EM modelling of arbitrary shaped dispersive chiral dielectric objects using a 3D leapfrog scheme on unstructured meshes

Abstract

The standard Yee FDTD algorithm is widely used in computational electromagnetics because of its simplicity and divergence free nature. A generalization of this classical scheme to 3D unstructured co-volume meshes is adopted, based on the use of a Delaunay primal mesh and its high quality Voronoi dual. This circumvents the problem of accuracy losses, which are normally associated with the use of a staircased representation of curved material interfaces in the standard Yee scheme. The procedure has been successfully employed for modelling problems involving both isotropic and anisotropic lossy materials. Here, we consider the novel extension of this approach to allow for the challenging modelling of chiral materials, where the material parameters are frequency dependent. To adequately model the dispersive behaviour, the Z-transform is employed, using second order Padé approximations to maintain the accuracy of the basic scheme. To validate the implementation, the numerical results produced are compared with available analytical solutions. The stability of the chiral algorithm is also studied.

1 Introduction

Innovative fabrication techniques are currently being employed to create new chiral materials for use in communication technologies. For such materials, the electric permittivity, magnetic permeability and chirality are all frequency dependent parameters. The chirality allows for a negative index of refraction with, simultaneously, a positive relative permittivity and permeability. In addition, chiral materials lead to optical rotatory dispersion (ORD) and circular dichroism (CD). In ORD, the polarization is continuously rotated inside the material, while CD refers to the change of polarization of the incident wave, from linear to elliptical, due to the different absorption coefficients of a right and a left circularly polarized wave. Such materials are being used to create smaller antennas, super lenses [1], polarizers and Radomes or radar cross section (RCS) reducing materials.

The Yee FDTD algorithm is widely used for general computational electromagnetic simulations. The advantages of the algorithm are its explicit nature, simplicity, low computational costs and divergence free nature. A major limitation of the standard implementation is the requirement for a structured Cartesian mesh, which can result in accuracy losses in simulations involving curved material surfaces. This limitation can be alleviated, though not removed, by employing finer meshes, but with a consequent increase in computational costs. To combine geometric flexibility with the efficiency of the Yee FDTD algorithm, a novel hybrid solution method has been developed in which an unstructured mesh procedure is used in the vicinity of material interfaces, while the standard Yee FDTD scheme is used elsewhere [2, 3]. The unstructured mesh procedure is essentially an unstructured implementation of the FDTD method, using a primal Delaunay and its Voronoi dual mesh [4]. The approach, which has already been employed for the analysis of scattering and transmission problems involving both isotropic and anisotropic materials, has been shown to require the use of meshes that are up to eight times coarser than those required by standard FDTD methods [5, 6].

In this paper, we will consider an extension of this procedure to enable the modelling of problems involving chiral dispersive materials. The approach adopted will employ a Lorentz model for the electric permittivity and magnetic permeability and a Condon model for the chirality [7]. Several methods have been developed for modelling frequency dependent materials within a time domain method, including the auxiliary differential equation method [8], the piecewise recursive convolution method [9] and the Z-transform technique [10]. As these three methods have been found to produce generally comparable results, the Z-transform technique was selected and implemented here. This approach is widely used in signal processing and can be viewed as the discrete version of the Laplace transform. It is readily implemented within the proposed solution algorithm and demonstrates good convergence close to the resonant frequency [11]. Demir et al. [12] appear to have been the first to model chiral materials in 3D with FDTD and using the Z-transform to handle the frequency dependence of the material parameters. In their method, first order approximations were used in the Z-domain and the Z-transform coefficients were derived analytically. Pereda et al. [13] used a different approach, which achieved second order accuracy in the Z-domain by employing a bilinear transformation for calculating Padé approximants [14].

In this paper, we present a hybrid unstructured mesh FDTD approach, in which chiral materials are modelled by employing a generalization of the method introduced by Pereda et al. [13]. The implementation is validated by simulating the transmission of a pulse through a 3D chiral slab in free space and by calculating the RCS of a sphere. The stability of the resulting numerical algorithm, with respect to changes in the mesh and the chirality, is also investigated.

2 Problem formulation for isotropic dielectric materials

We start with the equations for an isotropic material, in order to review the basic idea of the solution algorithm and to highlight the changes required to enable the modelling of frequency dependent chiral materials. If we assume that that material is non-lossy [5], Ampère’s Law and Faraday’s Law may be expressed, in scattered field form, as

$$\begin{aligned} \intop _{A} \varepsilon \frac{\partial }{\partial t} {{\mathbf {E}}}_{scat}\, \cdot \mathrm {d}{{\mathbf {A}}} = \ointop _{\partial A} {{\mathbf {H}}}_{scat}\,\cdot \mathrm {d}{{\mathbf {l}}} - \frac{\partial }{\partial t}\intop _{A}\left( \varepsilon -\varepsilon _{0}\right) {\mathbf {E}}_{inc}\,\cdot \mathrm {d}{\mathbf {A}} \end{aligned}$$

(1)

and

$$\begin{aligned} \intop _{A} \mu \frac{\partial }{\partial t} {\mathbf {H}}_{scat}\,\cdot \mathrm {d}{\mathbf {A}} = - \ointop _{\partial A} {\mathbf {E}}_{scat}\,\cdot \mathrm {d}{\mathbf {l}} - \frac{\partial }{\partial t} \intop _{A}\left( \mu -\mu _{0}\right) {\mathbf {H}}_{inc}\,\cdot \mathrm {d}{\mathbf {A}} \end{aligned}$$

(2)

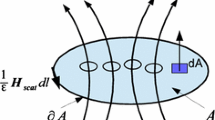
Here, $\partial A$ denotes the closed curve bounding a surface $A, \mathrm {d}{\mathbf {A}}$ is an element of surface area, directed normal to the surface and $\mathrm {d}{\mathbf {l}}$ is an element of contour length in the direction of the tangent to the curve. In addition, $\varepsilon$ is the electric permittivity and $\mu$ is the magnetic permeability. The total electric field, ${\mathbf {E}}_{tot}$, and the total magnetic field, ${\mathbf {H}}_{tot}$, are each regarded as being formed as the sum of incident and scattered fields, with the subscripts inc and scat being employed to indicate incident and scattered components respectively. The incident field is assumed to be a plane wave, generated in the far field, which has the form ${\mathbf {E}}_{inc}={\mathbf {E}}_{0}\,\cos (\omega t-{\mathbf {k}}\cdot {\mathbf {r}})$, where ${\mathbf {E}}_{0}$ is the polarization vector of the electric field, ${\mathbf {k}}$ is the wave vector, ${\mathbf {r}}$ is the position vector, $\omega$ is the angular frequency and t is the time. The incident magnetic field may be determined, using Faraday’s Law, as

$$\begin{aligned} {\mathbf {H}}_{inc}=\frac{\hat{{\mathbf {k}}}\times {\mathbf {E}}_{inc}}{\eta } \end{aligned}$$

(3)

where $\hat{{\mathbf {k}}}$ is the unit wave vector and $\eta =\sqrt{\mu _{o}/\varepsilon _{o}}$ is the impedance of free space.

For numerical solution, Eqs. (1) and (2) are discretized using two mutually orthogonal co-volume meshes. Although the approach is more general, we describe the implementation here on a primal tetrahedral mesh generated, using a standard Delaunay method [15], and its associated dual Voronoi diagram. Each Voronoi face is a perpendicular bisector of the corresponding Delaunay edge and each Delaunay face is perpendicular to the corresponding Voronoi edge. It is assumed that the Delaunay mesh has $N_{e}^{D}$ edges and that the Voronoi mesh has $N_{e}^{V}$ edges. Each Delaunay edge has an associated perpendicular closed loop of Voronoi edges and, similarly, each Voronoi edge is surrounded by a closed loop of Delaunay edges. The unknowns are located at the midpoints of these edges. At the center of the ith Delauany edge, the unknown is the projection, $E_{scat,i}$, of the scattered electric field onto the direction of the edge. The unknown at the center of the jth Voronoi edge corresponds to the projection, $H_{scat,j}$, of the scattered magnetic field onto the direction of the edge. Using the leapfrog time stepping scheme, discretization of Eqs. (1) and (2) results in

$$\begin{aligned} E_{scat,i}^{n+1}= & {} E_{scat,i}^{n} + \frac{\varDelta t}{\varepsilon A_{i}^{V}} \left[ \sum _{k=1}^{M_{i}^{V}}H_{scat,j_{i,k}}^{n+0.5} l_{j_{i,k}}^{V}-(\varepsilon -\varepsilon _{0})A_{i}^{V}\frac{\partial }{\partial t}E_{inc,i}^{n+0.5}\right] \nonumber \\ \end{aligned}$$

(4)

and

$$\begin{aligned} H_{scat,j}^{n+0.5}= & {} H_{scat,j}^{n-0.5} + \frac{\varDelta t}{\mu A_{j}^{D}}\left[ -\sum _{k=1}^{M_{j}^{D}}E_{scat,i_{j,k}}^{n}l_{i_{j,k}}^{D}-(\mu -\mu _{0})A_{j}^{D}\frac{\partial }{\partial t}H_{inc,j}^{n}\right] \nonumber \\ \end{aligned}$$

(5)

Here, $\varDelta t$ denotes the time step, the superscript n denotes an evaluation at time level $t^n=n\varDelta t, l_{i}^{D}$ is the length of the ith Delaunay edge and $A_{i}^{V}$ corresponds to the area of the Voronoi face spanned by the Voronoi edges surrounding Delaunay edge i. Similarly, $l_{j}^{V}$ represents the length of the jth Voronoi edge and $A_{j}^{D}$ corresponds to the area of the Delaunay face spanned by the Delaunay edges surrounding Voronoi edge j. The numbers $j_{i,k}, k=1,\ldots ,M_{i}^{V}$ refer to the $M_{i}^{V}$ edges of the Voronoi face corresponding to the ith Delaunay edge, as illustrated in Fig. 1, while the numbers $i_{j,k}, k=1,\ldots ,M_{j}^{D}$ refer to the $M_{j}^{D}$ edges of the Delaunay face corresponding to the jth Voronoi edge, as illustrated in Fig. 2.

Fig. 1

The ith Delaunay edge, connecting Delaunay vertices $p_{1}$ and $p_{2}$, and the corresponding Voronoi face, formed by the Voronoi edges $j_{i,1},\ldots ,j_{i,6}$

Fig. 2

The jth Voronoi edge, connecting Voronoi vertices $v_{1}$ and $v_{2}$, and the corresponding Delaunay face, formed by the Delaunay edges $i_{j,1},i_{j,2},i_{j,3}$

With these staggered equations, the magnetic field is updated over the dual graph at the half time step, using Eq. (5), and the electric field is updated over the primal graph at the full time step, using Eq. (4). At interface boundaries, the material parameters are not constant over the area of integration and, in this case, average values of $\varepsilon , \mu$ are adopted [6].

The extension of this implementation to any primal polyhedral mesh and its orthogonal dual is direct. In particular, the method reverts to the standard Yee FDTD algorithm when hexahedral meshes are employed.

3 Mesh generation

Consider the problem of generating a body fitted mesh to discretise the computational domain for a general problem of interest. For the solution of wave propagation problems with the FDTD method, a mesh of uniform size is generally desired. The procedure adopted for constructing a suitable mesh can be decomposed into four main stages, making full use of the ability of the algorithm to be implemented on general polyhedral meshes.

In the first stage, an unstructured triangulation of the surface of the object is produced [16] and this triangulation is then placed inside a hexahedral box. The region inside this box is discretized using a regular Cartesian mesh of cubes, of a uniform edge length. Cubes within a prescribed distance of the object, or lying internal to the object, are removed in a second stage, to create a staircase shaped surface that completely encloses the object [15]. A pyramidal element is added to each exposed internal square face. In the third stage, a standard Delaunay mesh generator is used to create a uniform unstructured tetrahedral mesh that completely covers the unmeshed region. The fourth stage consists of stitching together the hexahedral and tetrahedral meshes [17].

The resulting unstructured mesh is optimized to ensure that both the primal and the dual mesh are of the highest possible quality. The approach adopted is to relax, if necessary, the requirement that a dual edge must be a bisector of the corresponding Delaunay edge. At the same time, the corresponding dual mesh vertex is moved to a point which still ensures orthogonality between the two grids and which lies inside the corresponding primal element. Primal elements with a common circumcenter, and hence, a corresponding Voronoi edge length of zero, will automatically be merged prior to the solution process, creating a mesh consisting of general polyhedral cells [4].

4 Problem formulation for dispersive chiral materials

The approach outlined above requires some modification before it can be used to model problems involving frequency dependent chiral materials. Incorporation of the Z-transform method enables the development of a time domain formulation that takes into account materials with frequency dependent parameters. It is not possible to employ a pure scattered field formulation and an intermediate total field step is found to be required.

In this case, in the frequency domain, Ampère’s Law and Faraday’s Law may be expressed in the integral form

$$\begin{aligned} \intop _{A^V} \mathrm {j}\omega {\mathbf {D}}_{scat}(\omega ) \,\cdot \mathrm {d}{\mathbf {A}}= & {} \intop _{\partial A^V} {\mathbf {H}}_{scat}\cdot \mathrm {d}{\mathbf {l}}\nonumber \\&+\intop _{A^V}(\varepsilon (\omega )-\varepsilon _0)\mathrm {j}\omega {\mathbf {E}}_{inc}(\omega )\,\cdot \mathrm {d}{\mathbf {A}} \end{aligned}$$

(6)

$$\begin{aligned} \intop _{A^D} \mathrm {j}\omega {\mathbf {B}}_{scat}\,\cdot \mathrm {d}{\mathbf {A}}= & {} -\intop _{\partial A^D} {\mathbf {E}}_{scat}\cdot \mathrm {d}{\mathbf {l}}\nonumber \\&+\intop _{A^D}(\mu (\omega )-\mu _0) \mathrm {j}\omega {\mathbf {H}}_{inc}\,\cdot \mathrm {d}{\mathbf {A}} \end{aligned}$$

(7)

Here, $\mathrm {j}=\sqrt{-1}$ and ${\mathbf {D}}$ and ${\mathbf {B}}$ represent the electric flux density and the magnetic flux density respectively. The total field formulation

$$\begin{aligned} \intop _{A^V} \mathrm {j}\omega {\mathbf {D}}_{tot}(\omega ) \,\cdot \mathrm {d}{\mathbf {A}}= & {} \intop _{\partial A^V} {\mathbf {H}}_{scat}\cdot \mathrm {d}{\mathbf {l}}+\intop _{A^V}\varepsilon _0\mathrm {j}\omega {\mathbf {E}}_{inc}(\omega )\,\cdot \mathrm {d}{\mathbf {A}} \nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned} \intop _{A^D} \mathrm {j}\omega {\mathbf {B}}_{tot}\,\cdot \mathrm {d}{\mathbf {A}}= & {} -\intop _{\partial A^D} {\mathbf {E}}_{scat}\cdot \mathrm {d}{\mathbf {l}}+\intop _{A^D}\mu _0 \mathrm {j}\omega {\mathbf {H}}_{inc}\,\cdot \mathrm {d}{\mathbf {A}}\nonumber \\ \end{aligned}$$

(9)

removes the terms $\varepsilon (\omega )$ and $\mu (\omega )$. The constitutive equations for chiral materials are expressed in the form

$$\begin{aligned} {\mathbf {D}}_{tot}=\varepsilon {\mathbf {E}}_{tot}+\frac{\mathrm {j}\kappa }{c}{\mathbf {H}}_{tot} \quad {\mathbf {B}}_{tot}=\mu {\mathbf {H}}_{tot}-\frac{\mathrm {j}\kappa }{c}{\mathbf {E}}_{tot} \end{aligned}$$

(10)

where c is the speed of light and $\kappa$ the chiral parameter coupling the electric and magnetic fields. Implementing these relationships within the numerical scheme provides computational challenges, as the electric field projection is stored on the Delaunay mesh while the magnetic field projection is stored on the Voronoi mesh. The Lorentzian model

$$\begin{aligned} \varepsilon (\omega )= & {} \varepsilon _{\infty }+\frac{\left( \varepsilon _{\ell }-\varepsilon _{\infty }\right) \omega _e^2}{\omega _e^2+2\,\omega _e\,\xi _e\, \mathrm {j}\,\omega -\omega ^2}\nonumber \\ \mu (\omega )= & {} \mu _{\infty }+\frac{\left( \mu _{\ell }-\mu _{\infty }\right) \omega _h^2}{\omega _h^2+2\,\omega _h\,\xi _h\, j\,\omega -\omega ^2} \end{aligned}$$

(11)

is employed to determine the variation of the permittivity and the permeability with frequency. Here, the subscript $\infty$ denotes high frequency values, while the subscript $\ell$ refers to the low frequency limit. $\omega _e,\omega _h$ refer to the resonance frequency and $\xi _e,\xi _h,$ to the damping coefficients for the Lorentz model. The value of the chiral parameter is obtained, from the Condon model, as

$$\begin{aligned} \mathrm {j}\kappa (\omega )=\hat{\kappa }=\frac{\tau _k\, \omega _k^2\,\mathrm {j}\,\omega }{\omega _k^2+2\,\omega _k\,\xi _k\, \mathrm {j}\,\omega -\omega ^2} \end{aligned}$$

(12)

where $\omega _k$ denotes the resonance frequency, while $\xi _k$ corresponds to the damping coefficient for the chiral material. The coupling constant, $\tau _k$, defines the magnitude of the chirality.

Using these relations, Eqs. (6) and (7) may then be expressed as

$$\begin{aligned} \intop _{A^V} \mathrm {j}\omega \varepsilon _{\infty }{\mathbf {E}}_{tot}\, \cdot \mathrm {d}{\mathbf {A}}= & {} \intop _{\partial A^V} {\mathbf {H}}_{scat}\cdot \mathrm {d}{\mathbf {l}}+ \intop _{A^V}\varepsilon _0\mathrm {j}\omega {\mathbf {E}}_{inc}\cdot \mathrm {d}{\mathbf {A}}\nonumber \\&-\intop _{A^V} \mathbf {J}_{ee}\cdot \mathrm {d}{\mathbf {A}} +\intop _{A^V}\mathbf {J}_{\kappa h}\cdot \mathrm {d}{\mathbf {A}} \end{aligned}$$

(13)

$$\begin{aligned} \intop _{A^D} \mathrm {j}\omega \mu _{\infty }{\mathbf {H}}_{tot}\, \cdot \mathrm {d}{\mathbf {A}}= & {} -\intop _{\partial A^D} {\mathbf {E}}_{scat}\cdot \mathrm {d}{\mathbf {l}}+ \intop _{A^D}\mu _0\mathrm {j}\omega {\mathbf {H}}_{inc}\cdot \mathrm {d}{\mathbf {A}}\nonumber \\&-\intop _{A^D} \mathbf {J}_{hh}\cdot \mathrm {d}{\mathbf {A}} -\intop _{A^D}\mathbf {J}_{\kappa e}\cdot \mathrm {d}{\mathbf {A}} \end{aligned}$$

(14)

where

$$\begin{aligned} {\mathbf {J}}_{hh}=\mathrm {j}\omega (\mu -\mu _{\infty }){\mathbf {H}}_{tot}\quad {\mathbf {J}}_{\kappa h}=\frac{\mathrm {j}\omega \hat{\kappa }}{c}\,{\mathbf {H}}_{tot} \end{aligned}$$

(15)

$$\begin{aligned} {\mathbf {J}}_{ee}=\mathrm {j}\omega (\varepsilon -\varepsilon _{\infty }){\mathbf {E}}_{tot}\quad {\mathbf {J}}_{\kappa e}=\frac{\mathrm {j}\omega \hat{\kappa }}{c}\,{\mathbf {E}}_{tot} \end{aligned}$$

(16)

Fig. 3

Determining the electric field on the Voronoi edges: a reconstruct the electric field vector from its projections on the Delaunay edges and link this vector to the corresponding cell center and b average the electric field vectors from the cell centers linked to the same Voronoi edge $\mathbf {v}$ and project them to the corresponding edge

5 Discrete equations and the Z-transform

To convert Eqs. (13) and (14) from the frequency to the time domain, we use the substitution $\mathrm {j}\omega \rightarrow \frac{\partial }{\partial t}$. The staggered leapfrog scheme is then applied to discretize the resulting equations. The bilinear transformation

$$\begin{aligned} \mathrm {j}\omega =\frac{2}{\varDelta t}\frac{1-Z^{-1}}{1+Z^{-1}} \end{aligned}$$

(17)

is used, to convert a frequency dependent function to the Z-domain [10]. Equations (15) and (16) can be expressed, with second order accuracy in the Z-domain, by adopting the Padé approximants $b_0^{ij},b_1^{ij},b_2^{ij},a_1^{ij},a_2^{ij}$ with $ij=ee,\kappa e, hh ,\kappa h$. In this manner, we obtain the approximation

$$\begin{aligned} \mathbf {J}_{ee}=\frac{b_0^{ee}+b_1^{ee}Z^{-1}+b_2^{ee}Z^{-2}}{1+a_1^{ee}Z^{-1}+a_2^{ee}Z^{-2}} \end{aligned}$$

(18)

Transferring to the time domain is straightforward, as $Z^{-m}$ acts as a backwards operator in time, e.g. with $m=1, Z^{-1}\mathbf {J}_{ee}^{n+1}=\mathbf {J}_{ee}^n$. Rearranging Eq. (18) and, for an arbitrary field, $\mathbf {F}$, using the notation $Z^{-m}\mathbf {F}^{n}=\mathbf {F}^{n-m}$, we obtain

$$\begin{aligned} \mathbf {J}_{ee}^{n+1}&=\mathbf {W}_{ee}^{n}+b_0^{ee}{\mathbf {E}}_{tot}^{n+1}\nonumber \\ \mathbf {W}_{ee}^{n+1}&=b_1^{ee}{\mathbf {E}}_{tot}^{n+1}-a_1^{ee}\mathbf {J}_{ee}^{n+1}+b_2^{ee}{\mathbf {E}}_{tot}^n-a_2^{ee}\mathbf {J}_{ee}^n \end{aligned}$$

(19)

Similar approximations may be written for the terms $\mathbf {J}_{\kappa h}^{n-1/2}, \mathbf {J}_{hh}^{n+1/2}$ and $\mathbf {J}_{\kappa e}^{n+1}$. Using this notation, discretizing the time dependent form of Eqs. (13) and (14) on our unstructured mesh leads to the update equations

$$\begin{aligned} E_{tot,i}^{n+1}= & {} \frac{1}{2\varepsilon _{\infty }+b_0^{ee}\varDelta t}\left[ 2\varepsilon _{\infty }E_{tot,i}^n \right. \nonumber \\&+ \varDelta t\left\{ 2\left( \frac{1}{A^V} \sum _{k=1}^{M_{i}^{V}} H_{scat,j_{i,k}}^{n+1/2}l_{j_{i,k}}^{V}+\varepsilon _0 \frac{\partial E_{inc,i}^{n+1/2}}{\partial t}\right) \right. \nonumber \\&- \left. \left. W_{ee,i}^n-J_{ee,i}^n+2J_{{\kappa h,i}_{av}}^{n+1/2}\right\} \right] \end{aligned}$$

(20)

$$\begin{aligned} H_{tot,j}^{n+1/2}= & {} \frac{1}{2\mu _{\infty }+b_0^{hh}\varDelta t}\left[ 2\mu _{\infty }H_{tot,j}^{n-1/2} \right. \nonumber \\&+ \varDelta t\left\{ 2\left( \frac{-1}{A^D}\sum _{k=1}^{M_{j}^{D}}E_{scat,i_{j,k}}^{n}l_{i_{j,k}}^{D}+\mu _0 \frac{\partial H_{inc,j}^{n}}{\partial t}\right) \right. \nonumber \\&- \left. \left. W_{hh,j}^{n-1/2}-J_{hh,j}^{n-1/2}-2J_{{\kappa e,j}_{av}}^n\right\} \right] \end{aligned}$$

(21)

For a dispersive non-chiral material, $J_{{\kappa e,j}_{av}}$ and $J_{{\kappa h,i}_{av}}$ are identically equal to zero. The difficulty in dealing with Eqs. (20), (21) lies in the coupling terms $J_{{\kappa h,i}_{av}}^{n+1/2}$ and $J_{{\kappa e,j}_{av}}^n$. For example, $J_{{\kappa e,j}_{av}}^n$ is required on the Voronoi edges, but it includes the electric field projections, that are only available on the Delaunay edges. In Fig. 3, we illustrate how we overcome this problem. In the case of a tetrahedron, we have six Delaunay edges and the electric field projection $E_i,i=1,\ldots ,6$ is stored on each edge. Using these projections, the electric field vector ${\mathbf {E}}_{Cell_1}$ can be reconstructed and linked to the center of the corresponding cell, in this case cell 1. To achieve this, the equation set is as follows

$$\begin{aligned} {\bar{\bar{\mathbf{P}}}} {\mathbf {E}}_{Cell_1}=\left( {\mathbf {E}}_{Cell_1} \cdot {\hat{\mathbf {e}}}_i\right) {\hat{\mathbf {e}}}_i \end{aligned}$$

(22)

is constructed, where

$$\begin{aligned} {\bar{\bar{\mathbf{P}}}}= \left[ \begin{array}{ccccc} e_{i_x} e_{i_x} &{} \quad &{} e_{i_x} e_{i_y} &{} \quad &{} e_{i_x} e_{i_z} \\ e_{i_y} e_{i_x} &{} &{} e_{i_y} e_{i_y} &{} &{}e_{i_y} e_{i_z} \\ e_{i_z} e_{i_x} &{} &{} e_{i_z} e_{i_y} &{} &{} e_{i_z} e_{i_z} \end{array} \right] \end{aligned}$$

(23)

Here, $\left( {\mathbf {E}}_{Cell_1} \cdot \hat{\mathbf {e}}_i\right)$ corresponds to the projection of the electric field vector ${\mathbf {E}}_{Cell_1}$ in the direction of the Delaunay edge $\hat{\mathbf {e}}_i$. The unknown electric field vector at the center of a given cell is approximated by writing Eq. (22) for each of the N Delaunay edges forming the corresponding cell in turn and summing these equations, as depicted in Fig. 3b. In this case, for each cell center, we solve the system

$$\begin{aligned} \bar{\bar{\mathbf {P}}}' {\mathbf {E}}_{Cell_1}=\sum _{q=1}^{N} \left( {\mathbf {E}}_{Cell_1,q} \cdot \hat{\mathbf {e}}_{q}\right) \hat{\mathbf {e}}_{q} \end{aligned}$$

(24)

with

$$\begin{aligned} \bar{\bar{\mathbf {P}}}_{l,m}' = \sum _{q=1}^{N} \sum _{l=1}^3 \sum _{m=1}^3 e_{q_l}e_{q_m} \end{aligned}$$

(25)

where $e_{i_1}=e_{i_x}, e_{i_2}=e_{i_y}$ and $e_{i_3}=e_{i_z}$. The resulting field vector is then associated to the corresponding cell center. As a Voronoi edge connects two cells, we need to repeat this procedure for the second cell leading to ${\mathbf {E}}_{Cell_2}$. In the next step, the field vectors linked to these cells are averaged and projected to the corresponding Voronoi edge ${\mathbf {v}}$ according to $({\mathbf {E}}_{Cell1}+{\mathbf {E}}_{Cell2})/2\cdot {\mathbf {v}}$, as illustrated in Fig. 3b. With the electric field defined on the Voronoi edges in this manner, we may then compute $J_{{\kappa e,i}_{av}}^n$. We proceed analogously for the magnetic field, but in this case we have a point from the Delaunay mesh inside a Voronoi cell [6].

5.1 Updating scheme

With the total field formulation employed as an intermediate step, to obtain the desired scattered fields, the complete solution algorithm may be described by the steps:

• 1. Magnetic field loop. Calculation of $H_{scat,j}^{n+1/2}$

  • (a) reconstruct $\mathbf {E_{scat}}^n$ from Delaunay edges and project to the Voronoi edges leading to $E_{scat,j}^n$

  • (b) add the incident field to obtain the total field vector $E_{tot,j}^n=E_{scat,j}^n+E_{inc,j}^n$

  • (c) compute $J_{ke,j}^n, H_{tot,j}^{n+1/2}$ and $J_{hh,j}^{n+1/2}$

  • (d) compute $H_{scat,j}^{n+1/2}=H_{tot,j}^{n+1/2}-H_{inc,j}^{n+1/2}$

• 2. Electric field loop. Calculation of $E_{scat,i}^{n+1}$

  • (a) reconstruct $\mathbf {H_{scat}}^{n+1/2}$ from Voronoi edges and project to the Delaunay edges leading to $H_{scat,i}^{n+1/2}$

  • (b) add the incident field to obtain the total field vector $H_{tot,i}^{n+1/2}=H_{scat,i}^{n+1/2}+H_{inc,i}^{n+1/2}$

  • (c) compute $J_{kh,i}^{n+1/2}, E_{tot,i}^{n+1}$ and $J_{ee,i}^{n+1}$

  • (d) compute $E_{scat,i}^{n+1}=E_{tot,i}^{n+1}-E_{inc,i}^{n+1}$.

6 Interface boundary conditions

To satisfy the boundary conditions at interfaces between different materials, a weighted averaging is applied to the Padé approximants. This is similar to the process that has already been successfully employed for simulations involving isotropic and anisotropic media [5]. However, for the Padé approximants, which are required in expressions such as Eq. (18), we only average the coefficients in the numerator. To illustrate this process, consider two elements, separated by a boundary face, as illustrated in Fig. 4, and consider the calculation of the permeability for the corresponding Voronoi edge. Applying the bilinear transformation to $\mu _{\infty }-\mu$ from Eq. (11) leads to $(\mu _{\infty }-P(z))$, where

$$\begin{aligned} P(z)=\frac{b_0+b_{1} z^{-1}+b_{2} z^{-2}}{1+a_{1} z^-{1}+a_{2} z^{-2}} \end{aligned}$$

(26)

The magnetic flux is determined as

$$\begin{aligned} \mathbf {B}(z)_i=\mu (z){\mathbf {H}}(z)_i=(\mu _\infty -P(z)){\mathbf {H}}(z)_i \end{aligned}$$

(27)

where the subscript $i(=1,2)$ refers to the medium 1 or 2. The average magnetic flux at the interface is calculated as

$$\begin{aligned} \mathbf {B}(z)_{av}= & {} \frac{l_1\mathbf {B}(z)_1+l_2\mathbf {B}(z)_2}{l_1+l_2}= w_1(\mu _{\infty ,1}-P(z)_1){\mathbf {H}}(z)_1 \nonumber \\&+w_2(\mu _{\infty ,2}-P(z)_2){\mathbf {H}}(z)_2 \end{aligned}$$

(28)

where $w_i=l_i/(l_1+l_2)$ for $i=1,2$.

Fig. 4

Representation of a Voronoi edge and the corresponding cells

7 Numerical examples

7.1 Rotation of the plane of polarization

To verify the implementation of the scheme, the transmission coefficients for an EM pulse incident upon a chiral slab are computed, along with an evaluation of the variation of the angle of the plane of polarisation of the incident field. The dielectric slab has dimensions 0.3 m, 0.3 m and 0.1 m in the x, y, and z directions respectively. The mesh employed is such that 40 cells are used to discretise a length of 0.1 m. The electric permittivity and magnetic permeability of the slab are described by a Lorentz model and the chirality by a Condon model. The slab is located in free space, as depicted in Fig. 5.

Fig. 5

Chiral slab (shown in green) in free space (blue). (Color figure online)

In total the mesh with $\varDelta z=0.0025$ m consists of 3, 512, 025 cells corresponding to 10, 676, 124 Delaunay and 10, 417, 154 Voronoi edges. The PML is represented in terms of 1, 220, 300 hexahedral cells. We only consider a real chirality, which induces a rotation of the plane of polarization of the incident field (ORD). In this case, the variation of the angle of polarization, $\varPhi$, can be computed as

$$\begin{aligned} \varPhi =\kappa \omega L \end{aligned}$$

(29)

where $\kappa$ is the real value of the chirality, $\omega$ is the angular frequency of the incident wave and L is the thickness of the slab [18]. To compute this angle, we use a Fourier transform, which allows us to evaluate the variation of the amplitude without time dependence. A point in the Delaunay mesh is selected, such that, with respect to the incident wave, it lies behind the chiral slab. Then, for a wave propagating in z direction,

$$\begin{aligned} \varPhi _{num}=\frac{\text{ FT }(\mathbf {E_y)}}{\text{ FT }(\mathbf {E_x})} \end{aligned}$$

(30)

where FT denotes the Fourier transform.

Fig. 6

Rotation of the plane of polarization over time for 6 different values of the chirality. The black lines correspond to the theoretical values and the coloured lines to the numerically computed values over several cycles

Figure 6 shows the numerically computed rotation compared to the theoretical result, for different values of the chirality. For values of $\kappa$ less than 0.0407, the numerically computed angles of rotation of the plane of polarization remain almost constant over time and are in good agreement with the theoretical values. For higher chiralities, however, the numerical solution shows very strong fluctuations indicating an instability of the scheme.

7.2 Stability investigation

Initially, to investigated the effect of the time step size on the results, we performed calculations on the same mesh but with different time steps. From the results of these calculations, presented in Fig. 7a, it is apparent that reducing the time step has little effect on the stability of the scheme.

Next, we investigated the effect of spatial step size on the numerical stability. The slab thickness, L, is expressed as $L=n\varDelta z$, where n is the number of cells through the slab, in the z direction, and $\varDelta z$ is the edge length of a given cell. A cell normalized rotation of the plane of polarization may then be defined as

$$\begin{aligned} \varPhi _{cell}=\frac{\varPhi }{n}=\kappa \omega \varDelta z \end{aligned}$$

(31)

In the next step, we fix the chirality and create different meshes by just increasing the spatial step $\varDelta z$ and compute the relative error of $\varPhi _{cell}$.This leads to an increase in $\varPhi _{cell}$ for coarser meshes, as represented in Fig. 7b.

Finally, for several real chiralities we employ two meshes with $\varDelta z=0.0025$ m for the finer mesh and $\varDelta z=0.003$ m for the coarser mesh. The results produced after 20 cycles are displayed in Fig. 8a, b.

It can be clearly seen that, for the same chirality, the oscillations decrease when the mesh size reduces.

Fig. 7

a Same mesh, different time step and b same chirality, different meshes

Fig. 8

Relative error of the numerically computed rotation of the plane of polarization with increasing chirality compared to analytical values for two meshes. a Mesh with $\varDelta z=0.0025$ and b mesh with $\varDelta z=0.003$

We conclude that the chirality induced instabilities are directly linked to the spatial discretisation and not to the time step. For a stable simulation, the results suggest that the mesh used should ensure that $\varPhi _{Cell}\le 0.4^{\circ }$ for each cell.

7.3 Stability in the presence of damping

In this subsection, we demonstrate the stabilizing effects of damping applied to the numerical scheme. The coupling coefficient $\tau _k=2\cdot 10^-{12}$ s leads to strong instabilities in the scheme without damping. We increase the damping, using $\xi _k=0.01,0.025,0.05$ and 0.1 in turn, and again plot the angles over 20 cycles. From the results, shown in Fig. 9, we see that the scheme is now stable well above the $\varPhi _{Cell}=0.4^{\circ }$ limit suggested for the non-damped case. It appears that, provided $Im(\kappa )\ge Re(\kappa )/15$, the scheme is stable. But, in this case, we are no longer dealing with a pure ORD.

Fig. 9

Relative error of computed angle over 20 cycles

7.4 Reflection/transmission on a chiral slab

Consider the problem of determining the transmission and reflection coefficients for a chiral slab, of infinite length and width, with a finite thickness L, set between two isotropic media. The first medium extends from $z\in ]-\infty ,-L[$, the bi-isotropic chiral slab forms the second medium that extends from $z\in [-L,0[$ and the third medium extends from $z\in [0,+\infty [$. For our case, medium 1 and 3 will be taken to be free space. This problem has an analytical solution [18]. The linearly polarized narrowband pulse

Fig. 10

Comparison between analytical and numerical transmission coefficients. a $T_{co}$ and b $T_{cr}$

$$\begin{aligned} {\mathbf {E}}_{inc,y}({\mathbf {r}},t)=e^{-(t-{\mathbf {k}}\cdot {\mathbf {r}}/\omega )^2/2\tau ^2}\sin (\omega t -{\mathbf {k}}\cdot {\mathbf {r}}) \end{aligned}$$

(32)

propagating in the z direction, is sent towards the slab. The values adopted for the material parameters are $\varepsilon _s=1.8\varepsilon _0, \varepsilon _{\infty }=1.8\varepsilon _0, \mu _s=1.1\mu _0, \mu _{\infty }=1.0\mu _0, \omega _e=\omega _h=\omega _k=2 \pi \times 3.5$ GHz, $\xi _e=0.14, \xi _h=0.12, \xi _k=0.1$ and $\tau _k=1$ ps. To compute the frequency dependent reflection, we chose a point p1 in the mesh located in free space just ahead of the slab. For the transmission coefficient, a point p2, slightly behind the slab, is selected. The co-polarized reflection coefficient, $R_{co}$, the co-polarized transmission coefficient, $T_{co}$, and the cross polarized transmission coefficient, $T_{cr}$, are then determined as

$$\begin{aligned} R_{co}= & {} \frac{FT({\mathbf {E}}_{scat,y,p1})}{FT({\mathbf {E}}_{inc,y,p1})}\nonumber \\ T_{co}= & {} \frac{FT({\mathbf {E}}_{scat,y,p2})}{FT({\mathbf {E}}_{inc,y,p2})}\nonumber \\ T_{cr}= & {} \frac{FT({\mathbf {E}}_{scat,x,p2})}{FT({\mathbf {E}}_{inc,y,p2})} \end{aligned}$$

(33)

The results for the transmission and reflection coefficients are displayed in Figs. 10 and 11 respectively.

Fig. 11

Comparison between analytical and numerical reflection coefficients $R_{co}$

For a simple isotropic material, $T_{cr}$ is equal to zero. Overall, good agreement is obtained between the numerical and the analytical solution. The differences in the results arise because the analytical model assumes a slab with infinite extension in the directions perpendicular to the propagation. In addition, the numerical dispersion inherent in the scattered field formulation leads to a shift in the peaks for the reflection coefficient.

8 Radar cross section (RCS)

This case involves the computation of the radar cross section (RCS) of a chiral sphere. The RCS corresponds to the amount of scattered power from a target towards a radar and may be readily determined from the numerical solution [5, 6]. This problem is chosen as an analytical solution is available [19]. The scattered wave is decomposed into co-polarized and cross-polarized components. We consider a $\lambda /40$ sphere and employ a mesh consisting of 4,742,854 Delaunay cells, 1,727,445 Delaunay vertices, 7,604,002 Delaunay edges and 10,544,148 Voronoi edges. The expression $\lambda /n$ expresses the fact that our mesh consists of a spacing of n points per wavelength. We will use three different wavelengths, 0.8 m, 1.0 m and 1.2 m, corresponding to spheres of electrical length 2.5 m, 2.0 m and 1.66 m respectively. A PML region consisting of 10 layers of cells was found to be sufficient for this case. As this mesh is too dense to display, the form of a coarser mesh, suitable for the analysis of a $\lambda /15$ sphere, is shown in Fig. 12.

Fig. 12

Cut through a typical mesh for a $\lambda /15$ sphere

Fig. 13

Scattering of a plane wave by a chiral sphere with $\lambda _{0}=1$ m, $\xi _{k}=0.3$ and $\tau _{k}=16.7$ ps: a co-polarized RCS distribution and b cross-polarized RCS distribution

Fig. 14

Scattering of a plane wave by a chiral sphere with $\lambda _{0}=1$ m, $\xi _{k}=0.3$ and $\tau _{k}=10$ ps; a co-polarized RCS distribution and b cross-polarized RCS distribution

Fig. 15

Scattering of a plane wave by a chiral sphere with $\lambda _{0}=0.8$ m, $\xi _{k}=0.3$ and $\tau _{k}=16.7$ ps: a co-polarized RCS distribution and b cross-polarized RCS distribution

Fig. 16

Scattering of a plane wave by a chiral sphere with $\lambda _{0}=1.2$ m, $\xi _{k}=0.3$ and $\tau _{k}=16.$ ps; a co-polarized RCS distribution and b cross-polarized RCS distribution

The bi-static RCS of a $\lambda /40$ sphere, with varying free space wavelength $\lambda _{0}$ and coupling constants between the electric and magnetic fields, is computed. The wavelength $\lambda$ inside a dielectric shrinks with respect to free space according to $\lambda =\lambda _0/\sqrt{\varepsilon _r\mu _r-\kappa ^2}$. The material parameters for the electric permittivity and permeability remain the same, because we are interested in the effect of chirality on the RCS. For the simulations, the values $\varepsilon _{s}=1.8\,\varepsilon _{0}, \varepsilon _{\infty }=1.6\,\varepsilon _{0}, \mu _{s}=1.1\,\mu _{0}, \mu _{\infty }=1.0\,\mu _{0}, \omega _{e}=\omega _{h}=\omega _{k}=2\pi \times 1\,\hbox {GHz}, \xi _{e}=0.12, \xi _{h}=0.12$ were employed for the material parameters. A time step size $\varDelta t=6.18$ ps was used and the wavelength $\lambda _{0}$ of the incident wave took the values 0.8 m, 1.0 m and 1.2 m. The numerical solution was advanced through 20 cycles and the results produced were compared to the analytical solution, using the program developed by Demir et al. [19].

As the RCS distributions will be symmetrical in this case, only the results for angles lying between 180$^{\circ }$ and 360$^{\circ }$ are shown in Figs. 13, 14, 15 and 16. All the results demonstrate a very good agreement between the numerical and analytical solution for different values of the coupling constants $\tau _{k}$ and the wavelength $\lambda _{0}$. In particular, the very weak signal at high angles, from $300^{\circ }$ to $360^{\circ }$, is well captured.

9 Practical example

The final example demonstrates the use of the method in a predictive mode and involves the calculation of the transmission coefficient of a dielectric radome. The radome is in the form of half of an ellipsoidal shell, with a lateral radius of 0.5 m, a length of 1 m and a thickness of 0.05 m. A triangulation of the radome surface is shown in Fig. 17a. The shell is made of a chiral material, with properties characterised by the Lorentz and Condon models of Eqs. (11) and (12), with parameters values $\varepsilon _{s}=1.8\,\varepsilon _{0}, \varepsilon _{\infty }=1.6\,\varepsilon _{0}, \mu _{s}=1.1\,\mu _{0}, \mu _{\infty }=1.0\,\mu _{0}, \omega _{e}=\omega _{h}=\omega _{k}=2\pi \times 1$ GHz, $\xi _{e}=0.12$ and $\xi _{h}=0.12$.

Fig. 17

a View of the surface discretisation of a portion of the radome shell and b contours of $E_{scat,y}$, and a view of the mesh employed, after propagation of the narrowband pulse for 8 ns

A narrowband pulse, as defined in Eq. (32), is used to illuminate the radome, with a central frequency at 1.2 GHz and a width of 1 ns. Relative to an (x, y, z) cartesian coordinate system, the pulse is polarized in the y direction and propagates in the x direction. The mesh employed is designed to have 40 degrees of freedom per wavelength on the shell and a PML represented by 10 layers of hexahedral elements. The shortest distance between the inner boundary of the PML and the radome surface is discretised with 8 cells. This mesh, which is illustrated in Fig. 17b, contains 876,314 cells, 1,673,283 Delaunay edges and 2,076,114 Voronoi edges. The simulation is stopped after 20 periods, a time of 16.6 ns, when all the wave reverberations become insignificant. This required 40 min of CPU time on a single Intel Nehalem processor. Figure 17b also shows computed contours of the scattered field component $E_{scat,y}$ at a time corresponding to 8 ns of propagation of the narrowband pulse.

The transmission coefficient spectrum is computed using a Fourier transform of the time domain solution, as indicated in Eq. (33). For this example, the reference points p1 and p2 are chosen to lie outside and inside the radome respectively. Figure 18 shows the variation of the computed co-polarized reflection and transmission coefficients, $R_{co}$ and $T_{co}$ respectively, and the cross-polarized transmission coefficient, $T_{cr}$. The results show that the reflection is higher below 3 GHz. At this frequency, the cross-polarized transmission factor shows its maximum and above this frequency the transmission is higher.

Fig. 18

Calculated variation of the co-polarized reflection coefficient, $R_{co}$, the co-polarized transmission coefficient, $T_{co}$, and the cross polarized transmission, $T_{cr}$, for the radome example

10 Conclusion

In this paper, we have demonstrated how a co-volume solution method, originally developed for applications involving PECs, isotropic dielectric and anisotropic dielectric materials [5, 6], can be further extended to enable the modelling of isotropic frequency dependent materials and chirality. These additional features have been incorporated with the use of the Z-transform method [10, 13]. We have investigated the effect of the chirality on the stability of the resulting scheme and demonstrated that stability is enhanced by the use of a finer mesh or by reducing the real part of the chirality. Increasing the damping also has a stabilising effect. As the chirality is obtained by fitting the Condon model to experimental data, varying $Re(\kappa )$ or $Im(\kappa )$ is not possible, so that, normally, a stable solution can only be obtained by using finer meshes. With an appropriate mesh, we have successfully simulated the transmission and reflection of an electromagnetic pulse through a chiral slab and computed the RCS of a sphere. The modelling of chiral materials requires the use of a fine mesh, with $\varPhi _{Cell}<0.4^{\circ }$ for stability.