Explicit, fully implicit and forward gradient numerical integration of a hyperelasto-viscoplastic constitutive model for amorphous polymers undergoing finite deformation

Abstract

Following the growing use of amorphous polymers in an expanding range of applications, interest for numerical modeling of polymer behavior has greatly increased. Together with reliable constitutive models, stable, accurate and rapid integration algorithms valid for large deformations need to be developed. Here, in the framework of hyperelasto-viscoplasticity and multiplicative split formulation, three integration algorithms (explicit, fully implicit and forward gradient) are generated for a constitutive polymer model and respective stability is investigated. The algorithms are furthermore implemented in a commercial Finite Element code and simulation of a full field tensile test is shown to capture the actual deformation behavior of polymers.

1 Introduction

Three main groups of polymers have emerged since the discovery of natural rubber: thermoplastics (also called glassy polymers), thermosettings and elastomers. Thermoplastics are made of long covalent chains only linked together by weak Hydrogen and Van der Waals bonds. With increasing temperature, these bonds gradually weaken and eventually break, resulting in the existence of a so-called glass transition temperature $T_{\mathrm{g}}$. Thermoplastics behave therefore like solids below $T_{\mathrm{g}}$ and like viscous fluids above $T_{\mathrm{g}}$. Thermosettings on the other hand can be seen as three-dimensional networks where numerous covalent bonds tie polymer chains together; thermosettings are therefore by nature stiff. Finally, elastomers lie in between the two previous groups as usually being made of a soft thermosetting with very few covalent bonds or a blend of two thermoplastics, one being used above its glass transition temperature and the other one below. As a result, elastomers show a pure elastic response up to very high strains ($\sim \,400\%$).

Thermoplastics can be further split into two sub-groups: amorphous and semi-crystalline. Crystallinity depends on the chains ability to align themselves and therefore polymers with small and regular monomers are more prone to crystallinity than large monomers with bulky side groups. Only amorphous thermoplastics are considered here.

Amorphous thermoplastics being relatively new and increasingly used, their mechanical behavior is currently a field of active research. Noticeable progress has been made by Boyce and coworkers in [1,2,3,4,5,6,7] as well as in [8], where a new mechanical model is presented and the two distinct phenomena occurring during deformation are identified, namely: chain segment rotation and molecular alignment.

Intermolecular resistance to chain segment rotation by surrounding chains occurs first and is responsible for the typical hardening–softening sequence observed at relatively low strains, giving rise to a local stress maximum. Segment rotation causes the rupture of previously mentioned Hydrogen and Van der Waals bonds as well as an increase of the local free volume which together result in micro-shear banding (comparable to Piobert–Lüders bands in metals) and softening. Being non-directional by nature this phenomenon is modeled as isotropic hardening–softening by an Eyring dashpot.

Intramolecular resistance to molecular alignment occurs at larger strains and comes from the polymer chain itself. In principle, elastic stretching of an elastomer is similar to permanent orientation of molecular chains of glassy polymers (where entanglements replace chemical cross-links). Intramolecular resistance is therefore naturally modeled as rubber elasticity by a Langevin spring leading to kinematic hardening.

Whether a polymer behaves in a ductile or brittle manner is influenced by stability issues in the hardening-softening-rehardening sequence and is coupled to the relationship between the magnitude of isotropic and kinematic hardening. A high isotropic hardening peak combined to a weak kinematic hardening imply that large strains must develop in order to recover the peak stress level. This leads to localization and possible formation of crazes and failure in a brittle manner. Conversely, a low isotropic hardening peak combined to a strong kinematic hardening result in stabilization, as only small additional strains suffice to retrieve the peak stress level, see Fig. 1.

Fig. 1

Typical stress–strain curves for polymers: illustration of how the relationship between isotropic and kinematic hardening of two different polymers influences the recovery strain and therefore the global behavior

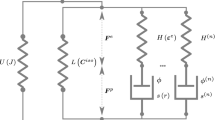
Subsequent to and, to some extent, in parallel with Boyce and coworkers, Anand and coworkers [9,10,11,12,13,14,15,16] have also made notable contributions to the development of the mechanical modeling of polymers. In an early paper [9], benefits of using the Hencky strain for large deformations are presented. In a series of publications devoted to metals subjected to deformations at high temperatures [10,11,12], modeling aspects subsequently applicable to polymers are developed; in particular, identification of state variables for large deformations is carefully studied in [11]. The original polymer model from Boyce is generalized in [13] to include both compressibility and thermal expansion and resulting model predictions are compared to a large amount of experimental data. In [14] the original Boyce model is reformulated within a firm thermodynamical framework, where the consequences of frame invariance on the principal of virtual power as well as consequences of the dissipation inequality on the flow rule are discussed. Note that both Boyce and Anand switch between two back-stress definitions, one based on the plastic deformation gradient (multiplicative split) and one based on the total deformation gradient, see the two one-dimensional rheological models shown in Fig. 2. The model presented in [14] is extended in [15] to a fully coupled thermomechanical theory, where also the response at large deformations and unloading is addressed differently. A model based on an elastic-viscoplastic mechanism and a hyperelastic network mechanism is developed in [16] to specifically address the response of thermoplastic polyurethanes. A large deformation viscoelastic-viscoplastic constitutive framework that also allows for a recovery strain at zero stress as observed in experiments is presented in [17]. In addition, constitutive models accounting for damage in thermoplastic polymers is emerging as proposed in [18, 19]. Numerical algorithms are also provided in [19], as well as in [20].

Fig. 2

One-dimensional rheological models: a original model and b modified model, (see [4, 6])

In this work, numerical aspects of the constitutive model for glassy polymers developed by Boyce and co-workers and modified by Anand and Gurtin [14] are studied. Specifically, three different integration schemes: explicit, fully implicit and forward gradient are developed and their robustness examined. The resulting algorithms are then implemented into an explicit finite element code as user material routines. The outline of the paper is therefore as follows: first, a summary of the constitutive model for glassy polymers according to [14] is presented. A discussion to highlight key features of the different integration schemes is then given. Finally, a three dimensional model simulation illustrates the capability of capturing typical polymer mechanical behavior.

2 Constitutive model

The constitutive model to be explored here, pertinent for glassy polymers, is thoroughly described in [14]. In particular, a version suitable for large elastic stretches similar to the one proposed in [21, 22] is scrutinized in the following. The material model is based on the multiplicative split of the deformation gradient $\mathbf{F}=\mathbf{F}^{\mathrm{e}}{} \mathbf{F}^{\mathrm{p}}$ into an elastic part, $\mathbf{F}^{\mathrm{e}}$ and a plastic part, $\mathbf{F}^{\mathrm{p}}$ (Kröner–Lee decomposition [23, 24]) and it contains two internal variables ($s, \eta$) representing an intermolecular resistance to plastic flow and the local free volume, respectively. A summary of the constitutive model is given next.

The constitutive relations are expressed in the relaxed configuration in terms of the elastic Hencky strain $\mathbf{E}^{\mathrm{e}}$ and the co-rotated Kirchhoff stress $\mathbf{T}^{\mathrm{e}}$ (conjugate to the elastic Hencky strain). The relaxed configuration is taken to be rotation free, i.e. $\mathbf{F}^{\mathrm{e}}=\mathbf{R}^{\mathrm{e}}{} \mathbf{U}^{\mathrm{e}}=\mathbf{RU}^{\mathrm{e}}$, and $\mathbf{F}^{\mathrm{p}}=\mathbf{U}^{\mathrm{p}}$, as proposed in [14], where $\mathbf{R}$ is the rotation tensor and $\mathbf{U}^{\mathrm{e}}$ and $\mathbf{U}^{\mathrm{p}}$ is the elastic and plastic right stretch tensor, respectively. The Hencky strain is defined as $\mathbf{E}^{\mathrm{e}} =\frac{1}{2}\hbox {log}({\mathbf{C}^{\mathrm{e}}})$, where $\mathbf{C}^{\mathrm{e}}=\mathbf{F}^{\mathrm{eT}}{} \mathbf{F}^{\mathrm{e}} =({\mathbf{U}^{\mathrm{e}}})^{2}$ is the elastic right Cauchy–Green deformation tensor. The co-rotated Kirchhoff stress tensor $\mathbf{T}^{\mathrm{e}}$ is related to the Cauchy stress tensor by the pull-back operation

$$\begin{aligned} \mathbf{T}^{\mathrm{e}}=\det ( {\mathbf{F}^{\mathrm{e}}}\,) \mathbf{R}^{\mathrm{eT}}{} \mathbf{TR}^{\mathrm{e}}. \end{aligned}$$

(1)

The equation of stress derives from an elastic free energy and can be expressed by use of the standard isotropic elasticity tensor as

$$\begin{aligned} \mathbf{T}^{\mathrm{e}}=2G\mathbf{E}_0^{\mathrm{e}} +K({\hbox {tr}{} \mathbf{E}^{\mathrm{e}}})\mathbf{I}, \end{aligned}$$

(2)

where $\mathbf{E}_0^{\mathrm{e}} =\mathbf{E}^{\mathrm{e}} -({\hbox {tr} \mathbf{E}^{\mathrm{e}}})\mathbf{I}/3$ and G and K are the shear and bulk moduli, respectively.

As discussed above, resistance to plastic flow is initially governed by isotropic hardening/softening and at higher stretches by orientation hardening. The orientation hardening is taken to be associated with plastic stretch and modeled as kinematic hardening with a back-stress $\mathbf{S}^{\mathrm{b}}$ defined as follows. From the left plastic Cauchy–Green deformation tensor $\mathbf{B}^{\mathrm{p}} ={\mathbf{F}^{\mathrm{p}}{} \mathbf{F}^{\mathrm{p}}}^{\mathrm{T}}$, an effective plastic stretch governing the orientation hardening (and thus the back-stress modulus) is introduced as

$$\begin{aligned} \lambda ^{\mathrm{P}}=\sqrt{\hbox {tr}({\mathbf{B}^{\mathrm{p}}})/3}. \end{aligned}$$

(3)

The back stress modulus $\mu$ is expressed by

$$\begin{aligned} \mu =\mu _{\mathrm{R}}\left( {\frac{\lambda _{\mathrm{L}}}{3\lambda ^{\mathrm{P}}}}\right) L^{-1}\left( {\frac{\lambda ^{\mathrm{P}}}{\lambda _{\mathrm{L}}}}\right) , \end{aligned}$$

(4)

where $L^{-1}$ is the inverse of the Langevin function defined by $L(x)=\coth (x)-1/x$ for $x>0, \mu _{\mathrm{R}}$ is a material parameter called the rubbery modulus and $\lambda _{\mathrm{L}}$ a material parameter representing the network locking stretch.

Finally, with $\mathbf{B}_0^{\mathrm{p}} =\mathbf{B}^{\mathrm{p}} -\frac{1}{3}\hbox {tr}({\mathbf{B}^{\mathrm{p}}})\mathbf{I}$ being the deviatoric part of $\mathbf{B}^{\mathrm{p}}$, the kinematic hardening or back stress $S^{\mathrm{b}}$ is defined as

$$\begin{aligned} \mathbf{S}^{\mathrm{b}}=\mu \mathbf{B}_0^{\mathrm{p}} . \end{aligned}$$

(5)

By assuming that the plastic flow is irrotational (zero plastic spin) and incompressible on the relaxed configuration, the evolution law for the plastic part of the deformation gradient can be written as

$$\begin{aligned} \dot{\mathbf{F}}^{\mathrm{p}} = \mathbf{D}^{\mathrm{p}}{} \mathbf{F}^{\mathrm{p}}, \end{aligned}$$

(6)

with $\mathbf{D}^{\mathrm{p}}$ being deviatoric. Then, $\mathbf{D}^{\mathrm{p}}$ directly corresponds to the plastic part of the velocity gradient on the relaxed configuration, and is given by a standard Mises-type flow rule that accounts for a back stress,

$$\begin{aligned} \mathbf{D}^{\mathrm{p}}=\upsilon ^{\mathrm{p}}\left( {\frac{\mathbf{S}_0 -\mathbf{S}^{\mathrm{b}}}{2\bar{\tau } }} \right) , \end{aligned}$$

(7)

where $\mathbf{S}_0 =\hbox {dev}(\mathbf{C}^{\mathrm{e}}\hbox {det} ({\mathbf{F}^{\mathrm{e}}}){\mathbf{F}^{\mathrm{e}}}^{-1} {\mathbf{TF}^{\mathrm{e}}}^{-\mathrm{T}}) =2G\mathbf{E}_0^{\mathrm{e}}$ is the deviatoric part of the Mandel stress which is work conjugate to $\mathbf{D}^{\mathrm{p}}$ on the relaxed configuration, and $\bar{\tau }$ is the equivalent shear stress defined as

$$\begin{aligned} \bar{\tau } =\frac{1}{\sqrt{2}}|{\mathbf{S}_0 -\mathbf{S}^{\mathrm{b}}}|. \end{aligned}$$

(8)

Here, $|\mathbf{A}|=\sqrt{\mathbf{A}:\mathbf{A}}$ denotes the magnitude of a $2{\mathrm{nd}}$ order tensor A. Thus, the magnitude of $\mathbf{D}^{\mathrm{p}}$ defined in (6) is proportional to the equivalent plastic shear strain rate, which is defined by a viscosity law as

$$\begin{aligned} \upsilon ^{\mathrm{p}}=\upsilon _0 \left( {\frac{\bar{\tau }}{s+\alpha \pi }}\right) ^{\frac{1}{m}}, \end{aligned}$$

(9)

where $\upsilon _0$ is a reference plastic shear strain-rate, $m\in ]0;1]$ is a strain-rate sensitivity parameter, s represents the intermolecular resistance to plastic flow and $\alpha$ is a pressure sensitivity parameter governing the influence of the mean normal stress $\pi =\hbox {tr}(\mathbf{T})/3$.

The evolution laws for the two internal variables governing the isotropic hardening/softening are given by the coupled differential equations

$$\begin{aligned} \left\{ \begin{array}{l} \dot{s} = h_{0}\left( 1-\frac{s}{\tilde{s}}\right) \upsilon ^{\mathrm{p}} \\ \dot{\eta } = g_0 \left( \frac{s}{s_{\mathrm{cv}} -1}\right) \upsilon ^{\mathrm{p}} \end{array} \right. \end{aligned}$$

(10)

where $\tilde{s} = s_{\mathrm{cv}} [1+b(\eta _{\mathrm{cv}} -\eta )]$ and $\{h_0$, $g_0$, $s_0$, $s_{\mathrm{cv}}$, b, $\eta _{\mathrm{cv}}\}$ are additional material parameters. The initial conditions are given by $s(0)=s_0$ and $\eta (0)=0$.

Fig. 3

Geometric interpretation in the stress space of a the generalized trapezoidal rule and b the generalized midpoint rule for inviscid plasticity. Subscripts n and $n+1$ refer to two consecutive time steps and $n+\alpha$ to an intermediate state. r is the plastic flow direction tensor, $\sigma$ the stress tensor and $\Delta \lambda$ the plastic strain increment

In summary, this model contains 13 model parameters: two associated with elasticity $\{G,K\}$, three associated with the rate of plastic flow $\{\upsilon _0 , m, \alpha \}$; two associated with kinematic (orientation) hardening $\{\mu _{\mathrm{R}} , \lambda _{\mathrm{L}}\}$; and six associated with isotropic hardening/softening $\{h_0$, $g_0$, $s_0$, $s_{\mathrm{cv}}$, b, $\eta _{\mathrm{cv}}\}$.

3 Methods for integration of finite strain rate constitutive equations: explicit, fully implicit and forward gradient

The constitutive models presented in the previous section is expressed in terms of rates and derivatives. The resulting system of coupled differential equations is non-linear and must be integrated numerically. Such an integration inevitably raises the questions of stability, accuracy and efficiency. All integration strategies are indeed a compromise between these three issues. Two well-established integration methods: the generalized trapezoidal rule and the generalized midpoint rule are presented in [25] for inviscid plasticity. Both methods make use of known quantities at step n and a priori unknown quantities at step $n+1$, where a scalar coefficient, say $\theta \in [0;1]$, weights the influence of the two contributions. An illustration of the generalized trapezoidal and the midpoint rules is shown in Fig. 3 for elasto-plasticity. Depending on the value taken by $\theta$: $\theta =0$, $\theta =1$, or $0<\theta <1$, the method is referred to as an explicit formulation, a fully implicit formulation or a gradient forward formulation. The fully implicit formulation reduces to the well-known radial return method for J2 plasticity. Note that for the extreme cases to be considered here, i.e. $\uptheta =0$ or 1, the generalized midpoint rule becomes the same as the generalized trapezoidal rule.

Fig. 4

Kinematic interpretation of the integration algorithms. $D^{\mathrm{p}}=\upsilon _n^{\mathrm{p}} N_n$ leads to the explicit formulation, $D^{\mathrm{p}}=\upsilon _{n+1}^{\mathrm{p}} N_{n+1}$ to the fully implicit formulation and $D^{\mathrm{p}}=[(1-\theta )\upsilon _n^{\mathrm{p}} +\theta \upsilon _{n+1}^{\mathrm{p}}]N_n$ to the gradient forward formulation

Box 1 Newton scheme for the three formulations

The two integration methods can be shown to be first-order accurate for all $\theta$-values, except for $\theta =1/2$, where second-order accuracy prevails. When it comes to stability, the midpoint rule is unconditionally stable for $\theta \ge 1/2$, whereas the generalized trapezoidal rule is unconditionally stable for values of $\theta$ depending on the shape of the yield surface but still always greater than 1 / 2. As opposed to unconditionally stable, conditionally stable means that stability depends on the incremental step size. For conditionally stable methods applied to viscoplasticity and creep, stability issues are discussed in [26], where a critical time step is put forward. This criterion is illustrated by several examples in [27] and is shown to be very much case specific: the time step increment limit depends on the viscoplastic properties of the material, the current elastic state and the current viscoplastic rate of deformation. To partially circumvent this time step limitation, a forward gradient time integration scheme is developed in [28], where the plastic strain directions are taken from step n as in an explicit method but the effective plastic strain increment is calculated from both step n and a forward gradient estimation of step $n+1$. This method, which was applied in [29] to integrate the constitutive equations of the Boyce model, is explored in Sect. 4. Note that this time step limitation is purely material related and has nothing to do with the limitation imposed by the Courant criterion derived in the context of explicit time integration within finite element analysis.

Another issue of considerable importance when integrating constitutive equations in the context of finite deformation is rotation neutralization. Roughly two main strategies have been employed: one illustrated in [30, 31] where quantities are rotated by the small rotation increment between two consecutive steps and one presented in [32] where all quantities are systematically rotated to an additional rotation-free configuration (pull-back), integrated and rotated back to the current configuration (push-forward). The second strategy is used in the following.

Iterative integrations schemes for hyperelasto-viscoplasticityicity also aim at, from quantities at step n, calculating quantities at step $n+1$. Kinematic quantities known at the beginning of the time step are the deformation gradients: $\mathbf{F}_n$, $\mathbf{F}_n^{\mathrm{e}}$, $\mathbf{F}_n^{\mathrm{p}}$ and $\mathbf{F}_{n+1}$; in addition, the (Cauchy) stress $\mathbf{T}_n$ and the internal variables are known. As for small deformations, it seems natural to define trial quantities and, to begin with, a trial elastic deformation gradient: $\mathbf{F}_{*}^{\mathrm{e}} =\mathbf{F}_{n+1} {\mathbf{F}_n^{\mathrm{p}}}^{-1}$. Carrying out the polar decomposition $\mathbf{F}_{*}^{\mathrm{e}} =\mathbf{R}_{*}^{\mathrm{e}} \mathbf{U}_{*}^{\mathrm{e}}$ and invoking isotropy leads to two interesting results: $\mathbf{R}_{n+1}^{\mathrm{e}} =\mathbf{R}_{*}^{\mathrm{e}}$ and $\mathbf{U}_{n+1}^{\mathrm{e}} =\mathbf{U}_{*}^{\mathrm{e}} \hbox {exp}(-\Delta t\mathbf{D}^{\mathrm{p}})$; see [32] for details and Fig. 4 for an overview of the different configurations. With $\upsilon ^{\mathrm{p}}$ being the plastic shear strain rate and $\mathbf{N}=(\frac{\mathbf{T}_0^{\mathrm{e}} -\mathbf{S}^{\mathrm{b}}}{2\bar{\tau }})$ the plastic strain directions, $\mathbf{D}^{\mathrm{p}}$ reads $\mathbf{D}^{\mathrm{p}}=\upsilon ^{\mathrm{p}}\mathbf{N}$. The step at which $\mathbf{D}^{\mathrm{p}}$ is evaluated determines the nature of the algorithm (explicit, fully implicit or forward gradient). Using the definition of the elastic Hencky strain $\mathbf{E}^{\mathrm{e}} =\hbox {log}(\mathbf{U}^{\mathrm{e}})$ and the isotropic elasticity ${\varvec{\mathcal {L}}}$ tensor leads directly to: $\mathbf{T}_{n+1}^{\mathrm{e}} =\mathbf{T}_{*}^{\mathrm{e}} -{{\varvec{\mathcal {L}}}}:(\Delta t\mathbf{D}^{\mathrm{p}})$. Note that thanks to the use of the Hencky strain this expression is exact (no approximation was made in the derivation) and that it is precisely the same expression as for small strain plasticity. The Newton scheme is outlined below in Box 1.

The explicit formulation is by far the simplest of the three alternatives to implement. It makes straight-forward use of quantities at step n; it does not require internal Newton–Raphson iterations and it is therefore relatively fast to execute. The fully implicit formulation is as expected of much higher complexity as it contains an iterative Newton–Raphson algorithm built to converge towards the sought solution; this obviously increases the running time substantially. Finally, the forward gradient formulation is of intermediate complexity: it does not require additional internal Newton–Raphson iterations but still the expression for $\upsilon _{n+1}^{\mathrm{p}}$ is quite tedious and involves quite intricate algebra. Note that in this formulation, according to [28], $\upsilon _{n+1}^{\mathrm{p}}$ is only an approximation of the effective value at $n+1$. The three algorithms are presented in detail in “Appendices A, B and C”.

At first glance, the explicit formulation of “Appendix A” does not seem to follow the update scheme presented above mainly because no trial stress is calculated. The explanation is as follows: instead of first removing the rotation from $\mathbf{F}_{*}^{\mathrm{e}}$ and then removing the plastic strain from the total strain, it is also possible to first remove the plastic contribution from $F_{n+1}$ before removing rotation effects in $\mathbf{F}_{n+1}^{\mathrm{e}}$.

When it comes to practical implementation, two important issues should be mentioned. Firstly, both the fully implicit and the forward gradient algorithms make use of numerous 4th order tensors and of their inverse. As inversion of 4th order tensors is very time consuming and can lead to numerical instability, it was here chosen to rewrite all four order tensors as 9 by 9 and subsequently 6 by 6 matrices which are much more easily invertible. Secondly, care should be taken when approximating derivatives of the exponential of a matrix: use of less than four terms in the Taylor expansion has proven to be inaccurate enough to jeopardize the whole solution (see [33] for details).

4 Results

The algorithms presented above were implemented and tested in two different software: Matlab [34]—for simple homogeneous deformation fields, and Abaqus Explicit [35]—for full field solutions. The material parameters used for Polycarbonate are listed in Table 1.

Table 1 Material parameters for polycarbonate [14]

Fig. 5

Explicit algorithm results; uniaxial tension; Cauchy stress versus Hencky strain. Number of time steps: from 800 to 1800. The vertical scale is only valid for the for lowest curve (800 time steps); all subsequent curves are translated upwards 10 MPa for clarity

4.1 Stability analysis

To analyze the characteristics of stability of the different algorithms, a homogeneous solid subjected to uniform stretching is considered. The directions of principal stretches are held constant in time. Specifically, a deformation history of relevance for uniaxial tension is examined, i.e. one stretch amplitude increases, here denoted $\lambda _1$, whereas the other two decreases as $\lambda _2 =\lambda _3 =1/ \sqrt{\lambda _1}$. During loading $\lambda _1$ is increased from 1 to 2. The total loading time is set to 1 s and it is divided into equally long time steps. This implies that the tensile stretch rate is constant and equal to 1/s whereas the corresponding logarithmic strain rate decreases from 1/s to 0.5/s. For figure clarity only the tensile stress is plotted in the figures. For this first problem, direct integration of the constitutive equation system is carried out for all three algorithms: explicit, fully implicit and forward gradient. This is accomplished by implementing the algorithms in Matlab. Results for the explicit algorithm are given in Fig. 5 and show a gradual loss of stability between 1800 and 800 steps eventually ending in fatal instability around 700 steps (not shown in the figure). Results for the fully implicit algorithm are given in Fig. 6 and as expected, complete stability can be observed irrespective of the number of steps. Finally results for the forward gradient algorithm are given in Fig. 7 and show no observable loss of stability between 1800 and 1000 steps. Some instability can be spotted at 900 steps and fatal instability eventually occurs around 800 steps. Note that compared to the explicit algorithm, the forward gradient algorithm improves the solution quality up the fatal instability but it does not substantially change the limit number of steps at which fatal instability occurs.

Fig. 6

Fully implicit algorithm results; uniaxial tension; Cauchy stress versus Hencky strain. Number of time steps: 10, 20, 40, 80, 160, 320. The vertical scale is only valid for the for lowest curve (10 time steps); all subsequent curves are translated upwards 10 MPa for clarity

Fig. 7

Forward gradient algorithm results; uniaxial tension; Cauchy stress verus Hencky strain. Number of time steps: from 800 to 1800. The vertical scale is only valid for the lowest curve (800 time steps); all subsequent curves are translated upwards 10 MPa for clarity

Fig. 8

Dog-bone specimen geometry (thickness 10 mm) loaded in uniaxial tension (displacement control)

4.2 FEM simulations of a dog bone specimen

To illustrate the ability of the algorithms developed for the polymer material model to accurately capture mechanical behavior in three-dimensional tensile loading, a standard dog bone specimen is analyzed as a second problem, see Fig. 8 for geometry and dimensions. For this full field analysis, the algorithms are implemented in Abaqus Explicit as user defined material subroutines VUMAT. Full symmetry is assumed allowing for only 1/8 of the geometry to be modelled. The rate of loading is small enough to limit effects of inertia and hence the time step imposed by the Courant condition is significantly smaller than the one required for a stable solution based on the explicit stress integration algorithms. For this reason, no difference is observed between the three different algorithms and only the results from the implicit algorithm are presented here. The force displacement curve is plotted in Fig. 9 and a series of corresponding field results (total strain in the loading direction) are shown in Fig. 10, where the degree of loading increases from left to right. It can be observed that localization sets in already at small strains but instead of catastrophic localization (as would be the case for metals) the region with smaller cross section gradually extends throughout the specimen in a stable manner since material re-hardening overcomes area reduction causing the deformed region to be stronger than the neighboring undeformed regions.

Fig. 9

Force displacement curve showing that the force required for necking propagation is nearly constant. Arrows indicate the displacements at which field results are extracted

Fig. 10

Finite Element simulations of a dog-bone specimen submitted to tensile loading at locations indicated in Fig. 9. Due to symmetry, only a 1/8 of the specimen is modeled. The scale and colors quantify the total strain in the loading direction

5 Conclusion

Three integration algorithms (explicit, fully implicit and forward gradient) are developed and presented in this paper, which all capture the specific behavior of amorphous polymer at large deformations. As expected, higher degree of complexity leads to higher stability: both the explicit and the forward gradient algorithms are only conditionally stable whereas the fully implicit algorithm is unconditionally stable. Implementation in Abaqus of these algorithms is also carried out as user defined subroutines. Due to the large number of time steps inherent to explicit solvers, simulation of a tensile test gave the same results for all subroutines. To make full use of the implicit algorithm, computation of the consistent tangent stiffness matrix would need to be performed.

Appendices

Appendix

One first order and two second order tensor products are used in the following.

$$\begin{aligned}&(\mathbf{u} \otimes \mathbf{v})_{ij} = u_i v_j \\&(\mathbf{A} \otimes \mathbf{B})_{ijkl} = A_{ij} B_{kl} \\&(\mathbf{A} \boxtimes \mathbf{B})_{ijkl} = A_{ik} B_{jl} \end{aligned}$$

Inner product of two tensors $\mathbf{A}$ and $\mathbf{B}$ is noted $\mathbf{A}:\mathbf{B}$ and the deviatoric part of a tensor $\mathbf{A}$ is noted $\mathbf{A}_0$. The first and second order identity tensors are noted $\mathbf{I}$ and ${\varvec{\mathcal {I}}}$ respectively; the fourth order isotropic elasticity tensor is noted ${\varvec{\mathcal {L}}}$ and the Langevin function L is definined according to: $L(x) = \cot (x)-1/x$ for $x>0$. Square root, exponential and logarithm of symmetric and real second order tensors $\mathbf{M}$ are, as follows, defined through their spectral decomposition.

$$\begin{aligned}&{} \mathbf{M} = \sum _{i=1}^3 \lambda ^{(i)}{} \mathbf{e}^{(i)} \otimes \mathbf{e}^{(i)} \\&\sqrt{\mathbf{M}} = \sum _{i=1}^3 \sqrt{\lambda ^{(i)}}{} \mathbf{e}^{(i)} \otimes \mathbf{e}^{(i)} \\&\hbox {exp}(\mathbf{M}) = \sum _{i=1}^3 \hbox {exp}(\lambda ^{(i)})\mathbf{e}^{(i)} \otimes \mathbf{e}^{(i)} \\&\hbox {log}(\mathbf{M}) = \sum _{i=1}^3 \hbox {log}(\lambda ^{(i)})\mathbf{e}^{(i)} \otimes \mathbf{e}^{(i)} \end{aligned}$$

Appendix A: Explicit algorithm

Quantities known at the beginning of the time-step:

• $\mathbf{F}_n$, $\mathbf{T}_n$, $\mathbf{R}_n^{\mathrm{e}}$, $\mathbf{F}_n^{\mathrm{p}}$, $s_n$, $\eta _n$ (saved as internal variables)

• $\mathbf{F}_{n+1}$ (deformation gradient calculated at the end of the step)

(a) Quantities at time step n:

Stress pull-back; Cauchy stress, $\mathbf{T}_n$, to corotated Kirchhoff, $\mathbf{T}_n^{\mathrm{e}}$, stress transformation:

$$\begin{aligned} \mathbf{T}_n^{\mathrm{e}} =\hbox {det}(\mathbf{F}_n){\mathbf{R}_n^{\mathrm{e}}}^{\mathrm{T}} \mathbf{T}_n \mathbf{R}_n^{\mathrm{e}} \end{aligned}$$

(A1)

Left plastic Cauchy–Green deformation tensor:

$$\begin{aligned} \mathbf{B}_n^{\mathrm{p}} =\mathbf{F}_n^{\mathrm{p}} {\mathbf{F}_n^{\mathrm{p}}}^{\mathrm{T}} \end{aligned}$$

(A2)

Deviatoric parts:

$$\begin{aligned} \mathbf{T}_{0n}^{\mathrm{e}}= & {} \mathbf{T}_n^{\mathrm{e}} -\frac{1}{3}\hbox {tr}(\mathbf{T}_n^{\mathrm{e}})\mathbf{I} \end{aligned}$$

(A3a)

$$\begin{aligned} \mathbf{B}_{0n}^{\mathrm{p}}= & {} \mathbf{B}_n^{\mathrm{p}} -\frac{1}{3}\hbox {tr}(\mathbf{B}_n^{\mathrm{p}})\mathbf{I} \end{aligned}$$

(A3b)

Mean normal pressure and effective plastic stretch:

$$\begin{aligned} \pi _n= & {} -\hbox {tr}(\mathbf{T}_n)/3 \end{aligned}$$

(A4a)

$$\begin{aligned} \lambda _n^{\mathrm{P}}= & {} \sqrt{\hbox {tr}(\mathbf{B}_n^{\mathrm{p}})/3} \end{aligned}$$

(A4b)

Back stress modulus and back stress tensor:

$$\begin{aligned} \mu _n= & {} \mu _{\mathrm{R}} \left( \frac{\lambda _{\mathrm{L}}}{3\lambda _n^{\mathrm{P}}}\right) L^{-1}\left( \frac{\lambda _n^{\mathrm{P}}}{\lambda _{\mathrm{L}}}\right) \end{aligned}$$

(A5a)

$$\begin{aligned} \mathbf{S}_n^{\mathrm{b}}= & {} \mu _n \mathbf{B}_{0n}^{\mathrm{p}} \end{aligned}$$

(A5b)

Equivalent shear stress:

$$\begin{aligned} \bar{\tau } _n =\frac{1}{\sqrt{2}} |\mathbf{T}_{0n}^{\mathrm{e}}-\mathbf{S}_n^{\mathrm{b}}| \end{aligned}$$

(A6)

Equivalent plastic shear strain rate:

$$\begin{aligned} \upsilon _n^{\mathrm{p}} = \upsilon _0 \left( \frac{\bar{\tau }_n}{s_n +\alpha \pi _n}\right) ^{\frac{1}{m}} \end{aligned}$$

(A7)

Plastic strain rate tensor:

$$\begin{aligned} \mathbf{D}^{\mathrm{p}} = \upsilon _n^{\mathrm{p}} \left( \frac{\mathbf{T}_{0n}^{\mathrm{e}} -\mathbf{S}_n^{\mathrm{b}}}{2\bar{\tau }_n}\right) \end{aligned}$$

(A8)

(b) Update from time-step n to time-step $n+1$:

New plastic deformation gradient tensor:

$$\begin{aligned} \mathbf{F}_{n+1}^{\mathrm{p}} = \hbox {exp} (\Delta t\mathbf{D}^{\mathrm{p}}) \mathbf{F}_n^{\mathrm{p}} \end{aligned}$$

(A9)

New elastic deformation gradient tensor:

$$\begin{aligned} \mathbf{F}_{n+1}^{\mathrm{e}} = \mathbf{F}_{n+1} {\mathbf{F}_{n+1}^{\mathrm{p}}}^{-1} \end{aligned}$$

(A10)

New elastic right Cauchy–Green deformation tensor:

$$\begin{aligned} \mathbf{C}_{n+1}^{\mathrm{e}} = {\mathbf{F}_{n+1}^{\mathrm{e}}}^{\mathrm{T}} \mathbf{F}_{n+1}^{\mathrm{e}} \end{aligned}$$

(A11)

New elastic stretch tensor:

$$\begin{aligned} \mathbf{U}_{n+1}^{\mathrm{e}} =\sqrt{\mathbf{C}_{n+1}^{\mathrm{e}}} \end{aligned}$$

(A12)

New elastic Hencky strain tensor:

$$\begin{aligned} \mathbf{E}_{n+1}^{\mathrm{e}} =\hbox {log}(\mathbf{U}_{n+1}^{\mathrm{e}}) \end{aligned}$$

(A13)

New rotation tensor:

$$\begin{aligned} \mathbf{R}_{n+1}^{\mathrm{e}} = \mathbf{F}_{n+1}^{\mathrm{e}} {\mathbf{U}_{n+1}^{\mathrm{e}}}^{-1} \end{aligned}$$

(A14)

New corotated Kirchhoff stress tensor:

$$\begin{aligned} \mathbf{T}_{n+1}^{\mathrm{e}} ={\varvec{\mathcal {L}}}: (\mathbf{E}_{n+1}^{\mathrm{e}}) \end{aligned}$$

(A15)

Stress push-forward; corotated Kirchhoff stress to Cauchy stress transformation:

$$\begin{aligned} \mathbf{T}_{n+1} = 1/\hbox {det}(\mathbf{F}_{n+1}) \mathbf{R}_{n+1}^{\mathrm{e}} \mathbf{T}_{n+1}^{\mathrm{e}} {\mathbf{R}_{n+1}^{\mathrm{e}}}^{\mathrm{T}} \end{aligned}$$

(A16)

New isotropic hardening internal variables:

$$\begin{aligned}&s_{n+1} = s_n +h_0 \left( 1-\frac{s_n }{\tilde{s}_n}\right) \Delta t\upsilon _n^{\mathrm{p}} \end{aligned}$$

(A17)

$$\begin{aligned}&\eta _{n+1} = \eta _n +g_0 \left( \frac{s_n}{s_{\mathrm{cv}}}-1\right) \Delta t\upsilon _n^{\mathrm{p}} \end{aligned}$$

(A18)

$$\begin{aligned}&\tilde{s}_n = s_{\mathrm{cv}}[1+b(\eta _{\mathrm{cv}} -\eta _n)] \end{aligned}$$

(A19)

Appendix B: Fully implicit algorithm

Quantities known at the beginning of the time-step:

• $\mathbf{T}_n$, $\mathbf{F}_n^{\mathrm{p}}$, $s_n$, $\eta _n$ (saved as internal variables)

• $\mathbf{F}_{n+1}$ (deformation gradient calculated at the end of the step)

(a) Trial quantities:

Trial elastic deformation gradient tensor:

$$\begin{aligned} \mathbf{F}_{*}^{\mathrm{e}} = \mathbf{F}_{n+1} {\mathbf{F}_n^{\mathrm{p}}}^{-1} \end{aligned}$$

(B1)

Trial elastic right Cauchy–Green deformation tensor:

$$\begin{aligned} \mathbf{C}_{*}^{\mathrm{e}} = {\mathbf{F}_{*}^{\mathrm{e}}}^{\mathrm{T}} \mathbf{F}_{*}^{\mathrm{e}} \end{aligned}$$

(B2)

Trial elastic stretch tensor:

$$\begin{aligned} \mathbf{U}_{*}^{\mathrm{e}} = \sqrt{\mathbf{C}_{*}^{\mathrm{e}}} \end{aligned}$$

(B3)

Trial elastic Hencky strain tensor:

$$\begin{aligned} \mathbf{E}_{*}^{\mathrm{e}} = \hbox {log}(\mathbf{U}_{*}^{\mathrm{e}}) \end{aligned}$$

(B4)

Deviatoric trial corotated Kirchhoff stress tensor:

$$\begin{aligned}&{} \mathbf{T}_{*}^{\mathrm{e}} = {\varvec{\mathcal {L}}}: (\mathbf{E}_{*}^{\mathrm{e}}) \end{aligned}$$

(B5a)

$$\begin{aligned}&{} \mathbf{T}_{0*}^{\mathrm{e}} = \mathbf{T}_{*}^{\mathrm{e}} - \frac{1}{3}\hbox {tr}(\mathbf{T}_{*}^{\mathrm{e}})\mathbf{I} \end{aligned}$$

(B5b)

Trial elastic rotation tensor:

$$\begin{aligned} \mathbf{R}_{*}^{\mathrm{e}} = \mathbf{F}_{*}^{\mathrm{e}} {\mathbf{U}_{*}^{\mathrm{e}}}^{-1} \end{aligned}$$

(B6)

(b) Initializations:

$$\begin{aligned}&\Delta \lambda ^{(k=1)} = 0 \end{aligned}$$

(B7a)

$$\begin{aligned}&{\mathbf{T}_0^{\mathrm{e}}}^{(k=1)} = \mathbf{T}_{0*}^{\mathrm{e}} \end{aligned}$$

(B7b)

$$\begin{aligned}&{\mathbf{F}^{\mathrm{p}}}^{(k=1)} = \mathbf{F}_n^{\mathrm{p}} \end{aligned}$$

(B7c)

$$\begin{aligned}&s^{(k=1)} = s_n \end{aligned}$$

(B7d)

$$\begin{aligned}&\eta ^{(k=1)} = \eta _n \end{aligned}$$

(B7e)

(c) Iterations:

Deviatoric left Cauchy–Green deformation tensor:

$$\begin{aligned} {\mathbf{B}^{\mathrm{p}}}^{(k)}= & {} {{\mathbf{F}^{\mathrm{p}}}}^{(k)} {\mathbf{F}^{\mathrm{p}^{\mathrm{T}}}}^{(k)} \end{aligned}$$

(B8a)

$$\begin{aligned} {\mathbf{B}_0^{\mathrm{p}}}^{(k)}= & {} {\mathbf{B}^{\mathrm{p}}}^{(k)} -\frac{1}{3} \hbox {tr}\left( {\mathbf{B}^{\mathrm{p}}}^{(k)}\right) \mathbf{I} \end{aligned}$$

(B8b)

Mean trial normal pressure and effective plastic stretch:

$$\begin{aligned}&\pi _{*} = -\hbox {tr}(\mathbf{T}_{*}^{\mathrm{e}})/3 \end{aligned}$$

(B9a)

$$\begin{aligned}&{\lambda ^{\mathrm{P}}}^{(k)} = \sqrt{\hbox {tr}\left( {\mathbf{B}_0^{\mathrm{p}}}^{(k)}\right) /3} \end{aligned}$$

(B9b)

Back stress modulus and back stress tensor:

$$\begin{aligned}&\mu ^{(k)} = \mu _{\mathrm{R}} \left( \frac{\lambda _{\mathrm{L}}}{3{\lambda ^{\mathrm{P}}}^{(k)}}\right) L^{-1} \left( \frac{{\lambda ^{\mathrm{P}}}^{(k)}}{\lambda _{\mathrm{L}}}\right) \end{aligned}$$

(B10a)

$$\begin{aligned}&{\mathbf{S}^{\mathrm{b}}}^{(k)} = \mu ^{(k)}{\mathbf{B}_0^{\mathrm{p}}}^{(k)} \end{aligned}$$

(B10b)

Equivalent shear stress:

$$\begin{aligned} \bar{\tau }^{(k)}=\frac{1}{\sqrt{2}} \left| {\mathbf{T}_0^{\mathrm{e}}}^{(k)}- {\mathbf{S}^{\mathrm{b}}}^{(k)}\right| \end{aligned}$$

(B11)

Plastic strain increment tensor:

$$\begin{aligned} \Delta t{\mathbf{D}^{\mathrm{p}}}^{(k)} = \Delta \lambda ^{(k)} \left( \frac{{\mathbf{T}_0^{\mathrm{e}}}^{(k)} - {\mathbf{S}^{\mathrm{b}}}^{(k)}}{2\bar{\tau }^{(k)}}\right) \end{aligned}$$

(B12)

Equivalent plastic shear strain increment:

$$\begin{aligned} \Delta t{\upsilon ^{\mathrm{p}}}^{(k)} = \Delta t\upsilon _0 \left( \frac{\bar{\tau }^{(k)}}{s^{(k)} +\alpha \pi _{*}}\right) ^{\frac{1}{m}} \end{aligned}$$

(B13)

Deviatoric stress–strain relations residual and viscosity law residual:

$$\begin{aligned} {\mathbf{R}_1}^{(k)}= & {} {\mathbf{T}_0^{e}}^{(k)} - \mathbf{T}_{0*}^e +2G\Delta t{\mathbf{D}^{\mathrm{p}}}^{(k)} \end{aligned}$$

(B14a)

$$\begin{aligned} {R_2}^{(k)}= & {} \Delta \lambda ^{(k)} - \Delta {t\upsilon ^{p}}^{(k)} \end{aligned}$$

(B14b)

Residuals Taylor expansion:

$$\begin{aligned} \mathbf{R}_1^{(k+1)}&= R_1^{(k)} +{\left( \frac{\partial R_1}{\partial \mathbf{T}_0^e}\right) }^{(k)}: \delta {\mathbf{T}_0^{e}}^{(k)} +{\left( \frac{\partial R_1}{\partial \Delta \lambda }\right) }^{(k)} \delta \Delta \lambda ^{(k)} \end{aligned}$$

(B15a)

$$\begin{aligned} R_2^{(k+1)}&= R_2^{(k)} +{\left( \frac{\partial R_2}{\partial \mathbf{T}_0^e}\right) }^{(k)}: \delta {\mathbf{T}_0^{e}}^{(k)} +{\left( \frac{\partial R_2}{\partial \Delta \lambda }\right) }^{(k)} \delta \Delta \lambda ^{(k)} \end{aligned}$$

(B15b)

Setting $R_1^{(k+1)}$ and $R_2^{(k+1)}$ to zero and solving for $\delta \Delta \lambda ^{(k)}$ gives:

$$\begin{aligned} \delta \Delta \lambda ^{(k)} =\frac{R_2^{(k)} -{\left( \frac{\partial R_2}{\partial \mathbf{T}_0^e}\right) }^{(k)}: {\left( {\left( \frac{\partial \mathbf{R}_1}{\partial \mathbf{T}_0^e}\right) }^{(k)}\right) }^{-1} : \mathbf{R}_1^{(k)}}{\left( \frac{\partial R_2}{\partial \mathbf{T}_{0n+1}^e}\right) ^{(k)}: {\left( {\left( \frac{\partial \mathbf{R}_1}{\partial \mathbf{T}_0^e}\right) }^{(k)}\right) }^{-1}: {\left( \frac{\partial \mathbf{R}_1}{\partial \Delta \lambda }\right) }^{(k)} -{\left( \frac{\partial R_2}{\partial \Delta \lambda }\right) }^{(k)}} \end{aligned}$$

(B16)

where:

$$\begin{aligned} {\left( \frac{\partial \mathbf{R}_1}{\partial \mathbf{T}_0^e}\right) }^{(k)}= & {} {\varvec{\mathcal {I}}} + 2G\mathbf{M}^{(k)} \end{aligned}$$

(B17)

$$\begin{aligned} {\left( \frac{\partial \mathbf{R}_1}{\partial \Delta \lambda }\right) }^{(k)}= & {} 2G{(\mathbf{P}^{(k)})}^{-1} : \mathbf{N}^{(k)} \end{aligned}$$

(B18)

$$\begin{aligned} {\left( \frac{\partial R_2}{\partial \mathbf{T}_0^e}\right) }^{(k)}= & {} -\frac{\Delta t{\upsilon ^{p}}^{(k)}}{m\bar{\tau }^{(k)}} \mathbf{N}^{(k)} \end{aligned}$$

(B19)

$$\begin{aligned} {\left( \frac{\partial R_2}{\partial \Delta \lambda }\right) }^{(k)}= & {} 1 \nonumber \\&-\frac{\Delta t{\upsilon ^{p}}^{(k)}}{m} \left[ \frac{1}{\bar{\tau }^{(k)}}{} \mathbf{N}^{(k)} : \mathbf{H}^{(k)}: {(\mathbf{P}^{(k)})}^{-1}:\mathbf{N}^{(k)}\right. \nonumber \\&-\left. \frac{1}{s^{(k)}+\alpha \pi _n} \left( \frac{\hbox {d}s}{\hbox {d}\Delta \lambda }\right) ^{(k)}\right] \end{aligned}$$

(B20)

with:

$$\begin{aligned}&{} \mathbf{N}^{(k)} = \frac{{\mathbf{T}_0^{\mathrm{e}}}^{(k)} -{\mathbf{S}^{\mathrm{b}}}^{(k)}}{2\bar{\tau }^{(k)}} \end{aligned}$$

(B21)

$$\begin{aligned}&{} \mathbf{M}^{(k)} = \frac{\Delta \lambda ^{(k)}}{2\bar{\tau }^{(k)}} ({\varvec{\mathcal {I}}}-2\mathbf{N}^{(k)}\otimes \mathbf{N}^{(k)}) \end{aligned}$$

(B22)

$$\begin{aligned}&{} \mathbf{P}^{(k)} = {\varvec{\mathcal {I}}} +\frac{\Delta \lambda ^{(k)}}{2\bar{\tau }^{(k)}} (2\mathbf{N}^{(k)} \otimes (\mathbf{N}^{(k)}: \mathbf{H}^{(k)})-\mathbf{H}^{(k)}) \end{aligned}$$

(B23)

$$\begin{aligned}&{} \mathbf{H}^{(k)} = {\mathbf{H}_1}^{(k)}: {\mathbf{H}_{2}}^{(k)} \end{aligned}$$

(B24)

$$\begin{aligned}&{\mathbf{H}_1}^{(k)} = \mu ^{(k)}\left[ \frac{1}{6{\lambda ^{{\mathrm{p}}^{2}}}^{(k)}} {\mathbf{B}_0^{\mathrm{p}}}^{(k)} \otimes \mathbf{I}-{\varvec{\mathcal {I}}} +\frac{1}{3}{} \mathbf{I} \otimes \mathbf{I}\right] \end{aligned}$$

(B25)

$$\begin{aligned}&{\mathbf{H}_2}^{(k)} = \frac{\hbox {dexp}\left( \Delta t{\mathbf{D}^{\mathrm{p}}}^{(k)}\right) }{d\Delta t{\mathbf{D}^{\mathrm{p}}}^{(k)}}\boxtimes \mathbf{B}_n^{\mathrm{p}} \exp \left( \Delta t{\mathbf{D}^{\mathrm{p}}}^{(k)}\right) \nonumber \\&\qquad \qquad +\mathbf{B}_n^{\mathrm{p}}\exp \left( \Delta t{\mathbf{D}^{\mathrm{p}}}^{(k)}\right) \boxtimes \frac{\hbox {dexp}\left( \Delta t{\mathbf{D}^{\mathrm{p}}}^{(k)}\right) }{\hbox {d}\Delta t{\mathbf{D}^{\mathrm{p}}}^{(k)}}\nonumber \\ \end{aligned}$$

(B26)

$$\begin{aligned}&{\left( \frac{\hbox {d}s}{\hbox {d}\Delta \lambda }\right) }^{(k)} = \frac{(\tilde{s}^{(k)}-s^{(k)})-bg_0\frac{s^{(k)}}{\tilde{s}^{(k)}} (s^{(k)}-s_{\mathrm{cv}}) \Delta \lambda ^{(k)}}{\frac{\tilde{s}^{(k)}}{h_0}+\left( 1+bg_0\frac{s^{(k)}}{\tilde{s}^{(k)}} \Delta \lambda ^{(k)}\right) \Delta \lambda ^{(k)}}\nonumber \\ \end{aligned}$$

(B27)

(d) Update from iteration k to iteration $k+1$:

New plastic strain increment:

$$\begin{aligned} \Delta \lambda ^{(k+1)}=\Delta \lambda ^{(k)}+\delta \Delta \lambda ^{(k)} \end{aligned}$$

(B28)

New isotropic hardening internal variables:

$$\begin{aligned} \hbox {s}^{(k+1)}&= \hbox {s}^{(k)} +{\left( \frac{\hbox {d}s}{\hbox {d}\Delta \lambda }\right) }^{(k)} \delta \Delta \lambda ^{(k)} \end{aligned}$$

(B29a)

$$\begin{aligned} \eta ^{(k+1)}&= \eta ^{(k)}+\frac{g_0}{s_{\mathrm{cv}}} \left[ \Delta \lambda ^{(k)} {\left( \frac{\hbox {d}s}{\hbox {d}\Delta \lambda }\right) }^{(k)} +(s^{(k)}-s_{\mathrm{cv}})\right] \delta \Delta \lambda ^{(k)} \end{aligned}$$

(B29b)

New corotated Kirchhoff stress tensor:

$$\begin{aligned} {\mathbf{T}_o^{\mathrm{e}}}^{(k+1)} =\,&{\mathbf{T}_o^{\mathrm{e}}}^{(k)} \nonumber \\&-{\left( {\left( \frac{\partial \mathbf{R}_1}{\partial \mathbf{T}_0^{e}}\right) }^{(k)}\right) }^{-1}: \left( \mathbf{R}_1^{(k)} + {\left( \frac{\partial \mathbf{R}_1}{\partial \Delta \lambda }\right) }^{(k)} \delta \Delta \lambda ^{(k)}\right) \end{aligned}$$

(B30)

New plastic strain increment tensor:

$$\begin{aligned} \Delta t{\mathbf{D}^{\mathrm{p}}}^{(k+1)} = \Delta t {\mathbf{D}^{\mathrm{p}}}^{(k)} +{(\mathbf{P}^{(k)})}^{-1} :\mathbf{N}^{(k)}\delta \Delta \lambda ^{(k)} \end{aligned}$$

(B31)

New plastic deformation gradient tensor:

$$\begin{aligned} {\mathbf{F}^{\mathrm{p}}}^{(k+1)} = \hbox {exp} \left( \Delta t{\mathbf{D}^{\mathrm{p}}}^{(k+1)}\right) \mathbf{F}_n^{\mathrm{p}} \end{aligned}$$

(B32)

(e) Final values when convergence criterion is met:

$$\begin{aligned}&{} \mathbf{T}_{0n+1}^{\mathrm{e}} = {\mathbf{T}_0^{\mathrm{e}}}^{(k+1)} \end{aligned}$$

(B33a)

$$\begin{aligned}&{} \mathbf{F}_{n+1}^{\mathrm{p}} = {\mathbf{F}^{\mathrm{p}}}^{(k+1)} \end{aligned}$$

(B33b)

$$\begin{aligned}&s_{n+1} = s^{(k+1)} \end{aligned}$$

(B33c)

$$\begin{aligned}&\eta _{n+1} = \eta ^{(k+1)} \end{aligned}$$

(B33d)

(f) Stress push-forward; corotated Kirchhoff stress to Cauchy stress transformation:

$$\begin{aligned} \mathbf{T}_{n+1} = 1/\hbox {det}(\mathbf{F}_{n+1}) \mathbf{R}_{*}^{\mathrm{e}}{} \mathbf{T}_{n+1}^{\mathrm{e}} {\mathbf{R}_{*}^{\mathrm{e}}}^{\mathrm{T}} \end{aligned}$$

(B34)

Appendix C: Forward gradient algorithm

This algorithm differs from the explicit algorithm in the calculation of equivalent plastic shear strain rate, $\upsilon ^{\mathrm{p}}$, which is presented below.

Quantities known at the beginning of the time-step:

• $\mathbf{F}_n$, $\mathbf{T}_n$, $\mathbf{R}_n^{\mathrm{e}}$, $\mathbf{F}_n^{\mathrm{p}}$, $s_n$, $\eta _n$ (saved as internal variables)

• $\mathbf{F}_{n+1}$ (deformation gradient calculated at the end of the step)

• $\theta \in ]0;1]$

(a) Quantities at time step n:

Stress pull-back; Cauchy stress, $\mathbf{T}_n$, to corotated Kirchhoff, $\mathbf{T}_n^{\mathrm{e}}$, stress transformation:

$$\begin{aligned} \mathbf{T}_n^{\mathrm{e}} = \hbox {det}(\mathbf{F}_n) {\mathbf{R}_n^{\mathrm{e}}}^{\mathrm{T}} \mathbf{T}_n \mathbf{R}_n^{\mathrm{e}} \end{aligned}$$

(C1)

Left plastic Cauchy–Green deformation tensor:

$$\begin{aligned} \mathbf{B}_n^{\mathrm{p}} = \mathbf{F}_n^{\mathrm{p}} {\mathbf{F}_n^{\mathrm{p}}}^{\mathrm{T}} \end{aligned}$$

(C2)

Deviatoric parts:

$$\begin{aligned} \mathbf{T}_{0n}^{\mathrm{e}}= & {} \mathbf{T}_n^{\mathrm{e}} -\frac{1}{3}\hbox {tr}(\mathbf{T}_n^{\mathrm{e}})\mathbf{I} \end{aligned}$$

(C3a)

$$\begin{aligned} \mathbf{B}_{0n}^{\mathrm{p}}= & {} \mathbf{B}_n^{\mathrm{p}} -\frac{1}{3}\hbox {tr}(\mathbf{B}_n^{\mathrm{p}})\mathbf{I} \end{aligned}$$

(C3b)

Mean normal pressure and effective plastic stretch:

$$\begin{aligned} \pi _n= & {} -\hbox {tr}(\mathbf{T}_n)/3 \end{aligned}$$

(C4a)

$$\begin{aligned} \lambda _n^{\mathrm{P}}= & {} \sqrt{\hbox {tr}(\mathbf{B}_n^{\mathrm{p}})/3} \end{aligned}$$

(C4b)

Back stress modulus and back stress tensor:

$$\begin{aligned} \mu _n= & {} \mu _{\mathrm{R}} \left( \frac{\lambda _{\mathrm{L}}}{3\lambda _n^{\mathrm{P}}}\right) L^{-1} \left( \frac{\lambda _n^{\mathrm{P}}}{\lambda _{\mathrm{L}}}\right) \end{aligned}$$

(C5a)

$$\begin{aligned} \mathbf{S}_n^{\mathrm{b}}= & {} \mu _n \mathbf{B}_{0n}^{\mathrm{p}} \end{aligned}$$

(C5b)

Equivalent shear stress:

$$\begin{aligned} \bar{\tau } _n = \frac{1}{\sqrt{2}} |\mathbf{T}_{0n}^{\mathrm{e}} - \mathbf{S}_n^{\mathrm{b}}| \end{aligned}$$

(C6)

Equivalent plastic shear strain rate:

$$\begin{aligned} \upsilon _n^{\mathrm{p}} = \upsilon _0 \left( \frac{\bar{\tau }_n}{s_n +\alpha \pi _n}\right) ^{\frac{1}{m}} \end{aligned}$$

(C7)

Variation of the equivalent plastic shear strain rate:

$$\begin{aligned} \Delta \upsilon ^{\mathrm{p}}= & {} \frac{\upsilon _0}{m} \left( \frac{\bar{\tau }_n}{s_n +\alpha \pi _n}\right) ^{\frac{1}{m}-1}\nonumber \\&\left[ \frac{\Delta {\bar{\tau }}}{s_n +\alpha \pi _n} -\frac{\bar{\tau }}{(s_n +\alpha \pi _n)^{2}} \left( \Delta s +\alpha \Delta \pi \right) \right] \end{aligned}$$

(C8)

Equivalent shear stress:

$$\begin{aligned} \bar{\tau } _n = \frac{1}{\sqrt{2}} |\mathbf{T}_{0n}^{\mathrm{e}} -\mathbf{S}_n^{\mathrm{b}}| \end{aligned}$$

(C9)

Variation of the equivalent shear stress:

$$\begin{aligned} \Delta \bar{\tau } = \frac{1}{2\bar{\tau }_n} (\mathbf{T}_{0n}^{\mathrm{e}} - \mathbf{S}_n^{\mathrm{b}}) : (\Delta \mathbf{T}_0^{\mathrm{e}} - \Delta \mathbf{S}^{\mathrm{b}}) \end{aligned}$$

(C10)

Distortional part of the elastic right Cauchy–Green deformation tensor:

$$\begin{aligned} \mathbf{C}_n^{\mathrm{e}}= & {} {\mathbf{F}_{n}^{\mathrm{e}}}^{\mathrm{T}} \mathbf{F}_n^{\mathrm{e}} \end{aligned}$$

(C11)

$$\begin{aligned} \bar{\mathbf{C}}_n^{\mathrm{e}}= & {} \hbox {det} (\mathbf{C}_n^{\mathrm{e}})^{-1/3}{} \mathbf{C}_n^{\mathrm{e}} \end{aligned}$$

(C12)

Distortional part of the trial elastic right Cauchy–Green deformation tensor:

$$\begin{aligned} \mathbf{C}_{*}^{\mathrm{e}}= & {} {\mathbf{F}_{*}^{\mathrm{e}}}^{\mathrm{T}} \mathbf{F}_{*}^{\mathrm{e}} \end{aligned}$$

(C13)

$$\begin{aligned} \bar{\mathbf{C}}_{*}^{\mathrm{e}}= & {} \hbox {det} (\mathbf{C}_{*}^{\mathrm{e}})^{-1/3}{} \mathbf{C}_{*}^{\mathrm{e}} \end{aligned}$$

(C14)

Variation of the equivalent corotated Kirchhoff stress tensor:

$$\begin{aligned} \Delta \mathbf{T}_0^{\mathrm{e}} = {\varvec{\mathcal {L}}}: \frac{1}{2}[\log (\bar{\mathbf{C}}_{*}^{\mathrm{e}}) - \hbox {log} (\bar{\mathbf{C}}_n^{\mathrm{e}})] -2G\Delta t\mathbf{D}^{\mathrm{p}} \end{aligned}$$

(C15)

Plastic strain increment tensor:

$$\begin{aligned} \mathbf{D}^{\mathrm{p}}= (\upsilon _n^{\mathrm{p}} + \theta \Delta \upsilon ^{\mathrm{p}})\mathbf{N}_n \end{aligned}$$

(C16)

Variation of the back stress tensor:

$$\begin{aligned} \Delta \mathbf{S}^{\mathrm{b}} = -\mathbf{H}_n :\mathbf{P}_n^{-1} : (\mathbf{N}_n \Delta t\Delta \upsilon ^{\mathrm{p}} +\mathbf{M}_n \Delta T_0^{\mathrm{e}}) \end{aligned}$$

(C17)

where:

$$\begin{aligned}&{} \mathbf{N}_n = \frac{\mathbf{T}_{0n}^{\mathrm{e}} - \mathbf{S}_n^{\mathrm{b}}}{2\bar{\tau }_n} \end{aligned}$$

(C18)

$$\begin{aligned}&{} \mathbf{M}_n = \frac{\Delta t\upsilon _n^{\mathrm{p}}}{2\bar{\tau } _n} ({\varvec{\mathcal {I}}}-2\mathbf{N}_n \otimes \mathbf{N}_n) \end{aligned}$$

(C19)

$$\begin{aligned}&{} \mathbf{P}_n = {\varvec{\mathcal {I}}} +\frac{\Delta t\upsilon _n^{\mathrm{p}}}{2\bar{\tau }_n} (2\mathbf{N}_n \otimes (\mathbf{N}_n :\mathbf{H}_n)-\mathbf{H}_n) \end{aligned}$$

(C20)

$$\begin{aligned}&{} \mathbf{H}_n = \mathbf{H}_{1n} : \mathbf{H}_{2n} \end{aligned}$$

(C21)

$$\begin{aligned}&{} \mathbf{H}_{1n} = \mu ^{(k)} \left[ \frac{1}{6{\lambda ^{\mathrm{p}^{2}}}^{(k)}} {\mathbf{B}_0^{\mathrm{p}}}^{(k)}\otimes \mathbf{I} -{\varvec{\mathcal {I}}} +\frac{1}{3}{} \mathbf{I} \otimes \mathbf{I}\right] \end{aligned}$$

(C22)

$$\begin{aligned}&{} \mathbf{H}_{2n} = \frac{\hbox {dexp}(\Delta t\mathbf{D}^{\mathrm{p}})}{d\Delta t\mathbf{D}^{\mathrm{p}}} \boxtimes \mathbf{B}_n^{\mathrm{p}}\exp (\Delta t\mathbf{D}^{\mathrm{p}})\nonumber \\&\qquad \qquad +\,\mathbf{B}_n^{\mathrm{p}} \exp (\Delta t\mathbf{D}^{\mathrm{p}})\boxtimes \frac{\hbox {dexp}(\Delta t\mathbf{D}^{\mathrm{p}})}{\hbox {d}\Delta t\mathbf{D}^{\mathrm{p}}} \end{aligned}$$

(C23)

Variation of the isotropic hardening internal variable:

$$\begin{aligned} \Delta s= & {} \left( \frac{\hbox {d}s}{\hbox {d}\Delta t\upsilon ^{\mathrm{p}}}\right) _n\nonumber \\= & {} \frac{(\tilde{s}_n -s_n)-bg_0\frac{s_n}{\tilde{s}_n} (s_n -s_{\mathrm{cv}}) \Delta t\upsilon ^{\mathrm{p}}}{\frac{\tilde{s}_n}{h_0} +\left( 1+bg_0\frac{s_n}{\tilde{s}_n}\Delta t\upsilon ^{\mathrm{p}}\right) \Delta t\upsilon ^{\mathrm{p}}} \Delta t\Delta \upsilon ^{\mathrm{p}} \end{aligned}$$

(C24)

Variation of the mean normal pressure:

$$\begin{aligned} \Delta \pi = -\frac{1}{3}\hbox {tr}(\Delta \mathbf{T}_0^{\mathrm{e}}) = -\frac{1}{3}\hbox {tr}\left\{ {\varvec{\mathcal {L}}}: \frac{1}{2}[\log (\bar{\mathbf{C}}_{*}^{\mathrm{e}}) -\hbox {log}(\bar{\mathbf{C}}_n^{\mathrm{e}})]\right\} \end{aligned}$$

(C25)

Inserting (C16) in (C15) and (C23); (C15) and (C17) in (C10); (C10), (C24) and (C25) in (C8) and solving for $\Delta \upsilon ^{\mathrm{p}}$ gives:

$$\begin{aligned}&\Delta \upsilon ^{\mathrm{p}}= \frac{\frac{\rho _{1n}}{s_n +\alpha \pi _n} -\frac{\bar{\tau }_n}{(s_n +\alpha \pi _n)^{2}}\alpha \Delta \pi }{\frac{m}{\upsilon _0} \left( \frac{\bar{\tau }_n}{s_n +\alpha \pi _n}\right) ^{1-\frac{1}{m}} -\frac{\rho _{2n}}{s_n +\alpha \pi _n}\Delta t +\frac{\bar{\tau }_n}{(s_n +\alpha \pi _n)^{2}} \left( \frac{\hbox {d}s}{\hbox {d}\Delta t\upsilon ^{\mathrm{p}}}\right) _{n} \Delta t} \end{aligned}$$

(C26)

where:

$$\begin{aligned} \rho _{1n} =\,&\mathbf{N}_n : \{{\varvec{\mathcal {I}}}+\mathbf{H}_n:\mathbf{P}_n^{-1} :\mathbf{M}_n\}\nonumber \\&:\left\{ {\varvec{\mathcal {L}}}: \frac{1}{2} [\log (\bar{\mathbf{C}}_{*}^{\mathrm{e}}) -\hbox {log} (\bar{\mathbf{C}}_n^{\mathrm{e}})] -2G\Delta t\upsilon _n^{\mathrm{p}} \mathbf{N}_n\right\} \end{aligned}$$

(C27)

$$\begin{aligned} \rho _{2n} =\,&\mathbf{N}_n : \{-2G\theta ({\varvec{\mathcal {I}}}+\mathbf{H}_n :\mathbf{P}_n^{-1}: \mathbf{M}_n) +\mathbf{H}_n :\mathbf{P}_n^{-1}\}:\mathbf{N}_n \end{aligned}$$

(C28)

Equivalent plastic shear strain rate:

$$\begin{aligned} \upsilon _{n+1}^{\mathrm{p}} = \upsilon _n^{\mathrm{p}} +\theta \Delta \upsilon ^{\mathrm{p}} \end{aligned}$$

(C29)

Plastic strain rate tensor:

$$\begin{aligned} \mathbf{D}^{\mathrm{p}} = \upsilon _{n+1}^{\mathrm{p}} \mathbf{N}_n \end{aligned}$$

(C30)

(b) Update from time-step n to time-step $n+1$: New plastic deformation gradient tensor:

$$\begin{aligned} \mathbf{F}_{n+1}^{\mathrm{p}} = \hbox {exp} (\Delta t\mathbf{D}^{\mathrm{p}}) \mathbf{F}_n^{\mathrm{p}} \end{aligned}$$

(C31)

New elastic deformation gradient tensor:

$$\begin{aligned} \mathbf{F}_{n+1}^{\mathrm{e}} = \mathbf{F}_{n+1} {\mathbf{F}_{n+1}^{\mathrm{p}}}^{-1} \end{aligned}$$

(C32)

New elastic right Cauchy–Green deformation tensor:

$$\begin{aligned} \mathbf{C}_{n+1}^{\mathrm{e}} = {\mathbf{F}_{n+1}^{\mathrm{e}}}^{\mathrm{T}} \mathbf{F}_{n+1}^{\mathrm{e}} \end{aligned}$$

(C33)

New elastic stretch tensor:

$$\begin{aligned} \mathbf{U}_{n+1}^{\mathrm{e}} = \sqrt{\mathbf{C}_{n+1}^{\mathrm{e}}} \end{aligned}$$

(C34)

New elastic Hencky strain tensor:

$$\begin{aligned} \mathbf{E}_{n+1}^{\mathrm{e}} = \hbox {log}(\mathbf{U}_{n+1}^{\mathrm{e}}) \end{aligned}$$

(C35)

New rotation tensor:

$$\begin{aligned} \mathbf{R}_{n+1}^{\mathrm{e}} = \mathbf{F}_{n+1}^{\mathrm{e}} {\mathbf{U}_{n+1}^{\mathrm{e}}}^{-1} \end{aligned}$$

(C36)

New corotated Kirchhoff stress tensor:

$$\begin{aligned} \mathbf{T}_{n+1}^{\mathrm{e}} = {\varvec{\mathcal {L}}}: (\mathbf{E}_{n+1}^{\mathrm{e}}) \end{aligned}$$

(C37)

Stress push-forward; corotated Kirchhoff stress to Cauchy stress transformation:

$$\begin{aligned} \mathbf{T}_{n+1} = 1/\hbox {det}(\mathbf{F}_{n+1}) \mathbf{R}_{n+1}^{\mathrm{e}} \mathbf{T}_{n+1}^{\mathrm{e}} {\mathbf{R}_{n+1}^{\mathrm{e}}}^{\mathrm{T}} \end{aligned}$$

(C38)

New isotropic hardening internal variables:

$$\begin{aligned}&s_{n+1} = s_n +h_0 \left( 1-\frac{s_n}{\tilde{s}_n}\right) \Delta t\upsilon _n^{\mathrm{p}} \end{aligned}$$

(C39)

$$\begin{aligned}&\eta _{n+1} = \eta _n +g_0 \left( \frac{s_n }{s_{\mathrm{cv}}}-1\right) \Delta t\upsilon _n^{\mathrm{p}} \end{aligned}$$

(C40)

$$\begin{aligned}&\tilde{s}_n = s_{\mathrm{cv}} [1+b(\eta _{\mathrm{cv}}-\eta _n)] \end{aligned}$$

(C41)