Abstract
This work presents a new finite element treatment of the coupled problem of Darcy–Biot-type fluid transport in porous media undergoing large deformations, that is free from any stabilization techniques. The formulation bases on an incremental two-field minimization principle that is constrained by the equation of continuity for the fluid mass content and determines at a given state the deformation and the fluid mass flux vector. The big advantage of the minimization formulation over classical saddle point principles of poroelasticity is the omission of the inf-sup condition—a condition that makes the construction of stable and computationally efficient finite element formulations difficult. Due to the \(H(\hbox {Div}, {\mathcal B}_0)\) variational structure of the minimization principle on the fluid side, lowest order Raviart–Thomas elements are used for the conforming approximation of the fluid mass flux. Furthermore, a standard nodal-based element using bilinear interpolation for both fields combined with a reduced numerical integration of the (volumetric) coupling term is analyzed and used for the solution of the minimization principle. Representative numerical examples demonstrate the performance of the proposed finite element designs of the minimization principle and clearly underline advantages over finite element formulations of the classical two-field saddle point principle formulated in deformation and fluid potential.






















Similar content being viewed by others
Notes
Note, that since the dissipation potential \(\widehat{\phi }\) defined in (20) is a homogeneous function of degree two, the dissipation potential functional D is half the dissipation in the overall body.
Note, that the solid grains forming the matrix still can be modelled as incompressible by setting Biot’s coefficient to \(b=1\).
The restriction \({\varvec{v}}\in {\varvec{H}}^1_0({\mathcal B})\) is in line with the additive split (48)\(_1\) of the displacement field into an extension \({\varvec{u}}_D \in {\varvec{H}}^1({\mathcal B})\) that fulfills the Dirichlet boundary condition and \({\varvec{u}}_0 \in {\varvec{H}}^1_0({\mathcal B})\) that is zero on the Dirichlet boundary.
A fourth-order tensor
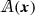 is called positive definite if the inequality
is called positive definite if the inequality 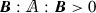 is satisfied for all second-order tensors \({\varvec{B}}\ne {\varvec{0}}\) at all points \({\varvec{x}}\in {\mathcal B}\). Alternatively, one can define positive definitness in the following way: there exists a constant \(A_0>0\) such that the inequality
is satisfied for all second-order tensors \({\varvec{B}}\ne {\varvec{0}}\) at all points \({\varvec{x}}\in {\mathcal B}\). Alternatively, one can define positive definitness in the following way: there exists a constant \(A_0>0\) such that the inequality 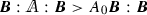 holds for all second-order tensors \({\varvec{B}}\ne {\varvec{0}}\) at all points \({\varvec{x}}\in {\mathcal B}\). This definition is equivalent to the previous one if
holds for all second-order tensors \({\varvec{B}}\ne {\varvec{0}}\) at all points \({\varvec{x}}\in {\mathcal B}\). This definition is equivalent to the previous one if 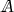 as well as \({\varvec{B}}\) are continuous. Note that if
as well as \({\varvec{B}}\) are continuous. Note that if 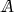 has minor symmetries we have to restrict \({\varvec{B}}\) to the set of symmetric second-order tensors \({\varvec{B}}= {\varvec{B}}^T\).
has minor symmetries we have to restrict \({\varvec{B}}\) to the set of symmetric second-order tensors \({\varvec{B}}= {\varvec{B}}^T\).The index \(k \in {\mathcal N}_0\) indicates the polynomial degree of the normal component of the fluid flux on the element edges.
For \({\varvec{H}}^1({\mathcal B}_0)\)-conformity, piecewise polynomial vector functions have to satisfy continuity in every component across element boundaries, i.e. \({\varvec{H}}^1({\mathcal B}_0) \subset H(\hbox {Div}, {\mathcal B}_0)\).
Finite Element Shapes. Associated with a node I of a two-dimensional finite element \({\mathcal B}_{0}^e\), the interpolation matrix has the form

in terms of the shape function \(N^I\) and its derivatives.
Note, that the mixed variables (126) do not arise in the presented reduced integration formulation. Latter is fully governed by the algebraic minimization principle (66) in terms of the potential (80). Hence, the reduced integration approach is not constrained by the discrete inf-sup condition which is algebraic in nature.
We use an Enhanced-Assumed-Strain element with a strain enhancement of the standard \(\hbox {Q}_1\) element with two vectorial parameters \(\underline{{\varvec{\alpha }}}_I^e \in {\mathbb {R}}^2\), \(I=1,2\), per element, see Simo and Armero [56].
Another possibility to overcome locking could be the increase of the polynomial degree of the finite element shape functions (\(\hbox {Q}_1\hbox {--}\hbox {RT}_1\), \(\hbox {Q}_2\hbox {--}\hbox {RT}_1\),...). Due to the higher computational costs this approach is not further investigated.
References
Abousleiman Y, Cheng A, Cui L, Detournay E, Roegiers J-C (1996) Mandel’s problem revisited. Géotechnique 46(2):187–195
Aguilar G, Gaspar FJ, Lisbona F, Rodrigo C (2008) Numerical stabilization of Biot’s consolidation model by a perturbation on the flow equation. Int J Numer Method Eng 75(11):1282–1300
Armero F (1999) Formulation and finite element implementation of a multiplicative model of coupled poro-plasticity at finite strains under fully saturated conditions. Comput Methods Appl Mech Eng 171(34):205–241
Arnold DN, Brezzi F, Fortin M (1984) A stable finite element for the Stokes equations. Calcolo 21:337–344
Arnold DN, Boffi D, Falk RS (2005) Quadrilateral \({H}(\text{ div })\) finite elements. SIAM J Numer Anal 42(6):2429–2451
Babuska I (1973) The finite element method with Lagrangian multipliers. Numer Math 20:179–192
Bear J (1972) Dynamics of fluids in porous media. Dover Publications, New York
Berger L, Bordas R, Kay D, Tavener S (2017) A stabilized finite element method for finite-strain three-field poroelasticity. Comput Mech 60:51–68
Biot MA (1965) Mechanics of incremental deformations. Wiley, New York
Biot M (1941) General theory of three-dimensional consolidation. J Appl Phys 12:155–164
Biot M (1972) Theory of finite deformations of porous solids. Indiana Univ Math J 21:597–620
Böger L, Nateghi A, Miehe C (2017) A minimization principle for deformation-diffusion processes in polymeric hydrogels: constitutive modeling and FE implementation. Int J Solids Struct 121:257–274
Booker J, Small J (1975) An investigation of the stability of numerical solutions of Biot’s equations of consolidation. Int J Solids Struct 11:907–917
Borja R, Alarcon E (1995) A mathematical framework for finite strain elastoplastic consolidation. Part I: balance laws, variational formulation, and linearization. Comput Methods Appl Mech Eng 122:145–171
Bouklas N, Landis CM, Huang R (2015) A nonlinear, transient finite element method for coupled solvent diffusion and large deformation of hydrogels. J Mech Phys Solids 79:21–43
Brezzi F (1974) On the existence, uniqueness and approximation of saddle-point problems arising from lagrangian multipliers. Revue française d’automatique, informatique, recherche opérationnelle. Analyse Numérique 8:129–151
Brezzi F, Fortin M (1991) Mixed and hybrid finite element methods. Springer, Berlin
Brezzi F, Douglas J, Marini L (1985) Two families of mixed finite elements for second order elliptic problems. Numer Math 47:217–235
Carter JP, Booker JR, Small JC (1979) The analysis of finite elasto-plastic consolidation. Int J Numer Anal Methods Geomech 3(2):107–129
Carter J, Small J, Booker J (1977) A theory of finite elastic consolidation. Int J Solids Struct 13:467–478
Chapelle D, Bathe KJ (1993) The inf-sup test. Comput Struct 47:537–545
Choo J, Borja RI (2015) Stabilized mixed finite elements for deformable porous media with double porosity. Comput Methods Appl Mech Eng 293:131–154
Christian J (1977) Numerical methods in geotechnical engineering, chapter two- and three-dimensional consolidation, pp 399–426. McGraw-Hill, New York
Coussy O (1995) Mechanics of porous continua. Wiley, Chichester
Coussy O (2004) Poromechanics. Wiley, Chichester
Cryer CW (1963) A comparison of the three-dimensional consolidation theories of Biot and Terzaghi. Quart J Mech Appl Math 16:401–412
de Boer R (2000) Theory of porous media. Springer, Berlin
Detournay E, Cheng AH-D (1993) Fundamentals of poroelasticity. In Fairhurst C (ed) Comprehensive rock engineering: principles, practice and projects, Vol. II, Analysis and Design Method, chapter 5, pp 113–171. Pergamon Press, Oxford
Dortdivanlioglu B, Krischok A, Beirao da Veiga L, Linder C (2018) Mixed isogeometric analysis of strongly coupled diffusion in porous materials. Int J Numer Methods Eng 114:28–46
Douglas J, Wang J (1989) An absolutely stabilized finite element method for the Stokes problem. Math Comput 52(186):495–508
Ehlers W (2002) Foundations of multiphasic and porous materials. In: Ehlers W, Bluhm J (eds) Porous media: theory, experiments and numerical applications. Springer, Berlin, pp 3–86
Ferronato M, Gambolati G, Teatini P (2001) Ill-conditioning of finite element poroelasticity equations. Int J Solid Struct 38(34–35):5995–6014
Ferronato M, Castelletto N, Gambolati G (2010) A fully coupled 3-D mixed finite element model of Biot consolidation. J Comput Phys 229:4813–4830
Gresho PM, Lee RL (1981) Don’t suppress the wiggles–they’re telling you something. Comput Fluids 9:223–253
Haga JB, Osnes H, Langtangen HP (2012) On the causes of pressure oscillations in low-permeable and low-compressible porous media. Int J Numer Anal Methods Geomech 36(12):1507–1522
Hughes TJR, Franca LP (1987) A new finite element formulation for computational fluid dynamics: VII. The Stokes problem with various well-posed boundary conditions: symmetric formulations that converge for all velocity pressure spaces. Comput Methods Appl Mech Eng 65:85–96
Korsawe J, Starke G (2006) A least-squares mixed finite element method for Biot’s consolidation problem in porous media. SIAM J Numer Anal 43(1):318–339
Krischok A, Linder C (2016) On the enhancement of low-order mixed finite element methods for the large deformation analysis of diffusion in solids. Int J Numer Methods Eng 106:278–297
Lewis R, Schrefler B (1998) The finite element method in the static and dynamic deformation and consolidation of porous media. Wiley, New York
Linder C, Krischok A, Dortdivanlioglu B (2017) Stable computational methods for strongly coupled porous media. In 88th GAMM anual meeting
Mandel J (1953) Consolidation des sols. Géotechnique, 7
Miehe C, Mauthe S, Teichtmeister S (2015) Minimization principles for the coupled problem of Darcy-Biot-type fluid transport in porous media linked to phase field modeling of fracture. J Mech Phys Solids 82:186–217
Mira P, Pastor M, Li T, Liu X (2003) A new stabilized enhanced strain element with equal order of interpolation for soil consolidation problems. Comput Methods Appl Mech Eng 192:4257–4277
Pantuso D, Bathe KJ (1997) On the stability of mixed finite elements in large strain analysis of incompressible solids. Finite Elem Anal Des 28:83–104
Papastavrou A, Steinmann P, Stein E (1997) Enhanced finite element formulation for geometrically linear fluid saturated porous media. Mech Cohes-Frict Mater 2:185–203
Phillips PJ, Wheeler M (2007) A coupling of mixed and continuous Galerkin finite element methods for poroelasticity I: the continuous in time case. Comput Geosci 11:131–144
Phillips PJ, Wheeler M (2007) A coupling of mixed and continuous Galerkin finite element methods for poroelasticity II: the discrete-in-time case. Comput Geosci 11:131
Phillips PJ, Wheeler M (2008) A coupling of mixed and discontinuous Galerkin finite-element methods for poroelasticity. Comput Geosci 12:417–435
Phoon KK, Toh KC, Chan SH, Lee FH (2002) An efficient diagonal preconditioner for finite element solution of Biot’s consolidation equations. Int J Numer Methods Eng 55(4):377–400
Preisig M, Prévost JH (2011) Stabilization procedure in coupled poromechanics problems: a critical assessment. Int J Numer Anal Methods Geomech 35:1207–1225
Prévost JH (1980) Mechanics of continuous porous media. Int J Eng Sci 18(6):787–800
Prévost JH (1983) Implicit-explicit schemes for nonlinear consolidation. Comput Methods Appl Mech Eng 39(2):225–239
Raviart PA, Thomas JM (1977) Primal hybrid finite element methods for 2nd order elliptic equations. Math Comput 31(138):391–413
Rodrigo C, Gaspar FJ, Hu X, Zikatanov LT (2016) Stability and monotonicity for some discretizations of the Biot’s consolidation model. Comput Methods Appl Mech Eng 298:183–204
Sandhu R, Wilson E (1969) Finite-element analysis of seepage in elastic media. J Eng Mech Div 95:641–652
Simo J, Armero F (1992) Geometrically nonlinear enhanced strain mixed methods and the method of incompatible modes. Int J Numer Methods Eng 33:1413–1449
Simo J, Rifai MS (1990) A class of mixed assumed strain methods and the method of incompatible modes. Int J Numer Methods Eng 29:1595–1638
Sun W, Ostien J, Salinger A (2013) A stabilized assumed deformation gradient finite element formulation for strongly coupled poromechanical simulations at finite strain. Int J Numer Anal Methods Geomech 37:2755–2788
Taylor C, Hood P (1973) A numerical solution of the Navier–Stokes equations using the finite element technique. Comput Fluids 1(1):73–100
Tchonkova M, Peters J, Sture S (2008) A new mixed finite element method for poro-elasticity. Int J Numer Anal Methods Geomech 32:579–606
Terzaghi K (1925) Erdbaumechanik auf bodenphysikalischer Grundlage. F. Deuticke
Terzaghi K (1943) Theoretical soil mechanics. Wiley, New York
Toh K-C, Phoon K-K (2008) Comparison between iterative solution of symmetric and non-symmetric forms of Biot’s FEM equations using the generalized Jacobi preconditioner. Int J Numer Anal Methods Geomech 32(9):1131–1146
Truty A, Zimmermann T (2006) Stabilized mixed finite element formulations for materially nonlinear partially saturated two-phase media. Comput Methods Appl Mech Eng 195:1517–1546
Verfürth R (1984) Error estimates for a mixed finite element approximation of the Stokes equations. Rairo Anal Numér 18:175–182
Vermeer PA, Verruijt A (1981) An accuracy condition for consolidation by finite elements. Int J Numer Anal Methods Geomech 5:1–14
White JA, Borja RI (2008) Stabilized low-order finite elements for coupled solid-deformation/fluid-diffusion and their application to fault zone transients. Comput Methods Appl Mech Eng 197(49):4353–4366
Wriggers P, Reese S (1996) A note on enhanced strain methods for large deformations. Comput Methods Appl Mech Eng 135:201–209
Zhou XX, Chow YK, Leung CF (2007) Hybrid and enhanced finite element methods for problems of soil consolidation. Int J Numer Methods Eng 69:221–249
Acknowledgements
Steffen Mauthe and Stephan Teichtmeister thank their late advisor Prof. Christian Miehe for his guidance, intensive mentorship and unlimited support. The anonymous reviewers’ detailed comments and suggestions are highly acknowledged. Moreover, we thank the German Research Foundation (DFG) for funding this work within SFB 1313, Research Project B.01.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Teichtmeister, S., Mauthe, S. & Miehe, C. Aspects of finite element formulations for the coupled problem of poroelasticity based on a canonical minimization principle. Comput Mech 64, 685–716 (2019). https://doi.org/10.1007/s00466-019-01677-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-019-01677-4




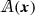 is called positive definite if the inequality
is called positive definite if the inequality 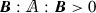 is satisfied for all second-order tensors
is satisfied for all second-order tensors 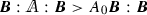 holds for all second-order tensors
holds for all second-order tensors 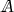 as well as
as well as 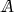 has minor symmetries we have to restrict
has minor symmetries we have to restrict 