Abstract
Generalized or extended finite element method (G/XFEM) models the crack by enriching functions of partition of unity type with discontinuous functions that represent well the physical behavior of the problem. However, this enrichment functions are not available for all problem types. Thus, one can use numerically-built (global-local) enrichment functions to have a better approximate procedure. This paper investigates the effects of micro-defects/inhomogeneities on a main crack behavior by modeling the micro-defects/inhomogeneities in the local problem using a two-scale G/XFEM. The global-local enrichment functions are influenced by the micro-defects/inhomogeneities from the local problem and thus change the approximate solution of the global problem with the main crack. This approach is presented in detail by solving three different linear elastic fracture mechanics problems for different cases: two plane stress and a Reissner–Mindlin plate problems. The numerical results obtained with the two-scale G/XFEM are compared with the reference solutions from the analytical, numerical solution using standard G/XFEM method and ABAQUS as well, and from the literature.


















Similar content being viewed by others
Abbreviations
- \( \varvec{{\bar{t}}} \) :
-
External traction vector
- \( \varvec{{\bar{u}}} \) :
-
Prescribed displacement
- \( \varvec{{\hat{n}}} \) :
-
Unit outward normal
- \( \varvec{b} \) :
-
Body force vector
- \( \varvec{m}_j, n_j \) :
-
Outward unit normal vectors in contour integral
- \( \varvec{u} \) :
-
Displacement field vector
- \( \varvec{v} \) :
-
Test function
- \( \delta \) :
-
Kronecker delta
- \( \epsilon _b, \epsilon _s \) :
-
Bending and shear strains
- \( \epsilon _{ij} \) :
-
Strain tensor
- \( \Gamma \) :
-
Inner J-integral boundary
- \( \kappa \) :
-
Material constant
- \( \mu \) :
-
Shear modulus
- \( \mu _d \) :
-
Inhomogeneities shear modulus
- \( \mu _m \) :
-
Main problem shear modulus
- \( \nu _d \) :
-
Inhomogeneities Poisson’s ratio
- \( \Omega \) :
-
Problem domain
- \( \omega _j\) :
-
Cloud of node j
- \( \partial \Omega \) :
-
Problem boundary
- \( \partial \Omega _c \) :
-
Crack surface
- \( \partial \Omega _t \) :
-
Surface traction boundary
- \( \partial \Omega _u \) :
-
Displacement boundary
- \( \phi _i \) :
-
Angle of micro-defect i and main crack-tip connection line with respect to the x-axis
- \( \psi \) :
-
Section rotation of the plate middle plane
- \( \sigma \) :
-
Cauchy stress tensor
- \( \sigma _{ij} \) :
-
Stress tensor
- \( \theta _i \) :
-
Micro-defect i direction angle
- \( \varepsilon \) :
-
Linear strain tensor
- \( a_{mc} \) :
-
Main crack length
- \( C_+, C_- \) :
-
Upper and lower crack surfaces
- \( C_0 \) :
-
Outer J-integral boundary
- \( d_i \) :
-
Distance of the micro-defect i to the main crack-tip
- detJ :
-
Determinant of the Jacobian
- \( h_{elem} \) :
-
Square root of the crack-tip element area
- I :
-
Interaction integral
- J :
-
J-integral
- \( l_{md} \) :
-
Characteristic length of the micro-defect
- M :
-
Bending moment
- \( N_{gp} \) :
-
Number of Gauss points
- Q :
-
Shear load
- q :
-
Weighting function
- \( q_j \) :
-
A set of linearly independent functions defined at each nodal cloud
- \( r_m \) :
-
Interaction integral scalar multiplier
- W :
-
Strain energy density
- w :
-
Transverse displacement of the plate
- \( w_{gp} \) :
-
Weight of each Gauss point
- \(\varvec{b}_{ji}\) :
-
Nodal parameters associated with G/XFEM
- \(\varvec{D}\) :
-
Hook’s tensor
- \({\mathbb {R}}^{2}\) :
-
Bi-dimensional domain
- \({\mathcal {N}}_j\) :
-
FE Shape function
- \(\nu \) :
-
Poisson ratio
- \(\Omega _{G}\) :
-
Global domain
- \(\Omega _{L}\) :
-
Local domain
- \(\phi _{ji}\) :
-
G/XFEM shape function
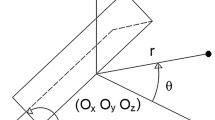
- \(\theta \) :
-
Angle between x coordinate and direction of the crack front
- \({\tilde{\varvec{u}}}(\varvec{x})\) :
-
G/XFEM displacement approximation
- E :
-
Young’s modulus
- \(K_I, K_{II}, K_{III} \) :
-
Mode-I, II and III stress intensity factors
- \(L_{ji}\) :
-
Local approximation function
References
Akbari A, Kerfriden P, Rabczuk T, Bordas SP (2012) An adaptive multiscale method for fracture based on concurrent-hierarchical hybrid modelling. In: Proceedings of the 20th UK conference of the association for computational mechanics in engineering, Manchester
Alves PD, Barros FB, Pitangueira RLS (2013) An object oriented approach to the generalized finite element method. Adv Eng Softw 59:1–18. https://doi.org/10.1016/j.advengsoft.2013.02.001
Barcellos CS, Mendonca PTR, Duarte CA (2009) A Ck continuous generalized finite element formulation applied to laminated kirchhoff plate model. Comput Mech 44:377–393. https://doi.org/10.1007/s00466-009-0376-5
Bazǎnt ZP (1976) Instability, ductility, and size effects in strain-softening concrete. J Eng Mech 102(2):331–344
Belytschko T, Black T (1999) Elastic crack growth in finite elements with minimal remeshing. Int J Numer Methods Eng 45:601–620. https://doi.org/10.1002/(SICI)1097-0207(19990620)45:5%3c601::AID-NME598%3e3.0.CO;2-S
Bhardwaj G, Singh S, Singh I, Mishra B, Rabczuk T (2016) Fatigue crack growth analysis of an interfacial crack in heterogeneous materials using homogenized XIGA. Theor Appl Fract Mech 85:294–319. https://doi.org/10.1016/j.tafmec.2016.04.004
Budarapu PR, Gracie R, Bordas SP, Rabczuk T (2014) An adaptive multiscale method for quasi-static crack growth. Comput Mech 53(6):1129–1148. https://doi.org/10.1007/s00466-013-0952-6
Budarapu PR, Gracie R, Yang SW, Zhuang X, Rabczuk T (2014b) Efficient coarse graining in multiscale modeling of fracture. Theor Appl Fract Mech 69:126–143. https://doi.org/10.1016/j.tafmec.2013.12.004
Camacho GT, Ortiz M (1996) Computational modelling of impact damage in brittle materials. Int J Solids Struct 33(20–22):2899–2938. https://doi.org/10.1016/0020-7683(95)00255-3
Chan SK, Tuba IS, Wilson WK (1970) On the finite element method in linear fracture mechanics. Eng Fract Mech 30:227–231. https://doi.org/10.1016/0013-7944(70)90026-3
Charalambides RP, Meeking Mc (1987) Finite element method simulation of crack propagation in a brittle microcracking solids. Mech Mater 6:71–87. https://doi.org/10.1016/0167-6636(87)90023-8
Chudnovsky AKMA, Dolgopolsky A (1987) Elastic interaction of a crack with a microcrack array-ii. Elastic solution for two crack configurations (piecewise constant and linear approximations). Int J Solids Struct 23(2):11–21. https://doi.org/10.1016/0020-7683(87)90029
Cook RD, Malkus DS, Plesha ME, Witt RJ (2002) Concepts and applications of finite element analysis. Wiley, New York
de Borst R, Sluys LJ, Muhlhaus HB, Pamin J (1993) Fundamental issues in finite element analyses of localisation of deformation. Eng Comput 10(2):99–121. https://doi.org/10.1108/eb023897
Dolbow J, Gosz M (2002) On the computation of mixed-mode stress intensity factors in functionally graded materials. Int J Solids Struct 39:2557–2574. https://doi.org/10.1016/S0020-7683(02)00114-2
Dolbow J, Moës N, Belytschko T (2000) Modeling fracture in mindlin-reissner plates with the extended finite element method. Int J Solids Struct 37:7161–7183. https://doi.org/10.1016/S0020-7683(00)00194-3
Duarte CA, Babuška IM (2005) A global-local approach for the construction of enrichment functions for the generalized fem and its application to propagating three-dimensional cracks. Technical report, ECCOMAS thematic conference on meshless methods, technical report 06
Duarte CA, Kim DJ (2008) Analysis and applications of a generalized finite element method with global-local enrichment functions. Comput Methods Appl Mech Eng 197:487–504. https://doi.org/10.1016/j.cma.2007.08.017
Duarte CA, Oden JT (1995) Hp clouds - a meshless method to solve boundary-value problem. Tech. rep., TICAM, The University of Texas at Austin, technical Report
Duarte CA, Babuška I, Oden JT (2000) Generalized finite element methods for three-dimensional structural mechanics problems. Comput Struct 77(2):215–232. https://doi.org/10.1016/S0045-7949(99)00211-4
Duarte CA, Kim DJ, Babuška I (2007) A global-local approach for the construction of enrichment functions for the generalized fem and its application to three-dimensional cracks. In: Leitão V, Alves C, Duarte CA (eds) Advances in meshfree techniques, pp 1–26. https://doi.org/10.1007/978-1-4020-6095-3-1
Holl M, Loehnert S, Wriggers P (2013) An adaptive multiscale method for crack propagation and crack coalescence. Int J Numer Meth Eng 93:23–51. https://doi.org/10.1002/nme.4373
Holl M, Rogge T, Loehnert S, Wriggers P, Rolfes R (2014) 3d multiscale crack propagation using the xfem applied to a gas turbine blade. Comput Mech 53:173–188. https://doi.org/10.1007/s00466-013-0900-5
Hu KX, Chandra A, Huang Y (1993) Multiple void-crack interaction. Int J Solids Struct 30(11):1473–1489. https://doi.org/10.1016/0020-7683(93)90072-F
Ingraffea AR, Saouma V (1985) Numerical modelling of discrete crack propagation in reinforced and plain concrete. Fracture mechanics of concrete. Martinus Nijhoff Publishers, Dordrecht, pp 171–225
Joseph P, Erdogan F (1991) Bending of a thin reissner plate with a through crack. J Appl Mech 58(3):842–846. https://doi.org/10.1115/1.2897273
Kim D, Duarte C, Pereira J (2008) Analysis of interacting cracks using the generalized finite element method with global-local enrichment functions. J Appl Mech 75(5):051107. https://doi.org/10.1115/1.2936240
Kim DJ, Pereira JP, Duarte CA (2010) Analysis of three-dimensional fracture mechanics problems: a two-scale approach using coarse-generalized fem meshes. Int J Numer Meth Eng 81:335–365. https://doi.org/10.1002/nme.2690
Lasry J, Pommier J, Renard Y, Salaun M (2010) eXtended finite element methods for thin cracked plates with kirchhoff-love theory. Int J Numer Meth Eng 84:1115–1138. https://doi.org/10.1002/nme.2939
Loehnert S, Belytschko T (2007a) Crack shielding and amplification due to multiple microcracks interacting with a macrocrack. Int J Fract 145:1–8. https://doi.org/10.1007/s10704-007-9094-1
Loehnert S, Belytschko T (2007b) A multiscale projection method for macro/microcrack simulations. Int J Numer Methods Geomech 71:1466–1482. https://doi.org/10.1002/nme.2001
Malekan M, Barros FB (2016) Well-conditioning global-local analysis using stable generalized/extended finite element method for linear elastic fracture mechanics. Comput Mech 58(5):819–831. https://doi.org/10.1007/s00466-016-1318-7
Malekan M, Barros FB, Pitangueira RLS, Alves PD (2016) An object-oriented class organization for global-local generalized finite element method. Latin Am J Solids Struct 13(13):2529–2551. https://doi.org/10.1590/1679-78252832
Malekan M, Barros FB, Pitangueira RLS, Alves PD, Penna SS (2017) A computational framework for a two-scale generalized/extended finite element method: generic imposition of boundary conditions. Eng Comput 34(3):988–1019. https://doi.org/10.1108/EC-02-2016-0050
Melenk JM, Babuška I (1996) The partition of unity finite element method: basic theory and applications. Comput Methods Appl Mech Eng 39:289–314. https://doi.org/10.1016/S0045-7825(96)01087-0
Mendonca PTR, Barcellos CS, Torres DAF (2011) Analysis of anisotropic mindlin plate model by continuous and non-continuous GFEM. Finite Elem Anal Des 47:698–717. https://doi.org/10.1016/j.finel.2011.02.002
Moës N, Dolbow J, Belytschko T (1999) A finite element method for crack growth without remeshing. Int J Numer Methods Eng 46:131–150. https://doi.org/10.1002/(SICI)1097-0207(19990910)46:1%3c131::AID-NME726%3e3.0.CO;2-J
Nguyen VP (2005) An object oriented approach to the xfem with applications to fracture mechanics. Master’s thesis, EMMC-Hochiminh University of Technology
Noor AK (1986) Global-local methodologies and their application to nonlinear analysis. Finite Elem Anal Des 2:333–346. https://doi.org/10.1016/0168-874X(86)90020-X
Oden JT, Duarte CA, Zienkiewicz OC (1998) A new cloud-based hp finite element method. Comput Methods Appl Mech Eng 153:117–126. https://doi.org/10.1016/S0045-7825(97)00039-X
O’Hara P, Duarte C, Eason T (2016) A two-scale GFEM for interaction and coalescence of multiple crack surfaces. Eng Fract Mech 163:274–302. https://doi.org/10.1016/j.engfracmech.2016.06.009
Rice J (1968) A path independent integral and the approximate analysis of strain concentration by notches and cracks. Trans ASME J Appl Mech 35:379–386. https://doi.org/10.1115/1.3601206
Rybicki EF, Kanninen MF (1977) A finite element calculation of stress intensity factors by a modified crack closure integral. Eng Fract Mech 9:931–938. https://doi.org/10.1016/0013-7944(77)90013-3
Singh I, Mishra B, Bhattacharya S (2011) XFEM simulation of cracks, holes and inclusions in functionally graded materials. Int J Mech Mater Des 7:199–218. https://doi.org/10.1007/s10999-011-9159-1
Soh A, Yang C (2004) Numerical modeling of interactions between a macro-crack and a cluster of micro-defects. Eng Fract Mech 71:193–217. https://doi.org/10.1016/S0013-7944(03)00097-3
Sosa HA, Eischen JW (1986) Computation of stress intensity factors for plate bending via a path-independent integral. Eng Fract Mech 25(4):451–462. https://doi.org/10.1016/0013-7944(86)90259-6
Strouboulis T, Copps K, Babuška I (2000) The generalized finite element method: an example of its implementation and illustration of its performance. Int J Numer Methods Eng 47:1401–1417. https://doi.org/10.1002/(SICI)1097-0207(20000320)47:8%3c1401::AID-NME835%3e3.0.CO;2-8
Strouboulis T, Copps K, Babuška I (2001) The generalized finite element method. Comput Methods Appl Mech Eng 190:4081–4193. https://doi.org/10.1016/S0045-7825(01)00188-8
Swenson DV, Ingraffea AR (1988) Modeling mixed-mode dynamic crack propagation using finite elements: theory and applications. Comput Mech 3(5):381–397. https://doi.org/10.1007/BF00301139
Szabo B, Babuška I (1991) Finite element analysis. Wiley, New York
Tada H, Paris PC, Irwin CR (2000) The stress analysis of cracks handbook, 3rd edn. ASME Press, New York. https://doi.org/10.1115/1.801535
Talebi H, Silani M, Bordas SPA, Kerfriden P, Rabczuk T (2014) A computational library for multiscale modeling of material failure. Comput Mech 53:104–1071. https://doi.org/10.1007/s00466-013-0948-2
Talebi H, Silani M, Rabczuk T (2015) Concurrent multiscale modeling of three dimensional crack and dislocation propagation. Adv Eng Softw 80:82–90. https://doi.org/10.1016/j.advengsoft.2014.09.016
Watwood V (1969) The finite element method for prediction of crack behaviour. Nucl Eng Des 11:323–332. https://doi.org/10.1016/0029-5493(70)90155-X
Yang SW, Budarapu PR, Mahapatra D, Bordas SP, Zi G, Rabczuk T (2015) A meshless adaptive multiscale method for fracture. Comput Mater Sci 96:382–395. https://doi.org/10.1016/j.commatsci.2014.08.054
Yau JF, Wang SS, Corten HT (1980) A mixed-mode crack analysis of isotropic solids using conservation laws of elasticity. Trans ASME J Appl Mech 47:335–341. https://doi.org/10.1115/1.3153665
Zeng Q, Liu Z, Xu D, Wang H, Zhuang Z (2016) Modeling arbitrary crack propagation in coupled shell/solid structures with x-fem. Int J Numer Meth Eng 106:1018–1040. https://doi.org/10.1002/nme.5157
Acknowledgements
The first author (CNPq Scholarship, Brazil—Grant No. 151003/2017-3) and the other author gratefully acknowledge the important support of the Brazilian research agencies CNPq (National Council for Scientific and Technological Developments—Grant No. 308932/2016-1), CAPES (Coordination for the Improvement of Higher Education Personnel), and FAPEMIG (Foundation for Research Support of the State of Minas Gerais—Grant No. APQ-02460-16).
Author information
Authors and Affiliations
Corresponding author
Appendix A: Intensity factors for Reissner–Mindlin plate problem
Appendix A: Intensity factors for Reissner–Mindlin plate problem
The J-integral contour for a Reissner–Mindlin plate problem is defined as [16]:
where \( M_{\alpha \beta } \) is the bending moment, \( Q_{\beta } \) is the shear, w is the transverse displacement and \( \psi _{\alpha } \) is section rotation about the \( x_{\alpha } \) axes that define the middle plane of the plate, in which \( \alpha \text { and } \beta \) ranging over the values 1,2.
Referring to Fig. 4a and following similar mathematical to the Sect. 4, one can reach following interaction energy integral equation for the Reissner–Mindlin plate, and for a crack with traction free faces as:
in which, similar to the Sect. 4, State (1) represents the current state and State (2) is an auxiliary state. The interaction strain energy, W, is defined by:
where \( \epsilon _b \) and \( \epsilon _s \) are bending and shear strains, respectively. Applying the divergence theorem to the integral over A, we obtain:
The above integral can be reduced depending on whether the quantity of interest is \( K_I \), \( K_{II} \), or \( K_{III} \), as certain terms in the auxiliary fields vanish for each case. For example, for \( K_I \) and \( K_{II} \) the integral takes the form:
whereas for \( K_{III} \) the integral is:
The auxiliary state for the displacement fields in Reissner–Mindlin plate theory can be found in Sosa [46] as a power series in \( \sqrt{r} \) and are shown in the following Table 6, in which \( C_{\theta } \) and \( S_{\theta } \) represent \( \cos \theta \) and \( \sin \theta \) functions, respectively. Moreover, the auxiliary bending moments and shear are as follows:
As an example, \( K_2 \) and \( K_3 \) must be set equal to zero in all equation in order to calculate auxiliary moment intensity factor of mode-I. The process of evaluating the mixed-mode intensity factors must be carried out with a judicious choice of the auxiliary moment and shear force intensity factors to evaluating the interaction energy integral. From the Eq. (A.1) and the energy release rate formulation, one can obtain the following expression:
where, to extract \( K_I \), the following values is chosen \(K_i^{(2)} = 1 , K_{II}^{(2)} = 0\), and \( K_{III}^{(2)} = 0 \). Then, the moment intensity factor \( K_I \) can be calculated as:
Rights and permissions
About this article
Cite this article
Malekan, M., Barros, F.B. Numerical analysis of a main crack interactions with micro-defects/inhomogeneities using two-scale generalized/extended finite element method. Comput Mech 62, 783–801 (2018). https://doi.org/10.1007/s00466-017-1527-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-017-1527-8