Abstract
We investigate how the complexity of Euclidean TSP for point sets P inside the strip \((-\infty ,+\infty )\times [0,\delta ]\) depends on the strip width \(\delta \). We obtain two main results.
-
For the case where the points have distinct integer x-coordinates, we prove that a shortest bitonic tour (which can be computed in \(O(n\log ^2 n)\) time using an existing algorithm) is guaranteed to be a shortest tour overall when \(\delta \leqslant 2\sqrt{2}\), a bound which is best possible.
-
We present an algorithm that is fixed-parameter tractable with respect to \(\delta \). Our algorithm has running time \(2^{O(\sqrt{\delta })} n + O(\delta ^2 n^2)\) for sparse point sets, where each \(1\times \delta \) rectangle inside the strip contains O(1) points. For random point sets, where the points are chosen uniformly at random from the rectangle \([0,n]\times [0,\delta ]\), it has an expected running time of \(2^{O(\sqrt{\delta })} n\). These results generalise to point sets P inside a hypercylinder of width \(\delta \). In this case, the factors \(2^{O(\sqrt{\delta })}\) become \(2^{O(\delta ^{1-1/d})}\).
























Similar content being viewed by others
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Notes
The separators given by Lemma 4.3 are not incident to any input points.
References
Alkema, H., de Berg, M.: Rectilinear Steiner trees in narrow strips. In: Proceedings of 37th International Symposium on Computational Geometry (SoCG), pp. 9:1–9:16 (2021)
Arora, S.: Polynomial time approximation schemes for Euclidean traveling salesman and other geometric problems. J. ACM 45(5), 753–782 (1998)
Bodlaender, H.L., Cygan, M., Kratsch, S., Nederlof, J.: Deterministic single exponential time algorithms for connectivity problems parameterized by treewidth. Inf. Comput. 243, 86–111 (2015)
Christofides, N.: Worst-case analysis of a new heuristic for the travelling salesman problem. Technical Report. Graduate School of Industrial Administration, Carnegie Mellon University (1976)
Cormen, T., Leiserson, C., Rivest, R., Stein, C.: Introduction to Algorithms, 3rd edn. MIT, Cambridge (2009)
Cutler, M.: Efficient special case algorithms for the \(n\)-line planar traveling salesman problem. Networks 10, 183–195 (1980)
Cygan, M., Kratsch, S., Nederlof, J.: Fast Hamiltonicity checking via bases of perfect matchings. J. ACM 65(3), 12:1-12:46 (2018)
Daley, D., Vere-Jones, D.: An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure. Probability and Its Applications. Springer, New York (2007)
de Berg, M., Cheong, O., van Kreveld, M., Overmars, M.: Computational Geometry: Algorithms and Applications. Springer, Berlin (2008)
de Berg, M., Buchin, K., Jansen, B., Woeginger, G.: Fine-grained complexity analysis of two classic TSP variants. In: Proceedings of 43rd International Colloquium on Automata, Languages, and Programming (ICALP), pp. 5:1–5:14 (2016)
de Berg, M., Buchin, K., Jansen, B.M.P., Woeginger, G.J.: Fine-grained complexity analysis of two classic TSP variants. ACM Trans. Algorithms 17(1), 1–29 (2016)
de Berg, M., Bodlaender, H., Kisfaludi-Bak, S., Kolay, S.: An ETH-tight exact algorithm for Euclidean TSP. In: Proceedings of 59th IEEE Symposium on Foundations of Computer Science (FOCS), pp. 450–461 (2018)
Deineko, V., Woeginger, G.: The convex-hull-and-$k$-lines traveling salesman problem. Inf. Proc. Lett. 59(3), 295–301 (1996)
Deineko, V., van Dal, R., Rote, G.: The convex-hull-and-line traveling salesman problem: a solvable case. Inf. Proc. Lett. 51, 141–148 (1994)
Deineko, V., Hoffmann, M., Okamoto, Y., Woeginger, G.: The traveling salesman problem with few inner points. Oper. Res. Lett. 34(1), 106–110 (2006)
Edelsbrunner, H., Rote, G., Welzl, E.: Testing the necklace condition for shortest tours and optimal factors in the plane. Theor. Comput. Sci. 66, 157–180 (1989)
Fomin, F., Lokshtanov, D., Kolay, S., Panolan, F., Saurabh, S.: Subexponential algorithms for rectilinear Steiner tree and arborescence problems. ACM Trans. Algorithms 16, 1–37 (2020). https://doi.org/10.1145/3381420
Garey, M., Graham, R., Johnson, D.: Some NP-complete geometric problems. In: Proceedings of the 8th Annual ACM Symposium on Theory of Computing (STOC), pp. 10–22 (1976)
Hwang, R., Chang, R., Lee, R.: The searching over separators strategy to solve some NP-hard problems in subexponential time. Algorithmica 9(4), 398–423 (1993)
Impagliazzo, R., Paturi, R.: On the complexity of \(k\)-SAT. J. Comput. Syst. Sci. 62(2), 367–375 (2001)
Kann, V.: On the approximability of NP-complete optimization problems. Ph.D. thesis, Royal Institute of Technology, Stockholm (1992)
Mitchell, J.: Guillotine subdivisions approximate polygonal subdivisions: a simple polynomial-time approximation scheme for geometric TSP, k-MST, and related problems. SIAM J. Comput. 28(4), 1298–1309 (1999)
Papadimitriou, C.: The Euclidean traveling salesman problem is NP-complete. Theor. Comput. Sci. 4(3), 237–244 (1977)
Rao, S., Smith, W.D.: Approximating geometrical graphs via ‘spanners’ and ‘banyans’. In: Proceedings of 30th ACM Symposium on Theory of Computing (STOC), pp. 540–550 (1998)
Reinhold, A.: Some results on minimal covertex polygons. Manuscript, City College of New York (1965)
Riordan, J.: Moment recurrence relations for binomial, Poisson and hypergeometric frequency distributions. Ann. Math. Stat. 8(2), 103–111 (1937). https://doi.org/10.1214/aoms/1177732430
Rote, G.: The \(n\)-line traveling salesman problem. Networks 22, 91–108 (1992)
Sanders, D.: On extreme circuits. Ph.D. thesis, City University of New York (1968)
Smith, W., Wormald, N.: Geometric separator theorems and applications. In: Proceedings 39th Annual Symposium on Foundations of Computer Science (FOCS), pp. 232–243 (1998)
Thorisson, H.: Coupling, Stationarity and Regeneration. Springer, New York (2000)
Funding
This study was supported by Dutch Research council (NWO) under project no. NETWORKS-024.002.003.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor in Charge: Kenneth Clarkson
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The work in this paper is supported by the Netherlands Organisation for Scientific Research (NWO) through Gravitation-grant NETWORKS-024.002.003.
We would like to thank the anonymous DCG reviewer for their exceptionally thorough review and insightful comments.
Appendices
Appendix A: The Automated Prover
Here, we will give an overview of the inner workings of the automated prover. See Algorithm 5 for pseudocode, which we will now explain. First, all candidate sets of edges \(\overline{F}'\) that form a tour together with \(\widetilde{E}\) are generated. Then, a set of cases is generated. Each case consists of the following:
-
The x-coordinates of each of the points, stored in \(\mathcal {X}\). Every point must have a different integer x-coordinate, and must adhere to the given bounds on the x-coordinates.
-
For every point, an interval denoting the range in which its y-coordinate must lie, stored in \(\mathcal {Y}\). When the cases are first generated, this is simply \([0,\delta ]\) for every point.
For each possible combination \(\mathcal {X}\) of x-coordinates of the points, one such case is generated. Note that every possible set of points in represented by one of these cases. Then, for every case, it does the following:
-
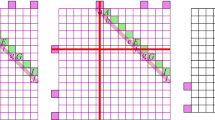
To prove a case, it calculates an upper bound on the total lengths of every candidate \(\overline{F}'\), and a lower bound of the total length of \(\overline{F}\). For every edge, a lower bound can be found by simply taking the points as close together as possible, and an upper bound is found by doing the opposite. See Fig. 21 for some examples. Suppose there exists a set \(\overline{F}'\) such that the upper bound on its length is guaranteed to be lower than the lower bound on the length of \(\overline{F}\). Then \(\Vert \overline{F}'\Vert < \Vert \overline{F}\Vert \) must hold, and the case holds. To counter rounding errors, the calculated upper bound must be more than some fixed \(\eta :=10^{-6}\) lower than the calculated lower bound for this to trigger. The prover has been implemented in Java using doubles, which have a precision of up to 15 to 16 decimal digits.
-
If it fails to prove the case, it splits the case into \(2^{n_\textrm{left}+ n_\textrm{right}}\) cases, by splitting the interval of every y-coordinate into two equal parts. For example, if a case has two points and intervals [0, 2] and [6, 8], it is split into the four cases ([0, 1], [6, 7]), ([0, 1], [7, 8]), ([1, 2], [6, 7]) and ([1, 2], [7, 8]). Then, it recursively tries to prove all of these cases. If, however, the intervals become too small (smaller than the given precision parameter \(\varepsilon \)), the prover gives up on proving this case.
This process continues until all cases have been either proven or given up on. Finally, the prover returns a list of all cases and whether it succeeded or failed on these cases. Note that the smaller the precision parameter \(\varepsilon \) is, the more precise the cases (and therefore the answer) will be. However, a smaller \(\varepsilon \) will also result in more cases, which increases both the running time and the number of lines of the output.
Appendix B: Omitted Proofs
1.1 Proof of Observation 6.2
See Fig. 22 for an example. Note that \(x_{st^+\hspace{-1.111pt}(i)}\) is the x-coordinate of the rightmost point to the left of \(t^+_i\), and that \(x_{st^+\hspace{-1.111pt}(i)+1}\) is the x-coordinate of the leftmost point to the right of \(t^+_i\). Therefore, \(x_{st^+\hspace{-1.111pt}(i)+1} - x_{st^+\hspace{-1.111pt}(i)} > \delta / (2k)\).
An example of Observation 6.2. Edges of T are shown in black, edges of \(T'\) are shown in red
W.l.o.g., T contains the directed edge from \(r_1\) to \(r_2\). Suppose for a contradiction that T is an optimal tour and not bitonic at \(t^+_i\). Then T must cross \(t^+_i\) at least four times, which implies that there must be another directed edge \(q_1 q_2\) with \(x(q_1) \leqslant x_{st^+\hspace{-1.111pt}(i)}\) and \(x_{st^+\hspace{-1.111pt}(i)+1} \leqslant x(q_2)\).
Note that \(q_1 \ne r_1\) and \(q_2 \ne r_2\), since a single point cannot have two incoming or two outgoing edges. We will now show that \(| r_1 q_1| + |r_2 q_2| < |q_1 q_2| + |r_1 r_2|\). By Observation 3.1, we then get an optimal tour \(T'\) shorter than T, thereby finishing the proof. First, we will simplify the problem using an argument similar to the proof of Observation 3.2. Suppose we move \(q_1\) towards \(q_2\) until \(x(q_1) = x_{st^+\hspace{-1.111pt}(i)}\). By doing so, \(|q_1 r_1|\) will never decrease more than \(|q_1 q_2|\). Therefore, it is sufficient to prove the statement for \(x(q_1) = x_{st^+\hspace{-1.111pt}(i)}\). Analogously, it is sufficient to prove the statement for \(x(q_2) = x_{st^+\hspace{-1.111pt}(i)+1}\) and \(x(r_1) + 2k \delta = x(q_1)\) and \(x(q_2) + 2k \delta = x(r_2)\). Finally, recall that \(x_{st^+\hspace{-1.111pt}(i)+1} - x_{st^+\hspace{-1.111pt}(i)} > \delta / (2k)\), so we will prove the statement for \(x_{st^+\hspace{-1.111pt}(i)+1} - x_{st^+\hspace{-1.111pt}(i)} = \delta / (2k)\). Together, we now have
We get
By Observation 3.1, this gives us an optimal tour \(T'\) shorter than T, thereby finishing the proof.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Alkema, H., de Berg, M., van der Hofstad, R. et al. Euclidean TSP in Narrow Strips. Discrete Comput Geom 71, 1456–1506 (2024). https://doi.org/10.1007/s00454-023-00609-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-023-00609-7