Smallest k-Enclosing Rectangle Revisited

Abstract

Given a set of n points in the plane, and a parameter $k$, we consider the problem of computing the minimum (perimeter or area) axis-aligned rectangle enclosing $k$ points. We present the first near quadratic time algorithm for this problem, improving over the previous near-$O(n^{5/2})$-time algorithm by Kaplan et al. (25th European Symposium on Algorithms. Leibniz Int Proc Inform, vol. 87, # 52. Leibniz-Zent Inform, Wadern, 2017). We provide an almost matching conditional lower bound, under the assumption that $(\min ,+)$-convolution cannot be solved in truly subquadratic time. Furthermore, we present a new reduction (for both perimeter and area) that can make the time bound sensitive to $k$, giving near $O(nk)$ time. We also present a near linear time $(1+\varepsilon )$-approximation algorithm to the minimum area of the optimal rectangle containing $k$ points. In addition, we study related problems including the 3-sided, arbitrarily oriented, weighted, and subset sum versions of the problem.

Appendix A Shallow Cutting for Points and 3-Sided Rectangles

Here, we prove a shallow cutting lemma due to Jørgensen and Larsen [23]—we provide the full details for the sake of completeness.

Let $P$ be a set of n points in general position (i.e., no two points share x or y values), let $\ell$ be a horizontal line below all the points of $P$, and let k be a parameter. For simplicity of exposition we assume $\ell$ is the x-axis. We generate $m = O(n/k)$ subsets $Q_1,\ldots , Q_m$ of $P$, each of size O(k), such that for any axis-parallel rectangle $R$ that has its bottom edge on $\ell$, and contains at most k points of $P$, its associated subset of $P$ is contained in one of these subsets.

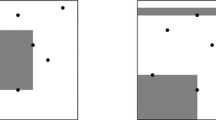
To this end, we sweep horizontally upward from $\ell$. At any point in time, the x-range is going to be split into interior disjoint intervals (the two extreme ones are rays). For an interval $I = [x_1,x_2]$, its weight at time t is $n(I,t) = \left| { P(I,t) } \right| \bigr .$, where is the active set of points associated with I. As soon as the weight of some active interval J becomes 2k, say at time t, we stop the sweep and split J into two intervals, by picking a value $m \in J$ between the kth rank and $(k+1)$th rank x-coordinates of the points of $P(I,t)$, and breaking I at m into two intervals. See Fig. 6. Let $I^-, I^+$ be the two intervals adjacent to I just before this split. We store the point $p_t = (m,t)$ into a set of splitting points $S$. Let be the rectangle associated with this split point, and add the set $P(I^- \cup I \cup I^+,t) = P\cap R(p_t)$ to the collection of subsets being computed.

For every two consecutive intervals J, K in the final partition in the end of the sweeping, we add the set $P(I\cup J,+\infty )$ to the collection. Let $\mathcal {F}$ be the resulting family of sets.

Fig. 6

An illustration of Lemma 2.4. The last pane on the right shows the point set associated with the last interval being split

1.1 Analysis

Observe that every time we insert a point $p$ into $S$, we are splitting a set of 2k points into two sets of k points. Since there are n points overall, this can happen at most n/k times. This readily implies that $\left| {\mathcal {F}} \right| \le 2 n/k$.

Lemma B.1

Let $R$ be any rectangle having its bottom edge on $\ell$ such that $\left| {R\cap P} \right| < k$. Then, there exists a set $Q\in \mathcal {F}$ such that $R\cap P\subseteq Q$. Furthermore, each set of $\mathcal {F}$ contains at most 6k points.

Fig. 7

$p$ is not in $R$

Fig. 8

The points $p$ and $q$ are both in $R$

Fig. 9

The point $p$ is in $R$, but $q$ is not

Proof

Let $I_R$ be the projection of $R$ onto the x-axis. Let I be the last active interval that contains $I_R$. If I is one of the final intervals, then all the points in the I strip are contained in the set that corresponds to I and its adjacent neighbor, and the claim immediately holds.

So, let t be the critical time, where I was split, and let $p$ be the splitting point. There are several possibilities.

I.:

If $p\notin R$, then $R(p_t)$ contains $R$—indeed, $R(p_t)$ x-axis extent contains I, which contains $I_R$, see Fig. 7. Now, $R\cap P\subseteq R(p_t) \cap P$ is in $\mathcal {F}$, and the claim holds.

II.:

If $p\in R$, then consider the lowest point $q$ (in the y-direction) of $S\setminus \left\{ {p} \right\}$ such that its x-axis coordinate is in $I_R$.

II.i.:

If $q$ does not exist, then $I_R$ is contained in two consecutive final intervals, and the claim readily holds.

II.ii.:

If $q\in R$, then the rectangle $R' = [x(p),x(q)] \times [0, t(q)] \subseteq R$ contains k points of $P$ (since it is one of the sides of the split created by $q$—which contains exactly k points by construction), see Fig. 8. But it is a contradiction to the assumption that $| R\cap P| < k$.

II.iii.:

If $q\notin R$ then when the upward sweep line hits $q$, the interval $I_R$ is contained in two consecutive intervals, where one of them is being split by $q$, see Fig. 9. But then, $R(q)$ is taller than $R$, and it spans these two intervals. We conclude that $R\subseteq R(q)$, which implies the claim.

As for the size, observe that a set in $\mathcal {F}$ is the union of at most three active sets, and each of these active sets contains at most 2k points. We conclude that a set of $\mathcal {F}$ contains at most 6k points.$\square$

The running time is dominated by O(n/k) queries, each of the following form: report the lowest O(k) points inside a given vertical slab. This is a generalization of range minimum queries, and known data structures [9] achieve O(k) query time after O(n) preprocessing time, assuming that the points are given in x-sorted order. The total construction time is $O(k\cdot n/k)=O(n)$. We thus get the following.

Restatement of Lemma 2.4 [23] Given a set $P$ of n points in the plane, lying above a horizontal line $\ell$, and a parameter k, one can compute a family $\mathcal {F}$ of at most $2\lceil {n/k}\rceil$ subsets of $P$, each of size at most 6k. The collection of sets can be computed in O(n) time if the x-coordinates have been pre-sorted. For any axis-aligned rectangle $R$ with its bottom edge lying on $\ell$, that contains less than k points of $P$, we have $P\cap R\subseteq Q$ for some $Q\in \mathcal {F}$.