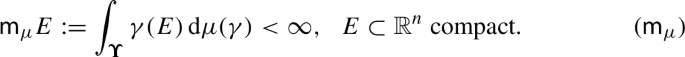On the ergodicity of interacting particle systems under number rigidity

Abstract

In this paper, we provide relations among the following properties:

• (a) the tail triviality of a probability measure $\mu$ on the configuration space ${\varvec{\Upsilon }}$;

• (b) the finiteness of a suitable $L^2$-transportation-type distance $\bar{\textsf {d} }_{\varvec{\Upsilon }}$;

• (c) the irreducibility of local ${\mu }$-symmetric Dirichlet forms on ${\varvec{\Upsilon }}$.

As an application, we obtain the ergodicity (i.e., the convergence to the equilibrium) of interacting infinite diffusions having logarithmic interaction and arising from determinantal/permanental point processes including $\text {sine}_{2}$, $\text {Airy}_{2}$, $\text {Bessel}_{\alpha , 2}$ ($\alpha \ge 1$), and $\text {Ginibre}$ point processes. In particular, the case of the unlabelled Dyson Brownian motion is covered. For the proof, the number rigidity of point processes in the sense of Ghosh–Peres plays a key role.

1 Introduction

The ergodicity (i.e., the convergence to the equilibrium) of interacting particle systems is one of the significant hypotheses supporting the foundation of statistical physics. In this paper, we study the ergodicity in terms of the theory of optimal transportation and of the theory of point processes. Configuration spaces. The configuration space ${\varvec{\Upsilon }}={\varvec{\Upsilon }}(X)$ over a locally compact Polish space X is the set of all locally finite point measures on X:

$$\begin{aligned} {\varvec{\Upsilon }}(X)\,{:=}\,\left\{ \gamma =\sum _{i=1}^N \delta _{x_i}: x_i\in X{,}\quad N \in {{\mathbb {N}}}_0\cup \left\{ +\infty \right\} {,}\quad \gamma (K)<\infty \quad K \Subset X \right\} {.}\end{aligned}$$

The space ${\varvec{\Upsilon }}$ is endowed with the vague topology $\tau _\text {v}$ defined by the duality of compactly supported continuous functions on X, and with a Borel probability measure ${\mu }$, understood as the law of a proper point process on X.

Interacting diffusions. A system of many interacting diffusions on the base space X can be thought of as a single diffusion on ${\varvec{\Upsilon }}$, provided the system does not condense too much by itself in the sense that every compact set in X contains only finitely many particles throughout the time evolution. There have been a large number of studies on a diffusion in ${\varvec{\Upsilon }}$, in particular, on a system of infinite stochastic differential equations on ${{\mathbb {R}}}^n$, written ‘formally’ as

$$\begin{aligned} \mathop {}\!\text {d}X_t^k= - \frac{\beta }{2}\nabla \Phi (X_t^k)\mathop {}\!\text {d}t - \frac{\beta }{2} \sum _{i \ne k} \nabla \Psi (X_t^k, X_t^i) \mathop {}\!\text {d}t + \mathop {}\!\text {d}B^k_t, \quad k \in {{\mathbb {N}}}{,}\end{aligned}$$

(1.1)

whereby $\Phi$ is a free potential, $\Psi$ is an interaction potential between particles, $\beta >0$ is a constant called inverse temperature, and $\left( B^k_t\right) _{k \in {{\mathbb {N}}}}$ are independent Brownian motions on ${{\mathbb {R}}}^n$. One approach addressing a solution to (1.1) is to construct a ${\mu }$-symmetric Dirichlet form $\big ({\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}}\big )$ on $L^2({\varvec{\Upsilon }}, {\mu })$, where ${\mu }$ is a (quasi-) Gibbs measure corresponding to the potentials $\Phi$ and $\Psi$, see, e.g., [4, 55] for Ruelle class potentials; [14, 26, 38, 40, 42, 50, 52, 54] for more general interactions including logarithmic potentials. Other approaches to tackle (1.1) have also been studied such as the construction of time-correlation functions in [16, 29, 35]; the construction of the unique strong solution to (1.1) in the case of the Dyson models in [53]. We refer the readers to Röckner [48] and Osada [41] and also to Dello Schiavo and Suzuki [14, Sect. 1.6] for more complete accounts and references.

Ergodicity. Regarding solutions to (1.1), the convergence to the equilibrium measure ${\mu }$ is characterised as the ergodicity of the $L^2({\mu })$-semigroup $\{S^{{\varvec{\Upsilon }}, {\mu }}_t\}$ corresponding to $\big ({\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, \mathcal F^{{\varvec{\Upsilon }}, {\mu }}}\big )$, which is defined as

$$\begin{aligned} \int _{{\varvec{\Upsilon }}} \biggl ( S^{{\varvec{\Upsilon }}, {\mu }}_t u - \int _{{\varvec{\Upsilon }}} u \mathop {}\!\text {d}{\mu }\biggr )^2 \mathop {}\!\text {d}{\mu }\xrightarrow {t \rightarrow \infty } 0, \quad u \in L^2({\mu }) {.}\end{aligned}$$

An equivalent characterisation is the irreducibility (also called the $L^2$-Liouville property) of $\big ({\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}}\big )$, i.e.,

$$\begin{aligned} \mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}(u)=0 \quad \implies \quad u \equiv \text { const.} \quad {\mu }\text {-a.e.} {.}\end{aligned}$$

See, e.g., Albeverio et al. [2, Proposition 2.3] for equivalent characterisations of the ergodicity. Up to now, there were only few known examples, where one could show the ergodicity of $\{S^{{\varvec{\Upsilon }}, {\mu }}_t\}$ in the case of infinite particle diffusions: one is a a class of Ruelle-type Gibbs measures with a compactly supported interaction potential and a small activity constant z [4, Corollary 6.2]; the other is a labelled particle system corresponding to the $\text {sine}_2$ process, which has been recently addressed in [44] by relying upon the arguments of strong solutions to (1.1) developed in [43]. The case of the unlabelled interacting diffusions corresponding to the $\text {sine}_2$ process (i.e., the unlabelled infinite Dyson Brownian motion) is addressed in this article as a particular case. The same case is dealt with in [37], which has been uploaded to arXiv almost at the same time as this article; however, Osada and Osada [37] deals with this particular case only.

Optimal transport theory on ${\varvec{\Upsilon }}$. If the base space X is equipped with a metric $\textsf {d}$, the configuration space ${\varvec{\Upsilon }}$ is equipped with the $L^2$-transportation (also called: $L^2$-Wasserstein, or $L^2$-Monge–Kantorovich–Rubinstein) distance

$$\begin{aligned} \textsf {d} _{\varvec{\Upsilon }}(\gamma , \eta ) \,{:=}\,\inf \left( \int _{X^{\scriptscriptstyle {\times 2}}} \textsf {d} ^2(x,y)\mathop {}\!\text {d}q(x,y)\right) ^{1/2}{,}\end{aligned}$$

where the infimum is taken over all measures $q$ on $X^{\scriptscriptstyle {\times 2}}$ with marginals $\gamma$ and $\eta$. As opposed to the case of the space of probability measures having finite second moment (i.e., the $L^2$-Wasserstein space), the function $\textsf {d} _{{\varvec{\Upsilon }}}$ is not a distance function since it attains the value $+\infty$ (e.g., when the total masses of $\gamma$ and $\eta$ are different, or the tails of $\gamma$ and $\eta$ are not close enough), and this happens often, in the sense that this occurs on sets of positive measure for any reasonable choice of a reference measure on ${\varvec{\Upsilon }}$. The function is, therefore, called extended distance. In this article, we use a variant of $\textsf {d} _{\varvec{\Upsilon }}$ defined as

$$\begin{aligned} \bar{\textsf {d} }_{\varvec{\Upsilon }}(\gamma , \eta ):= {\left\{ \begin{array}{ll} \textsf {d} _{\varvec{\Upsilon }}(\gamma , \eta ) \quad &{}\text {if } \gamma _{E^c}=\eta _{E^c} \text { for some bounded set }~E, \\ +\infty \quad &{}\text {otherwise} {.}\end{array}\right. } \end{aligned}$$

Recent studies have revealed that the $L^2$-transportation distance is the right object to describe geometry, analysis and stochastic analysis in ${\varvec{\Upsilon }}$ such as the curvature bounds on ${\varvec{\Upsilon }}$ [15, 17, 52], the consistency between metric measure geometry and Dirichlet forms [14, 46], characterisations of BV functions and sets of finite perimeters on ${\varvec{\Upsilon }}$ [8] and the integral Varadhan short-time asymptotic [15, 56].

Theory of point processes. A probability measure $\mu$ on ${\varvec{\Upsilon }}$ is said to be tail trivial $(\textsf {T})_{2.6}$ if (see Definition 2.6)

$$\begin{aligned} \mu (A) \in \{0, 1\}\quad \text {whenever } A \text { is a set in the tail } \sigma \text {-algebra} {.}\end{aligned}$$

From a probabilistic viewpoint, the tail triviality is in essence a form of 0–1 law. This property has been originally discussed in relation to phase transition of Gibbs states (i.e., non-uniqueness of Gibbs measures with a given potential) and it is equivalent to the extremality in the convex set of Gibbs measures with a given potential (see [21, Corollary 7.4]). The tail triviality has been extended also to determinantal/permanental point processes by Lyons [30] and Shirai and Takahashi [51] independently. Since then, it has been further developed for a wider class of determinantal/permantental processes both in continuous and discrete settings by various studies, see Example 2.7. A probability measure ${\mu }$ on ${\varvec{\Upsilon }}$ is said to be number rigid [Assumption $(\textsf {R})_{2.8}$] if the following holds ${\mu }$-almost surely for every bounded Borel set E:

$$\begin{aligned} \gamma \!\downharpoonright _{E^c} = \eta \!\downharpoonright _{E^c} \quad \implies \quad \gamma (E) = \eta (E){.}\end{aligned}$$

Namely, if two configurations $\gamma$ and $\eta$ coincide outside E, then the numbers of particles inside E for $\gamma$ and $\eta$ coincide. The study of this remarkable spatial correlation phenomenon has been initiated by Ghosh [22, 23] and Ghosh and Peres [25] for $\text {sine}_2$, $\text {Ginibre}$ and $\text {GAF}$ point processes and it has been further developed for other point processes, see Example 2.9 for further references.

Setting. In this article, we work in the following setting. Let $X={{\mathbb {R}}}^n$ be the n-dimensional Euclidean space and $\textsf {d}$ be the Euclidean distance on ${{\mathbb {R}}}^n$. Let $\left( B_r\right) _{r \in {{\mathbb {N}}}}$ be a monotone increasing sequence of convex compact domains covering ${{\mathbb {R}}}^n$ and $\textsf {m} _r$ be the Lebesgue measure restricted on $B_r$. For $E \subset {{\mathbb {R}}}^n$, define the projection $\text {pr} _{E}: {\varvec{\Upsilon }}\ni \gamma \mapsto \gamma _{E}:=\gamma \!\downharpoonright _{E}$ by the restriction of $\gamma$ on E. For a Borel probability measure ${\mu }$ on ${\varvec{\Upsilon }}$, define ${\mu }(\cdot \ |\ \cdot _{B_r^c}=\eta _{B_r^c})$ to be the regular conditional probability measure with respect to the $\sigma$-algebra $\sigma (\text {pr} _{B_r^c})$ conditioned to be $\eta \in {\varvec{\Upsilon }}$. Define the corresponding push-forward measure and its restriction on ${\varvec{\Upsilon }}^k(B_r):=\{\gamma \in {\varvec{\Upsilon }}(B_r): \gamma (B_r)=k\}$ by

$$\begin{aligned} {\mu }_r^\eta :=(\text {pr} _{B_r})_\#{\mu }(\cdot \ |\ \cdot _{B_r^c}=\eta _{B_r^c}) {,}\quad {\mu }_r^{\eta , k}:={\mu }_r^\eta \!\downharpoonright _{{{\varvec{\Upsilon }}^k(B_r)}}\!\!{.}\end{aligned}$$

We denote by $\pi _{\textsf {m} _r}$ the Poisson–Lebesgue measure on ${\varvec{\Upsilon }}(B_r)$ with intensity $\textsf {m} _r$ and by $\pi _{\textsf {m} _r}^k$ the restriction on ${\varvec{\Upsilon }}^k(B_r)$. Let $\Gamma ^{{\varvec{\Upsilon }}(B_r)}$ be the square field on ${\varvec{\Upsilon }}(B_r)$ defined as

$$\begin{aligned} \Gamma ^{{\varvec{\Upsilon }}(B_r)}(u):=\sum _{k=0}^\infty \Gamma ^{{\varvec{\Upsilon }}^k(B_r)}(u):=\sum _{k=0}^\infty \Bigl |\nabla ^{\odot k}u|_{{\varvec{\Upsilon }}^k(B_r)}\Bigr |^2 {,}\end{aligned}$$

where $\nabla ^{\odot k}$ is the symmetric product of the gradient operator $\nabla$ on ${{\mathbb {R}}}^n$.

List of assumptions. We say that ${\mu }$ satisfies

• strong conditional absolute continuity $(\textsf {CAC'})_{3.1}$ if

  $$\begin{aligned} {\mu }_r^{\eta , k} \sim \pi _{\textsf {m} _r}^k {,}\quad k \in \mathcal K_r^\eta :=\{k \in {{\mathbb {N}}}_0: {\mu }_r^\eta ({\varvec{\Upsilon }}^k(B_r))>0\} \quad r \in {{\mathbb {N}}}\quad {\mu }\text {-a.e. }~\eta \; \end{aligned}$$

• conditional closability $(\textsf {CC})_{3.2}$ if the form

  $$\begin{aligned} \mathcal {E}^{{\varvec{\Upsilon }}(B_r), {\mu }^{\eta }_{r}}(u) = \int _{{\varvec{\Upsilon }}(B_r)} \Gamma ^{{\varvec{\Upsilon }}(B_r)} (u) \mathop {}\!\text {d}{\mu }^{\eta }_{r} \end{aligned}$$

  is $L^2({\mu }_r^\eta )$-closable on a certain core (see Definition 3.2) for ${\mu }$-a.e. $\eta$ and every $r \in {{\mathbb {N}}}$. We denote its closure by $(\mathcal {E}^{{\varvec{\Upsilon }}(B_r), {\mu }^{\eta }_{r}}, \mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}(B_r), {\mu }^{\eta }_{r}}))$;

• conditional irreducibility $(\textsf {CI})_{4.1}$ if

  $$\begin{aligned} {\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }_r^\eta }(u) =0 {,}\quad u \in \mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}(B_r), {\mu }^{\eta }_{r}})\quad \implies \quad u|_{{\varvec{\Upsilon }}^k(B_r)} \equiv C_r^{\eta , k} \quad {\mu }_r^{\eta ,k} \text {-a.e.} {,}\end{aligned}$$

  for ${\mu }$-a.e. $\eta$, $r \in {{\mathbb {N}}}$, $k \in {\mathcal {K}}_r^\eta$, where $C_r^{\eta , k}$ is a constant depending on $r, \eta , k$.

Under $(\textsf {CAC'})_{3.1}$ and $(\textsf {CC})_{3.2}$, we construct a Dirichlet form $\big ({\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }},\mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})}\big )$ in Proposition 3.18. Let ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }} \subset \mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})$ be any closed subspace satisfying the Markovian property, i.e, ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ is a closed subspace in $\mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})$ and it is also closed under unit contraction [see (2.1)], which is called a Markovian subspace. We say that the form $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, \mathcal F^{{\varvec{\Upsilon }}, {\mu }})$ satisfies

• Rademacher-type property ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$ if

  $$\begin{aligned} \text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }) \subset {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}{,}\quad \Gamma ^{\varvec{\Upsilon }}(u) \le \text {Lip} _{\bar{\textsf {d} }_{\varvec{\Upsilon }}}(u)^2 {,}\end{aligned}$$

  where $\text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu })$ is the space of bounded $\bar{\textsf {d} }_{\varvec{\Upsilon }}$-Lipschitz ${\mu }$-measurable functions on ${\varvec{\Upsilon }}$;

• quasi-regularity $(\textsf {QR})_{3.20}$ if

  $$\begin{aligned} ({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}) \text { is quasi-regular in } ({\varvec{\Upsilon }}, \tau _\text {v} ){,}\end{aligned}$$

  see Sect. 2.2 for the definition of the quasi-regularity.

Main result. We define the following function associated with the $L^2$-transportation-type distance $\bar{\textsf {d} }_{{\varvec{\Upsilon }}}$:

$$\begin{aligned} \bar{\textsf {d} }^{\mu }_{\varvec{\Upsilon }}(\Xi , \Lambda ):={\mu }\text {-}{\mathop {\text { essinf}}\limits _{\gamma \in \Xi }}\,\inf _{\eta \in \Lambda }\bar{\textsf {d} }_{\varvec{\Upsilon }}(\gamma , \eta ) \quad \Xi , \Lambda \subset {\varvec{\Upsilon }}{.}\end{aligned}$$

We now state the main theorem, where we provide relations among the following three properties:

• (a) $\mu$ is tail trivial $(\textsf {T})_{2.6}$;

• (b) $\bar{\textsf {d} }_{{\varvec{\Upsilon }}}^{\mu }(A, B)<\infty$ whenever A is ${\mu }$-measurable, B is Borel and $\mu (A) \mu (B)>0$;

• (c) $(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }})$ is irreducible.

Theorem I

(Theorem  4.6) Let ${\mu }$ be a Borel probability measure on ${\varvec{\Upsilon }}$. Then,

• (b) $\implies$ (a);

• if $(\textsf {R})_{2.8}$ holds, then (a) $\implies$ (b).

Suppose that ${\mu }$ satisfies $(\textsf {CAC'})_{3.1}$ and $(\textsf {CC})_{3.2}$, and ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }} \subset \mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})$ is any closed Markovian subspace. Then the following hold.

• if $(\textsf {CI})_{4.1}$, $(\textsf {QR})_{3.20}$ and $(\textsf {R})_{2.8}$ hold, then (b) $\implies$ (c);

• if ${{\textsf {Rad}}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$ holds, then (c) $\implies$ (b).

We therefore have the following relation between the tail triviality and the irreducibility.

Corollary I

(Tail triviality and Irreducibility, Corollary 4.7) Let ${\mu }$ be a Borel probability measure on ${\varvec{\Upsilon }}$ satisfying $(\textsf {CAC'})_{3.1}$, $(\textsf {CC})_{3.2}$, and let ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }} \subset \mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})$ be any closed Markovian subspace. Then the following hold.

• If $(\textsf {CI})_{4.1}$, $(\textsf {QR})_{3.20}$ and $(\textsf {R})_{2.8}$ hold, then

  $$\begin{aligned} {\mu }\text { is tail trivial} \quad \implies \quad (\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}) \text { is irreducible} \; \end{aligned}$$

• If ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$ holds for ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$,

  $$\begin{aligned} (\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}) \text { is irreducible}\quad \implies \quad {\mu }\text { is tail trivial} {.}\end{aligned}$$

Applications. The first application of Theorem I as well as Corollary I is to considerably enlarge the list of (long-range) interactions for which one can prove the ergodicity of infinite particle systems. As an illustration, we will prove in Sect. 6 that $(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }})$ is irreducible (i.e., $\{S^{{\varvec{\Upsilon }}, {\mu }}_t\}$ is ergodic) for all the measures ${\mu }$ belonging to $\text {sine}_{2}$, $\text {Airy}_{2}$, $\text {Bessel}_{\alpha , 2}$ ($\alpha \ge 1$), and $\text {Ginibre}$ point processes. In particular, the semigroup $\{S^{{\varvec{\Upsilon }}, {\mu }}_t\}$ associated with the unlabelled Dyson Brownian motion is covered.

The second application is to show the finiteness of the $L^2$-transportation distance $\textsf {d} _{{\varvec{\Upsilon }}}(A, B)$, as well as of $\bar{\textsf {d} }_{{\varvec{\Upsilon }}}(A, B)$, between sets $A, B \subset {\varvec{\Upsilon }}$. As both $\textsf {d} _{{\varvec{\Upsilon }}}$ and $\bar{\textsf {d} }_{{\varvec{\Upsilon }}}$ take value $+\infty$ on sets of positive measure, it is not straightforward to answer the following geometric question:

$$\begin{aligned} \text {when are } \textsf {d} _{{\varvec{\Upsilon }}}(A, B) \text { and } \bar{\textsf {d} }_{{\varvec{\Upsilon }}}(A, B) \text { finite?} \end{aligned}$$

Theorem I tells us the finiteness of $\bar{\textsf {d} }_{{\varvec{\Upsilon }}}(A, B)$ (thus, also the finiteness of ${\textsf {d} }_{{\varvec{\Upsilon }}}(A, B)$ as $\textsf {d} _{\varvec{\Upsilon }}\le \bar{\textsf {d} }_{{\varvec{\Upsilon }}}$ by definition) only by checking the positivity of measures $\mu (A)\mu (B)>0$, due to the tail triviality $(\textsf {T})_{2.6}$ and the number rigidity $(\textsf {R})_{2.8}$ of ${\mu }$.

Comparisons with [4]. For a class of Gibbs measures or measures satisfying a certain integration-by-parts formula (denoted by (IbP1) and (IbP2) in [4, Theorem 6.2, 6.5]), relations between the ergodicity and the extremality of these measures have been studied. We compare our result with theirs in the following three points:

• Choice of a core. Albeverio et al. [4] studies Dirichlet forms whose core consists of cylinder functions while our Dirichlet forms have a flexibility for the choice of a core, which for instance allows us not only to choose cylinder functions, but also local functions as well as Lipschitz functions. This broadens the scope of applications significantly as cores of Dirichlet forms corresponding to long-range interactions constructed so far (e.g., [14, 26, 38, 40, 42, 50, 52]) are covered by our setting, but not necessarily covered by the setting of cylinder functions.

• Extremality vs.  tail-triviality. Albeverio et al. [4] proves that the extremality of a class of Gibbs measures implies the ergodicity. The concept of the extremality is equivalent to the tail triviality when Gibbs measures are considered, see [21, Corollary 7.4]. However, the extremality is not necessarily defined beyond Gibbs measures nor beyond measures satisfying (IbP1) and (IbP2), and many point processes coming from random matrix theory are not always described as Gibbs measures nor do they satisfy  (IbP1) and (IbP2). Rather they are described by determinantal or permanental structures or by a scaling limit of eigenvalue distributions of random matrices. In contrast, the tail triviality is a concept that can be defined for arbitrary point processes, because of which Theorem I can be applied also to the latter cases.

• Maximal domain vs. Rademacher-type property. Albeverio et al. [4] proves that the irreducibility of the maximal Dirichlet form implies the extremality of Gibbs measures, which corresponds to (c) $\implies$ (a) in Thereom I. We however only assume the Rademacher-type property ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$ of our Dirichlet form, whose domain is in general smaller than the maximal form. As the irreducibility of a larger domain is a stronger statement, Theorem I proves the extremality of Gibbs measures (as well as the tail triviality of general measures) under a weaker assumption.

Geometry and statistical physics. We would like to draw the reader’s attention to the fact that the relation between (b) and (c) in Theorem I provides a relation between the ergodicity of interacting diffusion processes and a quantitative information of the optimal transport distance, where the ergodicity is a statistical-physical concept, while the finiteness of the $L^2$-transportation distance between ${\mu }$-positive sets is a purely geometric concept of the extended metric measure space $({\varvec{\Upsilon }}, \bar{\textsf {d} }_{{\varvec{\Upsilon }}}, {\mu })$.

We close this introduction by providing an outlook on further improvements. The number rigidity $(\textsf {R})_{2.8}$ requires a strong spatial correlation to ${\mu }$, which is, however, not a necessary condition for the ergodicity. Indeed, Albeverio et al. [3, Theorem 4.3] proved the ergodicity for the Poisson measures, which obviously do not posses the number rigidity $(\textsf {R})_{2.8}$, since the laws of the Poisson point processes inside and outside bounded sets are independent. A challenging question is whether we can prove the ergodicity of Dirichlet forms for general tail trivial invariant measures without $(\textsf {R})_{2.8}$.

Organisation of the paper. In Sect. 2, we introduce necessary concepts and recall results used for the arguments in later sections. In Sect. 3, we construct Dirichlet forms on ${\varvec{\Upsilon }}$. In Sect. 4, we prove the main results. In Sect. 5, we give sufficient conditions to verify the main assumptions of Theorem I. In Sect. 6, we confirm that Theorem I can be applied to $\text {sine}_{2}$, $\text {Airy}_{2}$, $\text {Bessel}_{\alpha , 2}$ ($\alpha \ge 1$), and $\text {Ginibre}$ point processes.

2 Preliminaries

2.1 Numbers, tensors, function spaces

We write ${{\mathbb {N}}}:=\{1, 2, 3, \ldots \}$, ${{\mathbb {N}}}_0=\{0, 1, 2, \ldots \}$, $\overline{{{\mathbb {N}}}}:={{\mathbb {N}}}\cup \{+\infty \}$ and $\overline{{{\mathbb {N}}}}_0:={{\mathbb {N}}}_0 \cup \{+\infty \}$. The uppercase letter N is used for $N \in \overline{{{\mathbb {N}}}}_0$, while the lowercase letter n is used for $n \in {{\mathbb {N}}}_0$. We shall adhere to the following conventions:

• the superscript ${\square }^{\scriptscriptstyle {\times N}}$ (the subscript $\square _{\scriptscriptstyle {\times N}}$) denotes N-fold product objects;

• the superscript ${\square }^{\scriptscriptstyle {\otimes N}}$ (the subscript $\square _{\scriptscriptstyle {\otimes N}}$) denotes N-fold tensor objects;

• the superscript ${\square }^{\scriptscriptstyle {\odot N}}$ (the subscript $\square _{\scriptscriptstyle {\odot N}}$) denotes N-fold symmetric tensor objects.

Let $(X, \tau )$ be a topological space with $\sigma$-finite Borel measure $\nu$. A subset $A \subset X$ is called a domain if A is open and connected. A subset $A \subset X$ is called a closed domain if A is the union of a domain and all of its limit points. A subset $A \subset X$ is called a compact domain if A is a closed domain and compact. Throughout this article, we shall use the following symbols and phrases:

• (a) $L^p(\nu )$ $(1 \le p \le \infty )$ for the space of $\nu$-equivalence classes of real-valued functions u so that $|u|^p$ is $\nu$-integrable when $1 \le p<\infty$, and u is $\nu$-essentially bounded when $p=\infty$; The $L^p(\nu )$-norm is denoted by $\Vert u\Vert ^p_p=\Vert u\Vert ^p_{L^p(\nu )}:=\int _X |u|^p \mathop {}\!\text {d}\nu$ for $1 \le p <\infty$, and $\Vert u\Vert _\infty =\Vert u\Vert _{L^\infty (\nu )}:={{\,\textrm{esssup}\,}}_X |u|$; When $p=2$, the inner-product is denoted by $(u, v)_{2}=(u, v)_{L^2(\nu )}:=\int _X uv \mathop {}\!\text {d}\nu$;

• (b) $L^p_s(\nu ^{\otimes n}):=\{u \in L^p(\nu ^{\otimes n}): u\ \text {is symmetric}\}$ where u is said to be symmetric if $u(x_1, \ldots , x_k)=u(x_{\sigma (1)}, \ldots , x_{\sigma (k)})$ for every element $\sigma$ in the k-symmetric group ${\mathfrak {S}}_k$;

• (c) ${\mathscr {B}}(X, \tau )$ for the Borel $\sigma$-algebra; ${\mathscr {B}}(X, \tau )^{\nu }$ for the completion of ${\mathscr {B}}(X, \tau )$ with respect to $\nu$; ${\mathscr {B}}(X, \tau )^*$ for the universal $\sigma$-algebra, i.e., the intersection of ${\mathscr {B}}(X)^{\rho }$ among all Borel probability measures $\rho$ on X (we do not specify the topology and simply write ${\mathscr {B}}(X), {\mathscr {B}}(X)^{\nu }, {\mathscr {B}}(X)^*$ where the topology is clear from the context); Measurable functions with respect to ${\mathscr {B}}(X)$, ${\mathscr {B}}(X)^{\nu }$, ${\mathscr {B}}(X)^*$ are called Borel measurable, $\nu$-measurable, universally measurable respectively.

• (d) $C_b(X)$ for the space of $\tau$-continuous bounded functions on X; if X is locally compact, $C_0(X)$ denotes the space of $\tau$-continuous and compactly supported functions on X; $C_0^\infty ({{\mathbb {R}}}^n)$ for the space of compactly supported smooth functions on the n-dimensional Euclidean space ${{\mathbb {R}}}^n$;

• (e) ${{\textbf {1}}}_{A}$ for the indicator function on A, i.e., ${{\textbf {1}}}_{A}(x)=1$ if $x \in A$ and ${{\textbf {1}}}_A(x)=0$ otherwise; $\delta _x$ for the Dirac measure at x, i.e., $\delta _x(A)=1$ if $x \in A$ and $\delta _x(A)=0$ otherwise;

• (f) A sequence $(B_r)_{r \in {{\mathbb {N}}}}$ of subsets in X is called an exhaustion if $B_r \subset B_{r'}$ whenever $r \le r'$ and $\cup _{r \in {{\mathbb {N}}}} B_r = X$; If $B_r$ possesses a certain property P for every $r \in {{\mathbb {N}}}$ (e.g., $B_r$ is compact, convex, or a domain), we call it P exhaustion (e.g., compact exhaustion, compact convex exhaustion, domain exhaustion).

2.2 Dirichlet form

We refer the reader to Ma and Röckner [33] and Bouleau and Hirsch [5] for this subsection. Throughout this article, a Hilbert space always means a separable Hilbert space with inner product $(\cdot , \cdot )_H$ taking values in ${{\mathbb {R}}}$.

Dirichlet form. Given a bilinear form $(Q,\mathscr {D}(Q))$ on a Hilbert space H, we write

$$\begin{aligned} Q(u)\,{:=}\,Q(u,u) \,\,\text {,}\;\,\quad Q_\alpha (u,v)\,{:=}\,Q(u,v)+\alpha (u, v)_H\,\,\text {,}\;\,\alpha >0{.}\end{aligned}$$

Let $(X, \Sigma , \nu )$ be a $\sigma$-finite measure space. A symmetric Dirichlet form on $L^2(\nu )$ is a non-negative definite densely defined closed symmetric bilinear form $(Q,\mathscr {D}(Q))$ on $L^2(\nu )$ satisfying the Markov property (i.e., the closedness under unit contraction)

$$\begin{aligned} u_0\,{:=}\,0\vee u \wedge 1\in \mathscr {D}(Q) \quad \text {and} \quad Q(u_0)\le Q(u)\,\,\text {,}\;\,\quad u\in \mathscr {D}(Q){.}\end{aligned}$$

(2.1)

We note that (2.1) is equivalent to the closedness under normal contraction [18, Theorem  1.4.1]. Namely, if $u \in \mathscr {D}(Q)$ and v is a normal contraction of u, then $v \in \mathscr {D}(Q)$. Here v is a normal contraction of u if there exists a $\nu$-measurable version $\tilde{v}$ (resp. $\tilde{u}$) of v (resp. u) so that $|\tilde{v}(x)| \le |\tilde{u}(x)|$ for every $x \in X$ and $|\tilde{v}(x)-\tilde{v}(y)| \le |\tilde{u}(x)-\tilde{u}(y)|$ for every $x, y \in X$.

Throughout this article, Dirichlet form always means symmetric Dirichlet form. A subspace ${\mathcal {F}} \subset \mathscr {D}(Q)$ is called Markovian subspace if (2.1) holds for every $u \in {\mathcal {F}}$. If not otherwise stated, $\mathscr {D}(Q)$ is always regarded as a Hilbert space with norm

$$\begin{aligned} \left\Vert {\,\cdot \,}\right\Vert _{\mathscr {D}(Q)}\,{:=}\,Q_1({\,\cdot \,})^{1/2}:=\sqrt{Q({\,\cdot \,})+\left\Vert {\,\cdot \,}\right\Vert _{L^2(\nu )}^2}{.}\end{aligned}$$

To distinguish Dirichlet forms defined in different base spaces with different reference measures, we write $Q^{X, \nu }$ to specify the base space X and the reference measure $\nu$. We denote the extended domain of $\mathscr {D}(Q)$ by $\mathscr {D}(Q)_e$ defined as

$$\begin{aligned} \mathscr {D}(Q)_e:=&\{u: X \rightarrow {{\mathbb {R}}}:\ \nu \text {-measurable,}\ |u|<\infty \nu \text {-a.e.} \nonumber \\&\exists \{u_n\}_{n \in {{\mathbb {N}}}}\subset \mathscr {D}(Q) \ Q\text {-Cauchy s.t. } u_n \rightarrow u \ \nu \text {-a.e.}\} \end{aligned}$$

(2.2)

Square field. A Dirichlet form $(Q, \mathscr {D}(Q))$ admits square field $\Gamma$ if there exists a dense subspace $H \subset \mathscr {D}(Q) \cap L^\infty (\nu )$ so that for every $u \in H$, there exists $v \in L^1(\nu )$ so that

$$\begin{aligned} 2Q(uh, u) -Q(h, u^2) = \int _X h v \mathop {}\!\text {d}\nu \quad h \in \mathscr {D}(Q) \cap L^\infty (\nu ) {.}\end{aligned}$$

In this case, v is unique, and denoted by $\Gamma (u)$. The square field $\Gamma$ can be uniquely extended to an operator on $\mathscr {D}(Q) \times \mathscr {D}(Q) \rightarrow L^1(\nu )$ [5, Theorem I.4.1.3].

Resolvent, semigroup and generator. We refer the reader to [33, Chapter I, Sect. 2] for this paragraph. Let $(Q, \mathscr {D}(Q))$ be a symmetric closed form on a Hilbert space H. The infinitesimal generator $(A, \mathscr {D}(A))$ corresponding to $(Q, \mathscr {D}(Q))$ is the unique densely defined closed operator on H satisfying the following integration-by-parts formula:

$$\begin{aligned} -(u, Av)_{H}=Q(u, v) \quad \forall u \in \mathscr {D}(Q),\ v\in \mathscr {D}(A) {.}\end{aligned}$$

The resolvent operator. $\{R_\alpha \}_{\alpha > 0}$ is the unique bounded linear operator on H satisfying

$$\begin{aligned} Q_\alpha (R_\alpha u, v) = (u, v)_{H} \quad \forall u \in H \quad v \in \mathscr {D}(Q) {.}\end{aligned}$$

The semigroup. $\{T_t\}_{t > 0}$ is the unique bounded linear operator on H satisfying

$$\begin{aligned} G_\alpha u = \int _{0}^\infty e^{-\alpha t} T_{t}u \mathop {}\!\text {d}t \quad u \in H{.}\end{aligned}$$

Irreducibility. Let $(Q, \mathscr {D}(Q))$ be a Dirichlet from on $L^2(\nu )$ and $\{T_t\}_{t>0}$ be the corresponding $L^2(\nu )$-semigroup. A $\nu$-measurable set $A \subset X$ is $\{T_t\}_{t>0}$-invariant if $T_t({{\textbf {1}}}_A u) = {{\textbf {1}}}_A T_t u$ for every $u \in L^2(\nu )$ and $t>0$. We say that $\{T_t\}_{t>0}$ is irreducible if every $\{T_t\}_{t>0}$-invariant set A satisfies either $\nu (A)=0$ or $\nu (X \setminus A)=0$. If the total mass of $\nu$ is finite, the following are equivalent (see e.g., [2, Proposition 2.3]):

• (i) $\{T_t\}_{t>0}$ is irreducible;

• (ii) $(Q, \mathscr {D}(Q))$ possesses the $L^2$-Liouville property:

  $$\begin{aligned} Q(u)=0 \quad \implies \quad u \equiv \text { const.} \quad \nu \text {-a.e.} \ ; \end{aligned}$$

  (2.3)

• (iii) $\{T_t\}_{t>0}$ is ergodic:

  $$\begin{aligned} \int _X \biggl ( T_t u - \int _{X} u \mathop {}\!\text {d}\nu \biggr )^2 \mathop {}\!\text {d}\nu \xrightarrow {t \rightarrow \infty } 0, \quad u \in L^2(\nu ) {.}\end{aligned}$$

Following the convention of Albeverio et al. [2], we call $(Q, \mathscr {D}(Q))$ irreducible if (2.3) holds and $\nu (X)<\infty$.

Locality. Let $(Q, \mathscr {D}(Q))$ be a Dirichlet form on $L^2(\nu )$. It is called local if for every $F, G \in C_c^\infty ({{\mathbb {R}}})$ and $u \in \mathscr {D}(Q)$,

$$\begin{aligned} \text { supp}[F] \cap \text { supp}[G] = \emptyset \implies Q(F_0\circ u, G_0\circ u)=0 {,}\end{aligned}$$

where $F_0(x):=F(x)-F(0)$ and $G_0(x):=G(x)-G(0)$ (see [5, Definition 5.1.2 in Chapter I]).

Quasi-notion. Let $(X, \tau )$ be a Polish space and $\nu$ be a $\sigma$-finite Borel measure on X and $(Q, \mathscr {D}(Q))$ be a Dirichlet form on $L^2(\nu )$. For any $A\in {\mathscr {B}}(X)$, define

$$\begin{aligned} \mathscr {D}(Q)_A\,{:=}\,\left\{ u\in \mathscr {D}(Q): u= 0 \ \nu \text {-a.e. on}\ X\setminus A\right\} . \end{aligned}$$

A sequence $\left( A_n\right) _{n \in {{\mathbb {N}}}}\subset {\mathscr {B}}(X)$ is a Borel nest if $\cup _{n \in {{\mathbb {N}}}} \mathscr {D}(Q)_{A_n}$ is dense in $\mathscr {D}(Q)$. A closed (resp. compact) nest is a Borel nest consisting of closed (resp. compact) sets. A set $N\subset X$ is exceptional if there exists a closed nest $\left( F_n\right) _{n \in {{\mathbb {N}}}}$ so that $N\subset X{\setminus } \cup _n F_n$. It is a standard fact that any exceptional set N is $\nu$-negligible (see, e.g., [33, Exe. 2.3]). A property $(p_x)$ depending on $x\in X$ holds quasi-everywhere (in short: q.e.) if there exists a polar set N so that $(p_x)$ holds for every $x\in X\setminus N$. For a closed nest $\left( F_n\right) _{n \in {{\mathbb {N}}}}$, define

$$\begin{aligned} C(\left( F_n\right) _{n \in {{\mathbb {N}}}}):=\{u: A \rightarrow {{\mathbb {R}}}: \cup _{n \ge 1} F_n \subset A \subset X,\ u|_{F_n} \ \text {is continuous for every } n \in {{\mathbb {N}}}\} {.}\end{aligned}$$

A function u defined quasi-everywhere on X is quasi-continuous if there exists a closed nest $\left( F_n\right) _{n \in {{\mathbb {N}}}}$ so that $u \in C(\left( F_n\right) _{n \in {{\mathbb {N}}}})$.

A Dirichlet form $(Q, \mathscr {D}(Q))$ on $L^2(\nu )$ is quasi-regular if the following conditions hold:

• (QR1) there exists a compact nest $(A_n)_{n \in {{\mathbb {N}}}}$;

• (QR2) there exists a dense subspace ${\mathcal {D}} \subset \mathscr {D}(Q)$ so that every $u \in {\mathcal {D}}$ has a quasi-continuous $\nu$-version $\tilde{u}$;

• (QR3) there exists $\{u_n: n \in {{\mathbb {N}}}\} \subset \mathscr {D}(Q)$ and a polar set $N \subset X$ so that every $u_n$ has a quasi-continuous $\nu$-version $\tilde{u}_n$ and $\{\tilde{u}_n: n \in {{\mathbb {N}}}\}$ separates points in $X \setminus N$.

Maximal function. Let $(Q, \mathscr {D}(Q))$ be a local Dirichlet form on $L^2(\nu )$ with ${{\textbf {1}}} \in \mathscr {D}(Q)$ having a square field $\Gamma ^{Q}$. Define

$$\begin{aligned} {\mathbb {D}}_0:=\{u \in \mathscr {D}(Q) \cap L^\infty (\nu ): \Gamma ^{Q}(u) \le 1\} {.}\end{aligned}$$

By Hino and Ramírez [27, Theorem  1.2], for a $\nu$-positive measure set $A \subset X$, there exists a unique $\nu$-measurable function $\bar{\textsf {d}}_{\nu , A}$ called maximal function satisfying

• (a) $\bar{\textsf {d}}_{\nu , A} \wedge c \in {\mathbb {D}}_0$ for every $c \ge 0$;

• (b) $\bar{\textsf {d}}_{\nu , A} =0$ $\nu$-a.e. on A;

• (c) $\bar{\textsf {d}}_{\nu , A}$ is the largest function satisfying the previous two properties, i.e., if there exists a function v satisfying (a) and (b), then

  $$\begin{aligned} v \le \bar{\textsf {d}}_{\nu , A} \quad \nu \text {-a.e.} {.}\end{aligned}$$

  (2.4)

2.3 Extended metric space

Let X be any non-empty set. A function $\textsf {d} :X^{\scriptscriptstyle {\times 2}}\rightarrow [0,\infty ]$ is called an extended distance if it is symmetric, satisfying the triangle inequality and not vanishing outside the diagonal in $X^{{\scriptscriptstyle {\times 2}}}$, i.e. $\textsf {d} (x,y)=0$ iff $x=y$; a distance if it is finite, i.e., $\textsf {d} (x, y)<\infty$ for every $x, y \in X$. A space X equipped with an extended distance $\textsf {d}$ is called an extended metric space $(X, \textsf {d} )$. Let $\nu$ be a measure on a $\sigma$-algebra $\Sigma$ on X. Define

$$\begin{aligned} \textsf {d} (\cdot , B):=\inf _{y \in B}\textsf {d} (\cdot , y) {,}\quad \textsf {d} ^\nu (A, B):=\nu \text {-}{\mathop {\text { essinf}}\limits _{A}}\,\inf _{y \in B}\textsf {d} (\cdot , y){,}\quad A, B \in \Sigma ^\nu {,}\end{aligned}$$

(2.5)

the latter of which is well-defined whenever $\inf _{y \in B}\textsf {d} (\cdot , y)$ is $\nu$-measurable (i.e., $\Sigma ^\nu$-measurable).

Lipschitz algebra. A function $f:X\rightarrow {{\mathbb {R}}}$ is called $\textsf {d}$-Lipschitz if there exists a constant $L>0$ so that

$$\begin{aligned} \big | u(x)-u(y)\big |\le L\, \textsf {d} (x,y) \,\,\text {,}\;\,\quad x,y\in X {.}\end{aligned}$$

(2.6)

The smallest constant L satisfying (2.6) is called the (global) Lipschitz constant of u, denoted by $\text {Lip} _\textsf {d} {(u)}$. For any non-empty set $A\subset X$, define $\text {Lip} (A,\textsf {d} )$, resp. $\text {Lip}_b(A,\textsf {d} )$ as the space of all $\textsf {d}$-Lipschitz functions, resp. bounded $\textsf {d}$-Lipschitz functions on A. For simplicity of notation, we omit specifying the base space X and simply write  $\text {Lip} (\textsf {d} )\,{:=}\,\text {Lip} (X,\textsf {d} )$, resp. $\text {Lip}_b(\textsf {d} )\,{:=}\,\text {Lip}_b(X,\textsf {d} )$ if no confusion can occur. Define also $\text {Lip} ^\alpha (\textsf {d} ):=\{u \in \text {Lip} (\textsf {d} ): \text {Lip} _{\textsf {d} }(u) \le \alpha \}$ and $\text {Lip} ^\alpha _b(\textsf {d} ):=\text {Lip} ^\alpha (\textsf {d} ) \cap \text {Lip}_b(\textsf {d} ).$ For a measure $\nu$ on X defined on a $\sigma$-algebra $\Sigma$ and a topology $\tau$ on X, we define respectively

$$\begin{aligned}&\text {Lip} (\textsf {d} , \nu ):=\{u \in \text {Lip} (\textsf {d} ): u \text { is } \nu \text {-measurable}\} {,}\\&\text {Lip} (\textsf {d} , \tau ):=\{u \in \text {Lip} (\textsf {d} ): u \text { is } \tau \text {-continuous}\} {,}\end{aligned}$$

and we further define $\text {Lip} _b(\textsf {d} , \nu )$, $\text {Lip} ^\alpha _b(\textsf {d} , \nu )$, $\text {Lip} _b(\textsf {d} , \tau )$ and $\text {Lip} ^\alpha _b(\textsf {d} , \tau )$ for the corresponding subspaces of $\nu$-measurable functions (resp. $\tau$-continuous functions).

Let $\nu$ be a finite measure on X and let $(Q, \mathscr {D}(Q))$ be a local Dirichlet form on $L^2(\nu )$ having a square field $\Gamma ^{Q}$. We say that the Rademacher-type property holds for $\text {Lip} _b({\textsf {d} }, \nu )$ (resp. $\text {Lip} _b({\textsf {d} }, \tau )$) if

respectively.

2.4 Configuration space

A configuration on a locally compact Polish space X is an ${\overline{{{\mathbb {N}}}}}_0$-valued Radon measure $\gamma$ on X, which is expressed by $\gamma = \sum _{i=1}^N \delta _{x_i}$ for $N \in \overline{{{\mathbb {N}}}}_0$, where $x_i \in X$ for every i and $\gamma \equiv 0$ when $N=0$. The configuration space ${\varvec{\Upsilon }}={\varvec{\Upsilon }}(X)$ is the space of all configurations over X. The space ${\varvec{\Upsilon }}$ is equipped with the vague topology $\tau _\text {v}$, i.e., the topology generated by the duality of the space $C_0(X)$ of continuous functions with compact support. We write the restriction $\gamma _A\,{:=}\,\gamma \!\downharpoonright _{A}$ for $A \in {\mathscr {B}}(X)$ and the restriction map is denoted by

$$\begin{aligned} \gamma \longmapsto \text {pr} _A(\gamma ):=\gamma _{A}{.}\end{aligned}$$

(2.7)

The N-particle configuration space is denoted by

$$\begin{aligned} {\varvec{\Upsilon }}^N(X)\ \,{:=}\,&\ \left\{ \gamma \in {\varvec{\Upsilon }}: \gamma (X)=N\right\} {,}\quad N\in {\overline{{{\mathbb {N}}}}}_0 {.}\end{aligned}$$

Let ${\mathfrak {S}}_k$ be the k-symmetric group. It can be readily seen that the k-particle configuration space ${\varvec{\Upsilon }}^k$ is isomorphic to the quotient space $X^{\times k}/{\mathfrak {S}}_k$:

$$\begin{aligned} {\varvec{\Upsilon }}^k(X)\cong X^{\odot k}:=X^{\times k}/{\mathfrak {S}}_k {,}\quad k \in {{\mathbb {N}}}_0{.}\end{aligned}$$

(2.8)

The associated projection map from $X^{\times k}$ to the quotient space $X^{\times k}/{\mathfrak {S}}_k$ is denoted by $\textsf {P} _k$. For $\eta \in {\varvec{\Upsilon }}$ and $E\in {\mathscr {B}}(X)$, we define

$$\begin{aligned} {\varvec{\Upsilon }}_E^\eta :=\{\gamma \in {\varvec{\Upsilon }}: \gamma _{E^c}=\eta _{E^c}\} {.}\end{aligned}$$

(2.9)

Conditional probability. For a Borel probability measure $\mu$ on ${\varvec{\Upsilon }}$ and $E \in {\mathscr {B}}(X)$,

$$\begin{aligned} \mu (\ \cdot \ | \ \text {pr} _{E^c}(\cdot )=\eta _{E^c}) \end{aligned}$$

denotes the regular conditional probability of $\mu$ conditioned to be $\eta \in {\varvec{\Upsilon }}$ with respect to the $\sigma$-algebra generated by the projection map $\gamma \in {\varvec{\Upsilon }}\mapsto \text {pr} _{E}(\gamma )=\gamma _{E} \in {\varvec{\Upsilon }}(E)$ (see e.g., [14, Definition 3.32]). Let $\mu _{E}^\eta$ be the probability measure on ${\varvec{\Upsilon }}(E)$ defined as

$$\begin{aligned} \mu _{E}^\eta :=(\text {pr} _{E})_\#\mu (\ \cdot \ | \ \text {pr} _{E^c}(\cdot )=\eta _{E^c}) {,}\end{aligned}$$

(2.10)

and its restriction on the k-particle configuration space ${\varvec{\Upsilon }}^k(E)$ is denoted by $\mu _{E}^{\eta , k}:=\mu _{E}^\eta \!\downharpoonright _{{\varvec{\Upsilon }}^k(E)}$.

Remark 2.1

The conditional probability $\mu (\ \cdot \ | \ \text {pr} _{E^c}(\cdot )=\eta _{E^c})$ is a probability measure on ${\varvec{\Upsilon }}$ whose support is contained in ${\varvec{\Upsilon }}_E^\eta$ while $\mu _E^\eta$ is a probability measure on ${\varvec{\Upsilon }}(E)$. For every fixed $\eta$, we identify the two of them without loss of information in the sense that

$$\begin{aligned} \text {pr} _{E}: {\varvec{\Upsilon }}_E^\eta \rightarrow {\varvec{\Upsilon }}(E) \ \text {is a bi-measure-preserving bijection} {.}\end{aligned}$$

(2.11)

Namely, the projection map $\text {pr} _{E}$ is bijective with the inverse map $\text {pr} _{E}^{-1}$ defined as $\text {pr} ^{-1}_{E}(\gamma ):=\gamma +\eta _{E^c}$, and both $\text {pr} _{E}$ and $\text {pr} _{E}^{-1}$ are measure-preserving between the two measures $\mu (\ \cdot \ | \ \text {pr} _{E^c}(\cdot )=\eta _{E^c})$ and $\mu _{E}^\eta$.

For a measurable function $u:{\varvec{\Upsilon }}\rightarrow {{\mathbb {R}}}$, $E \in {\mathscr {B}}(X)$ and $\eta \in {\varvec{\Upsilon }}$, we define

$$\begin{aligned} u_{E}^\eta (\gamma )\,{:=}\,u(\gamma +\eta _{E^\text {c}}) \quad \gamma \in {\varvec{\Upsilon }}(E) {.}\end{aligned}$$

(2.12)

By the property of the conditional probability, it is straightforward to see that for every $u \in L^1(\mu )$,

$$\begin{aligned} \int _{{\varvec{\Upsilon }}} u \mathop {}\!\text {d}{\mu }= \int _{{\varvec{\Upsilon }}} \left[ \int _{{\varvec{\Upsilon }}(E)} u_{E}^\eta \mathop {}\!\text {d}{\mu }^\eta _E \right] \mathop {}\!\text {d}{\mu }(\eta ) {.}\end{aligned}$$

(2.13)

See, e.g., [14, Proposition 3.44]. For $\Omega \in {\mathscr {B}}({\varvec{\Upsilon }})$, $E \in {\mathscr {B}}(X)$ and $\eta \in {\varvec{\Upsilon }}$, define $\Omega _E^\eta \subset {\varvec{\Upsilon }}(E)$ as

$$\begin{aligned} \Omega _E^\eta :=\{\gamma \in {\varvec{\Upsilon }}(E): \gamma +\eta _{E^c} \in \Omega \} {.}\end{aligned}$$

(2.14)

By applying the disintegration formula (2.13) to $u={{\textbf {1}}}_{\Omega }$, we obtain

$$\begin{aligned} {\mu }(\Omega )=\int _{{\varvec{\Upsilon }}} {\mu }_E^\eta (\Omega _E^\eta ) \mathop {}\!\text {d}{\mu }(\eta ) {.}\end{aligned}$$

(2.15)

Poisson measure. Let $(X, \tau , \nu )$ be a locally compact Polish space endowed with a non-atomic Radon measure $\nu$ satisfying $\nu (X)<\infty$. The Poisson measure $\pi _{\nu }$ on ${\varvec{\Upsilon }}(X)$ with intensity $\nu$ is defined in terms of the symmetric tensor measures $\{\nu ^{\odot k}: k \in {{\mathbb {N}}}\}$ as follows:

$$\begin{aligned}&\pi _{\nu }(\cdot ):=\,e^{-\nu (X)}\sum _{k=1}^\infty \nu ^{\odot k}\bigl (\cdot \cap {{\varvec{\Upsilon }}^k(X)}\bigr )=e^{-\nu (X)}\sum _{k=1}^\infty \frac{1}{k!}(\textsf {P} _k)_\#\nu ^{\otimes k}\bigl (\cdot \cap {{\varvec{\Upsilon }}^k(X)} \bigr ) {,}\nonumber \\&\pi ^k_{\nu }(\cdot ):=\pi _{\nu }(\cdot )\!\downharpoonright _{{\varvec{\Upsilon }}^{k}(X)} {.}\end{aligned}$$

(2.16)

In the case that $\nu$ is $\sigma$-finite, take an exhaustion $\left( B_r\right) _{r \in {{\mathbb {N}}}}$ so that $\nu (B_r)<\infty$ for every $r \in {{\mathbb {N}}}$. The Poisson (random) measure ${\pi }_\nu$ with intensity $\nu$ is the unique probability measure on ${\varvec{\Upsilon }}$ satisfying

$$\begin{aligned} (\text {pr} _{B_r})_\sharp {\pi }_\nu ={\pi }_{\nu _{B_r}}{,}\quad r\in {{\mathbb {N}}}{.}\end{aligned}$$

(2.17)

The measure ${\pi }_\nu$ does not depend on the choice of $\left( B_r\right) _{r \in {{\mathbb {N}}}}$.

$L^2$-transportation distance. Let $(X, \textsf {d} )$ be a locally compact complete separable metric space. For $i=1,2$ let $\textsf {proj} ^i:X^{\times 2}\rightarrow X$ denote the projection to the $i^\text {th}$ coordinate for $i=1,2$. For $\gamma ,\eta \in {\varvec{\Upsilon }}$, let $\text {Cpl} (\gamma ,\eta )$ be the set of all couplings of $\gamma$ and $\eta$, i.e.,

$$\begin{aligned} \text {Cpl} (\gamma ,\eta )\,{:=}\,\left\{ q\in {\mathscr {M}}(X^{{\scriptscriptstyle {\times 2}}}) :\textsf {proj} ^1_\sharp q=\gamma {,}\quad \textsf {proj} ^2_\sharp q=\eta \right\} {.}\end{aligned}$$

(2.18)

Here ${\mathscr {M}}(X^{{\scriptscriptstyle {\times 2}}})$ denotes the space of all Radon measures on $X^{{\scriptscriptstyle {\times 2}}}$. The $L^2$-transportation extended distance on ${\varvec{\Upsilon }}(X)$ is

$$\begin{aligned} \textsf {d} _{{\varvec{\Upsilon }}}(\gamma ,\eta )\,{:=}\,\inf _{q\in \text {Cpl} (\gamma ,\eta )} \left( \int _{X^{\times 2}} \textsf {d} ^2(x,y) \mathop {}\!\text {d}q(x,y)\right) ^{1/2}{,}\quad \inf {\varnothing }=+\infty {.}\end{aligned}$$

(2.19)

We refer the reader to e.g., [14, Proposition 4.27, 4.29, Theorem  4.37, Proposition 5.12] and [46, Lemma 4.1, 4.2] for details regarding the $L^2$-transportation extended distance $\textsf {d} _{{\varvec{\Upsilon }}}$ and examples of $\textsf {d} _{{\varvec{\Upsilon }}}$-Lipschitz functions. It is important to note that $\textsf {d} _{\varvec{\Upsilon }}$ is an extended distance in general, attaining the value $+\infty$. Moreover, $\textsf {d} _{\varvec{\Upsilon }}$ is lower semi-continuous with respect to the product vague topology $\tau _\text {v} ^{\times 2}$ but not necessarily $\tau _\text {v} ^{\times 2}$-continuous.

We introduce a variant of the $L^2$-transportation extended distance, called $L^2$-transportation-type extended distance $\bar{\textsf {d} }_{\varvec{\Upsilon }}$ defined as

$$\begin{aligned} \bar{\textsf {d} }_{\varvec{\Upsilon }}(\gamma , \eta ):= {\left\{ \begin{array}{ll} \textsf {d} _{\varvec{\Upsilon }}(\gamma , \eta ) \quad &{}\text {if } \gamma _{B_r^c}=\eta _{B_r^c} \text { for some } r>0\ , \\ +\infty \quad &{}\text {otherwise} {,}\end{array}\right. } \end{aligned}$$

(2.20)

where $(B_r)_{r \in {{\mathbb {N}}}}$ is a compact exhaustion. The definition (2.20) does not depend on the choice of an exhaustion. By definition, $\textsf {d} _{\varvec{\Upsilon }}\le \bar{\textsf {d} }_{\varvec{\Upsilon }}$ on ${\varvec{\Upsilon }}$ and $\textsf {d} _{\varvec{\Upsilon }}= \bar{\textsf {d} }_{\varvec{\Upsilon }}$ on ${\varvec{\Upsilon }}(E)$ for every compact subset $E\subset X$. In particular, we have

$$\begin{aligned} \text {Lip} ({\varvec{\Upsilon }}, \textsf {d} _{\varvec{\Upsilon }}) \subset \text {Lip} ({\varvec{\Upsilon }}, \bar{\textsf {d} }_{\varvec{\Upsilon }}) {,}\quad \text {Lip} _{\bar{\textsf {d} }_{\varvec{\Upsilon }}}(u) \le \text {Lip} _{\textsf {d} _{\varvec{\Upsilon }}}(u){,}\quad u \in \text {Lip} ({\varvec{\Upsilon }}, \textsf {d} _{\varvec{\Upsilon }}){.}\end{aligned}$$

(2.21)

It can be readily seen readily that

$$\begin{aligned} \bar{\textsf {d} }_{\varvec{\Upsilon }}(\gamma , \eta ) <\infty \quad \iff \quad \gamma _{B_r^c}=\eta _{B_r^c} {,}\gamma (B_r)=\eta (B_r) \quad \text {for some } r>0{.}\end{aligned}$$

(2.22)

Proposition 2.2

The map $\bar{\textsf {d} }_{{\varvec{\Upsilon }}}: {\varvec{\Upsilon }}^{\times 2} \rightarrow {{\mathbb {R}}}$ is ${\mathscr {B}}({\varvec{\Upsilon }}^{\times 2}, \tau _\text {v} ^{\times 2})$-measurable.

Proof

According to (2.20), we can write

$$\begin{aligned} \bar{\textsf {d} }_{\varvec{\Upsilon }}= \textsf {d} _{\varvec{\Upsilon }}{{\textbf {1}}}_{\text {A}} + \infty {{\textbf {1}}}_{\text {A}^c} {,}\end{aligned}$$

(2.23)

where

$$\begin{aligned} \text {A}:=\{(\gamma , \eta ) \in {\varvec{\Upsilon }}^{\times 2}: \ \exists r>0 \ \text {s.t.}\ \gamma _{B_r^c}=\eta _{B_r^c} \}=\cup _{r \in {{\mathbb {N}}}}\{(\gamma , \eta ) \in {\varvec{\Upsilon }}^{\times 2}: \ \gamma _{B_r^c}=\eta _{B_r^c} \} {.}\end{aligned}$$

(2.24)

Let $\text {A}_r:=\{(\gamma , \eta ) \in {\varvec{\Upsilon }}^{\times 2}: \ \gamma _{B_r^c}=\eta _{B_r^c} \}$, which is $\tau _\text {v} ^{\times 2}$-closed. As $\text {A}$ is a countable union of closed sets, we obtain $\text {A}\in {\mathscr {B}}({\varvec{\Upsilon }}^{\times 2}, \tau _\text {v} ^{\times 2})$. Noting that $\textsf {d} _{\varvec{\Upsilon }}$ is $\tau _\text {v} ^{\times 2}$-lower semi-continuous ( [46, (vi) Lem.4.1], see also [14, (vii) Proposition 4.27]), the function $\textsf {d} _{\varvec{\Upsilon }}$ is in particular ${\mathscr {B}}({\varvec{\Upsilon }}^{\times 2}, \tau _\text {v} ^{\times 2})$-measurable, thus, the expression (2.23) concludes the ${\mathscr {B}}({\varvec{\Upsilon }}^{\times 2}, \tau _\text {v} ^{\times 2})$-measurablility of $\bar{\textsf {d} }_{\varvec{\Upsilon }}$. $\square$

The following universal measurability of the distance function from a set will be used in Theorem 4.6.

Proposition 2.3

Let $\Lambda \in {\mathscr {B}}({\varvec{\Upsilon }}, \tau _\text {v} )$ and

$$\begin{aligned} \bar{\textsf {d} }_{\varvec{\Upsilon }}(\gamma , \Lambda ):=\inf _{\eta \in \Lambda } \bar{\textsf {d} }_{\varvec{\Upsilon }}(\gamma , \eta ){.}\end{aligned}$$

(2.25)

The map ${\varvec{\Upsilon }}\ni \gamma \mapsto \bar{\textsf {d} }_{\varvec{\Upsilon }}(\gamma , \Lambda )$ is universally measurable (i.e., ${\mathscr {B}}({\varvec{\Upsilon }}, \tau _\text {v} )^*$-measurable).

Proof

It suffices to show that every sub-level set $\Lambda _r:=\{\gamma \in {\varvec{\Upsilon }}: \bar{\textsf {d} }_{\varvec{\Upsilon }}(\gamma , \Lambda ) \le r\}$ is universally measurable. Define $I: {\varvec{\Upsilon }}(X^{\times 2}) \rightarrow {{\mathbb {R}}}$ as

$$\begin{aligned} \alpha \mapsto \int _{X^{\times 2}} \textsf {d} (x, y) \mathop {}\!\text {d}\alpha (x, y) {.}\end{aligned}$$

The map I is lower semi-continuous in ${\varvec{\Upsilon }}(X^{\times 2})$ ([46, (i) Lemma 4.1], see also [14, (ii) Proposition 4.27]). The following set $\text {B}_r$ is, therefore, closed in ${\varvec{\Upsilon }}(X^{\times 2})$:

$$\begin{aligned} \text {B}_r:=\Bigl \{\alpha \in {\varvec{\Upsilon }}(X^{\times 2}): I(\alpha ) \le r^2\Bigr \}{.}\end{aligned}$$

Noting ${\varvec{\Upsilon }}^{\times 2} \subset {\varvec{\Upsilon }}(X^{\times 2})$ is a Borel subset, the Borel set $\text {A}\in {\mathscr {B}}({\varvec{\Upsilon }}^{\times 2})$ defined in (2.24) can be thought of as a Borel set in ${\varvec{\Upsilon }}(X^{\times 2}).$ Define $\tilde{\text {B}}_r:=\text {B}_r \cap \text {A}\in {\mathscr {B}}({\varvec{\Upsilon }}(X^{\times 2}))$. By (2.20),

$$\begin{aligned} \Lambda _r=\{\textsf {proj} ^1_\#\alpha : \alpha \in \tilde{\text {B}}_r{,}\textsf {proj} ^2_\#\alpha \in \Lambda \}=\textsf {proj} ^1_\#\Bigl (\tilde{\text {B}}_r \cap (\textsf {proj} ^2_\#)^{-1}(\Lambda )\Bigr ) {,}\end{aligned}$$

(2.26)

where $\textsf {proj} ^i$ has been defined just before (2.18). As the map $\textsf {proj} ^{i}_\#: {\varvec{\Upsilon }}(X^{\times 2}) \rightarrow {\varvec{\Upsilon }}$ is continuous, the set $\tilde{\text {B}}_r \cap (\textsf {proj} ^2_\#)^{-1}(\Lambda )$ is a Borel set in ${\varvec{\Upsilon }}(X^{\times 2})$. Noting the fact that a continuous image of a Borel set in a Polish space is Suslin (e.g., [28, Theorem  21.10]), we conclude by (2.26) that $\Lambda _r$ is a Suslin set in ${\varvec{\Upsilon }}$, therefore, universally measurable (see, e.g., [19, 431B Corollary]). $\square$

We present a lemma, which states that the operation $(\cdot )_{E}^\eta$ defined in (2.12) maps from $\text {Lip} ({\varvec{\Upsilon }}, \bar{\textsf {d} }_{\varvec{\Upsilon }})$ to $\text {Lip} ({\varvec{\Upsilon }}(E), \textsf {d} _{\varvec{\Upsilon }})$ and contracts Lipschitz constants.

Lemma 2.4

Let $u \in \text {Lip} ({\varvec{\Upsilon }}, \bar{\textsf {d} }_{\varvec{\Upsilon }})$ and $E \subset X$ be a Polish subset. Then, $u_{E}^\eta \in \text {Lip} ({\varvec{\Upsilon }}(E), \textsf {d} _{\varvec{\Upsilon }})$ and

$$\begin{aligned} \text {Lip} _{\textsf {d} _{\varvec{\Upsilon }}}(u_E^\eta ) \le \text {Lip} _{\bar{\textsf {d} }_{\varvec{\Upsilon }}}(u) {,}\quad \eta \in {\varvec{\Upsilon }}{.}\end{aligned}$$

(2.27)

Proof

Let $\gamma , \zeta \in {\varvec{\Upsilon }}(E)$ and $\eta \in {\varvec{\Upsilon }}$. Then,

$$\begin{aligned} |u_E^\eta (\gamma )-u_E^\eta (\zeta )|&=|u(\gamma +\eta _{E^c})-u(\zeta +\eta _{E^c})| \le \text {Lip} _{\bar{\textsf {d} }_{\varvec{\Upsilon }}}(u) \bar{\textsf {d} }_{\varvec{\Upsilon }}(\gamma +\eta _{E^c}, \zeta +\eta _{E^c})\\&= \text {Lip} _{\bar{\textsf {d} }_{\varvec{\Upsilon }}}(u) \textsf {d} _{\varvec{\Upsilon }}(\gamma , \zeta ) {.}\end{aligned}$$

The proof is completed. $\square$

Remark 2.5

By the same proof, one can replace $\bar{\textsf {d} }_{\varvec{\Upsilon }}$ with $\textsf {d} _{\varvec{\Upsilon }}$ in the statement of Lemma 2.4 and obtain

$$\begin{aligned} \text {Lip} _{\textsf {d} _{\varvec{\Upsilon }}}(u_E^\eta ) \le \text {Lip} _{{\textsf {d} }_{\varvec{\Upsilon }}}(u) {,}\quad \eta \in {\varvec{\Upsilon }}{.}\end{aligned}$$

(2.28)

2.5 Tail triviality

Let $\left( B_r\right) _{r \in {{\mathbb {N}}}}$ be a compact exhaustion. Let $\sigma (\text { pr}_{B_r^c})$ denote the $\sigma$-algebra generated by the projection map ${\varvec{\Upsilon }}\ni \gamma \mapsto \text { pr}_{B_r^c}(\gamma )=\gamma _{B_r^c} \in {\varvec{\Upsilon }}(B_r^c)$. We set ${\mathscr {T}}({\varvec{\Upsilon }}):=\cap _{r \in {{\mathbb {N}}}}\sigma (\text { pr}_{B_r^c})$ and call it tail $\sigma$-algebra. By the definition of the tail $\sigma$-algebra ${\mathscr {T}}({\varvec{\Upsilon }})$, every non-empty set $\Xi \in {\mathscr {T}}({\varvec{\Upsilon }})$ satisfies the following condition:

$$\begin{aligned} \Xi ={\varvec{\Upsilon }}(B_r) + \text { pr}_{B_r^c}(\Xi ), \quad r \in {{\mathbb {N}}}{.}\end{aligned}$$

(2.29)

For a set $\Xi \subset {\varvec{\Upsilon }}$, define ${\mathcal {T}}_{B_r}({\Xi }):=(\text { pr}_{B_r^c})^{-1}\circ \text { pr}_{B_r^c}(\Xi )$. By definition, $\Xi \subset {\mathcal {T}}_{B_r}(\Xi )$, and ${\mathcal {T}}_{B_r}({\Xi }) \subset {\mathcal {T}}_{B_{r'}}({\Xi })$ whenever $r\le r'$. Define the tail set of $\Xi$ by

$$\begin{aligned} {\mathcal {T}}(\Xi ):=\cup _{r \in {{\mathbb {N}}}} {\mathcal {T}}_{B_{r}}({\Xi }) {.}\end{aligned}$$

(2.30)

The tail set ${\mathcal {T}}(\Xi )$ of $\Xi$ does not depend on the choice of the exhaustion $\left( B_{r}\right)$. It can be readily shown that ${\mathcal {T}}(\Xi ) \in {\mathscr {T}}({\varvec{\Upsilon }})$ and $\Xi \subset {\mathcal {T}}({\Xi })$.

Definition 2.6

(Tail triviality) A Borel probability measure $\mu$ on ${\varvec{\Upsilon }}(X)$ is called tail trivial $(\textsf {T})_{2.6}$ if

Example 2.7

The tail triviality has been verified for a wide class of point processes.

• (i) (Determinantal point processes) Let X be a locally compact Polish space. Then, all determinantal point processes whose kernel are locally trace-class positive contraction satisfy the tail triviality (see [31, Theorem 2.1] and [7, 36, 51]). In particular, $\text {sine}_2$, $\text {Bessel}_{\alpha ,2}$, $\text {Airy}_2$ and Ginibre point processes are tail trivial.

• (ii) (Extremal Gibbs measure) A canonical Gibbs measure $\mu$ is tail trivial iff $\mu$ is extremal (see [21, Corollary 7.4]). In particular, Gibbs measures of the Ruelle type with sufficiently small activity constants are extremal (see [47, Theorem 5.7]).

2.6 Number-rigidity

The following definition of the number rigidity on the configuration space ${\varvec{\Upsilon }}$ over a locally compact Polish space X is an adaptation of the number rigidity originally introduced by Ghosh–Peres [25] in the setting of the configuration space over the complex plane.

Definition 2.8

(Number rigidity: cf. Ghosh–Peres [25, Theorem 1]) A Borel probability measure ${\mu }$ on ${\varvec{\Upsilon }}$ has the number rigidity (in short: $(\textsf {R})_{2.8}$) if, for every bounded Borel set $E\subset X$, there exists $\Omega \subset {\varvec{\Upsilon }}$ so that ${\mu }(\Omega )=1$ and, for every $\gamma , \eta \in \Omega$

Example 2.9

The number rigidity has been verified for a variety of point processes: Ginibre and GAF [25], $\text {sine}_\beta$ [23, Theorem 4.2], [10, 13], $\text {Airy}$,  $\text {Bessel}$, and $\text {Gamma}$ [9], and Pfaffian [6] point processes. We refer the readers also to the survey [24].

3 Construction of Dirichlet forms

In this section, we construct a Dirichlet form on ${\varvec{\Upsilon }}={\varvec{\Upsilon }}({{\mathbb {R}}}^n)$. Let $\left( B_r\right) _{r \in {{\mathbb {N}}}}$ be a compact convex domain exhaustion in ${{\mathbb {R}}}^n$. We first construct a Dirichlet form on ${\varvec{\Upsilon }}(B_r)$ called conditioned form with invariant measure ${\mu }_{B_r}^\eta$. We then lift it onto ${\varvec{\Upsilon }}$, which is called truncated form, whose gradient operator is truncated on $B_r$. Finally we take the monotone limit of the truncated forms as $r\rightarrow \infty$ and construct the limit Dirichlet form on ${\varvec{\Upsilon }}$.

Notation. Hereinafter, we use the following notation.

• $\textsf {m}$, $\textsf {m} _r$ for the Lebesgue measure on ${{\mathbb {R}}}^n$ and its restriction on $B_r$ respectively;

• $\textsf {d} (x, y):=|x-y|$ for the Euclidean distance in ${{\mathbb {R}}}^n$;

• ${\mu }_r^\eta :={\mu }_{B_r}^\eta$ for a probability measure ${\mu }$ on ${\varvec{\Upsilon }}$, defined in (2.10);

• $u_r^{\eta }:=u_{B_r}^\eta$ for a function $u: {\varvec{\Upsilon }}\rightarrow {{\mathbb {R}}}$, defined in (2.12).

3.1 Conditioned Dirichlet forms on $\varvec{\Upsilon }(B_r)$

Let $W^{1,2}_s(\textsf {m} ^{\otimes k}_r)$ be the space of $\textsf {m} ^{\otimes k}_r$-classes of symmetric (1, 2)-Sobolev functions on the product space $B_r^{\times k}$, i.e.,

$$\begin{aligned} W^{1,2}_s(\textsf {m} ^{\otimes k}_r):=\biggl \{u \in L^2_s(\textsf {m} ^{\otimes k}_{r}): \int _{B_r^{\times k}} |\nabla ^{\otimes k} u|^2 \mathop {}\!\text {d}\textsf {m} ^{\otimes k}_{r} <\infty \biggr \} {,}\end{aligned}$$

where $\nabla ^{\otimes k}$ denotes the distributional derivative on $({{\mathbb {R}}}^n)^{\times k}$: $\nabla ^{\otimes k}u:=(\partial _1 u, \ldots , \partial _ku)$. As the space $W^{1,2}_s(\textsf {m} ^{\otimes k}_r)$ consists of symmetric functions, the projection $\textsf {P} _k: B_r^{\times k} \rightarrow {\varvec{\Upsilon }}^k(B_r) \cong B_r^{\times k} /{\mathfrak {S}}_k$ acts on $W^{1,2}_s(\textsf {m} ^{\otimes k}_r)$ and the resulting quotient space is denoted by $W^{1,2}(\textsf {m} _r^{\odot k})$:

$$\begin{aligned} W^{1,2}(\textsf {m} ^{\odot k}_r):=\biggl \{u \in L^2(\textsf {m} ^{\odot k}_{r}): \int _{{\varvec{\Upsilon }}^k(B_r)} |\nabla ^{\odot k} u|^2 \mathop {}\!\text {d}\textsf {m} ^{\odot k}_{r} <\infty \biggr \} {,}\end{aligned}$$

where $\nabla ^{\odot k}$ is the quotient operator of the distributional gradient operator $\nabla ^{\otimes k}$ through the projection $\textsf {P} _k$ and $\textsf {m} _r^{\odot k}$ is the symmetric product measure defined as

$$\begin{aligned} \textsf {m} _r^{\odot k}:=\frac{1}{k!} (\textsf {P} _k)_\#\textsf {m} _r^{\otimes k} {.}\end{aligned}$$

Definition 3.1

(Conditional absolute continuity) A Borel probability measure ${\mu }$ on ${\varvec{\Upsilon }}$ is conditionally absolutely continuous (to ${\pi }_\textsf {m}$) if

Let ${\mathcal {K}}_r^\eta :=\{k \in {{\mathbb {N}}}_0: {\mu }_r^\eta ({\varvec{\Upsilon }}^k(B_r))>0\}$. We say that ${\mu }$ satisfies $(\textsf {CAC'})_{3.1}$ if

For $u, v: {\varvec{\Upsilon }}(B_r) \rightarrow {{\mathbb {R}}}$ satisfying $u|_{{\varvec{\Upsilon }}^{k}(B_r)}, v|_{{\varvec{\Upsilon }}^{k}(B_r)} \in W^{1,2}(\textsf {m} _r^{\odot k})$ for every $k \in {{\mathbb {N}}}$, set

$$\begin{aligned} \Gamma ^{{\varvec{\Upsilon }}(B_r)}(u, v)&:= \sum _{k=0}^\infty \Bigl \langle \nabla ^{\odot k} u|_{{\varvec{\Upsilon }}^{k}(B_r)}, \nabla ^{\odot k} v|_{{\varvec{\Upsilon }}^{k}(B_r)}\Bigr \rangle {,}\quad \Gamma ^{{\varvec{\Upsilon }}(B_r)}(u):=\Gamma ^{{\varvec{\Upsilon }}(B_r)}(u, u) {.}\end{aligned}$$

(3.1)

Let us define the following algebra of functions:

$$\begin{aligned} \text { LIP}_b({\varvec{\Upsilon }}(B_r), \textsf {d} _{\varvec{\Upsilon }}):= & {} \{u: {\varvec{\Upsilon }}(B_r) \rightarrow {{\mathbb {R}}}\ \text {bounded}:\\ {}{} & {} u|_{{\varvec{\Upsilon }}^k(B_r)} \in \text {Lip} _b({\varvec{\Upsilon }}^k(B_r), \textsf {d} _{\varvec{\Upsilon }}){,}k \in {{\mathbb {N}}}\}{.}\end{aligned}$$

Note that the Lipschitz constant $\text {Lip} _{\textsf {d} _{\varvec{\Upsilon }}}(u|_{{\varvec{\Upsilon }}^k(B_r)})$ may not be bounded in k for $u \in \text { LIP}_b({\varvec{\Upsilon }}(B_r), \textsf {d} _{\varvec{\Upsilon }})$, thus

$$\begin{aligned} \text {Lip} _b({\varvec{\Upsilon }}(B_r), \textsf {d} _{\varvec{\Upsilon }}) \subsetneq \text { LIP}_b({\varvec{\Upsilon }}(B_r), \textsf {d} _{\varvec{\Upsilon }}) {.}\end{aligned}$$

The quadratic functional associated with ${\mu }^{\eta , k}_{r}$ is denoted by

$$\begin{aligned}&\mathcal {E}^{{\varvec{\Upsilon }}(B_{r}), {\mu }^{\eta , k}_{r}}(u) \,{:=}\,\int _{{\varvec{\Upsilon }}(B_{r})} |\nabla ^{\odot k}u |^2\mathop {}\!\text {d}{\mu }^{\eta , k}_{r} {,}\end{aligned}$$

(3.2a)

$$\begin{aligned}&\mathcal {E}^{{\varvec{\Upsilon }}(B_{r}), {\mu }^\eta _{r}}(u) \,{:=}\,\int _{{\varvec{\Upsilon }}(B_r)} \Gamma ^{{\varvec{\Upsilon }}(B_r)}(u) \mathop {}\!\text {d}{\mu }_r^\eta {,}\quad u \in \text { LIP}_b({\varvec{\Upsilon }}(B_{r}), \textsf {d} _{{\varvec{\Upsilon }}}){.}\end{aligned}$$

(3.2b)

Definition 3.2

(Conditional closability) Let ${\mu }$ be a Borel probability measure on ${\varvec{\Upsilon }}$ satisfying $(\textsf {CAC})_{3.1}$. We say that ${\mu }$ satisfies the conditional closability $(\textsf {CC})_{3.2}$ if the form

is closable on $L^2\big ({{\varvec{\Upsilon }}(B_r),{\mu }^\eta _{r}}\big )$ for every $r \in {{\mathbb {N}}}$ and ${\mu }$-a.e. $\eta \in {\varvec{\Upsilon }}$.

Remark 3.3

We give two remarks on $(\textsf {CC})_{3.2}$.

• (i) The Rademacher theorem on convex domains in the Euclidean space implying

  $$\begin{aligned}&\text {Lip} _b({\varvec{\Upsilon }}(B_{r}), {\textsf {d} }_{{\varvec{\Upsilon }}})|_{{\varvec{\Upsilon }}^k(B_r)} \subset W^{1,\infty }(\textsf {m} ^{\odot k}_{r}){,}\nonumber \\&\quad \Bigl |\nabla ^{\odot k}u|_{{\varvec{\Upsilon }}^k(B_r)}\Bigr | \le \text {Lip} _{\textsf {d} _{\varvec{\Upsilon }}}(u) \quad \text {on} \quad {\varvec{\Upsilon }}^k(B_r){,}\quad k \in {{\mathbb {N}}}{,}\end{aligned}$$

  (3.3)

  the following bound follows:

  $$\begin{aligned} \Gamma ^{{\varvec{\Upsilon }}(B_r)}(u) \le \text {Lip} _{\textsf {d} _{\varvec{\Upsilon }}}(u)^2{,}\quad u \in \text {Lip} _b({\varvec{\Upsilon }}(B_{r}), \textsf {d} _{{\varvec{\Upsilon }}}) {,}\end{aligned}$$

  (3.4)

  which shows

  $$\begin{aligned} \text {Lip} _b({\varvec{\Upsilon }}(B_r), \textsf {d} _{\varvec{\Upsilon }}) \subset \text { LIP}_b({\varvec{\Upsilon }}(B_{r}), \textsf {d} _{{\varvec{\Upsilon }}}) \cap \{u: {\varvec{\Upsilon }}(B_r) \rightarrow {{\mathbb {R}}}: \mathcal {E}^{{\varvec{\Upsilon }}(B_{r}), {\mu }^\eta _{r}}(u)<\infty \} {.}\end{aligned}$$

  thus, the form (3.2b) is well-posed on $\text {Lip} _b({\varvec{\Upsilon }}(B_r), \textsf {d} _{\varvec{\Upsilon }})$.

• (ii) A simple sufficient condition for $(\textsf {CC})_{3.2}$ is

  $$\begin{aligned} \phi _{r}^{\eta , k}:=\frac{\mathop {}\!\text {d}{\mu }_{r}^\eta }{\mathop {}\!\text {d}\pi _{\textsf {m} _{r}}}\Big |_{{\varvec{\Upsilon }}^{k}(B_{r})} \in C_b({\varvec{\Upsilon }}^{k}(B_{r})) \quad r, k \in {{\mathbb {N}}}{.}\end{aligned}$$

  In this case, the closability of the form $\mathcal {E}^{{\varvec{\Upsilon }}(B_{r}), {\mu }^{\eta , k}_{r}}$ is a standard consequence of the Hamza-type argument by Ma and Röckner [32] and Fukushima [20]. For an accessible reference, see, e.g., [33, pp. 44–45]. The closability of the form $\mathcal {E}^{{\varvec{\Upsilon }}(B_{r}), {\mu }^\eta _{r}}$ then follows as it is a countable sum of the closable forms $\mathcal {E}^{{\varvec{\Upsilon }}(B_{r}), {\mu }^{\eta , k}_{r}}$ over $k \in {{\mathbb {N}}}_0$ (see e.g., [33, Proposition 3.7]). All examples we shall discuss in Sect. 6 fall into this case.

Definition 3.4

(Conditioned form) Under $(\textsf {CAC})_{3.1}$ and $(\textsf {CC})_{3.2}$, the closure of (3.2b) is called conditioned form and denoted by

$$\begin{aligned} \big ({\mathcal {E}^{{\varvec{\Upsilon }}(B_r), {\mu }^\eta _{r}},\mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}(B_r), {\mu }^\eta _{r}})}\big ) {.}\end{aligned}$$

(3.5)

The corresponding $L^2({\mu }^\eta _r)$-resolvent operator and the $L^2({\mu }^\eta _r)$-semigroup are denoted respectively by

$$\begin{aligned} \bigl \{G_{\alpha }^{{\varvec{\Upsilon }}(B_r), {\mu }^\eta _r}\bigr \}_{\alpha> 0} \quad \text {and} \quad \bigl \{T^{{\varvec{\Upsilon }}(B_r), {\mu }^\eta _r}_t\bigr \}_{t > 0}{.}\end{aligned}$$

The square field $\Gamma ^{{\varvec{\Upsilon }}(B_r)}$ naturally extends to the domain $\mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}(B_r), {\mu }^\eta _{r}})$, which is denoted by the same symbol $\Gamma ^{{\varvec{\Upsilon }}(B_r)}$.

3.2 Truncated Dirichlet forms

In this subsection, we construct the truncated Dirichlet form on ${\varvec{\Upsilon }}$. We start this section by giving an operator mapping functions on ${\varvec{\Upsilon }}$ to functions on ${{\mathbb {R}}}^n$.

Definition 3.5

([34, Lemma 1.2], see also [14, Lemma 2.16]) For $u: {\varvec{\Upsilon }}\rightarrow {{\mathbb {R}}}$, define ${\mathcal {U}}_{\gamma , x}(u): {{\mathbb {R}}}^n \rightarrow {{\mathbb {R}}}$ by

$$\begin{aligned} {\mathcal {U}}_{\gamma , x}(u)(y):=u\big ({\mathbb {1}_{X\setminus \left\{ x\right\} }\cdot \gamma + \delta _y}\big )-u\big ({\mathbb {1}_{X\setminus \left\{ x\right\} }\cdot \gamma }\big ) {,}\quad \gamma \in {\varvec{\Upsilon }},\quad x \in \gamma {.}\end{aligned}$$

(3.6)

We now define a square field operator on ${\varvec{\Upsilon }}$ truncated to particles inside $B_r$.

Definition 3.6

(Truncated square field on ${\varvec{\Upsilon }}$) Whenever $\nabla {\mathcal {U}}_{\gamma , x}(u)|_{B_r}$ makes sense $\textsf {m} _r$-a.e.  for $u:{\varvec{\Upsilon }}\rightarrow {{\mathbb {R}}}$, the truncated square field $\Gamma ^{\varvec{\Upsilon }}_r$ is defined as

$$\begin{aligned} \Gamma ^{{\varvec{\Upsilon }}}_r(u)(\gamma ):= \sum _{x\in \gamma _{B_r}} |\nabla {\mathcal {U}}_{\gamma , x}(u)|^2(x){.}\end{aligned}$$

(3.7)

Thanks to Lemma A.1, Formula (3.7) is well-defined for ${\mu }$-a.e. $\gamma$. Indeed, as the weak gradient $\nabla {\mathcal {U}}_{\gamma , x}(u)$ is well-defined pointwise on a measurable set $\Sigma \subset B_r$ with $\textsf {m} _r(\Sigma ^c)=0$, by applying Lemma A.1, Formula (3.7) is well-defined on a set $\Omega (r)$ of ${\mu }$-full measure.

Based on the truncated square field $\Gamma ^{\varvec{\Upsilon }}_r$, we introduce the truncated form on ${\varvec{\Upsilon }}$ defined on a certain core.

Definition 3.7

(Core) Let $\{{\mathcal {C}}_r\}_{r \in {{\mathbb {N}}}}$ be a sequence of algebras of $\mu$-classes of measurable functions so that ${\mathcal {C}}_r \supset {\mathcal {C}}_{r'}$ for $r \le r'$ and the following hold for every $r \in {{\mathbb {N}}}$:

• (a) ${\mathcal {C}}_r \subset L^\infty (\mu )$ and ${\mathcal {C}}_r \subset L^2({\mu })$ is dense;

• (b) $\Gamma ^{{\varvec{\Upsilon }}}_r(u)$ is well-defined ${\mu }$-a.e. for every $u \in {\mathcal {C}}_r$;

• (c) the following integral is well-defined and finite for every $u \in {\mathcal {C}}_r$:

  $$\begin{aligned} u_{r}^\eta \in \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\eta }) \quad {\mu }\text {-a.e.}~\eta {,}\quad {\mathcal {E}}^{{\varvec{\Upsilon }}, \mu }_r(u):= \int _{\varvec{\Upsilon }}{\mathcal {E}}^{{\varvec{\Upsilon }}(B_r), \mu _r^\eta }(u_{r}^\eta ) \mathop {}\!\text {d}{\mu }(\eta ) <\infty {,}\end{aligned}$$

  (3.8)

  and $({\mathcal {E}}^{{\varvec{\Upsilon }}, \mu }_r, {\mathcal {C}}_r)$ is Markovian.

Example 3.8

We have several choices of $\{{\mathcal {C}}_r\}_{r \in {{\mathbb {N}}}}$. In each of the following examples, we take a certain common core ${\mathcal {C}}$ and take ${\mathcal {C}}_r = {\mathcal {C}}$ for every $r>0$.

• (a) Cylinder functions. Take ${\mathcal {C}}_r={\mathcal {C}}=\mathcal {F}^{\varvec{\Upsilon }}\mathcal {C}^\infty _b$ for every $r \in {{\mathbb {N}}}$, where $\mathcal {F}^{\varvec{\Upsilon }}\mathcal {C}^\infty _b$ is the space of cylinder functions defined as

  $$\begin{aligned} \mathcal {F}^{\varvec{\Upsilon }}\mathcal {C}^\infty _b\,{:=}\,\left\{ \begin{matrix} u:{\varvec{\Upsilon }}\rightarrow {{\mathbb {R}}}: u=F\bigl (\gamma (f_1), \gamma (f_2), \ldots , \gamma (f_k)\bigr ) {,}F\in \mathcal {C}^\infty _b({{\mathbb {R}}}^k){,}\\ f_1,\dotsc , f_k\in C_0^\infty ({{\mathbb {R}}}^n){,}\quad k\in {{\mathbb {N}}}_0 \end{matrix}\right\} {,}\end{aligned}$$

  (3.9)

  where $\gamma (f):=\int _{{{\mathbb {R}}}^n} f \mathop {}\!\text {d}\gamma$. We say that ${\mu }$ satisfies $(\textsf {m} _{\mu })$ if the intensity measure $\textsf {m} _{\mu }$ is locally finite, viz.

  

  Under $(\textsf {m} _{\mu })$, $(\textsf {CAC})_{3.1}$ and $(\textsf {CC})_{3.2}$, all the conditions of Definition 3.7 are satisfied (see [14, Lemma 2.15, Proposition 3.45, Theorem  3.48]).

• (b) Lipschitz functions. Take ${\mathcal {C}}_r ={\mathcal {C}}$ for every $r \in {{\mathbb {N}}}$, where ${\mathcal {C}}$ is equal to either

  $$\begin{aligned} \text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }){,}\text {Lip} _b(\textsf {d} _{\varvec{\Upsilon }}, {\mu }){,}\text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }) \cap C_b(\tau _\text {v} ){,}\text {or} \ \ \text {Lip} _b(\textsf {d} _{\varvec{\Upsilon }}, {\mu }) \cap C_b(\tau _\text {v} ) {.}\end{aligned}$$

  (3.10)

  As $\text {Lip} _b(\textsf {d} _{\varvec{\Upsilon }}, {\mu }) \subset L^2(\mu )$ is dense (e.g., [1, Proposition 4.1]) and $\text {Lip} _b({\textsf {d} }_{\varvec{\Upsilon }}, {\mu }) \subset \text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu })$ by (2.21), $\text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }) \subset L^2({\mu })$ is dense as well. The density of $\text {Lip} _b({\textsf {d} }_{\varvec{\Upsilon }}, {\mu }) \cap C_b(\tau _\text {v} )$ follows e.g., by [49, Lemma 2.27] combined with the fact [14, Proposition 4.30] that $({\varvec{\Upsilon }}, \textsf {d} _{\varvec{\Upsilon }}, \tau _\text {v} )$ is an extended metric-topological space. This therefore implies the density of $\text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }) \cap C_b(\tau _\text {v} )$ as well. Thanks to the Lipschitz contraction property of $(\cdot )_r^\eta$ by Lemma 2.4 and of ${\mathcal {U}}_{\gamma , x}$ [52, Lemma 4.1] and by (3.4), the formula (3.8) readily follows. The Markov property follows from the Markov property of $({\mathcal {E}}^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\eta }, \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\eta }))$ by (3.8). Thus, all the conditions of Definition 3.7 are satisfied under $(\textsf {CAC})_{3.1}$ and $(\textsf {CC})_{3.2}$.

• (c) $C^1$-local functions (e.g. [11, Definition II.8]) Let $\Omega ^*:=\{(x, \gamma ) \in {{\mathbb {R}}}^n \times {\varvec{\Upsilon }}: x \in \gamma \}$ and we equip $\Omega ^*$ with the relative topology of the product topology in ${{\mathbb {R}}}^n \times {\varvec{\Upsilon }}$. Let $C^1_b({\varvec{\Upsilon }})$ be defined as the space of bounded $\tau _\text {v}$-continuous functions u satisfying

  • (i) the map $y \mapsto {\mathcal {U}}_{\gamma , x}(u)(y)$ is differentiable at x for every $(x, \gamma ) \in \Omega ^*$.

  • (ii) the map $\Omega ^* \ni (x, \gamma ) \mapsto \nabla {\mathcal {U}}_{\gamma , x}(x)$ is continuous.

  A function $u:{\varvec{\Upsilon }}\rightarrow {{\mathbb {R}}}$ is called local if u is $\sigma (\text {pr} _{B_r})$-measurable for some $r>0$, where $\sigma (\text {pr} _{B_r})$ is the $\sigma$-algebra generated by the map $\text {pr} _{B_r}$. Define

  $$\begin{aligned} C^1_{b, loc}({\varvec{\Upsilon }}):=\{u \in C^1_b({\varvec{\Upsilon }}): \ u \text { is local}{,}\limsup _{r \rightarrow \infty }{\mathcal {E}}^{{\varvec{\Upsilon }}, \mu }_r(u)<\infty \} {.}\end{aligned}$$

  (3.11)

  Assume $(\textsf {m} _{\mu })$, $(\textsf {CAC})_{3.1}$ and $(\textsf {CC})_{3.2}$, and take ${\mathcal {C}}_r={\mathcal {C}}=C^1_{b, loc}({\varvec{\Upsilon }})$ for every $r \in {{\mathbb {N}}}$.

  Then all the conditions of Definition 3.7 are satisfied.

The following proposition relates the two square fields $\Gamma ^{{\varvec{\Upsilon }}}_r$ and $\Gamma ^{{\varvec{\Upsilon }}(B_r)}$.

Proposition 3.9

(Truncated form cf. [52, Proposition 4.7]) Assume $(\textsf {CAC})_{3.1}$ and $(\textsf {CC})_{3.2}$ and take $\{{\mathcal {C}}_r\}_{r \in {{\mathbb {N}}}}$ as in Definition 3.7. The following relations hold for $u \in {\mathcal {C}}_r$ for every $r\in {{\mathbb {N}}}$:

$$\begin{aligned}&\Gamma ^{{\varvec{\Upsilon }}(B_r)}(u_{r}^\eta )(\gamma ) = \Gamma ^{{\varvec{\Upsilon }}}_r(u)(\gamma +\eta _{B_r^c}) {,}\quad {\mu }\text {-a.e.}~\eta , \ \mu _{r}^\eta \text {-a.e.}~\gamma \in {\varvec{\Upsilon }}(B_r) {,}\nonumber \\&{\mathcal {E}}^{{\varvec{\Upsilon }}, \mu }_r(u):= \int _{\varvec{\Upsilon }}{\mathcal {E}}^{{\varvec{\Upsilon }}(B_r), \mu _r^\eta }(u_{r}^\eta ) \mathop {}\!\text {d}{\mu }(\eta ) = \int _{\varvec{\Upsilon }}\Gamma ^{{\varvec{\Upsilon }}}_r(u) \mathop {}\!\text {d}{\mu }{.}\end{aligned}$$

(3.12)

As a consequence, the form $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_{r}, {\mathcal {C}}_r)$ is a densely defined closable Markovian form and the closure $({\mathcal {E}}_r^{{\varvec{\Upsilon }}, {\mu }}, \mathscr {D}({\mathcal {E}}_r^{{\varvec{\Upsilon }}, {\mu }}))$ is a local Dirichlet form on $L^2(\mu )$. The $L^2({\mu })$-semigroup and resolvent corresponding to $({\mathcal {E}}_{r}^{{\varvec{\Upsilon }}, \mu }, \mathscr {D}({\mathcal {E}}_{r}^{{\varvec{\Upsilon }}, \mu }))$ is denoted by $\{T_{r, t}^{{\varvec{\Upsilon }}, {\mu }}\}_{t > 0}$ and $\{G_{r, \alpha }^{{\varvec{\Upsilon }}, {\mu }}\}_{\alpha > 0}$ respectively.

Furthermore, if $\text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu })\subset {\mathcal {C}}_r$, then

$$\begin{aligned} \Gamma ^{\varvec{\Upsilon }}_r(u) \le \text {Lip} _{\bar{\textsf {d} }_{\varvec{\Upsilon }}}(u)^2{,}\quad u \in \text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }) {.}\end{aligned}$$

(3.13)

Proof

Although the idea of the proof is similar to Suzuki [52, Proposition 4.7], the core chosen there is different from the core ${\mathcal {C}}_r$ here. We therefore give the proof below for the sake of completeness.

We first prove (3.12). As the second line of (3.12) is an immediate consequence of the first line and the disintegration formula (2.13), we only give the proof of the first line of  (3.12). Let $u \in {\mathcal {C}}_r$. Then, the RHS of (3.12) is well-defined on a measurable set $\Omega$ of ${\mu }$-full measure by (b) in Definition 3.7. Let $\Omega _r^\eta$ be the section as defined in (2.14), which is of ${\mu }_r^\eta$-full measure for ${\mu }$-a.e. $\eta \in \Omega$ by (2.15). As $\mu _r^\eta$ is absolutely continuous with respect to the Poisson measure $\pi _{\textsf {m} _r}$ by $(\textsf {CAC})_{3.1}$ and the Poisson measure does not have multiple points almost everywhere, we may assume that every $\gamma \in \Omega _r^\eta$ does not have multiple points, i.e., $\gamma (\{x\}) \in \{0, 1\}$ for every $x \in B_r$. Let $\gamma \in \Omega _r^\eta \cap {\varvec{\Upsilon }}^k(B_r)$. Then,

$$\begin{aligned} \Gamma ^{\varvec{\Upsilon }}_r(u) (\gamma \!+\!\eta _{B_r^\text {c}})&\!=\! \sum _{x\in \gamma } \Bigl |\nabla \Bigl ( u\big ({\mathbb {1}_{X\setminus \left\{ x\right\} } \cdot (\gamma +\eta _{B_r^c})+\delta _\bullet }\big )-u\big ({\mathbb {1}_{X\setminus \left\{ x\right\} }\cdot (\gamma +\eta _{B_r^c})}\big ) \Bigr )\Bigl |^2(x) \\&=\sum _{x\in \gamma } \Bigl |\nabla \Bigl ( u_{r}^{\eta }\big ({\mathbb {1}_{X\setminus \left\{ x\right\} } \cdot \gamma +\delta _\bullet }\big )-u^\eta _{r}\big ({\mathbb {1}_{X\setminus \left\{ x\right\} }\cdot \gamma }\big ) \Bigr )\Bigr |^2(x) \\&= \sum _{x\in \gamma } \bigl |\nabla u_{r}^{\eta }\big ({\mathbb {1}_{X\setminus \left\{ x\right\} } \cdot \gamma +\delta _\bullet }\big )\bigr |^2(x) \\&= \Bigl |\nabla ^{\odot k} \bigl (u_r^\eta \bigr )\Bigr |^2(\gamma ) \\&= \Gamma ^{{\varvec{\Upsilon }}(B_r)}(u_{r}^\eta )(\gamma ) \end{aligned}$$

where the first equality is the definition of the square field $\Gamma ^{\varvec{\Upsilon }}_r$; the third equality holds as $u^\eta _{r}\big ({\mathbb {1}_{X\setminus \left\{ x\right\} }\cdot \gamma }\big )$ does not depend on the variable denoted as $\bullet$ on which the weak gradient $\nabla$ operates; the fourth equality follows from the definition of the symmetric gradient operator $\nabla ^{\odot k}$, for which we used the fact that $\gamma \in \Omega _r^\eta$ does not have multiple points. As this argument holds for arbitrary $k \in {{\mathbb {N}}}_0$, (3.12) has been shown. The local property follows immediately by (3.12) and the local property of $({\mathcal {E}}_r^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\eta }, \mathscr {D}({\mathcal {E}}_r^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\eta }))$. The Markov property of $({\mathcal {E}}_{r}^{{\varvec{\Upsilon }}, \mu }, {\mathcal {C}}_r)$ follows by Definition 3.7(c).

We now show the closability. Noting that ${\mathcal {E}}^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\eta }$ is closable for $\mu$-a.e. $\eta$ by $(\textsf {CC})_{3.2}$, the superposition form $(\bar{{\mathcal {E}}}^{{\varvec{\Upsilon }}, {\mu }}_r,\mathscr {D}(\bar{{\mathcal {E}}}^{{\varvec{\Upsilon }}, {\mu }}_r))$, which shall be defined below in Definition 3.10, is closed by [5, Proposition V.3.1.1]. As the two forms $({\mathcal {E}}_{r}^{{\varvec{\Upsilon }}, \mu }, {\mathcal {C}}_r)$ and $(\bar{{\mathcal {E}}}^{{\varvec{\Upsilon }}, {\mu }}_r,\mathscr {D}(\bar{{\mathcal {E}}}^{{\varvec{\Upsilon }}, {\mu }}_r))$ coincide on ${\mathcal {C}}_r$ by definition and ${\mathcal {C}}_r\subset \mathscr {D}(\bar{{\mathcal {E}}}^{{\varvec{\Upsilon }}, {\mu }}_r)$ by construction, the closability of $({\mathcal {E}}_{r}^{{\varvec{\Upsilon }}, \mu }, {\mathcal {C}}_r)$ is inherited from the closedness of the superposition form $(\bar{{\mathcal {E}}}^{{\varvec{\Upsilon }}, {\mu }}_r,\mathscr {D}(\bar{{\mathcal {E}}}^{{\varvec{\Upsilon }}, {\mu }}_r))$. As ${\mathcal {C}}_r \subset L^2({\mu })$ is dense by Definition 3.7(a), the form $({\mathcal {E}}_{r}^{{\varvec{\Upsilon }}, \mu }, {\mathcal {C}}_r)$ is densely defined. As the Markov property extends to the closure (e.g., [18, Theorem  3.1.1]), the form $({\mathcal {E}}_{r}^{{\varvec{\Upsilon }}, \mu }, \mathscr {D}({\mathcal {E}}_{r}^{{\varvec{\Upsilon }}, \mu }))$ is Markovian as well.

We now prove (3.13). By the Rademacher-type property of ${\mathcal {E}}^{{\varvec{\Upsilon }}(B_r), {\mu }_r^{k, \eta }}$, we have that

$$\begin{aligned} \Gamma ^{{\varvec{\Upsilon }}(B_r)}(u) \le \text {Lip} _{\textsf {d} _{\varvec{\Upsilon }}}(u)^2 {,}\quad u \in \text {Lip} ({\varvec{\Upsilon }}(B_r), \textsf {d} _{\varvec{\Upsilon }}) \quad r>0{.}\end{aligned}$$

(3.14)

In view of the relation between $\Gamma ^{\varvec{\Upsilon }}_r$ and $\Gamma ^{{\varvec{\Upsilon }}(B_r)}$ in (3.12) and the Lipschitz contractivity (2.27) of the operator $(\cdot )_r^\eta$, we concluded (3.13). $\square$

3.3 Superposition form

Definition 3.10

(Superposition Dirichlet form, e.g., [5, Proposition V.3.1.1]) Assume $(\textsf {CAC})_{3.1}$ and $(\textsf {CC})_{3.2}$.

$$\begin{aligned} {\mathcal {D}}(\bar{{\mathcal {E}}}^{{\varvec{\Upsilon }}, \mu }_r)&:= \biggl \{u \in L^2({\mu }): \ \int _{\varvec{\Upsilon }}{\mathcal {E}}^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\eta }(u_{r}^\eta ) \mathop {}\!\text {d}{\mu }(\eta )<\infty \biggr \} {,}\nonumber \\ \bar{{\mathcal {E}}}^{{\varvec{\Upsilon }}, {\mu }}_r(u)&:=\int _{\varvec{\Upsilon }}{\mathcal {E}}^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\eta }(u_{r}^\eta ) \mathop {}\!\text {d}{\mu }(\eta ) {.}\end{aligned}$$

(3.15)

It is known that $(\bar{{\mathcal {E}}}^{{\varvec{\Upsilon }}, {\mu }}_r,\mathscr {D}(\bar{{\mathcal {E}}}^{{\varvec{\Upsilon }}, {\mu }}_r))$ is a Dirichlet form on $L^2(\mu )$ [5, Proposition V.3.1.1]. The $L^2({\mu })$-semigroup and the infinitesimal generator corresponding to $(\bar{{\mathcal {E}}}^{{\varvec{\Upsilon }}, {\mu }}_r,\mathscr {D}(\bar{{\mathcal {E}}}^{{\varvec{\Upsilon }}, {\mu }}_r))$ are denoted by $\{\bar{T}_{r, t}^{{\varvec{\Upsilon }},{\mu }}\}_{t > 0}$ and $(\bar{A}_r^{{\varvec{\Upsilon }}, {\mu }}, \mathscr {D}(\bar{A}_r^{{\varvec{\Upsilon }}, {\mu }}))$ respectively.

The resolvent $\{\bar{G}_{r, \alpha }^{{\varvec{\Upsilon }}, {\mu }}\}_{\alpha > 0}$ and the semigroup $\{\bar{T}_{r, t}^{{\varvec{\Upsilon }}, {\mu }}\}_{t > 0}$ corresponding to the superposition form $\bar{{\mathcal {E}}}_r^{{\varvec{\Upsilon }}, {\mu }}$ can be obtained as the superposition of the resolvent $\{G^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\eta }_{\alpha }\}_{\alpha > 0}$ and the semigroup $\{T^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\eta }_{t}\}_{t > 0}$ associated with the form ${\mathcal {E}}^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\eta }$. The following proposition shows that the semigroup (resp. resolvent) corresponding to the superposition form is identified with the superposition of the semigroup (resp. resolvent), which has been proved by Dello Schiavo [12] in a general framework.

Proposition 3.11

(cf.  [12, (iii) Proposition 2.13]) Assume $(\textsf {CAC})_{3.1}$ and $(\textsf {CC})_{3.2}$. The following holds:

$$\begin{aligned} \bar{G}_{r,\alpha }^{{\varvec{\Upsilon }}, {\mu }}u(\gamma ) = G^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\gamma }_{\alpha } u_{r}^{\gamma }(\gamma _{B_r}) {,}\quad \bar{T}_{r,t}^{{\varvec{\Upsilon }}, {\mu }}u(\gamma ) = T^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\gamma }_{t} u_{r}^{\gamma }(\gamma _{B_r}) \, , \end{aligned}$$

(3.16)

for ${\mu }$-a.e. $\gamma \in {\varvec{\Upsilon }}$, every $t>0$.

Remark 3.12

The proof of Dello Schiavo [12, (iii) Proposition 2.13] has been given in terms of direct integral. As the measure ${\mu }_r^\eta$ can be identified to the conditional probability ${\mu }(\cdot \ |\ \cdot _{B_r^c}=\eta _{B_r^c})$ by a bi-measure-preserving isomorphism as remarked in (2.11), our setting can be identified with a particular case of direct integrals in [12].

As the former form is constructed as the smallest closed extension of $({\mathcal {E}}_r^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {C}}_r)$, it is clear by definition that

$$\begin{aligned} {\mathcal {E}}_r^{{\varvec{\Upsilon }}, {\mu }}=\bar{{\mathcal {E}}}_r^{{\varvec{\Upsilon }}, {\mu }} \quad \text {on} \quad {\mathcal {C}}_r {,}\quad \mathscr {D}({\mathcal {E}}_r^{{\varvec{\Upsilon }}, {\mu }}) \subset \mathscr {D}(\bar{{\mathcal {E}}}_r^{{\varvec{\Upsilon }}, {\mu }}) {.}\end{aligned}$$

We introduce a condition for the domain $\mathscr {D}({\mathcal {E}}_r^{{\varvec{\Upsilon }}, {\mu }})$.

Assumption 3.13

We say that $(\textsf {D})_{3.13}$ is satisfied if

Remark 3.14

• (i) For a suitable choice of $\{C_r\}_{r \in {{\mathbb {N}}}}$, Assumption $(\textsf {D})_{3.13}$ has been verified for a Dirichlet form whose invariant measure is $\textsf {sine}_\beta$ for every $\beta >0$, see [52, Theorem  4.11];

• (ii) $(\textsf {D})_{3.13}$ will be used only for (ii) in Theorem  4.3 below.

Under Assumption 3.13, Proposition 3.11 provides the superposition formula for the resolvent $\{G_{r, \alpha }^{{\varvec{\Upsilon }}, {\mu }}\}_{\alpha > 0}$ and the semigroup $\{T_{r, t}^{{\varvec{\Upsilon }}, {\mu }}\}_{t > 0}$ in terms of the resolvent $\{G_\alpha ^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\eta }\}_{\alpha > 0}$ and the semigroup $\{T_t^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\eta }\}_{t > 0}$ respectively.

Corollary 3.15

(Coincidence of semigroups) Assume $(\textsf {CAC})_{3.1}$, $(\textsf {CC})_{3.2}$ and $(\textsf {D})_{3.13}$.

The following three operators coincide:

$$\begin{aligned}&G_{r, \alpha }^{{\varvec{\Upsilon }}, {\mu }}u(\gamma ) = \bar{G}_{r, \alpha }^{{\varvec{\Upsilon }}, {\mu }}u(\gamma ) =G^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\gamma }_{\alpha } u_{r}^\gamma (\gamma _{B_r}), \end{aligned}$$

(3.17)

$$\begin{aligned}&T_{r, t}^{{\varvec{\Upsilon }}, {\mu }}u(\gamma ) = \bar{T}_{r, t}^{{\varvec{\Upsilon }}, {\mu }}u(\gamma ) =T^{{\varvec{\Upsilon }}(B_r), {\mu }_r^\gamma }_{t} u_{r}^\gamma (\gamma _{B_r}) \, , \end{aligned}$$

(3.18)

for ${\mu }$-a.e. $\gamma \in {\varvec{\Upsilon }}$, every $t>0$.

3.4 Monotone limit form

The following proposition follows immediately from the definitions of the square field $\Gamma ^{{\varvec{\Upsilon }}}_r$ and the core ${\mathcal {C}}_r$.

Proposition 3.16

(Monotonicity) Assume $(\textsf {CAC})_{3.1}$ and $(\textsf {CC})_{3.2}$. The form $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r, \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r))$ and the square field $\Gamma ^{\varvec{\Upsilon }}_r$ are monotone increasing as $r \uparrow \infty$, viz.,

$$\begin{aligned} \Gamma ^{\varvec{\Upsilon }}_r(u) \le \Gamma ^{\varvec{\Upsilon }}_s(u){,}\quad {\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r(u) \le {\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_s(u) {,}\quad \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_s) \subset \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r) \quad r\le s {.}\end{aligned}$$

Proof

As ${\mathcal {C}}_r$ is a core of the form $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r, \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r))$ and ${\mathcal {C}}_s \subset {\mathcal {C}}_r$ by Definition 3.7, it suffices to check that $\Gamma ^{\varvec{\Upsilon }}_r(u) \le \Gamma ^{\varvec{\Upsilon }}_s(u)$ on ${\mathcal {C}}_s$, which is a immediate consequence of the definition (3.7). The proof is complete. $\square$

Definition 3.17

(Monotone-limit form) The form $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}))$ is defined as the monotone limit:

$$\begin{aligned} \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }})&:=\{u \in \cap _{r>0} \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r): {\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}(u) = \lim _{r \rightarrow \infty }{\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r(u) <\infty \} {,}\nonumber \\ {\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}(u)&:=\lim _{r \rightarrow \infty }{\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r(u) {.}\end{aligned}$$

(3.19)

The form $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}))$ is a Dirichlet form on $L^2(\mu )$ as it is the monotone limit of Dirichlet forms (e.g., by Ma and Röckner [33, Exercise 3.9]). Note that the limit form does not depend on the choice of the exhaustion $\left( B_r\right) _{r \in {{\mathbb {N}}}}$. The square field $\Gamma ^{\varvec{\Upsilon }}$ is defined as the monotone limit of $\Gamma ^{\varvec{\Upsilon }}_r$ as well:

$$\begin{aligned} \Gamma ^{\varvec{\Upsilon }}(u):=\lim _{r \rightarrow \infty }\Gamma ^{\varvec{\Upsilon }}_r(u) \quad u \in \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}){.}\end{aligned}$$

(3.20)

We now show that the form $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}))$ is a local Dirichlet form on $L^2({\mu })$ and satisfies the Rademacher-type property with respect to the $L^2$-transportation-type distance $\bar{\textsf {d} }_{\varvec{\Upsilon }}$.

Proposition 3.18

Assume $(\textsf {CAC})_{3.1}$ and $(\textsf {CC})_{3.2}$. The form $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}))$ is a local Dirichlet form on $L^2({\mu })$. Furthermore, if $\text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }) \subset {\mathcal {C}}_r$ for every $r \in {{\mathbb {N}}}$, then $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}))$ satisfies Rademacher-type property:

$$\begin{aligned} \text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }) \subset \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}){,}\quad \Gamma ^{\varvec{\Upsilon }}(u) \le \text {Lip} _{\bar{\textsf {d} }_{\varvec{\Upsilon }}}(u)^2 {.}\end{aligned}$$

(3.21)

Proof

The local property of $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}))$ follows from (3.20). We show the Rademacher-type property. Since $\Gamma ^{\varvec{\Upsilon }}$ is the limit square field of $\Gamma ^{{\varvec{\Upsilon }}}_r$ as in (3.20), it suffices to show

$$\begin{aligned} \Gamma ^{\varvec{\Upsilon }}_r(u) \le \text {Lip} _{\bar{\textsf {d} }_{\varvec{\Upsilon }}}(u)^2 {,}\quad u \in \text {Lip} (\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }) \quad r>0{,}\end{aligned}$$

which has been already proven in Proposition 3.9. We verified ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$. The proof is complete. $\square$

The $L^2$-resolvent operators and the $L^2$-semigroups corresponding to the form (3.8) and the form (3.19) are denoted respectively by

$$\begin{aligned} \bigl \{G_{r, \alpha }^{{\varvec{\Upsilon }}, {\mu }}\bigr \}_{\alpha>0},\ \bigl \{T^{{\varvec{\Upsilon }}, {\mu }}_{r, t}\bigr \}_{t>0} \quad \text {and} \quad \bigl \{G_{\alpha }^{{\varvec{\Upsilon }}, {\mu }}\bigr \}_{\alpha>0}, \ \bigl \{T^{{\varvec{\Upsilon }}, {\mu }}_t\bigr \}_{t >0} {.}\end{aligned}$$

Proposition 3.19

Assume $(\textsf {CAC})_{3.1}$ and $(\textsf {CC})_{3.2}$. The semigroup $\{T^{{\varvec{\Upsilon }}, {\mu }}_{t}\}_{t \ge 0}$ is the $L^2({\mu })$-strong operator limit of the semigroups $\{T^{{\varvec{\Upsilon }}, {\mu }}_{r, t}\}_{t \ge 0}$, viz.,

$$\begin{aligned} L^2(\mu )\text {--}\lim _{r \rightarrow \infty } G^{{\varvec{\Upsilon }}, {\mu }}_{r, \alpha } u\!= \!G^{{\varvec{\Upsilon }}, {\mu }}_\alpha u, \quad L^2(\mu )\text {--}\lim _{r \rightarrow \infty } T^{{\varvec{\Upsilon }}, {\mu }}_{r, t} u\!=\! T^{{\varvec{\Upsilon }}, {\mu }}_t u \quad u \!\in \! L^2({\mu }){,}\quad t>0 {.}\end{aligned}$$

Proof

The statement follows from the monotonicity of $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r, \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r)$ as $r\uparrow \infty$ proven in Proposition 3.16 and [45, Sect. 14, p. 373]. $\square$

3.5 Quasi-regularity

In this subsection, we discuss a sufficient condition for the quasi-regularity.

Assumption 3.20

(Quasi-regularity) Let ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }} \subset \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }})$ be any closed Markovian subspace. We call $(\textsf {QR})_{3.20}$ for ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ if

In the following, we introduce another monotone-limit form having a (possibly) smaller domain. Recall that the Rademacher-type property $(\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, \tau _{\text {v} }})$ for $\tau _\text {v}$-continuous $\bar{\textsf {d} }_{\varvec{\Upsilon }}$-Lipschitz functions has been defined in Sect.  2.3.

Proposition 3.21

(Smaller domain) Assume $(\textsf {CAC})_{3.1}$ and $(\textsf {CC})_{3.2}$. Let $\left( {\mathcal {C}}_r\right) _{r \in {{\mathbb {N}}}}$ be a sequence of algebras in Definition 3.7. Then, the form $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {C}})$ defined as

$$\begin{aligned}&{\mathcal {C}}:=\{u \in \cap _{r \in {{\mathbb {N}}}} {\mathcal {C}}_r: \lim _{r \rightarrow \infty }{\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r(u) <\infty \} {,}\nonumber \\&{\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}(u):=\lim _{r \rightarrow \infty }{\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r(u) {,}\end{aligned}$$

(3.22)

is closable. Let $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }})$ be the closure $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, \overline{{\mathcal {C}}})$. Then, $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }})$ is a local Dirichlet form on $L^2({\mu })$. Furthermore, if either of the following holds for every $r \in {{\mathbb {N}}}$

$$\begin{aligned}{} & {} \text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }) \subset {\mathcal {C}}_r{,}\quad \text {resp.} \quad \text {Lip} _b({\textsf {d} }_{\varvec{\Upsilon }}, {\mu }) \subset {\mathcal {C}}_r{,}\quad \text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, \tau _\text {v} ) \subset {\mathcal {C}}_r{,}\quad \\{} & {} \quad \text {Lip} _b({\textsf {d} }_{\varvec{\Upsilon }}, \tau _\text {v} ) \subset {\mathcal {C}}_r {,}\end{aligned}$$

then $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }})$ satisfies Rademacher-type property

$(resp.~(\textsf {Rad}_{{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }})$, $(\textsf {Rad}_{\bar{\textsf {d} }_{\varvec{\Upsilon }}, \tau _\text {v} })$ and $(\textsf {Rad}_{{\textsf {d} }_{\varvec{\Upsilon }}, \tau _\text {v} }))$.

Proof

As ${\mathcal {C}} \subset \mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }})$ by definition, the closability of ${\mathcal {C}}$ follows by the closedness of $\mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }})$ proven in Proposition 3.18. The local property of ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ is inherited from $\mathscr {D}({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }})$. The Markov property of $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {C}})$ follows by the Markov property of $({\mathcal {E}}^{{\varvec{\Upsilon }}, {\mu }}_r, {\mathcal {C}}_r)$ and (3.22). As the Markov property is inherited to the closure by e.g., [18, Theorem  3.1.1], we concluded that ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ is Markovian. The rest of the arguments follows by the same proofs as in Proposition 3.18. $\square$

Corollary 3.22

Assume $(\textsf {CAC})_{3.1}$ and $(\textsf {CC})_{3.2}$. If ${\mathcal {C}}_r={\mathcal {C}}$ $(r \in {{\mathbb {N}}})$ is either one of the following:

$$\begin{aligned} {\mathcal {C}} = \text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, \tau _\text {v} ) \quad \textrm{or} \quad {\mathcal {C}} = \text {Lip} _b({\textsf {d} }_{\varvec{\Upsilon }}, \tau _\text {v} ) {,}\end{aligned}$$

(3.23)

and ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ is the closure $\overline{{\mathcal {C}}}$, then $(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }})$ is a quasi-regular local Dirichlet form.

Proof

First of all, the form is closable on ${\mathcal {C}}$ by Proposition 3.21 and the fact that ${\mathcal {C}}$ satisfies Definition 3.7 as seen in (b) Example 3.8. Furthermore, $(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }})$ is a local Dirichlet form and the Rademacher-type property $(\textsf {Rad}_{\bar{\textsf {d} }_{\varvec{\Upsilon }}, \tau _\text {v} })$ (resp. $(\textsf {Rad}_{{\textsf {d} }_{\varvec{\Upsilon }}, \tau _\text {v} })$) holds by Proposition 3.21. Thus, we conclude the quasi-regularity $(\textsf {QR})_{3.20}$ by the proof of [14, Corollary 6.3]. $\square$

Remark 3.23

(A different core) Another sufficient condition for $(\textsf {QR})_{3.20}$ has been studied in [38, Theorem  1] by taking a core ${\mathcal {C}}_r={\mathscr {D}}_\infty$ in Definition 3.7, where ${\mathscr {D}}_\infty$ is a space of smooth local functions (see, [38, (0.3)]) and take the domain to be the closure of ${\mathscr {D}}_\infty$. We note that functions in the core ${\mathcal {C}}$ in (3.23) are not necessarily local functions. The domain ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ defined as the closure of ${\mathcal {C}}$ in Corollary 3.22 is therefore not necessarily the same as the domain constructed as the closure of ${\mathscr {D}}_\infty$ in [38].

4 Tail-triviality, finiteness of $\bar{\textsf {d} }_{\varvec{\Upsilon }}$ and irreducibility

4.1 Irreducibility and tail-triviality

Recall that $\big ({\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}}\big )$ is irreducible if every $u \in {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ with $\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}(u)=0$ is equal to a constant ${\mu }$-almost everywhere, see (2.3). The following definition corresponds to the irreducibility of the conditioned form (3.5). Let $\left( B_{r}\right)$ be a compact convex domain exhaustion in ${{\mathbb {R}}}^n$.

Definition 4.1

(Conditional irreducibility) We say that the conditional irreducibility (in short: $(\textsf {CI})_{4.1}$) holds if, for every $r \in {{\mathbb {N}}}$, ${\mu }$-a.e. $\eta \in {\varvec{\Upsilon }}$ and $k \in {\mathcal {K}}_r^\eta$,

where $C_{r}^{\eta , k}$ is a constant depending on $r, \eta$ and k.

Remark 4.2

• (a) In terms of the corresponding diffusion process, Assumption $(\textsf {CI})_{4.1}$ can be understood as the ergodicity of the finite interacting particles in ${\varvec{\Upsilon }}(B_r)$ conditioned to be $\eta _{B_r^c}$ outside $B_r$.

• (b) Assumption $(\textsf {CI})_{4.1}$ can be verified for a wide class of invariant measures ${\mu }$ such as Gibbs measures including Ruelle measures, and determinantal/permanental point processes, including $\text {sine}_\beta$, $\text {Airy}_\beta$, $\text {Bessel}_{\alpha , \beta }$, Ginibre, which will be discussed in Sect. 6.

The main theorem of this section is the following:

Theorem 4.3

Let ${\mu }$ be a Borel probability measure on ${\varvec{\Upsilon }}$ satisfying $(\textsf {CAC})_{3.1}$ and $(\textsf {CC})_{3.2}$, and ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }} \subset \mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})$ be any closed Markovian subspace.

• (i) Suppose $(\textsf {D})_{3.13}$. Then

  $$\begin{aligned} \big ({\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, \mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})}\big )\, \mathrm{is\, irreducible} \quad \implies \quad {\mu }\,\mathrm{is\, tail\, trivial}~(\text {}\textsf {T}_{2.6}) \end{aligned}$$

• (ii) Suppose $(\textsf {CAC'})_{3.1}$, $(\textsf {CI})_{4.1}$, $(\textsf {QR})_{3.20}$ of ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ and $(\textsf {R})_{2.8}$. Then

  $$\begin{aligned} {\mu }\,\mathrm{is \,tail\, trivial }\, (\text {}\textsf {T}_{2.6}) \quad \implies \quad (\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }})\, \mathrm{is\, irreducible} \end{aligned}$$

In the following subsections, we give the proof of Theorem 4.3.

4.2 Proof of (i)

Recall that $\big ({\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }},\mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})}\big )$ is irreducible if and only if $\{T^{{\varvec{\Upsilon }}, {\mu }}_t\}_{t>0}$-invariant sets are trivial (see, e.g., [2, Proposition 2.3 and Appendix]), i.e., every $\Xi \subset {\varvec{\Upsilon }}$ satisfying

$$\begin{aligned} T^{{\varvec{\Upsilon }}, {\mu }}_t ({{\textbf {1}}}_{\Xi }u) = {{\textbf {1}}}_{\Xi }T^{{\varvec{\Upsilon }}, {\mu }}_t u,\quad u \in L^2({\mu }) {,}\end{aligned}$$

satisfies either ${\mu }(\Xi )=1$ or ${\mu }(\Xi )=0$. Therefore, it suffices to show that every set $\Xi \in {\mathscr {T}}({\varvec{\Upsilon }})$ is $\{T^{{\varvec{\Upsilon }}, {\mu }}_t\}_{t>0}$-invariant. By Proposition 3.19, we obtain $T^{{\varvec{\Upsilon }}, {\mu }}_{r, t}u \rightarrow T^{{\varvec{\Upsilon }}, {\mu }}_{t}u$ in $L^2(\mu )$ as $r \uparrow \infty$ for every $u \in L^2(\mu )$. Thus, it suffices to show that

$$\begin{aligned} \text {every tail set } \Xi \in {\mathscr {T}}({\varvec{\Upsilon }}) \text { is } \{T^{{\varvec{\Upsilon }}, {\mu }}_{r, t}\}_{t>0}\text {-invariant for every } r>0 {.}\end{aligned}$$

(4.1)

Indeed, if it is true, then

$$\begin{aligned} T^{{\varvec{\Upsilon }}, {\mu }}_t{{\textbf {1}}}_{\Xi }u = L^2(\mu ) \text {-}\lim _{r\rightarrow \infty } T^{{\varvec{\Upsilon }}, {\mu }}_{r, t}{{\textbf {1}}}_{\Xi }u = L^2(\mu )\text {-}\lim _{r\rightarrow \infty } {{\textbf {1}}}_{\Xi }T^{{\varvec{\Upsilon }}, {\mu }}_{r, t}u = {{\textbf {1}}}_{\Xi }T^{{\varvec{\Upsilon }}, {\mu }}_tu {.}\end{aligned}$$

We now show (4.1). By (2.29), every non-empty set $\Xi \in {\mathscr {T}}({\varvec{\Upsilon }})$ has the following expression:

$$\begin{aligned} \Xi ={\varvec{\Upsilon }}(B_r) + \text { pr}_{B_r^c}(\Xi ), \quad \text {for every}\ r \in {{\mathbb {N}}}{.}\end{aligned}$$

(4.2)

By Proposition 3.15, for $u \in L^2({\mu })$,

$$\begin{aligned} T^{{\varvec{\Upsilon }}, {\mu }}_{r, t}u(\gamma ) = T^{{\varvec{\Upsilon }}(B_r), {\mu }^\gamma _{r}}_t u_{r}^{\gamma }(\gamma _{B_r}), \quad \mu \text {-a.e.}\ \gamma {.}\end{aligned}$$

By (4.2), the function $({{\textbf {1}}}_{\Xi })_{r}^{\gamma } \equiv 1$ on ${\varvec{\Upsilon }}(B_r)$ if $\gamma \in \Xi$ and $({{\textbf {1}}}_{\Xi })_{r}^{\gamma } \equiv 0$ otherwise, which leads to

$$\begin{aligned} T^{{\varvec{\Upsilon }}(B_r), {\mu }^\gamma _{r}}_t (u{{\textbf {1}}}_{\Xi })_{r}^{\gamma }(\gamma _{B_r}) = {{\textbf {1}}}_{\Xi }(\gamma )T^{{\varvec{\Upsilon }}(B_r), {\mu }^\gamma _{r}}_t u_{r}^{\gamma }(\gamma _{B_r}) {.}\end{aligned}$$

Therefore, for every $r \in {{\mathbb {N}}}$

$$\begin{aligned} T^{{\varvec{\Upsilon }}, {\mu }}_{r, t}{{\textbf {1}}}_{\Xi } u(\gamma )&= T^{{\varvec{\Upsilon }}(B_r), {\mu }^\gamma _{r}}_t({{\textbf {1}}}_{\Xi }u)_{r}^{\gamma }(\gamma _{B_r}) = {{\textbf {1}}}_\Xi T^{{\varvec{\Upsilon }}(B_r), {\mu }^\gamma _{r}}_tu_{r}^{ \gamma }(\gamma _{B_r}) = {{\textbf {1}}}_{\Xi }T^{{\varvec{\Upsilon }}, {\mu }}_{r, t} u(\gamma ) {,}\end{aligned}$$

for $\mu$-a.e. $\gamma$. The proof of (i) is complete. $\square$

4.3 Proof of (ii)

By the number rigidity $(\textsf {R})_{2.8}$, we can take a measurable set $\Omega _\textsf {rig}^r \subset {\varvec{\Upsilon }}$ so that $\mu (\Omega _\textsf {rig}^{r})=1$ and if $\gamma , \eta \in \Omega _\textsf {rig}^r$ with $\gamma _{B_r^c} = \eta _{B_r^c}$, then $\gamma (B_r) = \eta (B_r)$. Let $\Omega _\textsf {rig} = \cap _{r \in {{\mathbb {N}}}} \Omega _\textsf {rig}^{r}$, which is of ${\mu }$-full measure as well. Let $u \in {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ be so that $\Gamma ^{{\varvec{\Upsilon }}}(u) =0$. By the monotonicity (3.20), we have $\Gamma ^{{\varvec{\Upsilon }}}_r(u)=0$. By the formula (3.12) and the same proof as [14, Proposition 5.14], for every $r \in {{\mathbb {N}}}$, there exists $\Omega ^r_0 \subset {\varvec{\Upsilon }}$ so that ${\mu }(\Omega ^r_0)=1$ and

$$\begin{aligned} \Gamma ^{{\varvec{\Upsilon }}(B_{r})}(u_{r}^{\eta }) =0 \quad {\mu }_{r}^\eta \text {-a.e.} {,}\quad \eta \in \Omega ^r_0 {.}\end{aligned}$$

By Assumption $(\textsf {CI})_{4.1}$, for $r \in {{\mathbb {N}}}$, there exists a measurable set $\Omega ^r_\textsf {rig, ic}\subset \Omega _0^r \cap \Omega _\textsf {rig}$ of full $\mu$-measure so that, for every $\eta \in \Omega ^r_\textsf {rig, ic}$, there exists $k=k(\eta ) \in {{\mathbb {N}}}_0$ and a constant $C^{\eta , k}_{r}$ satisfying

$$\begin{aligned} u_{r}^{\eta }\equiv C^{\eta , k}_{r} \quad {\mu }_{r}^\eta \text {-a.e.} {.}\end{aligned}$$

(4.3)

Note that the measure ${\mu }_{r}^\eta$ is fully supported on ${\varvec{\Upsilon }}^{k(\eta )}(B_{r})$ by the number rigidity $(\textsf {R})_{2.8}$ and $(\textsf {CAC'})_{3.1}$. Let $\Omega _\textsf {rig, ic}:= \cap _{r \in {{\mathbb {N}}}}\Omega ^r_\textsf {rig, ic}$ with $\mu (\Omega _\textsf {rig, ic})=1$.

By the quasi-regularity $(\textsf {QR})_{3.20}$, there exists a quasi-continuous ${\mu }$-version $\tilde{u}$ of u (see [33, Proposition 3.3 in Chapter IV]). Therefore, we can take a closed nest $(K_m)_m$ so that $\tilde{u}$ is $\tau _\text {v}$-continuous on $K_m$ for every $m \in {{\mathbb {N}}}$. Define $\Omega _\textsf {qc}:=\cup _{m \in {{\mathbb {N}}}} K_m$, which is of $\mu$-full measure since $\Omega _\textsf {qc}^c$ is an exceptional set with respect to $\big ({\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}}\big )$. Up to relabelling $K_m$, we may therefore assume that ${\mu }(K_m) >1-\frac{1}{2\,m}$. Let $\Omega _m:=\Omega _{\textsf {rig, ic}} \cap K_m$ for $m \in {{\mathbb {N}}}$. Since $\tilde{u}$ is $\tau _\text {v}$-continuous on $\Omega _m$, the function $\tilde{u}_{r}^{\eta }$ is continuous on $(\Omega _{m})_r^\eta$ for every $\eta \in \Omega _m$ and $r \in {{\mathbb {N}}}$ where $(\Omega _m)_{r}^\eta$ is the section defined in (2.14). By Proposition 2.13, we have that

$$\begin{aligned} {\mu }(\Omega _m)= \int _{{\varvec{\Upsilon }}}{\mu }_{r}^\eta \bigl ((\Omega _{m})_r^\eta \bigr ) \mathop {}\!\text {d}{\mu }(\eta ) {.}\end{aligned}$$

(4.4)

Thus, by noting that ${\mu }(\Omega _m) > 1-\frac{1}{2m}$ and that the integrand of the r.h.s. of (4.4) is non-negative and bounded from above by 1, there exists $\Omega _{m, r} \subset {\varvec{\Upsilon }}$ so that ${\mu }(\Omega _{m, r}) > 1-\frac{1}{2\,m}$ and

$$\begin{aligned} {\mu }_{r}^\eta \bigl ((\Omega _{m})_r^\eta \bigr )>0 \quad \forall \eta \in \Omega _{m, r}{.}\end{aligned}$$

(4.5)

Define $\Omega _{m}^r:= \Omega _m \cap \Omega _{m, r}$. As ${\mu }(\Omega _{m, r}), {\mu }(\Omega _m) > 1-\frac{1}{2m}$, by the Inclusion-Exclusion formula, it holds that

$$\begin{aligned} {\mu }(\Omega _{m}^r) > 1-\frac{1}{m}{,}\quad m \in {{\mathbb {N}}}{.}\end{aligned}$$

(4.6)

Combining (4.3) and (4.5) with the fact that ${\mu }_{r}^\eta \!\downharpoonright _{{{\varvec{\Upsilon }}^{k}(B_r)}}$ is fully supported in ${\varvec{\Upsilon }}^{k}(B_r)$ and $\tilde{u}$ is $\tau _\text {v}$-continuous on $(\Omega _{m})_r^\eta$, we obtain that

$$\begin{aligned} \tilde{u}_{r, \eta }\equiv C^k_{r, \eta } \textit{ everywhere } \text { in } (\Omega _{m})_r^\eta \text { for every } \eta \in \Omega _{m}^r\, {.}\end{aligned}$$

(4.7)

By Lemma A.2 in the Appendix applied to $\Omega _m^r$ in (4.6), we can take $n\mapsto m_n \in {{\mathbb {N}}}$ with $m_{n} \le m_{n'}$ for $n \le n'$ so that, by taking $\Omega =\limsup _{n \rightarrow \infty }\cap _{r=1}^n\Omega _{m_n}^r$, it holds that

$$\begin{aligned} {\mu }(\Omega ) = 1 {.}\end{aligned}$$

We now prove that

$$\begin{aligned} \tilde{u} \text { is constant }~{\mu }\text {-a.e.}~\text {on } \Omega {.}\end{aligned}$$

(4.8)

Claim 1

The statement (4.8) holds if the following statement is true: for every $\Xi _1, \Xi _2 \subset \Omega$ with $\mu (\Xi _1)\mu (\Xi _2)>0$, there exist $\gamma ^1 \in \Xi _1$ and $\gamma ^2 \in \Xi _2$ so that

$$\begin{aligned} \tilde{u}(\gamma ^1) =\tilde{u}(\gamma ^2){.}\end{aligned}$$

(4.9)

Proof of Claim 1

Assume that the statement (4.9) is true. Take $\Xi _1=\{\tilde{u}>a\}$ and $\Xi _2=\{\tilde{u} \le a\}$ for $a \in {{\mathbb {R}}}$. If there exists $a \in {{\mathbb {R}}}$ so that $\mu (\Xi _1)\mu (\Xi _2)>0$, then this contradicts (4.9). Thus, there is no such $a \in {{\mathbb {R}}}$, which means ${\mu }(\Xi _1){\mu }(\Xi _2)=0$ for every $a \in {{\mathbb {R}}}$. This concludes that $\tilde{u}$ is constant ${\mu }$-a.e. on $\Omega$. $\square$

We thus only have to prove (4.9). We may assume ${\mu }(\Xi _1)>0$, otherwise there is nothing to prove. Since $\mu$ is tail trivial, $\mu (\Xi _1)>0$ and $\Xi _1 \subset {\mathcal {T}}(\Xi _1)$, it holds that $\mu ({\mathcal {T}}(\Xi _1))=1$, where ${\mathcal {T}}(\Xi _1)$ is the tail set of $\Xi _1$ as defined in (2.30). Thus, $\mu ({\mathcal {T}}(\Xi _1) \cap \Xi _2)>0$, and ${\mathcal {T}}(\Xi _1) \cap \Xi _2$ is non-empty. Take an element $\gamma ^2 \in {\mathcal {T}}(\Xi _1) \cap \Xi _2$. By the definition (2.30) of the tail set ${\mathcal {T}}(\Xi _1)$ and since $\Omega \subset \Omega _\textsf {rig}$, there exists $r_0 \in {{\mathbb {N}}}$ and $\gamma ^1 \in \Xi _1$ so that

$$\begin{aligned} \gamma ^1_{B_{r_0}^c} = \gamma ^2_{B_{r_0}^c}, \quad \gamma ^1({B_{r_0}})=\gamma ^2({B_{r_0}}) {.}\end{aligned}$$

(4.10)

Claim 2

$\gamma ^1_{B_{j}}, \gamma ^2_{B_{j}}\in (\Omega _{m_j})_j^{\gamma ^2}$ for some $j \in {{\mathbb {N}}}$.

Proof of Claim 2

Recall

$$\begin{aligned} \Omega =\limsup _{n \rightarrow \infty }\cap _{r=1}^n\Omega _{m_n}^r := \bigcap _{n \ge 1} \bigcup _{j \ge n} \bigcap _{r=1}^j\Omega _{m_j}^r {.}\end{aligned}$$

(4.11)

As $\gamma ^1, \gamma ^2 \in \Omega$, there exist $j_1, j_2 \in {{\mathbb {N}}}$ with $j_1, j_2 \ge r_0$ so that

$$\begin{aligned} \gamma ^1 \in \bigcap _{r=1}^{j_1}\Omega _{m_{j_1}}^r {,}\quad \gamma ^2 \in \bigcap _{r=1}^{j_2}\Omega _{m_{j_2}}^r {,}\quad \text {in particular}{,}\quad \gamma ^1 \in \Omega _{m_{j_1}}^{j_1} \quad \gamma ^2 \in \Omega _{m_{j_2}}^{j_2} {.}\end{aligned}$$

We may assume without loss of generality $j_1 \le j_2$. As $\Omega _{m_{j_1}}^{j_1}\subset \Omega _{m_{j_1}}$ and $\Omega _{m_{j_2}}^{j_2}\subset \Omega _{m_{j_2}}$ by definition, and the monotonicity $\Omega _{m_{j_1}} \subset \Omega _{m_{j_2}}$ by construction, we have

$$\begin{aligned} \gamma ^1 \in \Omega _{m_{j_1}}^{j_1} \subset \Omega _{m_{j_1}} \subset \Omega _{m_{j_2}} {,}\quad \gamma ^2 \in \Omega _{m_{j_2}}^{j_2}\subset \Omega _{m_{j_2}} {.}\end{aligned}$$

(4.12)

As $j_2 \ge r_0$, (4.10) implies

$$\begin{aligned} \gamma ^1_{B_{j_2}^c} = \gamma ^2_{B_{j_2}^c}, \quad \gamma ^1({B_{j_2}})=\gamma ^2({B_{j_2}})=:k {.}\end{aligned}$$

(4.13)

By (4.12) and (4.13), we obtain

$$\begin{aligned} \gamma ^1_{B_{j_2}}, \gamma ^2_{B_{j_2}}\in (\Omega _{m_{j_2}})_{j_2}^{\gamma ^2} {.}\end{aligned}$$

(4.14)

$\square$

We now resume the proof of (4.9). In view of (4.7) and (4.14), we conclude

$$\begin{aligned} \tilde{u}(\gamma ^1)&\!=\! \tilde{u}(\gamma ^1_{B_{j_2}}+\gamma ^1_{B_{j_2}^c}) \!=\! \tilde{u}_{j_2}^{\gamma ^2}(\gamma ^1_{B_{j_2}}) \!=\! C^{\gamma ^2, k}_{j_2} \!=\!\tilde{u}_{j_2}^{\gamma ^2}(\gamma ^2_{B_{j_2}}) =\tilde{u}(\gamma ^2_{B_{j_2}}+\gamma ^2_{B_{j_2}^c}) =\tilde{u}(\gamma ^2) {,}\end{aligned}$$

which proves (4.9). The proof is complete. $\square$

For a closed Markovian subspace ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }} \subset \mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})$, let $S_t^{{\varvec{\Upsilon }}, {\mu }}$ be the corresponding $L^2({\mu })$-semigroup and $(L^{{\varvec{\Upsilon }}, {\mu }}, \mathscr {D}(L^{{\varvec{\Upsilon }}, {\mu }}))$ be the infinitesimal generator respectively.

Corollary 4.4

Let ${\mu }$ be a Borel probability measure on ${\varvec{\Upsilon }}$ and ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }} \subset \mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})$ be any closed Markovian subspace. Suppose $(\textsf {CAC'})_{3.1}$, $(\textsf {CC})_{3.2}$, $(\textsf {CI})_{4.1}$, $(\textsf {QR})_{3.20}$ of ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$,  $(\textsf {R})_{2.8}$ and $(\textsf {T})_{2.6}$. Then, the following hold:

• (i) $\big ({\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}}\big )$ is irreducible;

• (ii) $\{S^{{\varvec{\Upsilon }}, {\mu }}_t\}$ is irreducible, i.e., every $\Xi \in {\mathscr {B}}(\tau _\text {v} )^{\mu }$ with

  $$\begin{aligned} S^{{\varvec{\Upsilon }}, {\mu }}_t ({{\textbf {1}}}_{\Xi }f) = {{\textbf {1}}}_{\Xi }S^{{\varvec{\Upsilon }}, {\mu }}_t f,\quad f \in L^2({\mu }) \end{aligned}$$

  satisfies either ${\mu }(\Xi )=1$ or ${\mu }(\Xi )=0$;

• (iii) $\{S^{{\varvec{\Upsilon }}, {\mu }}_t\}$ is ergodic, i.e.,

  $$\begin{aligned} \int _{{\varvec{\Upsilon }}} \biggl (S^{{\varvec{\Upsilon }}, {\mu }}_t u - \int _{{\varvec{\Upsilon }}} u \mathop {}\!\text {d}{\mu }\biggr )^2 \mathop {}\!\text {d}{\mu }\xrightarrow {t \rightarrow \infty } 0, \quad u \in L^2({\mu }); \end{aligned}$$

• (iv) $L^{{\varvec{\Upsilon }}, {\mu }}$-harmonic functions are trivial, i.e.,

  $$\begin{aligned} \text {If}\ u \in \mathscr {D}(L^{{\varvec{\Upsilon }}, {\mu }})\ \text {and}\ L^{{\varvec{\Upsilon }}, {\mu }}u =0, \quad \text {then}\ \ u=\text {const.}. \end{aligned}$$

Proof

The statement (i) is the consequence of Theorem 4.3. The equivalences (i) $\iff$ (ii)$\iff$(iii) $\iff$ (iv) are standard in functional analysis. We refer the readers to, e.g., [2, Proposition 2.3 and Appendix]. $\square$

Let $({{\textbf {X}}}_t, {{\textbf {P}}}_\gamma )$ be the Markov process properly associated with the quasi-regular Dirichlet form $\big ({\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }},{\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}}\big )$ (see [33, Theorem 3.5 in Chapt. IV]). We write ${{\textbf {P}}}_{\nu }$ for $\int _{{\varvec{\Upsilon }}} {{\textbf {P}}}_\gamma (\cdot ) d\nu (\gamma )$ for a bounded Borel measure $\nu$ on ${\varvec{\Upsilon }}$. Recall that ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}_e$ is the extended domain of ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ defined in (2.2).

Corollary 4.5

Let ${\mu }$ be a Borel probability measure on ${\varvec{\Upsilon }}$ and ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }} \subset \mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})$ be any closed Markovian subspace. Suppose $(\textsf {CAC'})_{3.1}$, $(\textsf {CC})_{3.2}$, $(\textsf {CI})_{4.1}$, $(\textsf {QR})_{3.20}$ of ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$, $(\textsf {R})_{2.8}$, $(\textsf {T})_{2.6}$ and ${{\textbf {1}}} \in {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}_e$.

Then, the following hold:

• (i) for every Borel measurable ${\mu }$-integrable function u, it holds ${{\textbf {P}}}_{\mu }$-a.s. that

  $$\begin{aligned} \lim _{t \rightarrow \infty } \frac{1}{t} \int _0^t u({{\textbf {X}}}_s)ds = \int _{{\varvec{\Upsilon }}} u \mathop {}\!\text {d}{\mu }; \end{aligned}$$

  (4.15)

• (ii) for every non-negative bounded function h, (4.15) holds in $L^1({{\textbf {P}}}_{h\cdot {\mu }})$;

• (iii) the convergence (4.15) holds ${{\textbf {P}}}_\gamma$-a.s. for $\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}$-q.e. $\gamma$.

Proof

The form $\big ({\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }},{\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}}\big )$ is irreducible by Theorem 4.3. Furthermore, it is recurrent as ${{\textbf {1}}} \in {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}_e$ and $\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}({{\textbf {1}}})=0$, see Fukushima [18, Theorem 1.6.3]. Therefore, by Fukushima [18, Theorem 4.7.3], the proof is complete (although Fukushima [18, Theorem 4.7.3] assumes the local compactness of the state space, the same proof applies verbatim).

4.4 Finiteness of $\bar{\textsf {d} }_{\varvec{\Upsilon }}$

Recall that $\bar{\textsf {d} }_{{\varvec{\Upsilon }}}^{\mu }(\Xi , \Lambda )$ has been defined in (2.5) for $\Xi , \Lambda \subset {\varvec{\Upsilon }}$. In this subsection, we investigate relations among the tail triviality $(\textsf {T})_{2.6}$, the irreducibility, and the finiteness $\bar{\textsf {d} }_{{\varvec{\Upsilon }}}^{\mu }(\Xi , \Lambda )<\infty$. Namely, we discuss relations among the following statements:

• (a) $\mu$ is tail trivial $(\textsf {T})_{2.6}$;

• (b) $\bar{\textsf {d} }_{{\varvec{\Upsilon }}}^{\mu }(\Xi , \Lambda )<\infty$ whenever $\Xi \in {\mathscr {B}}(\tau _\text {v} )^{\mu }, \Lambda \in {\mathscr {B}}(\tau _\text {v} )$ and $\mu (\Xi ), \mu (\Lambda )>0$;

• (c) $\big ({\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }},{\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}}\big )$ is irreducible.

Theorem 4.6

Let ${\mu }$ be a Borel probability measure on ${\varvec{\Upsilon }}$. Then,

• (b) $\implies$ (a);

• if $(\textsf {R})_{2.8}$ holds, then (a) $\implies$ (b).

Suppose that ${\mu }$ satisfies $(\textsf {CAC'})_{3.1}$ and $(\textsf {CC})_{3.2}$, and ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }} \subset \mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})$ is any closed Markovian subspace. Then the following hold:

• if $(\textsf {CI})_{4.1}$, $(\textsf {QR})_{3.20}$ and $(\textsf {R})_{2.8}$ hold, then (b) $\implies$ (c);

• if ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$ holds, then (c) $\implies$ (b).

Proof

(b) $\implies$ (a). We argue by contradiction. Assume (b) and suppose that ${\mu }$ is not tail trivial. Then, there exists a tail-measurable set $\Xi \in {\mathscr {T}}({\varvec{\Upsilon }})$ so that ${\mu }(\Xi ), {\mu }(\Xi ^c)>0$. Note that $\Xi \in {\mathscr {B}}(\tau _\text {v} )$ as ${\mathscr {T}}({\varvec{\Upsilon }}) \subset {\mathscr {B}}(\tau _\text {v} )$ by construction. Also note that ${\mathcal {T}}(\Xi )=\Xi$ and ${\mathcal {T}}(\Xi ^c)=\Xi ^c$ as $\Xi , \Xi ^c \in {\mathscr {T}}({\varvec{\Upsilon }})$, where ${\mathcal {T}}(\Xi )$ is the tail set of $\Xi$ defined in (2.30). By (b), we have

$$\begin{aligned} \bar{\textsf {d} }_{{\varvec{\Upsilon }}}^{\mu }(\Xi , \Xi ^c)<\infty {.}\end{aligned}$$

(4.16)

By (2.22), this implies that there exist $\gamma ^1 \in \Xi$, $\gamma ^2 \in \Xi ^c$ and $r \in {{\mathbb {N}}}$ so that

$$\begin{aligned} \gamma ^1_{B_r^c} = \gamma ^2_{B_r^c} {,}\quad \gamma ^1(B_r)=\gamma ^2(B_r) {.}\end{aligned}$$

This however means that $\gamma ^1, \gamma ^2 \in {\mathcal {T}}(\Xi ) \cap {\mathcal {T}}(\Xi ^c) = \Xi \cap \Xi ^c=\emptyset$, which is a contradiction.

(a) $\implies$ (b). We argue by contradiction. Assume (a) and suppose that (b) does not hold. Then, there exist $\Xi , \Lambda \subset {\varvec{\Upsilon }}$ with ${\mu }(\Xi ), {\mu }(\Lambda )>0$ so that $\bar{\textsf {d} }_{{\varvec{\Upsilon }}}^{\mu }(\Xi , \Lambda )=\infty$. By modifying a ${\mu }$-negligible set in $\Xi$ (without relabelling $\Xi$), we have that

$$\begin{aligned} \bar{\textsf {d} }_{{\varvec{\Upsilon }}}(\cdot , \Lambda ) = \infty \quad \text {everywhere on } \Xi {.}\end{aligned}$$

(4.17)

Let $\Omega _\textsf {rig}$ be the set defined in the proof of (ii) of Theorem  4.3. Let $\tilde{\Lambda }:=\Lambda \cap \Omega _\textsf {rig}$. As $\tilde{\Lambda } \subset \Lambda$, we have

$$\begin{aligned} \infty =\bar{\textsf {d} }_{\varvec{\Upsilon }}(\cdot , \Lambda ) \le \bar{\textsf {d} }_{\varvec{\Upsilon }}(\cdot , \tilde{\Lambda }) \quad \text {everywhere on } \Xi {.}\end{aligned}$$

(4.18)

By (a), we have ${\mu }({\mathcal {T}}(\Xi ))={\mu }({\mathcal {T}}(\tilde{\Lambda }))=1$ as ${\mu }(\Xi ), {\mu }(\tilde{\Lambda })>0$, $\Xi \subset {\mathcal {T}}(\Xi )$ and $\tilde{\Lambda }\subset {\mathcal {T}}(\tilde{\Lambda })$. Therefore, ${\mu }({\mathcal {T}}(\Xi ) \cap \tilde{\Lambda })>0$ and ${\mathcal {T}}(\Xi ) \cap \tilde{\Lambda } \ne \emptyset$. Take $\gamma \in {\mathcal {T}}(\Xi ) \cap \tilde{\Lambda }$. By the definition of the tail-operation ${\mathcal {T}}$ and $(\textsf {R})_{2.8}$, there exist $\eta \in \Xi$ and $r \in {{\mathbb {N}}}$ so that

$$\begin{aligned} \gamma _{B_r^c}= \eta _{B_r^c} {,}\quad \gamma (B_r) = \eta (B_r) {.}\end{aligned}$$

Thus, by (2.22), we obtain $\bar{\textsf {d} }_{\varvec{\Upsilon }}(\gamma , \eta )<\infty$, which contradicts (4.18).

(b) $\implies$ (c). By (b) $\implies$ (a) and (a) $\implies$ (c) by (ii) of Theorem  4.3, we conclude (c).

(c) $\implies$ (b). By ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$, Proposition 2.3 and $\bar{\textsf {d} }_ {\varvec{\Upsilon }}(\cdot , \Lambda ) \wedge c \in \text {Lip} _b^1(\bar{\textsf {d} }, {\mu })$, it holds that

$$\begin{aligned} \bar{\textsf {d} }_{\varvec{\Upsilon }}(\cdot , \Lambda )\wedge c \in {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}, \quad \Gamma ^{{\varvec{\Upsilon }}, {\mu }}(\bar{\textsf {d} }_{\varvec{\Upsilon }}(\cdot , \Lambda ) \wedge c) \le 1 {,}\quad c >0{.}\end{aligned}$$

Let $\bar{\textsf {d}}_{\mu , \Lambda }$ be the maximal function associated with $\big ({\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }},{\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}}\big )$ defined in (2.4). By the definition of the maximal function $\bar{\textsf {d}}_{\mu , \Lambda }$, we obtain that

$$\begin{aligned} \bar{\textsf {d} }_{\varvec{\Upsilon }}(\cdot , \Lambda ) \wedge c \le \bar{\textsf {d}}_{\mu , \Lambda } \wedge c \quad {\mu }\text {-a.e.}{.}\end{aligned}$$

Passing to the limit $c \rightarrow \infty$, we obtain

$$\begin{aligned} \bar{\textsf {d} }_{{\varvec{\Upsilon }}}(\cdot , {\Lambda }) \le \bar{\textsf {d}}_{\mu , {\Lambda }} {,}\quad \Lambda \in {\mathscr {B}}(\tau _\text {v} ) {.}\end{aligned}$$

(4.19)

which leads to

$$\begin{aligned} \bar{\textsf {d} }^{\mu }_{{\varvec{\Upsilon }}}(\Xi ,\Lambda ) \le \mu \text {-}{\mathop {\text { essinf}}\limits _{\Xi }}\,\bar{\textsf {d}}_{\mu , \Lambda }{.}\end{aligned}$$

By Hino and Ramírez [27, Lemma 2.16], (c) implies $\mu \text {-}{{\,\textrm{essinf}\,}}_{\Xi }\bar{\textsf {d}}_{\mu , \Lambda }<\infty ,$ which concludes (b). $\square$

Corollary 4.7

Let ${\mu }$ be a Borel probability measure on ${\varvec{\Upsilon }}$ satisfying $(\textsf {CAC'})_{3.1}$, $(\textsf {CC})_{3.2}$, and let ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }} \subset \mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})$ be any closed Markovian subspace. Then the following hold.

• If $(\textsf {CI})_{4.1}$, $(\textsf {QR})_{3.20}$ and $(\textsf {R})_{2.8}$ hold, then

  $$\begin{aligned} {\mu }\text { is tail trivial} \quad \implies \quad (\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}) \text { is irreducible} \; \end{aligned}$$

• If ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$ holds for ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$,

  $$\begin{aligned} (\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}) \text { is irreducible}\quad \implies \quad {\mu }\text { is tail trivial} {.}\end{aligned}$$

Remark 4.8

We proved the implication (c) $\implies$ (b) in Theorem  4.3 under $(\textsf {D})_{3.13}$ with the domain $\mathscr {D}(\mathcal {E}^{{\varvec{\Upsilon }}, {\mu }})$. The same implication was proved in Corollary 4.7 under a different assumption ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$ with a smaller domain ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$. The assumption $(\textsf {D})_{3.13}$ is a condition for the truncated forms ${\mathcal {E}}_r^{{\varvec{\Upsilon }}, {\mu }}$ while ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$ is a condition for $({\mathcal {E}}^{{\varvec{\Upsilon }},{\mu }}, {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }})$. We do not have a simple comparison of these two different conditions: as the irreducibility with a smaller domain is a weaker statement than that with a larger domain, Corollary 4.7 looks providing the tail-triviality under a weaker assumption than Theorem  4.3. However, we do not know whether ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$ is weaker than $(\textsf {D})_{3.13}$. For the verification, Corollary 4.7 is more convenient as will be seen in Sect. 5.

5 Verifications of the main assumptions

In this section, we provide sufficient conditions for the verification of the main assumptions in Theorems 4.3,  4.6. See Examples 2.7, 2.9 for the tail triviality $(\textsf {T})_{2.6}$ and the number rigidity $(\textsf {R})_{2.8}$, and see Sect. 3.5 for the quasi-regularity $(\textsf {QR})_{3.20}$.

Quasi-Gibbs measures. We recall the definition of quasi-Gibbs measures. Several slightly different (possibly non-equivalent) definitions for this concept were introduced by H. Osada, see e.g. [40, Definition 2.1], [42, Dfn. 3.1], [41, Definition 5.1], or [43, Definition 2.2].

Let $\Phi :{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}$ be ${\mathscr {B}}(\tau _\text {v} )$-measurable, and by $\Psi :({{\mathbb {R}}}^n)^{\scriptscriptstyle {\times 2}}\rightarrow {{\mathbb {R}}}$ be ${\mathscr {B}}(\tau _\text {v} )^{\scriptscriptstyle {\otimes 2}}$-measurable and symmetric. The function $\Phi$ will be called the free potential, and $\Psi$ the interaction potential. These potentials define a Hamiltonian $\mathscr {H}_r:{\varvec{\Upsilon }}\rightarrow {{\mathbb {R}}}$ as

$$\begin{aligned} \mathscr {H}_r:\gamma \longmapsto \Phi ^{\star }\gamma _{B_r}+\tfrac{1}{2}\Psi ^{\star }\big ({\gamma _{B_r}^{\scriptscriptstyle {\otimes 2}}}\big ){,}\quad \gamma \in {\varvec{\Upsilon }}{.}\end{aligned}$$

Recall that ${\mathcal {K}}_r^\eta :=\{k \in {{\mathbb {N}}}_0: {\mu }_r^\eta ({\varvec{\Upsilon }}^k(B_r))>0\}$ has been defined in Definition 3.1.

Definition 5.1

(Quasi-Gibbs measures, cf. [43, Definition 2.2]) We say that a Borel probability ${\mu }$ on ${\varvec{\Upsilon }}$ is a $(\Phi ,\Psi )$-quasi-Gibbs measure if there exists a sequence $\{B_r\}_{r\in {{\mathbb {N}}}}$ of compact monotone increasing domains covering ${{\mathbb {R}}}^n$ so that, for ${\mu }$-a.e. $\eta \in {\varvec{\Upsilon }}$, every $r \in {{\mathbb {N}}}$, every $k\in {\mathcal {K}}_r^\eta$, there exists a constant $c_{r,\eta ,k}>0$ so that

$$\begin{aligned} c_{r,\eta ,k}^{-1}\, e^{-\mathscr {H}_r} \cdot {\pi }_{\textsf {m} _r}\!\downharpoonright _{{\varvec{\Upsilon }}^{k}(B_r)} \ \le {\mu }_r^{\eta , k} \ \le \ c_{r,\eta ,k}\, e^{-\mathscr {H}_r} \cdot {\pi }_{\textsf {m} _r}\!\downharpoonright _{{\varvec{\Upsilon }}^{k}(B_r)}{.}\end{aligned}$$

(5.1)

For quasi-Gibbs measures, $(\textsf {CAC'})_{3.1}$ follows immediately by (5.1).

Remark 5.2

• (a) The definition of quasi-Gibbs measures in [43, Definition 2.2] looks slightly different from Definition 5.1 as we assume (5.1) only for $k\in {\mathcal {K}}_r^\eta$ in place of $k\in {{\mathbb {N}}}$. These two definitions are, however, equivalent since the definitions of ${\mu }_r^{\eta , k}$ in this article is the restriction on ${\varvec{\Upsilon }}^k(B_r)$:

  $$\begin{aligned} {\mu }_r^{\eta , {k}}:={\mu }_r^\eta \!\downharpoonright _{{\varvec{\Upsilon }}^k(B_r)} {,}\end{aligned}$$

  while the corresponding measure in [43, Definition 2.2] has been defined as the measure conditioned on ${\varvec{\Upsilon }}^k(B_r)$.

• (b) “${\mu }$ belongs to $(\Phi ,\Psi )$-quasi-Gibbs measures” does not necessarily mean that ${\mu }$ is governed by the free potential $\Phi$ in the sense of the DLR equation. The symbol $\Phi$ here just plays a role as representative of the class of $(\Phi ,\Psi )$-quasi-Gibbs measures modulo perturbations by adding locally finite free potentials. To be more precise, noting that the constant $c_{r,\eta ,k}$ can depend on $r, \eta , k$, if ${\mu }$ is $(\Phi ,\Psi )$-quasi-Gibbs, then ${\mu }$ is $(\Phi +\Phi ',\Psi )$-quasi-Gibbs as well whenever $\Phi '|_{B_r}$ is bounded for every $r \in {{\mathbb {N}}}$. Therefore, in this case, we may write $(0,\Psi )$-quasi-Gibbs instead of $(\Phi ,\Psi )$-quasi-Gibbs.

Example 5.3

(See [41]) The class of quasi-Gibbs measures includes all canonical Gibbs measure, and the laws of some determinantal/permnental point processes, as for instance:

• (1) mixed Poisson measures;

• (2) canonical Gibbs measures;

• (3) the laws of some determinantal/permanental point processes and related point processes, e.g., $\text {sine}_\beta$, $\text {Bessel}_{\alpha ,\beta }$, $\text {Airy}_{\beta }$ ($\beta =1,2,4$) and Ginibre point processes.

5.1 Assumption $(\textsf {CC})_{3.2}$

According to Remark 3.3 and (5.1), The Conditional Closability $(\textsf {CC})_{3.2}$ holds if

$$\begin{aligned} e^{-\mathscr {H}_r}|_{{\varvec{\Upsilon }}^k(B_r)} \in C_b\bigl ({\varvec{\Upsilon }}^k(B_r)\bigr ) \quad k \in {{\mathbb {N}}}_0\, \quad r \in {{\mathbb {N}}}{.}\end{aligned}$$

(5.2)

Remark 5.4

While (5.2) is sufficient to cover all the examples discussed in Sect. 6, it is not necessary for $(\textsf {CC})_{3.2}$. Condition $(\textsf {CC})_{3.2}$ holds true if ${\mu }$ satisfies super-stability and lower regularity in the sense of Ruelle [39, 47], or the existence of upper semi-continuous bounds $(\Phi _0,\Psi _0)$ such that

$$\begin{aligned} c\, \Phi _0\le \Phi \le c^{-1} \Phi _0{,}\quad c\,\Psi _0\le \Psi \le c^{-1}\Psi _0 \end{aligned}$$

for some constant $c>0$, see [40, Eq. (A.3), p. 8]) and also [38, 39].

5.2 Assumptions $(\textsf {CI})_{4.1}$

In this subsection, we verify Assumptions $(\textsf {CI})_{4.1}$.

Assumption 5.5

Let $\mu$ be a quasi-Gibbs measure on ${\varvec{\Upsilon }}$ satisfying $(\textsf {CC})_{3.2}$, and suppose

• (1) there exists a closed $\textsf {m}$-negligible set $F\subset {{\mathbb {R}}}^n$ so that the free potential $\Phi$ of $\mu$ satisfies $\Phi \in L^\infty _{loc}({{\mathbb {R}}}^n{\setminus } F, \textsf {m} )$;

• (2) there exists a closed $\textsf {m} ^{\otimes 2}$-negligible set $F^{[2]}\subset {{\mathbb {R}}}^n \times {{\mathbb {R}}}^n$ so that the interaction potential $\Psi$ of $\mu$ satisfies $\Psi \in L^\infty _{loc}\bigl ({{\mathbb {R}}}^n \times {{\mathbb {R}}}^n {\setminus } F^{[2]},\textsf {m} ^{\otimes 2} \bigr )$.

Proposition 5.6

(Sufficient conditions for $(\textsf {CI})_{4.1}$ [14, Proposition 7.13]) Under Assumption 5.5, $(\textsf {CI})_{4.1}$ holds.

Proof

Noting that $(\textsf {CI})_{4.1}$ follows from the conditional Sobolev-to-Lipschitz property proven in [14, Proposition 7.13], we conclude the statement. $\square$

5.3 Markovian subspace with $(\textsf {QR})_{3.20}$ and  ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$

The quasi-regularity $(\textsf {QR})_{3.20}$ follows if ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ is chosen to be the closure of either:

• $\text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, \tau _\text {v} )$ or $\text {Lip} _b({\textsf {d} }_{\varvec{\Upsilon }}, \tau _\text {v} )$ by Corollary 3.22;

• smooth local functions ${\mathscr {D}}_\infty$ (see [38, Theorem 1]).

In the first case, Proposition 3.21 provides $(\textsf {Rad}_{\bar{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }})$, $(\textsf {Rad}_{{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }})$ respectively. For all these cores, the Markovian property of ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ has been proven in Proposition 3.21.

Corollary 5.7

(Corollary 3.22, Proposition 3.21) Let ${\mu }$ be a quasi-Gibbs measure.

• (i) If either ${\mathcal {C}}=\text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, \tau _\text {v} )$, or ${\mathcal {C}}=\text {Lip} _b({\textsf {d} }_{\varvec{\Upsilon }}, \tau _\text {v} )$, then ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}=\overline{{\mathcal {C}}}$ is Markovian and

  $$\begin{aligned} \text {}(\textsf {QR})_{3.20} \text { holds for } {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}\; \end{aligned}$$

• (ii) If ${\mathcal {C}}=\text {Lip} _b(\bar{\textsf {d} }_{\varvec{\Upsilon }}, \mu )$ (resp. ${\mathcal {C}}=\text {Lip} _b({\textsf {d} }_{\varvec{\Upsilon }}, \mu )$ $)$, then ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}=\overline{{\mathcal {C}}}$ is Markovian and

  $$\begin{aligned} \text {}{\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21} (resp.~(\textsf {Rad}_{{\textsf {d} }_{\varvec{\Upsilon }}, {\mu }})) \text { holds for } {\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}{.}\end{aligned}$$

6 Examples

Based on verifying the sufficient conditions provided in the previous section, we provide several examples to which our main results (Theorems 4.3, 4.6) applies. In the following, we discuss four classes of examples: $\text {sine}_2$, $\text {Airy}_2$, $\text {Bessel}_{\alpha ,2}$ ($\alpha \ge 1$), and $\text {Ginibre}$ point processes. They belong to the class of quasi-Gibbs measures as explained below, in particular, $(\textsf {CAC'})_{3.1}$ holds true. As all the examples discussed in the following are determinantal point processes, the tail triviality $(\textsf {T})_{2.6}$ is a consequence of e.g., [31, Theorem 2.1] (see Example 2.9 for more complete references).

As noted in (b) in Remark 5.2, the class of $(\Phi ,\Psi )$-quasi-Gibbs measures is stable under perturbations of $\Phi$ in terms of adding locally bounded free potentials. As seen in [40, Theorem 2.2], [42, Theorem 5.6] and [40, Theorem 2.3], the free potentials $\Phi$ representing the classes of quasi-Gibbs measures in the cases of $\text {sine}_2$, $\text {Airy}_2$, and $\text {Ginibre}$ are locally bounded, therefore $\Phi$ can be reduced to the representative

$$\begin{aligned} \Phi \equiv 0. \end{aligned}$$

Thus, we only discuss the interaction potentials $\Psi$ for the cases below.

Example 6.1

($\text {sine}_2$) By Osada [40, Theorem 2.2], the $\text {sine}_2$ ensemble belongs to the class of $(0,\Psi )$-quasi-Gibbs measures with the interaction potential

$$\begin{aligned} \Psi (x, y):=-2\log |x-y|, \quad x, y \in {{\mathbb {R}}}. \end{aligned}$$

Assumption $(\textsf {CC})_{3.2}$ follows from (5.2). Assumptions $(\textsf {CI})_{4.1}$ can be verified immediately by Proposition 5.6 by noting that Assumption 5.5 is satisfied by taking $F^{[2]}=\{(x, y) \in {{\mathbb {R}}}^{\times 2}: x=y\}$ as $\Psi \in L^\infty _{loc}({{\mathbb {R}}}^{\times 2} {\setminus } F^{[2]}, \textsf {m} ^{\otimes 2})$. The number rigidity $(\textsf {R})_{2.8}$ has been proved by Ghosh [23, Theorem 4.2] and Chhaibi and Najnundel [10]. A Markovian subspace ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ having the quasi-regularity $(\textsf {QR})_{3.20}$ and ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$ has been constructed in Corollary 5.7. We remark that the quasi-regularity $(\textsf {QR})_{3.20}$ with respect to ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}=\overline{{\mathscr {D}}}_\infty$ has been shown by a combination of Osada [40, Corollary 4.1] and [38, Theorem  1].

Example 6.2

($\text {Airy}_2$) By Osada [42, Theorem 4.7], the $\text {Airy}_2$ ensemble belongs to the class of $(0,\Psi )$-quasi-Gibbs measures with the interaction potential

$$\begin{aligned} \Psi (x, y):=-2\log |x-y|, \quad x, y \in {{\mathbb {R}}}. \end{aligned}$$

Thus the same arguments as in Example 6.1 apply to $(\textsf {CC})_{3.2}$,  $(\textsf {CI})_{4.1}$  and $(\textsf {QR})_{3.20}$. The number rigidity $(\textsf {R})_{2.8}$ has been proved in [9].

Example 6.3

($\text {Bessel}_{\alpha ,2}$, $\alpha \ge 1$) By Honda and Osada [26, Theorem 2.4], the class of measures $\text {Bessel}_{\alpha ,2}$ ($\alpha \ge 1$) belongs to the class of $(\Phi ,\Psi )$-quasi-Gibbs measures with potentials (the sign of the potentials in [26, Theorem 2.4] is opposite)

$$\begin{aligned} \Phi (x)=-\alpha \log x, \quad \Psi (x, y):=-2\log |x-y|, \quad x, y \in {{\mathbb {R}}}. \end{aligned}$$

Assumption $(\textsf {CC})_{3.2}$ follows from (5.2). Assumptions $(\textsf {CI})_{4.1}$ can be verified immediately by Proposition 5.6 by the same argument in Example 6.1 for $\Psi$. For $\Phi$, it suffices to take $F:=\{0\}$ in (i) in Assumption 5.5, with which $\Phi$ belongs to $L^\infty _{loc}({{\mathbb {R}}}{\setminus } F, \textsf {m} )$. The number rigidity $(\textsf {R})_{2.8}$ has been proved in [9]. A Markovian subspace ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ having the quasi-regularity $(\textsf {QR})_{3.20}$ and ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$ has been constructed in Corollary 5.7. We remark that the quasi-regularity $(\textsf {QR})_{3.20}$ with respect to ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}=\overline{{\mathscr {D}}}_\infty$ has been shown by combination of Honda and Osada [26, Theorem  2.4], Osada [40, Lemma 2.1] and [38, Theorem  1].

Example 6.4

($\text {Ginibre}$ ) By Osada [40, Theorem 2.3], the class of measures $\text {Ginibre}$ belongs to the class of $(\Phi ,\Psi )$-quasi-Gibbs measures with the interaction potential

$$\begin{aligned} \Psi (z_1, z_2):=-2\log |z_1-z_2|, \quad z_1, z_2 \in {{\mathbb {R}}}^{\times 2}. \end{aligned}$$

Assumption $(\textsf {CC})_{3.2}$ follows from (5.2). Assumptions $(\textsf {CI})_{4.1}$ can be verified immediately by Proposition 5.6. Note that Assumption 5.5 is satisfied since (ii) of Assumption 5.5 follows by taking $F^{[2]}=\{(x, y) \in ({{\mathbb {R}}}^{2})^{\times 2}: x=y\}$, with which $\Psi \in L^\infty _{loc}( ({{\mathbb {R}}}^{2})^{\times 2} {\setminus } F^{[2]}, \textsf {m} ^{\otimes 2})$. The number rigidity $(\textsf {R})_{2.8}$ has been proved by Ghosh and Peres [25, Theorem  1.1]. A Markovian subspace ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}$ having the quasi-regularity $(\textsf {QR})_{3.20}$ and ${\textsf {Rad}_{{\bar{\textsf {d} }}_{{\varvec{\Upsilon }}}, {\mu }}}_{3.21}$ has been constructed by Corollary 5.7. We remark that the quasi-regularity $(\textsf {QR})_{3.20}$ with respect to ${\mathcal {F}}^{{\varvec{\Upsilon }}, {\mu }}=\overline{{\mathscr {D}}}_\infty$ has been shown by combination of Osada [40, Corollary 4.1] and [38, Theorem  1].

Appendix A

Lemma A.1

[52, Lemma A.1] Let ${\mu }$ be a Borel probability on ${\varvec{\Upsilon }}$ satisfying that ${\mu }_r^\eta$ is absolutely continuous with respect to the Poisson measure $\pi _{\textsf {m} _r}$ for $r>0$ and ${\mu }$-a.e. $\eta$. Let $\Sigma \subset B_r$ so that $\textsf {m} _r(\Sigma ^c)=0$. Let $\Omega (r):=\{\gamma \in {\varvec{\Upsilon }}: \gamma _\Sigma =\gamma _{B_r}\}$. Then,

$$\begin{aligned} {\mu }\bigl (\Omega (r)\bigr )=1 \quad r>0 {.}\end{aligned}$$

Let $(\Omega , {\mathcal {F}}, P)$ be a probability space. Recall that, for a sequence $(A_n)$ of sets in ${\mathcal {F}}$, we define the limit superior of sets as

$$\begin{aligned} \limsup _{n \rightarrow \infty } A_n:=\bigcap _{n \ge 1} \bigcup _{j \ge n}A_j {.}\end{aligned}$$

By a simple application of the reverse Fatou’s lemma to the indicator function ${{\textbf {1}}}_{A_n^c}$, we see

$$\begin{aligned} P(\limsup _{n \rightarrow \infty } A_n) \ge \limsup _{n \rightarrow \infty } P(A_n) {.}\end{aligned}$$

Lemma A.2

Let $(\Omega , {\mathcal {F}}, P)$ be a probability space. Let $\{\Omega ^r_m\}_{m, r \in {{\mathbb {N}}}} \subset {\mathcal {F}}$ satisfy that, for any $\epsilon >0$, there exists $m_\epsilon$ so that for every $m \ge m_\epsilon$ and $r \in {{\mathbb {N}}}$,

$$\begin{aligned} P(\Omega ^r_m) \ge 1-\epsilon {.}\end{aligned}$$

Then, there exists $n \mapsto m_n \in {{\mathbb {N}}}$ with $m_{n} \le m_{n'}$ for $n \le n'$ so that

$$\begin{aligned} P\bigl (\limsup _{n \rightarrow \infty } \cap _{r=1}^n\Omega ^r_{m_n} \bigr ) = 1 {.}\end{aligned}$$

Proof

Define $\Omega ^{n, \epsilon }:=\cap _{r=1}^n \Omega ^r_{m_\epsilon }$. Then, by a simple application of Inclusion–Exclusion formula and the hypothesis $P(\Omega ^r_{m_\epsilon }) \ge 1-\epsilon$ for every $r \in {{\mathbb {N}}}$, it holds that

$$\begin{aligned} P(\Omega ^{n, \epsilon }) \ge 1-c(n) \epsilon {,}\end{aligned}$$

where c(n) is a constant monotone increasing in n. Let C(n) be a monotone increasing sequence so that $c(n)/C(n) <1$ and $c(n)/C(n) \downarrow 0$ as $n \rightarrow \infty$. Take $\epsilon _n:= \frac{1}{C(n)}$, and $\Omega ^{n}:=\Omega ^{n, \epsilon _n}$. By the upper semi-continuity of probability measures regarding the limit superior of sets, we obtain

$$\begin{aligned} P\bigl (\limsup _{n \rightarrow \infty }\Omega ^{n} \bigr ) \ge \limsup _{n\rightarrow \infty }P\bigl (\Omega ^{n} \bigr ) = \limsup _{n\rightarrow \infty }P\bigl (\Omega ^{n, \epsilon _n} \bigr ) \ge \lim _{n \rightarrow \infty } 1-\frac{c(n)}{C(n)} = 1 {.}\end{aligned}$$

The proof is complete. $\square$