1 Introduction

Stratospheric sudden warming (SSW) is one of the important weather processes that can affect the winter troposphere (Baldwin et al. 2021). The stratospheric polar vortex has formed in the Arctic stratosphere after autumn, and the polar vortex is strongest during the polar night (Waugh et al. 2017). However, this highly spinning weather system will be disrupted by SSWs, during which the upward propagating planetary waves cause the stratospheric polar vortex to shift, split, or even collapse (Charlton and Polvani 2007) and the temperatures in the polar region could rise significantly in a few days (Butler et al. 2015). There are two types of SSWs, major SSWs and minor SSWs. If the temperature gradient between 60° N and the pole reverses and the zonal-mean zonal wind at 60° N, 10 hPa reverses from westerly to easterly, the event is defined as a major SSW (Andrew 1987). The major SSW requires a reversal of the zonal winds at 60° latitude, while the minor SSW doesn’t. Studies show that SSWs have significant influences on the troposphere on the timescale of weeks to decades (e.g., Baldwin and Dunkerton 2001; Thompson and Wallace 2001; Reichler et al. 2012). Some minor SSWs occurred in the Northern Hemisphere (Wang and Chen 2010) and Southern Hemisphere (Hendon et al. 2019; Rao et al. 2020) were related to the weather anomalies in the troposphere, such as the bushfires in Australia (Lim et al. 2019).

Since SSWs have the potential to influence the weather and climate in the boreal winter, SSWs have received extensive attention from the science community, who want to find out whether there is any long-term trend in SSWs. There is high uncertainty in SSW trends simulated by models, e.g., simulations driven by the same greenhouse gases scenario obtain opposite trends in SSW frequency (e.g., Butchart et al. 2000). Rao and Garfinkel (2021) show that CMIP5/6 models project little change in the statistical characteristics of SSWs, including the duration, in the 21st century. Although recent model simulations showed that the increase of greenhouse gases after the industrial revolution would induce more SSWs (e.g., Schimanke et al. 2013), there is no significant increase in SSW frequency detected in the observation data until now. Domeisen (2019) inversely reconstructed the time series of SSW frequency since 1850 by utilizing the observed NAO index, which shows that there is high uncertainty in the SSW frequency and there is no trend in SSW frequency. Wang et al. (2017) analyzed the NCEP/NCAR reanalysis dataset and stated that from 1953 to 2016, the frequency of SSWs did not increase or decrease significantly. The result by Wang et al. (2017) is consistent with the previous research by Charlton and Polvani (2007), which stated that between the 1960 and 2000s, the number of SSWs did not show a recognizable trend. Although previous studies analyzed the frequency of SSWs, other characteristics of SSWs, such as the duration and strength, have not been analyzed. When analyzing interdecadal changes in SSWs, Li et al. (2018) combined minor SSWs and major SSWs together to analyze, in order to overcome the scarcity of major SSWs. The reason why these two types of SSWs can be analyzed together is that the dynamics of major SSWs and minor SSWs are quite similar Holton 1976; Matsuno 1971; Quiroz 1986). This article uses the same method in Li et al. (2018) to study the trend in the duration and strength of SSWs.

Many studies have found SSWs are influenced by the changes in tropical convective activities caused by sea surface temperature (SST) anomalies (e.g., Horel and Wallace 1981; Brönnimann 2007; Zhou et al. 2014; Zhang et al. 2015; Rao and Ren 2016a, b; Domeisen et al. 2019) or caused by the intraseasonal variability such as Madden-Julian Oscillation (MJO) (e.g., Garfinkel et al. 2012a; Garfinkel and Schwartz 2017; Kang and Tziperman 2017, 2018a, b). The vorticity perturbations triggered by the tropical convective activities propagate poleward and modulate planetary waves in the high latitude (Gill 1980; Seo and Son 2012; Lukens et al. 2017). Some studies such as Garfinkel et al. (2012b; Rao and Ren (2016a) revealed that some types of ENSO such as the moderate El Niño and the strong La Niña are much more efficient to impact the stratospheric polar vortex, because the tropical rainfall or convection anomalies induced by them are in the Central Pacific, while the convective activities of the strong El Niño or moderate La Niña are farther eastward. This inspires us to directly use convective activities to explain the trend in SSWs, considering that convective activities are the result of the combined effects of SSTs and various intraseasonal scale processes.

2 Data and method

2.1 Data

The meteorological fields are the National Centre for Environmental Prediction (NCEP) reanalysis dataset (Kalnay et al. 1996), which has a horizontal resolution of 2.5° × 2.5° and covers the period from 1948 to 2021. The Japanese 55-year (JRA55) Reanalysis dataset (Kobayashi et al. 2015; Harada et al. 2016) with a horizontal resolution of 1.25° × 1.25° is utilized to verify the trends in SSWs. The change in the tropical convective activities for the last 70 year cannot be directly derived from the precipitation or Outgoing Longwave Radiation (OLR) observations, since the observations are quite rare in the eastern Pacific before the satellites are used. An alternative method is to investigate the cloudiness, which is the total cloud amount from the observations of International Comprehensive Ocean-Atmosphere Data Set (ICOADS) (Woodruff et al. 2011) (https://data.nodc.noaa.gov/icoads/). The precipitation data for comparison and verification is derived from GPCP version 2.3 combined Precipitation Data Set (Adler et al. 2003). The SST data is the bucket-sampled SST from ICOADS. The solar irradiance is the radio emission from the Sun at a wavelength of 10.7 centimeters provided by Natural Resources Canada (http://www.spaceweather.ca/solarflux/sx-5-eng.php).

2.2 Definitions

The duration of SSWs is the number of days when the gradient of temperature between 60°–90° N at 10 hPa becomes positive. The strength of SSWs is defined as the maximum temperature gradient between 60°–90° N at 10 hPa during December to February. There is no SSW in the winters of 1948, 1949, 1952, 1954, 1955, 1956, 1957, 1960, 1963, 1966, 1969, 1975, 1985, 1996 and 2010, then the duration of SSWs should be 0 day. Although the maximum temperature gradients of these winters don’t represent the SSW strength, to keep the continuity of the time series when calculating the trend in the strength, the values of these winters are kept and shown as blue bars in Fig. 1b. The definition of SSWs based on temperature gradient would include both major and minor SSWs, which are not distinguished in this study.

Fig. 1
figure 1

Time series of a SSW duration (unit: days) and b SSW strength (unit: K/°) in winter (DJF) from 1948 to 2020 derived from NCEP. c SSW duration and d SSW strength from 1958 to 2020 derived from JRA55. The blue lines illustrate the linear trends

Full size image

The first leading mode (PC1) and the second leading mode (PC2) of winter North Pacific SST are calculated by the empirical orthogonal function (EOF) analysis following Li et al. (2018). PC1 and PC2 represent Pacific Decadal Oscillation (PDO) and Victoria mode of winter North Pacific SST, respectively.

The atmospheric heat source cannot be directly observed, while it can be measured with the reverse method by regarding the net heat source as the remaining term in the thermodynamic conservational equation. According to Ding (1989), the heat source Q1 is

$${Q}_{1}={c}_{p}\left[\frac{\partial T}{\partial t}+V\cdot \nabla T+{\left(\frac{P}{{P}_{0}}\right)}^{\kappa }\omega \frac{\partial \theta }{\partial p}\right]$$
(1)

where \({P}_{0}=1000 \text{h}\text{P}\text{a}\), \(\kappa =\frac{R}{{C}_{p}}\), R, and Cp are the gas constant and the specific heat at constant pressure of dry air, and θ is the potential temperature. Integrating Eq. (1) from 100 hPa to the surface pressure Ps, we obtain

$$\left\langle {{\text{Q}}_{1} } \right\rangle = \frac{1}{{\text{g}}}\int _{{100}}^{{p_{s} }} {\text{Q}}_{1} {\text{d}}_{p}$$
(2)

The monthly indices of Pacific North America (PNA), Western Pacific (WP) and North Atlantic Oscillation (NAO) are calculated by the Rotated Principal Component Analysis (RPCA) (Barnston and Livezey 1987), downloaded from NOAA Climate Prediction Center.

The Eliassen–Palm fluxes (EP fluxes) are calculated in log-pressure coordinates using the method given by Andrews et al. (1987):

$$F^{{\left( \phi \right)}} = \rho a\;\cos \phi \left( {\frac{{\overline{{\nu ^{\prime } \theta ^{\prime } }} }}{{\bar{\theta }_{z} }}\bar{u}_{z} - \overline{{\nu ^{\prime } u^{\prime } }} } \right)$$
(3)
$$F^{{(z)}} = \rho a\cos \phi \left[ {\left( {f - \frac{1}{{a\cos \phi }}(\bar{u}\cos \phi )_{\phi } } \right)\left( {\overline{{v^{\prime}\theta ^{\prime}}} } \right)/\overline{{\theta _{z} }} - \overline{{w^{\prime}u^{\prime}}} } \right]$$
(4)

The divergence of EP fluxes is defined as

$$\nabla \cdot {\text{F}}=\frac{1}{{a\cos \phi }}\frac{\partial }{{\partial \phi }}({F^{(\phi )}}cos\phi )+\frac{\partial }{{\partial z}}({F^{(z)}})$$
(5)

where u, v, and w are components of the vector wind, θ is the potential temperature, subscripts indicate derivatives, primes indicate deviations from the zonal mean and overbars indicate a zonal mean, a is the mean of Earth radius, z is the height in the log-pressure coordinate, \(\phi\) is latitude, H is the mean scale height of the atmosphere, \(\rho ={\rho _s}\exp ( - z/H)\) is the standard air density, \({\rho _s}\) is the sea level air density.

2.3 Statistics

Linear Regression is utilized to estimate the contribution of the driving variable X to the trend in the climate variable Y. The equation is

$$Y\left(i\right)={\alpha }_{0}+{\alpha }_{1}\times X\left(i\right)+r\left(i\right)$$
(6)

The ordinary least-squares estimation is utilized to obtain \({\alpha }_{0}\) and \({\alpha }_{1}\). \(Y\left(i\right)\) is a climate variable, which can represent the SSW duration, SSW strength, PW1, or PW2 in the following analysis. \(X\left(i\right)\) represents the driving factor such as the time series of cloudiness, NAO, PC1, PC2 or the solar irradiance. \(r\left(i\right)\) is the residual term.

$$X\left(i\right)={X}_{trend}\left(i\right)+{X}_{noise}\left(i\right)$$
(7)

The trend in the climate variable X is represented by \({X}_{trend}\left(i\right)\). The linear regression is a simple and convenient method to describe \({X}_{trend}\left(i\right)\) by the slope, β1. The equation is

$$X\left(i\right)={\beta }_{0}+{\beta }_{1}\times T\left(i\right)+{X}_{noise}\left(i\right)$$
(8)

\(T\left(i\right)\) is the time variable corresponding to \(X\left(i\right)\). The ordinary least-squares estimation is used to obtain \({\beta }_{0}\) and \({\beta }_{1}\). The detail can be found in Mudelsee (2019).

Substituting (8) into (6), we get

$$Y\left(i\right)={\alpha }_{1}{\beta }_{1}T\left(i\right)+r\left(i\right)$$
(9)

\({\alpha }_{1}{\beta }_{1}\) represents the contribution of the driving variable X to the trend in the climate variable Y. The trend of Y is the sum of the trend driven by X and the trend of the residual term. The trend of the residual term reflects the impacts of other driving factors.

Student’s t-test assesses the statistical significance of the trends in this study.

3 The trends in SSWs and tropical Pacific convection

Figure 1 shows the time series of the duration and strength of SSWs in winter. It can be seen from the NCEP data that although SSWs have a large inter-annual variability, during the period of 1948–2003, the increasing trend in the duration and strength of SSWs are statistically significant above 99% confidence level. But after 2003, the increasing trends in the duration and strength of SSWs did not continue. In the NCEP data, the increasing rate of the SSW duration and the SSW strength during 1948–2003 is 0.36 day/year and 0.006 K/°/year. Through JRA55, it further verified that SSWs had a growing trend before 2003. Since the starting year of JRA55 is 1958, the trend calculated from JRA55 is assigned to 1958–2003. In the JRA55 dataset, the increasing rate of the SSW duration and the SSW strength is 0.34 day/year and 0.007 K/°/year. Since there are consistent trends in both datasets, the following research is based on NCEP data. The correlation coefficient between the duration and the strength of SSWs is 0.7, which implies the winter with longer SSWs tends to have stronger SSWs. This is consistent with the study of the single SSW events, which shows that the SSW is more likely to have greater strength when it lasts longer (Li and Tian 2017).

According to whether an SSW event is driven by planetary waves originated from the troposphere or caused by the resonant wave amplification in the stratosphere, SSWs can be divided into non-self-generated SSWs and self-generated SSWs (Liu and Roble 2002). Mechanisms such as the blocking of PW2 (Smith and Avery 1987), the resonance of upper tropospheric stationary wave and stratospheric traveling wave (Plumb 1981) are proposed to explain the self-generated SSWs. In this research, the self-generated SSW days were selected by the following method, which is inspired by the method of distinguishing displacement SSWs and splitting SSWs (Ayarzagüena et al. 2019). The daily 200 hPa geopotential heights at 60° N are Fourier decomposed into PW1, PW2 and PW3 amplitudes. A day was defined as a self-generated SSW if the averaged amplitudes of PW1, PW2 and PW3 for [−10, 0] days before the SSW date are less than their winter climatology mean. Otherwise, the SSW days were defined as non-self-generated SSWs, which implies these SSWs are driven by the PW originated from the troposphere. The result is shown in Fig. 2. The duration of self-generated SSWs doesn’t have a long-term trend, but there was a peak in the 1960s. The peak of self-generated SSWs accounted for a considerable proportion of SSWs in the 1960s, which makes the increasing trend in SSWs less significant. After removing self-generated SSWs, the trend in the non-self-generated SSW duration from 1948 to 2003 is more significant. The long-term trend in SSWs is mainly driven by PW from the troposphere.

Fig. 2
figure 2

Time series of the duration (unit: days) of a self-generated and b non-self-generated SSWs from 1948 to 2020 derived from NCEP

Full size image

Due to the inter-annual variabilities of SSWs are remarkable, no matter what statistical method is adopted, the selection of the turning point of the trends in SSWs cannot be very accurate. For NCEP data, we set 1948 as the starting point, and use different endpoints to calculate the trends in the SSW duration (Fig. 3b). If 2003 is chosen as the endpoint, the trend in the SSW duration reaches the maximum. For JRA55 data, we set 1958 as the starting point, the result is almost the same as the result in NCEP. Figure 3c discusses the trends in the SSW strength calculated by selecting different endpoints. Although the selection of 2003 as the endpoint cannot make the trend in the SSW strength reach the maximum, it is still close to the maximum. Thus, choosing 2003 or early 2000s as the turning point to analyze the SSW trends and explore the influencing factors is suitable. In the lower row of Fig. 3, the endpoints of the trends are fixed at 2003 and the starting points are changed. The trends in the duration and strength of SSWs are statistically reliable if the starting points are selected before the 1960 s. The Mann-Kendall test (Gocic and Trajkovic 2013; Jaiswal et al. 2015) is used to test the monotonic trends before and after 2003. The results of the Mann-Kendall test show that there are monotonic increasing trends in the duration and strength of SSWs before 2003, which is significant at the 99% confidence level. The downward trends in SSWs after 2003 exist, but they have not passed the test.

Fig. 3
figure 3

The trends of a, d cloudiness (unit: okta/year), b, e SSW duration (unit: day/year), and c, f SSW strength (unit: K/°/year) calculated from a fixed start point to different endpoint (upper row), and from a fixed endpoint to different start point (bottom row). The years in the abscissa correspond to the different endpoints or start points. The black line in a, d is calculated from the time series in Fig. 4b. The blue line in b, e and c, f is calculated from the time series of Fig. 1a and b, and the orange line is calculated from the time series of Fig. 1c and d. Solid lines pass 99% confident level

Full size image

Figure 4a shows the trends in the cloudiness in the tropical Pacific region during 1948–2003, which implies the convective activities in the box region of 170° W–110° W, 18° S–3° N has increased significantly. Deser et al. (2010) found an eastward extension of atmospheric deep convection from the Maritime Continent to the central equatorial Pacific. The pattern of enhanced convective activities given by Deser et al. (2010) is similar to the pattern of increased cloudiness in Fig. 4a. Figure 4b shows the interannual variation of the winter-mean cloudiness averaged in the box region. During 1948–2003, the enhancement trend of cloudiness is statistically significant above the 99% confidence level, and the trend of enhancing convection ceased after 2003. The trend of the winter-mean cloudiness during 1948–2003 is 0. 18 okta/10 year. The turning point of the trend in the cloudiness is chosen based on Fig. 3a. Since the inter-annual variability of cloudiness is much smaller than that of SSW, the curve in Fig. 3a is smoother and reliable. The Mann-Kendall test shows that the monotonic upward trend in the cloudiness before 2003 is significant at the 99% confidence level, while the trend after 2003 has not passed the test. The curve in Fig. 3a is similar to that in Fig. 3b, which implies that there is a certain physical mechanism connection between the cloudiness and the duration of SSWs.

Fig. 4
figure 4

a Trends of winter cloudiness in the tropical Pacific region for 1948–2003 (unit: 10−3 okta/year). The trends over the black dotted regions are statistically significant at the 95% confidence level. The range of the box is [170° W–110° W, 18° S–3° N]. b Time series of winter cloudiness of the box region (unit: okta) for 1948–2020 and its trend. The cloudiness is observed data from ICOADS

Full size image

In this study, we adopt the cloudiness to measure the convective activities. Whether the cloudiness is capable of representing the convective activities in the tropical Pacific is assessed in Fig. 5a, which shows that the climatological pattern of cloudiness is consistent with that of precipitation. Figure 5b shows the cloudiness and precipitation have a proportional relationship in the interannual time scale. Thus, the cloudiness can replace the precipitation to indicate the convective activities in the box region. Winter tropical convective anomalies can release a large amount of latent heat energy, heating the atmosphere around, which would furtherly modulate circulations outside tropics (Guo et al. 2017). Figure 5b also shows the heating source in the box region is proportional to the intensity of convective activities. When the cloudiness in the box region is above (below) 4.5 okta, the values of the tropospheric heat source are above (below) zero, which means the troposphere in the box region is a heat source (sink). Figure 5d only lists the time series in which the winter heat source is positive. It can be seen that the heat source has a positive trend from 1948 to 2003.

Fig. 5
figure 5

a Climatological winter cloudiness (unit: okta) (color shadings) and precipitation rate (unit: mm/day) (contour). The precipitation data is derived from GPCP Version 2.3 Combined Precipitation Data Set for 1979–2020. b The scatter diagram of the winter cloudiness vs. precipitation rate (blue dots) and winter cloudiness vs. tropospheric heat source Q1 (unit: W/m2, orange dots). The tropospheric heat source is integrated from 1000 to 100 hPa over the box region using Eq. (2). c The ratio of the increment of cloudiness during 1948–2003 and the climatology mean. d Time series of winter tropospheric heat source in the box region

Full size image

The box region chosen is based on Fig. 4a, where cloudiness shows a positive trend and passes the statistic test. The box region is also the minimum area of the climatological cloudiness. Convective activities in the box area are surrounded by the intertropical convergence zone (ITCZ) and the South Pacific convergence zone (SPCZ), forming a valley area of convective activities. However, the relative change in the cloudiness is the largest in the whole tropical Pacific area. The change of cloudiness in the box region during 1948–2003 can reach approximately 20% of the amount of climatological mean (Fig. 5c). The convective activity in this convection valley is one of the most important factors influencing the trend of SSW.

Previous studies have mentioned that the extratropical SST anomalies (Jadin et al. 2010; Woo et al. 2015; Li et al. 2018), NAO (Choi et al. 2020) and solar activity (Shindell et al. 1999) would modulate SSWs. SST variations in the extratropical Pacific such as PDO (Mantua et al. 1997), which is the first mode of North Pacific SST anomalies, and Victoria mode, which is the second mode of North Pacific SST anomalies are reported to be capable to modulate the interannual variations of SSWs (Bond et al. 2003; Woo et al. 2015; Li et al. 2018; Hu et al. 2018). Though it is difficult to relate a single SSW event with solar activity, evidence shows that solar activity would modulate stratospheric winds, which are related to the conditions for PW to be transported to the stratosphere (Kodera 1991). The polar night jet is influenced by solar activity as well (Kuroda and Kodera 2002). Positive NAO favors displacement SSWs (Choi et al. 2020). A regression model (Eq. 9) is utilized to compare the influence of different factors on the SSW trend during 1948–2003. The contributions of convective activities and other factors on the SSW trend are shown in Fig. 6. The majority of the trends in the duration and strength of SSWs can be obtained from the enhancement of convective activities in the box region. The contributions of NAO, the extratropical SST signals and solar activities to the SSW trends are negligible. The influencing factors involved in Fig. 6 are only part of the factors that affect SSWs. This research only states the convection in the tropical Pacific is one of the most important factors influencing the SSW trends. The possibility that other factors may have a greater impact on the SSW trends still exists.

Fig. 6
figure 6

Contributions of different variables on the trends of a SSW duration (unit: day/year) and b SSW strength (unit: K/°/year). The trends are calculated in the period of 1948–2003. NCEP denotes the trend derived from reanalysis data. Cloud denotes the trend in SSWs contributed by the cloudiness. NAO denotes the contribution of North Atlantic Oscillation. PC1 and PC2 denote the contribution of the first and the second leading modes of winter North Pacific SST. Solar denotes the contribution of the solar irradiance

Full size image

4 Mechanism of the convection enhancement modulating SSW trends

Figure 7a shows the patterns of 200 hPa geopotential height and winds regressed on the standardized winter cloudiness in the box region. A north-south symmetrical anticyclonic structure appears in the tropical Central Pacific, which is triggered by the tropical convective activities. According to previous works such as Hoskins et al. (1977) and Gill (1980), the vorticity perturbations would propagate along the spherical surface to mid-high latitudes. The correlation coefficient between the winter-mean PNA and cloudiness is 0.52. The correlation coefficient between winter-mean WP and cloudiness is 0.42, which illustrated the enhancement of the convective activities in the box region would induce a wave train similar to PNA and WP. When PNA and WP are in the positive (negative) phase at the same time, the duration and strength of SSWs are reported longer and stronger (shorter and weaker) (Li and Wen 2021). Figure 7b shows the patterns of 200 hPa geopotential height regressed on the standardized time series of the SSW duration. In the middle and high latitudes, there exist negative geopotential height anomalies over North Pacific to Siberia and positive height anomalies over Canada. The results here are similar to the precursor of SSW obtained by Garfinkel et al. (2012b) in areas outside the tropics. Comparing Fig. 7a and b, both from the perspectives of pattern and magnitude, the height anomalies associated with SSWs resemble the extratropical anomalies caused by the enhancement of convective activities.

Fig. 7
figure 7

a Patterns of 200 hPa geopotential height (unit: gpm; color shadings) and winds (unit: m/s; vectors) regressed on the standardized winter cloudiness in Fig. 4b. b Patterns of 200 hPa geopotential height regressed on the standardized SSW duration index in Fig. 1a. The regions of dots pass the significance test. The data of height, wind, cloudiness and SSWs are detrended before regression

Full size image

Since the stratosphere can only allow large-scale planetary waves to propagate upward, SSWs are mainly regulated by the break of these planetary waves. Figure 8 shows how the enhancement of convective activities impacts PW1 and PW2. When the convective activities are active in the box region, the trough of PW1 aroused by convective activities is located from Siberia to Aleutian Islands, and the crest of PW1 is located from Northeast Canada to North Atlantic (Fig. 8a). Since PW1 anomalies coincide with the climatological pattern, PW1 in the troposphere is enhanced. The troughs of the climatological PW2 are located in Hudson Bay in Canada and Siberia, and the crests of the climatological PW2 are located in Northern Europe and Alaska. The troughs of PW2 aroused by convective activities are located in Sakhalin and North Atlantic, and the crests of PW2 are located in Northern America and Northern Asia (Fig. 8b). Since the anomalies of PW2 are 45° out of phase with the climatological PW2, the changes of PW2 caused by convection enhancement are not significant. The changes of PW1 caused by convection enhancement are significant and occupy the main component in the changes of large-scale PW.

Fig. 8
figure 8

a Planetary wave 1 (PW1) and b planetary wave 2 (PW2) components of the 200 hPa geopotential height regressed on the standardized winter cloudiness. Black contour lines with the intervals of ± 10, ± 20, ± 30 gpm. The color-filled contours show the climatological pattern of PW1 and PW2

Full size image

The contributions of convective activities and other factors on the trends in PW1 and PW2 in the upper troposphere are shown in Fig. 9. The majority of the trend in PW1 during 1948–2003 is contributed by the enhancement of convective activities in the box region. Although the intensity of PW2 also shows an increasing trend during 1948–2003, the rate is smaller than that of PW1.

Fig. 9
figure 9

Contributions (unit: m3/s2/year) of different independent variables on the trends of a PW1 and b PW2 at 200 hPa. The trends are calculated in the period of 1948–2003. The abbreviations are the same as Fig. 6

Full size image

Figure 10a and b show the time series of 100 hPa vertical component of EP flux averaged from 45° N to 75° N. During 1948–2003, the increasing trend of PW1 in mid-to-high latitudes is statistically significant above 99% confidence level. But after 2003, PW1 shows a decreasing trend. The trends of PW1 and convective activity are consistent. The trends in PW2 and convective activities are not consistent. Figure 10c and d illustrate the change of large-scale planetary waves in the middle stratosphere. PW1 showed changes of rising first and then falling around 2003. The change of the trend of PW2 is not significant. In the lower stratosphere, the intensity of PW1 is 1.7 times that of PW2. In the middle stratosphere, the intensity of PW1 is 2.8 times that of PW2. This is because the stratosphere has a filtering effect on planetary waves, and planetary waves with a small wavenumber are more penetrating than those with a large wavenumber. Therefore, PW1 has a greater impact on the SSW trend than PW2.

Fig. 10
figure 10

The time series of the winter F(z) (unit: 104 kg/s2) over the latitude of 45° N–75° N associated with a, c PW1 and b, d PW2 components at a, b 100 hPa and c, d 20 hPa derived from the NCEP/NCAR reanalysis data. The time series of the transmittance ratio of F(z) for e PW1 and f PW2. The blue line is the trend line from 1948 to 2003, and the black line is the trend line from 2004 to 2020

Full size image

Since the stratosphere has a filtering effect on planetary waves, Charney and Drazin (1961) proposed that the zonal wind must meet specific conditions for PW to propagate upward to the stratosphere. Subsequent studies showed that the vertical gradients of the zonal wind and the buoyancy frequency have essential influences on the vertical propagation of PW (Matsuno 1970; Limpasuvan and Hartmann 2000; Hu and Tung 2002; Karami et al. 2016). The stratospheric zonal wind and the buoyancy frequency before the onset of SSWs are important pre-conditioning factors for the occurrence of SSWs. The impact of the long-term trend of the pre-conditioning factor to the trend in SSWs is worth studying, but research on this issue is a sophistically systemic work. Here, we use a simplified analysis method to qualitatively estimate the impact of PW upward propagating conditions on the SSW trend. We defined the transmittance ratio of PW as the ratio of 20 hPa F(z) and 100 hPa F(z) over the band of 45° N–75° N. The time series of the transmittance ratio for PW1 and PW2 are shown in Fig. 10e and f. The transmittance of PW1 is decreasing in 1948–2003, which makes the growth of PW1 in the middle stratosphere smaller and the growth of PW1 in the lower stratosphere. The trend in the transmittance of PW2 is not significant.

5 Possible reasons for the trend of convective activities

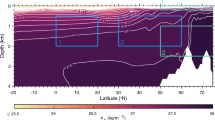
The tropical convective activity is strongly affected by the SST, because the saturated water pressure is related to temperature, and the higher temperature allows the atmosphere to contain more water vapor. Although there are high uncertainties in the SST measurement before satellites are used for observation, we attempt to investigate whether there are SST trends near the southeastern tropical Pacific corresponding with the change in the cloudiness. Figure 11 shows the winter SST trend derived from bucket-sampled SST in ICOADS. A significant warming pattern in the tropical southeastern Pacific appeared in 1948–2003, which is also reported by Tokinaga et al. (2012a, b). After 2003, the trend of SST warming did not continue.

Fig. 11
figure 11

Observed winter (December–February) SST trend (°C per year) for a 1948–2003 and b 2003–2020. c Averages of SST for 1948–2020. The contours of 25 and 27 °C SST are represented by black lines. SST data are bucket-sampled SST from ICOADS. The range of the box is [170° W–110° W, 18° S–3° N]. The trends over the dotted regions are statistically significant at the 95% confidence level

Full size image

The SST threshold for deep convection is estimated as 27 °C, where the precipitation rate exceeds 2 mm/day. The least SST threshold for convection is 25 °C if other estimation methods are used (Johnson and Xie 2010). Therefore, the convective activity in the tropical zone east of 25 °C will be not sensitive to the increase of SST (Fig. 11c). It can be seen from Fig. 11a that the SST in the tropical zone east of 110° W is also increasing, but due to its climatological average lower than 25 °C, even if SSTs increased, this region is still insufficient to generate more deep convective activities. Therefore, the eastern border of the box region of convection enhancement is near 110° W. The west boundary of the box region is 170° W since SSTs don’t have a significant positive trend in the area west of 170° W.

The increased pattern of tropical Pacific SST is closely related to ENSO, but not the same as typical El Niño. There are a lot of works have been done on the mechanism of ENSO to influence SSWs (e.g., Garfinkel and Hartmann 2008; Bell et al. 2009; Ren et al. 2012; Li and Tian 2017). From the perspective of inter-annual changes, the impact of ENSO on SSWs is significant and should not be ignored (the correlation coefficient of cloudiness and Niño 3.4 is 0.5). However, the commonly used indexes such as Niño 3.4 from Climate Prediction Center (CPC) did not have a significant trend from 1948 to 2003 (the slope of Niño 3.4 is about 0.01 °C/year). Niño 3.4 data from CPC is calculated based on changing base periods which consist of multiple centered 30-year base periods. These 30-year base periods will be used to calculate the anomalies for successive 5-year periods in the historical record. Therefore, the trend in the Niño 3.4 is negligible. In addition, Garfinkel et al. (2012b) found that although the influence of typical El Niño and La Niña on the polar vortex is significantly different, there is no significant difference in the frequency of SSW in the winter of typical El Niño and La Niña. Rao and Ren (2016a) found different types of El Niño and La Niña have different capacities to impact the stratosphere, which also makes ENSO index difficult to rebuilt the trend in SSWs.

However, SST is not the only factor that impacts the convective activities in the tropical Central Pacific. Eguchi and Kodera (2007; 2010) and Kodera et al. (2015) found during some SSW events, the enhancement of Brewer–Dobson (BD) circulation in the stratosphere has led to an increase in tropical convective activities. Kodera et al. (2011) and Eguchi et al. (2015) analyzed the model data and they found deep convective activities in the latitude 20–10° S were enhanced after the change of the stratospheric meridional circulation during SSW events. It is possible that the trend in the BD circulation also affects the trend in the convective activities in the tropical Central Pacific. The enhancement of the BD circulation in the lower stratosphere is reflected in the change of the tropical vertical wind and temperature. Figure 12 shows a scatter plot of the cloudiness vs. the vertical wind at 70 hPa and the potential temperature difference between 70 and 100 hPa. The enhancement of the BD circulation in the lower stratosphere is manifested as a decrease in ω, or a decrease in the potential temperature difference. For the seasonally averaged scale, the enhancement of BD circulation in the box region could strengthen the cloudiness. According to Eq. (9), the contribution of the change in the BD circulation on the trend of the cloudiness is much smaller than the contribution of SSTs. But this result does not conflict with the fact that during some strong SSW events, which are weather scale for weeks rather than the whole winter season, SSWs have significant impacts on tropical convection in some particular areas. For example, Eguchi and Kodera (2007, 2010) have found that in some strong SSW events, SSWs have significant impacts on convection in West Pacific, rather than the Central Pacific. This result does not rule out the possibility of SSWs affecting the long-term trend in the convective activities through other mechanisms.

Fig. 12
figure 12

Scatter plots of the winter cloudiness vs. a vertical wind at 70 hPa and b the potential temperature difference between 70 and 100 hPa. The parameters are winter mean over the box region, derived from JRA55 data

Full size image

6 Conclusion and discussion

This paper studies the trends in the convective activities in the tropical Central Pacific (box region of 170° W–110° W, 18° S–3° N) and SSWs from 1948 to 2020. Due to the lack of satellite observations of OLR, we used cloudiness observations from ICOADS. The convection activities in the tropical Central Pacific are enhanced during the period of 1948–2003. After 2003, the enhancement of the convective activities did not continue. The enhanced convective activities in the Central Pacific make the intensity of PW1 in the extratropical region significantly enhanced, while the impacts on PW2 are not significant. When the planetary waves in the troposphere are propagated to the stratosphere, the stratosphere has a filtering effect. PW1 with a small wavenumber is passed more than PW2. In the middle stratosphere, PW1 occupies a larger proportion of the planetary waves and has a greater impact on the SSW trend.

Through the analysis of NCEP data and JRA55 data, we found the duration and strength of SSWs had an increasing trend before 2003. Because SSW has large inter-annual variability, it is difficult to use statistical methods to obtain an accurate turning point of the SSW trend. Thus, we think it is appropriate to use the early 2000 s as a turning point. Previous studies on the trend in SSWs mostly used frequency as a measurement index, and draw conclusions from this index that there was no significant change in the trend in SSWs in the past few decades. This research studies SSWs from the perspective of duration and finds that the trend in SSWs has changed, which is the innovation of this article.

The regression model shows that convection in the tropical Central Pacific is one of the most important factors influencing the SSW trends. But, the relationship between cloudiness and SSWs is not strictly linear, and their relationship will be affected by other factors, such as the propagation conditions of planetary waves in the atmosphere. This work has not ruled out the possibility that other factors may have an important impact on the SSW trend. For example, model simulations showed that MJO would be enhanced significantly due to the increase of CO2 (Arnold et al. 2013, 2015). Studies have found SSWs are influenced by some MJO phases (Garfinkel et al. 2014; Garfinkel and Schwartz 2017; Wang et al. 2018; Kang and Tziperman 2018a, b; Wang et al. 2020). Kang and Tziperman (2017) find that having all MJO phases enhanced uniformly can also affect SSWs. It should be noted that because there are substantial uncertainties in stratospheric data in the pre-satellite era, changes in the adequacy of observation data have possibilities to produce partial artificial trends in SSWs (Ayrzagüena et al. 2019). However, the long-term trend in SSWs is possible due to the convective activities in the Central Pacific are enhanced.