1 Introduction

The distinct decrease of the surface wind speed (SWS) has been reported by several studies in different regions, such as in the Mediterranean and Adriatic areas (Pirazzoli and Tomasin 2003), the Black Sea region (Garmsshov and Polonskii 2011), Europe (Najac et al. 2009; Smits et al. 2005), North America (Greene et al. 2012; He et al. 2010; Pryor et al. 2007; Tuller 2004; Enloe 2003; Klink 2002), East Asia (Vautard et al. 2010), and China (Hu et al. 2011; McVicar et al. 2010; Jiang et al. 2010; Xu et al. 2006). The causes of these observed decreases in SWS remain unclear. Possible reasons for the SWS change include the influences of large-scale circulation and local changes in land use and cover change (LUCC). Some studies relate the decrease of the SWS with the weakening of large-scale circulation, Niño–Southern Oscillation (ENSO), and climate change. Pryor and Ledolter (2010), Pryor et al. (2005) and Enloe (2003) found some relations between the SWS change and ENSO, and Klink (2007) emphasized the importance of the pressure-gradient force (PGF) in the change of SWS, which means that the PGF should be a major cause of SWS change. Sušelj et al. (2010) showed that decreases in SWS were determined by the weakening of large-scale circulation. Xu et al. (2006) reported links between the weakening of the monsoon driving force and the SWS decrease in China, and Jiang et al. (2010) revealed a strong correlation between the changes in large-scale circulation and the SWS. Guo et al. (2011) reported a decreasing trend of the geostrophic current on the 850 hPa level in China; therefore, they noted that the decrease of SWS was caused by the weakening of circulation at high altitude.

Other studies found the cause of the SWS decrease to be anthropogenic activities (Gao et al. 2015; Pere et al. 2011), including the increase of surface roughness, which is induced by anthropogenic LUCC. Vautard et al. (2010) addressed the decreases in SWS could be determined by increases in surface roughness. Li et al. (2008) used the observation minus reanalysis (OMR) method to investigate the impact of the LUCC on the SWS, and their results suggest that the observed significant decrease of mean wind speeds was due to urbanization and other land-use changes in the last 40 years. In addition, SWS in urban areas was found to be lower than that in suburban regions in Shanghai (Zhou and Yu 1988) and Beijing (Li et al. 2011; Xu et al. 2009), two of China’s megacities, which linked the decrease of SWS to the increase in building area and height. Wu et al. (2016) used the frictional wind model (FWM), in which a balance among PGF, the Coriolis force, and the drag force was reached, to separate the effects of the PGF and LUCC on the SWS change and to quantitatively estimate the influence of the LUCC on the SWS change over the Eastern China Plain (ECP) region during the period of 1980–2011. Their results show that the drag coefficient induced by the LUCC has an increasing trend, which is consistent with the 30 % increase in the rate of urbanization. In addition, the long-term decrease of the SWS cannot be interpreted by the change of PGF alone because the PGF has an insignificant long-term increasing trend. The increase in the drag coefficient induced by the LUCC should account for the long-term decrease in the SWS. Furthermore, the long-term changes in East Asian monsoons may not completely account for the observed wind speed decrease near the surface, but the changes are an important factor in the SWS (Wu et al. 2016).

LUCC can affect SWS, especially in rapidly developing economic regions, but the issue is how to assess this influence quantitatively. Wu et al. (2016) established a reference SWS dataset without the influence from LUCC using the FWM to separate the influence of LUCC from other factors. At the same time, the reanalysis data include good long-term natural climate change signals and some important anthropogenic signals, such as the increase of greenhouse gases and aerosol (National Research Council 2005; Lim et al. 2005), but the reanalysis data do not include the impact of the regional and local surface processes associated with different land types (Li et al. 2008; Lim et al. 2005). Therefore, the OMR method has been used to investigate the influence of the LUCC on the regional and local climate (Wu et al. 2016; Kalnay and Cai 2003). Zhou et al. (2004) and Kalnay et al. (2006) investigated the effect of the LUCC on near-surface climate change by comparing observations and NCEP/NCAR reanalysis data. Frauenfeld et al. (2005) and Lim et al. (2005) also explored a similar subject based on the comparison between the meteorological station observations and the ERA-40 reanalysis data. Therefore, the wind speed difference between the observation and reanalysis data should reflect the influence of the LUCC on SWS. However, the reanalysis data include some kinds of error, despite the improvement of assimilation systems and numerical models in recent years. The successful use of reanalysis data in climate research indicates that the influence of LUCC on large-scale climate change may be smaller than other important factors, so the impact of LUCC on SWS may not be as distinct as other factors. Therefore, the quantitative assessment results of the SWS decrease induced by LUCC when using the traditional OMR method may include error from the reanalysis data, which are considered the reference data without effects from the LUCC in this assessment process. Hence, further improvement of the OMR method should focus on how to diminish the error included in the reanalysis data.

Statistical downscaling is a valid method to diminish the error in climate prediction versus observation that was induced by the local characteristics missing in the general circulation models or regional climate models (Busuioc et al. 1999; Murphy 1999; Wilby et al. 1999; Schubert 1998; Winkler et al. 1997). A wide range of wind variables have been predicted (Kirchmeier et al. 2014), including wind speed (De Rooy and Kok 2004), u and v components (Monahan 2012), wind gusts (Cheng et al. 2012), maximum wind speed (Yan et al. 2002), and energy density (Pryor et al. 2005), and some SDMs include neural networks (Sailor et al. 2000), probability methods (Kirchmeier et al. 2014), multivariable linear regression methods (Curry et al. 2012), the combined statistical-dynamical methods (Najac et al. 2011), and multiple linear regression models (Haas and Pinto 2012; Goubanova et al. 2010). These studies show that statistical downscaling can accurately capture large-scale information and regional climatic characteristic based on long-term observation data (predictand) and reanalysis data (predictor). The SDM can be used to revise the bias of the model results in climate prediction (Kazmi et al. 2015; Fan et al. 2007, 2010, 2013; Hanssen-Bauer et al. 2005; Mo and Straus 2002; Bergant et al. 2001). In addition, the reanalysis data are an assimilation result using the general circulation model and some observations, so they can be considered an approximation of climate variables. The statistical downscaling method can be used to optimize the reanalysis data to reduce the bias to a minimum. Then, the OMR method can be used to compare the difference between the observation and the downscaled reanalysis data, which should improve the result of the original OMR method.

This study performs a quantitative estimation of the influence of the LUCC on the SWS in China, using the difference between V10m-OBV and V10m-SDM. The data and methods used for the study are shown in Sect. 2. Section 3 describes the SDM and its validation, and the results and analysis are presented in Sect. 4. A discussion is given in Sect. 5, and the conclusions are summarized in Sect. 6.

2 Data and methods

2.1 Data

The ECP region is selected as the research region. The region spans from 21°N to 34.5°N and from 112°E to 123°E. The total number of meteorological stations in the ECP region is 153, but after the selection, 93 stations remained. The 93 stations used in this research were selected according to the following criteria: (1) the elevation of the station is below 200 m above sea level; (2) it is a national ground meteorological station; and (3) the missing data account for less than 1 % of the total period. Detailed information about the 93 stations can be found in the study by Wu et al. (2016). The wind speed is observed by the cup anemometer at the 10 m standard exposure height above ground according to the China Meteorological Administration (CMA) on the Observing System and Technical Regulations on Weather Observations (CMA 2003). The 93 stations are located in the ECP region, so the influence of typhoons on the wind speed is observed at all 93 stations. However, the impact of typhoons on the observed wind speed accounts for less than 1 % of the total period studied. The effect of typhoons on the SWS should be excluded because the typhoons can cause the observed wind speed to rise instantaneously. Typhoon track data from the Joint Typhoon Warning Center (JTWC) for 1980–2011 were used to remove wind speed observation data influenced by typhoons at stations located within a circle with a radius of 2° in latitude and longitude centered on the middle of each typhoon (Wu et al. 2013, 2016). In addition, to maintain the continuity of the wind speed data and compare these data with the reanalysis data, the missing day of data due to typhoons are interpolated by the adjacent 2 days in our research.

A homogeneity test of the annual wind speed at 347 stations selected from all of the stations in China has been conducted (Liu 2000), which included the 93 stations used in this research. All of the discontinuity points in the annual SWS dataset from 347 stations were found, and the reasons for the discontinuity points were analyzed using the historic records of these stations. There were 70 stations including discontinuity points in the SWS data, of which 47 stations were caused by the wind instrument replacement. Therefore, instrument replacement was the main factor leading to discontinuity points in the wind speed time series. Another factor resulting in discontinuity points was an observation height change, which was found in 14 stations. The last factor was station moving, which occurred at 11 stations (Liu 2000). All of the discontinuity points existing in the SWS dataset found by the homogeneous test and by both the extreme test and the temporal consistent test conducted by the National Meteorological Information Center (NMIC) of the CMA have been calibrated (CMA 2003); therefore, the SWS data are considered to be a credible dataset (Song et al. 2004; Liu 2000).

The four times per day (at UTC 00, 06, 12, and 18) wind speed data at 10 m height above the surface (V10m-ERA) and on the 850 hPa level (V850), geopotential height on 850 hPa (H850), and sea level pressure (SLP) from the latest ERA-Interim reanalysis data at 0.75° × 0.75° resolution during 1979–2011 are also used in our research. The ERA-Interim reanalysis data were produced via a sequential four-dimensional variational assimilation scheme and could be very beneficial, especially for stations in the topographically complex and data-sparse area (Dee et al. 2011; Frauenfeld et al. 2005). Compared to its original version, the ERA-40 reanalysis data, the representation of the hydrological cycle, the quality of the stratospheric circulation, and the consistency in time of the reanalysis fields were improved in the ERA-Interim (Dee et al. 2011). Berrisford et al. (2011) demonstrated that the ERA-Interim reanalysis data were superior in quality to ERA-40 and that the winds were improved in ERA-Interim. The land surface observations assimilated in ERA-Interim only include the 2-m temperature, 2-m humidity, and snow (Poli 2010), which means that wind speed observation data was not used in the ERA-Interim data assimilation process. In addition, Dee et al. (2011) indicated that the near-surface wind observations over land were not selected and that all the surface pressure observations over high terrain with elevations higher than 1500 m were not selected to assimilate in the ERA-Interim reanalysis data also. The effect of regional geographical distribution is controlled by the standard deviation of the small-scale orographic dataset, so the wind speed data in the mountainous regions are also reliable (Dee et al. 2011). In brief, the ERA-Interim data include self-contained large-, meso-, and small-scale characteristics, but the effect of the urban underlying surface variability and LUCC on the SWS was not explicitly included. The ERA-Interim reanalysis data are often used in the analysis of climatic change and can capture the inter-annual and inter-decadal change very well (Simmons et al. 2007, 2010, 2014). The ERA-Interim data were interpolated to the 93 meteorological stations over the ECP region using the bilinear interpolation method, which is suitable for converting a grid forecast field to another or discrete observation field (Mastylo 2013; Accadia et al. 2003). In addition, the urbanization rate is derived from the National Bureau of Statistics of China from 1980 to 2011, as the ratio between the urban population and the total population, and is considered an index of urbanization (Wu et al. 2016; Zhou et al. 2004).

2.2 Methods

The SDM is used to remove the systematic structural error from the reanalysis data and is established through multiple stepwise regressions of predictor principal components (PCs). Principal component analysis (PCA), also known as empirical orthogonal function (EOF) analysis in the meteorological community, has become a widely used tool in climate research. Such an approach to establish the SDM has been suggested by former studies (Fan et al. 2011, 2013; Kamp et al. 2012; Hanssen-Bauer et al. 2005; Mo and Straus 2002; Renwick and Wallace 1995).

The unique predictand of the SDM in this study is SWS at 10 m height, and the predictors include single fields of V850, H850, and SLP as well as the combinations of V850 + H850, V850 + SLP, and H850 + SLP. Fan et al. (2011, 2013) showed that the domain to compute PCs of the predictor should not be too big or too small in order to include proper large-scale signals. We compared different domain choices and chose the proper domain used in calculation PCs of the predictor for each station. The area of the predictor spans from 9.75°N to 45°N and from 99.75°E to 135°E (Figure not shown). Before using multiple stepwise regressions, both the predictors and predictand are normalized, and PCA is performed as the first step for predictors to remove noise and reduce the number of degrees of freedom. For the combinations of two predictors, such as V850 + H850, PCA analysis with the two fields combined spatially is used (Fan et al. 2013; Bretherton et al. 1992). The downscaling utilizes a stepwise screening procedure that aims to minimize the Akaike information criterion to obtain the skillful PCs (Wilks 1995). The choices of the number of PCs of each predictor variable are made when they are put into the stepwise regression equation to obtain the optimum linear regression models for each station (Fan et al. 2011, 2013). We set the criterion of explained variance exceeding 90 % for accumulative PCs; therefore, the number of PCs for each predictor can be determined in the SDM procedure with this criterion.

To evaluate the predicting skill of the method, the multiple correlation coefficients (MCC), error standard deviation (ESD) between the predictand and the predictors (Huang 2004), and the Brier Skill Score (BSS) (Bustamante et al. 2012) are used in this work. The MCC is used to measure the linear relation between predictand and predictors and is defined by Eq. (1).

$$R = \frac{{\sum\nolimits_{i = 1}^{n} {(y_{i} - \bar{y})(\hat{y}_{i} - \bar{y})} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {(y_{i} - \bar{y})^{2} \sum\nolimits_{i = 1}^{n} {(\hat{y}_{i} -\bar{y})^{2}}}}}}$$
(1)

where y i represents the predictand, \(\bar{y}\) represents the mean value of the predictand, and \(\hat{y}_{i}\) represents the downscaled values, n = 13. The Brier Skill Score is defined by Eq. (2).

$$BSS = 1 - [S_{ES}^{2} /S_{OB}^{2} ]$$
(2)

where S 2 ES represents the variance of the error between different estimations and the observation, and S 2 OB is the variance of an observation. Provided that the climatology is selected as a reference value to evaluate the error, in such conditions, BSS = 0 represents a prediction not better than climatology. If the estimation error variance is similar to that of the observation, a positive BSS is obtained, and the better the prediction is, the closer the value will be to 1 (Bustamante et al. 2012).

Additionally, Von Storch (1999) showed that \(\hat{y}\) have smaller variance than the local values y. \(\hat{y} = \alpha x\)(x represents the PC of predictors, 0 < α < 1), so \(\text{var} (\hat{y}) = \alpha^{2} \text{var} (x)\), and \(\text{var} (y) = \alpha^{2} \text{var} (x) + \alpha^{2}\) follows \(\text{var} (\hat{y}) < \text{var} (y)\). This result is important because the predictor x does not completely specify y. To directly compare with observations to estimate the anticipated climate change, the variances of \(\hat{y}\) are needed to enlarge (Huth 2004; Von Storch 1999). The detailed method can be found in Fan et al. (2007) and Huth (2004).

The SDM is established throughout the time period of 1980–1992 because the economic development in China during this period was lower than that in the following period and because LUCC was indistinct in this period relative to latter periods, which means that there was little LUCC influence on the observed SWS relative to the following period. The regression coefficients in the SDM, estimated by the least-squares fitting between V10m-OBV and the PCs in predictors, include the mutual link between V10m-OBV and large scale circulation only, so the SDM can calibrate the error in V10m-ERA versus the observation. The normalized V10m-ERA data are decomposed by the PCA in the following period of 1993–2011, and the downscaled SWS at 10 m height (V10m-SDM) is reconstructed using the linear combination between PCs of V10m-ERA and regression coefficients from the SDM, which can reduce error in the V10m-ERA data in maximum extent. This calibration may not bring the influence of LUCC into the V10m-SDM time series during 1993–2011. Then, the V10m-SDM data are compared with V10m-OBV to isolate the impact of LUCC on the SWS in the period of 1993–2011, and the surface wind speed difference (SWSD) between V10m-OBV and V10m-SDM is analyzed.

In addition, to quantitatively assess the consistency of the phase between the time series, the probability of extremes appearing at the same time point (represented by PEST) in the two time series is calculated. Student’s t test is used to determine the significance of the data. The linear trend coefficient is calculated using the least-squares method. The composite analysis is used to discuss the influence of PGF on the wind speed. A Gaussian low-pass filter is used to determine the interdecadal changes in the PGF (Ding et al. 2014; Li et al. 2010).

3 SDM and validation

The predictors selected to establish the SDM include the single fields of V850, H850, and SLP as well as the combination fields of V850 + H850, V850 + SLP, and H850 + SLP. V850 and H850 include the information of the large-scale circulation and pressure distribution over the ECP region because the elevation in this region is less than 200 m. The large-scale influence is an important background for SWS; therefore, the wind speed and geopotential height on 850 hPa are both selected as predictors. SLP represents the main characteristics of PGF on the sea level in the ECP region, which is the driving force of air motion. These predictors and V10m-ERA are decomposed by PCA, and the explained variance by accumulative PCs is given in Fig. 1. The first 3 PCs of H850, SLP, and their combination can explain more than 90 % of the variance. The lowest explained variance for the same number of PCs is V850, and 90 % of the explained variance needs 17 PCs of V850. Similar characteristics are found in V10m-ERA. The two combination fields involving V850 need the first 11 PCs to exceed 90 % of the explained variance. Therefore, we choose the first 17 PCs for all six predictors as the maximum PCs in the establishment of the SDM using stepwise regression, in which the exact number of PCs that are actually used in the SDM for each predictor is determined gradually in the regression process. In addition, we also investigate the seasonal changes in the first three PCs for the six predictors and V10m-ERA (figure not shown). The results show that the PC1s of all six predictors can capture the seasonal characteristics of V10m-ERA. The probability of the same sign of the anomaly appearing at the same time (represented by PAST) between the PC1s of V10m-ERA and V850 is 83 %, but PAST can reach 100 % between PC1 of V10m-ERA and the other five predictors. The seasonal characteristics of PC2 for V10m-ERA are also well-captured by V850 and V850 + SLP, with a PAST of 91.7 and 83.3 %, respectively (Table 1). PC2 of the predictors, other than V850 and V850 + SLP, shows inconsistent seasonal changes with respect to V10m-ERA with a lower PAST value, as shown in Table 1. When PC3 is considered, V850 + SLP always follow V10m-ERA, with a PAST of 75 %. The above-mentioned features indicate that the combination of V850 + SLP has the best performance in describing the seasonal change of V10m-ERA in all six predictors, which means that the combined use of V850 and SLP favors capturing the large-scale signals exactly. In addition, Table 1 also shows the performance of combined fields is better than that of single fields.

Fig. 1
figure 1

Accumulative explained variances for the first 17 principal components of the six predictors and wind speed at 10 m height in the ERA-Interim reanalysis data during 1980–1992

Full size image
Table 1 The probability of the same sign of the anomaly appearing at the same time (represented by PAST) between the first three principal components of six predictors and the wind speed at 10 m height of the ERA-Interim reanalysis data
Full size table

Six SDMs are constructed using the six predictors during 1980–1992, and the multiple correlation coefficients (MCC) between V10m-OBV and V10m-SDM, the BSS, and the ESD between the observation and estimators for the six SDMs during 1980–1992 are computed (Table 2). The mean MCC for V850, H850, and SLP is 0.60, 0.59, and 0.59, respectively, and the average MCC for V850 + SLP, H850 + SLP, and V850 + H850 is 0.69, 0.60, and 0.64, respectively, which is higher than the MCC of the single fields. The results of the MCC show that the SDM established by V850 + SLP has the best performance in downscaling the wind speed data at 10 m height in all six SDMs. The average BSS for V850 + SLP, H850 + SLP and V850 + H850 is higher than the BSS of three single fields. In all six SDMs, the highest BSS is reached in V850 + SLP (94 %), and the lowest BSS is reached in H850 (92.4 %). The average ESD for three combined fields is lower than three single fields. The mean ESD reaches the collective maximum value of 0.064 m s−1 in the three SDMs established by the single fields of V850, SLP, and H850, and the minimum value of 0.059 m s−1 is reached in V850 + SLP. Therefore, the maximum value of MCC and BSS and the minimum value of ESD are reached in the SDM constructed by the combined predictors of V850 + SLP at the same time (Table 2). The spatial distribution of MCC, BSS, and ESD for V850 + SLP is shown in Fig. 2. The MCC is greater in northeastern ECP, and MCC is smaller in the middle and southern part of this region (Fig. 2a). The spatial distribution of MCC for the other five predictors is consistent with that for V850 + SLP but is lower than that for V850 + SLP, and that the MCC for H850, SLP and H850 + SLP is also statistically insignificant in the middle reaches of the Yangtze River. Regions with smaller BSS for V850 + SLP are located in the middle reaches of the Yangtze River and the inshore area of the southeastern ECP, and the regions that have greater BSS for V850 + SLP are in the northern, central, and southwestern ECP, respectively (Fig. 2b). Similarly, the spatial distribution of BSS for the other five predictors is consistent with that for V850 + SLP but is lower than that for V850 + SLP in the same region. The main characteristics of ESD in V850 + SLP include a smaller ESD in the northern and southwestern ECP and a greater ESD in the central and southeastern ECP, which is opposite to the results of MCC and BSS in general (Fig. 2c). The spatial distribution of ESD for the other five predictors is consistent with that for V850 + SLP but is higher than that for V850 + SLP in the same regions. Therefore, the combination of V850 + SLP has the best performance in the establishment of the corresponding SDM. Therefore, we choose the SDM constructed by the predictor of V850 + SLP to downscale SWS during 1993–2011 in the following sections.

Table 2 Validation indices of the SDMs established by the six predictors during 1980–1992
Full size table
Fig. 2
figure 2

The spatial distribution of the multiple correlation coefficients (MCC) (a), Brier Skill Score (BSS) (unit: %) (b), and error standard deviation (ESD) (unit: m s−1) (c) during 1980–1992 for the V850 + SLP statistical downscaling model (the threshold of MCC is 0.41, which is the criterion of a significant F test at the 95 % significance level)

Full size image

The temporal changes in V10m-OBV, V10m-SDM, and V10m-ERA during 1980–1992 are shown in Fig. 3a. V10m-ERA and V10m-SDM have a weak increasing trend during 1980–1992, and their linear trend coefficients failed to pass the statistically significant t test at the 99 % level. However, V10m-OBV includes a statistically significant decreasing trend in the same period. Additionally, the correlation coefficient between V10m-OBV and V10m-ERA is 0.01, but the coefficient increased to 0.10 between the observation and V10m-SDM after downscaling. These results indicate that the long-term decreasing trend in V10m-OBV could not be changed by the downscaling method because the downscaling method requires complete large-scale information to calibrate V10m-ERA. Thus, the local information should account for the observed decreasing trend. The PEST between V10m-OBV and V10m-ERA is 80 % during this period, and the value does not change after downscaling.

Fig. 3
figure 3

Temporal change of V10m-OBV (black), V10m-SDM (red), and V10m-ERA (blue) (unit: m s−1) during 1980–1992 (a) and 1993–2011 (b). The annual mean values are indicated by triangles, rectangles, and circles (R is the correlation coefficient, Rc is the threshold, and P is 99 % the significance level)

Full size image

4 Result and analysis

4.1 Downscaled SWS during 1993–2011

The SDM used to downscale the V10m-ERA is a multi-stepwise regression model using stepwise screened skillful PCs of the combination of V850 + SLP during 1980–1992. The stepwise regression equation is used to choose the proper number of PCs decomposed from V850 + SLP when they are put into the SDM to obtain the optimum linear regression models for each station; then, the regression coefficients of the model are used to reconstruct the V10m-SDM serial for each station using the PCs decomposed from V10m-ERA during 1993–2011.

The temporal change of V10m-OBV, V10m-ERA, and V10m-SDM during 1993–2011 is shown in Fig. 3b, respectively. V10m-OBV shows an obvious decreasing trend, as reported by former, studies with decreasing rate of −0.15 m s−1 (10 year)−1. V10m-ERA and V10m-SDM have weak increasing trends, whose linear trend coefficients do not pass the significant t test at the 99 % confidence level. The PEST between V10m-OBV and V10m-ERA is 76.9 %, which is lower than that between V10m-OBV and V10m-SDM by 8 %. The average value of V10m-SDM is between V10m-OBV and V10m-ERA, which is greater than V10m-OBV by 0.46 m/s and smaller than V10m-ERA by 0.40 m/s during 1993–2011. The correlation coefficient between V10m-SDM and V10m-ERA is 0.63, which passed the significant t test at 99 % significance level.

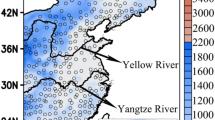
The spatial distribution of the V10m-OBV, V10m-SDM, and V10m-ERA during 1993–2011, as well as their linear trend coefficients and variances, are shown in Fig. 4. The average of V10m-OBV is 2.27 m s−1, and V10m-OBV is larger in the inshore region than in the inland region. The V10m-OBV is stronger in the northern ECP than in the southern ECP, with the largest value in the Yangtze River Delta Region. In addition, there are some regional fine differences in V10m-OBV, especially in the southern ECP region (Fig. 4a). V10m-ERA captures the features of “big inshore small inland” and “big north small south” in V10m-OBV but is distinctly stronger than V10m-OBV, with a mean value of 3.13 m s−1. Meanwhile, V10m-ERA fails to show the fine local features found in the observation because it includes obvious large-scale characteristics. The V10m-SDM can capture both the large-scale and local characteristics in the observations, and their patterns are very similar. In addition, the mean of V10m-SDM is 2.73 m s−1, which is closer to the observation data than V10m-ERA (Fig. 4b).

Fig. 4
figure 4

Spatial distribution of V10m-OBV, V10m-SDM, V10m-ERA (unit: m s−1), and their linear trend coefficients (unit: m s−1 (10 year)−1) and variances (unit: m−2 s−2) averaged during 1993–2011, respectively (a, d, g for V10m-OBV; b, e, h for V10m-SDM; c, f, i for V10m-ERA. Additionally, light blue, yellow, and red in (d–f) represent the criterion of the t test at the 90, 95, and 99 % significance levels, respectively)

Full size image

The linear trend coefficient of V10m-OBV is negative, with an average of −0.19 m s−1 (10 year)−1, and almost all of these coefficients pass the significant t test at the 90 % level in the ECP region (Fig. 4d). The linear trend coefficients range from 0.1 to −0.3 m s−1 (10 year)−1 with the most distinct decrease rate of −0.3 m s−1 (10 year)−1 near 116°E, 29°N. The linear trend coefficients in V10m-ERA and V10m-SDM are positive, but they fail to pass the significant t test at the 90 %. Simultaneously, both V10m-ERA and V10m-SDM have much smaller absolute values of linear trends than that of V10m-OBV (Fig. 4e, f), and the trend of V10m-SDM spreads in a very narrow range of −0.01 to 0.025 m s−1 (10 year)−1. In addition, the spatial pattern of the V10m-SDM linear trend is closer to V10m-OBV than that of V10m-ERA. The variance of V10m-OBV is the biggest among the three wind speeds (Fig. 4g), and V10m-SDM has the smallest variance (Fig. 4i). Therefore, the main spatial characteristics in the variance of V10m-OBV are captured by V10m-SDM, despite the small value in V10m-SDM. Based on the above-mentioned results, the long-term trend of V10m-ERA is maintained in V10m-SDM, which exhibits a better performance in the time points of extreme appearance than does V10m-ERA with respect to V10m-OBV.

4.2 Influence of LUCC on SWS during 1993–2011

The SWSD between V10m-SDM and V10m-OBV during 1993–2011 and its linear trend coefficient, as well as its variance, are displayed in Fig. 5. SWSD shows the pattern of “big north small south and big inshore small inland”, which is in agreement with the spatial characteristics of V10m-SDM (Fig. 4b). The most distinct SWSD in the inshore regions is found in Shanghai, Zhejiang, Jiangsu and Fujian Provinces, with an average of −0.4 m s−1, and these places are the most developed regions in China. There is a distinct SWSD belt extending from YRDR northwestward to the Huai River plain, with an extremum of −0.5 m s−1, and it is the most marked SWSD in the inland region. Similar results were reported by Li et al. (2008). A ring-shaped region is revealed in the southern ECP, which is the weakest SWSD in the whole ECP region, with an average of −0.26 m s−1. By comparing SWSD with V10m-SDM, it can be seen that the SWSD in regions with a larger V10m-SDM is more distinct than that in regions with a smaller SWS.

Fig. 5
figure 5

Spatial distribution of the wind speed differences between V10m-OBV and V10m-SDM (a) (unit: m s−1), as well as the linear trend coefficient (b) (unit: m s−1 (10 year)−1) and variance (c) (unit: m−2 s−2) averaged during 1993–2012 (light blue, yellow, and red in (b) represent the criterion of the t test at the 90, 95, and 99 % significance levels, respectively)

Full size image

The linear trend coefficient of SWSD is negative in almost the entire ECP region, with an average of −0.19 m s−1 (10 year)−1, except for a positive region on the western border of the ECP, which indicates that SWS is decreasing and the effect of LUCC is intensifying. There are two regions with the minimum slope of −0.3 m s−1 (10 year)−1 in the southern and northern part of the ECP, respectively, which are the most distinct regions of the SWS decrease. The spatial pattern of the SWSD variance has some discrete centers with big values, which shows that the linear trend has worse representation in these areas, and the average variance of the SWSD is 0.076 m−2 s−2 in the ECP region.

The temporal change of the SWSD and its linear regression with the urbanization rate is shown in Fig. 6. The average SWSD in the ECP is negative, and the SWSD was −0.24 m s−1 in 1993. A distinct decreasing trend can be found during 1993–2011, with a mean decreasing rate of −0.17 m s−1 (10 year)−1, which passed the statistical significance t test at the 99 % level. According to the temporal change of the SWSD, the most pronounced decrease of −0.56 m s−1 induced by LUCC was reached in 2011, and the average SWSD during 1993–2011 is −0.45 m s−1. In addition, there is a negative correlation between the SWSD and the urbanization rate passing the statistical significance t test at the 99 % confidence level, which means that each 10 percent increase of the urbanization rate leads to a 0.12 m s−1 decrease in SWS. In addition, the five-year mean SWSD in different scale cities are summarized in Table 3, and all 93 stations were classified into large, medium and small cities based on population sizes of more than 1,000,000, between 500,000 and 1,000,000, and under 500,000, respectively (Wu et al. 2012, 2016). SWSD in large cities is more distinct than that in small cities and the all stations mean, with values of −0.49, −0.38, and −0.45 m s−1, respectively. Further, a more distinct SWS decrease occurred during 1993–2007, and a slower SWS decreasing rate is found after 2007. These results indicate that LUCC is an important factor in the observed SWS decline in the ECP region.

Fig. 6
figure 6

Temporal change of the wind speed differences between V10m-OBV and V10m-SDM from 1993 to 2011 (a) (unit: m s−1) and its linear regression with urbanization rate (b) (R is the correlation coefficient, Rc is the threshold, and P is the 99 % significance level)

Full size image
Table 3 SWSD for every 5 years in different scale cities during 1993–2011 (unit: m s−1)
Full size table

4.3 Results comparison of different methods to evaluate the influence of LUCC on SWS

There are four methods used to estimate the impact of LUCC on SWS: comparison between rural and urban wind speed observations (represented by CRU) (Guo et al. 2011; Xu et al. 2006), the OMR method (Li et al. 2008), the FWM method (Wu et al. 2016), and the SDM method, which is an improvement of the original OMR method.

Due to the following factors, the CRU method may cause uncertainties in its results. First, strict rural stations are rare in long-term meteorological observation data in China, so some small cities and towns were selected as rural stations in some previous studies. Second, the influence of urbanization on the SWS in large cities can only be estimated under the premise that the LUCC in small city stations and rural station is ignorable in the CRU method. LUCC and urbanization are becoming more distinct in small cities. It is difficult to select appropriate rural or small city stations in the ECP region as reference stations without influence of LUCC because this region is one of fastest economic development regions in China, and the LUCC in the ECP be wider than that in other regions (Kuang et al. 2016; Liu et al. 2010; Liu and Tian 2010). Furthermore, the CRU method cannot be used to assess the LUCC impact on the SWS in small cities because the reference is missing under this condition. Therefore, we do not compare the results of the CRU method in this paper.

Figure 7 shows the average SWSD, the linear trend coefficient of the SWSD, and the variance of the SWSD in the ECP during 1993–2011 for the FWM and OMR methods, in which the results of FWM come from previous research (Wu et al. 2016). The distinct SWSD of the FWM method is found to the south of the Yangtze River, with the most distinct SWSD of −1.0 m s−1. The weak SWSD lies in the Yangtze River Delta Region (YRDR) and to the north of the Yangtze River, with representative value of −0.4 m s−1 (Fig. 7a). The distinct SWSD of the OMR method is found in the middle and low reaches of the Yangtze River and southern China, with the most distinct SWSD of −1.0 m s−1. The weak SWSD lies in southeast China, with a representative value of −0.5 m s−1 (Fig. 7b). The SWSD of the SDM method reveals a different pattern described in Fig. 5a; the most distinct SWSD is found in the YRDR and inshore region, which is consistent with the pattern of economic development and urbanization in this region (Wei and Liefner 2012; Lu and Liu 2000). In addition, regional differences in economic development and urbanization exist in the ECP region, for example, the YRDR region and some inshore regions in the southeast of the ECP are regarded as rapid development areas (Li and Wei 2010; Zhao and Wang 2007), but the OMR method fails to display the signal of regional differences. The spatial pattern of the SDM method is more reasonable than the OMR and FWM methods. Their regional mean SWSD is −0.46, −0.62, and −0.83 m s−1 for SDM, FWM, and OMR methods, respectively. The linear trend coefficients of the three methods are negative, with regional average values of −0.19 m s−1 (10 year)−1, −0.43 m s−1 (10 year)−1, and −0.16 m s−1 (10 year)−1 for SDM, FWM, and OMR, respectively. The most distinct SWSD induced by LUCC is reported by the OMR method, which is more than twice the SDM result, and the most rapid decrease of SWS is found by the FWM method, which is more than twice the SDM and OMR results. The patterns and values of the linear trend in the OMR and SDM methods are similar. In addition, the variances of the three methods have similar patterns, with the regional average values of 0.076, 0.13, and 0.065 m−2 s−2 for the SDM, FWM, and OMR methods, respectively. The downscaling method obtains the weakest influence from LUCC to SWS and the middle decreasing rate of SWS and variance of SWSD in the three methods. The downscaling method successfully reveals the fine characteristics in the spatial pattern of the SWSD, which is similar to the economic level in China in recent decades (Wei and Liefner 2012). In general, the results from different methods are dispersed, although the OMR and SDM methods have similar decreasing slopes of SWS and variances of SWSD. Additional methods should be used to explore the influence of LUCC on SWS to further decrease the uncertainty. The causes of these differences are complex. The OMR method causes error due to using the reanalysis data in the evaluation result, which may come from the bias of the model and assimilation systems used in the production of the reanalysis data, such as the low-resolution used to describe local terrain, regional climate, inaccurate land surface parameter, and inhomogeneous meteorological data. The SDM method belongs to the OMR method, but V10m-ERA is replaced by V10m-SDM. Thus, the original error in V10m-ERA is depressed to the maximum extent in the SDM method, which improves the results of the original OMR method. The FWM method only considers dynamic reasons by using the frictional wind model, which is one approximation model to describe surface wind, and the FWM method succeeds in isolating dynamic effects. LUCC leads to an increase in drag force in the canopy layer, which has blocking effects on the SWS, and changes thermodynamic characteristics of the surface, which can change the local circulation and turbulent flux, causing changes in the SWS. Many stations in the ECP region are located in the transition belt between the downtown and suburbs of a city, so urban expansion not only increases surface roughness but can also lead to heat island circulation and turbulent flux disturbance, which are important to the change of the local wind field. Consequently, thermodynamic effects should be considered in the analysis of the influence of LUCC on the SWS. Thermodynamic has no consideration in the FWM method, and some thermodynamic signals from large-scale LUCC may be included in the reanalysis data. Meso-scale and local thermodynamic signals are omitted in the reanalysis data. Although the quantitative evaluation for the influence of the thermodynamic factors on the observed SWS decrease remains difficult, including some thermodynamic information thus favors the objective evaluation of LUCC’s effects on the SWS change.

Fig. 7
figure 7

Spatial distribution of the wind speed decrease induced by LUCC (unit: m s−1), as well as its linear trend coefficient (unit: m s−1 (10 year)−1) and variance (unit: m−2 s−2) averaged during 1993–2011 estimated by FWM and OMR (a, c, e for the FWM method, and b, d, f for the OMR method. Additionally, light blue, yellow, and red in (c) and (d) represent the criterion of the t test at the 90, 95, and 99 % significance levels, respectively)

Full size image

5 Discussion

5.1 Analysis of causes of the SWS decrease

The PGF acts as the driving force of air motion, so a possible relation between the observed long-term decrease of the SWS and a change of PGF is an interesting issue. We calculated the PGF at near-surface, 925 and 850 hPa using the four-order differential scheme of Wu et al. (2016). The mean value of the wind speed, linear trend coefficients of wind speed, and the variances of wind speed at near-surface, 925 and 850 hPa are shown in Fig. 8. The wind speed at 925 and 850 hPa is larger than V10m-OBV, but the linear trend coefficients of the wind speed at 925 and 850 hPa fail to pass the statistical significance t test at the 90 % level in most areas over the ECP region, which differs from the distinct decrease of V10m-OBV spreading over the ECP region. The variances of wind speed at 925 and 850 hPa are smaller than on the near-surface. These characteristics mean that the long-term decrease in wind speed over most parts of the ECP region is evident at the near-surface only and that the temporal changes of wind speed at 925 and 850 hPa have no distinct decreasing trend over the ECP region. The temporal changes of the normalized PGF at the near-surface, 925 and 850 hPa are given in Fig. 9. The surface PGF shows an increasing trend with its linear trend coefficient passing the significant t test at the 99 % level, but the PGF at 925 and 850 hPa has no statistically significant increase during 1980–2011. The decadal-scale change determined using 9-year, Gaussian-type filtered values of the PGF shows that the interdecadal change of the PGF at the near-surface, 925 and 850 hPa is different. The PGF at the near-surface has a strong increasing trend during 1995–2011, but the PGFs at 925 and 850 hPa show the characteristics of fluctuation. In addition, the correlation coefficients between wind speed and PGF at the near-surface, 925 and 850 hPa are −0.31, 0.89, and 0.90, respectively, and the PEST between wind speed and PGF on the three levels is 50, 81.3, and 87.5 %, respectively. The ratio of positive and negative anomalies in the same year between PGF at the near-surface, 925 and 850 hPa is 72 and 63 %, respectively, and the PEST between PGF at the near-surface, 925 and 850 hPa is 65 and 60 %, respectively, which indicates different temporal change characteristics of the PGF at different heights. To clarify the effects of PGF on wind speed changes at different heights, the composite analysis is used in the following research (Fig. 10). The abnormal years of PGF are determined in the composite analysis based on the specific principle that the time series of the PGF should be normalized; then, if the value is more (less) than 0.9 (−0.9), its corresponding year is deemed as a strong (weak) PGF year (Jhun and Lee 2004). The wind speed difference at the near-surface is below 0.1 m s−1, and the difference is statistically insignificant in the ECP region, whereas the difference at 925 hPa is statistically significant, exceeding the 90 % level in most parts of the ECP region, except the southern bottom of the region. A much larger difference of wind speed can be found at 850 hPa, with the maximum of 0.7 m s−1, and the statistically significant region reaching the 95 % level spreads over the entire ECP region. PGF fails to dominate the long-term change of the wind speed at the near-surface, but it is a controlling factor for wind speed at higher levels. PGF is motive force for wind, but it has no distinct long-term decline during 1980–2011 in the ECP region, whereas SWS decreases distinctly in the same period, which should be interpreted from the viewpoint of the rise of the surface roughness by LUCC, as revealed by Vautard et al. (2010) and Wu et al. (2016).

Fig. 8
figure 8

Spatial distribution of the wind speed (unit: m s−1), as well as its linear trend coefficient (unit: m s−1 (10 year)−1) and variance (unit: m−2 s−2) at the near-surface, 925 and 850 hPa levels during 1980–2011 (a, d, g for V10m-OBV; b, e, h for 925 hPa; c, f, i for 850 hPa. Additionally, light blue, yellow, and red in (d–f) represent the criterion of the t test at the 90, 95, and 99 % significance levels, respectively)

Full size image
Fig. 9
figure 9

Temporal change of the normalized pressure-gradient force (PGF) during 1980–2011 at the near-surface, 925 and 850 hPa levels, respectively. The black solid lines denote a 9-year low-pass-filtered time series with the Gaussian-type filter and the pink solid lines denote the linear trend of the normalized PGF. (R is the correlation coefficient, Rc is the threshold, and P is the 99 % significance level)

Full size image
Fig. 10
figure 10

Spatial distribution of the composited wind speed difference (unit: m s−1) between the strong and weak pressure-gradient force years during 1980–2011 at the near-surface, 925 and 850 hPa levels, respectively (the light blue, yellow, and red represent the criterion of the t test at the 90, 95, and 99 % significance levels, respectively)

Full size image

5.2 Uncertainty in the SWSD from the evaluation of different SDMs established by different periods

The skill of SDM is related to the length of the period used to establish the model. In general, the longer the period that is used, the better the results will be. The longest observed SWS data in the ECP region exceed 50 years, beginning from 1960, but high-resolution, ERA-Interim reanalysis data are available from 1980. In addition, a reasonable period must be used to establish SDM, and this period should be selected from the earlier segment during 1980–2011 because stronger signals of LUCC may be included in the latter segment of the whole observed SWS dataset during 1980–2011. The period should not be too short to ensure the reliability of the SDM. Therefore, the period used to construct SDM, considering both the needs from the validation of SDM and the small amount of LUCC information existing in the observation, is 1980–1992 because (1) the 13-year length includes seasonal and annual cycling signals in the wind speed data; (2) 13-year data embody a complete decadal change; (3) 13-year data include a sufficient number of samples to perform validation of SDM; and (4) the LUCC signal contained in the period is weaker than in the later period. Chinese economic development appeared with the rise of manufacturing ability after the policy of Opening and Reform was implemented in 1980. Widespread urban expansion followed, regarded as a key LUCC type in China, began from the extensive construction of commercial residential buildings in the 1990s to feed the needs of population migration from the countryside and small towns or small cities to big cities (Liu et al. 2014; Liu and Tian 2010). Chen et al. (2004) showed that the rapid development of urbanization in China started in 1996. Therefore, LUCC signals contained in SWS observation during 1980–1992 are weaker than in the later period. These are the main reasons for selecting 1980–1992 to establish the SDM and estimate the influence of the LUCC on SWS quantitatively in Sects. 3 and 4.

A different selection of the time period used to construct SDM would result in a different assessment of the impact of LUCC on SWS in ECP region, but we consider 1980–1992 to be the most proper choice. We design comparisons of two extreme cases to reflect the uncertainty in the effect of LUCC on the SWS by using different time periods to establish the SDMs: 1980–1985 and 1980–2011. The two statistical downscaled wind speeds are defined as V10m-SDM-1 and V10m-SDM-2 for the periods of 1980–1985 and 1980–2011, respectively. The wind speed difference between the observations and downscaled SWS output by SDMs during the periods of 1980–1985 and 1980–2011 are defined as SWSD1 and SWSD2, respectively. The period of 1980–1985 is the 6 years of the available ERA-Interim reanalysis data, when the Chinese economy just began to develop; therefore, the potential influence from LUCC on the observed SWS should be negligible compared to the later period. The SDM based on the period of 1980–1985 diminishes the effect of LUCC in the regression coefficients, but the time length is shorter than the other two periods, and some seasonal signals of wind speed are ignored. When the full-length period of 1980–2011 is used to construct the SDM, the signals of LUCC are introduced into the regression coefficients that are used to calibrate V10m-ERA data because the observed SWS combined with the PCs of large scale circulation from ERA-Interim reanalysis data are used to solve the regression coefficients in SDM. Therefore, this comparison can determine the range of uncertainty in the evaluation of the effect of LUCC on SWS.

The temporal changes of SWSD of the two extreme SDMs are compared in Fig. 11. The temporal mean difference of the SWSD in the two extreme SDMs is 0.12 m s−1, which is close to the resolution of the cup anemometer (Zhang and Chen 1999; Kaganov and Yaglom 1976; Hyson 1972). The linear trend coefficients of the SWSD in the two extreme SDMs are negative, and they pass the statistical significance t test at the 99 % level. In addition, the two series have similar interannual and decadal changes, with the PEST between them reaching 70 %. The linear trend coefficients of SWSD1 and SWSD2 are −0.20 m s−1 (10 year−1) and −0.18 m s−1 (10 year−1), respectively, the variances of SWSD1 and SWSD2 are 0.02 and 0.014 m−2 s−2, respectively, and the correlation coefficient between SWSD1 and SWSD2 is 0.78, which passes the significant t test at the 99 % confidence level. Additionally, we also investigate the spatial characteristics of SWSD1 and SWSD2 (figure not shown). The patterns of the average wind speed of the two serials are similar, which is consistent with that of SWSD in Fig. 5a. SWSD1 is higher than SWSD2 by approximately 0.1 m s−1 in some regions to the north of the Yangtze River. The linear trend coefficients and variances of SWSD1 and SWSD2 are in agreement with that of SWSD in Fig. 5, and they are statistically significant at the 90 % confidence level. The variance of V10m-SDM-1 is larger than that of V10m-SDM-2 by 0.004 m−2 s−2, which is negligible.

Fig. 11
figure 11

Temporal change of the wind speed difference (unit: m s−1) during 1993–2011 between V10m-OBV and V10m-SDM using 1980–1985 (red line) and 1980–2011 (blue line) in establishing the statistical downscaling model (R is the correlation coefficient, Rc is the threshold, and P is the 99 % significance level)

Full size image

The mean results of the three SDMs established by the three different periods and V10m-ERA, as well as V10m-OBV, during 1980–2011 are summarized in Table 4. V10m-SDM is between V10m-SDM-1 and V10m-SDM-2, and the most distinct difference among the three serials is 0.12 m s−1. SWSD versus V10m-OBV is −0.46, −0.44, and −0.34 m s−1 for V10m-SDM-1, V10m-SDM, and V10m-SDM-2, respectively, and the biggest difference of 0.12 m s−1 is found between V10m-SDM-2 and V10m-SDM-1, which reaches 27 % of the SWSD of V10m-SDM and can be considered the uncertain range of the SWSD evaluated by SDM. In addition, the linear trend coefficients of SWSD versus observation are similar among the three SDMs.

Table 4 Comparison of the mean values from three SDMs with different periods used in establishing V10m-ERA and V10m-OBV during 1980–2011
Full size table

From the above-mentioned results of the average wind speed, temporal change, and spatial pattern, the most distinct difference among V10m-SDM, V10m-SDM-1, and V10m-SDM-2 reaches 27 % of the SWSD evaluated by the difference between V10m-OBV and V10m-SDM. The difference of the two SDMs is represented by their different regression coefficients between the observed SWS and large-scale signals from high levels in the reanalysis data. When the decomposed PCs of V10m-ERA are used to predict V10m-SDM, the two sets of regression coefficients are used as the weighting coefficients of the PCs in V10m-ERA. Therefore, the two sets of coefficients change only the relative importance of the PCs, and the temporal and spatial characteristics are determined mainly by the PCs of V10m-ERA.

6 Summary

The results of the combined use of statistical downscaling and the OMR method to evaluate the influence of LUCC on SWS quantitatively in the ECP region during 1993–2011 can be summarized as follows:

  1. 1.

    The surface wind speeds in the ERA-Interim reanalysis data and in the station observation show a pattern of “big inshore small inland” and “big north small south”, with averages of 3.16 and 2.38 m s−1, respectively. V10m-ERA captures obvious large-scale characteristics but fails to reveal the fine local spatial features in V10m-OBV. V10m-SDM captures both the large-scale and local characteristics in the observation, with an average speed of 2.76 m s−1, which approaches V10m-OBV much more than V10m-ERA. There is a statistically significant decrease in V10m-OBV, but V10m-ERA and V10m-SDM do not show apparent decreases and fail to pass the significant t test at the 90 % level. V10m-SDM has a more similar spatial pattern to V10m-OBV than V10m-ERA.

  2. 2.

    The impact of LUCC on SWS is signified by SWSD, which is the difference between V10m-OBV and V10m-SDM during 1993–2011, displaying a pattern of “big north small south and big inshore small inland”, with the most distinct SWSD of −0.4 and −0.38 m s−1 in inshore and inland regions, respectively. The SWSD in regions with more downscaled SWS is more distinct than in smaller SWS regions. The linear trend coefficient of SWSD indicates that LUCC induced a 0.17 m s−1 wind speed decrease per 10 years in the ECP region during 1993–2011. Furthermore, each 10 % increase of the urbanization rate could cause an approximately 0.12 m s−1 decrease of wind speed. Compared with the OMR and FWM methods, the SDM method obtains the weakest effect of LUCC on SWS and has the medium decreasing rate of SWS in three methods. In addition, the SDM method successfully reveals the fine characteristics of the spatial pattern for SWSD, which is similar to the economic level in China in recent decades.

  3. 3.

    Based on the comparison of the temporal patterns between PGF and SWS and the composite analysis of wind speed differences between strong and weak PGF years, it is obvious that PGF fails to dominate the long-term change of wind speed at the near-surface, but it is also an important control factor for wind speed on higher levels. The increase of surface roughness induced by LUCC is regarded as an important factor causing the observed SWS to decrease in the ECP region.

  4. 4.

    Different periods used to establish SDM can cause a maximum 27 % error in the regional mean SWSD of −0.44 m s−1 during the period of 1980–2011, and the linear trend of SWSD has a bias of 0.03 m s−1 (10 year)−1 and 0.01 m s−1 (10 year)−1 with the SWSD1 and SWSD2 respectively, which is lower than the linear trend of SWSD itself significantly.

In addition, there are some limitations and drawbacks in our research that are important to mention. There are other downscaling methods than the method used in this study; thus, these methods can also be used with OMR to evaluate the influence of LUCC, and potential differences in these results should be compared to verify the SDM method. We note the importance of dynamic and thermodynamic factors in the SWS change, but we have no special result in this research. In addition, the LUCC in the ECP region includes urbanization, forest cutting, farmland irrigation, returning farmland to forest and other types, but we cannot distinguish their contributions to the observed SWS decrease, and we hope to discuss this issue with reliable numerical models in the near future. Additionally, the potential reasons for the SWS decrease, except for the rise of the drag force caused by LUCC, contain the weakening of the general circulation, including the East Asian Monsoon, and local circulation changes, which are related to the change of stability and turbulent mixture in the boundary layer induced by global warming, surface albedo change, and even anthropogenic heat release. Therefore, the causes are complicated and further research from other viewpoints is required.