Improved spatial soliton theory on the example of photorefractive gallium arsenide

Abstract

This article presents a critical look at the standard theory of bright and dark photorefractive screening solitons. We pay attention to the commonly overlooked fact of the inconsistency of the theory in the context of the accordance of soliton solution with the microscopic band transport models. Taking into account the material equations for the semi-insulating semiconductor (SI-GaAs) and including the nonlinear transport of hot electrons, a simple differential equation has been developed to determine the distribution of refractive index changes in the material for a localized optical beam. An amendment to the standard solution of (1 + 1)D solitons has been proposed, which particularly should be used for dark solitons to obtain the plausible self-consistent solutions

1 Introduction

The photorefractive (PR) phenomenon is the high-sensitivity nonlinear optical effect in which the spatially nonuniform incident light induces changes in refractive index of photoconductive electrooptic materials. In the 1990s, the self-trapping effect of optical beams in photorefractive materials was observed. Soon after the possibility of generating bright and dark screening solitons was theoretically predicted [1, 2]. Those predictions were shortly thereafter confirmed experimentally [3,4,5], and the topic of solitons aroused great interest, which continues to this day [6,7,8,9,10,11]. So far, various types of PR solitons have been investigated, such as screening and photovoltaic solitons in materials with both linear and square electrooptic effect in geometry with bulk PR crystals as well as in planar waveguides.

However, it is commonly ignored that the standard PR soliton theory is internally inconsistent with respect to its compatibility with the microscopic model of the photorefractive phenomenon. The procedure for finding a soliton-state solution for an optical beam consists of two steps. In the first stage, exploiting the Kuhtarev-Vinetskii (K-V) band transport model, the dependence on the distribution of the space charge field is derived, which in turn induces changes in the refractive index Δn. Next, we look for a solution of a paraxial wave equation using the found expression for Δn. The problematic point is that when considering microscopic equations describing the properties of a specific material, commonly strong simplifying assumptions are made. As a result, the obtained soliton equation does not contain any microscopic parameter such as defect concentration, trapping coefficients, etc. Such result suggests that soliton solutions are universal and can be applied in the same form to various PR materials. Generally, such a conclusion is not correct. The present work is an attempt to reconcile the band transport model with the solution of the wave equation. It was pointed out that the commonly used expression for the distribution of the space charge field is a phenomenological approximation, which in some situations can be very different from the rigorous solution based on the microscopic model. A simple differential equation was derived that allows to determine the correct refractive index change profile in accordance with the material equations. Finally, it is shown how to modify the characteristic equation of soliton states to take into account the microscopic parameters of a given material. The proposed correction should be applied especially to the analysis of dark solitons. The band transport model for the PR semiconductor GaAs was adopted for the considerations. There were two reasons for this choice of material. Photorefractive semiconductors are characterized by electron–hole conductivity, which means that such a model of the PR effect includes cases of simpler band transport models with one type of carriers. In addition, in semiconductors such as GaAs, in strong electric fields, nonlinear electron transport appears, which was also included in the model under study. Secondly, according to authors’ knowledge photorefractive solitons have not been investigated in semi-insulating GaAs so far, therefore some criteria have been formulated that may be helpful in designing such an experiment. Also, it should be noted that photorefractive semiconductors have two attractive features: a short response time, which results from the high mobility of carriers, and sensitivity in the near infrared spectral range, including wavelengths of fiber optic telecommunications. Their disadvantage is low the electro-optic coefficients which means that high values of the external electric field are required to produce screening solitons.

2 Parameters of bright and dark beam

Further herein we consider the one-dimensional light beam with the intensity distribution I(x) in the x-direction. For solitary beams, a total power intensity of a light I(x) is generally a sum of a signal beam intensity I_s(x) and background intensity I_B = I_d + I_b, where I_d is the so-called equivalent dark irradiance corresponding to the rate of free carriers thermal generation, which can be increased by means of artificial illumination I_b. Taking as an example the optical beam described by the Gaussian function I_s(x) = I_m⋅exp(− ln2·x²/w²), where w = HWHM (width at a half maximum), the total intensity I(x) = I_s(x) + I_B can be written as

$$I(x) = I_{0} \left[ {1 \pm m\exp \left( { - \ln 2 \cdot {{x^{2} } \mathord{\left/ {\vphantom {{x^{2} } {w^{2} }}} \right. \kern-\nulldelimiterspace} {w^{2} }}} \right)} \right],$$

(1)

where for the bright beam (sign plus): I₀ = I_B, m = I_m/I₀, (m > 0) and for the dark beam (sign minus): I₀ = I_∞ + I_B, m = I_∞/I₀, (0 < m < 1); I_∞ is the signal beam intensity at a large distance from the center of the light distribution (I_∞ → 0 for bright beams and I_∞ → I_m > 0 for dark beams), m is the contrast beam parameter.

3 Standard description of the space-charge field as a phenomenological approach

The standard theoretical description of PR effect is usually based on the K-V band transport model which consists of a set of material equations involving optical excitation, transport and trapping of free carriers. In the first theoretical works [1, 2] concerning PR solitons, a few rather strong simplifying assumptions were formulated to determine the refractive index variation. The approach outlined therein that leads to the simple formula of the space-charge field E_sc(x) has been widely accepted by other researchers and up to now has been used in the analysis of one-dimensional PR solitons. Usually, the simplest version of the K-V model with the single trap level and one type of carriers is considered. This model is adequate for sillenites and ferroelectrics, but for semiconductors the model should be extended to include bipolar electron–hole transport. In both cases it can be shown that the standard solution for the space-charge field can be obtained through the phenomenological (macroscopic) approach in which only straightforward measurable parameters are taken into account. In the following the diffusion and photovoltaic effect are neglected. In that case the conduction current densities for electrons and holes are given through the differential Ohm law, respectively as

$$J_{{\text{n}}} = \sigma_{{\text{n}}} \left( x \right)E\left( x \right) \, = C_{{\text{n}}} I\left( x \right) \cdot E\left( x \right),$$

(2a)

$$J_{{\text{p}}} = \sigma_{{\text{p}}} \left( x \right)E\left( x \right) \, = C_{{\text{p}}} I\left( x \right) \cdot E\left( x \right)$$

(2b)

In the above equations, σ_n, σ_p are electron and hole photoconductivities, assuming that they are proportional to the light intensity I(x), where C_n and C_p denote quantities proportional to the carrier photogeneration rates. In the phenomenological approximation C_n and C_p do not depend on the electric field. In the steady state, for a conduction current we can write

$$J_{{\text{n}}} + J_{{\text{p}}} = J_{{{\text{total}}}} = J_{{{\text{n}}(\infty )}} + J_{{{\text{p}}(\infty )}} ,$$

(3)

where J_n(∞), J_p(∞) are the current densities at a sufficiently large distance from the beam center (formally infinitely large). Combining the equations given above, one gets

$$E(x)\left[ {C_{{\text{n}}} \left( {I_{{\text{s}}} (x) + I_{{\text{B}}} } \right) + C_{{\text{p}}} \left( {I_{{\text{s}}} (x) + I_{{\text{B}}} } \right)} \right] = E_{0} \left[ {C_{{\text{n}}} \left( {I_{\infty } + I_{{\text{B}}} } \right) + C_{{\text{p}}} \left( {I_{\infty } + I_{{\text{B}}} } \right)} \right],$$

(4a)

$$E(x) = E_{0} \frac{{I_{\infty } + I_{{\text{B}}} }}{{I_{{\text{s}}} (x) + I_{{\text{B}}} }} = E_{0} \frac{\rho + 1}{{\tilde{I}_{{\text{s}}} (x) + 1}} = \frac{{E_{0} }}{u(x)},$$

(4b)

where $\tilde{I}(x) = I(x)/I_{{\text{B}}}$, ρ = I_∞/I_B, E₀ = E(x → ∞) = E_∞ and for the simplicity of notation the function of relative light intensity $u(x) = \left[ {I_{{\text{s}}} (x) + I_{{\text{B}}} } \right]/\left( {I_{\infty } + I_{{\text{B}}} } \right) = \left[ {\tilde{I}(x) + 1} \right]/(\rho + 1)$ is introduced. In the case of bright beams: I_∞ = 0 and ρ = 0. The Eq. (4b) describes the nonlinear response which is spatially symmetric and local in respect to the light intensity pattern. If a constant voltage V is applied to the crystal of length L, additionally the external bias condition

$$V = \int_{ - L/2}^{L/2} {E(x)\;{\text{d}}x = E_{{\text{a}}} L}$$

(5)

is satisfied which permits to determine the value of E₀ = E_∞. Using Eqs. (4b) and (5) we find $E_{0} = {{E_{{\text{a}}} } \mathord{\left/ {\vphantom {{E_{{\text{a}}} } {\left\langle {u^{ - 1} (x)} \right\rangle }}} \right. \kern-\nulldelimiterspace} {\left\langle {u^{ - 1} (x)} \right\rangle }}$, where $\left\langle {u^{ - 1} (x)} \right\rangle = L^{ - 1} \int_{ - L/2}^{L/2} {u^{ - 1} (x)\;{\text{d}}x}$. If the crystal length is much larger than the width of the optical beam, one obtains $\left\langle {u^{ - 1} (x)} \right\rangle \to 1$ and E₀ → E_a. It should be noted that the field profile given by the expression (4b) depends only on the beam intensity distribution I(x) and is parameterized by the value of the coefficient ρ alone. No material parameters appear in the formula. For a symmetrical light beam, the distribution of the electric field is also symmetrical and spatially local, i.e. there is no shift of the space-charge field amplitude with respect to the light intensity. To the authors’ knowledge, the expression (4b) is used in all works concerning the analysis of screening (1 + 1)D solitons investigated not only in conventional PR crystals with linear electro-optics effect, but also in the analysis of two-photon screening-photovoltaic solitons [12, 13] or solitons in centrosymmetric materials with the quadratic electro-optic effect [14, 15].

4 Photorefractive screening solitons in semi-insulating GaAs

In what follows a more accurate expression describing the space-charge field distribution will be presented. Since the discussion is conducted in context of the possibility of generating photorefractive solitons (1 + 1D) in semiconductors, it is useful to recall shortly the basic assumptions of the commonly adopted theory of PR solitons taking the parameter values for semi-insulating GaAs.

If it is assumed that the light beam propagates along the z-axis and is allowed to diffract only in the x-direction, the intensity of the optical beam I = I(x, z) is related to the slow varying complex amplitude Φ(x,z) of the optical field E_opt(x,z,t) = Φ(x,z)exp(ikz − iωt) by the relationship: I = C·|Φ|², where C = (1/2)n_b(ε₀/μ₀)^1/2, k = (ω/c)n_b and n_b is the unperturbed index of refraction. The evolution of beam within the paraxial approximation obeys the wave equation

$$i\Phi_{z} + \frac{1}{{2k_{0} n_{{\text{b}}} }}\Phi_{xx} + k_{0} \Delta n_{{\text{b}}} (E)\Phi = 0,$$

(6a)

where Φ_z = ∂Φ/∂z, Φ_xx = ∂²Φ/∂x², Δn_b =  − (1/2)n_b³r_eff·E is the change in the refractive index induced by the linear electro-optic effect characterized by the effective coefficient r_eff. In the absence of applied voltage (E_a = 0) both bright and dark beams during propagation across a crystal spread out due to diffraction. With the proper bias electric field, this spreading of the beam can be exactly balanced by the PR nonlinearity and a spatial soliton state is formed. Forming of bright solitons requires the self-focusing nonlinearity, whereas the creation of dark solitons—self-defocusing effect. Both types of nonlinearity can be obtained in the same crystal exhibiting the electro-optic Pockels effect by reversing the biasing voltage polarity. It is convenient to write the Eq. (6a) in terms of normalized amplitude ϕ = (C/I_B)^1/2Φ and dimensionless coordinates $\zeta = z/Z_{E}$ with $Z_{E} = {2 \mathord{\left/ {\vphantom {2 {\left( {k_{0} n_{{\text{b}}}^{3} r_{{{\text{eff}}}} E} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {k_{0} n_{{\text{b}}}^{3} r_{{{\text{eff}}}} E} \right)}}$ and $\xi = x/X_{E}$ with $X_{E} = {1 \mathord{\left/ {\vphantom {1 {\left( {k_{0} n_{{\text{b}}}^{2} \sqrt {{{r_{{{\text{eff}}}} E_{0} } \mathord{\left/ {\vphantom {{r_{{{\text{eff}}}} E_{0} } 2}} \right. \kern-\nulldelimiterspace} 2}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {k_{0} n_{{\text{b}}}^{2} \sqrt {{{r_{{{\text{eff}}}} E_{0} } \mathord{\left/ {\vphantom {{r_{{{\text{eff}}}} E_{0} } 2}} \right. \kern-\nulldelimiterspace} 2}} } \right)}}$. In this case the expressions (4b) and (6a) may be written accordingly as E = E₀(1 +|ϕ_∞|²)/(1 +|ϕ |²) and

$$i\phi_{\zeta } + \frac{1}{2}\phi_{\xi \xi } \mp \left( {\frac{{1 + |\phi_{\infty } |^{2} }}{{1 + |\phi |^{2} }}} \right)\phi = 0$$

(6b)

Stationary solitons maintain the unchanged transverse profile during propagation hence the solution in the form ϕ(ξ, ζ) = y(ξ)·exp(iΓζ)·exp[iψ(ξ, ζ)] is assumed with the real amplitude y(ξ), the nonlinear propagation shift Γ and the phase function ψ(ξ, ζ). It turns out that for ψ = 0 such ansatz admits self-trapped solutions of Eq. (6b) corresponding to bright (the plus sign in the equation) and black solitons (the minus sign) not including, however, the so-called gray solitons, which have ψ ≠ 0 (phase is not constant across x), and propagate obliquely to the z-axis with the constant transverse velocity [6, 16, 17]. Using the appropriate boundary conditions for bright and dark beams and following the scheme developed in previous works [1, 2] we arrive at the characteristic equations for bright and black soliton states

$$\hat{y}_{\xi } = \left[ {F_{{{\text{bright}}}} (\rho_{0} ,\hat{y})} \right]^{1/2} ,{\text{where}}\;F_{{{\text{bright}}}} (\rho_{0} ,\hat{y}) = (2/\rho_{0} )\left[ { - \hat{y}^{2} \ln (1 + \rho_{0} ) + \ln (1 + \rho_{0} \hat{y}^{2} )} \right],$$

(7a)

$$\hat{y}_{\xi } = \left[ {F_{black} (\rho ,\hat{y})} \right]^{1/2} ,\;{\text{where}}\;F_{black} (\rho ,\hat{y}) = 2\left[ {\left( {\hat{y}^{2} - 1} \right) - \left( {1 + 1/\rho } \right)\ln \left( {\frac{{1 + \rho \hat{y}^{2} }}{1 + \rho }} \right)} \right],$$

(7b)

where ŷ denotes the amplitude normalized to unity, i.e. for bright beams ŷ = y/y_max, where y_max = y(ξ = 0), and for dark beams ŷ = y/y_max, where y_max = y(ξ → ∞). For bright and dark solitons, coefficients ρ₀, ρ are defined, respectively, as I₀/I_B (I₀ is the peak intensity value) and I_∞/I_B. Numerical integration of the above equations yields the profiles of the bright and black solitons described correspondingly by a symmetric and antisymmetric function. In turn, taking into account the inverse functions we can calculate and plot the soliton existence curves presenting the dependence of the characteristic beam width W (typically full width at half-maximum (FWHM)) as a function of the coefficients ρ₀, ρ for a given value of the electric field E_a:

$$W_{{{\text{bright}}}} (\rho_{0} ) = 2\int\limits_{1/\sqrt 2 }^{1} {F_{{{\text{bright}}}} (\rho_{0} ,\hat{y})^{ - 1/2} {\text{d}}\hat{y}} ,$$

(8a)

$$W_{{{\text{black}}}} (\rho ) = 2\int\limits_{0}^{1/\sqrt 2 } {F_{{{\text{black}}}} (\rho ,\hat{y})^{ - 1/2} {\text{d}}\hat{y}} .$$

(8b)

Fig. 1

a Existence curves for bright and black solitons for GaAs under the external field E_a = 20 kV/cm as the dependence of FWHM width of the soliton profile on the coefficients ρ₀ and ρ, b soliton width (FWHM) for bright and dark solitons as a function of an applied field for the given values of coefficients ρ₀ (bright beams) and ρ (dark beams)

Figure 1a shows the existence curves for GaAs for the intensity FWHM of bright and dark solitary waves at the applied field of 20 kV/cm.

To obtain the value of W in µm, the length X_E(20 kV/cm) ≈ 11 μm is included [introduced in the description of Eq. (6a)]. As it can be seen from Fig. 1b, the production of a soliton with a width of approximately 20 μm requires an external field of about 10 kV/cm for a black soliton, while for a bright soliton a field of up to 50 kV/cm is needed, which makes the latter impractical. Although dark solitons do not require very large electric fields, they can be unstable, leading, inter alia, to their splitting during propagation. As shown in the earlier works bright solitons are stable for any ρ₀ value, while black solitons reveal stability provided that ρ < 30 [17]. For this reason, ρ = 20 was adopted in further considerations.

5 Rate equations involving electron transport nonlinearity

To describe the PR effect in semiconductors, the K-V band model includes electron–hole transport. In the considered model inside the band gap it is assumed a single dominant deep level of photoactive centers (here donors of density N_D), responsible for the generation and recombination of both types of carriers. The shallow level of fully ionized acceptors of density N_A = N_A⁻ partially compensates of the deep donors. The shallow impurity species are inactive and do not participate in photorefractive transitions. The rate equations are [18, 19]

$${{\partial n} \mathord{\left/ {\vphantom {{\partial n} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}} = 0 = S_{{\text{n}}} \left( {I_{{\text{s}}} + I_{{\text{B}}} } \right)\left( {N_{{\text{D}}} - N_{{\text{D}}}^{ + } } \right) - \gamma_{{\text{n}}} nN_{D}^{ + } + (1/q)\nabla J_{{\text{n}}} ,$$

(9a)

$${{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}} = 0 = S_{{\text{p}}} \left( {I_{{\text{s}}} + I_{{\text{B}}} } \right)N_{{\text{D}}}^{ + } - \gamma_{{\text{p}}} p\left( {N_{{\text{D}}} - N_{{\text{D}}}^{ + } } \right) - (1/q)\nabla J_{{\text{p}}} ,$$

(9b)

$${{\partial \rho } \mathord{\left/ {\vphantom {{\partial \rho } {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}} = 0 = - \left( {1/q} \right)\nabla \left( {J_{{\text{n}}} + J_{{\text{p}}} } \right),$$

(9c)

$$J_{{\text{n}}} = q\mu_{{\text{n}}} (E)nE + qU_{T} \nabla \left[ {n\mu_{{\text{n}}} (E)T_{{\text{n}}} (E)/T} \right],$$

(9d)

$$J_{{\text{p}}} = q\mu_{{\text{p}}} pE + q\mu_{{\text{p}}} U_{T} \nabla p,$$

(9e)

$$\nabla E = {\rho \mathord{\left/ {\vphantom {\rho {\varepsilon ,}}} \right. \kern-\nulldelimiterspace} {\varepsilon ,}}$$

(9f)

$$\rho = q\left( {N_{{\text{D}}}^{ + } - N_{{\text{A}}}^{ - } + p - n} \right).$$

(9g)

Material equations are supplemented by the bias condition (5). In above equations to simplify the notation we use the symbol ∇ = d/dx. Light intensities I_s and I_B are defined in Sect. 2, S = s/hν is the photoionization cross section s per photon energy, ρ is the charge density, E is the total electric field inside a crystal, N_D, N_D⁺, N_A, n, p denote respectively the concentration of donors, ionized donors, acceptors, free electrons and holes; γ_n, γ_p are the recombination coefficients for electrons and holes, μ_n, μ_p—electron and hole mobility; J_n, J_p—the current densities; ε = ε₀ε_r, where ε₀ and ε_r are the vacuum and relative low frequency dielectric constants. U_T = k_BT/q is the thermal potential (U_T ≈ 26 mV at 300 K) where q is the elementary charge, k_B—the Boltzmann’s constant, T—the absolute temperature of lattice, T_n—the effective temperature of hot electrons. In above material equations thermal generation rate and the direct recombination rate are neglected as small. The parameters used to calculate the photorefractive response of SI-GaAs are listed in Table 1.

Table 1 Parameters used in calculations for SI-GaAs [19]

A characteristic property of GaAs is the nonlinear electron transport under electric fields exceeding 3 kV/cm, associated with the phenomenon of inter-valley electron scattering on phonons [20, 21]. This effect consists in transferring electrons (heated in a strong electric field) from the central valley Γ to the higher side L valley, where electrons have approximately 20 times lower mobility. As a result, with an increase in the electric field, the average mobility of electrons decreases, and with sufficiently strong fields (> 20 kV/cm), the drift velocity of carriers reaches an approximately constant value of saturation v_sat. The dependence of the electron drift velocity on the electric field can be modeled by an expression based on Monte-Carlo simulations [21]

$$v_{{\text{n}}} (E) = v_{{{\text{sat}}}} \left[ {1 + \frac{{E/E_{{{\text{sat}}}} - 1}}{{1 + 0.04 \cdot \left( {E/E_{{{\text{sat}}}} } \right)^{4} }}} \right].$$

(10)

The formula shows good agreement with experiments for GaAs at T = 300 K in the range of electric fields up to about 20 kV/cm [22]. Above this value, the electron drift velocity reveals a monotonic decline in the tested range to 200 kV/cm [22, 23]. Meanwhile, according to the expression (10) for E > 20 kV/cm, the electron velocity remains constant. In Eq. (10) v_sat is the saturation drift velocity, E_sat = v_sat/μ_e denotes the saturation field, v_sat = (0.6 + 0.6μ_n − 0.2μ_n²) × 10⁵ (m/s), where μ_n [m²/s] is the nonlinear mobility of electrons (μ_n(E) = v_n(E)/E) [21]. Assuming for GaAs the linear electron mobility μ_n = 0.5 m²/s = 5000 cm²/s we find v_sat = 8.5 × 10⁶ cm/s and E_sat ≈ 1.7 kV/cm. The effective temperature T_n(E) appearing in Eq. (9d) rises with the electric field approximately as T_n(E) ≈ 300 K + (1/1500)[K m/V] × E[V/m] and in strong electric fields it can exceed the lattice temperature by hundreds of degrees [18,19,20, 24]. On the other hand transport of hot holes remains linear under high fields [25]. Because experiments with generation of screening solitons require the application an external field higher than 10 kV/cm, for typical optical beams with FWHM widths of 10–20 µm, the drift transport strongly dominates over diffusion, so diffusion currents in Eqs. (9d) and (9e) may be ignored. This assumption is valid for both holes and electrons.

6 The space-charge field equation

Our aim is to find the equation describing the space charge field induced by the low-intensity 1D optical beam. By referring to the system of rate equations the assumption of low-intensity implies that free carrier concentrations are much smaller than the concentrations of impurities (n, p ≪ N_D, N_A). On the basis of Eqs. (9a)–(9g) a differential equation for ∇E can be obtained without any simplifications, but such equation is complex and illegible. More importantly, it may exhibit instability when integrating with standard numerical algorithms. We will show, that a much simpler equation can be given by using one additional assumption. The continuity Eq. (9c) states that the sum of electron and hole current densities is constant. Here, a stronger assumption is made that both the electron and hole current densities separately can be taken as constant i.e. J_n = const. and J_p = const. This result follows immediately from a macroscopic approach. Referring to the expressions (9a) and (9b) the electron conductivity is proportional to the hole conductivity, σ_n(x) = C·σ_p(x). Within the microscopic model, which means that the spatial distributions of electrons and holes are mutually proportional: n(x) ∝ p(x). In that case, from the continuity equation ∇J_n + ∇J_p = 0, one finds ∇σ_n·(1 + C)E + ∇E·σ_n(1 + C) = 0, thus ∇(σ_nE) = 0, that is J_n = const. and similarly J_p = const. Below, the above assumption is generalized by applying it to the microscopic model. This allows writing the equations J_n = J_n0, J_p = J_p0, where J_n0, J_p0 denote current densities sufficiently far from the beam: |x|≫ w. In that case concentrations of electrons and hole can be written as

$$n_{0} = {{S_{{\text{n}}} \left( {I_{\infty } + I_{{\text{B}}} } \right)(\tilde{r} - 1)} \mathord{\left/ {\vphantom {{S_{{\text{n}}} \left( {I_{\infty } + I_{{\text{B}}} } \right)(\tilde{r} - 1)} {\gamma_{{\text{n}}} }}} \right. \kern-\nulldelimiterspace} {\gamma_{{\text{n}}} }},$$

(11a)

$$p_{0} = {{S_{{\text{p}}} \left( {I_{\infty } + I_{{\text{B}}} } \right)} \mathord{\left/ {\vphantom {{S_{{\text{p}}} \left( {I_{\infty } + I_{{\text{B}}} } \right)} {\gamma_{{\text{p}}} (\tilde{r} - 1)}}} \right. \kern-\nulldelimiterspace} {\gamma_{{\text{p}}} (\tilde{r} - 1)}},$$

(11b)

where $\tilde{r}$ = r⁻¹ = N_D/N_A.

From Eqs. (9d) and (9e), omitting the diffusion component, we have μ_nn(x)E(x) = μ_n0n₀E₀, p(x)E(x) = p₀E₀, where μ_n0 denotes the low-field electron mobility. Hence, we find

$$n(x) = \left( {\mu_{{{\text{n}}0}} /\mu_{{\text{n}}} } \right)n_{0} /e(x),$$

(12a)

$$p(x) = p_{0} /e(x),$$

(12b)

where for clarity, the normalized field e(x) = E(x)/E₀ was introduced.

The space charge distribution N_D⁺ is directly related to the electric field in the crystal by Gauss’s law (9f), and assuming n, p, ≪ N_D⁺, N_A one gets

$$N_{{\text{D}}}^{ + } = N_{{\text{A}}} + (\varepsilon /q)\nabla E = N_{{\text{A}}} \left( {1 + X_{{\text{A}}} \nabla e} \right) = N_{{\text{A}}} \left( {1 + \tilde{r}X_{{\text{D}}} \nabla e} \right),$$

(13a)

and if we use the relationship (N_D − N_A)/N_A = N_DA/N_A = $\tilde{r}$ − 1, we can also write

$$N_{{\text{D}}} - N_{{\text{D}}}^{ + } = N_{{{\text{DA}}}} \left[ {1 - (\tilde{r} - 1)^{ - 1} X_{{\text{A}}} \nabla e} \right],$$

(13b)

where the two characteristic lengths X_D = εE₀/(qN_D), X_A = εE₀/(qN_A) = $\tilde{r}$ X_D and $\tilde{r}$ = r⁻¹ were defined.

By subtracting Eqs. (4a) and (4b) we arrive at the equation

$${{\partial \rho } \mathord{\left/ {\vphantom {{\partial \rho } {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}} = 0 = \left[ {S_{{\text{n}}} \left( {I_{{\text{s}}} + I_{{\text{B}}} } \right) + \gamma_{{\text{p}}} p} \right]\left( {N_{{\text{D}}} - N_{{\text{D}}}^{ + } } \right) - \left[ {S_{{\text{p}}} (I_{{\text{s}}} + I_{{\text{B}}} ) + \gamma_{{\text{n}}} n} \right]N_{{\text{D}}}^{ + }$$

(14)

which describes the dynamic equilibrium condition between the rates of photogeneration and recombination of carriers for charge density ρ. For low light intensities approximate equality ∂ρ/∂t ≈ ∂N_D⁺/∂t holds. Inserting expressions (11)–(13) into Eq. (14) after some algebra we find the looked-for equation

$$\nabla e(x) = X_{{\text{A}}}^{ - 1} \frac{{S(\tilde{r} - 1)\left[ {e(x)u(x) - \mu_{{{\text{n}}0}} /\mu_{{\text{n}}} } \right] - \left[ {e(x)u(x) - 1} \right]}}{{(S + 1)e(x)u(x) + \left( {\mu_{{{\text{n}}0}} /\mu_{{\text{n}}} } \right)S(\tilde{r} - 1) + (\tilde{r} - 1)^{ - 1} }}$$

(15)

where S = S_n/S_p.

The function f_μ(e) = μ_n0/μ_n(e) is given by the rather complicated dependence on the electric field. However, for fields E > 5 kV/cm a quasi-linear approximation f_μ(e) = e(x)^α can be used, where α ≈ 0.9. The important point regarding a stability of the solution is that the function f_μ(e) is sublinear. The accuracy of the solution according to Eq. (15) decreases in the case of a strong influence of the electron nonlinearity. The reason is that the assumption n(x) ∝ p(x) is no longer correct. However, it has been verified to be valid for the model with linear transport of carriers. In this case, setting μ_n0/μ_n = 1, Eq. (15) simplifies to the form

$$\nabla e(x) = \left( {\tilde{r}X_{{\text{D}}} } \right)^{ - 1} \frac{{\left[ {e(x)u(x) - 1} \right]\left[ {S(\tilde{r} - 1) - 1} \right]}}{{(S + 1)e(x)u(x) + S(\tilde{r} - 1) + (\tilde{r} - 1)^{ - 1} }},$$

(16)

where the distance X_A is written in terms of X_D and $\tilde{r}$. Equation (16) is a differential equation of the type de(x)/dx = [A(x)e(x) + B]/[C(x)e(x) + D]. It does not have an analytical solution in general, but is easy to integrate.

As seen, in addition to the macroscopic parameters, i.e. the electric field E₀ and electric permittivity ε, the Eq. (16) contains three microscopic material parameters: concentration of traps (N_D), impurity compensation ratio (r), and coefficient (S) that expresses the ratio of the electron to hole photogeneration rate. Note, that the equation does not contain recombination coefficients γ_n, γ_p. In the physical interpretation, this is due to the fact that in the steady state, the light-excited charge carriers in vast majority must finally be stored in the traps, building up the distribution of the space charge. Both the trapping cross-sections, as well as the mobility of carriers, affect only the dynamics of processes, determining the time of formation of the space charge. Equation (16) enables us to find the electric field distribution within the considered model of bipolar transport. Setting S = 0, (S_n = 0—only the hole transport remains), or alternatively 1/S = 0, (S_p = 0 − only the electron transport occurs), Eq. (16) can be written correspondingly as:

$$\nabla e_{{\text{p}}} (x) = (1 - r)X_{{\text{D}}}^{ - 1} \frac{{\left( {e_{{\text{p}}} u - 1} \right)r}}{{e_{{\text{p}}} u(1 - r) + r}},$$

(17a)

$$\nabla e_{{\text{n}}} (x) = rX_{{\text{D}}}^{ - 1} \frac{{\left( {e_{{\text{n}}} u - 1} \right)(1 - r)}}{{e_{{\text{n}}} u \cdot r + 1 - r}},$$

(17b)

where, to indicate the symmetry between the equations, they were written with coefficient r instead of $\tilde{r}$ = 1/r. When we replace the carrier type, symmetry relies on, as would be expected, the use of substitution r → 1 − r. For r = 0.5 ($\tilde{r}$ = 2) both equations give the same solutions.

In PR materials as ferroelectrics and sillenites, charge transport phenomena can be described by means of the band model with one type of carrier, usually electrons. Moreover, for most photorefractive crystals, the inequality N_A ≪ N_D i.e. r ≪ 1 is satisfied. In such case, Eq. (17b) takes the simple form [26]

$$\nabla e_{{\text{n}}} (x) = rX_{{\text{D}}}^{ - 1} \left[ {e_{{\text{n}}} (x)u(x) - 1} \right].$$

(17c)

Contrary to Eq. (16), based on the assumption that the electron and hole currents are constant, Eqs. (17a)–(17c) for one kind of carrier are fully consistent with the K-V model. In particular cases, e.g. for the Gaussian beam, analytical solution can be provided, expressed by the error function [27]. The electric field distribution obtained from Eq. (17c) is given by

$$e_{{\text{n}}} (x) = {1 \mathord{\left/ {\vphantom {1 {u(x)}}} \right. \kern-\nulldelimiterspace} {u(x)}} + X_{{\text{A}}} {{\nabla e_{{\text{n}}} (x)} \mathord{\left/ {\vphantom {{\nabla e_{{\text{n}}} (x)} {u(x)}}} \right. \kern-\nulldelimiterspace} {u(x)}}.$$

(18)

Referring to the above expression, we will examine the scope of validity of the approximation, where the second term may be omitted and the phenomenological formula (4b) can be applied.

7 The range of applicability of phenomenological approach

For typical optical beams with an intensity width FWHM of the order of 10–20 μm, the power intensity distribution I(x) may be treated as a slowly varying function, which suggests the assumption that the induced electric field profile has a similar property, hence inequality X_A·∇e(x) ≪ 1 is satisfied. This assumption is commonly used in the theoretical analysis concerning bright as well as dark solitons [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. As it will be shown this approximation is correct for bright beams, but has a limited applicability for dark beams. Here, we will estimate the approximate criteria when the formula e(x) ≈ 1/u(x) is correct, it means the second term in Eq. (18) can be ignored. For convenience, we assume that bright and dark beams are given by expressions $e_{{{\text{bright}}}} (\chi ) = 1/\left[ {1 + m_{0} \exp \left( { - \chi^{2} } \right)} \right]$, $e_{{{\text{dark}}}} (\chi ) = 1/\left[ {1 - m\exp \left( { - \chi^{2} } \right)} \right]$ respectively, where χ = (x/w) · (ln2)^1/2. Using parameters ρ₀ and ρ like in Fig. 2a, m₀ = ρ₀ and m = ρ/(ρ + 1). It should be noted, that if we take into consideration small values of ρ₀ and ρ = m/(1 − m) i.e. ρ₀, ρ ~ 1, the analysis can be omitted. In that case the derivatives ∇_χe are also small and it can be expected that the approximation e(χ) ≈ 1/u(χ) should not lead to major errors. Differences may appear for ρ₀, ρ ≫ 1. In the case of bright beams it can be found that in the range 20 < ρ₀ < 250 the derivate maximum ∇_χe∣_max ≈ 1 which takes place for χ ≈ 2. For dark beams, the value of the derivate maximum depends much more strongly on the parameter ρ. In the range 0.8 < m < 0.95 (4 < ρ < 20) the rough criterion can be written as ∇_χe∣_max ≈ 0.2 m/(1 − m)² = 0.2ρ(1 + ρ), for χ ≈ 0.15. To check the validity of the approximation e(χ) ≈ 1/u(χ), we take for semi-insulating GaAs the density of shallow impurities N_A = 10¹⁶ cm⁻³ and the external field E_a = 20 kV/cm, which corresponds to the characteristic length X_A = εE_a/qN_A ~ 0.1 μm. Considering the typical HWHM width of an optical beam w = 5 μm and assuming the intensity ratio ρ₀ = ρ = 20 for bright and dark beam, we obtain in the former case X_A·∇e∣_max ≈ X_A/(2 × 1.2w) ~ 0.01 << 1. The second term in Eq. (18) is negligible. Note also, that in photorefractive crystals belonging to ferroelectrics and sillenites as SBN and BSO—materials widely used in soliton experiments, one finds similar values of X_A under an external field E_a ~ 1 kV/cm [26].

Fig. 2

a The linear transport model with bipolar conductivity—comparison of analytical and numerical solutions for normalized electric field distribution, b the linear transport model with electron conductivity—comparing the macroscopic and microscopic solutions for different values of the coefficient r

As seen, in the vast majority of cases, the phenomenological approximation for bright beams is valid. The situation changes as regards dark beams. In that case the space-charge field distributions cannot be considered as slow-varying, because for ρ = 20 the derivative ∇_χe∣_max >  > 1 and X_A·∇e∣_max > 1. This shows that for dark beams the macroscopic scheme is not an appropriate approximation and the internal electric field profile should be determined on the basis of microscopic model equations i.e. using Eqs. (17) or (18).

It is worth looking at the phenomenological approximation also from another point of view. Referring to Eq. (13a), the assumption X_A∇e(x) ≪ 1 leads to the dependence N_D⁺(x) ≈ N_A, according to which depletion of ionized donor traps is negligible over all regions of the crystal. On the other hand, if we consider the model with one type of carrier, by combining the expression (13a) with (18) one obtains N_D⁺(x)/N_A = e(x)u(x). One can see immediately that for a dark beam distribution u(x), if the light intensity tends to zero at some point, a complete depletion of the available traps occurs at this point, regardless of the profile of function u(x). Moreover, it is easy to show that for dark beams with large values of ρ, the application of Eq. (18) yields the unphysical result—negative value of the donor density.

8 The microscopic versus macroscopic solution

In order to verify the accuracy of the solutions obtained from expressions (15)–(17), the system of material equations was solved using the numerical method. We have extended the numerical scheme described in [28] based on the semi-implicit algorithm, by including bipolar conductivity and hot electron transport. Figure 2a presents profiles of the internal electric field generated by a 10-μm-sized dark optical beam with the intensity factor ρ = 20. The rigorous numerical solution was compared with the solutions obtained according to Eq. (16). We find a good agreement, which also confirms the correctness of the assumption that the spatial distributions of electrons and holes are mutually proportional. Figure 2b shows the distributions of the normalized e(x) field for the dark beam, calculated according to the model with unipolar electron transport. The field profiles were plotted using Eq. (17b) and compared with the distribution resulting from the standard phenomenological approach—Eq. (4b). It is evident that the macroscopic solution may provide the result significantly different from the microscopic solution. In the presence of a strong electric field the space-charge field distribution reveals asymmetry and the peak is shifted from the center of light intensity distribution. For self-trapping beams such effect leads to bending the beam trajectory from the z-direction [6, 12, 16, 29].

In Fig. 2b, the maxima of the amplitude distribution lie exactly on the curve 1/u(x). The microscopic solution always leads to a lower field amplitude than predicted by the expression (4b). Note, the space charge field, being the response of the PR crystal to the dark beam, can reach values even tenfold times greater than the values of the applied field. The value of the crystal's internal electric field has a physical limit. It should not exceed the avalanche breakdown voltage. While for bright beams, the space-charge field (E_sc) tends to zero, completely screening the applied field (given the diffusion, the internal field can become negative), for dark beams with a high intensity ratio ρ, the E_sc field can exceed the applied field more than tenfold. The distribution of the space-charge in traps induced by a localized optical beam roughly resembles the linearly graded junction p–n. The breakdown voltage for such type of junction can be estimated using the relationship [30]

$$V_{{\text{B}}} = 60\left( {E_{{\text{g}}} /1.1} \right)^{6/5} \left[ {a/(3 \times 10^{20} )} \right]^{ - 2/5} [{\text{V}}],$$

(19)

where E_g is the energy band gap in eV, and a is the impurity gradient in cm⁻⁴. Knowing the width W_J of the space-charge region of linearly graded junction, we can find the maximum electric field from the relation [30] E_max = 1.5·V_B/W_J. In the case of GaAs (E_g = 1.42 eV) assuming N_A ~ 10¹⁶ cm⁻³ for a dark beam of half width w = 5 μm and the intensity ratio ρ = (10 − 20), we obtain a ~ 10¹⁶ cm⁻⁴, hence V_B a (100 − 150) V, and consequently, E_max ~ (350 − 400) kV/cm. According to the macroscopic description, the field amplitude attains a value about 20-fold larger than the external field—see Fig. 3b. At the applied field of 20 kV/cm it means E_max ≈ 400 kV/cm, a value comparable to an avalanche breakdown.

Fig. 3

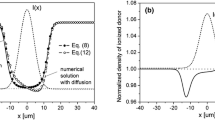
Spatial profiles of internal electric field as a response to a dark beam (ρ = 20). a Comparison of numerical solution (r = 0.2—relatively strong influence of hot electrons) with the one calculated from differential Eq. (15), b numerical solution for nonlinear transport model (r = 0.5—weak influence of hot electrons) and solutions obtained from Eqs. (15) and (16) (linear transport model) as well as (4b) (macroscopic approximation)

In the case of a significant influence of nonlinear electron transport (here r = 0.2), Eq. (15) gives only a rough approximation of the numerical solution, which reveals a strong asymmetry of the field distribution e(x) as shown in Fig. 3a. By reducing the concentration of electrons in relation to the holes (r = 0.5), the asymmetry of the field distribution decreases—Fig. 4b. In that case, Eq. (15) predicts the distribution profile close to the numerical solution. At the same time, Eq. (16) valid for the linear transport model yields an electric field profile e(x) which is always in agreement with numerical calculations.

Fig. 4

Distribution of the normalized space-charge field induced by the bright optical beam. a The linear model with electron–hole transport; solid and dashed lines—numerical solutions and phenomenological approximation (4b), b the nonlinear transport model—numerical solutions determined for r = 0.2 (comparable electron and hole densities), r = 0.5 (pronounced domination of hole density over electron density)

To sum up, it can be stated that the use of the standard relationship (4b) in the case of dark beams is generally incorrect. On the other hand, the macroscopic approach is almost always a good approximation for the study of bright solitons, as long as the model with linear transport is considered. As seen in Fig. 4a the analytical solution (4b) practically coincides with the numerical solution. However, if the influence of hot electron transport is strong, numerical methods are required to obtain the correct solution. In Fig. 4b we plotted field profiles of dark beam electric field calculated numerically for two values of the coefficient r considering the model with the nonlinear electron transport and the profile obtained according to Eq. (4b). Different values of the coefficient r imply a different ratio of hole to electron density, which for x → ∞ is given by the expression Q = p₀/n₀ = (S_p/S_n)(γ_n/γ_p)[r/(1 − r)]². Thus, for r = 0.2 we find Q = 1.2, which means that electron and hole currents are comparable, while for r = 0.5 (Q ≈ 20) the hole current clearly dominates. In the first case a relative strong impact of hot electrons results in a significant increase in the width and asymmetry of the electric field distribution—Fig. 4b. For r > 0.5 the profile of electric field approaches the shape described by the linear theory.

The applicability of the expression (15) including the electron transport nonlinearity deserves more detailed consideration. In semiconductors such as GaAs exhibiting the negative differential resistivity, instabilities of charge domains may appear at high electric fields, manifested by current oscillations. A well-known example are the microwave-frequency Gunn oscillations observed in n-type GaAs [31]. Gunn domains do not occur in semi-insulating GaAs, although light-triggered low-frequency oscillations can be excited using a localized optical beam [32]. Instability effects also appear within the numerical model used in the present work taking advantage the time equations describing the dynamics of transport processes [33]. However, carrier domains oscillations are observed provided that there is a sufficiently high concentration of electrons in relation to the concentration of holes. Since only stationary space-charge distributions are considered here, the analysis in the frame of the model with nonlinear transport was limited to the case of n₀/p₀ < 1 or n₀/p₀ ~ 1. For this reason under the strong influence of non-linear electron transport, the results predicted by expression (15) become unreliable.

9 Improved solution for dark solitons

Considering the obtained results in the context of the ability to generate black solitons in SI-GaAs, and taking into account the electron nonlinearity, we can observe stable distribution of the E_sc field with slight asymmetry and nonlocality when the hole concentration exceeds the electron concentration by at least an order of magnitude. At the same time, we can notice that the phenomenological approximation given by Eq. (4b) used in the standard soliton theory differs significantly from the solution resulting from the band transport model. If the nonlocality and asymmetry in the electric field distribution is small, the standard relationship (4b) can be modified, which provides a much better accordance with the correct solution e(x). For this purpose, we introduce three auxiliary parameters α, β, δ and write the formula (4b) in the form

$$e_{{{\text{approx}}}} (x) = \frac{\alpha }{\beta }\frac{(\rho + 1)}{{\left[ {\rho \tilde{I}_{s} (x) + 1/\beta } \right]}} + \delta .$$

(20a)

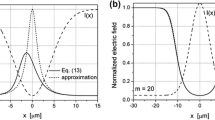
Parameters α and β control the height and width of the space-charge field profile, whereas the value of parameter δ ensures that the boundary condition e(x →  ± ∞) = 1 is satisfied, therefore we obtain δ = 1 − (α/β)(ρ + 1)/(ρ + 1/β). Let the factor α indicate how many times the amplitude of the exact distribution e(x) is reduced with respect to the macroscopic solution, i.e. α = max[e(x)]/max[1/u(x)], while the β value can be approximated as β ≈ α/2. Finally, we get the formula

$$e_{{{\text{approx}}}} (x,\rho ,\alpha ) = \frac{2(\rho + 1)}{{\tilde{I}_{{\text{s}}} (x) + \alpha /2}} - \frac{2(\rho + 1)}{{\rho + 2/\alpha }} + 1.$$

(20b)

The expression (20b) gives an acceptable approximation of the solution consistent with the numerical solution obtained from Eqs. (15)–(17a, 17b, 17c). In the following, we will consider the nonlinear model with a distinct advantage of the hole current over the electron current, assuming the coefficient r = 0.5. Figure 5 presents profiles of normalized field e(x) obtained from numerical integration of Eq. (15) and from the analytical formula (20b).

Fig. 5

Normalized electric field distribution formed by a dark beam for ρ = 20 calculated from differential Eq. (15) (solid line), centered profile e(x) (dash-dot line) and approximation based on Eq. (20b)

Having the distribution of the field e(x) and repeating the derivation given in Sect. 3, we arrive at the equation describing the black soliton, which is a corrected version of the Eq. (7b). The equation has the form

$$\hat{y}_{\xi } = \left[ {F_{{{\text{black}}}} (\rho ,\alpha ,\hat{y})} \right]^{1/2} = 2\left[ {\left( {\hat{y}^{2} - 1} \right)\frac{1 + \rho }{{2/\alpha + \rho }} - \left( {1 + 1/\rho } \right)\ln \left( {\frac{{2/\alpha + \rho \hat{y}^{2} }}{2/\alpha + \rho }} \right)} \right]^{1/2} .$$

(21)

In contrast to the standard theory, the soliton profile is now parameterized by two factors: the intensity ratio ρ and the coefficient α depending on the parameters of the microscopic model, in the general case α = α(r, N_D, S). Taking into account the field distribution shown in Fig. 5, after integration of Eq. (21) we find the intensity profile of the black soliton shown in Fig. 6a, which for comparison also includes the soliton profile according to the standard theory. Rather unexpectedly, despite significant discrepancies in the field profiles, the intensity profiles of solitons differ slightly. However, this is not always the case. In Fig. 6b, waveforms of solitons are plotted considering the model in which electrons are the sole charge carriers and assuming the impurity compensation ratio r = 0.01. In this case differences become clearly observable between outcomes of the standard and the corrected theory.

Fig. 6

Normalized black soliton intensity profiles according to the standard and revised theory obtained on the basis of: a the nonlinear transport K-V model with electron–hole conductivity, b the linear transport K-V model with one type of carrier (electrons)

The proposed amendment therefore comes down to two steps. In the first one, on the basis of Eqs. (4a, 4b), the amplitude of the field distribution e(x) is determined, which allows to find the value of the α coefficient. In the second step, using the characteristic Eq. (21), the corrected profile of the soliton is obtained.

10 Conclusions

In summary, it has been shown that the commonly used description of the space-charge electric field induced in PR material as a response to the localized (1 + 1)D optical beam is a macroscopic description. This approach is a good approximation for bright beams but is generally incorrect for dark beams leading to large unconformities with the photorefractive material equations. Taking into account the microscopic band transport model for semi-insulating GaAs, involving electron and hole competition as well as the nonlinear effect of hot electrons, a differential equation was developed, that allows to determine the correct profile of the space charge field E_sc(x). Using the obtained results for the theory of photorefractive black solitons, the a modification of the characteristic soliton state equation was presented which offers a good agreement with the numerical solution and permits to obtain the self-consistent solution between the paraxial wave equation and microscopic band transport model.