1 Introduction

Two decades ago, it was predicted that photorefractive crystals biased with a DC electric field could support the formation and propagation of the steady-state screening spatial solitons that could be generated at very low optical power of the order of μW. The theory of (1 + 1)D (one-transverse and one-propagation dimension) of such type of solitons was presented in works [1, 2] and shortly after experimentally confirmed [3–10]. Photorefractive (PR) crystals are photoconductive, specific doped electro-optics materials. When an optical beam propagates in a PR crystal, charge carriers are excited from photosensitive impurities into the conduction band where they move due to drift and diffusion and eventually are trapped in darker regions of the light intensity pattern. The resulting space–charge redistribution produces the spatially non-uniform internal electric field which in turn modulates the material refractive index through the linear electro-optic effect. Under an appropriate polarity of an external voltage, a local variation in the index of refraction leads to self-focusing or self-defocusing effect of an optical beam. This allows forming bright or dark soliton states when the nonlinearity compensates exactly the diffraction spreading of a light beam. As a result, the beam propagates in a PR medium without changing its transverse profile. For one-dimensional bright spatial solitons, a polarized optical beam in the form of a narrow stripe is launched at the entrance of a crystal together with orthogonally polarized background illumination. In the case of dark soliton, a black notch is superimposed on an otherwise uniform background illumination. Both types of solitons can be generated in the same crystal by reversing the bias voltage direction.

Due to a possibility of soliton creation at very low laser power levels, and their potential applications in all optical switching devices, PR screening solitons have been subjected to intensive theoretical and experimental works for the last two decades. So far, the formation of (1 + 1)D solitary waves has been demonstrated experimentally in various PR materials such as ferroelectrics (SBN) [3–5], (LiNbO3) [11, 12], sillenities (BTO) [6, 7], (BSO) [13] centrosymmetric paraelectrics (KLTN) [8], semiconductors (InP:Fe) [9, 14], and (CdZnTe) [15] both in geometry with bulk PR crystals and in planar waveguides [10, 16].

Typically, an analysis of optical beam propagation in PR media involves the transport equations of the so-called Kukhtarev–Vinetskii (K–V) model [17] to find the material response, then it consists in solving the paraxial wave equation with a nonlinearity term derived from the K–V model.

In original papers [1, 2], the theory of (1 + 1)D screening solitons was developed under an assumption of the slowly varying approximation for the optical field amplitude, which corresponds to typical experimental conditions. In both mentioned papers, the same approximate relation referring to the space–charge field was adopted. Using this approximation, we can derive the simple relationship representing the local saturable nonlinearity of a PR medium. As a result, we obtain the specific form of the paraxial wave equation describing both bright and dark solitary state solutions. Such form of the envelope wave equation has been commonly accepted by other researchers, and to date it has been treated as a standard in all theoretical and experimental works concerning the analysis of screening (1 + 1)D solitons [1–6, 18–33].

The purpose of this paper is to indicate that standard soliton solutions of the wave equation are not generally self-consistent with the K–V model as far as dark beams are concerned. More specifically, it is shown that the approximation made within the K–V model to determine the space–charge field induced by an optical beam has a limited range of applicability. Conditions for the validity of this approximation are discussed, and the standard relationship has been modified to ensure much better conformity with the equations of the band transport model. The modified intensity profiles of dark solitons are calculated and compared with profiles resulting from the standard theory. In particular, it has been found that a full width at half maximum (FWHM) for both profiles has very similar value. The FWHM of a beam is one of relevant experimentally accessible parameters employed to plot the soliton existence curve which constitutes the basic test in comparing experimental data with theoretical predictions. The similarity of existence curves derived from the standard theory and from the herein given revised theory explains why no discrepancies between experiments and standard soliton solutions have been reported.

2 The Kukhtarev–Vinetskii model and light-induced space–charge field

The description of photorefractive effect is based on equations of the Kukhtarev–Vinetskii band transport model including the photogeneration, transport, and trapping of the carriers. For many PR materials, we can use the simple one-carrier-type model that assumes the existence of two levels of impurities located in the energy band gap: one level of a photoactive donor species and a level of opposite species—acceptors. In that case, material equations in the steady state are read as follows [1, 2, 29]:

$$S\left( {I + I_{\text{b}} } \right)\left( {N_{\text{D}} - N_{\text{D}}^{ + } } \right) = \gamma nN_{\text{D}}^{ + } ,$$
(1a)
$$q\mu nE + q\mu U_{\text{T}}^{\prime } = J_{0} = {\text{const}} .,$$
(1b)
$$\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon q}} \right. \kern-0pt} q}} \right)E^{\prime } = N_{\text{D}}^{ + } - N_{\text{A}} - n,$$
(1c)

where the prime sign stands for a derivative with the respect to variable x.

In above equations, I is the power intensity of the optical beam, I b = I d + I B, where I d is the so-called equivalent dark irradiance corresponding to the rate of electron thermal generation, I B is the background uniform illumination used to artificially increase I d, and S = s/hν is the photoionization cross section s per photon energy hν. N D, N +D , N A, n denote the concentration of donors, ionized donors, acceptors, and free electrons, respectively; γ denotes the recombination coefficient, μ the electron mobility, q the elementary charge, E the total electric field inside a crystal, U T = k B T/q the thermal potential (U T ~ 26 mV at room temperature) where k B is the Boltzmann’s constant, and T the absolute temperature; J 0 is the current density; ε = ε 0 ε r, where ε 0 and ε r are the vacuum and relative low-frequency dielectric constants, respectively. If a constant voltage V is applied to the crystal of length L, Eqs. (1a)–(1c) are supplemented by the bias condition

$$V = \int\limits_{ - L/2}^{L/2} {E{\text{d}}x} = E_{\text{a}} L.$$
(1d)

In (1 + 1)D configuration, the light beam is allowed to diffract only in the x-direction and propagates along the z-axis. Light intensity of the optical beam I = I(x, z) is related to the slow varying complex amplitude Φ(x, z) of the optical field E opt(x, z, t) = Φ(x, z) exp(ikz − iωt) by the relationship: I = (1/2)n b(ε 0/μ 0)1/2|Φ|2, where k = (ω/c)n b and n b is the unperturbated index of refraction. The beam propagation within the paraxial approximation is governed by the wave equation:

$$i\Phi _{z} + \frac{1}{{2k_{0} n_{\text{b}} }}\Phi _{xx} + k_{0}\Delta n_{\text{b}} (E)\Phi = 0,$$
(1e)

where Φ z  = ∂Φ/∂z, Φ xx  = ∂2Φ/∂x 2, and

$$\Delta n_{\text{b}} \left( E \right) = - \left( {1/2} \right)n_{\text{b}}^{3} \cdot r_{\text{eff}} \cdot E$$
(1f)

is the change in the refractive index induced by the linear electro-optic effect, where r eff denotes the effective electro-optic coefficient.

On the basis of Eqs. (1a)–(1e), we aim to find the profile of amplitude Φ(x, z) in the case when a spatially localized optical beam with a known distribution Φ(x, 0) enters a PR crystal input plane. In particular, we can seek steady-state soliton states with the unchanged transverse profile described by a real function y(x)

$$\Phi (x,z) = y(x)\exp (i\Gamma z),$$
(2)

where Γ is the soliton propagation constant.

In order to determine the space–charge field induced by an optical beam, one needs to incorporate into Eqs. (1a)–(1d) the proper boundary conditions. The spatial x-width of the optical beam (~μm) is typically much less than the width L of the crystal (~mm). Hence, in a sufficient distance from the beam center (formally at x → ±∞), the electric field E ∞ tends to E a = V/L, and I ∞ → constant. Taking into account background illumination I b, the resulting light intensity is thus given by I total (x → ±∞, z) = I ∞ + I b. In this way, the current density in Eq. (1b) can be expressed through the free-electron density n 0 in regions with I total as J 0 = qμn 0 E a. Inserting this expression into Eq. (1b), one obtains the dependence:

$$n(x)E(x) + U_{\text{T}} n^{\prime } (x) = n_{0} E_{\text{a}} ,$$
(3)

where, for simplicity, the variable x will be hereafter neglected.

For further processing of Eq. (3), two assumptions are taken into account, which are satisfied in typical PR materials at moderate light intensity: (1) N D ≫ N A, N D ≫ N +D and (2) n ≪ N +D , N A. As a result, N +D can be neglected with respect to N D in Eq. (1a) and electron density can be omitted with respect to (N +D  − N A ) in Eq. (1c). Substituting N +D from Eq. (1c) to Eq. (1a) enables us to determine n(x), which together with Eq. (3) yields the following relation:

$$\frac{{S\left( {I + I_{\text{b}} } \right)N_{\text{D}} }}{{\gamma \left( {N_{\text{A}} + ({\varepsilon \mathord{\left/ {\vphantom {\varepsilon q}} \right. \kern-0pt} q})E^{\prime } } \right)}}E + U_{\text{T}} \left( {\frac{{S\left( {I + I_{\text{b}} } \right)N_{\text{D}} }}{{\gamma \left( {N_{\text{A}} + ({\varepsilon \mathord{\left/ {\vphantom {\varepsilon q}} \right. \kern-0pt} q})E^{\prime } } \right)}}} \right)^{\prime } = \frac{{S\left( {I_{\infty } + I_{\text{b}} } \right)N_{\text{D}} }}{{\gamma N_{\text{A}} }}E_{\text{a}} .$$
(4)

The Eq. (4) becomes more legible by introducing the normalized electric field e(x) = E(x)/E a, function u(x) of the relative light intensity, and the characteristic length X N, the latter two defined, respectively as:

$$u\left( x \right) \, = \, \left[ {I\left( x \right) + I_{\text{b}} } \right]/(I_{\infty } + I_{\text{b}} ),$$
(4a)
$$X_{\text{N}} = \varepsilon E_{\text{a}} /\left( {qN_{\text{A}} } \right).$$
(4b)

It allows us to rewrite Eq. (4) in the form:

$$e(x)\frac{u(x)}{{1 + X_{\text{N}} e^{\prime } (x)}} + \frac{{U_{\text{T}} }}{{E_{\text{a}} }}\left( {\frac{u(x)}{{1 + X_{\text{N}} e^{\prime } (x)}}} \right)^{\prime } = 1.$$
(5)

Additionally, introducing dimensionless coordinate χ = x/X N, we can write Eq. (5) as:

$$e(\chi ) = \frac{1}{u(\chi )} + \frac{{e^{\prime } (\chi )}}{u(\chi )} - \alpha_{\text{D}} \frac{{u^{\prime } (\chi )}}{u(\chi )} + \alpha_{\text{D}} \frac{{e^{\prime \prime } (\chi )}}{{1 + e^{\prime } (\chi )}},$$
(6)

where α D = U T/(X N E a).

3 Accuracy of the zero-order approximation of the distribution of e(χ)

The first component of Eq. (6) is a local term, i.e., maximum/minimum of the distribution of e(χ) coincides with the minimum/maximum of the light beam profile I(χ). The second term associated with application of an external field introduces the asymmetry in the e(χ) profile for a symmetric optical beam and leads to the appearance of spatial non-locality in the space–charge field distribution. Similarly, the third and fourth terms, associated with diffusion transport, cause the asymmetry and non-locality of e(χ). The formation of PR screening solitons requires the bias of PR crystal by a relatively large external field (~kV/cm). Considering typical experimental optical beams with an intensity FWHM ~ 10 μm, the drift components in Eq. (6) strongly dominate over the diffusion components, hence the terms with α D can be neglected in the first approximation. Therefore, from Eq. (6) one obtains:

$$e^{\prime}(\chi ) = e(\chi )u(\chi ) - 1.$$
(7)

Integration of Eq. (7) gives the looked-for profile of the internal electric field induced in a PR crystal by the optical beam described by the function u(χ). In works devoted to the analysis of PR screening solitons, the Eq. (7) is not used. Commonly, the assumption is made [1–6, 18–33] that similar to diffusion terms, the second term in (6) can be also omitted. Thus, Eq. (6) is reduced to the form:

$$e(\chi ) \simeq \frac{1}{u(\chi )} = \frac{{I_{\text{b}} + I_{\infty } }}{{I_{\text{b}} + I(\chi )}} = \frac{1 + \rho }{{1 + I(\chi )/I_{\text{b}} }},$$
(8)

which represents the local nonlinear saturable response of PR medium, where ρ = I ∞/I b is the intensity ratio of the beam at x → ±∞ with respect to the background intensity I b. For black beams, the intensity I b is equal to the equivalent dark irradiance, hence ρ = I ∞/I d.

The expression (8) is taken in literature to analyze bright solitons as well as dark solitons. It is worth noting that the above approximation is used in the analysis of solitary beams in conventional bulk materials and in the analysis of nonlinear propagation in PR centrosymmetric materials exhibiting the quadratic electro-optic effect [34, 35].

The approximation in question deserves some comment. First, it should be noted that in Eq. (8) no microscopic parameter appears, such as a recombination coefficient or trap density. In fact, the relationship (8) can be obtained directly from the macroscopic approach, without referring to the transport equations of the K–V model. Assuming that material photoconductivity is proportional to light intensity i.e., σ(x) = constant·I(x), and writing the continuity equation as J = σ(x)E(x) = σ ∞ E a, we get immediately the formula (8). Secondly, within the K–V model the assumption: \(\left| {e^{\prime } \left( \chi \right)} \right| = X_{\text{N}} \left| {e^{\prime } \left( x \right)} \right| \ll 1\) (see Eqs. 5, 7) according to Eq. (1c) yields:

$$\frac{{N_{\text{D}}^{ + } (x)}}{{N_{\text{A}} }} = 1 + X_{\text{N}} e^{\prime } (x) \simeq 1.$$
(9)

As seen, the approximation (8) is equivalent to the assumption that depletion of ionized donor traps is always negligible over all regions of the light intensity distribution, in other words N +D  ≈ N A. This conclusion seems to be a logic consequence of the assumption of low electron density n ≪ N A along with a slowly varying assumption of the power intensity function I(x). In typical photorefractive crystals, such as SBN or BSO, the characteristic length is X N ~ 0.1 μm under an external field of the order of E a ~ 1 kV/cm. Assuming that a typical beam size has an order of magnitude w ~ 10 μm, the induced space–charge field distribution should have a similar width, then Eq. (9) implies the inequality:

$$X_{\text{N}} e^{\prime } (x)_{x = w} \approx \frac{{X_{\text{N}} }}{w}\frac{{\Delta E_{\text{sc}} }}{{E_{\text{a}} }}\sim0.01 \ll 1.$$

In the following, it will be shown that this argumentation is incorrect for dark optical beams. Thirdly, if the relationship (8) constitutes the proper zero-order approximation of the exact solution of e(χ), then corrections given by the other terms in Eq. (6) can be evaluated by the perturbative solution scheme, as follows

$$e(\chi ) \approx e_{0} (\chi ) + e_{1} (\chi ) + \cdots ,$$
(10)

where e 0(χ) = 1/u(χ).

According to the perturbation approach, to obtain the higher-order correction terms, we introduce the auxiliary perturbative parameter p and write (6) as:

$$\begin{aligned} e_{0} + pe_{1} + p^{2} e_{2} \approx \frac{1}{u} + p\left( {\frac{{e_{0}^{\prime } + pe_{1}^{\prime } }}{u} - \alpha_{\text{D}} \frac{{u^{\prime } }}{u}} + \,\alpha_{\text{D}} {\left( {e_{0}^{{\prime \prime }} + pe_{1}^{{\prime \prime }} } \right)} \right) . \\ \end{aligned}$$
(11)

Equating powers of p, we find the corrections, respectively, of the first- and the second-order:

$$\begin{aligned} e_{1} & = \frac{{e_{0}^{\prime } }}{u} - \alpha_{\text{D}} \frac{{u^{\prime } }}{u} + \alpha_{\text{D}} e_{0}^{{\prime \prime }} = - \frac{{u^{\prime } }}{{u^{3} }} - \alpha_{\text{D}} \frac{{u^{\prime } }}{u} - \alpha_{\text{D}} \frac{{u^{{\prime \prime }} }}{{u^{2} }} + 2\alpha_{\text{D}} \frac{{(u^{\prime } )^{2} }}{{u^{3} }}, \\ e_{2} & = \frac{{e_{1}^{\prime } }}{u} + \alpha_{\text{D}} e_{1}^{{\prime \prime }}. \\ \end{aligned}$$
(12)

The above scheme is valid under the condition that all higher-order terms are much smaller than the leading term e 0. Such procedure has been applied in [21] to study the self-bending effect in propagation of bright PR solitons. To investigate the range of applicability of the approximation (9) let us consider the bright and dark optical beams described by the Gaussian function, given, respectively, as

$$I(\chi ) = I_{m} \exp ( - {{\chi^{2} } \mathord{\left/ {\vphantom {{\chi^{2} } {W^{2} }}} \right. \kern-0pt} {W^{2} }}),$$
(13a)
$$I(\chi ) = I_{m} \left( {1 - \exp ( - {{\chi^{2} } \mathord{\left/ {\vphantom {{\chi^{2} } {W^{2} }}} \right. \kern-0pt} {W^{2} }})} \right),$$
(13b)

where for the bright beam (13a): I(0) = I m , I ∞ = 0, and for the dark beam (13b): I(0) = 0, I ∞ = I m . W denotes the normalized width given by \(W = {w \mathord{\left/ {\vphantom {w {(X_{\text{N}} \sqrt {\ln 2} )}}} \right. \kern-0pt} {(X_{\text{N}} \sqrt {\ln 2} )}}\), where w = HWHM (half width at half maximum). The corresponding normalized light intensity function defined by Eq. (4a) may be now rewritten in the form:

$$u(\chi ) = 1 \pm m \cdot \exp ( - {{\chi^{2} } \mathord{\left/ {\vphantom {{\chi^{2} } {W^{2} }}} \right. \kern-0pt} {W^{2} }}),$$
(14)

where the contrast beam parameter is given by m = I m /I b for the bright beam and m = I ∞/(I b + I ∞) = ρ/(1 + ρ) for the dark beam.

In this study, calculations are carried out for cerium-doped strontium–barium–niobate (SBN) crystal—the material widely used in soliton experiments. Photorefractive transitions in SBN can be discussed in terms of a one-level model with electron conductivity [36] in accord to Eqs. (1a)–(1c). Photoactive centers occur at two valence states which act as donors (ions Cr3+) and acceptors (ions Cr4+). The values of the material parameters adopted for SBN:61:CeO2 crystal are as follows [36]: N D = 4 × 1018 cm−3, N A = 2 × 1016 cm−3, the photoionization cross section s = 2.6 × 10−19 cm2, which at a light wavelength λ 0 = 500 nm corresponds to S = 0.65 cm2/J, and the recombination coefficient γ = 1 × 10−10 cm3/s. In soliton experiments with SBN crystals, the optical beam is linearly polarized in the x-direction which coincides with the optical c-axis and direction of the external bias electric field. In that case, referring to Eq. (1f), coefficients n b and r eff denote, respectively, the extraordinary index of refraction n e = 2.33 and the electro-optic tensor element r 33 = 235 pm/V [20, 21, 36, 37]. Because SBN has a very large dielectric constant ε r = ε 33 = 880, screening solitons can be formed at a rather small applied electric field E a of the order of 1 kV/cm.

Based on Eqs. (7) and (8), three cases of distributions for the normalized electric field e(x) and ionized donors N +D (x)/N A will be investigated below. The solutions will be then compared with rigorous numerical solutions determined from material Eqs. (1a)–(1d).

3.1 Slowly varying bright optical beam (weak diffusion)

As a first example, let us consider a bright Gaussian beam described by Eq. (14) with parameter values m = 50, FWHM = 10 μm, and under the assumption of an applied field E a = 1 kV/cm. From Fig. 1, we can clearly see that in the case of bright optical beam, the accuracy of the approximation (6) is very good. The analytical solution (8) coincides almost wholly with the numerical solution. Distribution asymmetry arising from the application of external field is negligible, and concluding from numerical calculations, it becomes noticeable at field values above about 5 kV/cm. Influence of the diffusion can be satisfactorily studied by taking into account the second correction-perturbative term in Eq. (12), which is displayed in Fig. 1a.

Fig. 1
figure 1

a Normalized space–charge field distribution and b ionized donor density distribution induced by a Gaussian beam with FWHM = 10 μm and m = I(0)/I b = 50. In (a) solid and dashed lines display results of numerical integration of the K–V model equations, respectively, including and neglecting diffusion, whereas circle plots show solutions obtained, respectively, according to Eqs. (8) and (12)

Full size image

Notably, in the diffusionless case, the total internal field is close to zero in the central part of the beam as a result of the external field screening, while at the presence of the diffusion, the total field can be negative, that is it has an opposite polarization with respect to the applied field. Figure 1b indicates that local deviation of ionized donor density from the average value 〈N +D 〉 = N A is only a few percent, which is in agreement with Eq. (9).

3.2 Micro-sized bright optical beam (strong diffusion)

We can expect that approximation (8) becomes inaccurate if the transverse beam size is comparable with the characteristic length X N given by (4b) [38]. Here, for the assumed parameter values, we find X N ≈ 0.5 μm. In such case, simultaneously linked with the condition m ≫ 1, the adoption of the above approximation n ≪ N +D , N A is not longer valid. Note that within this approximation, we can obtain \(1 + X_{\text{N}} e^{\prime } \left( x \right) \to 0\), which means that the normalized electron density (see Eq. 5) \(\tilde{n} = n/N_{\text{A}}\) may tend to infinity

$$\tilde{n} = \frac{B}{{1 + X_{\text{N}} e^{\prime } }} \to \infty ,\quad {\text{where}}\quad B = \frac{{S\left( {I + I_{\text{b}} } \right)N_{\text{D}} }}{{\gamma N_{\text{A}}^{2} }}.$$
(15a)

Therefore, considering tight beams in size of the order of one micrometer, the full equations of the K–V model must be used. In particular, \(\tilde{n}\) should be determined from the expression:

$$\tilde{n} = \frac{1}{2}\left( {1 + X_{\text{N}} e^{\prime } } \right)\left( {\sqrt {1 + \frac{4B}{{\left( {1 + X_{\text{N}} e^{\prime } } \right)^{2} }}} - 1} \right).$$
(15b)

For illustration, Fig. 2 shows distributions of e(x) and N +D (x) for optical Gaussian beam with FWHM = 1 μm, m = 25 and for an applied field E a = 2 kV/cm.

Fig. 2
figure 2

a Micro-sized Gaussian beam (1 μm) generates the space–charge field profile which strongly deviates from the zero-order approximation (8). The diffusion effect on the considering distribution is very strong and must be taken into account. b Distribution of ionized donor density corresponding to profile in (a)

Full size image

It is evident from Fig. 2 that the zero-order approximation (8) fails under considerations of tight beams. The influence of diffusion is very strong and depletion of ionized donors amounts to about 75 % of the mean value. We can note that the resulting distribution of the space–charge resembles the depletion region of charge in the asymmetric p–n junction in semiconductors. For such micron-sized beams, it was found that states of screening and transient PR solitons are not allowed [38].

3.3 Slowly varying dark optical beam (weak diffusion)

In papers dealing with photorefractive (1 + 1)D screening solitons, the dependence (8) is also exploited for dark beams for which the light intensity pattern is a slowly varying function of x.

To show the problem, let us note first that, associated with the discussed approximation, the condition in Eq. (9): N +D /N A ≈ 1 is not fulfilled. For this purpose, consider the dark beam described by any function u(x) and take into account Eq. (9), for simplicity written here with the normalized coordinate χ = x/X N

$$\frac{{N_{\text{D}}^{ + } (\chi )}}{{N_{\text{A}} }} = 1 + e^{\prime } (\chi ).$$
(16)

Substitution of the dependence (7) into Eq. (16) leads to the equation:

$$\frac{{N_{\text{D}}^{ + } (\chi )}}{{N_{\text{A}} }} = e^{\prime } (\chi ) \cdot u(\chi ).$$
(17)

Let an optical beam be a black beam, where the term black indicates that its minimum intensity is zero at any point χ 0. From (17), one can see immediately that for a beam with u(χ 0) = 0 (for the symmetric beam χ 0 = 0), we get N +D (χ 0) = 0. Thus, in the center of a black beam, we always have 100 % depletion of donor traps regardless of the shape of function describing the profile u(χ). Adding the background illumination, the depletion will be smaller than 100 %; however, the above analysis reveals that for dark beams, taking into account only the zero-order term in (6) is not acceptable. In this case Eq. (7) should be applied. Since screening soliton beams propagate in biased PR crystals, the diffusion terms play a secondary role compared to the drift term, so the application of Eq. (7) provides a good accuracy.

Approximate and somewhat arbitrary assessment of the range of applicability of the dependence (8) can be made referring to Fig. 3. Figure 3a–c presents profiles of the internal electric field generated by a 10-μm-sized dark optical beam for three different values of the intensity factor ρ = 5, 10, and 50. One can infer that the reasonable agreement between solution (8) and numerical solution based on Eq. (7) occurs only for small values of ρ. Setting greater values of ρ leads to the very significant discrepancy, particularly noticeable in the ionized donor distribution depicted in Fig. 4c. In this event, the application of Eq. (8) yields the evident unphysical result, that is, a large negative value of the donor density. In contrast to this result, the rigorous numerical solution reveals that in accord with Eq. (17), the concentration of neutralized donor traps approaches the charge saturation state.

Fig. 3
figure 3

a–c Distributions of the internal electric field formed in SBN crystal by a dark optical Gaussian beam with FWHM = 10 μm for different intensity ratios ρ = I ∞/I b at the bias field E a = 1 kV/cm. Solid lines—numerical solutions, dashed lines—solution according to the dependence (8). d Distributions of ionized donor density corresponding to solutions shown in Fig. 3c

Full size image
Fig. 4
figure 4

Normalized electric field distribution formed by a Gaussian dark beam for ρ = 80 and an intensity FWHM = 10 μm to obtain the best reproduction of the numerically calculated profile by means of the relationship (20). Normalized coordinate is χ = x/X N, where X N taken from Eq. (4b) is equal to 0.24 μm

Full size image

For adopted parameter values, the solution obtained from Eq. (7) is practically identical with the numerical solution of material Eqs. (1a)–(1c). For the considered dark beam described by the Gaussian function (4), the Eq. (7) has an analytical solution in the integral form:

$$e(\chi ) = \left( {1 + \int\limits_{{ - \chi_{0} /2}}^{\chi } {\exp \left[ {P(\chi^{\prime } )} \right]{\text{d}}\chi^{\prime } } } \right)\exp \left[ { - P(\chi )} \right],$$
(18a)

where

$$P(\chi ) = \chi - \chi_{0} - \frac{\sqrt \pi }{2}W \cdot m\left[ {erf\left( {\frac{\chi }{W}} \right) - erf\left( {\frac{{\chi_{0} }}{W}} \right)} \right],\quad \chi_{0} = L/X_{\text{N}}$$
(18b)

and \(erf(s) = \frac{2}{\sqrt \pi }\int_{0}^{s} {\exp ( - p^{2} ){\text{d}}p}\) is the so-called error function.

There are a few worth noting differences as regards field distributions created by dark beams (Fig. 3) in comparison with field profiles induced by bright beams (Fig. 1). In the first case, the resulting electric field profile has a smaller width than the beam intensity FWHM and exhibits a distinct asymmetry as well as a spatial shift relative to the minimum light intensity. In contrast to the bright beam case, the shape of field distributions shown in Fig. 3 are slightly dependent on the influence of diffusion. In fact, in Fig. 3a–c, solutions with and without diffusion are virtually indistinguishable.

Since the relation (8) constitutes a rough approximation for dark beams, incorporation of higher-order terms in a perturbation scheme does not improve the accuracy of the solution. The zero-order approximation will be fully reliable only within the linear regime in which the distribution e(χ) mimics the optical beam shape given by u(χ) = 1 − m · f(χ) according to the dependence:

$$e(\chi ) \simeq \frac{1}{u(\chi )} = \frac{1}{1 - m \cdot f(\chi )} \approx 1 + m \cdot f(\chi ),$$
(19)

where the above approximation is valid for m < 1.

It is easy to point out the physical reason of observed differences in the space–charge distributions produced by bright and dark beam with a similar size and contrast. Under the influence of a bright beam, photoelectrons are excited mainly in the spatially localized region, much smaller than the crystal length. Consequently, a relatively small amount of charge is effectively transported between regions lying in the vicinity of beam edges. Thus, the induced space–charge field has a profile size wider than the beam intensity FWHM which is illustrated in Fig. 1.

The situation is different for a dark beam where photocarriers are generated in a large illuminated area of a crystal, and after transportation, free electrons are trapped in the central part of dark dip in the light intensity distribution. In consequence, a considerably larger number of charges are trapped than in the case of ‘point’ generation of photoelectrons by means of bright beam. Also, the resulting space–charge field distribution has now smaller width than FWHM of the dark wave.

As regards dark beams, we can distinguish three approximated ranges for the value of the factor ρ corresponding to the accuracy of the relationship (8) in the framework of the slowly varying approximation for the light intensity waveform: (1) range of linearity for ρ ≤ 1, in which the discussed approximation is right, (2) the range 1 < ρ < 5 in which the approximation leads to an acceptable agreement with the numerical solution, and (3) the range ρ > 5, in which one should apply Eq. (7).

However, as indicated earlier, the approximate relation (8) is generally adopted in literature for an arbitrary value of ρ for the analysis of (1 + 1)D dark solitons. Bearing this fact in mind, if we neglect the non-locality and asymmetry in the electric field distribution, one can propose a relatively simple modification of the standard relationship, which provides a much better accordance with the correct solution e(χ). For this purpose, by introducing three parameters α, β, and δ, the formula (8) is transformed to the following form:

$$e(\chi ) = \frac{\alpha }{\beta } \cdot \frac{1 + \rho }{{1/\beta + \rho \tilde{I}(\chi )}} + \delta ,$$
(20)

where Ĩ(χ) = I(χ)/I ∞ ≤ 1.

Two free parameters α ≤ 1 and β ≤ 1 control the height and width of the optical beam, respectively, whereas the value of parameter δ is determined in order to ensure the boundary condition e(χ → ±∞) = 1, then

$$\delta = 1 - \frac{\alpha }{\beta } \cdot \frac{1 + \rho }{1/\beta + \rho }.$$
(21)

The values of coefficients α and β must be found experimentally to obtain the best fit to the numerically determined profile e(χ) on the basis of (7). In the following, these coefficients are matched against the field profile to minimize the root-mean-square error with respect to the centered electric field distribution e(χ). Figure 4 depicts profiles of field e(χ) obtained from numerical integration of Eq. (7) and from the analytical formula (20). As seen, the dependence (20) permits to obtain an acceptable good fit to the numerical solution.

4 Solution for the dark soliton

To find the fundamental dark soliton solution, we will follow the scheme developed in original papers [1, 2] using a modified form of e(χ) given by Eq. (20). It is considered a one-dimensional light beam with the unknown slowly varying amplitude function describing the optical field Φ(x, z) in an input crystal plane. The optical beam propagates along the z-axis through the PR crystal and satisfies the envelope wave equation (1e). After substituting the normalized amplitude \(\phi (x,z) = {{\Phi (x,z)} \mathord{\left/ {\vphantom {{\Phi (x,z)} {\sqrt {I_{\text{b}} } }}} \right. \kern-0pt} {\sqrt {I_{\text{b}} } }} \propto \sqrt {{I \mathord{\left/ {\vphantom {I {I_{\text{b}} }}} \right. \kern-0pt} {I_{\text{b}} }}}\), together with (1f) and (20) into (1e) one gets:

$$i\phi_{z} + \frac{1}{{2k_{0} n_{e} }}\phi_{xx} \mp \frac{1}{2}k_{0} n_{e}^{3} r_{33} E_{0} \left( {\frac{\alpha }{\beta } \cdot \frac{{1 + |\phi_{\infty } |^{2} }}{{1/\beta + |\phi |^{2} }} + \delta } \right)\phi = 0 .$$
(22a)

For simplicity of calculations, Eq. (22a) is transformed to the normalized form:

$$i\phi_{\zeta } + \frac{1}{2}\phi_{\xi \xi } \mp \left( {\frac{\alpha }{\beta } \cdot \frac{{1 + |\phi_{\infty } |^{2} }}{{1/\beta + |\phi |^{2} }} + \delta } \right)\phi = 0,$$
(22b)

by inserting dimensionless coordinates: ς = z/Z E, Z E = 1/(0.5 k 0 n 3e r 33 E 0) and ξ = x/X E, \(X_{E} = {1 \mathord{\left/ {\vphantom {1 {\left( {k_{0} n_{e}^{2} \sqrt {{{r_{33} E_{0} } \mathord{\left/ {\vphantom {{r_{33} E_{0} } 2}} \right. \kern-0pt} 2}} } \right)}}} \right. \kern-0pt} {\left( {k_{0} n_{e}^{2} \sqrt {{{r_{33} E_{0} } \mathord{\left/ {\vphantom {{r_{33} E_{0} } 2}} \right. \kern-0pt} 2}} } \right)}}\).

In the absence of applied voltage, both bright and dark beams during propagation across a crystal spread out due to diffraction. With the proper bias field, this beam spreading can be exactly balanced by the PR nonlinearity and a spatial soliton state is formed. Forming of bright solitons requires the self-focusing effect, whereas the creation of dark solitons—a self-defocusing effect. Both types of nonlinearity can be obtained in the same crystal exhibiting the electro-optic Pockels effect by reversing the biasing voltage polarity. In both cases, the index of refraction increases locally in the central region of an optical beam. In Eq. (22), the minus sign corresponds with a self-focusing nonlinearity and bright beam trapping, while the plus sign with a self-defocusing nonlinearity and possibility to obtain a dark soliton. Looking for a stationary soliton state with unchanged transverse profile, we postulate the solution in the form:

$$\phi (\xi ,\varsigma ) = y(\xi )\exp (i\Gamma \varsigma ),$$
(23)

where y(ξ, ς) is assumed to be a real function as a condition of the stationary solution and Γ represents the nonlinear propagation shift, that is the difference between the soliton propagation constant and the wave number k e = k 0 n e for plane wave.

In the following, we consider only the wave equation (22b) which admits dark soliton solutions. Substitution (23) into Eq. (22b) yields:

$$y_{\xi \xi } = 2\Gamma y - 2\left( {\frac{\alpha }{\beta } \cdot \frac{{1 + y_{\infty }^{2} }}{{1/\beta + y^{2} }} + \delta } \right)y.$$
(24)

Noting that (y 2 ξ ) ξ  = 2y ξ y ξξ Eq. (24) can be easily integrated once, which leads to the equation

$$(y_{\xi } )^{2} = 2\Gamma y^{2} - 2\frac{\alpha }{\beta }\left( {1 + y_{\infty }^{2} } \right)\ln \left( {1 + \beta y^{2} } \right) - 2\delta y^{2} + C.$$
(25)

Constants Γ and C may be determined by imposing the boundary conditions at zero and infinity for the dark soliton solution i.e., y(0) = 0, y 2(ξ → ±∞) = y 2∞  = ρ = I ∞/I d, hence y ξ (±∞) = y ξξ (±∞) = 0. In this way, from Eq. (24) we find

$$\Gamma = \frac{\alpha }{\beta }\frac{1 + \rho }{1/\beta + \rho } + \delta$$
(26)

and taking into account (21) one obtains Γ = 1 as in the standard theory. For the dimensional coordinate z, we have Γ z  = Γ/Z E = (1/2)k 0 n 3e r 33 E 0, thus Γ z is independent of the intensity ratio ρ. The condition y ξ (±∞) = 0 inserted into (25) permits to find the integration constant C, and we finally arrive at the equation:

$$(y_{\xi } )^{2} = F\left( {y,y_{\infty }^{2} ,\alpha ,\beta } \right),$$
(27a)

where

$$F(y,y_{\infty }^{2} ,\alpha ,\beta ) = 2\frac{\alpha }{\beta }\left( {1 + y_{\infty }^{2} } \right)\left[ {\frac{{y^{2} - y_{\infty }^{2} }}{{1/\beta + y_{\infty }^{2} }} - \ln \left( {\frac{{1/\beta + y^{2} }}{{1/\beta + y_{\infty }^{2} }}} \right)} \right].$$
(27b)

The Eq. (27) is not integrable and has to be solved numerically to determine the looked-for profile of dark soliton. Unknown parameters α and β are adjusted so that the approximated solution for the internal electric field profile given by

$$e(\xi ) = \frac{\alpha }{\beta } \cdot \frac{{1 + y_{\infty }^{2} }}{{1/\beta + y^{2} (\xi )}} + \delta$$
(28a)

fitted to the numerical solution from Eq. (7):

$$e^{\prime}(\xi ) = \left[ {e(\xi )\frac{{1 + y^{2} (\xi )}}{{1 + y_{\infty }^{2} }} - 1} \right] \cdot \frac{{X_{\text{E}} }}{{X_{\text{N}} }}$$
(28b)

minimizes the mean square error. The Eq. (28b) is written with taking into account the scaled constant between coordinates χ and ξ.

The presented procedure provides the dark soliton solution of Eq. (27b) which is with a good approximation self-consistent with Eq. (28b) resulting directly from the Kukhtarev–Vinetskii model. The profile of dark soliton is described by an odd (antisymmetric) function which is easy to show by analysis of the structure of Eq. (27). For a coordinate ξ in the vicinity of ξ = 0, where y(0) = 0, for black solitons, the inequality y 2∞  ≫ y 2 holds, so Eq. (27) can be written approximately as

$$\begin{aligned} y_{\xi } & \approx \sqrt B ,\quad {\text{where}}\quad B = F(0,y_{\infty }^{2} ,\alpha ,\beta ) \\ & = 2\frac{\alpha }{\beta }\left( {1 + y_{\infty }^{2} } \right)\left[ {\ln \left( {1 + \beta y_{\infty }^{2} } \right) - \frac{{\beta y_{\infty }^{2} }}{{1 + \beta y_{\infty }^{2} }}} \right], \\ \end{aligned}$$

thus the function y(ξ → 0) is the linear function \(y \approx \xi \sqrt B\), therefore y(ξ) in the whole range of ξ has to be an odd function. The presented solution describes the so-called fundamental dark soliton that in a typical experimental configuration is created by introducing a phase shift of π into one half of the initial beam [4–6].

Figure 5a, b displays the normalized envelope of field profile (y norm = y/y ∞) and intensity profile (y/y ∞)2 for black solitons calculated on the basis on the standard relation with α = β = 1, δ = 0 in Eq. (28a) and according to the fitting procedure described above.

Fig. 5
figure 5

a The standard and revised normalized intensity profiles of the black soliton for ρ = 20 shown together with the corresponding distributions of the internal electric field and b envelope of the black soliton for intensity ratio ρ = 50. In both cases, a field E a = 1 kV/cm was applied. Normalized coordinate is ξ = x/X E, where X E ≈ 5 μm

Full size image

Figure 5a also includes distributions of the space–charge field obtained by using the standard dependence (8) and those based on Eq. (7). It can be seen that the difference is very distinct. For soliton beams, in comparison with previously considered dark Gaussian beams, the asymmetry in the space–charge field profile is noticeably smaller. As a result, the approximation of this profile by means of the dependence (28a) is more accurate.

As we can see in Fig. 5a, b, the improved intensity profiles are generally narrower that the profiles representing the standard solution. Differences between these profiles become clearly observable for the value of ρ = y 2∞ approximately >5. Below this value, both distributions practically overlap. It should be noted that half widths (FWHM) of these solutions are very similar, whereas a remarkable deviation is observed particularly for an upper part of the profile, i.e., for I(ξ) > 1/2.

On the basis of (27), we can determine the inverse function ξ(y norm) in the integral representation

$$\xi \left( {y_{\text{norm}} } \right) = \int\limits_{0}^{{y_{\text{norm}} }} {\frac{{{\text{d}}(\tilde{y}_{\text{norm}} )}}{{\sqrt {F(\tilde{y}_{\text{norm}} ,\rho ,\alpha ,\beta )} }}} .$$
(29)

Choosing an arbitrary characteristic width W of the dark soliton waveform, Eq. (28) enables us to calculate and plot the so-called existence curve for solitons, i.e., the dependence of W versus ρ (or y ∞) corresponding with a given external electric field E a. For this purpose, we write Eq. (29) as

$$W(\rho ) = \int\limits_{0}^{{y_{0} }} {\frac{{{\text{d}}(y_{\text{norm}} )}}{{\sqrt {F\left( {y_{\text{norm}} ,\rho ,\alpha ,\beta } \right)} }}} .$$
(30)

Typically the existence curve is constructed under an assumption that the characteristic width W is an intensity FWHM of a soliton beam at which \(y_{\text{norm}} = y_{0} = 1/\sqrt 2.\) However, to exhibit more clearly the difference between discussed soliton solutions, let us assume the width W corresponding to the definition of the Gaussian beam diameter at which \(y_{\text{norm}} = y_{0} = \sqrt {1 - 1/e^{2} } \approx 0.93\). Comparison of thus defined existence curves is shown in Fig. 6b. To obtain the value of W in micrometers, one should include the scaled length X E  ≈ 5 μm, introduced in the description of Eq. (22).

Fig. 6
figure 6

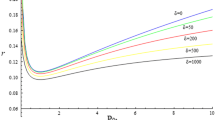
a Existence curves for black solitons obtained from the standard and improved theory for two various characteristic widths of soliton profiles: an intensity FWHW and the Gaussian width and b values of coefficients α, β (circle marks) found numerically and the matched curves α(ρ), β(ρ) described by the formula of type (30)

Full size image

An experimental investigation of one-dimensional dark solitons in conventional bulk PR crystals was reported in [4–6]. In this context, a question arises why, so far, any discrepancies between theory and experiments regarding the study of dark solitons have not been observed.

The explanation of this fact is relatively simple. As indicated, in the case of the determination of the space–charge field distribution in the frames of K–V model, the use of the approximation contained in Eq. (8) can lead to large errors concerning dark beams. If we improve this approximation toward better compatibility with the photorefractivity model, it turns out that soliton solutions derived from the wave equation with application of the standard and modified nonlinear term (see Eqs. 20, 1f) differ to an unexpectedly small extent. Thus, the commonly employed theory, despite inconsistencies with the K–V model, provides a similar profile of dark solitons as here presented revised theory.

It needs to be noted that the actual beam shape is not usually studied in the experiments. One of the most relevant measured parameters used for comparing experimental results with predictions of the theoretical model is the intensity FWHM of a beam which allows constructing and plotting the existence curve.

Although a good qualitative agreement between data and theory was found in experimental works, a quantitative agreement in some events is not fully satisfactory [39]. It is assumed that observed discrepancies are connected to extraneous effects not included in the applied theoretical model.

Figure 6a shows that the existence curves for FWHM of a beam plotted on the basis of the standard and improved theory are very similar and within the limits of measurement accuracy of the differences that are hardly visible in experiments. On the basis of the above comparison, such incompatibility should be observed by defining, for instance, the width of profile at a level of 90 % height of the soliton peak. In case of dark solitons, however, it is experimentally a hard challenge, because strong noise and fluctuations occur at a background intensity level [4–6], which makes beam width measurements difficult. The existence curves which are one of the basic tools related to the experiment run similarly for standard and modified solutions. As seen from Fig. 6a for y ∞ > 10, both curves tend to a constant value. Nevertheless, it is important to point out that, according to the standard theory, the steady-state soliton solutions for a given applied voltage are parameterized only through the intensity ratio ρ, which uniquely defines their profile shapes. In the case of the presented revised solutions, to obtain the transverse shape of soliton wave we need to know the values of coefficients α and β. These values are chosen toward the best fit of the solution (28a) for the numerical solution of the K–V model equations. The necessity to use such procedure complicates the determination of a correct profile of dark soliton compared to the standard approach, except for the range ρ < 5, where with good approximation one can assume that α ≈ β ≈ 1. Obviously, it is much more convenient to work with closed formulas for α(ρ) and β(ρ). It turns out that these relations are monotonically decreasing functions of the parameter ρ. For the assumed calculation parameters, these functions in the wide range of ρ (here: 5 < ρ < 500) can be quite well approximated by the formula of the type

$$\alpha (\rho ),\,\,\beta (\rho ) = \frac{{a_{1} }}{{\rho + a_{2} }}\exp \left( { - \frac{\rho }{{a_{3} }}} \right),$$
(31)

where a 1, a 2, and a 3 are free parameters, whose values have been selected to get the best conformity of the curve with numerical solutions. The appropriate form of the function (31) can be established from a relatively small number of specific values of α and β. Thanks to this, formula (31) permits to determine adjusting coefficient values without additional computational cost in a wide range of ρ changes. Thus, calculated curves α(ρ) and β(ρ) are plotted in Fig. 6b, where the following respective values were taken: a 1 = 8.5, a 2 = 4, a 3 = 8000 for the function α(ρ), and a 1 = 2, a 2 = 4, a 3 = 5000 for the function β(ρ).

Since the discovery of PR screening solitons in 1990s, during the recent two decades these self-trapping beams still have been the subject of interest and numerous publications. These include chapters in books and general reviews [29–33, 40, 41] concerning PR solitons, particularly dark solitons [40]. However, in all of the above works, the theoretical description of PR screening solitons is based on the approximation discussed in detail in the present article, hence as regards the dark solitons, the widely used solutions are formally incorrect. In this context, the herein presented outcomes providing the corrections to the standard solutions can be treated as a complement to previous works and should be taken into account in theoretical studies.

5 Summary

In summary, this paper examines the accuracy of commonly used approximation within the Kukhtarev–Vinetskii model, employed in an analysis of photorefractive material response to a slowly varying light beam. It has been indicated that for dark beams, the standard approximated formula describing the space–charge field distribution has a limited applicability and may lead to large unconformities with photorefractive transport equations. This author proposes a simple modification of the above formula which offers a substantially better agreement with the numerical solution and permits to obtain the self-consistent solution between the paraxial wave equation and the K–V model. The corrected profile of one-dimensional black soliton has been calculated. It has been found that soliton solutions according to the standard and modified theory yield soliton profiles exhibiting very similar half-widths. Also, the simple approximate analytical relationship has been given for the determination of adjusting parameters depending on the factor ρ.