Mathematical Analysis of Two Competing Cancer Cell Migration Mechanisms Driven by Interstitial Fluid Flow

Abstract

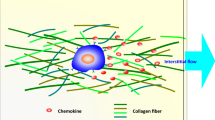
Recent experimental work has revealed that interstitial fluid flow can mobilize two types of tumor cell migration mechanisms. One is a chemotactic-driven mechanism where chemokine (chemical component) bounded to the extracellular matrix (ECM) is released and skewed in the flow direction. This leads to higher chemical concentrations downstream which the tumor cells can sense and migrate toward. The other is a mechanism where the flowing fluid imposes a stress on the tumor cells which triggers them to go in the upstream direction. Researchers have suggested that these two migration modes possibly can play a role in metastatic behavior, i.e., the process where tumor cells are able to break loose from the primary tumor and move to nearby lymphatic vessels. In Waldeland and Evje (J Biomech 81:22–35, 2018), a mathematical cell–fluid model was put forward based on a mixture theory formulation. It was demonstrated that the model was able to capture the main characteristics of the two competing migration mechanisms. The objective of the current work is to seek deeper insight into certain qualitative aspects of these competing mechanisms by means of mathematical methods. For that purpose, we propose a simpler version of the cell–fluid model mentioned above but such that the two competing migration mechanisms are retained. An initial cell distribution in a one-dimensional slab is exposed to a constant fluid flow from one end to the other, consistent with the experimental setup. Then, we explore by means of analytical estimates the long-time behavior of the two competing migration mechanisms for two different scenarios: (i) when the initial cell volume fraction is low and (ii) when the initial cell volume fraction is high. In particular, it is demonstrated in a strict mathematical sense that for a sufficiently low initial cell volume fraction, the downstream migration dominates in the sense that the solution converges to a downstream-dominated steady state as time elapses. On the other hand, with a sufficiently high initial cell volume fraction, the upstream migration mechanism is the stronger in the sense that the solution converges to an upstream-dominated steady state.

1 Introduction

1.1 Aggressive Cancer Cells and Fluid Flow

How and why is it so that aggressive cancer cells are able to detach from the primary tumor and migrate to nearby lymphatic vessels through which they can escape and give rise to formation of tumors at other places in the human body? This phenomenon of lymph node metastasis, which is a main reason why cancer becomes a deadly disease, has been recognized for a long time. However, the underlying mechanism by which malignant tumor cells leave the primary tumor site, invade the lymphatics and metastasize to lymph nodes is unclear (Shields et al. 2007; Polacheck et al. 2011). Many malignant tumors are associated with an elevated interstitial fluid pressure (IFP) caused by leaky blood vessels situated at the inside of the punctum. Lymphatic vessels normally adsorb this fluid and keep the IFP at a normal level. However, lymphatic vessels are often defective in the intratumoral region. This implies that the additional fluid oozes to the region outside the tumor periphery where it is adsorbed by collecting lymphatic vessels. It has been proposed that this elevated IF flow can be exploited by the tumor cells and has led researchers to systematically explore how tumor cells are sensitive to IF flow. In Shields et al. (2007), it was suggested that interstitial flow caused by lymphatic drainage directs tumor cell migration through chemotaxis. More precisely, the tumor cells utilize interstitial flow to create and amplify gradients in chemokine (a protein) and thus chemotact toward the adsorbing lymphatic vessels in a process termed autologous chemotaxis. Polacheck et al. Polacheck et al. (2011) extended the study by Shields et al. (2007), demonstrating that the IF velocity as well as the cell seeding density affected the migration direction. Experiments were conducted at two different seeding densities and at two different flow velocities. In particular, it was observed that for the low cell seeding density, culture tumor cells tended to migrate with the flow in accordance with the behavior reported in Shields et al. (2007). However, for the high cell seeding density, the migration was dominated by upstream migration.

1.2 A General Cell–Fluid–ECM Model

A rather general cell–fluid–ECM model was proposed in Waldeland and Evje (2018a) and further developed in Waldeland and Evje (2018b) and Evje and Waldeland (2019) to shed light on the above-mentioned competing cell migration mechanisms governed by interstitial fluid flow. A gently simplified version of the model, where we ignore certain details of the biochemical part by assuming that chemokine C is directly produced by the tumor cells instead of being released from ECM, takes the following form:

$$\begin{aligned} \begin{array}{lll} \alpha _{ct} + \nabla \cdot (\alpha _c \mathbf {u}_c)&{}=&{}+\,S_c \\ \alpha _{wt} + \nabla \cdot (\alpha _w \mathbf {u}_w)&{}=&{}-\,S_c \\ \alpha _c \nabla (P_{w}+\Delta P(\alpha _c) + \Lambda (C))&{}=&{}-\,{\hat{\zeta }}_c\mathbf {u}_c+ {\hat{\zeta }}(\mathbf {u}_w- \mathbf {u}_c)\\ \alpha _w \nabla P_{w}&{}=&{}-\,{\hat{\zeta }}_w\mathbf {u}_w- {\hat{\zeta }}(\mathbf {u}_w- \mathbf {u}_c) \\ C_t + \nabla \cdot (C \mathbf {u}_w) &{}=&{} \nabla \cdot (D_C \nabla C) + R_C \end{array} \end{aligned}$$

(1.1)

The model, which bears similarity to the model studied in Evje and Wen (2018), accounts for the volume fraction $\alpha _w$ of interstitial fluid (IF) and the volume fraction $\alpha _c$ of cancer cells such that $\alpha _c+\alpha _w=1$. In other words, the pore space is occupied by cancer cells and fluid and described my the two mass balance equations (1.1)$_{1,2}$. The two different phases move with their own interstitial velocity, respectively, $\mathbf {u}_w$ and $\mathbf {u}_c$. These are involved in the two momentum balance equations (1.1)$_{3,4}$. The momentum balance for the IF given by (1.1)$_{4}$ reflects that the interstitial fluid pressure gradient $\nabla P_w$ is balanced by two interaction forces whose coefficients are ${\hat{\zeta }}_w$ and ${\hat{\zeta }}$.

The first one reflects the resistance force felt by the fluid as it flows through the porous tissue, whereas the second reflects a drag force effect between the fluid and cells. Similarly, the momentum balance (1.1)$_{3}$ reflects that the cell phase pressure $P_w + \Delta P(\alpha _c) + \Lambda (C)$ differs from the IFP $P_w$ by two stress effects: $\Delta P(\alpha _c)$ is an increasing function which accounts for the effect that cells tend to move away from each other toward a region of lower cell volume fraction when they are densely packed to reduce the total cell phase pressure. $\Lambda (C)$ is a decreasing function which accounts for the cell’s ability to create directed motion toward higher concentration of C (i.e., toward positive gradients in C) to reduce the overall pressure. Similarly, ${\hat{\zeta }}_c$ represents cell–ECM interaction and ${\hat{\zeta }}$ the cell–fluid drag. The last equation (1.1)$_{5}$ reflects that the chemokine concentration C is advected according to the fluid velocity field $\mathbf {u}_w$, in addition to a diffusive spreading, combined with production and consumption as described by the source term $R_C$.

From the two momentum equations (1.1)$_{3,4}$, we can compute explicit expressions for the cell and fluid velocity, respectively, $\mathbf {u}_c$ and $\mathbf {u}_w$ (Waldeland and Evje 2018a). The following expressions are found:

$$\begin{aligned} \begin{array}{lll} \alpha _c\mathbf {u}_c&{}=&{} \mathbf {U}_T{\hat{f}}_c(\alpha _c) - {\hat{h}}(\alpha _c) \nabla (\Delta P(\alpha _c)) - {\hat{h}}(\alpha _c) \nabla \Lambda (C) \\ \alpha _w\mathbf {u}_w&{}=&{} \mathbf {U}_T{\hat{f}}_w(\alpha _c) + {\hat{h}}(\alpha _c)\nabla (\Delta P(\alpha _c)) + {\hat{h}}(\alpha _c)\nabla \Lambda (C) \end{array} \end{aligned}$$

(1.2)

with coefficients ${\hat{f}}_c(\alpha _c)$, ${\hat{f}}_w(\alpha _c)$ and ${\hat{h}}(\alpha _c)$ given by

$$\begin{aligned} \begin{array}{lll} {\hat{f}}_c(\alpha _c)&{}=&{} \frac{[\alpha _c^2{\hat{\zeta }}_w]+ \alpha _c{\hat{\zeta }}}{[\alpha _c^2{\hat{\zeta }}_w] + [\alpha _w^2{\hat{\zeta }}_c] + {\hat{\zeta }}} \\ {\hat{f}}_w(\alpha _c)&{}=&{} \frac{[\alpha _w^2{\hat{\zeta }}_c]+ \alpha _w{\hat{\zeta }}}{[\alpha _c^2{\hat{\zeta }}_w] + [\alpha _w^2{\hat{\zeta }}_c] + {\hat{\zeta }}} \\ {\hat{h}}(\alpha _c)&{}=&{}\frac{\alpha _c^2\alpha _w^2}{\alpha _c^2{\hat{\zeta }}_w + \alpha _w^2{\hat{\zeta }}_c+{\hat{\zeta }}} \end{array} \end{aligned}$$

(1.3)

and where the total velocity $\mathbf {U}_T=\alpha _c\mathbf {u}_c+\alpha _w\mathbf {u}_w$ is determined from the equation $\mathbf {U}_T=-{\hat{\lambda }}_T\nabla P_w - {\hat{\lambda }}_c\nabla (\Delta P +\Lambda )$ and the fact that $\nabla \cdot \mathbf {U}_T=0$. We refer to Waldeland and Evje (2018a) for details. Model (1.1) then takes the more compact form with unknowns $(\alpha _c,C)$:

$$\begin{aligned} \begin{array}{lll} \alpha _{ct} + \nabla \cdot (\alpha _c\mathbf {u}_c)&{}=&{}S_c \\ C_t + \nabla \cdot (C \mathbf {u}_w) &{}=&{} \nabla \cdot (D_C \nabla C) + R_C \end{array} \end{aligned}$$

(1.4)

where $\alpha _c \mathbf {u}_c$ is given by (1.2)$_1$. Note that ${\hat{f}}_c(\alpha _c)$ and ${\hat{h}}(\alpha _c)$ given by (1.3) are direct functions of the specified fluid–ECM interaction ${\hat{\zeta }}_w$, cell–ECM interaction ${\hat{\zeta }}_c$ and cell–fluid interaction ${\hat{\zeta }}$. These correlations reflect essential information in what way tumor cells respond and relate to their microenvironment. Moreover, we note that there are three different mechanisms involved in (1.2)$_1$: (i) the term $\mathbf {U}_T{\hat{f}}_c(\alpha _c)$ represents a cell migration effect due to fluid stress; (ii) ${\hat{h}}_c(\alpha _c) \nabla (\Delta P(\alpha _c))$ represents a diffusive cell–cell migration effect; and (iii) ${\hat{h}}_c(\alpha _c) \nabla (\Lambda (C))$ represents a chemotaxis migration effect.

Fig. 1

An illustration of typical examples of ${\hat{f}}_c(\alpha _c)$ (left) and $-\,{\hat{h}}(\alpha _c)$ (right) defined by (1.3) used in Waldeland and Evje (2018b)

For typical correlations used for ${\hat{\zeta }}_w$, ${\hat{\zeta }}_c$ and ${\hat{\zeta }}$, the shape of ${\hat{f}}_c(\alpha _c)$ and ${\hat{h}}(\alpha _c)$ will be as shown in Fig. 1. The resulting cell migration behavior is shown in Figs. 2 and 3, respectively, for the case with an initial low cell volume fraction and a high initial cell volume fraction. The numerical examples illustrate the competition between downstream and upstream migration as a function of cell volume fraction.

1.3 A Toy Model with Competing Downstream and Upstream Migration

In order to obtain a model that is more amenable for mathematical investigations, without losing the key characteristics of the cell–fluid model (1.4), we make the following assumptions:

• (i) We use the approximation $\mathbf {U}_T\approx \mathbf {u}_w\approx \hbox {const}$.

• (ii) ${\hat{h}}(\alpha _c) \Delta P'(\alpha _c) \sim \hbox {const}$.

• (iii) ${\hat{f}}_c(\alpha _c) \sim - \alpha _c^{\kappa }$ with $\kappa >1$.

• (iv) ${\hat{h}}(\alpha _c)\Lambda '(C) \sim -\alpha _c(1-\alpha _c)^{\lambda }$ with $\lambda >1$.

• (v) $D_C=1$, $S_c=0$, and $R_C=\alpha _c(1-C)$.

The IF velocity $\mathbf {u}_w$ typically is a 100-fold higher than the cell migration velocity $\mathbf {u}_c$ (Polacheck et al. 2011; Waldeland and Evje 2018a, b), which in turn is largely dictated by the linear pressure curve seen in Figs. 2 and 3 (panel B). This justifies assumption (i). The constant diffusion coefficient in (ii) is standard. The choice of ${\hat{f}}_c(\alpha _c)$ in (iii) accounts for the negative dip that gives rise to upstream migration for higher cell volume fraction $\alpha _c$, see Fig. 1 (left). The choice of ${\hat{h}}(\alpha _c)$ in (iv) is also consistent with the functional form of ${\hat{h}}(\alpha _c)$ in (1.3)$_3$ which amounts to a bell-shaped function starting and ending at 0, see Fig. 1 (right), combined with the fact that $\Lambda (C)$ is a decreasing function Waldeland and Evje (2018a, b). Finally, the choice of parameters and terms in (v) is standard.

Fig. 2

Competing tumor cell migration mechanisms for a cell aggregate with low volume fraction $\alpha _c\approx 0.1$. a cell volume fraction $\alpha _c$. The downstream chemotactic-driven mechanism dominates. b The interstitial fluid pressure $P_w$ gradient. High pressure at $x=0$ and low pressure at $x=1$ give rise to fluid flow from left to right. c The three different cell migration components. d Chemokine (chemical component) whose concentration is skewed in the downstream direction

Fig. 3

Competing tumor cell migration mechanisms. The situation is the same as in Fig. 2. The only difference is that we use the higher volume fraction $\alpha _c\approx 0.5$. The upstream mechanism now dominates. The reason for that can be seen from an inspection of ${\hat{f}}_c(\alpha _c)$ in Fig. 1. A larger cell volume fraction $\alpha _c$ means that a larger part of the downward dip is activated and therefore increases the impact from the upstream migration

With these assumptions and by replacing $\alpha _c$ and C by u and v, respectively, we obtain the following simplified version of (1.4):

$$\begin{aligned} \left\{ \begin{array}{lll} u_t - f(u)_x &{}=&{} u_{xx} - (h(u) v_x)_x, \\ v_t + v_x &{}=&{} v_{xx} + u(1-v). \end{array} \right. \end{aligned}$$

(1.5)

where f(u) and h(u) are given by

$$\begin{aligned} f(u)= u^\kappa \quad \hbox {and} \quad h(u)=u\psi (u)=u(1-u)^\lambda , \qquad u\in [0,1], \end{aligned}$$

(1.6)

where $\kappa >1$ and $\lambda >1$ are fixed parameters.

1.3.1 Analysis of Related Models for Chemotaxis–Fluid Interplay in the Literature

Understanding the interaction of chemotaxis systems with liquid environments has been the objective of a remarkably quickly growing literature during the past few years. Most analytical studies in this direction, however, focus on models addressing situations in which besides fluid-induced transport mechanisms, also certain buoyancy-driven gravitational forcing of the considered fluid flows is relevant; especially due the fact that then the fluid velocity forms a genuine unknown in the model, such additional feedback effects evidently go along with a noticeably higher complexity in comparison with (1.5); therefore, the analysis of accordingly obtained chemotaxis-(Navier–)Stokes systems (Tuval et al. 2005) has yet been predominantly concerned with rather basic issues such as questions from existence and regularity theory (Duan et al. 2010; Winkler 2012, 2016; Chae et al. 2014; Cao and Lankeit 2016; Kozono et al. 2016), and only few studies seem go beyond this by examining qualitative aspects such as large-time stabilization toward homogeneous equilibria (Lankeit 2016; Winkler 2014, 2017, 2019). Only for some more specialized and simplified variants involving suitably designed given fluid flows, more subtle findings on possible effects of fluid interaction, e.g., on taxis driven blowup or also certain spreading properties, are available (He and Tadmor 2019; Kiselev and Xu 2016; Kiselev and Ryzhik 2012).

1.3.2 Main Results I: Dominance of Downstream Migration in Sparsely Distributed Populations

In the first part of our analysis, we shall consider the fully no-flux-type initial-boundary value problem

$$\begin{aligned} \left\{ \begin{array}{llll} u_{\varepsilon t} - (u_\varepsilon ^\kappa )_x &{}=&{} u_{\varepsilon xx} - \Big (u_\varepsilon (1-u_\varepsilon )^\lambda v_{\varepsilon x}\Big )_x,\quad &{} x\in \Omega , \ t>0, \\ v_{\varepsilon t} + v_{\varepsilon x} &{}=&{} v_{\varepsilon xx} + u_\varepsilon (1-v_\varepsilon ),\quad &{} x\in \Omega , \ t>0, \\ u_{\varepsilon x} -u_\varepsilon (1-u_\varepsilon )^\lambda v_{\varepsilon x} + u_\varepsilon ^\kappa &{}=&{}0, \quad v_{\varepsilon x} - v_\varepsilon =0, \qquad &{} x\in \partial \Omega , \ t>0, \\ u_\varepsilon (x,0)&{}=&{}\varepsilon w_0(x), \quad v_\varepsilon (x,0)=v_0(x), \qquad &{} x\in \Omega , \end{array} \right. \end{aligned}$$

(1.7)

in the interval $\Omega =(0,L)$ with $L>0$, with suitably small and appropriately regular initial data in the sense that $\varepsilon >0$ is suitably small and that

$$\begin{aligned} \left\{ \begin{array}{l} w_0\in W^{1,\infty }(\Omega )\quad \hbox { is nonnegative with}\ w_0\not \equiv 0 \qquad \hbox {and} \\ v_0\in W^{1,\infty }(\Omega )\quad \hbox { is nonnegative with} v_0\not \equiv 0. \end{array} \right. \end{aligned}$$

(1.8)

Within this framework, the first of our main results states that indeed for appropriately small values of $\varepsilon$, this problem is classically solvable by functions which exhibit a certain tendency toward migration in the direction of the fluid flow, that is, toward large positive values of x, in the following sense.

Theorem 1.1

Let $L>0, \kappa>1, \lambda >1$ and $\Omega =(0,L)\subset \mathbb {R}$, and assume that $w_0$ and $v_0$ satisfy (1.8). Then, for all $\delta >0$, there exists $T(\delta )>0$ with the following property: Given any $T>T(\delta )$, one can find $\varepsilon _0(\delta ,T)>0$ such that for arbitrary $\varepsilon \in (0,\varepsilon _0(\delta ,T))$ the problem (1.7) possesses a classical solution $(u_\varepsilon ,v_\varepsilon )$ in $\Omega \times (0,T)$ with

$$\begin{aligned} \left\{ \begin{array}{l} u_\varepsilon \in C^0(\overline{\Omega }\times [0,T]) \cap C^{2,1}(\overline{\Omega }\times (0,T]) \qquad \hbox {and} \\ v_\varepsilon \in \bigcap _{q>1} C^0([0,T];W^{1,q}(\Omega )) \cap C^{2,1}(\overline{\Omega }\times (0,T]), \end{array} \right. \end{aligned}$$

(1.9)

which is such that $0\le u_\varepsilon \le 1$ and $v_\varepsilon \ge 0$ in $\Omega \times (0,T)$, and such that with some $\beta >0$ and $\gamma >0$, we have

$$\begin{aligned} \bigg | \frac{u_\varepsilon (x,t)}{\varepsilon } - \gamma e^{\beta e^x}\bigg | \le \delta \qquad \hbox {for all }x\in \overline{\Omega }\hbox { and any } t\in [T(\delta ),T]. \end{aligned}$$

(1.10)

1.3.3 Main Results II: Prevalence of Upstream Migration in Densely Populated Groups

In the second part of our study, we consider the parabolic system from (1.7) along with slightly different boundary conditions for the first solution component, which namely enforce the latter to attain the boundary value 1 on $\partial \Omega$ throughout evolution. Specifically, for $\varepsilon >0$ we shall be concerned with the problem

$$\begin{aligned} \left\{ \begin{array}{llll} u_{\varepsilon t} - (u_\varepsilon ^\kappa )_x &{}=&{} u_{\varepsilon xx} - \Big (u_\varepsilon (1-u_\varepsilon )^\lambda v_{\varepsilon x}\Big )_x, \qquad &{}\quad x\in \Omega , \ t>0, \\ v_{\varepsilon t} + v_{\varepsilon x} &{}=&{} v_{\varepsilon xx} + u_\varepsilon (1-v_\varepsilon ), \qquad &{}\quad x\in \Omega , \ t>0, \\ &{} &{} u_{\varepsilon x} =1, \quad v_{\varepsilon x} - v_\varepsilon =0, \qquad &{}\quad x\in \partial \Omega , \ t>0, \\ &{} &{} u_\varepsilon (x,0)=1-\varepsilon z_0(x), \quad v_\varepsilon (x,0)=v_0(x), \qquad &{}\quad x\in \Omega , \end{array} \right. \end{aligned}$$

(1.11)

under the assumptions that

$$\begin{aligned} \left\{ \begin{array}{l} z_0\in W^{1,\infty }(\Omega )\quad \hbox {is nonnegative with }z_0\not \equiv 0\hbox { and }z_0=0{ on}\partial \Omega \qquad \hbox {and} \\ v_0\in W^{1,\infty }(\Omega )\quad \hbox {is nonnegative with} v_0\not \equiv 0. \end{array} \right. \end{aligned}$$

(1.12)

Under these assumptions, we shall see that in sharp contrast to the above, the profiles of the deviations $1-u_\varepsilon$ from the level 1 will, throughout arbitrarily large time intervals, to a considerable extent remain near functions that are more concentrated near $x=0$ than near $x=L$.

Theorem 1.2

Let $\Omega =(0,L)$ with some $L>0$, let $\kappa >1$ and $\lambda >1$ and suppose that $z_0$ and $v_0$ satisfy (1.12). Then, given any $\delta >0$, one can find $T(\delta )>0$ with the property that for any choice of $T>T(\delta )$, it is possible to fix $\varepsilon _0(\delta ,T)>0$ such that whenever $\varepsilon \in (0,\varepsilon _0(\delta ,T))$, the problem (1.11) admits a classical solution $(u_\varepsilon ,v_\varepsilon )$ in $\Omega \times (0,T)$ fulfilling (1.9) as well as $0\le u_\varepsilon \le 1$ and $v_\varepsilon \ge 0$ in $\Omega \times (0,T)$, for which there exist $\beta >0$ and $\gamma >0$ such that

$$\begin{aligned} \bigg | e^{\beta t} \cdot \frac{1-u_\varepsilon (x,t)}{\varepsilon } - \gamma e^{-\frac{\kappa }{2}x} \sin \frac{\pi x}{L} \bigg | \le \delta \qquad \hbox {for all }x\in \overline{\Omega }\hbox { and each } t\in [T(\delta ),T]. \end{aligned}$$

(1.13)

2 Preferred Downstream Migration: Proof of Theorem 1.1

2.1 Classical Solutions to (1.7) in $\Omega \times (0,T)$ for Small $\varepsilon$

In order to construct solutions to (1.7) by means of a convenient approximation involving homogeneous Neumann boundary conditions in the first solution component, following precedent works pursuing a similar idea, we fix a family $(\zeta _j)_{j\in \mathbb {N}} \subset C_0^\infty (\Omega )$ such that $0\le \zeta _j\le 1$ in $\Omega$ for all $j\in \mathbb {N}$ and that $\zeta _j\rightarrow 1$ in $C^2_{loc}(\Omega )$ as $j\rightarrow \infty$. Then, for $\varepsilon >0$ and $j\in \mathbb {N}$, the problems

$$\begin{aligned} \left\{ \begin{array}{llll} u_{\varepsilon j t} - (\zeta _j(x)u_{\varepsilon j}^\kappa )_x &{}=&{} u_{\varepsilon jxx} - \Big (\zeta _j(x)u_{\varepsilon j}(1-u_{\varepsilon j})_+^\lambda v_{\varepsilon jx}\Big )_x, \qquad &{} x\in \Omega , \ t>0, \\ v_{\varepsilon jt} + v_{\varepsilon jx} &{}=&{} v_{\varepsilon jxx} + u_{\varepsilon j}(1-v_{\varepsilon j}), \qquad &{} x\in \Omega , \ t>0, \\ &{} &{} u_{\varepsilon jx} =0, \quad v_{\varepsilon jx} - v_{\varepsilon j}=0, \qquad &{} x\in \partial \Omega , \ t>0, \\ &{} &{} u_{\varepsilon j}(x,0)=\varepsilon w_0(x), \quad v_{\varepsilon j}(x,0)=v_0(x), \qquad &{} x\in \Omega , \end{array} \right. \end{aligned}$$

(2.1)

admit local classical solutions enjoying a handy extensibility criterion:

Lemma 2.1

Let $\varepsilon >0$ and $j\in \mathbb {N}$. Then, there exist $T_{\varepsilon j}$ and a unique pair of nonnegative functions

$$\begin{aligned} \left\{ \begin{array}{l} u_{\varepsilon j}\in C^0(\overline{\Omega }\times [0,T_{\varepsilon j})) \cap C^{2,1}(\overline{\Omega }\times (0,T_{\varepsilon j})) \qquad \hbox {and} \\ v_{\varepsilon j}\in \bigcap _{q>1} C^0([0,T_{\varepsilon j});W^{1,q}(\Omega )) \cap C^{2,1}(\overline{\Omega }\times (0,T_{\varepsilon j})) \end{array} \right. \end{aligned}$$

such that $(u_{\varepsilon j},v_{\varepsilon j})$ solves (2.1) classically in $\Omega \times (0,T_{\varepsilon j})$ and such that

$$\begin{aligned} \hbox {if }T_{\varepsilon j}<\infty ,\hbox { then } \quad \limsup _{t\nearrow T_{\varepsilon j}} \Big \{ \Vert u_{\varepsilon j}(\cdot ,t)\Vert _{L^\infty (\Omega )} + \Vert v_{\varepsilon j}(\cdot ,t)\Vert _{W^{1,q}(\Omega )} \Big \} =\infty \qquad \hbox {for all } q>1. \end{aligned}$$

(2.2)

Moreover,

$$\begin{aligned} \int _\Omega u_{\varepsilon j}(x,t)dx = \varepsilon \int _\Omega w_0 \qquad \hbox {for all } t\in (0,T_{\varepsilon j}). \end{aligned}$$

(2.3)

Proof

All statements can be verified by straightforward adaptation of well-known arguments to the present context, either following precedents concerned with taxis-type problems, such as e.g., Horstmann and Winkler (2005), or also directly resorting to general theory for abstract parabolic evolution problems (Amann 1989). $\square$

A first significant regularity information about these solutions, becoming important in our derivation of uniform bounds on $u_{\varepsilon j}$ in Lemma 2.3, can be obtained by conveniently transforming the second equation in (2.1) and then performing an essentially straightforward testing procedure.

Lemma 2.2

Let $q\ge 1$ and $T>0$. Then, there exists $C(q,T)>0$ such that for all $\varepsilon >0$ and $j\in \mathbb {N}$,

$$\begin{aligned} \Vert v_{\varepsilon j}(\cdot ,t)\Vert _{W^{1,q}(\Omega )} \le C(q,T) \cdot \bigg \{ 1 + \sup _{s\in (0,\widehat{T}_{\varepsilon j})} \Vert u_{\varepsilon j}(\cdot ,s)\Vert _{L^\infty (\Omega )}^2 \bigg \} \qquad \hbox {for all } t\in (0,\widehat{T}_{\varepsilon j}), \end{aligned}$$

(2.4)

where $\widehat{T}_{\varepsilon j}{:=}\min \{T,T_{\varepsilon j}\}$.

Proof

For $\varepsilon >0$ and $j\in \mathbb {N}$, we let $\widehat{v}_{\varepsilon j}(x,t){:=}e^{-x} v_{\varepsilon j}(x,t)$, $x\in \overline{\Omega }$, $t\ge 0$, and noting that then $v_{\varepsilon jx}= e^x(\widehat{v}_{\varepsilon jx}+\widehat{v}_{\varepsilon j})$ and $v_{\varepsilon jxx}=e^x (\widehat{v}_{\varepsilon jxx} + 2\widehat{v}_{\varepsilon jx} + \widehat{v}_{\varepsilon j})$, we obtain from (2.1) that

$$\begin{aligned} \left\{ \begin{array}{llll} \widehat{v}_{\varepsilon jt} &{}=&{} \widehat{v}_{\varepsilon jxx} + \widehat{v}_{\varepsilon jx} + h_{\varepsilon j}(x,t), \qquad &{}\quad x\in \Omega , \ t\in (0,T_{\varepsilon j}), \\ &{} &{} \widehat{v}_{\varepsilon jx}=0, \qquad &{}\quad x\in \partial \Omega , \ t\in (0,T_{\varepsilon j}), \\ &{} &{} \widehat{v}_{\varepsilon j}(x,0)=e^{-x} v_0(x), \qquad &{}\quad x\in \Omega , \end{array} \right. \end{aligned}$$

(2.5)

where

$$\begin{aligned} h_{\varepsilon j}(x,t){:=}e^{-x} u_{\varepsilon j}(x,t) \Big (1-v_{\varepsilon j}(x,t)\Big ), \qquad x\in \Omega , \ t\in (0,T_{\varepsilon j}). \end{aligned}$$

(2.6)

Thus, abbreviating $K_{\varepsilon j}(T){:=}\sup _{s\in (0,\widehat{T}_{\varepsilon j})} \Vert u_{\varepsilon j}(\cdot ,s)\Vert _{L^\infty (\Omega )}$ for $T>0, \varepsilon >0$ and $j\in \mathbb {N}$, and with $\widehat{T}_{\varepsilon j}{:=}\min \{T,T_{\varepsilon j}\}$, we see that since

$$\begin{aligned} h_{\varepsilon j}(x,t) \le e^{-x} u_{\varepsilon j}(x,t) \le K_{\varepsilon j}(T) \qquad \hbox {for all }x\in \Omega \hbox { and } t\in (0,\widehat{T}_{\varepsilon j}) \end{aligned}$$

by nonnegativity of $u_{\varepsilon j}$ and $v_{\varepsilon j}$, we have

$$\begin{aligned} \widehat{v}_{\varepsilon j t} \le \widehat{v}_{\varepsilon jxx} + \widehat{v}_{\varepsilon jx} + K_{\varepsilon j}(T) \qquad \hbox {in } \Omega \times (0,\widehat{T}_{\varepsilon j}). \end{aligned}$$

As $\overline{v}(x,t){:=}\Vert v_0\Vert _{L^\infty (\Omega )} + K_{\varepsilon j}(T) \cdot t$, $x\in \overline{\Omega }$, $t\ge 0$, satisfies $\overline{v}_t - \overline{v}_{xx} - \overline{v}_x - K_{\varepsilon j}(T) =0$ in $\Omega \times (0,\infty )$ as well as $\overline{v}(x,0) \ge e^{-x} v_0(x)$ for all $x\in \Omega$ and $\overline{v}_x(\cdot ,t)=0$ on $\partial \Omega$ for all $t>0$, by means of a comparison argument, we thus infer that

$$\begin{aligned} \Vert \widehat{v}_{\varepsilon j}(\cdot ,t)\Vert _{L^\infty (\Omega )} \le c_1(T) \cdot (1+K_{\varepsilon j}(T)) \qquad \hbox {for all } t\in (0,\widehat{T}_{\varepsilon j}) \end{aligned}$$

(2.7)

with $c_1(T){:=}\max \{ \Vert v_0\Vert _{L^\infty (\Omega )} \, , \, T \, , \, 1 \}$.

Now in view of the Hölder inequality, for verifying the statement of the lemma, it is sufficient to establish (2.4) for any fixed integer $q\ge 2$, and in order to achieve this, we again use the Neumann-type structure of the boundary condition in (2.5) to see that for any such q,

$$\begin{aligned} \frac{1}{q} \frac{d}{dt} \int _\Omega \widehat{v}_{\varepsilon jx}^q= & {} \int _\Omega \widehat{v}_{\varepsilon jx}^{q-1} \widehat{v}_{\varepsilon x jt} \\= & {} - \,(q-1) \int _\Omega \widehat{v}_{\varepsilon jx}^{q-2} \widehat{v}_{\varepsilon jxx} \widehat{v}_{\varepsilon jt} \\= & {} -\, (q-1) \int _\Omega \widehat{v}_{\varepsilon jx}^{q-2} \widehat{v}_{\varepsilon jxx}^2 - (q-1) \int _\Omega \widehat{v}_{\varepsilon jx}^{q-1} \widehat{v}_{\varepsilon jxx} - (q-1) \int _\Omega \widehat{v}_{\varepsilon jx}^{q-2} \widehat{v}_{\varepsilon jxx} h_{\varepsilon j} \\= & {} -\, (q-1) \int _\Omega \widehat{v}_{\varepsilon jx}^{q-2} \widehat{v}_{\varepsilon jxx}^2 - (q-1) \int _\Omega \widehat{v}_{\varepsilon jx}^{q-2} \widehat{v}_{\varepsilon jxx} h_{\varepsilon j} \qquad \hbox {for all } t\in (0,T_{\varepsilon j}). \end{aligned}$$

Here, observing that by (2.6), (2.7), Young’s inequality and the fact that $c_1(T)\ge 1$, we can estimate

$$\begin{aligned} |h_{\varepsilon j}|\le & {} u_{\varepsilon j}(1+v_{\varepsilon j}) \\\le & {} K_{\varepsilon j}(T) \cdot \Big \{ 1+c_1(T) \cdot (1+K_{\varepsilon j}(T))\Big \} \\\le & {} K_{\varepsilon j}(T) \cdot 2c_1(T) \cdot (1+K_{\varepsilon j}(T)) \\\le & {} 4 c_1(T) \cdot (1+K_{\varepsilon j}^2(T)) \qquad \hbox {in } \Omega \times (0,\widehat{T}_{\varepsilon j}), \end{aligned}$$

we see that once more due to Young’s inequality,

$$\begin{aligned} -(q-1) \int _\Omega \widehat{v}_{\varepsilon jx}^{q-2} \widehat{v}_{\varepsilon jxx} h_{\varepsilon j}\le & {} (q-1) \int _\Omega \widehat{v}_{\varepsilon jx}^{q-2} \widehat{v}_{\varepsilon jxx}^2 + \frac{q-1}{4} \int _\Omega \widehat{v}_{\varepsilon jx}^{q-2} h_{\varepsilon j}^2\\\le & {} (q-1) \int _\Omega \widehat{v}_{\varepsilon jx}^{q-2} \widehat{v}_{\varepsilon jxx}^2 + \frac{q-1}{4} \int _\Omega \widehat{v}_{\varepsilon jx}^q \\&+ \frac{(q-1)L}{4} \cdot 4^q c_1^q(T) \cdot (1+K_{\varepsilon j}^2(T))^q \end{aligned}$$

for all $t\in (0,\widehat{T}_{\varepsilon j})$, so that

$$\begin{aligned} \frac{d}{dt} \int _\Omega \widehat{v}_{\varepsilon jx}^q \le \frac{q(q-1)}{4} \int _\Omega \widehat{v}_{\varepsilon jx}^q + c_2(q,T) \cdot (1+K_{\varepsilon j}^2(T))^q \qquad \hbox {for all } t\in (0,\widehat{T}_{\varepsilon j}) \end{aligned}$$

with $c_2(q,T){:=}4^{q-1} q(q-1) c_1^q(T) L$. Integration in time gives

$$\begin{aligned} \int _\Omega \widehat{v}_{\varepsilon jx}^q\le & {} \bigg \{ \int _\Omega e^{-qx} \cdot (v_{0x}-v_0)^q \bigg \} \cdot e^\frac{q(q-1)t}{4} + c_2(q,T) \cdot (1+K_{\varepsilon j}^2(T))^q \int _0^t e^\frac{q(q-1)(t-s)}{4} ds \\= & {} \bigg \{ \int _\Omega e^{-qx} \cdot (v_{0x}-v_0)^q \bigg \} \cdot e^\frac{q(q-1)t}{4} + c_2(q,T) \cdot (1+K_{\varepsilon j}^2(T))^q \cdot \Big ( e^\frac{q(q-1)t}{4}-1\Big ) \end{aligned}$$

for all $t\in (0,\widehat{T}_{\varepsilon j})$, which in conjunction with (2.7) readily entails (2.4). $\square$

Thus, in particular, having at hand some information on integrability of the taxic gradient in (2.1), by making essential use of the presence of homogeneous Neumann boundary conditions for $u_{\varepsilon j}$, we can invoke smoothing estimates for the Neumann heat semigroup to assert a favorable uniform a priori bound for the first solution component, up to an arbitrary fixed time.

Lemma 2.3

Let $T>0$. Then, there exists $\varepsilon _\mathrm{down}(T)>0$ such that whenever $\varepsilon \in (0,\varepsilon _\mathrm{down}(T))$, for each $j\in \mathbb {N}$ the solution of (2.1) has the properties that $T_{\varepsilon j}>T$ and that

$$\begin{aligned} \Vert u_{\varepsilon j}(\cdot ,t)\Vert _{L^\infty (\Omega )} \le 1 \qquad \hbox {for all } t\in (0,T). \end{aligned}$$

(2.8)

Proof

Given $T>0$, on employing Lemma 2.2, we can find $c_1(T)>0$ such that for all $\varepsilon >0$ and $j\in \mathbb {N}$,

$$\begin{aligned} \Vert v_{\varepsilon jx}(\cdot ,t)\Vert _{L^4(\Omega )} \le c_1(T) \cdot \bigg \{ 1+\sup _{s\in (0,\widehat{T}_{\varepsilon j})} \Vert u_{\varepsilon j}(\cdot ,s)\Vert _{L^\infty (\Omega )}^2 \bigg \} \qquad \hbox {for all } t\in (0,\widehat{T}_{\varepsilon j}), \end{aligned}$$

(2.9)

where again $\widehat{T}_{\varepsilon j}{:=}\min \{T,T_{\varepsilon j}\}$. We furthermore recall a well-known smoothing property of the Neumann heat semigroup $(e^{\tau \Delta })_{\tau \ge 0}$ on $\Omega$ (Fujie et al. 2016) to fix $c_2(T)>0$ such that whenever $\varphi \in C^1(\overline{\Omega })$ satisfies $\varphi =0$ on $\partial \Omega$, then

$$\begin{aligned} \Vert e^{\tau \Delta }\varphi _x\Vert _{L^\infty (\Omega )} \le c_2(T) \tau ^{-\frac{3}{4}} \Vert \varphi \Vert _{L^2(\Omega )} \qquad \hbox {for all } \tau \in (0,T). \end{aligned}$$

(2.10)

As $\kappa >1$, it thereafter becomes possible to firstly pick $\delta (T)>0$ small enough such that $\delta (T)\le 1$ and

$$\begin{aligned} 4c_2(T) L^\frac{1}{2} T^\frac{1}{4} \delta ^\kappa (T) \le \frac{\delta (T)}{6}, \end{aligned}$$

(2.11)

and then choose $\varepsilon _\mathrm{down}(T)>0$ in such a way that

$$\begin{aligned} \Vert w_0\Vert _{L^\infty (\Omega )} \cdot \varepsilon _\mathrm{down}(T) \le \frac{\delta (T)}{6} \end{aligned}$$

(2.12)

as well as

$$\begin{aligned} 8c_1(T) c_2(T) \Vert w_0\Vert _{L^1(\Omega )}^\frac{1}{4} T^\frac{1}{4} \varepsilon ^\frac{1}{4} \delta ^\frac{3}{4}(T) \le \frac{\delta (T)}{6}. \end{aligned}$$

(2.13)

We now fix $\varepsilon \in (0,\varepsilon _\mathrm{down}(T))$, and we claim that then for each $j\in \mathbb {N}$,

$$\begin{aligned} \widetilde{T}_{\varepsilon j} {:=}\sup \bigg \{ {\widetilde{T}} \in (0,\widehat{T}_{\varepsilon j}) \ \bigg | \ \Vert u_{\varepsilon j}(\cdot ,t)\Vert _{L^\infty (\Omega )} < \delta (T) \hbox { for all } t\in (0,{\widetilde{T}}) \bigg \}, \end{aligned}$$

well-defined by continuity of $u_{\varepsilon j}$ in $\overline{\Omega }\times [0,T_{\varepsilon j})$ due to the fact that $\Vert u_{\varepsilon j}(\cdot ,0)\Vert _{L^\infty (\Omega )} \le \frac{\delta (T)}{6}<\delta (T)$ by (2.12), actually satisfies ${\widetilde{T}}_{\varepsilon j} =\widehat{T}_{\varepsilon j}$. In fact, if this was false, then again by continuity of $u_{\varepsilon j}$, we would have $\Vert u_{\varepsilon j}(\cdot ,t)\Vert _{L^\infty (\Omega )} < \delta (T)$ for all $t\in (0,{\widetilde{T}}_{\varepsilon j})$ but

$$\begin{aligned} \Vert u_{\varepsilon j}(\cdot ,{\widetilde{T}}_{\varepsilon j})\Vert _{L^\infty (\Omega )}=\delta (T). \end{aligned}$$

(2.14)

To see that this is impossible, we represent $u_{\varepsilon j}$ according to a Duhamel formula associated with the first equation in (2.1) and apply the maximum principle as well as (2.10) to infer that for all $t\in (0,{\widetilde{T}}_{\varepsilon j}]$,

$$\begin{aligned} \Vert u_{\varepsilon j}(\cdot ,t)\Vert _{L^\infty (\Omega )}= & {} \Bigg \Vert e^{t\Delta } \big ( \varepsilon w_0 \big ) - \int _0^t e^{(t-s)\Delta } \partial _x \Big \{ \zeta _j u_{\varepsilon j}(1-u_{\varepsilon j})_+^\lambda v_{\varepsilon jx} \Big \}(\cdot ,s) ds \\&+ \int _0^t e^{(t-s)\Delta } \partial _x \big \{ \zeta _j u_{\varepsilon j}^\kappa \big \} (\cdot ,s) ds \Bigg \Vert _{L^\infty (\Omega )} \\\le & {} \varepsilon \Vert w_0\Vert _{L^\infty (\Omega )} + c_2(T) \int _0^T (t-s)^{-\frac{3}{4}} \Vert u_{\varepsilon j}(\cdot ,s) v_{\varepsilon j x}(\cdot ,s)\Vert _{L^2(\Omega )} ds \\&+ c_2(T) \int _0^t (t-s)^{-\frac{3}{4}} \Vert u_{\varepsilon j}^\kappa (\cdot ,s)\Vert _{L^2(\Omega )} ds, \end{aligned}$$

because $0\le \zeta _j\le 1$ and $(1-u_{\varepsilon j})_+ \le 1$. Since clearly

$$\begin{aligned} \Vert u_{\varepsilon j}^\kappa (\cdot ,s)\Vert _{L^2(\Omega )} \le L^\frac{1}{2} \Vert u_{\varepsilon j}(\cdot ,s)\Vert _{L^\infty (\Omega )}^\kappa \le L^\frac{1}{2} \delta ^\kappa (T) \qquad \hbox {for all } s\in (0,{\widetilde{T}}_{\varepsilon j}), \end{aligned}$$

and since by the Cauchy–Schwarz inequality, (2.3), (2.9) and the inequality $\delta (T)\le 1$, we moreover have

$$\begin{aligned} \Vert u_{\varepsilon j}(\cdot ,s) v_{\varepsilon j x}(\cdot ,s)\Vert _{L^2(\Omega )}\le & {} \Vert u_{\varepsilon j}(\cdot ,s)\Vert _{L^\infty (\Omega )}^\frac{3}{4} \Vert u_{\varepsilon j}(\cdot ,s)\Vert _{L^1(\Omega )}^\frac{1}{4} \Vert v_{\varepsilon jx}(\cdot ,s)\Vert _{L^4(\Omega )} \\\le & {} \delta ^\frac{3}{4}(T) \cdot \big (\varepsilon \Vert w_0\Vert _{L^1(\Omega )} \big )^\frac{1}{4} \cdot c_1(T) (1+\delta ^2(T)) \\\le & {} 2 c_1(T) \Vert w_0\Vert _{L^1(\Omega )}^\frac{1}{4} \varepsilon ^\frac{1}{4} \delta ^\frac{3}{4}(T) \qquad \hbox {for all } s\in (0,{\widetilde{T}}_{\varepsilon j}); \end{aligned}$$

this entails that thanks to (2.11), (2.12) and (2.13),

$$\begin{aligned} \Vert u_{\varepsilon j}(\cdot ,t)\Vert _{L^\infty (\Omega )}\le & {} \varepsilon \Vert w_0\Vert _{L^\infty (\Omega )} + c_2(T) L^\frac{1}{2} \delta ^\kappa (T) \int _0^t (t-s)^{-\frac{3}{4}} ds \\&+ 2 c_1(T) c_2(T) \Vert w_0\Vert _{L^1(\Omega )}^\frac{1}{4} \varepsilon ^\frac{1}{4} \delta ^\frac{3}{4}(T) \int _0^t (t-s)^{-\frac{3}{4}} ds \\\le & {} \varepsilon \Vert w_0\Vert _{L^\infty (\Omega )} + 4 c_2(T) L^\frac{1}{2} T^\frac{1}{4} \delta ^\kappa (T)\\&+ 8 c_1(T) c_2(T) \Vert w_0\Vert _{L^1(\Omega )}^\frac{1}{4} T^\frac{1}{4} \varepsilon ^\frac{1}{4} \delta ^\frac{3}{4}(T) \qquad \hbox {for all } t\in (0,{\widetilde{T}}_{\varepsilon j}]. \end{aligned}$$

When evaluated at $t={\widetilde{T}}_{\varepsilon j}$, this contradicts (2.14) and thereby shows that indeed ${\widetilde{T}}_{\varepsilon j}=\widehat{T}_{\varepsilon j}$. As thus $\Vert u_{\varepsilon j}(\cdot ,t)\Vert _{L^\infty (\Omega )} \le \delta (T)\le 1$ for all $t\in (0,\widehat{T}_{\varepsilon j})$, in view of (2.9) and (2.2) this furthermore implies that we must have $T_{\varepsilon j}>\widehat{T}_{\varepsilon j}$ and that (2.8) holds.

$\square$

On the basis of the latter, straightforward application of parabolic regularity theory, followed by suitable compactness arguments, enables us to construct a solution of (1.7) in $\Omega \times (0,T)$ as a limit of solutions to (2.1), provided that $\varepsilon <\varepsilon _\mathrm{down}(T)$.

Lemma 2.4

Let $T>0$, and let $\varepsilon _\mathrm{down}(T)>0$ be as in Lemma 2.3. Then, for all $\varepsilon \in (0,\varepsilon _\mathrm{down}(T))$, there exist functions

$$\begin{aligned} \left\{ \begin{array}{l} u_\varepsilon \in C^0(\overline{\Omega }\times [0,T]) \cap C^{2,1}(\overline{\Omega }\times (0,T]) \qquad \hbox {and} \\ v_\varepsilon \in \bigcap _{q>1} C^0([0,T];W^{1,q}(\Omega )) \cap C^{2,1}(\overline{\Omega }\times (0,T]) \end{array} \right. \end{aligned}$$

such that $u_\varepsilon \ge 0$ and $v_\varepsilon \ge 0$ in $\overline{\Omega }\times (0,T]$, that $(u_\varepsilon ,v_\varepsilon )$ solves (1.7) in the classical sense in $\Omega \times (0,T)$ and that

$$\begin{aligned} \int _\Omega u_\varepsilon (x,t) dx = \varepsilon \int _\Omega w_0 \qquad \hbox {for all } t\in (0,T) \end{aligned}$$

(2.15)

as well as

$$\begin{aligned} \Vert u_\varepsilon (\cdot ,t)\Vert _{L^\infty (\Omega )} \le 1 \qquad \hbox {for all } t\in (0,T). \end{aligned}$$

(2.16)

This solution can be obtained as limits of the solutions to (2.1) in the sense that there exists a sequence $(j_k)_{k\in \mathbb {N}}\subset \mathbb {N}$ such that as $k\rightarrow \infty$, we have $j_k\rightarrow \infty$, $u_{\varepsilon j_k} \rightarrow u_\varepsilon$ and $v_{\varepsilon j_k} \rightarrow v_\varepsilon$ in $C^0(\overline{\Omega }\times [0,T]) \cap C^{2,1}_{loc}(\overline{\Omega }\times (0,T])$ as well as $v_{\varepsilon j_k x} {\mathop {\rightharpoonup }\limits ^{\star }}v_{\varepsilon x}$ in $L^\infty ((0,T);L^q(\Omega ))$ for all $q>1$.

Proof

Relying on Lemma 2.3 and a series of straightforward parabolic bootstrap arguments, thanks to the assumed limit behavior of $(\zeta _j)_{j\in \mathbb {N}}$ as $j\rightarrow \infty$, the part concerning existence and approximation can be seen by following a type of reasoning well-established in contexts of taxis problems involving no-flux boundary conditions different from homogeneous Neumann data; as concise derivations can be found in quite an elaborate manner in the literature on closely related problems, we may refrain from giving details here, and rather refer to, for example, Cao and Lankeit (2016) (see also Li et al. (2015) for a precedent). The properties (2.15) and (2.16) can thereupon easily be obtained on taking $j\rightarrow \infty$ in (2.3) and (2.8). $\square$

With regard to the rescaled version of $u_\varepsilon$ addressed in the finally intended estimate (1.10), this result can be rephrased as follows.

Corollary 2.5

Let $T>0$, and for $\varepsilon \in (0,\varepsilon _\mathrm{down}(T))$ let $u_\varepsilon$ and $v_\varepsilon$ be as provided by Lemma 2.4, with $\varepsilon _\mathrm{down}(T)>0$ taken from Lemma 2.3. Then, the pair $(w_\varepsilon ,v_\varepsilon )$, with $w_\varepsilon {:=}\frac{u_\varepsilon }{\varepsilon }$, forms a global classical solution of the problem

$$\begin{aligned} \left\{ \begin{array}{llll} w_{\varepsilon t} - \varepsilon ^{\kappa -1}(w_\varepsilon ^\kappa )_x &{}=&{} w_{\varepsilon xx} - \Big (w_\varepsilon (1-\varepsilon w_\varepsilon )^\lambda v_{\varepsilon x}\Big )_x, \qquad &{} x\in \Omega , \ t\in (0,T), \\ v_{\varepsilon t} + v_{\varepsilon x} &{}=&{} v_{\varepsilon xx} + \varepsilon w_\varepsilon (1-v_\varepsilon ), \qquad &{} x\in \Omega , \ t\in (0,T), \\ &{} &{} w_{\varepsilon x} -w_\varepsilon (1-\varepsilon w_\varepsilon )^\lambda v_{\varepsilon x}+ \varepsilon ^{\kappa -1} w_\varepsilon ^\kappa =0, \quad v_{\varepsilon x} - v_\varepsilon =0, \qquad &{} x\in \partial \Omega , \ t\in (0,T), \\ &{} &{} w_\varepsilon (x,0)=w_0(x), \quad v_\varepsilon (x,0)=v_0(x), \qquad &{} x\in \Omega , \end{array} \right. \end{aligned}$$

(2.17)

which is such that

$$\begin{aligned} \int _\Omega w_\varepsilon (x,t) dx = \int _\Omega w_0(x) dx \qquad \hbox {for all } t\in (0,T) \end{aligned}$$

(2.18)

and

$$\begin{aligned} 0 \le w_\varepsilon \le \frac{1}{\varepsilon } \qquad \hbox {in } \overline{\Omega }\times (0,T). \end{aligned}$$

(2.19)

Moreover, for any $q>1$, one can find $C(q,T)>0$ fulfilling

$$\begin{aligned} \Vert v_\varepsilon (\cdot ,t)\Vert _{W^{1,q}(\Omega )} \le C(q,T) \qquad \hbox {for all }t\in (0,T)\hbox { and each } \varepsilon \in (0,\varepsilon _\mathrm{down}(T)). \end{aligned}$$

(2.20)

Proof

The claimed solution features of $(w_\varepsilon ,v_\varepsilon )$ as well as (2.18) and (2.19) are obvious by-products of Lemma 2.4. In view of the statement from Lemma 2.4 on approximation of $(u_\varepsilon ,v_\varepsilon )$ by solutions to (2.1), property (2.20) is a consequence of Lemma 2.2 when combined with Lemma 2.3. $\square$

2.2 Existence, Uniqueness and Stabilization in a Formally Obtained Limit Problem

Motivated by formally taking $\varepsilon \searrow 0$ in the reformulation (2.17) of (1.7), in this section we shall analyze the behavior of solutions to the corresponding limit problem given by

$$\begin{aligned} \left\{ \begin{array}{llll} w_t &{}=&{} w_{xx} - (wv_x)_x, \qquad &{} x\in \Omega , \ t>0, \\ v_t +v_x &{}=&{} v_{xx}, \qquad &{} x\in \Omega , \ t>0, \\ w_x-wv_x&{}=&{}0, \quad v_x-v=0, \qquad &{} x\in \partial \Omega , \ t>0, \\ w(x,0)&{}=&{}w_0(x), \quad v(x,0)=v_0(x), \qquad &{} x\in \Omega , \end{array} \right. \end{aligned}$$

(2.21)

under the assumptions (1.8). In fact, a basic theory of well-posedness thereof can quite easily be obtained:

Lemma 2.6

Suppose that (1.8) holds. Then, (2.21) admits precisely one classical solution (w, v) such that

$$\begin{aligned} \left\{ \begin{array}{l} w\in C^0(\overline{\Omega }\times [0,\infty )) \cap C^{2,1}(\overline{\Omega }\times (0,\infty )), \\ v\in C^0(\overline{\Omega }\times [0,\infty )) \cap C^{2,1}(\overline{\Omega }\times (0,\infty )) \qquad \hbox {and} \\ v_x\in L^\infty _{loc}([0,\infty ;L^2(\Omega )). \end{array} \right. \end{aligned}$$

(2.22)

Proof

As (2.21) consists of two actually decoupled scalar and linear drift-diffusion problems with Robin-type boundary conditions, global existence of a classical solution enjoying the claimed regularity properties is asserted by standard parabolic Schauder theory (Ladyzenskaja et al. 1968).

To see its uniqueness within the indicated class, given two solutions (w, v) and $\widetilde{w},\widetilde{v})$ both fulfilling the regularity requirements in (2.22), we write $\varphi {:=}w-\widetilde{w}$ and $\psi {:=}v-\widetilde{v}$ to see using (2.21) that

$$\begin{aligned} \left\{ \begin{array}{llll} \varphi _t &{}=&{} \varphi _{xx}- (\varphi v_x)_x - (\widetilde{w}\psi _x)_x, \qquad &{} x\in \Omega , \ t>0, \\ \varphi _x-\varphi v_x - \widetilde{w}\psi _x&{}=&{}0, \qquad &{} x\in \partial \Omega , \ t>0, \\ \varphi (x,0)&{}=&{}0, \qquad &{} x\in \Omega , \end{array} \right. \end{aligned}$$

(2.23)

and that

$$\begin{aligned} \left\{ \begin{array}{llll} \psi _t -\psi _x &{}=&{} \psi _{xx}, \qquad &{} x\in \Omega , \ t>0, \\ \psi _x-\psi &{}=&{}0, \qquad &{} x\in \partial \Omega , \ t>0, \\ \psi (x,0)&{}=&{}0, \qquad &{} x\in \Omega . \end{array} \right. \end{aligned}$$

(2.24)

Therefore, by Young’s inequality,

$$\begin{aligned} \frac{1}{2} \frac{d}{dt} \int _\Omega \varphi ^2 + \int _\Omega \varphi _x^2= & {} \int _\Omega \varphi \varphi _x v_x + \int _\Omega \widetilde{w}\varphi _x \psi _x \nonumber \\\le & {} \frac{1}{2} \int _\Omega \varphi _x^2 + \int _\Omega \varphi ^2 v_x^2 + \int _\Omega \widetilde{w}^2 \psi _x^2 \nonumber \\\le & {} \frac{1}{2} \int _\Omega \varphi _x^2 + \Vert v_x\Vert _{L^2(\Omega )}^2 \Vert \varphi \Vert _{L^\infty (\Omega )}^2 \nonumber \\&+ \Vert \widetilde{w}\Vert _{L^\infty (\Omega )}^2 \Vert \psi _x\Vert _{L^2(\Omega )}^2 \qquad \hbox {for all } t>0 \end{aligned}$$

(2.25)

and

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \int _\Omega \psi ^2 + \int _\Omega \psi _x^2 = \int _\Omega \psi \psi _x \le \frac{1}{2} \int _\Omega \psi _x^2 + \frac{1}{2} \int _\Omega \psi ^2 \qquad \hbox {for all } t>0. \end{aligned}$$

(2.26)

Now for fixed $t>0$, (2.22) asserts the existence of $c_1=c_1(T)>0$ and $c_2=c_2(T)>0$ such that

$$\begin{aligned} \Vert v_x(\cdot ,t)\Vert _{L^2(\Omega )} \le c_1 \quad \hbox {and} \quad \Vert \widetilde{w}(\cdot ,t)\Vert _{L^\infty (\Omega )} \le c_2 \qquad \hbox {for all } t\in (0,T), \end{aligned}$$

whence in particular, using the Gagliardo–Nirenberg inequality and Young’s inequality, we see that with some $cx=c_3(T)>0$, we have

$$\begin{aligned} \Vert v_x\Vert _{L^2(\Omega )}^2 \Vert \varphi \Vert _{L^\infty (\Omega )}^2\le & {} c_3\Vert \varphi _x\Vert _{L^2(\Omega )} \Vert \varphi \Vert _{L^2(\Omega )} + c_3 \Vert \varphi \Vert _{L^2(\Omega )}^2 \\\le & {} \frac{1}{2} \Vert \varphi _x\Vert _{L^2(\Omega )}^2 + \Big (\frac{c_3^2}{2}+c_3\Big ) \Vert \varphi \Vert _{L^2(\Omega )}^2 \qquad \hbox {for all } t\in (0,T). \end{aligned}$$

By combining (2.25) with (2.26) we thus infer that

$$\begin{aligned} \frac{d}{dt} \bigg \{ \int _\Omega \varphi ^2 + c_2^2 \int _\Omega \psi ^2 \bigg \}\le & {} \Big (\frac{c_3^2}{2}+c_3\Big ) \int _\Omega \varphi ^2 + c_2^2 \int _\Omega \psi ^2 \\\le & {} \max \Big \{ 1 \, , \, \frac{C_3^2}{2}+c_3\Big \} \cdot \bigg \{ \int _\Omega \varphi ^2 + c_2^2 \int _\Omega \psi ^2 \bigg \} \qquad \hbox {for all } t\in (0,T). \end{aligned}$$

Thus, an integration using the initial conditions in (2.23) and (2.24) shows that $\int _\Omega \varphi ^2(\cdot ,t) + c_2^2 \int _\Omega \psi ^2(\cdot ,t) =0$ for all $t\in (0,T)$ and therefore implies that $\varphi \equiv \psi \equiv 0$, for $T>0$ was arbitrary. $\square$

Apart from that, thanks to the simple structure of the second equation in (2.21), one can readily achieve also some higher-order regularity information.

Lemma 2.7

If (1.8) holds, there exists $C>0$ such that the solution of (2.21) satisfies

$$\begin{aligned} \Vert w\Vert _{C^{2,1}(\overline{\Omega }\times [t,t+1])} \le C \qquad \hbox {for all } t>1 \end{aligned}$$

(2.27)

and

$$\begin{aligned} \Vert v\Vert _{C^{2,1}(\overline{\Omega }\times [t,t+1])} \le C \qquad \hbox {for all } t>1. \end{aligned}$$

(2.28)

Proof

An application of standard parabolic Schauder theory ( Ladyzenskaja et al. (1968)) to the second subproblem contained in (2.21) provides $\theta _1\in (0,1)$ and $c_1>0$ such that

$$\begin{aligned} \Vert v\Vert _{C^{2+\theta _1,1+\frac{\theta _1}{2}}(\overline{\Omega }\times [t,t+1])} \le c_1 \qquad \hbox {for all } t>\frac{1}{2}. \end{aligned}$$

(2.29)

Therefore, when rewritten in the form $w_t=w_{xx}+a(x,t)w_x+b(x,t)w$ with $a(x,t){:=}-v_x$ and $b(x,t){:=}-v_{xx}$ enjoying suitable Hölder bounds according to (2.29), also the first equation in (2.21) becomes accessible to the same tool so as to allow for the existence of $\theta _2\in (0,1)$ and $c_2>0$ fulfilling

$$\begin{aligned} \Vert w\Vert _{C^{2+\theta _1,1+\frac{\theta _1}{2}}(\overline{\Omega }\times [t,t+1])} \le c_1 \qquad \hbox {for all } t>1. \end{aligned}$$

This entails (2.27), whereas (2.28) directly results from (2.29). $\square$

Now by means of a transformation in the style of that from Lemma 2.2, we can detect an energy structure associated with the second equation in (2.21), in particular resulting in the following basic statement on stabilization of v.

Lemma 2.8

Assume (1.8). Then, the solution of (2.21) has the properties that

$$\begin{aligned} \int _\Omega (e^{-x} v)_x^2(\cdot ,t) \rightarrow 0 \qquad \hbox {as } t\rightarrow \infty \end{aligned}$$

(2.30)

and that

$$\begin{aligned} \int _0^\infty \int _\Omega v_t^2 <\infty . \end{aligned}$$

(2.31)

Proof

Abbreviating $\widehat{v}(x,t){:=}e^{-x} v(x,t)$ for $x\in \overline{\Omega }$ and $t\ge 0$, we compute $v_x= e^x(\widehat{v}_x+\widehat{v})$ and $v_{xx}=e^x(\widehat{v}_{xx}+2\widehat{v}_x+\widehat{v})$ and hence obtain from (2.21) that

$$\begin{aligned} \widehat{v}_t= e^{-x} v_{xx} - e^{-x} v_x = (\widehat{v}_{xx} + 2\widehat{v}_x +\widehat{v}) - (\widehat{v}_x+\widehat{v}) =\widehat{v}_{xx}+\widehat{v}_x \qquad \hbox {in } \Omega \times (0,\infty ) \end{aligned}$$

(2.32)

and that

$$\begin{aligned} \widehat{v}_x=0 \qquad \hbox {on } \partial \Omega \times (0,\infty ). \end{aligned}$$

(2.33)

Thanks to the latter, no nonzero boundary terms appear when we test (2.32) by $-\widehat{v}_{xx}$ and integrate by parts to see that

$$\begin{aligned} \frac{1}{2} \frac{d}{dt} \int _\Omega \widehat{v}_x^2 {=} \int _\Omega \widehat{v}_x \widehat{v}_{xt} {=} {-}\int _\Omega \widehat{v}_{xx} \widehat{v}_t {=} {-} \int _\Omega \widehat{v}_{xx}^2 {-} \int _\Omega \widehat{v}_x \widehat{v}_{xx} {=} {-} \int _\Omega \widehat{v}_{xx}^2 \qquad \hbox {for all } t>0. \end{aligned}$$

(2.34)

As (2.33) moreover enables us to invoke a Poincaré inequality to find $c_1>0$ fulfilling

$$\begin{aligned} \int _\Omega \widehat{v}_{xx}^2 \ge c_1 \int _\Omega \widehat{v}_x^2 \qquad \hbox {for all } t>0, \end{aligned}$$

this firstly implies that

$$\begin{aligned}\frac{d}{dt} \int _\Omega \widehat{v}_x^2 \le -2c_1 \int _\Omega \widehat{v}_x^2 \qquad \hbox {for all } t>0 \end{aligned}$$

and that hence, upon integration, writing $c_2{:=}\int _\Omega \widehat{v}_x^2(\cdot ,0)$, we have

$$\begin{aligned} \int _\Omega \widehat{v}_x^2 (\cdot ,t) \le c_2 e^{-2c_1 t} \qquad \hbox {for all } t>0, \end{aligned}$$

(2.35)

from which (2.30) immediately follows by definition of $\widehat{v}$ and the fact that $c_2$ is finite due to (1.8). Secondly, a direct integration in (2.34) shows that

$$\begin{aligned} \frac{1}{2} \int _\Omega \widehat{v}_x^2(\cdot ,t) + \int _0^t \int _\Omega \widehat{v}_{xx}^2 \le \frac{c_2}{2} \qquad \hbox {for all } t>0, \end{aligned}$$

(2.36)

where we once more use (2.32) to see that as a consequence of (2.35),

$$\begin{aligned} \int _0^t \int _\Omega \widehat{v}_{xx}^2= & {} \int _0^t \int _\Omega (\widehat{v}_t-\widehat{v}_x)^2 \\\ge & {} \frac{1}{2} \int _0^t \int _\Omega \widehat{v}_t^2 - \int _0^t \int _\Omega \widehat{v}_x^2 \\\ge & {} \frac{1}{2} \int _0^t \int _\Omega \widehat{v}_t^2 - c_2 \int _0^t e^{-2c_1 s} ds \\= & {} \frac{1}{2} \int _0^t \int _\Omega \widehat{v}_t^2 - \frac{c_2}{2c_1} (1-e^{-2c_1 t}) \\\ge & {} \frac{1}{2} \int _0^t \int _\Omega \widehat{v}_t^2 - \frac{c_2}{2c_1} \qquad \hbox {for all } t>0, \end{aligned}$$

because $(a-b)^2 \ge \frac{1}{2} a^2-b^2$ for all $a,b\in \mathbb R$. In conclusion, (2.36) thus in particular entails that

$$\begin{aligned} \frac{1}{2e^{2L}} \int _0^t \int _\Omega v_t^2\le & {} \frac{1}{2} \int _0^t \int _\Omega e^{-2x} \widehat{v}_t^2 \\= & {} \frac{1}{2} \int _0^t \int _\Omega \widehat{v}_t^2 \\\le & {} \int _0^t \int _\Omega \widehat{v}_{xx}^2 + \frac{c_2}{2c_1} \\\le & {} \frac{c_2}{2} + \frac{c_2}{2c_1} \qquad \hbox {for all } t>0 \end{aligned}$$

and thereby establishes (2.31). $\square$

Thanks to an evident mass conservation property of the second equation in (2.21), the latter in conjunction with one of the higher-order regularity features asserted by Lemma 2.7 already entails uniform stabilization of v toward one particular steady state:

Lemma 2.9

Suppose that (1.8) holds. Then, there exists $\beta >0$ such that the solution of (2.21) satisfies

$$\begin{aligned} v(\cdot ,t) \rightarrow \beta \cdot \exp \quad \hbox {in } L^\infty (\Omega ) \qquad \hbox {as } t\rightarrow \infty . \end{aligned}$$

(2.37)

Proof

We let $\beta {:=}\frac{\int _\Omega v_0}{\int _\Omega e^x dx}$ and note that then $\beta$ is positive by (1.8), and assuming (2.37) to be false, we could find $(t_k)_{k\in \mathbb {N}} \subset (1,\infty )$ and $c_1>0$ such that $t_k\rightarrow \infty$ as $k\rightarrow \infty$ and

$$\begin{aligned} \Vert v(\cdot ,t_k)-\beta \cdot \exp \Vert _{L^\infty (\Omega )} \ge c_1 \qquad \hbox {for all } k\in \mathbb {N}. \end{aligned}$$

(2.38)

Now since $(v(\cdot ,t))_{t>1}$ is bounded in $C^1(\overline{\Omega })$ and hence relatively compact in $C^0(\overline{\Omega })$ by Lemma 2.7 and the Arzelà-Ascoli theorem, upon passing to a subsequence if necessary we may assume that

$$\begin{aligned} v(\cdot ,t_k)\rightarrow v_\infty \quad \hbox {in } L^\infty (\Omega ) \qquad \hbox {as } k\rightarrow \infty \end{aligned}$$

(2.39)

with some nonnegative $v_\infty \in C^0(\overline{\Omega })$. Since therefore $\widehat{v}_k(x){:=}e^{-x} v(x,t_k)$, $x\in \overline{\Omega }$, $k\in \mathbb {N}$, and $\widehat{v}_\infty (x){:=} e^{-x} v_\infty (x)$, $x\in \overline{\Omega }$, satisfy

$$\begin{aligned} \widehat{v}_k\rightarrow \widehat{v}_\infty \quad \hbox {in } L^\infty (\Omega ) \qquad \hbox {as } k\rightarrow \infty , \end{aligned}$$

we may rely on Lemma 2.8 to infer the existence of $c_2>0$ such that

$$\begin{aligned} \widehat{v}_\infty (x) = c_2 \qquad \hbox {for all } x\in \Omega , \end{aligned}$$

(2.40)

because (2.30) warrants that $\widehat{v}_{kx} \rightarrow 0$ in $L^2(\Omega )$ and $k\rightarrow \infty$. By definition of $\widehat{v}_\infty$, in view of (2.39), this means that

$$\begin{aligned} v(\cdot ,t_k) \rightarrow c_2 \cdot \exp \quad \hbox {in } L^\infty (\Omega ) \qquad \hbox {as } k\rightarrow \infty , \end{aligned}$$

(2.41)

whence in particular

$$\begin{aligned} \int _\Omega v(\cdot ,t_k) \rightarrow c_2\int _\Omega e^x dx \qquad \hbox {as } k\rightarrow \infty . \end{aligned}$$

Since, on the other hand, a direct integration in (2.21) shows that

$$\begin{aligned} \frac{d}{dt} \int _\Omega v = \int _\Omega (v_{xx}-v_x)=0 \qquad \hbox {for all } t>0, \end{aligned}$$

this identifies $c_2$ according to $c_2=\frac{\int _\Omega v_0}{\int _\Omega e^x dx}=\beta$, so that (2.41) contradicts the hypothesis (2.38), thus altogether implying that actually (2.37) must have been valid. $\square$

Constituting the apparently most substantial part of this section, the following lemma turns the $L^2$ integrability property of $v_t$ contained in Lemma 2.8 into a first, though yet rather weak, information on stabilization in the first solution component.

Lemma 2.10

If (1.8) holds, then the solution of (2.21) has the property that

$$\begin{aligned} \int _\Omega (e^{-v} w)_x^2 \rightarrow 0 \qquad \hbox {as } t\rightarrow \infty . \end{aligned}$$

(2.42)

Proof

We substitute $\widehat{w}(x,t){:=} e^{-v(x,t)} w(x,t)$, $x\in \overline{\Omega }$, $t\ge 0$ and use the identity $w_x=e^v (\widehat{w}_x + v_x \widehat{w})$, as thereby implied, to see that

$$\begin{aligned} \widehat{w}_x=0 \qquad \hbox {on } \partial \Omega \times (0,\infty ) \end{aligned}$$

(2.43)

and that

$$\begin{aligned} \widehat{w}_t= & {} e^{-v} w_t - e^{-v} wv_t \nonumber \\= & {} e^{-v} (w_x -wv_x)_x - e^{-v} wv_t \nonumber \\= & {} e^{-v} \cdot (e^v \widehat{w}_x)_x - e^{-v} wv_t \qquad \hbox {in } \Omega \times (0,\infty ) \end{aligned}$$

(2.44)

because of (2.21). Thanks to (2.43), an integration by parts in (2.44) shows that

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} \int _\Omega e^v \widehat{w}_x^2= & {} 2\int _\Omega e^v \widehat{w}_x \widehat{w}_{xt} + \int _\Omega e^v \widehat{w}_x^2 v_t \nonumber \\= & {} -2\int _\Omega (e^v \widehat{w}_x)_x \widehat{w}_t + \int _\Omega e^v \widehat{w}_x^2 v_t \nonumber \\= & {} -2\int _\Omega e^{-v} \cdot (e^v \widehat{w}_x)_x^2 + 2\int _\Omega e^{-v} \cdot (e^v \widehat{w}_x)_x v_t + \int _\Omega e^v \widehat{w}_x^2 v_t \qquad \hbox {for all } t>0,\nonumber \\ \end{aligned}$$

(2.45)

in which we prepare an appropriate estimation of the two last summands by going back to Lemma 2.7 to find positive constants $c_i$, $i\in \{1,...,5\}$, such that

$$\begin{aligned} w \le c_1 \quad \hbox {and} \quad |w_x| \le c_2 \qquad \hbox {in } \Omega \times (1,\infty ) \end{aligned}$$

(2.46)

as well as

$$\begin{aligned} v \le c_3 \quad \hbox {and} \quad |v_x| \le c_4 \qquad \hbox {in } \Omega \times (1,\infty ) \end{aligned}$$

(2.47)

and

$$\begin{aligned} |v_t| \le c_5 \qquad \hbox {in } \Omega \times (1,\infty ), \end{aligned}$$

(2.48)

and by moreover relying on (2.43) in employing the Poincaré inequality to fix $c_6>0$ satisfying

$$\begin{aligned} \int _\Omega (e^v \widehat{w}_x)^2 \le c_6 \int _\Omega (e^v \widehat{w}_x)_x^2 \qquad \hbox {for all } t>0. \end{aligned}$$

(2.49)

Therefore, namely, by utilizing Young’s inequality, we can estimate

$$\begin{aligned} \int _\Omega e^v \widehat{w}_x^2 v_t\le & {} \Vert \widehat{w}_x\Vert _{L^\infty (\Omega )} \int _\Omega e^v |\widehat{w}_x| \cdot |v_t| \nonumber \\= & {} \Vert e^{-v} w_x - e^{-v} wv_x\Vert _{L^\infty (\Omega )} \int _\Omega e^v |\widehat{w}_x| \cdot |v_t| \nonumber \\\le & {} (c_2+c_1 c_4) \int _\Omega e^v |\widehat{w}_x| \cdot |v_t| \nonumber \\\le & {} \frac{1}{2c_6 e^{c_3}} \int _\Omega (e^v \widehat{w}_x)^2 + \frac{c_2 +c_1 c_4)^2 c_6 e^{c_3}}{2} \int _\Omega v_t^2 \nonumber \\\le & {} \frac{1}{2e^{c_3}} \int _\Omega (e^v \widehat{w}_x)_x^2 + \frac{c_2 +c_1 c_4)^2 c_6 e^{c_3}}{2} \int _\Omega v_t^2 \nonumber \\\le & {} \frac{1}{2} \int _\Omega e^{-v} (e^v \widehat{w}_x)_x^2 + \frac{c_2 +c_1 c_4)^2 c_6 e^{c_3}}{2} \int _\Omega v_t^2 \qquad \hbox {for all } t>1.\nonumber \\ \end{aligned}$$

(2.50)

Since furthermore, again due to Young’s inequality,

$$\begin{aligned} 2 \int _\Omega e^{-v} (e^v \widehat{w}_x)_x v_t\le & {} \frac{1}{2} \int _\Omega e^{-v} (e^v \widehat{w}_x)_x^2 + 2\int _\Omega e^{-v} v_t^2 \nonumber \\\le & {} \frac{1}{2} \int _\Omega e^{-v} (e^v \widehat{w}_x)_x^2 + 2\int _\Omega v_t^2 \qquad \hbox {for all } t>0, \end{aligned}$$

and since another application of (2.49) shows that

$$\begin{aligned} \int _\Omega e^v \widehat{w}_x^2= & {} \int _\Omega e^{-v} \cdot (e^v \widehat{w}_x)^2 \\\le & {} \int _\Omega (e^v \widehat{w}_x)^2 \\\le & {} c_6 \int _\Omega (e^v \widehat{w}_x)_x^2 \\\le & {} c_6 e^{c_3} \int _\Omega e^{-v} (e^v \widehat{w}_x)_x^2 \qquad \hbox {for all } t>1, \end{aligned}$$

from (2.45) we all in all obtain that $y(t){:=}\int _\Omega e^{v(\cdot ,t)} \widehat{w}_x^2(\cdot ,t)$ and $h(t){:=}\int _\Omega v_t^2(\cdot ,t)$, $t\ge 1$, satisfy

$$\begin{aligned} y'(t) + c_7 y(t) \le c_8 h(t) \qquad \hbox {for all } t>1 \end{aligned}$$

(2.51)

with $c_7{:=}\frac{1}{c_6 e^{c_3}}$ and $c_8{:=}\frac{(c_2+c_1c_4)^2 c_6 e^{c_3}}{2}+2$. By straightforward integration, we thus infer that for all $t>2$,

$$\begin{aligned} y(t)\le & {} y(1) e^{-c_7(t-1)} + c_8 \int _1^{\frac{t}{2}} e^{-c_7(t-s)} h(s)\hbox {d}s + c_8\int _{\frac{t}{2}}^t e^{-c_7(t-s)} h(s) \hbox {d}s \\\le & {} y(1) e^{-c_7(t-1)} + c_8 \cdot c_5^2 L \int _1^ {\frac{t}{2}} e^{-c_7(t-s)} \hbox {d}s + c_8 \int _{\frac{t}{2}}^t \int _\Omega v_t^2 \\= & {} y(1) e^{-c_7(t-1)} + \frac{c_5^2 c_8 L}{c_7} \cdot (e^{-\frac{c_7 t}{2}} - e^{-c_7(t-1)}) + c_8 \int _{\frac{t}{2}}^t \int _\Omega v_t^2 \\\le & {} y(1) e^{-c_7(t-1)} + \frac{c_5^2 c_8 L}{c_7} e^{-\frac{c_7 t}{2}} + c_8 \int _{\frac{t}{2}}^t \int _\Omega v_t^2, \end{aligned}$$

because $h(t) \le c_5^2 L$ for all $t>1$ according to (2.48). Now since Lemma 2.8 ensures that

$$\begin{aligned} \int _{\frac{t}{2}}^t \int _\Omega v_t^2 \rightarrow 0 \qquad \hbox {as } t\rightarrow \infty , \end{aligned}$$

this shows that

$$\begin{aligned} \int _\Omega e^v \widehat{w}_x^2 \rightarrow 0 \qquad \hbox {as } t\rightarrow \infty , \end{aligned}$$

which by definition of $\widehat{w}$ yields (2.42) due to the fact that $e^v \ge 1$. $\square$

Again relying on Lemma 2.7, this can be seen to imply convergence to some equilibrium also in the first solution component:

Lemma 2.11

Assume (1.8). Then, there exists $\gamma >0$ such that with $\beta >0$ taken from Lemma 2.9, for the solution of (2.21), we have

$$\begin{aligned} w(\cdot ,t) \rightarrow \gamma \cdot \exp \circ (\beta \cdot \exp ) \quad \hbox {in } L^\infty (\Omega ) \qquad \hbox {as } t\rightarrow \infty . \end{aligned}$$

(2.52)

Proof

Defining the number $\gamma$ according to

$$\begin{aligned} \gamma {:=}\frac{\int _\Omega w_0}{\int _\Omega e^{\beta e^x}\hbox {d}x}, \end{aligned}$$

positive due to (1.8), we proceed as in Lemma 2.9 by firstly relying on Lemma 2.7 and the Arzelà-Ascoli theorem to see that $(e^{-v(\cdot ,t)} w(\cdot ,t))_{t>1}$ is relatively compact in $C^0(\overline{\Omega })$, and by secondly identifying all corresponding $\omega$-limits: Indeed, whenever $(t_k)_{k\in \mathbb {N}}\subset (1,\infty )$ and $\varphi \in C^0(\overline{\Omega })$ are such that $t_k\rightarrow \infty$ and $e^{-v(\cdot ,t_k)} w(\cdot ,t_k) \rightarrow \varphi$ in $L^\infty (\Omega )$ as $k\rightarrow \infty$, in view of Lemma 2.10 we have $\varphi \equiv c_1$ in $\Omega$ with some $c_1\ge 0$, while Lemma 2.9 asserts that $e^{-v(\cdot ,t_k)} \rightarrow \exp \circ (-\beta \cdot \exp )$ in $L^\infty (\Omega )$ as $k\rightarrow \infty$. Therefore,

$$\begin{aligned} w(\cdot ,t_k) \rightarrow c_1 \cdot \exp \circ (\beta \cdot \exp ) \quad \hbox {in } L^\infty (\Omega ) \qquad \hbox {as } k\rightarrow \infty , \end{aligned}$$

so that since independently we obtain from (2.21) that $\frac{d}{dt} w=0$ for all $t>0$, we must have

$$\begin{aligned} \int _\Omega w_0=c_1\int _\Omega e^{\beta e^x} \hbox {d}x \end{aligned}$$

and hence $c_1=\gamma$. As $(t_k)_{k\in \mathbb {N}}$ was an arbitrary sequence having the indicated stabilization properties, by a standard reasoning in the style of that from Lemma 2.9, we readily infer (2.52). $\square$

2.3 Approaching (2.21) for Small Values of $\varepsilon$ in (1.7)

Our next goal consists in establishing a link between our solutions to (2.17) and those of (2.21) through an appropriate statement on convergence in the limit $\varepsilon \searrow 0$. The key ingredient toward this will be provided by the following outcome of a Moser-type iteration applied to the first equation in (2.17) on the basis of the taxic gradient estimate from (2.20).

Lemma 2.12

If (1.8) holds and $T>0$, and if $\varepsilon _\mathrm{down}(T)>0$ is taken from Lemma 2.4, then one can find $C(T)>0$ such that the solution of (2.17) from Corollary 2.5 has the property that

$$\begin{aligned} \Vert w_\varepsilon (\cdot ,t)\Vert _{L^\infty (\Omega )} \le C(T) \qquad \hbox {for all }t\in (0,T)\hbox { and any } \varepsilon \in (0,\varepsilon _\mathrm{down}(T)). \end{aligned}$$

(2.53)

Proof

For fixed $T>0$ and nonnegative integers k, we let $p_k{:=}2^k$ and estimate

$$\begin{aligned} M_k{:=}\sup _{\varepsilon \in (0,\varepsilon _\mathrm{down}(T))} \sup _{t\in (0,T)} \int _\Omega w_\varepsilon ^{p_k}(\cdot ,t) \ \in [0,\infty ] \end{aligned}$$

by testing the first equation in (2.17) against $w_\varepsilon ^{p_k-1}$ for $k\ge 1$ to see that due to Young’s inequality,

$$\begin{aligned} \frac{1}{p_k} \frac{d}{dt} \int _\Omega w_\varepsilon ^{p_k} + (p_k-1) \int _\Omega w_\varepsilon ^{p_k-2} w_{\varepsilon x}^2= & {} (p_k-1) \int _\Omega w_\varepsilon ^{p_k-1} (1-\varepsilon w_\varepsilon )^{\lambda -1} v_{\varepsilon x} w_{\varepsilon x} \\&+ (p_k-1) \varepsilon ^{\kappa -1} \int _\Omega w_\varepsilon ^{p_k+\kappa -2} w_{\varepsilon x} \\\le & {} \frac{p_k-1}{4} \int _\Omega w_\varepsilon ^{p_k-2} w_{\varepsilon x}^2 + (p_k-1) \int _\Omega w_\varepsilon ^{p_k} v_{\varepsilon x}^2 \\&+ \frac{p_k-1}{4} \int _\Omega w_\varepsilon ^{p_k-2} w_{\varepsilon x}^2 + (p_k-1) \varepsilon ^{2\kappa -2} \int _\Omega w_\varepsilon ^{p_k+2\kappa -2} \end{aligned}$$

for all $t>0$. Since herein $\varepsilon w_\varepsilon \le 1$ by (2.19), and since $\frac{p_k}{2} \le p_k-1 \le p_k$ for any such k, this shows that

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} \int _\Omega w_\varepsilon ^{p_k} + \int _\Omega (w_\varepsilon ^\frac{p_k}{2})_x^2 \le p_k^2 \int _\Omega w_\varepsilon ^{p_k} v_{\varepsilon x}^2 + p_k^2 \int _\Omega w_\varepsilon ^{p_k} \qquad \hbox {for all } t\in (0,T). \end{aligned}$$

(2.54)

Now an application of Corollary 2.5 to $q{:=}4$ yields $c_1=c_1(T)>0$ such that

$$\begin{aligned} \int _\Omega v_{\varepsilon x}^4 \le c_1 \qquad \hbox {for all }t\in (0,T)\hbox { and any } \varepsilon \in (0,\varepsilon _\mathrm{down}(T)), \end{aligned}$$

whence on the right-hand side of (2.54), we can use the Cauchy–Schwarz inequality to estimate

$$\begin{aligned} p_k^2 \int _\Omega w_\varepsilon ^{p_k} v_{\varepsilon x}^2 + p_k^2 \int _\Omega w_\varepsilon ^{p_k}\le & {} p_k^2 \cdot \bigg \{ \int _\Omega v_{\varepsilon x}^4 \bigg \}^\frac{1}{2} \cdot \bigg \{ \int _\Omega w_\varepsilon ^{2p_k}\bigg \}^\frac{1}{2} + p_k^2 L^\frac{1}{2} \cdot \bigg \{ \int _\Omega w_\varepsilon ^{2p_k}\bigg \}^\frac{1}{2} \nonumber \\&{\le }&c_2 p_k^2 \cdot \bigg \{ \int _\Omega w_\varepsilon ^{2p_k}\bigg \}^\frac{1}{2} \qquad \hbox {for all }t\in (0,T)\hbox { and } \varepsilon \in (0,\varepsilon _\mathrm{down}(T))\nonumber \\ \end{aligned}$$

(2.55)

with $c_2\equiv c_2(T){:=}c_1^\frac{1}{2} + L^\frac{1}{2}$. Here, by means of the Gagliardo–Nirenberg inequality, we can find $c_3=c_3(T)>0$ such that due to our definition of $(M_j)_{j\ge 0}$ and Young’s inequality,

$$\begin{aligned} c_2 p_k^2 \cdot \bigg \{ \int _\Omega w_\varepsilon ^{2p_k}\bigg \}^\frac{1}{2}= & {} c_2 p_k^2 \Vert w_\varepsilon ^\frac{p_k}{2}\Vert _{L^4(\Omega )}^4 \nonumber \\\le & {} c_3 p_k^2 \Vert (w_\varepsilon ^\frac{p_k}{2})_x\Vert _{L^2(\Omega )} \Vert w_\varepsilon ^\frac{p_k}{2}\Vert _{L^1(\Omega )} + c_3 p_k^2 \Vert w_\varepsilon ^\frac{p_k}{2}\Vert _{L^1(\Omega )}^2 \nonumber \\\le & {} c_3 p_k^2 M_{k-1} \Vert (w_\varepsilon ^\frac{p_k}{2})_x\Vert _{L^2(\Omega )} + c_3 p_k^2 M_{k-1}^2 \nonumber \\\le & {} \frac{1}{2} \Vert (w_\varepsilon ^\frac{p_k}{2})_x\Vert _{L^2(\Omega )}^2 + \Big ( \frac{c_3^2 p_k^4}{2} + c_3 p_k^2\Big ) M_{k-1}^2 \end{aligned}$$

(2.56)

for all $t\in (0,T)$ and $\varepsilon \in (0,\varepsilon _\mathrm{down}(T))$. As furthermore, for similar reasons, there exist $c_4>0$ and $c_5>0$ such that

$$\begin{aligned} \int _\Omega w_\varepsilon ^{p_k}\le & {} c_4 \Vert (w_\varepsilon ^\frac{p_k}{2})_x\Vert _{L^2(\Omega )}^\frac{2}{3} \Vert w_\varepsilon ^\frac{p_k}{2}\Vert _{L^1(\Omega )}^\frac{4}{3} + c_4\Vert w_\varepsilon ^\frac{p_k}{2}\Vert _{L^1(\Omega )}^2 \\\le & {} c_4 M_{k-1}^\frac{4}{3} \Vert (w_\varepsilon ^\frac{p_k}{2})_x\Vert _{L^2(\Omega )}^\frac{2}{3} + c_4 M_{k-1}^2 \\\le & {} \frac{1}{2} \Vert (w_\varepsilon ^\frac{p_k}{2})_x\Vert _{L^2(\Omega )}^2 + c_5 M_{k-1}^2 \qquad \hbox {for all }t\in (0,T)\hbox { and } \varepsilon \in (0,\varepsilon _\mathrm{down}(T)), \end{aligned}$$

by combining (2.54) with (2.55) and (2.56) and noting that $1\le p_k^2 \le p_k^4$, we readily infer the existence of $c_6=c_6(T)>0$ satisfying

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} \int _\Omega w_\varepsilon ^{p_k} + \int _\Omega w_\varepsilon ^{p_k} \le c_6 M_{k-1}^2 \qquad \hbox {for all} t\in (0,T)\hbox { and each } \varepsilon \in (0,\varepsilon _\mathrm{down}(T)). \end{aligned}$$

Through an ODE comparison argument, this entails that

$$\begin{aligned} \int _\Omega w_\varepsilon ^{p_k}(\cdot ,t) \le \max \bigg \{ \int _\Omega w_0^{p_k} \, , \, c_6 M_{k-1}^2 \bigg \} \qquad \hbox {for all }t\in (0,T)\hbox { and } \varepsilon \in (0,\varepsilon _\mathrm{down}(T)), \end{aligned}$$

and that thus, as the right-hand side herein neither depends on $t\in (0,T)$ nor on $\varepsilon \in (0,\varepsilon _\mathrm{down})$,

$$\begin{aligned} M_k \le \max \bigg \{ \int _\Omega w_0^{p_k} \, , \, c_6 M_{k-1}^2 \bigg \}. \end{aligned}$$

(2.57)

The remainder of the argument is quite standard: If incidentally $M_k \le \int _\Omega w_0^{p_k}$ for infinitely many $k\in \mathbb {N}$, then it immediately follows that whenever $\varepsilon \in (0,\varepsilon _\mathrm{down}(T))$,

$$\begin{aligned} \Vert w_\varepsilon (\cdot ,t)\Vert _{L^\infty (\Omega )}\le & {} \liminf _{k\rightarrow \infty } M_k^\frac{1}{p_k} \le \liminf _{k\rightarrow \infty } \Vert w_0\Vert _{L^{p_k}(\Omega )} = \Vert w_0\Vert _{L^\infty (\Omega )}\\&\hbox {for all }t\in (0,T). \end{aligned}$$

Otherwise, however, using that $M_0$ is finite according to (2.18), one can easily verify that (2.57) ensures finiteness of $M_k$ for all $k\ge 1$ and that with some $b>1$ we have

$$\begin{aligned} M_k \le b^k M_{k-1}^2 \qquad \hbox {for all } k\ge 1. \end{aligned}$$

By straightforward induction, this shows that

$$\begin{aligned} M_k \le b^{2^{k+1}-k-2} M_0^{2^k} \qquad \hbox {for all } k\ge 1 \end{aligned}$$

and therefore entails that

$$\begin{aligned} \Vert w_\varepsilon (\cdot ,t)\Vert _{L^\infty (\Omega )}\le & {} \liminf _{k\rightarrow \infty } M_k^\frac{1}{2^k} \le b^\frac{2^{k+1}-k-2}{2^k} M_0 \le b^2 M_0 \qquad \hbox {for all }t\in (0,T)\\&\hbox { and } \varepsilon \in (0,\varepsilon _\mathrm{down}(T)), \end{aligned}$$

thus implying (2.53) also in this case. $\square$

Indeed, thanks to a known result from scalar parabolic theory, the latter, once more in conjunction with (2.20), ensures bounds for both solution components in (2.17) in appropriate Hölder spaces.

Lemma 2.13

Suppose that (1.8) holds and that $T>0$, and let $\varepsilon _\mathrm{down}(T)>0$ be as in Lemma 2.4. Then, there exist $\theta =\theta (T)\in (0,1)$ and $C(T)>0$ such that the solution of (2.17) from Corollary 2.5 satisfies

$$\begin{aligned} \Vert w_\varepsilon \Vert _{C^{\theta ,\frac{\theta }{2}}(\overline{\Omega }\times [0,T])} \le C(T) \qquad \hbox {for all } \varepsilon \in (0,\varepsilon _\mathrm{down}(T)) \end{aligned}$$

(2.58)

and

$$\begin{aligned} \Vert v_\varepsilon \Vert _{C^{\theta ,\frac{\theta }{2}}(\overline{\Omega }\times [0,T])} \le C(T) \qquad \hbox {for all } \varepsilon \in (0,\varepsilon _\mathrm{down}(T)). \end{aligned}$$

(2.59)

Proof

In view of Corollary 2.5, Lemma 2.12 and (1.8), the estimate in (2.58) is a direct consequence of well-known theory on Hölder regularity in scalar parabolic equations under no-flux boundary conditions (Porzio and Vespri 1993). Likewise, (2.59) is ensured by the uniform bounds resulting from (2.19) and (2.20). $\square$

As a consequence of the latter, two successive applications of interior parabolic Schauder estimates provide higher-order regularity features:

Lemma 2.14

Assume (1.8) and that $T>0$, and let $\varepsilon _\mathrm{down}(T)>0$ be as in Lemma 2.4. Then, for all $\tau \in (0,T)$, one can find $\theta =\theta (\tau ,T)\in (0,1)$ and $C(\tau ,T)>0$ such that for the solution of (2.17), we have

$$\begin{aligned} \Vert w_\varepsilon \Vert _{C^{2+\theta ,1+\frac{\theta }{2}}(\overline{\Omega }\times [\tau ,T])} \le C(T) \qquad \hbox {for all } \varepsilon \in (0,\varepsilon _\mathrm{down}(T)) \end{aligned}$$

(2.60)

and

$$\begin{aligned} \Vert v_\varepsilon \Vert _{C^{2+\theta ,1+\frac{\theta }{2}}(\overline{\Omega }\times [\tau ,T])} \le C(T) \qquad \hbox {for all } \varepsilon \in (0,\varepsilon _\mathrm{down}(T)). \end{aligned}$$

(2.61)

Proof

Firstly, (2.61) results from Lemma 2.13 through standard parabolic Schauder theory (Ladyzenskaja et al. 1968) applied to the second equation in (2.17). Relying on the fact that $\tau \in (0,T)$ in (2.61) is arbitrary, we may thereafter apply the same tool to the first subproblem contained in (2.17) to readily infer from (2.61) that, possibly upon diminishing $\theta (\tau ,T)$ and enlarging $C(\tau ,T)$, also (2.60) can be achieved. $\square$

In quite a straightforward manner, the compactness features gathered above, along with the uniqueness statement contained in Lemma 2.6, enable us to take $\varepsilon \searrow 0$ in (2.17) with the desired result.

Lemma 2.15

Suppose that (1.8) is valid, and for $T>0$ let $\varepsilon _\mathrm{down}(T)>0$ be as given by Lemma 2.4. Then the solutions of (2.17) gained in Corollary 2.5 have the properties that

$$\begin{aligned}&w_\varepsilon \rightarrow w \qquad \hbox {in } C^0(\overline{\Omega }\times [0,T]) \cap C^{2,1}_{loc}(\overline{\Omega }\times (0,T]), \end{aligned}$$

(2.62)

$$\begin{aligned}&v_\varepsilon \rightarrow v \qquad \hbox {in } C^0(\overline{\Omega }\times [0,T]) \cap C^{2,1}_{loc}(\overline{\Omega }\times (0,T]) \qquad \hbox {and} \end{aligned}$$

(2.63)

$$\begin{aligned}&v_{\varepsilon x} {\mathop {\rightharpoonup }\limits ^{\star }}v_x \qquad \hbox {in } L^\infty ((0,T);L^2(\Omega )) \end{aligned}$$

(2.64)

as $\varepsilon \searrow 0$, where (w, v) denotes the unique classical solution of (2.21) satisfying (2.22).

Proof

In view of the uniqueness statement in Lemma 2.6, according to a standard argument, it is sufficient to make sure that with $\varepsilon _\mathrm{down}(T)>0$ taken from Lemma 2.4, each sequence $(\varepsilon _j)_{j\in \mathbb {N}} \subset (0,\varepsilon _\mathrm{down}(T))$ such that $\varepsilon _j\searrow 0$ as $j\rightarrow \infty$ contains a subsequence $(\varepsilon _{j_k})_{k\in \mathbb {N}}$ such that (2.62)–(2.64) hold as $\varepsilon =\varepsilon _{j_k}\searrow 0$, with some classical solution (w, v) of (2.21) fulfilling (2.22). To verify this, given any such $(\varepsilon _j)_{j\in \mathbb {N}}$, we may rely on the bounds provided by Lemmas 2.13, 2.14 and Corollary 2.5 to see upon a straightforward extraction procedure involving the Arzelà–Ascoli theorem that in fact it is possible to find a subsequence $(\varepsilon _{j_k})_{k\in \mathbb {N}}$ and functions w and v for which (2.62)–(2.64) hold as $\varepsilon =\varepsilon _{j_k}\searrow 0$. Since from (2.62) and (2.63), it is an evident consequence of the inequality $\kappa >1$ that the validity of (2.21) for these functions results in taking $\varepsilon =\varepsilon _{j_k}\searrow 0$ in each of the summands in (2.17) in the classical pointwise sense, we furthermore conclude that (w, v) indeed forms a classical solution of (2.21), having the additional feature (2.22) due to (2.64), whereby the proof becomes complete. $\square$

2.4 Proof of Theorem 1.1

We are now prepared to derive our main result on preferred downstream migration in the presence of suitably small population densities by simply combining Lemma 2.15 with Lemma 2.11.

proof of Theorem 1.1

Given $\delta >0$, by means of Lemma 2.11, we first choose $T(\delta )>0$ large enough such that the solution of (2.21) satisfies

$$\begin{aligned} \Big | w(x,t) - \gamma \cdot e^{\beta e^x}\Big | \le \frac{\delta }{2} \qquad \hbox {for all } x\in \overline{\Omega }\hbox { and } t\ge T(\delta ). \end{aligned}$$

(2.65)

We then fix any $T>T(\delta )$ and take $\varepsilon _\mathrm{down}(T)>0$ as accordingly provided by Lemma 2.4, and noting that then classical solvability of (1.7) in $\Omega \times (0,T)$ within the desired class is asserted by Lemma 2.4, we may rely on Lemma 2.15 to find some $\varepsilon _0(\delta ,T)\in (0,\varepsilon _\mathrm{down}(T))$ such that for the correspondingly obtained classical solution, we have

$$\begin{aligned} \Big \Vert \frac{u_\varepsilon (\cdot ,t)}{\varepsilon } - w(\cdot ,t)\Big \Vert _{L^\infty (\Omega )} \le \frac{\delta }{2} \quad \hbox { for all}\ t\in [0,T] \qquad \hbox {whenever } \varepsilon \in (0,\varepsilon _0(\delta ,T)). \end{aligned}$$

(2.66)

A simple combination of (2.65) and (2.66) thereupon directly yields (1.10) for any such $\varepsilon$. $\square$

3 Dominance of Upstream Migration for Large u: Proof of Theorem 1.2

In order to verify Theorem 1.2, following essentially the same basic approach as pursued in the previous part, we rescale (1.11) by substituting $u_\varepsilon =1-\varepsilon z_\varepsilon$, which in fact transforms (1.11) to the problem

$$\begin{aligned} \left\{ \begin{array}{llll} z_{\varepsilon t} - \kappa (1-\varepsilon z_\varepsilon )^{\kappa -1} z_{\varepsilon x} &{}=&{} z_{\varepsilon xx} + \varepsilon ^{\lambda -1} \Big (z_\varepsilon ^\lambda (1-\varepsilon z_\varepsilon ) v_{\varepsilon x}\Big )_x, \qquad &{} x\in \Omega , \ t>0, \\ v_{\varepsilon t} + v_{\varepsilon x} &{}=&{} v_{\varepsilon xx} + u_\varepsilon (1-v_\varepsilon ), \qquad &{} x\in \Omega , \ t>0, \\ z_\varepsilon &{}=&{}0, \quad v_{\varepsilon x} - v_\varepsilon =0, \qquad &{} x\in \partial \Omega , \ t>0, \\ z_\varepsilon (x,0)&{}=&{}z_0(x), \quad v_\varepsilon (x,0)=v_0(x), \qquad &{} x\in \Omega , \end{array} \right. \end{aligned}$$

(3.1)

that again turns out to be solvable in a convenient sense, now even globally in time, provided that the parameter $\varepsilon >0$ therein is suitably small:

Lemma 3.1

Assume (1.12). Then, there exists $\varepsilon _\mathrm{up}>0$ such that for each $\varepsilon \in (0,\varepsilon _\mathrm{up})$ the problem (3.1) possesses a global classical solution $(z_\varepsilon ,v_\varepsilon )$ with

$$\begin{aligned} \left\{ \begin{array}{l} z_\varepsilon \in C^0(\overline{\Omega }\times [0,\infty )) \cap C^{2,1}(\overline{\Omega }\times (0,\infty )) \qquad \hbox {and} \\ v_\varepsilon \in \bigcap _{q>1} C^0([0,\infty );W^{1,q}(\Omega )) \cap C^{2,1}(\overline{\Omega }\times (0,\infty )), \end{array} \right. \end{aligned}$$

which is such that $z_\varepsilon \ge 0$ and $v_\varepsilon \ge 0$ in $\Omega \times (0,\infty )$ and that moreover

$$\begin{aligned} \int _\Omega z_\varepsilon (x,t)dx \le \int _\Omega z_0(x)dx \qquad \hbox {for all } t>0 \end{aligned}$$

(3.2)

and

$$\begin{aligned} z_\varepsilon (x,t) \le \frac{1}{\varepsilon } \qquad \hbox {for all} x\in \overline{\Omega }\hbox { and } t>0. \end{aligned}$$

(3.3)

Apart from that, given any $q>1$ and $T>0$, one can find $C(q,T)>0$ fulfilling

$$\begin{aligned} \Vert v_\varepsilon (\cdot ,t)\Vert _{W^{1,q}(\Omega )} \le C(q,T) \qquad \hbox {for all} t\in (0,T)\hbox { and any } \varepsilon \in (0,\varepsilon _\mathrm{up}). \end{aligned}$$

(3.4)

Proof

We fix any $\varepsilon _\mathrm{up}>0$ such that $\varepsilon _\mathrm{up}\Vert z_0\Vert _{L^\infty (\Omega )}<1$ and then readily obtain, again by following standard arguments (Horstmann and Winkler 2005; Amann 1989), that for each $\varepsilon \in (0,\varepsilon _\mathrm{up})$, the auxiliary problem

$$\begin{aligned} \left\{ \begin{array}{llll} z_{\varepsilon t} - \kappa (1-\varepsilon z_\varepsilon )_+^{\kappa -1} z_{\varepsilon x} &{}=&{} z_{\varepsilon xx} + \varepsilon ^{\lambda -1} \Big (z_\varepsilon ^\lambda (1-\varepsilon z_\varepsilon ) v_{\varepsilon x}\Big )_x, \qquad &{} x\in \Omega , \ t>0, \\ v_{\varepsilon t} + v_{\varepsilon x} &{}=&{} v_{\varepsilon xx} + u_\varepsilon (1-v_\varepsilon ), \qquad &{} x\in \Omega , \ t>0, \\ z_\varepsilon &{}=&{}0, \quad v_{\varepsilon x} - v_\varepsilon =0, \qquad &{} x\in \partial \Omega , \ t>0, \\ z_\varepsilon (x,0)&{}=&{}z_0(x), \quad v_\varepsilon (x,0)=v_0(x), \qquad &{} x\in \Omega , \end{array} \right. \end{aligned}$$

(3.5)

possesses a nonnegative classical solution enjoying the claimed regularity properties and being extensible up to a maximal time $T_\mathrm{max}\in (0,\infty ]$ fulfilling

$$\begin{aligned} \hbox {either } T_\mathrm{max}=\infty ,\hbox { or } \limsup _{t\nearrow T_\mathrm{max}} \Big \{ \Vert z_\varepsilon (\cdot ,t)\Vert _{L^\infty (\Omega )} + \Vert v_\varepsilon (\cdot ,t)\Vert _{W^{1,q}(\Omega )} \Big \} =\infty \qquad \hbox {for all } q>1. \end{aligned}$$

(3.6)

But since $\overline{z}(x,t){:=}\frac{1}{\varepsilon }$, $x\in \overline{\Omega }$, $t\ge 0$, defines a supersolution of the considered homogeneous Dirichlet problem for the first equation in (3.5), it follows that $z_\varepsilon \le \frac{1}{\varepsilon }$ throughout $\Omega \times (0,T_\mathrm{max})$ and that hence $(z_\varepsilon ,v_\varepsilon )$ actually solves (3.1) in $\Omega \times (0,T_\mathrm{max})$. As this uniform upper bound together with standard parabolic estimates also warrants that $(v_\varepsilon (\cdot ,t))_{t\in (\min \{ 1,\frac{1}{2}T_\mathrm{max}\},\min \{T,T_\mathrm{max}\})}$ is bounded in $W^{1,q}(\Omega )$ for all $T>0$ and $q>1$, from (3.6) we conclude that indeed $T_\mathrm{max}=\infty$ and that hence $(z_\varepsilon ,v_\varepsilon )$ is global and satisfies (3.3). Finally, the mass control feature (3.2) can be obtained by direct integration in the first equation from (3.1) by observing that $z_{\varepsilon x}(0,t)\ge 0\ge z_{\varepsilon x}(L,t)$ for all $t>0$ by nonnegativity of $z_\varepsilon$ and the boundary condition in (3.1), and the estimate (3.4) can be derived by straightforward adaptation and simplification of the reasoning in Lemma 2.2. $\square$

3.1 Asymptotic Behavior in a Limit Problem

In comparison with that from Sect. 2, here the limit problem that is formally associated with (3.1) actually reduces, in its first component, to the Dirichlet problem for a scalar transport–diffusion equation, as given by

$$\begin{aligned} \left\{ \begin{array}{llll} z_t &{}=&{} z_{xx}+\kappa z_x, \qquad &{} x\in \Omega , \ t>0, \\ z&{}=&{}0, \qquad &{} x\in \partial \Omega , \ t>0, \\ z(x,0)&{}=&{}z_0(x). \qquad &{} x\in \Omega . \end{array} \right. \end{aligned}$$

(3.7)

This problem is well-understood and can in fact be reduced to the Dirichlet problem for the heat equation:

Lemma 3.2

Let $\kappa \in \mathbb {R}$ and $z_0\in C^0(\overline{\Omega })$ be nonnegative with $z_0=0$ on $\partial \Omega$. Then, there exists precisely one classical solution $z\in C^0(\overline{\Omega }\times [0,\infty )) \cap C^{2,1}(\overline{\Omega }\times (0,\infty ))$ of (3.7), namely the function given by

$$\begin{aligned} z(x,t){:=}e^{-\frac{\kappa ^2}{4}t} e^{-\frac{\kappa }{2}x} \widehat{z}(x,t), \qquad x\in \overline{\Omega }\, t\ge 0, \end{aligned}$$

(3.8)

with $\widehat{z}\in C^0(\overline{\Omega }\times [0,\infty )) \cap C^{2,1}(\overline{\Omega }\times (0,\infty ))$ denoting the classical solution of

$$\begin{aligned} \left\{ \begin{array}{llll} \widehat{z}_t &{}=&{} \widehat{z}_{xx}, \qquad &{}\quad x\in \Omega , \ t>0, \\ \widehat{z}&{}=&{}0, \qquad &{}\quad x\in \partial \Omega , \ t>0, \\ \widehat{z}(x,0)&{}=&{}e^{\frac{\kappa }{2}x} z_0(x), \qquad &{}\quad x\in \Omega . \end{array} \right. \end{aligned}$$

(3.9)

Proof

Since classical solutions of (3.7) in the indicated class are unique by the maximum principle, we only need to note that if z is as defined by (3.8), then

$$\begin{aligned} z_t= e^{-\frac{\kappa ^2}{4}t} e^{-\frac{\kappa }{2}x} \cdot \Big (\widehat{z}_t - \frac{\kappa ^2}{4}\widehat{z}\Big ) \qquad \hbox {in } \Omega \times (0,\infty ) \end{aligned}$$

as well as

$$\begin{aligned} z_x = e^{-\frac{\kappa ^2}{4}t} e^{-\frac{\kappa }{2}x} \cdot \Big ( \widehat{z}_x - \frac{\kappa }{2}\widehat{z}\Big ) \quad \hbox {and} \quad z_{xx} = e^{-\frac{\kappa ^2}{4}t} e^{-\frac{\kappa }{2}x} \cdot \Big ( \widehat{z}_{xx} - \kappa \widehat{z}_x + \frac{\kappa ^2}{4} \widehat{z}\Big ) \qquad \hbox {in } \Omega \times (0,\infty ), \end{aligned}$$

and that therefore z indeed solves (3.7) due to the observation that thus

$$\begin{aligned} e^{\frac{\kappa ^2}{4}t} e^{\frac{\kappa }{2}x} \cdot (z_t{-}z_{xx} {-} \kappa z_x)&{=}&\widehat{z}_t {-} \frac{\kappa ^2}{4} \widehat{z}{-} \Big (\widehat{z}_{xx}-\kappa \widehat{z}_x {+} \frac{\kappa ^2}{4}\widehat{z}\Big ) {-} \kappa \cdot \Big ( \widehat{z}_x -\frac{\kappa }{2}\widehat{z}\Big ) = 0\\&\quad \hbox {in}\, \Omega \times (0,\infty ) \end{aligned}$$

by (3.9).$\square$

Indeed, the asymptotic behavior in (3.7) can therefore be described quite exhaustively.

Lemma 3.3

Under the assumptions of Lemma 3.2, the classical solution $\widehat{z}\in C^0(\overline{\Omega }\times [0,\infty )) \cap C^{2,1}(\overline{\Omega }\times (0,\infty ))$ of (3.9) satisfies

$$\begin{aligned} \bigg \Vert e^{\frac{\pi ^2}{L^2} t} \widehat{z}(\cdot ,t) - \alpha \sin \frac{\pi (\cdot )}{L} \bigg \Vert _{L^\infty (\Omega )} \rightarrow 0 \qquad \hbox {as } t\rightarrow \infty , \end{aligned}$$

(3.10)

where

$$\begin{aligned} \alpha {:=}\frac{\int _\Omega e^{\frac{\kappa }{2}x} \sin \frac{\pi x}{L} z_0(x) \hbox {d}x}{\int _\Omega \sin ^2 \frac{\pi x}{L} \hbox {d}x} \ >0. \end{aligned}$$

(3.11)

Proof

We let $\mu _1{:=}\frac{\pi ^2}{L}$ denote the principal Dirichlet eigenvalue of $-(\cdot )_{xx}$ on $\Omega$ and take $\Theta (x){:=}\sin \frac{\pi x}{L}$, $x\in [0,L]$, as a corresponding eigenfunction. Then, abbreviating $\widetilde{z}(x,t){:=}e^{\mu _1 t} \widehat{z}(x,t)$ for $x\in \overline{\Omega }$ and $t\ge 0$, using (3.9) we see that

$$\begin{aligned} \left\{ \begin{array}{llll} &{}&{}\widetilde{z}_t = \widetilde{z}_{xx} + \mu _1 \widetilde{z}, \qquad &{}\quad x\in \Omega , \ t>0, \\ &{} &{} \widetilde{z}=0, \qquad &{}\quad x\in \partial \Omega , \, t>0, \\ &{} &{} \widetilde{z}(x,0)= e^{\frac{\kappa }{2}x} z_0(x), \qquad &{}\quad x\in \Omega , \end{array} \right. \end{aligned}$$

(3.12)

where we note that due to our assumptions that $z_0\in W^{1,\infty }(\Omega )$ and $z_0|_{\partial \Omega }=0$, we can fix $c_1>0$ large enough such that $e^{\frac{\kappa }{2}x} z_0(x) \le c_1 \Theta (x)$ for all $x\in \Omega$. As our choice of $\Theta$ ensures that $(c_1\Theta )_t - (c_1\Theta )_{xx} - \mu _1 \cdot (c_1\Theta ) = \mu _1 c_1\Theta -\mu _1 c_1\Theta =0$ in $\Omega \times (0,\infty )$, the classical comparison principle asserts that $\widetilde{z}(x,t)\le c_1\Theta (x) \le c_1$ for all $x\in \Omega$ and $t>0$, so that parabolic Schauder theory (Ladyzenskaja et al. 1968) together with the Arzelà-Ascoli theorem warrants that

$$\begin{aligned} \widetilde{z}_t \hbox { is uniformly continuous in } \Omega \times (1,\infty ) \end{aligned}$$

(3.13)

and that

$$\begin{aligned} (\widetilde{z}(\cdot ,t))_{t>1} \quad \hbox {is relatively compact in } C^2(\overline{\Omega }). \end{aligned}$$

(3.14)

In order to identify all elements of the corresponding $\omega$-limit set, we first test (3.12) by $\widetilde{z}_t$ to see that due to the variational characterization of $\mu _1$, we have

$$\begin{aligned} \int _1^t \int _\Omega \widetilde{z}_t^2= & {} - \,\frac{1}{2} \int _1^t \frac{\hbox {d}}{\hbox {d}t} \int _\Omega \widetilde{z}_x^2 + \frac{\mu _1}{2} \int _1^t \frac{\hbox {d}}{\hbox {d}t} \int _\Omega \widetilde{z}^2 \\= & {} -\, \frac{1}{2} \int _\Omega \widetilde{z}_x^2(\cdot ,t) + \frac{\mu _1}{2} \int _\Omega \widetilde{z}^2(\cdot ,t) + \frac{1}{2} \int _\Omega \widetilde{z}_x^2(\cdot ,1) - \frac{\mu _1}{2} \int _\Omega \widetilde{z}^2(\cdot ,1) \\\le & {} c_2{:=}\frac{1}{2} \int _\Omega \widetilde{z}_x^2(\cdot ,1) \qquad \hbox {for all } t>1, \end{aligned}$$

which according to (3.13) and an elementary argument ensures that in fact

$$\begin{aligned} \widetilde{z}(\cdot ,t) \rightarrow 0 \quad \hbox {in } L^\infty (\Omega ) \qquad \hbox {as } t\rightarrow \infty . \end{aligned}$$

(3.15)

Now if $(t_k)_{k\in \mathbb {N}} \subset (1,\infty )$ and $\widetilde{z}_\infty \in C^2(\overline{\Omega })$ are such that $t_k\rightarrow \infty$ and $tz(\cdot ,t_k)\rightarrow \widetilde{z}_\infty$ in $C^2(\overline{\Omega })$ as $k\rightarrow \infty$, then (3.15) together with (3.12) implies that $\widetilde{z}_{\infty xx}-\mu _1 \widetilde{z}_\infty =0$ and that thus there must exist ${{\widetilde{\alpha }}}\ge 0$ such that $\widetilde{z}_\infty \equiv {{\widetilde{\alpha }}}\Theta$, because the principal eigenspace of $-(\cdot )_{xx}$ is one-dimensional. But since testing (3.12) against $\Theta$ shows that $\frac{d}{dt} \int _\Omega \widetilde{z}\Theta =0$ for all $t>0$ and that thus $\int _\Omega \widetilde{z}(\cdot ,t)\Theta =\int _\Omega \widetilde{z}(\cdot ,0)\Theta$ for all $t>0$, we necessarily must have ${{\widetilde{\alpha }}} \int _\Omega \Theta ^2 \equiv \int _\Omega ({{\widetilde{\alpha }}} \widetilde{z}_\infty )\Theta = \int _\Omega (e^{\frac{\kappa }{2}x} z_0)\Theta$. As thus $\widetilde{z}_\infty \equiv \alpha \Theta$ in $\Omega$ according to (3.11), this establishes (3.10). $\square$

3.2 Approximation of (3.7) by Solutions to (3.1): Proof of Theorem 1.2

Again, the key observation that will finally enable us to safely take $\varepsilon \searrow 0$ in (3.1) consists in a uniform bound on the respective first solution component, to be achieved once more by means of a Moser-type recursive argument.

Lemma 3.4

Assume (1.12), and let $\varepsilon _\mathrm{up}>0$ be as provided by Lemma 3.1. Then, for all $T>0$, there exists $C(T)>0$ such that whenever $\varepsilon \in (0,\varepsilon _\mathrm{up})$, the solution of (3.1) from Lemma 3.1 satisfies

$$\begin{aligned} \Vert z_\varepsilon (\cdot ,t)\Vert _{L^\infty (\Omega )} \le C(T) \qquad \hbox {for all} t\in (0,T). \end{aligned}$$

(3.16)

Proof

Pursuing the same basic approach as in Lemma 2.12, fixing $T>0$, we let $p_k{:=}2^k$ and

$$\begin{aligned} M_k{:=}\sup _{\varepsilon \in (0,\varepsilon _\mathrm{up})} \sup _{t\in (0,T)} \int _\Omega z_\varepsilon ^{p_k}(\cdot ,t) \end{aligned}$$

for integers $k\ge 0$, and noting that $M_0 \le \int _\Omega z_0$ by (3.2), we proceed to recursively establish bounds on $M_k$ for $k\ge 1$ by differentiation and integration by parts on the basis of (3.1). Since $z_{\varepsilon x}(0,t) \ge 0 \ge z_{\varepsilon x}(L,t)$ for all $t>0$, namely we thereby obtain that

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} \int _\Omega z_\varepsilon ^{p_k} + p_k(p_k-1) \int _\Omega z_\varepsilon ^{p_k-2} z_{\varepsilon x}^2\le & {} - p_k(p_k-1) \varepsilon ^{\lambda -1} \int _\Omega z_\varepsilon ^{p_k+\lambda -2} (1-\varepsilon z_\varepsilon ) v_{\varepsilon x} z_{\varepsilon x} \nonumber \\&+ p_k \kappa \int _\Omega (1-\varepsilon z_\varepsilon )^{\kappa -1} z_\varepsilon ^{p_k-1} z_{\varepsilon x} \qquad \hbox {for all } t>0,\nonumber \\ \end{aligned}$$

(3.17)

where by Young’s inequality,

$$\begin{aligned} - p_k(p_k-1) \varepsilon ^{\lambda -1} \int _\Omega z_\varepsilon ^{p_k+\lambda -2} (1-\varepsilon z_\varepsilon ) v_{\varepsilon x} z_{\varepsilon x}\le & {} \frac{p_k(p_k-1)}{2} \int _\Omega z_\varepsilon ^{p_k-2} z_{\varepsilon x}^2 \nonumber \\&+ \frac{p_k(p_k-1)\varepsilon ^{2\lambda -2}}{2} \int _\Omega z_\varepsilon ^{p_k+2\lambda -2} (1-\varepsilon z_\varepsilon )^2 v_{\varepsilon x}^2 \nonumber \\\le & {} \frac{p_k(p_k-1)}{2} \int _\Omega z_\varepsilon ^{p_k-2} z_{\varepsilon x}^2 \nonumber \\&+ \frac{p_k(p_k-1)}{2} \int _\Omega z_\varepsilon ^{p_k} v_{\varepsilon x}^2 \qquad \hbox {for all } t>0\nonumber \\ \end{aligned}$$

(3.18)

due to (3.3). Here, using the Hölder inequality, (3.4), the Gagliardo–Nirenberg inequality and Young’s inequality, we can find $c_1=c_1(T)>0, c_2=c_2(T)>0$ and $c_3=c_3(T)>0$ such that

$$\begin{aligned} \frac{p_k(p_k-1)}{2} \int _\Omega z_\varepsilon ^{p_k} v_{\varepsilon x}^2 + \int _\Omega z_\varepsilon ^{p_k}\le & {} \frac{p_k(p_k-1)}{2} \Vert z_\varepsilon ^\frac{p_k}{2}\Vert _{L^4(\Omega )}^2 \cdot \Big \{ \Vert v_{\varepsilon x}\Vert _{L^4(\Omega )}^2+1\Big \} \nonumber \\\le & {} c_1 p_k(p_k-1) \Vert z_\varepsilon ^\frac{p_k}{2}\Vert _{L^4(\Omega )}^2 \nonumber \\\le & {} c_2 p_k(p_k-1) \Vert (z_\varepsilon ^\frac{p_k}{2})_x\Vert _{L^2(\Omega )} \Vert z_\varepsilon ^\frac{p_k}{2}\Vert _{L^1(\Omega )} \nonumber \\\le & {} \frac{p_k(p_k-1)}{2} \int _\Omega z_\varepsilon ^{p_k-2} z_{\varepsilon x}^2 + c_3 p_k^4 \Vert z_\varepsilon ^\frac{p_k}{2}\Vert _{L^1(\Omega )}^2 \nonumber \\\le & {} \frac{p_k(p_k-1)}{2} \int _\Omega z_\varepsilon ^{p_k-2} z_{\varepsilon x}^2 + c_3 p_k^4 M_{k-1}^2 \qquad \hbox {for all } t\in (0,T)\nonumber \\ \end{aligned}$$

(3.19)

whenever $k\ge 1$ and $\varepsilon \in (0,\varepsilon _\mathrm{up})$. Since furthermore, letting $\rho (s){:=}p_k\kappa \int _0^s (1-\varepsilon \sigma )^{\kappa -1} \sigma ^{p_k-1}\hbox {d}\sigma$, $s\in [0,\frac{1}{\varepsilon }]$, $\varepsilon \in (0,\varepsilon _\mathrm{up})$, we can compute

$$\begin{aligned} p_k\kappa \int _\Omega (1-\varepsilon z_\varepsilon )^{\kappa -1} z_\varepsilon ^{p_k-1} z_{\varepsilon x} = \int _\Omega (\rho (z_\varepsilon ))_x = \rho (z_\varepsilon (L,t)) - \rho (z_\varepsilon (0,t)) =0 \qquad \hbox {for all } t>0 \end{aligned}$$

due to the fact that $z_\varepsilon (0,t)=z_\varepsilon (L,t)=0$ for all $t>0$, from (3.17) to (3.19), we altogether obtain that for all $k\ge 1$ and $\varepsilon \in (0,\varepsilon _\mathrm{up})$,

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} \int _\Omega z_\varepsilon ^{p_k} + \int _\Omega z_\varepsilon ^{p_k} \le c_3 p_k^4 M_{k-1}^2 \qquad \hbox {for all } t\in (0,T) \end{aligned}$$

and that thus

$$\begin{aligned} K_m \le \max \bigg \{ \int _\Omega z_0^{p_k} \, , \, c_3 p_k^4 M_{k-1}^2 \bigg \} \qquad \hbox {for all }k\ge 1\hbox { and } \varepsilon \in (0,\varepsilon _\mathrm{up}). \end{aligned}$$

In much the same manner as detailed in Lemma 2.12, this can be seen to imply (3.16) with some suitably large $C(T)>0$. $\square$

In quite the same fashion as in Sect. 2, this can be seen to entail further estimates involving Hölder spaces.

Lemma 3.5

Suppose that (1.12) holds, and let $\varepsilon _\mathrm{up}>0$ be as in Lemma 3.1. Then, for all $\tau >0$ and any $T>\tau$, one can find $\theta (T)\in (0,1)$ and $C(T)>0$ as well as $\theta (\tau ,T)\in (0,1)$ and $C(\tau ,T)>0$ such that for the solutions of (3.1) obtained in Lemma 3.1, we have

$$\begin{aligned} \Vert z_\varepsilon \Vert _{C^{\theta (T),\frac{\theta (T)}{2}}(\overline{\Omega }\times [0,T])} +\Vert v_\varepsilon \Vert _{C^{\theta (T),\frac{\theta (T)}{2}}(\overline{\Omega }\times [0,T])} \le C(T) \qquad \hbox {for all } \varepsilon \in (0,\varepsilon _\mathrm{up}) \end{aligned}$$

(3.20)

and

$$\begin{aligned} \Vert z_\varepsilon \Vert _{C^{2{+}\theta (\tau {,}T){,}1{+}\frac{\theta (\tau {,}T)}{2}}(\overline{\Omega }\times [\tau {,}T])} {+} \Vert v_\varepsilon \Vert _{C^{2{+}\theta (\tau {,}T){,}1{+}\frac{\theta (\tau ,T)}{2}}(\overline{\Omega }\times [\tau {,}T])} \le C(\tau {,}T) \quad \hbox {for all } \varepsilon \in (0{,}\varepsilon _\mathrm{up}){.} \end{aligned}$$

(3.21)

Proof

These statements can be derived from Lemmas 3.1 and 3.4 along exactly the same lines as Lemmas 2.13 and 2.14 were deduced from Corollary 2.5 and Lemma 2.12. $\square$

Passing to the limit thereby becomes possible even throughout the entire positive half of the time axis.

Lemma 3.6

Suppose that (1.12) holds and that $\varepsilon _\mathrm{up}>0$ is as in Lemma 3.1. Then, the solutions of (3.1) from Lemma 3.1 have the property that

$$\begin{aligned} z_\varepsilon \rightarrow z \quad \hbox {in } C^0_{loc}(\overline{\Omega }\times [0,\infty )) \cap C^{2,1}(\overline{\Omega }\times (0,\infty )) \qquad \hbox {as } (0,\varepsilon _\mathrm{up}) \ni \varepsilon \searrow 0, \end{aligned}$$

(3.22)

where z denotes the unique solution in $C^0(\overline{\Omega }\times [0,\infty )) \cap C^{2,1}(\overline{\Omega }\times (0,\infty ))$ of (3.7).

Proof

Thanks to the Arzelà–Ascoli theorem, the estimates from Lemma 3.5 ensure that $(z_\varepsilon )_{\varepsilon \in (0,\varepsilon _\mathrm{up})}$ and $(v_\varepsilon )_{\varepsilon \in (0,\varepsilon _\mathrm{up})}$ are relatively compact in $X{:=}C^0_{loc}(\overline{\Omega }\times [0,\infty )) \cap C^{2,1}(\overline{\Omega }\times (0,\infty ))$. Since taking limits in (3.1) shows that any accumulation point (z, v) in $X\times X$ of $((z_{\varepsilon _j},v_{\varepsilon j}))_{j\in \mathbb {N}}$, with arbitrary sequences $(\varepsilon _j)_{j\in \mathbb {N}} \subset (0,\varepsilon _\mathrm{up})$ fulfilling $\varepsilon _j\searrow 0$ as $j\rightarrow \infty$, necessarily forms a classical solution of

$$\begin{aligned} \left\{ \begin{array}{llll} z_t &{}=&{}\quad z_{xx} + \kappa z_x, \qquad &{}\quad x\in \Omega , \ t>0, \\ v_t &{}=&{} v_{xx}-v_x, \qquad &{}\quad x\in \Omega , \ t>0, \\ z&{}=&{}0, \quad v_x=v, \qquad &{}\quad x\in \partial \Omega , \ t>0, \\ z(x,0)&{}=&{}z_0(x), \quad v(x,0)=v_0(x), \qquad &{}\quad x\in \Omega , \end{array} \right. \end{aligned}$$

(3.23)

and since another application of the maximum principle warrants uniqueness of classical solutions from $X\times X$ to these actually decoupled scalar transport–diffusion problems, this already implies the convergence property $(z_\varepsilon ,v_\varepsilon )\rightarrow (z,v)$ along the entire net $(0,\varepsilon _\mathrm{up})\ni \varepsilon \searrow 0$, with (z, v) solving (3.23). The claim of the lemma is an evident by-product thereof. $\square$

As a consequence, we infer that the behavior of solutions to (1.11) is essentially determined by that of solutions to (3.7) in the sense specified in our main statement on dominance of upstream migration:

proof of Theorem 1.2

Proceeding as in the proof of Theorem 1.1, for fixed $\delta >0$, we first invoke Lemmas 3.3 and 3.2 to pick $T(\delta )>0$ such that for the solution of the limit problem (3.7), abbreviating $\beta {:=}\frac{\kappa ^2}{4}+\frac{\pi ^2}{L^2}$ and taking $\alpha >0$ from (3.11), we have

$$\begin{aligned} \Big | e^{\beta t} e^{\frac{\kappa }{2}x} z(\cdot ,t) - \alpha \sin \frac{\pi x}{L} \Big | \le \frac{\delta }{2} \qquad \hbox {for all }x\in \overline{\Omega }\hbox { and } t \ge T(\delta ), \end{aligned}$$

which in particular entails that

$$\begin{aligned} \Big | e^{\beta t} z(x,t) - \alpha e^{-\frac{\kappa }{2}x} \sin \frac{\pi x}{L} \Big | \le \frac{\delta }{2} \qquad \hbox {for all }x\in \overline{\Omega }\hbox { and } t \ge T(\delta ). \end{aligned}$$

(3.24)

Then, letting $T>T(\delta )$ be given, we can thereafter rely on Lemma 3.6 in choosing $\varepsilon _0(\delta ,T)\in (0,\varepsilon _\mathrm{up})$ small enough such that

$$\begin{aligned} \Big | e^{\beta t} z_\varepsilon (x,t) - e^{\beta t} z(x,t) \Big | \le \frac{\delta }{2} \qquad \hbox {for all }x\in \overline{\Omega }\hbox { and } t \in [0,T], \end{aligned}$$

(3.25)

which when combined with (3.24) yields (1.13) with $\gamma {:=}\alpha$. $\square$

4 Numerical Investigations

We would like to carry out some numerical investigations that can illustrate the essence of Theorems 1.1 and 1.2. For that purpose we replace the model (1.5) by a discrete approximation. We refer to “Appendix A” for details.

For the parameters in (1.6), we set $\kappa =2=\lambda$. Then, we get $f(u)=u^2$, $h(u)=u\psi (u)=u(1-u)^2$ with $\psi (u)=(1-u)^2$, and $g(u)=\int ^u \frac{1}{h(s)}\,ds=-\log |{\frac{u-1}{u}}| + \frac{1}{1-u} + C$. The function g(u) is introduced to rewrite (1.5) in a form convenient for the discretization presented in “Appendix A.”

Fig. 4

Sparsely distributed cell population. The case with $\varepsilon =0.5$. Top: $T=0.1$. The solutions $w_\varepsilon$ and w (left figure) are close to each other but rather far from the steady state ${\overline{w}}$. Bottom: $T=0.5$. The solution w of the limit problem is close to the steady state ${\overline{w}}$; however, there is a certain discrepancy between $w_\varepsilon$ and the steady state ${\overline{w}}$, which is natural to be attributed to the relatively large $\varepsilon >0$

Fig. 5

Sparsely distributed cell population. The case with $\varepsilon =0.1$. Top: $T=0.1$. Bottom: $T=0.5$. We see that for this choice of $\varepsilon >0$, the discrepancy between $w_\varepsilon$ and the steady state ${\overline{w}}$ seen in Fig. 4 has essentially been eliminated

4.1 Case 1: Sparsely Distributed Cell Population

As initial data $w_0(x)$ and $v_0(x)$ to be used in (1.7), the following functions are specified

$$\begin{aligned} w_0(x) = \frac{1}{2}\exp (-\,200(x-1/2)^2), \qquad v_0(x) = 25\exp (-\,100(x-1/2)^2).\nonumber \\ \end{aligned}$$

(4.1)

We recall that the analytical steady-state solutions ${\overline{v}}(x)$ and ${\overline{w}}(x)$ of the limit problem (2.21) are found to be, see (2.37) and (2.52),

$$\begin{aligned}&{\overline{v}}(x)=\beta \exp (x), \quad {\overline{w}}(x)=\gamma \exp (\beta \exp (x)), \quad \beta =\frac{\int _0^1 v_0(x)\,\hbox {d}x}{\int _0^1 \exp (x)\,\hbox {d}x}, \nonumber \\&\quad \gamma =\frac{\int _0^1 w_0(x)\,\hbox {d}x}{\int _0^1 \exp (\beta \exp (x))\,\hbox {d}x}. \end{aligned}$$

(4.2)

We consider a numerical grid with $N=100$ grid cells on the spatial domain [0, 1]. We are interested in an illustration of the result of Theorem 1.1. We set $\varepsilon =0.5$. We compute numerical approximations of the solution $(u_{\varepsilon },v_{\varepsilon })$ of the initial boundary value problem (1.7) at a specified time T. We visualize $w_{\varepsilon }(x,T)=\varepsilon ^{-1}u_{\varepsilon }(x,T)$ and $v_{\varepsilon }(x,T)$, which naturally allow us to compare with numerical approximations to w(x, T) and v(x, T), i.e., the solution of the limit problem (2.21), as well as the analytically computed steady states ${\overline{w}}(x)$ and ${\overline{v}}(x)$. The results are shown in Fig. 4. Focusing on $w_{\varepsilon }$, the main observation is that for this choice of $\varepsilon$, there is a visible difference between $w_{\varepsilon }$ and the steady state ${\overline{w}}$ that remains. According to Theorem 1.1, this difference is controlled by $\varepsilon$. To test this, we reduce it by setting $\varepsilon =0.1$. The results are shown in Fig. 5 and clearly illustrate the essence of Theorem 1.1 as expressed by the precise estimate in (1.10): For a sufficiently small $\varepsilon >0$, we can ensure that the solution $w_\varepsilon =u_{\varepsilon }/\varepsilon$ is as close to the steady state ${\overline{w}}$ as we want, subject to the condition that t is sufficiently large.

4.2 Case 2: Densely Distributed Cell Population

We are interested in an illustration of the result of Theorem 1.2. For that purpose, we compute numerical approximations of the solution $(u_{\varepsilon },v_{\varepsilon })$ of the initial boundary value problem (1.11) at a specified time $T=0.1$, but now with initial data $u_{\varepsilon }(x,t=0)=1 - \varepsilon w_0$. First, we set $\varepsilon =0.5$, i.e., our initial data are close to 1 apart from a local region in the center of the domain. We compute the corresponding solution $u_{\varepsilon }$ by using the numerical scheme for (1.5) specified in “Appendix A” and then compute the corresponding $z_{\varepsilon }$ using the relation $u_{\varepsilon }=1-\varepsilon z_{\varepsilon }$. This allows us to compare $e^{\beta t} z_{\varepsilon }(x,T)$ and the steady-state expression $\alpha e^{-\frac{\kappa }{2}x}\sin {\pi x}$ where $\alpha$ is given by (3.11), $\beta =\frac{\kappa ^2}{4} + \pi ^2$, and we use that $L=1$. We want to show that we can control this discrepancy by the choice of $\varepsilon$, consistent with estimates (3.24) and (3.25). In Fig. 6, results are shown for $\varepsilon =0.5$ (left) and $\varepsilon =0.1$ (right). The numerical simulations indicate in accordance with Theorem 1.2 that by choosing $\varepsilon$ sufficiently small and time T sufficiently large, we ensure that the solution $u_{\varepsilon }$ is as close as we want to an analytical steady-state solution that is skewed in the upstream direction.

Fig. 6

Densely distributed cell population. $T=0.1$ The case with $\varepsilon =0.5$ (left) and $\varepsilon =0.1$ (right). We see that the discrepancy between $e^{\beta t}z_\varepsilon$ and the analytical steady state $\alpha e^{-\frac{\kappa }{2}x}\sin {\pi x}$ is controlled by $\varepsilon$

Appendix: A Discrete Scheme for the Model (1.5)

We may write model (1.5) in the following form:

$$\begin{aligned} \left\{ \begin{array}{lll} u_{t} + \Bigl (-f(u) + h(u)[v_x - \frac{1}{h(u)} u_{x}] \Bigr )_x &{}=&{}0, \\ v_{t} + v_{\varepsilon x} &{}=&{} v_{xx} + u(1-v). \end{array} \right. \end{aligned}$$

(4.3)

We introduce the notation $g(u)=\int _a^u \frac{1}{h(s)}\,\hbox {d}s$ for some constant a and write the first equation as

$$\begin{aligned} \begin{array}{lll} u_{t} + \Bigl (-\,f(u) + h(u)[v - g(u)]_x \Bigr )_x= & {} 0 \end{array} \end{aligned}$$

(4.4)

and the second as

$$\begin{aligned} \begin{array}{lll} v_{t} + \Bigl (v[1 - \ln (v)_x] \Bigr )_x= & {} u(1-v). \end{array} \end{aligned}$$

(4.5)

Based on (4.4) and (4.5), we consider a full discrete scheme where we have divided the spatial domain [0, L] into N grid cells of length $\Delta x$ such that $N\Delta x=L$ and with cell centers $x_j=(j-1/2)\Delta x$ for $j=1,\ldots ,N$ and cell interfaces $x_{j+1/2}=j\Delta x$ for $j=0,1,\ldots ,N$. The time period we consider is [0, T] with different time lines $t^n=n\Delta t$ where the number of time steps is M such that $M\Delta t=T$. The scheme which allows us to compute discrete approximations $\{u_{j}^n\}$ and $\{v_{j}^n\}$ takes the form

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{u_j^{n+1}-u_j^n}{\Delta t} + \frac{1}{\Delta x}(F_{j+1/2}^n -F_{j-1/2}^n) + \frac{1}{\Delta x}(G_{j+1/2}^{n} -G_{j-1/2}^{n}) &{}=&{} 0, \\ \frac{v_j^{n+1}-v_j^n}{\Delta t} + \frac{1}{\Delta x}(H_{j+1/2}^n - H_{j-1/2}^n) &{}=&{} u_j^{n}(1-v_j^{n}). \end{array} \right. \end{aligned}$$

(4.6)

with

$$\begin{aligned} \left\{ \begin{array}{lll} F_{j+1/2}^n &{}=&{} -f(u_{j+1}^n) \\ G_{j+1/2}^{n} &{}=&{} h_{j+1/2}^{n} \frac{1}{\Delta x}([v-g(u)]_{j+1}^{n} - [v-g(u)]_j^{n}) \\ H_{j+1/2}^n &{}=&{} v_{j+1/2}^n (1-D_+[\ln v]_j^n). \end{array} \right. \end{aligned}$$

(4.7)

where $D_+a_j=\frac{a_{j+1}-a_j}{\Delta x}$ and

$$\begin{aligned} h_{j+1/2}^{n}{:=} \left\{ \begin{array}{lll} u_j^{n}\psi (u_{j+1}^{n}) &{}\quad \hbox {when}&{} ([v-g(u)]_{j+1}^{n} - [v-g(u)]_j^{n} ) \ge 0 \\ u_{j+1}^{n}\psi (u_{j}^{n}) &{}\quad \hbox {when}&{} ([v-g(u)]_{j+1}^{n} - [v-g(u)]_j^{n}) < 0. \end{array} \right. \end{aligned}$$

(4.8)

and

$$\begin{aligned} v_{j+1/2}^{n}{:=} \left\{ \begin{array}{lll} v_j^n &{}\quad \hbox {when}&{} (1-D_+[\ln v]_j^n) \ge 0 \\ v_{j+1}^n &{}\quad \hbox {when}&{} (1-D_+[\ln v]_j^n) < 0. \end{array} \right. \end{aligned}$$

(4.9)

A similar discrete scheme can be defined for the limit problem (2.21) which allows us to compute discrete approximations $\{w_j^n\}$ and $\{v_j^n\}$.