Price of anarchy for parallel link networks with generalized mean objective

Abstract

The price of anarchy is the most well-known measure for quantifying the inefficiency of equilibrium flows in traffic networks and routing games. In this work, we give unifying price of anarchy bounds for atomic and non-atomic parallel link routing games with polynomial cost functions under various cost objectives including the arithmetic mean, geometric mean and worst-case cost objective. We do this through the study of the generalized p-mean as cost objective, and obtain upper bounds on the price of anarchy in terms of this parameter p. Our bounds unify existing results from the literature, and, in particular, give alternative proofs for price of anarchy results in parallel link routing games with polynomial cost functions under the geometric mean objective obtained by Vinci et al. (ACM Trans Econ Comput 10(2):41, 2022). We recover those simply as a limiting case. To the best of our knowledge, these are the first price of anarchy bounds that capture multiple cost objectives simultaneously in a closed-form expression.

1 Introduction

One of the fundamental problems at the intersection of transportation research and game theory is to quantify the inefficiency of equilibrium flows in traffic networks. Equilibrium flows, also known as Wardrop flows or Nash equilibria, arise as a result of autonomous users acting strategically to minimize their individual travel time. These flows often do not correpond to a system optimum, which is desired from a network designer’s point of view. Pigou (1920) was the first to (theoretically) demonstrate the possibility of inefficiency, and ever since, this topic has been of great interest to both researchers and practitioners in various areas, see, e.g., Dubey (1986), Roughgarden (2005), Braess et al. (2005).

Nowadays, the most well-known notion to quantify the inefficiency of equilibrium flows is the price of anarchy, introduced by Koutsoupias and Papadimitriou (1999, 2009). The price of anarchy has been studied extensively in the last 20 years in various routing models, both from a theoretical perspective, see, e.g., Roughgarden and Tardos (2002), Roughgarden (2003), Christodoulou and Koutsoupias (2005), Aland et al. (2011), Koutsoupias and Papadimitriou (1999), Caragiannis et al. (2011), Roughgarden (2015), as well as in practice, see, e.g., Monnot et al. (2017), Zhang et al. (2018), Benita et al. (2020). It is defined as the ratio between the quality of a (worst-case) equilibrium flow and a system optimum. The quality is measured with respect to a cost objective, such as the artithmetic mean (i.e. average) user cost, called the utilitarian objective, or the worst-case cost of any individual user, called the egalitarian objective. Recently, also the geometric mean of user costs has gained attention (Vinci et al. 2022). In the context of welfare maximization problems, the geometric mean of user costs is known as Nash social welfare (John 1950) in game theory and economics, where it has been studied extensively. However, much less is known about this objective in the context of cost minimization problems, which also was one of the motivations for studying this objective in Vinci et al. (2022). One appealing property of the geometric mean is that the price of anarchy is invariant with respect to rescaling the costs of individual users. This means users can measure their costs with respect to different units such as time or money.¹

The choice of cost objective, which is the topic of this work, plays an important role in how large the price of anarchy of equilibrium flows can be. For example, an equilibrium flow that might be considered “inefficient” under the utilitarian cost objective, can be efficient under the egalitarian objective as we will see in Example 1.1. The choice of cost objective is therefore also important for practitioners, who have to decide whether it is necessary to take measures to reduce the inefficiency, such as introducing road tolls.

Example 1.1 below can be seen as a discrete version of the well-known example of Pigou (1920) that first illustrated inefficieny in traffic networks. The atomic routing model used in Example 1.1 is formalized in Sect. 2. We study the three cost objectives mentioned above: the utilitarian, egalitarian and geometric mean objective.

Example 1.1

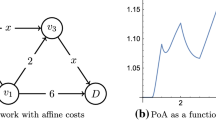
We consider an (atomic) routing game played on a parallel link network consisting of two links T and B, as illustrated in Fig. 1, that both are equipped with a cost (or latency) function $c_r(x)$ for $r \in \{T,B\}$. The game has two users, a and b, both represented by a unit of flow. Both have to choose one of the two links in the network over which they have to route their unsplittable unit of flow.

An assignment of users to links is called a strategy profile. For example, if both users choose link T, we have the strategy profile $s = (s_a,s_b) = (T,T)$. The cost $C_i(s)$ of player i in a strategy profile s is the cost incurred on the chosen links, which is $c_r(x_r)$ where $x_r$ is the the total amount of flow on link r. In the strategy profile $s = (T,T)$ this means both a and b have cost $C_a(s) = C_b(s) = c_T(2) = \frac{1}{2}\cdot 2 = 1$. A strategy profile is called a (pure) Nash equilibrium if no user can improve its cost by switching to the other link. The profile $s = (T,T)$ is then indeed a Nash equilibrium: If one of the users would deviate to link B, their new cost will equal one, which is the same as they have in the current profile s.

Fig. 1

Parallel link network consisting of two arcs

We next describe three possible cost objectives $C(\cdot )$ that can be used to quantify the inefficiency of the Nash equilibrium s. For all these objectives the profile $s^* = (s^*_a,s^*_b) = (T,B)$ minimizes the cost objective over all strategy profiles.

• Arithmetic mean cost (utilitarian objective): It holds that $C(s^*) = (C_a(s^*) + C_b(s^*))/2 = 0.75$. The Nash equilibrium $s = (2,2)$ has $C(s) = (1+1)/2 = 1$. This means the inefficiency of this Nash equilibrium is $C(s)/C(s^*) = 4/3$.

• Worst-case cost (egalitarian objective): It holds that $C(s^*) = \max \{C_a(s^*),C_b(s^*)\} = \max \{1,1/2\} =1$. The Nash equilibrium has $C(s) = \max \{1,1\} = 1$. This means that the inefficiency is $C(s)/C(s^*) = 1$.

• Geometric mean cost: It holds that $C(s^*) = \left( C_a(s^*)C_b(s^*)\right) ^{\frac{1}{2}} = (1\cdot 1/2)^{\frac{1}{2}} = 1/\sqrt{2}$. The Nash equilibrium has $C(s) = (1\cdot 1)^{\frac{1}{2}} = 1$. This means the inefficiency is $C(s)/C(s^*) = \sqrt{2}$.

As the above example illustrates, the choice of cost function indeed plays an important rule in how large the inefficiency of an equilibrium flow can be. In the case of the egalitarian objective, there is no inefficiency, whereas for the utilitarian and geometric mean objective, the inefficiency is roughly $33\%$ and $41\%$, respectively. These observations give rise to the following, somewhat informal, question:

Is it possible to quantify the price of anarchy for different cost objectives in one formula?

The main contribution of this work is that we answer the above question affirmatively for parallel link routing games with cost functions on the links being polynomials of degree at most d by considering the so-called generalized p-mean cost objective (defined in Sect. 1.1). We study both the atomic routing model of Rosenthal (1973) as well as the non-atomic routing model of Wardrop (1952). To the best of our knowledge, the results presented here are the first inefficiency results for routing games that capture multiple cost objectives such as the utilitarian, egalitarian and geometric mean objective at once. We remark that, although parallel link networks are the simplest type of traffic networks, they have been studied extensively in the areas of algorithmic game theory and operations research, see, e.g., Caragiannis (2008), Gairing et al. (2008), Vinci et al. (2022), Colini-Baldeschi et al. (2019), Bonifaci et al. (2011), Harks et al. (2019). Adding to their significance, they can also naturally be interpreted as scheduling, or load balancing, problems where the links play the roles of machines and users control jobs that have to be scheduled. See, e.g., Caragiannis (2008) and references therein.

In the utilitarian case, it is well-known that the price of anarchy typically can be characterized by the type of cost functions the links of the traffic network are allowed to have (e.g., polynomials of degree at most $d = 1,2,3,\dots$). This was first established in the seminal work of Roughgarden (2003); see also his smoothness framework (Roughgarden 2015) and Sect. 1.3 for more related work. Polynomial cost functions also have practical relevance, e.g., the cost functions proposed by the Bureau of Public Roads (States 1964) for modelling congestion in road networks are polynomials of degree $d = 4$.

1.1 Our contributions

Parallel link routing games² consist of a set $R = \{1,\dots ,m\}$ of parallel links between an origin O and destination D, and a set of users $N = \{1,\dots ,n\}$. Every user $i \in N$ has a subset of links ${\mathcal {S}}_i \subseteq R$, called its strategy set, that they are allowed to use. Every link is equipped with a nonnegative, nondecreasing cost function $c_r: {\mathbb {R}}_{\ge 0} \rightarrow {\mathbb {R}}_{\ge 0}$. The cost $C_i(s)$ of a player in strategy profile $s \in \times _i {\mathcal {S}}_i$ is the cost incurred on the chosen link. To get a general framework capturing all the different cost objectives, we consider the so-called generalized p-mean objective

$$\begin{aligned} C^p_w(s) = \displaystyle \left( \frac{1}{\sum _{i \in N} w_i}\sum _{i \in N} w_i\cdot C_i(s)^p\right) ^{\frac{1}{p}} \end{aligned}$$

(1.1)

for $p \in (0,\infty )$, where $w = (w_1,\dots ,w_n)$ is indicating for every $i \in N$ the amount of (unsplittable) flow $w_i$ that user i has to route over one of its links. If $w_i = 1$ for all $i \in N$, the game is called unweighted. Furthermore, we have

$$\begin{aligned} C^0_w(s) := \lim _{p \rightarrow 0} C^p_w(s) = \left( \prod _{i \in N} C_i(s)^{w_i}\right) ^{1/\sum _{i \in N} w_i} \ \text { and } \ C^\infty _w(s) := \lim _{p \rightarrow \infty } C^p_w(s) = \max _{i \in N} C_i(s). \end{aligned}$$

(1.2)

The generalized p-mean indeed captures the utilitarian objective $(p = 1)$, egalitarian objective $(p = \infty )$ and geometric mean objectives ($p = 0$) as special cases, as well as p-norm objectives for $p \ge 1$.

We next summarize our results for parallel link routing games with cost functions being polynomials of degree at most $d \in {\mathbb {N}}$. We emphasize that we obtain a price of anarchy bound for all values of $p \in [0,\infty ]$, which allows us to also go beyond the utilitarian, egalitarian and geometric mean cost objectives. A comparison with existing work, that we capture as special cases, is given in Table 1. We consider both the atomic model of Rosenthal (1973) and the non-atomic model of Wardrop (1952), whose difference, roughly speaking, lies in whether it is assumed that the $w_i$ are positive constants, or whether there is a continuum of players all controlling an infinitesimally small amount of flow (i.e., $w_i \rightarrow 0$). For all models, we first obtain a bound for $p \in (0,\infty )$, after which we obtain price of anarchy bounds for $p \in \{0,\infty \}$ simply as limiting cases, using the expressions in (1.2). In particular, for $p = 0$, this yields an alternative derivation of the price of anarchy results of Vinci et al. (2022) for games with polynomial cost functions and geometric mean objective, which is our main technical contribution.

• Non-atomic model: This is the model with a continuum of users that all control an infinitesimally small fraction of flow.³ We show in Theorem 3.2 that, for $p \in (0,\infty )$, the price of anarchy is upper bounded by

  $$\begin{aligned} \left( 1 - \frac{d p}{(d p+1)^{(d p+1)/(d p)}}\right) ^{-\frac{1}{p}}. \end{aligned}$$

  (1.3)

  As limiting cases we get that for $p = 0$ the price of anarchy is upper bounded by $(e^{1/e})^d$, and for $p = \infty$ by 1. These bounds also hold for atomic symmetric unweighted parallel link routing games, as explained in Remark 3.5. For an illustration of the obtained bounds in this case, see Fig. 2.

• Weighted atomic model: This is the general model as described above where user $i \in N$ has to route $w_i$ units of (unsplittable) flow over one of its links. We show in Theorem 3.6 that, for $p \in (0,\infty )$, the price of anarchy is upper bounded by

  $$\begin{aligned} (\Phi _{pd} + 1)^d, \end{aligned}$$

  (1.4)

  where $\Phi _{pd}$ is the unique nonnegative solution to $(x+1)^{pd} = x^{pd+1}$. As limiting cases, we obtain that for $p = 0$ the price of anarchy can be upper bounded by $2^d$, but it might be unbounded for $p \rightarrow \infty$.

• Unweighted atomic model: This is the above model with $w_i = 1$ for all $i \in N$. We show in Theorem 3.9 that, for $p \in (0,\infty )$, the price of anarchy is upper bounded by

  $$\begin{aligned} \left( \frac{(k+1)^{2pd+1} - k^{pd+1}(k+2)^{pd}}{(k+1)^{pd+1} - (k+2)^{pd} + (k+1)^{pd} - k^{pd+1}}\right) ^{\frac{1}{p}}, \end{aligned}$$

  (1.5)

  where $k = \lfloor \Phi _{pd} \rfloor$ and $\Phi _{pd}$ is again the unique nonnegative solution to $(x+1)^{pd} = x^{pd+1}$. Again, as limiting cases, we obtain that for $p = 0$ the price of anarchy can be upper bounded by $2^d$, but it might be unbounded for $p \rightarrow \infty$.

Fig. 2

Price of anarchy bounds under the generalized p-mean objective for non-atomic parallel link routing games for $d=1,2,3$ (bottom, middle and top function, respectively)

The bounds we obtain in (1.3)–(1.5) resemble those for the case $p = 1$ in Table 1. This follows from the fact that we derive our bounds by appropriately adjusting the proof techniques for the respective setting with $p = 1$. We do this by showing, roughly speaking, that it suffices to study the utilitarian objective in the game where the cost functions $c_r(x)$ are replaced by $c_r(x)^p$, i.e., the function $c_r$ raised to the power p. For the non-atomic case, this can be done by using the results of Correa et al. (2004), but for the atomic cases this requires non-trivial adjustments of the proofs by Aland et al. (2011). One of the technical tools we use for this is Descartes’ rule of signs (see Appendix 3), which allows one to say something about the number of nonnegative roots of a polynomial.

It is interesting to note that the bounds obtained by Vinci et al. (2022) for the geometric mean objective have a much easier form than their counterparts for the arithmetic mean cost objective. This also motivates the study of the price of anarchy of the geometric mean objective in other classes of (routing) games.

Table 1 Overview of special cases of the upper bounds in (1.3)–(1.5) for the price of anarchy in parallel link routing games for the geometric mean, utilitarian and egalitarian objectives

1.2 Discussion and lower bounds

It is interesting to note that there is a clear contrast in how the obtained price of anarchy bounds behave when comparing the non-atomic and atomic routing models. Whereas for the non-atomic model, the price of anarchy is a decreasing function of p (see Fig. 2), it is increasing for both the unweighted and weighted atomic model. This also shows that not only the choice of cost objective plays a large role, but also the underlying model being considered.

Studying the generalized p-mean objective on more general networks is a very interesting direction for future research. One of the technical issues that arises is that the reduction sketched at the end of Sect. 1.1 breaks down beyond parallel link networks, and various nonlinearity issues arise. In fact, Vinci et al. (2022) show that there exists a congestion game⁴ with affine cost functions where the inefficiency of a pure Nash equilibrium under the geometric mean objective can grow with the number of players of the game, which stands in stark contrast to the utilitarian setting, for which the price of anarchy is known to be at most 5/2 (Christodoulou and Koutsoupias 2005) in congestion games with affine cost functions.

Lower bounds. We note that the bounds we obtain in (1.3)–(1.5), and the special cases in Table 1, are known to be tight for various values of p and d. The non-atomic bound for $p \in (0,\infty )$ in Theorem 3.2 can be shown to be tight by using a similar construction as Correa et al. (2004) for polynomials of degree d (see Appendix 4). For the case $p = 0$, tightness is shown in Vinci et al. (2022).

For (symmetric) weighted atomic parallel link games, tightness for $p = 1$ is shown in Bhawalkar et al. (2014) for any d. A more general lower bound, using only mild assumptions on the cost functions, is provided in Bilò and Vinci (2017). Similar constructions and reasonings as in Bhawalkar et al. (2014), Bilò and Vinci (2017) seem to be able to give a tight lower bound for an arbitrary p. Indeed, Bilò and Vinci (2017, Theorem 1) should yield tightness of the bound in (1.4) for symmetric weighted atomic parallel link games; we leave the details of this to the interested reader.⁵ Tightness for $p = 0$ is shown in Vinci et al. (2022).

For unweighted atomic parallel link games, with $p = \infty$, Gairing et al. (2008) show that the price of anarchy grows with the number of players (or links) already in games with affine cost functions ($d=1$), which leads to a best possible upper bound of $\infty$ in case the price of anarchy is parameterized by the cost functions of the links. This explains the “$\infty$” price of anarchy bounds for $p = \infty$ in Table 1. Tightness of the bound in (1.5) for the case $d = 1$ and $p = 1$ is shown in Caragiannis et al. (2011), and for every d in the case of general network routing games, where the topology does not have to be a set of parallel links, still with $p = 1$, in Aland et al. (2011). The lower bound in Caragiannis et al. (2011) is generalized in Gairing and Schoppmann (2007) to arbitrary polynomical cost functions of degree at most d. Similary as for weighted games, using (Bilò and Vinci 2017, Theorem 3) this time, it should be possible to show that the bound in (1.5) is tight.

1.3 Further related work

The price of anarchy in general (network) routing and congestion games has been studied extensively in both the non-atomic and atomic setting. In one of the seminal works on the price of anarchy for routing games, Roughgarden and Tardos (2002) showed that the price of anarchy for affine cost functions equals 4/3 in the non-atomic case. Tight bounds for general classes of cost functions, including polynomial cost functions, were obtained by Roughgarden (2003) and Correa et al. (2004). In the atomic unweighted setting, Christodoulou and Koutsoupias (2005) first showed a bound of 5/2 for games with affine cost functions. Tight bounds for polynomial cost functions, both in the unweighted and weighted setting, were obtained by Aland et al. (2011). These results, applied to the special case of parallel link networks, are captured by our formulas in (1.3)–(1.5). Further works considering congestion games with polynomial cost functions are, e.g., Gairing et al. (2006), Gairing and Schoppmann (2007), Christodoulou et al. (2011), Bhawalkar et al. (2014), Bilò and Vinci (2017), Bilò and Vinci (2019).

Various extensions and variations on the classical models of Rosenthal (1973) and Wardrop (1952) have been proposed in the literature, which, from a technical perspective, can often be seen as quantifying the price of anarchy along one or more parameters induced by the extended setting of interest (similar to what we do in this work by means of the parameter p). Such models are used to capture, e.g., altruistic behavior (Chen et al. 2014; Schröder 2020), risk-aversion (Fotakis et al. 2015), tolls (or taxes) (Caragiannis et al. 2010; Bonifaci et al. 2011) or uncertainty (Piliouras et al. 2016; Cominetti et al. 2019). A unifying framework of such models in the case of affine cost functions can be found in Kleer and Schäfer (2019b), where the (utilitarian) cost objective, as well as the individual user costs, contain a parameter along which the price of anarchy is studied. There is also a line of work quantifying the impact on the quality of equilibrium flows, as a result of perturbation or uncertainties in the input of the game, where instead of comparing to an optimal flow, one instead compares the new (perturbed) equilibrium flow to the original (unperturbed) equilibrium flow. This leads to new inefficiency notions such as (in chronological order of introduction) the price of risk aversion (Nikolova and Stier-Moses 2014; Lianeas et al. 2019), the deviation ratio (Kleer and Schäfer 2017, 2019a) or the price of satisficing (Takalloo and Kwon 2020). Inefficiency results for such notions are typically also parameterized by an input parameter.

Another fundamental inefficiency notion that has been studied extensively is the price of stability (Anshelevich et al. 2008) that compares the best possible social cost of a Nash equilibrium with that of a social optimum, i.e., the minimal “price” a system designer has to pay in order to get a system which is stable from the players’ perspective. Further references here are, e.g., Christodoulou and Gairing (2015), Christodoulou et al. (2019), Kleer and Schäfer (2021).

1.4 Outline

We continue in Sect. 2 with a formal description of the routing models we consider in this work. After that, we prove our upper bounds on the price of anarchy under the generalized p-mean objective in Sect. 3. We conclude in Sect. 4.

2 Routing models

In this section we describe the routing models studied in this work together with the price of anarchy under the generalized p-mean objective.

2.1 Atomic parallel link routing game

A weighted atomic parallel link routing game $\Gamma = (N,R,(w_i)_{i \in N},(C_i)_{i \in N})$ is given by a set of users $N = \{1,\dots ,n\}$ and a set of parallel (directed) links $R = \{r_1,\dots ,r_m\}$ between an origin O and destination D (as in Fig. 1). Every user i has a strategy set ${\mathcal {S}}_i\subseteq R$ of links it is allowed to use, and a weight $w_i \ge 0$. In case ${\mathcal {S}}_i= R$ for every $i \in N$, the game is called symmetric.⁶ Every link $r \in R$ is equipped with a cost function $c_r : {\mathbb {R}}_{\ge 0} \rightarrow {\mathbb {R}}_{\ge 0}$ that is assumed to be non-decreasing (and non-negative by definition). User i places its (unpslittable) flow $w_i$ on one of its links $r \in {\mathcal {S}}_i$. That is, if in strategy profile s user i chooses link $s_i$, we write

$$\begin{aligned} x^i_j(s) = \left\{ \begin{array}{ll} w_i &{} \quad \text { if } j = s_i\\ 0 &{} \quad \text { otherwise.} \end{array} \right. \end{aligned}$$

The (total) flow on link $r \in R$ is defined as $x_r(s) = \sum _{i \in N} x^i_r(s)$. For convenience, we sometimes write $x_r$ instead of $x_r(s)$ if it’s clear what strategy profile we are considering. The cost of user i on its chosen link $s_i$ is given by

$$\begin{aligned} C_i(s) = c_{s_i}(x_{s_i}). \end{aligned}$$

⁷

Note that all users placing their weight on the same link, have the same cost.

We write $s_{-i} = (s_1,\dots ,s_{i-1},s_{i+1},\dots ,s_n)$ for the strategy profile in which $s_i$ is left out. Slightly abusing notation, we then write $(s_i',s_{-i}) =(s_1,\dots ,s_{i-1},s_i',s_{i+1},\dots ,s_n)$. A strategy profile $s \in \times _i {\mathcal {S}}_i$ is called pure Nash equilibrium if

$$\begin{aligned} C_i(s) \le C_i(s_i',s_{-i}) \end{aligned}$$

(2.1)

for all $i \in N$ and unilateral deviations $s_i' \in {\mathcal {S}}_i$. We write $\text {PNE}(\Gamma )$ for the set of all pure Nash equilibria of the game $\Gamma$.

We define the p-price of anarchy (p-PoA) as

$$\begin{aligned} p\text {-PoA}(\Gamma ) = \frac{\max _{s \in \text {PNE}(\Gamma )} C^p_w(s)}{\min _{t \in \times _i {\mathcal {S}}_i} C^p_w(t)} \end{aligned}$$

(2.2)

with $C^p_w(s)$ as in (1.1) for $p \in (0,\infty )$ or (1.2) for $p \in \{0,\infty \}$. It is important to note that the set $\text {PNE}(\Gamma )$ is the same for every value of $p \in [0,\infty ]$, as the inequality in (2.1) does not depend on p. A strategy minimizing the cost objective $C^p_w$ is called a socially optimal strategy profile (or system optimum). We next argue that in order to study the p-PoA, it suffices to study the utilitarian case in the game where the cost functions are raised to the power p.

For $p \in (0,\infty )$, in order to derive an upper bound of $\alpha \ge 1$ on the p-PoA, it suffices to show

$$\begin{aligned} C^p_w(s) \le \alpha \cdot C^p_w(s^*) \end{aligned}$$

where $s = (s_1,\dots ,s_n)$ is any pure Nash equilibrium and $s^* = (s_1^*,\dots ,s_n^*)$ a socially optimal strategy profile. This is equivalent to showing

$$\begin{aligned} \sum _{i \in N} w_i\cdot C_i(s)^p \le \alpha ^p \sum _{i \in N} w_i\cdot C_i(s^*)^p. \end{aligned}$$

(2.3)

As every user chooses one link, this reduces to

$$\begin{aligned} \sum _{i \in N} w_i \cdot c_{s_i}(x_{s_i})^p \le \alpha ^p \sum _{i \in N} w_i\cdot c_{s_i^*}(x_{s_i^*})^p \end{aligned}$$

(2.4)

Note that for any strategy profile $t = (t_1,\dots ,t_n)$, we may write the cost objective as an aggregation over link contributions,⁸ i.e.,

$$\begin{aligned} \sum _{i \in N} w_i\cdot c_{t_i}(x_{t_i})^p = \sum _{r \in R} x_r(t)c_r(x_r(t))^p, \end{aligned}$$

and so (2.3) is equivalent to showing

$$\begin{aligned} \sum _{r \in R} x_r(s)c_r(x_r(s))^p \le \alpha ^p \sum _{r \in R} x_r(s^*)c_r(x_r(s^*))^p. \end{aligned}$$

(2.5)

Moreover, for $p \in (0,\infty )$ it holds that (2.1) is true if and only if

$$\begin{aligned} c_{s_i}(x_{s_i})^p \le c_{t}(x_{t} + w_i)^p, \end{aligned}$$

(2.6)

for every $i \in N$ and $t \in {\mathcal {S}}_i$, as the mapping $x \mapsto x^p$ is increasing in $x \ge 0$ whenever $p > 0$. This means that in order to bound the p-price of anarchy, it suffices to study the utilitarian case for the game $\Gamma ^p$ in which for every $r \in R$, the cost function $c_r$ is replaced by $c_{r}^p$ defined by $c_{r}^p(x) = c_r(x)^p$ for all $x \ge 0$. In particular, the above discussion implies that for atomic parallel link routing games

$$\begin{aligned} p\text {-PoA}(\Gamma ) = \Big ( 1\text {-PoA}(\Gamma ^p)\Big )^{\frac{1}{p}}. \end{aligned}$$

(2.7)

A simple argument shows that upper bounds on the p-PoA for $p \in \{0,\infty \}$ can be obtained as limits of upper bounds on the p-PoA for $p \in (0,\infty )$. We will sketch this argument for $p = 0$. Let f(p) be an upper bound on $p\text {-PoA}(\Gamma )$. Let $s \in \text {PNE}(\Gamma )$ and $s^*$ be a worst-case Nash equilibrium and social optimum, respectively, with respect to $C_w^0(\cdot )$. Note that s is a Nash equilibrium, independent of the value of p, and that $C_w^p(s')$ is a continuous function w.r.t. p for any fixed strategy profile $s'$. This means that

$$\begin{aligned} 0\text {-PoA}(\Gamma ) = \frac{C_w^0(s)}{C_w^0(s^*)} = \lim _{p \rightarrow 0} \frac{C_w^p(s)}{C_w^p(s^*)} \le \lim _{p \rightarrow 0} p\text {-PoA}(\Gamma ) \le \lim _{p \rightarrow 0} f(p). \end{aligned}$$

(2.8)

The first inequality follows from the fact that $C^p_w(s)$ can always be upper bounded by $C^p_w(s(p))$, where s(p) is a worst-case Nash equilibrium w.r.t $C^p_w$ for a given p, and $C_w^p(s^*)$ can be lower bounded by $C_w^p(s^*(p))$ where $s^*(p)$ is a social optimum w.r.t $C^p_w$ for a given p. The same argument works for $p = \infty$.

2.2 Non-atomic parallel link routing game

In a non-atomic parallel link routing game there is a continuum of users that all control an infinitely small amount of flow that has to be assigned to one of the links in their strategy set. More formally, a non-atomic parallel link routing game $\Gamma = (R,(d_j)_{j \in [k]}, ({\mathcal {S}}_j)_{j \in [k]},(c_r)_{r \in R})$ is given by a set of links R and a number of commodities $[k] = \{1,\dots ,k\}$ where a commodity has demand $d_j > 0$ for $j \in [k]$ and strategy set ${\mathcal {S}}_j \subseteq R$. Every link is equipped with a cost function $c_r : {\mathbb {R}}_{\ge 0} \rightarrow {\mathbb {R}}_{\ge 0}$. A feasible flow for commodity j is a mapping $f^j : R \rightarrow {\mathbb {R}}_{\ge 0}$, where we write $f^j(r) = f^j_r$, such that $\sum _{r \in R} f^j_r = d_j$. A feasible flow for the non-atomic parallel link routing game is defined by the tuple $f = (f^1,\dots ,f^k)$. The aggregation of the feasible flows $f^1,\dots ,f^k$ for the individual commodities is defined by $f_r = f(r) = \sum _{j \in [k]} f^j_r$ for $r \in R$.

A feasible flow f is a Wardrop flow if for every $j \in [k]$ and $r \in {\mathcal {S}}_j$ with $f_r^j > 0$

$$\begin{aligned} c_r(f_r) \le c_t(f_t) \end{aligned}$$

(2.9)

for all $t \in {\mathcal {S}}_j$. The cost objective $C^p(f)$, the natural equivalent of the expressions in (2.10), is given by

$$\begin{aligned} C^p(f) = \left\{ \begin{array}{ll} \displaystyle \left( \sum _{i \in N} f_r\cdot \ell _r(f_r)^p\right) ^{\frac{1}{p}} &{} \quad \text { if } p \in (0,\infty )\\ \displaystyle \prod _{i \in N} \ell _r(f_r)^{f_r} &{} \quad \text { if } p = 0\\ \displaystyle \max _{i \in N} \ell _r(f_r) &{} \quad \text { if } p = \infty \end{array} \right. \end{aligned}$$

(2.10)

Similarly as for the atomic case, one may argue that in order to study the p-PoA for $p \in (0,\infty )$ it suffices to study the utilitarian case in the game $\Gamma$ where all the cost functions $c_r$ are replaced by $c_r^p$ (and the cases $p \in \{0,\infty \}$ can be studied by taking limits). That is, we have

$$\begin{aligned} p\text {-PoA}(\Gamma ) = \Big ( 1\text {-PoA}(\Gamma ^p)\Big )^{\frac{1}{p}}. \end{aligned}$$

(2.11)

2.3 Polynomial cost functions

In this work we will mostly be concerned with polynomial cost functions $c_r$ of maximum degree $d \in {\mathbb {N}}$, i.e.,

$$\begin{aligned} c_r(x) = \sum _{j=0}^d a_{j,r} x^j \end{aligned}$$

where $a_{j,r} \ge 0$ for all $j = 0,\dots ,d$. We write ${\mathcal {P}}_d$ for the collection of all polynomials of degree at most d. We emphasize that, in general, $c_r^p$ is not a polynomial function for $p > 0$.

3 Price of anarchy bounds

In this section we give all our unifying price of anarchy upper bounds. In Sects. 3.2 and 3.3, we rely on modified versions of lemmas from Aland et al. (2011). These are given in Appendix 2.

3.1 Non-atomic case

It is well-known that in non-atomic parallel link routing games (and more general non-atomic congestion games), the price of anarchy can be upper bounded by a so-called smoothness parameter defined based on the cost functions of the game. Let ${\mathcal {D}}$ be a class of continuous, non-decreasing cost functions. Define

$$\begin{aligned} \rho ({\mathcal {D}}) := (1 - \beta ({\mathcal {D}}))^{-1}, \quad \text {where}\quad \beta ({\mathcal {D}}) = \sup _{d \in {\mathcal {D}}} \sup _{x,y \in {\mathbb {R}}: x \ge y > 0} \frac{y(d(x) - d(y))}{xd(x)}. \end{aligned}$$

(3.1)

Theorem 3.1

(Roughgarden 2003; Correa et al. 2004) Let $\Gamma$ be a non-atomic parallel link routing game with cost functions from class ${\mathcal {D}}$. Then $1\text {-PoA}(\Gamma ) \le \rho ({\mathcal {D}}).$

The value of $\rho ({\mathcal {D}})$ is well-understood for many important classes of functions. Relevant to us is the class

$$\begin{aligned} {\mathcal {D}}_k = \{g: {\mathbb {R}}_{\ge 0} \rightarrow {\mathbb {R}}_{\ge 0} \, : \, g(\mu x) \ge \mu ^k g(x)\ \forall \mu \in [0,1]\} \end{aligned}$$

for given $k \in {\mathbb {R}}_{\ge 0}$. In Correa et al. (2004), it is shown that

$$\begin{aligned} \beta ({\mathcal {D}}_k) \le \frac{k}{(k+1)^{(k+1)/k}} \end{aligned}$$

and thus

$$\begin{aligned} \rho ({\mathcal {D}}_k) \le \left( 1 - \frac{k}{(k+1)^{(k+1)/k}}\right) ^{-1}. \end{aligned}$$

An obvious fact is that for $p \in (0,\infty )$

$$\begin{aligned} c_r \in {\mathcal {D}}_k \Rightarrow c_r^p \in {\mathcal {D}}_{k \cdot p}. \end{aligned}$$

(3.2)

This readily implies the following result based on (2.11).

Theorem 3.2

Let $\Gamma$ be a non-atomic parallel link routing game whose cost functions are polynomials of degree at most d for some $d \in {\mathbb {N}}$. Then for $p \in (0,\infty )$, we have

$$\begin{aligned} p\text {-PoA}(\Gamma ) \le \left( 1 - \frac{d p}{(d p+1)^{(d p+1)/(d p)}}\right) ^{-\frac{1}{p}}. \end{aligned}$$

(3.3)

An example illustrating tightness of the bound in (3.3) is given in Appendix 4. As a direct corollary, we obtain an alternative proof of the price of anarchy bound for the geometric mean objective of Vinci et al. (2022).

Corollary 3.3

(Vinci et al. 2022) Let $\Gamma$ be a non-atomic parallel link routing game whose cost functions are polynomials of degree at most d for some $d \in {\mathbb {N}}$. The price of anarchy for the geometric mean objective satisfies

$$\begin{aligned} 0\text {-PoA}(\Gamma ) \le \left( e^{\frac{1}{e}}\right) ^d \approx 1.44^d. \end{aligned}$$

Proof

Take the limit $p \rightarrow 0$ in the right hand side of (3.3). An explanation of the calculation of this limit is deferred to Proposition 5.1 in Appendix 1. $\square$

Corollary 3.4

Let $\Gamma$ be a non-atomic parallel link routing game whose cost functions are polynomials of degree at most d for some $d \in {\mathbb {N}}$. The price of anarchy for the egalitarian cost objective satisfies

$$\begin{aligned} \infty \text {-PoA}(\Gamma ) = 1. \end{aligned}$$

Proof

Take the limit $p \rightarrow \infty$ in the right hand side of (3.3). An explanation of the calculation of this limit is deferred to Proposition 5.1 in Appendix 1. $\square$

Remark 3.5

(Symmetric unweighted atomic parallel link routing games) Fotakis (2010) showed that for symmetric unweighted atomic parallel link routing games with utilitarian cost objective, the price of anarchy can also be upper bounded by the smoothness parameter $\rho ({\mathcal {D}})$. This implies that the results in Theorem 3.2, Corollary 3.3 and Corollary 3.4 also hold for symmetric unweighted atomic parallel link routing games $\Gamma$.

3.2 Weighted atomic case

In order to upper bound the price of anarchy for weighted atomic parallel link routing games, we follow the ideas of Aland et al. (2011) who study (un)weighted atomic congestion games under the utalitarian cost objective. We generalize their bounds, obtained by setting $p = 1$, for the case of parallel link routing games. The main result is as follows.

Theorem 3.6

Let $\Gamma$ be a atomic weighted parallel link routing game whose cost functions are polynomials of degree at most $d \in {\mathbb {N}}$, and let $p \in (0,\infty )$. Let $\Phi _{pd}$ be the unique non-negative solution to $(x+1)^{pd} = x^{pd+1}$. Then

$$\begin{aligned} p\text {-PoA}(\Gamma ) \le \left( \Phi _{pd}^{pd+1}\right) ^{\frac{1}{p}} = (\Phi _{pd} + 1)^d. \end{aligned}$$

(3.4)

As a limiting case, we obtain an alternative proof of the result of Vinci et al. (2022) for the geometric mean objective.

Corollary 3.7

(Vinci et al. 2022) Let $\Gamma$ be a weighted atomic parallel link routing game whose cost functions are polynomials of degree at most d for some $d \in {\mathbb {N}}$. The price of anarchy for the geometric mean objective satisfies

$$\begin{aligned} 0\text {-PoA}(\Gamma ) \le 2^d. \end{aligned}$$

Proof

Rewriting the definition of $\Phi _{pd}$, we have

$$\begin{aligned} \left( 1 + \frac{1}{\Phi _{pd}}\right) ^{pd} = \Phi _{pd}. \end{aligned}$$

From this it follows directly that $\Phi _{pd} \ge 1$ for all $pd \in {\mathbb {R}}_{>0}$, and then also

$$\begin{aligned} \lim _{p \rightarrow 0} \Phi _{pd} = 1 \end{aligned}$$

(3.5)

since $1 \le 1 + 1/\Phi _{pd} \le 2$. Now, by definition of $\Phi _{pd}$ it holds that $\Phi _{pd}^{pd+1} = (\Phi _{pd} + 1)^{pd}$. We then have

$$\begin{aligned} \lim _{p \rightarrow 0} \left( \Phi _{pd}^{pd+1}\right) ^{\frac{1}{p}} = \lim _{p \rightarrow 0} \left( (\Phi _{pd} + 1)^{pd}\right) ^{\frac{1}{p}} = \lim _{p \rightarrow 0} (\Phi _{pd} + 1)^{d} = 2^d \end{aligned}$$

where we use (3.5) in the last step (and the fact that $y \mapsto y^d$ is a continuous function). $\square$

We continue with the proof of Theorem 3.6.

Proof of Theorem 3.6

We start with a technical lemma to simplify the analysis. It essentially states (as will follow from the arguments that we give later) that it suffices to focus on cost functions of the form $c_r(x) = x^d$ in the main technical argument needed to prove (3.4). The proof of Lemma 3.8 uses Descartes’ rule of signs (see Appendix 3), which is of independent interest. $\square$

Lemma 3.8

Let $d \in {\mathbb {N}}$, $p \in (0,\infty )$, and $(\lambda ,\mu ) \in {\mathbb {R}}_{\ge 0} \times (0,1)$ be a given pair. Then

$$\begin{aligned} y\cdot (x + y)^{pd} \le \lambda \cdot y^{pd+1} + \mu \cdot x^{pd+1} \end{aligned}$$

(3.6)

for all $x,y \in {\mathbb {R}}_{\ge 0}$ if and only if for all $\ell \in {\mathcal {P}}_d$

$$\begin{aligned} y\cdot [\ell (x+y)]^p \le \lambda \cdot y \cdot [\ell (y)]^p + \mu \cdot x \cdot [\ell (x)]^p \end{aligned}$$

(3.7)

for all $x,y \in {\mathbb {R}}_{\ge 0}$.

Proof

First note that if (3.7) holds for all $\ell \in {\mathcal {P}}_d$, then (3.6) certainly also holds, by taking $\ell (x) = x^d$. We continue with the other, more involved, implication.

The statement is clearly true when $y = 0$, so assume $y > 0$. We write

$$\begin{aligned} \ell (z) = \sum _{j=0}^d a_j z^j \end{aligned}$$

where $a_0,\dots ,a_d \ge 0$. Let $h := \max \{x,y\} > 0$ and set ${\tilde{\ell }}(z) = {\tilde{a}} \cdot z^d$ where

$$\begin{aligned} {\tilde{a}} = \frac{1}{h^d}\sum _{j=0}^d a_j h^j, \end{aligned}$$

i.e., ${\tilde{a}}$ is chosen so that $\ell (h) = {\tilde{\ell }}(h)$. The polynomial

$$\begin{aligned} g(z) = \ell (z) - {\tilde{\ell }}(z) = (a_d - {\tilde{a}})x^d + \sum _{j=0}^{d-1} a_j z^j \end{aligned}$$

has non-negative coefficients, except for $a_d - {\tilde{a}}$. Descartes’ rule of signs (see Appendix 3) implies that g has at most one positive root (which is h). As ${\tilde{\ell }}(0) \le \ell (0)$, it follows that

$$\begin{aligned} \left\{ \begin{array}{ll} {\tilde{\ell }}(z) \ge \ell (z) &{} \quad \text { for } z \ge h\\ {\tilde{\ell }}(z) \le \ell (z) &{} \quad \text { for } 0 \le z \le h \end{array}\right. \end{aligned}$$

and then also

$$\begin{aligned} \left\{ \begin{array}{ll} {\tilde{\ell }}(z)^p \ge \ell (z)^p &{} \quad \text { for } z \ge h\\ {\tilde{\ell }}(z)^p \le \ell (z)^p &{} \quad \text { for } 0 \le z \le h \end{array}\right. \end{aligned}$$

(3.8)

as for $p \in (0,\infty )$ the mapping $z \mapsto z^p$ is an increasing function for $z \ge 0$. Multiplying (3.6) with ${\tilde{a}}^p$ we obtain

$$\begin{aligned} y\cdot [{\tilde{\ell }}(x+y)]^p \le \lambda \cdot y \cdot [{\tilde{\ell }}(y)]^p + \mu \cdot x \cdot [{\tilde{\ell }}(x)]^p. \end{aligned}$$

(3.9)

It then follows that

$$\begin{aligned}&y\cdot [\ell (x+y)]^p \le y\cdot [{\tilde{\ell }}(x+y)]^p \le \lambda \cdot y \cdot [{\tilde{\ell }}(y)]^p + \mu \cdot x \cdot [{\tilde{\ell }}(x)]^p \le \lambda \cdot y \cdot [\ell (y)]^{p} \nonumber \\&\quad + \mu \cdot x \cdot [\ell (x)]^{p}, \end{aligned}$$

(3.10)

where we use (3.9) in the second inequality, and (3.8) in the first and last inequality based on the fact that $x, y \le h \le x + y$. This proves the claim. $\square$

Now, let $(x_r)_{r \in R}$ be the (total) flow vector of a pure Nash equilibrium s and $(y_r)_{r \in R}$ that of a system optimum $s^*$. Assume that for a given pair $(\lambda ,\mu ) \in {\mathbb {R}}_{\ge 0} \times (0,1)$ it holds that

$$\begin{aligned} y_r \cdot c_r^p(x_r + y_r) \le \lambda \cdot y_r c_r^p(y_r) + \mu \cdot x_r c_r^p(x_r) \end{aligned}$$

(3.11)

for all $r \in R$. Following a standard argument, see, e.g., Aland et al. (2011, Theorem 3.2), we first apply the Nash inequality (2.1) once for every user $i \in N$, with the deviation of every user being the resource they use in the system optimum. We then find

$$\begin{aligned} c_{s_i}(x_{s_i})^p \le c_{s_i^*}(x_{s_i^*} + w_i)^p \le c_{s_i^*}(x_{s_i^*} + y_{s_i^*}) ^p \end{aligned}$$

for every user i, where the second inequality holds, because user i uses resource $s_i^*$ in the system optimum, and hence $w_i \le y_{s_i^*}$. Summing up these inequalities (and rewriting the resulting sum in terms of resource loads), it then follows that

$$\begin{aligned} \sum _{r \in R} x_rc_r^p(x_r)&\le \sum _{r \in R} y_r \cdot c_r^p(x_r + y_r)\\&\le \lambda \sum _{r \in R} y_r \cdot c_r^p(y_r) + \mu \sum _{r \in R}x_r \cdot c_r^p(x_r) \ \ \ (\text {using} \;3.11) \end{aligned}$$

and, hence, by rearranging,

$$\begin{aligned} p\text {-PoA}(\Gamma ) \le \left( \frac{\lambda }{1 - \mu }\right) ^{\frac{1}{p}}. \end{aligned}$$

In order to find the best bound on the $p\text {-PoA}$, we consider the infimum over all possible choices of $(\lambda , \mu )$. By Lemma 3.8, it follows that

$$\begin{aligned}&\inf _{(\lambda ,\mu ) \in {\mathbb {R}}_{\ge 0} \times (0,1)} \left\{ \frac{\lambda }{1 - \mu } \ \Bigg | \ \forall x,y \in {\mathbb {R}}_{\ge 0}, \ell \in {\mathcal {P}}_d : y\cdot [\ell (x+y)]^p \le \lambda \cdot y \cdot [\ell (y)]^p + \mu \cdot x \cdot [\ell (x)]^p \right\} \nonumber \\& \quad \quad \quad=\inf _{(\lambda ,\mu ) \in {\mathbb {R}}_{\ge 0} \times (0,1)} \left\{ \frac{\lambda }{1 - \mu } \ \Bigg | \ \forall x,y \in {\mathbb {R}}_{\ge 0} : y\cdot (x + y)^{pd} \le \lambda \cdot y^{pd+1} + \mu \cdot x^{pd+1} \right\} \\& \quad \quad \quad = \inf _{\mu \in (0,1)} \left\{ \max _{x \in {\mathbb {R}}_{\ge 0}}\left\{ \frac{(x+1)^{pd} - \mu \cdot x^{pd+1}}{1 - \mu }\right\} \right\} \end{aligned}$$

(3.12)

where the last equality holds because of Lemma 6.2 in Appendix 2.

In order to analyse the infimum in (3.12), we may use Lemma 6.3 in Appendix 2. In particular, the infimum in (3.12) is equal to $\Phi _{pd}^{pd+1}.$ This then completes the proof of Theorem 3.6.

3.3 Unweighted atomic case

We continue with the price of anarchy for unweighted atomic parallel link routing games. The main result is as follows.

Theorem 3.9

Let $\Gamma$ be an atomic unweighted parallel link routing game whose cost functions are polynomials of degree at most d for some $d \in {\mathbb {N}}$, and let $p \in (0,\infty )$. Let $\Phi _{pd}$ be the unique non-negative solution to $(x+1)^{pd} = x^{pd+1}$ and $k = \lfloor \Phi _{pd}\rfloor$. Then

$$\begin{aligned} p\text {-PoA}(\Gamma ) \le \left( \frac{(k+1)^{2pd+1} - k^{pd+1}(k+2)^{pd}}{(k+1)^{pd+1} - (k+2)^{pd} + (k+1)^{pd} - k^{pd+1}}\right) ^{\frac{1}{p}}. \end{aligned}$$

(3.13)

As a limiting case, we obtain the result of Vinci et al. (2022) for the geometric mean objective.

Corollary 3.10

(Vinci et al. 2022) Let $\Gamma$ be an unweighted atomic parallel link routing game whose cost functions are polynomials of degree at most d for some $d \in {\mathbb {N}}$. The price of anarchy for the geometric mean objective satisfies

$$\begin{aligned} 0\text {-PoA}(\Gamma ) \le 2^d. \end{aligned}$$

Proof

Take the limit $p \rightarrow 0$ in the right hand side of (3.13). A sketch of the calculation of this limit is deferred to Proposition 5.2 in Appendix 1. $\square$

It is known that for the egalitarian cost objective, the price of anarchy is unbounded, already for unweighted atomic parallel link routing games with linear cost functions (Czumaj and Vöcking 2007). Indeed, the bound from Theorem 3.9 grows indefinitely as $p \rightarrow \infty$, already for $d=1$.

Proof of Theorem 3.9

The proof uses the same approach as for the weighted case, with some differences. It is again based on the analysis of Aland et al. (2011). We start with a technical lemma that will simplify the analysis later on. It is the analogue of Lemma 3.8. Although we require $\lambda \ge 0$ in the statement of Lemma 3.11, we will in fact only apply it for the case $\lambda \ge 1$ later on. $\square$

Lemma 3.11

Let $d \in {\mathbb {N}}$, $p \in (0,\infty )$, and $(\lambda ,\mu ) \in {\mathbb {R}}_{\ge 0} \times (0,1)$ be a given pair. Then

$$\begin{aligned} y\cdot (x + 1)^{pd} \le \lambda \cdot y^{pd+1} + \mu \cdot x^{pd+1} \end{aligned}$$

(3.14)

for all $x,y \in {\mathbb {N}}$ with $x \ge y > 0$ if and only if for all $\ell \in {\mathcal {P}}_d$.

$$\begin{aligned} y\cdot [\ell (x+1)]^p \le \lambda \cdot y \cdot [\ell (y)]^p + \mu \cdot x \cdot [\ell (x)]^p \end{aligned}$$

(3.15)

for all $x,y \in {\mathbb {N}}$ with $x \ge y > 0$.

Proof

The proof is similar to the proof of Lemma 3.8. Rouhgly speaking, the only difference is that $``x + y"$ is replaced by $``x+1"$ in the left hand side of (3.6) and (3.7). This is not a problem as the argument in (3.10) still works, since $x,y \le \max \{x,y\} \le x+1$ by assumption of $x \ge y$. $\square$

Now, let $(x_r)_{r \in R}$ be the (total) flow vector of a pure Nash equilibrium s and $(y_r)_{r \in R}$ that of a system optimum $s^*$. We write $R^* = \{r \in R : y_r > 0\}$ and partition it as

$$\begin{aligned} R^+ = \{r \in R : x_r \ge y_r> 0\} \ \ \text { and } \ \ R^- = \{r \in R : x_r < y_r \text { with } y_r > 0\}. \end{aligned}$$

Assume that for a given pair $(\lambda ,\mu ) \in [1,\infty ) \times (0,1)$ it holds that

$$\begin{aligned} y_r \cdot c_r^p(x_r + 1) \le \lambda \cdot y_r c_r^p(y_r) + \mu \cdot x_r c_r^p(x_r) \end{aligned}$$

(3.16)

for all $r \in R^+$. Note that, as we require $\lambda \ge 1$, it also holds that

$$\begin{aligned} y_r \cdot c_r^p(x_r + 1) \le \lambda \cdot y_r c_r^p(y_r) + \mu \cdot x_r c_r^p(x_r) \end{aligned}$$

(3.17)

for all $r \in R^-$ as in that case $x_r + 1 \le y_r$.

Again, using the same standard argument as in the proof of Theorem 3.6, we find

$$\begin{aligned} \sum _{r \in R} x_rc_r^p(x_r)&\le \sum _{r \in R} y_rc_r^p(x_r + 1) = \sum _{r \in R^*} y_rc_r^p(x_r + 1) \\&= \sum _{r \in R^+} y_rc_r^p(x_r + 1) + \sum _{r \in R^-} y_rc_r^p(x_r + 1)\\&\le \lambda \sum _{r \in R^*} y_rc_r^p(y_r) + \mu \sum _{r \in R^*} x_rc_r^p(x_r)\\&\le \lambda \sum _{r \in R} y_rc_r^p(y_r) + \mu \sum _{r \in R} x_rc_r^p(x_r) \end{aligned}$$

using (3.16) and (3.17) in the second inequality, and the fact that all cost functions are non-negative.

Rewriting gives that

$$\begin{aligned} p\text {-PoA}(\Gamma ) \le \left( \frac{\lambda }{1 - \mu }\right) ^{\frac{1}{p}}. \end{aligned}$$

In order to find the best pair $(\lambda , \mu )$, we consider (an upper bound on) the infimum over all possible choices. By Lemma 3.11 we have that

$$\begin{aligned}&\inf _{(\lambda ,\mu ) \in {\mathbb {R}}_{\ge 1} \times (0,1)} \left\{ \frac{\lambda }{1 - \mu } \ \Bigg | \ \forall x,y \in {\mathbb {N}}\text { with } x \ge y, \ell \in {\mathcal {P}}_d : y\cdot [\ell (x+1)]^p \right. \nonumber \\&\quad \quad \left. \le \lambda \cdot y \cdot [\ell (y)]^p + \mu \cdot x \cdot [\ell (x)]^p \right\} \nonumber \\& \quad \quad=\inf _{(\lambda ,\mu ) \in {\mathbb {R}}_{\ge 1} \times (0,1)} \left\{ \frac{\lambda }{1 - \mu } \ \Bigg | \ \forall x,y \in {\mathbb {N}}\text { with } x \ge y: \ y\cdot (x + 1)^{pd} \le \lambda \cdot y^{pd+1} + \mu \cdot x^{pd+1} \right\} \nonumber \\& \quad \quad \le \inf _{(\lambda ,\mu ) \in {\mathbb {R}}_{\ge 0} \times (0,1)} \left\{ \frac{\lambda }{1 - \mu } \ \Bigg | \ \forall x,y \in {\mathbb {N}}_0 : \ y\cdot (x + 1)^{pd} \le \lambda \cdot y^{pd+1} + \mu \cdot x^{pd+1} \right\} \end{aligned}$$

(3.18)

$$\begin{aligned}&= \inf _{\mu \in (0,1)} \left\{ \max _{x \in {\mathbb {N}}_{0}}\left\{ \frac{(x+1)^{pd} - \mu \cdot x^{pd+1}}{1 - \mu }\right\} \right\} \end{aligned}$$

(3.19)

where the last equality holds because of Lemma 6.4 in Appendix 2. The inequality in (3.18), where we switch from $\lambda \ge 0$ to $\lambda \ge 1$ is justified by setting $x = 0$, as it then follows that the optimal choice of $\lambda$ in (3.18) satisfies $\lambda \ge 1$.

In order to compute the final infimum in (3.19) we may use the same analysis as in the proof of Aland et al. (2011, Lemma 5.9) which also works for real values of $t = pd$ instead of only integral values of t. This computation results in the expression in the right hand side of (3.13) without the exponent 1/p. This completes the proof of Theorem 3.9.

4 Conclusion

In this work we have given bounds on the p-price of anarchy for atomic and non-atomic parallel link routing games that unify many results in the literature for different cost objectives. To the best of our knowledge, these are the first price of anarchy bounds that unify various different well-known cost objectives such as the egalitarian, utilitarian and geometric mean objective. Our unification through the generalized p-mean objective also allows one to obtain price of anarchy bounds that can be seen as an interpolation between, e.g., the utilitarian objective and the geometric mean objective (by choosing $p \in [0,1]$). Understanding how the price of anarchy behaves under different cost objectives is important to decide how inefficient (from a quantitative point of view) an equilibrium flow actually is, and whether or not measures are needed to reduce it.

We note that Vinci et al. (2022) also obtain a result for the geometric mean objective in the setting of online load balancing using a greedy algorithm. In Appendix 5 we show that there exists a unification of their result and that of Caragiannis (2008), who studies the same greedy algorithm under the $L_p$-norm objective, when the links $r \in R$ have cost functions of the form $c_r(x) = a_rx^d$ for a given $d \in {\mathbb {N}}$. We suspect a similar result holds true for general polynomial cost functions of degree at most d, but leave this as a problem for future work. Further related works on online load balancing are, e.g., Awerbuch et al. (1995), Bilò and Vinci (2017), Klimm et al. (2019).

Appendices

Appendix 1: Limit calculations

Proposition 5.1

Let $d>0$ be given. Then

$$\begin{aligned} \lim _{p \rightarrow 0} \left( 1 - \frac{d p}{(d p+1)^{(d p+1)/(d p)}}\right) ^{-\frac{1}{p}} = \left( e^{\frac{1}{e}}\right) ^d \end{aligned}$$

and

$$\begin{aligned} \lim _{p \rightarrow \infty } \left( 1 - \frac{d p}{(d p+1)^{(d p+1)/(d p)}}\right) ^{-\frac{1}{p}} = 1 \end{aligned}$$

Proof

Setting $t = dp$, we obtain

$$\begin{aligned} \left( 1 - \frac{d p}{(d p+1)^{(d p+1)/(d p)}}\right) ^{-\frac{1}{p}} = \left[ \left( 1 - \frac{t}{(t+1)^{(t+1)/t}}\right) ^{-\frac{1}{t}}\right] ^d \end{aligned}$$

It now suffices to study the limit $t \rightarrow 0$, or $t \rightarrow \infty$, as d is fixed. We have

$$\begin{aligned} \left( 1 - \frac{t}{(t+1)^{(t+1)/t}}\right) ^{-\frac{1}{t}} = e^{-\frac{\ln \left( 1 - \frac{t}{(t+1)^{(t+1)/t}}\right) }{t}} \end{aligned}$$

Therefore, it suffices to show that

$$\begin{aligned} \lim _{t \rightarrow 0} \frac{\ln \left( 1 - \frac{t}{(t+1)^{(t+1)/t}}\right) }{t} = - \frac{1}{e} \end{aligned}$$

(5.1)

and

$$\begin{aligned} \lim _{t \rightarrow \infty } \frac{\ln \left( 1 - \frac{t}{(t+1)^{(t+1)/t}}\right) }{t} = 0 \end{aligned}$$

(5.2)

In order to prove these identities, one may use L’Hôpital’s rule (i.e., replace the functions in the nominator and denominator by their derivatives). These are somewhat tedious, but elementary, calculus exercises for which we only give informal sketches here.

For $t \rightarrow 0$, note that $(t+1)^{\frac{t+1}{t}} = (1+t)(1+t)^\frac{1}{t} \approx e$ as $\lim _{t \rightarrow 0} (1+t)^\frac{1}{t} = e$. Substituting this in (5.1) gives

$$\begin{aligned} \lim _{t \rightarrow 0} \frac{\ln \left( 1 - \frac{t}{(t+1)^{(t+1)/t}}\right) }{t} \approx \lim _{t \rightarrow 0} \frac{\ln \left( 1 - \frac{t}{e}\right) }{t} = \lim _{t \rightarrow 0} \frac{-\frac{1}{e}}{1 - \frac{t}{e}} = - \frac{1}{e} \end{aligned}$$

where the second to last equality is an application of L’Hôpital’s rule.

For $t \rightarrow \infty$, note that $(t+1)^{\frac{t+1}{t}} = (1+t)(1+t)^\frac{1}{t} \approx 1 + t$ as $\lim _{t \rightarrow \infty } (1+t)^\frac{1}{t} = 1$. Then (5.2) becomes

$$\begin{aligned} \lim _{t \rightarrow \infty } \frac{\ln \left( 1 - \frac{t}{(t+1)^{(t+1)/t}}\right) }{t} \approx \lim _{t \rightarrow \infty } \frac{\ln \left( 1 - \frac{t}{t+1}\right) }{t} = \lim _{t \rightarrow \infty } \frac{\ln \left( \frac{1}{t+1}\right) }{t} = \lim _{t \rightarrow \infty } \frac{t+1}{-(1+t)^2} = 0, \end{aligned}$$

where again the second to last equality is an application of L’Hôpital’s rule. $\square$

Proposition 5.2

Let $d > 0$ be given and let $p \in (0,\infty )$. Let $\Phi _{pd}$ be the unique non-negative solution to $(x+1)^{pd} = x^{pd+1}$ and $k = \lfloor \Phi _{pd}\rfloor$. Then

$$\begin{aligned} \lim _{p \rightarrow 0} \left( \frac{(k+1)^{2pd+1} - k^{pd+1}(k+2)^{pd}}{(k+1)^{pd+1} - (k+2)^{pd} + (k+1)^{pd} - k^{pd+1}}\right) ^{\frac{1}{p}} = 2^d \end{aligned}$$

Proof

Setting $t = dp$, we obtain

$$\begin{aligned}&\left( \frac{(k+1)^{2pd+1} - k^{pd+1}(k+2)^{pd}}{(k+1)^{pd+1} - (k+2)^{pd} + (k+1)^{pd} - k^{pd+1}}\right) ^{\frac{1}{p}} \nonumber \\&\quad = \left[ \left( \frac{(k+1)^{2t+1} - k^{t+1}(k+2)^{t}}{(k+1)^{t+1} - (k+2)^{t} + (k+1)^{t} - k^{t+1}}\right) ^{\frac{1}{t}}\right] ^d. \end{aligned}$$

Therefore, it suffices to show

$$\begin{aligned} \lim _{t \rightarrow 0} \left( \frac{(k+1)^{2t+1} - k^{t+1}(k+2)^{t}}{(k+1)^{t+1} - (k+2)^{t} + (k+1)^{t} - k^{t+1}}\right) ^{\frac{1}{t}} = 2 \end{aligned}$$

(5.3)

For $t = pd$ small enough, it holds that $k = \lfloor \Phi _{pd}\rfloor = 1$. To see this, note that if $x \ge 0$ is such that $(x+1)^t = x^{t+1}$ then we must have $x \ge 1$, and $x = x(t)$ is increasing in t. Then (5.3) reduces to

$$\begin{aligned} \lim _{t \rightarrow 0} \left( \frac{2^{2t+1} - 3^{t}}{2^{t+1} - 3^{t} + 2^{t} -1}\right) ^{\frac{1}{t}} = 2 \end{aligned}$$

(5.4)

This identity can be shown using L’Hôpital’s rule after exponentiating the left hand side similar to what was done in the proof of Proposition 5.1. That is, it suffices to show that

$$\begin{aligned} \lim _{t \rightarrow 0} \frac{\ln \left( \frac{2^{2t+1} - 3^{t}}{2^{t+1} - 3^{t} + 2^{t} -1}\right) }{t} = \lim _{t \rightarrow 0} \frac{\ln \left( 2^{2t+1} - 3^{t}\right) }{t} - \lim _{t \rightarrow 0} \frac{\ln \left( 2^{t+1} - 3^{t} + 2^{t} - 1\right) }{t} = \ln (2) \end{aligned}$$

Using L’Hôpital’s rule, we have

$$\begin{aligned} \lim _{t \rightarrow 0} \frac{\ln \left( 2^{2t+1} - 3^{t}\right) }{t} = \lim _{t \rightarrow 0} \frac{2\ln (4)4^t - \ln (3)3^t}{2^{2t+1} - 3^{t}} = 2\ln (4) - \ln (3) = \ln (16/3) \end{aligned}$$

and

$$\begin{aligned} \lim _{t \rightarrow 0} \frac{\ln \left( 2^{t+1} - 3^{t} + 2^{t} - 1\right) }{t} = \lim _{t \rightarrow 0} \frac{2\ln (2)2^t - \ln (3)3^t + \ln (2)2^t - 1}{2^{t+1} - 3^{t} + 2^{t} - 1} = 2\ln (2) - \ln (3) + \ln (2) \end{aligned}$$

Substracting $2\ln (2) - \ln (3) + \ln (2) = \ln (8/3)$ from $\ln (16/3)$ then indeed gives us $\ln (2)$, as desired. $\square$

Appendix 2: Lemmas from Aland et al. (2011)

This section contains all the lemmata from Aland et al. (2011) that we rely on. Lemma 6.1 can be proved using the proof of Aland et al. (2011, Lemma 5.2) verbatim.

Lemma 6.1

Let $\mu \in (0,1]$ and $t >0$. Define $g : {\mathbb {R}}_{\ge 0} \rightarrow {\mathbb {R}}$ as $g(x) = (x+1)^t - \mu \cdot x^{t+1}$. Then it holds that g has exactly one local maximum at some $\xi \in {\mathbb {R}}_{>0}$. Moreover, g is strictly increasing in $[0,\xi )$, and strictly decreasing in $(\xi ,\infty )$.

The following lemma is a relaxed version of Aland et al. (2011, Lemma 5.5).

Lemma 6.2

Let $t = pd > 0$. Then

$$\begin{aligned}&\inf _{(\lambda ,\mu ) \in {\mathbb {R}}_{\ge 0} \times (0,1)} \left\{ \frac{\lambda }{1 - \mu } \ \Bigg | \ \forall x,y \in {\mathbb {R}}_{\ge 0} : y\cdot (x + y)^{pd} \le \lambda \cdot y^{pd+1} + \mu \cdot x^{pd+1} \right\} \nonumber \\& \quad \quad = \inf _{\mu \in (0,1)} \left\{ \max _{x \in {\mathbb {R}}_{\ge 0}}\left\{ \frac{(x+1)^{pd} - \mu \cdot x^{pd+1}}{1 - \mu }\right\} \right\} \end{aligned}$$

(6.1)

In order to prove Lemma 6.2 one may follow the proof of Aland et al. (2011, Lemma 5.5). Aland et al. (2011) give the proof for $t \in {\mathbb {N}}$, but the only time this assumption is used, is when the proof relies on Aland et al. (2011, Lemma 5.5), which in fact also holds for any real $t > 0$, as summarized in Lemma 6.1. Furthermore, the statement of Aland et al. (2011, Lemma 5.5) is phrased in terms of general polynomials, but the proof proceeds by making a reduction to monomials with coefficient 1, which is our starting point (as we reduced to monomials already in Lemma 3.8).

Lemma 6.3

Let $t = pd > 0$. Then

$$\begin{aligned} \inf _{\mu \in (0,1)} \left\{ \max _{x \in {\mathbb {R}}_{\ge 0}}\left\{ \frac{(x+1)^{pd} - \mu \cdot x^{pd+1}}{1 - \mu }\right\} \right\} = \Phi _{pd}^{pd+1}. \end{aligned}$$

In order to prove Lemma 6.3 we may use the calculus proof of Aland et al. (2011, Lemma 5.6) by observing that it also verbatim works for real values of $t = pd$ instead of only $t \in {\mathbb {N}}$ by using Lemmas 6.1 and 6.2 in the argumentation as opposed to Aland et al. (2011, Lemmas 5.2 and 5.5), respectively.

Lemma 6.4

Let $t = pd > 0$. Then

$$\begin{aligned}&\inf _{(\lambda ,\mu ) \in {\mathbb {R}}_{\ge 0} \times (0,1)} \left\{ \frac{\lambda }{1 - \mu } \ \Bigg | \ \forall x,y \in {\mathbb {N}}_0 : \ y\cdot (x + 1)^{pd} \le \lambda \cdot y^{pd+1} + \mu \cdot x^{pd+1} \right\} \\& \quad \quad = \inf _{\mu \in (0,1)} \left\{ \max _{x \in {{\mathbb {N}}_{0}}}\left\{ \frac{(x+1)^{pd} - \mu \cdot x^{pd+1}}{1 - \mu }\right\} \right\} \\& \quad \quad = \frac{(k+1)^{2pd+1} - k^{pd+1}(k+2)^{pd}}{(k+1)^{pd+1} - (k+2)^{pd} + (k+1)^{pd} - k^{pd+1}}. \end{aligned}$$

The first equality can be proved in a similar way as the proofs of Aland et al. (2011, Lemmas 5.7 and 5.8). The second equality can be proved similarly as Aland et al. (2011, Lemmas 5.9). The proofs of these lemmas also hold verbatim for real $t = pd$ instead of only $t \in {\mathbb {N}}$.

Appendix 3: Descartes’ rule of signs

Descartes’ rule of signs can be used to upper bound the number of positive roots of a polynomial in terms of the number of sign changes of the coefficients of the polynomial. The version that we use of it in this work can be summarized as follows.

Let $f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x + a_0$ be a polynomial of degree (at most) n with real coefficients $a_{n},\dots ,a_0$. Define

$$\begin{aligned} SC(f) = \{i \in [n]: \text {sgn}(a_i) \ne \text {sgn}(a_{i-1})\} \end{aligned}$$

where $[n] = \{1,2,\dots ,n\}$. Here we use the sign function $\text {sgn}: {\mathbb {R}}\rightarrow \{-1,+1\}$ defined by $\text {sgn}(a) = 1$ if $a > 0$ and $\text {sgn}(a) = -1$ if $a < 0$. We refer to |SC(f)| as the number of sign changes of f. Descartes’ rule of signs (in particular) says that the number of positive real roots of f is at most the number of sign changes of f.

Appendix 4: Lower bound for non-atomic games

In this section we give a lower bound on a parallel link network with two links, illustrating the tightness of the bound in Theorem 3.2. This is the same example as used in Correa et al. (2004); Roughgarden (2003). We have one link B with $c_B(x) = 1$ and one link T with $c_T(x) = x^d$; see also Fig. 3. There is one commodity with a total flow of $d_1 = 1$. It is not hard to see that a Wardrop flow f is given by routing the whole unit of flow of the commodity over T. The social optimum w.r.t. $C^p(f)$ is given by routing $1 - dp(dp+1)^\frac{dp+1}{dp}$ units of flow over link T, and the remainder over link B. A simple calculation of the resulting price of anarchy shows that this gives the desired bound as in Theorem 3.2.

Fig. 3

Parallel link network consisting of two arcs

Appendix 5: Online load balancing and the greedy algorithm

An instance of online load balancing consists of the same components as an atomic weighted parallel link routing game, but proceeds differently. The users in $N = \{1,\dots ,n\}$, often called clients, arrive online and have to irrevocably be assigned to some link $r \in R$ from their strategy set. We assume without loss of generality that the clients arrive according to the permutation $(1,2,\dots ,n)$, so in step t of this process, client t has to be assigned. The goal is to find an assignment that minimizes the social cost, which in our case, based on (2.7), is equivalent to

$$\begin{aligned} \left( \sum _{r \in R} x_r c_r^p(x_r)\right) ^\frac{1}{p} \end{aligned}$$

The greedy algorithm, as the name suggests, makes the assignment decision “greedily” meaning that we assign a client to a link in her strategy set that yields the smallest increase in cost objective $C^p_w$ (based on the clients that have been assigned so far). To be precise, suppose that $s^{(t)} = (s_1,\dots ,s_t) \in \times _{i=1}^t {\mathcal {S}}_i$ is the profile in which clients $1,\dots ,t$ have been assigned so far. Then we assign client $t + 1$ to the link

$$\begin{aligned} \displaystyle s_{t+1} = \text {argmin}_{r \in {\mathcal {S}}_{t+1}} C^p_w(s^{(t)},r) \end{aligned}$$

(5.1)

If $p \in (0,\infty )$, we equivalently have

$$\begin{aligned} \displaystyle s_{t+1} = \text {argmin}_{r \in {\mathcal {S}}_{t+1}} \sum _{r \in R} x_r c_r^p(x_r) \end{aligned}$$

(5.2)

as the function $y \mapsto y^p$ is increasing in $y \ge 0$.

If, for some $d \in {\mathbb {N}}$, we have $c_r(x) = a_rx^d$ with $a_r > 0$ for every $r \in R$, then we have

$$\begin{aligned} \sum _{r \in R} x_r c_r^p(x_r) = \sum _{r \in R} a_r x_r^{dp + 1} = \sum _{r \in R} (a_r^{1/(dp+1)}x_r)^{dp + 1} \end{aligned}$$

We define

$$\begin{aligned} w_{ir} = a_r^{1/(dp+1)}w_i \end{aligned}$$

for $r \in R$. With the definition of $w_{ir}$ in hand, we can rephrase the social cost as

$$\begin{aligned} \left[ \left( \sum _{r \in R} \ell _r(z_r(s))^{1 + dp}\right) ^{\frac{1}{1 + dp}}\right] ^{\frac{dp+1}{p}} \end{aligned}$$

(5.3)

where $z_r(s) = \sum _{i : s_i = r} w_{ir}$ is the sum of the weights of the clients assigned to resource r. If we define $q = 1 + dp$, we have arrived at (a special case of) the setting of Caragiannis (2008). To be more precise, (5.3) corresponds to studying the $L_{dp+1}$-norm cost objective raised to the power $(dp+1)/p$.⁹

We next restate (Caragiannis 2008, Theorem 3.1) in a slightly different form. The guarantee given in (5.4) is the same as that in Caragiannis (2008, Theorem 3.1), with the parameter p in Caragiannis (2008) replaced by $dp+1$, and raised to the power $(dp+1)/p$ as a consequence of (5.3).

Theorem 5.1

(Caragiannis 2008) For $d \in {\mathbb {N}}$ and $p \in (0,\infty )$, consider an instance of online load balancing with cost functions of the form $c_r(x) = a_rx^d$ for $r \in R$. Let s be the strategy profile obtained with the greedy algorithm defined by the rule in (5.2), and let $s^*$ be a system optimum. Then

$$\begin{aligned} \frac{C^p_w(s)}{C^p_w(s^*)} \le (2^{1/(dp+1)}-1)^{-(dp+1)/p}. \end{aligned}$$

(5.4)

As a corollary we obtain the bound of Vinci et al. (2022) for this class of cost functions. We note that their result for $p = 0$ holds for arbitrary polynomials of degree d with non-negative coefficients.

Corollary 5.2

For $d \in {\mathbb {N}}$, consider an instance of online load balancing with cost functions of the form $c_r(x) = a_rx^d$ for $r \in R$. Let s be the strategy profile obtained with the greedy algorithm defined by the rule in (5.2), and let $s^*$ be a system optimum. Then

$$\begin{aligned} \frac{C^0_w(s)}{C^0_w(s^*)} \le 4^d. \end{aligned}$$

(5.5)

Proof

We take the limit $p \rightarrow 0$ on the right hand side of (5.4), i.e.,

$$\begin{aligned} \lim _{p \rightarrow 0} (2^{1/(dp+1)}-1)^{-(dp+1)/p} = 4^d \end{aligned}$$

which can be shown by setting $t = pd$, and then exponentiating and applying L’Hôpital’s rule (as for the limits analysed in Appendix 1). That is, we can write

$$\begin{aligned} \displaystyle \left( 2^{1/(dp+1)}-1\right) ^{-\frac{dp+1}{p}} = \left[ \left( 2^\frac{1}{t+1} - 1\right) ^\frac{t+1}{t}\right] ^d. \end{aligned}$$

It suffices to show that

$$\begin{aligned} \lim _{t \rightarrow 0} \frac{t+1}{t}\ln \left( 2^\frac{1}{t+1} - 1\right) = \ln (4) \end{aligned}$$

We have

$$\begin{aligned} \frac{t+1}{t}\ln \left( 2^\frac{1}{t+1} - 1\right) = \ln \left( 2^\frac{1}{t+1} - 1\right) + \frac{\ln \left( 2^\frac{1}{t+1} - 1\right) }{t} \end{aligned}$$

Taking $t \rightarrow 0$ in the first term gives zero. Applying L’Hôpital’s rule to the second term gives

$$\begin{aligned} \lim _{t \rightarrow 0} \frac{\ln \left( 2^\frac{1}{t+1} - 1\right) }{t} = \lim _{t \rightarrow 0} \frac{2\ln (2)\left( \frac{1}{2}\right) ^t}{2^\frac{1}{t+1} - 1} = 2\ln (2) = \ln (4) \end{aligned}$$

which gives the desired result. $\square$