Analysis of the onset of a regime shift and detecting early warning signs of major population changes in a two-trophic three-species predator-prey model with long-term transients

Abstract

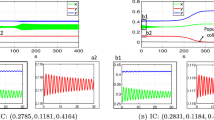
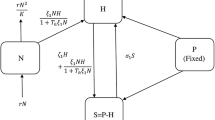
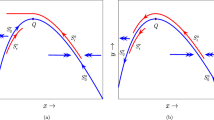
Identifying early warning signs of sudden population changes and mechanisms leading to regime shifts are highly desirable in population biology. In this paper, a two-trophic ecosystem comprising of two species of predators, competing for their common prey, with explicit interference competition is considered. With proper rescaling, the model is portrayed as a singularly perturbed system with fast prey dynamics and slow dynamics of the predators. In a parameter regime near singular Hopf bifurcation, chaotic mixed-mode oscillations (MMOs), featuring concatenation of small and large amplitude oscillations are observed as long-lasting transients before the system approaches its asymptotic state. To analyze the dynamical cause that initiates a large amplitude oscillation in an MMO orbit, the model is reduced to a suitable normal form near the singular-Hopf point. The normal form possesses a separatrix surface that separates two different types of oscillations. A large amplitude oscillation is initiated if a trajectory moves from the “inner” to the “outer side” of this surface. A set of conditions on the normal form variables are obtained to determine whether a trajectory would exhibit another cycle of MMO dynamics before experiencing a regime shift (i.e. approaching its asymptotic state). These conditions serve as early warning signs for a sudden population shift as well as detect the onset of a regime shift in this ecological model.

Appendix

1.1 Center manifold reduction

The center manifold can be expressed as a graph

$$\begin{aligned} w=\kappa (u, v, \delta )= & {} \frac{1}{2}\kappa _{uu}^0 u^2+ \kappa _{uv}^0 uv+ \frac{1}{2}\kappa _{vv}^0 v^2 +O(3)\nonumber \\&+ \delta \left( \frac{1}{2}\kappa _{uu}^1 u^2+ \kappa _{uv}^1 uv+ \frac{1}{2}\kappa _{vv}^1 v^2 +O(3)\right) \\&+O(\delta ^2), \end{aligned}$$

where O(3) represents cubic and higher-order terms in u and v. The function $\kappa$ can be determined by solving the equation $\frac{d \kappa }{d \tau } = \delta (H_3 \kappa +\frac{1}{2}H_{11} u^2)+O(\delta ^2)$. Using the equation for w and the above equation and equating the coefficients of like terms, (see Braaksma 1998 for details) one obtains that

$$\begin{aligned} w=\kappa (u, v, \delta )=-\frac{H_{11}}{4H_{3}}(u^2+v^2) +O(3)+O(\delta ). \end{aligned}$$

The corresponding equations in the center manifold up to higher order terms are

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{du}{d\tau } &{}=v+\frac{u^2}{2}+\delta \Big (\alpha u +\Big (-\frac{F_{13}H_{11}}{4H_{3}}+\frac{1}{6}F_{111}\Big )u^3-\frac{F_{13}H_{11}}{4H_3} uv^2 \Big )\\ \frac{dv}{d\tau } &{}=-u. \end{array}\right. \end{aligned}$$

(32)

It is clear from the governing equations of the two-dimensional center manifold that the equilibrium (0, 0, 0) (up to $O(\delta )$) is asymptotically stable if and only if $\alpha <0$, where $\alpha$ is given by (6).

1.2 Special Cases of the normal form

The FSN II point $(\bar{x}, \bar{y}, \bar{z}, \bar{h})$ can be explicitly computed for the following special cases:

Equal predation efficiencies: When $\beta _1=\beta _2$, one can solve for $\bar{h}$ in terms of the other parameters and can compute $(\bar{x}, \bar{y},\bar{z})$. In this case,

$$\begin{aligned} \bar{h}=\frac{4\Big [(\alpha _{12}+\alpha _{21})(1-\beta _1)-(c\alpha _{21}+d\alpha _{12})(1+\beta _1)\Big ] -\alpha _{12}\alpha _{21}(1+\beta _1)^3}{4(1-\beta _1-c(1+\beta _1))}, \end{aligned}$$

where $\alpha _{12}, \alpha _{21}, c, d$ are free parameters that satisfy (33)-(34) below:

$$\begin{aligned} \alpha _{12}(1+\beta _1)^2>4\Big (\frac{1-\beta _1}{1+\beta _1}-c\Big )> & {} 0 \end{aligned}$$

(33)

$$\begin{aligned} \ \alpha _{21}(1+\beta _1)^2 -4(c-d)\ne & {} 0. \end{aligned}$$

(34)

Furthermore,

$$\begin{aligned} \bar{x}= & {} \frac{1-\beta _1}{2},\\ \bar{y}= & {} \frac{\alpha _{12}(1+\beta _1)^3-4(1-\beta _1)+4c(1+\beta _1)}{4\alpha _{12}(1+\beta _1)},\\ \bar{z}= & {} \frac{1-\beta _1-c(1+\beta _1)}{\alpha _{12}(1+\beta _1)}. \end{aligned}$$

For biological significance, in addition to (33)- (34) we will choose $\alpha _{12}, \alpha _{21}, c, d$ so that that the expression in the numerator of $\bar{h}$ is positive, i.e.

$$\begin{aligned} 4\Big [(\alpha _{12}+\alpha _{21})(1-\beta _1)-(c\alpha _{21}+d\alpha _{12})(1+\beta _1)\Big ] > \alpha _{12}\alpha _{21}(1+\beta _1)^3. \end{aligned}$$

No exclusive competition: Assuming that the predators do not exhibit interference competition, i.e. $\alpha _{12}=\alpha _{21}=0$, one can explicitly solve for $(\bar{x}, \bar{y},\bar{z}, \bar{h})$, namely,

$$\begin{aligned} \bar{x}= & {} \frac{c\beta _1}{1-c},\\ \bar{y}= & {} \frac{\beta _1^2}{(1-c)^3(\beta _1-\beta _2)}((1-c)(1-\beta _2)-2c\beta _1),\\ \bar{z}= & {} \frac{(c\beta _1 +\beta _2(1-c))^2}{(1-c)^3(\beta _2-\beta _1)}((1-c)-\beta _1(1+c)) \end{aligned}$$

with

$$\begin{aligned} \bar{h} = \frac{(\beta _2-\beta _1)(\frac{\bar{x}}{\beta _2+\bar{x}} -d)}{(1-\beta _1-2\bar{x})(\beta _2+\bar{x})^2}. \end{aligned}$$

(35)