Skip to main content
SpringerLink
Log in

Numerical rate function determination in partial differential equations modeling cell population dynamics

  • Published:
Journal of Mathematical Biology Aims and scope Submit manuscript

Abstract

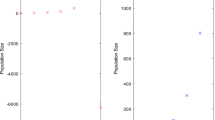
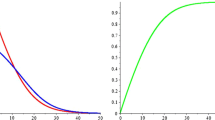
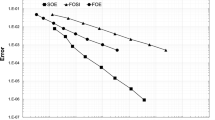
This paper introduces a method to solve the inverse problem of determining an unknown rate function in a partial differential equation (PDE) based on discrete measurements of the modeled quantity. The focus is put on a size-structured population balance equation (PBE) predicting the evolution of the number distribution of a single cell population as a function of the size variable. Since the inverse problem at hand is ill-posed, an adequate regularization scheme is required to avoid amplification of measurement errors in the solution method. The technique developed in this work to determine a rate function in a PBE is based on the approximate inverse method, a pointwise regularization scheme, which employs two key ideas. Firstly, the mollification in the directions of time and size variables are separated. Secondly, instable numerical data derivatives are circumvented by shifting the differentiation to an analytically given function. To examine the performance of the introduced scheme, adapted test scenarios have been designed with different levels of data disturbance simulating the model and measurement errors in practice. The success of the method is substantiated by visualizing the results of these numerical experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Abu-Absi NR, Zamamiri A, Kacmar J, Balogh SJ, Srienc F (2003) Automated flow cytometry for acquisition of time-dependent population data. Cytom Part A 51A(2):87–96

    Article  Google Scholar 

  • Anderson EC, Bell GI, Petersen DF, Tobey RA (1969) Cell growth and division IV. Determination of volume growth rate and division probability. Biophys J 9(2):246–263

    Article  Google Scholar 

  • Arino O (1995) A survey of structured cell population dynamics. Acta Biotheor 43:3–25

    Article  Google Scholar 

  • Banks HT, Sutton KL, Thompson WC, Bocharov G, Roose D, Schenkel T, Meyerhans A (2011) Estimation of cell proliferation dynamics using CFSE data. Bull Math Biol 73:116–150

    Article  MathSciNet  MATH  Google Scholar 

  • Bell GI (1968) Cell growth and division III. Conditions for balanced exponential growth in a mathematical model. Biophys J 8(4):431–444

    Article  Google Scholar 

  • Bell GI, Anderson EC (1967) Cell growth and division I. A mathematical model with applications to cell volume distributions in mammalian suspension cultures. Biophys J 7(4):329–351

    Article  Google Scholar 

  • Bourgeron T, Doumic M, Escobedo M (2014) Estimating the division rate of the growth-fragmentation equation with a self-similar kernel. Inverse Probl 30(2):025007

    Article  MathSciNet  MATH  Google Scholar 

  • Diekmann O (1984) The stable size distribution: an example in structured population dynamics. In: Mathematical ecology: proceedings of the autumn course (research seminars) held at the International Centre for Theoretical Physics, Miramare-Trieste, Italy, 1982, no. 54, pp 90-96

  • Diekmann O, Heijmans HJ, Thieme HR (1984) On the stability of the cell size distribution. J Math Biol 19:227–248

    Article  MathSciNet  MATH  Google Scholar 

  • Diekmann O, Lauwerier HA, Aldenberg T, Metz JAJ (1983) Growth, fission and the stable size distribution. J Math Biol 18:135-148

  • Doumic M (2007) Analysis of a population model structured by the cells molecular content. Math Model Nat Phenom 2(03):121–152

    Article  MathSciNet  MATH  Google Scholar 

  • Doumic M, Maia P, Zubelli JP (2010) On the calibration of a size-structured population model from experimental data. Acta Biotheor 58:405–413

    Article  Google Scholar 

  • Doumic M, Perthame B, Zubelli JP (2009) Numerical solution of an inverse problem in size-structured population dynamics. Inverse Probl 25(4):045008 (pp 25)

  • Doumic M, Tine LM (2013) Estimating the division rate for the growth-fragmentation equation. J Mathl Biol 67(1):69–103

    Article  MathSciNet  MATH  Google Scholar 

  • Doumic-Jauffret M, Gabriel P (2010) Eigenelements of a general aggregation-fragmentation model. Math Mod Meth Appl Sci 20(5):757–783

    Article  MathSciNet  MATH  Google Scholar 

  • Doumic-Jauffret M, Hoffmann M, Reynaud-Bouret P, Rivoirard V (2012) Nonparametric estimation of the division rate of a size-structured population. SIAM J Numer Anal 50(2):925–950

    Article  MathSciNet  MATH  Google Scholar 

  • Doumic-Jauffret M, Tine LM (2011) A general inverse problem for the growth-fragmentation equation. Technical Report arXiv:1110.4798, INRIA Rocquencour

  • Eakman JM, Fredrickson AG, Tsuchiya HM (1966) Statistics and dynamics of microbial cell populations. Chem Eng Prog Symp Ser 69(62):37–49

    Google Scholar 

  • Engl HW, Flamm C, Kügler P, Lu J, Müller S, Schuster P (2009) Inverse problems in systems biology. Inverse Probl 25(12):123014 (pp 51)

  • Engl HW, Hanke M, Neubauer A (1996) Regularization of inverse problems. Mathematics and its applications, vol 375. Kluwer Academic Publishers, Dordrecht

  • Engl HW, Rundell W, Scherzer O (1994) A regularization scheme for an inverse problem in age-structured populations. J Math Anal Appl 182(3):658–679

    Article  MathSciNet  MATH  Google Scholar 

  • Fredrickson AG, Ramkrishna D, Tsuchiya HM (1967) Statistics and dynamics of procaryotic cell populations. Math Biosci 1(3):327–374

    Article  MATH  Google Scholar 

  • Groh A, Krebs J, Wagner M (2011) Efficient solution of an inverse problem in cell population dynamics. Inverse Probl 27:065009 (pp 25)

  • Gyllenberg M (2007) Mathematical aspects of physiologically structured populations: the contributions of J A J metz. J Biol Dyn 1(1):3–44

    Article  MathSciNet  MATH  Google Scholar 

  • Gyllenberg M, Osipov A, Päivärinta L (2002) The inverse problem of linear age-structured population dynamics. J Evol Equ 2(2):223–239

    Article  MathSciNet  MATH  Google Scholar 

  • Gyllenberg M, Osipov A, Päivärinta L (2003) On determining individual behaviour from population data. In: Haroske D, Runst T, Schmeisser H-J (eds) Function spaces, differential operators, and nonlinear analysis: the Hans Triebel anniversary volume. Birkhäuser, Boston

  • Heijmans HJAM (1984) On the stable size distribution of populations reproducing by fission into two unequal parts. Math Biosci 72(1):19–50

    Article  MathSciNet  MATH  Google Scholar 

  • Henson MA (2003) Dynamic modeling of microbial cell populations. Curr Opin Biotechnol 14:460–467

    Article  Google Scholar 

  • Kohr H (2013) A linear regularization scheme for inverse problems with unbounded linear operators on Banach spaces. Inverse Probl 29(6):065015

    Article  MathSciNet  MATH  Google Scholar 

  • Kolewe ME, Roberts SC, Henson MA (2012) A population balance equation model of aggregation dynamics in Taxus suspension cell cultures. Biotechnol Bioeng 109(2):472–482

    Article  Google Scholar 

  • Laurençot P, Perthame B (2009) Exponential decay for the growth-fragmentation/cell-division equation. Commun Math Sci 7(2):503–510

    Article  MathSciNet  MATH  Google Scholar 

  • Liou JJ, Srienc F, Fredrickson AG (1997) Solutions of population balance models based on a successive generations approach. Chem Eng Sci 52(9):1529–1540

    Article  Google Scholar 

  • Liu YH, Bi JX, Zeng AP, Yuan JQ (2007) A population balance model describing the cell cycle dynamics of myeloma cell cultivation. Biotechnol prog 23(5):1198–1209

    Google Scholar 

  • Louis AK (1989) Inverse und schlecht gestellte Probleme. Teubner Studienbücher Mathematik, Teubner, Stuttgart

  • Louis AK (1996) Approximate inverse for linear and some nonlinear problems. Inverse Probl 12(2):175–190

    Article  MATH  Google Scholar 

  • Louis AK (2011) Feature reconstruction in inverse problems. Inverse Probl 27(6):065010 (pp 21)

  • Louis AK, Maass P (1990) A mollifier method for linear operator equations of the first kind. Inverse Probl 6:427–440

    Article  MathSciNet  MATH  Google Scholar 

  • Luzyanina T, Roose D, Schenkel T, Sester M, Ehl S, Meyerhans A, Bocharov G (2007) Numerical modelling of label-structured cell population growth using CFSE distribution data. Theor Biol Med Model 4(26):

  • Mancuso L, Liuzzo MI, Fadda S, Pisu M, Cincotti A, Arras M, Nasa GL, Concas A, Cao G (2010a) In vitro ovine articular chondrocyte proliferation: experiments and modelling. Cell Prolif 43(3):310–320

    Article  Google Scholar 

  • Mancuso L, Scanu M, Pisu M, Concas A, Cao G (2010b) Experimental analysis and modelling of in vitro HUVECs proliferation in the presence of various types of drugs. Cell Prolif 43(6):617–628

    Article  Google Scholar 

  • Mantzaris NV, Liou JJ, Daoutidis P, Srienc F (1999) Numerical solution of a mass structured cell population balance model in an environment of changing substrate concentration. J Biotechnol 71(1–3):157–174

    Article  Google Scholar 

  • Metz JAJ, Diekmann O (1986) The dynamics of physiologically structured populations. Lecture notes in biomathematics, 68

  • Michel P (2006a) Existence of a solution to the cell division eigenproblem. Math Mod Meth in Appl Sci 16(Suppl. Issue 1):1125-1154

  • Michel P (2006b) Optimal proliferation rate in a cell division model. Math Model Nat Phenom 1(2):23–44

    Article  MathSciNet  MATH  Google Scholar 

  • Michel P, Mischler S, Perthame B (2005) General relative entropy inequality: an illustration on growth models. J Math Pure Appl 84(9):1235–1260

    Article  MathSciNet  MATH  Google Scholar 

  • Perthame B (2006) Transport equations in biology. Frontiers in mathematics. Birkhäuser, Basel

    Google Scholar 

  • Perthame B, Ryzhik L (2005) Exponential decay for the fragmentation or cell-division equation. J Differ Equ 210(1):155–177

    Article  MathSciNet  MATH  Google Scholar 

  • Perthame B, Zubelli JP (2007) On the inverse problem for a size-structured population model. Inverse Probl 23(3):1037–1052

    Article  MathSciNet  MATH  Google Scholar 

  • Pilant M, Rundell W (1991a) Determining a coefficient in a first-order hyperbolic equation. SIAM J Appl Math 51(2):494–506

    Article  MathSciNet  MATH  Google Scholar 

  • Pilant M, Rundell W (1991b) Determining the initial age distribution for an age structured population. Math Popul Stud 3(1):3–20

    Article  MATH  Google Scholar 

  • Ramkrishna D (2000) Population balances: theory and applications to particulate systems in engineering. Academic Press, San Diego

    Google Scholar 

  • Ramkrishna D, Fredrickson AG, Tsuchiya HM (1968) On relationships between various distribution functions in balanced unicellular growth. Bull Math Biol 30:319–323

    Google Scholar 

  • Rieder A, Schuster T (2000) The approximate inverse in action with an application to computerized tomography. SIAM J Numer Anal 37(6):1909–1929

    Article  MathSciNet  MATH  Google Scholar 

  • Rieder A, Schuster T (2003) The approximate inverse in action II: convergence and stability. Math comput 72(243):1399–1415

    Article  MathSciNet  MATH  Google Scholar 

  • Rundell W (1989) Determining the birth function for an age structured population. Math Popul Stud 1(4):377–395

    Article  MathSciNet  MATH  Google Scholar 

  • Rundell W (1993) Determining the death rate for an age-structured population from census data. SIAM J Appl Math 53(6):1731–1746

    Article  MathSciNet  MATH  Google Scholar 

  • Schuster T (2007) The method of approximate inverse: theory and applications, vol 1906, Lecture notes in mathematics. Springer, Berlin-Heidelberg-New York

  • Schuster T, Schöpfer F (2010) Solving linear operator equations in Banach spaces non-iteratively by the method of approximate inverse. Inverse Probl 26(8):085006 (pp 19)

  • Sidoli FR, Mantalaris A, Asprey SP (2004) Modelling of mammalian cells and cell culture processes. Cytotechnology 44(1):27–46

    Article  Google Scholar 

  • Sinko JW, Streifer W (1967) A new model for age-size structure of a population. Ecology 48(6):910–918

    Article  Google Scholar 

  • Sinko JW, Streifer W (1969) Applying models incorporating age-size structure of a population to daphnia. Ecology 50(4):608–615

    Article  Google Scholar 

  • Sinko JW, Streifer W (1971) A model for population reproducing by fission. Ecology 52(2):330–335

    Article  Google Scholar 

  • Subramanian G, Ramkrishna D, Fredricksson AG, Tsuchiya HM (1970) On the mass distribution model for microbial cell populations. Bull Math Biol 32:521–537

    Google Scholar 

  • Tsuchiya HM, Fredricksson AG, Aris R (1966) Dynamics of microbial cell populations. Adv Chem Eng 6:125–206

    Article  Google Scholar 

  • Webb GF (2008) Population models structured by age, size, and spatial position. Structured population models in biology and epidemiology, vol 1936., Lecture notes in mathematicsSpringer, Berlin, pp 1–49

    Chapter  Google Scholar 

  • Wendland H (2005) Scattered data approximation, 1st edn. Cambridge University Press, Cambridge

  • Yosida K (1995) Functional analysis. Reprint of the sixth (1980) edition. Classics in mathematics, vol 11. Springer, Berlin

Download references

Author information

Authors and Affiliations

  1. Hexagon Metrology PTS, Walter-Zapp-Strasse 4, 35578, Wetzlar, Germany

    Andreas Groh

  2. Royal Institute of Technology (KTH), Lindstedtsvägen 25, 10044, Stockholm, Sweden

    Holger Kohr

  3. Saarland University, POB: 151150, 66041, Saarbrücken, Germany

    Alfred K. Louis

Authors
  1. Andreas Groh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Holger Kohr
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alfred K. Louis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Andreas Groh.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Groh, A., Kohr, H. & Louis, A.K. Numerical rate function determination in partial differential equations modeling cell population dynamics. J. Math. Biol. 74, 533–565 (2017). https://doi.org/10.1007/s00285-016-1032-2

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00285-016-1032-2

Keywords

Mathematics Subject Classification

Search

Navigation