Derivation of Kubo’s formula for disordered systems at zero temperature

Abstract

This work justifies the linear response formula for the Hall conductance of a two-dimensional disordered system. The proof rests on controlling the dynamics associated with a random time-dependent Hamiltonian.

The principal challenge is related to the fact that spectral and dynamical localization are intrinsically unstable under perturbation, and the exact spectral flow - the tool used previously to control the dynamics in this context - does not exist. We resolve this problem by proving a local adiabatic theorem: With high probability, the physical evolution of a localized eigenstate $\psi$ associated with a random system remains close to the spectral flow for a restriction of the instantaneous Hamiltonian to a region $R$ where the bulk of $\psi$ is supported. Allowing $R$ to grow at most logarithmically in time ensures that the deviation of the physical evolution from this spectral flow is small.

To substantiate our claim on the failure of the global spectral flow in disordered systems, we prove eigenvector hybridization in a one-dimensional Anderson model at all scales.

Appendices

Appendix A: Hybridization in $1D$

In this appendix, we show eigenvector hybridization for a family of $1D$ Anderson Hamiltonians. Apart from an occasional reference to a definition or a technical lemma, this appendix is self-contained. In some places, the notation used here conflicts with the notation used in the main text.

We consider the Hilbert space $\ell ^{2}\left ( {\mathbb{Z}} \right )$ and denote its scalar product by $\langle \cdot , \cdot \rangle$. Delta functions $\{\delta _{x}\}_{x \in \mathbb{Z}}$, equal to 1 at $x$ and 0 elsewhere, form a basis for the Hilbert space. The discrete Laplacian $\Delta$ is the operator given by

$$ \langle \delta _{x}, \Delta \delta _{y} \rangle = \textstyle\begin{cases} -2 & x=y, \\ 1 & x \sim y, \\ 0 & \text{otherwise}, \end{cases} $$

where $x \sim y$ denotes that $|x - y| =1$. We recall that $\sigma (-\Delta )=[0,4]$. We will use a decomposition $\Delta = \sum _{x \sim y} \Gamma _{xy}-2$, where $\Gamma _{xy}$ is a rank one operator defined by $\Gamma _{xy} f = f(x)\delta _{y}$ for $f\in \ell ^{2}({\mathbb{Z}})$. For a set $Z \subset \mathbb{Z}$, we let $\chi _{Z} = \sum _{x \in Z} \Gamma _{xx}$ be the orthogonal projection onto $Z$.

Our results concern the analytic family of Hamiltonians $H(\beta )$ with $\beta \in (-1,1)$ of the form

$$ H(\beta )=-\Delta +V_{\omega}+\beta W $$

(A.1)

acting on $\ell ^{2}\left ( {\mathbb{Z}} \right )$. Here, $V_{\omega}$ is a random potential, with $V_{\omega}(x)=\omega _{x}$ the i.i.d. random coupling variables distributed according to the Borel probability measure $\mathbb{P}:=\otimes _{{\mathbb{Z}}} P_{0}$. We will assume that the single-site distribution $P_{0}$ is absolutely continuous with respect to Lebesgue measure on ℝ. We assume that the corresponding Lebesgue density $\mu$ is bounded with $\operatorname*{supp}(\mu )\subset [0,1]$, and that the single-site probability density is bounded away from zero on its support. We denote the configuration space by $\Omega$. The perturbation $W$ is a compactly supported non-negative potential. For concreteness, we anchor $W$ at the origin by assuming that $W(0) =1$ and $\|W\| = 1$, in particular $\|H(\beta )\| \leq 6$ in our setup. We remark that $\sigma (H(0))$ is a ℙ-a.s. deterministic set (see e.g., [3, Theorem 3.10]), which we denote by $\Sigma$, and that $\Sigma \supset [0,5]$.

For a region $Z \subset {\mathbb{Z}}$, we write $H^{Z} = \chi _{Z} H \chi _{Z}$, understood as an operator acting on $\ell ^{2}(Z)$. We will use the natural embedding $\ell ^{2}(Z) \subset \ell ^{2}\left ( {\mathbb{Z}} \right )$ without further comment. With some slight abuse of notation, $(a,b)$ denotes $(a,b) \cap {\mathbb{Z}}$ whenever it signifies a subset of the lattice.

We consider a length scale ℒ, a symmetric region $\Lambda _{full}: = (-{\mathcal {L}}, {\mathcal {L}})$, and an asymmetric region $\Lambda : = (-{\mathcal {L}}, 2\sqrt {\mathcal {L}}/\ln {\mathcal {L}})$ that we divide into a right region $\Lambda _{R} = (-2\sqrt {\mathcal {L}}/\ln {\mathcal {L}}, 2\sqrt { \mathcal {L}}/\ln {\mathcal {L}})$, and a left region $\Lambda _{L} = \Lambda \setminus \Lambda _{R}$ (the reasons for this asymmetry will be clear later on). We denote by $r$ the leftmost point of $\Lambda _{R}$ and by $l$ the rightmost point of $\Lambda _{L}$, so by construction $l \sim r$. We consider the Hamiltonians associated with these regions, $H_{full}:=H^{\Lambda _{full}}, H: = H^{\Lambda}, H_{L}: = H^{ \Lambda _{L}}$, and $H_{R}: = H^{\Lambda _{R}}$, as well as the decoupled Hamiltonian $H_{dec}$ obtained by erasing the coupling between the left and right regions, i.e. $H_{dec} = H_{L} + H_{R} = H - \Gamma _{lr} - \Gamma _{rl}$. All of these Hamiltonians a priori depend on $\beta$. Here and later, we only stress the dependence on $\beta$ in some equations, and suppress the dependence in others. We will assume henceforth that ℒ is large enough so that $\operatorname*{supp}(W) \subset \Lambda _{R}$. In particular, $H_{L}$ does not depend on $\beta$.

We consider an eigenvector $\varphi _{L}$ of $H_{L}$ with eigenvalue $E_{L} \equiv E$ and a continuous family of eigenvectors $\varphi _{R}(\beta )$ of $H_{R}(\beta )$ with eigenvalues $E_{R}(\beta )$. We will assume that these two energy levels cross, i.e. $E - E_{R}(\beta )$ changes sign as $\beta$ varies. In Sect. A.2, we will show that such levels exist with large probability thanks to two-sided Wegner estimates.

For a typical realization of the disorder, the eigenvectors $\varphi _{L}$, $\varphi _{R}:=\varphi _{R}(0)$ are well localized with localization centers $x_{L}$, $x_{R}$, respectively (we will make this statement quantitative later on). We pick the eigenvectors in such a way that $x_{R}$ is close to the origin and $x_{L}$ is located at least a distance of $\sqrt {\mathcal {L}}$ away from $\Lambda _{R}$. Let $P_{dec}$ be the orthogonal projection onto $Span(\varphi _{L}, \varphi _{R})$. Let us consider the rank two operator $\mathbb{H}:=P_{dec} H P_{dec}$ acting on $Ran(P_{dec})$. We note that the matrix representation for ℍ with respect to the $\left \{ \varphi _{L}, \varphi _{R} \right \}$ basis is given by a $2\times 2$ matrix

$$ M_{\beta}:= \left ( \textstyle\begin{array}{c@{\quad}c} E & gap \\ gap & E_{R} + \beta \langle W \rangle _{\varphi _{R}} \end{array}\displaystyle \right ) $$

(A.2)

with $gap: = \langle \varphi _{L}, H(0) \varphi _{R} \rangle = \varphi _{L}(l) \varphi _{R}(r)$, $\langle W \rangle _{\varphi _{R}}:=\langle \varphi _{R}, W \varphi _{R} \rangle$. Moreover, $gap\neq 0$ since eigenfunctions of a Schrödinger operator restricted to an interval do not vanish on its boundary. We now note that for $\beta$ such that $E_{L} = E_{R} + \beta \langle W \rangle _{\varphi _{R}}$, the eigenvectors $\varphi _{\pm }:= \varphi _{R} \pm \varphi _{L}$ of ℍ are delocalized in a sense that these functions are not small at both of the points $x_{R}$ and $x_{L}$, which are separated by a distance comparable with the system’s size. We call this phenomenon a hybridization across lengthscale ℒ. We are going to show that such hybridization also occurs for eigenvectors of the full Hamiltonian $H_{full}(\beta )$.

Definition A.1

Let $F\in (0,1/2]$ be a parameter. We say that $H_{full}(\beta )$ $F$-hybridize on a length scale ℒ if there exists an analytical family of eigenvectors $\varphi (\beta )$ of $H_{full}(\beta )$ for $\beta \in (-1,1)$ such that

• (i) $\|\chi _{|x| \geq \sqrt {\mathcal {L}}/\ln {\mathcal {L}}} \varphi (0)\| \leq e^{-c \sqrt {\mathcal {L}}/\ln {\mathcal {L}}}$,

• (ii) There exists $\beta$ such that $\|\chi _{\Lambda _{L}} \varphi (\beta ) \|^{2} \geq F$, and $\|\chi _{|x| <\sqrt {\mathcal {L}}/\ln {\mathcal {L}}} \varphi (\beta ) \|^{2} \geq F$.

We call $F$ a hybridization strength and denote by $\Omega _{F, {\mathcal {L}}} \subset \Omega$ all realizations for which $H_{full}(\beta )$ $F$-hybridize.

Theorem A.2

For any $F < 1/2$, $\liminf _{{\mathcal {L}}\to \infty} \mathbb{P}(\Omega _{F, {\mathcal {L}}}) > 0$.

If we now consider an infinite volume operator $H(\beta )$ (i.e., $\Lambda _{full}={\mathbb{Z}}$), any $F<\frac{1}{2}$, and an arbitrary sequence $\mathcal {L}_{n}\to \infty$, then by the Borel-Cantelli lemma, for almost all random configurations $\omega \in \Omega$ we can find a subsequence $\mathcal {L}_{n_{k}}\to \infty$ such that $H^{\Lambda _{{\mathcal {L}}_{n_{k}}}}(\beta )$ $F$-hybridizes.

While there could potentially be different mechanisms leading to the hybridization phenomenon, our construction below hinges on the behavior of the simple two-level system (characterized by the avoided eigenvalue crossing) discussed above. Since the probability of multiple level crossings is much smaller than that of two-level ones, we expect that this is the only possible mechanism of hybridization, but in this work we have not tried to formalize this statement. We chose this definition for its simplicity; our construction of the hybridization event is more detailed and exactly matches the underlying motivation.

1.1 A.1 Perturbation of a non-avoided crossing

We consider the eigenvalues $E_{L} \equiv E, E_{R}(\beta )$ of $H_{dec}(\beta )$ for $\beta$ in a compact interval $J$ associated with the (normalized) eigenvectors $\varphi _{L}, \varphi _{R}(\beta )$. Later, the notation $E_{L}$ will stand more generally for an eigenvalue of $H_{L}$ and $E_{R}$ will stand for an eigenvalue of $H_{R}$, but this is not important at the moment. We assume that $\varphi _{R}(\beta )$ is continuous, which implies that $E_{R}(\beta )$ is continuous.

Let

$$ h := \min \{ \max _{\beta \in (-1,1)}(E - E_{R}(\beta ))_{+}, \max _{ \beta \in (-1,1)} (E_{R}(\beta )-E)_{+} \}, $$

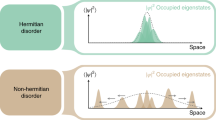
where $(x)_{+}$ is equal to $x$ for positive $x$ and zero otherwise. If the eigenvalues $E_{R}(\beta )$ do not intersect $E$, then $h=0$, otherwise $h$ is a maximal number such that both $E -h$ and $E+h$ intersect $E_{R}(\beta )$, see Figure 1 for an illustration.

Fig. 1

The left panel shows the crossing of $E$ and $E_{R}$ (colored in cyan and red, respectively) as $\beta$ varies in $(-1,1)$. The parameter $h>0$ captures the crossing width. The right panel shows the avoided crossing, $h=0$. (Color figure online)

Suppose now that the Hamiltonian $H(\beta )$ has a continuous family of spectral projections $P(\beta )$ such that (suppressing the $\beta$ dependence)

$$ \| P - P_{dec}\| \leq \varepsilon , \quad \| H_{dec} P_{dec} - H P\| \leq \varepsilon , $$

(A.3)

for some $\varepsilon \ll 1$. The range of $P$ is then two-dimensional and is spanned by (normalized) eigenvectors of $H$ that we denote $\varphi _{\pm}$. We denote the associated eigenvalues $E_{\pm}$. Let $c_{L}^{\pm},c_{R}^{\pm}$ be the Fourier coefficients of $\varphi _{\pm}$ with respect to the elements $\varphi _{L}, \varphi _{R}$ of an eigenbasis of $H_{dec}$, i.e.,

$$ \varphi _{\pm} = c_{L}^{\pm} \varphi _{L} + c_{R}^{\pm} \varphi _{R} + \varphi _{\perp}^{\pm}, $$

with $\langle \varphi _{\perp}^{\pm},\varphi _{L}\rangle =\langle \varphi _{ \perp}^{\pm},\varphi _{R}\rangle =0$, and let

$$ F: = \max _{\beta \in (-1,1)} \min \left ( |c^{+}_{L}(\beta )|^{2}, |c^{+}_{R}( \beta )|^{2} \right ). $$

(This value will be used for the parameter $F$ introduced in Definition A.1.)

Since $|c^{+}_{L}(\beta )|^{2}+|c^{+}_{R}(\beta )|^{2}\le 1$, we know that $F \leq 1/2$. For $\epsilon =0$, $F$ equals zero by the continuity of $\beta$ dependence in $H$, $H_{dec}$, $P$, and $P_{dec}$, so there is no hybridization. As can be seen from the two-level system described in (A.2), $F$ can be equal to $1/2$ for an arbitrarily small but non-zero value of $\epsilon$. Indeed, in this example $\epsilon >0$ corresponds to $gap>0$ and $F=1/2$ is achieved for $\beta$ that solves $E_{L}= E_{R} + \beta \langle W \rangle _{\varphi _{R}}$.

Our principle indicator of hybridization will be the fact that $F$ has to be close to $1/2$ whenever the level crossing for $H_{dec}$ is avoided for the full $H$.

Lemma A.3

Suppose that $E_{+}(\beta ), E_{-}(\beta )$ do not intersect in $J$, and $h\ge 4\varepsilon$. Then

$$ F \geq \frac{1 - \varepsilon ^{2}}{2}. $$

Proof

By the continuity of $E_{\pm}$ and the non-crossing condition, we may assume without loss of generality that $E_{+}(\beta )-E_{-}(\beta )>0$ for $\beta \in (-1,1)$. By the first equation in (A.3), we know that $\|\varphi _{\perp}^{+}\| \leq \varepsilon$, hence

$$ |c^{+}_{L}(\beta )|^{2} + |c^{+}_{R}(\beta )|^{2} \geq 1- \varepsilon ^{2}. $$

(A.4)

By the same equation,

$$ \varepsilon \ge {\langle \varphi _{\sharp},\varphi _{\sharp}-P \varphi _{\sharp}\rangle}=1- \left ( |c^{-}_{\sharp }|^{2} + |c^{+}_{ \sharp }|^{2} \right ),\quad \sharp =L,R. $$

(A.5)

On the other hand, the second equation in (A.3) implies

$$ |c_{\sharp}^{\pm}|^{2}(E_{\sharp }- E_{\pm})^{2}\le \varepsilon ^{2} , \quad \sharp =L,R. $$

(A.6)

Using the second equation in (A.3) and Weyl’s theorem, [40, Theorem 4.3.1] we get

$$ \mathrm{dist}_{H}(\{0,E_{L}, E_{R}\}, \{0,E_{-}, E_{+}\})= \mathrm{dist}_{H}(\sigma (H_{dec} P_{dec}),\sigma (HP)) \leq \varepsilon , $$

(A.7)

where $\mathrm{dist}_{H}$ stands for the Hausdorff distance between a pair of sets. Hence,

$$ \mathrm{dist}_{H}(\{E_{L}, E_{R}\}, \{E_{-}, E_{+}\}) \leq 2 \varepsilon . $$

(A.8)

The definition of $h$ implies that there exist $\beta _{1}, \beta _{2}\in (-1,1)$ such that $E_{L} - E_{R}(\beta _{1}) = h$ and $E_{R}(\beta _{2}) - E_{L} =h$. Thus, it follows from (A.8) and $E_{+}(\beta )-E_{-}(\beta )>0$ for $\beta \in (-1,1)$ that

$$\begin{aligned} &\max \left ( |E_{R}(\beta _{1}) - E_{-}(\beta _{1})|,|E_{L}-E_{+}( \beta _{1}) |,|E_{R}(\beta _{2}) - E_{+}(\beta _{2})|,|E_{L}-E_{-}( \beta _{2}) | \right ) \\ &\quad\leq 2\varepsilon . \end{aligned}$$

Using (A.6) at $\beta _{1,2}$ with $\sharp =R$, we get $|c_{R}^{+}(\beta _{1})|^{2}(h - 2\varepsilon )^{2} \leq \varepsilon ^{2}$ and $|c_{R}^{-}(\beta _{2})|^{2}(h - 2\varepsilon )^{2} \leq \varepsilon ^{2}$, which imply $|c_{R}^{+}(\beta _{1})|^{2}\le \frac{1}{4}$ and $|c_{R}^{-}(\beta _{2})|^{2}\le \frac{1}{4}$. The latter relation yields $|c_{R}^{+}(\beta _{2})|^{2}\ge \frac{3}{4}-\varepsilon >\frac{1}{2}$ by (A.5). It follows from the continuity of the coefficient $c^{+}_{R}$ that there exists $\beta \in (\beta _{1},\beta _{2})$ such that $|c^{+}_{R}(\beta )|^{2} = \frac{1- \epsilon ^{2}}{2}$. Hence, by (A.4) we also have $|c^{+}_{L}(\beta )|^{2} \geq \frac{1- \epsilon ^{2}}{2}$, completing the proof. □

1.2 A.2 Construction of the non-avoided crossing

We first give a precise notion of eigenvector localization.

Definition A.4

For $\omega \in \Omega$ and a pair $\left ( \nu ,\theta \right )$ of positive parameters, we will say that $H$ is $\left ( \nu ,\theta \right )$-localized if all eigenvalues of $H$ are simple and for each $E\in \sigma (H)$, the corresponding eigenvector $\psi _{E}$ satisfies

$$ \left \vert \psi _{E}(y,\omega ) \right \vert ^{2}\le \frac{1}{\theta}\langle x_{E}(\omega )\rangle ^{2}\mathrm{e}^{-\nu \left \vert y-x_{E}(\omega ) \right \vert }. $$

(A.9)

We call $x_{E}$ the localization center of the eigenvector $\psi _{E}$.

One of the key results we will use in this appendix is

Theorem A.5

Eigenfunctions localization

There exist $C,\nu >0$ such that

$$ \mathbb{P}\left ( \left \{ \omega \in \Omega :\ \textit{$H^{\sharp }(0)$ is $\left ( \nu ,\theta \right )$-localized} \right \} \right )\le 1-C\theta ,\quad \sharp =\Lambda ,\Lambda _{L}, \Lambda _{R}. $$

(A.10)

Proof

This is a consequence of [3, Theorems 5.8, 7.4, and 12.11] and Markov’s inequality. □

We will fix this value of $\nu$ henceforth.

Definition A.6

In this definition, we gather requirements on $\omega \in \Omega$ used in our construction. The requirements depend on a small parameter $\theta < 1$, and a large parameter $b$.

There exists eigenvalues $E_{R}(0)$ (resp. $E_{L}$) of $H_{R}(0)$ (resp. $H_{L}$) with eigenvectors $\varphi _{L}, \varphi _{R}$ such that

• (i) $H_{L}$, $H_{R}(0)$ are $\left ( \nu ,\theta \right )$-localizing; In particular, $\varphi _{L}, \varphi _{R}$ are localized;

• (ii) $|E_{L} - E_{R}(0)| \leq b \theta /{\mathcal {L}}$;

• (iii) Let

  $$ J: = \{\lambda \in \mathbb{R}:\ \mathrm{dist}(\lambda ,\left \{ E_{L},E_{R}(0) \right \})\le \sqrt{\theta}/{\mathcal {L}}\} $$

  (A.11)

  Then $\sigma (H_{L})\cap J=\{E_{L}\}$ and $\sigma (H_{R}(0))\cap J=\{E_{R}(0)\}$.

• (iv) $|\varphi _{R}(0)|^{2} \geq - C_{\nu}/\ln \theta$. Here $C_{\nu}$ is an explicit constant given in Theorem C.2.

We will denote by ${\mathcal {C}}$ a set of all $\omega \in \Omega$ for which (i)-(iv) hold true.

For $\omega \in {\mathcal {C}}$, let $(E_{R}(\beta ), \varphi _{R}(\beta ))$ be the eigenpair of $H_{R}(\beta )$ that depends smoothly on $\beta \in J$.

Proposition A.7

Suppose that $\omega \in {\mathcal {C}}$ and that $\theta$ is small enough. Then $E_{R}(\beta ), E_{L}$ intersect for some $\beta \in I$, where

$$ I :=[-a,a],\quad a=4 \frac{b}{C_{\nu}} \frac{\theta \ln \theta}{{\mathcal {L}}}, $$

(A.12)

and the associated function $h$ satisfies $h \geq b \theta / {\mathcal {L}}$.

Proof

Let $P_{R}(\beta )$ be the projection on $\varphi _{R}(\beta )$. By the Hellmann-Feynman theorem

$$ \dot{E}_{R}(\beta ) = \mathrm{tr}{\left(P_{R}(\beta ) W\right)};\quad \ddot{E}_{R}( \beta ) = \mathrm{tr}{\left(\dot{P}_{R}(\beta ) W\right)}. $$

Since $\left \Vert H_{R}(\beta )-H_{R}(0) \right \Vert \le \beta$, by Weyl’s theorem

$$ \mathrm{dist}\left ( E_{R}(\beta ), \sigma (H_{R}(\beta )) \setminus \left \{ E_{R}(\beta ) \right \} \right ) \geq \mathrm{dist}\left ( E_{R}(0), \sigma (H_{R}(0)) \setminus \left \{ E_{R}(0) \right \} \right )-2 \beta \geq \frac{\sqrt{\theta}}{2 {\mathcal {L}}} $$

for $\beta \in I$ and $\theta$ sufficiently small. Hence, by standard perturbation theory,

$$ \| \dot{P}_{R}(\beta ) \| \leq \beta /{\mathrm{dist}\left ( E_{R}( \beta ), \sigma (H_{R}(\beta )) \setminus \left \{ E_{R}(\beta ) \right \} \right )} \leq 2\beta \frac{ {\mathcal {L}}}{\sqrt{\theta}}. $$

We now estimate

$$ \dot{E}_{R}(\beta ) =\dot{E}_{R}(0)+\int _{0}^{\beta }\ddot{E}_{R}(s) ds \ge -\frac{C_{\nu}}{ \ln \theta }-2\beta ^{2} \frac{ {\mathcal {L}}}{\sqrt{\theta}}\ge -\frac{C_{\nu}}{2 \ln \theta }, \quad \beta \in I, $$

using Definition A.6(iv), $Rank(P_{R})=1$, and $\left \Vert W \right \Vert \le 1$ in the second step. Hence

$$ E_{R}\left ( a \right )-{E}_{R}(0), {E}_{R}(0)-{E}_{R}\left ( -a \right )\ge 2b\frac{ \theta }{{\mathcal {L}}}. $$

Using Definition A.6(ii), we see that $h \geq b \theta / {\mathcal {L}}$, completing the proof. □

Lemma A.8

For $b$ large enough, $\mathbb{P}({\mathcal {C}}) \geq c b \theta$ for some constant $c$ independent of $\theta$ and $b$.

Proof

Let ${\mathcal {C}}_{k}$ denote the event that the property (k) with $k=i,ii,iii,iv$ in Definition A.6 holds. By (A.10), $\mathbb{P}\left ( {\mathcal {C}}_{i} \right )\ge 1 - C \theta$.

If $H_{R}(0)$ is $(\nu , \theta )$ localizing and (C.2) is satisfied for some interval $J$ and constant $c$, it follows from Lemma C.2 that there exists an eigenvalue $E_{R}$ of $H_{R}(0)$ and the associated eigenvector $\varphi _{R}$ such that $|\varphi _{R}(0)|^{2} > -C_{\nu }/\ln (\theta )$. As shown in Lemma C.1, (C.2) indeed holds deterministically with the choice $J=[\tfrac{1}{4},\tfrac{15}{4}]$, $c=\tfrac{1}{49}$. Thus we can pick ${\mathcal {C}}_{iv}:={\mathcal {C}}_{i}$.

To bound $\mathbb{P}\left ( {\mathcal {C}}_{ii} \right )$ we will invoke

Theorem A.9

Two-sided Wegner estimate

Let $K\subset {\mathbb{Z}}$ be an interval. Then for any compact subinterval $J$ of $(0,4)$ there exist $L_{0}>0$ and constants $C_{+}\ge C_{-}>0$ such that we have

$$ C_{-}\left \vert J \right \vert \left \vert K \right \vert \le \mathbb{E}\left ( \mathrm{tr}\left(\chi _{J}( H^{K} ) \right)\right ) \le C_{+}\left \vert J \right \vert \left \vert K \right \vert , $$

(A.13)

provided $\left \vert K \right \vert >L_{0}$.

Proof

The upper bound is well known, see e.g., [3, Corollary 4.9]. The lower bound was recently established in [31, Theorem 1.1] in the continuum setting, but the same proof works for the lattice systems considered here as well. □

We will also need the following extension of the upper Wegner bound, known as the Minami estimate:

Theorem A.10

Minami estimate

Under the same assumptions as in Theorem A.9, for any $n\in \mathbb{N}$ we have

$$ \mathbb{P}\left ( \mathrm{tr}\left (\chi _{J} ( H^{K}) \right )\ge n \right )\le \frac{1}{n!}\left ( C_{+}\left \vert J \right \vert \left \vert K \right \vert \right )^{n}. $$

(A.14)

Proof

In this generality, the bound goes back to [21], see also [3, Theorem 17.11]. □

Let $\check{I}:=[ E_{R}(0)-b \theta /{\mathcal {L}},E_{R}(0)+ b \theta /{ \mathcal {L}}]$. Combining the lower bound in (A.13) with (A.14) and using the statistical independence of $H_{L}$ and $H_{R}(0)$, we see that

$$ \mathbb{P}\left ( \mathrm{tr}\left(\chi _{\check{I}}\left ( H_{L} \right )\right) \ge 1 \right )\ge \mathbb{E}\left ( \mathrm{tr}\chi _{\check{I}}\left ( H_{L} \right ) \right )-\sum _{n=2}^{\infty }\left ( n-1 \right ) \mathbb{P} \left ( \mathrm{tr}\left(\chi _{\check{I}}\left ( H_{L}\right) \right )\ge n \right )\geq c b \theta $$

(A.15)

for some $b$-independent constant $c>0$. This implies that $\mathbb{P}\left ( {\mathcal {C}}_{ii} \right ) \geq c b \theta$ for such $b$.

This leaves us with estimating $\mathbb{P}\left ( {\mathcal {C}}_{iii} \right )$. Let $\hat{J}: = \{\lambda \in \mathbb{R}:\ \left \vert \lambda -E_{R}(0) \right \vert \le 2\sqrt{\theta}/{\mathcal {L}}\}$. Then $J\subset \hat{J}$ for $J$ specified in (A.11) and, using the statistical independence of $H_{L}$ and $H_{R}(0)$, by (A.14)

$$ \mathbb{P}\left ( \mathrm{tr}\left(\chi _{J}\left ( H_{L} \right )\right)\ge 2 \right )\le \mathbb{P}\left ( \mathrm{tr}\left(\chi _{\hat{J}}\left ( H_{L} \right )\right)\ge 2 \right )\le C\theta . $$

(A.16)

To complete the argument, we will use the following consequence of Theorem A.10.

Theorem A.11

Let $\delta >0$ and let $\mathcal {E}_{\omega}$ be an event

$$ \mathcal {E}_{\omega}:=\left \{ \sigma (H^{K})\textit{ is } \delta \textit{-level spaced on } \Lambda \right \}. $$

Then there exists $C>0$ such that

$$ \mathbb{P}\left ( \mathcal {E}_{\omega }\right )\ge 1-C\delta \left \vert K \right \vert ^{2}. $$

Proof

This statement is essentially [44, Lemma 2], in the formulation given in [25, Lemma B.1]. □

Applying this with the choice $K=\Lambda _{R}$, we deduce that

$$ \mathbb{P}\left ( \mathrm{tr}\left(\chi _{J}\left ( H_{R} \right )\right)\ge 2 \right )\le C\sqrt{\theta}/\ln ^{2}{\mathcal {L}}\le {\theta} $$

(A.17)

for ℒ large enough. This yields $\mathbb{P}\left ( {\mathcal {C}}_{iii} \right )\ge 1 - C \theta$.

Putting our bounds on $\left ( {\mathcal {C}}_{i} \right )$–$\left ( { \mathcal {C}}_{iv} \right )$ together, we see that for $b$ large enough $\mathbb{P}({\mathcal {C}}) \geq c b \theta$ for some constant $c>0$. □

1.3 A.3 Construction of the avoided crossing

In addition to $\omega \in {\mathcal {C}}$, we will assume further properties of $\omega$ that will allow us to use perturbation theory to study the crossing.

Definition A.12

Let $\Lambda _{B}$ be a region of size ${\mathcal {L}}^{1/8}$, centered at the boundary between $\Lambda _{L}$ and $\Lambda _{R}$, i.e. (recall (3.1)–(3.2)) $\Lambda _{B} = \left ( \partial \Lambda _{R} \right )_{{\mathcal {L}}^{1/8}}$. We pick $b_{L}, b_{R}\in {\mathbb{Z}}$ so that $\Lambda _{B}=(b_{L}, b_{R})$. We denote by $H_{B} := H^{\Lambda _{B}}$ the Hamiltonian restricted to this region. We will say that $\omega \in {\mathcal {A}}$ if $\omega \in {\mathcal {C}}$ and the following items hold true

• (i) $H_{B}$ has no spectrum in the interval $\hat{J}:=(E_{L} - \theta ^{-1}{\mathcal {L}}^{-1/2}, E_{L} +\theta ^{-1} {\mathcal {L}}^{-1/2})$.

• (ii) There are at most two eigenvalues of $H(0)$ in the interval $J$ defined in (A.11).

• (iii) The centers of $\varphi _{L}$ and $\varphi _{R}$ are a distance of order $\sqrt {\mathcal {L}}/\ln {\mathcal {L}}$ away from the boundary of $\Lambda _{R}$. Specifically,

  $$ \left \Vert \chi _{\{\left \vert x \right \vert >\sqrt{\mathcal {L}}/(4 \ln{\mathcal {L}})\}} \varphi _{R} \right \Vert + \left \Vert \chi _{\{x>-3 \sqrt{\mathcal {L}}/\ln{\mathcal {L}}\}} \varphi _{L} \right \Vert \leq e^{-c \sqrt {\mathcal {L}}/\ln {\mathcal {L}}}. $$

  (A.18)

• (iv) For $\lambda \in \hat{J}$,

  $$ \left \Vert \chi _{\{\left \vert x-l \right \vert \ge{\mathcal {L}}^{1/8} \}}(H_{B} - \lambda )^{-1} \delta _{l} \right \Vert \leq e^{-c { \mathcal {L}}^{1/8}}. $$

• (v) For $\sharp =L,R$,

  $$ \left \vert \langle \delta _{r}, \left ( H_{B} - E_{\sharp }\right )^{-1} \delta _{l}\rangle -1 \right \vert \ge 2\theta ^{\frac{1}{4}}. $$

  We note that condition (i) above ensures that the resolvents in (iv)-(v) are well-defined.

The dependence on the parameter $\theta$ in the above definition is chosen so that $\mathbb{P}\left ( {\mathcal {A}} \right )=O\left ( \theta \right )$. We will establish this at the end of the section.

Let $\varphi _{R}(\beta )$ be an eigenvector of $H_{R}(\beta )$, which is an analytic continuation of $\varphi _{R}(0)$. (Note that $H_{R}(\beta )$ is a finite rank operator, so its eigenvectors do have analytical continuation on the real line, c.f. [43]). We recall that $H_{L}(\beta )$ is $\beta$-independent, so $\varphi _{L}(\beta ) \equiv \varphi _{L}$. We first show that the analogue of (A.18) holds if we replace $\varphi _{R}(0)$ with $\varphi _{R}(\beta )$. For an interval $J$, we set $J_{a} := a J$.

Lemma A.13

Assume that $\omega \in {\mathcal {A}}$. For $\beta \in I$ defined in (A.12),

$$ \left \Vert \chi _{\{\left \vert x \right \vert > \sqrt{\mathcal {L}}/(2 \ln{\mathcal {L}})\}} \varphi _{R}(\beta ) \right \Vert \leq e^{-c \sqrt {\mathcal {L}}/\ln {\mathcal {L}}}. $$

(A.19)

Proof

Let $\hat{H}_{R}(0)=H_{R}(0)+(1-E_{R}(0))P_{R}(0)$, where $P_{R}(0)$ is an orthogonal projection onto $Span( \varphi _{R}(0) )$. We observe that by Definition A.6(iii) and $\left \vert E_{R}(\beta )-E_{R}(\beta ) \right \vert \le \beta$,

$$ \left \Vert \left ( \hat{H}_{R}(0)-E_{R}(\beta ) \right )^{-1} \right \Vert \le \frac{2 {\mathcal {L}}}{\sqrt{\theta}},\quad \beta \in I. $$

(A.20)

We have

$$ \begin{aligned} &\chi _{\{\left \vert x \right \vert > \sqrt {\mathcal {L}}/(2\ln { \mathcal {L}})\}} \varphi _{R}(\beta ) \\ &\quad=\chi _{\{\left \vert x \right \vert > \sqrt {\mathcal {L}}/(2\ln {\mathcal {L}})\}} \left ( \hat{H}_{R}(0)-E_{R}( \beta ) \right )^{-1}\left ( \hat{H}_{R}(0)-E_{R}(\beta ) \right ) \varphi _{R}(\beta ) \\ &\quad =\chi _{\{\left \vert x \right \vert > \sqrt {\mathcal {L}}/(2\ln { \mathcal {L}})\}} \left ( \hat{H}_{R}(0)-E_{R}(\beta ) \right )^{-1} \left ( (1-E_{R}(0))P_{R}(0)+\beta W \right )\varphi _{R}(\beta ). \end{aligned} $$

To estimate the right hand side, we note that

$$ \left \Vert \chi _{\{\left \vert x \right \vert > \sqrt{\mathcal {L}}/(4 \ln{\mathcal {L}})\}}\left ( P_{R}(0)+\beta W \right ) \right \Vert \le \mathrm{e}^{-c \sqrt {\mathcal {L}}/\ln {\mathcal {L}}} $$

by (A.18) and the compactness of $\operatorname*{supp}(W)$. Hence (A.19) will follow once we show that

$$ \left \Vert \chi _{\{\left \vert x \right \vert > \sqrt{\mathcal {L}}/(2 \ln{\mathcal {L}})\}} \left ( \hat{H}_{R}(0)-E_{R}(\beta ) \right )^{-1}{ \chi _{\{\left \vert x \right \vert \le \sqrt{\mathcal {L}}/(4\ln{ \mathcal {L}})\}}} \right \Vert \leq e^{-c \sqrt {\mathcal {L}}/\ln { \mathcal {L}}}. $$

The latter bound is a consequence of the spectral theorem, the estimate (A.20), and the fact that $H_{R}(0)$ (and hence $\hat{H}_{R}(0)$) is $\left ( \nu ,\theta \right )$-localizing for $\omega \in {\mathcal {A}}$. □

We recall that $P_{dec}(\beta )$ denotes the orthogonal projection onto $Span\left ( \varphi _{L}, \varphi _{R}(\beta ) \right )$. By standard perturbation theory, $P_{dec}(\beta )$ is a spectral projection of $H_{dec}(\beta )$ for all $\beta \in I$. We first establish that $P_{dec}(\beta )$ is close to a spectral projection of $H(\beta )$.

Proposition A.14

Assume that $\omega \in {\mathcal {A}}$. Then for $\beta \in I$ (recall (A.11) and (A.12)) we have

• (i) $\sigma (H(\beta ))\cap J=\left \{ E_{-}(\beta ),E_{+}(\beta ) \right \}$ where $E_{\pm}(\beta )$ are real analytic in $\beta$;

• (ii) $\mathrm{dist}(\left \{ E_{-}(\beta ),E_{+}(\beta ) \right \},\left \{ E_{L},E_{R}(\beta ) \right \}) \leq \mathrm{e}^{-c \sqrt { \mathcal {L}}/\ln {\mathcal {L}}}$;

• (iii) Let $P(\beta )$ be the spectral projection on $E_{\pm}(\beta )$, then $\|{P}(\beta ) - P_{dec}(\beta )\|\le \mathrm{e}^{-c \sqrt { \mathcal {L}}/\ln {\mathcal {L}}}$;

• (iv) We can label $E_{\pm}(\beta )$ so that the associated eigenfunctions $\varphi _{\pm}(\beta )$ satisfy

  $$ |\langle \varphi _{-}(0),\varphi _{R}(0) \rangle |^{2} \leq e^{-c \sqrt {\mathcal {L}}/\ln {\mathcal {L}}},\quad |\langle \varphi _{+}(0), \varphi _{L} \rangle |^{2} \leq e^{-c\sqrt {\mathcal {L}}/\ln { \mathcal {L}}}. $$

Proof

By Lemma C.4, (A.18), and Lemma A.13 we deduce that

$$ \mathrm{dist}\left ( \sigma (H(\beta )),E_{\sharp }(\beta ) \right ) \le \mathrm{e}^{-c \sqrt {\mathcal {L}}/\ln {\mathcal {L}}},\quad \sharp =L,R. $$

It follows that $H(\beta )$ has at least two eigenvalues in the interval $I$. Combined with standard perturbation theory and the fact that for $\omega \in {\mathcal {A}}$ the operator $H(0)$ has at most two eigenvalues in $J$, see Definition A.12(ii), we see that Proposition A.14(i)–A.14(iii) holds. The last statement follows from (A.18), Lemma A.13, and Lemma C.4. □

Proposition A.15

Suppose that $\omega \in {\mathcal {A}}$, then the eigenvalues $E_{\pm}(\beta )$ cannot intersect each other in the interval $I$.

We start with the following preliminary observation.

Lemma A.16

The operator $\bar{P}_{dec}(\beta ) \left ( H(\beta )-\lambda \right ) \bar{P}_{dec}( \beta )$ is invertible on the range of $\bar{P}_{dec}(\beta )$ for all $\lambda \in J$ and $\beta \in I$, and the norm of the inverse is bounded by $C {\mathcal {L}}/\sqrt{\theta}$.

Proof

It is a standard result in perturbation theory that if $B$ is invertible and $\|B^{-1}\| \|(A- B) \| <1$, then $A$ is invertible and

$$ \|A^{-1}\| \leq \frac{\|B^{-1}\|}{1 - \|B^{-1}\| \|A-B\|}. $$

To prove Lemma A.16, we combine this observation with

$$ B = \bar{P}(\beta ) (H(\beta ) - \lambda ) \bar{P}(\beta ) + P(\beta ), \quad A = \bar{P}_{dec}(\beta ) \left ( H({\beta })-\lambda \right ) \bar{P}_{dec}(\beta ) + P_{dec}(\beta ). $$

By Proposition A.14, $\|A - B\| \leq e^{-c \sqrt {\mathcal {L}}/\ln {\mathcal {L}}}$. By $\omega \in {\mathcal {A}}$, $B^{-1}$ is invertible with

$$ \|B^{-1}\| \leq C \frac{{\mathcal {L}}}{\sqrt{\theta}}. $$

We now note that $A$ is block diagonal with respect to $P_{dec}(\beta ),\bar{P}_{dec}(\beta )$, and that its inverse exists if and only if each associated block has an inverse. □

Proof of Proposition A.15

We will suppress the $\beta$ dependence and use the shorthand $P$ for $P_{dec}(\beta )$ in this proof. Here, the idea is to use Schur complementation. Namely, given $\lambda \in J$, we consider $M=M(\beta ,\lambda )$, the Schur complement of $H$ in $Ran(\bar{P})$, defined as

$$ M:=P\left ( H-\lambda \right )P-PH \bar{P}\left ( \bar{P} \left ( H- \lambda \right ) \bar{P} \right )^{-1}\bar{P}H P. $$

We note that by Lemma A.16, $M$ is well-defined for our range of $\lambda$s and $\beta$s. $M$ is a rank-two operator whose range is spanned by $(\varphi _{R}, \varphi _{L})$. Using the Guttman rank additivity formula, [68, Sect. 0.9], we see that $\mathrm{tr}{\left(\chi _{\left \{ \lambda \right \}}(H)\right)}=2$ (a sufficient and necessary condition for the intersection of two eigenvalues) if and only if $M=0$. In particular, the non-intersection property will follow if we can show that in this range we have $M_{LR} = \langle \varphi _{L}, M \varphi _{R} \rangle \neq 0$. We claim that

$$ M_{LR} = \varphi _{L}(l) \varphi _{R}(r) \left (1 - \langle \delta _{r},(H_{B} - E_{-})^{-1}\delta _{l}\rangle + Error \right ), $$

(A.21)

where $|Error| \leq \theta ^{2}$. Since $\omega \in {\mathcal {A}}$, by Definition A.12(v) we have

$$ \left \vert \langle \delta _{r}, \left ( H_{B} - E_{-} \right )^{-1} \delta _{l}\rangle -1 \right \vert \ge \theta ^{\frac{1}{4}}. $$

Hence, for sufficiently large ℒ, $M_{LR}\neq 0$ as the eigenfunctions of $H_{L,R}$ cannot vanish at the respective boundary points.

It remains to derive (A.21). We recall that $\Gamma := \Gamma _{lr} + \Gamma _{rl}$ is the hopping term connecting the region $\Lambda _{R}$ to the region $\Lambda _{L}$. In particular, $\Gamma \varphi _{L} = \varphi _{L}(l) \delta _{r}$ and $\Gamma \varphi _{R} = \varphi _{R}(r) \delta _{l}$. We use these equations to evaluate the terms in

$$ M_{LR}=\langle \varphi _{L}, \left ( H-\lambda \right ) \varphi _{R} \rangle -\langle \varphi _{L},PH \bar{P}\left ( \bar{H}-\lambda \right )^{-1}\bar{P}H P\varphi _{R}\rangle , $$

where we denote $\bar{H}= \bar{P} H \bar{P}$, and let $\left ( \bar{H}-\lambda \right )^{-1}$ denote the inverse of $\bar{H}-\lambda$ on the $Ran\left ( \bar{P} \right )$. The first term is equal to

$$ \langle \varphi _{L},H\varphi _{R}\rangle =\langle \varphi _{L}, \Gamma \varphi _{R}\rangle =\varphi _{L}(l)\varphi _{R}(r). $$

To evaluate the second term, we use the identity $\bar{P}H P = \bar{P} \Gamma P$ to get

$$ \langle \varphi _{L},PH \bar{P}\left ( \bar{H}-\lambda \right )^{-1} \bar{P}HP\varphi _{R}\rangle = \varphi _{L}(l)\varphi _{R}(r) \langle \delta _{r},\left ( \bar{H}-\lambda \right )^{-1}\delta _{l}\rangle . $$

We next use the resolvent identity

$$ \left ( \bar{H}-\lambda \right )^{-1} = \left ( H_{B} - \lambda \right )^{-1} +T , \quad T := \left ( \bar{H}-\lambda \right )^{-1} (H_{B} - H +\bar{P}HP)\left ( H_{B} - \lambda \right )^{-1}. $$

We note that since $\omega \in {\mathcal {A}}$, by Definition A.12(iii) the resolvent $(H_{B} - \lambda )^{-1}$ is well-defined and its norm is bounded by $C {\mathcal {L}}^{1/4}$. Moreover, since $(H_{B} - H)\chi _{\{\left \vert x-l \right \vert < {\mathcal {L}}^{1/8} \}}=0$, by Definition A.12(iv), (A.18), and Lemma A.13 we get

$$ \begin{aligned} \left \Vert T\delta _{l} \right \Vert \le 5&\left \Vert \left ( \bar{H}-\lambda \right )^{-1} \right \Vert \left \Vert \chi _{\{\left \vert x-l \right \vert \ge{\mathcal {L}}^{1/8}\}}(H_{B} - \lambda )^{-1} \delta _{l} \right \Vert \\ +&\left \Vert \left ( \bar{H}-\lambda \right )^{-1} \right \Vert \left \Vert P\chi _{\{\left \vert x-l \right \vert < {\mathcal {L}}^{1/8} \}} \right \Vert \left \Vert (H_{B} - \lambda )^{-1} \right \Vert \le C e^{-c {\mathcal {L}}^{1/8}}, \end{aligned} $$

which implies that

$$ \left \vert \langle \delta _{r},T\delta _{l}\rangle \right \vert \leq C e^{-c {\mathcal {L}}^{1/8}}. $$

Furthermore, by standard perturbation theory and Definition A.12(iii),

$$ \left \Vert \left ( H_{B} - \lambda \right )^{-1} - \left ( H_{B} - E_{-} \right )^{-1} \right \Vert \leq C |E_{-} - \lambda | \theta ^{2}{ \mathcal {L}}. $$

Since $E_{-} - \lambda$ is of order ${\mathcal {L}}^{-1}$ for $\lambda \in J$, we get (A.21). □

We now show

Lemma A.17

$\mathbb{P}({\mathcal {A}}) \geq c \theta$ for some constant $c$.

Proof

Let ${\mathcal {A}}_{k}$ denote the event that property (k) in Definition A.12 holds.

Using the upper bound in (A.13), we get $\mathbb{P}({\mathcal {A}}_{i}) \geq \mathbb{P}({\mathcal {C}})- C\theta ^{-1}{ \mathcal {L}}^{-1/2}{\mathcal {L}}^{1/8}\ge c b \theta$ for ℒ large enough. On the other hand, using (A.14), we deduce that

$$ \mathbb{P}({\mathcal {A}}_{ii}\cap {\mathcal {A}}_{i})\ge \mathbb{P}({ \mathcal {A}}_{i})- \mathbb{P}\left ( \mathrm{tr}\chi _{J}\left ( H(0) \right )\ge 3 \right )\ge \mathbb{P}({\mathcal {A}}_{i})-C\theta ^{3/2} \le c b \theta . $$

Let $\hat{\Lambda}_{L}=[-4\sqrt {\mathcal {L}}/\ln {\mathcal {L}},l]$. Then, using the upper bound in (A.13), for ℒ large enough,

$$ \mathbb{P}\left ( \mathrm{tr}\left(\chi _{\hat{J}} ( H^{\hat{\Lambda}_{L}}) \right )=0 \right )\ge 1-C(\sqrt {\mathcal {L}}/\ln {\mathcal {L}}) \theta ^{-1}{\mathcal {L}}^{-1/2}\ge 1-\theta ^{2}. $$

Let ${\mathcal {E}}:={\mathcal {A}}_{ii}\cap {\mathcal {D}}$, where ${\mathcal {D}}$ is the event $\mathrm{tr}\left(\chi _{\hat{J}} ( H^{\hat{\Lambda}_{L}}) \right )=0$. Then we see that

$$ \mathbb{P}({\mathcal {E}}) \geq \mathbb{P}({\mathcal {A}}_{ii})-\theta ^{2} \ge c b \theta . $$

We claim that (A.18) holds for $\omega \in {\mathcal {E}}$, implying that $\mathbb{P}({\mathcal {A}}_{iii}\cap {\mathcal {A}}_{ii}) \geq c b \theta$. Indeed, the bound $\left \Vert \chi _{\{\left \vert x \right \vert >\sqrt{\mathcal {L}}/(4 \ln{\mathcal {L}})\}} \varphi _{R} \right \Vert \leq e^{-c \sqrt { \mathcal {L}}/\ln {\mathcal {L}}}$ follows directly from Definition A.6, parts (i,iv) (we recall that ${\mathcal {A}}\subset {\mathcal {C}}$). On the other hand, if the localization center for $\varphi _{L}$ were located in $[-\frac{7}{2}\sqrt {\mathcal {L}}/\ln {\mathcal {L}},l]$, Definition A.6(i) would imply that $\left \Vert \chi _{x<-4\sqrt{\mathcal {L}}/\ln{\mathcal {L}}}\varphi _{L} \right \Vert \le \mathrm{e}^{-c\sqrt {\mathcal {L}}/\ln {\mathcal {L}}}$. But then we would have $\mathrm{dist}\left ( E_{L},\sigma (H^{\hat{\Lambda}_{L})} \right ) \le \mathrm{e}^{-c\sqrt {\mathcal {L}}/\ln {\mathcal {L}}}$ thanks to Lemma C.4, contradicting $\mathrm{tr}\left(\chi _{\hat{J}} ( H^{\hat{\Lambda}_{L}} )\right)=0$. This implies that the localization center for $\varphi _{L}$ is located in $\Lambda _{L}\setminus [-\frac{7}{2}\sqrt {\mathcal {L}}/\ln { \mathcal {L}},l]$, which in turn implies that $\left \Vert \chi _{\{x>-3\sqrt{\mathcal {L}}/\ln{\mathcal {L}}\}} \varphi _{L} \right \Vert \leq e^{-c \sqrt {\mathcal {L}}/\ln { \mathcal {L}}}$ by Definition A.6(i).

To estimate $\mathbb{P}({\mathcal {A}}_{iv}\cap {\mathcal {A}}_{iii})$, we note that our assumptions on randomness imply

$$ \sup _{\lambda \in \mathbb{R}} \mathbb{E}\left \Vert \chi _{\{\left \vert x-l \right \vert \ge{\mathcal {L}}^{1/8}\}}(H_{B} - \lambda -i0)^{-1} \delta _{l} \right \Vert \le Ce^{-c {\mathcal {L}}^{1/8}}, $$

[3, Theorem 12.11]. Hence, denoting

$$ {\mathcal {F}}:=\left \{ \omega \in \Omega :\ \left \Vert \chi _{\{ \left \vert x-l \right \vert \ge{\mathcal {L}}^{1/8}\}}(H_{B} - \lambda )^{-1} \delta _{l} \right \Vert \leq e^{-c {\mathcal {L}}^{1/8}} \right \}, $$

we see that $\mathbb{P}({\mathcal {A}}_{iv}\cap {\mathcal {A}}_{iii})\ge c b \theta$ for ℒ large enough by Markov’s inequality.

Finally, the bound $\mathbb{P}({\mathcal {A}}_{v}\cap {\mathcal {A}}_{iv})\ge c b \theta$ is a direct consequence of □

Lemma A.18

For a fixed $s \in (0,1/2)$ and $\lambda \in I$, we have

$$ \mathbb{P}\left ( \left \{ \omega \in \Omega : \ \left \vert \langle \delta _{r}, \left ( H_{B} - E \right )^{-1}\delta _{l}\rangle -1 \right \vert \ge \theta ^{\frac{1}{s}} \right \} \right ) \ge 1- C_{s} \theta . $$

Proof of Lemma A.18

Let $G(x,y):=\langle \delta _{x},\left ( H_{B} - \lambda \right )^{-1} \delta _{y}\rangle$. We first observe that, thanks to the geometric resolvent identity (or directly by [3, Eq. 12.7]),

$$ G(l,r)= \hat{G}(l,l)G(r,r), $$

(A.22)

where $\hat{G}(x,y)=\langle \delta _{x},\left ( \hat{H}_{B} - \lambda \right )^{-1} \delta _{y}\rangle$ and $\hat{H}_{B}$ is obtained from $H_{B}$ by the removal of the $( l,r)$ bond, i.e., $\hat{H}_{B}=H_{B}-\Gamma _{(l,r)} - \Gamma _{(r,l)}$. We use the resolvent identity

$$ \tilde{G}(r,r) = G(r,r) - \tilde{G}(r,r) \hat{G}(l,l) G(r,r) $$

to obtain

$$ \frac{1}{\hat{G}(l,l)G(r,r)-1}=-\frac{\tilde{G}(r,r)}{ G(r,r)}, $$

where $\tilde{G}(x,y):=\langle \delta _{x},\left ( H_{B}+\hat{G}(l,l)\chi _{ \left \{ r \right \}} - \lambda \right )^{-1}\delta _{y}\rangle$. An important fact to note here is that $\hat{G}(l,l)$ is independent of the $\omega _{r}$ random variable. This independence allows us to conclude that

$$ \mathbb{E}_{\omega _{1}}\left \vert \tilde{G}(r,r) \right \vert ^{s} \le C_{s},\quad s\in (0,1). $$

On the other hand, under our conditions on the probability distribution $\mu$, we also have (see [3, Theorem 12.8]

$$ \mathbb{E}\left \vert G(r,r) \right \vert ^{-s}\le C_{s},\quad s\in (0,1). $$

Combining these two bounds and using the Hölder inequality, we deduce that

$$ \mathbb{E}\left \vert \frac{1}{\hat{G}(l,l)G(r,r)-1} \right \vert ^{s} \le C_{s},\quad s\in (0,1/2), $$

from which the assertion follows by the Markov inequality. □

1.4 A.4 Proof of Theorem A.2

Theorem A.19

Let us denote by $\tilde{\Omega}_{F, {\mathcal {L}}} \subset \Omega$ all realizations for which $H(\beta )$ $F$-hybridize. Let $\omega \in {\mathcal {A}}$ and $F < 1/2$. Then for ℒ large enough, $\omega \in \tilde{\Omega}_{F, {\mathcal {L}}}$.

Proof

Consider the analytical family of eigenvectors $\varphi _{R}(\beta )$, $\varphi _{L}$ of $H_{dec}(\beta )$ and the analytical family $\varphi _{\pm}(\beta )$ of eigenvectors of $H(\beta )$. We will show that $\varphi (\beta ):=\varphi _{+}(\beta )$ is an analytical family whose existence is required in Definition A.1 of $\Omega _{F, {\mathcal {L}}}$. We recall that the families are labeled in such a way that at $\beta =0$, $\varphi _{+}$ has exponentially small overlap with $\varphi _{L}$. In particular, $\varphi _{+}(0)$ satisfies item (i) in Definition A.1.

By Proposition A.14, the families satisfy (A.3) with $\varepsilon = \mathrm{e}^{-c \sqrt {\mathcal {L}}/\ln {\mathcal {L}}}$. Proposition A.7 implies that the bandwidth of the crossing satisfies $h > 4 \varepsilon$. It then follows from Lemma A.3 that there exists $\beta$ such that

$$ \varphi _{+}(\beta ) = c_{L}^{+}(\beta ) \varphi _{L} + c_{R}^{+}( \beta ) \varphi _{R} + \varphi ^{\perp}, $$

with

$$ |c^{+}_{L}(\beta )|^{2} = |c^{+}_{R}(\beta )|^{2} \geq \frac{1- \epsilon ^{2}}{2}. $$

It follows that item (ii) of Definition A.1 is satisfied for any $F<1/2$, provided ℒ is large enough. □

As a corollary of the above result and Lemma A.17, we get that for any $F < 1/2$,

$$ \liminf _{{\mathcal {L}}\to \infty} \mathbb{P}(\tilde{\Omega}_{F, { \mathcal {L}}}) > 0. $$

The assertion of Theorem A.2 is established completely analogously, by splitting $\Lambda _{full}$ into $\Lambda _{L}$, $\Lambda _{R}$, and $-\Lambda _{L}$, and then repeating the same steps as above. The reason that we present a proof for the asymmetric region is related to the fact that, in this case, the boundary of $\Lambda _{R}$ consists of a single point $r$, whereas in the symmetric case it consists of two points $\pm r$, making the presentation slightly more cumbersome.  □

Appendix B: A Wannier basis for quasi-local projections

Here, we show the existence of a (generalized) Wannier basis, consisting of exponentially localized functions, for a rank $m$ orthogonal projection $P$ on $\ell ^{2}({\mathbb{Z}}^{d})$ that satisfies the quasi-locality property (B.4) below. The motivation for constructing such a basis is related to the fact that it allows showing the localization property (2.1) without assuming spectrum simplicity.

To illustrate the idea behind this construction, we start with the case $m=1$.

Lemma B.1

Suppose that the normalized vector $\psi \in \ell ^{2}\left ( \mathbb{T}_{L} \right )$ satisfies

$$ \max _{x,y\in \mathbb{T}_{L}}\left ( \left \vert \psi (x) \right \vert \left \vert \psi (y) \right \vert \mathrm{e}^{c\left \vert x-y \right \vert } \right )\le \frac{1}{\theta}. $$

(B.1)

Then, for any sufficiently small (but $L$-independent) $\theta$, we have $\|\psi \|_{\infty}^{2} \ge \left \vert \ln \theta \right \vert ^{-d-1}$, and there exists $x_{o}\in \mathbb{T}\,_{L}$ such that

$$ \left \vert \psi (y) \right \vert \le \frac{\left \vert \ln \theta \right \vert ^{\frac{d+1}{2}}}{\theta} \mathrm{e}^{-c\left \vert y-x_{o} \right \vert },\quad \forall y\in \mathbb{T}_{L}. $$

Proof of Lemma B.1

The second bound is an immediate consequence of the first with a (non unique, in general) choice of $x_{o}$ such that $\left \vert \psi (x_{o}) \right \vert =\|\psi \|_{\infty}$, so we only need to show that $\|\psi \|^{2}_{\infty}\ge \left \vert \ln \theta \right \vert ^{-d-1}$. Let $r=r(c,\theta )>0$ be such that

$$ \sum _{{y\in {\mathbb{Z}}^{d}:\ \left \vert y \right \vert >r}} \mathrm{e}^{-2c\left \vert y \right \vert }\le \frac{\theta ^{2} \|\psi \|_{\infty}^{2}}{2}. $$

In particular, for a fixed $c$ there exists $C$ such that we can choose $r=-C\ln \left ( {\theta \|\psi \|^{2}_{\infty }} \right )$ for $\theta$ sufficiently small. Then by (B.1) we can bound

$$\begin{aligned} 1&=\sum _{x\in \mathbb{T}_{L}}\left \vert \psi (x) \right \vert ^{2} \le {\|\psi \|^{2}_{\infty}} \sum _{ \substack{x\in \mathbb{T}_{L}:\\ \left \vert x-x_{o} \right \vert \le r}}1+ \sum _{ \substack{x\in \mathbb{T}_{L}:\\ \left \vert x-x_{o} \right \vert > r}} \frac{\mathrm{e}^{-2 c \left \vert x-x_{o} \right \vert }}{{\|\psi \|^{2}_{\infty}}\theta ^{2}} \\ &\le {\|\psi \|^{2}_{\infty}} (2r+1)^{d}+\frac{1}{2}. \end{aligned}$$

(B.2)

This implies that ${\|\psi \|^{2}_{\infty}}\ge \frac{1}{2(2r+1)^{d}}$ or, in view of the definition of $r$, ${\|\psi \|^{2}_{\infty}}\ge u$, where $u$ is a unique positive solution of

$$ \mathrm{e}^{-C u^{1/d}}= \theta u^{2}. $$

(B.3)

Since $u>\left \vert \ln \theta \right \vert ^{-d-1}$ for $\theta$ sufficiently small, we get ${\|\psi \|^{2}_{\infty}}\ge \left \vert \ln \theta \right \vert ^{-d-1}$. □

While considering the rank one projection $P$ is sometimes enough for random operators (e.g., for the randomness given by the rank one single site potential as in the standard Anderson model), in general it is not known whether the spectrum of a random operator that satisfies Assumptions 2.3–2.4 is a.s. simple or even has finite multiplicities. For our applications, one needs to be able to decompose $P$ into a sum of rank one mutually orthogonal projections that individually exhibit exponential decay. Such a decomposition is called a (generalized) Wannier basis for $P$. In general, finding a Wannier basis is a hard problem, due to a topological obstruction, see e.g., [51]. Here, we assert its existence for a finite rank $P$ with explicit control over its rank $m$, which is sufficient for our purposes.

Theorem B.2

Let $m\in {\mathbb{N}}$, $\theta >0$ be such that $m^{3}\theta \ll 1$. Suppose that a rank $m$ orthonormal projection $P\in {\mathcal {L}}({\mathcal {H}})$, ${\mathcal {H}}=\ell ^{2}\left ( {\mathbb{Z}}^{d} \right )$ satisfies

$$ \max _{x,y\in {\mathbb{Z}}^{d}}\left ( \left \vert P(x,y) \right \vert \mathrm{e}^{c\left \vert x-y \right \vert } \right )\le \theta ^{-1}. $$

(B.4)

Then we can decompose $P$ as $P=\sum _{i=1}^{m}P_{i}$, where $P_{i}=\left \vert \psi _{i}\rangle \langle \psi _{i} \right \vert$ are rank one mutually orthogonal projections that satisfy ${\|\psi _{i}\|_{\infty}}\ge \left \vert \ln \theta \right \vert ^{-d-1}$ and, for some $x_{i}\in {\mathbb{Z}}^{d}$,

$$ \left \vert \psi _{i}(y) \right \vert \le {\theta}^{-2}\mathrm{e}^{-c \left \vert y-x_{i} \right \vert /m},\quad y\in {\mathbb{Z}}^{d}. $$

We stress that the constant $c$ here is $m$-independent.

Proof

We will need some preparatory results. Using the argument identical to the one used in Lemma B.1 we obtain

Lemma B.3

Let $M=\max _{x\in {\mathbb{Z}}^{d}}P(x,x)$. Then there exists a ($\theta$-independent) $C>0$ such that $M\ge u$, where $u$ is a unique positive solution of (B.3). In particular, for $\theta$ sufficiently small, $M\ge \left \vert \ln \theta \right \vert ^{-d-1}$.

Let $L=L(c,\theta )>0$ be such that

$$ \sum _{\Lambda ^{c}_{L/4}(0)}\mathrm{e}^{-2c\left \vert y \right \vert }\le {\theta ^{6} M} $$

(B.5)

with $M$ as above. In particular, there exists $C$ such that we can choose

$$ L=-C\ln{\theta } $$

(B.6)

for $\theta$ sufficiently small. Consider

$$ \Xi _{L}:= \left ( \tfrac {3}{2}L {\mathbb{Z}} \right )^{d}, $$

(B.7)

cf. (4.14), and an $L$-cover of ${\mathbb{Z}}^{d}$ of the form

$$ {\mathbb{Z}}^{d}=\bigcup _{a \in \Xi _{L}} {\Lambda}_{L}(a). $$

We note that for any $x\in {\mathbb{Z}}^{d}$ we can find $a \in \Xi _{L}$ such that $\mathrm{dist}\left ( {\Lambda }_{L}^{c}(a),x \right )\ge L/4$.

Lemma B.4

For $L$ as above, let $T=\max _{a \in \Xi _{L}}\mathrm{tr}\left ( P\chi _{\Lambda _{L}(a)} \right )$. Then $T\ge 1/2$ for $\theta$ sufficiently small.

Proof

Suppose in contradiction that $\mathrm{tr}{\left(P\chi _{\Lambda _{L}(a)}\right)}< 1/2$ for any $a \in \Xi _{L}$. Picking $x_{o}$ as in the previous lemma and letting $a\in \Xi _{L}$ be such that $\mathrm{dist}\left ( {\Lambda }_{L}^{c}(a),x_{o} \right )\ge L/4$, we have

$$\begin{aligned} M&\le P(x_{o},x_{o})\sum _{y\in \Lambda _{L}(a)}P(y,y)+\sum _{y\in \Lambda _{L}^{c}(a)}\left \vert P(x_{o},y) \right \vert ^{2}\\ &\le M \sum _{y\in \Lambda _{L}(a)}P(y,y)+\theta ^{4} M< 2M/3, \end{aligned}$$

a contradiction. □

We now observe that since $\mathrm{tr}{(P)}=m$, the cardinality of a set

$$ {\mathcal {S}}:=\left \{ a \in \Xi _{L}:\ \mathrm{tr}{\left(P\chi _{\Lambda _{L}(a)}\right)} \ge 1/2 \right \} $$

cannot exceed $2\cdot 3^{d} m$ as each box $\Lambda _{L}(a)$ can overlap with at most $3^{d}$ other boxes.

Let ${\mathcal {R}}:=\cup \Lambda _{L}(a)$, where the union is taken over boxes with $a\in {\mathcal {S}}$ and boxes that overlap with them. We note that if $y\notin {\mathcal {R}}$, then

$$ P(y,y)< {2M}\theta ^{4} $$

(B.8)

for $\theta$ sufficiently small. Indeed, if $y\notin {\mathcal {R}}$, then $\mathrm{dist}\left ( y,\cup _{a\in{\mathcal {S}}} \Lambda _{L}(a) \right )\ge L/2$. In particular,

$$ P(y,y)\le P(y,y)\sum _{z\in \Lambda _{L/2}(y)}P(z,z)+\sum _{z\in \Lambda _{L/2}^{c}(y)}\left \vert P(z,y) \right \vert ^{2}\le \frac{1}{2}P(y,y)+\theta ^{4} M, $$

which yields (B.8).

Lemma B.5

Let $Q=P\chi _{{\mathcal {R}}} P$. Then $Q$ is close to $P$, namely $\left \Vert P-Q \right \Vert \le \theta ^{3}$ for $\theta$ sufficiently small. In particular, $Q$ is invertible as an operator on $Ran(P)$, with $Q\ge 1-\theta ^{3}$.

Proof

We have $Q^{2}=Q-P\chi _{{\mathcal {R}}^{c}} P\chi _{{\mathcal {R}}} P$ and

$$ \begin{aligned} \left \Vert \chi _{{\mathcal {R}}^{c}}P\chi _{{\mathcal {R}}} \right \Vert _{HS}= \sum _{y\in {\mathcal {R}}_{1}^{c},x\in {\mathcal {R}}} \left \vert P(x,y) \right \vert ^{2} &=\sum _{0< \mathrm{dist}\left ( y,{ \mathcal {R}} \right )\le L/2,x\in {\mathcal {R}}}\left \vert P(x,y) \right \vert ^{2} \\ &+\sum _{\mathrm{dist}\left ( y,{\mathcal {R}} \right ) > L/2,x\in { \mathcal {R}}}\left \vert P(x,y) \right \vert ^{2}. \end{aligned} $$

The first term can be estimated by $CmM^{2}\theta ^{4}\left \vert \ln \theta \right \vert ^{d}\le \theta ^{3}/2$ using $\left \vert P(x,y) \right \vert ^{2}\le P(x,x)P(y,y)$ and (B.8). For the second sum, we use (B.5) to bound it by $CmM\theta ^{4}\left \vert \ln \theta \right \vert ^{d} <\theta ^{3}/2$. This shows that

$$ \left \Vert \chi _{{\mathcal {R}}^{c}}P\chi _{{\mathcal {R}}} \right \Vert _{HS}\le \theta ^{3}, $$

(B.9)

so $\left \Vert Q^{2}-Q \right \Vert _{HS}\le \theta ^{3}$ for $\theta$ sufficiently small.

We next observe that, in view of (B.4),

$$ \left \vert Q(x,y) \right \vert =\left \vert \sum _{z\in{\mathcal {R}}}P(x,z)P(z,y) \right \vert \le C\theta ^{-2}\mathrm{e}^{-c\left \vert x-y \right \vert } $$

(B.10)

by the properties of exponential sums. Let $\bar{Q}=P-Q$. Then $\bar{Q}$ is (a) close to be a projection on $Ran(P)$ and (b) $\left \vert \bar{Q}(x,y) \right \vert \le C\theta ^{-2}\mathrm{e}^{-c \left \vert x-y \right \vert }$. Indeed, (a) follows from

$$ \tilde{Q}^{2}=P-2Q+Q^{2}=\tilde{Q}-(Q-Q^{2})=\tilde{Q}+O(\theta ^{3}), $$

while (b) follows directly from the decay properties of $P(x,y)$ and $Q(x,y)$.

We next show that $\bar{Q}$ is close to zero, which implies the result. Indeed, suppose in contradiction that $\bar{Q}$ is close to a non-trivial projection, i.e., $\mathrm{dist}\left ( \sigma (\bar{Q}),1 \right )=O(\theta ^{3})$. Let $y_{o}\in {\mathbb{Z}}^{d}$ be such that $\bar{M}:=\max \bar{Q}(x,x)=\bar{Q}(y_{o},y_{o})$ for some $y_{o}$ which is not necessary unique. Just as in the proof of Lemma B.3, let $\bar{r}=\bar{r}(c,\theta )>0$ be such that $\sum _{{y\in {\mathbb{Z}}^{d}:\ \left \vert y \right \vert >\bar{r}}} \mathrm{e}^{-2c\left \vert y \right \vert }\le {\theta ^{4} \bar{M}^{2}}$. In particular, there exists $C$ such that we can choose $r=-C\ln \left ( \theta ^{2}\bar{M} \right )$ for $\theta$ sufficiently small.

Essentially repeating the argument of Lemma B.3, we have

$$ \begin{aligned} \bar{M}&=\bar{Q}(y_{o},y_{o})=\left ( \bar{Q}-\bar{Q}^{2} \right )(y_{o},y_{o})+( \bar{Q}^{2})(y_{o},y_{o}) \\ & =O(\theta ^{3})+\sum _{y\in {\mathbb{Z}}^{d}}\left \vert \bar{Q}(y_{o},y) \right \vert ^{2}\\ &=O(\theta ^{3})+\sum _{y\in \Lambda _{r}(y_{o})} \left \vert Q(y_{o},y) \right \vert ^{2}+\sum _{y\in \Lambda ^{c}_{r}(x_{o})} \left \vert \bar{Q}(y_{o},y) \right \vert ^{2} \\ & \le O(\theta ^{3})+3^{d}\bar{M}^{2} r^{d}. \end{aligned} $$

This yields $\bar{M}\le 3^{d+1}\bar{M}^{2} r^{d}$, which in turn yields $\bar{M}\ge \bar{u}$, where $u$ is implicitly given by the analogue of (B.3). Since $\bar{u}>\left \vert \ln \theta \right \vert ^{-d-1}$ for $\theta$ sufficiently small, we get $\bar{M}\ge \left \vert \ln \theta \right \vert ^{-d-1}$. But then (B.8) implies

$$\begin{aligned} \theta ^{4}>P(y_{o},y_{o})&=\left ( P\chi _{{\mathcal {R}}^{c}}P \right )(y_{o},y_{o})+ \left ( P\chi _{{\mathcal {R}}}P \right )(y_{o},y_{o})\ge \left ( P \chi _{{\mathcal {R}}^{c}}P \right )(y_{o},y_{o})\\ &=\tilde{Q}(y_{o},y_{o})> \theta , \end{aligned}$$

a contradiction. □

Let ${\mathcal {R}}=\cup _{i=j}^{n} {\mathcal {R}}_{i}$ be a partition of ℛ into connected components. We note that $n\le 2m$, and that by construction,

$$ \mathrm{dist}_{i\neq j}\left ( {\mathcal {R}}_{i},{\mathcal {R}}_{j} \right )\ge L/2 $$

(B.11)

We now introduce the operator

$$ X=\sum _{j=1}^{n} j P \chi _{{\mathcal {R}}_{j}} P, $$

(B.12)

which acts on $Ran(P)$. Clearly, $X$ is hermitian.

Lemma B.6

Let $\lambda \in \sigma (X)$. Then there exists $j\in \left \{ 1,\ldots ,n \right \}$ such that $\left \vert \lambda -j \right \vert \le \theta$ for $\theta$ sufficiently small.

Proof

For any $\lambda \in \sigma (X)$, we have

$$ \left ( X-\lambda \right )^{2}=\sum _{j=1}^{n} \left ( j-\lambda \right )^{2} P \chi _{{\mathcal {R}}_{j}} P+\sum _{j\neq j'}\left ( j- \lambda \right )\left ( j'-\lambda \right )P \chi _{{\mathcal {R}}_{j}} P \chi _{{\mathcal {R}}_{j'}} P. $$

The second sum can be bounded in norm by $n^{2}\theta ^{3}$ using (B.11) and (B.5), while the first one satisfies

$$ \sum _{j=1}^{n} \left ( j-\lambda \right )^{2} P \chi _{{\mathcal {R}}_{j}} P\ge \min _{j} \left ( j-\lambda \right )^{2} Q\ge \min _{j} \left ( j- \lambda \right )^{2}\left ( 1-\theta ^{3} \right ) $$

using Lemma B.5. But $0\in \sigma \left ( \left ( X-\lambda \right )^{2} \right )$, from which the result follows. □

The assertion of Theorem B.2 will follow from

Lemma B.7

Let $(\lambda ,\psi _{\lambda})$ be an eigenpair for $X$ with normalized $\psi _{\lambda}$. Then

$$ \left \vert \psi _{\lambda }(x) \right \vert \le C\theta ^{-2} \mathrm{e}^{-c\,\mathrm{dist}\left ( x, {\mathcal {R}}_{j_{o}} \right )}, $$

(B.13)

where $j_{o}$ is chosen so that $\left \vert \lambda -j_{o} \right \vert \le \theta$.

Proof

Let

$$ Y_{\lambda}:=P\chi _{{\mathcal {R}}_{j_{o}}} P+\sum _{j\neq j_{o}} \left ( j-\lambda \right ) P \chi _{{\mathcal {R}}_{j}} P,\ Z_{\lambda}:=P \chi _{{\mathcal {R}}_{j_{o}}} P+\sum _{j\neq j_{o}}\left ( j-\lambda \right )^{-1} P \chi _{{\mathcal {R}}_{j}} P. $$

We have

$$ Y_{\lambda}\,Z_{\lambda}=P+\sum _{j\neq j'}f(j,j')\left ( j'-\lambda \right )P \chi _{{\mathcal {R}}_{j}} P \chi _{{\mathcal {R}}_{j'}} P=:P+W, $$

where $\left \vert f(j,j') \right \vert \le 2n$ for all $j\neq j'$. We have $\left \Vert W \right \Vert \le n^{3}\theta ^{3}$ using (B.9). Hence by standard perturbation theory, the operator $Y_{\lambda}$ is invertible on $Ran(P)$, with

$$ Y_{\lambda}^{-1}=Z_{\lambda}\left ( P+W \right )^{-1}=Z_{\lambda} \sum _{i=0}^{\infty }(-W)^{i}. $$

(B.14)

We now note that, analogously to (B.10),

$$ \left \vert Z_{\lambda }(x,y) \right \vert \le C\theta ^{-2} \mathrm{e}^{-c\left \vert x-y \right \vert }, $$

while

$$ \begin{aligned} \left \vert W(x,y) \right \vert &\le n^{3}\max _{j\neq j'}\left \vert \sum _{z\in{\mathcal {R}}_{j},w\in{\mathcal {R}}_{j'}}P(x,z)P(z,w)P(w,y) \right \vert \\ &\le Cn^{3}\theta ^{-3}\mathrm{e}^{-c\left \vert x-y \right \vert /2} \max _{j\neq j'}{\sum _{z\in {\mathcal {R}}_{j},w\in {\mathcal {R}}_{j'}} \mathrm{e}^{-c\left \vert z-w \right \vert /2}}\le \theta ^{2} \mathrm{e}^{-c\left \vert x-y \right \vert /2} \end{aligned} $$

using (B.11), (B.5), and (B.6). This in turn implies that

$$ \left \vert W^{i}(x,y) \right \vert \le \theta ^{i}\mathrm{e}^{-c \left \vert x-y \right \vert /2}, \quad i\in {\mathbb{N}}. $$

Using these bounds in (B.14), we deduce that

$$ \left \vert Y_{\lambda }^{-1}(x,y) \right \vert \le C\theta ^{-2} \mathrm{e}^{-c\left \vert x-y \right \vert /2}. $$

Hence we have

$$ \begin{aligned} \left \vert \psi _{\lambda }(x) \right \vert &=\left \Vert \chi _{ \left \{ x \right \}}\psi _{\lambda }\right \Vert =\left \Vert \chi _{ \left \{ x \right \}}Y_{\lambda }^{-1}Y_{\lambda }\psi _{\lambda } \right \Vert \\ &=\left \Vert \chi _{\left \{ x \right \}}Y_{\lambda }^{-1}\left ( Y_{ \lambda }-X+\lambda \right )\psi _{\lambda }\right \Vert \\ &=\left \vert 1-j_{o}+\lambda \right \vert \left \Vert \chi _{\left \{ x \right \}}Y_{\lambda }^{-1}P\chi _{{\mathcal {R}}_{j_{o}}} P\psi _{ \lambda }\right \Vert \le C\theta ^{-2}\mathrm{e}^{-c\,\mathrm{dist} \left ( x, {\mathcal {R}}_{j_{o}} \right )}. \end{aligned} $$

 □

We are now ready to complete the proof of Theorem B.2. We pick the set $\{\psi _{i}\}$ to be $\left \{ \psi _{\lambda }\right \}_{\lambda \in \sigma (X)}$, which is an orthonormal basis for $Ran(P)$ since $X$ is hermitian. Since

$$ \max _{j}\mathrm{diam}({\mathcal {R}}_{j})\le 2mL=-mC\ln \theta , $$

picking some $x_{j}\in {\mathcal {R}}_{j}$, we have

$$ \mathrm{e}^{-c\,\mathrm{dist}\left ( x, {\mathcal {R}}_{j_{o}} \right )} \le \mathrm{e}^{-c\left ( \left \vert x-x_{j} \right \vert -2mL \right )}\le \mathrm{e}^{-c\left \vert x-x_{j} \right \vert /m} \text{ for } \left \vert x-x_{j} \right \vert \ge 3mL. $$

On the other hand, since $\left \vert \psi (x) \right \vert \le 1$ for all $x$, we can pick $c$ sufficiently small so that

$$ \mathrm{e}^{-c\left \vert x-x_{j} \right \vert /m} \ge \theta ^{2} \text{ for } \left \vert x-x_{j} \right \vert < 3mL, $$

and the assertion follows.  □

Appendix C: Auxiliary results

Lemma C.1

Let $H=-\Delta +V_{\omega}$ be the random operator on $\ell ^{2}({\mathbb{Z}})$ with $V_{\omega}$ that satisfies assumptions introduced in Appendix A. Let $J=[\tfrac{1}{4},\tfrac{15}{4}]$ and $c=\tfrac{1}{49}$. Then

$$ \sum _{E\in \sigma (H)\cap J}\left \vert \psi _{E}(y) \right \vert ^{2} \ge c,\quad y\in {\mathbb{Z}}, $$

(C.1)

and the same bound holds for any Dirichlet restriction $H^{\Lambda}$ of $H$.

Proof

Let $P_{J}:=P_{J}(H)$. Suppose in contradiction that $\mathrm{tr}{\left(\chi _{\left \{ y \right \}}P_{J}\right)}< c$ for some $y\in {\mathbb{Z}}$. Then we have

$$ \mathrm{tr}{\left(\chi _{\left \{ y \right \}}\left ( H-2 \right )^{2}\right)}\ge \mathrm{tr}{\left(\chi _{\left \{ y \right \}}\left ( H-2 \right )^{2} \bar{P}_{J}\right)}\ge \tfrac{49}{16}\,\mathrm{tr}{\left(\chi _{\left \{ y \right \}}\bar{P}_{J}\right)}> 3. $$

However, the left hand side can be computed explicitly: $\mathrm{tr}{\left(\chi _{\left \{ y \right \}}\left ( H-2 \right )^{2}\right)}=2+V_{ \omega}^{2}(y)\le 3$, a contradiction. The proof for $H^{\Lambda}$ is identical. □

Theorem C.2

Assume that $H$ is $\left ( \nu ,\theta \right )$-localized on ℤ and that there exists $c>0$ and a compact interval $J$ such that

$$ \sum _{E\in \sigma (H)\cap J}\left \vert \psi _{E}(y) \right \vert ^{2} \ge c,\quad y\in {\mathbb{Z}}. $$

(C.2)

Then there exists $C_{\nu}>0$ and $E\in \sigma (H)\cap J$ such that $\left \vert \psi _{E}(0) \right \vert ^{2}\ge \frac{-C_{\nu}}{\ln \theta}$ and $\left \vert x_{E} \right \vert \le \frac{-\ln \theta}{C_{\nu}}$. The same result holds for $H$ replaced by the finite volume Hamiltonian $H^{\Lambda}$, provided that $\left \vert \Lambda \right \vert$ is sufficiently large, namely $\left \vert \Lambda \right \vert \gg \left \vert \ln \theta \right \vert$.

Proof

We first observe that for any $L\in \mathbb{N}$ and $E\in \sigma (H)$ we have

$$\begin{array}{c}\sum _{\begin{array}{c}y\in \mathbb{Z}:\\ |y-x_E|\ge \frac{1}{2}(\left|x_E\right|+L)\end{array}}{|{\psi }_E(y)|}^2\le \frac{{〈x_E〉}^2}{\theta }\sum _{\begin{array}{c}y\in \mathbb{Z}:\\ |y-x_E|\ge \frac{1}{2}(\left|x_E\right|+L)\end{array}}{\mathrm{e}}^{-\nu |y-x_E|}\hfill \\ =\frac{{〈x_E〉}^2}{\theta }\sum _{\begin{array}{c}u\in \mathbb{Z}:\\ \left|u\right|\ge \frac{1}{2}(\left|x_E\right|+L)\end{array}}{\mathrm{e}}^{-\nu \left|u\right|}\\ \hfill =\frac{{〈x_E〉}^2}{\theta }{\mathrm{e}}^{-\frac{\nu }{2}(L+\left|x_E\right|)}\frac{2}{1-{\mathrm{e}}^{-\nu }}\le \frac{C_{\nu }}{\theta }{\mathrm{e}}^{-\frac{\nu }{2}(L+\left|x_E\right|)}\end{array}$$

(C.3)

for some $C_{\nu}>0$.

We next note that by the orthonormality of $\left \{ \psi _{E} \right \}$ we have

$$ \sum _{y\in {\mathbb{Z}}}\left \vert \psi _{E}(y) \right \vert ^{2}=1, \quad E\in \sigma (H). $$

(C.4)

Hence, using (C.2) and (C.3), there exists $K_{\nu}>0$ such that

$$\begin{aligned} {4L+1}&\ge \sum _{\left \vert y \right \vert \le 2L}\sum _{E\in \sigma (H)\cap J}\left \vert \psi _{E}(y) \right \vert ^{2}\ge \sum _{ \left \vert y \right \vert \le 2L}\sum _{ \substack{E\in \sigma (H):\\ \left \vert x_{E} \right \vert \le L}} \left \vert \psi _{E}(y) \right \vert ^{2} \\ &=\sum _{ \substack{E\in \sigma (H)\cap J:\\ \left \vert x_{E} \right \vert \le L}} \left ( 1-\sum _{\left \vert y \right \vert > 2L}\left \vert \psi _{E}(y) \right \vert ^{2} \right ) \\ &\ge \#\left \{ E\in \sigma (H)\cap J:\ \left \vert x_{E} \right \vert \le L \right \}\left ( 1-\frac{C_{\nu }}{\theta }\mathrm{e}^{- \frac {\nu }{2} {L}} \right ) \\ &\ge \frac{1}{2}\#\left \{ E\in \sigma (H) \cap J:\ \left \vert x_{E} \right \vert \le L \right \} \end{aligned}$$

(C.5)

for $L\ge K_{\nu}\left \vert \ln \theta \right \vert$.

This bound together with (C.3) imply that for $L\ge K_{\nu}\left \vert \ln \theta \right \vert$ we have

$$\begin{array}{c}\sum _{\left|y\right|\le L}\sum _{\begin{array}{c}E\in \sigma (H)\cap J:\\ \left|x_E\right|>3L\end{array}}{|{\psi }_E(y)|}^2\le \sum _{k=4}^{\mathrm{\infty }}\mathrm{\#}\{E\in \sigma (H)\cap J:\left|x_E\right|\le kL\}\frac{C_{\nu }}{\theta }{\mathrm{e}}^{-\frac{\nu kL}{2}}\hfill \\ \hfill \le \frac{9C_{\nu }}{\theta }L\sum _{k=4}^{\mathrm{\infty }}k{\mathrm{e}}^{-\frac{\nu kL}{2}}<\frac{c}{2}\end{array}$$

(C.6)

for $L\ge M_{\nu}\left \vert \ln \theta \right \vert$ with some $M_{\nu}>0$.

Using this estimate, we get

$$ c\le \sum _{E\in \sigma (H)\cap J}\left \vert \psi _{E}(0) \right \vert ^{2}\le \sum _{ \substack{E\in \sigma (H)\cap J:\\ \left \vert x_{E} \right \vert \le 3L}} \left \vert \psi _{E}(0) \right \vert ^{2}+\frac {c}{2}, $$

for $L\ge M_{\nu}\left \vert \ln \theta \right \vert$, so

$$ \frac {c}{2}\le \sum _{ \substack{E\in \sigma (H)\cap J:\\ \left \vert x_{E} \right \vert \le 3L}} \left \vert \psi _{E}(0) \right \vert ^{2}, $$

and since $\#\left \{ E\in \sigma (H):\ \left \vert x_{E} \right \vert \le 3L \right \}\le 13L$ by (C.5), we deduce that there exists $C_{\nu}>0$ and $E\in \sigma (H)\cap J$ such that

$$ \left \vert \psi _{E}(0) \right \vert ^{2}\ge \frac {c}{26L}= \frac{-C_{\nu}}{\ln \theta},\quad \left \vert x_{E} \right \vert \le \frac{-\ln \theta}{C_{\nu}}. $$

 □

Let $H$ be a self-adjoint operator. Here we will often use the integral representation

$$ P_{[E_{1},E_{2}]}(H)=-\frac {1}{2\pi}\int _{-\infty}^{\infty }\sum _{j=1}^{2}(-1)^{j} \left ( H-ix-E_{j} \right )^{-1}dx,$$

(C.7)

which holds provided that $E_{1},E_{2}$ are not in the spectrum $\sigma (H)$. If in addition $H(s)$ is a differentiable family of operators, the formula

$$ \frac{d}{ds}\left ( H(s)-ix-E_{j} \right )^{-1}=-\left ( H(s)-ix-E_{j} \right )^{-1}\dot{H}(s)\left ( H(s)-ix-E_{j} \right )^{-1}$$

(C.8)

holds. Furthermore, for any operator $R$, we have

$$ [R, \frac{1}{H-z}]= -\frac{1}{H-z}[R,H] \frac{1}{H-z}. $$

(C.9)

Lemma C.3

Let $H_{1},H_{2},R$ be bounded operators on $\ell ^{2}\left ( \Lambda \right )$, with $H_{1},H_{2}$ self-adjoint. Let $J=[E_{1}, E_{2}]$ and denote by $J_{2\Delta}$ for $\Delta >0$, the widened interval $J+[-2\Delta ,2\Delta ]$. Suppose that for some $\epsilon _{1},\epsilon _{2}$,

• (i) $\left \Vert \left ( H_{1}-H_{2} \right )R \right \Vert =\epsilon _{1}$

• (ii) $\left \Vert [H_{2},R]P_{J}(H_{2}) \right \Vert \le \epsilon _{2}$.

Then

$$ \left \Vert \bar{P}_{J_{\Delta }}(H_{1})RP_{J}(H_{2}) \right \Vert \le \frac{\epsilon _{1}+\epsilon _{2}}{\Delta}. $$

Proof

Let $z_{1}=E_{1}-\Delta +ix$, $z_{2}=E_{2}+\Delta +ix$ and write

$$ G_{i,j}=\left ( H_{i}-z_{j} \right )^{-1}. $$

We first establish the identity

$$\begin{aligned} \bar{P}_{J_{\Delta}}(H_{1})RP_{J}(H_{2}) =&\frac {1}{2\pi}\sum _{j=1}^{2}(-1)^{j} \int _{-\infty}^{\infty }\bar{P}_{J_{\Delta}}(H_{1})G_{1,j}[H_{2},R]G_{2,j}P_{J}(H_{2})dx \\ +& \frac {1}{2\pi}\sum _{j=1}^{2}(-1)^{j}\int _{-\infty}^{\infty } \bar{P}_{J_{\Delta}}(H_{1})G_{1,j}\left ( H_{2}-H_{1} \right )R\,G_{2,j}P_{J}(H_{2})dx. \end{aligned}$$

Indeed, we start from

$$ G_{1,j}[H_{2},R] G_{2,j} = G_{1,j}(H_{2}-H_{1})R G_{2,j} +R G_{2,j} + G_{1,j}R. $$

Upon multiplying with $(-1)^{j}$, summing over $j=1,2$, integrating over $x$, and using (C.7) with $[E_{1},E_{2}]$ replaced by $[E_{1}-\Delta ,E_{2}+\Delta ]$, we get the desired identity. We next bound

$$ \max _{j=1,2}\left \Vert \bar{P}_{J_{\Delta }}(H_{1})G_{1,j} \right \Vert \le \frac{1}{\sqrt{x^{2}+\Delta ^{2}}}, \quad \max _{j=1,2} \left \Vert G_{2,j}P_{J}(H_{2}) \right \Vert \le \frac{1}{\sqrt{x^{2}+\Delta ^{2}}} $$

to get

$$ \left \Vert \bar{P}_{J_{\Delta }}(H_{1})RP_{J}(H_{2}) \right \Vert \le \left ( \epsilon _{1}+\epsilon _{2} \right )\frac {1}{\pi}\int _{- \infty}^{\infty }\frac{dx}{{x^{2}+\Delta ^{2}}}= \frac{\epsilon _{1}+\epsilon _{2}}{\Delta}. $$

 □

For the next lemma, we will use the notation $J_{a}(\mu )=[\mu -a,\mu +a]$, and will let $P^{\Theta}_{J_{a}(\mu )}$ denote the spectral projection of $H_{o}^{\Theta}$ onto $J_{a}(\mu )$.

Lemma C.4

Let $\Phi$ and $\Theta$, with $\Phi \subset \Theta$, be finite subsets of ${\mathbb{Z}}^{d}$. Let $(\phi ,\mu )$ be an eigenpair for $H_{o}^{\Phi}$. Then we have

$$ \mathrm{dist}\left ( \mu ,\sigma (H_{o}^{\Theta }) \right )\le C \left \vert \partial _{r}\Phi \right \vert \left \Vert \chi _{ \partial _{r}\Phi }\phi \right \Vert _{\infty}, $$

(C.10)

and

$$ \mathrm{dist}\left ( \phi ,Ran\left ( P^{\Theta }_{J_{a}(\mu )} \right ) \right )\le \frac {C}{a}\left \vert \partial _{r}\Phi \right \vert \left \Vert \chi _{\partial _{r}\Phi }\phi \right \Vert _{ \infty}. $$

(C.11)

Conversely, if $(\psi ,\lambda )$ is an eigenpair for $H^{\Theta}$, then

$$ \mathrm{dist}\left ( \lambda ,\sigma (H_{o}^{\Phi }) \right )\le C \left \vert \Theta \setminus \Phi \right \vert \left \Vert \chi _{ \Theta \setminus \Phi }\psi \right \Vert _{\infty }$$

(C.12)

and

$$ \mathrm{dist}\left ( \phi ,Ran\left ( P^{\Phi }_{J_{a}(\lambda )} \right ) \right )\le \frac {C}{a} \left \vert \Theta \setminus \Phi \right \vert \left \Vert \chi _{ \Theta \setminus \Phi }\psi \right \Vert _{\infty}. $$

(C.13)

Proof

We have

$$ \left ( \left ( H_{o}^{\Theta }-\mu \right )\phi \right )(y)= \textstyle\begin{cases} \sum _{\substack{y'\in \Phi :\\ \left \vert y-y' \right \vert \le r}}H_{o}(y,y') \phi (y') & \text{if } y\in \Theta \setminus \Phi \text{ and } \mathrm{dist}\left ( y, \Phi \right )\le r, \\ 0 & \text{otherwise}. \end{cases} $$

(C.14)

It follows that

$$ \left \Vert \left ( H_{o}^{\Theta }-\mu \right )\phi \right \Vert \le C\left \vert \partial _{r}\Phi \right \vert \left \Vert \chi _{ \partial _{r}\Phi }\phi \right \Vert _{\infty}. $$

(C.15)

Thus, recalling that $\phi$ is normalized,

$$ \mathrm{dist}\left ( \mu ,\sigma (H_{o}^{\Theta }) \right )\le \left \Vert \left ( H_{o}^{\Theta }-\mu \right )\phi \right \Vert \le C \left \vert \partial _{r}\Phi \right \vert \left \Vert \chi _{ \partial _{r}\Phi }\phi \right \Vert _{\infty}. $$

(C.16)

On the other hand, we have

$$ \left \Vert \bar{P}^{\Theta }_{J_{a}(\mu )}\phi \right \Vert \le \left \Vert{\bar{P}^{\Theta }_{J_{a}(\mu )}\left ( H_{o}^{\Theta }- \mu \right )^{-1}} \right \Vert \left \Vert \left ( H_{o}^{\Theta }- \mu \right )\phi \right \Vert \le \frac {C}{a} \left \Vert \chi _{ \Theta \setminus \Phi }\psi \right \Vert _{\infty}, $$

(C.17)

from which the second assertion of the lemma follows.

Similar considerations yield

$$ \left \Vert \left ( H_{o}^{\Phi }-\lambda \right )\phi \right \Vert \le C \left \vert \Theta \setminus \Phi \right \vert \left \Vert \chi _{ \Theta \setminus \Phi }\phi \right \Vert _{\infty}, $$

(C.18)

which in turn imply the bounds (C.12)–(C.13). □

In this paper we are interested in the evolution of the initial wave packet $\psi _{o}$ supported near some $x\in {\mathbb{Z}}^{d}$ up to the (rescaled) time $s$ of order 1. In this context, we can always approximate the dynamics generated by $H(s)$ with the one generated by $\hat{H}^{\mathbb{T}}(s)$, where $H^{\mathbb{T}}(s)$ is understood as an operator on $\ell ^{2}({\mathbb{Z}}^{d})$ (extending it by zero outside of the box $\Lambda _{L}$), in the following sense.

Proposition C.5

The finite speed of propagation bound

Let $\mathbb{T}$ be a torus of linear size $R$ and let $U_{\epsilon}(s)$, $U_{\epsilon}^{\mathbb{T}}(s)$ be the dynamics generated by $H(s)$ and $H^{\mathbb{T}}(s)$, respectively, i.e.,

$$\begin{aligned} i\epsilon \partial _{s}U_{\epsilon}(s) =&H(s)U_{\epsilon}(s), \quad U_{ \epsilon}(0)=1; \end{aligned}$$

(C.19)

$$\begin{aligned} i\epsilon \partial _{s} U^{\mathbb{T}}_{\epsilon}(s) =&H^{\mathbb{T}}(s) U^{\mathbb{T}}_{\epsilon}(s), \quad U^{\mathbb{T}}_{\epsilon}(0)=1. \end{aligned}$$

(C.20)

Then there exists $c>0$ such that for any ℒ satisfying $\mathcal{L}\ge C/\epsilon$ we have

$$ \max _{s}{ \left \vert{(U^{\sharp }_{\epsilon }(s))}(y,x) \right \vert \le \mathrm{e}^{-c\left \vert x-y \right \vert }, \quad \textit{ for } \left \vert x-y \right \vert \ge \frac {{\mathcal {L}}}{4}}, $$

(C.21)

where $U_{\epsilon}^{\sharp}$ is either $U$ or $U^{\mathbb{T}\,}$.

Proof

This is a standard fact for (local) lattice Hamiltonians, see e.g., the proof of [27, Lemma 5] for the time-independent case (which extends to the time-dependent one without effort), or, for a more general approach, [50]. □