Abstract
We explore three-dimensional gravity with negative cosmological constant via canonical quantization. We focus on chiral gravity which is related to a single copy of \(\text {PSL}(2,\mathbb {R})\) Chern-Simons theory and is simpler to treat in canonical quantization. Its phase space for an initial value surface \(\Sigma \) is given by the appropriate moduli space of Riemann surfaces. We use geometric quantization to compute partition functions of chiral gravity on three-manifolds of the form \(\Sigma \times {{\,\textrm{S}\,}}^1\), where \(\Sigma \) can have asymptotic boundaries. Most of these topologies do not admit a classical solution and are thus not amenable to a direct semiclassical path integral computation. We use an index theorem that expresses the partition function as an integral of characteristic classes over phase space. In the presence of n asymptotic boundaries, we use techniques from equivariant cohomology to localize the integral to a finite-dimensional integral over \(\overline{\mathcal {M}}_{g,n}\), which we evaluate in low genus cases. Higher genus partition functions quickly become complicated since they depend in an oscillatory way on Newton’s constant. There is a precise sense in which one can isolate the non-oscillatory part which we call the fake partition function. We establish that there is a topological recursion that computes the fake partition functions for arbitrary Riemann surfaces \(\Sigma \). There is a scaling limit in which the model reduces to JT gravity and our methods give a novel way to compute JT partition functions via equivariant localization.





Similar content being viewed by others
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Notes
Except in the case \(g=0\) and \(n=2\). Our formula is not modular invariant and we will discuss the precise reason for this in the Discussion 6.
This differs from the value \(\frac{\ell }{4G}\) that is usually stated in the literature by a factor of 4. The reason is that we are working with the gauge group \(\text {PSL}(2,\mathbb {R})\) instead of \(\text {SL}(2,\mathbb {R})\), which is more natural in the bosonic context.
As it stands, this quotient is not even a Hausdorff space. This can be avoided by taking the GIT-quotient instead, but it will not play a role in this paper.
In more down-to-earth terms, we can choose a canonical basis of paths \(\alpha _1,\dots ,\alpha _g,\beta _1,\dots ,\beta _g\) of \(\Sigma \) such that the only relation in \(\pi _1(\Sigma )\) is \(\alpha _1 \beta _1 \alpha _1^{-1} \beta _1^{-1} \alpha _2 \beta _2 \alpha _2^{-1} \beta _2^{-1} \cdots =1\). Then a homomorphism as in (2.3) is an assignment of matrices \(\rho (\alpha _i)=A_i\), \(\rho (\beta _i)=B_i\) with the same relation. We can then lift each \(A_i\) and \(B_i\) to the universal cover \(\widetilde{\text {PSL}(2,\mathbb {R})}\), which we denote by \({\widetilde{A}}_i\) and \({\widetilde{B}}_i\). We then have
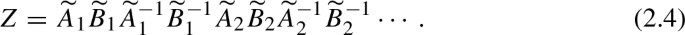
Z is an element of the center of \(\widetilde{\text {PSL}(2,\mathbb {R})}\), which can be identified with the integers. Since Z is also independent of the choices made in this construction, it gives an integer invariant of every bundle.
The dual bundle has opposite Euler number, so the component with minimal Euler number would work as well.
There is also a version of 3d gravity where one considers also non-orientable surfaces and gauges by non-orientable diffeomorphisms. We consider in this paper only orientable gravity in which orientation reversal is ungauged. In the context of JT gravity, all the different possibilities were discussed in [22].
This is always possible. The obstruction to the existence of such an extension with a G-bundle is captured by the oriented cobordism group \(\Omega _3(BG) \cong _3(G,\mathbb {Z})\), where the isomorphism follows from an application of the Atiyah-Hirzebruch spectral sequence. For \(G=\text {PSL}(2,\mathbb {R})\), the third homology group vanishes and thus such an extension always exists. See also the discussion in [60].
Also every integer can in fact appear, since different choices of four-manifolds are parametrized the oriented cobordism group \(\Omega _4(B \text {PSL}(2,\mathbb {R})) \cong \mathbb {Z}\).
There is another step that is sometimes done in the literature, which is the ‘metaplectic correction’. If we would follow the recipe as stated so far, one sometimes runs into problems with the ground state energies. For example, one finds that the energy levels of the harmonic oscillator are \(n \in \mathbb {Z}_{\ge 0}\) (in units where \(\hbar \omega =1\)) instead of the usual \(n+\frac{1}{2}\). To correct for this in geometric quantization, one changes the line bundle under consideration to \({\mathscr {L}}\) tensored with a choice of square root of the canonical line bundle of phase space. Such a square root may or may not exist depending on the specific situation. In the case of the moduli space of Riemann surfaces, the canonical bundle does generically not admit a square root. Thus we will not include a metaplectic correction in our analysis, since it would lead to inconsistencies.
In the presence of orbifold singularities, any divisor with enhanced symmetries is always counted with the additional factor \(|{{\,\textrm{Aut}\,}}|^{-1}\), where \({{\,\textrm{Aut}\,}}\) is the automorphism group.
We can confirm this by checking that the Gauss-Bonnet theorem works out, since the top Chern class of the tangent bundle gives the orbifold Euler characteristic of \(\overline{\mathcal {M}}_{1,1}\). This works, since the holomorphic tangent bundle is \({\mathscr {L}}^{10}\) and so
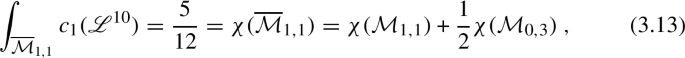
since the boundary divisor of \(\overline{\mathcal {M}}_{1,1}\) is isomorphic to \(\mathcal {M}_{0,3}/\mathbb {Z}_2\). The \(\mathbb {Z}_2\) interchanges the two nodes in the nodal sphere.
There is some care required to specify how these line bundles are defined for singular curves. A more rigorous definition can be given as follows. Let \(\pi : \overline{\mathcal {C}}_{g,n} \rightarrow \overline{\mathcal {M}}_{g,n}\) be the universal curve. Let \(\omega _\pi \) be the line bundle on \(\overline{\mathcal {C}}_{g,n}\) consisting of holomorphic differentials on the fiber. Sections are allowed to have simple poles at the nodes as long as the residues on the two branches of the node are opposite. This extends the definition of \(\omega _\pi \) to the boundary of \(\overline{\mathcal {C}}_{g,n}\), which technically is called the relative dualizing sheaf since it satisfies Serre-duality for the fiber. Let now \(\sigma _i: \overline{\mathcal {M}}_{g,n} \rightarrow \overline{\mathcal {C}}_{g,n}\) be the sections that take a curve to itself together with the i-th marked point. One then defines \(\mathbb {L}_i=\sigma _i^*(\omega _\pi )\). This description is explained and used further in Appendix B.
As in the previous footnote 14, some care has to be taken to properly define the Hodge bundle near the boundary divisors. By definition the fiber of \(\mathbb {E}\) is given by sections of \(\omega _\pi \), which are allowed to have simple poles at the nodes.
Since we forget a marked point, the component with the marked point of the nodal curve might become unstable through this procedure. It is then necessary to contract components until the curve becomes stable again, which is called stabilization.
It is often denoted by \(\delta \) in the literature.
We should note that this theorem shows that the canonical bundle \({\mathscr {K}}\) on moduli space does not possess a square root (at least for genera \(g \ge 3\)), since its Chern class cannot be written as an integer linear combination of \(\lambda \), \(\psi \) and \(\delta \) classes. Thus there is no consistent quantization scheme that employs a metaplectic correction.
This classical fact follows directly from the fact that \(f(z)=\frac{\omega _1(z)}{\omega _2(z)}\) with \(\omega _i(z)\) the two holomorphic differentials gives a degree 2 map to the Riemann sphere. A surface of this form is called hyperelliptic and the \(\mathbb {Z}_2\) automorphism interchanges the two sheets of the degree 2 map.
To see this, notice that the normal bundle is \(g-2\)-dimensional. Hence the \(\mathbb {Z}_2\)-automorphism acts as \(-1\) on \(g-2\) of the \(3g-3\) quadratic differentials. The g holomorphic differentials are all odd under the hyperelliptic involution, since they can be written as \(\omega _j(z)=\frac{z^{j-1}\, \textrm{d}z}{y}\), where y is defined as in eq. (C.1). Under the hyperelliptic involution \(y \mapsto -y\) and z stays invariant. Thus all the holomorphic differentials are odd. In total, this means that the action on \({\mathscr {L}}^k=(\det \mathbb {E}^{(2)})^k \otimes (\det \mathbb {E})^{-k}\) is \((-1)^{k(g-2-g)}=1\) for any k and thus the contribution is not oscillatory.
Actually for n odd the automorphism group is or order 2n since the rotation around the origin has to be combined with the hyperelliptic involution.
Contrary to what the notation might suggest, these moduli spaces are actually not compact (which is fairly clear in the simplest example \({\mathscr {M}}_0^{(1)}=\overline{{\mathscr {M}}}_0^{(1)}=\text {Diff}({{\,\textrm{S}\,}}^1)/\text {PSL}(2,\mathbb {R})\). However, we will see that equivariant localization reduces everything to an integral over \(\overline{\mathcal {M}}_{g,n}\).
It would be absent in the usual treatment of JT gravity, where one zeta-function regularizes the infinite product \(\prod _{n=2}^\infty \frac{n}{\beta ^\text {JT}}\) that appears in the disk partition function. Here we instead regularized it by interpreting it as a limit of the Dedekind eta-function. This is a divergent term in the regularization and as usual one should discard it and keep only the finite contribution.
The residue is only defined up to a sign since it involves choosing a branch of the surface. This means that the claimed isomorphism is true up to 2-torsion. However Chern-classes do not detect 2-torsion.
This relation is a gravitational analogue to the relation of \(\text {SU}(2)\) Chern-Simons theory and the conformal blocks of the \(\mathfrak {su}(2)\) Kac-Moody algebra [94].
Our analysis gives easy access to the regime of fixed g and large k, but not to fixed k and large g. Thus we do not know how to quantify this intuition.
This virtual bundle formally defines an element of the K-theory group \(K_0(I \mathcal {M}) \otimes _\mathbb {Z}\mathbb {C}\).
The preprint [105] also explains a similar computation, but we do not agree with their formula. Their formula fails in particular the checks that we perform here.
We use \(\nabla \) instead of the commonly used \(\Delta \) in the literature to avoid confusions with the cohomology classes \(\Delta _\ell \) that we introduced in Section 3.3.
These are not vector bundles anymore. Thus the exact sequence should be understood as a sequence in sheaf cohomology. Indeed, \({\mathscr {O}}_{{\mathscr {D}}_i}\) is a (coherent) sheaf that is entirely supported on the divisor \({\mathscr {D}}_i\).
This differs from the famous calculation for the Euler characteristic of \(\mathcal {M}_{g,n}\) by the inclusion of boundary divisors [108]. It is simple combinatorics to deduce \(\chi (\overline{\mathcal {M}}_{g,n})\) from \(\chi (\mathcal {M}_{g,n})\).
The reason to use \(q^2\) here is that \(\lambda _i-\lambda _j\) is only well-defined up to sign for small \(\lambda _i-\lambda _j\) and thus a good local parameter is \(q^2=\lambda _i-\lambda _j\).
References
Banados, M., Teitelboim, C., Zanelli, J.: The Black hole in three-dimensional space-time. Phys. Rev. Lett. 69, 1849 (1992). https://doi.org/10.1103/PhysRevLett.69.1849. [arXiv:hep-th/9204099]
Brown, J., Henneaux, M.: Central charges in the canonical realization of asymptotic symmetries: an example from three-dimensional gravity. Commun. Math. Phys. 104, 207 (1986). https://doi.org/10.1007/BF01211590
Coussaert, O., Henneaux, M., van Driel, P.: The Asymptotic Dynamics of Three-Dimensional Einstein Gravity with a Negative Cosmological Constant. Class. Quant. Grav. 12, 2961 (1995). https://doi.org/10.1088/0264-9381/12/12/012. [arXiv:gr-qc/9506019]
Witten, E.: Three-Dimensional Gravity Revisited. arXiv:0706.3359
Yin, X.: On non-handlebody instantons in 3D gravity. JHEP 09, 120 (2008). https://doi.org/10.1088/1126-6708/2008/09/120. [arXiv:0711.2803]
Yin, X.: Partition functions of three-dimensional pure gravity. Commun. Num. Theor. Phys. 2, 285 (2008). https://doi.org/10.4310/CNTP.2008.v2.n2.a1. [arXiv:0710.2129]
Maloney, A., Witten, E.: Quantum gravity partition functions in three dimensions. JHEP 02, 029 (2010). https://doi.org/10.1007/JHEP02(2010)029. [arXiv:0712.0155]
Gaberdiel, M.R.: Constraints on extremal self-dual CFTs. JHEP 11, 087 (2007). https://doi.org/10.1088/1126-6708/2007/11/087. [arXiv:0707.4073]
Giombi, S., Maloney, A., Yin, X.: One-loop partition functions of 3D gravity. JHEP 08, 007 (2008). https://doi.org/10.1088/1126-6708/2008/08/007. [arXiv:0804.1773]
Hartman, T., Keller, C.A., Stoica, B.: Universal spectrum of 2D conformal field theory in the large C limit. JHEP 09, 118 (2014). https://doi.org/10.1007/JHEP09(2014)118. [arXiv:1405.5137]
Keller, C.A., Maloney, A.: Poincare series, 3D gravity and CFT spectroscopy. JHEP 02, 080 (2015). https://doi.org/10.1007/JHEP02(2015)080. [arXiv:1407.6008]
Benjamin, N., Ooguri, H., Shao, S.-H., Wang, Y.: Light-cone modular bootstrap and pure gravity. Phys. Rev. D 100, 066029 (2019). https://doi.org/10.1103/PhysRevD.100.066029. [arXiv:1906.04184]
Hartman, T., Mazáč, D., Rastelli, L.: Sphere packing and quantum gravity. JHEP 12, 048 (2019). https://doi.org/10.1007/JHEP12(2019)048. [arXiv:1905.01319]
Afkhami-Jeddi, N., Hartman, T., Tajdini, A.: Fast conformal bootstrap and constraints on 3D gravity. JHEP 05, 087 (2019). https://doi.org/10.1007/JHEP05(2019)087. [arXiv:1903.06272]
Benjamin, N., Collier, S., Maloney, A.: Pure gravity and conical defects. JHEP 09, 034 (2020). https://doi.org/10.1007/JHEP09(2020)034. [arXiv:2004.14428]
Cotler, J., Jensen, K.: AdS\(_{3}\) gravity and random CFT. JHEP 04, 033 (2021). https://doi.org/10.1007/JHEP04(2021)033. [arXiv:2006.08648]
Maxfield, H., Turiaci, G.J.: The path integral of 3D gravity near extremality; or, JT gravity with defects as a matrix integral. JHEP 01, 118 (2021). https://doi.org/10.1007/JHEP01(2021)118. [arXiv:2006.11317]
Chandra, J., Collier, S., Hartman, T., Maloney, A.: Semiclassical 3D Gravity as an Average of Large c CFTs. arXiv:2203.06511
Schlenker, J.-M., Witten, E.: No Ensemble Averaging Below the Black Hole Threshold. arXiv:2202.01372
Jackiw, R.: Lower Dimensional Gravity. Nucl. Phys. B 252, 343 (1985). https://doi.org/10.1016/0550-3213(85)90448-1
Saad, P., Shenker, S.H., Stanford, D.: JT Gravity as a Matrix Integral. arXiv:1903.11115
Stanford, D., Witten, E.: JT Gravity and the Ensembles of Random Matrix Theory. arXiv:1907.03363
Witten, E.: On the structure of the topological phase of two-dimensional gravity. Nucl. Phys. B 340, 281 (1990). https://doi.org/10.1016/0550-3213(90)90449-N
Witten, E.: Two-dimensional gravity and intersection theory on moduli space. Surv. Diff. Geom. 1, 243 (1991). https://doi.org/10.4310/SDG.1990.v1.n1.a5
Dijkgraaf, R., Verlinde, H.L., Verlinde, E.P.: Loop equations and Virasoro constraints in nonperturbative 2-D quantum gravity. Nucl. Phys. B 348, 435 (1991). https://doi.org/10.1016/0550-3213(91)90199-8
Kontsevich, M.: Intersection theory on the moduli space of curves and the matrix Airy function. Commun. Math. Phys. 147, 1 (1992). https://doi.org/10.1007/BF02099526
Douglas, M.R., Shenker, S.H.: Strings in less than one-dimension. Nucl. Phys. B 335, 635 (1990). https://doi.org/10.1016/0550-3213(90)90522-F
Brezin, E., Kazakov, V.A.: Exactly solvable field theories of closed strings. Phys. Lett. B 236, 144 (1990). https://doi.org/10.1016/0370-2693(90)90818-Q
Gross, D.J., Migdal, A.A.: Nonperturbative two-dimensional quantum gravity. Phys. Rev. Lett. 64, 127 (1990). https://doi.org/10.1103/PhysRevLett.64.127
DeWitt, B.S.: Quantum theory of gravity. 1. The canonical theory. Phys. Rev. 160, 1113 (1967). https://doi.org/10.1103/PhysRev.160.1113
Kim, J., Porrati, M.: On a canonical quantization of 3D anti de Sitter pure gravity. JHEP 10, 096 (2015). https://doi.org/10.1007/JHEP10(2015)096. [arXiv:1508.03638]
Kim, H.K., Scarinci, C.: A quantization of moduli spaces of 3-dimensional gravity. arXiv:2112.13329
Moncrief, V.: Reduction of the Einstein equations in (2+1)-dimensions to a Hamiltonian system over Teichmuller space. J. Math. Phys. 30, 2907 (1989). https://doi.org/10.1063/1.528475
Krasnov, K., Schlenker, J.-M.: Minimal surfaces and particles in 3-manifolds. Geom. Dedicata 126, 187 (2007). https://doi.org/10.1007/s10711-007-9132-1. [arXiv:math/0511441]
Mess, G.: Lorentz spacetimes of constant curvature. arXiv:0706.1570
Scarinci, C., Krasnov, K.: The universal phase space of \(AdS_3\) gravity. Commun. Math. Phys. 322, 167 (2013). https://doi.org/10.1007/s00220-012-1655-0. [arXiv:1111.6507]
Verlinde, H.L.: Conformal field theory, 2-\(D\) quantum gravity and quantization of Teichmuller space. Nucl. Phys. B 337, 652 (1990). https://doi.org/10.1016/0550-3213(90)90510-K
Kashaev, R.M.: Quantization of Teichmueller spaces and the quantum dilogarithm. Lett. Math. Phys. 43, 105 (1998). https://doi.org/10.1023/A:1007460128279
Chekhov, L., Fock, V.V.: Quantum Teichmuller space. Theor. Math. Phys. 120, 1245 (1999). https://doi.org/10.1007/BF02557246. [arXiv:math/9908165]
Gaiotto, D., Yin, X.: Genus two partition functions of extremal conformal field theories. JHEP 08, 029 (2007). https://doi.org/10.1088/1126-6708/2007/08/029. [arXiv:0707.3437]
Gaberdiel, M.R., Gukov, S., Keller, C.A., Moore, G.W., Ooguri, H.: Extremal N=(2,2) 2D conformal field theories and constraints of modularity. Commun. Num. Theor. Phys. 2, 743 (2008). https://doi.org/10.4310/CNTP.2008.v2.n4.a3. [arXiv:0805.4216]
Lin, Y.-H., Pei, D.: Holomorphic CFTs and Topological Modular Forms. arXiv:2112.10724
Maloney, A.: Geometric microstates for the three dimensional black hole? arXiv:1508.04079
Cotler, J.S., Gur-Ari, G., Hanada, M., Polchinski, J., Saad, P., Shenker, S.H., et al.: Black holes and random matrices. JHEP 05, 118 (2017). https://doi.org/10.1007/JHEP05(2017)118. [arXiv:1611.04650]
Balasubramanian, V., de Boer, J., Sheikh-Jabbari, M.M., Simon, J.: What is a chiral 2D CFT? and what does it have to do with extremal black holes? JHEP 02, 017 (2010). https://doi.org/10.1007/JHEP02(2010)017. [arXiv:0906.3272]
Nayak, P., Shukla, A., Soni, R.M., Trivedi, S.P., Vishal, V.: On the dynamics of near-extremal black holes. JHEP 09, 048 (2018). https://doi.org/10.1007/JHEP09(2018)048. [arXiv:1802.09547]
Ghosh, A., Maxfield, H., Turiaci, G.J.: A universal Schwarzian sector in two-dimensional conformal field theories. JHEP 05, 104 (2020). https://doi.org/10.1007/JHEP05(2020)104. [arXiv:1912.07654]
Eynard, B., Orantin, N.: Invariants of algebraic curves and topological expansion. Commun. Num. Theor. Phys. 1, 347 (2007). https://doi.org/10.4310/CNTP.2007.v1.n2.a4. [arXiv:math-ph/0702045]
Eynard, B.: Intersection numbers of spectral curves. arXiv:1104.0176
Eynard, B.: Invariants of spectral curves and intersection theory of moduli spaces of complex curves. Commun. Num. Theor. Phys. 8, 541 (2014). https://doi.org/10.4310/CNTP.2014.v8.n3.a4. [arXiv:1110.2949]
Dunin-Barkowski, P., Orantin, N., Shadrin, S., Spitz, L.: Identification of the Givental formula with the spectral curve topological recursion procedure. Commun. Math. Phys. 328, 669 (2014). https://doi.org/10.1007/s00220-014-1887-2. [arXiv:1211.4021]
Stanford, D., Witten, E.: Fermionic localization of the Schwarzian theory. JHEP 10, 008 (2017). https://doi.org/10.1007/JHEP10(2017)008. [arXiv:1703.04612]
Mirzakhani, M.: Weil–Petersson volumes and intersection theory on the moduli space of curves. J. Am. Math. Soc. 20, 1 (2007). https://doi.org/10.1090/S0894-0347-06-00526-1
Witten, E.: (2+1)-Dimensional gravity as an exactly soluble system. Nucl. Phys. B 311, 46 (1988). https://doi.org/10.1016/0550-3213(88)90143-5
Milnor, J.: On the existence of a connection with curvature zero. Comment. Math. Helv. 32 (1957/58) 215. https://doi.org/10.1007/BF02564579
Wood, J.W.: Bundles with totally disconnected structure group. Comment. Math. Helv. 46, 257 (1971). https://doi.org/10.1007/BF02566843
Goldman, W.M.: Topological components of spaces of representations. Invent. Math. 93, 557 (1988). https://doi.org/10.1007/BF01410200
Atiyah, M.F., Bott, R.: The Yang–Mills equations over Riemann surfaces. Phil. Trans. R. Soc. A 308, 523 (1983). https://doi.org/10.1098/rsta.1983.0017
Goldman, W.M.: The symplectic nature of fundamental groups of surfaces. Adv. Math. 54, 200 (1984). https://doi.org/10.1016/0001-8708(84)90040-9
Dijkgraaf, R., Witten, E.: Topological Gauge theories and group Cohomology. Commun. Math. Phys. 129, 393 (1990). https://doi.org/10.1007/BF02096988
Deser, S., Jackiw, R., Templeton, S.: Topologically massive Gauge theories. Ann. Phys. 140, 372 (1982). https://doi.org/10.1016/0003-4916(82)90164-6
Deser, S., Jackiw, R., Templeton, S.: Three-dimensional massive Gauge theories. Phys. Rev. Lett. 48, 975 (1982). https://doi.org/10.1103/PhysRevLett.48.975
Li, W., Song, W., Strominger, A.: Chiral gravity in three dimensions. JHEP 04, 082 (2008). https://doi.org/10.1088/1126-6708/2008/04/082. [arXiv:0801.4566]
Maldacena, J.M.: The large \(N\) limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 38, 1113 (1999). https://doi.org/10.1023/A:1026654312961, https://doi.org/10.4310/ATMP.1998.v2.n2.a1, [arXiv:hep-th/9711200]
Chekhov, L.O., Fock, V.V.: Observables in 3D gravity and geodesic algebras. Czech. J. Phys. 50, 1201 (2000). https://doi.org/10.1023/A:1022844520574
Teschner, J.: An Analog of a Modular Functor from Quantized Teichmuller Theory. arXiv:math/0510174
Witten, E.: On quantum gauge theories in two-dimensions. Commun. Math. Phys. 141, 153 (1991). https://doi.org/10.1007/BF02100009
Cornalba, M.: On the locus of curves with automorphisms. Ann. Mat. Pura Appl. 149, 135 (1987). https://doi.org/10.1007/BF01773930
Givental, A., Tonita, V.: The Hirzebruch–Riemann–Roch theorem in true genus-0 quantum K-theory. arXiv:1106.3136
Zvonkine, D.: An introduction to moduli spaces of curves and their intersection theory. Handb. Teichmüller Theory 3, 667 (2012). https://doi.org/10.4171/103-1/12
Wolpert, S.: On the homology of the moduli space of stable curves. Ann. Math. 491, 1 (1983). https://doi.org/10.2307/2006980
Wolpert, S.: Chern forms and the Riemann tensor for the moduli space of curves. Invent. Math. 85, 119 (1986). https://doi.org/10.1007/BF01388794
Mumford, D.: Towards an enumerative geometry of the moduli space of curves. In: Arithmetic and Geometry, pp. 271–328. Springer (1983). https://doi.org/10.1007/978-1-4757-9286-7_12
Harris, J., Mumford, D.: On the Kodaira dimension of the moduli space of curves. Invent. Math. 67, 23 (1982). https://doi.org/10.1007/BF01393371
Boggi, M., Pikaart, M.: Galois covers of moduli of curves. Compos. Math. 120, 171–191 (2000). https://doi.org/10.1023/A:1001731524036
Harer, J.: The second homology group of the mapping class group of an orientable surface. Invent. Math. 72, 221 (1983). https://doi.org/10.1007/BF01389321
Arbarello, E., Cornalba, M.: The Picard groups of the moduli spaces of curves. Topology 26, 153 (1987). https://doi.org/10.1016/0040-9383(87)90056-5
Cornalba, M., Harris, J.: Divisor classes associated to families of stable varieties, with applications to the moduli space of curves. Ann. Sci. Éc. Norm. Supér. 21, 455 (1988). https://doi.org/10.24033/asens.1564
Gibney, A., Keel, S., Morrison, I.: Towards the ample cone of \(\overline{\cal{M} }_{g, n}\). J. Am. Math. Soc. 15, 273 (2002). https://doi.org/10.1090/S0894-0347-01-00384-8
Delecroix, V., Schmitt, J., van Zelm, J.: admcycles—a sage package for calculations in the tautological ring of the moduli space of stable curves. arXiv:2002.01709
Atiyah, M.F., Segal, G.B.: The index of elliptic operators: II. Ann. Math. 87, 531 (1968). https://doi.org/10.2307/1970716
Maldacena, J., Stanford, D., Yang, Z.: Conformal symmetry and its breaking in two dimensional nearly anti-de-Sitter space. PTEP 2016, 12C104 (2016). https://doi.org/10.1093/ptep/ptw124. [arXiv:1606.01857]
Witten, E.: Coadjoint orbits of the Virasoro group. Commun. Math. Phys. 114, 1 (1988). https://doi.org/10.1007/BF01218287
Chen, B., Wu, J.-q.: 1-loop partition function in \({{\rm AdS}}_{3}/{{\rm CFT}}_{2}\), JHEP 12, 109 (2015). https://doi.org/10.1007/JHEP12(2015)109, [arXiv:1509.02062]
Cotler, J., Jensen, K.: A theory of reparameterizations for \(\rm AdS _3\) gravity. JHEP 02, 079 (2019). https://doi.org/10.1007/JHEP02(2019)079. [arXiv:1808.03263]
Eichler, M., Zagier, D.: The Theory of Jacobi Forms. Birkhäuser, Boston, MA (1985). https://doi.org/10.1007/978-1-4684-9162-3
Okuyama, K., Sakai, K.: Multi-boundary correlators in JT gravity. JHEP 08, 126 (2020). https://doi.org/10.1007/JHEP08(2020)126. [arXiv:2004.07555]
Di Francesco, P., Ginsparg, P.H., Zinn-Justin, J.: 2-D Gravity and random matrices. Phys. Rep. 254, 1 (1995). https://doi.org/10.1016/0370-1573(94)00084-G. [arXiv:hep-th/9306153]
Eynard, B., Kimura, T., Ribault, S.: Random matrices. arXiv:1510.04430
Collier, S., Maloney, A.: Wormholes and spectral statistics in the Narain ensemble. JHEP 03, 004 (2022). https://doi.org/10.1007/JHEP03(2022)004. [arXiv:2106.12760]
Teschner, J.: From Liouville Theory to the Quantum Geometry of Riemann Surfaces, In: 14th International Congress on Mathematical Physics, vol. 8 (2003). arXiv:hep-th/0308031
Ellegaard Andersen, J., Kashaev, R.: A TQFT from Quantum Teichmüller Theory. Commun. Math. Phys. 330, 887 (2014). https://doi.org/10.1007/s00220-014-2073-2. [arXiv:1109.6295]
Mikhaylov, V.: Teichmüller TQFT vs. Chern–Simons theory. JHEP 04, 085 (2018). https://doi.org/10.1007/JHEP04(2018)085. [arXiv:1710.04354]
Witten, E.: Quantum field theory and the Jones polynomial. Commun. Math. Phys. 121, 351 (1989). https://doi.org/10.1007/BF01217730
Kashaev, R.M.: Liouville Central Charge in Quantum Teichmuller Theory. arXiv:hep-th/9811203
Marolf, D., Maxfield, H.: Transcending the Ensemble: Baby Universes, Spacetime Wormholes, and the Order and Disorder of Black Hole Information. JHEP 08, 044 (2020). https://doi.org/10.1007/JHEP08(2020)044. [arXiv:2002.08950]
Eberhardt, L.: Summing over Geometries in String Theory. JHEP 05, 233 (2021). https://doi.org/10.1007/JHEP05(2021)233. [arXiv:2102.12355]
Turiaci, G.J., Usatyuk, M., Weng, W.W.: 2D Dilaton–Gravity, Deformations of the Minimal String, and Matrix Models. Class. Quant. Grav. 38, 204001 (2021). https://doi.org/10.1088/1361-6382/ac25df. [arXiv:2011.06038]
Krasnov, K.: 3-D gravity, point particles and Liouville theory. Class. Quant. Grav. 18, 1291 (2001). https://doi.org/10.1088/0264-9381/18/7/311. [arXiv:hep-th/0008253]
Beasley, C., Witten, E.: Non-Abelian localization for Chern–Simons theory. J. Diff. Geom. 70, 183 (2005). [arXiv:hep-th/0503126]
Norbury, P.: A new cohomology class on the moduli space of curves. arXiv:1712.03662
Norbury, P.: Enumerative Geometry via the Moduli Space of Super Riemann Surfaces. arXiv:2005.04378
Kawasaki, T.: The Riemann–Roch theorem for complex \(V\)-manifolds. Osaka J. Math. 16, 151 (1979). https://doi.org/ojm/1200771835
Atiyah, M.F., Singer, I.M.: The index of elliptic operators: III. Ann. Math. 87, 546 (1968). https://doi.org/10.2307/1970717
Bini, G.: Chern classes of the moduli stack of curves. arXiv:math/0506084
Arbarello, E., Cornalba, M.: Combinatorial and algebro-geometric cohomology classes on the moduli spaces of curves. arXiv:alg-geom/9406008
Bini, G., Harer, J.: Euler characteristics of moduli spaces of curves. J. Eur. Math. Soc. 13, 487 (2010). https://doi.org/10.4171/JEMS/259
Harer, J., Zagier, D.: The Euler characteristic of the moduli space of curves. Invent. Math. 85, 457 (1986). https://doi.org/10.1007/BF01390325
Arbarello, E., Cornalba, M.: Calculating cohomology groups of moduli spaces of curves via algebraic geometry. Pub. Math. l’IHÉS 88, 97 (1998). https://doi.org/10.1007/BF02701767
Igusa, J.-I.: Modular forms and projective invariants. Am. J. Math. 89, 817 (1967). https://doi.org/10.2307/2373243
Acknowledgements
I thank Edward Witten for many interesting conversations and initial collaboration. I also thank Nathan Benjamin, Alexander Maloney and Gustavo Joaquin Turiaci for useful discussions. I thank Bertrand Eynard for correspondence and Jordan Cotler and Kristan Jensen for comments on the first version of this paper. I gratefully acknowledge support from the grant DE-SC0009988 from the U.S. Department of Energy.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
The Kawasaki Index Theorem
We describe here the modifications of the Riemann-Roch-Hirzebruch theorem to orbifolds due to Kawasaki [103]. It is a direct consequence of the Lefschetz fixed point formula that is derived in [81, 104]. In the following, \(\mathcal {M}\) denotes a smooth complex orbifold.
1.1 The inertia stack
To formulate the index theorem, one needs to integrate over a larger orbifold called the inertia stack \(I\mathcal {M}\) that is a disjoint union of orbifolds, one of which is \(\mathcal {M}\). In language familiar to physicists, \(\mathcal {M}\) consists of the untwisted sector of the orbifold, whereas \(I\mathcal {M}\) consists of both the untwisted and twisted sectors.
From the analytic viewpoint \(I\mathcal {M}\) is constructed as follows. Let \(\mathcal {U}=(U_i)_{i \in I}\) be an atlas for \(\mathcal {M}\). Every open set \(U_i\) comes equipped with a group action of a group \(G_i\) and a covering space \({\tilde{U}}_i\) such that \(U_i={\tilde{U}}_i/G_i\). Now for every \(g \in G_i\) consider the fixed point sets \({\tilde{U}}_i^g\) inside \({\tilde{U}}_i\). On \({\tilde{U}}_i^g\) we still have a well-defined group action of the centralizer \(Z_{G_i}(g)\) of the group element g in \(G_i\). We then set \(U^g_i={\tilde{U}}_i^g/Z_{G_i}(g)\). Clearly \(U_i^g\) only depends on the conjugacy class of \(g\in G_i\). The \(U_i^g\)’s with \(i \in I\) and \(g \in \text {Conj}(G_i)\) provide then an atlas for a disjoint union of orbifolds of different dimensions, since they can be patched together in an obvious way. This is the inertia stack \(I\mathcal {M}\). In particular, \(I\mathcal {M}\) contains \(\mathcal {M}\) as one of its components because we can always choose \(g=e\) the identity for any open set and since \(U_i^e=U_i\), patching these open sets together gives back the original orbifold. There is always a canonical map \(I\mathcal {M} \rightarrow \mathcal {M}\) given by inclusion of the fixed point sets into the original orbifolds.
For a stack of the form \(\mathcal {M}=X/G\) where G is a finite group and X a smooth manifold, one can define the inertia stack alternatively as follows. Define first the inertia manifold as
IX has a natural G action given by \(g \cdot (h,x)=(g h g^{-1},g \cdot x)\). Then one can define
Thus, points in the inertia stack are in general labeled by a point \(x\in \mathcal {M}\) together with a conjugacy class \([g] \subset G_x\), where \(G_x\) is the local isotropy group of x.
Let’s exemplify this construction on \(\overline{\mathcal {M}}_{1,1}\). In this case, the stabilizer groups are all abelian (\(\mathbb {Z}_2\) for a generic point, \(\mathbb {Z}_4\) for \(\tau =i\) and \(\mathbb {Z}_6\) for \(\tau =\textrm{e}^{\frac{2\pi i}{3}}\)). Hence the centralizers are all isomorphic to the group \(G_i\) itself. \(I\overline{\mathcal {M}}_{1,1}\) contains one component \(\overline{\mathcal {M}}_{1,1}\) for the identity acting at every point. But since any point carries also a \(\mathbb {Z}_2\) action, we get a further copy of \(\overline{\mathcal {M}}_{1,1}\). For \(\tau =i\), we get two more points that carry a \(\mathbb {Z}_4\) action and for \(\tau =\textrm{e}^{\frac{\pi i}{3}}\), we get four more points that carry a \(\mathbb {Z}_6\) action. Overall, we hence have
in hopefully obvious notation.
1.2 The index theorem
Let now E be a vector bundle on \(\mathcal {M}\). We can lift E to a vector bundle \(I\mathcal {M}\) in an obvious way by pulling it back along the natural map \(I \mathcal {M} \rightarrow \mathcal {M}\). On \(I\mathcal {M}\), g acts on the fiber of E at (x, [g]) and we may decompose the bundle according to the eigenspaces under the action of g. One then introduces the virtual trace bundleFootnote 27
i.e. an eigenspace is weighted by its eigenvalue. We also form the following formal linear combination of the conormal bundle \(\mathcal {N}^*\) of the component of \(I \mathcal {M}\) inside \(\mathcal {M}\)
i.e. the alternating sum of the exterior algebra. This bundle is also called the K-theoretic Euler character of \(\mathcal {N}^*\).
The index theorem now states
The normal bundle appears essentially because of the localization formula in equivariant cohomology. Since the Chern character respects tensor products and direct sums as \({{\,\textrm{ch}\,}}(E \otimes F)={{\,\textrm{ch}\,}}(E) {{\,\textrm{ch}\,}}(F)\) and \({{\,\textrm{ch}\,}}(E + F)={{\,\textrm{ch}\,}}(E) + {{\,\textrm{ch}\,}}(F)\) (i.e. it is a ring homomorphism from the K-theory ring to the ordinary cohomology ring), we can uniquely extend its definition to virtual bundles. For example
The action of g on the normal bundle can never have eigenvalue 1. This means that the Chern character \({{\,\textrm{ch}\,}}({{\,\textrm{tr}\,}}(\Lambda ^\bullet \mathcal {N}^*))\) can always be formally inverted.
1.3 Modular forms from the orbifold index theorem
Let’s exemplify the theorem with the help of \(\overline{\mathcal {M}}_{1,1}\) and the bundle \({\mathscr {L}}^k\) of modular forms. Sections satisfy by definition
under the natural \(\text {SL}(2,\mathbb {Z})\) action. Let us also recall from Section 3.2 that the canonical bundle of \(\overline{\mathcal {M}}_{1,1}\) was given by cusp forms of weight 2. The generic point is stabilized by \(-\mathbb {1}\) with eigenvalue \((-1)^k\). The additional stabilizers of the point \(\tau =i\) are the \(\text {SL}(2,\mathbb {Z})\) group elements
with eigenvalues \((-i)^k\) and \(i^k\) respectively. The additional stabilizers of the point \(\tau =\textrm{e}^{\frac{2\pi i}{3}}\) are
with eigenvalues \(\textrm{e}^{\frac{\pi ik}{3}}\), \(\textrm{e}^{\frac{2\pi ik}{3}}\), \(\textrm{e}^{\frac{4\pi ik}{3}}\) and \(\textrm{e}^{\frac{5\pi ik}{3}}\).
The action on the normal bundles follows immediately from the fact that the cotangent bundle is given by the bundle \({\mathscr {L}}^{-2}\) on \(\mathcal {M}_{1,1}\) and in particular on the fixed points. Thus in the cases in the cases with a non-trivial normal bundle we have
We can then evaluate the index theorem. Higher cohomology \(\textrm{H}^1(\overline{\mathcal {M}}_{1,1},{\mathscr {L}}^k)\) vanishes for \(k \ge 0\) and hence
Here the first two terms come from the identity element and the generic \(\mathbb {Z}_2\) automorphism. Since the integrals over \(i/\mathbb {Z}_4\) and \(\textrm{e}^{\frac{\pi i}{3}}\) are 0-dimensional, we just have to extract the degree 0 of the Chern characters. We have
The integral \(\int _{i/\mathbb {Z}_4} 1\) evaluates to \(\frac{1}{4}\) because we have to divide it as usual by the order of the automorphism group and similarly for the \(\mathbb {Z}_6\) fixed point. Using also the evaluation of the first integral explained in Section 3.2, we obtain
It is simple to check that the right-hand side is indeed an integer and predicts the correct dimensions consistent with the fact that the ring of modular forms is freely generated by the two Eisenstein series \(E_4\) and \(E_6\).
1.4 Leading correction to fake partition function
We can also use the Kawasaki index theorem to evaluate the leading correction to the fake partition function in the large k limit. There are some low-genus cases where where the following is not the leading correction, namely \((g,n)=(1,1)\), (2, 0), in which case the surface carries generically a \(\mathbb {Z}_2\)-automorphism. For \((g,n)=(1,1)\), (1, 2), (2, 0), (2, 1), (3, 0) there are also other corrections that contribute at the same order in k, since there are other components of \(I\overline{\mathcal {M}}_{g,n}\) with the same codimension. For example for \((g,n)=(3,0)\) to locus of hyperelliptic surfaces would lead to a correction of the same order.
As we mentioned in Section 3.7, the leading correction comes generically from the locus where a genus 1 component splits off from the surface, i.e. \({\mathscr {D}}_{1,\emptyset } \cong \overline{\mathcal {M}}_{g-1,n+1} \times \overline{\mathcal {M}}_{1,1}\) which has codimension 1 and automorphism group \(\mathbb {Z}_2\). The conormal bundle to such a divisor is
as was explained for example in Section 4.4. Let’s say that \(\mathbb {L}_\bullet \) lies on the \(\overline{\mathcal {M}}_{1,1}\). We have to work out the action of the non-trivial automorphism on the normal bundle and the prequantum line bundle \({\mathscr {L}}^k\). For \(\mathcal {N}^*\), this is easy. Since the \(\mathbb {Z}_2\) only acts on \(\overline{\mathcal {M}}_{1,1}\), sections of \(\mathbb {L}_\circ \) are invariant under the automorphisms. One the other hand, \(\mathbb {L}_\bullet \) is by definition the cotangent bundle at the node and the \(\mathbb {Z}_2\)-involution of the torus acts as \(-1\) on the cotangent bundle at every point on the torus. Thus the automorphism acts as \(-1\) on the conormal bundle. This had to be so, since it could only act as \(+1\) or \(-1\) and a \(+1\) action is not possible, since then the fixed point locus would be bigger. We can similarly work out the action of the \(\mathbb {Z}_2\) on the prequantum line bundle \({\mathscr {L}}^k\). \({\mathscr {L}}^k\) splits into an outer product \({\mathscr {L}}^k ={\mathscr {L}}_{\overline{\mathcal {M}}_{g-1,n+1}}^k \boxtimes {\mathscr {L}}_{\overline{\mathcal {M}}_{1,1}}^k\) on the two components. Again \(\mathbb {Z}_2\) does not act on the first factor. On the second factor, the line bundle corresponds to modular forms of weight k, on which the \(\mathbb {Z}_2\) automorphism acts as \((-1)^k\). Thus Kawasaki’s index theorem predicts (3.42) as leading correction to the naive index theorem in a large k limit.
Some Algebraic Geometry on \(\overline{\mathcal {M}}_{g,n}\)
In this appendix, we review some background about the cohomology of \(\overline{\mathcal {M}}_{g,n}\). We also explain the application of the Grothendieck-Riemann-Roch theorem to the universal curve \(\overline{\mathcal {C}}_{g,n}\) over \(\overline{\mathcal {M}}_{g,n}\) that leads to formulas for the Chern characters of the Hodge bundle and tangent bundle of moduli space in terms of the more basic cohomology classes. This computation is standard in algebraic geometry and far-reaching generalizations exist. Our presentation follows loosely [70]. Since we are not aware of an explicit formula for the Chern characters of the tangent bundle in the literature, we will explain the computation in detail. We also explain strong consistency checks on our formula.Footnote 28
1.1 The universal curve
Let us first recall the definition of the universal curve. The universal curve \(\overline{\mathcal {C}}_{g,n}\) is a fiber bundle over \(\overline{\mathcal {M}}_{g,n}\) whose fiber at a given curve in \(\overline{\mathcal {M}}_{g,n}\) is the (nodal stable) curve itself. Thus, the total space of \(\overline{\mathcal {C}}_{g,n}\) has one more complex dimension than \(\overline{\mathcal {M}}_{g,n}\) and consists of curves together with points on them, \((\Sigma _{g,n},z)\), \(z \in \Sigma _{g,n}\). There is a canonical projection map
that takes the pair \((\Sigma _{g,n},z)\) to the curve \(\Sigma _{g,n}\). We have the isomorphism \(\overline{\mathcal {M}}_{g,n+1} \cong \overline{\mathcal {C}}_{g,n}\), where the last point describes the location in the fiber and \(\pi \) becomes the usual forgetful morphism. The perspective of \(\overline{\mathcal {C}}_{g,n}\) is however slightly different. Because the fiber over \(\overline{\mathcal {M}}_{g,n}\) is described by any point on the curve, this point could also coincide with a marked point or a node. Thus the isomorphism with \(\overline{\mathcal {M}}_{g,n+1}\) involves collapsing components of the nodal curve that contain the marked point \(n+1\) and which become unstable when forgetting the \((n+1)\)-st marked point. We will in the following switch back and forth between the two points of view.
There is a natural line bundle on \(\overline{\mathcal {C}}_{g,n}\) that is called the relative dualizing sheaf \(\omega _\pi \), whose fiber at a curve with marked point is the cotangent bundle at the marked point. It is now very important that in the case of a nodal curve, \(\omega _\pi \) is defined to allow poles of the one-forms at the boundary divisors, as long as the residues on the two branches of the nodes are opposite. \(\omega _\pi \) is called the relative dualizing sheaf, because it is the sheaf that allows one to still write a natural Serre duality even in the presence of nodes.
The universal curve carries n canonical divisors \({\mathscr {D}}_i\). These are the divisors where the the point in the fiber coincides with the i-th marked point. Alternatively, we can also say that there are n sections of the universal curve
that map a curve to the curve together with the i-th marked point. Then \({\mathscr {D}}_i\) is the image of \(\sigma _i\). Similarly to the notation used in in Section 3.3, we denote the corresponding Poincaré dual classes by \(\delta _i \in ^2(\overline{\mathcal {C}}_{g,n},\mathbb {Q})\). Under the identification of \(\overline{\mathcal {C}}_{g,n}\) with \(\overline{\mathcal {M}}_{g,n+1}\), we identify \({\mathscr {D}}_i \cong {\mathscr {D}}_{0,\{i,n+1\}}\) and \(\delta _i \cong \delta _{0,\{i,n+1\}}\).
\(\overline{\mathcal {C}}_{g,n}\) has also a codimension 2 locus consisting of the nodes in singular curves, which we call \(\nabla \).Footnote 29 We will by abuse of notation also denote by \(\nabla \) the corresponding Poincaré dual class \(\nabla \in ^4(\overline{\mathcal {C}}_{g,n},\mathbb {Q})\). \(\nabla \) has natural double cover, whose fibers are a choice of branch of the node curve (i.e. on which of the two components of the curves it lies). Thus the double cover consists of the marked point of the normalization of the curve (which means that we separate the nodal curve at the nodes into several disconnected curves).
1.2 \(\psi \)- and \(\kappa \)-classes
Let us collect some further background on \(\psi \)- and \(\kappa \)-classes. The precise definition of \(\psi _i\) is
compare also with footnote 14.
There is an important comparison result. Under the projection
we can compare the classes \(\psi _i\) and \(\pi ^*(\psi _i)\), where the first is the \(\psi \)-class as defined in \(\overline{\mathcal {M}}_{g,n+1}\) and the second is the pullback of the corresponding \(\psi \)-class in \(\overline{\mathcal {M}}_{g,n}\). One might naively think that the two are the same, but this is incorrect. Essentially, \(\psi _i\) is defined in terms of the line bundle \(\omega _\pi \) on the universal curve \(\overline{\mathcal {C}}_{g,n+1}\) while the pullback \(\pi ^*(\psi _i)\) was defined through the line bundle \(\omega _\pi \) on the universal curve \(\overline{\mathcal {C}}_{g,n}\). In the former, we allow the holomorphic differential to have poles at the boundary divisor where the i-th and \((n+1)\)-st marked point coincide. In the latter case, there is no \((n+1)\)-st marked point and hence no corresponding pole is allowed. This means that
where we recall that \({\mathscr {D}}_{0,\{i,n+1\}}\) is the boundary divisor where the i-th and the \((n+1)\)-th marked point coincide and bubble off into a 3-pointed sphere and \(\delta _{0,\{i,n+1\}}\) the corresponding Poincaré dual class.
We furthermore also observe that the restriction of \(\mathbb {L}_i\) on \(\overline{\mathcal {M}}_{g,n+1}\) to the divisor \({\mathscr {D}}_{0,\{i,n+1\}}\) is trivial, since the i-th point on \({\mathscr {D}}_{0,\{i,n+1\}}\) lies on a genus 0 component with two marked point and one node. This component does not have any non-trivial moduli and thus \(\mathbb {L}_i\) is trivial. This means the the intersection \(\psi _i \, \delta _{0,\{i,n+1\}}=0\) vanishes.
One can derive the following immediate consequence from these results that we will need below. We will change our perspective and think about \(\overline{\mathcal {M}}_{g,n+1}\) as \(\overline{\mathcal {C}}_{g,n}\). Let us compute \(\pi _*(\delta _i^{m+1})\). For \(m=0\), this is clearly equal to one since every \({\mathscr {D}}_i\) intersects the fiber of the universal curve exactly once. We then have for \(m \ge 1\)
where the first equality is (B.5). The second follows from the vanishing intersection of \(\psi _i\) and \(\delta _i\) together with the general properties of the pushforward. Finally, the last equality follows by induction.
Let us also recall that we defined the \(\kappa \)-classes on \(\overline{\mathcal {M}}_{g,n}\) as
By definition, \(\psi _{n+1}\) is the first Chern class of the line bundle \(\mathbb {L}_{n+1}\) on \(\overline{\mathcal {M}}_{g,n+1}\). Let us work out the relation between \(\mathbb {L}_{n+1}\) and \(\omega _\pi \). Both are line bundles on \(\overline{\mathcal {M}}_{g,n+1} \cong \overline{\mathcal {C}}_{g,n}\). Away from singularities, the two line bundles are isomorphic, since the fiber is the cotangent space at the \((n+1)\)-th marked point. When the i-th marked point collides with the \((n+1)\)-th marked point, \(\omega _\pi \) is completely regular since its definition makes no reference to marked points. \(\mathbb {L}_{n+1}\) is however allowed to have poles which follows from the definition of \(\omega _\pi \) on \(\overline{\mathcal {C}}_{g,n+1}\). Thus we have
Here, we defined \(\omega _\pi ^\text {log}\) as the relative dualizing sheaf that also allows poles at the punctures. It is the usual dualizing sheaf twisted by the divisors \({\mathscr {D}}_i\). In particular this means that we can also define the \(\kappa \)-classes as
This is the definition of Arbarello and Cornalba [106]. It is aesthetically perhaps nicer since it only uses the universal curve for its definition.
1.3 The GRR formula
Let’s also recall the GRR formula. It states that for maps
the Chern characters of line bundles \({\mathscr {L}}\) (or more generally coherent sheaves) behave under pushforward as follows:
We explained the definition of \(\pi _*({\mathscr {L}})\) in Section 3.3. Here \({{\,\textrm{ch}\,}}\) is the Chern character and \({{\,\textrm{td}\,}}(\pi )\) is the relative Todd class, that can be defined as
We want to apply this to the situation where \(X=\overline{\mathcal {C}}_{g,n}\) and \(Y=\overline{\mathcal {M}}_{g.n}\). First, we should remark that GRR is applicable, since even though the space \(\overline{\mathcal {M}}_{g,n}\) has orbifold singularities, its fibers are stable Riemann surfaces without orbifold singularities. The GRR theorem is only sensible to the fibers which makes its application valid.
1.4 Computing \({{\,\textrm{td}\,}}(\pi )\)
The most non-trivial part of the application of the theorem is the computation of the relative Todd class. Naively one could have thought that we have a sequence
Here the first map is just the adjoint map of the differential \(\textrm{d}\pi \) between the tangent spaces of \(\overline{\mathcal {C}}_{g,n}\) and \(\overline{\mathcal {M}}_{g,n}\). The second map r is the restriction of a section of the cotangent bundle to the marked point of the universal curve, which gives by definition a cotangent vector of the marked point. We can hence view this as a holomorphic one-form on the fiber of the universal curve, which is hence a section of the relative dualizing sheaf.
However, the caveat is that this sequence is not exact, because contrary to \(\omega _\pi \), sections of \(T^* \overline{\mathcal {C}}_{g,n}\) are not allowed to have poles at the boundary divisors. Thus the last map r is not surjective. We now explain how to repair this problem and get an exact sequence. Let us use a local model of the singular locus. The universal curve close to the locus can be modeled as
Here q should be thought of as parametrizing the base \(\overline{\mathcal {M}}_{g,n}\) and (x, y) parametrize the fiber of the universal curve. All other coordinates will not be relevant. For \(q=0\) we obtain a nodal curve whose two components are described by \(x=0\) and \(y=0\). Thus the canonical projection \(\pi :\overline{\mathcal {C}}_{g,n} \rightarrow \overline{\mathcal {M}}_{g,n}\) takes the form
So the cotangent space \(T^* \overline{\mathcal {C}}_{g,n}\) is spanned by \(\textrm{d}x\) and \(\textrm{d}y\). The cotangent bundle of \(\pi ^*(T^* \overline{\mathcal {M}}_{g,n})\) is instead spanned by \(\textrm{d}q=x \, \textrm{d}y+y\, \textrm{d} x\). Finally, the line bundle \(\omega _\pi \) is generated by the forms \(\frac{\textrm{d}x}{x}\) and \(\frac{\textrm{d}y}{y}\) modulo the relation \(\frac{\textrm{d}x}{x}+\frac{\textrm{d}y}{y}=0\). Thus the composition of the two maps is trivial, \(r \circ (\textrm{d}\pi )^*=0\), but we already mentioned that they are not exact because r is not a surjective map.
One can repair this failure of exactness by considering the following sequence
Here we used \(\omega _\pi ^\text {log}\) instead of \(\omega _\pi \), which is the canonical bundle on the universal curve twisted by the divisors \({\mathscr {D}}_i\), see (B.8). In other words, sections are holomorphic differentials that are allowed to have simple poles at the marked points. This change is just convenient and will simplify later computations, because of the relation (B.9). We compensated for it by including \( \bigoplus _i \omega _\pi ^\text {log} \otimes {\mathscr {O}}_{{\mathscr {D}}_i}\) in the last term. Here \({\mathscr {O}}_\nabla \) and \({\mathscr {O}}_{{\mathscr {D}}_i}\) mean the sheaf of holomorphic functions on the corresponding subvarieties.Footnote 30 The last map is given by taking the residue at the nodes and the marked points respectively. It is now simple to check that this sequence is indeed exact, even in the vicinity of a node.
Using the multiplicative property of the Todd class, one finds the following formula for the relative Todd class (after dualizing the sequence)
Here, \({{\,\textrm{td}\,}}^*\) means the Todd class of the dual bundle (or sheaf).
To continue, one makes the following simple observations (for \(i \ne j\))
The first two formulas are obvious. By definition of \(\overline{\mathcal {M}}_{g,n}\), two marked points are never allowed to coincide and consequently the two divisors \({\mathscr {D}}_i\) and \({\mathscr {D}}_j\) do not intersect. The same goes for the intersection of \({\mathscr {D}}_i\) with \(\nabla \), since a marked point is never allowed to coincide with a node. The third identity holds because the restriction of \(\omega ^\text {log}_\pi \) to \({\mathscr {D}}_i\) is trivial. The same reasoning applies for the restriction of \(\omega ^\text {log}_\pi \) to \(\nabla \), except that there can be 2-torsion associated with the choice of branch. So the line bundle is rationally trivial, which is still good enough for \(c_1(\omega _\pi ^\text {log}) \, \nabla =0\) to hold in rational cohomology.
The triviality of \(\omega ^\text {log}_\pi \) when restricted to \({\mathscr {D}}_i\) or \(\nabla \) also implies that we can simplify (B.17) to
So it remains to compute these three Todd classes. We then take their pushforward below.
-
1.
Let us start with \({{\,\textrm{td}\,}}^*(\omega _\pi ^\text {log})\), which by simply takes the form
$$\begin{aligned} {{\,\textrm{td}\,}}^*(\omega _\pi ^\text {log})=\frac{c_1(\omega _\pi ^\text {log})}{\textrm{e}^{c_1(\omega _\pi ^\text {log})}-1} \end{aligned}$$(B.20)on \(\overline{\mathcal {C}}_{g,n} \cong \overline{\mathcal {M}}_{g,n+1}\).
-
2.
It is also straightforward to work out \({{\,\textrm{td}\,}}^*({\mathscr {O}}_{{\mathscr {D}}_i})\). We have the short exact sequence
$$\begin{aligned} 0 \longrightarrow {\mathscr {O}}(-{\mathscr {D}}_i) \longrightarrow {\mathscr {O}} \longrightarrow {\mathscr {O}}_{{\mathscr {D}}_i} \longrightarrow 0\ , \end{aligned}$$(B.21)where \({\mathscr {O}}(-{\mathscr {D}}_i)\) denotes functions on \(\overline{\mathcal {C}}_{g,n}\) with a simple zero on \({\mathscr {D}}_i\). Since \({\mathscr {O}}\) is the trivial line bundle, we have
$$\begin{aligned} \frac{1}{{{\,\textrm{td}\,}}^*({\mathscr {O}}_{{\mathscr {D}}_i})}={{\,\textrm{td}\,}}^*({\mathscr {O}}(-{\mathscr {D}}_i))={{\,\textrm{td}\,}}({\mathscr {O}}({\mathscr {D}}_i))=\frac{\delta _i}{1-\textrm{e}^{-\delta _i}}\ . \end{aligned}$$(B.22)The last equality follows from the definition of the Chern class by noting that the constant function is a section of \({\mathscr {O}}({\mathscr {D}}_i)\) with a simple zero on the divisor \({\mathscr {D}}_i\).
-
3.
One has to work a bit more for the Todd class of \({\mathscr {O}}_\nabla \). \(\nabla \) has several components, namely one associated to every boundary divisor of \(\overline{\mathcal {M}}_{g,n}\). Indeed, by definition \(\nabla \) is the set of all nodal surfaces together with a marked point that coincides with the node. In the language of \(\overline{\mathcal {M}}_{g,n+1}\), a component of \(\nabla \) thus looks like Figure 6.
Thus let us write \(\nabla =\sum _\Gamma \nabla _\Gamma \) as the sum of the different components and \(\nabla \) runs over the stable graphs (defined in Section 5.1) that correspond to codimension 1 boundary classes in \(\overline{\mathcal {M}}_{g,n}\). From the Figure 6 it should be clear that the intersection of any two distinct components vanishes and thus \(\nabla _\Gamma \, \nabla _{\Gamma '}=0\) for \(\Gamma \ne \Gamma '\). Thus we have
$$\begin{aligned} \frac{1}{{{\,\textrm{td}\,}}^*({\mathscr {O}}_\nabla )}=\prod _\Gamma \frac{1}{{{\,\textrm{td}\,}}^*({\mathscr {O}}_{\nabla _\Gamma })}=1+\sum _\Gamma \left( \frac{1}{{{\,\textrm{td}\,}}^*({\mathscr {O}}_{\nabla _\Gamma })}-1\right) \end{aligned}$$(B.23)and we can proceed to compute each \({{\,\textrm{td}\,}}^*({\mathscr {O}}_{\nabla _\Gamma })\) separately.
Since boundary divisors are normal crossing divisors in moduli space we can write locally \(\nabla _\Gamma ={\mathscr {D}}^{(1)}_\Gamma \cap {\mathscr {D}}^{(2)}_\Gamma \) as the intersection of the two divisors. Let us denote by \(\delta ^{(1)}_\Gamma \) and \(\delta ^{(2)}_\Gamma \) the corresponding cohomology classes. Then we have the exact sequence
$$\begin{aligned} 0 \longrightarrow {\mathscr {O}}(-{\mathscr {D}}_\Gamma ^{(1)}-{\mathscr {D}}_\Gamma ^{(2)}) \longrightarrow {\mathscr {O}}(-{\mathscr {D}}_\Gamma ^{(1)}) \oplus {\mathscr {O}}(-{\mathscr {D}}_\Gamma ^{(2)}) \longrightarrow {\mathscr {O}} \longrightarrow {\mathscr {O}}_{\nabla _\Gamma } \longrightarrow 0 .\nonumber \\ \end{aligned}$$(B.24)The maps are almost obvious. The first map maps a function f that vanishes on both divisors \({\mathscr {D}}_\Gamma ^{(1)}\) and \({\mathscr {D}}_\Gamma ^{(2)}\) to (f, f). The next map maps a pair of functions \((f^{(1)},f^{(2)})\) that vanish on the respective divisors to the difference \(f^{(1)}-f^{(2)}\). The final map is the restriction of a function f to \(\nabla _\Gamma \). This sequence is clearly exact. We thus have
$$\begin{aligned} \frac{1}{{{\,\textrm{td}\,}}^*({\mathscr {O}}_{\nabla _\Gamma })}&=\frac{{{\,\textrm{td}\,}}^*({\mathscr {O}}(-{\mathscr {D}}^{(1)}_\Gamma ) \oplus {\mathscr {O}}(-{\mathscr {D}}^{(2)}_\Gamma ))}{{{\,\textrm{td}\,}}^*({\mathscr {O}}(-{\mathscr {D}}^{(1)}_\Gamma -{\mathscr {D}}^{(2)}_\Gamma ))} \end{aligned}$$(B.25)$$\begin{aligned}&=\frac{\delta _\Gamma ^{(1)} \delta _\Gamma ^{(2)} (1-\textrm{e}^{-\delta _\Gamma ^{(1)}-\delta _\Gamma ^{(2)}})}{(\delta _\Gamma ^{(1)}+\delta _\Gamma ^{(2)})(1-\textrm{e}^{-\delta _\Gamma ^{(1)}})(1-\textrm{e}^{-\delta _\Gamma ^{(2)}})} \end{aligned}$$(B.26)$$\begin{aligned}&=\nabla _\Gamma \, \frac{ (1-\textrm{e}^{-\delta _\Gamma ^{(1)}-\delta _\Gamma ^{(2)}})}{(\delta _\Gamma ^{(1)}+\delta _\Gamma ^{(2)})(1-\textrm{e}^{-\delta _\Gamma ^{(1)}})(1-\textrm{e}^{-\delta _\Gamma ^{(2)}})}\ . \end{aligned}$$(B.27)
The GRR formula (B.11) involves the pushforward of the relative Todd class under \(\pi \) to \(\overline{\mathcal {M}}_{g,n}\) and hence we should determine the various pushforwards. Using eqs. (B.6) and (B.9), this is immediate for the first two cases discussed above,
We used that \(\kappa _0=\pi _*(\omega _\pi ^\text {log})\) computes the degree of the line bundle \(\omega _\pi ^\text {log}\) on the surface \(\Sigma \), which is \(2g-2+n\). Thus the main remaining work is to cast the pushforward of (B.27) in a useful form. Let us first rephrase (B.27) in terms of the Chern classes of the normal bundle to \(\nabla \). For any smooth divisor \({\mathscr {D}}\), \({\mathscr {O}}(-{\mathscr {D}})\) is in fact the same as the conormal line bundle. Indeed, sections of \({\mathscr {O}}(-{\mathscr {D}})\) are functions with a simple zero on the divisor \({\mathscr {D}}\), while sections of the conormal bundle are by definition first order approximations to such functions. Hence \(\delta _\Gamma ^{(1)}\) and \(\delta _\Gamma ^{(2)}\) are the two Chern roots of the normal bundle of \(\nabla _\Gamma \) in \(\overline{\mathcal {M}}_{g,n+1}\). In Section 4.4, we already discussed the normal bundles of divisors in moduli space and saw that the normal bundle to a divisor \({\mathscr {D}}\) is isomorphic to \(\mathbb {L}_\circ ^{-1} \otimes \mathbb {L}_\bullet ^{-1}\), where \(\mathbb {L}_\circ \) and \(\mathbb {L}_\bullet \) are the usual two line bundles of the two nodes. In our case, one of the nodes is on the 3-punctured sphere component in Figure 6 and thus does not contribute to the first Chern class. Using the definition of the \(\psi \)-classes, we hence find
on the singular locus \(\nabla _\Gamma \), where as usual \(\psi _\circ \) and \(\psi _\bullet \) denote the two \(\psi \)-classes of the two nodes (that are indistinguishable). We then have
where we recall that \(\xi _\Gamma \) is the inclusion of the boundary divisor \({\mathscr {D}}_\Gamma \) in \(\overline{\mathcal {M}}_{g,n}\).
1.5 Evaluating the GRR theorem
Now that we have explained how to compute \({{\,\textrm{td}\,}}(\pi )\), we can apply the theorem (B.11) to various instances of interest. For this, we can choose the line bundle \({\mathscr {L}}\) on \(\overline{\mathcal {C}}_{g,n}\) freely.
The Hodge bundle. We start by choosing \({\mathscr {L}}={\mathscr {O}}\), the trivial line bundle. Then the push-forward is
where we used Serre duality (and hence in \(\mathbb {E}\) we need to allow for simple poles at the nodes for this step to be valid). So
Here we first used that various intersections vanish to rewrite the product of classes as a sum, see eqs. (B.18) and (B.23). We then used eqs. (B.28) and (B.31) to rewrite the result in terms of known quantities. Finally upon taking the dual, we learn that
while the even Chern characters vanish (except for \({{\,\textrm{ch}\,}}_0(\mathbb {E})=g\)). Some further exercises in symmetric function theory turn this into a famous formula for the Chern classes \(\lambda _i=c_i(\mathbb {E})\), which was first found by Mumford [73].
The bundle of quadratic differentials. Let’s repeat the computation for the bundle of quadratic differentials that we denote by \(\mathbb {E}^{(2)}\). Quadratic differentials are by definition sections of \(\omega _\pi \otimes \omega _\pi ^\text {log}\), i.e. they are allowed to have simple poles at the marked points. Near a node, the quadratic differential is allowed to have double poles, but there are conditions on the singular terms at the node. We stress already here that these conditions are different than for the cotangent bundle of \(\overline{\mathcal {M}}_{g,n}\). In fact, quadratic differentials lead to the cotangent bundle of uncompactified moduli space, \(\mathcal {M}_{g,n}\). It will be slightly more convenient to start with the line bundle \((\omega _\pi ^\text {log})^{-1}\), which has the dual pushforward, since
So we get
Observe that
and hence
Te products in (B.41) can again be rewritten as a sum of the involved Todd classes because the intersections (B.18) are trivial. We can then compare with (B.34) and see that
where we used the definition (B.9). Finally, we can take the dual and use that the degree of \(\omega _\pi ^\text {log}\) is \(2g-2+n\) and hence \(\kappa _0=2g-2+n\) to get
where \({{\,\textrm{ch}\,}}(\mathbb {E})\) is given by (B.37) above. In particular,
gives the correct dimension of the space of quadratic differentials.
Tangent bundle. Finally, we want to repeat the same exercise for the cotangent bundle of \(\overline{\mathcal {M}}_{g,n}\). Let us first recall the following standard result of deformation theory due to Kodaira and Spencer. The Kodaira Spencer map identifies
But since \(^0(\Sigma ,T\Sigma )=0\), the right hand side is the pushforward of the relative tangent bundle (or sheaf), i.e.
\(T_{\overline{\mathcal {C}}_{g,n}/\overline{\mathcal {M}}_{g,n}}\) fits into the short exact sequence
After dualizing, we recognize this sequence essentially as (B.16). Let us denote
Then \(\Omega _\pi ^\text {log}\) is the sheaf of differentials on \(\Sigma \) with possible simple poles at the divisors \({\mathscr {D}}_i\). However, contrary to \(\omega _\pi ^\text {log}\), sections of \(\Omega _\pi ^\text {log}\) are not allowed to have simple poles at the nodes. To summarize, we have
To relate \(\Omega _\pi ^\text {log}\) to \(\omega _\pi ^\text {log}\), we combine the sequences (B.16) and (B.51), which gives
Thus we can dualize the sequence and conclude
where we again used the triviality of the line bundle \(\omega _\pi ^\text {log}\) when restricted to \(\nabla \). \({{\,\textrm{ch}\,}}^*\) denotes the Chern character of the dual bundle (or sheaf). We again use the exact sequence (B.24) to compute \({{\,\textrm{ch}\,}}^*({\mathscr {O}}_\nabla )\):
We then only have to put the pieces together. When comparing with the previous case for the quadratic differentials (B.41), we get
Since \(\delta _i\, \nabla =c_1(\omega _\pi ^\text {log})\, \nabla =0\), this simplifies with the help of (B.27) to
where we used the definition (3.23) for the boundary classes \(\Delta _m\). We can finally dualize to get the Chern character of the cotangent bundle,
So the full answer for the cotangent bundle is obtained by combining (B.37), (B.47) and (B.65). In particular, we have
which is the well-known formula by Mumford and Harris derived in [74]. In particular, \(\Delta _1\) is the total boundary class of \(\overline{\mathcal {M}}_{g,n}\), see eq. (3.22). We also have the following simple result for the even Chern characters
1.6 A consistency check
Let us explain a strong consistency check that one can perform on this result. The Gauss-Bonnet theorem predicts
where \(\chi (\overline{\mathcal {M}}_{g,n})\) is the orbifold Euler characteristic of compactified moduli space. For small values of \(3g-3+n\) one can check this explicitly. Using the program admcycles [80], we computed the left hand sides of (B.68) for the following values of (g, n). They agree with the known values of the Euler characteristics of \(\overline{\mathcal {M}}_{g,n}\) [107],Footnote 31 which are
This computation involves all the terms in the Chern characters and thus provides a simple check on our formula (B.64).
Some Details About Genus 2
In this appendix, we work out explicitly the sections of \({\mathscr {L}}^k\) in the case of a surface of genus 2.
1.1 Hyperelliptic surfaces
We use an explicit parametrization of the genus 2 moduli space. First, we recall that every genus 2 surface can be written as a hyperelliptic surface of the form
Thus, we can view the \(\lambda _i\)’s as coordinates on \(\mathcal {M}_2\). Of course permuting them leads to equivalent surfaces and there is an action of \(\textrm{PSL}(2,\mathbb {C})\) acting on them. So the moduli space \(\mathcal {M}_{2}\) consists of unordered tuples \(\lambda _i\) up to the action of \(\textrm{PSL}(2,\mathbb {C})\). Another way to think about unordered tuples \(\lambda _i\) is to consider homogeneous polynomials or degree 6 in two variables, traditionally called binary sextics in the literature. Their zeros parametrize 6 values in \(\mathbb{C}\mathbb{P}^1\).
Thus a section of a line bundle over \(\overline{\mathcal {M}}_{2}\) is simply a symmetric function depending on the 6 variables \(\lambda _i\) that satisfies certain boundary conditions at the boundary divisors and certain invariance conditions under the action of \(\text {PSL}(2,\mathbb {C})\).
1.2 Invariance conditions
We first explain the invariance condition under \(\text {PSL}(2,\mathbb {C})\) that a section of the prequantum line bundle \({\mathscr {L}}^k\) has to satisfy. On a hyperelliptic genus 2 surface, there are two holomorphic differentials, which we can take to be of the form
There are three quadratic differentials, namely
Recall from the discussion in Section 3.3 that the prequantum line bundle can be realized as \({\mathscr {L}}^k=(\det \mathbb {E}^{(2)})^k \otimes (\det \mathbb {E})^{-k}\). A section can thus be written as
Let us work out the invariance conditions on \(f_k(\lambda _1,\lambda _2\dots )\). Clearly, \(f_k(\lambda _1,\lambda _2,\dots )\) has to be a symmetric function, but it also has to satisfy a further condition due to \(\textrm{PSL}(2,\mathbb {C})\) invariance. A simple computation yields the transformation
under \(\lambda _i \rightarrow \frac{a \lambda _i+b}{c \lambda _i+d}\) with \(ad-bc=1\). We also transformed z in the same fashion on the right hand side in order to bring the differentials back into their standard form. Consequently,
and thus we should have
for a section of \({\mathscr {L}}^k\).
1.3 Non-separating degeneration
Let us next discuss what sort of behaviour we expect near the degenerations. There are two types of degenerations, namely the separating and the non-separating type. To keep formulas shorter, we will gauge fix \(\lambda _4=0\), \(\lambda _5=1\) and \(\lambda _6=\infty \). The non-separating degeneration corresponds to the collision of two \(\lambda _i\)’s. Since any two collisions are equivalent, we can consider \(\lambda _3 \rightarrow 0\). In this limit, the hyperelliptic equation becomes
Upon defining \({\tilde{y}}=\frac{y}{z}\), this becomes the standard hyperelliptic surface of a genus 1 surface,
The differentials become
\(\omega _2(z)\) is the standard differential on the genus 1 surface, whereas \(\omega _1(z)\) has two additional poles at \(z=0\), \({\tilde{y}}=\pm \sqrt{-\lambda _1\lambda _2}\), which are the two nodes of the surface. Similarly, \(\omega _1^2\), \(\omega _1\omega _2\) and \(\omega _2^2\) are quadratic differentials that have up to second order poles at the nodes. These are the standard differentials on the nodal surface and we hence conclude that \(f_k(\lambda _1,\lambda _2,\dots )\) should be regular in the limit \(\lambda _i \rightarrow \lambda _j\).
1.4 Separating degeneration
Next we discuss the separating degeneration. It can be identified with the limit where both \(\lambda _2 \rightarrow 0\) and \(\lambda _3 \rightarrow 0\) at the same rate, but their ratio is kept fixed. So let’s set \(\lambda _2=q^2\), \(\lambda _3=q^2 \lambda \) and send \(q \rightarrow 0\).Footnote 32 Then the hyperelliptic equation becomes
There are now two different ways to take the limit. We can either naively proceed and obtain
where \({\tilde{y}}=\frac{y}{z_\text {L}}\). We wrote \(z_\text {L}\) for z. This again a genus 1 surface. We can also first rescale \(z \rightarrow q^2 z_\text {R}\) and \(y \rightarrow q^3 {\tilde{y}}\), which presents the surface in the form
The limit \(q \rightarrow 0\) now gives again a genus 1 surface of the form
We thus obtain two genus 1 surfaces that are connected at a single node. The node is located at \(z_\text {L}=0\) and \(z_\text {R}=\infty \). Let’s work out what happens to the differentials. We start with the left surface.
which is the standard differential on the surface. For \(\omega _1(z)\), we find instead
A good local parameter of the surface near \(z_\text {L}=0\) is given by \({\tilde{y}}\), since \(z_\text {L}=\lambda _1^{-1} {\tilde{y}}^2\). The differential near \(z_\text {L}\) behaves as
Thus the differential has a double pole at the node and is thus not a valid differential on the left surface. Similarly we find
The limit of \(\omega _2(z)\) has again a double pole at the node \(z_\text {R}=\infty \). For the wedge products, \(q \omega _1 \wedge \omega _2\) tends to a well-defined object in the limit, because the correct combination
survives, whereas the terms with the double poles vanish in the limit. For the quadratic differentials, we note that \(\omega _2^2\) tends to the quadratic differential that is only non-zero on the left part of the surface and \(q^2 \omega _1^2\) tends to the quadratic differential that is only non-zero on the right part of the surface. Finally \(\omega _1\omega _2\) tends to a quadratic differential that is non-zero on both sides of the surface and has double poles at the residues. So we find that
tends to a well-defined product of the three quadratic differentials on the surface. Overall we find that
tends to a well-defined element of the fiber of \({\mathscr {L}}\) in the limit. Thus, we need to require that \(f_k(\lambda _1,\lambda _2,\dots )\) has a zero of order \(q^k\) at this degeneration in order to get a well-defined section of \({\mathscr {L}}^k\) that also extends to the boundary of \(\overline{\mathcal {M}}_2\).
1.5 A side note about a relation in cohomology
Our discussion here can be used to derive a relation in \(^2(\overline{\mathcal {M}}_2,\mathbb {Q})\), which we can compare with the literature in order to cross-check our analysis. Let’s consider a section of the line bundle
In this case, the invariance conditions on such a section simply means that it is a function on moduli space (i.e. a section of the trivial line bundle on \(\mathcal {M}_2\)). However, writing the section as
f can behave non-trivially near the boundary of moduli space. From our discussion, it follows that f behaves regularly near the non-separating degeneration of moduli space. Near the separating degeneration, the discussion of C.4 implies that f is allowed to have a first order pole there. Let’s denote as in Section 3.3 by \(\delta _1\equiv \delta _{1,\emptyset }\) the cohomology class of the separating divisor in \(^2(\mathcal {M}_{2,0})\) and by \(\delta _\text {irr}\) the cohomology class of the non-separating divisor. We thus learn that
since the first Chern class is by definition the zero divisor minus the pole divisor. Recalling the definition \(c_1(\mathbb {E})=\lambda _1\) and from (B.47) that \(c_1(\mathbb {E}^{(2)})=\lambda _1+\kappa _1\), this reads
We can furthermore use Mumford’s formula (3.24a)
We can thus solve for \(\kappa _1\) in terms of boundary divisors, which yields
This relation in cohomology is well-known [109]. No similar relation exists for \(g \ge 3\).
1.6 The classical invariants
Let us get back to our study of sections of \({\mathscr {L}}^k\). We learned from our study of the degenerations that \(f_k(\lambda _1,\lambda _2,\dots )\) does not have any poles, even at the degenerations. Thus, it has to be a polynomial. The invariance condition under \(\text {PSL}(2,\mathbb {C})\) then tells us that the order of the polynomial is 2k in every variable. The symmetric polynomials satisfying
for some weight w (but without the further condition at the degenerations) are well-known. A list of generators is (see e.g. [110])
Here the notation (ij) means \(\lambda _i-\lambda _j\). The sums and products run over all permutations of the labels \(1,\dots ,6\) that act non-trivially on the given expression. One readily checks that A has weight 2, B has weight 4, C has weight 6, D has weight 10 and E has weight 15. The generators satisfy a single relation of the form
where F is of graded polynomial of degree 30 in the other generators.
1.7 Sections of \((\det \mathbb {E})^k\) and Siegel modular forms
In order to make contact with more classical results in the literature, we will first determine a set of generators for sections of \((\det \mathbb {E})^k\). These can be identified with Siegel modular forms of genus 2. On top of the invariance requirement that is solved by the invariants A, B, C, D and E, we also need to impose that
This comes from the fact that \(q \omega _1 \wedge \omega _2\) is a well-defined section as \(q \rightarrow 0\). In fact, this requirement is already satisfied by B and D that vanish to orders \(q^4\) and \(q^{12}\), respectively. So D vanishes faster than required and is hence a cusp form. The complete list of generators that satisfy these requirements are
They satisfy a single relation of the form
where F is a graded homogeneous polynomial in the generators. In particular, the Hilbert series of the Siegel modular forms of genus 2 is
This is a classical result of Igusa [110].
1.8 Sections of \({\mathscr {L}}^k\)
Finally, we can discuss the matter of interest and determine the ring of sections of the prequantum line bundle \({\mathscr {L}}^k\). By definition from (C.7), the weight \(w=2k\) is even and hence the ring in question will be a subring of the free polynomial algebra \(\mathbb {C}[A,B,C,D]\). It will be more convenient to use instead similar generators as the one that appeared for the Siegel modular forms and consider
These generators still do not have any relation, but \(\gamma \) has a higher order of vanishing at the separating degeneration than C. In fact, let \(\ell \) denote the order of vanishing at the separating degeneration as in (C.36). Then the weights and orders of vanishing of the generators \(\alpha \), \(\beta \), \(\gamma \) and \(\delta \) are
We need the order of vanishing to be at least as high as the order of vanishing. Thus, \(\beta \), \(\gamma \) and \(\delta \) give directly generators of the ring \(\bigoplus _{k \ge 0} ^0(\overline{\mathcal {M}}_2,{\mathscr {L}}^k)\). Any element in the ring \(\bigoplus _{k \ge 0} ^0(\overline{\mathcal {M}}_2,{\mathscr {L}}^k)\) can thus be written as
where
Thus all that remains is to count the number of integer solutions to these constraints, which will give the Hilbert series. Let us first consider the refined Hilbert series that also keeps track of the order of vanishing. The Hilbert series that only accounts for the use of \(\beta \), \(\gamma \) and \(\delta \) is
where t keeps track of the weight of the generators and x of the order of vanishing. Now in the formal expansion around \(t=0\), every term of the form \(x^\ell t^k\) gives rise to several terms in the actual Hilbert series. In fact, we should replace every monomial
to get the actual Hilbert series for the number of sections of \({\mathscr {L}}^k\). This is because every monomial in \(\beta \), \(\gamma \) and \(\delta \) whose weight and order of vanishing are k and \(\ell \) can be multiplied by \(\alpha ^m\) with \(0 \le m \le \ell -k\) to give a section of \({\mathscr {L}}^{k+m}\). Thus it follows that the full Hilbert series takes the form
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Eberhardt, L. Off-shell Partition Functions in 3d Gravity. Commun. Math. Phys. 405, 76 (2024). https://doi.org/10.1007/s00220-024-04963-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00220-024-04963-2