Random Quantum Circuits Transform Local Noise into Global White Noise

Abstract

We study the distribution over measurement outcomes of noisy random quantum circuits in the regime of low fidelity, which corresponds to the setting where the computation experiences at least one gate-level error with probability close to one. We model noise by adding a pair of weak, unital, single-qubit noise channels after each two-qubit gate, and we show that for typical random circuit instances, correlations between the noisy output distribution $p_{\text {noisy}}$ and the corresponding noiseless output distribution $p_{\text {ideal}}$ shrink exponentially with the expected number of gate-level errors. Specifically, the linear cross-entropy benchmark F that measures this correlation behaves as $F=\text {exp}(-2s\epsilon \pm O(s\epsilon ^2))$, where $\epsilon$ is the probability of error per circuit location and s is the number of two-qubit gates. Furthermore, if the noise is incoherent—for example, depolarizing or dephasing noise—the total variation distance between the noisy output distribution $p_{\text {noisy}}$ and the uniform distribution $p_{\text {unif}}$ decays at precisely the same rate. Consequently, the noisy output distribution can be approximated as $p_{\text {noisy}}\approx Fp_{\text {ideal}}+ (1-F)p_{\text {unif}}$. In other words, although at least one local error occurs with probability $1-F$, the errors are scrambled by the random quantum circuit and can be treated as global white noise, contributing completely uniform output. Importantly, we upper bound the average total variation error in this approximation by $O(F\epsilon \sqrt{s})$. Thus, the “white-noise approximation” is meaningful when $\epsilon \sqrt{s} \ll 1$, a quadratically weaker condition than the $\epsilon s\ll 1$ requirement to maintain high fidelity. The bound applies if the circuit size satisfies $s \ge \Omega (n\log (n))$, which corresponds to only logarithmic depth circuits, and if, additionally, the inverse error rate satisfies $\epsilon ^{-1} \ge {\tilde{\Omega }}(n)$, which is needed to ensure errors are scrambled faster than F decays. The white-noise approximation is useful for salvaging the signal from a noisy quantum computation; for example, it was an underlying assumption in complexity-theoretic arguments that noisy random quantum circuits cannot be efficiently sampled classically, even when the fidelity is low. Our method is based on a map from second-moment quantities in random quantum circuits to expectation values of certain stochastic processes for which we compute upper and lower bounds.

1 Introduction

There is a fundamental trade-off in quantum computation between computation size and error rate. Naturally, the longer the computation, the lower the physical error rate must be to maintain a high probability of an errorless computation. Once the error rate is beneath a constant threshold, the theory of fault tolerance and quantum error correction [1, 2] may be employed to push the probability of a logical error arbitrarily close to zero, despite the prevalence of many physical errors during the computation; however, error correction comes at the cost of additional qubits and gates. These overheads, while acceptable in an asymptotic sense, are likely to be overwhelming in the near and intermediate term. This inspires the idea of an upcoming Noisy Intermediate-Scale Quantum (NISQ) era [3], where hardware capabilities are good enough to perform non-trivial quantum tasks on dozens or hundreds of qubits, but quantum error correction, which might require thousands or millions of qubits, remains beyond reach.

In this paper, we study a model of NISQ devices performing random computations and prove a precise sense in which, for typical circuit instances, local errors are quickly scrambled and can be treated as white noise. For some applications, this phenomenon makes it possible for the signal of the noiseless computation to be extracted by repetition despite a large overall chance that at least one error occurs.

Our local error model assumes that each two-qubit gate in the quantum circuit is followed by a pair of gate-independent single-qubit unital noise channels acting on the two qubits involved in the gate. For simplicity and ease of analysis, we assume each of these noise channels is identical, but we fully expect the takeaways from our work to apply when the noise strength is allowed to vary from location to location. For concreteness in this introduction, we can consider the depolarizing channel with error probability $\epsilon$. The fidelity of the noisy computation with respect to the ideal computation is defined as $f=\textrm{tr}(\rho _{\text {ideal}}\rho _{\text {noisy}})$ where $\rho _{\text {ideal}}$ is the (pure) density matrix output by the ideal circuit and $\rho _{\text {noisy}}$ is the (generally mixed) density matrix ouput by the noisy circuit. In this case, f is expected to be roughly equal to the probability that no errors occur, denoted here by F. We see that, for a circuit with s two-qubit gates, the quantity $F = (1-\epsilon )^{2s}$ is close to 1 only if the quantity $2\epsilon s$—the average number of errors—satisfies $2\epsilon s \ll 1$.

However, this high-fidelity requirement is quite restrictive in practice. Already for circuits with 50 qubits at depth 20, the error rate $\epsilon$ must be on the order of $10^{-4}$ for the whole computation to run without error at least 90% of the time; this error rate is more than an order of magnitude smaller than what has been achievable in recent experiments on superconducting qubit systems of that size [4,5,6]. Indeed, in their landmark 2019 quantum computational supremacy experiment [4], a group at Google performed random circuits on 53 qubits of depth 20, but the fidelity of the computation was estimated to be $f \approx 0.002$, suggesting that at least one error occurs in all but a tiny fraction of the trials. Similar experiments at the University of Science and Technology of China on 56 [5] and 60 [6] qubits reported even smaller fidelities of 0.0007 [5] and 0.0004 [6]. This would not be an issue if one could determine when a trial is errorless: in this case, one could just repeat the experiment 1/f times. However, error detection requires overheads similar to error correction.

Rather, low-fidelity random circuit sampling experiments and their claim of quantum computational supremacy benefit from a key assumption [4, 7]: when at least one error does occur, the output of the experiment is well approximated by white noise, that is, the output is random and uncorrelated with the ideal (i.e., noiseless) output. When this is the case, the signal of diminished size F can, at least for some applications, be extracted from the white noise using $O(1/F^2)$ trials, as we explain later. Specifically, for quantum computational supremacy, the white-noise assumption is that the distribution $p_{\text {noisy}}$ over measurement outcomes of their noisy device is close to what we call the “white-noise distribution”

$$\begin{aligned} p_{\text {wn}}= F p_{\text {ideal}}+ (1-F)p_{\text {unif}}, \end{aligned}$$

(1)

with $p_{\text {ideal}}$ the ideal distribution and $p_{\text {unif}}$ the uniform¹ distribution. In particular, for the approximation to be non-trivial, we demand that the total variation distance between $p_{\text {noisy}}$ and $p_{\text {wn}}$ be a small fraction of F, that is

$$\begin{aligned} \hspace{72 pt}\frac{1}{2}\Vert p_{\text {wn}}-p_{\text {noisy}}\Vert _1 \ll F . \qquad \text {(white-noise assumption)} \end{aligned}$$

(2)

This demand is necessary because we expect that $p_{\text {noisy}}$ also decays toward $p_{\text {unif}}$ such that $\frac{1}{2}\Vert p_{\text {noisy}}- p_{\text {unif}}\Vert _1 = \Theta (F)$, and thus $p_{\text {unif}}$ is a trivial approximation for $p_{\text {noisy}}$ with error $\Theta (F)$.

Prior to their experiment, the Google group provided numerical evidence [7] in favor of the white-noise assumption² for randomly chosen circuits. They found that the output distribution of random circuits of depth 40 on a 2D lattice of 20 qubits approaches the uniform distribution when a local Pauli error model is applied. Furthermore, they observed that the correlation of $p_{\text {noisy}}$ with respect to $p_{\text {ideal}}$ appears to decay exponentially, consistent with $p_{\text {noisy}}\approx p_{\text {wn}}$. However, their analysis did not specifically estimate the distance³ between $p_{\text {noisy}}$ and $p_{\text {wn}}$. The white-noise condition in Eq. (2) requires that the distance between $p_{\text {noisy}}$ and $p_{\text {wn}}$ decrease as the expected number of errors increases and F decays, so quantifying the differences between the distributions is vital for determining how well the white-noise approximation is obeyed.

Here we prove rigorous bounds on the error in the white-noise approximation, averaged over circuits with randomly chosen gates. Our results fully apply in two random quantum circuit architectures: first, the 1D architecture with periodic boundary conditions, where qubits are arranged in a ring and alternating layers of nearest-neighbor gates are applied; and second, the complete-graph architecture, where each gate is chosen to act on a pair of qubits chosen uniformly at random among all $n(n-1)/2$ pairs.⁴ We show that, for Pauli noise channels, the error in the white-noise approximation is small as long as (1) $\epsilon ^2 s \ll 1$, (2) $s \ge \Omega (n\log (n))$, and (3) $\epsilon \ll 1/(n\log (n))$. We believe that condition (3) could be relaxed to read $\epsilon < c/n$ for some universal constant $c = O(1)$; numerics suggest $c=0.3$ for the complete-graph architecture. Condition (1) is a quadratic improvement over the condition $\epsilon s \ll 1$ needed for high fidelity. For circuits with $\epsilon < 0.005$, as is the case in recent experiments [4,5,6], thousands of gates could potentially be implemented before condition (1) fails. Note that our technical statements hold for general (non-Pauli) error channels as well, but we find that the error in the white-noise approximation is small only for incoherent noise channels, which includes depolarizing and dephasing noise, but not unitary noise. We complement this analysis with numerical results that confirm the picture presented by our theoretical proofs for the complete-graph architecture, and demonstrate that realistic NISQ-era values of the error rate and circuit size can lead to a good white-noise approximation.

By putting the white-noise approximation for random quantum circuits on stronger theoretical footing, our work has several applications. First, the white-noise assumption has been an ingredient in formal complexity-theoretic arguments that the task accomplished on noisy devices running random quantum circuits is hard for classical computers, enabling the declaration of quantum computational supremacy [4]. We complement our main result by showing in Appendix C that classically sampling from the white-noise distribution within total variation distance $\eta F$ is, in a certain complexity-theoretic sense, equivalent to sampling from the ideal output distribution within total variation distance $O(\eta )$, up to a factor of F in the complexity. This makes low-fidelity experiments where errors are common nearly as defensible for quantum computational supremacy as high-fidelity experiments where errors are rare, at least in principle. However, by identifying a barrier at $\epsilon = O(1/n)$ above which the white-noise assumption is expected to fail, our work accentuates limitations of existing high-noise quantum computational supremacy proposals: if the noise rate is order-1 as n increases—a more realistic experimental scenario—one should not rely on the white-noise assumption as Google [4, 7] did to justify an asymptotic advantage for the sampling problem. Second, our result lends theoretical justification to the usage [4,5,6] of the linear cross-entropy metric proposed in Ref. [4] to benchmark noise in random circuit experiments and verify that hardware has correctly performed the quantum computational supremacy task. Indeed, as a side result, we show that, for both incoherent and coherent noise, the metric decays precisely as $e^{-2s\epsilon \pm O(s\epsilon ^2)}$ when $\epsilon$ is sufficiently small, matching the expectation that it should be roughly equal to the probability that all 2s noise locations are error free. This also suggests that the linear cross-entropy benchmark could be reliably used to accurately estimate the underlying local noise rate $\epsilon$ [9].

Beyond random circuit experiments for quantum computational supremacy, our work suggests that other scenarios where the white-noise assumption holds may be advantageous in the NISQ era, as one can eschew error correction and nonetheless perform a fairly long quantum computation, as long as one is willing to repeat the experiment $O(1/F^2)$ times. One example of a scenario where the assumption may hold is quantum simulation of fixed chaotic Hamiltonians, since they are also believed to be efficient at scrambling errors.

The remainder of the paper is structured as follows: in Sect. 2, we describe our setup and in particular our model for local noise within a random quantum circuit; in Sect. 3, we precisely state our results; in Sect. 4, we discuss further implications and how our results fit in with prior work; in Sect. 5, we give an overview of the intuition behind our result and the method we use in our proofs, which is based on a map from random quantum circuits to certain stochastic processes. These stochastic processes can also be interpreted as partition functions of statistical mechanical systems. This method might be regarded as an extension of the method in Ref. [8], where we studied anti-concentration in noiseless random quantum circuits. In Sect. 6, we present a numerical calculation of our bound for the realistic values of the circuit parameters informed by the experiments in Refs. [4,5,6] (although for the complete-graph architecture, rather than 2D). We conclude the main text with an outlook in Sect. 7. The rigorous proofs and details behind the map to stochastic processes then appear in the appendices.

2 A Model of Noisy Random Quantum Circuits

Here we describe our model of noisy random quantum circuits. Let the circuit consist of s two-qudit gates acting on n qudits, each with local Hilbert space dimension q. We follow Ref. [8] in defining a random quantum circuit architecture as an efficient algorithm that takes the circuit specifications (n, s) as input and outputs a quantum circuit diagram with s two-qudit gates, that is, a length-s sequence of qudit pairs, without specifying the actual gates that populate the diagram. Our results fully apply for two specific architectures: the 1D architecture with periodic boundary conditions, and the complete-graph architecture, which were previously shown in Ref. [8] to have the anti-concentration property as long as $s \ge \Omega (n\log (n))$, with a particular constant prefactor. Our results would also fully apply for standard architectures in D spatial dimensions with periodic boundary conditions if it could be proved that they also achieve anti-concentration whenever $s \ge \Omega (n \log (n))$, as was conjectured in Ref. [8].

Given an architecture and parameters (n, s), we can generate a circuit instance by choosing the circuit diagram according to the architecture and then choosing each of the unitary gates in the diagram at random according to the Haar measure. Each instance is associated with an output probability distribution $p_{\text {ideal}}$ over $q^n$ possible computational basis measurement outcomes $x \in [q]^n$ (where $[q] = \{0,1,\ldots ,q-1\}$) that would be sampled if the circuit were implemented noiselessly. Note that in the formal analysis we include a layer of n (also Haar-random) single-qudit gates at the beginning and end of the circuit without counting these 2n gates toward the circuit size; these might be regarded as fixing the local basis for the input product state and the measurement of the output.⁵

2.1 Local noise model

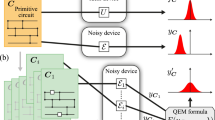
We augment this setup by inserting single-qudit noise channels into the circuit diagram, which act on qudits involved in a multi-qudit gate immediately following the gate, as shown in the example in Fig. 1. In our model, the single-qudit gates remain noiseless and measurements are assumed to be perfect.⁶

Fig. 1

Example of a noisy quantum circuit diagram on $n=4$ qudits with $s=5$ two-qudit gates. A pair of single-qudit noise channels ${\mathcal {N}}$ follow each two-qudit gate. The circuit begins and ends with a layer of noiseless single-qudit gates

Thus, the core assumption is that the noise is local, i.e. independent from qudit to qudit. We assume each noise channel ${\mathcal {N}}$ is a unital⁷ and completely positive trace-preserving map.

For a given noise channel, there are only two parameters that matter for our analysis, the average infidelity and the unitarity of the channel. The average infidelity for a channel ${\mathcal {N}}$ is defined as

$$\begin{aligned} r = 1-\int dV \textrm{tr}\left[ V |{\psi }\rangle \!\langle {\psi }| V^{\dagger }{\mathcal {N}}(V |{\psi }\rangle \!\langle {\psi }| V^{\dagger })\right] , \end{aligned}$$

(3)

where the integral is over the Haar-measure on $q \times q$ unitary matrices V and $|{\psi }\rangle \!\langle {\psi }|$ is any pure state. The average infidelity is one measure of the overall noise strength of the channel ${\mathcal {N}}$. Following Refs. [10, 11], the unitarity is defined for unital channels as

$$\begin{aligned} u = \frac{q}{q-1}\left( \int dV \textrm{tr}\left[ {\mathcal {N}}\left( V |{\psi }\rangle \!\langle {\psi }| V^{\dagger }\right) ^2\right] -\frac{1}{q}\right) . \end{aligned}$$

(4)

The unitarity is the expected purity of the output state under random choice of input state, scaled to have minimum value of 0 and maximum value of 1.

Examples: depolarizing, dephasing, and rotation channels

It is helpful to consider explicitly the following three channels. First, the depolarizing channel

$$\begin{aligned} {\mathcal {N}}_{\textrm{depo}}(\rho )&= (1-\gamma )\rho + \gamma \frac{I}{q} = (1-\epsilon )\rho +\frac{\epsilon }{q^2-1} \sum _{i=1}^{q^2-1}P_i \rho P_i^\dagger \,, \end{aligned}$$

(5)

where $\gamma = \epsilon q^2/(q^2-1)$, $\{P_i\}_{i=1}^{q^2-1}$ is the set of single-qudit Pauli matrices (appropriately generalized to higher q), and I is the $q \times q$ identity matrix. There are two ways to think of the channel: first, with probability $1-\gamma$ doing nothing and with probability $\gamma$ resetting the state to the maximally mixed state on that qudit; second, with probability $1-\epsilon$ doing nothing and with probability $\epsilon$ choosing a Pauli operator at random to apply to the qudit.

We can also consider the dephasing channel

$$\begin{aligned} {\mathcal {N}}_{\textrm{deph}}(\rho )&= (1-\frac{q}{q-1}\epsilon )\rho +\frac{q}{q-1}\epsilon \sum _{i=0}^{q-1} |{i}\rangle \!\langle {i}| \rho |{i}\rangle \!\langle {i}| \,, \end{aligned}$$

(6)

which represents doing nothing with probability $1-q\epsilon /(q-1)$ and performing a measurement in the computational basis with probability $q\epsilon /(q-1)$.

Finally, we can consider a coherent noise channel, for example the rotation channel

$$\begin{aligned} {\mathcal {N}}_{\textrm{rot}}(\rho )&= e^{-i\theta |{0}\rangle \!\langle {0}| }\rho e^{i\theta |{0}\rangle \!\langle {0}| }\,, \end{aligned}$$

(7)

which applies a small unitary rotation by angle $\theta$ to the state.

The average infidelity and unitary of these channels are given in Table 1. The core fact that differentiates the coherent rotation error channel from the incoherent depolarizing and dephasing error channels is how the size of the errors grow under repeated application of the channel. If an incoherent channel is applied m times, the average infidelity grows linearly in m, which is seen in our examples by replacing $\epsilon$ with $1-(1-\epsilon )^m$ and noting $r=O(m\epsilon )$ up to leading order. However, if a coherent channel is applied m times, the average infidelity grows quadratically in m, which is seen in the rotation channel by replacing $\theta$ with $m\theta$ and noting $r = O(m^2\theta ^2)$ up to leading order. Given r and u, the amount of coherence in the channel can be quantified by the parameter $\delta = 2r(1+q^{-1}) - (1-u)(1-q^{-2})$ [12].

Table 1 Average infidelity and unitarity for three different single-qudit noise channels, where q denotes the local dimension of the qudits ($q=2$ for qubits)

2.2 Output distributions of the quantum circuit

Suppose the locations of the s two-qudit gates have been fixed, with gate t acting on qudits $\{i_t,j_t\}$. Then a circuit instance is specified by a sequence $(U^{(-n+1)},\ldots , U^{(s+n)})$, where $U^{(t)}$ is a $q^2 \times q^2$ (two-qudit) unitary matrix if $1\le t \le s$ and a $q \times q$ (single-qudit) unitary matrix otherwise. Accordingly, for each t, let

$$\begin{aligned} {\mathcal {U}}^{(t)}(\sigma ) = \left( {\mathcal {I}}_{[n]\setminus \{i_t,j_t\}} \otimes U_{\{i_t,j_t\}}^{(t)} \right) \sigma \left( {\mathcal {I}}_{[n]\setminus \{i_t,j_t\}} \otimes U_{\{i_t,j_t\}}^{ \dagger (t)} \right) \end{aligned}$$

(8)

denote the unitary channel that acts as $U^{(t)}$ on qudits $i_t$ and $j_t$ and as the identity channel, denoted by ${\mathcal {I}}$, on the other qudits. To account for noise, let

$$\begin{aligned} \widetilde{{\mathcal {U}}}^{(t)} = {\left\{ \begin{array}{ll} \left( {\mathcal {I}}_{[n]\setminus \{i_t,j_t\}}\otimes {\mathcal {N}}_{\{i_t\}} \otimes {\mathcal {N}}_{\{j_t\}}\right) \circ {\mathcal {U}}^{(t)} &{} \text {if } 1 \le t \le s \text { (two-qudit)}\\ {\mathcal {U}}^{(t)} &{} \text {if } t \le 0 \text { (single-qudit)} \end{array}\right. } \end{aligned}$$

(9)

be the channel that applies noise channels after applying the unitary gate. Now we can define the ideal and noisy output distributions by

$$\begin{aligned} p_{\text {ideal}}(x)&= \textrm{tr}\left[ |{x}\rangle \!\langle {x}| \; {\mathcal {U}}^{(s+n)}\circ \cdots \circ {\mathcal {U}}^{(-n+1)}\left( |{0^n}\rangle \!\langle {0^n}| \right) \right] \end{aligned}$$

(10)

$$\begin{aligned} p_{\text {noisy}}(x)&= \textrm{tr}\left[ |{x}\rangle \!\langle {x}| \; \widetilde{{\mathcal {U}}}^{(s+n)}\circ \cdots \circ \widetilde{{\mathcal {U}}}^{(-n+1)}\left( |{0^n}\rangle \!\langle {0^n}| \right) \right] \,. \end{aligned}$$

(11)

Our work compares the distribution $p_{\text {noisy}}$ to the white-noise distribution $p_{\text {wn}}$ (defined in Eq. (1) and repeated here)

$$\begin{aligned} p_{\text {wn}}(x) = Fp_{\text {ideal}}(x) + (1-F)q^{-n} \end{aligned}$$

(12)

for some choice of F. In the introduction, for simplicity our discussion set F to be equal to the probability of an errorless computation; in our more precise analysis below, we find that the choice of F that minimizes the distance between $p_{\text {wn}}$ and $p_{\text {noisy}}$ is given by a normalized version of the linear cross-entropy benchmark, which we show is nearly equal to the quantity chosen in the introduction.

The white-noise distribution is a mixture of the ideal distribution and the uniform distribution. Note that $p_{\text {ideal}}$, $p_{\text {noisy}}$, and $p_{\text {wn}}$ all depend implicitly on the circuit instance U. In the analysis we treat F as a free parameter, and we choose it such that our bound on the distance between $p_{\text {noisy}}$ and $p_{\text {wn}}$ is minimized. The total variation distance between two distributions $p_1$ and $p_2$ is defined as

$$\begin{aligned} \text {TVD}(p_1,p_2) = \frac{1}{2}\Vert p_1 - p_2 \Vert _1 = \frac{1}{2}\sum _{x}|p_1(x)-p_2(x)| . \end{aligned}$$

(13)

Comment on randomness in our setup

There are multiple types of randomness in our analysis, and in understanding our result it is important to keep track of how they interplay. First of all, the noiseless circuit instance U is generated randomly by choosing each gate to be Haar random—in an experimental setting, U is chosen randomly but known to the experimenter. The choice of U determines an ideal pure output state. Second of all, for each fixed choice of U, the noise channels may introduce randomness that makes the noisy output state mixed. When the noise is depolarizing noise, this might be regarded as the insertion of a randomly chosen pattern of Pauli errors. Lastly, the measurement of the state in the computational basis gives rise to a random measurement outcome drawn from a certain classical probability distribution: $p_{\text {ideal}}$ if we are considering the noiseless circuit, and $p_{\text {noisy}}$ if we are considering the noisy circuit. The important thing to remember is that we are primarily concerned with thinking about fixed instances U and the interplay between the resulting probability distributions $p_{\text {ideal}}$, $p_{\text {noisy}}$ and $p_{\text {wn}}$ for that instance. Then, we make a statement about these distributions that holds in expectation over random choice of U. If desired, one could then use Markov’s inequality to form bounds on the fraction of instances U for which the white-noise approximation must be good. In practice, we expect strong concentration of typical instances near their expectation.

Comment on more general (universal) gate sets

We consider random quantum circuits built from local two-site unitary gates drawn randomly with respect to the Haar measure. As our analysis involves only second moment quantities, our results therefore directly apply to any gate set (or distribution on the 2-site unitary group) that forms an exact unitary 2-design, e.g. random Clifford circuits with each two-qubit gate drawn uniformly at random from the Clifford group. Furthermore, circuits constructed with gates drawn randomly from universal gate sets should give rise to similar scrambling phenomena and we expect that our results hold for such circuits, including the actual random circuit experiments performed in Refs. [4,5,6]. While our method is not directly generalizable to other gate sets, we anticipate that if our analysis were extendable to such gate sets, the results would only change by constant factors.

Some evidence for this is provided by the independence of the spectral gap for universal gate sets [13]. This implies that the depth at which random quantum circuits scramble (and converge to approximate unitary designs) only changes by a constant factor when one considers circuits comprised of gates drawn randomly for any universal gate set [14].

3 Overview of Contributions

The main result of this paper is a proof that, for typical random circuits, the output distribution $p_{\text {noisy}}$ of the quantum circuit with local noise is very close to the white-noise distribution $p_{\text {wn}}$ if the noise is sufficiently weak—for our results to apply, the noise strength must decay with the system size. Specifically, we prove an upper bound on the expectation value of the total variation distance between the two distributions. In proving that result, we also prove a statement about the expected linear cross-entropy benchmark—a proxy for fidelity—in noisy random quantum circuits, and another statement about the speed at which $p_{\text {noisy}}$ approaches the uniform distribution. For all statements, the notation ${\mathbb {E}}_U$ denotes expectation over choice of Haar-random single-qudit and two-qudit gates.

In the rest of this section, we state our results for general noise channels, deferring the proofs to Appendix B, but first we summarize the contributions specifically applied to the depolarizing channel in Table 2.

Table 2 Summary of results when the noise is depolarizing (Eq. (5)) with error parameter $\epsilon$

Comment on architectures

The theorem statements below are expressed only for the 1D and complete-graph architectures, which are known to anti-concentrate after circuit size $\Theta (n\log (n))$. In the appendix, we prove slightly more general statements that also hold for any architecture consisting of layers and satisfying a natural connectivity property (this includes standard architectures in D spatial dimensions with periodic boundary conditions). These statements depend on the anti-concentration size $s_{AC}$ of these architectures, which is conjectured to be $\Theta (n\log (n))$ but for which the best known upper bound is $O(n^2)$ [8].

3.1 Decay of linear cross-entropy benchmark

Define the quantity

$$\begin{aligned} {\bar{F}} = \frac{{{\mathbb {E}}}_U\Big [ \sum _x p_{\text {noisy}}(x)(q^np_{\text {ideal}}(x)-1)\Big ]}{{{\mathbb {E}}}_U\Big [ \sum _x p_{\text {ideal}}(x)(q^np_{\text {ideal}}(x)-1)\Big ]}. \end{aligned}$$

(14)

The quantity ${\bar{F}}$ may be regarded as an estimate of the fidelity of the noisy quantum device with respect to the ideal computation; however, we emphasize that it is a distinct quantity. When $p_{\text {noisy}}(x)$ and $p_{\text {ideal}}(x)$ are viewed as random variables in the instance U, ${\bar{F}}$ is equal to their covariance, normalized by the variance of $p_{\text {ideal}}$. Note also that the numerator of ${\bar{F}}$ is the expected score on the linear cross-entropy benchmark, as proposed in Ref. [4], using samples from the noisy device, and the denominator is the expected score using samples from the ideal output distribution. Refs. [9, 15] studied a similar quantity, the difference being that the ${\mathbb {E}}_U$ appears outside the fraction in their case. Additionally, note that the denominator is given by $q^n Z-1$, where Z is the collision probability studied in Refs. [8, 16]. The results of Ref. [8] imply that the denominator becomes within a small constant factor of $(q^n-1)/(q^n+1) \approx 1$ after $\Theta (n\log (n))$ gates. Therefore, while our results are stated for the normalized linear cross-entropy benchmark, they apply equally well for the linear cross-entropy benchmark when the depth is at least logarithmic.

Theorem 1

Consider either the complete-graph architecture or the 1D architecture with periodic boundary conditions on n qudits of local Hilbert space dimension q and comprised of s gates. Let r be the average infidelity of the local noise channels. Then there exists constants c and $n_0$ such that whenever $r \le c/n$ and $n \ge n_0$, the following holds:

$$\begin{aligned} {\bar{F}}&\ge \exp \left( -2sr(1+q^{-1})\right) e^{-O(sr^2)-O(sq^{-2n})-e^{O(\log (n))-\Omega (s/n)}} \end{aligned}$$

(15)

$$\begin{aligned} {\bar{F}}&\le \exp \left( -2sr(1+q^{-1})\right) Q_1 \,, \end{aligned}$$

(16)

where

$$\begin{aligned} Q_1 = \exp \left( O(sr^2) + O(rn\log (n)) + e^{O(\log (n))-\Omega (s/n)} + O(nr \log (1/(nr)))\right) .\quad \end{aligned}$$

(17)

Note that the relationship $\epsilon = r(q+1)/q$ holds for the depolarizing channel as defined in Eq. (5), so, ignoring the $O(q^{-2n})$ corrections,

$$\begin{aligned} e^{-2s\epsilon - O(s\epsilon ^2) } \le {\bar{F}} \le e^{-2s\epsilon + O(s\epsilon ^2) + O(\epsilon n\log (n))+O(n\epsilon \log (1/(n\epsilon ))}, \end{aligned}$$

(18)

indicating that the linear cross-entropy metric decreases exponentially with the expected number of Pauli errors $2s\epsilon$, as long as the noise is sufficiently weak that the other terms can be ignored. In particular, three conditions must be met to approximate $Q_1$ by 1 in Eq. (16): (1) $\epsilon ^2 s \ll 1$; (2) $s \ge \Omega (n\log (n))$, i.e., anti-concentration has been reached; and (3) $\epsilon \ll 1/(n\log (n))$. One implication of Theorem 1 is that the same kind of decay extends to general noise channels and is observed even for coherent noise channels like the rotation channel.

3.2 Convergence to uniform

We show an upper bound on the expected total variation distance between the output of the noisy quantum device $p_{\text {noisy}}$ and the uniform distribution. Our bound decays exponentially in the number of error locations, under certain circumstances. In particular, it decays exponentially in $(1-u)(1-q^{-2})s$ where u is the unitarity of the local noise channels.

Theorem 2

Consider either the complete-graph architecture or the 1D architecture with periodic boundary conditions on n qudits of local Hilbert space dimension q and s gates. Let u be the unitarity of the local noise channels (and define $v=1-u$). Then there exist constants c and $n_0$ such that as long as $v \le c/n$ and $n \ge n_0$

$$\begin{aligned} \mathop {\mathbb {E}}\limits _U \left[ \frac{1}{2}\Vert p_{\text {noisy}}- p_{\text {unif}}\Vert _1 \right] \le \exp (-sv(1-q^{-2})) Q_2 , \end{aligned}$$

(19)

where $p_{\text {unif}}$ is the uniform distribution, and

$$\begin{aligned} Q_2 = \exp \left( O(sv^2) + O(v n \log (n)) + e^{O(\log (n))-\Omega (s/n)}+O(nv \log (1/(nv))\right) . \end{aligned}$$

(20)

Note that $Q_2$ is small under a similar three conditions as in the cross-entropy decay result: (1) $s(1-u)^2 \ll 1$, (2) anti-concentration has been reached, and (3) $n\log (n)(1-u) \ll 1$.

For the depolarizing channel, $u = 1-2\epsilon (1-q^{-2})^{-1}$ up to first order in $\epsilon$, so the distance to uniform decays like $e^{-2s\epsilon }$, which is identical to the rate of linear cross-entropy decay. On the other hand, the unitarity of the rotation channel is $u=1$, so our upper bound does not decay with s, even though ${\bar{F}}$ does decay for the rotation channel. This is expected because the rotation channel is coherent; indeed, unlike the other two examples, it sends pure states to pure states. The ideal pure state and the noisy pure state will become less and less correlated as more noise channels act, which explains why ${\bar{F}}$ decays, but the output distribution for the noisy pure state will not converge to uniform.

3.3 Distance to white-noise distribution

We also show a stronger statement: not only does the output distribution decay to uniform, it does so in a very particular way, preserving an uncorrupted signal from the ideal distribution. That is, we show that $p_{\text {noisy}}$ is close to $p_{\text {wn}}$ by upper bounding the expected total variation distance between the two distributions. Our bound can be applied for any noise channel, but it only evaluates to a small and meaningful number for incoherent noise channels.

Theorem 3

Consider either the complete-graph architecture or the 1D architecture with periodic boundary conditions on n qudits of local Hilbert space dimension q and s gates. Let r be the average infidelity and u the unitarity of the local noise channels (and define $v=1-u$). Let

$$\begin{aligned} \delta =2r(1+q^{-1})-(1-u)(1-q^{-2}) . \end{aligned}$$

(21)

Then, when we choose $F = {\bar{F}}$ as in Eq. (14), there exist constants $c_1$, $c_2$, and $n_0$ such that as long as $v \le c_1/n$, $r \le c_2/n$, and $n \ge n_0$,

$$\begin{aligned} \mathop {\mathbb {E}}\limits _U \left[ \frac{1}{2}\Vert p_{\text {noisy}}- p_{\text {wn}}\Vert _1 \right] \le {}&{\bar{F}}\sqrt{s}\left( \sqrt{\delta }+O(v)+O(r)\right) + O\big ({\bar{F}}\sqrt{vn\log (n)}\big ) \nonumber \\&\quad +O\big ({\bar{F}}\sqrt{nv\log (1/nv)}\big )+ {\bar{F}}e^{O(\log (n))-\Omega (s/n)}\,, \end{aligned}$$

(22)

whenever the right-hand side of Eq. (22) is less than ${\bar{F}}$.

We make a couple of comments. First, we emphasize how small the right-hand side of Eq. (22) is. The quantity ${\bar{F}}$ is decaying exponentially in the number of expected errors, as shown in Theorem 1. We showed in Theorem 2 that $p_{\text {noisy}}$ converges to uniform at roughly the same rate. However, the distance between $p_{\text {noisy}}$ and $p_{\text {wn}}$ is much smaller than ${\bar{F}}$ if the parameters are sufficiently weak, demonstrating that the noisy and white-noise distribution are much closer to each other than either are to uniform.

Second, let us examine the quantity $\delta$. For the depolarizing channel and the dephasing channel, the leading term in $\delta$ cancels out leaving $\delta = O(\epsilon ^2)$, so the $\sqrt{\delta }$ term in Eq. (22) is on the same order as the other terms. This is a signature of incoherent noise. The coherent rotation channel, which has $u=1$ and $r = O(\theta ^2)$, has $\delta = O(\theta ^2)$, so $\sqrt{\delta }$ is large compared to the other terms in the expression. In this case, we would need $sr \ll 1$ for the approximation to be good, but if this is true, then ${\bar{F}} \approx 1$ and the white-noise approximation is trivial.

Relatedly, the parameter $\delta$ can be connected to the diamond distance between the channel ${\mathcal {N}}$ and the identity channel. This distance, denoted by D, is defined as the trace distance between the input state $\phi$ and the state $\phi '$ obtained by applying the noise channel to $\phi$, maximized over all possible $\phi$, including $\phi$ that are entangled with an auxiliary system of arbitrary size. If ${\mathcal {N}}$ is applied 2s times, the total deviation in trace norm from the ideal output can be as large as 2sD in the worst case. It was shown in Ref. [12] that $D = O(\sqrt{\delta })$, specifically

$$\begin{aligned} \frac{1}{2}\sqrt{\delta }\le D \le \frac{q^2}{2}\sqrt{\delta }. \end{aligned}$$

(23)

It is also known that $r \le O(D)$ and $1-u \le O(D)$. Thus, working at sufficiently large circuit size and sufficiently small noise rate to neglect the final three terms in Eq. (22), we can write our result as

$$\begin{aligned} \mathop {\mathbb {E}}\limits _U\left[ \frac{1}{2}\Vert p_{\text {noisy}}- p_{\text {wn}}\Vert _1\right] \le O(F D\sqrt{s}). \end{aligned}$$

(24)

This emphasizes that the fundamental result is an improved trade-off between noise and circuit size; the strength of the signal decays exponentially, but the error on the renormalized signal grows quadratically slower (as $O(D\sqrt{s})$) in the case of random quantum circuits with incoherent noise than it does in the worst case (as O(Ds)) for arbitrary circuits and arbitrary noise channels with diamond distance D.

4 Related Work and Implications

4.1 Quantum computational supremacy

A central motivation for our work has been recent quantum computational supremacy experiments [4, 5] that sampled from the output of noisy random quantum circuits on superconducting devices. In this context, the main claim is that no classical computer could have performed the same feat in any reasonable amount of time. While no efficient classical algorithms to simulate the quantum device performing this task are known, there is a lack of concrete theoretical evidence that no such algorithm exists.

Our work bolsters the theory behind these experiments in two ways, assuming noise in the device is sufficiently well described by our local noise model. First, our result on the decay of ${\bar{F}}$ justifies the usage of the linear cross-entropy metric to benchmark the overall noise rate in the device, and to quantify the amount of signal from the ideal computation that survives the noise. Second, convergence to the white-noise distribution has theoretical benefits with respect to a potential proof that the random circuit sampling task accomplished by the device is actually hard for classical computers.

4.1.1 Linear cross-entropy benchmarking

Quantum computational supremacy experiments are complicated by the fact that since (by definition) they cannot be replicated on a classical computer, it is non-trivial to classically verify that they actually performed the correct computational task. A partial solution to this issue has been the proposal of linear cross-entropy benchmarking, whereby a sample x is generated by the device according to the noisy output distribution $p_{\text {noisy}}$, and a classical supercomputer is used to compute $p_{\text {ideal}}(x)$.⁸ When T samples $\{x_1,\ldots ,x_T\}$ are chosen, the average

$$\begin{aligned} {\mathcal {F}} = \frac{1}{T}\sum _{i=1}^T (q^np_{\text {ideal}}(x_i) -1) \end{aligned}$$

(25)

is calculated, which is an empirical proxy for the circuit fidelity. We can see that the expected value of ${\mathcal {F}}$ is precisely $\sum _x p_{\text {noisy}}(x)(q^n p_{\text {ideal}}(x) - 1)$, which is the numerator of the quantity ${\bar{F}}$ defined in Eq. (14). Meanwhile, the denominator of ${\bar{F}}$ becomes close to 1, so long as the output is anti-concentrated. In Theorem 1, we show that if the depolarizing error rate $\epsilon$ satisfies $\epsilon \ll 1/(n\log (n))$ and as long as $\epsilon ^2 s \ll 1$, then there are matching upper and lower bounds on the expected value of ${\mathcal {F}}$, which decays with the circuit size like $e^{-2\epsilon s}$. Thus, assuming our local noise model, we prove that one can infer $\epsilon$ given ${\mathcal {F}}$ and s. The inferred value of $\epsilon$ can then be compared to the noise strength estimated when testing each circuit component individually, thus providing one method of verification that the components are behaving as expected during the experiment.

Indeed, the idea of using random circuit sampling as an alternative to randomized benchmarking was formally proposed in Ref. [9], a work that has certain similarities to ours. In particular, like us, they find that the condition $1/\epsilon \ge \Omega (n)$ appears necessary for controlled decay of the fidelity—our result can be expressed as requiring $1/\epsilon \ge {\tilde{\Omega }}(n)$, where the tilde hides log factors, and we believe those log factors are not necessary for our result. They give analytical and numerical evidence that the fidelity decays as $e^{-2 \epsilon s}$. Additionally, like us, they use a map from random quantum circuits to identity-swap configurations to motivate their results. However, they only analytically study the fidelity decay up to first order in the error rate for a 1D architecture; that is, they compute the expected fidelity due to contributions with an error at only one location or at a correlated set of locations all at the same depth. On the other hand, their error model is more general than ours as we do not consider correlated errors, while their theoretical analysis handles Pauli errors of up to weight three; in the context of noise characterization, this is important as correlated errors are often the most difficult to diagnose. On this point, we believe correlated errors could be handled by our method with a more intricate analysis, but we leave that for future work. Relatedly, exponential decay of fidelity in noisy systems has been proposed [17] as an experimentally detectable signature of quantum mechanics that distinguishes it from theories where quantum mechanics emerges from an underlying classical theory. Our work may help justify these proposals.

Note that as the fidelity decays, more samples must be generated to form a good estimate of the mean of ${\mathcal {F}}$. Since $p_{\text {ideal}}(x)$ for uniformly random x has standard deviation on the order of $q^{-n}$ (assuming anti-concentration), the standard deviation of ${\mathcal {F}}$ is expected to decay with the number of samples like $1/\sqrt{T}$. Thus, resolving the mean of ${\mathcal {F}}$ with enough precision to differentiate it from 0 requires $T = \Omega (1/{\mathcal {F}}^2)$ samples.

We comment that while our analysis assumes that each noise location has the same value of $\epsilon$, this is not essential to our method. We expect it could be shown that the expected value of ${\mathcal {F}}$ decays like $\exp (-\sum _i \epsilon _i)$ where i runs over all possible noise locations. Moreover, our analysis works for any kind of local noise, not just depolarizing noise; the only relevant parameter is the average infidelity of the noise channels. This includes coherent noise; for example, the average infidelity of the coherent rotation channel given in Eq. (7) is less than 1 and thus leads to exponential decay of ${\mathcal {F}}$. This is consistent with Ref. [9], which previously showed that from the perspective of fidelity decay, every channel is equivalent to an (incoherent) Pauli noise channel.

4.1.2 Classical hardness of sampling from the noisy output distribution

To claim to have achieved quantum computational supremacy, the low-fidelity random circuit sampling experiments in Refs. [4, 5] should be able to identify a concrete computational problem that their device solved, but a classical device could not also solve in any reasonable amount of time. Here there are a couple of options. One option is to simply rely directly on the linear cross-entropy benchmark and define the task to be generating a set of samples that scores at least ${\mathcal {F}} \ge 1/{{\,\textrm{poly}\,}}(n)$. A related idea is the task of Heavy Output Generation (HOG) [18], which is to generate outputs x for which $p_{\text {ideal}}(x)$ is large (i.e. “heavy outputs”) significantly more often than a uniform generator. The upshot of these definitions is that in the regime where $p_{\text {ideal}}(x)$ can be calculated classically with an exponential-time algorithm, it can be verified that the quantum device successfully performed the task. Their main drawback is that it is not clear whether running a (noisy) quantum computation is the only way to perform these tasks. Perhaps a (yet-to-be-discovered) classical algorithm can score well on the linear cross-entropy benchmark without performing an actual random circuit simulation; for example, this was the goal in Refs. [19, 20], both of which utilized similar techniques as the present paper in their analyses.

Another option is to define the task specifically in terms of the white-noise distribution. Namely, one must produce samples from a distribution $p_{\text {noisy}}$ for which $\frac{1}{2}\Vert p_{\text {noisy}}- p_{\text {wn}}\Vert _1 \le \eta F$ where F is not too small (ideally at least inverse polynomial⁹ in n) and some small constant $\eta$. We refer to this task as “white-noise random circuit sampling (RCS).” A downside of this option is that even with unlimited computational power, an exponential number of samples from the device would be needed to definitively verify that the distribution is close to $p_{\text {wn}}$ in total variation distance. Our work provides a partial solution here, as we show that a local error model allows a device to accomplish the white-noise RCS task, as long as the error rate is sufficiently weak compared to the number of qubits. Thus, if the experimenters are sufficiently confident in the error model that describes their device, they can rely on our work to be confident they are performing the white-noise RCS task. This observation is especially important after recent work of Ref. [20] suggests that using the linear cross-entropy benchmark is insufficient as a way of verifying that the sampling task has been correctly performed. In that light, our results show that a high-score on the benchmark is sufficient when paired with an assumption on the underlying local error model.

The major upside of the white-noise RCS task is that one can give stronger evidence that it is classically hard to perform. For example, in the Supplementary Material of Ref. [4], it was shown that exactly (i.e. $\eta = 0$) sampling from $p_{\text {wn}}$ (a task they called “unbiased noise F-approximate random circuit sampling”) in the worst case is a hard computational task in the sense that an efficient classical algorithm for it would cause the collapse of the polynomial hierarchy ($\textsf {PH}{}$), and further that its computational cost should be at most a factor of F smaller than sampling exactly from $p_{\text {ideal}}$. In that spirit, we show in Theorem 4, in the appendix, that the more realistic task of sampling approximately from $p_{\text {wn}}$ is essentially just as hard as sampling approximately from $p_{\text {ideal}}$, up to a linear factor of F in the classical computational cost. This is important because some mild progress has been made toward establishing that approximately sampling from $p_{\text {ideal}}$ is hard for the polynomial hierarchy, through a series of work that reduce the task of computing $p_{\text {ideal}}(x)$ in the worst case to the task of computing $p_{\text {ideal}}(x)$ in the average case up to some small error [21,22,23,24,25]. Weaknesses in this result as evidence for hardness of approximate sampling were discussed in more detail in Refs. [23, 26], but it remains true that the white-noise-centered definition of the computational task is the likeliest route to a more robust version of quantum computational supremacy that can be grounded in well-studied complexity theoretic principles.

Recently, Ref. [27] showed that in the regime of constant $\epsilon =\Omega (1)$ local noise, the output of a typical random circuit can be classically sampled up to total variation distance error $\delta$ in time ${{\,\textrm{poly}\,}}(n,1/\delta )$ whenever anti-concentration holds. This result is not in tension with our analysis since the runtime of their algorithm is exponential in $1/\epsilon$ and thus exponential in n in the noise regime we study. The existence of their algorithm is further evidence that the assumption $\epsilon = O(1/n)$ is necessary (and sufficient) for a successful hardness argument.

4.2 Convergence to uniform with circuit size

It is widely understood that incoherent and uncorrected unital noise in quantum circuits should typically lead the output of a quantum circuit to lose all correlation with the ideal circuit and become nearly uniform. It is further asserted that the decay to uniform should scale with the circuit size; however, rigorous results have only shown a decay in total variation distance to uniform with the circuit depth d, following the form $e^{-\Omega (\epsilon d)}$. In particular, Ref. [28] showed that any (even non-random) circuit with interspersed local depolarizing noise approaches uniform at least this quickly. Later, Ref. [29] showed the same is true for any Pauli noise model, at least for most circuits chosen from a particular random ensemble. However, in Ref. [23], a stronger convergence at the rate of $e^{-\Omega (\epsilon s)}$ in random quantum circuits like ours was desired in order to show a barrier on further improvements of their worst-to-average-case reduction for computing entries of $p_{\text {ideal}}$. To that end, they showed that exponential convergence in circuit size occurs in a toy model where each layer of unitary evolution enacts an exact global unitary 2-design, and they conjectured the same is true in the local noise model we consider in this paper. Thus, our result in Theorem 2 gets close to providing the missing ingredient for their claim; for their application, we would need to extend our result to show $e^{-\Omega (\epsilon s)}$ even in the regime where $\epsilon = O(1)$, independent of n. However, recent work of Ref. [30] (which appeared roughly simultaneously with the first version of this work) casts doubt that this extension would be possible by showing a lower bound of $e^{-O(\epsilon d)}$ in the regime where $\epsilon = O(1)$. Our results are not in tension with theirs since our results apply only when $\epsilon = O(1/n)$.

4.3 Signal extraction in noisy experiments

One implication of our work is that, in the parameter regime where our results apply, the signal from the noiseless random circuit experiment can be extracted by taking many samples. To illustrate this, suppose we are interested in some classical function f(x) for $x\in [q]^n$ that takes values in the interval $[-1,1]$. Choosing x randomly from $p_{\text {ideal}}$ induces a probability distribution over the resulting values of f(x). To understand this distribution empirically (e.g., estimate its mean or variance), samples $x_i$ might be generated on a quantum device, but if the device is noisy, these samples will be drawn from $p_{\text {noisy}}$ instead of $p_{\text {ideal}}$. However, if $p_{\text {noisy}}\approx p_{\text {wn}}$, then the sampled distribution over f(x) will be a mixture of the ideal with weight F, and the distribution that arises from uniform choice of x with weight $1-F$. Supposing the latter is well understood, inferences can be made about the former by repetition. For example, if $\sum _x p_{\text {ideal}}(x) f(x) = \mu = O(1)$ and $\sum _x f(x)/q^n = 0$,¹⁰ then the mean of f under samples from $p_{\text {wn}}$ is $F\mu$. Meanwhile, the standard deviation of f can be as large as O(1), indicating that $O(1/F^2)$ samples from $p_{\text {wn}}$ are required to compute the mean $F\mu$ up to O(F) precision. Generally, this procedure requires knowing the value of F.

A concrete example of such a situation is the Quantum Approximate Optimization Algorithm (QAOA) [31], where samples x from the output of a parameterized quantum circuit are used to estimate the expectation of a classical cost function C(x). The parameters can then be varied to optimize the expected value of the cost function. Our work is for Haar-random local quantum circuits, which are, in a sense, very different from QAOA circuits. For example, the marginal of typical random circuits on any constant number of qubits is very close to maximally mixed, whereas QAOA circuits optimized for local cost functions will, by design, not have this property. Nevertheless, it is plausible that generic QAOA circuits might respond to local noise in a similar way as random quantum circuits. Indeed, in Refs. [32,33,34], numerical and analytic evidence was given for the conclusion that the expectation value of the cost function and its gradient with respect to the circuit parameters decay toward zero when local noise is inserted into a QAOA circuit. This behavior would be consistent with a stronger conclusion that the output is well described by $p_{\text {wn}}$.

5 Summary of Method and Intuition

In this section, we present a heuristic argument about why the technical statements above should hold. Then we give an overview of how we actually show it using our method, which analyzes certain Markov processes derived from the quantum circuits, extending our previous work in Ref. [8].

5.1 Intuition behind error scrambling and error in white-noise approximation

Our result that $p_{\text {noisy}}$ is very close to $p_{\text {wn}}$ requires three conditions to be satisfied: (1) $\epsilon ^2 s \ll 1$; (2) anti-concentration has been achieved, i.e. $s \ge \Omega (n\log (n))$; and (3) $\epsilon n\log (n) \ll 1$. Here, we try to motivate why these conditions should be sufficient and speculate about whether they are also necessary. In particular, we believe condition (3) can be significantly relaxed.

For simplicity, lets restrict to qubits ($q=2$). Let U denote the unitary enacted by the noiseless quantum circuit instance, so the ideal output state is the pure state $\rho _{\text {ideal}} = U |{0^n}\rangle \!\langle {0^n}| U^{\dagger }$. If a location somewhere in the middle of the circuit experiences a Pauli error, then we could write the output state as $U_2 P U_1 |{0^n}\rangle \!\langle {0^n}| U_1^{\dagger } P^\dagger U_2^{\dagger }$, where P is a Pauli operator with support on only one qubit, and $U=U_2U_1$ is a decomposition of the unitary into gates that act before and after the error location. If we like, we can conjugate P so that it acts at the end of the circuit, giving $O_PU |{0^n}\rangle \!\langle {0^n}| U^{\dagger }O_P^{\dagger }$ where $O_P = U_2 P U_2^\dagger$. Unlike P, the operator $O_P$ will likely have support over many qubits. Indeed, this is what we mean by scrambling; the portion of the circuit acting after the error location scrambles the local noise P into more global noise $O_P$. We can handle error patterns E with multiple Pauli errors similarly, by commuting each to the end one at a time and forming an associated global noise operator $O_E$.

Next, we expand the output quantum state $\rho _{\text {noisy}}$ of the noisy circuit as a sum over all possible Pauli error patterns, weighted by the probability that each pattern occurs. Assuming the local noise is depolarizing, the probability of a pattern E depends only on the number of non-identity Pauli operators in the error pattern, denoted by |E|.

$$\begin{aligned} \rho _{\text {noisy}} = \sum _E \left( \frac{\epsilon }{3}\right) ^{|E|}(1-\epsilon )^{2s-|E|} O_E \rho _{\text {ideal}} O_E^{\dagger } . \end{aligned}$$

(26)

The classical probability distribution $p_{\text {noisy}}$ is then given by $p_{\text {noisy}}(x) = \langle x | \rho _{\text {noisy}} |x\rangle$ for each measurement outcome x. Observe that for the error pattern with $|E| = 0$ (no errors), we have $\text{\O }_E\rho _{\text {ideal}}O_E^{\dagger } = \rho _{\text {ideal}}$. There can be other error patterns for which $O_E\rho _{\text {ideal}}O_E^{\dagger } = \rho _{\text {ideal}}$; for example, when a lone Pauli-Z error acts prior to any non-trivial gates, the state is unchanged since the initial state $|0^n\rangle$ is an eigenstate of all the Pauli-Z operators. However, these error patterns are rare and for the sake of intuition we ignore this possibility. In essence, the white-noise assumption is the claim that when we take the mixture over output states for all of the error patterns, we arrive at a state $\rho _{\text {err}}$ that produces measurement outcomes that are very close to uniform. (Note that in general $\rho _{\text {err}}$ need not be close to maximally mixed to yield uniformly random measurement outcomes.) Letting $F = (1-\epsilon )^{2\,s}$, we may write

$$\begin{aligned} \rho _{\text {noisy}}&= F \rho _{\text {ideal}} + F \sum _{E: |E| > 0} \left( \frac{\epsilon /3}{1-\epsilon }\right) ^{|E|} O_E \rho _{\text {ideal}} O_E^{\dagger } \end{aligned}$$

(27)

$$\begin{aligned}&= F \rho _{\text {ideal}} + (1-F) \frac{I}{2^n} + F \sum _{E: |E| > 0} \left( \frac{\epsilon /3}{1-\epsilon }\right) ^{|E|} \left( O_E \rho _{\text {ideal}} O_E^{\dagger }- \frac{I}{2^n}\right) \,, \end{aligned}$$

(28)

where $I/2^n$ denotes the maximally mixed state. This final term gives the deviations of the noisy output state $\rho _{\text {noisy}}$ from a linear combination of the ideal state and $I/2^n$.

This allows us to state more clearly the intuition for our result. Since the circuit is randomly chosen and scrambles the local error patterns, the operators $O_E$ generally have large support and are essentially uncorrelated for different choices of error pattern E. Suppose we measure in the computational basis, and examine the probability of obtaining the outcome x. We can calculate the squared deviation between this value and the white-noise value under expectation over instance U.

$$\begin{aligned} \mathop {\mathbb {E}}\limits _U[(p_{\text {noisy}}(x) - p_{\text {wn}}(x))^2] ={}&\mathop {\mathbb {E}}\limits _U\left[ \left( \langle x | \rho _{\text {noisy}} |x\rangle - (F \langle x | \rho _{\text {ideal}} |x\rangle + (1-F) 2^{-n} )\right) ^2\right] \end{aligned}$$

(29)

$$\begin{aligned} ={}&F^2 \sum _{\begin{array}{c} E,E'\\ |E|,|E'| > 0 \end{array}} \left( \frac{\epsilon /3}{1-\epsilon }\right) ^{|E|+|E'|}\nonumber \\&\mathop {\mathbb {E}}\limits _U\left[ \left( p_E(x)- 2^{-n}\right) \left( p_{E'}(x)- 2^{-n}\right) \right] \,, \end{aligned}$$

(30)

where $p_{E}(x) = \langle x |O_E \rho _{\text {ideal}} O_E^{\dagger } |x\rangle$. Suppose we now make the approximation that the quantities $p_E(x)$ and $p_{E'}(x)$, when considered as functions of the random instance U, are independently distributed unless $E = E'$. Their mean is $2^{-n}$ and, assuming anti-concentration (condition (2)), their standard deviation is $O(2^{-n})$. Then we have

$$\begin{aligned} \mathop {\mathbb {E}}\limits _U[(p_{\text {noisy}}(x) - p_{\text {wn}}(x))^2] \approx {}&F^2\sum _{E: |E|> 0} \left( \frac{\epsilon /3}{1-\epsilon }\right) ^{2|E|}\mathop {\mathbb {E}}\limits _U \left[ \left( p_E(x)- 2^{-n}\right) ^2 \right] \nonumber \\ ={}&F^2\sum _{E: |E| > 0} \left( \frac{\epsilon /3}{1-\epsilon }\right) ^{2|E|}O(2^{-2n}) \end{aligned}$$

(31)

$$\begin{aligned} ={}&F^2\cdot O(2^{-2n}) \cdot \left( (1+O(\epsilon ^2))^{2s}-1\right) \end{aligned}$$

(32)

$$\begin{aligned} \approx {}&O(F^2 2^{-2n}\epsilon ^2 s)\, \end{aligned}$$

(33)

where the last line is true when $\epsilon ^2 s \ll 1$. This implies that the deviation of each entry in the probability distribution $p_{\text {noisy}}$ from the white-noise distribution is on the order of $F2^{-n}\epsilon \sqrt{s}$, and since there are $2^n$ entries, we have

$$\begin{aligned} \mathop {\mathbb {E}}\limits _U\left[ \frac{1}{2}\Vert p_{\text {wn}}-p_{\text {noisy}}\Vert _1 \right] \approx O(F \epsilon \sqrt{s}). \end{aligned}$$

(34)

In other words, the total variation distance is much smaller than F when $\epsilon ^2 s \ll 1$, giving an intuitive reason for condition (1). Moreover, without condition (2), the contribution of each term would be much larger than $O(2^{-2n})$, which illustrates why condition (2) is necessary.

The key step in this analysis was the assumption of independence between $p_E$ and $p_{E'}$ when $E \ne E'$. This is only approximately true; indeed for a circuit that does not scramble errors, this will be a bad approximation because it might be common to have different error patterns E, $E'$ that produce the same (or approximately the same) effective error $O_E = O_{E'}$. However, for random quantum circuits, this outcome is unlikely for the vast majority of error pairs. Our rigorous proof, later, might be regarded as a justification of this intuition above.

Condition (3) is more subtle to motivate. In our analysis we require $\epsilon \ll 1/(n\log (n))$ so that the chance an error occurs while the circuit is still anti-concentrating, which takes $\Omega (n\log (n))$ gates, is small. This is helpful in the analysis because it allows us to essentially ignore the possibility that an error P occurs near the beginning or end of the circuit, where there is insufficient time to scramble the error (either forward or backward in time). However, a finer-grained analysis might be able to handle these kinds of errors: we believe condition (3) can be improved from $\epsilon ^{-1} \gg \Omega (n\log (n)) = {\tilde{\Omega }}(n)$ to simply $\epsilon ^{-1} \ge n/c$ for some constant c that depends only on the architecture (1D vs. complete-graph etc.). However, we do not believe that improvement beyond this point would be possible; there is a fundamental barrier that requires $\epsilon$ to scale as O(1/n).

The reason for this is essentially that if the white-noise approximation is to hold, the errors need to be scrambled at least as fast as they appear. The probability of an errorless computation F decreases like $(1-\epsilon )^{2\,s} = \exp (-2\,s\epsilon - O(s\epsilon ^2))$, so each layer of O(n) gates causes a decrease by a factor $\exp (-\Theta (n\epsilon ))$. Recall that we demand that the total variation distance between $p_{\text {noisy}}$ and $p_{\text {wn}}$ be much smaller than F, so as F decreases, this condition becomes increasingly stringent. Meanwhile, scrambling is fundamentally happening at the rate of increasing circuit depth, not size. One way to see this is simply that local Pauli errors P that appear at a certain circuit location are expected to be scrambled into larger operators that grow ballistically with the depth [35, 36]; each layer of O(n) gates yields a constant amount of operator growth. Another way to see this is to consider a pair of error patterns E and $E'$, where E consists of a single Pauli error on qudit j at layer d and $E'$ consists of a single Pauli error on qudit j at layer $d + \Delta$. The correlation between $p_E(x)$ and $p_{E'}(x)$, as a function of the random instance U, which is roughly speaking the chance that the random circuit transforms the first error into something resembling the second error, will decay exponentially with $\Delta$, the separation in depth between the two errors.¹¹ Yet a third way to see this fact is to notice that, after a circuit has initially reached anti-concentration, convergence of the collision probability $Z={\mathbb {E}}_U[\sum _x p_{\text {ideal}}(x)^2]$ to its limiting value $Z_H$ occurs like $Z = Z_H + O(Z_H)\exp (-O(s/n))$ [8]. Each additional layer of O(n) gates only decreases the deviation of Z from $Z_H$ by a constant factor. The terms ${\mathbb {E}}_U[(p_E - 2^{-n})(p_{E'}-2^{-n})]$ for $E \ne E'$ that were ignored above are expected to obey a similar kind of decay to the value 0 for most choices of $(E,E')$, but if F is decaying too fast, we are not able to neglect these terms. Each layer of O(n) gates must incur at most a constant-factor decay of F to not exceed the rate of scrambling; equivalently, $n\epsilon < c$ must hold for some constant c.

5.2 Noisy random quantum circuits as a stochastic process

Our method is a manifestation of the “stat mech method” for random quantum circuits, developed in Refs. [35,36,37,38] and further utilized in Refs. [8, 9, 19, 26, 39,40,41,42,43,44], whereby averages over k copies of random quantum circuits are mapped to partition functions of classical statistical mechanical systems. The mapping for $k=2$, corresponding to second-moment quantities, is particularly simple and amenable to analysis [8, 26, 38, 39].

In Ref. [8], we analyzed the collision probability $Z = {\mathbb {E}}_U[\sum _x p_{\text {ideal}}(x)^2]$, a second-moment quantity, using the stat mech method, although we found it more useful to interpret the result as the expectation value of a certain stochastic process, rather than as a partition function. As we will see, this work is essentially an extension of the analysis in Ref. [8] to account for the action of the single-qudit noise channels ${\mathcal {N}}$ that act after two-qudit gates. We explain the steps in this analysis below, and leave the formal proofs for the appendices.

We also mention that a number of works [16, 45,46,47,48,49,50,51,52] study noiseless random quantum circuits using a distinct technique that also maps certain second-moment quantities to a stochastic process; however, we emphasize that this results in a different stochastic process than the one studied here, and extending it to noisy random quantum circuits would require a distinct analysis.

Expressing the total variation distance in terms of second-moment quantities

To apply this method, the first step is to express $\frac{1}{2}\Vert p_{\text {noisy}}-p_{\text {wn}}\Vert _1$ in terms of second-moment quantities. To do so, we use the general 1-norm to 2-norm bound: when $p_1$ and $p_2$ are vectors on a $q^n$-dimensional vector space, then

$$\begin{aligned} \Vert p_1-p_2 \Vert _1 \le q^{n/2} \Vert p_1-p_2 \Vert _2 , \end{aligned}$$

(35)

where $\Vert p_1-p_2 \Vert _2 = \sqrt{\sum _x (p_1(x)-p_2(x))^2}$. Applying this identity with $p_1 = p_{\text {wn}}$ and $p_2 = p_{\text {noisy}}$ and invoking Jensen’s inequality for the concave function $\sqrt{\cdot }$, we find

$$\begin{aligned} \mathop {\mathbb {E}}\limits _U\left[ \frac{1}{2}\Vert p_{\text {wn}}-p_{\text {noisy}}\Vert _1\right]\le & {} q^{n/2} \mathop {\mathbb {E}}\limits _U\left[ \frac{1}{2}\Vert p_{\text {wn}}-p_{\text {noisy}}\Vert _2\right] \nonumber \\\le & {} \frac{1}{2}\sqrt{q^n\mathop {\mathbb {E}}\limits _U\left[ \Vert p_{\text {wn}}-p_{\text {noisy}}\Vert ^2_2\right] }. \end{aligned}$$

(36)

Now we can expand

$$\begin{aligned} q^n\mathop {\mathbb {E}}\limits _U \left[ \Vert p_{\text {wn}}- p_{\text {noisy}}\Vert _2^2 \right]&= q^n\mathop {\mathbb {E}}\limits _U\left[ \sum _x\left( \left( F p_{\text {ideal}}(x) + (1-F)q^{-n}\right) -p_{\text {noisy}}(x)\right) ^2 \right] \end{aligned}$$

(37)

$$\begin{aligned}&= (Z_2-1)-2F (Z_1-1) + F^2 (Z_0-1) \,, \end{aligned}$$

(38)

where

$$\begin{aligned} Z_0&= q^{n}\mathop {\mathbb {E}}\limits _U\left[ \sum _xp_{\text {ideal}}(x)^2\right] = q^{2n}\mathop {\mathbb {E}}\limits _U\left[ p_{\text {ideal}}(0^n)^2\right] \end{aligned}$$

(39)

$$\begin{aligned} Z_1&= q^{n}\mathop {\mathbb {E}}\limits _U\left[ \sum _xp_{\text {noisy}}(x)p_{\text {ideal}}(x)\right] = q^{2n}\mathop {\mathbb {E}}\limits _U\left[ p_{\text {noisy}}(0^n)p_{\text {ideal}}(0^n)\right] \end{aligned}$$

(40)

$$\begin{aligned} Z_2&= q^{n}\mathop {\mathbb {E}}\limits _U\left[ \sum _xp_{\text {noisy}}(x)^2\right] = q^{2n}\mathop {\mathbb {E}}\limits _U\left[ p_{\text {noisy}}(0^n)^2\right] \end{aligned}$$

(41)

are second-moment quantities (the second equality holds since by symmetry each term in the sum has the same value under expectation), with $Z_w$ containing w copies of the noisy output and $2-w$ copies of the ideal output for each $w \in \{0,1,2\}$. Note that $Z_0 =q^n Z$ with Z the collision probability studied in Refs. [8, 16]. Furthermore, note that F is a free parameter, and we may choose it so that it minimizes the right-hand side¹² of Eq. (38), which occurs when

$$\begin{aligned} F={\bar{F}} = \frac{Z_1-1}{Z_0-1}, \end{aligned}$$

(42)

matching the definition for ${\bar{F}}$ in Eq. (14). Plugging in $F={\bar{F}}$ yields

$$\begin{aligned} \mathop {\mathbb {E}}\limits _U\left[ \frac{1}{2}\Vert p_{\text {wn}}-p_{\text {noisy}}\Vert _1\right] \le \frac{1}{2} {\bar{F}} \sqrt{(Z_0-1)\left( \frac{(Z_0-1)(Z_2-1)}{(Z_1-1)^2}-1\right) }. \end{aligned}$$

(43)

Mapping second-moment quantities to stochastic processes

We bound the quantities $Z_0$, $Z_1$, and $Z_2$ by mapping them to stochastic processes. These stochastic processes are the same as the stochastic process we studied in Ref. [8], except that the noise channels introduce slightly modified transition rules, as we now discuss.

Second moment quantities include two copies of each random unitary gate in the circuit. The idea in Ref. [8] was to perform the expectation over the two copies of each gate independently, using Haar-integration techniques. For a density matrix $\rho$ on two copies of a Hilbert space of dimension q, let

$$\begin{aligned} M[\rho ] = \mathop {\mathbb {E}}\limits _{V}\left[ V^{\otimes 2} \rho {V^{\dagger }}^{\otimes 2}\right] , \end{aligned}$$

(44)

where ${\mathbb {E}}_V$ denotes expecation over choice of V from the Haar measure over $q \times q$ matrices. Then, we have the following well-known formula (for which a derivation is provided in Ref. [8])

$$\begin{aligned} M[\rho ] = \frac{\textrm{tr}(\rho ) - q^{-1}\textrm{tr}(\rho S)}{q^2-1}I + \frac{\textrm{tr}(\rho S) - q^{-1}\textrm{tr}(\rho )}{q^2-1}S, \end{aligned}$$

(45)

where I is the identity operation and S is the swap operation on two copies of the single-qudit system. The equation above states that, after Haar averaging, the state of the system is simply a linear combination of identity and swap, with certain coefficients that can be readily calculated. For an n-qudit system acted upon by a sequence of single and two-qudit gates, this formula can be applied sequentially to each gate. After t gates have been applied, the Haar-averaged state of the system can be expressed as a linear combination of n-fold tensor products of I and S (e.g. for $n=3$, the state would be given by $c_1 I \otimes I \otimes I + c_2 I \otimes I \otimes S + c_3 I \otimes S \otimes I + \ldots +c_8 S \otimes S \otimes S$).

The important takeaway from Ref. [8] was to interpret the coefficients of these $2^n$ terms as probabilities of a certain stochastic process over the set of length-n bit strings $\{I,S\}^n$, which were called “configurations.” The stochastic process generates a sequence of $s+1$ configurations $\gamma ={(\vec {\gamma }^{(0)},\ldots ,\vec {\gamma }^{(s)})}$, which was called a “trajectory,” where the probabilistic transition from $\vec {\gamma }^{(t-1)}$ to $\vec {\gamma }^{(t)}$ depends only on the value of $\vec {\gamma }^{(t-1)}$ (Markov property).

The transition rules of the stochastic process are calculated by computing the coefficients in Eq. (45); here we state the result¹³ of that calculation; more details can be found in Appendix A.1. First of all, the initial configuration $\vec {\gamma }^{(0)}$ is chosen at random by independently choosing each of the n bits to be I with probability $q/(q+1)$ and S with probability $1/(q+1)$. Then, for each time step t, if the tth gate acts on qudits $i_t$ and $j_t$, then the transition from $\vec {\gamma }^{(t-1)}$ to $\vec {\gamma }^{(t)}$ can involve a bit flip at position $i_t$, at position $j_t$, or neither (but not at both), and no bit can flip at any other position. Moreover, ${\gamma _{i_t}^{(t)}}={\gamma _{j_t}^{(t)}}$ must hold, so if ${\gamma _{i_t}^{(t-1)}} \ne {\gamma _{j_t}^{(t-1)}}$, then one of the two bits must be flipped. In this situation, when one bit is assigned I and one is assigned S, the S is flipped to I with probability $q^2/(q^2+1)$, and the I is flipped to S with probability $1/(q^2+1)$. Thus, there is a bias toward making more of the assignments I. The quantity $Z_0$ is given exactly by the expectation value of the quantity $q^{|\vec {\gamma }^{(s)}|}$ when trajectories $\gamma$ are generated in this fashion, where $|\vec {\nu }|$ denotes the Hamming weight of the bit string $\vec {\nu }$, that is, the number of S assignments out of n.

$$\begin{aligned} Z_0 = {\mathbb {E}}_0\left[ q^{|\vec {\gamma }^{(s)}|}\right] , \end{aligned}$$

(46)

where here ${\mathbb {E}}_0$ denotes evolution by the stochastic process described above.

With the stochastic process now defined, a vital observation is that the process has two fixed points, the $I^n$ configuration and the $S^n$ configuration, since whenever all the bits agree, none can be flipped. In Ref. [8], we could precisely compute the fraction of the probability mass that eventually reaches each of these fixed points if the circuit is infinitely long. Specifically, $q^n/(q^n+1)$ of the probability mass converges to $I^n$ and $1/(q^n+1)$ converges to $S^n$.¹⁴ Then, since the $S^n$ fixed point receives a weighting of $q^n$ and the $I^n$ fixed point receives a weighting of 1 in Eq. (46), we find that $Z_0 \rightarrow 2q^n/(q^n+1)$.

Noise introduces new rules into this stochastic process. Suppose the configuration immediately after the tth two-qudit gate is $\vec {\nu }$, and a noise channel ${\mathcal {N}}$ acts on qudit $i_t$. Since the noise channel is unital, if $\nu _{i_t} = I$, representing the identity operator on a two-qudit system, then the configuration is left unchanged. However, if $\nu _{i_t} = S$, then the action of the noise may cause a flip from S to I. For the calculation of $Z_0$, there is no noise, so this happens with probability 0. For the calculation of $Z_1$, where there is one copy of the noisy distribution and one copy of the ideal, we can again use the formula in Eq. (45) to compute the $S \rightarrow I$ transition probability to be $rq/(q-1)$, where r is the average infidelity given in Eq. (3). This is explained in Appendix A.2. For $Z_2$, where there are two copies of the noisy distribution, the probability of an $S \rightarrow I$ transition is calculated to be $1-u$, where u is the unitarity of the noise channel given in Eq. (4). The values of $Z_1$ and $Z_2$ are thus given by

$$\begin{aligned} Z_1&= {\mathbb {E}}_{rq/(q-1)}\left[ q^{|\vec {\gamma }^{(s)}|}\right] \end{aligned}$$

(47)

$$\begin{aligned} Z_2&= {\mathbb {E}}_{1-u}\left[ q^{|\vec {\gamma }^{(s)}|}\right] \,, \end{aligned}$$

(48)

where ${\mathbb {E}}_\sigma$ denotes the stochastic process where $S\rightarrow I$ bit flips occur at each noise location with probability $\sigma$, generalizing Eq. (46).

Since noise can flip an S to an I but not vice versa, $I^n$ is the only fixed point of the stochastic processes for $Z_1$ and $Z_2$; the $S^n$ fixed point is only metastable: eventually, the action of noise will flip one of the S bits to an I, and the trajectory might re-equilibrate to the $I^n$ fixed point. Our analysis consists of a careful accounting of the leakage of probability mass away from the metastable $S^n$ fixed point.

Analyzing the stochastic processes for a toy example

Now, we consider a toy example which captures the essence of our analysis. Suppose a circuit consists of alternating rounds of (1) a global Haar-random transformation and (2) a depolarizing noise channel on a single qudit, as depicted in Fig. 2. Step (1) can be approximately accomplished by performing a very large number of two-qudit gates.

Fig. 2

Toy example where global Haar-random gates $U^{(t)}$ act in between a depolarizing noise channel on a single qudit. In this model we can exactly compute quantities $Z_0$, $Z_1$, and $Z_2$ because the global Haar-random gates cause the probability mass in the stochastic process to fully re-equilibrate to one of the fixed points, $I^n$ or $S^n$

This model is similar to the toy model considered in Ref. [23] (the difference being that they considered single-qudit noise channels on all n qudits in step (2)), which they analyzed using the Pauli string method of Refs. [45, 46].

The initial global Haar-random transformation induces perfect equilibration to the two fixed points, with $q^n/(q^n+1)$ mass reaching the $I^n$ fixed point and $1/(q^n+1)$ mass reaching the (metastable) $S^n$ fixed point. This is already sufficient to compute $Z_0-1$, which is not sensitive to the noise.

$$\begin{aligned} Z_0-1 = \frac{q^n-1}{q^n+1} . \end{aligned}$$

(49)

Now suppose we want to calculate $Z_1$. Consider a piece of probabiltiy mass that is part of the $1/(q^n+1)$ fraction at the $S^n$ fixed point. The single-qudit depolarizing noise channel will flip one of the S assignments to an I assignment with probability $rq/(q-1) = \epsilon (1-q^{-2})^{-1}$. If this happens, there are $n-1$ S assignments and 1 I assignment. While it may seem that this new configuration is still close to the $S^n$ fixed point, we must remember that the random walk is biased in the I direction. When we perform the next global Haar-random transformation, we get perfect re-equilibration back to the two fixed points; with probability $\frac{1-q^{-2}}{1-q^{-2n}}$ we end at the $I^n$ fixed point, and with probability $\frac{q^{-2}-q^{-2n}}{1-q^{-2n}}$ we end at the $S^n$ fixed point. These probabilities were derived in Ref. [8], and are a basic consequence of Eq. (45). Now, the total mass that remains at the $S^n$ fixed point is the $\frac{1}{q^n+1}(1-\frac{\epsilon }{1-q^{-2}})$ that never left and the $\frac{\epsilon }{1-q^{-2}}\frac{q^{-2}-q^{-2n}}{1-q^{-2n}}$ that left and returned, which comes out to $\frac{1}{q^n+1}(1-\frac{\epsilon }{1-q^{-2n}})$. After 2s single-qudit error channels have been applied, the probability mass remaining at the $S^n$ fixed point is precisely

$$\begin{aligned} \begin{array}{c} \text {probability mass at } S^n \\ \text {after } 2s \text { noise locations} \end{array} = \frac{1}{q^n+1}\left( 1-\frac{\epsilon }{1-q^{-2n}} \right) ^{2s} \approx \frac{1}{q^n+1}e^{-2\epsilon s}. \end{aligned}$$

(50)

This mass receives weighting of $q^n$ toward $Z_1$. Meanwhile the rest of the mass is at the $I^n$ fixed point and receives weighting of 1. This tells us that

$$\begin{aligned} Z_1-1 = \frac{q^n-1}{q^n+1}\left( 1-\frac{\epsilon }{1-q^{-2n}} \right) ^{2s}. \end{aligned}$$

(51)

We see that in this toy model, the quantity ${\bar{F}} = (Z_1-1)/(Z_0-1)$ is precisely given by the fraction of probability mass originally destined for the $S^n$ fixed point that remains at the $S^n$ fixed point even after the noise locations have acted. Thus, the leakage of probability mass from $S^n$ to $I^n$ in the calculation of $Z_1$ corresponds exactly to the decay of the linear cross-entropy benchmark.

Calculating $Z_2-1$ is just as easy. Here transitions due to noise occur with probability $1-u$ where u is the unitarity of the noise channel. For depolarizing noise, we have $1-u = 2\epsilon (1-q^{-2})^{-1} - O(\epsilon ^2)$, so $Z_2-1$ is the same as $Z_1-1$ with the replacement $\epsilon \rightarrow 2\epsilon - O(\epsilon ^2)$, giving

$$\begin{aligned} Z_2-1 = \frac{q^n-1}{q^n+1}\left( 1-\frac{2\epsilon }{1-q^{-2n}} +O(\epsilon ^2)\right) ^{2s} = \frac{q^n-1}{q^n+1}\left( 1-\frac{\epsilon }{1-q^{-2n}} \right) ^{4s} e^{O(s\epsilon ^2)}.\nonumber \\ \end{aligned}$$

(52)

We can plug these calculations into Eq. (43) to find that

$$\begin{aligned} \mathop {\mathbb {E}}\limits _U\left[ \frac{1}{2}\Vert p_{\text {wn}}-p_{\text {noisy}}\Vert _1\right] \le \frac{1}{2} {\bar{F}} \sqrt{\frac{q^n-1}{q^n+1}\left( e^{O(\epsilon ^2s)}-1\right) } = O({\bar{F}}\epsilon \sqrt{s}). \end{aligned}$$

(53)

Extending the analysis to a full proof

In the proofs of our theorems, the difficulty is that the probability mass does not fully equilibrate to a fixed point before the next error location acts. Nonetheless, we manage to calculate tight bounds on $Z_1$ and $Z_2$ by keeping track of the amount of probability mass that would re-equilibrate back to $S^n$ and $I^n$ if the rest of the gates were noiseless, which we refer to as S-destined and I-destined probability mass. We show that, as long as $\epsilon < c/n$ for some constant c, the S-destined probability mass is exponentially clustered near the $S^n$ fixed point in the sense that the probability of being x bit flips away from $S^n$ conditioned on being S-destined decays exponentially in x. Thus, for a piece of S-destined probability mass, nearly all the bits will be assigned S, and the action of a noise channel reduces the amount of S-destined mass by a factor of roughly $1-\epsilon$. To see why exponential clustering of S-destined mass is necessary, suppose that this were not the case, and that at a certain point in the evolution, a considerable fraction of the S-destined probability mass has a constant fraction r of its bits assigned I. Then, if a noise channel acts on a random bit, the probability that the bit is already assigned I is equal to r, in which case the noise has no impact on the configuration. With probability $1-r$, the bit will be assigned S, and the noise will cause a fraction roughly equal to $1-\epsilon$ of the S-destined probability mass to become I-destined. Thus, the fraction of probability mass that remains S-destined after the noise channel would be roughly $1-(1-r)\epsilon$, which is larger than $1-\epsilon$ by an $\Omega (\epsilon )$ amount. In this scenario, there would be significantly slower leakage from the $S^n$ fixed point to the $I^n$ fixed point, and we would not be able to assert that Eq. (50) is approximately true, ruining the delicate analysis that require $Z_1-1$ and $Z_2-1$ to have very precise rates of decay with s.

The reason $\epsilon < c/n$ is required for the exponential clustering effect is that errors need to be rare enough for the S-destined mass to mostly re-equilibrate back to $S^n$ before new errors pop up; to say it another way, the errors must get scrambled at a faster rate than they appear. If a configuration has $n-1$ S assignments and 1 I assignment, it will take $\Theta (n)$ gates before the single I-assigned qudit participates in a gate. Thus, if errors occur at a slower rate than one per $\Theta (n)$ gates, full re-equilibration will happen before a new error pops up most of the time. It is not clear if this condition is truly necessary for the clustering statement to hold, but we show at the very least that it is sufficient.

However, we need $\epsilon < c/n$ to hold for another (related) reason: the leakage from $S^n$ to $I^n$ must occur more slowly than the anti-concentration rate, which corresponds to the speed at which the probability mass initially equilibrates to $I^n$ and $S^n$. After all, even though the stochastic process is I-biased, the I-destined mass does not make it to the $I^n$ fixed point instantaneously. After s gates, there will be some residual contribution from the not-yet-equilibrated I-destined mass to the calculation of quantities $Z_0-1$, $Z_1-1$, and $Z_2-1$; this contribution decays by a constant factor with every additional O(n) gates. If $\epsilon =O(1/n)$, a constant fraction of the S-destined mass will leak away with each set of O(n) gates, and if the constant prefactor on this leakage is too large, the I-destined mass will contribute more than the S-destined mass to the expectation values; as a result, the right-hand-side of Eq. (43) will not exhibit the same kind of cancellations observed for the toy example.

In our formal analysis, we actually assume something even stronger: we require that $\epsilon \ll 1/(n\log (n))$, which essentially means that very few errors occur during the initial anti-concentration period. However, this is done to make the analysis easier, and we do not believe this condition is necessary.

6 Numerical Estimates of Error in White-Noise Approximation

In principle, it would be possible to determine the constant factors under the big-O notation in our proofs, but the result of this exercise would likely yield extremely unfavorable numbers due to our lack of optimization throughout, and the fact that it might be possible to eliminate some of the terms in our error expression altogether with a more fine-grained analysis. The goal of this section is to provide a numerical assessment of the bound on the error in the white-noise approximation for realistic values of the circuit parameters. We find that realistic NISQ-era values of the circuit parameters can lead to a small upper bound on the white-noise approximation error, even for circuits with several thousand gates, but we confirm that the noise rate needs to decrease like O(1/n) as the system size scales up for our upper bound to be meaningful.

6.1 Numerical method

The numerics we present are for the complete-graph architecture. In general, the stochastic process underlying our method (described in Sect. 5.2 and presented formally in the appendix) is a random walk over $2^n$ possible configurations of a length-n bit string. However, for the complete-graph architecture there is an equivalence between all configurations with the same Hamming weight. Thus, the state space for the stochastic process is reduced to $n+1$ distinct groups of configurations (associated with Hamming weights $0,1,\ldots ,n$). The quantities $Z_0$, $Z_1$, and $Z_2$, as defined in Eqs. (39), (40), and (41) can then be precisely computed by multiplying the (sparse) $(n+1) \times (n+1)$ transition matrices for the stochastic process. This allows us to compute the right-hand-side of Eq. (43) for n substantially large, giving a bound on ${\mathbb {E}}_U[\frac{1}{2}\Vert p_{\text {noisy}}-p_{\text {wn}}\Vert _1]$.

In our analysis below, we suppose all noise locations are subject to depolarizing noise with error probability $\epsilon$, given as in Eq. (5). We also restrict to $q=2$ (qubits). We do not model readout errors, which are a large source of error in the actual experiments of Refs. [4,5,6]. We plug in specifications $(n,\epsilon ,s)$ and exactly compute the quantity

$$\begin{aligned} \frac{1}{2}\sqrt{(Z_0-1)\left( \frac{(Z_0-1)(Z_2-1)}{(Z_1-1)^2}-1\right) } \end{aligned}$$

(54)

which gives the ratio of the bound in Eq. (43) to the normalized linear cross-entropy metric ${\bar{F}}$.

6.2 Numerical bound for realistic circuit parameters

We first examine the bound using the circuit parameters of existing experimental setups. The Google experiment [4] ran $s=430$ gates on their $n=53$ qubit processor called Sycamore, and their error rate per cycle, which is the analogous quantity to the total error in a two-qubit gate in our setup, was reported to be $0.9\%$. This corresponds to $\epsilon \approx 0.0045$ in our model where separate noise channels act on each of the two qubits. Meanwhile, the largest experiment from USTC [6] ran $s=594$ gates on their $n=60$ qubit processor called Zuchongzhi, with a similar overall error rate per cycle. In Fig. 3, we plot the numerically calculated bound on $\frac{1}{{\bar{F}}}{\mathbb {E}}_U[\frac{1}{2}\Vert p_{\text {noisy}}-p_{\text {wn}}\Vert _1]$ as a function of circuit size for complete-graph circuits with $n=53$ and $n=60$ at $\epsilon =0.0045$. The circuit sizes $s=430$ and $s=594$ appear as large dots.

Fig. 3

Plot of the numerically calculated upper bound on the expected total variation distance between $p_{\text {noisy}}$ and $p_{\text {wn}}$ divided by F for a complete-graph version of recent random quantum circuit experiments by Google (53 qubits) [4] and USTC (60 qubits) [6]. The large dots represent the circuit sizes (number of two-qubit gates) implemented in those experiments. The dotted black line is the function $2\epsilon \sqrt{s}/3$ for each experiment

We find that, as expected, the bound is bad if the circuit size is too small. There is an initial spike in the bound due to the first few layers of noisy gates, which subsides quickly as those initial errors are scrambled. The behavior that follows reflects the race between decay of F and anti-concentration. For these values of the error rate, the decay of F is happening at a slower rate than anti-concentration, but it has a head start, since it takes $\Theta (n\log (n))$ gates for anti-concentration to initially be reached [8]; this explains why the bound is decreasing (relative to F) even as the circuit size passes 1000. For large s, both curves approach the function $2\epsilon \sqrt{s}/3$. This indicates that the constant factor underneath the $O(\epsilon \sqrt{s})$ is less than 1, at least for depolarizing noise in the complete-graph architecture. The point at which we expect the $O(\epsilon \sqrt{s})$ behavior to take over will generally be $\Theta (n\log (n)) + \Theta (n)$, where the first term corresponds to the initial anti-concentration period, and the second term corresponds to the additional time needed for anti-concentration to catch up to F. The constant prefactor under the second term will be larger when $\epsilon$ is larger and F decays more rapidly.

Interestingly, the circuit size actually implemented in both of the experiments falls in a region where the bound on approximation error relative to F is decreasing with circuit size, suggesting the white-noise approximation would become more meaningful if more gates were applied (at the expense of smaller fidelity). In fact, for Google’s experiment, the upper bound yields a value close to 1, and for USTC, it yields a value larger than 1, indicating that, in this idealized complete-graph version of their experiments, the white-noise assumption may not hold (we would need a lower bound to know for sure).

There are a few caveats to these conclusions. First, what we plot is only an upper bound, and it is not clear whether this upper bound is tight. Second, this is for the complete-graph architecture, but the experiments of Refs. [4,5,6] had a 2D architecture (although one might speculate that a 2D architecture would only scramble less efficiently than the complete-graph architecture). Third, we have not modeled readout errors in the device. Fourth, we have an idealized error model of depolarizing single-qubit noise. As has been mentioned in footnotes throughout this paper, the goal of our work is not to justify the claims of quantum computational supremacy by specific noisy random quantum circuit experiments. Rather, we aim to show that the white-noise phenomenon is possible and can be proved analytically, and that this adds some justification to claims that a low-fidelity random quantum circuit experiment could in principle accomplish quantum computational supremacy.

6.3 Threshold error rate for good white-noise bound

A key feature we observed in our theoretical analysis was the need for the error rate $\epsilon$ to decrease with n. For each value of n, we observe a threshold error rate such that, if $\epsilon$ is beneath the threshold, our upper bound on the total variation distance follows $O(F\epsilon \sqrt{s})$ at large values of s, and if $\epsilon$ is above the threshold, our bound becomes (empirically) $O(Fe^{\Theta (s)})$. Without a lower bound, we cannot be sure if this is the actual behavior of the approximation error.

In Fig. 4, we present a log plot of the numerically calculated bound on the approximation error (relative to F) for different values of $\epsilon$ at system sizes $n=53, 106, 159, 212$ (corresponding to integer multiples of the size of Google’s 53-qubit experiment). For $n=53$, we see that choices of $\epsilon$ beneath roughly 0.0057 appear to approach $O(\epsilon \sqrt{s})$ scaling at large s, while choices of $\epsilon$ above that threshold increase exponentially with s. For $n=106$, $n=159$, and $n=212$, the apparent threshold decreases to roughly $\epsilon =0.0028$, $\epsilon =0.0019$, and $\epsilon =0.0014$, respectively. This is consistent with a general threshold of roughly $\epsilon = 0.3/n$. We expect the $\epsilon = O(1/n)$ threshold to exist in other architectures as well, but with a modified constant prefactor. Architectures with a faster anti-concentration rate should have larger thresholds.

7 Outlook

We have presented a comprehensive picture of how the output distribution of typical random quantum circuits behaves under a weak incoherent local noise model. As more gates are applied, the output distribution decays toward the uniform distribution in total variation distance like $e^{-2\epsilon s}$ where $\epsilon$ is the local noise strength in a Pauli error model (for non-Pauli models, this can be expressed in terms of the average infidelity r) and s is the number of gates. Moreover, we show that the convergence to uniform happens in a very special way: the residual non-uniform component of the noisy distribution is approximately in the direction of the ideal distribution. The random quantum circuits scramble the errors that occur locally during the evolution so that they can ultimately be treated as global white noise, allowing some signal of the ideal computation to be extracted even from a noisy device. While this property had previously been conjectured—it was an underlying assumption of quantum computational supremacy experiments [4, 5]—it had not received rigorous analytical study. Basic questions like how the error in the white-noise approximation scales with $\epsilon$ and s had not been investigated.

Fig. 4

Plot of the numerically calculated upper bound on the expected total variation distance between $p_{\text {noisy}}$ and $p_{\text {wn}}$ divided by F for the complete-graph architecture at various values of n, $\epsilon$ and s. For each value of n, a threshold in $\epsilon$ is observed where error rates above the threshold lead to a bad approximation, while error rates below the threshold lead the approximation to become $O(F\epsilon \sqrt{s})$ once s is sufficiently large. The threshold value of $\epsilon$ appears to be roughly 0.3/n

Our theorem statements are given for general, possibly coherent, noise channels. While we show that local coherent noise channels lead the output distribution to exhibit exponential decay in the linear cross-entropy benchmark for the fidelity, there is not generally also a decay toward the uniform distribution. As a result, the white-noise approximation is not good for coherent noise channels. Moreover, even for incoherent noise channels, our technical statements are only applicable if the Pauli noise strength $\epsilon$ (or for non-Pauli noise channels, the average infidelity) is beneath a threshold that shrinks with system size like O(1/n) and if the circuit size is at least $\Omega (n\log (n))$. Furthermore, our bound on error in the white-noise approximation is only meaningful if $\epsilon \ll 1/(n\log (n))$. We believe the $\epsilon \ll 1/(n\log (n))$ requirement is merely a result of suboptimal analysis, but that the assumption $\epsilon < O(1/n)$ is fundamentally necessary for the approximation to be good: errors must be scrambled faster than the fidelity-proxy $F \approx e^{-2\epsilon s}$ decays.

One implication of our result is to put low-fidelity random-circuit-based quantum computational supremacy experiments on stronger theoretical footing by showing that, as long as our local noise model is a reasonable approximation of noise in actual devices, the device produces samples from a well-understood output distribution, which can subsequently be argued is hard to classically sample. Indeed, in Appendix C, we combine observations from previous work to show that the task of classically sampling from the white-noise distribution with fidelity-proxy parameter F up to $\eta F$ error is essentially just as hard, in a certain complexity-theoretic sense, as the task of classically sampling from the ideal distribution up to a $O(\eta )$ error. This is important because the latter task (and variants of it in other computational models [53, 54]) has previously garnered significant theoretical scrutiny [21,22,23], although it is still not known whether it is hard in a formal complexity-theoretic sense.

These results are good news for the utility of NISQ devices more broadly. In order to perform a larger and more interesting computation, noise rates must become smaller; our work shows that, in some applications, for circuits with s gates, noise rates need only decrease like $1/\sqrt{s}$, rather than 1/s, as long as one is willing to repeat the experiment many times to extract the signal from the global white noise. A natural next question is when, besides the case of random quantum circuits, do we expect a similar white-noise phenomenon to occur? Our result shows that convergence to white-noise is a generic property, occurring for a large fraction of randomly chosen circuits. Heuristically, this is because random quantum circuits are known to be good scramblers. However, most interesting quantum circuits are non-generic in some way. An extreme example is quantum error-correcting circuits, which are specifically designed not to scramble errors (so that they can be corrected). The output of these circuits will not be close to the white-noise distribution. A fascinating follow-up question is whether other computations proposed for NISQ devices appear to scramble errors well enough that a similar approximation can be made. One leading candidate with relevance for many-body physics is circuits that simulate evolution by fixed chaotic Hamiltonians, since these systems are thought to scramble information efficiently. Indeed, a central motivation for studying random quantum circuits in the first place has been to model the scrambling properties of chaotic many-body systems [35, 36, 55].

Appendices

Framework for Noisy Circuit Analysis

1.1 Action of averaged noiseless gate on identity and swap

The contents of this subsection contain analysis from Ref. [8], which we include again here for completeness. We also slightly modify the notation from Ref. [8] so that the two-qudit identity operator I is always normalized by $q^2$ and the two-qudit swap operator S is always normalized by q, such that their traces are one.

   Since we study second-moment properties, we work with two copies of the n-qudit state. The initial state is $|{0^n}\rangle \!\langle {0^n}| ^{\otimes 2}$. Suppose the gate at time step t acts on qudits in the set $A^{(t)} \subset [n]$ (of size either 1 or 2), and let

$$\begin{aligned} M^{(t)}[\rho ] = \mathop {\mathbb {E}}\limits _{U^{(t)}}\left[ {U^{(t)}_{A^{(t)}}}^{\otimes 2} \rho \, {{U^{(t)}_{A^{(t)}}}^\dagger }^{\otimes 2}\right] , \end{aligned}$$

(A1)

where the average is over Haar-random choice of $U^{(t)}$ and $U^{(t)}_{A^{(t)}}$ denotes the operation that acts as $U^{(t)}$ on qudits in region $A^{(t)}$ and as identity on all other qudits.

   Application of the first layer of n single-qudit gates in Fig. 1 corresponds to application of $M^{(-n+1)}\circ \cdots \circ M^{(0)}$ to the initial state $|{0^n}\rangle \!\langle {0^n}| ^{\otimes 2}$. Applying the Haar integration formula in Eq. (45) to each qubit, we find

$$\begin{aligned} M^{(-n+1)}\circ \cdots \circ M^{(0)}[ |{0^n}\rangle \!\langle {0^n}| ]= & {} \frac{1}{q^n(q+1)^n}\bigotimes _{j=0}^{n-1} \left( I + S\right) _{\{j\}} \nonumber \\= & {} \bigotimes _{j=0}^{n-1} \left( \frac{q}{q+1}\frac{I}{q^2} + \frac{1}{q+1}\frac{S}{q}\right) _{\{j\}}, \end{aligned}$$

(A2)

where the second equality expresses the formula as a linear combination of $I/q^2$ and S/q, both of which have trace one. The coefficients $q/(q+1)$ and $1/(q+1)$ are interpreted as probabilities that each bit of the initial configuration $\vec {\gamma }^{(0)}$ as described in Sect. 5.2 is I or S, respectively.

   Since the averaged state is a linear combination of tensor products of I and S already after the first layer, we need only compute the action of an averaged two-qudit gate on $I \otimes I$, $I \otimes S$, $S\otimes I$, and $S \otimes S$, properly normalized. Suppose gate t acts on qudits $\{i_t,j_t\}$. Then $M^{(t)}$ acts trivially on all qudits outside of $\{i_t,j_t\}$ and its action on $\{i_t,j_t\}$ is computed using the Haar integration formula in Eq. (45) (note that since the gates are $q^2 \times q^2$ matrices, we replace q by $q^2$, I by $I \otimes I$, and S by $S \otimes S$), yielding

$$\begin{aligned} M^{(t)}\left[ \frac{I}{q^2} \otimes \frac{I}{q^2}\right]&= \frac{I}{q^2} \otimes \frac{I}{q^2} \end{aligned}$$

(A3)

$$\begin{aligned} M^{(t)}\left[ \frac{S}{q} \otimes \frac{S}{q}\right]&= \frac{S}{q} \otimes \frac{S}{q} \end{aligned}$$

(A4)

$$\begin{aligned} M^{(t)}\left[ \frac{I}{q^2} \otimes \frac{S}{q}\right] = M^{(t)}\left[ \frac{S}{q} \otimes \frac{I}{q^2}\right]&= \frac{q^2}{q^2+1}\frac{I}{q^2} \otimes \frac{I}{q^2} + \frac{1}{q^2+1}\frac{S}{q} \otimes \frac{S}{q} \end{aligned}$$

(A5)

The above equations correspond to the transition rules for the noiseless stochastic process mentioned in Sect. 5.2: if both bits are I or both are S, then there is no change, but if one is I and one is S, they are both set to I with probability $q^2/(q^2+1)$ and both set to S with probability $1/(q^2+1)$.

   This illustrates that sequential application of $M^{(t)}$ on the state will map linear combinations of tensor products of $I/q^2$ and S/q to other linear combinations of tensor products of $I/q^2$ and S/q. The coefficients of these linear combinations transform linearly. When written in terms of the trace-one operators $I/q^2$ and S/q, this linear transformation will be stochastic, i.e. the sum of the coefficients of the linear combination over tensor products will be conserved (note that the sum of coefficients in Eqs. (A3), (A4), and (A5) is one). Now, let us associate the configuration $\vec {\nu } \in \{I,S\}^n$ by the tensor product $\bigotimes _{j=0}^{n-1} \frac{\nu _j}{\textrm{tr}(\nu _j)}$, which is a basis state for the vector space acted upon by $M^{(t)}$. For configurations $\vec {\nu }, \vec {\gamma } \in \{I,S\}^n$, denote the matrix elements of this (stochastic) transformation by $M^{(t)}_{\vec {\nu }\vec {\gamma }}$, that is

$$\begin{aligned} M^{(t)}\left[ \bigotimes _{j=0}^{n-1} \frac{\gamma _j}{\textrm{tr}(\gamma _j)}\right] = \sum _{\vec {\nu } \in \{I,S\}^n}M_{\vec {\nu }\vec {\gamma }}^{(t)}\bigotimes _{j=0}^{n-1} \frac{\nu _j}{\textrm{tr}(\nu _j)} . \end{aligned}$$

(A6)

The matrix elements are given explicitly by

$$\begin{aligned} M^{(t)}_{\vec {\nu }\vec {\gamma }}={\left\{ \begin{array}{ll} 1 &{} \text {if } \gamma _{i_t} = \gamma _{j_t} \text { and } \vec {\gamma } = \vec {\nu } \\ \frac{q^2}{q^2+1} &{} \text {if } \gamma _{i_t} \ne \gamma _{j_t} \text { and } \nu _{i_t} = \nu _{j_t}=I \text { and } \gamma _c = \nu _c \;\forall c \in [n]\setminus \{i_t,j_t\} \\ \frac{1}{q^2+1} &{} \text {if } \gamma _{i_t} \ne \gamma _{j_t} \text { and } \nu _{i_t} = \nu _{j_t}=S \text { and } \gamma _c = \nu _c \;\forall c \in [n]\setminus \{i_t,j_t\} \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(A7)

Now, note that

$$\begin{aligned} \textrm{tr}\left[ |{0}\rangle \!\langle {0}| ^{\otimes 2} \frac{I}{q^2}\right]&= \frac{1}{q^2} \end{aligned}$$

(A8)

$$\begin{aligned} \textrm{tr}\left[ |{0}\rangle \!\langle {0}| ^{\otimes 2} \frac{S}{q}\right]&= \frac{1}{q} \end{aligned}$$

(A9)

so, for $\vec {\nu } \in \{I,S\}^n$,

$$\begin{aligned} \textrm{tr}\left[ |{0^n}\rangle \!\langle {0^n}| ^{\otimes 2} \bigotimes _{j=0}^{n-1}\frac{\nu _j}{\textrm{tr}(\nu _j)} \right] = \frac{q^{|\vec {\nu }|}}{q^{2n}}\,, \end{aligned}$$

(A10)

where $|\vec {\nu }|$ denotes the Hamming weight of the bit string $\vec {\nu }$, that is, the number of S assignments. Working now from the definition of $Z_0$ in Eq. (39) and $p_{\text {ideal}}$ in Eq. (10), we have the matrix equation

$$\begin{aligned} Z_0= & {} q^{2n}\textrm{tr}\left[ |{0^n}\rangle \!\langle {0^n}| M^{(s)} \circ \cdots M^{(-n+1)} ( |{0^n}\rangle \!\langle {0^n}| )\right] \nonumber \\= & {} \sum _{\gamma \in \{I,S\}^{n\times (s+1)}} \frac{q^{n-|\vec {\gamma }^{(0)}|}}{(q+1)^n}\left( \prod _{t=1}^s M^{(t)}_{\vec {\gamma }^{(t)}\vec {\gamma }^{(t-1)}}\right) q^{|\vec {\gamma }^{(s)}|}. \end{aligned}$$

(A11)

The $q^{n-|\vec {\gamma }^{(0)}|}/(q+1)^n$ factor is the probability of starting in $\vec {\gamma }^{(0)}$. Thus, this can be re-expressed as

$$\begin{aligned} Z_0 = {\mathbb {E}}_0\left[ q^{|\vec {\gamma }^{(s)}|}\right] , \end{aligned}$$

(A12)

where ${\mathbb {E}}_0$ denotes expectation over the stochastic process that generates the trajectory $\gamma = (\gamma ^{(0)},\ldots ,\gamma ^{(s)})$, as described above, and as concluded in Eq. (46) of Sect. 5.2. In Ref. [8], this stochastic process was termed the “biased random walk.”

1.2 Action of averaged noise channel on identity and swap

Since every single-qudit noise channel is followed by a Haar-random (either single-qudit or two-qudit) gate in the circuit diagram, we are free to add a single-qudit Haar-random gate immediately after every noise channel without changing the overall circuit ensemble (the Haar measure is invariant under multiplication by any unitary). Denote this single-qudit Haar-random matrix by V. There will be a difference in the analysis between the calculation of $Z_0$, $Z_1$ and $Z_2$, where $Z_w$ contains w copies of the noisy output as defined in Eqs. (39), (40), (41). Define

$$\begin{aligned} {\mathcal {N}}_0&= {\mathcal {I}} \otimes {\mathcal {I}} \end{aligned}$$

(A13)

$$\begin{aligned} {\mathcal {N}}_1&= {\mathcal {I}} \otimes {\mathcal {N}} \end{aligned}$$

(A14)

$$\begin{aligned} {\mathcal {N}}_2&= {\mathcal {N}} \otimes {\mathcal {N}} \end{aligned}$$

(A15)

with ${\mathcal {I}}$ denoting the single-qudit identity channel. Let $\rho$ be a state on two copies of a single-qudit Hilbert space. Then for $w \in \{0,1,2\}$, let

$$\begin{aligned} N_w[\rho ]&= \mathop {\mathbb {E}}\limits _V\left[ V^{\otimes 2} \; {\mathcal {N}}_w(\rho ) V^{\dagger \otimes 2}\right] \end{aligned}$$

(A16)

be the Haar-averaged noise channel.

   We will only need to compute the action of $N_w$ on input states $\rho = I/q^2$ (here I is the two-qudit identity operator) or $\rho = S/q$ since, as shown above, the random gates turn the initial state $|{0^n}\rangle \!\langle {0^n}|$ into a linear combination of tensor products of $I/q^2$ or S/q on each qudit. Note that since ${\mathcal {N}}$ is assumed to be unital, we have

$$\begin{aligned} N_w\left[ \frac{I}{q^2}\right]&= \frac{I}{q^2} \end{aligned}$$

(A17)

for all $w \in \{0,1,2\}$. However, computing the action on S/q is not as simple. Let

$$\begin{aligned} Y_w&= \textrm{tr}\left( S {\mathcal {N}}_w(S)\right) \,. \end{aligned}$$

(A18)

(Note that $Y_0 = q^2$ since ${\mathcal {N}}_0$ is the identity channel.) Then, use Eq. (45) and the fact that ${\mathcal {N}}$ is trace-preserving to show

$$\begin{aligned} N_w\left[ \frac{S}{q}\right]&= \frac{q^2-Y_w}{q^2-1} \frac{I}{q^2} + \frac{Y_w-1}{q^2-1}\frac{S}{q} \,. \end{aligned}$$

(A19)

Now we relate the quantities $Y_1$ and $Y_2$ to the average infidelity and the unitarity, respectively. Recall that $\textrm{tr}(AB) = \textrm{tr}(S(A \otimes B))$. Using this trick and Eq. (45), the average infidelity from Eq. (3), can be evaluated as follows:

$$\begin{aligned} r&= 1-\int dV \textrm{tr}\left[ V |{\psi }\rangle \!\langle {\psi }| V^{\dagger }{\mathcal {N}}(V |{\psi }\rangle \!\langle {\psi }| V^{\dagger })\right] \end{aligned}$$

(A20)

$$\begin{aligned}&= 1-\int dV \textrm{tr}\left[ S\left( V |{\psi }\rangle \!\langle {\psi }| V^{\dagger }\otimes {\mathcal {N}}(V |{\psi }\rangle \!\langle {\psi }| V^{\dagger })\right) \right] \end{aligned}$$

(A21)

$$\begin{aligned}&= 1-\int dV \textrm{tr}\left[ S({\mathcal {I}} \otimes {\mathcal {N}})\left( \left( V |{\psi }\rangle \!\langle {\psi }| V^{\dagger }\right) ^{\otimes 2}\right) \right] \end{aligned}$$

(A22)

$$\begin{aligned}&= 1-\textrm{tr}\left[ S{\mathcal {N}}_1 \left( \frac{I+S}{q(q+1)}\right) \right] \end{aligned}$$

(A23)

$$\begin{aligned}&= 1-\frac{1-q^{-1}Y_1}{q+1} = \frac{q-q^{-1}Y_1}{q+1}\,. \end{aligned}$$

(A24)

The unitarity from Eq. (4), can be evaluated in a similar way.

$$\begin{aligned} u&=\frac{q}{q-1}\left( \int dV \textrm{tr}\left[ {\mathcal {N}}\left( V |{\psi }\rangle \!\langle {\psi }| V^{\dagger }\right) ^2\right] -\frac{1}{q}\right) \end{aligned}$$

(A25)

$$\begin{aligned}&=\frac{q}{q-1}\int dV \textrm{tr}\left[ S\left( {\mathcal {N}}\left( V |{\psi }\rangle \!\langle {\psi }| V^{\dagger }\right) \right) ^{\otimes 2}\right] -\frac{1}{q-1} \end{aligned}$$

(A26)

$$\begin{aligned}&= \frac{q}{q-1}\int dV \textrm{tr}\left[ S({\mathcal {N}} \otimes {\mathcal {N}})\left( \left( V |{\psi }\rangle \!\langle {\psi }| V^{\dagger }\right) ^{\otimes 2}\right) \right] -\frac{1}{q-1} \end{aligned}$$

(A27)

$$\begin{aligned}&=\frac{q}{q-1} \textrm{tr}\left[ S {\mathcal {N}}_2\left( \frac{I+S}{q(q+1)}\right) \right] -\frac{1}{q-1} \end{aligned}$$

(A28)

$$\begin{aligned}&=\frac{q +Y_2}{(q-1)(q+1)}-\frac{1}{q-1} \end{aligned}$$

(A29)

$$\begin{aligned}&= \frac{Y_2 -1}{q^2-1} \,. \end{aligned}$$

(A30)

Plugging these relations back into Eq. (A19) gives us

$$\begin{aligned} N_0\left[ \frac{S}{q} \right]&= \frac{S}{q} \end{aligned}$$

(A31)

$$\begin{aligned} N_1\left[ \frac{S}{q} \right]&= \frac{qr}{q-1} \frac{I}{q^2} + \left( 1-\frac{qr}{q-1}\right) \frac{S}{q} \end{aligned}$$

(A32)

$$\begin{aligned} N_2\left[ \frac{S}{q} \right]&= (1-u) \frac{I}{q^2} + u \frac{S}{q} \,. \end{aligned}$$

(A33)

For weak noise channels, r is close to 0 and u is close to 1. In this case we see that the noise causes some small amount of leakage from the S state to the I state, but no leakage from the I state to the S state, introducing an asymmetry into the problem that did not exist in the noiseless analysis.

   For $t=1,\ldots , s$, let $N_w^{(t)} = {\mathcal {I}}_{[n]{\setminus }\{i_t\}} \otimes N_{w,\{i_t\}}$ be the channel that acts with the averaged noise channel on site $i_t$ and identity elsewhere, and let $N_w^{\prime \,(t)} = {\mathcal {I}}_{[n]{\setminus }\{j_t\}} \otimes N_{w,\{j_t\}}$ be the same for site $j_t$. For $t\le 0$ and $t > s$, let $N_w^{(t)}$ be the identity channel. If $\rho$ is a linear combination of tensor products of $I/q^2$ and S/q, $N_w^{(t)}(\rho )$ and $N_w^{\prime \,(t)}(\rho )$ will be as well, with coefficients that transform linearly (and stochastically). For configurations $\vec {\gamma }, \vec {\nu } \in \{I,S\}^n$, let $N_{w,\vec {\nu }\vec {\gamma }}^{(t)}$ denote the matrix elements of this transformation, that is

$$\begin{aligned} N_w^{(t)}\left[ \bigotimes _{j=0}^{n-1} \frac{\gamma _j}{\textrm{tr}(\gamma _j)}\right] = \sum _{\vec {\nu } \in \{I,S\}^n}N_{w,\vec {\nu }\vec {\gamma }}^{(t)}\bigotimes _{j=0}^{n-1} \frac{\nu _j}{\textrm{tr}(\nu _j)} , \end{aligned}$$

(A34)

where for $1 \le t \le s$,

$$\begin{aligned} N_{0,\vec {\nu }\vec {\gamma }}^{(t)}&= {\left\{ \begin{array}{ll} 1 &{} \text {if } \vec {\gamma } = \vec {\nu } \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(A35)

$$\begin{aligned} N_{1,\vec {\nu }\vec {\gamma }}^{(t)}&= {\left\{ \begin{array}{ll} 1 &{} \text {if } \gamma _{i_t} = \nu _{i_t} = I \text { and } \vec {\gamma } = \vec {\nu }\\ 1-\frac{qr}{q-1} &{} \text {if } \gamma _{i_t} = S \text { and } \nu _{i_t} = S \text { and } \vec {\gamma } = \vec {\nu }\\ \frac{qr}{q-1} &{} \text {if } \gamma _{i_t} = S \text { and } \nu _{i_t} = I \text { and } \gamma _a = \nu _a \forall a \ne i_t\\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(A36)

$$\begin{aligned} N_{2,\vec {\nu }\vec {\gamma }}^{(t)}&= {\left\{ \begin{array}{ll} 1 &{} \text {if } \gamma _{i_t} = \nu _{i_t} = I \text { and } \vec {\gamma } = \vec {\nu }\\ u &{} \text {if } \gamma _{i_t} = S \text { and } \nu _{i_t} = S \text { and } \vec {\gamma } = \vec {\nu }\\ 1-u &{} \text {if } \gamma _{i_t} = S \text { and } \nu _{i_t} = I \text { and } \gamma _a = \nu _a\; \forall a \ne i_t\\ 0 &{} \text {otherwise}\,, \end{array}\right. } \end{aligned}$$

(A37)

and $N_w^{\prime \,(t)}$ are given by the same equations, with $j_t$ replacing $i_t$.

1.3 Mapping noisy circuits to stochastic processes

Define

$$\begin{aligned} {\mathcal {U}}_0^{(t)}&= {\mathcal {U}}^{(t)} \otimes {\mathcal {U}}^{(t)} \end{aligned}$$

(A38)

$$\begin{aligned} {\mathcal {U}}_1^{(t)}&= \widetilde{{\mathcal {U}}}^{(t)} \otimes {\mathcal {U}}^{(t)} \end{aligned}$$

(A39)

$$\begin{aligned} {\mathcal {U}}_2^{(t)}&= \widetilde{{\mathcal {U}}}^{(t)} \otimes \widetilde{{\mathcal {U}}}^{(t)}\,, \end{aligned}$$

(A40)

where ${\mathcal {U}}^{(t)}$ and $\widetilde{{\mathcal {U}}}^{(t)}$ are given in Eqs. (8) and (9). Then we may write, for $w \in \{0,1,2\}$

$$\begin{aligned} Z_w = q^{2n} \mathop {\mathbb {E}}\limits _U \left[ \textrm{tr}\left[ |{0^n}\rangle \!\langle {0^n}| ^{\otimes 2}\;{\mathcal {U}}_w^{(n+s)} \circ \cdots \circ {\mathcal {U}}_w^{(-n+1)}\left( |{0^n}\rangle \!\langle {0^n}| ^{\otimes 2}\right) \right] \right] \,. \end{aligned}$$

(A41)

Since each $U^{(t)}$ is chosen independently, we are free to perform the expectation value individually over each ${\mathcal {U}}_w^{(t)}$ channel. The noiseless channel ${\mathcal {U}}^{(t)}_0 = {\mathcal {U}}^{(t)\otimes 2}$ averages to $M^{(t)}$, where $M^{(t)}$ is given in Eq. (A1). The action of the noise may also be averaged, since, as discussed in Appendix A.2, we may pull out a single-qudit Haar random gate to act after each noise location. Thus, the noiseless single qudit gates at the end of the circuit may be dropped as they are being absorbed into the noise. Let

$$\begin{aligned} M_w^{(t)} = N_w^{\prime \,(t)} \circ N_w^{(t)} \circ M^{(t)} \end{aligned}$$

(A42)

so that

$$\begin{aligned} Z_w = q^{2n} \textrm{tr}\left[ |{0^n}\rangle \!\langle {0^n}| ^{\otimes 2}\;M_w^{(s)} \circ \cdots \circ M_w^{(-n+1)}\left( |{0^n}\rangle \!\langle {0^n}| ^{\otimes 2}\right) \right] \,. \end{aligned}$$

(A43)

Following the noiseless analysis of Appendix A.1, we may now write $Z_w$ as a product of matrices

$$\begin{aligned} Z_w&= \sum _{\gamma \in \{I,S\}^{n \times (3s+1)}}\frac{q^{n-|\vec {\gamma }^{(0)}|}}{(q+1)^n} \left( \prod _{t=1}^{s} N^{\prime \,(t)}_{w,\vec {\gamma }^{(t)}\vec {\gamma }^{(t-1/3)}} N^{(t)}_{w,\vec {\gamma }^{(t-1/3)}\vec {\gamma }^{(t-2/3)}} M^{(t)}_{\vec {\gamma }^{(t-2/3)}\vec {\gamma }^{(t-1)}}\right) q^{|\vec {\gamma }^{(s)}|} \end{aligned}$$

(A44)

generalizing Eq. (A11). In the notation of Sect. 5.2, for $w=1$ this can be expressed as $Z_1={\mathbb {E}}_{rq/(q+1)}[q^{|\vec {\gamma }^{(s)}|}]$ where the expectation is over the stochastic process that generates a trajectory with $3s+1$ configurations (at time values $t=0,1/3,2/3,1,\ldots ,s$). For $w=2$, it reads $Z_2={\mathbb {E}}_{1-u}[q^{|\vec {\gamma }^{(s)}|}]$.

   The expressions for $Z_w$ as weighted sums over trajectories can alternatively be interpreted as partition functions of an Ising-like stat mech model where each $\gamma _a^{(t)}$ is an Ising variable $\{+1,-1\}$. There are interactions between adjacent Ising variables whenever a gate or noise location acts between them; the associated interaction strengths can be calculated from the matrix elements listed above.

1.4 Bra-ket notation for the stochastic process

We now write the above insights in a notation that offers slightly more flexibility, which we will utilize in our proofs. The reader need only read this section to verify the proofs that appear later. Consider a $2^n$-dimensional vector space, where orthonormal basis states are labeled by configurations $|\vec {\nu }\rangle$ for each $\vec {\nu } \in \{I,S\}^n$. Define the vectors

$$\begin{aligned} |\textbf{1}\rangle&= \sum _{\vec {\nu } \in \{I,S\}^n} |\vec {\nu }\rangle \end{aligned}$$

(A45)

$$\begin{aligned} |\textbf{q}\rangle&= \sum _{\vec {\nu } \in \{I,S\}^n} q^{|\vec {\nu }|}|\vec {\nu }\rangle \end{aligned}$$

(A46)

$$\begin{aligned} |\Lambda \rangle&= \frac{1}{(q+1)^n}\sum _{\vec {\nu } \in \{I,S\}^n} q^{n-|\vec {\nu }|}|\vec {\nu }\rangle \,. \end{aligned}$$

(A47)

Then we may define $2^n \times 2^n$ transition matrices $P^{(t)}$, which enact the tth step of the noiseless stochastic process, as well as matrices $Q_{\sigma }^{(t)}$ and $Q'^{(t)}_{\sigma }$ which enact the $S \rightarrow I$ transition with probability $\sigma$ on qudits $i_t$ and $j_t$, respectively. Explicitly we let

$$\begin{aligned} P^{(t)}&= {\mathcal {I}}_{[n]\setminus \{i_t,j_t\}} \otimes P_{\{i_t,j_t\}} \end{aligned}$$

(A48)

$$\begin{aligned} Q_\sigma ^{(t)}&= {\mathcal {I}}_{[n]\setminus \{i_t\}} \otimes \Big ( |{I}\rangle \!\langle {I}| + (1-\sigma ) |{S}\rangle \!\langle {S}| + \sigma |{I}\rangle \!\langle {S}| \Big )_{\{i_t\}} \end{aligned}$$

(A49)

$$\begin{aligned} Q'^{(t)}_{\sigma }&= {\mathcal {I}}_{[n]\setminus \{j_t\}} \otimes \Big ( |{I}\rangle \!\langle {I}| + (1-\sigma ) |{S}\rangle \!\langle {S}| + \sigma |{I}\rangle \!\langle {S}| \Big )_{\{j_t\}}\,, \end{aligned}$$

(A50)

where the subscripts on the right-hand side denote which bits are acted upon by which operators, and

$$\begin{aligned} D ={}&|{II}\rangle \!\langle {II}| + |{SS}\rangle \!\langle {SS}| \end{aligned}$$

(A51)

$$\begin{aligned} T ={}&\frac{q^2}{q^2+1} |{II}\rangle \!\langle {IS}| +\frac{q^2}{q^2+1} |{II}\rangle \!\langle {SI}| + \frac{1}{q^2+1} |{SS}\rangle \!\langle {SI}| +\frac{1}{q^2+1} |{SS}\rangle \!\langle {IS}| \end{aligned}$$

(A52)

$$\begin{aligned} P ={}&D+ T \,. \end{aligned}$$

(A53)

Note that P is a stochastic $4 \times 4$ matrix. Then, define

$$\begin{aligned} {\mathcal {Z}}_\sigma = \langle \textbf{q} |\left( \prod _{t=1}^s Q'^{(t)}_{\sigma }Q^{(t)}_{\sigma } P^{(t)}\right) |\Lambda \rangle , \end{aligned}$$

(A54)

If the circuit diagram is generated randomly, as is the case for the complete-graph architecture, then ${\mathcal {Z}}_\sigma$ is defined instead as the mean of the above expression over choice of circuit diagram. For the specific case of the complete-graph architecture (where the pair of qudits acted upon by each gate is chosen independently from all other gates), the average of ${\mathcal {Z}}_\sigma$ over different circuit diagrams can be accomplished by averaging the matrix $Q'^{(t)}_{\sigma }Q^{(t)}_{\sigma } P^{(t)}$ over all choices of $\{i_t,j_t\}$. This is the convention we follow when analyzing the complete-graph architecture.

   The $|\Lambda \rangle$ in the equation above represents the distribution over the initial configuration $\vec {\gamma }^{(0)}$, and the $\langle \textbf{q} |$ represents the weighting given to the final configuration $\vec {\gamma }^{(s)}$. Thus, the equation for $Z_w$ in Eq. (A44) implies that

$$\begin{aligned} Z_0&= {\mathcal {Z}}_0 \end{aligned}$$

(A55)

$$\begin{aligned} Z_1&= {\mathcal {Z}}_{r q/(q-1)} \end{aligned}$$

(A56)

$$\begin{aligned} Z_2&= {\mathcal {Z}}_{1-u}\,. \end{aligned}$$

(A57)

Detailed Proofs

The statements of our main theorems in the appendix are slightly more general than in the main text: we consider a general class of architectures that are both “layered” and “regularly connected,” which we define below. The theorem statements are in terms of the anti-concentration size $s_{AC}$ of the architecture, which is defined [8] to be the minimum circuit size s such that $Z_0 \le 4q^n/(q^n+1)$. The 1D architecture and complete-graph architecture are the only architectures known to have $s_{AC} = \Theta (n\log (n))$, so for clarity, we previously restricted our statements to those architectures.

   First, in Appendix B.1, we present definitions and our main lemmas, which are themselves dependent on more minor lemmas. Then, in Appendix B.2, we prove a slightly generalized version of our theorems from the main text, based on the main lemmas. Afterward, in Appendix B.3, we develop some more machinery and state the minor lemmas, deferring their proofs to Appendix B.8.

1.1 Definitions and main lemmas

Our proofs apply to architectures that are layered and h-regularly connected for some constant $h=O(1)$. The regularly connected property was defined in Ref. [8], where it was conjectured to imply anti-concentration after $\Theta (n\log (n))$ gates, and we repeat its definition here.

   First, define an architecture as in Ref. [8] to be an efficient (possibly randomized) algorithm that takes as input circuit parameters (n, s) and outputs a length-s sequence of size-2 subsets $(A^{(1)},\ldots ,A^{(s)})$, where $A^{(t)} \subset [n]$ and $|A^{(t)}| = 2$ for each t. The subsets $A^{(t)}$ correspond to the pair of qudits acted upon by a gate at time step t.

Definition 1

(Regularly connected [8]) We say a random quantum circuit architecture is h-regularly connected if for any n, any t, any subsequence $A=(A^{(1)},\ldots ,A^{(t)})$ and any proper subset $R \subset [n]$ of qudit indices, there is at least a 1/2 probability that, conditioned on the first t gates in the gate sequence being A, there exists some index $t'$ for which $t< t' \le t+hn$, $A^{(t')} \cap R \ne \emptyset$, and $A^{(t')} \not \subset R$.

   If $h=O(1)$, we often simply call the architecture regularly connected, without specifying h. This property is a precise way of saying that the circuit does not break into multiple distinct parts that rarely interact with each other (a feature that would prevent scrambling): for any bipartition, there is usually a gate that couples one qubit from each half at least once every O(n) time steps. Nearly all natural architectures are regularly connected. For example, many architectures, such as those based on lattices in d dimensions, can be associated with a graph where vertices represent the n qubits and edges represent the allowable gates between those qubits. Suppose the graph is connected and has degree O(1), and furthermore that gates are performed by repeatedly iterating through the edges of the graph. It is straightforward to see that for any bipartition, there will be a gate connecting the two parts at least once every O(n) gates, and thus the architecture is regularly connected. In the complete-graph architecture, the degree of the graph is $n-1$, but gates are chosen randomly rather than iteratively, ensuring that any bipartition is spanned by a gate with 1/2 probability every O(n) gates. An example of an architecture that is not regularly connected is the hypercube architecture, which is associated with a graph of superconstant degree equal to $\log _2(n)$. If we partition the qubits into two equal size sets, it is possible for there to be a sequence of $O(n \log (n))$ consecutive gates that do not connect the two sets.

   Next, we define layered, which simply means that the gates can always be neatly arranged into layers of n/2 non-overlapping gates.

Definition 2

An architecture is layered if any sequence of gates $(A^{(1)},\ldots ,A^{(s)})$ it generates with non-zero probability has the property that for any integer $d\ge 0$, and any pair of gates in the same “layer”

$$\begin{aligned} t_1,t_2 \in \{dn/2+1, dn/2+2,\ldots , (d+1)n/2\} \end{aligned}$$

(B58)

with $t_1 \ne t_2$, we have $A^{(t_1)} \cap A^{(t_2)} = \emptyset$. Thus, all n qudits are acted upon by exactly one gate out of every n/2 gates.

   For layered architectures we can speak clearly about the depth $d = 2\,s/n$. The anti-concentration depth is then defined as $d_{AC} = 2s_{AC}/n$. We will generally require s be a multiple of n/2 so that there are an integer number of layers. Regular lattice architectures in D spatial dimensions are typically layered, although adhering strictly to the definition would require applying periodic boundary conditions. We do not expect this condition is actually necessary for our results, but it is analytically convenient. The only place we need it is in Lemma 12.

   Our theorems are corollaries of the following lemmas. Recall the definition of ${\mathcal {Z}}_\sigma$ from Eq. (A54). Note that in these proofs, all constants are dependent on q as well as h (the regularly connected parameter), but independent of n and the noise parameters.

Lemma 1

If the random quantum circuit architecture is h-regularly connected and layered with anti-concentration depth $d_{AC}$, then there exist constants $c_0$, $c_1$, $c_2$, $c_3$, $c_4$, $c_5$, and $n_0'$ that depend on h and q but not on n or $\sigma$, such that as long as $\sigma \le c_5/n$ and $n \ge n_0'$, for any value of the circuit depth d,

$$\begin{aligned} \frac{q^n-1}{q^n+1}\left( 1-f_\sigma \right) ^{d}\le {}&{\mathcal {Z}}_\sigma -1 \le \frac{q^n-1}{q^n+1}\left( 1-f_\sigma \right) ^{d} e^{K_\sigma } \,, \end{aligned}$$

(B59)

where

$$\begin{aligned} f_\sigma&= \frac{1-(1-\sigma (1-q^{-2}))^n}{1-q^{-2n}} \end{aligned}$$

(B60)

$$\begin{aligned} K_\sigma&= c_0 n d \sigma ^2 + c_1 n \sigma d_{AC}+c_2e^{-c_3(d-d_{AC})+2\sigma d n} + c_4 n \sigma \log (1/(n\sigma ))\,. \end{aligned}$$

(B61)

Proof

The lower bound is an immediate consequence of two lemmas that appear later, Lemma 11 and Lemma 12. The upper bound is also an immediate consequence, with the constant $c_1$ absorbing an $O(n\sigma )$ term since $d_{AC} = 2s_{AC}/n \ge \Omega (\log (n))$ by the results of Ref. [8]. $\square$

   We show the analogous statement for the complete-graph architecture.

Lemma 2

If the random quantum circuit architecture is the complete-graph architecture, then there exist constants $c'_0$, $c'_1$, $c'_2$, $c'_3$, $c'_4$, $c'_5$, and $n_0$ that depend on q but not on n or $\sigma$, such that as long as $\sigma \le c'_5/n$ and $n \ge n_0$, for any value of the circuit size s,

$$\begin{aligned} \frac{q^n-1}{q^n+1}\left( 1-f'_\sigma \right) ^{s}\le {}&{\mathcal {Z}}_\sigma -1 \le \frac{q^n-1}{q^n+1}\left( 1-f'_\sigma \right) ^{s} e^{K'_\sigma } \,, \end{aligned}$$

(B62)

where

$$\begin{aligned} f'_\sigma&= \frac{1-(1-\sigma (1-q^{-2}))^2}{1-q^{-2n}} \end{aligned}$$

(B63)

$$\begin{aligned} K'_\sigma&= c'_0 s \sigma ^2 + c'_1 \sigma s_{AC}+c'_2e^{-c'_3(s-s_{AC})/n + 4 \sigma s} + c'_4 n \sigma \log (1/(n\sigma )) \,, \end{aligned}$$

(B64)

and $s_{AC} = \Theta (n\log (n))$ is the anti-concentration size for the complete-graph architecture.

Proof

The proof is the same as Lemma 1 except using Lemma 13 in place of Lemma 12. $\square$

Note that in the regime $\sigma \le O(1/n)$, we can bound $1-\sigma (1-q^{-2}) \ge e^{-\sigma (1-q^{-2})}e^{-O(\sigma ^2)}$ and the following holds

$$\begin{aligned} e^{-n\sigma (1-q^{-2})} e^{-O(n\sigma ^2)-O(q^{-2n})}&\le 1-f_{\sigma } \le e^{-n\sigma (1-q^{-2})} \end{aligned}$$

(B65)

$$\begin{aligned} e^{-2\sigma (1-q^{-2})} e^{-O(\sigma ^2)-O(q^{-2n})}&\le 1-f'_{\sigma } \le e^{-2\sigma (1-q^{-2})} \,. \end{aligned}$$

(B66)

The upper bound in Eqs. (B65) and (B66) actually holds generally for all $\sigma$.

1.2 Proofs of main theorems from main lemmas

1.2.1 Proof of Theorem 1: linear cross-entropy decay

Theorem 1

(Generalized and restated). Consider either the complete-graph architecture or a regularly connected, layered random quantum circuit architecture with n qudits of local Hilbert space dimension q and s gates, where the anti-concentration size is given by $s_{AC}$. Let r be the average infidelity of the local noise channels. Then there exists constants c and $n_0$ such that whenever $r \le c/n$ and $n \ge n_0$, the following holds:

$$\begin{aligned} {\bar{F}}&\ge \exp \left( -2sr(1+q^{-1})\right) e^{-O(sr^2)-O(sq^{-2n})-e^{O(\log (n))-\Omega (s/n)}} \end{aligned}$$

(B67)

$$\begin{aligned} {\bar{F}}&\le \exp \left( -2sr(1+q^{-1})\right) Q_1 \,, \end{aligned}$$

(B68)

where ${\bar{F}}$ is given in Eq. (14), and

$$\begin{aligned} Q_1 = \exp \left( O(sr^2) + O(s_{AC}r) + e^{O(s_{AC}/n)}e^{-\Omega (s/n)} + O(nr \log (1/(nr)))\right) . \end{aligned}$$

(B69)

Proof

The quantity ${\bar{F}}$ is precisely $(Z_1-1)/(Z_0-1) = ({\mathcal {Z}}_{\sigma }-1)/({\mathcal {Z}}_{0}-1)$ with $\sigma =r q/(q-1)$. The statements are then direct consequences of Lemma 1 for layered architectures and Lemma 2 for the complete-graph architecture, combined with the observation in Eqs. (B65) and (B66). Note also that $nd=2s$. $\square$

1.2.2 Proof of Theorem 2: convergence to the uniform distribution

Theorem 2

(Generalized and restated). Consider either the complete-graph architecture or a regularly connected, layered random quantum circuit architecture with n qudits of local Hilbert space dimension q and s gates, where the anti-concentration size is given by $s_{AC}$. Let u be the unitarity of the local noise channels (and define $v=1-u$). Then there exist constants c and $n_0$ such that as long as $v \le c/n$ and $n \ge n_0$

$$\begin{aligned} \mathop {\mathbb {E}}\limits _U \left[ \frac{1}{2}\Vert p_{\text {noisy}}- p_{\text {unif}}\Vert _1 \right] \le \exp (-sv(1-q^{-2})) Q_2 , \end{aligned}$$

(B70)

where $p_{\text {unif}}$ is the uniform distribution and

$$\begin{aligned} Q_2 = \exp \left( O(sv^2) + O(s_{AC}v) + e^{O(s_{AC}/n)}e^{-\Omega (s/n)}+O(nv \log (1/(nv))\right) . \end{aligned}$$

(B71)

Proof

We can use the 1-norm to 2-norm inequality in Eq. (35), along with Jensen’s inequality for the concave $\sqrt{\cdot }$ function to say

$$\begin{aligned} \mathop {\mathbb {E}}\limits _U \left[ \frac{1}{2}\Vert p_{\text {noisy}}- p_{\text {unif}}\Vert _1 \right]&\le \frac{1}{2}\sqrt{q^n\mathop {\mathbb {E}}\limits _U\left[ \sum _x\left( p_{\text {noisy}}(x) - q^{-n}\right) ^2\right] } \end{aligned}$$

(B72)

$$\begin{aligned}&= \frac{1}{2}\sqrt{q^{2n}\mathop {\mathbb {E}}\limits _U\left[ p_{\text {noisy}}(0^n)^2\right] -1} = \frac{1}{2}\sqrt{Z_2-1} \end{aligned}$$

(B73)

$$\begin{aligned}&= \frac{1}{2}\sqrt{{\mathcal {Z}}_v-1} \end{aligned}$$

(B74)

Then, the theorem follows from the upper bound in Lemma 1 for layered architectures and Lemma 2 for the complete-graph architecture, with $\sigma = v$, combined with the observation in Eqs. (B65) and (B66). Note also that $nd=2s$. $\square$

1.2.3 Proof of Theorem 3: approximation by white noise

Theorem 3

(Generalized and restated). Consider either the complete-graph architecture or a regularly connected, layered random quantum circuit architecture with n qudits of local Hilbert space dimension q and s gates, where the anti-concentration size is given by $s_{AC}$. Let r be the average infidelity and u the unitarity of the local noise channels (and define $v=1-u$). Let

$$\begin{aligned} \delta =2r(1+q^{-1})-(1-u)(1-q^{-2}) . \end{aligned}$$

(B75)

Then, when we choose $F = {\bar{F}}$ as in Eq. (14), there exist constants $c_1$, $c_2$, and $n_0$ such that as long as $v \le c_1/n$, $r \le c_2/n$, and $n \ge n_0$,

$$\begin{aligned} \mathop {\mathbb {E}}\limits _U \left[ \frac{1}{2}\Vert p_{\text {noisy}}- p_{\text {wn}}\Vert _1 \right]&\le {} {\bar{F}}\sqrt{s}\left( \sqrt{\delta }+O(v)+O(r)\right) + O({\bar{F}}\sqrt{s_{AC}v}) \nonumber \\&\quad +O({\bar{F}}\sqrt{nv\log (1/nv)})+ {\bar{F}}e^{O(s_{AC}/n)-\Omega (s/n)}\,, \end{aligned}$$

(B76)

whenever the right-hand side of Eq. (B76) is less than ${\bar{F}}$.

Proof

Following Sect. 5.2, we first use the 1-norm to 2-norm bound and Jensen’s inequality, and then we optimize the value of F. The bound on the distance between $p_{\text {wn}}$ and $p_{\text {noisy}}$ is minimized when we choose $F = {\bar{F}} = (Z_1-1)/(Z_0-1)$. When this value is chosen, the bound can be expressed as

$$\begin{aligned} \mathop {\mathbb {E}}\limits _U \left[ \frac{1}{2}\Vert p_{\text {noisy}}- p_{\text {wn}}\Vert _1 \right] \le \frac{1}{2}{\bar{F}}\sqrt{\frac{(Z_2-1)(Z_0-1)^2}{(Z_1-1)^2}-(Z_0-1)} \end{aligned}$$

(B77)

Note that after the anti-concentration size has been surpassed, the quantity $Z_0-1$ rapidly approaches $\frac{q^n-1}{q^n+1}\approx 1$ from above. To evaluate $Z_0$, $Z_1$ and $Z_2$ we use the correspondence $Z_0 = {\mathcal {Z}}_0$, $Z_1 = {\mathcal {Z}}_{r q /(q-1)}$ and $Z_2 = {\mathcal {Z}}_v$. The bounds from Lemma 1 for layered architectures and Lemma 2 for the complete-graph architecture then allow us to upper bound $(Z_2-1)(Z_0-1)^2/(Z_1-1)^2$, arriving at

$$\begin{aligned} \frac{(Z_2-1)(Z_0-1)^2}{(Z_1-1)^2} \le {}&\frac{q^n-1}{q^n+1}e^{2s\left( 2r(1+q^{-1})-v(1-q^{-2})\right) }e^{O(sr^2)+O(sq^{-2n})+e^{O(s_{AC}/n)}e^{-\Omega (s/n)}}Q_2 \end{aligned}$$

(B78)

$$\begin{aligned} =&\frac{q^n-1}{q^n+1} e^{2s\delta }e^{O(sr^2+sq^{-2n}+sv^2+s_{AC}v-nv \log (nv))+ e^{O(s_{AC}/n)}e^{-\Omega (s/n)}} \,, \end{aligned}$$

(B79)

where $Q_2$ is given in Eq. (B71), and $\delta$ is given in Eq. (B75). Now, working back from Eq. (B77), and noting that $e^x-1 < 2x$ for all $x \le 1$, we have

$$\begin{aligned}&\mathop {\mathbb {E}}\limits _U \left[ \frac{1}{2}\Vert p_{\text {noisy}}- p_{\text {wn}}\Vert _1 \right] \nonumber \\&\quad \le {} \frac{{\bar{F}}}{2}\sqrt{4s\delta +O(sr^2+sq^{-2n}+sv^2+s_{AC}v-nv \log (nv))+ e^{O(s_{AC}/n)}e^{-\Omega (s/n)}} \end{aligned}$$

(B80)

$$\begin{aligned}&\quad ={} {\bar{F}}\sqrt{s}\left( \sqrt{\delta }+O(v)+O(r)\right) + O({\bar{F}}\sqrt{s_{AC}v}) \nonumber \\&\qquad +O({\bar{F}}\sqrt{nv\log (1/nv)})+ {\bar{F}}e^{O(s_{AC}/n)-\Omega (s/n)} \end{aligned}$$

(B81)

when the quantity under the square root is less than 1 (and using $\sqrt{A+B} \le \sqrt{A}+\sqrt{B}$).

$\square$

1.3 Machinery for proof

We now develop some more notation, and we precisely state some of our lemmas. We defer the proofs of these lemmas to Appendix B.8. As we state them, we attempt to give some commentary about the meaning and purpose of the different objects that we define and the related lemmas.

Fig. 5

Illustration of dynamics of coupled noiseless and noisy stochastic process. The gate at time step t acts on sites $\{i_t,j_t\}$; the transition from time step $t-1$ to time step t can modify the assignment only at these locations. In the example above, at time step $t-1$ (left), both the X and Y systems are assigned I at position $i_t$ and S at position $j_t$. Since $i_t$ and $j_t$ are assigned different values, the transformation $R_0^{(t)}$ forces a bit flip at one of the positions, but the same bit is flipped for the X and Y systems. In this example, the I is flipped to S. Then the configuration at time step t (right) is formed by applying noise operators $Q'^{(t)}_\sigma Q^{(t)}_\sigma$ only to the Y copy, which results in a bit flip from S to I independently on each location with probability $\sigma$. In the example above, only the $i_t$ assignment is flipped. The system W captures the difference between the X and Y copies; it is assigned S wherever they agree and I wherever they disagree. This formalism allows us to isolate the impact of the noise on a trajectory of the stochastic process compared to what “would have” happened had there been no noise

1.3.1 Coupling a noiseless and noisy copy of the dynamics

We have a fairly good understanding of the noiseless stochastic process from Ref. [8]. Our strategy here is to examine how introducing noise perturbs that process. To that end, we consider two copies of the random walk, where one is noiseless and one is noisy, but where they are correlated so that we can isolate the impact of the noise.

   Recall that we have reduced the calculation of ${\mathcal {Z}}_\sigma$ to the expectation value of a random variable (the configuration) that evolves according to the stochastic transition matrix $P^{(t)}$ (representing the noiseless gate) followed by transition matrices $Q^{(t)}_\sigma$ and $Q'^{(t)}_\sigma$, which represent the impact of noise.

   Let X denote the $2^n$-dimensional vector space for the first “noiseless” copy and Y for the second “noisy” copy. To define the dynamics formally, recall the definition of D and T from Eqs. (A51) and (A52), and define the following matrix that acts on four bits.

$$\begin{aligned} R&=D \otimes D + D \otimes T + T \otimes D + T \otimes T \left( |{IS,SI}\rangle \!\langle {IS,SI}| + |{SI,IS}\rangle \!\langle {SI,IS}| \right) \nonumber \\&\quad + \frac{q^2}{q^2+1} |{II,II}\rangle \!\langle {IS,IS}| +\frac{1}{q^2+1} |{SS,SS}\rangle \!\langle {IS,IS}| \nonumber \\&\quad +\frac{q^2}{q^2+1}|{II,II}\rangle \!\langle {SI,SI}| +\frac{1}{q^2+1} |{SS,SS}\rangle \!\langle {SI,SI}| \,. \end{aligned}$$

(B82)

The matrix R is stochastic. It should be understood as a correlated bit flip where, if the first and third bits are equal and the second and fourth bits are equal, they are sent to a state where that is still true. However, its marginal on either the first two bits or the last two bits is precisely P from Eq. (A53). Refer to the ith bit of the first random variable as $X_i$ and the ith bit of the second random variable as $Y_i$. Then define

$$\begin{aligned} R_\sigma ^{(t)} = \left( {\mathcal {I}}_X \otimes (Q'^{(t)}_{\sigma } Q_\sigma ^{(t)})_Y\right) \left( {\mathcal {I}}_{XY\setminus \{X_{i_t}X_{j_t},Y_{i_t}Y_{j_t}\}} \otimes R_{\{X_{i_t}X_{j_t},Y_{i_t}Y_{j_t}\}}\right) . \end{aligned}$$

(B83)

In words, what $R_\sigma ^{(t)}$ does is first generate a correlated noiseless transition among the bits involved in the gate $\{X_{i_t}X_{j_t},Y_{i_t}Y_{j_t}\}$ for both the first “noiseless” X copy and the second “noisy” Y copy, and then apply the noise transitions only to the Y copy. Since the marginal dynamics of the matrix R restricted either to the first two bits or to the last two bits is the matrix P, the marginal dynamics of $R_\sigma ^{(t)}$ are $P^{(t)}$ on the X copy and $Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}P^{(t)}$ on the Y copy. The action of $R^{(t)}_\sigma$ on an example configuration is illustrated in Fig. 5.

   An additional property of $R_\sigma ^{(t)}$ is that it preserves a certain subspace of the $2^n \times 2^n$ Hilbert space. If we define the projector $\pi _i = \left( |{II}\rangle \!\langle {II}| + |{SS}\rangle \!\langle {SS}| + |{SI}\rangle \!\langle {SI}| \right) _{\{X_iY_i\}}$, then the support of $\bigotimes _{i=0}^{n-1} \pi _i$ is not coupled with its orthogonal complement by the matrix $R_\sigma ^{(t)}$. Let us refer to this subspace as the accessible subspace. This corresponds to the fact that the noise can send $S \rightarrow I$ but not vice versa.

We define the initial state to be the correlated version of $|\Lambda \rangle$

$$\begin{aligned} |\Lambda \Lambda \rangle = \frac{1}{(q+1)^n}\sum _{\vec {\nu }} q^{n-|\vec {\nu }|}|\vec {\nu }\rangle _X \otimes |\vec {\nu }\rangle _Y, \end{aligned}$$

(B84)

which lies in the accessible subspace, so evolution by $R_\sigma ^{(t)}$ is guaranteed to remain within the accessible subspace for the entire evolution.

   In terms of $R_\sigma ^{(t)}$ we can rewrite Eq. (A54) as

$$\begin{aligned} {\mathcal {Z}}_\sigma = \langle \textbf{1},\textbf{q} |\prod _{t=1}^s R_\sigma ^{(t)}|\Lambda \Lambda \rangle , \end{aligned}$$

(B85)

where $|a,b\rangle$ is shorthand for $|a\rangle _X \otimes |b\rangle _Y$. Inner product with $\langle \textbf{1} |$ in the equation above simply marginalizes over the noiseless X copy (since the vector is normalized in the 1-norm), and in our proofs, we will use this notation often.

   Note also that since the marginal dynamics of the X copy is the noiseless dynamics, we can marginalize over the Y copy and conclude that

$$\begin{aligned} {\mathcal {Z}}_0 = \langle \textbf{q},\textbf{1} |\prod _{t=1}^s R_\sigma ^{(t)}|\Lambda \Lambda \rangle \end{aligned}$$

(B86)

for any $\sigma$.

In our proof, we find it convenient to define

$$\begin{aligned} |v^{(t)}\rangle = \prod _{t'=1}^t R_\sigma ^{(t')}|\Lambda \Lambda \rangle , \end{aligned}$$

(B87)

which represents the joint probability distribution over the $2^n$ configurations after t gates (and their associated noise channels) have been applied. Note that for circuit architectures where the circuit diagram is chosen randomly, such as the complete-graph architecture, $|v^{(t)}\rangle$ is defined as the above expression averaged over all circuit diagrams.

   Finally, let W refer to a third copy of the $2^n$-dimensional Hilbert space and define a mapping from the ith bits of X and Y to the ith bit of W, as follows:

$$\begin{aligned} \Delta _i = |S\rangle _{W_i}\langle SS |_{X_iY_i} + |S\rangle _{W_i}\langle II |_{X_iY_i} + |I\rangle _{W_i}\langle IS |_{X_iY_i} + |I\rangle _{W_i}\langle SI |_{X_iY_i} . \end{aligned}$$

(B88)

It maps a bit pair to $|S\rangle$ if they agree and $|I\rangle$ if they disagree. Let

$$\begin{aligned} \Delta = \bigotimes _{i=0}^{n-1} \Delta _i \end{aligned}$$

(B89)

be the map from $X \otimes Y$ to W. Note that $\Delta |\Lambda \Lambda \rangle = |S^n\rangle$.

1.3.2 I-destined and S-destined probability mass

Fig. 6

Schematic of the concept of I-destined and S-destined probability mass in an $n=6$ example. Each of the $2^n$ configurations corresponds to a Hamming weight between 0 and n, that is, the number of S assignments out of n. For a given configuration, the mass can be broken into an I-destined and an S-destined portion corresponding to the fraction that would end at Hamming weight 0 and Hamming weight n, respectively, if an infinite number of noiseless gates were applied. In the diagram, this corresponds to a division of the mass into the blue and red circles within each Hamming weight bucket. For each x, the ratio of I-destined to S-destined mass at Hamming weight x is always precisely $(1-q^{-2n+2x})/(q^{-2n+2x}-q^{-2n})$. A portion of probability mass that is conditioned on being I-destined or S-destined obeys effective transition dynamics (given by transition matrices $P_I^{(t)}$ and $P_S^{(t)}$, respectively) that preserve which fixed-point the portion of probability mass is destined for. The allowed transitions of these conditional noiseless dynamics are given by blue and red arrows in the diagram. The allowed transitions associated with action of a noise location are given by yellow lines: a portion of S-destined mass that experiences a $S \rightarrow I$ flip due to noise can remain S-destined, or it can become I-destined, but I-destined mass can never become S-destined. The proof decomposes the I-destined mass according to which time step it first became I-destined

We view $|v^{(t)}\rangle$ as the probability vector for the correlated stochastic process. Suppose starting at timestep $t+1$, we begin running noiseless dynamics on both copies, i.e. we apply $R_0^{(t)}$, and we continue for an infinite number of gates. Then we will get full convergence to the fixed points $|I^n\rangle \otimes |I^n\rangle$, $|S^n\rangle \otimes |S^n\rangle$ and $|S^n\rangle \otimes |I^n\rangle$. The fourth fixed point $|I^n\rangle \otimes |S^n\rangle$ is not in the accessible subspace. We can compute precisely the probability of each of these outcomes. In Ref. [8], we arrived at an expression for these probabilities by solving a certain recursion relation. Here, we need only the result of that calculation to inform how we define the diagonal matrices $L_I$ and $L_S$:

$$\begin{aligned} L_I&= \sum _{\vec {\nu }} \frac{1-q^{-2n+2|\vec {\nu }|}}{1-q^{-2n}} |{\vec {\nu }}\rangle \!\langle {\vec {\nu }}| \end{aligned}$$

(B90)

$$\begin{aligned} L_S&= \sum _{\vec {\nu }} \frac{q^{-2n+2|\vec {\nu }|}-q^{-2n}}{1-q^{-2n}} |{\vec {\nu }}\rangle \!\langle {\vec {\nu }}| \,. \end{aligned}$$

(B91)

Note that $L_I+L_S$ is the identity matrix ${\mathcal {I}}$. The coefficient of $|{\vec {\nu }}\rangle \!\langle {\vec {\nu }}|$ in $L_I$ gives the probability that a configuration that starts at $|\vec {\nu }\rangle$ ends at the $I^n$ fixed point if it undergoes completely noiseless dynamics, and the coefficient in $L_S$ gives the probability of ending at the $S^n$ fixed point [8].

Then define

$$\begin{aligned} L_{II}&= L_I \otimes {\mathcal {I}} \end{aligned}$$

(B92)

$$\begin{aligned} L_{SS}&= {\mathcal {I}} \otimes L_S \end{aligned}$$

(B93)

$$\begin{aligned} L_{SI}&= {\mathcal {I}} \otimes L_I - L_I \otimes {\mathcal {I}} \,, \end{aligned}$$

(B94)

which are the analogous matrices for the joint dynamics to end at $|I^n\rangle \otimes |I^n\rangle$, $|S^n\rangle \otimes |S^n\rangle$, and $|S^n\rangle \otimes |I^n\rangle$, respectively. The final equation can be understood as a mathematical representation of the following observation: the probability that the X copy ends at $S^n$ while the Y copy ends at $I^n$ is equal to the probability that both copies end at $I^n$ minus the probability that the X copy ends at $I^n$. Recall that if the X copy ends at $I^n$, the Y copy must also end there, as the number of S entries in the Y copy may not exceed that of the X copy.

   Now we may define

$$\begin{aligned} P^{(t)}_I&= L_I P^{(t)} L_I^{-1} \end{aligned}$$

(B95)

$$\begin{aligned} P^{(t)}_S&= L_S P^{(t)} L_S^{-1} \end{aligned}$$

(B96)

and

$$\begin{aligned} R^{(t)}_{II}&= L_{II} R_0^{(t)} L_{II}^{-1} \end{aligned}$$

(B97)

$$\begin{aligned} R^{(t)}_{SS}&= L_{SS} R_0^{(t)} L_{SS}^{-1} \end{aligned}$$

(B98)

$$\begin{aligned} R^{(t)}_{SI}&= L_{SI} R_0^{(t)} L_{SI}^{-1}\,, \end{aligned}$$

(B99)

where in each case $O^{-1}$ denotes the Moore-Penrose pseudo-inverse of O—that is, working in the basis where O is diagonal, $O^{-1}$ is formed by inverting all non-zero diagonal entries, and leaving the zero diagonal entries equal to zero. We interpret these matrices as the transition operators for probability mass that has been conditioned to end up at a certain fixed point. For example, $P^{(t)}_S$ is the transition operator for a single copy conditioned on eventually ending up at the $S^n$ fixed point. Even though the walk is generally biased toward I, it will be biased toward S when conditioned on ending at the $S^n$ fixed point. The following lemma asserts that these are indeed stochastic matrices. All lemmas stated here are proved in Appendix B.8.

Lemma 3

The matrices $P^{(t)}_I$, $P^{(t)}_S$, $R^{(t)}_{II}$, $R^{(t)}_{SS}$, $R^{(t)}_{SI}$, restricted to their support, are stochastic matrices.

   The next lemma asserts that if the $X \otimes Y$ system undergoes dynamics under $R_{SI}^{(t)}$, then the W system undergoes dynamics under $P_I^{(t)}$. This makes sense, since conditioning on X to go to $S^n$ and Y to go to $I^n$ should be equivalent to conditioning the W system to go to $I^n$.

Lemma 4

Within the accessible subspace, the following holds.

$$\begin{aligned} \Delta R^{(t)}_{SI} = P^{(t)}_I \Delta . \end{aligned}$$

(B100)

We now introduce some more notation. For any vector $|x\rangle$ on a single copy of the vector space, let

$$\begin{aligned} |x_I\rangle&= L_I |x\rangle \end{aligned}$$

(B101)

$$\begin{aligned} |x_S\rangle&= L_S |x\rangle \,, \end{aligned}$$

(B102)

and for any vector $|v\rangle$ on two copies of the vector space, let

$$\begin{aligned} |v_{II}\rangle&= L_{II} |v\rangle \end{aligned}$$

(B103)

$$\begin{aligned} |v_{SS}\rangle&= L_{SS} |v\rangle \end{aligned}$$

(B104)

$$\begin{aligned} |v_{SI}\rangle&= L_{SI} |v\rangle \,. \end{aligned}$$

(B105)

Thus, if $|x\rangle$ represents a probability distribution over the $2^n$ basis states on a single copy of the Hilbert space, then the vector $|x_I\rangle$ is the portion of $|x\rangle$ that is destined to end at the fixed point $I^n$, and $|x_S\rangle$ is the portion destined to end at $S^n$ (if all future gates are noiseless). The division of probability mass into separate I and S-destined parts is depicted schematically in Fig. 6.

   The amount of probability mass for which the noisy copy is destined for the $S^n$ fixed point cannot decay too quickly with the number of noise locations (note that if the noisy copy ends at $S^n$, the noiseless copy must also end at $S^n$). In Fig. 6, this is depicted by the fact that the only way to transition from the S-destined to an I-destined division of probability mass is due to the action of a noise location, which induces a $S\rightarrow I$ transition with probability $\sigma$.

Lemma 5

The S-destined probability mass obeys the following inequality, for any $t' \ge t$.

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(t')}\rangle \ge (1-\sigma )^{2(t'-t)}\langle \textbf{1}, \textbf{1} | v_{SS}^{(t)}\rangle . \end{aligned}$$

(B106)

Proof idea

Recall that the inner product with $\langle \textbf{1},\textbf{1} |$ gives the sum of the entries of the vector. We interpret $|v_{SS}^{(t)}\rangle$ as the probability vector of mass destined to reach the $S^n$ fixed point on both copies. Each time a noise location acts, it can affect at most a $\sigma$ fraction of the mass, so even after two noise locations act, at least a $(1-\sigma )^2$ fraction of the mass that was S-destined before will still be S-destined. $\square$

1.3.3 Decomposing the I-destined probability mass

The final piece of machinery we need is an accounting of which error leads to each piece of I-destined probability mass. To do this, for each $t \ge 1$ define

$$\begin{aligned} |v_{SI}^{(t,t)}\rangle ={}&|v_{SI}^{(t)}\rangle -({\mathcal {I}} \otimes Q'^{(t)}_{\sigma } Q_\sigma ^{(t)})R_{SI}^{(t)}|v_{SI}^{(t-1)}\rangle \end{aligned}$$

(B107)

$$\begin{aligned} ={}&\left( L_{SI} \left( {\mathcal {I}} \otimes Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}\right) -\left( {\mathcal {I}} \otimes Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}\right) L_{SI}\right) R_0^{(t)}|v^{(t-1)}\rangle \,, \end{aligned}$$

(B108)

and define the evolution rule

$$\begin{aligned} |v_{SI}^{(t'+1,t)}\rangle = Q'^{(t'+1)}_\sigma Q_\sigma ^{(t'+1)}R_{SI}^{(t'+1)}|v_{SI}^{(t',t)}\rangle . \end{aligned}$$

(B109)

The vector $|v_{SI}^{(t',t)}\rangle$ represents the probability mass that would have gone to the $S^n$ fixed point, but the noise at time step t caused it to be redirected to the $I^n$ fixed point, and we have subsequently evolved it forward to timestep $t'$.

   Importantly, we can verify from the definition that

$$\begin{aligned} \sum _{t=1}^{t'} |v_{SI}^{(t',t)}\rangle = |v_{SI}^{(t')} \rangle \,, \end{aligned}$$

(B110)

indicating that all of the mass at time step $t'$ is accounted for as having originated at some previous time step t.

Lemma 6

For all t and $t'\ge t$,

$$\begin{aligned} \langle \textbf{1},\textbf{1} | v_{SI}^{(t',t)}\rangle \le (1-(1-\sigma )^2) \langle \textbf{1},\textbf{1} | v_{SS}^{(t-1)}\rangle . \end{aligned}$$

(B111)

Proof idea

The vector $|v_{SI}^{(t,t)}\rangle$ represents the mass that satisfies two conditions: (1) it was destined for the $|S^n\rangle \otimes |S^n\rangle$ fixed point at time step $t-1$, and (2) the noise at time step t caused it to be destined for the $|S^n\rangle \otimes |I^n\rangle$ fixed point at time step t. At most $\langle \textbf{1},\textbf{1} | v_{SS}^{(t-1)}\rangle$ mass qualifies under condition (1). Among that mass, each of the two noise location can only impact a $\sigma$ fraction of the mass, so the fraction of mass that can be re-directed is at most $(1-(1-\sigma )^2)$. $\square$

1.4 Consequences of anti-concentration

In all of our rigorous proofs, we assume we have a random quantum circuit architecture that is h-regularly connected for some constant $h=O(1)$, and has anti-concentration size equal to $s_{AC}$. Recall that this means that $Z_0$ becomes twice its limiting value at $s_{AC}$. When this is the case, we have the following lemmas. All constants are dependent on q and h, but not on n or any noise parameters.

Lemma 7

Suppose the random quantum circuit architecture is regularly connected. There exist constants $\chi _1$ and $\chi _2$ such that for all $t \ge s_{AC}$

$$\begin{aligned} \langle \textbf{q},\textbf{1} | v^{(t)}\rangle \le \frac{2q^n}{q^n+1} + \eta _t, \end{aligned}$$

(B112)

where

$$\begin{aligned} \eta _t = \chi _2 \exp \left( -\frac{\chi _1}{n}(t-s_{AC})\right) . \end{aligned}$$

(B113)

Proof idea

The left-hand side is precisely $Z_0$ for a circuit with size t. The regularly connected property indicates that for any configuration not at a fixed point, there will be a gate that couples an I with an S roughly once every O(n) gates. When this happens, the difference between $Z_0$ and its infinite-size limit is reduced by a constant factor, leading to the scaling in the lemma. $\square$

Lemma 8

Suppose the random quantum circuit architecture is regularly connected. There exist constants $\chi _3$ and $\chi _4$ such that for all t

$$\begin{aligned} \langle S^n,\textbf{1} | v^{(t)}\rangle \ge \frac{1-\eta '_t}{q^n+1}, \end{aligned}$$

(B114)

where

$$\begin{aligned} \eta '_t = \chi _4 \exp \left( -\frac{\chi _3}{n}(t-s_{AC})\right) . \end{aligned}$$

(B115)

Proof idea

Anti-concentration happens because most of the probability mass makes it to one of the fixed points. This lemma states that after the anti-concentration size, most of the mass destined for the $S^n$ fixed point has already reached it. The fraction that has not yet reached is $\eta _t'$, which decays exponentially with t/n. We show that if this were not the case, then the bound in Lemma 7 could not hold. $\square$

Lemma 9

Suppose the random quantum circuit architecture is regularly connected. There exist constants $\chi _5$ and $\chi _6$ such that for any non-negative vector $|v\rangle$ that is normalized (i.e. $\langle \textbf{1},\textbf{1} | v\rangle =1$), the following holds for any $t_0$ and any $t_1\ge t_0$.

$$\begin{aligned}&\langle \textbf{q} |\Delta \prod _{t=t_0+1}^{t_1}\left( ({\mathcal {I}} \otimes Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}) R_{SI}^{(t)}\right) |v\rangle -1 \nonumber \\&\quad \le {} \left( \langle \textbf{q} |\Delta |v\rangle -1\right) \chi _6 \exp \left( -\frac{\chi _5 (t_1-t_0)}{n}\right) \,. \end{aligned}$$

(B116)

Proof idea

Recall from Lemma 4 that if $|v\rangle$ evolves by $R_{SI}^{(t)}$, then $\Delta |v\rangle$ evolves by $P_{I}^{(t)}$. The transition matrix $P_I^{(t)}$ is the matrix that conditions on sending the vector to the $I^n$ fixed point, so it is even more I-biased than the transition matrix $P^{(t)}$. Thus, each time a bit is flipped, the Hamming weight is likely to decrease, and the inner product with $\langle \textbf{q} |-\langle \textbf{1} |$ will be reduced by a constant factor. This will (usually) happen once every O(n) gates if the architecture is regularly connected. The insertion of the $Q_\sigma ^{(t)}$ operators will only make the Hamming weight smaller since they can only flip $S \rightarrow I$. $\square$

1.5 Exponential clustering of S-destined probability mass

A key step in our analysis is that the S-destined mass stays close to the $S^n$ fixed point, as long as $\sigma = O(1/n)$. In fact, the probability of deviating from the fixed point by x bit flips decays exponentially in x. Intuitively, this is because the S-destined mass is biased to move upward in Hamming weight, and when $\sigma$ is small enough, this upward pressure will be greater than the downward pressure coming from the noise itself.

   We prove this for the W system, which captures the difference between the (noiseless) X and (noisy) Y systems. We cannot directly analyze the Y system because at time step 0, the statement is definitively not true. It takes $s_{AC}$ gates for the S-destined mass in the Y system to initially converge. Meanwhile, the W system begins at the $S^n$ fixed point. This is the main reason we introduced the W system in the first place.

   Define the projector

$$\begin{aligned} \Pi _w = \sum _{\vec {\nu }: |\vec {\nu }| = w} |{\vec {\nu }}\rangle \!\langle {\vec {\nu }}| . \end{aligned}$$

(B117)

Lemma 10

There exist constants $\chi _7$, $\chi _8$, $\chi _9$, and $n_0$ such that as long as $\sigma \le \chi _7/n$ and $n \ge n_0$, the following holds for any t and any integer w with $1 \le w < n$.

$$\begin{aligned} \frac{\langle \textbf{1} |\Pi _w\Delta |v^{(t)}_{SS}\rangle }{\langle \textbf{1},\textbf{1} | v^{(t)}_{SS}\rangle }\le n \sigma \xi _{w}, \end{aligned}$$

(B118)

where

$$\begin{aligned} \xi _{w}= \chi _9(n-w) q^{-(n-w)}e^{-\chi _8 (n-w)}. \end{aligned}$$

(B119)

Proof idea

The S-destined portion of the mass within the W system starts at the $S^n$ fixed point. When noise acts at time step t, some of the mass moves to Hamming weight $n-1$ but continues to be S-destined, and some of it is “redirected” to become I-destined, which is captured in the $|v_{SI}^{(t,t)}\rangle$ vector. The total amount of redirected mass cannot be too large, as we see in Lemma 6. Moreover, the redirected mass must steadily move downward in Hamming weight (after all, it is I-destined), which we quantify with Lemma 9. This is important because for each value of the Hamming weight w, the amount of S-destined mass divided by the amount of I-destined mass at that Hamming weight is precisely $\frac{q^{-2n+2w} - q^{-2n}}{1-q^{-2n+2w}} \approx q^{-2(n-w)}$, so as the I-destined mass moves down in Hamming weight, the S-destined mass that corresponds to it decreases exponentially. After accounting for each bit of I-destined mass by summing over all $|v_{SI}^{(t',t)}\rangle$, we can prove the lemma. $\square$

1.6 Relating ${\mathcal {Z}}_\sigma$ to the amount of S-destined probability mass

The following lemma states that keeping track of the amount of S-destined mass is sufficient to get good upper and lower bounds on the quantity ${\mathcal {Z}}_\sigma$.

Lemma 11

The following lower bound always holds

$$\begin{aligned} {\mathcal {Z}}_\sigma -1 \ge \left( q^n-1\right) \langle \textbf{1},\textbf{1} | v_{SS}^{(s)}\rangle \end{aligned}$$

(B120)

Moreover, there exist constants $\chi _{10}$, $\chi _{11}$, $\chi _{12}$, $\chi _{13}$, and $n_0$ such that as long as $\sigma \le \chi _{13}/n$ and $n\ge n_0$, the following upper bound holds.

$$\begin{aligned} {\mathcal {Z}}_\sigma - 1 \le \left( q^n-1\right) \langle \textbf{1},\textbf{1} | v_{SS}^{(s)}\rangle \exp \left( 1+\chi _{10} n\sigma +\chi _{12} e^{-\frac{\chi _{11}}{n}(s-s_{AC})+4s\sigma }\right) \end{aligned}$$

(B121)

Proof idea

For each w, we know the ratio of the I-destined and S-destined mass at Hamming weight w: for each portion of S-destined probability mass, there is roughly $q^{2(n-w)}$ I-destined probability mass. This decreases with w like $q^{-2w}$. The contribution of mass at Hamming weight w to ${\mathcal {Z}}_\sigma$ increases, but at the slower rate of $q^{w}$. Thus, for a fixed amount of S-destined mass, ${\mathcal {Z}}_\sigma$ is minimized when all of it is at the $S^n$ fixed point, leading to our lower bound. On the other hand, we know that the S-destined mass is exponentially clustered near the $S^n$ fixed point (Lemma 10), so this lower bound cannot be too loose, which we leverage into an upper bound. $\square$

1.7 Bounding the S-destined mass

Now, all that remains is to compute the amount of S-destined mass. Here we show upper and lower bounds on this quantity for layered architectures and for the complete-graph architecture.

Lemma 12

Suppose the random quantum circuit architecture is regularly connected and layered. Let $d_{AC}$ be its anti-concentration depth. Then, for any d,

$$\begin{aligned} \langle \textbf{1},\textbf{1} | v_{SS}^{(dn/2)}\rangle \ge \frac{\left( 1-\frac{1-(1-\sigma (1-q^{-2}))^n}{1-q^{-2n}}\right) ^d }{q^n+1} . \end{aligned}$$

(B122)

Moreover, there exist constants $a_0$, $a_1$, $a_2$, $a_3$, and $n_0$ such that, as long as $\sigma \le a_3/n$ and $n \ge n_0$,

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(dn/2)}\rangle \le \frac{\left( 1-\frac{1-(1-\sigma (1-q^{-2}))^n}{1-q^{-2n}}\right) ^d }{q^n+1}e^{a_0\sigma ^2 dn+ a_1\sigma n d_{AC} +a_2 n\sigma \log (1/(n\sigma ))}\,, \end{aligned}$$

(B123)

where $d_{AC}$ is the anti-concentration depth.

Lemma 13

Suppose the random quantum circuit architecture is the complete-graph architecture. Let $s_{AC}$ be its anti-concentration size. Then, for any s,

$$\begin{aligned} \langle \textbf{1},\textbf{1} | v_{SS}^{(s)}\rangle \ge \frac{\left( 1-\frac{1-(1-\sigma (1-q^{-2}))^2}{1-q^{-2n}}\right) ^s }{q^n+1} . \end{aligned}$$

(B124)

Moreover, there exist constants $b_0$, $b_1$, $b_2$, $b_3$, and $n_0$ such that, as long as $\sigma \le b_3/n$ and $n \ge n_0$,

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(s)}\rangle \le \frac{\left( 1-\frac{1-(1-\sigma (1-q^{-2}))^2}{1-q^{-2n}}\right) ^s }{q^n+1}e^{b_0\sigma ^2 s + b_1\sigma s_{AC} +b_2 n\sigma \log (1/(n\sigma ))} \end{aligned}$$

(B125)

Proof idea for Lemma 12 and Lemma 13

When a portion of S-destined mass is at the $S^n$ fixed point, and noise acts to move it to Hamming weight $n-1$, we have a good understanding of what fraction remains S-destined. Specifically, there is a $\frac{q^{-2}-q^{-2n}}{1-q^{-2n}}$ chance that it re-equilibrates to $S^n$. We also know the chance that it will make the transition in the first place; the transition from $S \rightarrow I$ happens with probability precisely $\sigma$. This scenario gives the maximum amount of lost S-destined mass, and gives rise to our lower bound. However, if the portion of S-destined mass is not at the $S^n$ fixed point, then this is complicated in two ways. First, the probability of re-equilibrating back to $S^n$ is a slightly different expression, and, more importantly, the noise will not cause a transition as often, as there is a chance it acts on a bit that is already I. If the configuration has Hamming weight w and the noise acts on a random bit, the chance of a transition is $\frac{n-w}{n}\sigma$ so a smaller amount of S-destined mass is lost at each step. Luckily, we know that the S-destined mass is exponentially clustered near $w=n$ (Lemma 10), so the corrections are small, which gives rise to the upper bound.

   We utilize the layered architecture property to be able to say that every qudit is acted upon by noise after each layer, and thus, from the perspective of the amount of S-destined mass, all that matters is the Hamming weight of the configuration prior to the noise. The same is true for the complete-graph case because the gates are chosen randomly and each qudit is equally likely to participate. However, we do not believe this property is necessary for our result to be true. $\square$

1.8 Deferred proofs of lemmas

1.8.1 Proof of Lemma 3

Proof

We demonstrate this for $P^{(t)}_I$ and leave the others to be verified in a similar fashion. First of all, since $P^{(t)}$ is a stochastic matrix, its matrix elements are non-negative. Since $L_I$ and $L_I^{-1}$ are diagonal matrices with non-negative entries, $P^{(t)}_I = L_I P^{(t)} L_I^{-1}$ also has non-negative matrix elements. The support of $P_I$ is the entire vector space except for the span of $|S^n\rangle$. Consider another basis state $|\vec {\nu }\rangle$. Since gate t acts on qudits $\{i_t,j_t\}$, if $\nu _{i_t} = \nu _{j_t}$ then it is a $+1$ eigenvector of $|P^{(t)}\rangle$ and

$$\begin{aligned} \langle \textbf{1} |P^{(t)}_I|\vec {\nu }\rangle&= \sum _{\vec {\mu }} \langle \vec {\mu } | L_I P^{(t)} L_I^{-1} |\vec {\nu }\rangle \end{aligned}$$

(B126)

$$\begin{aligned}&= \sum _{\vec {\mu }} \frac{1-q^{-2n+2|\vec {\mu }|}}{1-q^{-2n+2|\vec {\nu }|}} \langle \vec {\mu } | P^{(t)} |\vec {\nu }\rangle \end{aligned}$$

(B127)

$$\begin{aligned}&=\sum _{\vec {\mu }} \frac{1-q^{-2n+2|\vec {\mu }|}}{1-q^{-2n+2|\vec {\nu }|}} \langle \vec {\mu } | \vec {\nu }\rangle = 1\,. \end{aligned}$$

(B128)

If $\nu _{i_t} \ne \nu _{j_t}$, then $P^{(t)}$ sends $|\vec {\nu }\rangle$ to a basis state with Hamming weight reduced by 1 with probability $q^2/(q^2+1)$, and to Hamming weight increased by 1 with probability $1/(q^2+1)$, so

$$\begin{aligned} \langle \textbf{1} |P^{(t)}_I|\vec {\nu }\rangle&= \sum _{\vec {\mu }} \frac{1-q^{-2n+2|\vec {\mu }|}}{1-q^{-2n+2|\vec {\nu }|}} \langle \vec {\mu } | P^{(t)} |\vec {\nu }\rangle \end{aligned}$$

(B129)

$$\begin{aligned}&=\left( \frac{q^2}{q^2+1}\frac{1-q^{-2n+2|\vec {\nu }|-2}}{1-q^{-2n+2|\vec {\nu }|}}+\frac{1}{q^2+1}\frac{1-q^{-2n+2|\vec {\nu }|+2}}{1-q^{-2n+2|\vec {\nu }|}} \right) = 1\,. \end{aligned}$$

(B130)

This demonstrates $P_I^{(t)}$ is a stochastic matrix when restricted to its support. $\square$

1.8.2 Proof of Lemma 4

Proof

We consider the action of both sides of the equation on an input state $|\vec {\nu },\vec {\mu }\rangle$. Let a and b be the number of 1 entries in $\vec {\nu }$ and $\vec {\mu }$, excluding the positions $\{i_t,j_t\}$, respectively, and let c be the number of entries on which $\vec {\nu }$ and $\vec {\mu }$ agree. Since we are restricting to the accessible subspace, we have $c=n-2-a+b$. Since $\Delta$ is a tensor product across all bits $i \in \{0,\ldots ,n-1\}$, and both $P_I^{(t)}$ and $R_{SI}^{(t)}$ modify only bits $i_t$ and $j_t$, it is sufficient to consider the transitions among just bits $i_t$ and $j_t$. First, define

$$\begin{aligned} c_0&= \frac{1-q^{-2n+2c}}{1-q^{-2n+2c+2}}\frac{q^2}{q^2+1} \end{aligned}$$

(B131)

$$\begin{aligned} c_1&= \frac{1-q^{-2n+2c+4}}{1-q^{-2n+2c+2}}\frac{1}{q^2+1} \,. \end{aligned}$$

(B132)

Let the four bits below be ordered $X_{i_t}X_{j_t},\,Y_{i_t}Y_{j_t}$. The right-hand side has the following effect, where the first arrow is application of $\Delta$ and the second is application of $P_I^{(t)}$.

$$\begin{aligned} |SS,SS\rangle&\rightarrow |SS\rangle \rightarrow |SS\rangle \\ |SS,SI\rangle&\rightarrow |SI\rangle \rightarrow c_0|II\rangle + c_1|SS\rangle \\ |SS,IS\rangle&\rightarrow |IS\rangle \rightarrow c_0|II\rangle + c_1|SS\rangle \\ |SS,II\rangle&\rightarrow |II\rangle \rightarrow |II\rangle \\ |SI,SI\rangle&\rightarrow |SS\rangle \rightarrow |SS\rangle \\ |SI,II\rangle&\rightarrow |IS\rangle \rightarrow c_0|II\rangle + c_1|SS\rangle \\ |IS,IS\rangle&\rightarrow |SS\rangle \rightarrow |SS\rangle \\ |IS,II\rangle&\rightarrow |SI\rangle \rightarrow c_0|II\rangle + c_1|SS\rangle \\ |II,II\rangle&\rightarrow |SS\rangle \rightarrow |SS\rangle \,. \end{aligned}$$

Now, we can do the same for the left-hand side. For example, consider the input state $|SS,SI\rangle$. Action by $R_{SI}^{(t)}$ sends it to

$$\begin{aligned} |SS,SI\rangle \rightarrow {}&\frac{q^{-2n+2a+4}-q^{-2n+2b}}{q^{-2n+2a+4} - q^{-2n+2b+2}}\frac{q^2}{q^2+1}|SS,II\rangle \nonumber \\&+ \frac{q^{-2n+2a+4}-q^{-2n+2b+4}}{q^{-2n+2a+4} - q^{-2n+2b+2}}\frac{1}{q^2+1}|SS,SS\rangle \end{aligned}$$

(B133)

$$\begin{aligned} ={}&c_0 |SS,II\rangle + c_1 |SS,SS\rangle \,, \end{aligned}$$

(B134)

where the last line follows by recalling the relation $c=n-2-a+b$. Action by $\Delta$ then yields the state $c_0 |II\rangle + c_1 |SS\rangle$. We can now list this calculation for each input state, where the first arrow is action by $R_{SI}^{(t)}$ and the second by $\Delta$.

$$\begin{aligned} |SS,SS\rangle \rightarrow {}&|SS,SS\rangle \rightarrow |SS\rangle \end{aligned}$$

(B135)

$$\begin{aligned} |SS,SI\rangle \rightarrow {}&c_0|SS,II\rangle + c_1|SS,SS\rangle \rightarrow c_0|II\rangle + c_1 |SS\rangle \end{aligned}$$

(B136)

$$\begin{aligned} |SS,IS\rangle \rightarrow {}&c_0|SS,II\rangle + c_1|SS,SS\rangle \rightarrow c_0|II\rangle + c_1 |SS\rangle \end{aligned}$$

(B137)

$$\begin{aligned} |SS,II\rangle \rightarrow {}&|SS,II\rangle \rightarrow |II\rangle \end{aligned}$$

(B138)

$$\begin{aligned} |SI,SI\rangle \rightarrow {}&\frac{q^{-2n+2a}-q^{-2n+2b}}{q^{-2n+2a+2}-q^{-2n+2b+2}}\frac{q^2}{q^2+1}|II,II\rangle \nonumber \\&+\frac{q^{-2n+2a+4}-q^{-2n+2b+4}}{q^{-2n+2a+2}-q^{-2n+2b+2}}\frac{1}{q^2+1}|SS,SS\rangle \end{aligned}$$

(B139)

$$\begin{aligned} \rightarrow {}&|SS\rangle \end{aligned}$$

(B140)

$$\begin{aligned} |SI,II\rangle \rightarrow {}&c_1|II,II\rangle + c_0 |SS,II\rangle \rightarrow c_0|II\rangle + c_1 |SS\rangle \end{aligned}$$

(B141)

$$\begin{aligned} |IS,IS\rangle \rightarrow {}&\frac{q^{-2n+2a}-q^{-2n+2b}}{q^{-2n+2a+2}-q^{-2n+2b+2}}\frac{q^2}{q^2+1}|II,II\rangle \nonumber \\&+\frac{q^{-2n+2a+4}-q^{-2n+2b+4}}{q^{-2n+2a+2}-q^{-2n+2b+2}}\frac{1}{q^2+1}|SS,SS\rangle \end{aligned}$$

(B142)

$$\begin{aligned} \rightarrow {}&|SS\rangle \end{aligned}$$

(B143)

$$\begin{aligned} |IS,II\rangle \rightarrow {}&c_1|II,II\rangle + c_0 |SS,II\rangle \rightarrow c_0|II\rangle + c_1 |SS\rangle \end{aligned}$$

(B144)

$$\begin{aligned} |II,II\rangle \rightarrow {}&|II,II\rangle \rightarrow |SS\rangle \,, \end{aligned}$$

(B145)

which verifies that the left-hand and right-hand sides are equal.$\square$

1.8.3 Proof of Lemma 5

Proof

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(t)}\rangle&=\langle \textbf{1}, \textbf{1} |L_{SS}R_\sigma ^{(t)}|v^{(t-1)}\rangle = \langle \textbf{1}, \textbf{1} |L_{SS}R^{(t)}_\sigma L_{SS}^{-1}|v_{SS}^{(t-1)}\rangle \end{aligned}$$

(B146)

$$\begin{aligned}&={}\sum _{\begin{array}{c} \vec {\mu }\\ \vec {\nu } \ne I^n \end{array}} \langle \textbf{1}, \textbf{1} |L_{SS} |{\textbf{1},\vec {\mu }}\rangle \!\langle {\textbf{1},\vec {\mu }}| R^{(t)}_\sigma |{\textbf{1},\vec {\nu }}\rangle \!\langle {\textbf{1},\vec {\nu }}| L_{SS}^{-1}|v_{SS}^{(t-1)}\rangle \end{aligned}$$

(B147)

$$\begin{aligned}&={} \sum _{\begin{array}{c} \vec {\mu }\\ \vec {\nu } \ne I^n \end{array}} \frac{q^{-2n+2|\vec {\mu }|}-q^{-2n}}{q^{-2n+2|\vec {\nu }|}-q^{-2n}} \langle \textbf{1},\vec {\mu } |R^{(t)}_\sigma |\textbf{1},\vec {\nu }\rangle \langle \textbf{1},\vec {\nu } | v_{SS}^{(t-1)}\rangle \end{aligned}$$

(B148)

$$\begin{aligned}&={} \sum _{\begin{array}{c} \vec {\mu }\\ \vec {\nu } \ne I^n \end{array}} \frac{q^{-2n+2|\vec {\mu }|}-q^{-2n}}{q^{-2n+2|\vec {\nu }|}-q^{-2n}} \langle \vec {\mu } |Q'^{(t)}_\sigma Q^{(t)}_\sigma P^{(t)} |\vec {\nu }\rangle \langle \textbf{1},\vec {\nu } | v_{SS}^{(t-1)}\rangle \end{aligned}$$

(B149)

$$\begin{aligned}&={} \sum _{\begin{array}{c} \vec {\mu }\\ \vec {\nu }, \vec {\zeta } \ne I^n \end{array}} E_{\vec {\mu }\vec {\zeta }} G_{\vec {\zeta }\vec {\nu }} \langle \textbf{1},\vec {\nu } | v_{SS}^{(t-1)}\rangle \end{aligned}$$

(B150)

where

$$\begin{aligned} E_{\vec {\mu }\vec {\zeta }}&= \frac{q^{-2n+2|\vec {\mu }|}-q^{-2n}}{q^{-2n+2|\vec {\zeta }|}-q^{-2n}} \langle \vec {\mu } |Q'^{(t)}_\sigma Q^{(t)}_\sigma |\vec {\zeta }\rangle \end{aligned}$$

(B151)

$$\begin{aligned} G_{\vec {\zeta }\vec {\nu }}&= \frac{q^{-2n+2|\vec {\zeta }|}-q^{-2n}}{q^{-2n+2|\vec {\nu }|}-q^{-2n}}\langle \vec {\zeta } |P^{(t)} |\vec {\nu }\rangle = \langle \vec {\zeta } |P_S^{(t)} |\vec {\nu }\rangle \end{aligned}$$

(B152)

However, note that $E_{\vec {\zeta }\vec {\zeta }} \ge (1-\sigma )^2$ (with equality when $\zeta _{i_t} = \zeta _{j_t} = 1$), and all $E_{\vec {\mu }\vec {\zeta }}$ are non-negative. Moreover, note that

$$\begin{aligned} \sum _{\vec {\zeta }} G_{\vec {\zeta }\vec {\nu }} = 1, \end{aligned}$$

(B153)

owing to the fact that $P_S^{(t)}$ is stochastic. Thus $\langle \textbf{1}, \textbf{1} | v_{SS}^{(t)}\rangle \ge (1-\sigma )^2 \langle \textbf{1}, \textbf{1} | v_{SS}^{(t-1)}\rangle$, and by recursion, the statement holds. $\square$

1.8.4 Proof of Lemma 6

Proof

Recall that $L_{SI} = {\mathcal {I}} \otimes L_I - L_I \otimes {\mathcal {I}}$, but the second term commutes with ${\mathcal {I}} \otimes Q'^{(t)}_\sigma Q_\sigma ^{(t)}$, thus we may ignore it in the following calculation.

$$\begin{aligned} \langle \textbf{1},\textbf{1} | v_{SI}^{(t,t)}\rangle&= \sum _{\vec {\mu },\vec {\nu }} \langle \vec {\mu } | L_IQ'^{(t)}_{\sigma } Q_\sigma ^{(t)}-Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}L_I|\vec {\nu }\rangle \langle \textbf{1},\vec {\nu } |R_0^{(t)}|v^{(t-1)}\rangle \end{aligned}$$

(B154)

$$\begin{aligned}&= \sum _{\vec {\mu },\vec {\nu }}\frac{q^{-2n+2|\vec {\nu }|}-q^{-2n+2|\vec {\mu }|}}{1-q^{-2n}} \langle \vec {\mu } | Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}|\vec {\nu }\rangle \langle \textbf{1},\vec {\nu } |R_0^{(t)}|v^{(t-1)}\rangle \end{aligned}$$

(B155)

If $\vec {\mu } = \vec {\nu }$ the factor gives 0. For each $\vec {\nu }$ there are at most three possible $\vec {\mu } \ne \vec {\nu }$ for which the matrix element $\langle \vec {\mu } | Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}|\vec {\nu }\rangle \ne 0$, corresponding to a single error on either qudit or an error on both at once. In those cases, the matrix element is $\sigma (1-\sigma )$ (for single error) or $\sigma ^2$ (for double error). The double error is only possible if $|\vec {\nu }| \ge 2$, but note that we may assume $|\vec {\nu }| \ne 1$ since action by $R_0^{(t)}$ will leave the two bits it acts on equal, and cannot lead to a configuration with Hamming weight 1. We have

$$\begin{aligned}&\sum _{\vec {\mu }}\frac{q^{-2n+2|\vec {\nu }|}-q^{-2n+2|\vec {\mu }|}}{1-q^{-2n}} \langle \vec {\mu } | Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}|\vec {\nu }\rangle \nonumber \\&\quad \le {} 2\sigma (1-\sigma )\frac{q^{-2n+2|\vec {\nu }|}-q^{-2n+2|\vec {\nu }|-2}}{1-q^{-2n}}+\sigma ^2\frac{q^{-2n+2|\vec {\nu }|}-q^{-2n+2|\vec {\nu }|-4}}{1-q^{-2n}} \end{aligned}$$

(B156)

$$\begin{aligned}&\quad ={} \left( \frac{q^{-2n+2|\vec {\nu }|}-q^{-2n}}{1-q^{-2n}}\right) \frac{2\sigma (1-\sigma )(1-q^{-2}) + \sigma ^2(1-q^{-4})}{1-q^{-2|\vec {\nu }|}} \end{aligned}$$

(B157)

$$\begin{aligned}&\quad \le {} \left( \frac{q^{-2n+2|\vec {\nu }|}-q^{-2n}}{1-q^{-2n}}\right) \left( 2\sigma -\sigma ^2\right) \,. \end{aligned}$$

(B158)

This lets us say

$$\begin{aligned} \langle \textbf{1},\textbf{1} | v_{SI}^{(t,t)}\rangle&\le \sum _{\vec {\nu }}\left( \frac{q^{-2n+2|\vec {\nu }|}-q^{-2n}}{1-q^{-2n}}\right) \left( 2\sigma -\sigma ^2\right) \langle \textbf{1},\vec {\nu } |R_0^{(t)}|v^{(t-1)}\rangle \end{aligned}$$

(B159)

$$\begin{aligned}&=\sum _{\vec {\nu }}\left( 2\sigma -\sigma ^2\right) \langle \textbf{1},\vec {\nu } |L_{SS}R_0^{(t)}|v^{(t-1)}\rangle \end{aligned}$$

(B160)

$$\begin{aligned}&=\sum _{\vec {\nu }}\left( 2\sigma -\sigma ^2\right) \langle \textbf{1},\vec {\nu } |R_{SS}^{(t)}L_{SS}|v^{(t-1)}\rangle \end{aligned}$$

(B161)

$$\begin{aligned}&=\left( 2\sigma -\sigma ^2\right) \sum _{\vec {\nu }}\langle \textbf{1},\vec {\nu } |R_{SS}^{(t)}|v_{SS}^{(t-1)}\rangle \end{aligned}$$

(B162)

$$\begin{aligned}&= (1-(1-\sigma )^2) \langle \textbf{1},\textbf{1} | v_{SS}^{(t-1)}\rangle \,, \end{aligned}$$

(B163)

where the last equality follows because $R_{SS}$ is stochastic.

   The fact that this is also true for $|v^{(t',t)}\rangle$ with $t' >t$ follows from the fact that $|v^{(t',t)}\rangle$ is related to $|v^{(t,t)}\rangle$ by a sequence of stochastic matrices, which preserves the left-hand side of the lemma statement. $\square$

1.8.5 Proof of Lemma 7

Proof

This proof is similar to the proof of the general upper bound on the collision probability in Ref. [8]. Define $Z^{(t')} = \langle \textbf{q},\textbf{1} | v^{(t')}\rangle$. If the anti-concentration size is $s_{AC}$, this means that

$$\begin{aligned} Z^{(s_{AC})} \le 2q^n Z_H = \frac{4q^n}{q^n+1}. \end{aligned}$$

(B164)

where $Z_H=2/(q^n+1)$ is the limiting value of the collision probability studied in Ref. [8]. Note that $Z^{(t')}$ is monotonically non-increasing with $t'$ (i.e., collision probability only decreases as more gates are applied). Recall that for architectures where the circuit diagram is random, $|v^{(t')}\rangle$ represents an average over choice of circuit diagram. The h-regularly connected property says that, no matter what the circuit diagram has looked like up to time step $t'$, given any partition of the qudits into two parts, there is at least a 1/2 probability that the next hn gates in the circuit diagram will include at least one gate that couples qudits from opposite parts. Conditioned on coupling the two parts, the portion of the collision probability associated with configurations not already at a fixed point will decrease by a factor $2q/(q^2+1)$, as was seen in the general upper bound on the collision probability in Ref. [8]. Thus for all $t'$,

$$\begin{aligned} Z^{(t'+rn)}-\frac{2q^n}{q^n+1}&\le \left( \frac{1}{2} + \frac{1}{2}\frac{2q}{q^2+1}\right) \left( Z^{(t')}-\frac{2q^n}{q^n+1}\right) \end{aligned}$$

(B165)

$$\begin{aligned}&=\frac{(q+1)^2}{2(q^2+1)}\left( Z^{(t')} -\frac{2q^n}{q^n+1}\right) \,. \end{aligned}$$

(B166)

Applying the above recursively, we have

$$\begin{aligned} Z^{(s_{AC}+zhn)} -\frac{2q^n}{q^n+1} \le \left( \frac{(q+1)^2}{2(q^2+1)}\right) ^z \frac{2q^n}{q^n+1} \le 2\left( \frac{(q+1)^2}{2(q^2+1)}\right) ^z. \end{aligned}$$

(B167)

Now we ensure something similar holds for every value of t and not just $t=s_{AC} +zhn$ for integers z. Let $t_0$ be the maximum integer for which $t_0 \le t$, and $t_0=s_{AC}+z_0hn$ for some integer $z_0$. So $t-t_0 \le hn$ and $z_0 \ge (t-s_{AC})/(hn)-1$. Moreover, by monotonicity, we have $Z^{(t)} \le Z^{(t_0)}$. Together, this implies

$$\begin{aligned} Z^{(t)}&\le \frac{2q^n}{q^n+1} + 2\left( \frac{(q+1)^2}{2(q^2+1)}\right) ^{z_0} ={} \frac{2q^n}{q^n+1} + 2\left( \frac{(q+1)^2}{2(q^2+1)}\right) ^{\frac{t-s_{AC}}{hn}-1} \end{aligned}$$

(B168)

$$\begin{aligned}&= \frac{2q^n}{q^n+1} + \chi _2 e^{-\chi _1 (t-s_{AC})/n}\,, \end{aligned}$$

(B169)

where $\chi _2 = 4(q^2+1)/(q+1)^2$ and $\chi _1 = \frac{1}{h}\log (2(q^2+1)/(q+1)^2)$. $\square$

1.8.6 Proof of Lemma 8

Proof

We have

$$\begin{aligned} \frac{\langle \textbf{q},\textbf{1} | v^{(t)}\rangle -1}{q^n-1} ={}&\sum _{\vec {\nu }}\frac{q^{|\vec {\nu }|}-1}{q^n-1} \langle \vec {\nu },\textbf{1} | v^{(t)}\rangle \end{aligned}$$

(B170)

$$\begin{aligned} ={}&\langle S^n,\textbf{1} | v^{(t)}\rangle +\sum _{\vec {\nu } \ne I^n,S^n} \frac{q^{|\vec {\nu }|}-1}{q^n-1} \langle \vec {\nu },\textbf{1} | v^{(t)}\rangle \end{aligned}$$

(B171)

$$\begin{aligned} ={}&\langle S^n,\textbf{1} | v^{(t)}\rangle +\sum _{\vec {\nu } \ne I^n,S^n} \frac{q^{|\vec {\nu }|}-1}{q^n-1} \langle \vec {\nu },\textbf{1} |(L_S^{-1}L_S \otimes {\mathcal {I}})|v^{(t)}\rangle \end{aligned}$$

(B172)

$$\begin{aligned} ={}&\langle S^n,\textbf{1} | v^{(t)}\rangle +\sum _{\vec {\nu } \ne I^n,S^n}\frac{\left( 1-q^{-2n}\right) \left( q^{|\vec {\nu }|}-1\right) }{(q^{-2n+2|\vec {\nu }|} - q^{-2n})(q^n-1)} \langle \vec {\nu },\textbf{1} |L_S \otimes {\mathcal {I}}|v^{(t)}\rangle \end{aligned}$$

(B173)

$$\begin{aligned} \ge {}&\langle S^n,\textbf{1} | v^{(t)}\rangle +\frac{\left( 1-q^{-2n}\right) \left( q^{n-1}-1\right) }{(q^{-2} - q^{-2n})(q^n-1)}\sum _{\vec {\nu } \ne I^n,S^n} \langle \vec {\nu },\textbf{1} |L_S \otimes {\mathcal {I}}|v^{(t)}\rangle \end{aligned}$$

(B174)

$$\begin{aligned} ={}&\langle S^n,\textbf{1} | v^{(t)}\rangle +\frac{q\left( 1+q^{-n}\right) }{1 + q^{-n+1}}\sum _{\vec {\nu } \ne I^n,S^n} \langle \vec {\nu },\textbf{1} |L_S \otimes {\mathcal {I}}|v^{(t)}\rangle \end{aligned}$$

(B175)

$$\begin{aligned} ={}&-\left( \frac{q\left( 1+q^{-n}\right) }{1 + q^{-n+1}}-1\right) \langle S^n,\textbf{1} | v^{(t)}\rangle \nonumber \\&+\frac{q\left( 1+q^{-n}\right) }{1 + q^{-n+1}}\sum _{\vec {\nu } \ne I^n} \langle \vec {\nu },\textbf{1} |L_S \otimes {\mathcal {I}}|v^{(t)}\rangle \end{aligned}$$

(B176)

$$\begin{aligned} ={}&-\frac{q-1}{1+q^{-n+1}}\langle S^n,\textbf{1} | v^{(t)}\rangle +\frac{q\left( 1+q^{-n}\right) }{1 + q^{-n+1}}\langle \textbf{1},\textbf{1} |L_S \otimes {\mathcal {I}}|v^{(t)}\rangle \end{aligned}$$

(B177)

$$\begin{aligned} ={}&-\frac{q-1}{1+q^{-n+1}}\langle S^n,\textbf{1} | v^{(t)}\rangle +\frac{q\left( 1+q^{-n}\right) }{1 + q^{-n+1}}\frac{1}{q^n+1}\,, \end{aligned}$$

(B178)

where the last line follows because the total amount of S-destined mass for the noiseless copy is exactly $1/(q^n+1)$. From Lemma 7, we have

$$\begin{aligned} \frac{\langle \textbf{q},\textbf{1} | v^{(t)}\rangle -1}{q^n-1}&\le \frac{1}{q^n+1} + \frac{\eta _t}{q^n-1}\,. \end{aligned}$$

(B179)

Combining the above, we have

$$\begin{aligned} \langle S^n,\textbf{1} | v^{(t)}\rangle \frac{q-1}{1+q^{-n+1}} \ge \frac{1}{q^n+1}\left( \frac{q\left( 1+q^{-n}\right) }{1 + q^{-n+1}}-1\right) - \frac{\eta _t}{q^n-1}\,, \end{aligned}$$

(B180)

and hence

$$\begin{aligned} \langle S^n,\textbf{1} | v^{(t)}\rangle \ge \frac{1-\eta '_t}{q^n+1}\,, \end{aligned}$$

(B181)

where

$$\begin{aligned} \eta '_t = \eta _t\frac{(q^n+1)(1+q^{-n+1})}{(q-1)(q^n-1)} \le 6\eta _t = 6\chi _2e^{-\frac{\chi _1}{n}(t-s_{AC})}. \end{aligned}$$

(B182)

The inequality above is true for all $n \ge 1$ and $q \ge 2$. We choose $\chi _4 = 6\chi _2$ and $\chi _3 = \chi _1$, and the lemma is proved. $\square$

1.8.7 Proof of Lemma 9

Proof

The gate at time step t acts on bits $i_{t}$ and $j_t$. Suppose for some configuration $\vec {\nu }$ these bits disagree, i.e. $\nu _{i_t} \ne \nu _{j_t}$. Consider a state $|\vec {\eta },\vec {\eta }'\rangle$ for which $\Delta |\vec {\eta },\vec {\eta }'\rangle = |\vec {\nu }\rangle$. Then consider the quantity

$$\begin{aligned} \langle \textbf{q} |\Delta R_{SI}^{(t)}|\vec {\eta },\vec {\eta }'\rangle -1&= \langle \textbf{q} |P_I^{(t)}\Delta |\vec {\eta },\vec {\eta }'\rangle -1 = \langle \textbf{q} |P_I^{(t)}|\vec {\nu }\rangle -1 \end{aligned}$$

(B183)

$$\begin{aligned}&= \sum _{\vec {\mu }} (q^{|\vec {\mu }|}-1)\langle \vec {\mu } | L_I P^{(t)} L_I^{-1}|\vec {\nu }\rangle \end{aligned}$$

(B184)

$$\begin{aligned}&=\sum _{\vec {\mu }}\frac{(q^{|\vec {\mu }|}-1)(1-q^{-2n+2|\vec {\mu }|})}{1-q^{-2n+2|\vec {\nu }|}} \langle \vec {\mu } |P^{(t)}|\vec {\nu }\rangle \,. \end{aligned}$$

(B185)

The action of $P^{(t)}$ on $|\vec {\nu }\rangle$ will force a bit flip, so there are only two possible $\vec {\mu }$ that lead to a non-zero contribution, one for which $|\vec {\mu }|=|\vec {\nu }|+1$ and one for which $|\vec {\mu }|=|\vec {\nu }|-1$. The matrix element (probability) of the former is $1/(q^2+1)$ and the matrix element for the latter is $q^2/(q^2+1)$. Thus, we have

$$\begin{aligned} \langle \textbf{q} |P_I^{(t)}|\vec {\nu }\rangle -1&= \frac{q^2(q^{|\vec {\nu }|-1}-1)(1-q^{-2n+2|\vec {\nu }|-2})}{(q^2+1)(1-q^{-2n+2|\vec {\nu }|})} + \frac{(q^{|\vec {\nu }|+1}-1)(1-q^{-2n+2|\vec {\nu }|+2})}{(q^2+1)(1-q^{-2n+2|\vec {\nu }|})} \end{aligned}$$

(B186)

$$\begin{aligned}&=\frac{2q}{q^2+1}\frac{q^{|\vec {\nu }|}-\frac{q+q^{-1}}{2} - q^{-2n+2|\vec {\nu }|}\left( q^{|\vec {\nu }|}\frac{q^2+q^{-2}}{2}-\frac{q+q^{-1}}{2}\right) }{1-q^{-2n+2|\vec {\nu }|}} \end{aligned}$$

(B187)

$$\begin{aligned}&\le \frac{2q}{q^2+1}(q^{|\vec {\nu }|}-1) = \frac{2q}{q^2+1} \left( \langle \textbf{q} | \vec {\nu }\rangle -1\right) \,. \end{aligned}$$

(B188)

The above is true for all $\vec {\nu }$, and demonstrates that each time disagreeing bits are coupled, the total contribution under inner product with $(\langle \textbf{q} |-\langle \textbf{1} |)\Delta$ decreases by a constant factor.

   Now consider the sequence $\prod _{t=t_0+1}^{t_1}\left( {\mathcal {I}} \otimes Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}\right) R_{SI}^{(t)}$ acting on $|\vec {\eta },\vec {\eta }'\rangle$. Since the architecture is h-regularly connected, for any t there is at least a 1/2 chance that there will be some pair $(i_{t'},j_{t'})$ with $t < t' \le t+hn$ for which $\nu _{i_{t'}} \ne \nu _{j_{t'}}$ (assuming $\vec {\nu }$ is not a fixed point). The first time this happens, it will lead to a decrease in inner product with $(\langle \textbf{q} |-\langle \textbf{1} |)\Delta$ by the factor $2q/(q^2+1)$. The only way this would not happen is if one of the bits $\nu _{i_{t'}}$ or $\nu _{j_{t'}}$ was flipped already by action by one of the operators $Q^{(t'')}$. However, since the $Q^{(t)}_\sigma$ operators act only on the noisy Y copy, they can only flip a bit of $\vec {\eta }'$ from a 1 to a 0, which would also induce a bit flip in $\vec {\nu }$ from a 1 to a 0. In this case, the Hamming weight decreases by 1 and the inner product with $(\langle \textbf{q} |-\langle \textbf{1} |)\Delta$ would decrease by a factor of $\frac{q^{|\vec {\nu }|-1}-1}{q^{|\vec {\nu }|}-1}$ which is less than $2q/(q^2+1)$.

   Thus, if $z_0$ is the largest integer such that $t_0 + z_0 hn \le t_1$, then

$$\begin{aligned} \langle \textbf{q} |\Delta \prod _{t=t_0+1}^{t_1}\left( ({\mathcal {I}} \otimes Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}) R_{SI}^{(t)}\right) |v\rangle -1 \le {}&\left( \frac{1}{2} + \frac{1}{2}\frac{2q}{q^2+1}\right) ^{z_0}\left( \langle \textbf{q} |\Delta |v\rangle -1\right) \end{aligned}$$

(B189)

$$\begin{aligned} \le {}&\left( \frac{1}{2} + \frac{1}{2}\frac{2q}{q^2+1}\right) ^{\frac{t_1-t_0}{hn}-1}\left( \langle \textbf{q} |\Delta |v\rangle -1\right) \end{aligned}$$

(B190)

$$\begin{aligned} ={}&\chi _6\exp \left( -\frac{\chi _5 (t_1-t_0)}{n}\right) \left( \langle \textbf{q} |\Delta |v\rangle -1\right) \end{aligned}$$

(B191)

for appropriate choice of $\chi _5$ and $\chi _6$. $\square$

1.8.8 Proof of Lemma 10

Proof

When probability mass is redirected from S-destined at time step $t-1$ to I-destined at time step $t'$, it may begin with Hamming weight as large as $n-1$. But since it is I-destined, it will quickly move down in Hamming weight. We wish to quantify this phenomenon. First of all,

$$\begin{aligned} \langle \textbf{1} |\Pi _{ w}\Delta |v_{SI}^{(t,t')}\rangle&= \sum _{\vec {\mu }:|\vec {\mu }| = w} \langle \vec {\mu } |\Delta |v_{SI}^{(t,t')}\rangle = \frac{\sum _{\vec {\mu }:|\vec {\mu }| = w}(q^{|\vec {\mu }|}-1) \langle \vec {\mu } |\Delta |v_{SI}^{(t,t')}\rangle }{q^w-1} \end{aligned}$$

(B192)

$$\begin{aligned}&\le \frac{\langle \textbf{q} |\Delta |v_{SI}^{(t,t')}\rangle -\langle \textbf{1} | v_{SI}^{(t,t')}\rangle }{q^w-1}\,. \end{aligned}$$

(B193)

Now, note that $|v_{SI}^{(t,t')}\rangle = \prod _{t''=t'+1}^{t}\left( ({\mathcal {I}} \otimes Q'^{(t'')}_\sigma Q_\sigma ^{(t'')}) R_{SI}^{(t'')}\right) |v_{SI}^{(t',t')}\rangle$, so we can invoke Lemma 9.

$$\begin{aligned} \langle \textbf{1} |\Pi _{w}\Delta |v_{SI}^{(t,t')}\rangle&\le \frac{\langle \textbf{q} |\Delta |v_{SI}^{(t',t')}\rangle -\langle \textbf{1} | v_{SI}^{(t,t')}\rangle }{q^w-1}\chi _6 \exp \left( -\frac{\chi _5 (t-t')}{n}\right) \end{aligned}$$

(B194)

$$\begin{aligned}&\le \frac{q^{n}-1}{q^w-1}\langle \textbf{1},\textbf{1} | v_{SI}^{(t',t')}\rangle \chi _6 \exp \left( -\frac{\chi _5 (t-t')}{n}\right) \,, \end{aligned}$$

(B195)

where the second line follows because $q^n$ is the maximum entry in $\langle \textbf{q} |$, and the quantity $\langle \textbf{1} | v_{SI}^{(t,t')}\rangle$ does not change as t increases (it evolves by stochastic transformations).

We now invoke Lemma 6 (in the first line) and Lemma 5 (in the second line) to say

$$\begin{aligned}&\langle \textbf{1} |\Pi _{w}\Delta |v_{SI}^{(t,t')}\rangle \le {} \frac{q^{n}-1}{q^w-1}(2\sigma -\sigma ^2)\langle \textbf{1},\textbf{1} | v_{SS}^{(t'-1)}\rangle \chi _6 e^{-\frac{\chi _5 (t-t')}{n}} \end{aligned}$$

(B196)

$$\begin{aligned}&\quad \le {} \frac{q^{n}-1}{q^w-1}(2\sigma -\sigma ^2)(1-\sigma )^{-2(t-t'+1)}\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \chi _6 e^{-\frac{\chi _5 (t-t')}{n}} \end{aligned}$$

(B197)

$$\begin{aligned}&\quad \le {} \sigma (4\chi _6 q^{n-w}) \exp \left( -\frac{\chi _5 (t-t')}{n}+ 2(t-t'+1)\log \left( \frac{1}{1-\sigma }\right) \right) \langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \,, \end{aligned}$$

(B198)

where the extra factor of 2 comes from a very crude bound $(q^n-1)/(q^w-1) \le 2q^{n-w}$. As long as $\chi _5/n$ is greater than $2\log (1/(1-\sigma ))$, the above is exponentially decaying in t. This will be the case whenever $\sigma \le 1-\exp (-\chi _5/2n))$. There is an $n_0$ and $\chi _7$ such that $\sigma \le \chi _7/n$ whenever $n \ge n_0$ is a weaker condition. Alternatively, we could make a simpler bound by invoking Lemma 6 and Lemma 5, but not Lemma 9.

$$\begin{aligned} \langle \textbf{1} |\Pi _{w}\Delta |v_{SI}^{(t,t')}\rangle&\le \langle \textbf{1},\textbf{1} | v_{SI}^{(t,t')}\rangle \le 2\sigma \langle \textbf{1},\textbf{1} | v_{SS}^{(t'-1)}\rangle \end{aligned}$$

(B199)

$$\begin{aligned}&\le 2\sigma (1-\sigma )^{-2(t-t'+1)} \langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \end{aligned}$$

(B200)

Both Eq. (B198) and Eq. (B200) will be useful.

Now, we connect $|v^{(t)}_{SS}\rangle$ to $|v_{SI}^{(t,t')}\rangle$. First we note

$$\begin{aligned} \langle \textbf{1} |\Pi _{w}\Delta |v^{(t)}_{SS}\rangle ={}&\langle \textbf{1} |\Pi _{w} \Delta L_{SS}|v^{(t)}\rangle ={}\sum _{\vec {\mu },\vec {\nu }} \langle \textbf{1} | \Pi _{w} \Delta |{\vec {\mu },\vec {\nu }}\rangle \!\langle {\vec {\mu },\vec {\nu }}| L_{SS}|v^{(t)}\rangle \end{aligned}$$

(B201)

$$\begin{aligned} ={}&\sum _{\begin{array}{c} \vec {\mu },\vec {\nu } \\ |\vec {\mu }| = |\vec {\nu }| +n-w \end{array}}\langle \vec {\mu },\vec {\nu } |L_{SS}|v^{(t)}\rangle ={} \sum _{\begin{array}{c} \vec {\mu },\vec {\nu } \\ |\vec {\mu }| = |\vec {\nu }|+n-w \end{array}}\frac{q^{-2n+2|\vec {\nu }|}-q^{-2n}}{1-q^{-2n}}\langle \vec {\mu },\vec {\nu } | v^{(t)}\rangle \end{aligned}$$

(B202)

$$\begin{aligned} ={}&\sum _{\begin{array}{c} \vec {\mu },\vec {\nu } \\ |\vec {\mu }| = |\vec {\nu }|+n-w \end{array}}\frac{q^{2|\vec {\nu }|}-1}{q^{2|\vec {\mu }|}-q^{2|\vec {\nu }|}}\frac{q^{-2n+2|\vec {\mu }|}-q^{-2n+2|\vec {\nu }|}}{1-q^{-2n}}\langle \vec {\mu },\vec {\nu } | v^{(t)}\rangle \end{aligned}$$

(B203)

$$\begin{aligned} ={}&\sum _{\begin{array}{c} \vec {\mu },\vec {\nu } \\ |\vec {\mu }| = |\vec {\nu }|+n-w \end{array}}q^{-2(n-w)}\frac{1-q^{-2|\vec {\nu }|}}{1-q^{-2(n-w)}}\langle \vec {\mu },\vec {\nu } |L_{SI}|v^{(t)}\rangle \end{aligned}$$

(B204)

$$\begin{aligned} \le {}&\frac{q^{-2(n-w)}}{1-q^{-2}}\sum _{\begin{array}{c} \vec {\mu },\vec {\nu } \\ |\vec {\mu }| = |\vec {\nu }|+n-w \end{array}}\langle \vec {\mu },\vec {\nu } | v_{SI}^{(t)}\rangle = \frac{q^{-2(n-w)}}{1-q^{-2}}\langle \textbf{1} |\Pi _w \Delta |v_{SI}^{(t)}\rangle \,. \end{aligned}$$

(B205)

This allows us to use Eq. (B110) and assert

$$\begin{aligned} \langle \textbf{1} |\Pi _w\Delta |v^{(t)}_{SS}\rangle = \frac{q^{-2(n-w)}}{1-q^{-2}}\sum _{t' = 1}^{t}\langle \textbf{1} |\Pi _w \Delta |v_{SI}^{(t,t')}\rangle . \end{aligned}$$

(B206)

Let $t_w = t-\lceil n(n-w)\log (q)/\chi _5 \rceil$. For $t' > t_w$, we will bound $|v_{SI}^{(t,t')}\rangle$ with Eq. (B200), and for $t' \le t_w$, we will use Eq. (B198). Let us examine these sums separately. For the $t' > t_w$ portion, we make the substitution $a=t'-t_w-1$, and we have

$$\begin{aligned} \sum _{t'=t_w+1}^{t}\langle \textbf{1} |\Pi _{w}\Delta |v_{SI}^{(t,t')}\rangle \le {}&\sum _{t'=t_w+1}^{t} 2\sigma (1-\sigma )^{-2(t-t'+1)} \langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \end{aligned}$$

(B207)

$$\begin{aligned} ={}&\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle 2\sigma (1-\sigma )^{-2(t-t_w)}\sum _{a=0}^{t-t_w-1} (1-\sigma )^{2a} \end{aligned}$$

(B208)

$$\begin{aligned} ={}&\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle 2\sigma (1-\sigma )^{-2(t-t_w)}\frac{1-(1-\sigma )^{2(t-t_w-1)}}{2\sigma -\sigma ^2} \end{aligned}$$

(B209)

$$\begin{aligned} \le {}&\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle (1-\sigma )^{-2(t-t_w)}\left( 4\sigma (t-t_w)\right) \end{aligned}$$

(B210)

$$\begin{aligned} \le {}&\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle (1-\sigma )^{-2\lceil n(n-w)\log (q)/\chi _5 \rceil }\nonumber \\&\left( 4\sigma \lceil n(n-w)\log (q)/\chi _5 \rceil \right) \end{aligned}$$

(B211)

$$\begin{aligned} \le {}&\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle q^{-2n(n-w)\log (1-\sigma )/\chi _5}\chi _5'n\sigma (n-w)\, \end{aligned}$$

(B212)

for some constant $\chi _5'$ slightly larger than $4\log (q)/\chi _5$ to account for dropping the ceiling in the last line. Note that in the third-to-last line, the extra factor of 2 comes from the bound $2\sigma /(2\sigma - \sigma ^2) \le 2$.

   For the $t \le t_w$ portion, we use the substitution $a = t_w-t'$ and find (assuming $\chi _5/n \ge 2\log (1/(1-\sigma ))$)

$$\begin{aligned} \sum _{t'=1}^{t_w}\langle \textbf{1} |\Pi _{w}\Delta |v_{SI}^{(t,t')}\rangle \le {}&\sum _{t'=1}^{t_w} \sigma (4\chi _6 q^{n-w}) e^{-\frac{\chi _5 (t-t')}{n}+ 2(t-t'+1)\log \left( \frac{1}{1-\sigma }\right) }\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \end{aligned}$$

(B213)

$$\begin{aligned} ={}&\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \sigma (4\chi _6 q^{n-w})\sum _{a=0}^{t_w-1}e^{-\frac{\chi _5 (t-t_w+a)}{n}+ 2(t-t_w+a+1)\log \left( \frac{1}{1-\sigma }\right) } \end{aligned}$$

(B214)

$$\begin{aligned} \le {}&\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \sigma (4\chi _6 q^{n-w})\sum _{a=0}^{\infty }e^{-\frac{\chi _5 (t-t_w+a)}{n}+ 2(t-t_w+a+1)\log \left( \frac{1}{1-\sigma }\right) } \end{aligned}$$

(B215)

$$\begin{aligned} ={}&\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \sigma (4\chi _6 q^{n-w})\nonumber \\&\frac{\exp \left( -\lceil n(n-w)\log (q)/\chi _5 \rceil (\frac{\chi _5}{n}+2\log (1-\sigma ))\right) }{ (1-e^{-\chi _5/n-2\log (1-\sigma )})(1-\sigma )^2} \end{aligned}$$

(B216)

$$\begin{aligned} \le {}&\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \sigma (4\chi _6)\nonumber \\&\frac{\exp \left( -2\lceil n(n-w)\log (q)/\chi _5 \rceil \log (1-\sigma )\right) }{ (1-e^{-\chi _5/n-2\log (1-\sigma )})(1-\sigma )^2} \end{aligned}$$

(B217)

$$\begin{aligned} \le {}&\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \sigma \chi _6'q^{-2n(n-w)\log (1-\sigma )/\chi _5} \end{aligned}$$

(B218)

for some constant $\chi _6'$. Plugging the bounds on the two parts of the sum into Eq. (B206), we find

$$\begin{aligned} \frac{\langle \textbf{1} |\Pi _w\Delta |v^{(t)}_{SS}\rangle }{\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle }&\le \frac{q^{-2(n-w)}}{1-q^{-2}}n\sigma q^{-2n(n-w)\log (1-\sigma )/\chi _5}\left( \chi _5'(n-w)+\frac{\chi _6'}{n}\right) \end{aligned}$$

(B219)

$$\begin{aligned}&\le \chi _9 q^{-2(n-w)}n\sigma (n-w) q^{c'(n-w)} \end{aligned}$$

(B220)

$$\begin{aligned}&= \chi _9n\sigma (n-w) q^{-(n-w)}q^{-(1-c')(n-w)} \end{aligned}$$

(B221)

for some constants $\chi _9$ and $c'$ which is less than 1 whenever $\sigma \le \chi _7/n$ and $n \ge n_0$ hold. Thus we may define $\chi _8=(1-c')\log (q)$ and the lemma is proved. $\square$

1.8.9 Proof of Lemma 11

Proof

Recall that ${\mathcal {Z}}_\sigma = \langle \textbf{1},\textbf{q} | v^{(s)}\rangle$. and that $|v^{(t)}_{SS}\rangle = L_{SS} |v^{(t)}\rangle$. The matrix $L_{SS}^{-1}$ is defined to be the Moore-Penrose pseudo-inverse of $L_{SS}$ and note that the null space of $L_{SS}$ is the space spanned by $|\vec {\nu },I^n\rangle$ for all $\vec {\nu }$. The projector onto this subspace is $|{\textbf{1},I^n}\rangle \!\langle {\textbf{1},I^n}|$. Thus,

$$\begin{aligned} |v^{(s)}\rangle&= {\mathcal {I}} |v^{(s)}\rangle = ( |{\textbf{1},I^n}\rangle \!\langle {\textbf{1},I^n}| + L_{SS}^{-1}L_{SS}) |v^{(s)}\rangle \end{aligned}$$

(B222)

$$\begin{aligned}&= |\textbf{1},I^n\rangle \langle \textbf{1},I^n | v^{(s)}\rangle + L_{SS}^{-1}|v_{SS}^{(s)}\rangle \,. \end{aligned}$$

(B223)

The lower bound is shown as follows:

$$\begin{aligned} {\mathcal {Z}}_\sigma -1&= \sum _{\vec {\nu }}\left( q^{|\vec {\nu }|}-1\right) \langle \textbf{1},\vec {\nu } | v^{(s)}\rangle =\sum _{\vec {\nu } \ne I^n}\left( q^{|\vec {\nu }|}-1\right) \langle \textbf{1},\vec {\nu } | v^{(s)}\rangle \end{aligned}$$

(B224)

$$\begin{aligned}&=\sum _{\vec {\nu } \ne I^n} \left( q^{|\vec {\nu }|}-1\right) \langle \textbf{1},\vec {\nu } |\left( |\textbf{1},I^n\rangle \langle \textbf{1},I^n | v^{(s)}\rangle + L_{SS}^{-1}|v_{SS}^{(s)}\rangle \right) \end{aligned}$$

(B225)

$$\begin{aligned}&=\sum _{\vec {\nu } \ne I^n} \left( q^{|\vec {\nu }|}-1\right) \langle \textbf{1},\vec {\nu } | L_{SS}^{-1}|v_{SS}^{(s)}\rangle \end{aligned}$$

(B226)

$$\begin{aligned}&=\sum _{\vec {\nu } \ne I^n} \left( q^{|\vec {\nu }|}-1\right) \langle \vec {\nu } |\frac{1-q^{-2n}}{q^{-2n+2|\vec {\nu }|}-q^{-2n}}|v_S^{(s)}\rangle \end{aligned}$$

(B227)

$$\begin{aligned}&=\sum _{\vec {\nu } \ne I^n}\left( q^n-1\right) \left( \frac{1+q^n}{1+q^{|\vec {\nu }|}}\right) \langle \textbf{1},\vec {\nu } | v_{SS}^{(s)}\rangle \end{aligned}$$

(B228)

$$\begin{aligned}&\ge \sum _{\vec {\nu } \ne I^n}\left( q^n-1\right) \langle \textbf{1},\vec {\nu } | v_{SS}^{(s)}\rangle \end{aligned}$$

(B229)

$$\begin{aligned}&= (q^n-1) \langle \textbf{1},\textbf{1} | v_{SS}^{(s)}\rangle \,. \end{aligned}$$

(B230)

Now, we will show the upper bound.

$$\begin{aligned} {\mathcal {Z}}_\sigma -1&= \sum _{\vec {\nu }}\left( q^{|\vec {\nu }|}-1\right) \langle \textbf{1},\vec {\nu } | v^{(s)}\rangle \end{aligned}$$

(B231)

$$\begin{aligned}&= \sum _{\vec {\nu }}\left( q^{|\vec {\nu }|}-1\right) \left( \langle S^n,\vec {\nu } | + \sum _{\vec {\mu } \ne S^n}\langle \vec {\mu },\vec {\nu } |\right) |v^{(s)}\rangle \end{aligned}$$

(B232)

$$\begin{aligned}&= \sum _{\vec {\nu }}\left( \left( q^{|\vec {\nu }|}-1\right) \langle S^n,\vec {\nu } | v^{(s)}\rangle + \sum _{\vec {\mu } \ne S^n}\left( q^{|\vec {\nu }|}-1\right) \langle \vec {\mu },\vec {\nu } | v^{(s)}\rangle \right) \end{aligned}$$

(B233)

$$\begin{aligned}&\le \sum _{\vec {\nu }}\left( \left( q^{|\vec {\nu }|}-1\right) \langle S^n,\vec {\nu } | v^{(s)}\rangle + \sum _{\vec {\mu } \ne S^n}\left( q^{|\vec {\mu }|}-1\right) \langle \vec {\mu },\vec {\nu } | v^{(s)}\rangle \right) \end{aligned}$$

(B234)

$$\begin{aligned}&= \sum _{\vec {\nu }}\left( \left( q^{|\vec {\nu }|}-1\right) \langle S^n,\vec {\nu } | v^{(s)}\rangle \right) + Z_0-1 - (q^n-1)\langle S^n,\textbf{1} | v^{(s)}\rangle \,, \end{aligned}$$

(B235)

where we have used $Z_0 = \sum _{\vec {\nu }}\sum _{\vec {\mu }}q^{|\vec {\mu }|}\langle \vec {\mu },\vec {\nu } | v^{(s)}\rangle$. Now we invoke Lemma 8, to say

$$\begin{aligned} {\mathcal {Z}}_\sigma -1&\le \sum _{\vec {\nu }}\left( q^{|\vec {\nu }|}-1\right) \langle S^n,\vec {\nu } | v^{(s)}\rangle + Z_0-1 - \frac{q^n-1}{q^n+1}(1-\eta '_s) \end{aligned}$$

(B236)

$$\begin{aligned}&= \sum _{\vec {\nu }} \left( q^{|\vec {\nu }|}-1\right) \langle S^n,\vec {\nu } | v^{(s)}\rangle + \left( Z_0 - \frac{2q^n}{q^n+1}\right) + \eta '_s\left( \frac{q^n-1}{q^n+1}\right) \end{aligned}$$

(B237)

$$\begin{aligned}&\le \sum _{\vec {\nu }}\left( q^{|\vec {\nu }|}-1\right) \langle S^n,\vec {\nu } | v^{(s)}\rangle + \left( Z_0 - \frac{2q^n}{q^n+1}\right) + \eta '_s \,. \end{aligned}$$

(B238)

Now we invoke Lemma 7 to bound $Z_0 - 2q^{n}/(q^n+1)$ in the first step below, and continue on. Denote $\eta _s'' = \eta _s + \eta '_s$.

$$\begin{aligned} {\mathcal {Z}}_\sigma -1 \le {}&\sum _{\vec {\nu }}\left( q^{|\vec {\nu }|}-1\right) \langle S^n,\vec {\nu } | v^{(s)}\rangle + \eta '_s + \eta _s \end{aligned}$$

(B239)

$$\begin{aligned} ={}&\sum _{\vec {\nu }}\left( q^{|\vec {\nu }|}-1\right) \langle S^n,\vec {\nu } |L_{SS}^{-1}L_{SS}|v^{(s)}\rangle + \eta _s'' \end{aligned}$$

(B240)

$$\begin{aligned} ={}&\sum _{\vec {\nu }}\left( \frac{(q^{|\vec {\nu }|}-1)(1-q^{-2n})}{q^{-2n+2|\vec {\nu }|}-q^{-2n}}\right) \langle S^n,\vec {\nu } | v_{SS}^{(s)}\rangle + \eta _s'' \end{aligned}$$

(B241)

$$\begin{aligned} ={}&\sum _{\vec {\nu }}(q^n-1)\left( \frac{q^{n}+1}{q^{|\vec {\nu }|}+1}\right) \langle S^n,\vec {\nu } | v_{SS}^{(s)}\rangle + \eta _s'' \end{aligned}$$

(B242)

$$\begin{aligned} \le {}&\eta _s'' +(q^n-1)\sum _{\vec {\nu }}q^{n-|\vec {\nu }|}\langle S^n,\vec {\nu } | v_{SS}^{(s)}\rangle \end{aligned}$$

(B243)

$$\begin{aligned} ={}&\eta _s'' +(q^n-1)\sum _{\vec {\nu }}q^{n-|\vec {\nu }|}\langle \vec {\nu } |\Delta |v_{SS}^{(s)}\rangle \end{aligned}$$

(B244)

$$\begin{aligned} ={}&\eta _s'' +(q^n-1)\langle S^n,S^n | v_{SS}^{(s)}\rangle +(q^n-1)\sum _{w=1}^{n-1}q^{n-w}\langle \textbf{1} |\Pi _w\Delta |v_{SS}^{(s)}\rangle \end{aligned}$$

(B245)

$$\begin{aligned} \le {}&\eta _s'' +(q^n-1)\langle S^n,S^n | v_{SS}^{(s)}\rangle +(q^n-1)\sum _{w=1}^{n-1}q^{n-w}n\sigma \xi _w\langle \textbf{1},\textbf{1} | v_{SS}^{(s)}\rangle \end{aligned}$$

(B246)

$$\begin{aligned} \le {}&\eta _s'' +(q^n-1)\langle \textbf{1},\textbf{1} | v_{SS}^{(s)}\rangle \left( 1+\chi _9 n \sigma \sum _{w=1}^{n-1}(n-w) e^{-\chi _8(n-w)}\right) \,, \end{aligned}$$

(B247)

where in the second-to-last line we have invoked Lemma 10, which requires $\sigma \le \chi _7/n$ and $n \ge n_0$ (leading to our requirements in this lemma that $\sigma \le \chi _{13}/n$ and $n \ge n_0$). Now, we make the choice of $\chi _{10}=\chi _9\sum _{w=1}^{n-1}(n-w)e^{-\chi _8 (n-w)}\le \chi _9\sum _{w=1}^{\infty }w e^{-\chi _8 w} = O(1)$, which yields the following. (In line 2, we invoke Lemma 5.)

$$\begin{aligned} {\mathcal {Z}}_\sigma -1&\le (q^n-1)\langle \textbf{1},\textbf{1} | v_{SS}^{(s)}\rangle \left( 1+\chi _{10} n\sigma +\frac{\eta ''_s}{(q^n-1)\langle \textbf{1},\textbf{1} | v_{SS}^{(s)}\rangle }\right) \end{aligned}$$

(B248)

$$\begin{aligned}&\le (q^n-1)\langle \textbf{1},\textbf{1} | v_{SS}^{(s)}\rangle \left( 1+\chi _{10} n\sigma +\frac{q^n+1}{q^n-1}\eta ''_s(1-\sigma )^{-2s}\right) \end{aligned}$$

(B249)

$$\begin{aligned}&\le (q^n-1)\langle \textbf{1},\textbf{1} | v_{SS}^{(s)}\rangle \left( 1+\chi _{10} n\sigma +3\eta ''_s(1-\sigma )^{-2s}\right) \end{aligned}$$

(B250)

$$\begin{aligned}&\le (q^n-1)\langle \textbf{1},\textbf{1} | v_{SS}^{(s)}\rangle \left( 1+\chi _{10} n\sigma +\chi _{12} e^{-\frac{\chi _{11}}{n}(s-s_{AC})+4s\sigma }\right) \end{aligned}$$

(B251)

$$\begin{aligned}&\le (q^n-1)\langle \textbf{1},\textbf{1} | v_{SS}^{(s)}\rangle \exp \left( 1+\chi _{10} n\sigma +\chi _{12} e^{-\frac{\chi _{11}}{n}(s-s_{AC})+4s\sigma }\right) \,, \end{aligned}$$

(B252)

where the third-to-last line is true for all $q\ge 2$ and $n \ge 1$, and the second-to-last line plugs in the equations for $\eta _s$ and $\eta '_s$, chooses constants $\chi _{11}$ and $\chi _{12}$ appropriately, and asserts $(1-\sigma )^{2s} \le e^{-4\sigma s}$, which is true whenever $\sigma \le 0.79$, so it is certainly true under the assumption $\sigma \le \chi _7/n$ for sufficiently large n. $\square$

1.8.10 Proof of Lemma 12

Proof

Recall that $\langle \textbf{1},\textbf{1} | v_{SS}^{(0)}\rangle = 1/(q^n+1)$. Let $t_0 = dn/2$.

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(t_0+n/2)}\rangle ={}&\langle \textbf{1}, \textbf{1} |L_{SS}\prod _{t=t_0+1}^{t_0+n/2}R_\sigma ^{(t)}|v^{(t_0)}\rangle \end{aligned}$$

(B253)

$$\begin{aligned} ={}&\langle \textbf{1}, \textbf{1} |L_{SS}\prod _{t=t_0+1}^{t_0+n/2}R^{(t)}_\sigma L_{SS}^{-1}|v_{SS}^{(t_0)}\rangle \end{aligned}$$

(B254)

$$\begin{aligned} ={}&\langle \textbf{1}, \textbf{1} |L_{SS}\prod _{t=t_0+1}^{t_0+n/2}({\mathcal {I}} \otimes Q'^{(t)}_{\sigma } Q_\sigma ^{(t)})\prod _{t=t_0+1}^{t_0+n/2}({\mathcal {I}} \otimes R_0^{(t)}) L_{SS}^{-1}|v_{SS}^{(t_0)}\rangle \end{aligned}$$

(B255)

$$\begin{aligned} ={}&\langle \textbf{1}, \textbf{1} |L_{SS}\prod _{t=t_0+1}^{t_0+n/2}({\mathcal {I}} \otimes Q'^{(t)}_{\sigma } Q_\sigma ^{(t)})L_{SS}^{-1}\prod _{t=t_0+1}^{t_0+n/2} R_{SS}^{(t)}|v_{SS}^{(t_0)}\rangle \end{aligned}$$

(B256)

$$\begin{aligned} ={}&\langle \textbf{1}, \textbf{1} |({\mathcal {I}} \otimes L_S)\prod _{t=t_0+1}^{t_0+n/2}({\mathcal {I}} \otimes Q'^{(t)}_{\sigma } Q_\sigma ^{(t)})({\mathcal {I}} \otimes L_{S}^{-1})\prod _{t=t_0+1}^{t_0+n/2} R_{SS}^{(t)}|v_{SS}^{(t_0)}\rangle \end{aligned}$$

(B257)

$$\begin{aligned} ={}&\langle \textbf{1} | L_S\prod _{t=t_0+1}^{t_0+n/2}( Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}) L_{S}^{-1}(\langle \textbf{1} |\otimes {\mathcal {I}})\prod _{t=t_0+1}^{t_0+n/2}R_{SS}^{(t)}|v_{SS}^{(t_0)}\rangle \end{aligned}$$

(B258)

$$\begin{aligned} ={}&\sum _{\vec {\nu }\ne I^n}\langle \textbf{1} | L_S\prod _{t=t_0+1}^{t_0+n/2}( Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}) L_{S}^{-1}|\vec {\nu }\rangle \langle \textbf{1},\vec {\nu } |\prod _{t=t_0+1}^{t_0+n/2}R_{SS}^{(t)}|v_{SS}^{(t_0)}\rangle \,. \end{aligned}$$

(B259)

We now examine the quantity

$$\begin{aligned} \langle \textbf{1} | L_S\prod _{t=t_0+1}^{t_0+n/2}( Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}) L_{S}^{-1} |\vec {\nu }\rangle ={}&\sum _{\vec {\mu }} \langle \vec {\mu } |L_S\prod _{t=t_0+1}^{t_0+n/2}( Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}) L_{S}^{-1} |\vec {\nu }\rangle \end{aligned}$$

(B260)

$$\begin{aligned} ={}&\sum _{\vec {\mu }} \frac{q^{-2n+2|\vec {\mu }|}-q^{-2n}}{q^{-2n+2|\vec {\nu }|}-q^{-2n}}\langle \vec {\mu } | \prod _{t=t_0+1}^{t_0+n/2}( Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}) |\vec {\nu }\rangle \,. \end{aligned}$$

(B261)

Note that, because of the layered property, all n qudits are acted upon by one of the $Q_\sigma ^{(t)}$ or $Q'^{(t)}_{\sigma }$. This can cause some S bits to flip to I bits (with probability $\sigma$). For a configuration $\vec {\mu }$ to have non-zero contribution in the above sum, it must have $\mu _i \le \nu _i$ for all i (under the ordering $I < S$), a condition we denote by $\vec {\mu } \le \vec {\nu }$, and in this case we have

$$\begin{aligned} \langle \vec {\mu } | \prod _{t=t_0+1}^{t_0+n/2}( Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}) |\vec {\nu }\rangle = (1-\sigma )^{|\vec {\mu }|}\sigma ^{|\vec {\nu }| - |\vec {\mu }|}. \end{aligned}$$

(B262)

Note also the following sum formula, which holds for any real number z.

$$\begin{aligned} \sum _{\vec {\mu }\le \vec {\nu }}q^{z|\vec {\mu }|} (1-\sigma )^{|\vec {\mu }|}\sigma ^{|\vec {\nu }| - |\vec {\mu }|}= & {} \sum _{x=0}^{|\vec {\nu }|} \left( {\begin{array}{c}|\vec {\nu }|\\ x\end{array}}\right) q^{zx}(1-\sigma )^{x}\sigma ^{|\vec {\nu }| - x} \nonumber \\= & {} (\sigma +q^z(1-\sigma ))^{|\vec {\nu }|}. \end{aligned}$$

(B263)

We find

$$\begin{aligned} \langle \textbf{1} | L_S\prod _{t=t_0+1}^{t_0+n/2}( Q'^{(t)}_{\sigma } Q_\sigma ^{(t)}) L_{S}^{-1} |\vec {\nu }\rangle ={}&\frac{1}{q^{2|\vec {\nu }|}-1}\sum _{\vec {\mu }\le \vec {\nu }} (q^{2|\vec {\mu }|}-1)(1-\sigma )^{|\vec {\mu }|}\sigma ^{|\vec {\nu }| - |\vec {\mu }|} \end{aligned}$$

(B264)

$$\begin{aligned} ={}&\frac{(\sigma + q^2(1-\sigma ))^{|\vec {\nu }|}-1}{q^{2|\vec {\nu }|}-1} = \frac{(1-\sigma ')^{|\vec {\nu }|}-q^{-2|\vec {\nu }|}}{1-q^{-2|\vec {\nu }|}} \,, \end{aligned}$$

(B265)

where $\sigma ' = \sigma (1-q^{-2})$. Denote this final expression by

$$\begin{aligned} E_w = \frac{(1-\sigma ')^{w}-q^{-2w}}{1-q^{-2w}}, \end{aligned}$$

(B266)

which allows us to rewrite Eq. (B259) as

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(t_0+n/2)}\rangle = \sum _{\vec {\nu }\ne I^n}E_{|\vec {\nu }|}\langle \textbf{1},\vec {\nu } |\prod _{t=t_0+1}^{t_0+n/2}R_{SS}^{(t)}|v_{SS}^{(t_0)}\rangle . \end{aligned}$$

(B267)

Now we claim that, for any $|\vec {\nu }| \ne 0$,

$$\begin{aligned} E_n \le E_{|\vec {\nu }|} . \end{aligned}$$

(B268)

We can prove the statement above by noting that it holds for $|\vec {\nu }| = n$ and observing that the derivative with respect to $|\vec {\nu }|$ is always negative (in this verification, note that $(1-\sigma ') \ge 1/q$ holds for all $\sigma \le 1$).

Collecting these observations, we have

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(t_0+n/2)}\rangle&\ge \sum _{\vec {\nu } \ne I^n}E_n \langle \textbf{1},\vec {\nu } |\prod _{t=t_0+1}^{t_0+n/2}R_{SS}^{(t)}|v_{SS}^{(t_0)}\rangle \end{aligned}$$

(B269)

$$\begin{aligned}&=E_n \langle \textbf{1},\textbf{1} |\prod _{t=t_0+1}^{t_0+n/2}R_{SS}^{(t)}|v_{SS}^{(t_0)}\rangle \end{aligned}$$

(B270)

$$\begin{aligned}&=E_n\langle \textbf{1},\textbf{1} | v_{SS}^{(t_0)}\rangle \,. \end{aligned}$$

(B271)

Hence, the lower bound in the lemma statement follows by recursively applying the above conclusion for increasing d.

To show the upper bound, we return to Eq. (B267). Note that $E_w \le 1$. We can restate what we know and divide the mass into whether or not the noiseless copy has reached the $S^n$ fixed point, and if it has, what value w for the Hamming weight the noisy copy ends up at.

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(t_0+n/2)}\rangle&= A_{not} + \sum _{w=1}^n E_w A_w\,, \end{aligned}$$

(B272)

where

$$\begin{aligned} A_{not}&= \sum _{\vec {\nu }\ne I^n,\vec {\mu } \ne S^n}E_{|\vec {\nu }|}\langle \textbf{1},\vec {\nu } |\prod _{t=t_0+1}^{t_0+n/2}R_{SS}^{(t)}\left( |{\vec {\mu }}\rangle \!\langle {\vec {\mu }}| \otimes {\mathcal {I}}\right) |v_{SS}^{(t_0)}\rangle \end{aligned}$$

(B273)

$$\begin{aligned} A_{w}&= \sum _{\vec {\nu }:|\vec {\nu }|=w}\langle \textbf{1},\vec {\nu } |\prod _{t=t_0+1}^{t_0+n/2}R_{SS}^{(t)}\left( |{S^n}\rangle \!\langle {S^n}| \otimes {\mathcal {I}}\right) |v_{SS}^{(t_0)}\rangle \,. \end{aligned}$$

(B274)

Since $E_{|\vec {\nu }|} \le 1$, we may directly apply Lemma 8 and bound $A_{not} \le \eta _{t_0}'/(q^n+1)$.

To bound $A_w$, we will need to use Lemma 10. Applying the layer of $R_{SS}^{(t)}$ from $t=t_0+1$ to $t=t_0+n/2$ can at most double the number of I-assigned bits, since each qudit participates in at most one gate. So, in order to land at a configuration with Hamming weight w at time step $t_0+n/2$, the configuration at time step $t_0$ must have Hamming weight at most $\lfloor \frac{n+w}{2}\rfloor$. In other words,

$$\begin{aligned} A_w \le \sum _{w'=1}^{\lfloor \frac{n+w}{2}\rfloor } \sum _{\vec {\mu }:|\vec {\mu }| = w'}\langle S^n,\vec {\mu } | v_{SS}^{(t_0)}\rangle \,. \end{aligned}$$

(B275)

When $w < n$, the right-hand side of the above is then bounded with Lemma 10, which requires $\sigma \le \chi _7/n$ and $n \ge n_0$ (and thus the upper bound portion of lemma inherits these requirements).

$$\begin{aligned} A_w&\le \sum _{w'=1}^{\lfloor \frac{n+w}{2}\rfloor } \sum _{\vec {\mu }:|\vec {\mu }| = w'}\langle \vec {\mu } |\Delta |v_{SS}^{(t_0)}\rangle = \sum _{w'=1}^{\lfloor \frac{n+w}{2}\rfloor } \langle \textbf{1} |\Pi _{w'}\Delta |v_{SS}^{(t_0)}\rangle \end{aligned}$$

(B276)

$$\begin{aligned}&\le \sum _{w'=1}^{\lfloor \frac{n+w}{2}\rfloor } n \sigma \chi _9 (n-w')q^{-(n-w')}e^{-\chi _8(n-w')}\langle \textbf{1},\textbf{1} | v_{SS}^{(t_0)}\rangle \end{aligned}$$

(B277)

$$\begin{aligned}&\le n\sigma \chi _9 \langle \textbf{1},\textbf{1} | v_{SS}^{(t_0)}\rangle \sum _{a=\lceil \frac{n-w}{2}\rceil }^\infty a e^{-a(\chi _8+\log (q))}\,, \end{aligned}$$

(B278)

where we have used the substitution $a=n-w'$. For any c, there is a constant $c''$ such that $\sum _{a=a_0}^{\infty } ae^{-ca}$ is bounded by $c''e^{-ca_0}$. Thus, there is a constant $c''$ such that

$$\begin{aligned} A_w&\le \langle \textbf{1},\textbf{1} | v_{SS}^{(t_0)}\rangle n\sigma \chi _9c''e^{-(\chi _8+\log (q))\lceil \frac{n-w}{2}\rceil } \le \langle \textbf{1},\textbf{1} | v_{SS}^{(t_0)}\rangle n\sigma \chi _9c''e^{-(\chi _8+\log (q)) \frac{n-w}{2}} \end{aligned}$$

(B279)

$$\begin{aligned}&= \langle \textbf{1},\textbf{1} | v_{SS}^{(t_0)}\rangle f n \sigma e^{-f'(n-w)}\,, \end{aligned}$$

(B280)

with the definitions $f = \chi _9c'' = O(1)$ and $f' = \chi _8+\log (q) = O(1)$. Note also that by construction $\sum _{w=1}^n A_w \le \langle \textbf{1},\textbf{1} | v_{SS}^{(t_0)}\rangle$. Thus,

$$\begin{aligned} \sum _{w=1}^n E_w A_w = \sum _{w=1}^n (E_n+E_w-E_n) A_w \le E_n\langle \textbf{1},\textbf{1} | v_{SS}^{(t_0)}\rangle + \sum _{w=1}^{n-1} (E_w-E_n)A_w ,\nonumber \\ \end{aligned}$$

(B281)

which we can insert into Eq. (B272), along with the bounds on $A_w$, giving

$$\begin{aligned}&\langle \textbf{1}, \textbf{1} | v_{SS}^{(t_0+n/2)}\rangle \le \langle \textbf{1},\textbf{1} | v_{SS}^{(t_0)}\rangle \left( E_n+n\sigma \sum _{w=1}^{n-1}(E_{w}-E_n)fe^{-f' (n-w)}\right) +\frac{\eta _{t_0}'}{q^n+1} \end{aligned}$$

(B282)

We also have

$$\begin{aligned} \frac{E_w}{E_n} = \frac{1-q^{-2n}}{1-q^{-2w}}\frac{(1-\sigma ')^{w}-q^{-2w}}{(1-\sigma ')^{n}-q^{-2n}} \le (1-\sigma ')^{-(n-w)}, \end{aligned}$$

(B283)

which can be verified by observing that the quantity

$$\begin{aligned} \frac{E_w}{E_n}(1-\sigma ')^{n-w}=\frac{(1-q^{-2n})(1-(q\sqrt{1-\sigma '})^{-2w})}{(1-q^{-2w})(1-(q\sqrt{1-\sigma '})^{-2n})} \end{aligned}$$

(B284)

achieves its maximum with respect to $\sigma '$ when $\sigma '=0$, where it equals 1. The quantity in parentheses in Eq. (B282) is now at most

$$\begin{aligned}&\left( E_n+n\sigma E_n\sum _{w=1}^{n-1}fe^{-f'(n-w)}(e^{-\log (1-\sigma ') (n-w)}-1)\right) \nonumber \\&\quad \le {}\left( E_n+n\sigma E_n\sum _{w=1}^{n-1}fe^{-f'(n-w)}\tau \sigma (n-w)\right) \end{aligned}$$

(B285)

$$\begin{aligned}&\quad \le {} E_n\left( 1+f''n\sigma ^2 \right) \,, \end{aligned}$$

(B286)

where in the first line, we bound $e^{-x\log (1-\sigma )}-1$ by $\tau \sigma x$ for some constant $\tau$, which holds for x sufficiently small, as is the case when $\sigma \le O(1/n)$ with n sufficiently large; in the second line, we choose the appropriate constant $f''$ as a bound for the sum $f\tau \sum _{a=1}^{n-1} ae^{-a}$. This gives us the recursion relation

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(t_0+n/2)}\rangle \le \langle \textbf{1},\textbf{1} | v_{SS}^{(t_0)}\rangle E_n(1+f''n\sigma ^2)+\frac{\eta _{t_0}'}{q^n+1}. \end{aligned}$$

(B287)

For the first few layers, before anti-concentration has been reached and $\eta _{t_0}'$ has become small, we will just use the simpler naive bound $\langle \textbf{1}, \textbf{1} | v_{SS}^{(t_0+n/2)}\rangle \le \langle \textbf{1},\textbf{1} | v_{SS}^{(t_0)}\rangle$. Define the anti-concentration depth as $d_{AC} = 2s_{AC}/n$. Then we have

$$\begin{aligned} \frac{\eta _{dn/2}'}{q^n+1}&\le \frac{\chi _4}{q^n+1} e^{-\chi _3(d-d_{AC})/2}\le \frac{\chi _4'}{q^n+1} E_n e^{-\chi _3(d-d_{AC})/2-n\log (1-\sigma )} \end{aligned}$$

(B288)

$$\begin{aligned}&\le \chi _4' E_n \langle \textbf{1},\textbf{1} | v_{SS}^{(dn/2)}\rangle e^{-\chi _3(d-d_{AC})/2-n\log (1-\sigma )-dn\log (1-\sigma )} \end{aligned}$$

(B289)

$$\begin{aligned}&\le E_n \langle \textbf{1},\textbf{1} | v_{SS}^{(dn/2)}\rangle n \sigma e^{-\chi _3'(d-d^*)}\,, \end{aligned}$$

(B290)

where in line 1, we refer back to the definition of $E_n$ and choose $\chi _4'$ slightly larger than $\chi _4$, in line 2, we use Lemma 5, and in line 3 we choose

$$\begin{aligned} d^* = d_{AC}\chi _3/2\chi '_3 + f''' + \log (1/n\sigma )/\chi _3' \end{aligned}$$

(B291)

for some constant $f'''$ that is O(1) whenever $-n\log (1-\sigma )$ is O(1). Note that this also requires $n\log (1-\sigma ) \le \chi _3$. We can choose the constant $a_3$ such that the condition $\sigma \le a_3/n$ implies these requirements hold. Note we also must choose a weaker exponential decay constant $\chi _3'$. Thus our recursion relation is

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(t_0+n/2)}\rangle \le \langle \textbf{1},\textbf{1} | v_{SS}^{(t_0)}\rangle E_n(1+f''n\sigma ^2 + n\sigma e^{-\chi _3'(d-d^*)}). \end{aligned}$$

(B292)

Iterating this equation starting at $d=d^*$, we get

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(dn/2)}\rangle&\le \frac{E_n^{d-d^*}}{q^n+1}\prod _{d'=d^*+1}^{d}(1+f''n\sigma ^2 + n\sigma e^{-\chi _3'(d'-d^*)}) \end{aligned}$$

(B293)

$$\begin{aligned}&\le \frac{E_n^{d-d^*}}{q^n+1}\exp \left( \sum _{d'=d^*+1}^{d}(f''n\sigma ^2 + n\sigma e^{-\chi _3'(d'-d^*)})\right) \end{aligned}$$

(B294)

$$\begin{aligned}&\le \frac{E_n^{d-d^*}}{q^n+1}\exp \left( (d-d^*)(f''n\sigma ^2) + n\sigma \chi _3''\right) \end{aligned}$$

(B295)

for some choice of $\chi _3''$ (the exponentially decaying sum is bounded). Now, we note from the definition of $E_n$ that as long as $\sigma \le O(1/n)$, there is a constant g (slightly larger than 1) such that $E_n \ge \exp (-g n\sigma ')$, allowing us to say

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(dn/2)}\rangle \le \frac{E_n^d}{q^n+1}\exp \left( f''n\sigma ^2d+ gn\sigma 'd^* + n\sigma \chi _3''\right) \,, \end{aligned}$$

(B296)

which, recalling the definition of $d^*$ in Eq. (B291), implies the lemma statement for appropriate choices of $a_0$, $a_1$, and $a_2$. $\square$

1.8.11 Proof of Lemma 13

Proof

In the layered case (proof of Lemma 12), we considered the action of all n/2 gates in a layer at once. For complete-graph, we can treat each gate individually. Following the layered derivation to Eq. (B259), for complete-graph we have

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(t)}\rangle ={}&\sum _{\vec {\nu }\ne I^n}\langle \textbf{1} | L_S Q'^{(t)}_{\sigma } Q_\sigma ^{(t)} L_{S}^{-1}|\vec {\nu }\rangle \langle \textbf{1},\vec {\nu } |R_{SS}^{(t)}|v_{SS}^{(t-1)}\rangle \,. \end{aligned}$$

Here the tth gate acts on two qudits $i_t$ and $j_t$, but in forming $|v_{SS}^{(t)}\rangle$ from $|v_{SS}^{(t-1)}\rangle$, we take the average over all possible choices of $\{i_t, j_t\}$, as the complete-graph architecture chooses the pair of qudits to act on uniformly at random. After action by $R_{SS}^{(t)}$ the values assigned at position $i_t$ and $j_t$ must be set equal. If they are assigned S, then errors can send the new configuration to one of four possible configurations, corresponding to errors on none, one, or both qudits. If they are assigned I then no errors are possible. If we assume $\nu _{i_t} = \nu _{j_t} = S$, then zero errors occurs with probability $(1-\sigma )^2$, one error with probability $2\sigma (1-\sigma )$, and two errors with probability $\sigma ^2$. Thus, we have

$$\begin{aligned} \langle \textbf{1} | L_S Q'^{(t)}_{\sigma } Q_\sigma ^{(t)} L_{S}^{-1}|\vec {\nu }\rangle ={}&(1-\sigma )^2+ 2\sigma (1-\sigma ) \frac{q^{-2n+2|\vec {\nu }|-2}-q^{-2n}}{q^{-2n+2|\vec {\nu }|}-q^{-2n}} \nonumber \\&+\sigma ^2 \frac{q^{-2n+2|\vec {\nu }|-4}-q^{-2n}}{q^{-2n+2|\vec {\nu }|}-q^{-2n}} \end{aligned}$$

(B297)

$$\begin{aligned} ={}&\frac{(1-\sigma ')^2 - q^{-2|\vec {\nu }|}}{1 - q^{-2|\vec {\nu }|}}\,, \end{aligned}$$

(B298)

where $\sigma ' = \sigma (1-q^{-2})$. Define the final expression as

$$\begin{aligned} J_{w} = \frac{(1-\sigma ')^2 - q^{-2w}}{1 - q^{-2w}}. \end{aligned}$$

(B299)

The quantity $J_w$ is monotonically increasing in w and satisfies $J_w \le J_n$ for all w. Meanwhile, if $\nu _{i_t} = \nu _{j_t} = I$, then $\langle \textbf{1} | L_S Q'^{(t)}_{\sigma } Q_\sigma ^{(t)} L_{S}^{-1}|\vec {\nu }\rangle = 1$.

   Recall the marginal dynamics of $R^{(t)}_{SS}$ on the noisy copy are simply $P_S^{(t)}$. Suppose the noisy copy starts at a configuration $|\vec {\eta }\rangle$. If $|\vec {\eta }| = w$, then let $\phi _{SS,w}$ be the probability that the qudits $i_t$ and $j_t$ are both assigned S, $\phi _{IS,w}$ be the probability one is assigned S and one is assigned I, and $\phi _{II,w}$ be the probability both are assigned I.

$$\begin{aligned} \phi _{SS,w}&= \frac{w(w-1)}{n(n-1)} \end{aligned}$$

(B300)

$$\begin{aligned} \phi _{IS,w}&= \frac{2w(n-w)}{n(n-1)} \end{aligned}$$

(B301)

$$\begin{aligned} \phi _{II,w}&= \frac{(n-w)(n-w-1)}{n(n-1)}\,. \end{aligned}$$

(B302)

Note that $\phi _{SS,w} + \phi _{IS,w} + \phi _{II,w} = 1$. In the case where one is I and one is S, the I is flipped to S by $P_S^{(t)}$ with probability $P_{\uparrow ,w}$ and the S is flipped to I with probability $P_{\downarrow ,w}$, where

$$\begin{aligned} P_{\uparrow ,w}&= \frac{1}{q^2+1}\frac{q^{-2n + 2w + 2}-q^{-2n}}{q^{-2n + 2w}-q^{-2n}} \end{aligned}$$

(B303)

$$\begin{aligned} P_{\downarrow ,w}&= 1-P_{\uparrow ,w} \,, \end{aligned}$$

(B304)

which increases or decreases the Hamming weight of w by 1. Note the following equalities and inequalities:

$$\begin{aligned} P_{\downarrow ,w}&= \frac{1}{q^2+1}\frac{1-q^{-2w+2}}{1-q^{-2w}} \ge \frac{1}{q^2+1}-q^{-2w} \end{aligned}$$

(B305)

$$\begin{aligned} 1-J_w&= \frac{1-(1-\sigma ')^2}{1-q^{-2w}} =\frac{2\sigma '-\sigma '^2}{1-q^{-2w}} \end{aligned}$$

(B306)

$$\begin{aligned} J_n-J_w&= \frac{(1-(1-\sigma ')^2)(q^{-2w}-q^{-2n})}{(1-q^{-2n})(1-q^{-2w})} \le \frac{q^{-2w}(2\sigma '-\sigma '^2)}{1-q^{-2w}} \end{aligned}$$

(B307)

$$\begin{aligned} \phi _{II,w} + \phi _{IS,w}P_{\downarrow ,w}&\ge {\left\{ \begin{array}{ll} \frac{n-w}{n-1}\left( \frac{1}{q^2+1}-q^{-2w}\right) \ge \frac{n-w}{n-1}\frac{1}{q^2+1} - q^{-2w}&{} \text {if } w \ge n/2 \\ \frac{1}{4}&{} \text {if } w < n/2 \end{array}\right. }\,, \end{aligned}$$

(B308)

where the last inequality follows because, when $w \ge n/2$, $\phi _{IS,w} \ge \frac{n-w}{n-1}$, and when $w < n/2$, $\phi _{II,w} \ge \frac{1}{4}$.

   We may now define $G_w$ by the following equation, where $|\vec {\eta }|=w$,

$$\begin{aligned} G_w ={}&\sum _{\vec {\nu }\ne I^n}\langle \textbf{1} | L_S Q'^{(t)}_{\sigma } Q_\sigma ^{(t)} L_{S}^{-1}|\vec {\nu }\rangle \langle \vec {\nu } |P_{S}^{(t)}|\vec {\eta }\rangle \end{aligned}$$

(B309)

$$\begin{aligned} ={}&\phi _{SS,w}J_w + \phi _{IS,w}(P_{\uparrow ,w}J_{w+1} + P_{\downarrow ,w}) + \phi _{II,w} \,. \end{aligned}$$

(B310)

We want to lower bound this quantity. If $n=2$, then $G_1=G_2=J_2$. If $n > 2$, we have

$$\begin{aligned} G_w \ge {}&\phi _{SS,w}J_w + \phi _{IS,w}(P_{\uparrow ,w}J_{w} + P_{\downarrow ,w}) + \phi _{II,w} \end{aligned}$$

(B311)

$$\begin{aligned} ={}&J_n + (1-J_w)(\phi _{II,w} + P_{\downarrow ,w}\phi _{IS,w}) - (J_n-J_w) \end{aligned}$$

(B312)

$$\begin{aligned} \ge {}&J_n + \frac{2\sigma '-\sigma '^2}{1-q^{-2w}}{\left\{ \begin{array}{ll} \frac{n-w}{n-1}\frac{1}{q^2+1}- 2q^{-2w} &{} \text {if } w \ge n/2 \\ \frac{1}{4}- q^{-2w} &{} \text {if } w < n/2 \end{array}\right. } \,. \end{aligned}$$

(B313)

By inspection of the final equation, we see that $G_w \ge J_n$ for every combination $n>2$, $w\ge 1$ (since $q>2$) except when $w = n$, but for $w=n$, $G_w=J_n$ by definition, so $G_w \ge J_n$ also holds.

   This immediately gives us

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(t)}\rangle ={}&\sum _{w=1}^n G_w\sum _{\vec {\eta }:|\vec {\eta }|=w}\langle \textbf{1},\vec {\eta } | v_{SS}^{(t-1)}\rangle \ge J_n \sum _{w=1}^n \sum _{\vec {\eta }:|\vec {\eta }|=w}\langle \textbf{1},\vec {\eta } | v_{SS}^{(t-1)}\rangle = J_n\langle \textbf{1},\textbf{1} | v_{SS}^{(t-1)}\rangle \,, \end{aligned}$$

(B314)

which proves the lower bound by recursion on increasing t and the fact that $\langle \textbf{1},\textbf{1} | v_{SS}^{(0)}\rangle =1/(q^n+1)$.

To show the upper bound, we first observe

$$\begin{aligned} G_w \le J_n + (1-J_n)(\phi _{II,w} + P_{\downarrow ,w}\phi _{IS,w})\,. \end{aligned}$$

(B315)

We have the inequalities

$$\begin{aligned} 1-J_n&= \frac{2\sigma '-\sigma '^2}{1-q^{-2n}} \le 2\sigma \end{aligned}$$

(B316)

$$\begin{aligned} \phi _{II,w} + P_{\downarrow ,w}\phi _{IS,w}&\le \phi _{II,w} + \frac{1}{2}\phi _{IS,w} = \frac{n-w}{n}\,. \end{aligned}$$

(B317)

Moreover, there exists a constant b such that $J_n \ge 1/b$ as long as $n \ge 2$ and $\sigma \le 0.5$. and thus

$$\begin{aligned} G_w \le J_n(1 + 2b\sigma \frac{n-w}{n})\,. \end{aligned}$$

(B318)

Similar to the proof of Lemma 12, we can split the initial weight into parts for which the noiseless copy has reached the $S^n$ fixed point, and a part that has not.

$$\begin{aligned} \langle \textbf{1}, \textbf{1} | v_{SS}^{(t)}\rangle&= A_{not} + \sum _{w=1}^n G_w A_w\,, \end{aligned}$$

(B319)

where

$$\begin{aligned} A_{not}&= \sum _{\vec {\eta },\vec {\mu } \ne S^n}G_{|\vec {\eta }|}\langle \vec {\mu },\vec {\eta } | v_{SS}^{(t-1)}\rangle \end{aligned}$$

(B320)

$$\begin{aligned} A_{w}&= \sum _{\vec {\eta }:|\vec {\eta }|=w}\langle S^n,\vec {\eta } | v_{SS}^{(t-1)}\rangle \,. \end{aligned}$$

(B321)

Since $G_{|\vec {\eta }|} \le 1$ by definition, we may directly apply Lemma 8 and bound $A_{not} \le \eta _{{t-1}}'/(q^n+1)$.

When $w<n$, we also have

$$\begin{aligned} A_w&\le \sum _{\vec {\eta }:|\vec {\eta }|=w}\langle \vec {\eta } |\Delta |v_{SS}^{(t-1)}\rangle \le n\sigma (n-w) q^{-(n-w)} \chi _9 e^{-\chi _8(n-w)} \langle \textbf{1},\textbf{1} | v^{(t-1)}_{SS}\rangle \end{aligned}$$

(B322)

by Lemma 10. This requires $\sigma \le \chi _7/n$ and $n \ge n_0$, so the upper bound inherits these requirements. Meanwhile by definition $\sum _{w=1}^n A_w \le \langle \textbf{1},\textbf{1} | v_{SS}^{(t-1)}\rangle$.

   Thus we have

$$\begin{aligned} \sum _{w=1}^n G_w A_w&= G_n\sum _{w=1}^n A_w + \sum _{w=1}^n(G_w-G_n)A_w \end{aligned}$$

(B323)

$$\begin{aligned}&\le \langle \textbf{1},\textbf{1} | v_{SS}^{(t-1)}\rangle \left( G_n + \sum _{w=1}^{n-1} (G_w-G_n) n\sigma (n-w) q^{-(n-w)} \chi _9 e^{-\chi _8(n-w)} \right) \end{aligned}$$

(B324)

$$\begin{aligned}&\le \langle \textbf{1},\textbf{1} | v_{SS}^{(t-1)}\rangle J_n\left( 1 + \sum _{w=1}^{n-1} 2b\sigma \frac{n-w}{n} n\sigma (n-w) q^{-(n-w)} \chi _9 e^{-\chi _8(n-w)} \right) \end{aligned}$$

(B325)

$$\begin{aligned}&\le \langle \textbf{1},\textbf{1} | v_{SS}^{(t-1)}\rangle J_n(1 + f\sigma ^2) \end{aligned}$$

(B326)

for some constant f, since $\sum _{a=1}^\infty a^2 e^{-ca}$ is bounded by a constant.

   This gives us the recursion relation

$$\begin{aligned} \langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \le \langle \textbf{1},\textbf{1} | v_{SS}^{(t-1)}\rangle J_n(1 + f\sigma ^2) + \frac{\eta '_{t-1}}{q^n+1}. \end{aligned}$$

(B327)

However, for the first roughly $s_{AC}$ gates, we will use the naive recursion relation $\langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \le \langle \textbf{1},\textbf{1} | v_{SS}^{(t-1)}\rangle$. We will begin to use Eq. (B327) once $\eta _{t-1}'$ is small. We have

$$\begin{aligned} \frac{\eta _{t-1}'}{q^n+1}&\le \frac{\chi _4}{q^n+1} e^{-\chi _3(t-1-s_{AC})/n}\le \frac{\chi _4}{q^n+1} J_n e^{-\chi _3(t-1-s_{AC})/n-2\log (1-\sigma )} \end{aligned}$$

(B328)

$$\begin{aligned}&\le \chi _4 J_n \langle \textbf{1},\textbf{1} | v_{SS}^{(t-1)}\rangle e^{-\chi _3(t-1-s_{AC})/n-2\log (1-\sigma )-2(t-1)\log (1-\sigma )} \end{aligned}$$

(B329)

$$\begin{aligned}&\le J_n n\sigma \langle \textbf{1},\textbf{1} | v_{SS}^{(t-1)}\rangle e^{-\chi _3'(t-s^*)/n}\,, \end{aligned}$$

(B330)

where in the first line we used the fact that $J_n \ge (1-\sigma )^2$, in the second line we invoked Lemma 5, and in the third line we have defined

$$\begin{aligned} s^* = s_{AC} + n\log (1/n\sigma )/\chi _3' + f'' + n \log (\chi _4)/\chi _3' \end{aligned}$$

(B331)

for an appropriate constant $f''$ and a weaker exponential decay coefficient $\chi _3'$. This requires $-2\log (1-\sigma ) < \chi _3/n$, which will hold as long as $\sigma \le b_3/n$ for a properly chosen constant $b_3$. This gives us

$$\begin{aligned} \langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \le \langle \textbf{1},\textbf{1} | v_{SS}^{(t-1)}\rangle J_n(1 + f\sigma ^2 + n\sigma e^{-\chi _3'(s-s^*)/n}). \end{aligned}$$

(B332)

Iterating this equation starting at $t=s^*$, and recalling that $\langle \textbf{1},\textbf{1} | v_{SS}^{(s^*)}\rangle \le 1/(q^n+1)$,

$$\begin{aligned} \langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle&\le \frac{J_n^{t-s^*}}{q^n+1}\prod _{t'=s^*+1}^t\left( 1 + f\sigma ^2 + n\sigma e^{-\chi _3'(t'-s^*)/n}\right) \end{aligned}$$

(B333)

$$\begin{aligned}&\le \frac{J_n^{t-s^*}}{q^n+1}\exp \left( \sum _{t'=s^*+1}^t\left( f\sigma ^2 + n\sigma e^{-\chi _3'(t'-s^*)/n}\right) \right) \end{aligned}$$

(B334)

$$\begin{aligned}&\le \frac{J_n^{t-s^*}}{q^n+1}e^{ft\sigma ^2 + \chi _3'' n \sigma } \end{aligned}$$

(B335)

for some choice of $\chi _3'' = O(1)$ (the exponentially decaying sum is bounded). Now, we note that $J_n \ge \exp (-g\sigma ')$ for a constant g slightly larger than 2 (when $\sigma$ is beneath some constant), allowing us to say

$$\begin{aligned} \langle \textbf{1},\textbf{1} | v_{SS}^{(t)}\rangle \le \frac{J_n^{t}}{q^n+1}e^{ft\sigma ^2 + \chi _3'' n \sigma + g\sigma 's^*}, \end{aligned}$$

(B336)

which, recalling the definition of $s^*$ in Eq. (B331), implies the lemma statement for appropriate choices of $b_0$, $b_1$, and $b_2$. Note that the $O(n\sigma )$ term can be collected with the $O(s_{AC}\sigma )$ term since $s_{AC} \ge \Omega (n \log (n))$. $\square$

Complexity Theory of the White-Noise Sampling Problem

Recent experiments on superconducting qubit devices [4,5,6] have claimed that the output distribution $p_{\text {noisy}}$ sampled by their device would be intractable to sample on a classical computer. This claim is motivated by progress in complexity theory on showing that sampling the outputs of quantum computations is hard, but ultimately these claims must rely on conjecture.

The argument that quantum computations should be hard to simulate classically begins with the observation that an efficient classical algorithm for sampling $p_{\text {ideal}}$ exactly with probability 1 over choice of U (i.e. in the worst case) would lead to a contradiction of the widely believed conjecture that the polynomial hierarchy (PH) does not collapse [56]. The main problem with this result in practice is that noisy quantum devices cannot sample exactly from $p_{\text {ideal}}$. It has been conjectured that the task of approximately sampling $p_{\text {ideal}}$ with high probability over circuit instance cannot be efficiently classically performed, assuming the PH does not collapse. Here “approximate” means that the sampled distribution $p_{\text {noisy}}$ is close to $p_{\text {ideal}}$ in total variation distance. Henceforth we refer to this task as approximate Random Circuit Sampling (RCS).

   To state the conjecture more precisely, we use the language of the PH [57]. The PH consists of an infinite number of “levels,” each containing a set of problems; the zeroth and first levels are the familiar P and NP complexity classes, respectively. Level j can be defined recursively as the set of problems solvable in NP with access to an oracle to level $j-1$ of the PH. In this spirit, we say that a sampling task has a PH protocol if there is a classical algorithm that solves the task in polynomial time while making a polynomial number of calls to an oracle that lies in one of the levels of the PH. The crucial aspect to note is that if we construct an algorithm by calling a PH protocol and an NP oracle as subroutines, each at most a polynomial number of times, then this algorithm will itself be a PH protocol. If one can show that one level of the PH contains the entire PH, then this is known to imply that the entire PH “collapses,” meaning that all higher levels are equal to that level. It is conjectured that the PH does not collapse for reasons similar to the belief that P does not equal NP.

Conjecture 1

(PH protocol for approximate RCS implies collapse of PH). Consider the task of sampling from a distribution $p_{\text {noisy}}$ for which the bound $\frac{1}{2}\Vert p_{\text {noisy}}-p_{\text {ideal}}\Vert _1 \le \varepsilon$ holds for at least a $1-\delta$ fraction of random quantum circuit instances. There exists a choice of $\varepsilon =O(1)$ and $\delta \ge 1/{{\,\textrm{poly}\,}}(n)$ such that the existence of a PH protocol for this task would imply that the polynomial hierarchy collapses.

This conjecture mirrors similar conjectures for random linear optical networks and random “instantaneous” quantum (IQP) circuits in Refs. [53, 54]. There is weak evidence for these conjectures in the form of worst-to-average case reductions for computing the entries of $p_{\text {ideal}}$ with very small error tolerance [21,22,23,24, 53, 58], but these results are multiple steps away from proving Conjecture 1 because they concern computing probabilities (strong simulation) as opposed to sampling (weak simulation), and furthermore they cannot tolerate errors of size O(1) in total variation distance.

   However, another issue with applying the conjecture in practice is that actual devices are unlikely to be able to sample from a distribution with such small total variation distance from ideal, as doing so requires error rates to be exceedingly small. Sampling from a distribution $p_{\text {noisy}}$ that is close in total variation distance to $p_{\text {wn}}$ (for some non-negligible choice of F) is potentially much more tractable in the near term; indeed, the experiments from Refs. [4,5,6] claim to have performed this task—although note that their random circuits were not Haar random, but rather chosen from some other discrete random ensemble. We refer to this task as white-noise RCS.

Conjecture 2

(PH protocol for white-noise RCS implies collapse of PH). Consider the task of sampling from a distribution $p_{\text {noisy}}$ for which the bound $\frac{1}{2}\Vert p_{\text {wn}}-p_{\text {noisy}}\Vert _1 \le \varepsilon F$ holds for at least a $1-\delta$ fraction of random quantum circuit instances. There exists a choice of $\varepsilon =O(1)$ and $\delta \ge 1/{{\,\textrm{poly}\,}}(n)$ such that whenever the white-noise parameter F satisfies $F \ge 1/{{\,\textrm{poly}\,}}(n)$, the existence of a PH protocol for this task would imply that the polynomial hierarchy collapses.

   It is important to note that the task of exactly sampling the white-noise distribution in the worst case is known to have the property that a PH protocol would imply the collapse of the PH (as long as F is at least inverse polynomial). A version of this statement, which further claims that the exact worst-case white-noise task can be at most a factor of F easier for classical computers than the exact worst-case noiseless task, appears in the Supplementary Material of Ref. [4]. However, allowing error of size $\varepsilon F$ was not explicitly considered. Here we show that this is not an issue, and that approximate white-noise RCS and approximate RCS are essentially equivalent in this context, up to a linear factor in $F^{-1}$ in computational complexity, whenever the underlying random quantum circuits have the anti-concentration property.

Theorem 4

Consider a random quantum circuit architecture that has the anti-concentration property. That is, there is a constant z such that ${\mathbb {E}}_U[\sum _xp_{\text {ideal}}(x)^2] \le z q^{-n}$. Define an oracle ${\mathcal {O}}$ as follows. On input (U, b), where U is a description of a n-qudit circuit with ${{\,\textrm{poly}\,}}(n)$ gates drawn randomly from the architecture, and b is a string of ${{\,\textrm{poly}\,}}(n)$ uniformly random bits, ${\mathcal {O}}$ produces an output x from a distribution $p_{\text {noisy}}$ for which $\frac{1}{2}\Vert p_{\text {noisy}}- p_{\text {wn}}\Vert _1 \le \varepsilon F$ holds for a certain (known) constant F on at least $1-\delta$ fraction of random circuit instances U.

   Then, given access to ${\mathcal {O}}$ and an NP oracle, there is an algorithm with runtime $F^{-1}{{\,\textrm{poly}\,}}(n)$ that produces samples from a distribution p for which $\frac{1}{2}\Vert p-p_{\text {ideal}}\Vert _1 \le \varepsilon '$ on at least $1-\delta '$ fraction of circuit instances, with

$$\begin{aligned} \varepsilon '&= 5\varepsilon + 1/{{\,\textrm{poly}\,}}(n) \end{aligned}$$

(C337)

$$\begin{aligned} \delta '&= \delta + 1/{{\,\textrm{poly}\,}}(n) \end{aligned}$$

(C338)

Corollary 1

For a random quantum circuit architecture with the anti-concentration property, Conjecture 1 is true if and only if Conjecture 2 is true.

Proof of Corollary 1

It is straightforward to show that Conjecture 2 implies Conjecture 1 simply by reduction from the white-noise RCS task to the approximate RCS task, as follows. Assume Conjecture 2 is true, and let $(\varepsilon ,\delta )$ be the parameters for which a PH protocol for white-noise RCS implies the collapse of the PH. Suppose there existed a PH protocol for approximate RCS with those parameters, that is, a PH protocol that produces samples from a distribution $p_{\text {noisy}}$ for which $\frac{1}{2}\Vert p_{\text {noisy}}-p_{\text {ideal}}\Vert _1 \le \varepsilon$. Then, for any choice of F, one can design another PH protocol that samples from a distribution $p_{\text {noisy}}'$ by producing a uniformly random output with probability $1-F$ and an output drawn from $p_{\text {noisy}}$ with probability F. This protocol performs the white-noise RCS task since $\frac{1}{2}\Vert p_{\text {noisy}}'-p_{\text {wn}}\Vert _1 \le \varepsilon F$. Thus, if Conjecture 2 is true, then the polynomial hierarchy collapses, implying that Conjecture 1 is also true..

   The fact that Conjecture 1 implies Conjecture 2 is a direct implication of Theorem 4. Assume Conjecture 1 is true, and let $(\varepsilon ',\delta ')$ be a parameter choice for which a PH protocol for approximate RCS would imply that the PH collapses. Theorem 4 imples that we can then choose $\varepsilon = O(1)$ and $\delta \ge 1/{{\,\textrm{poly}\,}}(n)$ such that if there exists a PH protocol for the white-noise RCS task with parameters $(\varepsilon ,\delta )$, then there is also a PH protocol for approximate RCS with parameters $(\varepsilon ',\delta ')$—this PH protocol will call as a subroutine the PH protocol for white-noise RCS as well as an NP oracle. Assuming Conjecture 1, this implies that the PH collapses, and hence that Conjecture 2 is true. $\square$

   Theorem 4 asserts that if one has an efficient classical algorithm that approximately samples from the white-noise distribution, one can construct another efficient classical algorithm (that uses an NP oracle) that approximately samples from the ideal distribution. This incurs a blowup in runtime by a factor of $F^{-1}$. The part of the proof of Corollary 1 that shows Conjecture 2 implies Conjecture 1 also illustrates why this factor of $F^{-1}$ is optimal. To simulate a white-noise output, one need only produce an output from $p_{\text {ideal}}$ on a fraction F of the samples, outputting a sample from $p_{\text {unif}}$ on the other $1-F$ fraction. Thus, producing T samples requires only FT queries to a sampler for $p_{\text {ideal}}$. If sampling from $p_{\text {ideal}}$ is a hard classical task, sampling from $p_{\text {wn}}$ is thus at least a factor of F easier. Theorem 4 shows that, in a sense, it is also at most a factor of F easier.

   This observation essentially puts the low-fidelity and high-fidelity noise regimes on the same theoretical footing when it comes to hardness of sampling, as long as the probability of an errorless computation is at least inverse polynomial in n. One might object that $F \ge 1/{{\,\textrm{poly}\,}}(n)$ is unrealistic in an asymptotic sense, and in many cases, this may be true. However, one way to achieve $F \ge 1/{{\,\textrm{poly}\,}}(n)$ is to run circuits with Pauli error rate $\epsilon = \Theta (1/n)$ and circuit size $s = \Theta (n\log (n))$, which, conveniently, is precisely the size required to achieve the anti-concentration property, as shown in Ref. [8]. Moreover, when the probability of an errorless computation is inverse exponential in n (but larger than $2^{-n}$), there is still a sense in which the low-fidelity regime can be at most a factor of F easier for a classical computer than the high-noise regime.

Proof idea of Theorem 4

The idea behind our reduction is to combine two ingredients: Stockmeyer’s approximate counting algorithm [59] and approximate rejection sampling. We sketch the role of each ingredient here. For any input x and any positive real number $\nu < 1$, Stockmeyer’s counting algorithm is used to produce an estimate of the quantity $p_{\text {noisy}}(x) \approx p_{\text {wn}}(x)= Fp_{\text {ideal}}(x) + (1-F)p_{\text {unif}}(x)$ that is correct up to a factor $O(\nu )$ in relative error, with high probability over the internal randomness of the algorithm. The algorithm makes at most $\nu ^{-1} \cdot \text {poly}(n)$ calls to an NP oracle, and to the oracle ${\mathcal {O}}$. If $\nu < O(F)$, we can subsequently subtract out $(1-F)p_{\text {unif}}(x)$ and divide by F to obtain an estimate for $p_{\text {ideal}}(x)$ up to relative error $O(\nu /F)$.

However, we desire an algorithm that samples from $p_{\text {ideal}}$. Turning estimates of $p_{\text {ideal}}(x)$ into samples from $p_{\text {ideal}}$ is accomplished with approximate rejection sampling. The idea is as follows. Since we have assumed anti-concentration, we know that most samples x drawn from $p_{\text {ideal}}$ will satisfy $p_{\text {ideal}}(x) \le O(q^{-n})$. We choose a cutoff at $kq^{-n}$. We perform rejection sampling by choosing x uniformly at random, computing (an estimate of) $p_{\text {ideal}}(x)$, and accepting the choice of x with probability $p_{\text {ideal}}(x)/(kq^{-n})$ if $p_{\text {ideal}}(x) \le kq^{-n}$; otherwise, we reject the choice of x and draw a new uniform sample. If every x satisfied the relation $p_{\text {ideal}}(x) \le kq^{-n}$, this procedure would exactly produce a sample from $p_{\text {ideal}}$, and it would accept after at most O(k) attempts on average. The rejection sampling is approximate because $p_{\text {ideal}}(x)$ exceeds the threshold for some x, and also because our estimates for $p_{\text {ideal}}(x)$ are not exact. However, in the full proof, we perform a careful accounting of the errors, which can be made small by taking k sufficiently large and $\nu$ sufficiently small. $\square$

Proof of Theorem 4

We first apply Stockmeyer’s approximate counting algorithm [59] to produce estimates of $p_{\text {noisy}}(x)$ using the oracle ${\mathcal {O}}$ and an NP oracle. To be precise, for any $\nu$, any $\mu '$, and any x, there is a randomized algorithm (with access to $\textsf {NP}{}$ oracle) that produces a number, denoted $p'$ such that with probability at least $1-\mu '$,

$$\begin{aligned} |p_{\text {noisy}}(x) - p'| \le 2\nu p_{\text {noisy}}(x). \end{aligned}$$

(C339)

The runtime of the algorithm and the number of queries it makes to the oracle ${\mathcal {O}}$ and the NP oracle is at most $\nu ^{-1} \cdot {{\,\textrm{poly}\,}}(n, \log (1/\mu '))$. To verify the $\text {polylog}(\mu '^{-1})$ dependence, note that constant failure probability may always be boosted to be exponentially small: given r independent estimates of $p_{\text {noisy}}(x)$, each satisfying Eq. (C339) with probability more than 1/2, Lemma 1 of Ref.  [60] implies that the median of these r estimates will satisfy Eq. (C339) with probability at least $1-e^{-\Omega (r)}$. To verify the linear dependence on $\nu ^{-1}$, see the Supplementary Information of Ref. [4] or Theorem 38 of the lecture notes in Ref. [61].

   The algorithm is a randomized algorithm; denote the random bits it takes as input by $\omega$. For each choice of x, the algorithm fails on at most $\mu '$ fraction of the choices of $\omega$. Since there are $q^n$ possible inputs x, by the union bound, the fraction of choices of $\omega$ for which the algorithm fails for at least one input x is upper bounded $q^n \mu '$. Thus, to achieve overall error probability $\mu$ across all inputs x, we may choose $\mu ' = \mu /q^n$, noting that $\log (1/\mu ') = \log (1/\mu ) + \text {poly}(n)$.

Now, suppose that we feed the same random bits $\omega$ into the approximate counting algorithm for every choice of x with parameters $\nu$ and $\mu '$, yielding a fixed set of outputs $p_{\text {noisy}}'(x)$ for each possible x. The logic above implies that these values satisfy

$$\begin{aligned} |p_{\text {noisy}}(x) - p_{\text {noisy}}'(x)| \le 2\nu p_{\text {noisy}}(x) \end{aligned}$$

(C340)

for every x simultaneously with probability at least $1-\mu$ over the choice of $\omega$. On any particular x, the algorithm still runs in time $\nu ^{-1}{{\,\textrm{poly}\,}}(n, \log (1/\mu ))$. When this is the case,

$$\begin{aligned} \frac{1}{2}\Vert p_{\text {noisy}}- p_{\text {noisy}}'\Vert _1 \le \nu . \end{aligned}$$

(C341)

The idea is to try to infer the value of $p_{\text {ideal}}$ from the estimate of $p_{\text {noisy}}$ by subtracting out the uniform component of the white noise distribution, and dividing by F. Specifically, let

$$\begin{aligned} {\overline{p_{\text {ideal}}}}(x) = \frac{p_{\text {noisy}}(x)-(1-F)q^{-n}}{F} \end{aligned}$$

(C342)

and

$$\begin{aligned} {\overline{p_{\text {ideal}}}}'(x) = {\left\{ \begin{array}{ll} \frac{p_{\text {noisy}}'(x)-(1-F)q^{-n}}{F} &{} \text {if } p_{\text {noisy}}'(x) > (1-F)q^{-n}\\ 0 &{} \text {otherwise} \end{array}\right. } . \end{aligned}$$

(C343)

The former quantity is the estimate for $p_{\text {ideal}}$ we would make if we had exactly computed $p_{\text {noisy}}$, and the latter is the estimate we make using the approximate counting algorithm. Recall from the theorem statement that for a fraction at least $1-\delta$ of instances U, ${\mathcal {O}}$ succeeds at producing samples that satisfy $\frac{1}{2}\Vert p_{\text {noisy}}- p_{\text {wn}}\Vert _1 \le \varepsilon F$. We can say that, as long as the instance U is among this $1-\delta$ fraction and the choice of random bits $\omega$ is among the $1-\mu$ fraction for which Eq. (C341) holds, the following relations are true:

$$\begin{aligned} \frac{1}{2}\Vert {\overline{p_{\text {ideal}}}} - p_{\text {ideal}}\Vert _1&\le \varepsilon \end{aligned}$$

(C344)

$$\begin{aligned} \frac{1}{2}\Vert {\overline{p_{\text {ideal}}}} - {\overline{p_{\text {ideal}}}}' \Vert _1&\le \nu /F \,, \end{aligned}$$

(C345)

and by the triangle inequality

$$\begin{aligned} \frac{1}{2}\Vert p_{\text {ideal}}- {\overline{p_{\text {ideal}}}}' \Vert _1 \le \nu /F + \varepsilon . \end{aligned}$$

(C346)

Note that in general the function ${\overline{p_{\text {ideal}}}}'$ as defined does not describe a probability distribution since it is not necessarily normalized.

   Having described how to produce estimates ${\overline{p_{\text {ideal}}}}'(x)$ approximating $p_{\text {ideal}}(x)$, we now describe how to use these estimates to approximately sample from $p_{\text {ideal}}$. Let $k > 1$ and consider the following approximate rejection sampling algorithm, similar to that in the Supplementary Information of Ref. [62].

• 1. Choose a set of random bits $\omega$, which implicitly determines a function $p_{\text {noisy}}'$.

• 2. Choose an x uniformly at random, and use the estimation algorithm with bits $\omega$ to produce $p_{\text {noisy}}'(x)$. Compute ${\overline{p_{\text {ideal}}}}'(x)$ using Eq. (C343).

• 3. Generate a random real number $0 \le \eta \le 1$

• 4. If ${\overline{p_{\text {ideal}}}}'(x) \le 2k q^{-n}$ and if $\eta \le {\overline{p_{\text {ideal}}}}'(x)q^n/(2k)$, output x (accept); otherwise, return to step 2 (reject).

   Following the observations in Ref. [62], we first analyze the output distribution, denoted by $p_\omega$, of the above algorithm for a certain choice of $\omega$ in step 1. We see that $p_\omega$ is precisely the distribution ${\overline{p_{\text {ideal}}}}'$ conditioned on $x \in W$ where W is the set of x for which ${\overline{p_{\text {ideal}}}}'(x) \le 2k q^{-n}$. That is, we may define

$$\begin{aligned} {\mathcal {M}}&= \sum _x {\overline{p_{\text {ideal}}}}'(x) \end{aligned}$$

(C347)

$$\begin{aligned} {\mathcal {N}}&= \sum _{x\in W} {\overline{p_{\text {ideal}}}}'(x) \,, \end{aligned}$$

(C348)

and conclude that

$$\begin{aligned} p_\omega (x) = {\left\{ \begin{array}{ll} {\mathcal {N}}^{-1}{\overline{p_{\text {ideal}}}}'(x) &{} \text {if } x \in W \\ 0 &{} \text {otherwise} \end{array}\right. } . \end{aligned}$$

(C349)

Hence,

$$\begin{aligned} \frac{1}{2} \Vert p_\omega - {\overline{p_{\text {ideal}}}}' \Vert _1&= \frac{1}{2}\sum _{x \in W} |{\mathcal {N}}^{-1}{\overline{p_{\text {ideal}}}}'(x)-{\overline{p_{\text {ideal}}}}'(x)| + \frac{1}{2}\sum _{x\not \in W} {\overline{p_{\text {ideal}}}}'(x) \end{aligned}$$

(C350)

$$\begin{aligned}&= \frac{1}{2}|1-{\mathcal {N}}| + \frac{1}{2}({\mathcal {M}}-{\mathcal {N}}) \end{aligned}$$

(C351)

$$\begin{aligned}&\le \frac{1}{2}|1-{\mathcal {M}}| + ({\mathcal {M}}-{\mathcal {N}}) \,. \end{aligned}$$

(C352)

Note that $|1-{\mathcal {M}}| \le 2\nu /F$ is an implication of Eq. (C345). Also note that the values of ${\overline{p_{\text {ideal}}}}$ sum to 1 (although some can in principle be negative). To handle the quantity ${\mathcal {M}}-{\mathcal {N}} = \sum _{x \not \in W} {\overline{p_{\text {ideal}}}}'(x)$, we invoke Lemma 14, with $p_1 = {\overline{p_{\text {ideal}}}}'$, $p_2 = p_{\text {ideal}}$ and $T = 2kq^{-n}$. It shows that

$$\begin{aligned} {\mathcal {M}}-{\mathcal {N}} \le 4\varepsilon + 4\nu /F + \sum _{x: p_{\text {ideal}}(x) > kq^{-n}} p_{\text {ideal}}(x) , \end{aligned}$$

(C353)

and thus

$$\begin{aligned} \frac{1}{2} \Vert p_\omega - {\overline{p_{\text {ideal}}}}' \Vert _1 \le 5\nu /F + 4\varepsilon + \sum _{x: p_{\text {ideal}}(x) > kq^{-n}} p_{\text {ideal}}(x) . \end{aligned}$$

(C354)

This is progress because the right-hand side only has dependence on the ideal distribution $p_{\text {ideal}}$, and not the approximate distribution output by the estimator.

   Now, recall that we assume that ${\mathbb {E}}_U[\sum _x p_{\text {ideal}}(x)^2] \le z q^{-n}$. By Markov’s inequality, for any $z'$, $\sum _x p_{\text {ideal}}(x)^2 \le z' q^{-n}$ for at least $1-z/z'$ fraction of instances U. Suppose we have such an instance. Then

$$\begin{aligned} \sum _{x: p_{\text {ideal}}(x)> kq^{-n}} p_{\text {ideal}}(x)&= \sum _{x: p_{\text {ideal}}(x)> kq^{-n}} \frac{p_{\text {ideal}}(x)^2}{p_{\text {ideal}}(x)} \le \sum _{x: p_{\text {ideal}}(x) > kq^{-n}} \frac{p_{\text {ideal}}(x)^2}{kq^{-n}} \le z'/k \,. \end{aligned}$$

(C355)

Combining Eqs. (C346), (C354), and (C355), we conclude that the algorithm produces outputs from a distribution $p_\omega$ for which

$$\begin{aligned} \frac{1}{2}\Vert p_\omega - p_{\text {ideal}}\Vert _1 \le 6\nu /F + 5\varepsilon + z'/k \end{aligned}$$

(C356)

(with probability at least $1-\mu$ over its internal randomness) and succeeds on at least $1-\delta '$ fraction of circuit instances, where

$$\begin{aligned} \delta ' = \delta + z/z' . \end{aligned}$$

(C357)

The $\delta '$ fraction of failed instances arise either because the underlying white-noise sampler also fails on those instances or because the output distribution is not sufficiently anti-concentrated. Either way, whether an instance is among this $\delta '$ fraction is independent of the choice of $\omega$. Thus, we may note that in the $\mu$ chance that the total variation distance bound is not satisfied for the random choice of $\omega$, the total variation distance will still be upper bounded by its maximal value of 1, and thus, for any of the $1-\delta '$ successful instances, the overall total variation distance of the sampler is at most $\varepsilon '$, where

$$\begin{aligned} \varepsilon '&= 6\nu /F + 5\varepsilon + z'/k + \mu \,. \end{aligned}$$

(C358)

   Now, we analyze the algorithm’s runtime. Each random choice of x and subsequent calculation of ${\overline{p_{\text {ideal}}}}'(x)$ takes at most $\nu ^{-1}{{\,\textrm{poly}\,}}(n, \log (1/\mu ))$ time, but sometimes this step must be repeated. Each time the algorithm returns to step 2, it will end up accepting on step 4 with probability ${\mathcal {N}}/2k$. By the above analysis,

$$\begin{aligned} |{\mathcal {N}}-1| \le |{\mathcal {M}}-1| + ({\mathcal {M}}-{\mathcal {N}}) \le 4\varepsilon + 6\nu /F + z'/k \,. \end{aligned}$$

(C359)

Thus, as long $4\varepsilon + 6\nu /F + z'/k \le 1/2$, then the acceptance probability will be at least 1/4k, and the expected number of repetitions required to produce an output is at most 4k.

   Recall that $z = O(1)$. Then we may choose $z' = {{\,\textrm{poly}\,}}(n)$ sufficiently large, $k = {{\,\textrm{poly}\,}}(n)$ even larger, $\nu ^{-1} = F^{-1}\cdot {{\,\textrm{poly}\,}}(n)$ sufficiently large, and $\mu ^{-1} = {{\,\textrm{poly}\,}}(n)$ sufficiently large that the algorithm runs in expected¹⁵ time $F^{-1}{{\,\textrm{poly}\,}}(n)$ and solves the approximate RCS task with parameters $\varepsilon ' = 5\varepsilon + 1/{{\,\textrm{poly}\,}}(n)$ and $\delta ' = \delta + 1/{{\,\textrm{poly}\,}}(n)$. It is likely the factor of 5 could be optimized. $\square$

Lemma 14

Suppose $p_1$ and $p_2$ are two real functions on $[q]^n$ for which

$$\begin{aligned} \frac{1}{2}\Vert p_1-p_2 \Vert _1 \le \varepsilon . \end{aligned}$$

(C360)

Let $\textbf{1}(\cdot )$ be the indicator function. Then for any threshold $T>0$, we have

$$\begin{aligned} \sum _x p_1(x) \textbf{1}(p_1(x)> T) \le 4\varepsilon + \sum _x p_2(x) \textbf{1}(p_2(x) > T/2) \,. \end{aligned}$$

(C361)

Proof

Let $A_1$ be the subset of $[q]^n$ for which $p_1(x) > T$, $A_2$ be the subset for which $p_2(x) > T$, and $A_3$ be the subset for which $p_2(x) > T/2$. For a subset X let ${\overline{X}}$ denote its complement.

$$\begin{aligned} \sum _x p_1(x) \textbf{1}(p_1(x) > T)={}&\sum _{x \in A_1} p_1(x) ={} \sum _{x \in A_1} (p_1(x)-p_2(x)) + \sum _{x \in A_1} p_2(x) \end{aligned}$$

(C362)

$$\begin{aligned} \le {}&2\varepsilon + \sum _{x \in A_1} p_2(x) \end{aligned}$$

(C363)

$$\begin{aligned} ={}&2\varepsilon + \sum _{x \in A_1 \cap {\overline{A}}_3} p_2(x)+\sum _{x \in A_1 \cap A_3} p_2(x) \end{aligned}$$

(C364)

$$\begin{aligned} \le {}&2\varepsilon + \sum _{x \in A_1 \cap {\overline{A}}_3} p_2(x)+ \sum _{x \in A_3} p_2(x) \end{aligned}$$

(C365)

$$\begin{aligned} \le {}&2\varepsilon + (T/2)|A_1 \cap {\overline{A}}_3|+ \sum _{x \in A_3} p_2(x) \end{aligned}$$

(C366)

$$\begin{aligned} \le {}&2\varepsilon + (T/2)\frac{2\varepsilon }{T/2}+ \sum _{x \in A_3} p_2(x) \end{aligned}$$

(C367)

$$\begin{aligned} ={}&4\varepsilon + \sum _x p_2(x) \textbf{1}(p_2(x) > T/2)\,, \end{aligned}$$

(C368)

where the second-to-last line follows because any element of $A_1 \cap {\overline{A}}_3$ must contribute at least T/2 toward the $2\varepsilon$ total allowed deviation between the two functions. $\square$