Error statistics and scalability of quantum error mitigation formulas

Abstract

Quantum computing promises advantages over classical computing in many problems. Nevertheless, noise in quantum devices prevents most quantum algorithms from achieving the quantum advantage. Quantum error mitigation provides a variety of protocols to handle such noise using minimal qubit resources. While some of those protocols have been implemented in experiments for a few qubits, it remains unclear whether error mitigation will be effective in quantum circuits with tens to hundreds of qubits. In this paper, we apply statistics principles to quantum error mitigation and analyse the scaling behaviour of its intrinsic error. We find that the error increases linearly O(ϵN) with the gate number N before mitigation and sublinearly $O({\epsilon }^{{\prime} }{N}^{\gamma })$ after mitigation, where γ ≈ 0.5, ϵ is the error rate of a quantum gate, and ${\epsilon }^{{\prime} }$ is a protocol-dependent factor. The $\sqrt{N}$ scaling is a consequence of the law of large numbers, and it indicates that error mitigation can suppress the error by a larger factor in larger circuits. We propose the importance Clifford sampling as a key technique for error mitigation in large circuits to obtain this result.

Introduction

With the recent progress that quantum computers can have more than half a hundred qubits^1,2, it is widely accepted that we are in the era of noisy intermediate-scale quantum (NISQ) technologies³. A prominent feature of NISQ technologies is the potential for surpassing all classical computers in certain tasks, yet they cannot realise full quantum error correction and achieve fault tolerance due to noise and the limited number of physical qubits. Under the assumption of realistic noise models, the qubit overhead is thousands of physical qubits per logical qubit to reduce the chance of a logical error to the negligible level^4,5. This requirement of quantum error correction is considerably beyond today’s technologies.

Nevertheless, we can still perform computation tasks with NISQ devices. Protocols proposed recently allow us to bypass quantum error correction, which are termed quantum error mitigation^{6,7,8,9,10,11,12,13,14,15,16,17}. Unlike error correction preserving the logical quantum state, error mitigation aims at recovering the error-free measurement outcome without physically preparing the error-free state. It can extract the correct computation result from a noisy device as long as the physical quantum state is not excessively damaged by the error accumulation¹⁸. For example, if the state becomes the maximally mixed state due to noise, there is nothing we can do to extract any useful information about the noise-free state. Recently, quantum algorithms using shallow circuits have been developed to minimise error accumulation. Quantum simulation algorithms based on variational, Lanczos and Monte Carlo methods are promising examples of such algorithms^{19,20,21,22,23}. Although shallow-circuit algorithms and error mitigation protocols have been successful in proof-of-principle experiments^{12,24,25,26,27,28,29,30}, it remains unexplored how they will perform as we venture into the regime of useful applications, where the computation involves more than half a hundred qubits and the device noise permits error mitigation but not yet error correction.

In this work, we address how the computation error after mitigation scales with the circuit size. In many quantum algorithms, we use quantum circuits to evaluate the expected values of observables. For example, the Hamiltonian is evaluated in the variational quantum eigensolver²⁰. Because of noise, an actual quantum computer produces a biased expected value, and the bias usually increases with the circuit size due to the error accumulation. Among the error mitigation protocols, probabilistic error cancellation can completely remove the bias under ideal conditions^7,8. Under realistic conditions, however, all protocols leave a residual bias in the computation result. This residual bias depends on the protocol and circuit depth.

To draw a conclusion regardless of the protocol, we utilise a general formalism of error mitigation. In this formalism, we recover the observable in the error-free circuit using an error mitigation formula, which is a function of observables directly measured with noisy circuits. Many such formulas are inspired by our knowledge of quantum physics, such as error extrapolation^6,7,31,32, probabilistic error cancellation^7,8 and virtual distillation^{13,14,33,34,35}. Throughout this work, when a concrete error mitigation formula is needed for analysis, we take the three aforementioned protocols as examples. An alternative way to construct the formula is optimising a parameterised function with data of selected training circuits^36,37. We find that the optimisation can suppress the scaling of the residual bias with respect to the circuit size.

For optimisation-based error mitigation protocols, we propose the importance Clifford sampling (ICS) as an efficient and scalable method to generate training circuits. Other than being practically useful in its own right, ICS lends us a tool to analyse the residual bias in the computation result. With its help, we show that the global depolarising model with circuit-dependent fluctuation is an effective phenomenological-error model, which describes the impact of realistic error models. Using this phenomenological model, we analyse the scaling behaviour of the residual bias. We find that the bias in the computation result after an optimised error mitigation process increases in proportion to $\sqrt{N}$, where N is the gate number. In contrast, the bias is usually proportional to N without error mitigation. Because error mitigation can suppress the error by a factor increasing with the circuit size, it is a feasible technique for large circuits.

The Results section is organised as follows. After introducing the general formalism of error mitigation, we discuss the error scaling in the mitigation protocols using the global depolarising model, which will be validated subsequently as the effective phenomenological-error model. Then we propose the ICS protocol, followed by a description of the important training circuits, the algorithms to generate them and an analysis of the sampling cost. We introduce the phenomenological-error model and show that the fluctuation of the effective depolarising rate follows the $\sqrt{N}$ scaling, which is numerically verified. Finally, we show the same scaling relation between the bias and the gate number in error extrapolation, probabilistic error cancellation and virtual distillation.

Results

Error mitigation formula

First, we introduce the notations. In quantum computing, a quantum circuit consists of quantum gates. Let U_j be the unitary operator of the jth gate. The circuit with N gates realises the transformation U = U_N ⋯ U₂U₁. Given the initial state of n qubits ${\left\vert 0\right\rangle }^{\otimes n}$ and observable Q, the expected value in the error-free circuit is ${f}_{{{{\boldsymbol{C}}}}}={{{\rm{Tr}}}}[Q[U](\left\vert 0\right\rangle {\left\langle 0\right\vert }^{\otimes n})]$, where [U](•) = U•U^†. Here we use C = (U₁, …, U_N, Q) to denote the circuit with the observable specified. If the circuit is noisy, the transformation is inexact, and we use the completely positive map ${{{\mathcal{E}}}}$ to denote the erroneous transformation. The expected value becomes ${y}_{{{{\boldsymbol{C}}}}}={{{\rm{Tr}}}}[Q{{{\mathcal{E}}}}(\left\vert 0\right\rangle {\left\langle 0\right\vert }^{\otimes n})]$. Then, y_C − f_C is the bias without error mitigation. Note that the error in the actual computing also depends on the statistical error due to finite measurement shots.

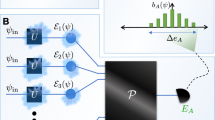
The general form of error mitigation formulas reads

$${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }=F({y}_{{{{{\boldsymbol{C}}}}}_{1}},{y}_{{{{{\boldsymbol{C}}}}}_{2}},\ldots ,{\lambda }_{1},{\lambda }_{2},\ldots )$$

(1)

where ${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }$ is the result of the circuit C after error mitigation, C₁, C₂, … are circuits generated from the primitive circuit C, and λ’s denote parameters determined via error mitigation protocols. See Fig. 1. In quantum computing, we evaluate ${y}_{{{{{\boldsymbol{C}}}}}_{i}}$ using the noisy quantum computer and calculate the error-mitigated value ${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }$ according to the formula. The bias after error mitigation is ${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }-{f}_{{{{\boldsymbol{C}}}}}$. Next, we show how some specific error mitigation protocols fit into the general form.

Fig. 1: Schematic illustration of quantum error mitigation formulas.

a Ideal and noisy quantum computing for the expected value of an observable. The distribution of the expected value is biased because of noise. b Error-mitigated quantum computing. The bias is corrected in quantum error mitigation (QEM).

Many error mitigation protocols have been proposed. See Ref. ¹⁷ for a review. In this work, we take three protocols as examples: error extrapolation, probabilistic error cancellation and virtual distillation. These protocols are applicable to any quantum algorithm evaluating expected values and can largely reduce the error. We give a minimal description here and leave a more detailed overview to Supplementary Note 1.

In error extrapolation using a polynomial fitting function^7,31, the error mitigation formula is

$${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }=\mathop{\sum}\limits_{i}{q}_{i}{y}_{{{{{\boldsymbol{C}}}}}_{i}},$$

(2)

where C_i is the primitive circuit with noise increased by a factor of r_i, and coefficients q_i are determined by noise amplification factors (i.e. r_i). For example, for the linear extrapolation with r₁ = 1 and r₂ = 2, the formula is

$${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }=2{y}_{{{{{\boldsymbol{C}}}}}_{1}}-{y}_{{{{{\boldsymbol{C}}}}}_{2}}.$$

(3)

In probabilistic error cancellation, the completely positive map of the error-free circuit is expressed as a linear combination of erroneous maps, i.e.

$$[U]=\mathop{\sum}\limits_{i}{q}_{i}{{{{\mathcal{E}}}}}_{i},$$

(4)

where q_i are quasi-probabilities, and ${{{{\mathcal{E}}}}}_{i}$ is the map of a noisy circuit C_i. Here C_i is generated by, for example, replacing or adding some gates in the primitive circuit C. We can work out the quasi-probability decomposition with gate set tomography data⁸ or in a learning manner³⁶. Given the decomposition, the error mitigation formula is the same as Eq. (2), but coefficients and circuits are different from error extrapolation.

In virtual distillation, k copies of the erroneous state ρ are used to evaluate the observable in a distilled state without physically preparing it. Given the primitive circuit C that prepares the state ρ, the circuit C₁ is to evaluate ${y}_{{{{{\boldsymbol{C}}}}}_{1}}={{{\rm{Tr}}}}(Q{\rho }^{k})$, and the circuit C₂ is to evaluate ${y}_{{{{{\boldsymbol{C}}}}}_{2}}={{{\rm{Tr}}}}({\rho }^{k})$. Then the error mitigation formula reads

$${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }=\frac{{y}_{{{{{\boldsymbol{C}}}}}_{1}}}{{y}_{{{{{\boldsymbol{C}}}}}_{2}}}.$$

(5)

It is similar in related protocols, e.g. verified phase estimation³⁴ and dual-state purification³⁵.

Bias in the global depolarising model

Before considering realistic error models, we take the global depolarising model as an example to discuss the bias in error mitigation formulas. In this section, we show that, if the error mitigation protocols are perfectly implemented, probabilistic error cancellation and learning-based error mitigation can reduce the bias to zero, while linear extrapolation and virtual distillation with two copies can reduce the bias from O(Nϵ) to O(N²ϵ²), where N is the gate number and ϵ is the depolarising rate per gate. In the section of “Phenomenological-error model” we will show that the global depolarising model successfully captures the influence of realistic noise and can be used as a phenomenological model.

In the global depolarising model, the j-th gate with error is described by the map ${{{{\mathcal{G}}}}}_{j}=(1-\epsilon )[{U}_{j}]+\epsilon {{{\mathcal{D}}}}$ acting on the whole input state, where ϵ is the gate depolarising rate, ${{{\mathcal{D}}}}(\bullet )={{{\rm{Tr}}}}(\bullet ){\rho }_{m}$ is the depolarising map, and ${\rho }_{m}={\mathbb{1}}/{2}^{n}$ is the maximally mixed state. Without loss of generality, we assume that the observable is a traceless operator, and we have y_C = (1−ϵ)^Nf_C = f_C + O(ϵN). The bias increases linearly with the gate number when N is significantly smaller than ϵ⁻¹. In the limit of large N, the bias approaches a finite value if the observable is bounded.

We take linear extrapolation as an example of error extrapolation. We can construct two noisy circuits using original gates and double-noise gates, respectively. Let ${{{{\mathcal{G}}}}}_{j}^{{\prime} }=(1-2\epsilon )[{U}_{j}]+2\epsilon {{{\mathcal{D}}}}$ be the gate with the doubled depolarising rate, two circuits labelled by i = 1, 2 produce expected values ${y}_{{{{{\boldsymbol{C}}}}}_{i}}={{{\rm{Tr}}}}[Q{{{{\mathcal{E}}}}}_{i}(\left\vert 0\right\rangle {\left\langle 0\right\vert }^{\otimes n})]$, where ${{{{\mathcal{E}}}}}_{1}={{{{\mathcal{G}}}}}_{N}\cdots {{{{\mathcal{G}}}}}_{2}{{{{\mathcal{G}}}}}_{1}$ and ${{{{\mathcal{E}}}}}_{2}={{{{\mathcal{G}}}}}_{N}^{{\prime} }\cdots {{{{\mathcal{G}}}}}_{2}^{{\prime} }{{{{\mathcal{G}}}}}_{1}^{{\prime} }$. Then, Eq. (3) leads to the error-mitigated expected value

$$\begin{array}{lll}{y}_{{{{\boldsymbol{C}}}}}^{{\prime} }&=&2{(1-\epsilon )}^{N}{f}_{{{{\boldsymbol{C}}}}}-{(1-2\epsilon )}^{N}{f}_{{{{\boldsymbol{C}}}}}\\ &=&{f}_{{{{\boldsymbol{C}}}}}+O({\epsilon }^{2}{N}^{2}).\end{array}$$

(6)

We can find that the bias in the linear extrapolation formula increases quadratically with the gate number because the linear extrapolation eliminates the first-order contribution of errors.

In probabilistic error cancellation, we take the quasi-probability decomposition of each gate as

$$[{U}_{j}]=\frac{1}{1-\epsilon }{{{{\mathcal{G}}}}}_{j}-\frac{\epsilon }{1-\epsilon }{{{\mathcal{D}}}}.$$

(7)

This decomposition means that we can correct the error by stochastically replacing the original gate ${{{{\mathcal{G}}}}}_{j}$ with the depolarising map ${{{\mathcal{D}}}}$ according to a quasi-probability distribution. The decomposition formula of the entire circuit reads

$$\begin{array}{lll}[U]&=&\mathop{\prod }\limits_{j=1}^{N}\left[\frac{1}{1-\epsilon }{{{{\mathcal{G}}}}}_{j}-\frac{\epsilon }{1-\epsilon }{{{\mathcal{D}}}}\right]\\ &=&\frac{1}{{(1-\epsilon )}^{N}}{{{{\mathcal{E}}}}}_{1}-\frac{\epsilon }{{(1-\epsilon )}^{N}}{{{{\mathcal{E}}}}}_{2}+\cdots \,,\end{array}$$

(8)

where ${{{{\mathcal{E}}}}}_{1}={{{{\mathcal{G}}}}}_{N}\cdots {{{{\mathcal{G}}}}}_{2}{{{{\mathcal{G}}}}}_{1}$ corresponding to the primitive circuit, ${{{{\mathcal{E}}}}}_{2}={{{{\mathcal{G}}}}}_{N}\cdots {{{{\mathcal{G}}}}}_{2}{{{\mathcal{D}}}}$ in which the first gate is replaced, and so on. Then the error mitigation formula is

$${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }=\frac{1}{{(1-\epsilon )}^{N}}{y}_{{{{{\boldsymbol{C}}}}}_{1}}-\frac{\epsilon }{{(1-\epsilon )}^{N}}{y}_{{{{{\boldsymbol{C}}}}}_{2}}+\cdots ={f}_{{{{\boldsymbol{C}}}}}.$$

(9)

Here, we have used that ${y}_{{{{{\boldsymbol{C}}}}}_{i}}=0$ if any gate is replaced with ${{{\mathcal{D}}}}$. Therefore, the residual bias is zero.

Lastly, we consider virtual distillation. The final state of N gates with the depolarising error is

$$\rho =(1-{\epsilon }_{t})U\left\vert 0\right\rangle {\left\langle 0\right\vert }^{\otimes n}{U}^{{\dagger} }+{\epsilon }_{t}{\rho }_{m},$$

(10)

where ϵ_t = 1 − (1−ϵ)^N. Take the second-order virtual distillation (i.e. k = 2) as an example, the error-mitigated expected value is

$$\begin{array}{lll}{y}_{{{{\boldsymbol{C}}}}}^{{\prime} }&=&\frac{{(1-{\epsilon }_{t})}^{2}+{2}^{1-n}(1-{\epsilon }_{t}){\epsilon }_{t}}{{(1-{\epsilon }_{t})}^{2}+{2}^{1-n}(1-{\epsilon }_{t}){\epsilon }_{t}+{2}^{-n}{\epsilon }_{t}^{2}}{f}_{{{{\boldsymbol{C}}}}}\\ &=&{f}_{{{{\boldsymbol{C}}}}}+O({\epsilon }^{2}{N}^{2}).\end{array}$$

(11)

Therefore, the bias in the second-order virtual distillation increases quadratically with the gate number, which is the natural consequence of the second-order distillation formalism.

So far we have been considering ideal conditions. Under realistic conditions, imperfections in the implementation cause an additional contribution to the bias. For example, zero-bias probabilistic error cancellation requires exact knowledge about the depolarising rate. If the depolarising rate is thought to be ${\epsilon }^{{\prime} }$ instead of its actual value ϵ and we work out the error mitigation formula with ${\epsilon }^{{\prime} }$, we have ${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }={(1-\epsilon )}^{N}/{(1-{\epsilon }^{{\prime} })}^{N}{f}_{{{{\boldsymbol{C}}}}}$. Then, the bias of the error mitigation formula is O((ϵ^″ − ϵ)N), which is finite and increases linearly with the gate number. It is similar for error extrapolation, in which the bias scales linearly if the noise is not increased exactly as designed.

Next, we analyse the bias in learning-based error mitigation. The optimisation of an ansatz function is a flexible approach for working out a proper error mitigation formula. Various ansatz functions have been proposed^36,37,38. In this work, we consider a general framework of this approach and focus on the scaling of the bias with respect to the gate number.

One way to compose an ansatz function is by modifying a specific-form formula. Taking the linear error extrapolation as an example, we parameterise the formula as

$${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }=\lambda {y}_{{{{{\boldsymbol{C}}}}}_{1}}+(1-\lambda ){y}_{{{{{\boldsymbol{C}}}}}_{2}}.$$

(12)

We determine λ by minimising the bias for a set of circuits, which are called training circuits. To evaluate the bias, the error-free expected value must be known. This condition limits the choice of training circuits. We can use only one training circuit T and the corresponding data $({y}_{{{{{\boldsymbol{T}}}}}_{1}},{y}_{{{{{\boldsymbol{T}}}}}_{2}},{f}_{{{{\boldsymbol{T}}}}})$ to determine λ for the ansatz considered here. The bias of the training circuit is minimised at

$${\lambda }^{* }=\frac{{f}_{{{{\boldsymbol{T}}}}}-{y}_{{{{{\boldsymbol{T}}}}}_{2}}}{{y}_{{{{{\boldsymbol{T}}}}}_{1}}-{y}_{{{{{\boldsymbol{T}}}}}_{2}}}.$$

(13)

For the global depolarising model, the optimal parameter is λ^* = [1 − (1−2ϵ)^N]/[(1−ϵ)^N − (1−2ϵ)^N]. If we take λ = λ^* in the error mitigation formula, the bias is zero for all circuits with the same gate number N. Therefore, the linear error extrapolation becomes bias-free after the optimisation.

It is similar for other error mitigation protocols. For probabilistic error cancellation, we can take the depolarising rate ϵ in Eq. (9) as the variational parameter, assuming the actual depolarising rate is unknown. We can find the optimal value of ϵ with data of a training circuit, and the optimal value must be the actual depolarising rate. Then, the error mitigation formula taking the optimal parameter is bias-free for all circuits. For virtual distillation, we can choose the ansatz ${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }=\lambda \frac{{y}_{{{{{\boldsymbol{C}}}}}_{1}}}{{y}_{{{{{\boldsymbol{C}}}}}_{2}}}$. According to Eq. (11), the bias is zero when λ cancels the factor before f_C.

We have seen that the learning-based approach can reduce the bias in error mitigation. According to the global depolarising model, the bias is zero in all examples. We get this perfect result because the global depolarising model is free of fluctuation, i.e. errors of all gates have the same impact on the expected value. The impact is a factor of 1−ϵ. Without the fluctuation, there are many simple error mitigation formulas that can simultaneously and completely correct the bias for all circuits.

In error models with fluctuation, the optimised error mitigation formula has a finite bias, and the bias increases with the gate number. Usually, errors are localised in many actual quantum computing systems, e.g. superconducting qubits and trapped ions. The error associated with a gate only affects qubits at the location of the gate (rather than the entire quantum register as in the global depolarising model). The contribution of an error to the bias depends on its location and the circuit. For example, if the observable is the Pauli operator X of qubit-1, errors localised on qubit-2 do not affect the observable; A phase-flip error before the measurement changes the sign of X but preserves the sign if we modify the circuit by inserting a Hadamard gate before the measurement. The fluctuation of error contributions causes a finite bias, i.e. the error mitigation formula cannot simultaneously compensate for all errors for all circuits. Assuming we can successfully compensate for the average contribution of errors, the residual bias is due to the fluctuation across different circuits. We find that in a large class of error mitigation formulas, the fluctuation-caused bias is proportional to $\sqrt{N}$. Later, we will show that the global depolarising model with fluctuation is an effective phenomenological model to characterise the impact of errors in realistic error models, see Fig. 2.

Fig. 2: Distribution of the effective depolarising rate in the phenomenological-error model.

In the model, the impact of errors in a noisy circuit is characterised by the global depolarising model with the circuit-dependent depolarising rate ϵ_C. The histogram is generated using six-qubit periodic-cycling circuits with 72 two-qubit gates under the gate depolarising noise. The error rate per gate is 0.001. Single-qubit gates are randomly sampled from the set of single-qubit unitaries with the weight ${f}_{{{{\boldsymbol{C}}}}}^{2}$. The average depolarising rate is proportional to the gate number N, and the standard deviation is proportional to $\sqrt{N}$.

Importance Clifford sampling

In this section, we address the question of how to efficiently sample large training circuits by proposing sampling algorithms whose resource costs scale linearly with the circuit size. These training circuits are Clifford circuits sharing the same circuit frame as the original noisy circuit, for which the ideal measurements take non-zero expected values.

A classical computer can efficiently simulate Clifford circuits, in which all gates are Clifford gates. Because the error-free expected value f_C of a Clifford circuit is computable^39,40, we can take them as training circuits. However, not every Clifford circuit is suitable. We take Eq. (13) as an example. If the training circuit T has a zero expected value, i.e. f_T = 0, erroneous expected values are all zero, i.e. ${y}_{{{{{\boldsymbol{T}}}}}_{1}}={y}_{{{{{\boldsymbol{T}}}}}_{2}}=0$. In this case, we cannot use the equation to determine the optimal parameter. Therefore, to find the optimal parameter, we need a training circuit T whose expected value is non-zero.

It is general that some training circuits are more important than others in the learning-based approach. To optimise the error mitigation formula, we need a measure of its overall performance in various circuits. We take the mean squared error (MSE) as an example, which reads

$${L}_{{\mathbb{R}}}={\langle {({y}_{{{{\boldsymbol{C}}}}}-{f}_{{{{\boldsymbol{C}}}}})}^{2}\rangle }_{{\mathbb{R}}},$$

(14)

where ${\langle g({{{\boldsymbol{C}}}})\rangle }_{{\mathbb{R}}}\equiv \frac{1}{| {\mathbb{R}}| }{\sum }_{{{{\boldsymbol{C}}}}\in {\mathbb{R}}}g({{{\boldsymbol{C}}}})$ is the average of the real-valued circuit function g(C) over the circuit set ${\mathbb{R}}$. Importance sampling is a crucial technique in statistics, in which the probability of a sample is proportional to the magnitude of its value, i.e. ${({y}_{{{{\boldsymbol{C}}}}}-{f}_{{{{\boldsymbol{C}}}}})}^{2}$ in MSE. According to importance sampling, we prefer training circuits with a larger bias over those with a smaller bias. The larger bias circuits, i.e. error-sensitive circuits, can provide more information about noise in the circuit.

The question of sampling training circuits has two parts. The first part is how to efficiently generate an error-sensitive circuit. The second part is how to draw samples according to a distribution. We address the first part in the “Circuit generation” section and the second part in the “Circuit frame” and “Sampling algorithms” sections.

Circuit generation

There are different approaches of generating an error-sensitive circuit. For example, we can randomly select a circuit and calculate the expected value, and we take it as a training circuit only if the expected value is non-zero. This approach works only when the circuit size is small because circuits with a non-zero expected value are rare in large Clifford circuits. An approach usually used in randomised benchmarking is reversing the transformation by adding an additional unitary at the end of the circuit⁴¹. We will not take this approach because the additional unitary may significantly increase the total gate number in multi-qubit circuits. We want to generate training circuits with a specific gate number, such that the error mitigation formula is optimised for circuits with the same gate number.

In the following, we focus on the case that the observable Q is a Pauli operator. In the standard model of quantum computing, qubits at the end of the circuit are measured in the computation basis, i.e. the Pauli operator Z is measured. One can adjust the measurement basis by inserting gates before the measurement. For example, by inserting single-qubit Clifford gates before the measurement, we can measure any Pauli operator. For a general observable, a way to evaluate its expected value is by expressing it as a linear combination of Pauli operators and computing the expected value of each term.

The expected value of a Pauli operator in a Clifford circuit takes three values 0 and ± 1. We can reexpress the error-free expected value as ${f}_{{{{\boldsymbol{C}}}}}={{{\rm{Tr}}}}({Q}_{U}\left\vert 0\right\rangle {\left\langle 0\right\vert }^{\otimes n})$, where Q_U = U^†QU is the effective observable. When U is Clifford, Q_U is a Pauli operator. Let P_i = I, X, Y, Z be the single-qubit Pauli operator on qubit-i, Q_U = ± P₁ ⊗ P₂ ⊗ ⋯ ⊗ P_n. Then ${f}_{{{{\boldsymbol{C}}}}}=\pm \mathop{\prod }\nolimits_{i = 1}^{n}\left\langle 0\right\vert {P}_{i}\left\vert 0\right\rangle$. If any single-qubit Pauli operator P_i is X or Y, the expected value is zero. If all P_i are I or Z, f_C = ± 1, and the sign is the same as Q_U. For a randomly generated Clifford circuit, it is likely that some single-qubit Pauli operators contained in Q_U are X or Y, i.e. f_C = 0.

We can deterministically generate an error-sensitive circuit as follows. The setup is shown in Fig. 3. The overall unitary transformation of the circuit is $U={U}^{{\prime} }{U}_{0}$, where U₀ = R₁ ⊗ R₂ ⊗ ⋯ ⊗ R_n is one layer of single-qubit gates, and R_i is the gate on qubit-i. First, given the gate number, we generate a random Clifford circuit, which realises the unitary ${U}^{{\prime} }$. If ${U}_{0}={\mathbb{1}}$, the effective observable is ${Q}_{{U}^{{\prime} }}=\pm {P}_{1}^{{\prime} }\otimes {P}_{2}^{{\prime} }\otimes \cdots \otimes {P}_{n}^{{\prime} }$. Given Q and ${U}^{{\prime} }$, we can efficiently work out this expression of ${Q}_{{U}^{{\prime} }}$ on a classical computer. Second, we determine single-qubit gates in U₀: we take a Clifford R_i satisfying ${R}_{i}^{{\dagger} }{P}_{i}^{{\prime} }{R}_{i}=\pm Z,I$. For the final circuit $U={U}^{{\prime} }{U}_{0}$, single-qubit Pauli operators in its effective observable Q_U are either I or Z. Then, the expected value is f_C = ± 1.

Fig. 3: Error-sensitive circuit generation.

We compose an error-sensitive circuit with two sections U₀ and ${U}^{{\prime} }$, as shown in (a). ${U}^{{\prime} }$ is a Clifford operator. The observable is a Pauli operator, e.g. Q = Z ⊗ I ⊗ ⋯ ⊗ I. ${U}^{{\prime} }$ and the observable is equivalent to an effective observable ${Q}_{{U}^{{\prime} }}=X\otimes I\otimes \cdots \otimes Z$, as shown in (b). Gates in U₀ are taken from the group of single-qubit Clifford gates. We choose the gates such that all non-identity Pauli operators in ${Q}_{{U}^{{\prime} }}$ are mapped to ± Z, as shown in (c).

Circuit frame

In the learning-based error mitigation, we aim at an optimised error mitigation formula that works for a set of circuits, including training circuits and circuits useful in some computation tasks. Choosing the target circuit set is important. When the circuit set is larger, it is harder to find a formula suitable for every circuit. Therefore, we want to be focusing on a circuit set relevant to some tasks to minimise bias. A way to construct a task-relevant circuit set is by taking circuits with the same pattern of multi-qubit Clifford gates, see Fig. 4. This pattern is called the circuit frame. In many quantum computing systems, such as superconducting qubits and trapped ions, the error rates of single-qubit gates are much lower than multi-qubit gates. Errors occurring in a circuit are mainly determined by multi-qubit gates. Therefore, all the circuits with the same frame have approximately the same errors, and we are able to correct them using the same error mitigation formula.

Fig. 4: Quantum circuit and circuit frame.

a The circuit for a specific task. Single-qubit gates X, H and S are Clifford, and gates T and R are non-Clifford. b The task-dependent circuit frame. Green boxes are slots for variable single-qubit gates. Clifford gates in the yellow region with dashed borders form a composite Clifford gate.

In the fixed-frame circuit set, single-qubit gates are variables. As shown in Fig. 4, the frame includes the qubit initialisation, multi-qubit Clifford gates and measurement. Fixing these operations, we change single-qubit gates to generate the circuit set. We call each variable single-qubit gate a slot. In Ref. ³⁶, a setup with slots after each multi-qubit gate is proposed. Here we reduce the slot number to minimise the circuit set. We only take locations of single-qubit non-Clifford gates in the task circuit as slots and add two layers of slots after the initialisation and before the measurement, respectively. The reason is that a sequence of Clifford gates not interrupted by any non-Clifford gate can be treated as one multi-qubit Clifford gate.

The minimised slots have sufficient degrees of freedom for implementing Pauli twirling and probabilistic error cancellation for general error models. A Pauli error is an unwanted Pauli transformation stochastically occurring in the circuit. In Pauli twirling, we convert general errors into Pauli errors by randomly applying Pauli gates before and after each Clifford gate. We can correct a Pauli error by applying a Pauli gate to undo the error. Relevant discussions can be found in ref. ³⁶.

With the frame determined, a circuit depends on the choice of single-qubit gates. Let C = (U₁, …, U_N, Q) be a circuit (with two layers of single-qubit gates after the initialisation and before the measurement, respectively). The corresponding frame is F = (…, U_i, •_k, …, U_j, •_q, …, Q), where U_i is a gate on the frame, and •_k denotes a slot on qubit-k. In other words, F is the same as C except that gates in slots are replaced with •_k. Formally, if S = {i₁, i₂, … } are labels of slots and $K=\{{k}_{{i}_{1}},{k}_{{i}_{2}},\ldots \,\}$ are corresponding qubits, the frame is F = (F₁, …, F_N, Q), where F_i = U_i if i ∉ S, and ${F}_{i}={\bullet }_{{k}_{i}}$ if i ∈ S. Then, we can reexpress the circuit as C = [F, R₁, R₂, …], where R_l is the single-qubit gate in the l-th slot, i.e. ${U}_{{i}_{l}}={I}^{\otimes ({k}_{{i}_{l}}-1)}\otimes {R}_{l}\otimes {I}^{\otimes (n-{k}_{{i}_{l}})}$.

To generate training circuits of the fixed frame, we can randomly draw the gate on each slot from the 24 single-qubit Clifford gates. Because the frame is formed of Clifford gates, the entire circuit constructed in this way is Clifford. It is likely that such a random circuit has a zero expected value. We can work out a circuit with a non-zero expected value by adjusting the first-layer gates, i.e. gates after the initialisation, as described in in the previous section. We give details of this procedure in Algorithm 1.

Algorithm 1

Generation of error-sensitive circuits.

1: function EScircuit$(F,\bar{R})$

2: Compose the candidate circuit ${{{{\boldsymbol{C}}}}}^{{\prime} }=[F,I,\ldots ,I,{R}_{n+1},\ldots ,{R}_{{N}_{R}}]$.

3: Calculate ${Q}_{{U}^{{\prime} }}={U}^{{\prime} {\dagger} }Q{U}^{{\prime} }$.

4: Calculate $({P}_{1}^{{\prime} },{P}_{2}^{{\prime} },\ldots ,{P}_{n}^{{\prime} })$ according to ${Q}_{{U}^{{\prime} }}=\pm {P}_{1}^{{\prime} }\otimes {P}_{2}^{{\prime} }\otimes \cdots \otimes {P}_{n}^{{\prime} }$.

5: for i = 1 to n do

6: repeat

7: Choose a random R_i from C₁.

8: until ${R}_{i}^{{\dagger} }{P}_{i}^{{\prime} }{R}_{i}=\pm Z,I$

9: Compose the error-sensitive circuit ${{{\boldsymbol{C}}}}=[F,{R}_{1},\ldots ,{R}_{n},{R}_{n+1},\ldots ,{R}_{{N}_{R}}]$.

10: Output C.

Sampling algorithms

We give two algorithms for sampling error-sensitive Clifford circuits in Algorithms 2 and 3. For clarity, we use the following notations in the algorithms. F is the circuit frame, Q is the observable, n is the qubit number, N_R is the slot number, and N_T is the sample number. C₁ is the single-qubit Clifford group with 24 elements. U = U_N ⋯ U₂U₁ is the unitary transformation of the circuit C = (U₁, …, U_N, Q) = [F, R₁, R₂, …]. We use $\bar{R}=({R}_{n+1},{R}_{n+2},\ldots ,{R}_{{N}_{R}})$ to denote an ordered set of single-qubit Clifford gates, and R₁, R₂, …, R_n are gates in the first-layer slots. w(C) is the weight of the Clifford circuit C: Q_U = U^†QU = ± P₁ ⊗ P₂ ⊗ ⋯ ⊗ P_n is a tensor product of Pauli operators, then w(C) is the number of non-identity Pauli operators in the product, i.e.

$$w({{{\boldsymbol{C}}}})\equiv n-\mathop{\sum }\limits_{i=1}^{n}{\delta }_{I,{P}_{i}},$$

(15)

where ${\delta }_{I,{P}_{i}}=1$ if P_i = I, and ${\delta }_{I,{P}_{i}}=0$ otherwise. In Algorithm 3, we employ the Metropolis-Hasting algorithm to realise a uniform distribution of error-sensitive circuits, which requires a conditional distribution $g({\bar{R}}^{{\prime} }| \bar{R})$ for suggesting a candidate sample. For example, we can take the conditional distribution as follows: we update gates in some randomly selected slots with newly generated random gates and keep gates in other slots unchanged.

Algorithm 2

Non-uniform importance Clifford sampling.

1: Input F.

2: for t = 1 to N_T do

3: for i = n + 1 to N_R do

4: Choose a random R_i from C₁.

5: Call EScircuit $F,\bar{R}$ to generate C.

6: Output C_t = C.

Algorithm 3

Uniform importance Clifford sampling.

1: Input F, a conditional distribution $g({\bar{R}}^{{\prime} }| \bar{R})$ and an initial slot-gate pattern ${\bar{R}}^{(0)}$.

2: Set t = 0.

3: Call EScircuit$F,{\bar{R}}^{(0)}$ to generate C.

4: Take C₀ = C.

5: for t = 1 to N_T do

6: Generate a random candidate of slot-gate pattern ${\bar{R}}^{(t)}$ according to $g({\bar{R}}^{(t)}| {\bar{R}}^{(t-1)})$.

7: Call EScircuit$F,{\bar{R}}^{(t)}$ to generate C.

8: Calculate the acceptance probability

$$A=\min \left(1,\frac{{3}^{-w({{{\boldsymbol{C}}}})}}{{3}^{-w({{{{\boldsymbol{C}}}}}_{t-1})}}\frac{g({\bar{R}}^{(t-1)}| {\bar{R}}^{(t)})}{g({\bar{R}}^{(t)}| {\bar{R}}^{(t-1)})}\right).$$

9: Generate a uniform random number u ∈ [0, 1].

10: Accept and set C_t = C if u≤A.

11: Reject and set C_t = C_t−1 if u > A.

12: Output C_t.

There is a relation between Clifford sampling and unitary sampling which allows us to estimate the bias distribution in general unitary circuits using Clifford circuits. We use ${\mathbb{C}}$ to denote the set of Clifford circuits and ${\mathbb{U}}$ to denote the set of all unitary circuits with the same frame. For a frame with N_R slots, the total number of Clifford circuits is $| {\mathbb{C}}| =2{4}^{{N}_{R}}$, i.e. each slot takes one of 24 single-qubit Clifford gates. In ${\mathbb{U}}$, each slot can take any single-qubit unitary. When errors are independent of the choice of single-qubit gates, MSEs are the same for the two circuit sets, i.e. ${L}_{{\mathbb{U}}}={L}_{{\mathbb{C}}}$⁴². Because the set ${\mathbb{C}}$ is large, we need to use the Monte Carlo method to evaluate ${L}_{{\mathbb{C}}}$.

There is a similar relation between ICS and unitary sampling. Error-sensitive circuits are a subset of all Clifford circuits, denoted by ${{\mathbb{C}}}^{ES}$. According to Algorithm 1, given slot gates $\bar{R}=({R}_{n+1},{R}_{n+2},\ldots ,{R}_{{N}_{R}})$, the number of error-sensitive circuits is 8^w(C)24^n−w(C). If ${P}_{i}^{{\prime} }=I$, ${R}_{i}^{{\dagger} }{P}_{i}^{{\prime} }{R}_{i}=I$ for all 24 single-qubit Clifford gates, which contributes a factor of 24; If ${P}_{i}^{{\prime} }\ne I$, ${R}_{i}^{{\dagger} }{P}_{i}^{{\prime} }{R}_{i}=\pm Z$ for 8 single-qubit Clifford gates, which contributes a factor of 8. The number of different $\bar{R}$’s is $2{4}^{{N}_{R}-n}$, then the total number of error-sensitive circuits is

$$| {{\mathbb{C}}}^{ES}| =\mathop{\sum }\limits_{j=1}^{2{4}^{{N}_{R}-n}}{8}^{w({{{{\boldsymbol{C}}}}}_{j})}2{4}^{n-w({{{{\boldsymbol{C}}}}}_{j})},$$

(16)

where C_j are circuits with different $\bar{R}$’s. In a Clifford circuit, a Pauli error either preserves the Pauli observable or flips its sign. As a result, non-sensitive Clifford circuits do not respond to Pauli errors, i.e y_C = f_C if f_C = 0. Therefore,

$${L}_{{\mathbb{U}}}={L}_{{\mathbb{C}}}=\eta {L}_{{{\mathbb{C}}}^{ES}},$$

(17)

for Pauli error models, where $\eta \equiv | {{\mathbb{C}}}^{ES}| /| {\mathbb{C}}|$ is the proportion of error-sensitive circuits in all Clifford circuits.

The distribution of error-sensitive circuits from Algorithm 2 is non-uniform. Because we uniformly choose slot gates in $\bar{R}$, the probability of an error-sensitive circuit C is

$$\begin{array}{lll}{P}_{nu}({{{\boldsymbol{C}}}})&=&2{4}^{-({N}_{R}-n)}{8}^{-w({{{\boldsymbol{C}}}})}2{4}^{-[n-w({{{\boldsymbol{C}}}})]}\\ &=&2{4}^{-{N}_{R}}{3}^{w({{{\boldsymbol{C}}}})}.\end{array}$$

(18)

Therefore, the probability of C is proportional to 3^w(C). If we use Algorithm 2 to sample circuits, we can evaluate ${L}_{{{\mathbb{C}}}^{ES}}$ according to

$${L}_{{{\mathbb{C}}}^{ES}}={\eta }^{-1}{{{\rm{E}}}}{[{3}^{-w({{{\boldsymbol{C}}}})}{({y}_{{{{\boldsymbol{C}}}}}-{f}_{{{{\boldsymbol{C}}}}})}^{2}]}_{nu},$$

(19)

where the expected value is taken over the distribution P_nu(C).

We can generate a uniform distribution of error-sensitive circuits as shown in Algorithm 3. In the uniform distribution, the probability of an error-sensitive circuit is ${P}_{u}({{{\boldsymbol{C}}}})=| {{\mathbb{C}}}^{ES}{| }^{-1}$. Then, we can evaluate ${L}_{{{\mathbb{C}}}^{ES}}$ with ${L}_{{{\mathbb{C}}}^{ES}}={{{\rm{E}}}}{[{({y}_{{{{\boldsymbol{C}}}}}-{f}_{{{{\boldsymbol{C}}}}})}^{2}]}_{u}$, where the expected value is taken over the distribution P_u(C). By changing the formula of the acceptance probability, we can use the same algorithm to generate other distributions of error-sensitive circuits.

We now summarise the algorithms and analyse their classical-computing costs. Algorithm 1 is used to generate an error-sensitive circuit. Provided with an observable Q and a frame with n qubits and N two-qubit gates, Algorithm 1 includes operations that conjugate Q (line 3) via O(N) Clifford gates and a conditioned random selection for the single-qubit gates in the first layer (line 5 to 8). The time cost of the conjugating operations is O(nN) according to the efficient simulation algorithm for Clifford gates³⁹, and the time cost of selecting gates in the first layer is O(n). Thus, the cost of Algorithm 1 is O(nN). Algorithm 2 and Algorithm 3 are used to sample error-sensitive circuits according to the non-uniform distribution P_nu(C) and uniform distribution P_u(C), respectively. To generate N_T circuits, the costs for both algorithms are O(N_TnN), because the elementary building block of both algorithms is nothing but the circuit generation given in Algorithm 1, which is repeated for N_T times. The numerical result in Supplementary Note 3 demonstrates that the number of error-sensitive circuits N_T required to perform learning-based error mitigation does not increase (as far as we have observed) with either the number of gates or the number of qubits. Overall, the cost scales linearly with the number of qubits and the number of gates. Noting that the sampling algorithms assume that two-qubit gates are Clifford and errors are independent of single-qubit gates. We give discussion in Supplementary Note 4 about the implementation of the algorithms when the assumptions are not satisfied.

Phenomenological-error model

In this section, we introduce the phenomenological-error model which quantifies the bias caused by realistic errors in a circuit. Then, we show that the phenomenological-error model can be effectively represented by a global depolarising model with fluctuation, and the fluctuation is $O(1/\sqrt{N})$ times smaller than the depolarising rate. This result suggests that, if we are able to use error mitigation to cancel the impact of the effective global depolarising error, we can reduce the bias caused by realistic errors by a factor of $O(1/\sqrt{N})$.

Before introducing our phenomenological-error model, we give a brief overview of realistic error models. Consider a quantum gate with the unitary operator U_i, the error-free output state of the gate is [U_i]ρ_i, where ρ_i is the input state. When the gate is imperfect, we can always express the output state with error as ${{{{\mathcal{N}}}}}_{i}[{U}_{i}]{\rho }_{i}$ (assuming the noisy circuit is a Markov process), where the completely positive map ${{{{\mathcal{N}}}}}_{i}$ describes the effect of noise associated with the gate. In the global depolarising model, ${{{{\mathcal{N}}}}}_{i}=(1-\epsilon )[{\mathbb{1}}]+\epsilon {{{\mathcal{D}}}}$. In realistic error models, ${{{{\mathcal{N}}}}}_{i}$ is usually caused by local processes, such as dephasing, dissipation and imperfections in the coherent evolution. If the gate acts on qubit-1 and qubit-2, the noise mainly affects these two qubits. Taking a Pauli error model as an example, the noise map reads

$${{{{\mathcal{N}}}}}_{i}=\left(1-\frac{16\epsilon }{15}\right)[{I}^{\otimes n}]+\frac{16\epsilon }{15}{{{{\mathcal{D}}}}}_{1,2},$$

(20)

where

$${{{{\mathcal{D}}}}}_{1,2}\equiv \frac{1}{16}\mathop{\sum}\limits_{{P}_{1},{P}_{2}=I,X,Y,Z}[{P}_{1}\otimes {P}_{2}\otimes {I}^{\otimes (n-2)}].$$

(21)

We call this particular Pauli error model the gate depolarising model, in which probabilities of Pauli errors are the same. We can rewrite this summation-form error model into the product form

$${{{{\mathcal{N}}}}}_{i}=\mathop{\prod}\limits_{{P}_{1},{P}_{2}=I,X,Y,Z}\left[(1-p)[{I}^{\otimes n}]+p[{P}_{1}\otimes {P}_{2}\otimes {I}^{\otimes (n-2)}]\right],$$

(22)

where p ≃ ϵ/15. In the product form, the noise map is a product of 15 independent maps, and we call each of them a Pauli error channel.

The global depolarising model with fluctuation can characterise the impact of realistic errors in large circuits. Given a circuit C, the error-free final state is ${\rho }_{0}=U\left\vert 0\right\rangle {\left\langle 0\right\vert }^{\otimes n}{U}^{{\dagger} }$. In our error model, the erroneous final state is ρ = (1 − ϵ_C)ρ₀ + ϵ_Cρ_m, where ϵ_C is the circuit-dependent depolarising rate. According to this model, we have y_C = (1 − ϵ_C)f_C. If we allow ϵ_C to be any value (rather than limited in the interval [0, 1]), this error model is a general phenomenological-error model. Given any f_C and y_C, the corresponding depolarising rate is ϵ_C = 1 − y_C/f_C. Note that the bias is ϵ_Cf_C, which is always finite even when f_C = 0 and ϵ_C is infinite.

We write the circuit-dependent depolarising rate as two terms, the average and fluctuation, i.e. ϵ_C = ϵ₀ + δϵ_C, where

$${\epsilon }_{0}\equiv \frac{{\langle {\epsilon }_{{{{\boldsymbol{C}}}}}{f}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{\mathbb{U}}}}{{\langle {f}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{\mathbb{U}}}}$$

(23)

is the average depolarising rate with the weight ${f}_{{{{\boldsymbol{C}}}}}^{2}$, and δϵ_C is the circuit-dependent fluctuation. We characterise the fluctuation with the weighted standard deviation

$$\Delta \equiv \sqrt{\frac{{\langle \delta {\epsilon }_{{{{\boldsymbol{C}}}}}^{2}{f}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{\mathbb{U}}}}{{\langle {f}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{\mathbb{U}}}}}.$$

(24)

The key result is that Δ increases with the gate number as O(N^γ), and γ ≈ 0.5, see Fig. 2.

In the rest part of this section, we show theoretically that the standard deviation Δ is proportional to $\sqrt{N}$ using a Pauli error model. In the next two sections, we introduce an error mitigation protocol inspired by the phenomenological-error model, then we verify the scaling behaviour in numerical simulations of the gate depolarising model, composite error models involving Pauli, amplitude damping and coherent errors, and a model with single-qubit-gate-dependent errors. The $\sqrt{N}$ scaling is observed in all the error models.

We focus on Pauli errors to analyse the fluctuation in the phenomenological-error model. For general errors, we can use Pauli twirling to convert them into Pauli errors. If error mitigation is concatenated with error correction, logical errors after correction are mainly Pauli errors⁴³. Suppose errors are independent of single-qubit gates, we have the following relations,

$${\langle {f}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{\mathbb{U}}}={\langle {f}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{\mathbb{C}}}=\eta {\langle {f}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{{\mathbb{C}}}^{ES}},$$

(25)

$${\langle {f}_{{{{\boldsymbol{C}}}}}{y}_{{{{\boldsymbol{C}}}}}\rangle }_{{\mathbb{U}}}={\langle {f}_{{{{\boldsymbol{C}}}}}{y}_{{{{\boldsymbol{C}}}}}\rangle }_{{\mathbb{C}}}=\eta {\langle {f}_{{{{\boldsymbol{C}}}}}{y}_{{{{\boldsymbol{C}}}}}\rangle }_{{{\mathbb{C}}}^{ES}},$$

(26)

$${\langle {y}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{\mathbb{U}}}={\langle {y}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{\mathbb{C}}}=\eta {\langle {y}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{{\mathbb{C}}}^{ES}},$$

(27)

where ${\mathbb{U}}$, ${\mathbb{C}}$ and ${{\mathbb{C}}}^{ES}$ are circuit sets with the same frame. In the above equations, the first equal sign follows because the Clifford group is a unitary-2 design^42,44, and therefore ${\langle \bullet \rangle }_{{\mathbb{U}}}={\langle \bullet \rangle }_{{\mathbb{C}}}$ holds if • is a polynomial of degree two in the gate unitaries. The second equal sign is a consequence of f_C = 0 when ${{{\boldsymbol{C}}}}\notin {{\mathbb{C}}}^{ES}$ and $\eta =| {{\mathbb{C}}}^{ES}| /| {\mathbb{C}}|$. Using f_C = ± 1 for error-sensitive circuits, we can obtain

$$\eta ={\langle {f}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{\mathbb{U}}},$$

(28)

$${\epsilon }_{0}={\langle {\epsilon }_{{{{\boldsymbol{C}}}}}\rangle }_{{{\mathbb{C}}}^{ES}},$$

(29)

$$\Delta =\sqrt{{\langle \delta {\epsilon }_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{{\mathbb{C}}}^{ES}}}.$$

(30)

These relations allow us to study ϵ₀ and Δ with error-sensitive circuits.

For simplicity, we consider an error model where two-qubit gates are the dominant sources of errors in actual quantum computing devices. We assume that the initialisation, single-qubit gates and measurement are perfect. In a two-qubit gate, we assume that the probability of Pauli errors are the same, i.e. the gate depolarising model. We use ${N}^{{\prime} }$ to denote the number of two-qubit gates.

The effect of local Pauli errors is equivalent to that of global depolarising errors in error-sensitive circuits. The unitary transformation of a circuit with N gates is U = U_N ⋯ U₁. If a Pauli error σ occurs after the ith gate, the transformation becomes ${U}^{{\prime} }={U}_{N}\cdots {U}_{i+1}\sigma {U}_{i}\cdots {U}_{1}={\sigma }_{{{{\boldsymbol{C}}}}}^{{\prime} }U$, where ${\sigma }_{{{{\boldsymbol{C}}}}}^{{\prime} }={U}_{N}\cdots {U}_{i+1}\sigma {U}_{i+1}^{{\dagger} }\cdots {U}_{N}^{{\dagger} }$ is the Pauli error propagated to the end of the circuit. Because gates are Clifford, ${\sigma }_{{{{\boldsymbol{C}}}}}^{{\prime} }$ is also a Pauli operator, i.e. any Pauli error in the circuit is equivalent to a Pauli error at the end of the circuit. If the probability of the Pauli error is p, i.e. the error channel is $(1-p)[{\mathbb{1}}]+p[\sigma ]$, the final state of the circuit is transformed from ρ₀ to $(1-p){\rho }_{0}+p[{\sigma }_{{{{\boldsymbol{C}}}}}^{{\prime} }]{\rho }_{0}$. Then there are two cases: If ${\sigma }_{{{{\boldsymbol{C}}}}}^{{\prime} }$ and the Pauli observable Q are commutative, the expected value is preserved under the Pauli error; otherwise, the expected value is changed from f_C to (1 − 2p)f_C, i.e. the equivalent depolarising rate is 2p.

The overall depolarising rate depends on the number of Pauli error channels. Each two-qubit gate contributes 15 Pauli error channels according to the product form of the Pauli error model. For a circuit with ${N}^{{\prime} }$ two-qubit gates, there are $M=15{N}^{{\prime} }$ error channels. Let $(1-p)[{\mathbb{1}}]+p[{\sigma }_{k}]$ be the k-th error channel, $(1-p)[{\mathbb{1}}]+p[{\sigma }_{k,{{{\boldsymbol{C}}}}}^{{\prime} }]$ is the corresponding error channel at the end of the circuit. We use the binary number t_k(C) to denote whether the k-th error channel affect the observable, i.e. t_k(C) = 0 if ${\sigma }_{k,{{{\boldsymbol{C}}}}}^{{\prime} }$ and Q are commutative, and t_k(C) = 1 otherwise. Then, the expected value is changed to $\mathop{\prod }\nolimits_{k = 1}^{M}{(1-2p)}^{{t}_{k}({{{\boldsymbol{C}}}})}{f}_{{{{\boldsymbol{C}}}}}$. The equivalent depolarising rate is

$${\epsilon }_{{{{\boldsymbol{C}}}}}=1-\mathop{\prod }\limits_{k=1}^{M}{(1-2p)}^{{t}_{k}({{{\boldsymbol{C}}}})}=\mathop{\sum }\limits_{k=1}^{M}2{t}_{k}({{{\boldsymbol{C}}}})p+O({p}^{2}).$$

(31)

The average depolarising rate is proportional to the gate number, and the standard deviation is proportional to the square root of the gate number. We can understand this phenomenon as follows. If we choose the circuit randomly from the circuit set, each error channel is switched on and off randomly, i.e. each t_k takes a random value. Under the assumption that t_k are independent and identically distributed random variables, the distribution of ϵ_C is binomial. Let P be the probability of t_k = 1 and neglect O(p²) terms, the average depolarising rate is ϵ₀ ≃ 2pMP, and the standard deviation is $\Delta \simeq \sqrt{2pMP(1-P)}$. Note that M is proportional to the gate number.

In large circuits, the global depolarising model with the depolarising rate ϵ₀ is an approximate phenomenological-error model. When we sample circuits composed of noisy gates, the circuit plays the role of a sampler, i.e. the impact of each gate error is a random variable dependent on the circuit configuration. In a certain regime, the total impact is the summation of individual gate errors. When the gate number is larger, the number of random variables in the summation is larger. According to the law of large numbers, the relative standard deviation of the summation decreases with the number of random variables, i.e.

$$\frac{\Delta }{{\epsilon }_{0}}\propto \frac{1}{\sqrt{M}},$$

(32)

where $M\propto {N}^{{\prime} } \sim N$. Therefore, ϵ_C is in the vicinity of ϵ₀ with a high probability in large circuits.

The analysis above has shown that local gate errors can be represented by a fluctuating global depolarising error, and the ratio of the fluctuation Δ to the depolarising rate ϵ₀ is in proportion to $1/\sqrt{N}$. This result will be verified by the numerical simulations in the next two sections. We will show that, if the effective global depolarising error is removed by error mitigation, the remaining error (caused by the fluctuation) scales with the gate number as $1/\sqrt{N}$. In addition, we numerically illustrate the error propagation model used in the above analysis. We show that the overall effect of propagated gate errors will become close to the global depolarising error and the relative difference between them decreases as $1/\sqrt{N}$. We leave the numerical result of error propagation to Supplementary Note 2.

The analysis in this section assumes a small total error rate pM. Under this assumption, we can neglect contributions from the second order in Eq. (31). In the section of “Numerical results of the scaling behaviour”, we randomly take total error rates from about 0.003 to 0.3, and we observe the $\sqrt{N}$ scaling behaviour. We remark that a modest total error rate is a general requirement of quantum error mitigation^45,46. Unlike quantum error correction, which actively detects and corrects errors in the circuit, most quantum error mitigation protocols correct the result by post-processing the noisy experimental data. When the total error rate is high, i.e. the fidelity approaches zero, the raw data lose the information about the correct quantum state, from which post-processing cannot recover the information. For example, in probabilistic error cancellation, the sampling overhead is exponential in the number of gates given a constant error rate per gate^7,8.

Error mitigation according to the phenomenological-error model

According to the phenomenological-error model, the effective depolarising rate in large circuits is ϵ₀ with a small fluctuation. We can mitigate errors by compensating the effect of ϵ₀. We use the root mean square error (RMSE) as the measure of the overall accuracy of an error mitigation formula in a circuit set. Before error mitigation, RMSE of unitary circuits with the same frame is $\scriptstyle\sqrt{{\langle {({y}_{{{{\boldsymbol{C}}}}}-{f}_{{{{\boldsymbol{C}}}}})}^{2}\rangle }_{{\mathbb{U}}}}=\sqrt{\eta ({\epsilon }_{0}^{2}+{\Delta }^{2})}\simeq \sqrt{\eta }{\epsilon }_{0}$, which increases linearly with the gate number. Using the error mitigation formula ${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }={(1-{\epsilon }_{0})}^{-1}{y}_{{{{\boldsymbol{C}}}}}$, we can reduce RMSE to $\scriptstyle\sqrt{{\langle {({y}_{{{{\boldsymbol{C}}}}}^{{\prime} }-{f}_{{{{\boldsymbol{C}}}}})}^{2}\rangle }_{{\mathbb{U}}}}={(1-{\epsilon }_{0})}^{-1}\sqrt{\eta }\Delta \simeq \sqrt{\eta }\Delta$, which increases sublinearly with the gate number. Because ${\epsilon }_{0}=1-{\langle {y}_{{{{\boldsymbol{C}}}}}{f}_{{{{\boldsymbol{C}}}}}\rangle }_{{{\mathbb{C}}}^{ES}}$, we can measure ϵ₀ (and Δ) by uniformly sampling error-sensitive circuits. Actually, because the fluctuation is small, we can even take ${\hat{\epsilon }}_{0}=1-{y}_{{{{\boldsymbol{C}}}}}{f}_{{{{\boldsymbol{C}}}}}$ for one randomly generated error-sensitive circuit ${{{\boldsymbol{C}}}}\in {{\mathbb{C}}}^{ES}$, and it is likely that the error mitigation formula still works. This phenomenological-error-model inspired (PEMI) error mitigation protocol is illustrated in Fig. 5.

Fig. 5: Distributions of the bias for six-qubit periodic-cycling circuits with 72 two-qubit gates under the gate depolarising noise.

The error rate per gate is 0.001. Before error mitigation, the bias distribution of unitary circuits (the blue histogram) has a shape similar to the Gaussian distribution, and the bias distribution of error-sensitive circuits (the orange histogram) is concentrated at two values. When we mitigate errors according to the average depolarising rate ϵ₀, we move the two peaks to the centre, and the residual bias is determined by the width of the two peaks. Because of the equivalence between the importance Clifford sampling and unitary sampling, the bias of unitary circuits is significantly reduced after error mitigation (the red histogram).

Similar protocols that mitigate errors according to the global depolarising model have been proposed in Refs. ^37,47,48. In these protocols, the effective depolarising rate is measured in different ways. Before considering general error mitigation formulas, we take the PEMI protocol as an example to verify the phenomenological-error model, because the bias of this protocol is directly related to the fluctuation.

In the PEMI protocol, we can further reduce RMSE by optimising the error mitigation formula. If we take

$${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }=\frac{1-{\epsilon }_{0}}{{(1-{\epsilon }_{0})}^{2}+{\Delta }^{2}}{y}_{{{{\boldsymbol{C}}}}},$$

(33)

RMSE after mitigation is reduced to

$$\sqrt{{\langle {({y}_{{{{\boldsymbol{C}}}}}^{{\prime} }-{f}_{{{{\boldsymbol{C}}}}})}^{2}\rangle }_{{\mathbb{U}}}}=\frac{\sqrt{\eta }\Delta }{\sqrt{{(1-{\epsilon }_{0})}^{2}+{\Delta }^{2}}}.$$

(34)

Numerical results of the scaling behaviour

In this section, we numerically test the PEMI error mitigation formula and verify the scaling behaviour of ϵ₀ and Δ. Results of other error mitigation formulas will be given in the next section.

To demonstrate the scaling behaviour, we generate three families of circuits. In periodic-cycling circuits, two-qubit gates are arranged according to a fixed pattern, and we increase the circuit depth by repeating the pattern. Therefore, periodic-cycling circuits are deterministic. In linear-network circuits, two-qubit gates only act on the nearest neighbouring qubits on a one-dimensional qubit array, and we randomly place two-qubit gates in the circuit. In all-to-all-network circuits, two-qubit gates are also arranged randomly but they can act on any pair of qubits.

We use three types of error models in our numerical calculations: the gate depolarising model with a randomly selected error rate, randomly generated composite error models and a model with single-qubit-gate-dependent errors. The gate depolarising model is used to derive the phenomenological-error model, but the conclusion holds for other error models. The composite error model involves gate depolarising, dephasing, amplitude damping and coherent errors, which are the typical error sources in actual devices. We generate different composite error models by randomly choosing the weight of each component and observe the same scaling behaviour as the gate depolarising model. The equivalence between Clifford sampling and unitary sampling is also used in deriving the phenomenological-error model, which is under the condition that errors are single-qubit-gate independent. In the numerical result, we find that the conclusion on the scaling behaviour holds even if errors are single-qubit-gate dependent. See the Methods section for details of numerical calculations.

By compensating the average depolarising rate, we can reduce RMSE from $\scriptstyle\sqrt{L}=\sqrt{{\langle {({y}_{{{{\boldsymbol{C}}}}}-{f}_{{{{\boldsymbol{C}}}}})}^{2}\rangle }_{{\mathbb{U}}}}\simeq \sqrt{\eta }{\epsilon }_{0}$ to $\scriptstyle\sqrt{{L}^{{\prime} }}=\sqrt{{\langle {({y}_{{{{\boldsymbol{C}}}}}^{{\prime} }-{f}_{{{{\boldsymbol{C}}}}})}^{2}\rangle }_{{\mathbb{U}}}}\simeq \sqrt{\eta }\Delta$. According to the discussion in the section of “Phenomenological-error model”, ϵ₀ ∝ N and $\Delta \propto \sqrt{N}$. Therefore, RMSE is reduced in error mitigation by a factor of $\Delta /{\epsilon }_{0}\propto 1/\sqrt{N}$. We verify these scaling behaviours by applying the error mitigation formula in Eq. (33) to randomly generated circuits with up to ten qubits and more than a thousand two-qubit gates. To implement the formula, ϵ₀ and Δ are measured by sampling error-sensitive circuits. RMSEs before and after error mitigation $\sqrt{L}$ and $\sqrt{{L}^{{\prime} }}$ are calculated and plotted in Figs. 6 and 7. For the model with single-qubit-gate-dependent errors, we directly calculate and plot ϵ₀ and Δ in Fig. 8. We can find that numerical results are consistent with scaling behaviours predicted by the phenomenological-error model. In addition, we perform experiments on IBM quantum computers⁴⁹ and observe good agreement between the numerical and experimental results. We include the experimental results in Supplementary Note 6.

Fig. 6: Root mean square errors of linear-network circuits with the gate depolarising model.

a Root mean square error $\sqrt{L}$ before error mitigation. b Root mean square error $\sqrt{{L}^{{\prime} }}$ after error mitigation. In the numerical simulation, we randomly generate a circuit frame with n qubits and N two-qubit gates, and we randomly take the error rate per gate ϵ. We generate 1000 Clifford circuits according to Algorithm 2 to estimate the phenomenological-error rate and then generate 1000 random unitary circuits to compute L and ${L}^{{\prime} }$.

Fig. 7: Root mean square errors of all-to-all-network circuits.

a, c Root mean square error $\sqrt{L}$ before error mitigation. b, d Root mean square error $\sqrt{{L}^{{\prime} }}$ after error mitigation. The results in (a) and (b) are obtained with the gate depolarising model, and the results in (c) and (d) are obtained with the composite model. In the numerical simulation, we randomly generate a circuit frame with n qubits and N two-qubit gates, and we randomly take the error rate per gate ϵ. We generate 1000 Clifford circuits according to Algorithm 2 to estimate the phenomenological-error rate and then generate 1000 random unitary circuits to compute L and ${L}^{{\prime} }$.

Fig. 8: Average depolarising rate ϵ₀ and standard deviation Δ in six-qubit periodic-cycling circuits.

The axis on the left corresponds to ϵ₀ and the axis on the right corresponds to Δ. The error rate per two-qubit gate is ϵ = 2 × 10⁻⁴, and the error rate of a single-qubit gate R is $0.1{\pi }^{-1}\epsilon \arccos \frac{| {{{\rm{Tr}}}}(R)| }{2}$. The error bar represents one standard deviation.

In Fig. 7, the error suppression ratio $\sqrt{L/{L}^{{\prime} }}$ for all-to-all-network circuits meets $\sqrt{L/{L}^{{\prime} }}=a\sqrt{N}$ and a is a positive number independent of the qubit number. However, in Fig. 6, we find that a for linear-network circuits decreases with the qubit number. The difference between all-to-all-network and linear-network circuits is that two-qubit gates in linear-network circuits are short-range, thus it requires more gates for the error on one qubit to propagate across the circuit network.

The error suppression ratio $\sqrt{L/{L}^{{\prime} }}$ are obtained via averaging random unitary circuits, which usually have near-zero expected values. However, in common quantum applications such as variational quantum eigensolver, the expected value is far from zero, which is atypical for random unitary circuits. Thus, we come to ask the question of whether the average suppression ratio of random unitary circuits is also the error suppression ratio of these atypical circuits. To answer this question, we numerically investigate the dependence of the error suppression ratio on the error-free expectation. The numerical result is illustrated in Supplementary Note 5, and the answer is which demonstrates that the average error suppression ratio can be applied to these atypical circuits.

We note that the $\sqrt{N}$ scaling of error-mitigated result relies on a modest total error rate. This condition is essential for quantum error mitigation methods to work properly^45,46 and is considered as a general requirement of NISQ computation³. For each data point in Figs. 6 and 7, we randomly choose the error rate per gate ϵ such that the total error rate Nϵ is in the interval about 0.003 to 0.3.

Error scaling in optimised error mitigation formulas

In this section, we utilise the phenomenological-error model to show that one can suppress the scaling of the residual bias in a learning-based manner. For imperfect error extrapolation and probabilistic error cancellation, the error scaling after the optimisation is $\propto \sqrt{N}$. The imperfections are due to the imperfect control of noise in error extrapolation and inaccurate knowledge of the error model in probabilistic error cancellation. For virtual distillation, the result is similar.

First, we analyse the error scaling of error extrapolation. An error mitigation formula usually involves multiple circuits. For each of them, we can effectively characterise the impact of noise using our phenomenological-error model. Taking the linear error extrapolation as an example, the two circuits C₁ and C₂ are the same as the primitive circuit C, but the noise level is doubled in C₂. In the phenomenological-error model of the circuit C_i, the average depolarising rate is ϵ_i, the rate fluctuation is δϵ_C,i, and the standard deviation is Δ_i. Because C₁ and C₂ are the same circuit, their fluctuations are correlated: Suppose effective depolarising rates are approximately proportional to the noise level, we have ϵ₂ ≃ 2ϵ₁ and δϵ_C,2 = 2δϵ_C,1. Therefore, the fluctuation-caused bias depends on the covariance matrix ${K}_{i,j}\equiv {\eta }^{-1}{\langle \delta {\epsilon }_{{{{\boldsymbol{C}}}},i}\delta {\epsilon }_{{{{\boldsymbol{C}}}},j}{f}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{\mathbb{U}}}$.

For the linear extrapolation formula in Eq. (12), RMSE after mitigation depends on average depolarising rates ϵ_i and the covariance matrix K, i.e.

$$\sqrt{{\langle {({y}_{{{{\boldsymbol{C}}}}}^{{\prime} }-{f}_{{{{\boldsymbol{C}}}}})}^{2}\rangle }_{{\mathbb{U}}}}=\sqrt{\eta [{({E}^{{\dagger} }\Lambda -1)}^{2}+{\Lambda }^{{\dagger} }K\Lambda ]},$$

(35)

where $E={(1-{\epsilon }_{1},1-{\epsilon }_{2})}^{{{{\rm{T}}}}}$ and Λ = (λ, 1−λ)^T. Taking λ = ϵ₂/(ϵ₂ − ϵ₁), we can remove the contribution of average depolarising rates, and RMSE becomes $\scriptstyle\sqrt{{\langle {({y}_{{{{\boldsymbol{C}}}}}^{{\prime} }-{f}_{{{{\boldsymbol{C}}}}})}^{2}\rangle }_{{\mathbb{U}}}}=\sqrt{\eta {\Lambda }^{{\dagger} }K\Lambda }\le \sqrt{\eta ({\Delta }_{1}^{2}+{\Delta }_{2}^{2})}\parallel \Lambda \parallel \propto \sqrt{N}$. Here, we have used that K is positive semi-definite, ${\Delta }_{1}^{2}$ and ${\Delta }_{2}^{2}$ are diagonal elements of K, and $\parallel \Lambda \parallel \simeq \sqrt{5}$ does not change significantly with the gate number. Note that this upper bound holds even if the noise is not increased as designed, and we can further reduce RMSE by optimising the parameter λ. In Fig. 9, we plot RMSE before and after error mitigation. In the optimised error mitigation formula, we take λ = ϵ₂/(ϵ₂ − ϵ₁). The numerical result is consistent with the scaling behaviour predicted by the phenomenological-error model.

Fig. 9: Root mean square errors (RMSE) in error mitigation protocols.

The result is obtained using ten-qubit periodic-cycling circuits under the error model in Eq. (36) with ϵ_d = 8 × 10⁻⁵ and ϵ_z = 2 × 10⁻⁵, and we use 1000 Clifford circuits generated via Algorithm 2 for the training and 1000 unitary circuits to compute the RMSE. The error bar represents one standard deviation. In the raw result without error mitigation, RMSE increases linearly with the gate number. In error extrapolation (EE), noise is increased imperfectly: ϵ_d = 1.8 × 10⁻⁴ and ϵ_z = 2 × 10⁻⁵ in the error model with a doubled error rate, i.e. only the gate depolarising component is increased. In probabilistic error cancellation (PEC), we take the inverse map in Eq. (37) according to an inaccurate error model with only gate depolarising errors, i.e. we take λ = − 16ϵ_d/(15 − 16ϵ_d) before the optimisation and the optimal value after the optimisation.

Theorem 1

Consider the general extrapolation formula in Eq. (2), let ϵ_i, δϵ_C,i and Δ_i be the average depolarising rate, rate fluctuation and standard deviation of the circuit C_i, respectively, then

$$\mathop{\min }\limits_{\{{q}_{i}\}}\sqrt{{\langle {({y}_{{{{\boldsymbol{C}}}}}^{{\prime} }-{f}_{{{{\boldsymbol{C}}}}})}^{2}\rangle }_{{\mathbb{U}}}}\le \frac{\sqrt{\eta {E}^{{\dagger} }KE}}{\parallel E{\parallel }^{2}}\le \frac{\sqrt{\eta {\sum }_{i}{\Delta }_{i}^{2}}}{\parallel E\parallel }.$$

where $E={(1-{\epsilon }_{1},1-{\epsilon }_{2},\ldots )}^{{{{\rm{T}}}}}$, ${K}_{i,j}={\eta }^{-1}{\langle \delta {\epsilon }_{{{{\boldsymbol{C}}}},i}\delta {\epsilon }_{{{{\boldsymbol{C}}}},j}{f}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{\mathbb{U}}}$ and $\eta ={\langle {f}_{{{{\boldsymbol{C}}}}}^{2}\rangle }_{{\mathbb{U}}}$.

The proof is straightforward. Let $\Lambda ={({q}_{1},{q}_{2},\ldots )}^{{{{\rm{T}}}}}$, the expression of RMSE is the same as Eq. (35). We can prove the theorem by taking Λ = E/∥E∥².

Second, we investigate the error scaling of probabilistic error cancellation. In probabilistic error cancellation, we reconstruct the transformation of the ideal circuit as a linear combination of transformations of noisy circuits. A practical way is decomposing each ideal gate in the circuit as a linear combination of noisy gates. In general, we can work out the decomposition as follows. If U_i is the unitary operator of the ideal gate, the completely positive map of the noisy gate is ${{{{\mathcal{N}}}}}_{i}[U]$. We can cancel the noise by applying an inverse noise $\scriptstyle{\widetilde{{{{\mathcal{N}}}}}}_{i}^{-1}={\sum }_{k}{q}_{i,k}{{{{\mathcal{E}}}}}_{i,k}$ after the noisy gate, and the overall effective gate is $\scriptstyle{\widetilde{{{{\mathcal{N}}}}}}_{i}^{-1}{{{{\mathcal{N}}}}}_{i}[U]$. Here, ${{{{\mathcal{E}}}}}_{i,k}$ are some noisy gates, i.e. we insert the gate ${{{{\mathcal{E}}}}}_{i,k}$ after the gate ${{{{\mathcal{N}}}}}_{i}[U]$ with the quasi-probability q_i,k. If $\scriptstyle{\widetilde{{{{\mathcal{N}}}}}}_{i}^{-1}={{{{\mathcal{N}}}}}_{i}^{-1}$, the error in the gate is completely removed; otherwise, effective noise in the gate is $\scriptstyle{\widetilde{{{{\mathcal{N}}}}}}_{i}^{-1}{{{{\mathcal{N}}}}}_{i}$.

We consider a Pauli error model with gate depolarising errors and dephasing errors as an example. For a two-qubit gate on qubit-1 and qubit-2, the noise map is

$$\begin{array}{lll}{{{{\mathcal{N}}}}}_{i}&=&\left(1-\frac{16{\epsilon }_{d}}{15}-{\epsilon }_{z}\right)[{I}^{\otimes n}]\\ &&+\frac{16{\epsilon }_{d}}{15}{{{{\mathcal{D}}}}}_{1,2}+\frac{{\epsilon }_{z}}{2}([{Z}_{1}]+[{Z}_{2}]),\end{array}$$

(36)

where Z_i = [I^⊗(i−1) ⊗ Z ⊗ I^⊗(n−i)]. Suppose our knowledge about the noise map is inaccurate and we correct the error according to the gate depolarising model, we have

$${\widetilde{{{{\mathcal{N}}}}}}_{i}^{-1}=(1-\lambda )[{I}^{\otimes n}]+\lambda {{{{\mathcal{D}}}}}_{1,2}.$$

(37)

When λ = − 16ϵ_d/(15 − 16ϵ_d) and ϵ_z = 0, we can correct all errors in the gate; otherwise, the effective gate has a finite error rate.

We can suppress the error scaling in imperfect probabilistic error cancellation by optimisation. For an error mitigation formula worked out according to an inaccurate error model, we can treat it as having a virtual quantum computer, in which the error model is given by $\scriptstyle{\widetilde{{{{\mathcal{N}}}}}}_{i}^{-1}{{{{\mathcal{N}}}}}_{i}$. Then, we can describe the error in this virtual machine using the phenomenological-error model and reduce the bias using the PEMI protocol. We can use the formula ${y}_{{{{\boldsymbol{C}}}}}^{{\prime\prime} }=(1-{\epsilon }_{0}^{{\prime} }){y}_{{{{\boldsymbol{C}}}}}^{{\prime} }$, where ${\epsilon }_{0}^{{\prime} }$ and ${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }$ are respectively the average depolarising rate and expected value in the virtual machine. Then the residual bias of ${y}_{{{{\boldsymbol{C}}}}}^{{\prime\prime} }$ is determined by the standard deviation ${\Delta }^{{\prime} }$ of the virtual machine. Actually, it is not necessary to modify the formula to suppress the error scaling. For example, we can take λ in Eq. (37) as a variational parameter and optimise it in ICS. The numerical result in Fig. 9 shows that RMSE of probabilistic error cancellation with the optimised λ scales as $\propto \sqrt{N}$.

Third, we investigate the error scaling of virtual distillation. The virtual distillation formula is nonlinear unlike error extrapolation and cancellation. For a general error mitigation formula, suppose the truncation on the Taylor expansion is valid, we have

$${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }\simeq F({a}_{1}{f}_{{{{{\boldsymbol{C}}}}}_{1}},{a}_{2}{f}_{{{{{\boldsymbol{C}}}}}_{2}},\cdots \,)+\mathop{\sum}\limits_{i}\frac{\partial F}{\partial {y}_{{{{\boldsymbol{C}}}},i}}\delta {\epsilon }_{{{{\boldsymbol{C}}}},i},$$

(38)

where a_i = 1 − ϵ_i. In Eq. (38), we have considered the general error mitigation formula in Eq. (1) and ${y}_{{{{\boldsymbol{C}}}},i}=(1-{\epsilon }_{i}+\delta {\epsilon }_{{{{\boldsymbol{C}}}},i}){f}_{{{{{\boldsymbol{C}}}}}_{i}}$. If we can remove the zeroth-order term (contribution of average depolarising rates) by taking proper variational parameters in the formula, the bias is determined by fluctuations. For virtual distillation, $F({a}_{1}{f}_{{{{{\boldsymbol{C}}}}}_{1}},{a}_{2}{f}_{{{{{\boldsymbol{C}}}}}_{2}})={a}_{1}{f}_{{{{{\boldsymbol{C}}}}}_{1}}/({a}_{2}{f}_{{{{{\boldsymbol{C}}}}}_{2}})$, therefore, we can compensate average depolarising rates by a factor. In the numerical simulation, we determine the factor by taking the original virtual distillation formula ${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }={y}_{{{{{\boldsymbol{C}}}}}_{1}}/{y}_{{{{{\boldsymbol{C}}}}}_{2}}$ as a virtual machine and concatenating it with the PEMI protocol according to the formula ${y}_{{{{\boldsymbol{C}}}}}^{{\prime\prime} }=(1-{\epsilon }_{0}^{{\prime} }){y}_{{{{\boldsymbol{C}}}}}^{{\prime} }$, where ${\epsilon }_{0}^{{\prime} }$ is the average depolarising rate of ${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }$. We find that RMSE of the optimised formula scales as N^α and α < 1/2 as shown in Fig. 10.

Fig. 10: Root mean square errors (RMSE) in virtual distillation (VD) protocols.

The error bar represents one standard deviation. Other details such as the circuit configuration and error model are the same as Fig. 9.

The remaining error after virtual distillation changes from the coherent mismatch¹⁴ to decoherence error when the gate number increases. With the error-mitigation formula ${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }={{{\rm{Tr}}}}(Q{\rho }^{2})/{{{\rm{Tr}}}}({\rho }^{2})$, the decoherence error is reduced from Nϵ (gate number times error rate per gate) to (Nϵ)², while the coherent mismatch is not suppressed, about which we give a short introduction in Supplementary Note 1.3. Because the remaining decoherence error increases quadratically with the gate number, the coherent mismatch is the dominant component in the remaining error when the gate number is small, and the decoherence error is the dominant component when the gate number is large. This change in the type of error could explain the bifurcation in Fig. 10, and the result suggests that the optimisation protocol can further reduce the remaining decoherence error but not the coherent mismatch.

In the numerical simulations, we have taken into account imperfect implementations in probabilistic error cancellation and error extrapolation. Assuming the implementation is perfect, probabilistic error cancellation can reduce RMSE to zero, and error extrapolation can reduce RMSE to a much lower level. Note that perfect implementation requires the exact knowledge of the error model or exact control of the error model. In virtual distillation, we have only taken into account errors in those gates that prepare the state ρ and neglected errors in those gates that implement virtual distillation, e.g. the controlled-swaps in Ref. ¹⁴.

Discussion

In this work, we show that the residual bias in the computation result after error mitigation scales with the gate number N as $O({\epsilon }^{{\prime} }{N}^{\gamma })$ if the error mitigation formula is optimised. Here, γ ≈ 0.5, and ${\epsilon }^{{\prime} }$ is a parameter depending on the error rate of quantum gates and the error mitigation formula. In contrast, the bias in the computation result before error mitigation scales linearly with N. The two scaling relations lead to a somewhat surprising result: We can suppress the computation error by a larger factor in larger circuits.

In the analysis, we introduce a phenomenological-error model characterising errors as the global depolarisation with fluctuation, which captures the impact of realistic noise on the computation result. For the optimisation of an error mitigation formula, we propose ICS as an efficient method of generating training circuits, where only those Clifford circuits sensitive to Pauli errors are selected. The optimised formula removes the average contribution of noise and leaves the fluctuation proportional to $\sqrt{N}$. We verify this result with the numerical simulation of various circuits, error models and error mitigation formulas, from which we observe that the scaling behaviour is universal.

Despite the encouraging scaling of bias in error mitigation, we point out that the circuit size is still limited by the quality of quantum devices. On a quantum device with a finite error rate per gate, the bias increases with the circuit size. Although the bias scaling after error mitigation is advantageous in comparison with the linear error accumulation before mitigation, at certain circuit sizes the computation result becomes sufficiently random that error mitigation cannot faithfully recover the information. Therefore, the efficacy of error mitigation is conditional on the quality of the quantum device. In general, the minimum requirement for error mitigation to take effect is a non-zero fidelity between the error-free and erroneous circuits, and the performance is better with higher fidelity. Beyond this, the impact of the unmitigated error rate on the accuracy of the mitigated result depends on the mitigation method. In probabilistic error cancellation, for example, the variance in calculating the expectation value of the result increases with the error rate. Another example is that, after the virtual distillation using two copies, the bias in the expectation value scales quadratically with the error rate. Once the device can implement the circuit with sufficiently high fidelity (which is not necessarily close to one but we take a fidelity of 0.9 as an example), error mitigation can improve the computation result to a much higher accuracy (equivalent to quantum computing with fidelity of 0.99 if the error is reduced by a factor of ten).

In scalable quantum computers, we can adopt quantum error correction to increase the fidelity of logical qubits. Protocols concatenating error correction with error mitigation have been proposed recently^50,51,52. Fault-tolerant devices will enable the implementation of much deeper circuits than NISQ hardware. Our result of the scaling behaviours suggests that error mitigation can perform even better in the fault-tolerant regime than in the NISQ regime.

Methods

Circuits

We use three families of circuits: periodic-cycling circuits, linear-network circuits and all-to-all-network circuits.

Periodic-cycling circuits. The qubit array has n qubits, and n is even. All qubits are initialised in the state $\left\vert 0\right\rangle$. After initialisation, a layer of single-qubit gates is placed, see Supplementary Figure 1(a). The circuit pattern is periodic, and each period has two layers of two-qubit gates. In the first layer, a controlled-Z gate is applied on qubit-(2i − 1) and qubit-(2i), where i = 1, 2, …, n/2. In the second layer, a controlled-Z gate is applied on qubit-(2i − 1) and qubit-(2i − 2), and qubit-0 and qubit-n are the same qubits. After each two-qubit gate, a single-qubit gate is applied to each of the two qubits. The observable O is Z of the first qubit. All single-qubit gates are taken as slots in the corresponding circuit frame.

Linear-network circuits. Except for the pattern of two-qubit gates and observable, the setup is the same as periodic-cycling circuits. All two-qubit gates are controlled-Z gates. For each of them, we randomly generate an integer i ∈ [1, n] and apply the two-qubit gate on qubit-(i − 1) and qubit-i, see Supplementary Figure 1(b). The observable is O = P₁ ⊗ P₂ ⊗ ⋯ ⊗ P_n, where P = I, Z is taken randomly.

All-to-all-network circuits. It is similar to linear-network circuits. For each of the two-qubit gates, we randomly generate two different integers i, j ∈ [1, n] and apply the two-qubit gate on qubit-i and qubit-j, see Supplementary Figure 1(c).

Error models

Several error models are used in the numerical simulations.

Gate depolarising model. The model is given in Eq. (20), and only two-qubit gates have errors. This model is used to generated data shown in Figs. 2, 5 and 6. In Figs. 2 and 5, we take ϵ = 0.001. In Figs. 6, for each data point, we randomly generate a circuit (and the corresponding circuit frame) and an error rate. For a circuit with N two-qubit gates, we generate a random real number η ∈ [ − 2.5, − 0.5], and we take ϵ = 10^η/N as the error rate per gate. Notice that 10^η is the total error rate.

Composite error model. Only two-qubit gates have errors. For a two-qubit gate U, the gate with errors is

$${{{{\mathcal{A}}}}}_{2}{{{{\mathcal{A}}}}}_{1}[{R}_{2,Z}{R}_{2,Y}{R}_{2,X}][{R}_{1,Z}{R}_{1,Y}{R}_{1,X}]{{{{\mathcal{Z}}}}}_{2}{{{{\mathcal{Z}}}}}_{1}{{{\mathcal{N}}}}[U],$$

where ${{{\mathcal{N}}}}$ is the gate depolarising error in Eq. (20) with the error rate ϵ_d, ${{{{\mathcal{Z}}}}}_{i}=(1-{\epsilon }_{i,z})[I]+{\epsilon }_{i,z}[Z]$ is the dephasing error on qubit-i, $\scriptstyle{R}_{i,P}={e}^{-i\frac{{\theta }_{i,P}}{2}P}$ is a single-qubit rotation on qubit-i, and

$$\begin{array}{lll}{{{{\mathcal{A}}}}}_{i}&=&\left[\frac{{\mathbb{1}}+Z}{2}+\sqrt{1-{\epsilon }_{i,a}}\frac{{\mathbb{1}}-Z}{2}\right]\\ &&+\left[\sqrt{{\epsilon }_{i,a}}\frac{X+iY}{2}\right]\end{array}$$

(39)

is the amplitude damping on qubit-i. This model is used to generate data shown in Fig. 7 (c) and (d). For each data point, we randomly generate the error model parameters as follows. For a circuit with N two-qubit gates, we generate a random real number η ∈ [ − 2.5, − 0.5], and we take ϵ = 10^η/N as the error rate per gate. Then, we take ϵ_d = (1 + 0.2κ_d)ϵ/9, ϵ_i,z = (1 + 0.2κ_i,z)ϵ/9, θ_i,P = κ_i,Pϵ/9 and ϵ_i,a = (1 + 0.2κ_i,a)ϵ/6. Each κ is taken randomly in the interval [ − 1, 1].

Gate-dependent error model. In this model, both single-qubit and two-qubit gates have errors. The error model is the gate depolarising model. For two-qubit gates, the noise map is given by Eq. (20). For a single-qubit gate R, the gate with error is ${{{\mathcal{S}}}}[R]$, where

$${{{\mathcal{S}}}}=\left(1-\frac{4{\epsilon}_{s}}{3}\right)[I]+\frac{{\epsilon}_{s}}{3}{\sum}_{P = I,X,Y,Z}[P],$$

(40)

and ${\epsilon }_{s}=0.1{\pi }^{-1}\epsilon \arccos \frac{| {{{\rm{Tr}}}}(R)| }{2}$. This model is used to generate data shown in Fig. 8, and we estimate ϵ₀ and Δ using 10000 unitary circuits in ${\mathbb{U}}$.

Gate depolarising and dephasing model. The model is given in Eq. (36), and only two-qubit gates have errors. This model is used to generate data shown in Figs. 9 and 10. In the numerical simulation, we approximate the error model with ${{{{\mathcal{Z}}}}}_{2}{{{{\mathcal{Z}}}}}_{1}{{{\mathcal{N}}}}$ for simplicity in coding, which only causes a small difference and will not change the conclusion.

The above error models take into consideration kinds of physical noise processes and are able to simulate noises in realistic quantum devices. The depolarising error ${{{\mathcal{N}}}}$ and dephasing error ${{{\mathcal{Z}}}}$ simulates the relaxation process and the dephasing process^53,54, which are the main contributions to noise in realistic quantum devices. Amplitude damping ${{{\mathcal{A}}}}$ refers to the infidelity caused by energy dissipation. Random rotations R refer to coherent errors caused by imperfect controls. This composite model takes into consideration all the above realistic imperfections and it was demonstrated in Ref. ⁴² that the composite model can produce error distributions resembling that in experiments on a superconducting quantum processor. The single-qubit-gate-dependent error model ${{{\mathcal{S}}}}$ is the single-qubit depolarising error with an error rate depending on the gate parameters. This error model takes into consideration the realistic situation that gate errors increase with the gate time. Additionally, we will make a direct comparison between the experimental results and simulation results in Supplementary Note 6 and show that experimental results are consistent with simulation results.

Error mitigation protocols

We verified the scaling behaviour by simulating various error mitigation protocols. The formula in Eq. (33) is used to generate data shown in Figs. 5, 6 and 7. The PEMI protocol in Fig. 9 is ${y}_{{{{\boldsymbol{C}}}}}^{{\prime} }={(1-{\epsilon }_{0})}^{-1}{y}_{{{{\boldsymbol{C}}}}}$. In optimised error extrapolation, we take λ = ϵ₂/(ϵ₂ − ϵ₁). In optimised probabilistic error cancellation, we take λ = − 16ϵ_d/(15 − 16ϵ_d) − 2ϵ_z: We have searched for the optimal λ using ICS data and found that the numerical optimal value is close to it. In optimised virtual distillation in Fig. 10, the formula is ${y}_{{{{\boldsymbol{C}}}}}^{{\prime\prime} }={(1-{\epsilon }_{0}^{{\prime} })}^{-1}{y}_{{{{\boldsymbol{C}}}}}^{{\prime} }$. To implement optimised error mitigation formulas, we estimate ϵ₀, Δ, ϵ₁, ϵ₂ or ${\epsilon }_{0}^{{\prime} }$ using 1000 error-sensitive circuits, according to Algorithm 2. Then, we generate 1000 unitary circuits with the same frame to estimate RMSE.