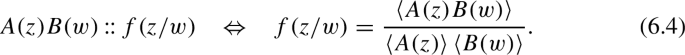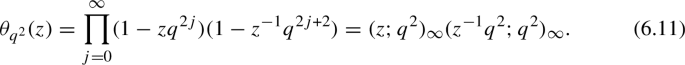Abstract
The notion of shifted quantum groups has recently played an important role in algebraic geometry. This subtle modification of the original definition brings more flexibility in the representation theory of quantum groups. The first part of this paper presents new mathematical results for the shifted quantum toroidal \(\mathfrak {gl}(1)\) and quantum affine \(\mathfrak {sl}(2)\) algebras (resp. denoted \({\ddot{U}}_{q_1,q_2}^{\varvec{\mu }}(\mathfrak {gl}(1))\) and \({\dot{U}}_q^{\varvec{\mu }}(\mathfrak {sl}(2))\)). It defines several new representations, including finite dimensional highest \(\ell \)-weight representations for the toroidal algebra, and a vertex representation of \({\dot{U}}_q^{\varvec{\mu }}(\mathfrak {sl}(2))\) acting on Hall–Littlewood polynomials. It also explores the relations between representations of \({\dot{U}}_q^{\varvec{\mu }}(\mathfrak {sl}(2))\) and \({\ddot{U}}_{q_1,q_2}^{\varvec{\mu }}(\mathfrak {gl}(1))\) in the limit \(q_1\rightarrow \infty \) (\(q_2\) fixed), and present the construction of several new intertwiners. These results are used in the second part to construct BPS observables for 5d \({{\mathcal {N}}}=1\) and 3d \({{\mathcal {N}}}=2\) gauge theories. In particular, it is shown that 5d hypermultiplets and 3d chiral multiplets can be introduced in the algebraic engineering framework using shifted representations, and the Higgsing procedure is revisited from this perspective.
















Similar content being viewed by others
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Notes
The shifted quantum affine \(\mathfrak {sl}(2)\) algebra with antidominant shift had appeared before in [6] in the context of quantum Q-systems of type A and cluster algebras.
Explicitly, we can choose the following isomorphism \(X^+(z)\rightarrow z^n X^+(z)\), \(X^-(z)\rightarrow X^-(z)\) and \(\Psi ^\pm (z)\rightarrow z^n\Psi ^\pm (z)\) in terms of the Drinfeld currents defined below.
It is shown in [5] in the case \(q^c=1\) and the central deformation is obvious.
More precisely, \(\iota _P\) and \(\iota _P^*\) send representations of \({{\mathcal {U}}}^{{\varvec{\mu }},\Omega }\) to representations of \({{\mathcal {U}}}^{{\varvec{\mu }}',\Omega '}\) with \({\varvec{\mu }}'={\varvec{\mu }}+{\varvec{\mu }}_P\) and \(\Omega '=\frac{\alpha _P^2}{\prod _a(-\nu _a)}\Omega \). Thus, to preserve the relation \(\Psi _{-\mu _+}^+\Psi _{\mu _-}^-=\Omega \), we would need to require \(\alpha _P^2=\prod _a(-\nu _a)\).
To compare with the standard literature on quantum groups, on may denote the weight \(a=v q^N\), replace \(q\rightarrow q^{-1}\) using \(\sigma _H\), and use the spectral parameter \(u=z^{-1}\). Then, the action of the Cartan on the vacuum state takes the familiar form of a ratio of Drinfeld polynomials,
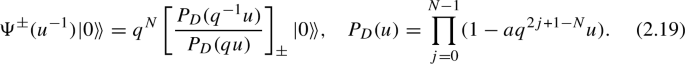
They are unrelated to the twisted vertex representations introduced by Jing in [30].
We made a minor modification of the zero modes to ease the comparison with the twisted Fock representations of the previous section.
Comparing the presentation 3.2 with the definition of the algebra \({{\mathcal {E}}}\) used in the work of Feigin, Jimbo, Miwa and Mukhin (e.g. [35]), we note that the Cartan currents have been twisted by the central element \({{\hat{\gamma }}}\) (denoted C in [35]) as \(\psi ^\pm (z)\rightarrow \psi ^\pm ({{\hat{\gamma }}}^{\pm 1/2}z)\), and the currents have also been rescaled which gives a different value for \(\kappa \). Besides, we do not include the grading elements in the definition of the algebra. These small differences should be kept in mind when comparing the papers.
Note that we use here a different notation than in [36].
The factors \(q_2^{k}\) and \(q_2^{1-k}\) in the matrix elements of \(x^+(z)\) and \(x^-(z)\) resp. can be eliminated by the rescaling \(\vert k\rangle \!\rangle \rightarrow q_2^{-k(k-1)/2}\vert k\rangle \!\rangle \) of the states. We kept these factors here to simplify the comparison with other representations.
Choosing more generally \(P(z)=\alpha _Pz^k(1-vq_2^{-1}/z)\), we would find a lowest weight representation of \({{\mathcal {E}}}^{(k,1-k)}\) on \({{\mathcal {L}}}\).
To be really precise and recover the formulas given in [36] for the matrix elements of the Drinfeld currents, we would need to take \(\iota _{P_1}\iota _{P_2}^*\rho _v^{{{\mathcal {L}}}^-}\) with \(P_1(z)=1-K^{-1}v/z\) and \(P_2(z)=K^{1/2}\) but these algebras are isomorphic when K is invertible.
It is possible to use different normalizations of the Heisenberg algebra, sending \(J_k\rightarrow r_kJ_k\) with \(r_kr_{-k}=1\). The choice taken here identifies the elementary symmetric polynomials \(p_k\) with \(q_3^{k/2}(1-q_2^k)J_{-k}\) so that the zero mode \(\eta _0^+\) in the expansion \(\eta ^+(z)=\sum _{k\in {{\mathbb {C}}}}z^{-k}\eta _k^+\) acts as the Macdonald operator [38].
We keep here the same notation as in 3.17 since the quantities coincide for \(k\ge 0\) if we replace \(q_2=\rightarrow q^2\).
This is also one of the reasons why Miki’s automorphism [34] cannot be extended to the quantum affine algebra in a simple way.
Note that we use here a standard Kronecker delta, instead of the Kronecker delta modulo p used in [44].
This expression follows from the limit of the functions \({{\mathcal {Y}}}_\lambda (z)\),
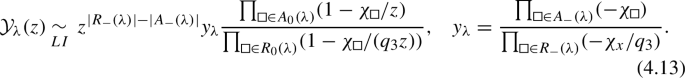
We also note that \(|A_-(\lambda )|-|R_-(\lambda )|\) is one if \(|A_0(\lambda )|=0\) and zero otherwise.
This argument works also at the level of modes. For instance, the exchange relation for \({\bar{\psi }}(z)\) reads in terms modes \(\eta _{A,n+1}{\bar{\psi }}_m-q_1\eta _{A,n}{\bar{\psi }}_{m+1}={\bar{\psi }}_m\eta _{A,n+1}-q_1q_2{\bar{\psi }}_{m+1}\eta _{A,n}\), and gives in the limit LII \({\hat{\eta }}_{A,n}{\bar{\psi }}_{m+1}=q^2{\bar{\psi }}_{m+1}{\hat{\eta }}_{A,n}\) which is independent of n.
In the first line, an extra factor \(q^{-2}\) arise from changing the position of \({\hat{\eta }}_A\) in the normal ordering, it compensates the limit \(-q_1^{-1}{\tilde{\kappa }}\rightarrow q^2\).
Alternatively, it can be seen as the brane web realizing the 4D \({{\mathcal {N}}}=2\) gauge theory obtained in the compactification limit \(R\rightarrow 0\). This theory is realized in type IIA string theory by suspending D4-branes (drawn vertically) between NS5-branes (drawn horizontally), while matter hypermultiplets are inserted using D6-branes transversal to the (56)-plane. However, in this case, the algebraic engineering is based on the affine Yangian double of \(\mathfrak {gl}(1)\) that is obtained from \({{\mathcal {E}}}\) in the limit \(R\rightarrow 0\) (see [55]).
Unfortunately, the case of fundamental hypermultiplets is not so clear.
This factor can be displaced by taking e.g. \(n_\lambda ={\bar{n}}_\lambda ^P\) but it is a purely cosmetic change.
Recall that the brane web is flattened and rotated by 90\(^\circ \), so that D5-branes become vertical lines and dressed NS5-branes horizontal lines.
This equality requires to adjust the weights and level according to the intermediate representation which is different. It is easy to see that the operator part matches on both sides, and the result follows from comparing the vevs
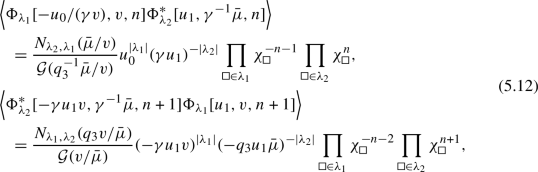
using the reflection formula for the Nekrasov factor (see e.g. footnote 6 in [16]). The two expressions match up to the one-loop factor involving the function \({{\mathcal {G}}}(z)\), and the result follows from the specialization at \(\lambda _2=\emptyset \). We refer to the appendix B of [16] for the definition of the function \({{\mathcal {G}}}(z)\).
Note that when \(\iota _P\rho _v^{(0,1)}\) is of dimension one, there is no difference between the operators \(\Phi \) and \(\Phi ^P\) since
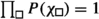 .
.In contrast with the ‘complex masses’ entering in the superpotential, ‘real masses’ correspond to a deformation of the supersymmetry algebra.
In these expressions, we used the shortcut notation \(A(z)B(w)\,{:}{:}\,f(z/w)\) for \(A(z)B(w)=f(z/w):A(z)B(w):\). To say it differently,
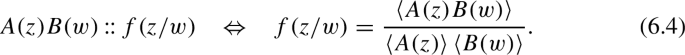
Normal-ordering relations of this type appear often in this context, and this trick shortens many formulas.
We recall the definition
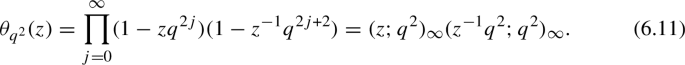
One should not confuse the transformation \(\iota _{P_\nu ^*}\), that is \(\iota _P\) with the polynomial \(P_\nu ^*\), and \(\iota _{P_\nu }^*\) which corresponds to \(\iota _P^*\) with the polynomial \(P_\nu \). In the same way, \(\Phi ^{P_\nu *}\) denotes the intertwiner \(\Phi ^*\) shifted by the polynomial \(P_\nu \) while \(\Phi ^{P_\nu ^*}\) is the intertwiner \(\Phi \) shifted by \(P_\nu ^*\).
While the limit LII of \({{\mathcal {G}}}(q_3^{-1}z)\) (with z finite) is well defined and produces the factor \((zq^2;q^2)_\infty ^{-1}\), the limit of \({{\mathcal {G}}}(z)\) requires a regularization that we simply denote \({{\mathcal {G}}}_{LII}(z)\) since we are not interested in the perturbative contributions.
In this appendix, we denote n the rank of the gauge group to avoid a conflict of notation with the vector space \(N={{\mathbb {C}}}^n\).
When the two n-tuples of Young diagrams \({\varvec{\lambda }}\) and \({\varvec{\lambda }}'\) differ, the quantity \(\chi _{{\varvec{\lambda }},{\varvec{\lambda }}'}\) is in fact the equivariant character of a fiber defined using the Hecke correspondence introduced in [81] as a generalization of the moduli space of nested Hilbert scheme to \(n>1\).
The presence of the extra factor \(q_3^{-1}\) in the argument of the function \({{\mathcal {Y}}}^*_{\varvec{\lambda }}(z)\) is a convention related to the property \(\chi _{{\varvec{\lambda }},{\varvec{\lambda }}'}^\vee =q_3\chi _{{\varvec{\lambda }}',{\varvec{\lambda }}}\) in the absence of hypermultiplets (symplectic quiver) which leads to the relation \({{\mathcal {Y}}}_{\varvec{\lambda }}^*(z)=\prod _l(-z/v_l)\ {{\mathcal {Y}}}_{\varvec{\lambda }}(z)\).
References
Brundan, J., Kleshchev, A.: Shifted Yangians and finite W-algebras. Adv. Math. 200(1), 136–195 (2006). https://doi.org/10.1016/j.aim.2004.11.004
Braverman, A., Feigin, B., Finkelberg, M., Rybnikov, L.: A Finite analog of the AGT relation I: finite \(W\)-algebras and quasimaps’ spaces. Commun. Math. Phys. 308, 457–478 (2011). https://doi.org/10.1007/s00220-011-1300-3. arXiv:1008.3655 [math.AG]
Braverman, A., Finkelberg, M., Nakajima, H.: Coulomb branches of \(3d\)\({\cal{N} }=4\) quiver gauge theories and slices in the affine Grassmannian. Adv. Theor. Math. Phys. 23, 75–166 (2019). https://doi.org/10.4310/ATMP.2019.v23.n1.a3. arXiv:1604.03625 [math.RT]
Nakajima, H., Weekes, A.: Coulomb branches of quiver gauge theories with symmetrizers. J. Eur. Math. Soc. (2021). arXiv:1907.06552 [math.QA]
Finkelberg, M., Tsymbaliuk, A.: Multiplicative slices, relativistic Toda and shifted quantum affine algebras. arXiv:1708.01795 [math.RT]
Di Francesco, P., Kedem, R.: Quantum Q systems: from cluster algebras to quantum current algebras. Lett. Math. Phys. 107(2), 301–341 (2016). https://doi.org/10.1007/s11005-016-0902-2. arXiv:1606.09052 [math.QA]
Hernandez, D., Jimbo, M.: Asymptotic representations and Drinfeld rational fractions. Compos. Math. 148(5), 1593–1623 (2012). https://doi.org/10.1112/S0010437X12000267
Bazhanov, V.V., Lukyanov, S.L., Zamolodchikov, A.B.: Integrable structure of conformal field theory. 3. The Yang–Baxter relation. Commun. Math. Phys. 200, 297–324 (1999). https://doi.org/10.1007/s002200050531. arXiv:hep-th/9805008
Hernandez, D.: Representations of shifted quantum affine algebras. arXiv:2010.06996 [math.RT]
Hernandez, D., Zhang, H.: Shifted Yangians and polynomial R-matrices. arXiv:2103.10993 [math.QA]
Bourgine, J.-E.: Engineering 3D \({\cal{N}}=2\) theories using the quantum affine \(\mathfrak{sl} (2)\) algebra. arXiv:2107.10063 [hep-th]
Bourgine, J.-E.: Webs of quantum algebra representations in 5d \(\cal{N} =1\) super Yang–Mills. Proc. Math. Stat. 263, 209–218 (2017). https://doi.org/10.1007/978-981-13-2715-5_11
Awata, H., Feigin, B., Shiraishi, J.: Quantum algebraic approach to refined topological vertex. JHEP 03, 041 (2012). https://doi.org/10.1007/JHEP03(2012)041. arXiv:1112.6074 [hep-th]
Awata, H., Kanno, H., Matsumoto, T., Mironov, A., Morozov, A., Morozov, A., Ohkubo, Y., Zenkevich, Y.: Explicit examples of DIM constraints for network matrix models. JHEP 07, 103 (2016). https://doi.org/10.1007/JHEP07(2016)103. arXiv:1604.08366 [hep-th]
Mironov, A., Morozov, A., Zenkevich, Y.: Ding–Iohara–Miki symmetry of network matrix models. Phys. Lett. B 762, 196–208 (2016). https://doi.org/10.1016/j.physletb.2016.09.033. arXiv:1603.05467 [hep-th]
Bourgine, J.-E., Fukuda, M., Harada, K., Matsuo, Y., Zhu, R.-D.: (p, q)-webs of DIM representations, 5d \( {\cal{N} }=1 \) instanton partition functions and qq-characters. JHEP 11, 034 (2017). https://doi.org/10.1007/JHEP11(2017)034. arXiv:1703.10759 [hep-th]
Bourgine, J.-E., Fukuda, M., Matsuo, Y., Zhu, R.-D.: Reflection states in Ding–Iohara–Miki algebra and brane-web for D-type quiver. JHEP 12, 015 (2017). https://doi.org/10.1007/JHEP12(2017)015. arXiv:1709.01954 [hep-th]
Zhu, R.-D.: An elliptic vertex of Awata–Feigin–Shiraishi type for M-strings. JHEP 08, 050 (2018). https://doi.org/10.1007/JHEP08(2018)050. arXiv:1712.10255 [hep-th]
Zenkevich, Y.: Higgsed network calculus. arXiv:1812.11961 [hep-th]
Zenkevich, Y.: Mixed network calculus. arXiv:2012.15563 [hep-th]
Ghoneim, M., Kozçaz, C., Kurşun, K., Zenkevich, Y.: 4d higgsed network calculus and elliptic DIM algebra. arXiv:2012.15352 [hep-th]
Galakhov, D., Li, W., Yamazaki, M.: Shifted Quiver Yangians and Representations from BPS Crystals. arXiv:2106.01230 [hep-th]
Noshita, G., Watanabe, A.: Shifted quiver quantum toroidal algebra and subcrystal representations. arXiv:2109.02045 [hep-th]
Feigin, B., Feigin, E., Jimbo, M., Miwa, T., Mukhin, E.: Quantum continuous \(\mathfrak{gl}_\infty \): semi-infinite construction of representations. Kyoto J. Math. 51(2), 337–364 (2011). https://doi.org/10.1215/21562261-1214375. arXiv:1002.3100 [math.QA]
Ding, J., Frenkel, I.B.: Isomorphism of two realizations of quantum affine algebras \(U_q(gl(n))\). Commun. Math. Phys. 156, 277–300 (1993)
Khoroshkin, S., Pakuliak, S., Tarasov, V.: Off-shell Bethe vectors and Drinfeld currents. J. Geom. Phys. 57(8), 1713–1732 (2007). https://doi.org/10.1016/j.geomphys.2007.02.005
Chari, V., Pressley, A.: A Guide to Quantum Groups. Cambridge University Press, Cambridge (1995)
Ding, J., Pakuliak, S., Khoroshkin, S.: Factorization of the universal R-matrix for \(U_q \left( \hat{\text{ sl }}_2\right)\). Theor. Math. Phys. 124(2), 1007–1037 (2000). https://doi.org/10.1007/bf02551074. arXiv:math/0008227 [math.QA]
Hernandez, D.: Quantum toroidal algebras and their representations. Sel. Math. New Ser. 14(3–4), 701–725 (2009). arXiv:0801.2397 [math.QA]
Jing, N.: Twisted vertex representations of quantum affine algebras. Invent. Math. 102, 663–690 (1990)
Frenkel, I.B., Jing, N.: Vertex representations of quantum affine algebras. Proc. Natl. Acad. Sci. U.S.A. 85(24), 9373–9377 (1988). https://doi.org/10.1073/pnas.85.24.9373
Jimbo, M., Miwa, T.: Algebraic Analysis of Solvable Lattice Models, vol. 85. American Mathematical Society, Providence (1994)
Ding, J., Iohara, K.: Generalization of Drinfeld quantum affine algebras. Lett. Math. Phys. 41(2), 181–193 (1997). https://doi.org/10.1023/A:1007341410987
Miki, K.: A (q, \(\gamma \)) analog of the \(W_{1+\infty }\) algebra. J. Math. Phys. 48(12), 3520 (2007). https://doi.org/10.1063/1.2823979
Feigin, B., Jimbo, M., Miwa, T., Mukhin, E.: Quantum toroidal \(\mathfrak{gl} _1\) and Bethe ansatz. J. Phys. A 48(24), 244001 (2015). https://doi.org/10.1088/1751-8113/48/24/244001. arXiv:1502.07194 [math.QA]
Feigin, B., Jimbo, M., Miwa, T., Mukhin, E.: Finite Type Modules and Bethe Ansatz for Quantum Toroidal \(\mathfrak{gl} _1\). Commun. Math. Phys. (2017). https://doi.org/10.1007/s00220-017-2984-9. arXiv:1603.02765 [math.QA]
Bourgine, J.-E.: Fiber-base duality from the algebraic perspective. JHEP 03, 003 (2019). https://doi.org/10.1007/JHEP03(2019)003. arXiv:1810.00301 [hep-th]
Feigin, B., Hashizume, K., Hoshino, A., Shiraishi, J., Yanagida, S.: A commutative algebra on degenerate CP\(^{1}\) and Macdonald polynomials. J. Math. Phys. 50(9), 095215 (2009). https://doi.org/10.1063/1.3192773. arXiv:0904.2291 [math.CO]
Bershtein, M., Feigin, B., Merzon, G.: Plane partitions with a “pit’’: generating functions and representation theory. Sel. Math. New Ser. 24(1), 21–62 (2018). https://doi.org/10.1007/s00029-018-0389-z
Litvinov, A., Vilkoviskiy, I.: Liouville reflection operator, affine Yangian and Bethe ansatz. JHEP 12, 100 (2020). https://doi.org/10.1007/JHEP12(2020)100. arXiv:2007.00535 [hep-th]
Hernandez, D.: Stable maps, Q-operators and category O. J. Am. Math. Soc. 26, 179–210 (2022). arXiv:1902.02843 [math.RT]
Maulik, D., Okounkov, A.: Quantum groups and quantum cohomology. arXiv:1512.05388 [math.AG]
Feigin, B., Jimbo, M., Miwa, T., Mukhin, E.: Quantum toroidal \(\mathfrak{gl} _{1}\)-algebra: plane partitions. Kyoto J. Math. 52(3), 621–659 (2012). https://doi.org/10.1215/21562261-1625217
Bourgine, J.-E., Jeong, S.: New quantum toroidal algebras from 5D \({\cal{N}}=1\) instantons on orbifolds. arXiv:1906.01625 [hep-th]
Garbali, A., Zinn-Justin, P.: Shuffle algebras, lattice paths and the commuting scheme. arXiv:2110.07155 [math.RT]
Jing, N.: Vertex operators and Hall–Littlewood symmetric functions. Adv. Math. 87(2), 226–248 (1991). https://doi.org/10.1016/0001-8708(91)90072-F
Macdonald, I.: Symmetric Functions and Hall Polynomials. Oxford University Press, Oxford (1998)
Gerasimov, A., Lebedev, D., Oblezin, S.: On q-deformed \(\mathfrak{gl} _{\ell +1}\) Whittaker function III. Lett. Math. Phys. 97, 1–24 (2011). arXiv:0805.3754 [math.RT]
Awata, H., Fujino, H., Ohkubo, Y.: Crystallization of deformed Virasoro algebra, Ding–Iohara–Miki algebra and 5D AGT correspondence. J. Math. Phys. 58(7), 071704 (2017). https://doi.org/10.1063/1.4993773. arXiv:1512.08016 [math-ph]
Ohkubo, Y.: Singular Vector of Ding–Iohara-Miki algebra and Hall–Littlewood limit of 5D AGT conjecture. Ph.D. thesis, Nagoya U., Math. Dept. (2017). arXiv:1703.10990 [math-ph]
Awata, H., Kubo, H., Odake, S., Shiraishi, J.: Virasoro type symmetries in solvable models. In: Extended and Quantum Algebras and their Applications to Physics. (1996). arXiv:hep-th/9612233
Nekrasov, N.: Seiberg–Witten prepotential from instanton counting. Adv. Theor. Math. Phys. 7, 831 (2004). arXiv:hep-th/0306211
Aharony, O., Hanany, A.: Branes, superpotentials and superconformal fixed points. Nucl. Phys. B 504, 239–271 (1997). https://doi.org/10.1016/S0550-3213(97)00472-0. arXiv:hep-th/9704170 [hep-th]
Aharony, O., Hanany, A., Kol, B.: Webs of (p, q) 5-branes, five dimensional field theories and grid diagrams. JHEP 9801, 002 (1998). arXiv:hep-th/9710116 [hep-th]
Bourgine, J.E., Zhang, K.: A note on the algebraic engineering of 4D \({\cal{N} }=2\) super Yang–Mills theories. Phys. Lett. B 789, 610–619 (2019). https://doi.org/10.1016/j.physletb.2018.11.066. arXiv:1809.08861 [hep-th]
Nekrasov, N.: BPS/CFT correspondence: non-perturbative Dyson–Schwinger equations and qq-characters. JHEP 03, 181 (2016). https://doi.org/10.1007/JHEP03(2016)181. arXiv:1512.05388 [hep-th]
Frenkel, E., Reshetikhin, N.: The q-characters of representations of quantum affine algebras and deformations of W-algebras. arXiv:math/9810055
Nekrasov, N.: BPS/CFT correspondence II: instantons at crossroads, moduli and compactness theorem. Adv. Theor. Math. Phys. 21, 503–583 (2017). https://doi.org/10.4310/ATMP.2017.v21.n2.a4. arXiv:1608.07272 [hep-th]
Bourgine, J.-E., Matsuo, Y., Zhang, H.: Holomorphic field realization of SH\(^c\) and quantum geometry of quiver gauge theories. JHEP 04, 167 (2016). https://doi.org/10.1007/JHEP04(2016)167. arXiv:1512.02492 [hep-th]
Bourgine, J.-E., Fukuda, M., Matsuo, Y., Zhang, H., Zhu, R.-D.: Coherent states in quantum \({\cal{W}}_{1+\infty }\) algebra and qq-character for 5d Super Yang–Mills. PTEP2016(12), 123B05 (2016) https://doi.org/10.1093/ptep. arXiv:1606.08020 [hep-th]
Kimura, T., Pestun, V.: Quiver W-algebras. Lett. Math. Phys. 108(6), 1351–1381 (2018). https://doi.org/10.1007/s11005-018-1072-1. arXiv:1512.08533 [hep-th]
Feigin, B., Jimbo, M., Mukhin, E., Vilkoviskiy, I.: Deformations of \({\cal{W}}\) algebras via quantum toroidal algebras. Selecta Mathematica 27(52) (2020). arXiv:2003.04234 [math.QA]
Hellerman, S., Orlando, D., Reffert, S.: String theory of the Omega deformation. JHEP 01, 148 (2012). https://doi.org/10.1007/JHEP01(2012)148. arXiv:1106.0279 [hep-th]
Nedelin, A., Pasquetti, S., Zenkevich, Y.: T[SU(N)] duality webs: mirror symmetry, spectral duality and gauge/CFT correspondences. JHEP 02, 176 (2019). https://doi.org/10.1007/JHEP02(2019)176. arXiv:1712.08140 [hep-th]
Aprile, F., Pasquetti, S., Zenkevich, Y.: Flipping the head of \(T[SU(N)]\): mirror symmetry, spectral duality and monopoles. JHEP 04, 138 (2019). https://doi.org/10.1007/JHEP04(2019)138. arXiv:1812.08142 [hep-th]
Yoshida, Y.: Localization of Vortex Partition Functions in \({\cal{N}}=(2,2) \) Super Yang-Mills theory. arXiv:1101.0872 [hep-th]
Fujitsuka, M., Honda, M., Yoshida, Y.: Higgs branch localization of 3d \({\cal{N}} = 2\) theories PTEP2014(12), (2014) 123B02. https://doi.org/10.1093/ptep/ptu158. arXiv:1312.3627 [hep-th]
Chen, H.-Y., Chen, H.-Y., Ho, J.-K.: Connecting mirror symmetry in 3d and 2d via localization. Int. J. Mod. Phys. A 29(32), 1530004 (2014). https://doi.org/10.1142/S0217751X15300045. arXiv:1312.2361 [hep-th]
Hanany, A., Witten, E.: Type IIB superstrings, BPS monopoles, and three-dimensional gauge dynamics. Nucl. Phys. B 492, 152–190 (1997). https://doi.org/10.1016/S0550-3213(97)00157-0. arXiv:hep-th/9611230
Kimura, T., Nieri, F.: Intersecting defects and supergroup gauge theory. arXiv:2105.02776 [hep-th]
Fukuda, M., Ohkubo, Y., Shiraishi, J.: Generalized Macdonald functions on Fock tensor spaces and duality formula for changing preferred direction. arXiv:1903.05905 [math.QA]
Intriligator, K.A., Seiberg, N.: Mirror symmetry in three-dimensional gauge theories. Phys. Lett. B 387, 513–519 (1996). https://doi.org/10.1016/0370-2693(96)01088-X. arXiv:hep-th/9607207
de Boer, J., Hori, K., Ooguri, H., Oz, Y., Yin, Z.: Mirror symmetry in three-dimensional theories, SL(2, Z) and D-brane moduli spaces. Nucl. Phys. B 493, 148–176 (1997). https://doi.org/10.1016/S0550-3213(97)00115-6. arXiv:hep-th/9612131
Nieri, F., Pan, Y., Zabzine, M.: 3d mirror symmetry from S-duality. Phys. Rev. D 98(12), 126002 (2018). https://doi.org/10.1103/PhysRevD.98.126002. arXiv:1809.00736 [hep-th]
Cheng, S.: 3d \({\cal{N}}=2\) brane webs and quivers. arXiv:2108.03696 [hep-th]
Gaiotto, D., Koroteev, P.: On three dimensional quiver gauge theories and integrability. JHEP 05, 126 (2013). https://doi.org/10.1007/JHEP05(2013)126. arXiv:1304.0779 [hep-th]
Gadde, A., Gukov, S., Putrov, P.: Walls, lines, and spectral dualities in 3d gauge theories. JHEP 05, 047 (2014). https://doi.org/10.1007/JHEP05(2014)047. arXiv:1302.0015 [hep-th]
Atiyah, M., Hitchin, N., Drinfeld, V., Manin, Y.: Construction of instantons. Phys. Lett. A 65(3), 185–187 (1978). https://doi.org/10.1016/0375-9601(78)90141-X
Nakajima, H.: Instantons on ALE spaces, quiver varieties, and Kac–Moody algebras. Duke Math. J. 76(2), 365–416 (1994). https://doi.org/10.1215/S0012-7094-94-07613-8
Nekrasov, N., Schwarz, A.S.: Instantons on noncommutative R**4 and (2,0) superconformal six-dimensional theory. Commun. Math. Phys. 198, 689–703 (1998). https://doi.org/10.1007/s002200050490. arXiv:hep-th/9802068
Schiffmann, O., Vasserot, E.: Cherednik algebras, W algebras and the equivariant cohomology of the moduli space of instantons on \({{\mathbb{A} }}^2\). Pub. Math. de l’IHES 118(1), 213–342 (2013). arXiv:1202.2756v2 [math.QA]
Nekrasov, N., Pestun, V., Shatashvili, S.: Quantum geometry and quiver gauge theories. arXiv:1312.6689 [hep-th]
Rapcak, M., Soibelman, Y., Yang, Y., Zhao, G.: Cohomological Hall algebras and perverse coherent sheaves on toric Calabi–Yau 3-folds. arXiv:2007.13365 [math.QA]
Hanany, A., Tong, D.: Vortices, instantons and branes. JHEP 07, 037 (2003). https://doi.org/10.1088/1126-6708/2003/07/037. arXiv:hep-th/0306150
Franzen, H.: On cohomology rings of non-commutative Hilbert schemes and CoHa-modules. Math. Res. Lett. 23, 805–840 (2016). arXiv:1312.1499 [math.RT]
Ginzburg, V., Kapranov, M., Vasserot, E.: Langlands reciprocity for algebraic surfaces. arXiv:q-alg/9502013 [math.QA]
Vasserot, E.: Affine quantum groups and equivariant K-theory. Transform. Groups 3, 269–299 (1998). arXiv:math/9803024 [math.QA]
Nakajima, H.: Quiver varieties and finite dimensional representations of quantum affine algebras. arXiv:math/9912158 [math.QA]
Acknowledgements
The author would like to thank Sasha Garbali, David Hernandez, Taro Kimura and Gufang Zhao for discussions.
Funding
This research was partly supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education through the Center for Quantum Spacetime (CQUeST) of Sogang University (NRF-2020R1A6A1A03047877). The author also gratefully acknowledges support from the Australian Research Council Centre of Excellence for Mathematical and Statistical Frontiers (ACEMS).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author have no competing interests to declare that are relevant to the content of this article.
Additional information
Communicated by Y. Kawahigashi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Example of a Finite Dimensional Shifted Representation
In this appendix, we provide some explicit formulas for the action of the Drinfeld currents defining the algebra \({{\mathcal {E}}}^{(0,3)}\) on the five dimensional module \({{\mathcal {M}}}_\mu \) indexed by the Young diagram \(\mu =21\). The representation is obtained as \(\iota _{P_\mu }\rho _v^{(0,1)}\) with
In the basis \(e_0=\vert \emptyset \rangle \!\rangle \), \(e_1=\vert 1\rangle \!\rangle \), \(e_2=\vert 2\rangle \!\rangle \), \(e_3=\vert 1^2\rangle \!\rangle \) and \(e_4=\vert 21\rangle \!\rangle \), the currents \(x^\pm (z)\) have the form of \(5\times 5\) matrices
The expression of the coefficients shortens if we introduce the notation \(p_{i,j}=1-q_1^iq_2^j\),
The action of the Cartan currents on the state \(e_i\) is diagonal, with the eigenvalue \(q_3^{-1/2}[{\tilde{\psi }}_i(z)]_\pm \) obtained by expanding the following rational functions,
Equivariant Characters
In this appendix, we analyze the 5d hypermultiplets and the Higgsing procedure from the point of view of the equivariant characters of instantons and vortex moduli spaces. The moduli space of U(n) framed instantons of charge k on the \(\Omega \)-deformed non-commutative \({{\mathbb {R}}}^4\) follows from the ADHM construction [78,79,80].Footnote 31 It is a quiver variety with a single node \(K={{\mathbb {C}}}^k\) framed by \(N={{\mathbb {C}}}^n\),
with the moment maps
The corresponding quiver is represented on Fig. 17. When \(\zeta >0\), the real moment map can be replaced by the stability condition \({{\mathbb {C}}}[B_1,B_2]IN=K\) provided that we quotient by the action of GL(k) instead of U(k). The torus \({\mathfrak {t}}=U(1)_{\varepsilon _1}\times U(1)_{\varepsilon _2}\times U(1)^n\) acts on this moduli space, and the fixed point are labeled by n-tuples of partitions \({\varvec{\lambda }}\) with \(|{\varvec{\lambda }}|=k\) boxes. At the fixed point \({\varvec{\lambda }}\), we have the following decomposition of N and K into one-dimensional subspaces
As a result, the characters for the action of the torus \({\mathfrak {t}}\) on the spaces N and K are given by

The characters \(v_l\) and  are resp. identified with the exponentiated Coulomb branches and the box contents \(\chi _{(l,i,j)}=v_lq_1^{i-1}q_2^{j-1}\).
are resp. identified with the exponentiated Coulomb branches and the box contents \(\chi _{(l,i,j)}=v_lq_1^{i-1}q_2^{j-1}\).
The Nekrasov instanton partition function is a sum over the fixed points \({\varvec{\lambda }}\), the summands are obtained from the character \(\chi _{{\varvec{\lambda }},{\varvec{\lambda }}}\) of the torus action on the tangent space \(T_{\varvec{\lambda }}{{\mathcal {M}}}^I_{k,N}\) at the fixed point, withFootnote 32
with the linear operation \(v_l^\vee =v_l^{-1}\), \(q_\alpha ^\vee =q_\alpha ^{-1}\). The vector contribution is obtained by applying the index functor to this expression,
and the Nekrasov factor corresponds to the case \(n=1\): \({{\mathcal {N}}}_{\lambda ,\lambda '}(v/v')={{\mathbb {I}}}[\chi _{\lambda ,\lambda '}]\).
1.1 Massive hypermultiplets
In the presence of \(N^f\) fundamental and \(N^{{\bar{f}}}\) antifundamental hypermultiplets, the equivariant character is replaced by,
with \({{\mathcal {M}}}=\sum _{a=1}^{N^f}\mu _a\) and \(\overline{{\mathcal {M}}}=\sum _{a=1}^{N^{{\bar{f}}}}{\bar{\mu }}_a\) [82] (neglecting the one-loop terms). The summands of the instanton partition function are again obtained as
The extra terms \(-{\bar{{{\mathcal {M}}}}}{{\mathcal {K}}}_{{\varvec{\lambda }}'}^\vee -q_1q_2{{\mathcal {K}}}_{\varvec{\lambda }}{{\mathcal {M}}}^\vee \) in the character also induce an extra factor in the \({{\mathcal {Y}}}\)-observables. These observables were introduced by Nekrasov in [56], they can be obtained as a variation of the equivariant character (see [44]),Footnote 33

From the bilinear expression of the character B.7, we deduce that the r.h.s. of these formulas is indeed independent of the second Young diagram. The \({{\mathcal {Y}}}\)-observables are the unique rational functions satisfying these constraints for the infinite set of points \(\chi _{(l,i,j)}=v_lq_1^{i-1}q_2^{j-1}\). The extra factors in the \({{\mathcal {Y}}}\)-observables coming from the deformation of the character in the presence of hypermultiplets are simply the inverse of the polynomials defined in 5.4 and involved in the shift of representations,e

Using the shell formula, it is seen that the \({{\mathcal {Y}}}\)-observable \({{\mathcal {Y}}}_\lambda (z)\) coincides with the function 3.19 defining the vertical Fock representation. Thus, restricting ourselves to U(1) instantons, the algebra \({{\mathcal {E}}}\) acts on the fixed point \(\vert \lambda \rangle \!\rangle \) of the torus action by the vertical Fock representation given in 3.20. This action is the (K-theoretic) (double) Cohomological Hall algebra of the instanton moduli space. Matrix elements of the currents are expressed in terms of the \({{\mathcal {Y}}}\)-observables, and so they are expected to be modified in the presence of hypermultiplets as follows,

Comparing with 3.20, we deduce that antifundamental hypermultiplets lead to the shift \(\iota _P\rho _v^{(0,1)}\) of the vertical representation with the polynomial \(P=P_{\bar{{\varvec{\mu }}}}^{{\bar{f}}}\). Naively, fundamental hypermultiplets would introduce a similar shift \(\iota _{P^{-1}}^*\rho _v^{(0,1)}\) with \(P=P_{\varvec{\mu }}^f\). However, in this case \(P(z)^{-1}\) is no longer a finite Laurent series, it introduce extra poles in the action of the Cartan current that cannot be accounted for by the commutator \([x^+(z),x^-(w)]\). Thus, it is not clear how to define properly the vertical action there. This is a limitation of our simplified approach, and this issue could be resolved using the more involved geometric techniques employed e.g. in [81, 83].
1.2 Higgsing and the vortex moduli space
The relation between the instanton moduli space and the vortex moduli space has been investigated in [84] from the point of view of the \({{\mathcal {N}}}=(2,2)\) quantum mechanics on the worldvolume of D1-branes. By weakly gauging a U(1) subgroup of the total symmetry group, it is possible to give a large mass to some of the fields and decouple them. It corresponds to imposing \(B_1=J=0\) in the ADHM construction, and we find the vortex moduli space given by the quiver variety of Fig. 18,
with the real moment map \(2\mu _{{\mathbb {R}}}=II^\dagger +[B_2,B_2^\dagger ]\). The torus \(U(1)_{\varepsilon _2}\times U(1)^n\) acts on \({{\mathcal {M}}}_{k,n}^V\) and the fixed point are labeled by n-tuple of positive integers \({{\varvec{k}}}=(k_1,\ldots ,k_n)\) such that \(|{{\varvec{k}}}|=\sum _lk_l=k\). At each fixed point, we have the following decomposition of K and N and the corresponding characters \({{\mathcal {K}}}_{{{\varvec{k}}}}\) and \({{\mathcal {N}}}\),
The equivariant character of the tangent space of the vortex moduli space has been computed in [66], it corresponds to \(\chi ^\text {3d}_{{{\varvec{k}}},{{\varvec{k}}}}\) with
Taking the index functor, this character produces the 3d version of the Nekrasov factor defined in 6.3, \(N_{k,k'}(v/v')={{\mathbb {I}}}[\chi _{k,k'}]\).
The vortex moduli space studied here corresponds to a non-commutative Hilbert scheme [85], but unfortunately we were unable to find a derivation of the K-theoretic COHA for this variety. A possible approach could be to start from the K-theoretic COHA derivation of the finite dimensional module of quantum affine algebras performed in [86,87,88]. Specializing to the Kirillov–Reshetikhin representation of dimension N for the quantum affine \(\mathfrak {sl}(2)\) algebra, it might be possible to consider the limit \(N\rightarrow \infty \) of this geometric construction. Here, again, we will be more modest and simply consider the variation of the equivariant character. In this way, we define 3d analog of Nekrasov’s \({{\mathcal {Y}}}\)-observables,
where \(\delta _l=(0,\ldots ,1,0,\ldots )\in {{\mathbb {Z}}}^n\) is a vector with a 1 in the lth row and zero elsewhere. It gives indeed the functions defined in [11],
In the case of U(1) vortices, the prefundamental representation acts on a module spanned by states \(\vert k\rangle \!\rangle \) labeled by the fixed point of the equivariant action on the vortex moduli space, its action can be expressed using \({{\mathcal {Y}}}\)-observables as
It reproduces the prefundamental action 2.18 up to a change in the normalization of the states and a rescaling of the currents by harmless factors.
Higgsing Recall that the 3d gauge theories are obtained from a two steps procedure that consists in (1) adjusting the mass of n hypermultiplets to a critical value and (2) taking the limit \(q_1\rightarrow \infty \) to decouple the adjoint chiral multiplet. Once the mass takes its critical value, the set of fixed points is restricted to n-tuples of single column Young diagrams identified with the n positive integers \({{\varvec{k}}}=(k_1,\ldots ,k_n)\), and the characters \({{\mathcal {K}}}_{\varvec{\lambda }}\) should be replaced by \({{\mathcal {K}}}_{{\varvec{k}}}\). Furthermore, adjusting the mass of n antifundamental hypermultiplets to \(\bar{\mu }_l=q_1v_l\) corresponds to setting \({\bar{{{\mathcal {M}}}}}=q_1{{\mathcal {N}}}\) and \({{\mathcal {M}}}=0\) in the expression B.7 of the equivariant character, and we find
In the limit \(q_1\rightarrow \infty \), only the finite terms in \(\chi _{{{\varvec{k}}},{{\varvec{k}}}'}^\text {5d}\) will contribute once the index functor is applied. Examining the term of power \(q_1^0\), we find indeed \(\left[ \chi _{{{\varvec{k}}},{{\varvec{k}}}'}^\text {5d}\right] _0=\chi _{{{\varvec{k}}},{{\varvec{k}}}'}^\text {3d}\). We would arrive at the same conclusion if we had adjusted instead the mass of fundamental hypermultiplet, i.e. setting \({{\mathcal {M}}}=q_1^2q_2{{\mathcal {N}}}\) and \({\bar{{{\mathcal {M}}}}}=0\) in B.7. This relation between the equivariant characters justifies our approach of the limit of highest \(\ell \)-weight representation, and we can check that the \({{\mathcal {Y}}}\)-observables have indeed the proper limit (the factor \(q^{-2k}\) can be absorbed in a renormalization of the states)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Bourgine, JE. Shifted Quantum Groups and Matter Multiplets in Supersymmetric Gauge Theories. Commun. Math. Phys. 401, 2051–2114 (2023). https://doi.org/10.1007/s00220-023-04685-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-023-04685-x



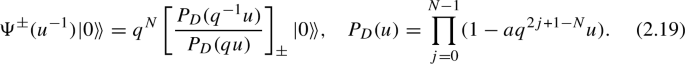
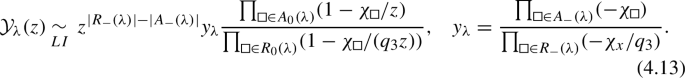
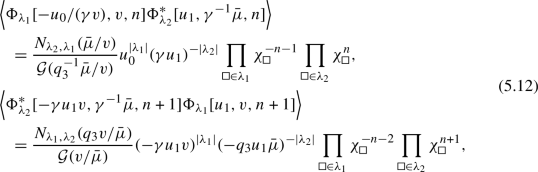
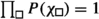 .
.