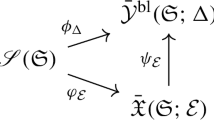Abstract
We study the stated skein modules of marked \(3-\)manifolds. We generalize the splitting homomorphism for stated skein algebras of surfaces to a splitting homomorphism for stated skein modules of \(3-\)manifolds. We show that there exists a Chebyshev–Frobenius homomorphism for the stated skein modules of 3-manifolds which extends the Chebyshev homomorphism of the skein algebras of unmarked surfaces originally constructed by Bonahon and Wong. Additionally, we show that the Chebyshev–Frobenius map commutes with the splitting homomorphism. This is then used to show that in the case of the stated skein algebra of a surface, the Chebyshev–Frobenius map is the unique extension of the dual Frobenius map (in the sense of Lusztig) of \({\mathcal {O}}_{q^2}(SL(2))\) through the triangular decomposition afforded by an ideal triangulation of the surface. In particular, this gives a skein theoretic construction of the Hopf dual of Lusztig’s Frobenius homomorphism. A second conceptual framework is given, which shows that the Chebyshev–Frobenius homomorphism for the stated skein algebra of a surface is the unique restriction of the Frobenius homomorphism of quantum tori through the quantum trace map.



























Similar content being viewed by others
References
Baseilhac, S., Roche, P.: Unrestricted quantum moduli algebras, I: The case of punctured spheres, preprint arXiv:1912.02440
Bonahon, F.: Miraculous cancellations for quantum SL2, Annales de la Faculté des sciences de Toulouse : Mathématiques, Série 6. Tome 28(3), 523–557 (2019)
Bonahon, F., Wong, H.: Quantum traces for representations of surface groups in SL2(C). Geom. Topol. 15(3), 1569–1615 (2011)
Bonahon, F., Wong, H.: Representations of the Kauffman skein algebra I: invariants and miraculous cancellations. Invent. Math. 204(1), 195–243 (2016)
Bonahon, F., Wong, H.: Representations of the Kauffman bracket skein algebra II: Punctured surfaces. Algebr. Geom. Topol. 17(6), 3399–3434 (2017)
Bonahon, F., Wong, H.: Representations of the Kauffman bracket skein algebra III: closed surfaces and naturality. Quantum Topol. 10(2), 325–398 (2019)
Chari, V., Pressley, A.: A guide to quantum groups. Cambridge University Press, Cambridge (1995)
Chekhov, L., Fock, V.: Quantum Teichmüller spaces (Russian) Teoret. Mat. Fiz. 120(3), 511–528 (1999). translation in Theoret. and Math. Phys. 120(3), 1245–1259 (1999)
F. Costantino and T.T.Q. Lê, Stated skein algebras of surfaces. To appear in Journal of EMS, arXiv:1907.11400 [math.GT], (2019)
Costantino, F., Lê, T.T.Q.: In preparation
De Concini, C., Lyubashenko, V.: Quantum Function Algebra at Roots of 1. Adv. Math. 108(2), 205–262 (1994)
Frohman, C., Kania-Bartoszynska, J., Lê, T.T.Q.: In preperation
Frohman, C., Gelca, R.: Skein modules and the noncommutative torus. Trans. Am. Math. Soc. 352(10), 4877–4888 (2000)
Frohman, C., Kania-Bartoszynska, J., Lê, T.T.Q.: Unicity for Representations of the Kauffman bracket skein algebra. Invent. Math. 215(2), 609–650 (2019)
Frohman, C., Kania-Bartoszynska, J., Lê, T.T.Q.: Dimension and Trace of the Kauffman Bracket Skein Algebra. Trans. Am. Math. Soc. Ser. B 8, 510–547 (2021)
Ganev, I., Jordan, D., Safronov, P.: The quantum Frobenius for character varieties and multiplictative quiver varieties, preprint arXiv:1901.11450
Kashiwara, M.: On crystal bases of the q-analogue of universal enveloping algebras. Duke Math. J. 63(2), 465–516 (1991)
Kassel, C.: Quantum groups, Springer Verlag, New York, 1995, Graduate Texts in Mathematics, No. 155
Kauffman, L.: States models and the Jones polynomial. Topology 26, 395–407 (1987)
Korinman, J., Quesney, A.: Classical shadows of stated skein representations at roots of unity, arXiv:1905.03441 [math.GT] (2019)
Lê T.T.Q., Yu, T.: Quantum traces and embeddings of stated skein algebras into quantum tori, arXiv:2012.15272 [math.GT]
Lê, T.T.Q.: Quantum Teichmüller spaces and quantum trace map. J. Inst. Math. Jussieu 1–43 (2017). https://doi.org/10.1017/S1474748017000068
Lê, T.T.Q.: On Kauffman bracket skein modules at roots of unity. Alg. Geol. Top. 15(2), 1093–1117 (2015)
Lê, T.T.Q.: Triangular Decomposition of Skein Algebras. Quantum Topol. 9(3), 591–632 (2018)
Lê, T.T.Q., Paprocki, J.: On Kauffman bracket skein modules Of marked 3-manifolds and the Chebyshev-Frobenius homomorphism. Algebra Geom. Topol. 19(7), 3453–3509 (2019)
Lê, T.T.Q., Yu, T.: Stated skein modules of marked 3-manifolds/surfaces, a survey. Acta Math. Vietnam. 46(2), 265–287 (2021)
Lusztig, G.: Introduction to quantum groups, Progress in Mathematics, 110. Birkhäuser, (1993)
Lusztig, G.: Quantum Groups at Roots of \(1\). Geom. Dedicata 35(1–3), 89–113 (1990)
Majid, S.: Foundations of quantum group theory, Cambridge University Press (1995) 1-640 pp. (2nd edn.) 2000
Muller, G.: Skein algebras and cluster algebras of marked surfaces, Quan. Topol., to appear. (2012)
Parshall, B., Wang, J.P.: Quantum Linear Groups. Mem. Am. Math. Soc. 439, (1991)
Penner, R.C.: Decorated Teichmüller Theory, with a foreward by Yuri I. Manin, QGM Master Class Series, European Mathematical Society, Zürich, (2012)
Przytycki, J.: Fundamentals of Kauffman bracket skein modules. Kobe J. Math. 16, 45–66 (1999)
Turaev, V.: Conway and Kauffman modules of a solid torus. J. Soviet. Math. 52, 2799–2805 (1990)
Turaev, V.: Skein quantization of Poisson algebras of loops on surfaces. Ann. Sci. Sc. Norm. Sup. (4) 24(6), 635–704 (1991)
Acknowledgements
The authors would like to thank F. Bonahon, C. Frohman, J. Kania-Bartozynska, A. Kricker, G. Masbaum, G. Muller, A. Sikora, D. Thurston. The second author would like to thank the CIMI Excellence Laboratory, Toulouse, France, for inviting him on a Excellence Chair during the period of January – July 2017 when part of this work was done. The second author is supported in part by NSF grant DMS 1811114. The first author is supported in part by NSF Grant DMS-1745583.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A Divided powers and the Hopf pairing
A Divided powers and the Hopf pairing
In this appendix we provide the computations required to show that \(\varPhi _\omega \) is the Hopf dual of the Frobenius homomorphism.
Note that the Hopf pairing
is defined on generators as
This non-degenerate Hopf pairing \(\langle , \rangle \) restricted to \(U^L_{q^2}({\mathfrak {sl}}_2)\) is integral, meaning
Proposition 5
With the notation of Sect. 6, we have for any m and any p.
and
and
Proof
This result follows from a direct computation based induction using the coproduct in \(U_{q^2}({\mathfrak {sl}}_{{\mathfrak {2}}})\). \(\square \)
Proposition 6
Let \(\omega \) be a root of unity with \(N=\mathrm{ord}(\omega ^8)\) and \(\eta =\omega ^{N^2}\). We have that the Frobenius map f and the map \(\varPhi _\omega \) are dual with respect to the Hopf pairings between \({\mathcal {O}}_{\eta ^4}(SL(2))\) and \(U_{\eta ^4}({\mathfrak {sl}}_2)\) and between \({\mathcal {O}}_{\omega ^4}(SL(2))\) and \(U_{\omega ^4}({\mathfrak {sl}}_2)\), meaning the following diagram commutes:

Proof
This is a direct computation on the generators of the algebras. We will use matrix notation to indicate the map applied to each entry of the matrix.
Where the first equality uses the definition of the pairing, the second equality uses that \(\eta =\omega ^{N^2}\), and the last equality comes from Equation 49 with \(m=N\).
Where the first equality uses the definition of the pairing and the second equality uses Equation 50 with \(m=N\) and \(p=1\).
Where the first equality uses the definition of the pairing and the second equality uses Equation 51 with \(m=N\) and \(p=1\).
Where the first equality uses the definition of the pairing and the second equality uses Equation 50 with \(m=N\) and \(p=N\).
Where the first equality uses the definition of the pairing and the second equality uses Equation 51 with \(m=N\) and \(p=N\). \(\square \)
Rights and permissions
About this article
Cite this article
Bloomquist, W., Lê, T.T.Q. The Chebyshev–Frobenius homomorphism for stated skein modules of 3-manifolds. Math. Z. 301, 1063–1105 (2022). https://doi.org/10.1007/s00209-021-02904-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-021-02904-6