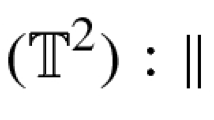Abstract
We consider the two-dimensional plasma-vacuum interface problem in ideal compressible magnetohydrodynamics (MHD). This is a hyperbolic-elliptic coupled system with a characteristic free boundary. In the plasma region the 2D planar flow is governed by the hyperbolic equations of ideal compressible MHD, while in the vacuum region the magnetic field obeys the elliptic system of pre-Maxwell dynamics. At the free interface moving with the velocity of plasma particles, the total pressure is continuous and the magnetic field on both sides is tangent to the boundary. The plasma-vacuum system is not isolated from the outside world, since it is driven by a given surface current which forces oscillations onto the system. We prove the local-in-time existence and uniqueness of solutions to this nonlinear free boundary problem, provided that at least one of the two magnetic fields, in the plasma or in the vacuum region, is non-zero at each point of the initial interface. The proof follows from the analysis of the linearized MHD equations in the plasma region and the elliptic system for the vacuum magnetic field, suitable tame estimates in Sobolev spaces for the full linearized problem, and a Nash–Moser iteration.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Consider the equations of ideal compressible MHD (see [13, 14, 20])
where the density \(\rho ,\) the velocity \({\textbf{u}}\in {{\mathbb {R}}}^3\), the magnetic field \({\textbf{H}}\in {{\mathbb {R}}}^3\) and the pressure \(p=p(\rho ,S)\) are unknown functions of the spacial variables \({\textbf{x}}\in {{\mathbb {R}}}^3\) and the time t. Here S is the entropy, \(e=E+\frac{1}{2}|{\textbf{u}}|^2\) is the total energy and \(E=E(\rho ,S)\) stands for the internal energy. By using the state equation of gas, \(\rho =\rho (p,S),\) and the first principle of thermodynamics, we have that (1.1) is a closed system. System (1.1) is endowed with the divergence constraint
on the Cauchy initial data.
In this paper we restrict ourselves to 2D planar MHD flows. This means that the flow is \(x_3\)-invariant and the velocity and the magnetic field are shearless, i.e., the unknowns do not depend on \(x_3\) and \(u_3=H_3=0\). It follows from the 4th and 7th scalar equations of system (1.1) for \(x_3\)-invariant flows that \(u_3|_{t=0}=H_3|_{t=0}=0\) implies \(u_3=H_3=0\) for all \(t>0\). That is, the restriction that the velocity and the magnetic field are shearless at a first moment guarantees that 2D flows are planar. In other words, without loss of generality we may assume that the space variables, the velocity and the magnetic field have only two components: \({\textbf{x}}=(x_1,x_2)\in {\mathbb {R}}^2\), \({\textbf{u}}=(u_1,u_2)\in {\mathbb {R}}^2\), \({\textbf{H}}=(H_1,H_2)\in {\mathbb {R}}^2\).
By (1.2), we can rewrite (1.1) in the non-conservative form
where \(\rho _p=\frac{\partial \rho }{\partial p}\) and \(q=p+\frac{1}{2}|{\textbf{H}}|^2\) denotes the total pressure. Equation (1.3) form a symmetric system for the unknown vector \((p,{\textbf{u}},{\textbf{H}},S)\). In the following, we shall adopt a different symmetrization form of (1.3), namely we choose the basic unknown q instead of p. Denote \(\textrm{d} /\textrm{d} t =\partial _t+( {\textbf{u}}\cdot {\nabla } )\). Then, the equation for the pressure in (1.3) has the form
where in this case \(\rho =\rho (q -|{\textbf{H}} |^2/2,S)\) and similarly for \(\rho _p \). We then derive \(\textrm{div}\,{\textbf{u}} \) from (1.4) and rewrite the equation for the magnetic field in (1.3) as
Substituting (1.4), (1.5) into (1.3) yields the symmetric system
where \({\textbf{I}}_2\) denotes the \(2\times 2\) identity matrix and \({\underline{0}}=(0,0)\). System (1.6) can be written in the matrix form as
where \(\mathbf{{U}}=\mathbf{{U}}(t,{\textbf{x}})=(q,{\textbf{u}},{\textbf{H}},S),\) with the initial data \(\mathbf{{U}}(0,{\textbf{x}})=\mathbf{{U}}_0({\textbf{x}}).\) The symmetric matrices \(A_{\alpha }\) (\(\alpha =0,1,2\)) can be easily written down if necessary. The quasilinear symmetric system (1.7) is hyperbolic if the state equation \(\rho =\rho (p,S)\) satisfies the hyperbolicity condition \(A_0>0:\)
Let \(\Omega ^+(t)\) and \(\Omega ^-(t)\) be the regions occupied by the plasma and the vacuum respectively. That is, in \(\Omega ^+(t)\) the motion of an ideal plasma is governed by the MHD system (1.1) (or (1.7)) whereas in \(\Omega ^-(t)\) the vacuum magnetic field \({\mathcal {H}}\) obeys the pre-Maxwell equations [4, 14] that in 3D read as
In order to write down the 2D version of (1.9) we are considering, we assume that no variable depends on \(x_3\) and that \({\mathcal {H}}_3=0\) in \(\Omega ^-(t)\). That is, the 2D version of (1.9) reads as
where we have denoted
for the vacuum magnetic field \({\mathcal {H}}=({\mathcal {H}}_1,{\mathcal {H}}_2)\).
Let us assume that the moving interface \(\Gamma (t)\) between plasma and vacuum (which is a curve in 2D) is given by a smooth function \(F(t,{\textbf{x}})\): \(\Gamma (t)=\{F(t,{\textbf{x}})= 0\}\). It is to be determined and moves with the velocity of plasma particles at the boundary:
As the interface function F is one of the unknowns of the problem, we deal with a free-boundary problem. The plasma variable \({\textbf{U}}\) is connected with the vacuum magnetic field \({\mathcal {H}}\) through the relations [4, 14]
where \(N=\nabla F\) and \([q]= q|_{\Gamma }-\frac{1}{2}|{\mathcal {H}}|^2|_{\Gamma }\) denotes the jump of the total pressure across the interface. These relations together with (1.11) are the boundary conditions at the interface \(\Gamma (t)\).
As in [35, 36], we assume that for problem (1.7), (1.10)–(1.12) the hyperbolicity conditions (1.8) are satisfied in \(\Omega ^+(t)\) up to the boundary \(\Gamma (t)\), i.e., the plasma density does not go to zero continuously, but has a jump (clearly in the vacuum region \(\Omega ^-(t)\) the density is identically zero). This assumption is compatible with the continuity of the total pressure in (1.12). Moreover, as in [35, 36], for technical simplicity we will assume that the moving interface \(\Gamma (t)\) takes the form of a graph with periodic boundary conditions in the tangential direction:
there \(t \in [0,T]\) and \({\mathbb {T}}\) denotes the 1-torus. It is assumed that \(-1<\varphi (t,\cdot )<1.\) Then
where \(\Omega =(-1,1)\times {\mathbb {T}}\) is the space domain occupied by plasma and vacuum.
With our parametrization of \(\Gamma (t)\), the boundary conditions (1.11), (1.12) become
where \(u_N={\textbf{u}}\cdot N\), \(H_N={\textbf{H}}\cdot N\), \({\mathcal {H}}_N={\mathcal {H}}\cdot N\), \(N=(1,-\partial _2\varphi )\).
On the fixed top and bottom boundaries
of the domain \(\Omega \), we prescribe the boundary conditions
where \({\mathcal {J}}={\mathcal {J}}(t,x_2)\) is a given function. The last boundary condition in (1.14) is the 2D version of the standard physical boundary condition
on the fixed bottom boundary \(x_1=-1\) of a 3D space domain \(\Omega ^-(t)\), where \({\textbf{e}}_1= (1,0,0)\) and \({\mathfrak {J}}\) is a given surface current, which forces oscillations onto the plasma-vacuum system (see [36] for further discussions). In our 2D planar case, the scalar function \({\mathcal {J}}\) is just the third component of the vector function \({\mathfrak {J}}\).
System (1.7), (1.9), (1.13) is supplemented with initial conditions
Note that we must regard (1.2) as well as the boundary conditions \(H_N|_{\Gamma }=0\) and \(H_1|_{\Gamma _+}=0\) in (1.13) and(1.14) as the restrictions on the initial data (1.15). More precisely, we can prove that a solution of problem (1.7), (1.10), (1.13)–(1.15) (if it exists for all \(t\in [0,T]\)) satisfies
for all \(t\in [0,T]\), if the latter is satisfied at \(t=0\), i.e., for the initial data (1.15). In particular, the fulfillment of the divergence constraint (1.2) implies that systems (1.1) and (1.7) are equivalent on solutions of this problem.
The main goal in this paper is to find conditions on the initial data (1.15) providing the existence and uniqueness on some time interval [0, T] of a solution \(({{\textbf{U}}},{\mathcal {H}},\varphi )\) to problem (1.7), (1.10), (1.13)–(1.15) in Sobolev spaces. Since (1.1) is a system of hyperbolic conservation laws that can produce shock waves and other types of strong discontinuities (e.g., current-vortex sheets [7, 8, 40]), it is natural to expect to obtain only local-in-time existence theorems. In this paper, we successfully find a new “stability” condition on the initial data, namely,
for some fixed \(\delta >0\), which is sufficient for local well-posedness of problem (1.7), (1.10), (1.13)–(1.15) (together with the hyperbolicity conditions (1.8) and appropriate compatibility conditions).
In view of the last two boundary condition in (1.13), inequality (1.17) is equivalent to the requirement that at each point of the interface at least one of the two magnetic fields is non-zero:
Mathematically, condition (1.17) (or equivalently (1.18)) appears as the requirement that the interface symbol is elliptic, i.e., the boundary conditions are resolvable for the space-time gradient \((\partial _t\varphi ,\partial _2\varphi )\) of the interface function \(\varphi \).
Remark 1.1
In the case of ideal polytropic gases where \(p=A\rho ^\gamma e^S\) (\(A>0, \gamma >1\)), the hyperbolicity condition \(\rho >0\) implies \(p>0\) and then \(\frac{1}{2}|{\mathcal {H}}|^2=q=p+\frac{1}{2}|\textbf{H}|^2>0\) on \(\Gamma (t)\). Thus the stability condition (1.18) is always satisfied. We can repeat word by word the same argument for general gases that satisfy the conventional assumption that \(p>0\) if \(\rho >0\) and show again that the hyperbolicity condition implies (1.18). This argument excludes the case of Chaplygin gases where p can be negative for small densities; in such a case the stability condition (1.18) does not seem a consequence of the hyperbolicity. Notice that (1.18) can hold in the form \(|{\textbf{H}}|>0, |{\mathcal {H}}|=0\) on \(\Gamma (t)\), only for a Chaplygin-type gas with \(p=-\frac{1}{2}|\textbf{H}|^2<0\) on \(\Gamma (t)\).
Plasma-vacuum interface problems for system (1.7) appear in the mathematical modeling of plasma confinement by magnetic fields (see, e.g., [4,5,6, 14]). In this model the plasma is confined inside a perfectly conducting rigid wall and isolated from it by a vacuum region, due to the effect of strong magnetic fields. In astrophysics, the plasma-vacuum interface problem can be used for modeling the motion of a star or the solar corona when magnetic fields are taken into account.
For the linearization of the 3D version of the plasma-vacuum interface problem formulated above, the third author [41] proposed two different well-posedness conditions for the basic state around which the problem was linearized. The first one is the non-collinearity condition, stating that the magnetic fields on either side of the interface are not collinear:
The second one is the MHD counterpart of the Rayleigh–Taylor sign condition, which reads as
In [41], basic a priori estimates were derived respectively for the variable coefficient linearized problem under the non-collinearity condition (1.19) and for the frozen coefficient linearized problem under the Rayleigh–Taylor-type sign condition (1.20).
In [36], the second and third authors proved the first local well-posedness theorem for the full plasma-vacuum interface problem under condition (1.19). However, the non-collinearity condition (1.19) excludes physically or mathematically important cases, such as the case with zero vacuum magnetic field. Motivated by this fact, the third author and Wang [44] studied the 3D version of the free boundary problem (1.7), (1.10), (1.13)–(1.15) for \({\mathcal {H}}\equiv 0\) and showed the first local well-posedness result under the Rayleigh–Taylor sign condition (1.20). Recently Lindblad and Zhang [22] improved the result in [44] by establishing the a priori estimate without loss of anisotropic regularity for the nonlinear problem.
The local well-posedness for the 3D plasma-vacuum interface problem is still unknown for nontrivial vacuum magnetic field without the non-collinearity condition (1.19). However, as was proved in [43], the simultaneous failure of the non-collinearity condition and the Rayleigh–Taylor sign condition leads to the ill-posedness of the frozen coefficient linearized problem. The most general open problem is, of course, the proof of local well-posedness provided that at each point of the initial interface \(\Gamma (0)\) either the non-collinearity condition (1.19) or the Rayleigh-Taylor sign condition (1.20) holds.
At the same time, our goal in this paper is to show that for 2D planar flows neither the non-collinearity condition nor the Rayleigh-Taylor sign condition are necessary for local well-posedness. Indeed, for the 2D planar case, in view of the last two boundary conditions in (1.13), the magnetic fields on either side of the interface are always collinear by definition. The only stability condition which we require in our well-posedness theorem for problem (1.7), (1.10), (1.13)–(1.15) is assumption (1.18), in agreement with the analysis of [6]. The assumption (1.18) shows that, as in the 3D case, the magnetic field plays a stabilizing role because, in contrast with the free boundary problem for the compressible Euler equations (for \(\rho |_{\Gamma }>0\), see [21, 39]), the Rayleigh–Taylor sign condition is not necessary for well-posedness.
At last, we note that neither the non-collinearity condition nor the Rayleigh-Taylor sign condition are necessary for well-posedness if the effect of surface tension is taken into account. For the 3D version of problem (1.7), (1.10), (1.13)–(1.15), this was recently proved by the third author and Wang in [45] for \({\mathcal {H}}\equiv 0\) and in [46] for nontrivial vacuum magnetic field. Clearly, the same is true for the 2D problem (1.7), (1.10), (1.13)–(1.15). Regarding the incompressible plasma-vacuum interfaces, we refer to [33, 37] for the qualitative behavior of surface waves, [15,16,17, 19, 24, 38] and [18], respectively for the well-posedness and ill-posedness without surface tension. For more references see the bibliography of the cited papers.
The rest of the paper is organized as follows: in Sect. 2 we reformulate the nonlinear problem and state the main result of the paper. In Sect. 3 we introduce our function spaces. In Sect. 4 we linearize the problem around a basic state and reduce the linearized problem to that with the homogeneous version (with zero right-hand sides) of the linearized constraints (1.16) and the linearized elliptic system (1.10). In Sect. 5 we write down a hyperbolic approximation of the hyperbolic-elliptic linear plasma-vacuum system. In Sect. 6 we obtain a basic a priori estimate and in Sect. 7 we prove the well-posedness of the hyperbolic approximation problem. In Sect. 8 we give the proof of Theorem 4.1 containing the basic a priori estimate for the coupled linear problem with the homogeneous constraints and elliptic system. In Sect. 9 we study the elliptic part of the linear problem. For the linearized problem (4.15), in Sect. 10 we provide an \(H^1\) a priori estimate and in Sect. 11 the tame estimate in anisotropic Sobolev estimate. In the final Sect. 13 we explain how the remaining part of the proof of the main Theorem 2.1 can be proved following the same arguments of [36].
2 Reformulation in the Fixed Domain and Main Result
Let us denote that
We want to reduce the free boundary problem (1.7), (1.9), (1.13), (1.15) to the fixed domains \(\Omega ^\pm \). In all what follows, \(H^s(\omega )\) denotes the Sobolev space of order s on a domain \(\omega \). \(H^s({\mathbb {T}})\) can be defined by using the Fourier coefficients and coincides with the set of distributions \({\textbf{u}}\) such that
\(c_k({\textbf{u}})\) denotes the kth Fourier coefficients of \({\textbf{u}}.\) The following lemma shows how to lift functions from \(\Gamma \) to \(\Omega \):
Lemma 2.1
Let \(m \ge 1\) be an integer and let \(T>0\). Then there exists a continuous linear map \(\varphi \in \cap _{j=0}^{m-1} {\mathcal C}^j([0,T];H^{m-j-0.5}(\Gamma )) \mapsto \Psi \in \cap _{j=0}^{m-1} {{\mathcal {C}}}^j([0,T];H^{m-j}(\Omega ))\) such that \(\Psi (t,0,x_2)=\varphi (t,x_2)\), \(\Psi (t,\pm 1,x_2)=0\) on \(\Gamma \), and moreover \(\partial _1\Psi (t,0,x_2)=0,\) if \(m\ge 2.\)
Furthermore, there exists a constant \(C>0\) that is independent of T and only depends on m, such that
The proof of Lemma 2.1 can be found in [10]. The diffeomorphism that reduces the free boundary problem (1.7), (1.13), (1.15) to the fixed domains \(\Omega ^\pm \) is given in the following lemma, (see [10, Lemma 3] and [36, Lemma 3]):
Lemma 2.2
Let \(m \ge 3\) be an integer. Then, there exists a constant \(\varepsilon _0>0\) such that for all \(T>0\), and for all \(\varphi \in \cap _{j=0}^{m-1} {{\mathcal {C}}}^j([0,T];H^{m-j-0.5}(\Gamma ))\), satisfying \(\Vert \varphi \Vert _{{{\mathcal {C}}} ([0,T];H^{2.5}(\Gamma ))} \le \varepsilon _0\), there exists a function \(\Psi \in \cap _{j=0}^{m-1} {{\mathcal {C}}}^j([0,T];H^{m-j}(\Omega ))\) constructed in Lemma 2.1, such that the function
defines an \(H^m\)-diffeomorphism of \(\Omega ,\) for all \(t \in [0,T]\). Moreover, it holds that \(\partial ^j_t (\Phi - Id) \in {\mathcal C}([0,T];H^{m-j}(\Omega ))\) for \(j=0,\dots , m-1\), \(\Phi (t,0,x_2)=(\varphi (t,x_2),x_2)\), \(\Phi (t,\pm 1,x_2)=(\pm 1,x_2),\) \(\partial _1\Phi (t,0,x_2)=(1,0)\).
We introduce the change of independent variables defined by (2.1) by setting
Dropping for convenience tildes in \(\widetilde{{\textbf{U}}}\) and \(\widetilde{{\mathcal {H}}}\), problem (1.7), (1.9) (1.13), (1.15) can be reformulated on the fixed reference domains \(\Omega ^\pm \) as
where \({\mathbb {P}}({\textbf{U}},\Psi )=P({\textbf{U}},\Psi ){\textbf{U}}\),
In (2.3) the notation \([0,T]\times (\Gamma ^3\times \Gamma _+\times \Gamma _-)\) means that the first three components of this vector equation are taken on \([0,T]\times \Gamma \), the fourth one on \([0,T]\times \Gamma _+\) and the fifth one on \([0,T]\times \Gamma _-\).
To avoid an overload of notation we have denoted by the same symbols \(u_N,{\mathcal {H}}_N\) here above and \(u_N,{\mathcal {H}}_N\) as in (1.13). Notice that \(u_{N |x_1=0}=u_1- u_2\partial _2\varphi ,\) \({\mathcal {H}}_{N |x_1=0}= {\mathcal {H}}_1- {\mathcal {H}}_2\partial _2\varphi \), as in the previous definition in (1.13).
We did not include in problem (2.2)–(2.4) the equation
and the boundary conditions
where \({\textbf{h}}=(H_{N},H_2\partial _1\Phi _1)\), \(H_{N}=H_1-H_2\partial _2\Psi \), because they are just restrictions on the initial data (2.4). More precisely, referring to [40] for the proof, we have the following proposition:
Proposition 2.1
Let the initial data (2.4) satisfy (2.5) and (2.6) for \(t=0\). If \(({\textbf{U}},{\mathcal {H}},\varphi )\) is a solution of problem (2.2)–(2.4), then this solution satisfies (2.5) and (2.6) for all \(t\in [0,T]\).
Note that Proposition 2.1 remains valid if in (2.2) we replace system \({\mathbb {P}}({\textbf{U}},\Psi )=0\) by system (1.1) in the straightened variables. This means that these systems are equivalent on solutions of our plasma-vacuum interface problem and we may justifiably replace the conservation laws (1.1) by their nonconservative form (1.3).
Remark 2.1
For each time t the vacuum magnetic field \({\mathcal {H}}\) solves the elliptic problem
We remark that, by the uniqueness of the solution to (2.1), see Proposition 9.1, \({\mathcal {H}}\not \equiv 0\) in \(\Omega ^-\) if and only if \({\mathcal {J}}\not \equiv 0\) in \(\Gamma _-\).
Now, we are in the position to state the main theorem of this paper.
Theorem 2.1
Let \(m\in {\mathbb {N}},\) \(m\ge 15,\) and \({\mathcal {J}}\in H^{m+9}([0,T_0]\times \Gamma _{-})\) for some \(T_0>0.\) Consider the initial data \({\textbf{U}}_0\in H^{m+9.5}(\Omega ^+),\) \({\mathcal {H}}^0\in H^{m+9.5}(\Omega ^-),\) and \(\varphi _0\in H^{m+10}(\Gamma ).\) Moreover, the initial data satisfy (1.8), (1.18), (12.2), (12.3) and are compatible up to order \(m+9\) in the sense of Definition 12.1. Then, there exists \(0<T\le T_0,\) \(\epsilon _1>0\) and \(\gamma _0\ge 1\) such that if \(||\varphi _0||_{H^{2.5}(\Gamma )}\le \epsilon _1\) and \(\gamma \ge \gamma _0,\) there exists a unique solution \(({\textbf{U}},{\mathcal {H}},\varphi )\) of problem (2.2)–(2.4) in [0, T], with
The function spaces involved in the statement above are introduced in the next section.
Remark 2.2
The initial vacuum magnetic field \({\mathcal {H}}^0\) is assumed to satisfy (12.3), which is a uniquely solvable elliptic system, and therefore it is uniquely determined by Proposition 9.1 from \(\varphi _0\) (i.e. the initial space domain) and \({\mathcal {J}}(0)\) (the external density current at the initial time). In this sense, for a given \({\mathcal {J}}\), the actual initial data of the problem may be only considered \({\textbf{U}}_0,\varphi _0\).
Remark 2.3
For polytropic gases, the hyperbolicity condition (1.8) at any given time t gives \(|{\mathcal {H}}|>0\) on \(\Gamma \), see Remark 1.1, which in turn from (2.1) and the uniqueness of its solution implies that \({\mathcal {J}}\not \equiv 0\) on \(\Gamma _-\), which is equivalent to \({\mathcal {H}}\not \equiv 0\) in \(\Omega ^-\). The same remark is true for general gases that satisfy the conventional assumption that \(p>0\) if \(\rho >0\).
Remark 2.4
The statement of the main Theorem 2.1 appears essentially equal to the statement of [36, Theorem 5], except for the lower bound on the required regularity \(m\ge 15\), instead of \(m\ge 13\) as the second and the third authors wrote in [36, Theorem 5]. From the similar construction of the modified state for the Nash–Moser iteration made in [27, Section 10.2.3] on 2D current-vortex sheets, it appears that some more regularity is needed, and after the iteration this fact is reflected into the increased regularity needed for the solution; see also Remark 13.1.
3 Function Spaces
Now we introduce the main function spaces to be used in what follows.
Let us denote that
3.1 Weighted Sobolev Spaces
For \(\gamma \ge 1\) and \(s\in {\mathbb {N}}\), \(H^s_\gamma (\Omega )\) denotes the Sobolev space of order s, equipped with the norm \(||\cdot ||_{H^s_{\gamma }(\Omega )}\) defined by
For functions defined over \(Q_T\) we will consider the weighted Sobolev spaces \(H^m_{\gamma }(Q_T)\) equipped with the \(\gamma -\)dependent norm
Similar weighted Sobolev spaces will be considered for functions defined on \(\Omega ^{\pm },Q^{\pm }_T, Q^\pm , \omega ^\pm , \omega \).
3.2 Conormal Sobolev Spaces
Let us introduce some classes of function spaces of Sobolev type, defined over the half-space \(Q^+_T\). We set
where \(\sigma (x_1)=x_1(1-x_1)\in C^{\infty }(0,1)\) is a smooth and nonnegative function. Then, for every multi-index \(\alpha =(\alpha _0,\alpha _1,\alpha _2)\in {\mathbb {N}}^3\), the conormal derivative \(Z^{\alpha }\) is defined by
we also write \(\partial ^{\alpha }=\partial ^{\alpha _0}_0\partial ^{\alpha _1}_1\partial ^{\alpha _2}_2\) for the usual partial derivative corresponding to \(\alpha \).
Given an integer \(m\ge 1\), the conormal Sobolev space \(H^m_{tan}(Q^+_T)\) is defined as the set of functions \(u\in L^2(Q^+_T)\) such that \(Z^\alpha u\in L^2(Q^+_T)\), for all multi-indices \(\alpha \) with \(|\alpha |\le m\). Agreeing with the notations set for the usual Sobolev spaces, for \(\gamma \ge 1\), \(H^m_{tan,\gamma }(Q^+_T)\) will denote the conormal space of order m equipped with the \(\gamma \)-dependent norm
and we have \(H^m_{tan}(Q^+_T):=H^m_{tan,1}(Q^+_T)\). Similarly, the function space can be defined on \(Q^-_T.\) If the \(Z_0\) derivatives are ignored, similar conormal Sobolev spaces with \(\gamma \)-dependent norms can be defined on \(\Omega ^{\pm }\),.
Now, we introduce the definition of anisotropic Sobolev spaces, which was firstly introduced by Chen [9] in the study of hyperbolic characteristic problem. Also see Secchi [31, 32] for general theory.
3.3 Anisotropic Sobolev Spaces
For every positive integer m, the anisotropic Sobolev space \(H^m_{*}(\Omega ^+)\) is defined as follows:
Define \(H^0_{*}(\Omega ^+)=H^0_{tan}(\Omega ^+)=L^2(\Omega ^+).\) The anisotropic space \(H^m_{*,\gamma }(\Omega ^+)\) is the same space equipped with the \(\gamma \)-dependent norm
We have \(H^m_*(\Omega ^+)=H^m_{*,1}(\Omega ^+)\). In a similar way, we define the anisotropic space \(H^m_{*,\gamma }(Q^+_T)\) equipped with its natural norm.
3.4 Moser-Type Calculus Inequalities
Let us define the space
equipped with the natural norm.
Lemma 3.1
([26, 40]) Let \(m\in {\mathbb {N}}_+.\) Assume that F is a \(C^{\infty }-\)function and \(u,v\in H^m_{*,\gamma }(Q^+_T)\cap W^{1,\infty }_*(Q^+_T)\). Then, there holds
Let \(M_*\) be a positive constant such that
If we assume that \(F(0)=0\), then there holds
3.5 Embedding Theorem
We introduce the Sobolev embedding theorem for \(H^m_{*,\gamma }(Q^+_T)\).
Theorem 3.1
([25]) Let \(n\ge 2\) and \(\gamma \ge 1\). Let \(\Omega \) be either \({{\mathbb {R}}}^n_+\) or a bounded open subset of \({{\mathbb {R}}}^n\) with \(C^\infty \) boundary. For every integer \(m\ge \left[ \frac{n+1}{2}\right] +1\) the continuous imbedding \(H^{m}_{*,\gamma }(\Omega )\hookrightarrow C^0_B(\Omega )\) (the space of bounded continuous functions) holds. Moreover, there exists a constant C such that for every \(u\in H^m_{*,\gamma }(\Omega )\)
Remark 3.1
Applying the above theorem for \(\Omega =Q^+_T\) (here the dimension is \(n=3\)) we obtain the following inequalities:
Observe that the same inequalities hold if the space dimension is 3, so that in space-time \(n=4\). This is the main reason why the loss of regularity of the solution from the initial data obtained in the present paper, see Theorem 2.1, is the same of the 3D case considered in [36].
4 The Linearized Problem
4.1 Basic State
Let us denote that
Let
be a given sufficiently smooth vector-function with \(\widehat{{\textbf{U}}}=({\hat{q}},\hat{{\textbf{u}}},\widehat{{\textbf{H}}},{\widehat{S}})\), respectively defined on \(Q^+_T,Q^-_T,\omega _T\), with
where \(K>0\) is a constant, \(\varepsilon _0\) is the arbitrary constant introduced in Lemma 2.2. Corresponding to the given \({{\hat{\varphi }}}\) we construct \({{\hat{\Psi }}}\) and the diffeomorphism \({{\hat{\Phi }}}\) as in Lemmata 2.1 and 2.2 such that
It is noted that the Sobolev inequality (recall that in 2D the following imbeddings \(H^2_*(\Omega ^+)\hookrightarrow C^0(\overline{\Omega ^+})\), \(H^3_*(Q^+_T)\hookrightarrow C^0(\overline{Q^+_T})\) hold true) implies that
where \(\nabla _{t,x}=(\partial _t,\nabla )\) and \(C=C(K)>0\) is a constant depending on K.
We assume that the basic state (4.2) satisfies (for some positive \(\rho _0,\rho _1\in {{\mathbb {R}}}\))
where all the “hat” values are determined like corresponding values for \(({\textbf{U}},{\mathcal {H}},\varphi )\), i.e.
and where
It follows from (4.5) that the constraints
are satisfied for the basic state (4.2) if they hold at \(t=0\) (see [40] for the proof). Thus, for the basic state we also require the fulfillment of conditions (4.10) at \(t=0\).
4.2 Linearized Problem
The linearized equations for (2.2), (2.3) read as
where \({\textbf{U}}_{\varepsilon }=\widehat{{\textbf{U}}}+ \varepsilon \,\delta {\textbf{U}}\), \({\mathcal {H}}_{\varepsilon }= \widehat{{\mathcal {H}}}+\varepsilon \,\delta {\mathcal {H}}\), \(\varphi _{\varepsilon }={\hat{\varphi }}+ \varepsilon \,\delta \varphi \); \(\delta \Psi \) is constructed from \(\delta \varphi \) as in Lemma 2.1 and \(\Psi _{\varepsilon }={{\hat{\Psi }}} + \varepsilon \,\delta \Psi \).
Here we introduce the source terms \(f=(f_1,\ldots ,f_6)\), \({\mathcal {G}}'=(\chi , \Xi )\) and \(g=(g_1,\dots ,g_5)\) to make the interior equations and the boundary conditions inhomogeneous.
We compute the exact form of the linearized equations (below we drop \(\delta \)):
there \(u_{N}:= u_1-u_2\partial _2{\widehat{\Psi }}\), and the matrix \({{\mathcal {C}}}(\widehat{{\textbf{U}}},{\widehat{\Psi }})\) is determined as follows:
Since the differential operators \({\mathbb {P}}'(\widehat{{\textbf{U}}},{\widehat{\Psi }})\) and \({\mathbb {V}}'(\widehat{{\mathcal {H}}},{\widehat{\Psi }})\) are first-order operators in \(\Psi \), as in [1] the linearized problem is rewritten in terms of the “good unknown”
Taking into account assumptions (4.7) and omitting detailed calculations, we rewrite our linearized equations in terms of the new unknowns (4.11):
there \({\dot{u}}_{\textrm{N}}={\dot{u}}_1-{\dot{u}}_2\partial _2{\hat{\Psi }}\), \(\dot{{\mathcal {H}}}_{N}=\dot{{\mathcal {H}}}_1-\dot{{\mathcal {H}}}_2\partial _2{\hat{\Psi }}\), and
We used (4.6), taken at \(x_1=0\), while writing down the third boundary condition in (4.14).
As in [1, 12, 40], we drop the zeroth-order term in \(\Psi \) in (4.12), (4.13) and consider the effective linear operators
In the proof of nonlinear analysis, we shall treat the dropped terms in (4.12), (4.13) as error terms. The new form of our linearized problem for \((\dot{{\textbf{U}}},\dot{{\mathcal {H}}},\varphi )\) reads as
where we denote that
We assume that the source terms \(f, \chi ,\Xi \) and the boundary datum g vanish in the past and consider the case of zero initial data. We postpone the case of nonzero initial data to the nonlinear analysis (see e.g. [12, 40]).
4.3 Reduction to Homogeneous Constraints in the “Vacuum part”
We decompose \(\dot{{\mathcal {H}}}\) in (4.15) as \(\dot{{\mathcal {H}}}={\mathcal {H}}'+{\mathcal {H}}''\) (and accordingly \(\dot{{\mathfrak {h}}}={\mathfrak {h}}'+{\mathfrak {h}}''\), \(\dot{{\mathfrak {H}}}={\mathfrak {H}}'+{\mathfrak {H}}''\)), where \({\mathcal {H}}''\) is required to solve for each t the elliptic problem
Let us observe that, for the resolution of (4.16), the data do not need to satisfy necessary compatibility conditions, see Auchmuty–Alexander [3], because this problem has boundary conditions of mixed type. The resolution of (4.16) is given in Sect. 9.
Given \({\mathcal {H}}''\), we look for \({\mathcal {H}}'\) such that
where we write \(g_2'=g_2+\widehat{{\mathcal {H}}}\cdot {{\mathcal {H}}}''.\) If \({\mathcal {H}}''\) solves (4.16) and \({\mathcal {H}}'\) is a solution of (4.17) then \(\dot{{\mathcal {H}}}={\mathcal {H}}'+{\mathcal {H}}''\) clearly solves (4.15b), (4.15d), (4.15e), (4.15g).
From (4.15), (4.17), the new form of the reduced linearized problem with unknowns (\(\dot{{\textbf{U}}},{\mathcal {H}}'\)) can be written as
4.4 Reduction to Homogeneous Constraints in the “Plasma part”
From problem (4.18) we can deduce nonhomogeneous equations associated with the divergence constraint \(\textrm{div}\,\dot{{\textbf{h}}}=0\) and the “redundant” boundary conditions \({\dot{H}}_N|_{x_1=0}=0\) and \({\dot{H}}_1|_{x_1=1}=0\) for the nonlinear problem. More precisely, with reference to [40, Proposition 2] for the proof, we have
Proposition 4.1
Let the basic state (4.2) satisfies assumptions (4.3)–(4.10). Then solutions of problem (4.18) satisfy
Here, we denote that
The functions \(r= r(t,x ),\) \(R= R(t,x_2)\) and \(R^+= R^+(t,x_2)\) which vanish in the past, are determined by the source terms and the basic state as solutions to the linear inhomogeneous equations
where \(a=r/\partial _1{\widehat{\Phi }}_1,\quad {{\mathcal {F}}}_H=(\textrm{div}\, {f}_{H})/\partial _1{\widehat{\Phi }}_1\), \({f}_{H}= (f_{N},f_5),\quad f_{N}=f_4-f_5\partial _2{\widehat{\Psi }},\)
Let us reduce (4.18) to a problem with homogeneous boundary conditions (4.18c), (4.18d), (4.18f) (i.e. \(g_1=g'_2=g_4=0\)) and homogeneous constraints (4.19) and (4.20) (i.e. \(r=R=R^+=0\)). More precisely, we describe a “lifting” function as
where \({\tilde{q}}= {g}'_2,{\tilde{u}}_1=-g_1\) on \(\omega _T\), \({\tilde{u}}_1=g_4\) on \(\omega ^+_T\) and where \(\widetilde{{\textbf{H}}}\) solves the equation for \(\dot{{\textbf{H}}}\) contained in (4.18a) with \(\dot{{\textbf{u}}}=\tilde{\textbf{u}}=({\tilde{u}}_1,0)\):
where \(\tilde{{\textbf{h}}}=({\widetilde{H}}_1-{\widetilde{H}}_2\partial _2{\hat{\Psi }},{\widetilde{H}}_2)\), \(f_H=(f_4,f_5)\). It is very important that, in view of (4.7), we have \({\hat{w}}_1|_{x_1=0}={\hat{w}}_1|_{x_1=1}=0\); therefore the linear Eq. (4.24) does not need any boundary condition. Then the new unknown
satisfies problem (4.18) with \(f=F\), where
In view of (4.24), \(F_4=F_5=0\), and it follows from Proposition 4.1 that \({\textbf{U}}^{\natural }\) satisfies (4.19) and (4.20) with \(r=R=R^+=0\). As in [36, Section 4.4] we obtain the estimates
Dropping for convenience the indices \(^{\natural }\) in (4.25), the new form of our reduced linearized problem now reads as
and solutions should satisfy
All the notations here for \({\textbf{U}}\) and \({\mathcal {H}}\) (e.g., h,\({\mathfrak {h}}\), etc.) are analogous to the corresponding ones for \(\dot{{\textbf{U}}}\) and \(\dot{{\mathcal {H}}}\) introduced above.
4.5 An Equivalent Formulation of (4.28)
In the following analysis it is convenient to make use of different “plasma” variables and an equivalent form of Eq. (4.28a). We define the matrix
It follows that
Multiplying (4.28a) on the left side by the matrix
after some calculations, we get the symmetric hyperbolic system for the new vector of unknowns \({\mathcal {U}}=(q,{\textbf{v}},{\textbf{h}},S)\) (compare with (1.6), (4.28a)):
there \({{\hat{a}}}_0\) is the symmetric and positive definite matrix
with a new matrix \(\widehat{{\mathcal {C}}}'\) in the zero-order term (whose precise form has no importance) and where we have set \( {\mathcal {F}}=\partial _1{{\widehat{\Phi }}}_1 \, {{\widehat{R}}} F.\) We write system (4.34) in compact form as
where
The formulation (4.35) has the advantage of the form of the boundary matrix of the system \(\widehat{{\mathcal {A}}}_1+{{\mathcal {E}}}_{12}\), with
because \({{\hat{w}}}_1={{\hat{h}}}_1=0\), and \({{\mathcal {E}}}_{12}\) a constant matrix. Thus system (4.35) is symmetric hyperbolic with characteristic boundary of constant multiplicity (see [28,29,30] for maximally dissipative boundary conditions). Thus, the final form of our reduced linearized problem is
under the constraints (4.29), (4.30) and (4.31) (recall that \(u_1=v_1\) on \(\omega ^+_T\)).
In order to prove Theorem 2.1, we need to prove the following theorem for the well-posedness of linearized problem. Recall that \({\mathcal {U}}=(q,{\textbf{v}},{\textbf{h}},S)\), where \({\textbf{v}}\) and \({\textbf{h}}\) were defined in (4.32).
Theorem 4.1
Let \(T>0\). Let the basic state (4.2) satisfies assumptions (4.3)–(4.10) and
where \(\delta \) is a fixed constant. There exists \(\gamma _0\ge 1\) such that for all \(\gamma \ge \gamma _0\) and for all \({\mathcal {F}}_\gamma \in H^1_{tan,\gamma }(Q^+_T)\), vanishing in the past, namely for \(t<0\), problem (4.37) has a unique solution \(({\mathcal {U}}_\gamma ,{{\mathcal {H}}}_\gamma ,\varphi _\gamma )\in H^1_{tan,\gamma }(Q^+_T)\times H^1_{\gamma }(Q^-_T)\times H^{3/2}_\gamma (\omega _T)\) with trace \((q_\gamma ,v_{1\gamma },h_{1\gamma })|_{\omega _T\cup \omega ^+_T}\in {H^{1/2}_\gamma (\omega _T\cup \omega ^+_T)}\). Moreover, the solution obeys the a priori estimate
where we have set \({\mathcal {U}}_\gamma =e^{-\gamma t}\,{\mathcal {U}}, {\mathcal {H}}_\gamma =e^{-\gamma t}\, {\mathcal {H}}, \varphi _\gamma = e^{-\gamma t}\, \varphi \) and so on. Here \(C=C(K,T,\delta )>0\) is a constant independent of the data \({\mathcal {F}}\) and \(\gamma \).
5 Hyperbolic Approximation of the Reduced Problem
The problem (4.37) is a nonstandard initial-boundary value problem for a coupled hyperbolic-elliptic system. For its resolution we introduce a hyperbolic approximation of the elliptic system (4.37b). We will prove the existence of solutions for such approximating problem by referring to the well-posedness theory for linear symmetric hyperbolic systems with characteristic boundary and maximally nonnegative boundary conditions [29, 30]. After showing suitable a priori estimate uniform in \(\varepsilon \), we will pass to the limit as \(\varepsilon \rightarrow 0\), to get the solution of (4.37).
The approximation of problem (4.37) is inspired by a corresponding problem in relativistic MHD [42]. In our non-relativistic case the displacement current \((1/c)\partial _t{\mathcal {E}}\) is neglected in the vacuum Maxwell equations, where c is the speed of light and \({\mathcal {E}}\) is the electric field. Now, in some sense, we restore this neglected term. Namely, we consider a hyperbolic approximation of the elliptic system (4.37b) by introducing a new auxiliary unknown \({\mathcal {E}}^{\varepsilon }\) which plays a role of the vacuum electric field, and the small parameter \(\varepsilon \) is associated with the physical parameter 1/c. We also approximate the second boundary condition in (4.37d) and introduce one boundary condition for the unknown \({\mathcal {E}}^{\varepsilon }\).
Let us denote \(V^{\varepsilon }=({\mathcal {H}}^{\varepsilon },{\mathcal {E}}^{\varepsilon })\). Given a small parameter \(\varepsilon >0\), we consider the following problem for the unknown \(({\mathcal {U}}^{\varepsilon },V^{\varepsilon },\varphi ^{\varepsilon })\):
where in the following we shall write
All the other notations for \({\mathcal {H}}^{\varepsilon }\) are analogous to those for \({\mathcal {H}}\), i.e.
The \(\textrm{Curl}\) of a scalar function \({\mathcal {E}}\) is the vector field defined by
If \(\Psi =0, \Phi _1=x_1\), then \({{\mathfrak {h}}}^{\varepsilon }={{\mathcal {H}}}^{\varepsilon }\,, {{\mathfrak {e}}}^{\varepsilon }={{{\mathcal {E}}}}^{\varepsilon }\), and when \(\varepsilon =1\) (5.1b) turns out to be nothing else than the Maxwell equations.
It is noteworthy that solutions to problem (5.1) satisfy
because (5.2)–(5.5) are just restrictions on the initial data which are automatically satisfied in view of (5.1h). Indeed, the derivation of (5.2) and (5.4) is absolutely the same as that of (4.29) and (4.30). Equation (5.3) trivially follow from (5.1b), (5.1h). Moreover, condition (5.5) is obtained by considering the first component of the first equation in (5.1b) at \(x_1=0\) and taking into account (5.1e)–(5.1h).
5.1 An Equivalent Formulation of (5.1)
In the following analysis it is convenient to make use of a different formulation of the approximating problem (5.1), as far as the vacuum part is concerned.
First we introduce the matrices which are coefficients of the space derivatives in (5.1b) (for \(\varepsilon =1\) the matrices below are those for the vacuum Maxwell equations):
Then system (5.1b) can be written in terms of the “curved” unknown \(W^{\varepsilon }=({\mathfrak {H}}^{\varepsilon },{\mathcal {E}}^{\varepsilon })\) as
where
The matrices \(B_0\) and K are found from the relations
so that
System (5.6) is symmetric hyperbolic. The convenience of the use of variables \(W^{\varepsilon }\) rather than \(V^{\varepsilon }\) stays mainly in that the matrices \(B_j^{\varepsilon }\) of (5.6), containing the singular multiplier \(\varepsilon ^{-1}\), are constant.
Finally, we write the boundary conditions (5.1c)–(5.1e) in terms of \(({\mathcal {U}}^{\varepsilon }, W^{\varepsilon })\), where we observe that (recalling that \({\partial _1{\widehat{\Phi }}_1}=1\) on \(\omega _T\))
Concerning the first equality above in (5.8) we notice that \(\hat{{\mathfrak {h}}}_1= \widehat{{\mathcal {H}}}_N=0\) on \(\omega _T\), so that \({\mathfrak {H}}^{\varepsilon }_1\) does not appear in the boundary condition.
From (5.6), (5.8) we get the new formulation of problem (5.1) for the unknowns \(({\mathcal {U}}^{\varepsilon }, W^{\varepsilon })\):
From (5.2)–(5.5) we get that solutions \(({\mathcal {U}}^{\varepsilon }, W^{\varepsilon })\) to problem (5.9) satisfy
Remark 5.1
The invertible part of the boundary matrix of a system allows to control the trace at the boundary of the so-called noncharacteristic component of the vector solution. Thus, with the system (5.9a) (whose boundary matrix is \(-{{\mathcal {E}}}_{12}\), because of (4.36)) we have the control of \(q^{\varepsilon },v_1^{\varepsilon }=u^{\varepsilon }_N\) at the boundary; therefore the components of \({{\mathcal {U}}}^{\varepsilon }\) appearing in the boundary conditions (5.9c), (5.9d) are well defined.
The same holds true for (5.9b) where we can get the control of \({\mathfrak {H}}_2^{\varepsilon },{\mathcal {E}}^{\varepsilon }\). We recall that \({\mathfrak {H}}_1^{\varepsilon }\) does not appear in the boundary condition (10.2) because \(\hat{{\mathfrak {h}}}_1=\hat{{\mathcal {H}}}_N=0\).
Before studying problem (5.9) (or equivalently (5.1)), we should be sure that the number of boundary conditions is in agreement with the number of incoming characteristics for the hyperbolic systems (5.9). Since one of the three boundary conditions (5.9c)–(5.9e) is needed for determining the function \(\varphi ^{\varepsilon } (t,x_2)\), the total number of “incoming” characteristics should be two. Let us check that this is true.
Proposition 5.1
If \(0<\varepsilon <1\) system (5.9a) has one incoming characteristic for the boundary \(\omega _T\) of the domain \(Q_T^+\). If \(\varepsilon >0\) is sufficiently small, system (5.9b) has one incoming characteristic for the boundary \(\omega _T\) of the domain \(Q_T^-\).
Proof
Consider first system (5.9a). In view of (4.36), the boundary matrix on \(\omega _T\) is \(-{\mathcal {E}}_{12}\) which has one negative (incoming in the domain \(Q_T^+\)) and one positive eigenvalue, while all other eigenvalues are zero.
Now consider system (5.9b). The boundary matrix \(B_1^\varepsilon \) has eigenvalues \( \lambda _{1}=-\varepsilon ^{-1},\, \lambda _{2}=\varepsilon ^{-1},\, \lambda _{3}=0. \) Thus, system (5.9b) has indeed one incoming characteristic in the domain \(Q_T^-\) (\(\lambda _{1}<0\)). \(\square \)
6 Basic a Priori Estimate for a Boundary Value Problem Associated to the Hyperbolic Approximation Problem (5.1)
Our goal now is to justify rigorously the formal limit \(\varepsilon \rightarrow 0\) in (5.1)–(5.5), or alternatively in (5.9)–(5.13). To this end we will prove the existence of solutions to problem (5.9)–(5.13) and a uniform in \(\varepsilon \) a priori estimate. This work will be done in several steps.
6.1 The Boundary Value Problem
Assuming that all coefficients and data appearing in (5.9) are extended for all times to the whole real line, let us consider the boundary value problem (recall the definition of \(Q^\pm ,\omega ,\omega ^\pm \) in (3.1))
In this section we prove a uniform in \(\varepsilon \) a priori estimate of smooth solutions of (6.1).
Theorem 6.1
Let the basic state (4.2) satisfies assumptions (4.3)–(4.10) and (4.38) for all times. There exist \({\varepsilon }_0>0,\,\gamma _0\ge 1\) such that if \(0<{\varepsilon }<{\varepsilon }_0\) and \(\gamma \ge \gamma _0\) then all sufficiently smooth solutions \(({\mathcal {U}}^{\varepsilon },W^{\varepsilon },\varphi ^{\varepsilon })\) of problem (6.1) obey the estimate
where we have set \({\mathcal {U}}^{\varepsilon }_\gamma =e^{-\gamma t}\,{\mathcal {U}}^{\varepsilon }, W^{\varepsilon }_\gamma =e^{-\gamma t}\, W^{\varepsilon }, \varphi ^{\varepsilon }_\gamma = e^{-\gamma t}\, \varphi ^{\varepsilon }\) and so on, and where \(C=C(K,\delta )>0\) is a constant independent of the data \({\mathcal {F}}\) and the parameters \(\varepsilon ,\gamma \).
Passing to the limit \(\varepsilon \rightarrow 0\) in this estimate will give the a priori estimate (4.39).
Since problem (6.1) looks similar to a corresponding one in relativistic MHD [42], for the deduction of estimate (6.2) we use the same ideas as in [42]. It is worth to point out that we need to be more careful with lower-order terms than in [42], because we must avoid the appearance of terms with \(\varepsilon ^{-1}\) (otherwise, our estimate would not be uniform in \(\varepsilon \)). Also for this reason we are using the variables \(({\mathcal {U}}^{\varepsilon }, W^{\varepsilon })\) rather than \(({\textbf{U}}^{\varepsilon },V^{\varepsilon })\).
For the proof of (6.2) we will need a secondary symmetrization of the transformed Maxwell equations in vacuum (5.1b), (5.3).
6.2 A Secondary Symmetrization
In order to show how to get the secondary symmetrization, for the sake of simplicity we first consider a planar unperturbed interface, i.e. the case \({\hat{\varphi }}\equiv 0\). For this case (5.1b), (5.3) become
We write for system (6.3) the following secondary symmetrization (for a similar secondary symmetrization of the 3D Maxwell equations in vacuum see [35, 42]):
there
The arbitrary functions \(\nu _i(t,\textbf{x})\) will be chosen in appropriate way later on. It may be useful to notice that system (6.5) can also be written as
where we write \(\mathbf {\nu }:=(\nu _1, \nu _2)\), \(\mathbf {\nu }^{\perp }:=(\nu _2,-\nu _1)\) and for any two vectors \(\textbf{v}=(v_1,v_2)\), \(\textbf{w}=(w_1,w_2)\) their vector product is the scalar given by
The symmetric system (6.5) (or (6.7)) is hyperbolic if \({\mathfrak {B}}_0^{\varepsilon }>0\), i.e. for
The last inequality is satisfied for any given \(\mathbf {\nu }\) and small \({\varepsilon }\). We compute that
Therefore the boundary is noncharacteristic for system (6.5) provided (6.9) and \(\nu _1\not =0\) hold.
Consider now a nonplanar unperturbed interface, i.e., the general case when \({\hat{\varphi }}\) is not identically zero. Similarly to (6.5), from (5.6) and (5.11), we get the secondary symmetrization
We write the system as
where (recall the definition of \(B_0\) in (5.7))
The explicit form of the matrix coefficient \(M^\varepsilon _3\) is useless in view of the subsequent analysis. The only important point is its behaviour with respect to \(\varepsilon \); namely one can check that all its entries are bounded as \(\varepsilon \rightarrow 0^+\), see (6.14).
System (6.10) is symmetric hyperbolic provided that (6.9) holds. We compute that
and so the boundary is noncharacteristic for system (6.10) if and only if (6.9) holds and \(\nu _1\not =\nu _2\partial _2{{\hat{\varphi }}}\). It is also useful to notice that system (6.10) originates from a linear combination of Eq. (5.1b) similarly to (6.7), namely from
We need to know which is the behaviour of the above matrices in (6.11) w.r.t. \(\varepsilon \) as \(\varepsilon \rightarrow 0\). In view of this, let us denote a generic matrix which is bounded w.r.t. \(\varepsilon \) by O(1). It is easy to find that
As the matrices \(M_0^{\varepsilon }\) and \({M}_3^{\varepsilon }\) do not contain the multiplier \(\varepsilon ^{-1}\), their norms are bounded as \(\varepsilon \rightarrow 0\). Recalling that the matrices \(B_j^{\varepsilon }\) are constant, we deduce as well that all the possible derivatives (with respect to t and \(x_j\)) of the matrices \(M_j^{\varepsilon }\) have bounded norms as \(\varepsilon \rightarrow 0\).
Remark 6.1
Following the same arguments of [35], it can be proved that systems (6.1b) and (6.10) are effectively equivalent, in the sense that they have the same solutions.
6.3 Proof of Theorem 6.1
For the proof of our basic a priori estimate (6.2) we will apply the energy method to the symmetric hyperbolic systems (6.1a) and (6.10). In the sequel \(\gamma _0\ge 1\) denotes a generic constant sufficiently large which may increase from formula to formula, and C is a generic constant that may change from line to line.
First of all we provide some preparatory estimates. In particular, to estimate the weighted conormal derivative \(Z_1=\sigma \partial _1\) of \({\mathcal {U}}^{\varepsilon }\) (recall the definition (3.2) of the \(\gamma \)-dependent norm of \(H^1_{tan,\gamma }\)) we do not need any boundary condition because the weight \(\sigma \) vanishes on \(\omega \). Applying to system (6.1a) the operator \(Z_1\) and using standard arguments of the energy method, multiplying \(Z_1\)(6.1a) by \(e^{-\gamma t}\,Z_1{\mathcal {U}}^{\varepsilon }_\gamma \) and integrate by parts over \(Q^+\), then we use the Cauchy-Schwarz inequality yields the inequality
for \(\gamma \ge \gamma _0\). On the other hand, directly from the Eq. (6.1a) we have
where C(K) is independent of \({\varepsilon },\gamma \). Thus from (6.15), (6.16) we get
where C(K) is independent of \({\varepsilon },\gamma \). Furthermore, using the special structure of the boundary matrix in (6.1a) (see (4.36)) and the divergence constraint (5.10), we may estimate the normal derivative of the noncharacteristic part \({\mathcal {U}}_{n\gamma }^{\varepsilon }=e^{-\gamma t}(q^{\varepsilon },v_1^{\varepsilon },h_1^{\varepsilon })\) of the “plasma” unknown \({\mathcal {U}}_{\gamma }^{\varepsilon }\):
where C(K) is independent of \({\varepsilon },\gamma \). In a similar way we wish to express the normal derivative of \(W^{\varepsilon }\) through its tangential derivatives. Here it is convenient to use system (6.1b) rather than (6.10). We multiply (6.1b) by \(\varepsilon \) and find from the obtained equation an explicit expression for the normal derivatives of \({\mathfrak {H}}_2^{\varepsilon },{\mathcal {E}}^{\varepsilon }\). An explicit expression for the normal derivatives of \({\mathfrak {H}}^{\varepsilon }_1\) is found through the divergence constraints (5.11). Thus we can estimate the normal derivatives of all the components of \(W^{\varepsilon }\) through its tangential derivatives:
where C(K) does not depend on \(\varepsilon \) and \(\gamma \), for all \({\varepsilon }\le {\varepsilon }_0\).
As for the front function \(\varphi ^\epsilon \) we easily obtain from (6.1c) the \(L^2\) estimate
where C is independent of \(\gamma \). Furthermore, thanks to our basic assumption (4.38), we can resolve (5.12), (5.13) and (6.1c) for the space-time gradient \(\nabla _{t,x_2}\varphi _\gamma ^{\varepsilon } =(\partial _t\varphi ^{\varepsilon }_\gamma ,\partial _2\varphi ^{\varepsilon }_\gamma )\):
where the vector-functions \({\hat{a}}_{\alpha }={a}_{\alpha }(\widehat{{\textbf{U}}}_{|\omega },\widehat{{\mathcal {H}}}_{|\omega })\) of coefficients can be easily written in explicit form. From (6.21) we get
Now we prove a \(L^2\) energy estimate for \(({\mathcal {U}}^{\varepsilon },W^{\varepsilon })\). We multiply (6.1a) by \(e^{-\gamma t}\,{\mathcal {U}}^{\varepsilon }_\gamma \) and (6.10) by \(e^{-\gamma t}\,W^{\varepsilon }_\gamma \), integrate by parts over \(Q^\pm \), then we use the Cauchy-Schwarz inequality. We easily obtain
where we have denoted that
Thanks to the properties of the matrices \(M_{\alpha }^{\varepsilon }\) (\(\alpha =0,1,2,3\)) described in (6.14), the constant C(K) in (6.23) is uniformly bounded in \({\varepsilon }\) and \(\gamma \).
Let us calculate the quadratic form \({\mathcal {A}}^{\varepsilon }\) for the following choice of the functions \(\nu _j\) in the secondary symmetrization:
there the cut-off function \(\chi (x_1)\in C^{\infty }([-1,0])\) is well-defined, such that \(\chi (0)=1\) and \(\chi (-1)=0.\) It has to be noted that the choice (6.24) makes the boundary characteristic, see (6.12).
After long calculations we get (for simplicity we drop the index \(\gamma \))
Now we insert the boundary conditions (5.13) (written in \(\omega \)), (6.1c)–(6.1e) in the quadratic form \({\mathcal {A}}^{\varepsilon }\), recalling also \(\hat{{\mathcal {H}}}_{N}|_{\omega }=0\). Again after some calculations we get
Thanks to the multiplicative factor \(\varepsilon \) in the boundary condition (6.1e), the critical term with the multiplier \({\varepsilon }^{-1}\) in (6.25) has been dropped out.
In the energy identity, there are also the boundary integrals for the outer top and bottom boundaries:
(recall that \(v_{1}=u_{1}\) on \(\omega ^+\)) and
By the choice of (6.24), we have \(\nu _i|_{x_1=-1}=0, i=1,2\) and it follows that
Then,
By using (6.1f) and (6.1g), \({\mathcal {I}}^{\pm }=0.\) From (6.23), (6.26) we obtain that
where C is independent of \({\varepsilon },\gamma \). Thus if \(\gamma _0\) is large enough we obtain from (6.20), (6.28) the inequality
where C is independent of \({\varepsilon },\gamma \).
Now we derive the a priori estimate of tangential derivatives. Differentiating systems (6.1a) and (6.10) with respect to \(x_0=t\), \(x_2\), using standard arguments of the energy method, and applying (6.18), (6.19), gives the energy inequality
where \(\ell =0,2\), and where we have denoted that
Thanks to the properties of the matrices \(M_{\alpha }^{\varepsilon }\) (\(\alpha =0,1,2,3\)) described in (6.14), the constant C in (6.30) is uniformly bounded in \({\varepsilon }\) and \(\gamma \). We repeat for \(\displaystyle {\mathcal {A}}^{\varepsilon }_{\ell }\) the calculations leading to (6.26) for \(\displaystyle {\mathcal {A}}^{\varepsilon }\). Clearly, for the same choice (6.24) we obtain (for simplicity we drop again the index \(\gamma \))
where l.o.t. is the sum of lower-order terms. Using (6.21) and the boundary condition (6.1d), we reduce the above terms to those like
terms as above with \({\mathfrak {h}}_1^{\varepsilon },v_1^{\varepsilon }\) instead of \(h_1^{\varepsilon }\), or even “better” terms like
Here and below \({\hat{c}}\) is the common notation for a generic coefficient depending on the basic state (4.2). By integration by parts such “better” terms can be reduced to the above ones and terms of lower order.
The terms like \({\hat{c}}\,h_1^{\varepsilon }Z_{\ell } v^{\varepsilon }_{1|x_1=0}\) are estimated by passing to the volume integral and integrating by parts,
where \({\tilde{c}}|_{x_1=0}={\hat{c}}\). Estimating the right-hand side by Hölder’s inequality and (6.18) gives
In the same way we estimate the other similar terms \( {\hat{c}}\, {h}_1^{\varepsilon }Z_{\ell }{\mathfrak {H}}_j^{\varepsilon }, {\hat{c}}\, {h}_1^{\varepsilon }Z_{\ell }{\mathcal {E}}^{\varepsilon },\) etc. Notice that we only need to estimate normal derivatives either of components of \({\mathcal {U}}_{n\gamma }^{\varepsilon }\) or \(W_{\gamma }^{\varepsilon }\). For terms like \({\hat{c}}\,{{\mathfrak {h}}}^{\varepsilon }_{1}Z_{\ell }v_1^{\varepsilon }, {\hat{c}}\,{{\mathfrak {h}}}^{\varepsilon }_{1}Z_{\ell }{\mathcal {E}}^{\varepsilon }\), etc. we use (6.19) instead of (6.18).
We treat the terms like \({\hat{c}}\,h_{1|x_1=0}^{\varepsilon }Z_{\ell } \varphi ^{\varepsilon }\) by substituting (6.21) again:
Combining (6.30), (6.32), (6.33) and similar inequalities for the other terms of (6.31) yields (we restore the index \(\gamma \))
where C is independent of \({\varepsilon },\gamma \). Then, from (6.17), (6.19), (6.29), (6.34), we obtain
where C is independent of \({\varepsilon },\gamma \). We need the following estimate for the traces of \({\mathcal {U}}^{\varepsilon }_n,W^{\varepsilon }\):
Lemma 6.1
The functions \({\mathcal {U}}^{\varepsilon }_n,W^{\varepsilon }\) satisfy
Proof
See [35, Lemma 6.2]. \(\square \)
Substituting (6.36), (6.37) in (6.35) and taking \(\gamma _0\) large enough yields
where C is independent of \({\varepsilon },\gamma \). Finally, from (6.22), (6.36) and (6.38) we get
Adding (6.38), (6.39) gives (6.2), The proof of Theorem 6.1 is complete.
7 Well-Posedness of the Boundary Value Problem Associated to the Hyperbolic Approximation Problem (5.1)
In this section we prove the existence of the solution of (6.1). Its restriction to the time interval \((-\infty ,T]\) will provide the solution of problem (5.9). From now on, in the proof of the existence of the solution, \(\varepsilon \) is fixed and so we omit it and we simply write \({\mathcal {U}}\) instead of \({\mathcal {U}}^{\varepsilon }\), W instead of \(W^{\varepsilon }\), \(\varphi \) instead of \(\varphi ^{\varepsilon }\).
In what follows, we can consider system (6.10) instead of (6.1b), because, following the same arguments of [35], these two systems are shown to be equivalent, in the sense that they have the same solutions. First of all, we write the boundary conditions in different form, by eliminating the derivatives of \(\varphi \). We substitute (6.1c) in the boundary conditions for \({\mathcal {E}}\) and take account of the constraint (5.13) and the choice (6.24). We get
where the precise form of the coefficients a is not important. For later use we observe that (5.13), (6.1c)–(6.1e) is equivalent to (5.13), (6.1c), (7.1).
Let us write the system (6.1a), (6.10), (7.1) in compact form as
where the matrix M and the vector b are implicitly defined by (7.1).
Let us multiply (7.2) by \(e^{-\gamma t}\) with \(\gamma \ge 1\); according to the rule \(e^{-\gamma t}\partial _tu=(\gamma +\partial _t)e^{-\gamma t}u\), (7.2) becomes equivalent to
where
\({\mathcal {U}}_{\gamma }=e^{-\gamma t}\,{\mathcal {U}}, W_{\gamma }=e^{-\gamma t}\, W, \varphi _{\gamma }=e^{-\gamma t}\varphi \), etc.
First we solve (7.3) under the assumption that \(\varphi _{\gamma }\) is given.
Lemma 7.1
There exists \(\gamma _0>0\) such that for all \(\gamma \ge \gamma _0\) and for all given \({\mathcal {F}} \in e^{\gamma t} H^1_{tan,\gamma }(Q^+)\) and \(\varphi \in e^{\gamma t}H^{3/2}_\gamma (\omega )\) vanishing in the past, the problem (7.3) has a unique solution \(({\mathcal {U}},W)\in e^{\gamma t} H^1_{tan,\gamma }(Q^+)\times e^{\gamma t} H^1_\gamma (Q^-)\) with \((q,v_{1}, h_1,W)_{|\omega }\in e^{\gamma t}{H^{1/2}_\gamma (\omega )}\), such that
Proof
Here we follow the same lines of [35]. We insert the new boundary conditions (7.1) in the quadratic form \({\mathcal {A}}^{\varepsilon }\) (see (6.25)) and we get
If we consider the boundary conditions (7.1) in homogeneous form, namely if we set \(\varphi =0\), then from (7.5)
We deduce that the boundary conditions (7.1) are nonnegative for \({{\mathcal {L}}}_\gamma \). As the number of boundary conditions in (7.1) is in agreement with the number of incoming characteristics for the operator \({{\mathcal {L}}}_\gamma \) (see Proposition 5.1) we infer that the boundary conditions (7.1) are maximally nonnegative (but not strictly dissipative). Then we reduce the problem to one with homogeneous boundary conditions by subtracting from \(({\mathcal {U}}_{\gamma },W_{\gamma })\) a function \(({\mathcal {U}}'_{\gamma },W'_{\gamma })\in H^2_\gamma (Q^+) \times H^2_\gamma (Q^-)\) such that
Finally, as the boundary is characteristic of constant multiplicity [28], we may apply the result of [29, 30] and we get the solution with the prescribed regularity. \(\square \)
The well-posedness of (6.1) in \(H^1_{tan}\times H^1\) is given by the following theorem.
Theorem 7.1
There exists \(\gamma _0>0\) such that for all \(\gamma \ge \gamma _0\) and \({\mathcal {F}} \in e^{\gamma t} H^1_{tan,\gamma }(Q^+)\) vanishing in the past, the problem (6.1) has a unique solution \(({\mathcal {U}},W)\in e^{\gamma t} H^1_{tan,\gamma }(Q^+)\times e^{\gamma t} H^1_{\gamma }(Q^-)\) with \((q,v_{1}, h_1,W)_{|\omega }\in e^{\gamma t}{H^{1/2}_\gamma (\omega )}\), \(\varphi \in e^{\gamma t}H^{3/2}_\gamma (\omega )\).
Proof
Again, we follow the same lines of [35]. We prove the existence of the solution to (6.1) by a fixed point argument. Let \({{\overline{\varphi }}}\in e^{\gamma t} H^{3/2}_{\gamma }(\omega )\) vanishing in the past. By Lemma 7.1, for \(\gamma \) sufficiently large there exists a unique solution \(({\mathcal {U}},W)\in e^{\gamma t} H^1_{tan,\gamma }(Q^+)\times e^{\gamma t} H^1_\gamma (Q^-)\), with \((q,v_1,h_1,W)_{|\omega } \in e^{\gamma t} H^{1/2}_\gamma (\omega )\) of
enjoying the a priori estimate (7.4) with \({{\overline{\varphi }}}\) instead of \(\varphi \). Now consider the equation
where \(v_{1\gamma } \in {H^{1/2}_{\gamma }(\omega )}\) is the trace of the component of \({\mathcal {U}}_\gamma \) that is the solution of problem (7.6) given in the previous step, vanishing for \(t<0\). For \(\gamma \) sufficiently large there exists a unique solution \(\varphi _{\gamma }\in H^{1/2}_{\gamma }(\omega )\), vanishing in the past, such that
From the plasma equation in (7.6) and from (7.7) we deduce the boundary constraint
Since in the right-hand side of (7.6) we have \({{\overline{\varphi }}}\) instead of \(\varphi \) we are not able to deduce the similar boundary constraint for the vacuum magnetic field. Instead, we obtain
where \(G_{\gamma }\) solves
for \({\tilde{\mathrm{{d}}}}/\mathrm{{d}}t=\gamma +\partial _t+\partial _2({\hat{u}}_2\,\cdot )\) and where the coefficient a is the same of (7.1). Condition (7.11) is derived from the first equation of the vacuum part of (7.6), (7.7) and the boundary condition for \({\mathcal {E}}\) in (7.6).
Let us consider the linear system for \(\nabla _{t,x_2}\varphi _\gamma \) provided by Eqs. (7.7), (7.9) and (7.10). We can represent \(\nabla _{t,x_2}\varphi _\gamma \) through \((h_{1\gamma }, {\mathfrak {h}}_{1\gamma }, v_{1\gamma })_{|\omega }, \varphi _\gamma , G_\gamma \) by using the stability condition (4.38), that is,
where the precise form of the coefficients \(a_i'\) has no interest. Then, substituting into (7.11) yields
with suitable coefficients \(b_i\).
From (7.13), for \(\gamma \) sufficiently large, we get the estimate
where we have applied (7.4) (with \({{\overline{\varphi }}}\) in place of \(\varphi \)) and (7.8). Thus, from (7.12) again, we obtain the estimate
Combining (7.4) (with \({{\overline{\varphi }}}\) in place of \(\varphi \)), (7.8) and (7.15) gives
This defines a map \({{\overline{\varphi }}}\rightarrow \varphi \) in \(e^{\gamma t} H^{3/2}_{\gamma }(\omega )\). Let \({{\overline{\varphi }}}^1, {{\overline{\varphi }}}^2\in e^{\gamma t} H^{3/2}_{\gamma }(\omega )\), and \(({\mathcal {U}}^1,W^1), ({\mathcal {U}}^2,W^2)\), \(\varphi ^1, \varphi ^2 \) be the corresponding solutions of (7.6), (7.7), respectively. Thanks to the linearity of the problems (7.6), (7.7) we obtain, as for (7.16),
Then there exists \(\gamma _0>0\) such that for all \(\gamma \ge \gamma _0\) the map \({{\overline{\varphi }}}\rightarrow \varphi \) has a unique fixed point, by the contraction mapping principle. The fixed point \({{\overline{\varphi }}}=\varphi \), together with the corresponding solution of (7.6), provides the solution of (7.3), (7.7), that is a solution of (6.1). As for the boundary conditions, we have already observed that (5.13) written on \(\omega \) instead of \(\omega _T\), (6.1c)–(6.1e) is equivalent to (5.13) written on \(\omega \) instead of \(\omega _T\), (6.1c), (7.1). The proof is complete. \(\square \)
Remark 7.1
We observe that, from the well-posedness of the boundary value problem (6.1), stated in Theorem 7.1, we get the well-posedness of the initial boundary value problem (5.9), indeed, the restriction of the solution of (6.1) to the time interval \((-\infty ,T]\) will provide the solution of problem (5.9).
8 Proof of Theorem 4.1
For all \(\varepsilon \) sufficiently small, problem (5.9) admits a unique solution with the regularity described in Theorem 7.1, see Remark 7.1. Due to the uniform a priori estimate (6.2) we can estract a subsequence weakly convergent to functions \(({\mathcal {U}},W,\varphi )\) with \(({\mathcal {U}}_\gamma ,W_\gamma )\in {H^{1}_{tan,\gamma }(Q^+_T)}\times {H^{1}_\gamma (Q^-_T)}\) and \((q_\gamma ,v_{1\gamma },h_{1\gamma })|_{\omega _T}\in {H^{1/2}_\gamma (\omega _T)}\), \(W_{\gamma }|_{\omega _T}\in {H^{1}_\gamma (\omega _T)}\) and \(\varphi _\gamma \in {H^1_\gamma (\omega _T)}\) (we use obvious notations). Let us decompose \(W=({\mathfrak {H}},{\mathcal {E}})\) and perform a inverse change of unknown with respect to that of Sect. 5.1 to define \({\mathcal {H}}\) from \({\mathfrak {H}}\). Passing to the limit in (5.1b), (5.9)–(5.13) as \(\varepsilon \rightarrow 0\) immediately gives that \(({{\textbf{U}}},{\mathcal {H}},\varphi )\) is a solution to (4.37), (4.29), (4.30) and \(\lim \limits _{\varepsilon \rightarrow 0}{\mathcal {E}}^{\varepsilon }={\mathcal {E}}=0\). Passing to the limit in (6.2) gives the a priori estimate (4.39). The proof of Theorem 4.1 is complete.
9 The Div-Curl Problem
This section is devoted to study the following div-curl system with mixed boundary condition. For fixed time t, we consider the elliptic system (4.16). Because \({\mathfrak {h}}=A{\mathfrak {H}}\) problem (4.16) can be equivalently rewritten as
where \(A=A(\nabla {\hat{\Psi }})=(\partial _1{\hat{\Phi }}_1)^{-1}{\hat{\eta }}{\hat{\eta }}^T,\) with \({\hat{\eta }}\) defined in (4.32) (recall that \(\mathfrak H_2={\mathcal {H}}_\tau ={\mathcal {H}}_2\) on \(\Gamma _-\)). The problem above is of the type of the div-curl boundary problems with mixed boundary conditions studied by Auchmuty–Alexander [3]; in particular, A is a symmetric positive-definite matrix in the sense of [3, Condition E1]. Therefore, we can apply to the problem above the well-posedness Theorem [3, Theorem 31], adapted to the case of the domain \(\Omega ^-\) which is periodic in the tangential \(x_2-\)variable.
In view of [3, Sect. 15], the mixed boundary-value problem (9.1) decouples into two separate elliptic problems for scalar functions, according to the decomposition of \(L^2(\Omega ^-)\) as
where \(\oplus \) denotes the direct sum of the spaces
and \(H^1_{\Gamma 0}(\Omega ^-)\) and \(H^1_{\Gamma _- 0}(\Omega ^-)\) are respectively the spaces of functions from \( H^1(\Omega ^-)\) with zero trace on \(\Gamma \) or \(\Gamma _-\).
Remark 9.1
In [3, Theorem 21], the decomposition of the space \(L^2(\Omega ^-)\) as the direct sum of subspaces involves an additional finite-dimensional space consisting of suitable A-harmonic vector fields on \(\Omega ^-\), whose dimension depends on the topology of the domain \(\Omega ^-\) and its boundary; however in the case of a simply connected domain, as \(\Omega ^-\) is in our case, this space of A-harmonic vector fields reduces to the null space.
According to the decomposition (9.2), we seek a solution to problem (9.1) in the form
where \(\varphi \) and \(\psi \) have to belong respectively to \(G_{\Gamma _-}(\Omega ^-)\) and \({\mathcal {C}}_{A\Gamma }(\Omega ^-)\). Substituting (9.5) in (9.1), we find that \(\varphi \) and \(\psi \) must solve the problems (see [3, Sect. 15])
and
where \(\textbf{e}_1:=(1,0)\) is the normal vector to \(\Gamma \) and \(\textbf{e}_2:=(0,1)\) is the tangential vector to \(\Gamma _-\). In view of [3, Theorem 31], problem (9.1) is well-posed in \(L^2(\Omega ^-)\). It is specially worth noting that no compatibility conditions are required when mixed boundary conditions are imposed, see again [3, Section 15].
Proposition 9.1
Assume that for each fixed t, the data \((\chi ,\Xi , g_3, g_5)\) in (9.1) satisfy \((\chi , \Xi )\in L^2(\Omega ^-)\), \(g_3\in H^{1/2}(\Gamma )\), \(g_5\in H^{1/2}(\Gamma _-)\). Then there exists a unique solution \({\mathfrak {H}}\in H^1(\Omega ^-)\) of (9.1) and
where \(H^{-1}_{\Gamma 0}(\Omega ^-)\) and \(H^{-1}_{\Gamma _- 0}(\Omega ^-)\) are respectively the dual spaces of \(H^1_{\Gamma 0}(\Omega ^-)\) and \(H^1_{\Gamma _- 0}(\Omega ^-)\) endowed with their natural norms.
If \((\chi ,\Xi )\in H^1(\Omega ^-)\), \(g_3\in H^{3/2}(\Gamma )\), \(g_5\in H^{3/2}(\Gamma _-)\), then \({\mathfrak {H}}\in H^2(\Omega ^-)\) and
In (9.8)–(9.10), \(C=C(K)\) is a positive constant depending only on K defined in (4.3).
Proof
The existence of \(\varphi \in H^1_{\Gamma _- 0}(\Omega ^-)\) and \(\psi \in H^1_{\Gamma 0}(\Omega ^-)\), respectively solutions of (9.6) and (9.7), follows from [3, Theorem 28, Theorem 29]. From (9.5) we obtain \({\mathfrak {H}}\in L^2(\Omega ^-)\). The estimate (9.8) follows from the equalities obtained from (9.6), (9.7) and integrations by parts,
by using that A and \(A^{-1}\) are positive definite and the Poincaré inequality. (9.9) and (9.10) follow from standard elliptic estimates for (9.6), (9.7). \(\square \)
10 Final \(H^1\) Estimate for the Nonhomogeneous Linearized Problem (4.15)
It is convenient to work in the plasma part with system analogous to (4.35) and write the vacuum equations in terms of \(\dot{{\mathfrak {H}}}\). Denoting \(\dot{{\mathcal {U}}}=({\dot{q}},\dot{{\textbf{v}}},\dot{{\textbf{h}}},{\dot{S}}),\) where
the nonhomogeneous linearized problem (4.15) becomes
Here, we define \({\tilde{f}}=\partial _1{\hat{\Phi }}_1{\hat{R}}f\), where \({{\hat{R}}}\) is defined in (4.33). Then we have
Theorem 10.1
Let \(T>0\). Let the basic state (4.2) satisfy the assumptions (4.3)–(4.10), (4.38). Then there exists \(\gamma _1\ge 1\) such that for all \(\gamma \ge \gamma _1\) and for all \({\tilde{f}}_\gamma \in H^2_{\gamma }(Q^+_T)\), \(\chi _\gamma \in {H}^{1}_\gamma (Q_T^-)\cap H^2_\gamma (-\infty ,T;H^{-1}_{\Gamma 0})\), \(\Xi _\gamma \in {H}^{1}_\gamma (Q_T^-)\cap H^2_\gamma (-\infty ,T;H^{-1}_{\Gamma _- 0})\), \((g_{1\gamma },g_{2\gamma })\in {H}_\gamma ^{3/2}(\omega _T)\), \(g_{3\gamma }\in {H}^{3/2}_\gamma (\omega _T)\cap H^2_\gamma (-\infty ,T;{H}^{-1/2}_\gamma (\Gamma ))\), \(g_{4\gamma }\in H^{3/2}_\gamma (\omega _T^+)\), \(g_{5\gamma }\in {H}^{3/2}_\gamma (\omega _T^-)\cap H^2_\gamma (-\infty ,T;{H}^{-1/2}_\gamma (\Gamma _-))\), and all functions vanishing in the past, problem (10.1) has a unique solution \((\dot{{\mathcal {U}}}_\gamma ,\dot{{\mathfrak {H}}}_\gamma ,\varphi _\gamma )\in H^1_{tan,\gamma }(Q^+_T)\times {H}^1_{\gamma }(Q^-_T)\times H^{3/2}_\gamma (\omega _T)\) with trace \(({\dot{q}}_\gamma ,{\dot{u}}_{1\gamma },{\dot{h}}_{1\gamma })|_{\omega _T}\in {H^{1/2}_\gamma (\omega _T)}\). Moreover, the solution obeys the a priori estimates
where we have set \(\dot{{\mathcal {U}}}_\gamma =e^{-\gamma t}\,{\dot{U}}, \dot{{\mathfrak {H}}}_\gamma =e^{-\gamma t}\, \dot{{\mathcal {H}}}, \varphi _\gamma = e^{-\gamma t}\, \varphi \) and so on. Here \(C=C(K,T,\delta )>0\) is a constant independent of the data \({\tilde{f}},\chi ,\Xi ,g\) and \(\gamma \).
Proof
Recalling the decomposition \(\dot{{\mathfrak {H}}}={\mathfrak {H}}'+{\mathfrak {H}}''\), see Sect. 4.3, the proof follows from the estimates (4.26), (4.27), Theorem 4.1, (9.9) for the space derivatives of \({{\mathfrak {H}}}''\), (9.8) for the time derivative of \({{\mathfrak {H}}}''\), and (9.10) for the trace estimate of \(g_2'\). \(\square \)
11 Well-Posedness of the Linearized Problem (4.15) in Anisotropic Sobolev Spaces
Then, we can prove the following well-posedness of the linearized problem in anisotropic Sobolev spaces:
Theorem 11.1
Let \(T>0,\) \(m\in {\mathbb {N}},m\ge 1\) and \(s=\max \{m+2,9\}.\) Let the basic state (4.2) satisfy the assumptions (4.3)–(4.10), (4.38) and
There exists \(\gamma _m\ge 1\) such that for all \(\gamma \ge \gamma _m\) and for all \(f_{\gamma }\in H^{m+1}_{*,\gamma }(Q^+_T),\) \((\chi _{\gamma },\Xi _{\gamma })\in H^{m+1}_{\gamma }(Q^-_T)\), \((g_{1\gamma },g_{2\gamma },g_{3\gamma })\in H^{m+1.5}_{\gamma }(\omega _T),\) \(g_{4\gamma }\in H^{m+1.5}_{\gamma }(\omega ^+_T), g_{5\gamma }\in H^{m+1}_{\gamma }(\omega ^-_T),\) all functions vanishing in the past, (10.1) has a solution \((\dot{{\mathcal {U}}}_{\gamma },\dot{{\mathfrak {H}}}_{\gamma },\varphi _{\gamma })\in H^m_{*,\gamma }(Q^+_T)\times H^m_{\gamma }(Q^-_T)\times H^{m+0.5}_{\gamma }(\omega _T),\) with trace \(({\dot{q}}_{\gamma },{\dot{v}}_{1\gamma },{\dot{h}}_{1\gamma })|_{\omega _T}\in H^{m-0.5}_{\gamma }(\omega _T).\) The solution obeys the tame estimate
where the constant \(C=C(K,T,\delta )\) is independent of the data \(f,\chi ,\Xi ,g\) and \(\gamma ,\) where we set
Proof
The proof of the theorem is entirely similar to that of [36, Theorem 16], using the \(H^1\) estimate (5.9d) in Theorem 10.1, the elliptic estimates (9.8), (9.9), (9.10) and estimates of commutators. \(\square \)
12 Compatibility Conditions on the Initial Data
Assume that the initial data \({\textbf{U}}_0=(q_0,{\textbf{u}}^0,{\textbf{H}}^0,S_0),\) \({\mathcal {H}}^0\) and \(\varphi _0\) that satisfy the hyperbolicity condition (1.8) and the stability condition (4.38). It is also assumed that
Let the functions \(\Psi _0,\Phi ^0\) be defined from \(\varphi _0,\) as in Lemmas 2.1 and 2.2. It is also assumed that the initial plasma magnetic field \({\textbf{H}}^0\) satisfy
where \(h^0=(H^0_{N_0},H^0_{2}\partial _1\Phi ^0_1),\) \(H^0_{N_0}=H^0_1-H^0_2\partial _2\Psi _0,\) and the initial vacuum magnetic field \({\mathcal {H}}^0\) satisfies
where \({\mathfrak {h}}^0,{\mathfrak {H}}^0\) are defined by
for \(j=0.\) Define \({\textbf{U}}_j=(q_j,{\textbf{u}}^j,{\textbf{H}}^j,S_j),\) with \({\textbf{u}}^j=(u^j_1,u^j_2)\) and \({\textbf{H}}^j=(H^j_1,H^j_2)\) and \(\varphi _j\) by formally taking \(j-1\) time derivatives of (2.2) and the boundary equation \(\partial _t\varphi -u_N=0,\) evaluating at time \(t=0\) and solving for \(\partial ^j_t{\textbf{U}}(0),\partial ^j_t\varphi (0).\) This process inductively determines \(\partial ^j_t{\textbf{U}}(0),\partial ^j_t\varphi (0)\) in terms of \({\textbf{U}}_0,\varphi _0.\) Denote \({\textbf{U}}_j=\partial ^j_t{\textbf{U}}(0),\varphi _j=\partial ^j_t\varphi (0).\) Corresponding to \(\varphi _j,\) we compute the functions \(\Psi _j,\Phi ^j.\) Finally, we define the time derivatives at initial time \({\mathcal {H}}^j\)
where \({\mathfrak {h}}^j,{\mathfrak {H}}^j\) are defined in (12.4) and \(\alpha _j,\beta _j,\vartheta _j\) are suitable commutators. From the second boundary equation in (2.3), we have that
The compatibility conditions are as follows:
Note that the other boundary conditions in (2.3) do not give raise to compatibility conditions as these are implicitly included in the above definitions of \(\varphi _j, {\mathcal {H}}^j\).
Lemma 12.1
Let \(k\in {\mathbb {N}},k\ge 4,\) \({\textbf{U}}_0\in H^{k-0.5}(\Omega ^+),\) \({\mathcal {H}}^0\in H^{k-0.5}(\Omega ^-),\) \(\varphi _0\in H^{k}(\Gamma )\) and \({\mathcal {J}}\in H^{k-0.5}([0,T_0]\times \Gamma _-).\) Then, the above procedure determines \({{\textbf{U}}}_j\in H^{k-j-0.5}(\Omega ^+),\) \({{\mathcal {H}}}^j\in H^{k-j-0.5}(\Omega ^-)\) and \(\varphi _j\in H^{k-j}(\Gamma )\) by induction for \(j=1,\cdots ,k-1\). Besides we prove
where \(C=C(M_0)>0\) depends on
Proof
See [36, Lemma 19]. \(\square \)
Definition 12.1
Let \(k\in {\mathbb {N}},k\ge 4\). The initial data \({\textbf{U}}_0\in H^{k-0.5}(\Omega ^+),\) \({\mathcal {H}}^0\in H^{k-0.5}(\Omega ^-)\) and \(\varphi _0\in H^k(\Gamma )\) are assumed to satisfy (1.8), (4.38), (12.1), (12.2), (12.3). The initial data \(({\textbf{U}}_0,{\mathcal {H}}^0,\varphi _0)\) are said to be compatible up to order \(k-1\) if they satisfy (12.6) on \(\Gamma ,\) \(u^j_1=0\) on \(\Gamma _+,\) for \(j=0,\cdots ,k-2\) and
Observe that \({\textbf{U}}_j\in H^{k-j-0.5}(\Omega ^+),\) \({\mathcal {H}}^j\in H^{k-j-0.5}(\Omega ^-),\) for \(j=0,\dots ,k-2\), so it is legitimate to take the traces at \(\{x_1=0\}\) and \(\{x_1=1\}\). The compatibility condition (12.9) is motivated by the lifting Theorem 2.3 in [23].
13 Proof of the Main Theorem 2.1
The proof of our main Theorem 2.1 follows by repeating entirely the same arguments used to show the similar result for the 3D problem in [36]. Starting from compatible initial data, we first construct a suitable approximate solution, which reduces (by subtraction) the original problem (2.2)–(2.4) on the fixed reference domain to a new nonlinear problem with zero initial data. Then we construct a modified Nash–Moser iteration scheme to solve this reduced problem. Our Nash–Moser scheme is not standard in the sense that we have to incorporate the specific constraints that need to be satisfied at each iteration step, namely the assumptions (4.3)–(4.10), (4.38) for the background state needed for the resolution of the linearized problem (4.15).
The details of the proof are similar to those in [36], in particular because the tame estimate (11.2) of Theorem 11.1 is exactly the same of [36, Theorem 16]. The modified state in the plasma part, satisfying the above mentioned constraints, is constructed in an alternative way as in [27, Section 10.2.3] on current-vortex sheets.
Remark 13.1
With respect to the similar construction of the modified state in [36], it appears that some more regularity is needed, and after the iteration this fact is reflected into the increased lower bound of the regularity needed for the solution, that is \(m\ge 15\) in Theorem 2.1, instead of \(m\ge 13\), as the second and the third authors wrote in [36, Theorem 5].
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Alinhac, S.: Existence d’ondes de raréfaction pour des systèmes quasi-linéaires hyperboliques multidimensionnels. Commun. Part. Differ. Eqs. 14(2), 173–230, 1989
Alinhac, S., Gérard, P.: Pseudo-differential Operators and the Nash-Moser Theorem. American Mathematical Society, Providence (2007)
Auchmuty, G., Alexander, J.C.: \(L^2\) well-posedness of planar div-curl systems. Arch. Ration. Mech. Anal. 160(2), 91–134, 2001
Bernstein, I.B., Frieman, E.A., Kruskal, M.D., Kulsrud, R.M.: An energy principle for hydromagnetic stability problems. Proc. R. Soc. Lond. A 244, 17–40, 1958
Blank, A.A., Friedrichs, K.O., Grad, H.: Notes on magneto-hydrodynamics. Theory of Maxwell’s Equations Without Displacement Current. New York University, Report NYO-6486-V p. 1957
Catania, D., D’Abbicco, M., Secchi, P.: Weak stability of the plasma-vacuum interface problem. J. Differ. Equ. 261(6), 3169–3219, 2016
Chen, G.-Q., Wang, Y.-G.: Existence and stability of compressible current-vortex sheets in three-dimensional magnetohydrodynamics. Arch. Ration. Mech. Anal. 187, 369–408, 2008
Chen, G.-Q., Wang, Y.-G.: Characteristic discontinuities and free boundary problems for hyperbolic conservation laws. in: Nonlinear Partial Differential Equations Abel Symp., vol. 7, pp. 53–81. Springer, Heidelberg (2012)
Chen, S.: Initial boundary value problems for quasilinear symmetric hyperbolic systems with characteristic boundary. Front. Math. China 2(1), 87–102, 2007
Coulombel, J.-F., Morando, A., Secchi, P., Trebeschi, P.: A priori estimates for 3D incompressible current-vortex sheets. Commun. Math. Phys. 311(1), 247–275, 2012
Coulombel, J.-F., Secchi, P.: The stability of compressible vortex sheets in two space dimensions. Indiana Univ. Math. J. 53, 941–1012, 2004
Coulombel, J.-F., Secchi, P.: Nonlinear compressible vortex sheets in two space dimensions. Ann. Sci. Ec. Norm. Super. 41, 85–139, 2008
Dafermos, C.M.: Hyperbolic Conservation Laws in Continuum Physics. Third Edition, Grundlehren der Mathematischen Wissenschaften (Fundatmental Principles of Mathematical Sciences), vol. 235, Springer-Verlag, Berlin (2010)
Goedbloed, J.P., Poedts, S.: Principles of Magnetohydrodynamics with Applications to Laboratory and Astrophysical Plasmas. Cambridge University Press, Cambridge (2004)
Gu, X., Wang, Y.: On the construction of solutions to the free-surface incompressible ideal magnetohydrodynamic equations. J. Math. Pures Appl. 128, 1–41, 2019
Hao, C.: On the motion of free interface in ideal incompressible MHD. Arch. Ration. Mech. Anal. 224, 515–553, 2017
Hao, C., Luo, T.: A priori estimates for free boundary problem of incompressible inviscid magnetohydrodynamic flows. Arch. Ration. Mech. Anal. 212, 805–847, 2014
Hao, C., Luo, T.: Ill-posedness of free boundary problem of the incompressible ideal MHD. Comm. Math. Phys. 376, 259–286, 2020
Hao, C., Luo, T.: Well-posedness for the linearized free boundary problem of incompressible ideal magnetohydrodynamics equations. J. Differ. Equ. 299, 542–601, 2021
Landau, L.D., Lifshiz, E.M., Pitaevskii, L.P.: Electrodynamics of Continuous Media. Pergamon Press, Oxford (1984)
Lindblad, H.: Well posedness for the motion of a compressible liquid with free surface boundary. Commun. Math. Phys. 260, 319–392, 2005
Lindblad, H., Zhang, J.: Anisotropic regularity of the free-boundary problem in compressible ideal magnetohydrodynamics, preprint at arXiv:2106.12173 (2021)
Lions, J.-L. Magenes, E.: Problèmes aux limites non homogènes et applications. Vol. 2. Travaux et Recherches Mathématiques, No. 18. Dunod, Paris (1968)
Morando, A., Trakhinin, Y., Trebeschi, P.: Well-posedness of the linearized plasma-vacuum interface problem in ideal incompressible MHD. Quart. Appl. Math. 72, 549–587, 2014
Morando, A., Secchi, P.: Regularity of weakly well posed hyperbolic mixed problems with characteristic boundary. J. Hyperbolic Differ. Equ. 8(1), 37–99, 2011
Morando, A., Secchi, P., Trebeschi, P.: Regularity of solutions to characteristic initial-boundary value problems for symmetrizable systems. J. Hyperbolic Differ. Equ. 6(4), 753–808, 2009
Morando, A., Secchi, P., Trebeschi, P., Yuan, D.: Nonlinear stability and existence of two-dimensional compressible current-vortex sheets. Arch. Ration. Mech. Anal. 247, 50, 2023. https://doi.org/10.1007/s00205-023-01865-w
Rauch, J.: Symmetric positive systems with boundary characteristic of constant multiplicity. Trans. Am. Math. Soc. 291, 167–187, 1985
Secchi, P.: Linear symmetric hyperbolic systems with characteristic boundary. Math. Methods Appl. Sci. 18, 855–870, 1995
Secchi, P.: The initial-boundary value problem for linear symmetric hyperbolic systems with characteristic boundary of constant multiplicity. Differ. Integr. Equ. 9(4), 671–700, 1996
Secchi, P.: Well-posedness of characteristic symmetric hyperbolic systems. Arch. Ration. Mech. Anal. 134, 155–197, 1996
Secchi, P.: A higher-order Hardy-type inequality in anisotropic Sobolev spaces. Int. J. Differ. Equ. 2012, 129691, 2012
Secchi, P.: Nonlinear surface waves on the plasma-vacuum interface. Quart. Appl. Math. 73, 711–737, 2015
Secchi, P.: On the Nash-Moser iteration technique. In: Amann, H., Giga, Y., Kozono, H., Okamoto, H., Yamazaki, M. (eds.) Recent Developments of Mathematical Fluid Mechanics, pp. 443–457. Birkhäuser, Basel (2016)
Secchi, P., Trakhinin, Y.: Well-posedness of the linearized plasma-vacuum interface problem. Interfaces Free Bound. 15, 323–357, 2013
Secchi, P., Trakhinin, Y.: Well-posedness of plasma-vacuum interface problem. Nonlinearity 27, 105–169, 2014
Secchi, P., Yuan, Y.: Weakly nonlinear surface waves on the plasma-vacuum interface. J. Math. Pures Appl. 163, 132–203, 2022
Sun, Y., Wang, W., Zhang, Z.: Well-posedness of the plasma-vacuum interface problem for ideal incompressible MHD. Arch. Ration. Mech. Anal. 234, 81–113, 2019
Trakhinin, Y.: Local existence for the free boundary problem for nonrelativistic and relativistic compressible Euler equations with a vacuum boundary condition. Commun. Pure Appl. Math. 62, 1551–1594, 2009
Trakhinin, Y.: The existence of current-vortex sheets in ideal compressible magnetohydrodynamics. Arch. Ration. Mech. Anal. 191, 245–310, 2009
Trakhinin, Y.: On the well-posedness of a linearized plasma-vacuum interface problem in ideal compressible MHD. J. Differ. Equ. 249, 2577–2599, 2010
Trakhinin, Y.: Stability of relativistic plasma-vacuum interfaces. J. Hyperbol. Differ. Equ. 9, 469–509, 2012
Trakhinin, Y.: On well-posedness of the plasma-vacuum interface problem: the case of non-elliptic interface symbol. Commun. Pure Appl. Anal. 15, 1371–1399, 2016
Trakhinin, Y., Wang, T.: Well-posedness of free boundary problem in non-relativistic and relativistic ideal compressible magnetohydrodynamics. Arch. Ration. Mech. Anal. 239, 1131–1176, 2021
Trakhinin, Y., Wang, T.: Well-posedness for the free-boundary ideal compressible magnetohydrodynamic equations with surface tension. Math. Ann. 383, 761–808, 2022
Trakhinin, Y., Wang, T.: Well-posedness for moving interfaces with surface tension in ideal compressible MHD. SIAM J. Math. Anal. 54, 5888–5921, 2022
Acknowledgements
The research of A. Morando, P. Secchi, P. Trebeschi was supported in part by the Italian MUR Project PRIN prot. 20204NT8W4. The research of Y. Trakhinin was supported by Mathematical Center in Akademgorodok under Agreement No. 075-15-2022-282 with the Ministry of Science and Higher Education of the Russian Federation. D. Yuan was supported by NSFC Grant No.12001045 and China Postdoctoral Science Foundation No. 2020M680428, No. 2021T140063. D. Yuan thanks the University of Brescia for its kind hospitality.
Funding
Open access funding provided by Università degli Studi di Brescia within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by T.-P. Liu.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Morando, A., Secchi, P., Trakhinin, Y. et al. Well-Posedness of the Two-Dimensional Compressible Plasma-Vacuum Interface Problem. Arch Rational Mech Anal 248, 56 (2024). https://doi.org/10.1007/s00205-024-02001-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00205-024-02001-y