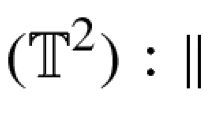Abstract
We consider the plasma-vacuum interface problem in a horizontally periodic slab impressed by a uniform non-horizontal magnetic field. The lower plasma region is governed by the incompressible inviscid and resistive MHD, the upper vacuum region is governed by the pre-Maxwell equations, and the effect of surface tension is taken into account on the free interface. The global well-posedness of the problem, supplemented with physical boundary conditions, around the equilibrium is established, and the solution is shown to decay to the equilibrium almost exponentially. Our results reveal the strong stabilizing effect of the magnetic field as the global well-posedness of the free-boundary incompressible Euler equations, without the irrotational assumption, around the equilibrium is unknown. One of the key observations here is an induced damping structure for the fluid vorticity due to the resistivity and transversal magnetic field. A similar global well-posedness for the plasma-plasma interface problem is obtained, where the vacuum is replaced by another plasma.
Similar content being viewed by others
References
Alazard, T., Delort, J.M.: Global solutions and asymptotic behavior for two dimensional gravity water waves. Ann. Sci. Éc. Norm. Supér. 48(5), 1149–1238 (2015)
Beale, J.: The initial value problem for the Navier–Stokes equations with a free surface. Commun. Pure Appl. Math. 34(3), 359–392 (1981)
Beale, J.: Large-time regularity of viscous surface waves. Arch. Ration. Mech. Anal.84(4), 307–252 (1983/84)
Caflisch, R.E., Orellana, O.F.: Singular solutions and ill-posedness for the evolution of vortex sheets. SIAM J. Math. Anal. 20(2), 293–307 (1989)
Castro, A., Córdoba, D., Fefferman, C., Gancedo, F., Gómez-Serrano, J.: Finite time singularities for the free boundary incompressible Euler equations. Ann. Math. (2) 178(3), 1061–1134 (2013)
Castro, A., Córdoba, D., Fefferman, C., Gancedo, F., Gómez-Serrano, J.: Splash singularities for the free boundary Navier–Stokes equations. Ann. PDE5(1), (2019) Art. 12, 117 pp
Chandrasekhar, S.: Hydrodynamic and Hydromagnetic Stability. The International Series of Monographs on Physics, Clarendon Press, Oxford (1981)
Cheng, C.H.A., Coutand, D., Shkoller, S.: On the motion of vortex sheets with surface tension in three-dimensional Euler equations with vorticity. Commun. Pure Appl. Math. 61(12), 1715–1752 (2008)
Cheng, C.A., Shkoller, S.: Solvability and regularity for an elliptic system prescribing the curl, divergence, and partial trace of a vector field on Sobolev-class domains. J. Math. Fluid Mech. 19(3), 375–422 (2017)
Christodoulou, D., Lindblad, H.: On the motion of the free surface of a liquid. Commun. Pure Appl. Math. 53(12), 1536–1602 (2000)
Coulombel, J.F., Morando, A., Secchi, P., Trebeschi, P.: A priori estimates for 3D incompressible current-vortex sheets. Commun. Math. Phys. 311(1), 247–275 (2012)
Coutand, D.: Finite-time singularity formation for incompressible Euler moving interfaces in the plane. Arch. Ration. Mech. Anal. 232(1), 337–387 (2019)
Coutand, D., Shkoller, S.: Well-posedness of the free-surface incompressible Euler equations with or without surface tension. J. Am. Math. Soc. 20(3), 829–930 (2007)
Davidson, P.A.: An Introduction to Magnetohydrodynamics. Cambridge Texts in Applied Mathematics., 2nd edn. Cambridge University Press, Cambridge (2001)
Deng, Y., Ionescu, A., Pausader, B., Pusateri, F.: Global solutions of the gravity-capillary water-wave system in three dimensions. Acta Math. 219(2), 213–402 (2017)
Ebin, D.: The equations of motion of a perfect fluid with free boundary are not well posed. Commun. Partial Differ. Equ. 12(10), 1175–1201 (1987)
Ebin, D.: Ill-posedness of the Rayleigh-Taylor and Helmholtz problems for incompressible fluids. Commun. Partial Differ. Equ. 13(10), 1265–1295 (1988)
Fefferman, C., Ionescu, A., Lie, V.: On the absence of splash singularities in the case of two-fluid interfaces. Duke Math. J. 165(3), 417–462 (2016)
Freidberg, J.P.: Ideal Magnetohydrodynamics. Plenum Press, New York (1987)
Germain, P., Masmoudi, N., Shatah, J.: Global solutions for the gravity water waves equation in dimension 3. Ann. Math. (2) 175(2), 691–754 (2012)
Germain, P., Masmoudi, N., Shatah, J.: Global solutions for capillary waves equation. Commun. Pure Appl. Math. 68(4), 625–487 (2015)
Goedbloed, J., Poedts, S.: Principles of Magnetohydrodynamics with Applications to Laboratory and Astrophysical Plasmas. Cambridge University Press, Cambridge (2004)
Gu, X., Wang, Y.J.: On the construction of solutions to the free-surface incompressible ideal magnetohydrodynamic equations. J. Math. Pures Appl. (9) 128, 1–41 (2019)
Guo, Y., Tice, I.: Local well-posedness of the viscous surface wave problem without surface tension. Anal. PDE 6(2), 287–369 (2013)
Guo, Y., Tice, I.: Almost exponential decay of periodic viscous surface waves without surface tension. Arch. Ration. Mech. Anal. 207(2), 459–531 (2013)
Guo, Y., Tice, I.: Decay of viscous surface waves without surface tension in horizontally infinite domains. Anal. PDE 6(6), 1429–1533 (2013)
Hao, C., Luo, T.: A priori estimates for free boundary problem of incompressible inviscid magnetohydrodynamic flows. Arch. Ration. Mech. Anal. 212(3), 805–847 (2014)
Hataya, Y.: Decaying solution of a Navier–Stokes flow without surface tension. J. Math. Kyoto Univ. 49(4), 691–717 (2009)
Ionescu, A., Pusateri, F.: Global solutions for the gravity water waves system in 2D. Invent. Math. 199(3), 653–804 (2015)
Ionescu, A., Pusateri, F.: Global regularity for 2D water waves with surface tension. Mem. Am. Math. Soc. 256(1227), v+124 pp (2018)
Jang, J., Tice, I.: Instability theory of the Navier–Stokes–Poisson equations. Anal. PDE 6(5), 1121–1181 (2013)
Ladyženskaya, O.A., Solonnikov, V.A.: Solutions of some non-stationary problems of magnetohydrodynamics for a viscous incompressible fluid. Trudy Mat. Inst. Steklov. 59, 115–173 (1960)
Ladyženskaya, O.A., Solonnikov, V.A.: The linearization principle and invariant manifolds for problems of magnetohydrodynamics. Zap. Naun. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 38, 46–93 (1973)
Lindblad, H.: Well-posedness for the motion of an incompressible liquid with free surface boundary. Ann. Math. (2) 162(1), 109–194 (2005)
Lions, J.L., Magenes, E.: Nonhomogeneous Boundary Value Problems and Applications. Springer-Verlag, Berlin (1972)
Morando, A., Trakhinin, Y., Trebeschi, P.: Well-posedness of the linearized plasma-vacuum interface problem in ideal incompressible MHD. Q. Appl. Math. 72(3), 549–587 (2014)
Nalimov, V.I.: The Cauchy-Poisson problem. (Russian) Dinamika Splo\(\breve{s}\)n. Sredy Vyp. 18 Dinamika \(\breve{Z}\)idkost. so Svobod. Granicami. 254, 104–210 (1974)
Padula, M., Solonnikov, V.A.: On the free boundary problem of magnetohydrodynamics. J. Math. Sci. (N.Y.) 178(3), 313–344 (2011)
Roberts, P.H.: An Introduction to Magnetohydrodynamics. Longmans, Green and Co Ltd., London (1967)
Shatah, J., Zeng, C.: Geometry and a priori estimates for free boundary problems of the Euler equation. Commun. Pure Appl. Math. 61(5), 698–744 (2008)
Shatah, J., Zeng, C.: A priori estimates for fluid interface problems. Commun. Pure Appl. Math. 61(6), 848–876 (2008)
Shatah, J., Zeng, C.: Local well-posedness for fluid interface problems. Arch. Ration. Mech. Anal. 199(2), 653–705 (2011)
Solonnikov, V.A.: Solvability of the problem of the motion of a viscous incompressible fluid that is bounded by a free surface. Math. USSR-Izv (1977) 11(6) , 1323–1358 (1978)
Solonnikov, V.A.: Unsteady flow of a finite mass of a fluid bounded by a free surface. J. Soviet Math. 40(5), 672–686 (1988)
Solonnikov, V.A.: Free boundary problems of magnetohydrodynamics in multi-connected domains. Interfaces Free Bound. 14(4), 569–602 (2012)
Solonnikov, V.A.: On a free boundary problem of magnetohydrodynamics for a viscous incompressible fluid not subjected to capillary forces. Recent advances in partial differential equations and applications, 357–383, Contemp. Math., 666, American Mathematical Society, Providence, RI (2016)
Solonnikov, V.A., Frolova, E.V.: Solvability of a free boundary problem of magnetohydrodynamics in an infinite time interval. J. Math. Sci. (N.Y.) 195(1), 76–97 (2013)
Ströhmer, G.: About an initial-boundary value problem from magnetohydrodynamics. Math. Z. 209, 345–362 (1992)
Sun, Y., Wang, W., Zhang, Z.: Nonlinear stability of current-vortex sheet to the incompressible MHD equations. Commun. Pure Appl. Math. 71(2), 356–403 (2018)
Sun, Y., Wang, W., Zhang, Z.: Well-posedness of the plasma-vacuum interface problem for ideal incompressible MHD. Arch. Ration. Mech. Anal. 234(1), 81–113 (2019)
Wang, Y.J.: Anisotropic decay and global well-posedness of viscous surface waves without surface tension. Adv. Math. 374(2020), 107330, 54 pp
Wang, Y.J.: Sharp nonlinear stability criterion of viscous non-resistive MHD internal waves in 3D. Arch. Ration. Mech. Anal. 231(3), 1675–1743 (2019)
Wang, Y.J., Tice, I., Kim, C.: The viscous surface-internal wave problem: global well-posedness and decay. Arch. Ration. Mech. Anal. 212(1), 1–92 (2014)
Wang, Y.J., Xin, Z.P.: Vanishing viscosity and surface tension limits of incompressible viscous surface waves. SIAM J. Math. Anal. 53(1), 574–648 (2021)
Wu, S.: Well-posedness in Sobolev spaces of the full water wave problem in 2-D. Invent. Math. 130(1), 39–72 (1997)
Wu, S.: Well-posedness in Sobolev spaces of the full water wave problem in 3-D. J. Am. Math. Soc. 12(2), 445–495 (1999)
Wu, S.: Almost global wellposedness of the 2-D full water wave problem. Invent. Math. 177(1), 45–135 (2009)
Wu, S.: Global wellposedness of the 3-D full water wave problem. Invent. Math. 184(1), 125–220 (2011)
Zhang, P., Zhang, Z.: On the free boundary problem of three-dimensional incompressible Euler equations. Commun. Pure Appl. Math. 61(7), 877–940 (2008)
Acknowledgements
The authors are grateful to the referees for insightful comments and suggestions. This research was supported by Zheng Ge Ru Foundation, HongKong RGC Earmarked Research Grants CUHK14305315, CUHK14302819, CUHK14300917, CUHK14302917, CUHK14300819 and Basic and Applied Basic Research Foundation of Guangdong Province 2020B1515310002. Y. J. Wang was also supported by the National Natural Science Foundation of China (11771360, 12171401) and the Natural Science Foundation of Fujian Province of China (2019J02003).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Ionescu
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A. Analytic tools
Appendix A. Analytic tools
In this appendix we will collect the analytic tools which are used throughout the paper.
1.1 Harmonic extension
Define the specialized Poisson sum in \( \mathbb {T}^2\times \mathbb {R}\) by (see [53])
where
Here \(0<\lambda _0<\lambda _1<\cdots<\lambda _m<\infty \) for \(m\in \mathbb {N}\), and \(\alpha =(\alpha _0,\alpha _1,\dots ,\alpha _m)^T\) is the solution to
where V is the \((m+1) \times (m+1)\) Vandermonde matrix. The Poisson sum (A.1) is specialized in that \(\mathcal {P} f\) is differentially continuous across \(\Sigma \) up to any order as needed provided that m is sufficiently large. Moreover, the following estimate holds.
Lemma A.1
It holds that for all \(s\in \mathbb {R}\),
Proof
One may refer to Lemma A.9 of [24] for instance. \(\quad \square \)
1.2 Time extension
The following lemmas allow one to extend the initial data to be time-dependent functions, which are “hyperbolic” versions of the “parabolic” ones in [24] with some minor modifications.
Lemma A.2
Suppose that \(\partial _t^j \eta (0) \in H^{2N-j+3/2}(\Sigma )\) for \(j=0,\dotsc ,2N-1\). There exists an extension \(\eta ^0\) defined on \([0,\infty )\), achieving the initial data, so that
Proof
For each \(j=0,\dotsc ,2N-1\), we denote \(f_j = \partial _t^j \eta (0)\) and let \(\varphi _j \in C_0^\infty (\mathbb {R}^{})\) be such that \(\varphi _j^{(k)}(0) = \delta _{j,k}\) for \(k=0,\dotsc ,2N-1\). Then \(\eta ^0\) is constructed as a sum \(\eta ^0 = \sum _{j=0}^{2N-1} F_j\), where \(F_j\) is defined via its Fourier coefficients:
where \(\left\langle \xi \right\rangle = \sqrt{1+ \left| \xi \right| ^2}\). It follows by modifying the proof of Lemma A.5 of [24] suitably that \(\eta ^0\) satisfies the conclusion. \(\quad \square \)
Lemma A.3
Suppose that \(\partial _t^j u(0) \in H^{2N-j}(\Omega _-)\) for \(j=0,\dotsc ,2N-1\). There exists an extension \(u^0\) defined on \([0,\infty )\), achieving the initial data, so that
Proof
It follows similarly as Lemma A.2, by using additionally the usual theory of extensions and restrictions in Sobolev spaces between \(H^k(\Omega _-)\) and \(H^k(\mathbb {R}^3)\) for \(k\ge 0\).
\(\square \)
Lemma A.4
Suppose that \(\partial _t^j b(0) \in H^{2N-j+1}(\Omega _-)\) for \(j=0,\dotsc ,2N-1\). There exists an extension \(b^0\) defined on \([0,\infty )\), achieving the initial data, so that
Proof
It follows in the same way as Lemma A.3. \(\quad \square \)
1.3 Product estimates
The following standard estimates in Sobolev spaces are needed.
Lemma A.5
Let the domains below be either \(\Omega _\pm \), \(\Sigma \) or \(\Sigma _\pm \), and d be the dimension.
-
(1)
Let \(0\le r \le s_1 \le s_2\) be such that \(s_1 > d/2\). Then
$$\begin{aligned} \left\| fg\right\| _{H^r} \lesssim \left\| f\right\| _{H^{s_1}} \left\| g\right\| _{H^{s_2}}. \end{aligned}$$(A.8) -
(2)
Let \(0\le r \le s_1 \le s_2\) be such that \(s_2 >r+ d/2\). Then
$$\begin{aligned} \left\| fg\right\| _{H^r} \lesssim \left\| f\right\| _{H^{s_1}} \left\| g\right\| _{H^{s_2}}. \end{aligned}$$(A.9)
Lemma A.6
It holds that for \(s>5/2\),
1.4 Poincaré-type inequality
The following Poincaré-type inequality related to \({\bar{B}}\cdot \nabla \) holds.
Lemma A.7
For any constant vector \({\bar{B}} \in \mathbb {R}^3\) with \({\bar{B}}_3\ne 0\), it holds that
and
Proof
It follows by the fundamental theorem of calculus, see Lemma A.4 in [52]. \(\square \)
1.5 Normal trace estimates
The following \(H^{-1/2}\) boundary estimate holds for functions satisfying \(v\in L^2\) and \({{\,\mathrm{div}\,}}^{\varphi }v \in L^2\).
Lemma A.8
Assume that \(\left\| \nabla \varphi \right\| _{L^\infty } \le C\), then
Proof
One may refer to Lemma 3.3 in [24]. \(\quad \square \)
1.6 Hodge-type estimates
The following Hodge-type estimate holds, when the boundary conditions are not specified. Let the domain be either \(\Omega _-\) or \(\Omega +\) or \(\Omega \).
Lemma A.9
Let \(r\ge 1\) be an integer. Then it holds that
Proof
Notice that (A.14) follows easily for \(r=1\). Now for \(r\ge 2\), applying the previous estimate of \(r=1\) gives that for \(\ell =1,\dots , r\),
By an induction argument on \(\ell =1,\dots , r\), one gets (A.14). \(\quad \square \)
Rights and permissions
About this article
Cite this article
Wang, Y., Xin, Z. Global Well-Posedness of Free Interface Problems for the Incompressible Inviscid Resistive MHD. Commun. Math. Phys. 388, 1323–1401 (2021). https://doi.org/10.1007/s00220-021-04235-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-04235-3