Abstract
We are concerned with the nonlinear stability and existence of two-dimensional current-vortex sheets in ideal compressible magnetohydrodynamics. This is a nonlinear hyperbolic initial-boundary value problem with a characteristic free boundary. It is well-known that current-vortex sheets may be at most weakly (neutrally) stable due to the existence of surface waves solutions that yield a loss of derivatives in the energy estimate of the solution with respect to the source terms. We first identify a sufficient condition ensuring the weak stability of the linearized current-vortex sheets problem. Under this stability condition for the background state, we show that the linearized problem obeys an energy estimate in anisotropic weighted Sobolev spaces with a loss of derivatives. Based on the weakly linear stability results, we then establish the local-in-time existence and nonlinear stability of current-vortex sheets by a suitable Nash–Moser iteration, provided that the stability condition is satisfied at each point of the initial discontinuity. This result gives a new confirmation of the stabilizing effect of sufficiently strong magnetic fields on Kelvin–Helmholtz instabilities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we are focusing on two-dimensional ideal compressible magnetohydrodynamics (MHD)(see [15, 18, 19])
supplemented with
on the initial data for the Cauchy problem. Here density \(\rho ,\) velocity \({\textbf{u}}=(u_1,u_2)\), magnetic field \({\textbf{H}}=(H_1,H_2)\) and pressure p are unknown functions of time t and spacial variables \({\textbf{x}}=(x_1,x_2)\). \(p=p(\rho ,S)\) stands for the pressure, S is the entropy, \(e=E+\frac{1}{2}|{\textbf{u}}|^2\), where \(E=E(\rho ,S)\) stands for the internal energy. By using the state equation of gas, \(\rho =\rho (p,S),\) and the first principle of thermodynamics, we have that (1.1) is a closed system. We write \(\mathbf{{U}}=\mathbf{{U}}(t,{\textbf{x}})=(p,{\textbf{u}},{\textbf{H}},S)^T,\) with initial data \(\mathbf{{U}}(0,{\textbf{x}})=\mathbf{{U}}_0({\textbf{x}}).\) By (1.2), we can rewrite (1.1) into the form
where \(q=p+\frac{1}{2}|{\textbf{H}}|^2\) represents the total pressure, c denotes the speed of sound and \(\frac{1}{c^2}:=\frac{\partial \rho }{\partial p}(\rho ,S)=\rho _p(p,S)\). (1.3) can be written in the matrix form as
where
The quasilinear system (1.4) is symmetric hyperbolic if the state equation \(\rho =\rho (p,S)\) satisfies the hyperbolicity condition \(A_0>0:\)
We suppose that \(\Gamma :=\bigcup \limits _{t\in [0,T]}\Gamma (t)\), where \(\Gamma (t):=\{\textbf{x}\in {\mathbb {R}}^2\,:\,\,x_1-\varphi (t,x_2)=0\}\), is a smooth hypersurface in \([0,T]\times {{\mathbb {R}}}^2.\) The weak solutions of (1.1) satisfy the following Rankine–Hugoniot jump conditions on \(\Gamma (t)\):
Here we denote \([\upsilon ]=(\upsilon ^+-\upsilon ^-)|_{\Gamma }\) the jump of \(\upsilon \), with \(\upsilon ^{\pm }:=\upsilon \) in \(\Omega ^{\pm }(t)=\{\pm (x_1-\varphi (t,x_2))>0\},\) and \(j=\rho (u_N-\partial _t\varphi )\) is the mass transfer flux across the discontinuity surface. We also denote the tangential and normal components of velocity and magnetic fields \(u_{\tau }={\textbf{u}}\cdot \tau ,H_{\tau }={\textbf{H}}\cdot \tau ,\) \(u_N={\textbf{u}}\cdot N, H_N={\textbf{H}}\cdot N,\) where \(N=(1,-\partial _2\varphi ),\tau =(\partial _2\varphi ,1).\)
We are focusing on the current-vortex sheets solutions, which obey the following additional conditions along the interface \(\Gamma \):
Then, the Rankine–Hugoniot conditions reduce to the boundary conditions
on \(\Gamma (t).\)
The tangential components of the velocity and the magnetic field may undergo any jumps: \([u_{\tau }]\ne 0,\quad [H_{\tau }]\ne 0.\) The initial data are given as follows:
It is obvious that there exist trivial vortex sheets (contact discontinuity) solutions consisting of two constant states separated by a flat surface as
where on account of (1.8), we require that
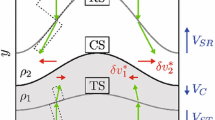
Compressible vortex sheets are fundamental waves in the study of entropy solutions to multidimensional hyperbolic conservation laws, arising in many important physical phenomena. For the two-dimensional compressible flows governed by the Euler equations, Fejer and Miles [16, 22, 23], see also [12, 35], proved that vortex sheets are unstable when \(M<\sqrt{2}\), while the vortex sheets in three-dimensional Euler flows are always violently unstable (the violent instability is the analogue of the Kelvin-Helmholtz instability for incompressible fluids).
In their pioneering works [13, 14] Coulombel and Secchi proved the nonlinear stability and existence of two-dimensional vortex sheets when the Mach number \(M>\sqrt{2}\). The linear and nonlinear stability of vortex sheets has also been established in [25, 26] for two-dimensional nonisentropic Euler flows, in [4] for two-dimensional relativistic fluids, in [41, 42] for three-dimensional steady Euler flows.
For the three-dimensional compressible flows, various stabilizing effects on vortex sheets have been considered. Taking into account the effect of magnetic fields, Chen–Wang [5, 6] and Trakhinin [38, 39] proved that large non-parallel magnetic fields stabilize the motion of three dimensional current-vortex sheets. Elasticity can also provide stabilization of vortex sheets: Chen–Hu–Wang [7, 8] and Chen–Hu–Wang–Wang–Yuan [9] successfully proved the linear stability and nonlinear stability, respectively, of two-dimensional compressible vortex sheets in elastodynamics by introducing the upper-triangularization method. More recently, Chen–Huang–Wang–Yuan [10] confirmed the stabilizing effect of elasticity also on three dimensional compressible vortex sheets. Another stabilizing effect on vortex sheets is provided by surface tension: for the three-dimensional compressible Euler flows, the local existence and structural stability were proved in Stevens [36].
The analysis of three-dimensional current-vortex sheets in [5, 6, 38, 39] does not cover the two dimensional case. In fact, such a case can be considered as the case when the third component of magnetic field \({\textbf{H}}=(H_1,H_2,H_3)\) is zero, i.e. \(H_3=0,\) and therefore the non-collinear stability conditions in [5, 38, 39] fail. As was shown in Trakhinin [38], the case when either tangential magnetic fields are collinear or one of them is zero corresponds to the transition to violent instability.
For the two-dimensional compressible flows, Wang and Yu [40] proved the linear stability of rectilinear current-vortex sheets under suitable stability conditions by the spectral analysis technique, through the computation of the roots of the Lopatinski determinant and construction of a Kreiss symmetrizer.
In the present paper we investigate the nonlinear stability and existence of two dimensional current-vortex sheets. From the mathematical point of view, this is a nonlinear hyperbolic free boundary problem. Since the Kreiss–Lopatinski condition does not hold uniformly, there is a loss of tangential derivatives in the estimates of the solution. The free boundary is characteristic, which yields a possible loss of regularity in the normal direction to the boundary, and the loss of control of the traces of the characteristic part of the solution.
Differently from [40], we consider the nonisentropic flows and for the analysis of linear stability, instead of spectral analysis, we use a direct energy estimate argument, adapting the dissipative symmetrizer technique introduced by Chen–Wang [5, 6] and Trakhinin [38, 39] for the three-dimensional problem. Moreover, in our linear stability result we study a general case of 2D current-vortex sheets, while in [40] both states of the background magnetic field are assumed to have the same strength, see the subsequent Remark 5.2.
First, we introduce a secondary symmetrization of the system of equations by multiplying by a suitable “secondary generalized Friedrichs symmetrizer” and impose the hyperbolicity of the new system of equations. Then, we identify a sufficient stability condition that makes the boundary conditions dissipative for the new symmetrized system. The new stability condition on the boundary takes the form
where \(c^{\pm }_A={\vert {\textbf{H}}^{\pm }\vert }/{\sqrt{\rho ^{\pm }}}\) stands for the Alfvén speed. This condition indicates that larger magnetic fields than the jump of tangential velocity play a stabilization effect; in some sense this corresponds to the “subsonic” bubble in linear stability result of [40], see Remark 5.2. Condition (1.11) is in agreement with the stability result found for the three-dimensional current-vortex sheets of [5, 38, 39] that only holds in the subsonic regime.
We observe that condition (1.11) has a strong similarity with the Syrovatskij stability condition [3, 21, 37] that is necessary and sufficient for the linear stability of the two-dimensional incompressible current-vortex sheets. For our problem we show that condition (1.11) is sufficient for the linear stability and optimal with respect to the specific dissipative symmetrizer technique that we use in our proof. On the other hand, it is likely that (1.11) is not necessary for the linear and nonlinear stability. Indeed, by taking the incompressible limit as \(c^\pm \rightarrow +\infty \) in (1.11), we formally get the inequality
where, because the incompressible flow has uniform density, \(\rho ^\pm \) have been replaced by a constant \(\bar{\rho }>0\). This inequality describes somehow the “half” of the whole 2D neutral stability domain from [21]. Moreover, in Wang-Yu [40] even a “supersonic” linear stability domain is found for the studied case of particular piece-wise constant background states; the same kind of “supersonic” region is therefore expected to appear for a general case of 2D current-vortex sheet; see again Remark 5.2.
Under condition (1.11) for the background state, we show that the linearized problem obeys an energy estimate in anisotropic weighted Sobolev spaces (see [11, 28, 30, 31]) with a loss of derivatives. The energy estimate for the linearized problem takes the form of a \({ tame}\) estimate, since it exhibits a fixed loss of derivatives from the basic state to the solutions. In order to compensate the loss of derivatives, for the proof of the existence of the solution to the nonlinear problem, we apply a modified Nash–Moser iteration scheme. For an introduction to the Nash–Moser technique, refer to [2, 33].
Compared to [5, 39] for the three-dimensional problem, our existence result shows a lower loss of regularity from the initial data to the solution. This is mainly due to the use of finer Moser-type and imbedding estimates in anisotropic Sobolev spaces.
The rest of the paper is organized as follows: In Section 2 we formulate the nonlinear problem for the current-vortex sheets in a fixed domain. In Section 3 we introduce the definition of anisotropic Sobolev spaces and then state our main Theorem 3.1. In Section 4 we linearize the nonlinear problem with respect to the basic state. Then, we introduce dissipative Friedrichs symmetrizer for two dimensional MHD equations. In Section 5 we study the well-posedness of the linearized problems (4.20), (4.31) and determine the stability condition. In Sects. 6 and 7 we prove the tame estimate in anisotropic Sobolev spaces for the linearized problems (4.31) and (4.20), respectively. In Section 8 we formulate the compatibility conditions for the initial data and construct the approximate solution. In Section 9 we introduce the Nash–Moser iteration scheme and in Section 10 we prove the existence of the solution to the nonlinear problem. In this section one important step is the new construction of the modified state, notably the modified magnetic field, and the delicate derivation of its estimates. In Appendix A1 we recall the trace theorem in anisotropic Sobolev space \(H^m_{*}\) and in Appendix A2 we give a detailed proof of the well-posedness of the homogeneous linearized problem (4.31) stated in Theorem 5.1.
2 Reformulate Current-Vortex Sheets Problem in a Fixed Domain
Let us reformulate the current-vortex sheets problem into an equivalent one posed in a fixed domain. Motivated by Métivier [20], we introduce the functions
where \(\chi \in C^{\infty }_0({{\mathbb {R}}}),\quad \chi \equiv 1 \text { on } [-1,1],\) and \(||\chi '||_{L^{\infty }({{\mathbb {R}}})}\le \frac{1}{2}\). Here, as in [20], we use the cut-off function \(\chi \) to avoid assumptions about compact support of the initial data in our subsequent nonlinear existence Theorem 3.1. The unknowns \({{\textbf{U}}}^{\pm }\) are smooth in \(\Omega ^{\pm }(t)\) and can be replaced by
after changing the variables, which are smooth in the fixed domain \(\Omega ={{\mathbb {R}}}^2_{+}=\{x_1>0, x_2\in {{\mathbb {R}}}\}\). Dropping \(\natural \) in \({{\textbf{U}}}^{\pm }_{\natural }\) for convenience, we reduce (1.1), (1.8) and (1.9) into the initial boundary value problem (IBVP)
where \(\Gamma :=\{x_1=0\}\times {{\mathbb {R}}},\) \({\mathbb {L}}({{\textbf{U}}}^\pm ,\Psi ^\pm )=L({{\textbf{U}}}^\pm ,\Psi ^\pm ){{\textbf{U}}}^\pm \),
with
where \(\partial _1\Phi ^{\pm }=\pm 1+\partial _1\Psi ^{\pm }.\) The boundary condition in (2.1) takes the form
where \(u^{\pm }_{N}=u^{\pm }_1-u^{\pm }_2\partial _2\varphi \).
The following Lemma 2.1 yields that the divergence constraints (1.2) and the boundary conditions \(H^{\pm }_N|_{x_1=0}=0\) on \(\Gamma \) (that is not included in (2.1)) can be regarded as the conditions on the initial data. The proof follows by similar calculations as to those in [39, Proposition 1].
Lemma 2.1
Let the initial data in (2.1) satisfy
and the boundary conditions
where
If the IBVP (2.1) admits a solution \(({{\textbf{U}}}^{\pm },\varphi ),\) then this solution satisfies (2.4) and (2.5) for all \(t\in [0,T].\)
3 Properties of Function Spaces and Main Theorem
In this section, we first introduce some notations, then anisotropic Sobolev spaces are defined. At the end, we are ready to state the main result of this paper.
3.1 Notations
Let us denote \(\Omega _T:=(-\infty ,T)\times \Omega \) and \(\Gamma _T:=(-\infty ,T)\times \Gamma \) for \(T>0.\) We write \(\partial _t=\frac{\partial }{\partial t}, \partial _i=\frac{\partial }{\partial x_i},i=1,2, \nabla _{t,{\textbf{x}}}=(\partial _t,\nabla ).\) \(D^{\alpha }_{*}:=\partial ^{\alpha _0}_t(\sigma \partial _1)^{\alpha _1}\partial ^{\alpha _2}_2\partial ^{\alpha _3}_1, \alpha :=(\alpha _0,\alpha _1,\alpha _2,\alpha _3),\quad |\alpha |=\alpha _0+\alpha _1+\alpha _2+\alpha _3.\) Here \(\sigma \) is an increasing smooth function, which satisfies \(\sigma (x_1)=x_1\) for \(0\le x_1\le \frac{1}{2}\) and \(\sigma (x_1)=1\) for \(x_1\ge 1.\) The symbol \(A\lesssim B\) represents that \(A\le CB\) holds uniformly for some universal positive constant C.
3.2 Anisotropic Sobolev spaces
For any integer \(m\in {\mathbb {N}}\) and the interval \(I\subseteq {{\mathbb {R}}},\) function spaces \(H^m_{*}(\Omega )\) and \(H^{m}_{*}(I\times \Omega )\) are defined by
and equipped with the norm \(||\cdot ||_{H^m_{*}(\Omega )}\) and \(||\cdot ||_{H^m_{*}(I\times \Omega )}\) respectively, where
Define the norm
We also write \(||\cdot ||_{m,*,t}:=||u||_{H^m_{*}(\Omega _t)}\) for convenience. Then, from (3.2), we have
3.3 Moser-type calculus inequalities
Now, we introduce two lemmata, which will be useful in the proof of tame estimates in \(H^m_{*}(\Omega _T)\) for the problem (4.20) when m is large enough. We first introduce the Moser-type calculus inequalities in \(H^m,\) see [2, Propositions 2.1.2 and 2.2].
Lemma 3.1
Let \(m\in {\mathbb {N}}_+.\) Let \({\mathcal {O}}\) be an open subset of \({{\mathbb {R}}}^n\) with Lipschitz boundary. Assume that \(F\in C^{\infty }\) in a neighbourhood of the origin with \(F(0)=0\) and that \(u,v\in H^m({\mathcal {O}})\cap L^\infty ({\mathcal {O}})\). Then,
for all \(\alpha ,\beta \in {\mathbb {N}}^n\) with \(|\alpha |+|\beta |\le m\) and where C depends only on F and \(\Vert u\Vert _{L^\infty }\).
Next, we introduce the Moser-type calculus inequalities for \(H^m_{*}\).
Let us define the space
equipped with the natural norm
where \(D^{\alpha }_{*}\) and \(\langle \alpha \rangle \) are defined in Section 3.1.
Lemma 3.2
([24, 39]) Let \(m\in {\mathbb {N}}_+.\) Assume that F is a \(C^{\infty }-\)function and \(u,v\in H^m_{*}(\Omega _T)\cap W^{1,\infty }(\Omega _T)\). Then, hold that
for any multi-index \(\alpha ,\beta \in {\mathbb {N}}^4\) with \(\langle \alpha \rangle +\langle \beta \rangle \le m.\) Let \(M_*\) be a positive constant such that
Moreover, if we assume that \(F(0)=0\), then holds that
For the proof of (3.6) and (3.7), one can check [24]. For (3.8) one can check [39].
3.4 Embedding and trace theorem
Now, we introduce the Sobolev embedding theorem for \(H^m_{*}(\Omega _T)\).
Lemma 3.3
[24] The following inequalities hold:
where \(||u||_{W^{1,\infty }_{*}(\Omega _T)}\) is defined by (3.5) and
Proof
Using [24, Theorem B.4], we obtain the first inequality in (3.9) in \(\Omega _T\subseteq {{\mathbb {R}}}^3.\) Then, the second one in (3.9) can be obtained by definition. Observing that
we can obtain the first inequality in (3.10) from the first inequality in (3.9). Similarly the second one in (3.10) can be obtained by definition. \(\square \)
For higher order energy estimate, we also need to use the following trace theorem by Ohno, Shizuta, Yanagisawa [27] for the anisotropic Sobolev spaces \(H^m_{*}\)(see also Appendix A1).
Lemma 3.4
[27] Let \(m\ge 1\) be an integer. Then, the following arguments hold:
(i) If \(u\in H^{m+1}_{*}(\Omega _T),\) then its trace \(u|_{x_1=0}\) belongs to \(H^m(\Gamma _T),\) and it satisfies
(ii) There exists a continuous lifting operator \({\mathcal {R}}_T:\)
such that \(({\mathcal {R}}_Tu)|_{x_1=0}=u \text { and } ||{\mathcal {R}}_Tu||_{m+1,*,T}\lesssim ||u||_{H^m({\Gamma _T})}.\)
3.5 Main theorem
Theorem 3.1
Let \(m\in {\mathbb {N}}\) and \(m\ge 15,\) and let \(\bar{{\textbf{U}}}^{\pm }\) be defined in (1.10). Suppose that the initial data in (2.1) satisfy
and also satisfy the hyperbolicity condition (1.6), the divergence-free constraint (2.4) for all \({\textbf{x}}\in {{\mathbb {R}}}^2_+.\) Let the initial data at \(x_1=0\) satisfy the stability condition (1.11). The hyperbolicity condition (1.6) and the stability condition (1.11) have to be satisfied uniformly in the sense of (4.2) and (4.4), for suitable \(k>0\). Assume that the initial data are compatible up to order m+10 in the sense of Definition 8.1 and satisfy the boundary constraints (2.5). Assume also that
Then, there exists a sufficiently short time \(T>0\) such that problem (2.1) has a unique solution on the time interval [0, T] satisfying
Remark 3.1
Since the initial data \(\textbf{U}_0^\pm \) have the form \(\textbf{U}_0^\pm =\overline{\textbf{U}}^\pm +\tilde{\textbf{U}}_0^\pm \), with \(\tilde{\textbf{U}}_0^\pm \in H^m({\mathbb {R}}^2_+)\) vanishing at infinity (as \(\vert \textbf{x}\vert \rightarrow +\infty \)), the hyperbolicity and stability conditions satisfied in the sense of (4.2), (4.4) (see Remark 4.1) yield that the same conditions hold for the constant states (1.10).
Remark 3.2
We note that Theorem 3.1 implies corresponding results for the original free boundary problem (1.1), (1.8) and (1.9), posed in the moving domain, because Lemma 2.1 and the relation \(\partial _1\Phi ^+\ge \frac{1}{2}\) and \(\partial _1\Phi ^-\le -\frac{1}{2}\) hold in \([0,T]\times {{\mathbb {R}}}^2_+\) for sufficiently small \(T>0.\)
Remark 3.3
Compared to [5, 39], in Theorem 3.1 there is less loss of regularity from the initial data to the solution. This is mainly due to the use of finer Moser-type and imbedding estimates in anisotropic Sobolev spaces.
Remark 3.4
The analysis in this paper could also be applied to prove the nonlinear stability and existence of two dimensional relativistic current-vortex sheets; see [4, 17].
4 Linearized Problem
4.1 The basic state
Let the basic state
be a given vector-valued and sufficiently smooth function, where \(\hat{{{\textbf{U}}}}^{\pm }=({\hat{p}}^{\pm },\hat{{\textbf{u}}}^{\pm }, \hat{{\textbf{H}}}^{\pm },{\hat{S}}^{\pm })^T\) are defined in \(\Omega _T.\) We assume that we shall linearize the problem (2.1) around the basic state (4.1), which satisfy the hyperbolicity condition (1.6) in \(\Omega _T\)
the Rankine–Hugoniot jump condition
where \({\hat{u}}^{\pm }_{N}={\hat{u}}^{\pm }_1-{\hat{u}}^{\pm }_2\partial _2{\hat{\varphi }}\), and the stability condition on the boundary
for a suitable constant k, where \({\hat{c}}^{\pm }_A=\frac{\vert \hat{{\textbf{H}}}^{\pm }\vert }{\sqrt{{\hat{\rho }}^{\pm }}}\) denotes the Alfvén speed and
Remark 4.1
The stability condition (1.11) can be written in uniform form as (4.4) by making use of (4.3) and the following boundary constraint in (4.10).
Remark 4.2
Let us observe that, differently from [39], in the Rankine–Hugoniot conditions we dot not require that the basic state satisfies \([{{\hat{q}}}]=0\). It seems that this condition could not be helpful to simplify the boundary quadratic form which appear from the application of the energy method to the linearized problem.
Remark 4.3
Estimate (4.4) implies in particular that at least one among \({{\hat{H}}}^+_2\) and \({{\hat{H}}}^-_2\) must be nonzero along the boundary.
Remark 4.4
The presence of the positive constant k in the hyperbolicity and stability assumptions (4.2), (4.4) is needed in order to ensure the boundedness of all coefficients, nonlinearly depending on the basic state \(\hat{{\textbf{U}}}^\pm \), \({{\hat{\varphi }}}\), appearing in the arguments of the energy method developed in the sequel.
Let us assume
where \(K>0\) is a constant. Moreover, without loss of generality, we assume
This implies
with
We also assume the following nonlinear constraints on the background states:
where
Then, we can obtain that the constraints (2.4) and (2.5), that is,
hold for all times \(t>0\) if they hold initially (see Appendix A in [39]), where \({\hat{H}}^{\pm }_N={\hat{H}}^{\pm }_1-{\hat{H}}^{\pm }_2\partial _2{\hat{\varphi }}.\)
4.2 The linearized equations
The linearized equations for (2.1) around the basic state (4.1) can be defined as
where \({{\textbf{U}}}^{\pm }_{\varepsilon }=\hat{{{\textbf{U}}}}^{\pm }+\varepsilon \delta {{\textbf{U}}}^{\pm },\quad \varphi _{\varepsilon }={\hat{\varphi }}+\varepsilon \delta \varphi \) and
In the following argument, we shall drop \(\delta \) for simplicity. The linearized operators have the following form:
where the operator \(L(\hat{{{\textbf{U}}}}^{\pm },{\hat{\Psi }}^{\pm })\) is defined in (2.2), \(q^{\pm }=p^{\pm }+\hat{{\textbf{H}}}^{\pm }\cdot {\textbf{H}}^{\pm },u^{\pm }_N=u^{\pm }_1-u^{\pm }_2\partial _2{\hat{\varphi }},\) and the matrix \(C(\hat{{{\textbf{U}}}}^{\pm },{\hat{\Psi }}^{\pm })\) is defined as follows:
We introduce the Alinhac’s good unknown [1]
In terms of (4.13), the linearized interior equations have the following form:
Since the zero order terms in \(\Psi ^{\pm }\) can be regarded as the error terms in the Nash–Moser iteration, we drop these terms and consider the effective linear operators
Concerning the boundary differential operator \({\mathbb {B}}'\), we rewrite (4.12) in terms of the Alinhac’s good unknowns (4.13) to get
where \({\dot{u}}^{\pm }_N={\dot{u}}^{\pm }_1-{\dot{u}}^{\pm }_2\partial _2{\hat{\varphi }}\) (recall also that \(\partial _1{{\hat{\Phi }}}^\pm \vert _{x_1=0}=\pm 1\)).
Remark 4.5
Notice that, due to the fact that we have transformed the domains \(\Omega ^\pm (t)\) into the same half-space \({\mathbb {R}}^2_+\), the jump on the boundary of a normal derivative of a function \(a=a(t,\textbf{x})\) is defined as follows:
This is why the jump of the total pressure q in the last row of (4.16) reduces under Alinhac’s change of unknowns to
In the following, according to (4.17), we will set
Denote the operator
Now, we are focusing on the following linear problem for \((\dot{{{\textbf{U}}}}^{\pm },\varphi ):\)
where \({\textbf{f}}=({\textbf{f}}^+,{\textbf{f}}^-)=(f^+_1,\cdots ,f^+_6,f^-_1,\cdots ,f^-_6),\) and \({\textbf{g}}=(g^+_1,g^-_1,g_2)\) vanish in the past. In order to prove the well-posedness of the linearized problem (4.20), we can state the following Lemma 4.1, that can be proven as in [39, Proposition 2].
Lemma 4.1
Let the basic state (4.1) satisfy the assumption (4.8) and (4.10). Then, the solutions of the problem (4.20) satisfy
Here
where \(r^{\pm }=r^{\pm }(t,{\textbf{x}}),\quad g^{\pm }_3=g^{\pm }_3(t,x_2),\) which vanish in the past, are determined by the source terms and the basic state as solutions to the linear equations
where \(R^{\pm }=\frac{r^{\pm }}{\partial _1{\hat{\Phi }}^{\pm }},\quad {\mathcal {F}}^{\pm }=\frac{\textrm{div} {\textbf{f}}^{\pm }_h}{\partial _1{\hat{\Phi }}^{\pm }}, \quad {\textbf{f}}^{\pm }_h=(f^{\pm }_n,f^{\pm }_5),\quad f^{\pm }_n=f^{\pm }_4-f^{\pm }_5\partial _2{\hat{\Psi }}^{\pm }\),
\({\mathcal {G}}^{\pm }=\{\partial _2({\hat{H}}^{\pm }_2g^{\pm }_1)-f^{\pm }_n\}|_{x_1=0}\), with \(\hat{{\textbf{w}}}^\pm \) and \(\hat{{\textbf{v}}}^\pm \) defined in (4.9).
4.3 Reduction to homogeneous boundary conditions
In this section, we reduce the inhomogeneous boundary condition in (4.20) to the homogeneous one. We follow the same ideas in Trakhinin [39], that for reader’s convenience, we recall here. Suppose there exists a solution \((\dot{{{\textbf{U}}}},\varphi )\in H^s_{*}(\Omega _T)\times H^s({\Gamma _T})\) to problem (4.20), with a given \(s\in {\mathbb {N}}.\) We define a vector-valued function
that vanishes in the past and such that it is a “suitable lifting" of the boundary data \(({{\textbf{g}}}, g^+_3, g^-_3)\in H^{s+1}(\Gamma _T)\). We choose \(\tilde{{{\textbf{U}}}}\) such that on the boundary \(\Gamma _T\), it satisfies the boundary conditions in (4.20) with \(\varphi =0\), i.e.
and both conditions (4.22) and (4.24) with \(\varphi =0\) (where \({{\tilde{q}}}\), \({{\tilde{u}}}^\pm _N\), \({{\tilde{H}}}_N^\pm \) are defined similarly to \(\dot{q}\), \(\dot{u}_N^\pm \) and \(\dot{H}_N^\pm \)). More explicitly we require
with \(g^\pm _3\) solution of (4.24). Then, we define \(\tilde{q}^\pm \), \({{\tilde{u}}}_n^\pm \) and \({{\tilde{H}}}_n^\pm \) in the interior domain \(\Omega _T\) by using the lifting operator (that exists thanks to the trace theorem in anisotropic Sobolev spaces \(H^s_*\), see [27] and Appendix A1)
which gives
Let also \({{\tilde{u}}}_1^\pm \) and \({{\tilde{H}}}^\pm _1\) be such that
where \({{\tilde{u}}}_2^\pm \) is arbitrary and can be taken for instance as zero, and where we can define \({{\tilde{H}}}^\pm _2\) in such a way that it satisfies equation (4.23) for \(R^\pm =\frac{\text {div} \tilde{{\textbf{h}}}^\pm }{\partial _1{{\hat{\Phi }}}^\pm }\), where \(\tilde{{\textbf{h}}}^\pm =({{\tilde{H}}}_n^\pm , \tilde{H}_2^\pm \partial _1{{\hat{\Phi }}}^\pm )\) (this is possible since we have a freedom in the choice of “characteristic unknown" \({{\tilde{H}}}^\pm _2\) ). The last components \({{\tilde{S}}}^\pm \) of \(\tilde{{\textbf{U}}}\) can again be taken as zero. To sum up, the vector \(\tilde{{\textbf{U}}}\) is defined as
where \({{\tilde{H}}}^\pm _2\) satisfies equation (4.23) for \(R^\pm =\frac{\text {div} \tilde{{\textbf{h}}}^\pm }{\partial _1{{\hat{\Phi }}}^\pm }\) and \(\tilde{{\textbf{h}}}^\pm =(\tilde{H}_n^\pm , {{\tilde{H}}}_2^\pm \partial _1{{\hat{\Phi }}}^\pm )\).
We define \(\dot{{{\textbf{U}}}}^{\natural }=\dot{{{\textbf{U}}}}-\tilde{{{\textbf{U}}}},\) then \(\dot{{{\textbf{U}}}}^{\natural }\) satisfies
Here \({\textbf{F}}=(F^+_1,\cdots ,F^+_6,F^-_1,\cdots ,F^-_6).\) Moreover, in view of equations (4.23) for \(R^{\pm }=\frac{\textrm{div}\tilde{{\textbf{h}}}^{\pm }}{\partial _1{\hat{\Phi }}^{\pm }},\) condition (4.22) for \(\tilde{{\textbf{U}}}\) with \(\varphi =0,\) and (4.24), we have, from (4.25), that (4.23) and (4.24) are satisfied for \(R^{\pm }=\frac{\textrm{div}\dot{{\textbf{h}}}^{\natural \pm }}{\partial _1{\hat{\Phi }}^{\pm }},\) \(g^{\pm }_3=({\hat{H}}^{\pm }_2\partial _2\varphi -{\dot{H}}^{\natural \pm }_N\mp \varphi \partial _1{\hat{H}}^{\pm }_N)|_{x_1=0}\) with right-hand sides \({\mathcal {F}}^{\pm }={\mathcal {G}}^{\pm }=0\). Here \(\dot{{\textbf{h}}}^{\natural \pm }\) and \({\dot{H}}^{\natural \pm }_N\) are defined similarly to \(\dot{{\textbf{h}}}^{\pm }\) and \({\dot{H}}^{\pm }_N.\) Notice that \(\dot{{{\textbf{U}}}}^{\natural }=0, \text { for } t<0.\) Hence, the conditions
hold for \(t<0\). Then, by standard method of characteristic curves, we get that equations (4.26) are satisfied for all \(t\in (-\infty ,T].\) Notice that from
we have that
By the definition of \({{\textbf{F}}}\), using (4.27) and the definition of \(\tilde{{\textbf{U}}}\) as a lifting of the boundary data \(({{\textbf{g}}},g_3^+, g_3^-)\), we obtain that
Using (4.24) and the trace Theorem in the anisotropic Sobolev spaces to estimate
we get
Then, from (4.28) and (4.29), we derive
We obtain that \(\dot{{{\textbf{U}}}}^{\natural }\) solves the problem
where the source term \({\textbf{F}}\) satisfies the estimate (4.30) and solutions of (4.31) satisfy the constraints
We have thus proved the following result:
Lemma 4.2
Let problem (4.31) be well-posed and its unique solution \((\dot{{{\textbf{U}}}^\natural },\varphi )\) belongs to \(H^s_{*}(\Omega _T)\times H^s({\Gamma _T})\) for \({\textbf{F}}\in H^s_{*}(\Omega _T),\) where \(s\in {\mathbb {N}}\) is a given number. Then problem (4.20) is well-posed, namely it admits a unique solution \((\dot{{\textbf{U}}},\varphi ) \in H^s_{*}(\Omega _T)\times H^s({\Gamma _T})\) for data \(({\textbf{f}},{\textbf{g}})\in H^{s+2}_{*}(\Omega _T)\times H^{s+2}(\Gamma _T).\)
Remark 4.6
Let us observe that loss of regularity from the data to the solution in the inhomogeneous problem (4.20) is due to the introduction of lifting function \(\tilde{{{\textbf{U}}}}\).
4.4 New Friedrichs Symmetrizer for 2D MHD equations
Motivated by the idea of Trakhinin [39], in the following we will make use of a new symmetric form of the MHD system. This symmetric form is the result of the application of a “secondary generalized Friedrichs symmetrizer” \({\mathbb {S}}=(S({{\textbf{U}}}), {\mathcal {T}}({{\textbf{U}}}))\) to system (1.4):
The Friedrichs symmetrizer can be written as (see [38])
where \(\lambda =\lambda ({\textbf{U}})\) is an arbitrary function.
In order to make system (4.34) symmetric hyperbolic, we need \(B_0>0,\) i.e.,
Condition (4.37) ensures the equivalence of system (1.4) and (4.34) on smooth solutions if \(\lambda ({{\textbf{U}}})\) is a smooth function of \({{\textbf{U}}}\) (see Trakhinin [38] and [39]).
Now let us apply the new symmetrization to the homogeneous linearized problem (4.31). From now on we drop the index \(\natural \) from the unknown \(\dot{{\textbf{U}}}^\natural \) of system (4.31).
Multiplying (4.31) on the left by \({\mathcal {S}}(\hat{{{\textbf{U}}}})\) and adding to the result the vector
we obtain
where \({\tilde{C}}(\hat{{{\textbf{U}}}},{\hat{\Psi }})={\mathcal {S}}(\hat{{{\textbf{U}}}})C(\hat{{{\textbf{U}}}},{\hat{\Psi }}),\quad \tilde{{\textbf{F}}}(\hat{{{\textbf{U}}}})={\mathcal {S}}(\hat{{{\textbf{U}}}}){{\textbf{F}}}\),
5 Stability condition and well-posedness of the linearized problem
In this section, let us introduce the new unknown \({\textbf{V}}=({\textbf{V}}^+,{\textbf{V}}^-),\) where
Rewriting system (4.31) in terms of \({\textbf{V}}\) shows in clear way that the boundary matrix of the resulting system has constant rank at the boundary (see (5.6)), i.e. the system is symmetric hyperbolic with characteristic boundary of constant multiplicity (in the sense of Rauch [29]). Indeed, we obtain that
where \(J=\textrm{diag}(J^+,J^-),\)
with \({\hat{H}}^{\pm }_{\tau }={\hat{H}}\cdot \tau ^{\pm },\quad \tau ^{\pm }=(\partial _2{\hat{\Psi }}^{\pm },1).\) In terms of \({\textbf{V}}\), systems (4.31) and (4.39) can be equivalently rewritten as
where \({\mathcal {A}}_{\alpha }=J^TA_{\alpha }J,\quad {\mathcal {B}}_{\alpha }=J^TB_{\alpha }J,\quad \alpha =0,2,\)
In view of constraints (4.3) and (4.10) on the basic state \(\hat{{\textbf{U}}}\), the boundary matrix in (5.3) has the following form:
Here, \({\mathcal {E}}_{ij}\) is a \(6\times 6\) symmetric matrix, in which (ij)th and (ji)th elements are 1 and the remaining elements are 0. The explicit form of \({\mathcal {A}}_{(0)}\) is of no interest and it is only important that the all non zero elements of \({\mathcal {A}}_{(0)}\) are multiplied either by the function \({\hat{u}}_n -\partial _t {\hat{\Psi }}\) or by the function \({\hat{H}}_n\). Therefore, the boundary matrix
This is a matrix of constant rank 4 and has two positive and two negative eigenvalues.
Concerning system (5.4), note that \({\mathcal {B}}_0>0\) because of the hyperbolicity condition (4.37) satisfied for the basic state, hence the symmetric system (5.4) is hyperbolic. Moreover, considering the boundary matrix \({\mathcal {B}}_1\) in (5.4), we will only need its explicit form on the boundary
which gives
with \({{\hat{\lambda }}}:= \lambda (\hat{{\textbf{U}}})\).
Using (4.31) and (4.33) (see also (4.16)) for \({\dot{u}}^{\pm }_{N}\) and \({\dot{H}}^{\pm }_N,\) (recall that we have dropped the index \(\natural \) from the unknown) and the boundary constraint \([{\dot{q}}]=-\varphi [\partial _{1}{\hat{q}}]\) (recall the definition of \([\partial _1{{\hat{q}}}]\) in (4.18)) we obtain that
with
We use “l.o.t." to mean boundary terms that can be manipulated in the energy estimate by passing to volume integral and using integration by parts, so that they do not give any trouble in the derivation of the energy estimate, see Appendix A2.
Let us now make a suitable choice of the function \({\hat{\lambda }}=\lambda (\hat{{\textbf{U}}})\). We first take \({\hat{\lambda }}\) as, (see [39])
with \(\eta (x_1)\) a smooth monotone decreasing function satisfying \(\eta (0)=1\) and \(\eta (x_1)=0,\) for \(x_1>\varepsilon \), with \(\varepsilon >0\) sufficiently small. The functions \(\lambda ^{\pm }\) will be chosen below.
Remark 5.1
The motivation of the definition of \({\hat{\lambda }}\) by using the cut-off function \(\eta =\eta (x_1)\) is that it guarantees that the hyperbolicity condition (4.37), that trivially holds for \({{\hat{\lambda }}}=0\) remains true for the basic state in a small neighborhood \(\{0<x_1<\varepsilon \}\) of the boundary, thanks to the continuity of the basic state. Hence, by definition of \(\eta \), the hyperbolicity condition still holds in the whole domain \(\Omega _T\); see [39] for more details.
The functions \(\lambda ^{\pm }(t,x_2)\) are chosen in this way: if the jump \([{\hat{u}}_2](t,x_2)=0,\) we define \(\lambda ^{\pm }(t,x_2)=0\); otherwise, if the jump \([{\hat{u}}_2](t,x_2)\ne 0,\) we choose \(\lambda ^{+}(t,x_2)\) and \(\lambda ^{-}(t,x_2)\) satisfying the following relation:
The following Lemma ensures the existence of such functions \(\lambda ^{+}(t,x_2)\), \(\lambda ^{-}(t,x_2)\) satisfying the above equation and the hyperbolicity assumption (4.37) written for the basic state, see (5.12):
Lemma 5.1
For all \((t,x_2)\in \Gamma _T\), there exist \(\lambda ^{\pm }(t,x_2)\) satisfying
and the hyperbolicity conditions
if and only if the basic states \(\hat{{\textbf{U}}}^\pm \) obey the stability estimate
where \({{\hat{a}}}^\pm \) are defined in (4.5). In particular, under (5.13) we can set
Proof
For shortness in the proof we drop the hat and the subscript 2 on the variables, moreover we do not write the considered variables are restricted along the boundary \(\{x_1=0\}\), that is, we write
Let us first note that equation (5.11) can be restated as
Let us consider the simple case \(H^+\ne 0\) and \(H^-=0\). Then, from equation (5.15) we immediately get
and plugging the above into the constraint in (5.12) for \(\lambda ^+\) gives
that is, (5.13). In this case \(\lambda ^-\) can be whatever function satisfying the corresponding constraint (5.12)
(for instance \(\lambda ^-\equiv 0\)); it does not yield any condition on the background state in addition to (5.16). Of course the symmetric case \(H^+=0\) and \(H^-\ne 0\) is treated similarly, by choosing
and making the condition
to be satisfied on the background state, which is again (5.13).
Let us consider now the case \(H^+\ne 0\) and \(H^-\ne 0\). From (5.15), we write \(\lambda ^+\) as a known function of \(\lambda ^-\) as
and plug the above into \(|\lambda ^+| < a^+\) to get, after simple manipulations,
We have that \(\lambda ^-\) must obey simultaneously the two constraints (5.19) and
Let assume now that \(\frac{H^-}{H^+}>0\). Then equation (5.19) becomes
where
A necessary condition for (5.20) and (5.21) to hold simultaneously is that
After some calculations, in view of the definition (5.22), the above becomes equivalent to
Assuming \(H^- <0\) (hence \(H^+<0\)) the above is equivalent to
which is the estimate (5.13). Similar calculation in the case \(H^- >0\) and \(H^+ >0\) still yield to (5.13).
To sum up if \(\frac{H^-}{H^+} >0\) we get that condition (5.13) is at least necessary in order to find \(\lambda ^-\) satisfying (5.20) and (5.21), that is,
If such \(\lambda ^-\) actually exists, then \(\lambda ^+\) will be defined by (5.18).
From (5.19), arguing in the same way as above when \(\frac{H^-}{H^+}<0\) we obtain once again that (5.13) is at least necessary for the existence of such a \(\lambda ^-\) satisfying both (5.19) and (5.20), that in this case are equivalent to
where \(b_1\) and \(b_2\) are defined in (5.22).
To complete the proof, it remains to show that condition (5.13) is also sufficient for the existence of functions \(\lambda ^\pm \) satisfying (5.11) and (5.12).
We already proved it in the simplest cases \(H^+\ne 0\) and \(H^-=0\) or viceversa. Now let us do the same in the case \(H^+\ne 0\) and \(H^-\ne 0\). Thus let us assume that the background state satisfies condition (5.13). If we assume for a while that \(\lambda ^\pm \) exist and satisfy (5.11) and (5.12), we derive that
that is
The last inequality (5.24) suggests to take \(\lambda ^\pm \) such that
Indeed from (5.24) it immediately follows that \(\lambda ^\pm \) as above satisfy the constraint (5.12). Formula (5.25) defines \(\lambda ^\pm \) up to the sign. One can directly check that taking
makes the equation (5.11) to be satisfied. The above definitions of \(\lambda ^\pm \) are just equal to (5.14). This ends the proof. \(\square \)
Remark 5.2
In order to make a comparison between our stability condition (5.13) and the subsonic part of the stability condition found in [40], let us consider the case of background piece-wise constant state
Then the right-hand side of estimate (5.13) can be restated in terms of sound speeds \({{\hat{c}}}^\pm \) and the Alfvén speeds \({{\hat{c}}}^\pm _A=\frac{\vert \hat{{\textbf{H}}}^\pm \vert }{\sqrt{\rho ^\pm }}=\frac{\vert {{\hat{H}}}^\pm _2\vert }{\sqrt{\rho ^\pm }}\) as
and (5.13) becomes
In their two dimensional linear stability analysis [40], Wang and Yu are able to perform a complete normal modes analysis of the linearized problem for an isentropic flow, when the planar piece-wise constant basic state (5.27) (without \({{\hat{S}}}^\pm \)) satisfies suitable technical restrictions. Precisely, the constant components of \(\hat{{{\textbf{U}}}}^\pm \) are required to satisfy, besides the Rankine–Hugoniot conditions
the additional assumptions
(here the notation of [40] is adapted to our current setting). Notice in particular that, since the flow is isentropic, the assumption \(|{{\hat{H}}}_{2}^+|=|{{\hat{H}}}_{2}^-|\) and the last Rankine–Hugoniot condition in (5.29) imply \({{\hat{\rho }}}^-={{\hat{\rho }}}^+=:{{\hat{\rho }}}\) so that the sound speed and the Alfvén speed take the same value \({{\hat{c}}}=c({{\hat{\rho }}}):=\sqrt{p^\prime ({{\hat{\rho }}})}\) and \({{\hat{c}}}_A:=\sqrt{\frac{\vert {{\hat{H}}}_2\vert ^2}{{{\hat{\rho }}}}}\) on both ±-states of the flow.
The linear stability conditions by Wang-Yu [40] read as follows:
The left inequality in (5.31) identifies a “subsonic” weak stability region, becoming empty in the absence of a magnetic field (namely for compressible Euler equations), whereas the right inequality corresponds to the “supersonic” weak stability region of 2D compressible vortex sheets (to which it reduces, when formally setting \({{\hat{c}}}_A=0\)). With respect to (5.31), our stability condition in (5.28) provides only a subsonic stability domain. For a planar isentropic background state obeying (5.30), condition (5.28) reduces to
To compare the left inequality in (5.31) and (5.32), one can easily check that
so that our subsonic condition (5.32) is more restrictive than the one in [40].
Let us also note that we are not able, by our approach, to obtain a counterpart of the supersonic condition in [40] for isentropic flows in the constant coefficients case (that is the right inequality in (5.31)). On the other hand, our stability condition applies also to nonisentropic flows and to general (non piece-wise constant) background states.
We are now in the position to state the well-posedness of the “homogeneous” linearized problem (4.31).
Theorem 5.1
Let all assumptions (4.2)–(4.10) be satisfied for the basic state (4.1) (note that (4.4) implies the stability condition (5.13)). Then, for all \({\textbf{F}}\in H^1_{*}(\Omega _T)\) that vanish in the past, problem (4.31) has a unique solution \((\dot{{{\textbf{U}}}}^\natural ,\varphi )\in H^{1}_{*}(\Omega _T)\times H^1(\Gamma _T).\) The solution satisfies the a priori estimate
where \(C=C(K,T)>0\) is a constant independent of the data \({\textbf{F}}\).
The proof of Theorem 5.1 is given in Appendix A2.
As a consequence of Lemma 4.2 we have the following well-posedness result for the nonhomogeneous problem (4.20):
Theorem 5.2
Let all assumptions of Theorem 5.1 be satisfied for the basic state (4.1). Then, for all \(({\textbf{f}},{\textbf{g}})\in H^3_{*}(\Omega _T)\times H^{3}(\Gamma _T)\) that vanish in the past, problem (4.20) has a unique solution \((\dot{{{\textbf{U}}}},\varphi )\in H^{1}_{*}(\Omega _T)\times H^1(\Gamma _T)\). The solution satisfies the a priori estimate
where \(C=C(K,T)>0\) is a constant independent of the data \({\textbf{f}},{\textbf{g}}.\)
6 Higher-order energy estimates for the homogeneous problem (4.31)
In order to get an a priori tame estimate in \(H^s_{*}\) for solution of problem (4.20) with s sufficiently large, as a preliminary step we derive a tame estimate for the homogenous problem (4.31), that we state in the that theorem.
For shortness, in all this section we write \(\dot{{{\textbf{U}}}}^\natural =\dot{{{\textbf{U}}}}\).
Theorem 6.1
Let \(T>0\) and s be positive integer, \(s\ge 6.\) Assume that the basic state \((\breve{{\textbf{U}}}^{\pm },{\hat{\varphi }})\in H^{s+4}_{*}(\Omega _T)\times H^{s+5}(\Gamma _T),\)
Assume that \({\textbf{F}}\in H^s_{*}(\Omega _T)\) vanishes in the past. Then, there exists a positive constant \(K_0,\) that does not depend on s and T, and there exists a constant \(C(K_0)>0\) such that if \({\hat{K}}\le K_0,\) then there exists a unique solution \((\dot{{{\textbf{U}}}},\varphi )\in H^s_{*}(\Omega _T)\times H^s(\Gamma _T)\) to homogeneous problem (4.31) satisfying the estimate
for T small enough, where \({\hat{W}}=(\breve{{\textbf{U}}},\nabla _{t,\textbf{x}}{\hat{\Psi }}).\)
To prove the above theorem we need to obtain several higher-order energy estimates.
6.1 Estimate of the normal derivative of the “non-characteristic” unknown
In this section we will prove the estimate of the normal derivative of the “non-characteristic” unknown
Let s be positive integer, we need to estimate \(\partial _1{{\textbf{V}}}_n\) in \(H^{s-1}_{*},\) obtained from (5.3) and the divergence constraint (4.32) as follows:
Here \({\mathcal {K}}_{i}\in {{\mathbb {R}}}\) is the \(i-\)th scalar component of the vector
where \(\tilde{{\mathcal {A}}}=\textrm{diag}\Big ((\partial _1{\hat{\Phi }}^+){\mathcal {E}}_{12},(\partial _1{\hat{\Phi }}^-){\mathcal {E}}_{12}\Big ),\) \(\partial _1{\hat{\Phi }}^{\pm }=\pm 1+\partial _1{\hat{\Psi }}^{\pm },\) \({\mathcal {F}}=J^T{\textbf{F}}.\)
Now, we are ready to prove the following Lemma, which is needed in the proof of weighted normal derivatives and non-weighted tangential derivatives; see Sections 6.2 and 6.4.
Lemma 6.1
The estimate
with
holds for problem (4.31) for all \(t\le T.\)
Proof
Using Moser-type calculus inequalities (3.7) and (3.8), we can estimate the right-hand side of (6.4) as
For \(j=0,2,\)
where C(K) stands for positive constants that depends on K and we used that \(\tilde{{\mathcal {A}}}J^T\), \(\tilde{{\mathcal {A}}}{\mathcal {A}}_j\) for \(j=0,2\) and \(\tilde{{\mathcal {A}}}{\mathcal {A}}_3\) are all nonlinear smooth functions of the basic state \({\hat{W}}\).
Now, we estimate the last term in (6.4), where for simplicity we denote \({\mathcal {A}}=\tilde{{\mathcal {A}}}{\mathcal {A}}_{(0)}\). We get
where we used that \({\mathcal {A}}\vert _{x_1=0}=0\), thus the \(L^\infty -\)norm of \({\mathcal {A}}/\sigma \) can be estimated by the \(L^\infty \)-norms of \({\mathcal {A}}\) and \(\partial _1{\mathcal {A}}\), see [24, Lemma B.9], [32].
For the rest of the term in (6.3), using (3.7) and (3.8), we obtain that
The second term in (6.3) can be controlled similarly. Summarizing all the estimates (6.7)–(6.11) for the terms in (6.3) and (6.4), Lemma 6.1 is concluded. \(\square \)
We also need the following estimate, still for \(\partial _1{{\textbf{V}}}_n\), which is also essential in the proof of non-weighted tangential derivatives, see (6.47) in Section 6.4:
Lemma 6.2
The estimate
holds for problem (4.31) for all \(t\le T\), where s is a positive integer and \({\mathcal {M}}(t)\) is defined in (6.6).
Proof
Denote the differential operator \(D^{\alpha }_{*}=\partial ^{\alpha _0}_t(\sigma \partial _1)^{\alpha _1}\partial ^{\alpha _2}_2\partial ^{\alpha _3}_1\), \(\langle \alpha \rangle :=|\alpha |+\alpha _3.\) We estimate the right-hand side of (6.4). Using the elementary estimate
we get
The second term of (6.4) can be controlled as follows:
where \(D_*\) denotes any tangential derivative in t or \(\textbf{x}\) of order one, and \(D^{\alpha -1}_*\) denotes the derivative of order \(\langle \alpha \rangle -1\) obtained “subtracting" \(D_*\) from \(D_{*}^\alpha \).
We estimate separately each \(\Sigma ^\prime _i\), \(i=1,2,3\) as follows:
Adding the above inequalities, we get
Similarly, the third term can be estimated by
Using Moser-type calculus inequalities (3.7) and (3.8), we can estimate
Now, we estimate the last term \(\tilde{{\mathcal {A}}}{\mathcal {A}}_{(0)}\partial _1{{\textbf{V}}}\) as
where
and where we exploit again the vanishing of \(\tilde{{\mathcal {A}}}{\mathcal {A}}_{(0)}\) and \(D_*(\tilde{{\mathcal {A}}}{\mathcal {A}}_{(0)})\) along the boundary \(\{x_1=0\}\) in the estimates of \(\Sigma _1\) and \(\Sigma _2\), see [24, Lemma B.9], [32].
Adding the estimates of \(\Sigma _i\), \(i=1,2,3\) above, we get
For the rest of the term in (6.3), using (3.7) and (3.8), we obtain that
The second term in (6.3) can be controlled similarly. Summarizing from (6.14)–(6.19), we conclude that (6.12) holds. \(\square \)
The following lemma gives the estimate of the normal derivative of the entropy, which is treated differently from the other components of the vector \({{\textbf{V}}}\):
Lemma 6.3
The estimate
holds for problem (4.31) for all \(t\le T\), where s is a positive integer and \({\mathcal {M}}(t)\) is defined in (6.6).
Proof
The linearized equation for the entropy \( S^\pm \) is an evolution-like equation because the coefficient of the normal derivative of the entropy vanishes on the boundary; this yields that no boundary conditions are needed to be coupled to the equation in order to derive an a priori energy estimate. Thus, to estimate \( S^\pm \), we just handle the equation of \( S^\pm \) alone by the standard energy method tools. The details of the proof are similar to those of the following Lemma 6.4. \(\square \)
Now, we derive weighted derivative estimates.
6.2 Estimate of weighted derivatives
Since the differential operators \((\sigma \partial _1)^{\alpha _1}\) and \(\sigma ^{\alpha _1}\partial ^{\alpha _1}_1\) are equivalent, see [28], in the following we discuss the term \(D^{\alpha }_{*}{{\textbf{V}}}\), with \(\alpha _1>0\) and \(\langle \alpha \rangle =|\alpha |+\alpha _3\le s\), in its equivalent form \(\sigma ^{\alpha _1}D^{\alpha ^\prime }_{t,x}\partial ^{\alpha _3}_1{\textbf{V}}\), where \(D^{\alpha ^\prime }_{t,x}:=\partial ^{\alpha _0}_t\partial ^{\alpha _1}_{1}\partial ^{\alpha _2}_{2}\) (\(\alpha ^\prime =(\alpha _0,\alpha _1,\alpha _2)\)).
Lemma 6.4
The following estimate holds for (4.31) for all \(t\le T:\)
there s is a positive integer and \({\mathcal {M}}(t)\) is defined in (6.6).
Proof
It is obvious that when \(\alpha _1>0,\) \(D^{\alpha }_{*}{{\textbf{V}}}|_{x_1=0}=0.\) Note that
for some nonnegative integer m. Applying \(D^{\alpha }_{*}\) to (5.3) and using the standard energy method, we obtain that
where
(the brackets \([\cdot ,\cdot ]\) here denotes the commutator between the operators). Notice that \({\mathcal {A}}_0\) is positive definite, then
where \(c_0\) depends on the number k in (4.2) and (4.4). Hence, we obtain that
Now, we estimate \(||{\mathcal {R}}||^2_{L^2(\Omega _t)}\) in (6.22). Recall that \({\mathcal {R}}=D^{\alpha }_{*}{\mathcal {F}}+{\mathcal {R}}_0+{\mathcal {R}}_1.\) Using Moser-type calculus inequalities (3.7) and (3.8), we can prove that
Using the decomposition of boundary matrix \({\mathcal {A}}_1\) in (5.5), \({\mathcal {A}}_1={\mathcal {A}}+{\mathcal {A}}_{(0)}\), following arguments similar to those used in Lemma 6.1, we obtain that
recall here above that the matrix \({\mathcal {A}}\) acts only on the noncharacteristic part \({{\textbf{V}}}_n\) of the unknown \({\textbf{V}}\).
Now, we estimate the commutators in \({\mathcal {R}}_1:\) For \(j=0,2,\) we obtain that
For \(\langle \beta \rangle =1\), we get
For \(\langle \beta \rangle \ge 2,\) we obtain that
For \(j=1,\) we need to be very careful. We have
For \(\langle \beta \rangle =1\) we get \(\beta _3=0.\) Therefore, from (5.5) it follows that \(D^{\beta }_{*}{\mathcal {A}}_1|_{x_1=0}=0\) and we use Moser-type calculus inequalities (3.7), (3.8) to obtain
For \(\langle \beta \rangle \ge 2\), we have
Using Moser-type calculus inequalities (3.7), (3.8), we can prove that
Notice that summing up (6.25)–(6.31) gives
Hence, using (6.23), (6.24) and (6.32), we obtain (6.21). Lemma 6.4 is concluded. \(\square \)
Now, we are going to estimate the non-weighted normal derivatives.
6.3 Estimate of non-weighted normal derivatives
Now we perform the differential operator \(D^{\alpha }_{*}\), in the case \(\alpha _1=0, \alpha _3\ge 1\), that is \(D^\alpha _*=\partial ^{\alpha _0}_t\partial ^{\alpha _2}_2\partial ^{\alpha _3}_1\) with \(\langle \alpha \rangle \le s\). Now, we are ready to prove the following:
Lemma 6.5
The estimate
holds for problem (4.31) for all \(t\le T,\) where s is a positive integer, \({\mathcal {M}}(t)\) is given in (6.6).
Proof
Similar as in Lemma 6.4, applying the operator \(D^{\alpha }_{*}\) on (5.3) and using the standard energy method, we obtain that
where \({\mathcal {R}}\) is defined as in the proof of Lemma 6.4. Thus
where
When \(\alpha _1=0,\) by definition, \({\mathcal {R}}_0=0.\) Hence, we obtain the estimate
This yields that
Using (6.3) and (6.4), we obtain that
where \({\mathcal {K}}\) is defined in (6.4). Moreover, recalling that \(\tilde{{\mathcal {A}}}|_{x_1=0}=\textrm{diag}\Big ({\mathcal {E}}_{12},-{\mathcal {E}}_{12}\Big )\) because \(\partial _1{\hat{\Phi }}^{\pm }|_{x_1=0}=\pm 1,\) we notice that \(||\tilde{{\mathcal {A}}}|_{x_1=0}||_{L^{\infty }(\Gamma _t)}=1.\) Using \({\mathcal {A}}_{(0)}|_{x_1=0}=0\) we obtain that
where
notice that in spite of the notation here \(D^{\beta '}_*\) and \(D^{\beta ''}_*\) dot not involve any weighted derivative \(\sigma \partial _1\) (see the beginning of this section); notice also that \(\beta '+\beta ''=(\alpha _0,\alpha _2,\alpha _3-1)\) implies that \(\langle \beta '\rangle +\langle \beta ''\rangle \le s-2\);
Now, we estimate \(\Sigma _2(t)\) and \(\Sigma _3(t)\), which can be controlled by using Lemma 3.4 (i) and Moser-type calculus inequalities (3.7) and (3.8) as follows:
In the above estimate it is noted that \(\langle \beta ''\rangle \le s-3\).Then
For the term \(\Sigma _1(t),\) passing to the volume integral then using Leibniz’s rule, we get (for shortness, in the sequel we denote \(D^\alpha :=\partial ^{\alpha _0}_t\partial ^{\alpha _2}_2\) whereas \(D^\alpha _*:=\partial ^{\alpha _0}_t\partial ^{\alpha _2}_2\partial ^{\alpha _3}_1\))
Then integration by parts with respect to \(\partial _j\) (for \(j=0,2)\) gives
where
Since \(|\alpha |+2+2(\alpha _3-1)\le s\) we obtain that
Using Young’s inequality, we obtain that
for small \(\varepsilon .\) Therefore, we conclude from (6.38), (6.39) and elementary inequalities (6.13) that
The last two terms in (6.35) can be estimated by using Lemma 3.4 (i), Moser-type calculus inequalities (3.7) and (3.8) as
Summarizing (6.34)–(6.37) and using (6.40) and (6.41), taking \(\varepsilon \) sufficiently small, we get the estimate (6.33). Therefore, Lemma 6.5 is proven. \(\square \)
6.4 Estimate of non-weighted tangential derivatives
Now, we are going to obtain estimates of non-weighted tangential derivatives, i.e. \(\alpha _1=\alpha _3=0\), that is \(D^\alpha _*=\partial ^{\alpha _0}_t\partial ^{\alpha _2}_2\) with \(|\alpha |\le s\). This is the most important case because we shall use the boundary conditions. This gives the loss of two additional derivatives that imply that in final tame estimate we will have the “\(s+4, *, t\)" loss of derivatives from the coefficients, see Theorem 6.1. This loss is caused by the presence of zero order terms in \(\varphi \) (see (4.16)).
Lemma 6.6
The following estimate holds for (4.31) for all \(t\le T:\)
where s is positive integer, \(\varepsilon \) is a positive constant and \({\mathcal {M}}(t)\) is defined in (6.6).
Proof
We only need to estimate the highest-order tangential derivatives with \(|\alpha |=s, \) since the lower order terms can be controlled by definition of the anisotropic Sobolev norm, through the following estimate:
Therefore, applying same argument as in Lemmata 6.4 and 6.5, we obtain that
for \(\alpha =(\alpha _0,\alpha _2),\) with \(|\alpha |=s,\) where
Taking into account the boundary conditions (4.31) and (4.33), and also the important dissipative structure (5.8), the explicit quadratic boundary term in the integral can be rewritten in a suitable form: let us denote
where
and \({{\hat{\lambda }}}^\pm \) were defined in (5.10); see also Lemma 5.1.
The boundary quadratic form becomes
where lower order term l.o.t can be expressed by
Since the boundary conditions are dissipative, it is noted that first term on the right-hand side of (6.45) vanish by Lemma 5.1. The boundary terms can be estimated separately,as
where
Recall that \(|\alpha |=s\ge 2.\) We denote \(D^{\alpha }_{*}=\partial _lD^{\gamma }\), \(D^\gamma :=\partial ^{\gamma _0}_t\partial ^{\gamma _2}_2\) for \(\gamma =(\gamma _0,\gamma _2),|\gamma |=s-1\ge 1\), where
In the ensuring estimate of \({\mathcal {J}}^{+}_1(t)\), we separate the analysis into two cases.
Case A: When \(\alpha _0=s\), then \(l=0, D^{\alpha }_{*}=\partial _tD^{\gamma }.\) Using the normal derivative estimates (6.5), (6.12) for non-characteristic variables, the elementary inequality (6.13) and integration by parts, we obtain that
Here, \(\varepsilon \) is an arbitrary fixed constant. Similar argument also holds for \({\mathcal {J}}^-_1(t).\) Therefore, we obtain that
Case B: When \(\alpha _0\ne s\), then \(l=2, D^{\alpha }_{*}=\partial _2D^{\gamma }.\) Using integration by parts, we could deduce that
Next, we estimate \({\mathcal {J}}^+_3\) and separate this term into two parts,
where
For the term \({\mathcal {J}}_0(t),\) after integrating by parts, we obtain that
We note that to estimate \(\partial ^2_1D^{\alpha }_{*}{\hat{u}}^+_n\), we need \({\hat{W}}\) with regularity \(s+4.\) For the term \({\mathcal {J}}_0(t),\) using Moser-type calculus inequalities (3.7), (3.8), (6.5) and (6.12) we get
Now, we start to estimate \(\Sigma _4.\) It is noted that for \(|\alpha '|\ge 1,\) we can isolate one tangential derivative in the differential operator
Using (A.54) and (A.42) we obtain that
Here \({\textbf{H}}(\hat{{{\textbf{U}}}},{\hat{\varphi }}),{\textbf{G}}(\hat{{{\textbf{U}}}},{\hat{\varphi }})\) depend on \(\hat{{{\textbf{U}}}}|_{x_1=0},\partial _1\hat{{{\textbf{U}}}}|_{x_1=0}\) and second order derivatives of \({\hat{\varphi }}.\)
Using (6.49), we can write the derivatives of \(\varphi \) by using the non-characteristic unknown \({{\textbf{V}}}_n\). We insert these derivatives \(D^{\alpha '}_{*}\varphi =D^{\gamma '}(\cdots )\), with \(|\gamma '|\le s-1\), into \(\Sigma _4\) to obtain
which can be controlled by the right-hand side of (6.42). Indeed, by passing to the volume integral on \(\Omega _t\), we note that the highest order of regularity for \(D^{\alpha ''}_{*}\partial _1^2{\hat{u}}^+_n\) is \(s+3\) because \(|\gamma '|+|\alpha ''|=s-1\) (since \(|\alpha '|= |\gamma '|+1\) and \(|\alpha '|+|\alpha ''|=s\)). Similar estimates also hold for \({\mathcal {J}}^-_3,{\mathcal {J}}^{\pm }_2,{\mathcal {J}}^{\pm }_4.\) Using (6.43), (6.44), (6.46), (6.47), (6.48), we obtain the estimate (6.42). Therefore, Lemma 6.6 is concluded. \(\square \)
6.5 Estimate of front
Now, we are going to estimate the front \(\varphi (t)\) in \(H^{s-1}({{\mathbb {R}}})\) and its tangential derivatives \(\nabla _{t,x_2}\varphi \) in \(H^{s-1}(\Gamma _t).\)
Lemma 6.7
Given the solution \(\varphi \) of (4.31), for all \(t\le T\) and positive integer s, the following estimate holds:
Proof
Applying tangential derivatives on the first boundary conditions in (4.31), we obtain that
where
For the first term on the right-hand side of (6.51), using trace Theorem in Lemma 3.4, we obtain that
For the third term on the right-hand side of (6.51), when \(|\alpha |\le s-1,\) we obtain that
Hence, we obtain the estimate of the first term in the left-hand side of (6.50).
For the estimate of the second term in the left-hand side of (6.50), we use the relation (6.49), \(||{\hat{\varphi }}||_{H^s(\Gamma _t)}\lesssim ||{\hat{\Psi }}||_{s,*,t}\le ||{\hat{\varphi }}||_{H^s(\Gamma _t)},\) and Moser-type calculus inequalities (3.7) and (3.8) to obtain that
Therefore, Lemma 6.7 is concluded. \(\square \)
Collecting all the previously established higher order estimates, we can prove the following lemma:
Lemma 6.8
The solution of the homogeneous problem (4.31) satisfies the following a priori estimate
for positive integer s, where
Proof
Combining the estimates (6.21), (6.33), (6.42) choosing \(\varepsilon \) small enough and (6.50), we obtain that
where
Notice that
Then, using Grönwall’s lemma to (6.55), we obtain
Integrating (6.55) with respect to \(t\in (-\infty ,T],\) we get
Notice that \(\dot{{{\textbf{U}}}}=J{{\textbf{V}}}.\) Then, using the decomposition \(J=J({\hat{W}})=I+J_0({\hat{W}}),\) where \(J_0\) satisfies \(J_0(0)=0,\) we apply the Moser-type calculus inequalities (3.7) and (3.8) and derive
and, using (6.50) with \(t=T\),
In the proof of last inequalities in (6.57), (6.58), we have used the following relation by applying Sobolev imbedding:
Using (6.56) and (6.57), we obtain
Similar to (6.57), we can get
Adding (6.58) and (6.59), and using (6.60), we conclude Lemma 6.8. \(\square \)
Using (6.54), we are ready to prove the tame estimate for the homogeneous problem (4.31).
Proof of Theorem 6.1
Using Lemma 6.8, the Sobolev inequalities (3.9), (3.10) for \(s\ge 6,\) we obtain
Taking T sufficiently small and \(s=6,\) using (6.1), we obtain that
Hence, (6.61) and (6.62) implies (6.2). The existence and uniqueness of the solution comes from Theorem 5.1. The proof of Theorem 6.1 is complete.
7 Higher order energy estimate for problem (4.20)
Now, we are ready to obtain an a priori tame estimate in \(H^s_{*}\) for the nonhomogeneous problem (4.20).
Theorem 7.1
Let \(T>0\) and s be an integer, \(s\ge 6.\) Assume that the basic state \((\hat{{{\textbf{U}}}},{\hat{\varphi }})\) satisfies (4.2)–(4.10), and \((\breve{{\textbf{U}}}^{\pm },{\hat{\varphi }})\in H^{s+4}_{*}(\Omega _T)\times H^{s+5}(\Gamma _T)\) satisfies (6.1). Assume that \({\textbf{f}}\in H^{s+2}_{*}(\Omega _T)\), \({\textbf{g}}\in H^{s+2}(\Gamma _T)\) vanish in the past. Then, there exists a positive constant \(K_0,\) that does not depend on s and T, and there exists a constant \(C(K_0)>0\) such that if \({\hat{K}}\le K_0\), then there exists a unique solution \((\dot{{{\textbf{U}}}},\varphi )\in H^{s}_{*}(\Omega _T)\times H^s({\Gamma _T})\) to the problem (4.20) that allows the tame estimate
for T small enough, where \({\hat{W}}=(\breve{{\textbf{U}}},\nabla _{t, \textbf{x}}{\hat{\Psi }}).\)
Remark 7.1
The lower regularity in (6.1) and low norms in (6.2) and (7.1), for both the even and odd case, differ from Trakhinin [39], see Theorem 3 and Theorem 4, due to finer Sobolev imbeddings (3.9), (3.10).
Proof
Using the Moser-type calculus inequalities (3.7) and (3.8), we obtain a refined version of estimate (4.27) in tame form
Then, using Sobolev embedding inequalities (3.10), we get
Using the above estimate, (4.30) and recalling the definition of \(\tilde{{\textbf{U}}}\), see Section 4.3, it holds that
Using the assumption (6.1) and (7.2) with \(s=6\), we get
Combining the estimates (6.61), (7.2) and (7.3), we obtain the tame estimate (7.1). \(\square \)
8 Construction of Approximate Solutions
Suppose the initial data
satisfy the stability condition (4.4) and restriction (2.5) at \(x_1=0\) for \(x_2\in {{\mathbb {R}}}\). Since \({H}^+_{2,0}\ne 0\) or \({H}^-_{2,0}\ne 0\) at \({x_1=0}\), see also Remark 4.3, from (2.5) we can solve \(\partial _2\varphi \) as follows (we drop the sub-index 0 for simplicity):
where \({{\textbf{U}}}:=({{\textbf{U}}}^+,{{\textbf{U}}}^-).\) Then, using the boundary condition (4.3), we have
with
By using the hyperbolicity condition (1.6), we can write the system in (2.1) as
where \(\Psi :=(\Psi ^+,\Psi ^-)\), and the matrices \(A_0,A_2,{\tilde{A}}_1\) are defined by (1.5) and (2.3). The traces
and
can be defined step by step by applying operator \(\partial ^{j-1}_t\) to (8.2) and (8.3), for \(j\ge 1\) and evaluating \(\partial ^j_t{{\textbf{U}}}\) and \(\partial ^j_t\varphi \) at \(t=0\) in terms of the initial data. Notice that
Define the zero-th order compatibility condition as
Taking (8.1), (8.2) evaluated at \(t=0,\) and using (8.4), we obtain that
Denote \((H^{\pm }_N)_j=\partial ^j_tH^{\pm }_N\Big |_{t=0}.\) Using (8.3) and (8.5), taking \(t=0,\) we obtain that
Therefore, \((H^{\pm }_N)_0|_{x_1=0}=0\) implies \((H^{\pm }_N)_1|_{x_1=0}=0.\) Once we have defined \({{\textbf{U}}}_1,\varphi _1,\) we can deduce \({{\textbf{U}}}_2,\varphi _2\) and so on. Moreover, at each step, we can prove that
provided that \({{\textbf{U}}}_j\), \(\varphi _j\) satisfy the compatibility condition (see Definition 8.1).
The following Lemma 8.1 is necessary for the approximate solutions; we refer to [14] and [20, Lemma 4.2.1]. Differently from [39], we take the initial data in the standard Sobolev spaces.
Lemma 8.1
Let \(\mu \in {\mathbb {N}},\mu \ge 3,\) \(\tilde{{{\textbf{U}}}}_0:= {\textbf{U}}_0-\bar{{\textbf{U}}}\in H^{\mu +1.5}({\mathbb {R}}^2_+)\) and \(\varphi _0\in H^{\mu +1.5}({{\mathbb {R}}})\). Then, we can determine \(\tilde{{{\textbf{U}}}}_j\in H^{\mu +1.5-j}({\mathbb {R}}^2_+)\) and \(\varphi _j\in H^{\mu +1.5-j}({{\mathbb {R}}})\) by induction and set \({\textbf{U}}_j=\tilde{{\textbf{U}}}_j +\bar{{\textbf{U}}},\) for \(j=1,\cdots ,\mu \). In addition, we prove
where \(C>0\) depends only on \(\mu \), \(||\tilde{{{\textbf{U}}}}_0||_{W^{1,\infty }({\mathbb {R}}^2_+)}\) and \(||\varphi _0||_{W^{1,\infty }({{\mathbb {R}}})}\), and
Definition 8.1
Let \(\mu \in {\mathbb {N}},\mu \ge 3\). The initial data \((\tilde{{{\textbf{U}}}}_0,\varphi _0)\in H^{\mu +1.5}({\mathbb {R}}^2_+)\times H^{\mu +1.5}({{\mathbb {R}}})\) are defined to be compatible up to order \(\mu \) if \((\tilde{{{\textbf{U}}}}_j,\varphi _j)\) satisfy (8.4) for \(j=0\) and
for \(j=1,\cdots ,\mu \), where \(C_{l,j-1}\) are suitable constants.
To use the tame estimate for the proof of convergence of the Nash–Moser iteration, we should reduce our nonlinear problem to that whose solution vanishes in the past. This is achieved by the construction of the so-called “approximate solution" that allows to “absorb" the initial data into the interior equation. The “approximate solution" is in the sense of Taylor’s series at \(t=0\).
Below, we will use the notation
Lemma 8.2
Let \(\mu \in {\mathbb {N}}, \mu \ge 3\) and let \(\delta >0\). Suppose the initial data \((\tilde{{{\textbf{U}}}}_0,\varphi _0)\in H^{\mu +1.5}({\mathbb {R}}^2_+)\times H^{\mu +1.5}({{\mathbb {R}}})\) are compatible up to order \(\mu \) and satisfy the assumptions (1.6), (2.4), (2.5), (4.4). Then, there exist \(T>0\) and \(({\tilde{{\textbf{U}}}}^a,\varphi ^a)\in H^{\mu +2}(\Omega _T)\times H^{\mu +2}(\Gamma _T)\) such that
where
We call \(({\textbf{U}}^a, \varphi ^a)\) the approximate solution to problem (4.20). Moreover the approximate solution satisfies the estimate
the stability conditions (4.4) on \(\Gamma _T\), the hyperbolicity condition (4.2) on \(\Omega _T\).
Proof
Let us first denote \(\Phi ^{a\,\pm }=\pm x_1+\Psi ^{a\,\pm }\), \(\tilde{{\textbf{U}}}^a=(\tilde{{\textbf{U}}}^{a+},\tilde{{\textbf{U}}}^{a-})^T\), \({{\tilde{p}}}^a=({{\tilde{p}}}^{a+}, {\tilde{p}}^{a-})^T\), \({\tilde{u}}^a=({\tilde{u}}^{a+},{\tilde{u}}^{a-})^T\), \({\tilde{H}}^a=({\tilde{H}}^{a+},{\tilde{H}}^{a-})^T\), \({\tilde{S}}^a=({\tilde{S}}^{a+},{\tilde{S}}^{a-})^T\). Consider \(\tilde{{\textbf{U}}}^a\in H^{\mu +2}({{\mathbb {R}}}\times {\mathbb {R}}^2_+),\varphi ^a\in H^{\mu +2}({{\mathbb {R}}}^2)\), such that
where \(\tilde{{\textbf{U}}}_j\) and \(\varphi _j\) are given by Lemma 8.1. Since \((\tilde{{\textbf{U}}}^a,\varphi ^a)\) satisfies the hyperbolicity condition (4.2) and the stability condition (4.4) at \(t=0\), by continuity \((\tilde{{\textbf{U}}}^a,\varphi ^a)\) satisfy (4.4) at \(x_1=0\) and (4.2) for small times. By multiplication of \((\tilde{{\textbf{U}}}^a,\varphi ^a)\) by a cut-off function in time supported on \([-T,T]\) we can assume that (4.2), (4.4) hold for all times (in this regard, recall Remark 3.1). Given any \(\delta >0\), by taking \(T>0\) sufficiently small, we can assume that \(\tilde{{\textbf{U}}}^a\), \(\varphi ^a\) are small in the sense of (8.9). \(\square \)
Remark 8.1
Let us remark that we do not require any constraint (that is interior equations or boundary condition) to be satisfied by the approximate solution constructed above. This allows us to the use of cut-off argument making the hyperbolicity condition (4.2) and the stability condition (4.4) to be satisfied globally in time, without any trouble.
Remark 8.2
In the sequel, in the proof of the main Theorem 3.1, estimate (8.9) will be used with \(\mu =m+10\), being m an integer as in the statement of that theorem.
We assume that
then we fix \(T>0\) sufficiently small so that \(||\varphi ^a||_{L^{\infty }([0,T]\times {{\mathbb {R}}})}\le \frac{1}{2}.\) Hence, we get
(recall that \(||\chi ^\prime ||_{L^\infty ({{\mathbb {R}}})}\le 1/2\), see Section 2).
The approximate solution \(({{\textbf{U}}}^a,\varphi ^a)\) enables us to reformulate the original problem (2.1) as a nonlinear problem with zero initial data. Set
From \(\tilde{{{\textbf{U}}}}^a\in H^{\mu +2}(\Omega _T)\) and \(\varphi ^a\in H^{\mu +2}(\Gamma _T),\) we have \({\mathcal {F}}^a\in H^{\mu +1}(\Omega _T)\).
Given the approximate solution \((\tilde{{{\textbf{U}}}}^a,\varphi ^a)\) of Lemma 8.2 and \({\mathcal {F}}^a\) defined in (8.10), we see that \(({{\textbf{U}}},\varphi )=({{\textbf{U}}}^a,\varphi ^a)+({{\textbf{V}}},\psi )\) is a solution of the original problem (2.1) if \({{\textbf{V}}}=({{\textbf{V}}}^+,{{\textbf{V}}}^-)^T,\Psi =(\Psi ^+,\Psi ^-)^T,\) \(\Psi |_{x_1=0}:=\psi \) satisfy the following problem:
The original nonlinear problem on \([0,T]\times {\mathbb {R}}^2_+\) is thus reformulated as a problem on \(\Omega _T\) whose solutions vanish in the past.
9 Nash–Moser Iteration
In this section, we recall the Nash–Moser iteration for reader’s convenience. First, we introduce the smoothing operators \(S_{\theta }\) and describe the iterative scheme for problem (8.11). For more details refer to [5, 14, 39].
Lemma 9.1
Let \(\mu \in {\mathbb {N}},\) with \(\mu \ge 4\). \({\mathcal {F}}^s_{*}(\Omega _T):=\{u\in H^s_{*}(\Omega _T): u=0 \text { for }t<0\}.\) Define a family of smoothing operators \(\{S_{\theta }\}_{{\theta \ge 1}}\) on the anisotropic Sobolev space from \({\mathcal {F}}^{3}_{*}(\Omega _T)\) to \(\bigcap _{s\ge 3}{\mathcal {F}}^{s}_{*}(\Omega _T)\), such that
where C is positive constant and \(k,j\in {\mathbb {N}},(k-j)_+:=\max \{0,k-j\}.\) In particular, if \(u=v\) on \(\Gamma _T,\) then \(S_{\theta }u=S_{\theta }v\) on \(\Gamma _T\). The definition of \({\mathcal {F}}^s(\Gamma _T)\) is entirely similar.
Now, we begin to formulate the Nash–Moser iteration scheme.
The iteration scheme starts from \(({{\textbf{V}}}_0,\Psi _0,\psi _0)=(0,0,0),\) and \(({{\textbf{V}}}_i,\Psi _i,\psi _i)\) is given such that
Let us consider
where the differences \((\delta {{{\textbf{V}}}}_i,\delta \psi _i)\) will be determined below. First, we can obtain \((\delta \dot{{{\textbf{V}}}}_i,\delta \psi _i)\) by solving the effective linear problem
where operators \({\mathbb {L}}_e', {\mathbb {B}}_e'\) are defined in (4.15) and (4.16),
is the Alinhac “good unknown" and \(({{\textbf{V}}}_{i+\frac{1}{2}},\Psi _{i+\frac{1}{2}})\) is a smooth modified state such that \(({{\textbf{U}}}^a+{{\textbf{V}}}_{i+\frac{1}{2}},\Psi ^a+\Psi _{i+\frac{1}{2}})\) satisfies (4.2)–(4.8) and (4.10). The source terms \((f_i,g_i)\) will be defined through the accumulated errors at step i. \(S_{\theta _i}\) is the smoothing operator with \({\theta _i}\) defined by
The errors at step i can be defined from the decompositions
and
where we write
and have used (4.14) to get the last identity in (9.9). Denote
We assume \(f_0:=S_{\theta _0}{\mathcal {F}}^a,(E_0,{\tilde{E}}_0,g_0):=(0,0,0)\) and \((f_k,g_k,e_k,{\tilde{e}}_k)\) are already given and vanish in the past for \(k\in \{0,\cdots ,i-1\}.\) We can calculate the accumulated errors at step \(i,i\ge 1\), by
Then, we obtain \(f_i\) and \(g_i\) for \(i\ge 1\) from the equations
Then, given suitable \(({{\textbf{V}}}_{i+\frac{1}{2}},\Psi _{i+\frac{1}{2}})\), we can obtain \((\delta \dot{{{\textbf{V}}}}_i,\delta \psi _i)\) as the solutions of the linear problem (9.6), \(\delta {{\textbf{V}}}_i\) from (9.7), \(({{\textbf{V}}}_{i+1},\Psi _{i+1}, \psi _{i+1})\) from (9.5). Since \(S_{\theta _i}\rightarrow I \) as \(i\rightarrow \infty ,\) we can formally obtain the solution to problem (8.11) from \({\mathcal {L}}({{\textbf{V}}}_{i},\Psi _{i})\rightarrow {\mathcal {F}}^a,{\mathcal {B}}({{\textbf{V}}}_{i}|_{x_1=0},\psi _{i})\rightarrow 0,\) as error terms \((e_i,{\tilde{e}}_i)\rightarrow 0.\)
10 Proof of the Main Result
Now, we prove the local existence of solutions to (8.11) by a modified iteration scheme of Nash–Moser type. From the sequence \(\{\theta _i\}\) defined in (9.8), we set \(\Delta _i:=\theta _{i+1}-\theta _i.\) Then, the sequence \(\{\Delta _i\}\) is decreasing and tends to 0 as i goes to infinity. Moreover, we have
10.1 Inductive analysis
Given a small fixed \(\delta >0\), and an integer \({{\tilde{\alpha }}}\) that will be chosen later on, we assume that the following estimate holds:
We may assume that (10.1) holds, by taking \(T>0\) sufficiently small.
Given the integer \(\alpha \), our inductive assumptions read as
Our goal is to show that \((H_0)\) holds and \((H_{i-1})\) implies \((H_i)\), for a suitable choice of the parameters \(\alpha \), \({{\tilde{\alpha }}}\), for \(\delta >0\) and \(T>0\) sufficiently small, for \(\theta _0\ge 1\) sufficiently large. Then, we conclude that \((H_i)\) holds for all \(i\in {\mathbb {N}}.\)
Lemma 10.1
If \(T>0\) is sufficiently small, then \((H_0)\) holds.
Proof
The proof follows as in [39, Lemma 17]. \(\square \)
Now we prove that \((H_{i-1})\) implies \((H_i)\). The hypothesis \((H_{i-1})\) yields the following lemma:
Lemma 10.2
[39, Lemma 7], [14, Lemma 7] If \(\theta _0\) is large enough, then, for each \(k\in \{0,\cdots ,i\}\), and each integer \(s\in \{6,\cdots ,{\tilde{\alpha }}\},\)
Furthermore, for each \(k\in \{0,\cdots ,i\}\), and each integer \(s\in \{6,\cdots ,{\tilde{\alpha }}+8\},\)
10.2 Estimate of the error terms
To derive \((H_{i})\) from \((H_{i-1})\), we need to estimate the quadratic error terms \(e'_k\) and \({\tilde{e}}'_k,\) the first substitution error terms \(e''_k\) and \({\tilde{e}}''_k,\) the second substitution error terms \(e'''_k\) and \({\tilde{e}}'''_k\) and the last error term \(D_{k+\frac{1}{2}}\delta \Psi _k\) (cf. (9.9)–(9.11)).
First, we denote the quadratic error terms by
Then, we get
where \({\mathbb {L}}'',{\mathbb {B}}''\) denote the second order derivatives of the operators \({\mathbb {L}}\) and \({\mathbb {B}}.\) To be more precise, we define
where \({\mathbb {L}}'\) and \({\mathbb {B}}'\) are defined in (4.11) and (4.12). Simple calculations yield that
To estimate the error terms, we need to estimate the operators \({\mathbb {L}}''\) and \({\mathbb {B}}''.\) Applying the Moser-type calculus inequalities in Lemma 3.1 and Lemma 3.2 and the explicit forms of \({\mathbb {L}}''\) and \({\mathbb {B}}''\), we can obtain the necessary estimates. Omitting the detailed calculation, we have the following Lemma 10.3:
Lemma 10.3
Let \(T>0,\) and \(s\in {\mathbb {N}}\) with \(s\ge 6.\) Assume that \((\breve{{\textbf{U}}},{\hat{\Psi }})\in H^{s+2}_{*}(\Omega _T)\) satisfies
(recall that \(\hat{{{\textbf{U}}}}=\bar{{{\textbf{U}}}}+\breve{{{\textbf{U}}}}\)) for some constant \({\tilde{K}}>0.\) Then, there exists a positive C depending on \({\tilde{K}},\) but not on T, such that if \(({{\textbf{V}}}_i,\Psi _i)\in H^{s+2}_{*}(\Omega _T)\) and \((W_i,\psi _i)\in H^{s}(\Gamma _T)\times H^{s+1}(\Gamma _T),\) for \(i=1,2,\) then
and
10.2.1 Estimate of the quadratic errors
We now apply Lemma 10.3 to prove the following estimate for the quadratic error terms:
Lemma 10.4
Let \(\alpha \ge 7.\) There exist \(\delta >0\) sufficiently small and \(\theta _0\ge 1\) sufficiently large such that, for all \(k\in \{0,\cdots ,i-1\},\) and all integers \(s\in \{6,\cdots ,{\tilde{\alpha }}-2\},\) we have
where \(L_1(s):=\max \{(s+2-\alpha )_++10-2\alpha ;s+6-2\alpha \}.\)
Proof
Using (10.1), the hypothesis \((H_{i-1})\) and the estimate (10.3), we use the Sobolev inequalities (3.10) to get
Then, we apply Lemma 10.3 and use Sobolev inequalities (3.10), the assumption (10.1) and the hypothesis \((H_{i-1})\) to give
for all \(s\in \{6,\cdots ,{\tilde{\alpha }}-2\}.\) If \(s+2\ne \alpha ,\) then it follows from (10.3) and \(2\theta _k\Delta _k\le 1,\) that
If \(s+2=\alpha ,\) then it follows from (10.3) and \(\alpha \ge 7,\) that
Therefore, we obtain (10.9). Now, we prove (10.10). Using Lemma 10.3 and trace Theorem A1.1, we obtain
This completes the proof of Lemma 10.4. \(\square \)
10.2.2 Estimate of the first substitution errors
We can estimate the first substitution errors \(e''_k, {\tilde{e}}''_k\) of the iteration scheme, defined in (9.9) and (9.10). We rewrite
Lemma 10.5
Let \(\alpha \ge 7.\) There exist \(\delta >0\) sufficiently small and \(\theta _0\ge 1\) sufficiently large, such that for all \(k\in \{0,\cdots ,i-1\}\) and for all integer \(s\in \{6,\cdots ,{\tilde{\alpha }}-2\},\) we have
where \(L_2(s):=\max \{(s+2-\alpha )_++12-2\alpha ;s+8-2\alpha \}.\)
Proof
In view of (10.11) and (10.12) we have
Using (10.4) and (10.5), we have
Next, we apply Lemma 10.3, use Sobolev inequalities (3.10), (10.1), the Hypothesis \((H_{i-1})\) and (10.4) to get that
for all \(s\in \{6,\cdots ,{\tilde{\alpha }}-2\}.\) Similar to the proof of Lemma 10.4, we can discuss \(s+2\ne \alpha \) and \(s+2=\alpha \) separately. Hence, using (10.5), we can obtain (10.13) and (10.14). The proof of Lemma 10.5 is completed. \(\square \)
10.2.3 Estimate of the modified state
We need to construct a smooth modified state \(({{\textbf{V}}}_{i+\frac{1}{2}},\psi _{i+\frac{1}{2}})\) such that \(({{\textbf{U}}}^a+{{\textbf{V}}}_{i+\frac{1}{2}},\varphi ^a+\psi _{i+\frac{1}{2}})\) satisfies the nonlinear constraints (4.2)–(4.8), (4.10) and (6.1). In this regard, we remark it is crucial that the sum of the approximate solution \(({{\textbf{U}}}^a,\varphi ^a)\) and the modified state \(({{\textbf{V}}}_{i+\frac{1}{2}},\psi _{i+\frac{1}{2}})\), instead of the latter two separately, satisfies the aforementioned nonlinear constraints; indeed it is just this sum which plays the role of basic state around which we need to linearize problem (2.1) in the iteration scheme leading to its solution, see problem (9.6). In the construction of some components of the modified state we follow an approach similar to that of [1, 14, 34], while for the magnetic field we are inspired by [34, 39].
Lemma 10.6
Let \(\alpha \ge 10\). There exist some functions \({{\textbf{V}}}_{i+\frac{1}{2}},\Psi _{i+\frac{1}{2}},\psi _{i+\frac{1}{2}}\) vanishing in the past, such that \(({{\textbf{U}}}^a+{{\textbf{V}}}_{i+\frac{1}{2}}, \Psi ^a+\Psi _{i+\frac{1}{2}}, \varphi ^a+\psi _{i+\frac{1}{2}})\) satisfy the constraints (4.2)– (4.8), (4.10) and (6.1); moreover,
for sufficiently small \(\delta >0\) and \(T>0,\) and sufficiently large \(\theta _0\ge 1.\)
Proof
To shortcut notation, in the proof the ± indices are omitted. Let us define \(\Psi _{i+1/2}\), \(\psi _{i+1/2}\), \(p_{i+1/2}\), \(S_{i+1/2}\) and the tangential component \(u_{2,i+1/2}\) of the velocity as in (10.15), (10.16); this is similar as in [1, 14, Proposition 7], [34, Proposition 28]. It is easily checked that all these functions vanish in the past.
Construction of the modified normal velocity.
In order to construct the normal component \(u_{1,i+1/2}\) of the velocity, we follow the idea of [1, 14]. We first introduce the following function \({\mathcal {G}}\):
The normal component of the velocity \(u_{1,i+1/2}\) is defined by
where \({\mathcal {R}}_T\) is the lifting operator \(H^{s-1}(\Gamma _T)\rightarrow H^s_*(\Omega _T)\), \(s>1\), see [27]. It is easily checked that \(u_{1,i+1/2}\) vanishes in the past.
Let us note that, by construction, \(u_{1,i+1/2}\) satisfies the following equation on the boundary:
We prove the estimate (10.17) for the part regarding \({{\textbf{u}}}_{i+1/2}\). We have
Now we rewrite \({\mathcal {G}}\) in a more convenient form, by using the error \(\varepsilon ^i\) defined by
In view of (10.16), by means of \(\varepsilon ^i\) we may rewrite \({\mathcal {G}}\) as
To estimate the first term \(S_{\theta _i}\varepsilon ^i\) on the right-hand side, we use the decomposition
Then we exploit point (c) of (\(H_{i-1}\)) and the properties of smoothing operators, to get
In order to make an estimate of the commutator term \([S_{\theta _i},\partial _t]\psi _i\), we use different arguments for large and small orders s.
For all \(s\in \{6,\dots ,\alpha \}\) we write the commutator as
then we use estimates (9.2), (10.3) and (10.4) to get
In order to get the similar estimate as (10.23) for \(s\in \{\alpha +1,\dots ,{{\tilde{\alpha }}}+6\}\), we directly estimate the two terms of the commutator \([\partial _t,S_{\theta _i}]\psi _i=\partial _tS_{\theta _i}\psi _i-S_{\theta _i}\partial _t\psi _i\), using (9.1) and (10.5).
To estimate the third term in the right-hand side of (10.21), we proceed as above by applying different arguments to small and large orders s.
For integers \(s\in \{6,\dots ,\alpha \}\), we apply (9.2) to get
in view of (10.1).
For integers \(s\in \{\alpha +1,\dots .{{\tilde{\alpha }}}+6\}\), we use (9.1) and (10.1) to estimate directly
where \(E^a:=\partial _t\varphi ^a-u^a_1+u_2^a\partial _2\varphi ^a\) has been set.
Let us now estimate the fourth term \(-\left( S_{\theta _i}(u^a_2\partial _2\psi _i)-u_2^a\partial _2 S_{\theta _i}\psi _i\right) \); once again we need to argue separately on different values of s.
For small integers \(s\in \{6,\dots ,{{\tilde{\alpha }}}\}\) we rewrite the above in the form
which takes advantage of the appearing of the difference \(I-S_{\theta _i}\); thus estimate (10.4) and Moser-type calculus inequalities of Lemma 3.1 yield
As for the second term in the right-hand side of (10.24), a further splitting of the range of s covered by estimate (10.25) is required. For integers s such that \(6\le s\le \alpha +1\), we apply (9.2), Moser-type calculus inequalities of Lemma 3.1 and (10.3) to obtain
On the other hand for integers s such that \(\alpha +1<s\le {{\tilde{\alpha }}}\), we use (9.1), Moser-type calculus inequalities and (10.3) to get
Gathering (10.25)–(10.27) we end up with
For higher integers \(s\in \{{{\tilde{\alpha }}}+1,\dots ,{{\tilde{\alpha }}}+6\}\), we estimate separately the two terms of the difference \(u_2^a\partial _2 S_{\theta _i}\psi _i-S_{\theta _i}(u^a_2\partial _2\psi _i)\); using again estimates (9.1), (10.3), (10.5) and Moser-type calculus inequalities, we obtain
Adding the last two inequalities we end up with
Gathering estimates (10.28) and (10.29) provide the estimate for all integers \(s\in \{6,\dots ,{{\tilde{\alpha }}}+6\}\).
For the last two terms in the right-hand side of (10.21) we use the same arguments as above, where we still separate small and large orders s; in the case of small s we manage to rewrite the expression in order to make advantage from the boundedness properties (9.2), (10.4) of \(I-S_{\theta _i}\); for large s we estimate separately each term of the difference using Moser-type calculus inequalities and (9.1), (10.3), (10.5). Doing so, we derive the following:
Gathering all the previously found estimates we end up with
In the above estimate it is fundamental that \(s\le {\tilde{\alpha }}+6\) in order to prove the following (10.40). Let us recall that the above estimate holds under the smallness assumption (10.1).
Construction of the modified magnetic field.
Let us see now how to define the modified magnetic field \({\textbf{H}}_{i+1/2}\), following [34, Proposition 28], [39, Proposition 12].
Let us denote the nonlinear equation satisfied by the magnetic field in (2.1) by
The field \({\textbf{H}}_{i+1/2}\) should be such that \(\textbf{H}^a+{\textbf{H}}_{i+1/2}\) satisfies (4.8), that is,
We note that equation (10.31) is linear in \({\textbf{H}}^a+{\textbf{H}}_{i+1/2}\) and does not need to be supplemented with any boundary condition; in fact, the coefficient of \(\partial _1({\textbf{H}}^a+{\textbf{H}}_{i+1/2})\) is zero along the boundary because of (10.19) (the left-hand side of (10.19) is nothing but \(w_1\vert _{x_1=0}\), computed for \({{\textbf{u}}}^a+{{\textbf{u}}}_{i+1/2}\) and \(\Psi ^a+\Psi _{i+1/2}\) instead of \({\textbf{u}}\) and \(\Psi \) respectively).
Therefore, for given \({{\textbf{u}}}_{i+1/2}\), \(\Psi _{i+1/2}\), \({{\textbf{U}}}^a\) and \(\Psi ^a\), (10.31) has a unique solution \({\textbf{H}}'\), from which we derive the existence of a unique \({\textbf{H}}_{i+1/2}={\textbf{H}}'-{\textbf{H}}^a\), vanishing in the past.
In order to estimate \({{\textbf{H}}}_{i+1/2}-S_{\theta _i}{{\textbf{H}}}_i\), we first observe that (10.31) yields
Then \({\textbf{H}}_{i+1/2}-S_{\theta _i}{\textbf{H}}_i\) solves the equation
where
Let us first write the explicit form of \(\Delta _1\). Using the definition of the nonlinear operator \({\mathbb {L}}_H(\textbf{u},\textbf{H},\Psi )\) we have
where
The vectors \(\textbf{v}[\textbf{u}^a+S_{\theta _i}{} \textbf{u}_i]\), \(\textbf{w}[\textbf{u}^a+S_{\theta _i}{} \textbf{u}_i]\), \(\textbf{h}[\textbf{H}^a+S_{\theta _i}{} \textbf{H}_i]\) are defined by completely similar expressions with \(S_{\theta _i}{} \textbf{u}_i\), \(S_{\theta _i}{} \textbf{H}_i\), \(S_{\theta _i}\Psi _i\) instead of \(\textbf{u}_i\), \(\textbf{H}_i\), \(\Psi _i\).
We split the range of s into small and large values (in order to take advantage of the continuity estimates of \(I-S_{\theta _i}\), see (9.2) and (10.4)). For small values of s, by using (10.3), (10.4), the smallness assumption (10.1) and Moser-type calculus inequalities we get
Adding (10.34), (10.35) gives an estimate of \(\textbf{v}[\textbf{u}^a+S_{\theta _i}{} \textbf{u}_{i}]\). We obtain similar estimates for \(\textbf{w}[\textbf{u}^a+\textbf{u}_{i}],\textbf{h}[\textbf{H}^a+\textbf{H}_{i}], \textbf{w}[\textbf{u}^a+S_{\theta _i}{} \textbf{u}_{i}]\) and \(\textbf{h}[\textbf{H}^a+S_{\theta _i}{} \textbf{H}_{i}]\).
We decompose \(\Delta _1\) as sum of terms with differences \(I-S_{\theta _i}\) put in evidence. Making repeated use of estimates (9.1), (9.2), (10.3)–(10.5), the smallness assumption (10.1), Moser-type calculus inequalities of Lemmata 3.1, 3.2, we get, for \(\alpha \ge 9\),
For large values \(s\ge {\alpha }-3\) we use (9.1), (10.5) to obtain
with similar estimates for \(\textbf{w}[\textbf{u}^a+S_{\theta _i}\textbf{u}_{i}]\) and \(\textbf{h}[\textbf{H}^a+S_{\theta _i}{} \textbf{H}_{i}]\). With a direct estimate of the terms in \(\Delta _1\) we extend (10.36) to the cases \(s\ge {\alpha }-2\) and finally obtain
In the above estimate (10.37) it is fundamental that \(s\le {\tilde{\alpha }}+6\). This is used for the estimate (10.38) of \(\Delta _1\), where the estimate of the normal derivative of \({\textbf{v}}[\cdot ]\) in the anisotropic space \(H^s_*\), for \(s\le {\tilde{\alpha }}+4\), requires an estimate of \({\textbf{v}}[\cdot ]\) in \(H^{s+2}_*\).
As for \(\Delta _2\), we have the explicit expression
where
From the definition (10.39), using Moser-type calculus inequalities, (10.1), (10.5), (10.15), and the estimate (10.30), we obtain
Again in (10.40) we need \(s\le {\tilde{\alpha }}+6\) in order to get the following estimate (10.41) of \(\Delta _2\), where the estimate of the normal derivative of \({\textbf{v}}[\cdot ]\) in the anisotropic space \(H^s_*\), for \(s\le {\tilde{\alpha }}+4\), requires an estimate of \({\textbf{v}}[\cdot ]\) in \(H^{s+2}_*\).
Making repeated use of Moser-type calculus inequalities, (10.1), (10.5), (10.15), the estimates (10.30) and (10.40), we get for \(\alpha \ge 9\)
To estimate the last term of \(F_H^{i+1/2}\) we write
where \({\mathcal {L}}_H,{\mathcal {F}}^a_H\) are the \({\textbf{H}}\)-component in (8.11), (8.10), respectively. From (9.1), \((H_{i-1})(b)\) we readily obtain
For the first difference in (10.42) let us denote
Hence we have
where, in particular, for the estimate of \(||\Delta _3||_{6,*,T}\), we have used \((H_{i-1})(a)\), (10.3), (10.34) and
used in the cases \(s=6\), \(s=8\) and a similar estimate for \(\textbf{w}[\textbf{u}^a+{\textbf{u}}_{i-1}+\delta {\textbf{u}}_{i-1}]-\textbf{w}[\textbf{u}^a+\textbf{u}_{i-1}]\) in case \(s=6\). Collecting (10.38), (10.41), (10.43), (10.44) we get
Equation (10.32) solved by \({\textbf{H}}_{i+1/2}-S_{\theta _i}{\textbf{H}}_i\) has the form
for \(Y={\textbf{H}}_{i+1/2}-S_{\theta _i}{\textbf{H}}_i\), \(b=({{\textbf{u}}}^a+{\textbf{u}}_{i+1/2},\Psi ^a+\Psi _{i+1/2})\), and where \({\mathcal {D}}_j\) and \({\mathcal {Q}}\) are some matrices. The matrices \({\mathcal {D}}_j\) are diagonal and, more important, \({\mathcal {D}}_1\) vanishes at the boundary. This yelds that system (10.46) does not need any boundary condition. A standard energy argument applied to (10.46) gives, in view of (10.45),
Collecting (10.30), (10.47) gives (10.17).
Using (8.9), (10.5), (10.17) for \(s=6\), and taking \(\delta >0\) sufficiently small we have that \(\varphi ^a+\psi _{i+\frac{1}{2}}\) and \(\tilde{{{\textbf{U}}}}^a+{\textbf{V}}_{i+\frac{1}{2}}\) are sufficiently small. Then, \(\varphi ^a+\psi _{i+\frac{1}{2}}\) satisfies (4.7) and, recalling Remark 3.1, \({{{\textbf{U}}}}^a+{\textbf{V}}_{i+\frac{1}{2}}\) satisfies (4.2), (4.4), (4.6), (6.1). \({{{\textbf{H}}}}^a+{\textbf{H}}_{i+\frac{1}{2}}\) satifies (4.8) by construction, see (10.31); the initial value at \(t=0\) of \({{{\textbf{H}}}}^a+{\textbf{H}}_{i+\frac{1}{2}}\) satisfies (4.10) since \({{{\textbf{H}}}}^a_{|t=0}={{\textbf{H}}}_0\) satisfies (4.10) by assumption, and \({{{\textbf{H}}}}_{i+\frac{1}{2}}=0\) for \(t\le 0\) by continuity. In conclusion, \({{{\textbf{U}}}}^a+{\textbf{V}}_{i+\frac{1}{2}}\) satisfies all the constraints (4.2)–(4.8), (4.10) and (6.1) for the background state. \(\square \)
10.2.4 Estimate of the second substitution errors
In the following Lemma, we can estimate the second substitution errors \(e'''_k,{\tilde{e}}'''_k\) of the iterative scheme. We define
We can write (10.48) and (10.49) as follows:
Lemma 10.7
Let \(\alpha \ge 10\). There exist \(\delta >0\) sufficiently small and \(\theta _0\ge 1\) sufficiently large such that, for all \(k\in \{0,\cdots ,i-1\}\) and for all integers \(s\in \{6,\cdots ,{\tilde{\alpha }}-2\},\) we have
where \(L_3(s):=\max \{(s+2-\alpha )_++16-2\alpha ;s+12-2\alpha \}.\)
Proof
Using (10.17) and Lemma 10.3, similar to the proof of Lemmata 10.4 and 10.5, we obtain (10.50) and (10.51). Here, we can calculate the explicit form of \({\tilde{e}}'''_k\) as
\(\square \)
10.2.5 Estimate of the last error term
We now estimate the last error term (9.11):
where \(R_k:=\partial _1[{\mathbb {L}}({{\textbf{U}}}^a+{{\textbf{V}}}_{k+\frac{1}{2}},\Psi ^a+\Psi _{k+\frac{1}{2}})].\) It is noted that
for \(\delta >0\) sufficiently small.
The following Lemma 10.8 can be proved by direct calculations:
Lemma 10.8
Let \(\alpha \ge 10,{\tilde{\alpha }}\ge \alpha -4.\) There exist \(\delta >0\) sufficiently small and \(\theta _0\ge 1\) sufficiently large, such that, for all \(k\in \{0,\cdots ,i-1\}\) and for all integers \(s\in \{6,\cdots ,{\tilde{\alpha }}-2\}\), we have
where \(L_4(s):=s+14-2\alpha \).
Proof
Using (3.7) and (3.9), we obtain that
Using (8.10) and (8.11), we can write
where
If \(s\in \{4,\cdots ,{\tilde{\alpha }}-4\},\) then using Hypothesis \((H_{i-1}),\) we obtain that
Using (10.3), (10.4), (10.15)–(10.17), (10.56),(10.57), Sobolev inequalities (3.10) and Moser-type calculus inequalities in Lemma 3.2, we have
If \(s\in \{{\tilde{\alpha }}-3,{\tilde{\alpha }}-2\}\), then, for \({{\tilde{\alpha }}}\ge \alpha -4\), using (10.3), (10.5) and (10.15)–(10.17), we can deduce directly from (10.56) that
Therefore, (10.58) holds for all \(s\in \{4,\cdots ,{\tilde{\alpha }}-2\}.\) Using Hypothesis \((H_{i-1}),\) (10.58), (10.5), (10.3) and (10.15)–(10.17) into (10.55), we can obtain (10.54). \(\square \)
Using Lemmata 10.4–10.8, we can conclude the following estimates of the error terms \(e_k, {\tilde{e}}_k,\) defined by (9.12):
Lemma 10.9
Let \(\alpha \ge 10,{\tilde{\alpha }}\ge \alpha -4.\) There exist \(\delta >0\) sufficiently small and \(\theta _0\ge 1\) sufficiently large, such that for all \(k\in \{0,\cdots ,i-1\}\) and for all integers \(s\in \{6,\cdots ,{\tilde{\alpha }}-2\}\), we have
where \(L_4(s)\) is defined in Lemma 10.8.
From Lemma 10.9, we obtain the estimate of the accumulated errors \(E_i,{\tilde{E}}_i,{\hat{E}}_i,\) which are defined in (9.13).
Lemma 10.10
Let \(\alpha \ge 16,{\tilde{\alpha }}=\alpha +5.\) There exist \(\delta >0\) sufficiently small and \(\theta _0\ge 1\) sufficiently large, such that
Proof
Using \(L_4(\alpha +3)\le 1\) if \(\alpha \ge 16\), it follows from (10.59) that
if \(\alpha +3\le {\tilde{\alpha }}-2\). Similar arguments also hold for \(||{\tilde{E}}_i||_{H^{\alpha +3}(\Gamma _T)}\). The minimal possible \({\tilde{\alpha }}\) is \(\alpha +5\). \(\square \)
10.3 Convergence of the iteration scheme
We still need to estimate the source terms \(f_{i},g_{i}.\)
Lemma 10.11
Let \(\alpha \ge 16\) and \({\tilde{\alpha }}=\alpha +5\). There exist \(\delta >0\) sufficiently small and \(\theta _0\ge 1\) sufficiently large, such that for all integers \(s\in \{6,\cdots ,{\tilde{\alpha }}+2\},\)
In the above inequalities we need the exponent \(s-\alpha -3\) of \(\theta _i\) to compensate the loss of 2 derivatives for the data in (10.64), in order to recover the exponent \(s-\alpha -1\) in the corresponding terms of (10.68).
Proof
As in [14, 34, 39], using (9.1)–(9.3), (9.14), (10.59), (10.60), we obtain that
Using (10.59) and (10.60) we can obtain (10.62). \(\square \)
Similar to the proof of [14, 34, 39], we can obtain the estimate of \((\delta {{\textbf{V}}}_i,\delta \Psi _i)\) by (10.17) and the tame estimate (7.1) applied to problem (9.6).
Lemma 10.12
Let \(\alpha \ge 16\) and \({\tilde{\alpha }}=\alpha +5\). If \(\delta >0\) and \(||{\mathcal {F}}^a||_{\alpha +2,*,T}/\delta \) are sufficiently small and \(\theta _0\ge 1\) is sufficiently large, then for all integers \(s\in \{6,\cdots ,{\tilde{\alpha }}\}\),
Proof
Let us consider problem (9.6) that will be solved by applying Theorem 7.1. We first notice that \(({{\textbf{U}}}^a+{{\textbf{V}}}_{i+\frac{1}{2}}, \Psi ^a+\Psi _{i+\frac{1}{2}}, \varphi ^a+\psi _{i+\frac{1}{2}})\) satisfy the constraints (4.2)–(4.8), (4.10), (6.1). Thus we may apply our tame estimate (7.1) and obtain
On the other hand, from (9.7) it follows that
From
(10.64) for \(s=4\) and (6.1) we have
Then, from (10.64) and (10.65) we obtain
Using (8.9), (10.5) and (10.17) for \(s=6\), taking \(\delta >0\) sufficiently small, we can absorb the last term in the right-hand side above into the left-hand side to get
The remaining part of the work is to estimate the right-hand side of (10.67).
Using Lemma 10.11, (10.5), Lemma 10.6 and (10.66), (10.67) becomes
One checks that, for \(\alpha \ge 16\) and \(6\le s\le {\tilde{\alpha }}\), the following inequalities hold true:
From (10.68) we thus obtain (10.63), provided \(\delta >0\) and \(||{\mathcal {F}}^a||_{\alpha +2,*,T}/\delta \) are sufficiently small and \(\theta _0\ge 1\) is sufficiently large. \(\square \)
Finally, similar to the proof of [14, 34, 39], we can obtain the remaining inequalities in \((H_i).\)
Lemma 10.13
Let \(\alpha \ge 16\). If \(\delta >0\) and \(||{\mathcal {F}}^a||_{\alpha +2,*,T}/\delta \) are sufficiently small and if \(\theta _0\ge 1\) is sufficiently large, then for all integers \(s\in \{6,\cdots ,{\tilde{\alpha }}-2\}\)
Moreover, for all integers \(s\in \{6,\cdots ,{\tilde{\alpha }}-2\}\)
Proof
Recall that, by summing the relations (9.9), we have
The proof of (10.69) then follows by applying (9.2), (10.59), (10.60), provided that \(\delta >0\) and \(||{\mathcal {F}}^a||_{\alpha +2,*,T}/\delta \) are sufficiently small and \(\theta _0\ge 1\) is sufficiently large. The proof of (10.70) is similar. \(\square \)
We are now in the position to prove the main theorem for the existence of the solution to the nonlinear problem (2.1).
Proof of Theorem 3.1
Let the initial data \(({{\textbf{U}}}^{\pm }_0,\varphi _0)\) satisfy all the assumptions of Theorem 3.1. Let \(\alpha =m+1\ge 16\), \({\tilde{\alpha }}=\alpha +5\), \(\mu =m+10\). Then the initial data \({{\textbf{U}}}^{\pm }_0\in H^{\mu +1.5}({\mathbb {R}}^2_+)\) and \(\varphi _0\in H^{\mu +1.5}({\mathbb {R}})\) are compatible up to order \(\mu \) and there exists an approximate solution \((\tilde{{\textbf{U}}}^a,\varphi ^a)\in H^{\mu +2}(\Omega _T)\times H^{\mu +2}(\Gamma _T)\) to problem (2.1). Observe that \(\mu +2={{\tilde{\alpha }}}+6\) as required in (10.1). We choose \(\delta >0\), \(T>0\) sufficiently small, \(\theta _0\ge 1\) sufficiently large as in the previous lemmata. We also assume \(T>0\) small enough so that \(||{\mathcal {F}}^a||_{\alpha +2,*,T}/\delta \) is sufficiently small. Then in view of Lemmata 10.1, 10.12, 10.13, property (\(H_i\)) holds for all integers i. In particular, we have
Thus, the sequence \(({{\textbf{V}}}_i,\Psi _i)\) converges to some limit \(({{\textbf{V}}},\Psi )\) in \(H^{\alpha -1}_{*}(\Omega _T),\) and sequence \(\psi _i\) converges to some limit \(\psi \) in \(H^{\alpha -1}(\Gamma _T).\) Passing to the limit in (10.69) and (10.70) for \(s=m=\alpha -1\), we obtain (8.11). Therefore, \(({{\textbf{U}}},\Phi )=({{\textbf{U}}}^a+{{\textbf{V}}},\Phi ^a+\Psi )\) is a solution on \(\Omega _T\) of nonlinear system (2.1).
References
Alinhac, S.: Existence d’ondes de raréfaction pour des systèmes quasi-linéaires hyperboliques multidimensionnels. Commun. Partial Differ. Eqs. 14(2), 173–230, 1989
Alinhac, S., Gérard, P.: Pseudo-differential Operators and the Nash–Moser Theorem. American Mathematical Society, Providence (2007)
Axford, W.I.: Note on a problem of magnetohydrodynamic stability. Canad. J. Phys 40, 654–655 (1962)
Chen, G.-Q., Secchi, P., Wang, T.: Nonlinear stability of relativistic vortex sheets in three dimensional Minkowski spacetime. Arch. Ration. Mech. Anal. 232, 591–695, 2019
Chen, G.-Q., Wang, Y.-G.: Existence and stability of compressible current-vortex sheets in three-dimensional magnetohydrodynamics. Arch. Ration. Mech. Anal. 187, 369–408 (2008)
Chen, G.-Q., Wang, Y.-G.: Characteristic discontinuities and free boundary problems for hyperbolic conservation laws, In: Nonlinear Partial Differential Equations, In: Abel Symp., vol.7, Springer, Heidelberg, pp. 53-81 (2012)
Chen, R.M., Hu, J., Wang, D.: Linear stability of compressible vortex sheets in two-dimensional elastodynamics. Adv. Math. 311, 18–60 (2017)
Chen, R.M., Hu, J., Wang, D.: Linear stability of compressible vortex sheets in 2D elastodynamics: variable coefficients, Math. Ann. 1–50 (2019)
Chen, R.M., Hu, J., Wang, D., Wang, T., Yuan, D.: Nonlinear stability and existence of compressible vortex sheets in 2D elastodynamics. J. Differ. Equ. 269, 6899–6940 (2020)
Chen, R.M., Huang, F.M., Wang, D., Yuan, D.: Stabilization effect of elasticity on three-dimensional compressible vortex sheets. J. Math. Pures Appl. 172(9), 105–138, 2023
Chen, S.: Initial boundary value problems for quasilinear symmetric hyperbolic systems with characteristic boundary. Translate from Chinese Ann. Math.3(2) (1982), 222–232. Front. Math. China 2(1), 87–102 (2007).
Coulombel, J.-F., Morando, A.: Stability of contact discontinuities for the nonisentropic Euler equations. Ann. Univ. Ferrara Sez. VII (N.S.) 50, 79–90 (2004)
Coulombel, J.-F., Secchi, P.: The stability of compressible vortex sheets in two space dimensions. Indiana Univ. Math. J. 53, 941–1012 (2004)
Coulombel, J.-F., Secchi, P.: Nonlinear compressible vortex sheets in two space dimensions. Ann. Sci. Ec. Norm. Super. 41, 85–139 (2008)
Dafermos, C.M.: Hyperbolic Conservation Laws in Continuum Physics. Third Edition, Grundlehren der Mathematischen Wissenschaften (Fundatmental Principles of Mathematical Sciences), vol. 235, Springer-Verlag, Berlin (2010)
Fejer, J.A., Miles, W.: On the stability of a plane vortex sheet with respect to three dimensional disturbances. J. Fluid Mech. 15, 335–336 (1963)
Freistühler, H., Trakhinin, Y.: Symmetrizations of RMHD equations and stability of relativistic current-vortex sheets. Class. Quantum Gravity 30(8), 85012–85028(17) (2012)
Goedbloed, J.P., Poedts, S.: Principles of Magnetohydrodynamics with Applications to Laboratory and Astrophysical Plasmas. Cambridge University Press, Cambridge (2004)
Landau, L.D., Lifshiz, E.M., Pitaevskii, L.P.: Electrodynamics of Continuous Media. Pergamon Press, Oxford (1984)
Métivier, G.: Stability of multidimensional shocks. In: Freistühler, H., Szepessy, A. (eds.) Advances in the Theory of Shock Waves, pp. 25–103. Birkhäuser, Boston (2001)
Michael, D.H.: The stability of a combined current and vortex sheet in a perfectly conducting fluid. Proc. Camb. Philos. Soc. 51, 528–532 (1955)
Miles, J.W.: On the reflection of sound at an interface of relative motion. J. Acoust. Soc. Am. 29, 226–228 (1957)
Miles, J.W.: On the disturbed motion of a plane vortex sheet. J. Fluid. Mech. 4, 538–552 (1958)
Morando, A., Secchi, P., Trebeschi, P.: Regularity of solutions to characteristic initial-boundary value problems for symmetrizable systems. J. Hyperbolic Differ. Equ 6(4), 753–808 (2009)
Morando, A., Trebeschi, P.: Two-dimensional vortex sheets for the nonisentropic Euler equations: linear stability. J. Hyperbolic Differ. Equ. 5(3), 487–518 (2008)
Morando, A., Trebeschi, P., Wang, T.: Two-dimensional vortex sheets for the nonisentropic Euler equations: nonlinear stability. J. Differ. Equ. 266(9), 5397–5430, 2019
Ohno, M., Shizuta, Y., Yanagisawa, T.: The trace theorem on anisotropic Sobolev spaces. Tôhoku Math. J. 46, 393–401 (1994)
Ohno, M., Shizuta, Y., Yanagisawa, T.: The initial boundary value problem for linear symmetric hyperbolic problems with boundary characteristic of constant multiplicity. J. Math. Kyoto Univ. 35, 143–210 (1995)
Rauch, J.: Symmetric positive systems with boundary characteristic of constant multiplicity. Trans. Am. Math. Soc. 291, 167–187 (1985)
Secchi, P.: The initial-boundary value problem for linear symmetric hyperbolic systems with characteristic boundary of constant multiplicity. Differ. Integ. Equ. 9(4), 671–700 (1996)
Secchi, P.: Well-posedness of characteristic symmetric hyperbolic systems. Arch. Ration. Mech. Anal. 134, 155–197 (1996)
Secchi, P.: A higher-order Hardy-type inequality in anisotropic Sobolev spaces. Int. J. Differ. Equ. Art. ID 129691 (2012)
Secchi, P.: On the Nash-Moser iteration technique. In: Amann, H., Giga, Y., Kozono, H., Okamoto, H., Yamazaki, M. (eds.) Recent Developments of Mathematical Fluid Mechanics, pp. 443–457. Birkhäuser, Basel (2016)
Secchi, P., Trakhinin, Y.: Well-posedness of plasma-vacuum interface problem. Nonlinearity 27, 105–169 (2014)
Serre, D.: Systems of Conservation Laws.2. Geometric Structure, Oscillations, and Initial-Boundary Value Problems. Cambridge University Press, Cambridge (2000)
Stevens, B.: Short-time structural stability of compressible vortex sheets with surface tension. Arch. Ration. Mech. Anal. 222(2), 603–730 (2016)
Syrovatskij, S.I.: The stability of tangential discontinuities in a magnetohydrodynamic medium. Zhurnal Eksper. Teor. Fiz. 24, 622–629 (1953)
Trakhinin, Y.: Existence of compressible current-vortex sheets: variable coefficients linear analysis. Arch. Ration. Mech. Anal. 177(3), 331–366 (2005)
Trakhinin, Y.: The existence of current-vortex sheets in ideal compressible magnetohydrodynamics. Arch. Ration. Mech. Anal. 191, 245–310 (2009)
Wang, Y.-G., Yu, F.: Stabilization effect of magnetic fields on two-dimensional compressible current-vortex sheets. Arch. Ration. Mech. Anal. 208, 341–389 (2013)
Wang, Y.-G., Yu, F.: Stability of contact discontinuities in three-dimensional compressible steady flows. J. Differ. Equ. 255, 1278–1356 (2013)
Wang, Y.-G., Yu, F.: Structural stability of supersonic contact discontinuities in three-dimensonal compressible steady flows. SIAM J. Math. Anal. 47, 1291–1329 (2015)
Acknowledgements
The authors are grateful to the anonymous referee for her/his comments and suggestions, that have contributed to improve this paper. The research of A. Morando, P. Secchi, P. Trebeschi was supported in part by the Italian MUR Project PRIN prot. 20204NT8W4. D. Yuan was supported by NSFC Grant No.12001045 and China Postdoctoral Science Foundation No.2020M680428, No.2021T140063. D. Yuan thanks the Department of Mathematics of the University of Brescia for its kind hospitality.
Funding
Open access funding provided by Università degli Studi di Brescia within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
This research does not have any associated data.
Additional information
Communicated by T.-P. Liu.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
Trace theorem in anisotropic space
In this Appendix let us recall the following trace theorem in the anisotropic space by Ohno, Shizuta, Yanagisawa [27].
Theorem A1.1
([27]) Let \(s\ge 2\) be an integer. Then the mapping
extends by continuity to a continuous linear mapping of
This mapping is surjective and there exists a continuous linear right-inverse
of
such that
Proof of Theorem 5.1
Here we focus only on the proof of the energy estimate (5.33); the existence and uniqueness of the solution can be shown by standard methods.
Let \({{\textbf{V}}}={{\textbf{V}}}(t,\textbf{x})=({{\textbf{V}}}^+,{{\textbf{V}}}^-)\), \(\varphi =\varphi (t,x_2)\), where \({{\textbf{V}}}^\pm :=(\dot{q}^\pm , \dot{u}^\pm _n, \dot{u}_2^\pm , \dot{H}^\pm _n, \dot{H}^\pm _2, \dot{S}^\pm )\), be sufficiently smooth vector fields respectively on \(\Omega _T\) and \(\Gamma _T\), satisfying the linear system (5.3), or its equivalent form (5.4), together with the boundary and the “initial" conditions from (4.31), that is,
Recall from Section 4 that \({{\hat{\Psi }}}^\pm ={{\hat{\Psi }}}^\pm (t,\textbf{x})\) are defined through the basic front function \({{\hat{\varphi }}}={{\hat{\varphi }}}(t,x_2)\) by
where \(\chi \in C^{\infty }_0({{\mathbb {R}}})\) satisfies \(\chi \equiv 1\) on \([-1,1]\), so that \(\partial _1{{\hat{\Psi }}}^\pm \vert _{x_1=0}=0\). We set
notice, in particular, that
Recall that \(({{\textbf{V}}},\varphi )\) as above must also satisfy the interior and boundary constraints
where
In the forthcoming calculations we will make use of the shortcut notation
and we set
In (A.6), \({{\textbf{V}}}^\pm _n\) denote the noncharacteristic part of the solution \({{\textbf{V}}}^\pm \), that is,
For all integers \(m\ge 0\), we will also write \(C_m\) to denote a generic positive constant depending (nonlinearly) on \(\Vert \hat{{\textbf{U}}}^\pm \Vert _{W^{m,\infty }(\Omega _T)}\) and \(\Vert \nabla _{t,x_2}{{\hat{\varphi }}}\Vert _{W^{m,\infty }(\Gamma _T)}\) and the positive number k from (4.2) and (4.4), that is,
which might possibly be different from an occurrence to another even within the same sequence of inequalities.
From the notation above and in view of (A.2), it straightforwardly turns out that
for all \(t\in (0,T]\), see (3.3), (3.4) and (5.1).
The estimate of Theorem 5.1 will be obtained by applying classical arguments from the energy method in order to get a control of the \(L^2\)-norm of the solution \({{\textbf{V}}}^\pm \) and the front \(\varphi \), as well as its tangential space time derivatives, corresponding to the different expressions listed in (A.4)–(A.8).
1.1 Estimate of I(t)
We scalarly multiply both sides of system (5.4) and integrate by parts in \(\Omega _t\) to get the energy identity
where, to shorcut notation, we write hereafter \({\mathcal {B}}_k\) instead of \({\mathcal {B}}_k(\hat{{{\textbf{U}}}},{\hat{\Psi }})\) for \(k=0,1,2,3\).
From Cauchy-Schwarz and Young inequality, the right-hand side above is estimated by
where
are used, together with (A.4), to make the last inequality above.
Now we need to get an estimate of the quadratic form \(({\mathcal {B}}_1{{\textbf{V}}}\cdot {{\textbf{V}}})\) under the second boundary integral in the left-hand side of (A.11).
From (5.7), a direct calculation gives (5.8), (5.9), where we have made use of the boundary conditions in (A.1) and (A.3). In (5.8) the initials “l.o.t” are used to mean “lower order terms” with respect to the leading part \([{{\hat{u}}}_2-{{\hat{\lambda }}}{{\hat{H}}}_2]\dot{q}^+\partial _2\varphi \) of the boundary quadratic form (5.8). All terms appearing in (5.9) are products of the form \(\varphi \,\partial _i\varphi \), with \(i=0,2\), or \(v_{j}^{\pm }\vert _{x_1=0}\,\varphi \), with \(j=1,\dots ,6\), up to some coefficients. To make uniform notation, here we have set \(\partial _0\equiv \partial _t\) and \({{\textbf{V}}}^\pm :=(v_1^\pm ,v^\pm _2,v^\pm _3,v^\pm _4,v^\pm _5,v^\pm _6)\).
As already shown in Section 5, the major advantage to settle the functions \({{\hat{\lambda }}}^\pm =\lambda (\hat{{\textbf{U}}}^\pm )\) as prescribed in Lemma 5.1 is making the leading term in the boundary quadratic form \(({\mathcal {B}}_1{{\textbf{V}}}\cdot {{\textbf{V}}})\vert _{x_1=0}\) to be identically zero. Under this choice, the latter reduces indeed to
We now focus on the estimate of the boundary integral of the different quadratic terms in (A.14). Because the explicit form of the coefficients involved in the different quadratic terms appearing in (A.14) is useless, hereafter we adopt the custom to denote as \({\hat{c}}={\hat{c}}(t,x_2)\) a generic function on \(\Gamma _T\) represented by some nonlinear smooth function of \(\hat{{\textbf{U}}}^\pm \vert _{x_1=0}\) and \(\nabla _{t,x_2}{{\hat{\varphi }}}\) only, that may be possibly different from a line to another within the same formula. From (A.14)
follows at once.
Hence Cauchy–Schwarz and Young’s inequalities together with Leibniz’s rule and integration by parts yields
Then we sum up the preceding estimates to get
Because functions \({{\hat{\lambda }}}^\pm \) chosen in Lemma 5.1 make \({\mathcal {B}}_0\) to be positive definite, we also have
with some constant \(c_0>0\) (depending on the number k in (4.2) and (4.4)).
Combining the latter with (A.11), (A.12) and (A.15) then leads to
Notice that in the right-hand side of (A.17) the \(L^2\)-norm of the trace of \(\dot{q}^+\) on the boundary \(\Gamma _t\) needs for a control of the normal derivative of \(\dot{q}^+\) in the interior of the domain \(\Omega _t\): indeed, we apply to \(\dot{q}^+\) the following trace type inequality
which holds true for an arbitrary sufficiently smooth scalar/vector-valued function \(f=f(t,\textbf{x})\) over \(\Omega _t\). The above estimate (A.18) follows by passing from a boundary integral on \({\mathbb {R}}\) to a spatial volume one on \({\mathbb {R}}^2_+\), at fixed t, as
from which (A.18) follows at once from integrating over \((-\infty ,t)\).
This clearly shows that inequality (A.17) cannot provide a closed \(L^2\)-estimate of the vector unknown \({{\textbf{V}}}\), since a control of the normal derivative of \(\dot{q}^+\) on \(\Omega _t\) is needed in the right-hand side. Fortunately, the component \(\dot{q}^+\) of \({{\textbf{V}}}\) belongs to the noncharacteristic components \(\textbf{V}^\pm _n=(\dot{q}^\pm ,\dot{u}_n^\pm , \dot{H}^\pm _n)\), whose normal derivative can be expressed directly from linear system (5.3) as a function of tangential derivatives of \(\textbf{V}\) only and the source term \({\mathcal {F}}\). Thus estimating the \(L^2-\)norm of \(\partial _1{{\textbf{V}}}^\pm _n\) reduces to estimate the \(L^2-\)norm of tangential derivatives of \(\textbf{V}\) and the \(L^2-\)norm of \({\mathcal {F}}\), as it will be detailed in the next section.
Applying (A.18) to \(f=\dot{q}^+\), from (A.17)
follows at once; see (A.6).
1.2 Estimate of \(I_{1,n}(t)\)
In this section we manage to find an “explicit" expression of the normal derivative of the noncharacteristic component \({{\textbf{V}}}^\pm _n\) of the unknowns directly from linear system (5.3). The key step is taking advantage of the form of the normal derivative coefficient \({\mathcal {A}}_1\) in (5.5) and noticing that from \({\mathcal {A}}_{(0)}\vert _{x_1=0}=0\) the identity
easily follows, where the matrix coefficient \({\mathcal {H}}_{(0)}={\mathcal {H}}_{(0)}(t,\textbf{x}):=\displaystyle \frac{{\mathcal {A}}_{(0)}(t,\textbf{x})}{\sigma (x_1)}\in L^\infty (\Omega _T)\) provided that \({\mathcal {A}}_{(0)}, \partial _1{\mathcal {A}}_{(0)}\in L^\infty (\Omega _T)\) and obeys the estimate
see [24, Lemma B.9] for details.
After (A.21), from (5.3) we derive
where the matrix \({\mathcal {A}}\) involved in the left-hand side above only applies to components \({\dot{q}}^\pm \), \({\dot{u}}^\pm _n\) of the noncharacteristic part \({{\textbf{V}}}_n\) of \({{\textbf{V}}}\), in view of (5.5); indeed an explicit calculation gives
By gathering (A.22), (A.23) we derive the announced explicit form of normal derivatives of the noncharacteristic components \((\dot{q}^\pm , \dot{u}_n^\pm )\) of \({{\textbf{V}}}^\pm \) as a function of space time tangential derivatives of \({{\textbf{V}}}^\pm \) and \({\mathcal {F}}^\pm \) alone, namely
where the subindices 1, 2 appearing above are referred to the first and the second components of the vectors.
As regards to the normal derivative of the noncharacteristic components \(\dot{H}^\pm _n\), they can be still derived from the first condition in (A.3) as a known function of tangential derivatives of \({{\textbf{V}}}^\pm \)
The estimate of \(I_{1,n}(t)\) then follows at once from (A.24) and (A.25); we get that
After estimate (A.26), it appears that the \(L^2-\)estimate of the normal derivative of the noncharacteristic part \({{\textbf{V}}}_n^\pm \) of the solution is reducted to control the \(L^2-\)norm of the tangential space time derivatives of \({{\textbf{V}}}\), that is \(I_\sigma (t)\), \(I_2(t)\) and \(I_0(t)\), which naturally leads to establish an \(H^1_*-\)estimate for \({{\textbf{V}}}\). The subsequent sections will be devoted to obtain the \(H^1_*-\)estimate.
1.3 Estimate of \(I_\sigma (t)\)
We set for shortness \({{\textbf{V}}}_\sigma :=\sigma \partial _1{{\textbf{V}}}\). Applying the conormal derivative \(\sigma \partial _1\) to both sides of system (5.4) we get a similar linear system satisfied by \({{\textbf{V}}}_\sigma \). We compute
From Leibniz’s rule,
plugging the latter into (A.27) and rewriting \(\sigma \partial _1{\mathcal {B}}_1\partial _1{{\textbf{V}}}=\partial _1{\mathcal {B}}_1{{\textbf{V}}}_\sigma \) gives
where
Performing on system (A.28) the same standard energy arguments as done for system (5.4) in Section A2.1, leads to the following energy identity for \({{\textbf{V}}}_\sigma \):
However, because \(\sigma \vert _{x_1=0}=0\), the quadratic form \(({\mathcal {B}}_1{{\textbf{V}}}_\sigma \cdot {{\textbf{V}}}_\sigma )\) under the boundary integral in the left-hand side above vanishes and the energy identity reduces to
The second integral in the right-hand side of the identity above is trivially estimated as in (A.12)
Now we focus on the estimate of the first integral
in the right-hand side of (A.30). Substituting the explicit form (A.29) of \({\tilde{F}}_\sigma \), using, similarly to \(A_1\) (see (5.5)), that
while \({\mathcal {B}}\) only “applies" to the noncharacteristic components \(\textbf{V}^\pm _n\) of \({{\textbf{V}}}^\pm \), and denoting \({\mathcal {K}}^{(0)}_1=\frac{{\mathcal {B}}^{(0)}_1}{\sigma },\) we have from Cauchy–Schwarz and Young’s inequalities
Finally, estimating from below the space integral in the left-hand side of (A.30) as in (A.16) (with \({{\textbf{V}}}_\sigma \) instead of \({{\textbf{V}}}\)) we end up with
1.4 Estimate of \(I_2(t)\)
We set for shortness \({{\textbf{V}}}_{x_2}:=\partial _2{{\textbf{V}}}\). Applying \(\partial _2\) to both sides of system (5.4) we get a similar linear system satisfied by \({{\textbf{V}}}_{x_2}\), that is,
where
As usual, from the above linear system we derive, by scalar multiplication by \({{\textbf{V}}}_{x_2}\) and integration by parts in \(\Omega _t\), the energy identity
The second integral in the right-hand side of the above identity is estimated as usual as
whereas to estimate the first integral in the right-hand side we still use the decomposition of \({\mathcal {B}}_1\) in (A.32) and repeat the same arguments used in the estimate of (A.31) and use (A.13), to get
Now we need to get an estimate of the quadratic form \(({\mathcal {B}}_1{{\textbf{V}}}_{x_2}\cdot {{\textbf{V}}}_{x_2})\) under the second boundary integral in the left-hand side of (A.35). The explicit expression of this quadratic form is in principle the same as the one for \({{\textbf{V}}}\) in (5.7), that is,
with \({{\hat{\lambda }}}:= \lambda (\hat{{\textbf{U}}})\).
As done to treat the quadratic form (5.7) for \({{\textbf{V}}}\), now we make use of the boundary conditions in (A.1) and the boundary constraint in (A.3), differentiated with respect to \(x_2\), to rewrite (A.38) as the sum of the same leading part as in (5.8), vanishing as a consequence of the choice of \({{\hat{\lambda }}}^\pm \), and lower order terms. We compute
where
As already announced the leading quadratic term \(2[{\hat{u}}_2-{{\hat{\lambda }}}{\hat{H}}_2]{\dot{q}}^+_{x_2}\partial _{2}\varphi \) in (A.39) vanishes because of the chosen \({{\hat{\lambda }}}^\pm \). We now focus on the estimate of the boundary integral of the different lower order quadratic terms in (A.40). Here below we denote again by \({\hat{c}}={\hat{c}}(t,x_2)\) the different coefficients of those boundary lower order terms, which are all smooth functions of \(\hat{{\textbf{U}}}^\pm \vert _{x_1=0}\) and \(\nabla _{t,x_2}{{\hat{\varphi }}}\) and their derivatives and whose explicit form is useless.
From (A.40), we get
To estimate the boundary integrals above, we follow similar arguments to those of [38].
The first step is to write \(\partial _2\varphi \) as a linear combination of \(\dot{H}^\pm _{N}\vert _{x_1=0}\) and \(\varphi \); this can be done by making use of boundary constraints (A.3) and exploiting that \({{\hat{H}}}_2^\pm \) are never simultaneously zero on the boundary as a consequence of the stability condition (4.4), see Remark 4.3. From the boundary conditions (A.3) we have
Then multiplying the first one by \({\hat{H}}^{+}_2\vert _{x_1=0}\) and the second one by \({\hat{H}}^{-}_2\vert _{x_1=0}\), then adding the results we get
where \({{\hat{d}}}_i={{\hat{d}}}_i(t,x_2)\) are suitable functions depending only on the boundary values of \({{\hat{H}}}^\pm \), \(\partial _1{{\hat{H}}}^\pm \) and second order derivatives of \({{\hat{\varphi }}}\), whose esplicit form could be easily deduced from above.
Let us start to estimate the first term in the right-hand side of (A.41). Inserting the expression of \(\partial _2\varphi \) provided by (A.42), we find
Let us estimate \({\mathcal {I}}_1\). Here the trick of passing from a boundary integral over \({\mathbb {R}}\) to a volume integral over \({\mathbb {R}}^2_+\) is used as already done to get the trace inequality (A.18). In the following we will adopt the notation \(\hat{{\textbf{c}}}=\hat{{\textbf{c}}}(t,\textbf{x})\) to mean a suitable lifting from \(\Gamma _t\) to \(\Omega _t\) of a boundary coefficient \({{\hat{c}}}={{\hat{c}}}(t,x_2)\). Then we have
\({\mathcal {I}}_{1,1}\) and \({\mathcal {I}}_{1,3}\) can be easily estimated by Cauchy-Schwarz and Young’s inequalities by
Recall that \({{\textbf{V}}}_n^\pm =(\dot{q}^\pm , \dot{u}^\pm _n, \dot{H}^\pm _n)\) are the noncharacteristic components of the solution \({{\textbf{V}}}^\pm \), see also (A.6).
As regards to \({\mathcal {I}}_{1,2}\), differently from above, we cannot immediately end up by Cauchy-Schwarz and Young’s inequality, because this should require a control of the \(L^2-\)norm of the second order derivative of \(\dot{q}^+\), preventing to close the \(H^1_*-\)estimate. Instead, here integration by parts with respect to the tangential space variable \(x_2\) and Leibiniz’s rule are used to further rewrite \({\mathcal {I}}_{1,2}\) as
then we observe that the last two integral above are similar to \({\mathcal {I}}_{1,1}\) and \({\mathcal {I}}_{1,3}\), and therefore can be estimated in the same way by
Adding (A.43) and (A.44) gives the estimate of \({\mathcal {I}}_1\)
It is clear that \({\mathcal {I}}_2:=\displaystyle \int _{0}^t\!\!\!\int _{{\mathbb {R}}}\!\!{{\hat{c}}}\,\partial _2{\dot{q}}^+{\dot{H}}^-_N dx_2ds\) can estimated by repeating exactly the same arguments applied to \({\mathcal {I}}_1\).
Concerning \({\mathcal {I}}_3=\displaystyle \int _{0}^t\!\!\!\int _{{\mathbb {R}}}\!\!{{\hat{c}}}\,\partial _2{\dot{q}}^+\varphi \,dx_2ds\), we are reduced to applying the same arguments as above by first integrating by parts and then using Leibniz’s rule and replacing, once again, \(\partial _2\varphi \) by the expression in the right-hand side of (A.42):
Since all the boundary traces under the integral are of noncharacteristic components of \({{\textbf{V}}}\), we end up by Cauchy-Schwarz, Young’s inequalities and trace type inequality (A.18) to get
To complete the estimate of the remaining boundary integrals involved in the right-hand side of (A.41), it is then sufficient to notice that the second boundary integral is exactly the same as \({\mathcal {I}}_3\), while the other boundary integrals are the same as the first and second ones, where \(\partial _2\dot{q}^+\vert _{x_1=0}\) is replaced by \(\partial _2\dot{u}^-_N\vert _{x_1=0}\) or by \(\partial _2\dot{H}^-_N\vert _{x_1=0}\) (but \(\dot{u}^-_n\) and \(\dot{H}^-_n\) are still noncharacteristic components of the vector solution \({{\textbf{V}}}\), so that they are treated along the same arguments as to \(\dot{q}^+\)). Therefore we end up with
Using (A.36), (A.37) and (A.46) together with the counterpart of (A.16) with \({{\textbf{V}}}_{x_2}\) instead of \({{\textbf{V}}}\), from (A.35) we obtain
1.5 Estimate of \(I_0(t)\)
We set for shortness \({{\textbf{V}}}_{t}:=\partial _t{{\textbf{V}}}\). Applying \(\partial _t\) to both sides of system (5.4) we get a similar linear system satisfied by \({{\textbf{V}}}_{t}\), that is,
where
As usual, from the above linear system we derive, by scalar multiplication by \({{\textbf{V}}}_{t}\) and integration by parts in \(\Omega _t\), the energy identity
The second integral in the right-hand side of the above identity is estimated as usual as
whereas to estimate the first integral in the right-hand side we still use the decomposition of \({\mathcal {B}}_1\) in (A.32) and repeat the same arguments used in the estimates (A.31), (A.37) and use (A.13), to get
Now we need to get an estimate of the quadratic form \(({\mathcal {B}}_1{{\textbf{V}}}_{t}\cdot {{\textbf{V}}}_{t})\) under the second boundary integral in the left-hand side of (A.49), whose explicit expression is
with \({{\hat{\lambda }}}:= \lambda (\hat{{\textbf{U}}})\).
As in the case of the quadratic form (A.38), we make use of the boundary conditions in (A.1), differentiated with respect to t, to rewrite (A.51) as the sum of the same leading part as in (A.39), vanishing as a consequence of the choice of \({{\hat{\lambda }}}^\pm \), and lower order terms. We compute
where
We solve the first boundary condition in (A.1) (we choose the \(+\) side) with respect to \(\partial _t\varphi \) and replace \(\partial _2\varphi \) by (A.42) to get
with suitable coefficients \({{\hat{D}}}_i={{\hat{D}}}_i(t,x_2)\), \(i=1,2,3\), smoothly depending on the boundary traces of \({{\hat{u}}}^+\), \({{\hat{H}}}^\pm \), \(\partial _1{{\hat{H}}}^\pm \), \(\partial _1{{\hat{u}}}^+\) and second order derivatives of \({{\hat{\varphi }}}\), whose explicit form is useless for the subsequent calculations.
Now we insert (A.54) and (A.42) in the expression (A.53) to rewrite the latter as
From the resulting expression above, it appears that the lower order terms above are reduced to a sum of two types of quadratic terms, namely,
where \(\alpha =\alpha (t,\textbf{x})\) and \(\beta =\beta (t,\textbf{x})\) are used to mean any component of the noncharacteristic part \({{\textbf{V}}}^\pm _n=(\dot{q}^\pm ,\dot{u}^\pm _n, \dot{H}^\pm _n)\) of the solution, while \({{\hat{c}}}={{\hat{c}}}(t,x_2)\) denotes, as usual, suitable functions on \(\Gamma _t\), smoothly depending on space-time derivatives of \(\hat{{\textbf{U}}}^\pm \) and \(\nabla _{t,x_2}{{\hat{\varphi }}}\) up to second order.
In view of the preceding manipulations, to get an estimate of the boundary integral of the quadratic form (A.51) we only need to estimate the following types of boundary integrals:
As it was done in Section A2.4, in \({\mathcal {J}}_1\) we pass to a volume integral over \({\mathbb {R}}^2_+\) and use Leibniz’s rule to get
By Cauchy–Schwarz and Young’s inequalities, \({\mathcal {J}}_{1,1}\) and \({\mathcal {J}}_{1,3}\) are estimated by
The middle integral \({\mathcal {J}}_{1,2}\) is the most involved one, because the second order derivative \(\partial _1\partial _t\alpha \) prevents from directly estimating \({\mathcal {J}}_{1,2}\) similarly to (A.56).
From Leibniz’s rule with respect to time (notice that \(\alpha |_{t=0}\equiv 0\) and \(\beta |_{t=0}\equiv 0\)), we rewrite \({\mathcal {J}}_{1,2}\) as
The last two integrals above are estimated exactly by the same right-hand side of (A.56).
Concerning, instead, the first spatial integral
in view of estimates (A.20), (A.26) (recall that \(\alpha \) is a noncharacteristic component of \({{\textbf{V}}}\)), the use of Cauchy–Schwarz and weighted Young’s inequalities gives
where \(\varepsilon >0\) will be chosen to be small enough.
Adding (A.58) and the analogous of (A.56) for the second and third integral in the right-hand side of (A.57) finally yields
and adding the latter and (A.56) we get
The boundary integral \({\mathcal {J}}_2\) is treated along the same lines as \({\mathcal {J}}_{1,2}\). After Leibniz’s rule with respect to time, we first rewrite
The middle integral \({\mathcal {J}}_{2,2}\) is estimated at once by Cauchy–Schwarz, Young’s inqualities and the trace type inequality (A.18)
Concerning \({\mathcal {J}}_{2,3}\), we substitute \(\partial _t\varphi \) with the right-hand side of (A.54) to rewrite it as
where the second type of boundary integral above is exactly the same as \({\mathcal {J}}_{2,2}\) and the first one is trivially estimated by using once again the trace type inequality, hence we get the same estimate (A.61)
Concerning, instead, the first spatial integral \({\mathcal {J}}_{2,1}\), the use of Cauchy–Schwarz and weighted Young’s inequalities and the trace type inequality (A.19) gives
Gathering (A.63), (A.61) and (A.62) we get
Summing the estimate of \({\mathcal {J}}_1\) and \({\mathcal {J}}_2\) above, we end up with the following estimate of the boundary integral of the quadratic form (A.51)
Using (A.50), (A.50) and (A.65) together with the counterpart of (A.16) with \({{\textbf{V}}}_{t}\) instead of \({{\textbf{V}}}\), from (A.49) we obtain
1.6 Estimate of the front \(\varphi \)
To estimate the \(L^2-\)norm of the front we multiply by \(\varphi \) the first boundary condition in (A.1) (we choose the \(+\) side) and integrate by parts over \(\Gamma _t\) to get
from which, by Cauchy–Schwarz and Young’s inequalities, and the trace type inequality (A.18)
Using the expressions of \(\partial _2\varphi \) and \(\partial _t\varphi \) in (A.42) and (A.54) we can recover an estimate of the \(L^2-\)norms of those derivatives from the estimate (A.68) and (A.18). Precisely, integrating over \({\mathbb {R}}\) (A.42) and (A.54) and using (A.18) we get
see (A.4), (A.6), and analogously
1.7 \(H^1_*-\)estimate
We add estimates (A.20), (A.33), (A.47), (A.66) and (A.68) to get
Then using (A.68) to estimate \(\Vert \varphi (t)\Vert _{L^2({\mathbb {R}})}^2\) in the right-hand side above, the previous inequality reduces to
Then we use (A.26) to get a control of the normal derivatives of \({{\textbf{V}}}^\pm _n\) involved in the term \(I_{1,n}\) in the right-hand side above to get
In order to estimate the spatial \(L^2-\)norm of the source \({{\textbf{F}}}(t)\) in the right-hand side above we use the following argument
so that
hence taking \(\varepsilon >0\) small enough in order to absorb \(C_1\varepsilon I_{1,*}(t)\) in the left-hand side above, we end up with
Applying Grönwall’s lemma, we obtain
and integrating on t over (0, T),
where C is a positive constant depending only on T and K from (4.6).
From the use of estimates (A.69), (A.70) we can manage to include the \(L^2(\Gamma _T)-\)norms of \(\nabla _{t,x_2}\varphi \) in the left-hand side of (A.71), so as to get a control of the \(H^1(\Gamma _T)-\)norm of the front \(\varphi \).
From integration of (A.69), (A.70) with respect to t over (0, T) and the use of (A.26) we get
where, in the last inequality, it is used that
Using (A.71) to estimate the right-hand side above, we end up with
Then adding the latter to (A.71) we get
which is just the estimate (5.33), in view of (5.1) (recalling that to shortcut notation we have set \(\dot{{\textbf{U}}}=\dot{{\textbf{U}}}^\natural \) and \(\dot{{\textbf{U}}}=J{{\textbf{V}}}\), see (5.1)).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Morando, A., Secchi, P., Trebeschi, P. et al. Nonlinear Stability and Existence of Two-Dimensional Compressible Current-Vortex Sheets. Arch Rational Mech Anal 247, 50 (2023). https://doi.org/10.1007/s00205-023-01865-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00205-023-01865-w