Abstract
We consider a family of vectorial models for cohesive fracture, which may incorporate \(\textrm{SO}(n)\)-invariance. The deformation belongs to the space of generalized functions of bounded variation and the energy contains an (elastic) volume energy, an opening-dependent jump energy concentrated on the fractured surface, and a Cantor part representing diffuse damage. We show that this type of functional can be naturally obtained as \(\Gamma \)-limit of an appropriate phase-field model. The energy densities entering the limiting functional can be expressed, in a partially implicit way, in terms of those appearing in the phase-field approximation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In variational models of nonlinear elasticity a hyper-elastic body with reference configuration \(\Omega \subset \mathbb {R}^n\) (\(n=2,3\)) undergoes a deformation \(u:\Omega \rightarrow \mathbb {R}^m\), whose stored energy reads as
External loads can be included, adding linear perturbations to this energy, and Dirichlet boundary conditions, restricting the set of admissible deformations u. The energy density \(\Psi :\mathbb {R}^{m\times n}\rightarrow [0,\infty )\), acting on the deformation gradient \(\nabla u\), is typically assumed to be minimized by matrices in the set of proper rotations \(\textrm{SO}(n)\) (with \(m=n\)) and to have p-growth at infinity, \(p>1\). Correspondingly, the natural space for the deformation u is a (subset of) the Sobolev space \(W^{1,p}(\Omega ;\mathbb {R}^m)\). There is an extensive literature on the theory of existence of minimizers of this type of functionals, and in particular the key property of weak lower semicontinuity of (1.1) is closely related to the quasiconvexity of the energy density \(\Psi \).
Fracture phenomena, both brittle and cohesive, require a richer modelling framework. Physically, cohesive fracture is often understood as a gradual separation phenomenon: load–displacement curves usually exhibit an initial increase of the load up to a critical value, and a subsequent decrease to zero, which is the value indicating the complete separation [12, 21, 49, 51]. See [47, 48] for discussions on different load–displacement behaviours. Evolutionary models (prescribing the crack path) have been studied in [2, 8, 21, 30, 38, 39, 46, 66, 68, 69, 73], see also references therein. See [31, 42] for further results on the topic.
Variational models of fracture are typically formulated using the space (G)BV of (generalised) functions of bounded variation [21, 58] and energy functionals of the form
The deformation \(u\in (G)BV(\Omega ;\mathbb {R}^m)\) may exhibit discontinuities along a \((n-1)\)-dimensional set \(J_u\). We denote by [u] and \(\nu _u\) the opening of the crack and the normal vector to the crack set \(J_u\), respectively, while \(D^cu\) represents the Cantor derivative of u (see [7] for the definition and the relevant properties of functions of bounded variation). Working within deformation theory, the functional (1.2) contains both energetic and dissipative terms, which are physically distinct but need not be separated for this variational modeling.
The densities W, l, and g entering (1.2) need to satisfy suitable growth conditions. The lower semicontinuity of the functional imposes several restrictions, such as, for example, that l is positively one-homogeneous and quasiconvex, W quasiconvex, and g subadditive. Furthermore, l needs to match, after appropriate scaling, both the behavior of W at infinity and the behavior of g near zero. These properties will be discussed in more detail below (see, for example, Proposition 3.11).
The qualitative properties of W, l and g are selected according to the specific model of interest. For instance, the brittle regime is modelled by a constant surface density g and a superlinear bulk energy density W. These choices in turn imply that \(l(\xi )=\infty \) for \(\xi \ne 0\), so that \(D^cu\) necessarily vanishes. The functional setting of the problem is then provided by the space of (generalised) special functions with bounded variation \((G)SBV(\Omega )\). In contrast, in cohesive models g is usually assumed to be approximately linear for small amplitudes and bounded.
The direct numerical simulation of functionals of the type (1.2) is highly problematic, due to the difficulty of finding good discretizations for (G)BV functions and of differentiating the functional with respect to the coefficients entering the finite-dimensional approximation. Therefore a number of regularizations have been proposed, of which one of the most successful is given by phase-field functionals. These are energies depending on a pair of variables (u, v), having a Sobolev regularity, where u represents a regularization of a discontinuous displacement, while \(v\in [0,1]\) can be interpreted as a damage parameter, indicating the amount of damage at each point of the body (where \(v=1\) corresponds to the undamaged material and \(v=0\) to the completely damaged material). The basic structure of a phase-field functional is
where \(\varepsilon >0\) is a small parameter, \(f_\varepsilon \) is a damage coefficient acting on the damage variable v, increasing from 0 to 1, and \(\Psi \) is an elastic energy density, as in (1.1). The first term in (1.3) represents the stored elastic energy, the other two terms represent the stored energy and dissipation due to the damage.
Despite the phase-field functional in (1.3) is introduced here as a regularization of the sharp-interface functional in (1.2), one may alternatively consider the functional in (1.3) as a physical model of its own, with v an internal variable representing local damage, and view the \(\Gamma \)-convergence result as a derivation of the sharp-interface functional in (1.2). This is frequently done in an evolutionary setting, where irreversibility of damage may be modeled by imposing monotonicity in time of v. Our mathematical result proves that the two models are, under suitable assumptions, closely related to each other, and so there is no requirement to choose one of these interpretations, we stick for simplicity to the first one. We stress that the relation between the three densities entering (1.2) and the functions entering (1.3) is implicit (see the discussion in what follows), and the problem of determining good choices of \(f_\varepsilon \) and \(\Psi \) for specific materials is not easy. Some progress has recently been obtained for related formulations [52] as discussed below.
Finding a variational approximation of the fracture model (1.2) by phase-field models means to construct \(f_\varepsilon \) and \(\Psi \) such that the functionals (1.3) converge, in the sense of \(\Gamma \)-convergence, to (1.2) as \(\varepsilon \rightarrow 0\). This is not an easy task in general. The brittle case (g constant) in an antiplane shear, linear, framework (\(m=1\), \(\Psi \) quadratic) was the first outcome of this type [10, 11]. It has been extended in several directions for different aims, giving rise to a very vast literature of both theoretical results [6, 9, 18, 35,36,37, 43, 53, 61,62,63, 71] and numerical simulations [13, 14, 21, 25,26,27, 29] (for other regularizations, see also [7, 17, 22, 28, 60] and references therein). In particular, the extension of the results in [11] to the vector-valued (nonlinear) brittle case has been provided in [59]. The variational approximation of cohesive models is considerably more involved. The antiplane shear linear case was obtained through a double \(\Gamma \)-limit of energies with 1-growth in [1], then generalized to the vector-valued case in [5]. A drawback of these results is the 1-growth with respect to \(\nabla u\), which makes the approximants mechanically less meaningful and numerically less helpful.
To overcome these problems, in [33] we proposed a different approximation of (1.2) in the antiplane shear case, with quadratic models of the form (1.3), based on a damage coefficient \(f_\varepsilon \) of the type

and obtained \(\Gamma \)-convergence to a model of the type (1.2) in the scalar (\(m=1\)) case. We remark that \(f_\varepsilon \) is equal to 1 when \(v\sim 1\) (elastic response) and to 0 when \(v\sim 0\) (brittle fracture response). Moreover, the first addend in the energy in (1.3) competes against the second term if v is less than but close to 1, and with all the terms of (1.3) otherwise (pre-fracture response). This phase-field approximation of this scalar cohesive fracture was investigated numerically in [54]. A 1D cohesive quasistatic evolution (not prescribing the crack path) is presented in [16] and related to the phase-field models of [33]. A different approximation of (1.2), still in the scalar-valued framework, is obtained in [44] using elasto-plastic models.
The class of phase-field functionals introduced in [33], summarized in (1.3) and (1.4), has recently received strong attention in the mechanics literature, specifically from a computational perspective. Many variants have been proposed, including for example extension to vectorial linear elasticity, finite elasticity, directional dependence, irreversibility as well as the application to specific materials, and many numerical simulations have been carried out, but up to now a rigorous mathematical analysis of convergence has remained restricted to the scalar case [33]. A first numerical study in a simplified setting appeared in [54], it uses a convex variant of (1.4) that renders the model more amenable to numerical simulation, (for a mathematical analysis of this variant, we refer to [65, Sect. 4.1 and App. B]). In addition, Wu [77] proposed to use a functional of the type (1.3) with the damage function \(f_\varepsilon \) in (1.4) replaced by a regular function of the form
where \(p>0\) and P is a low-degree polynomial with \(P(0)=1\) whose coefficients can be fitted in order to reproduce specific material properties, and possibly the quadratic term \((1-v)^2/4\varepsilon \) in (1.3) is replaced by a linear one (to compare equations one should note that in [77] \(d:=1-v\) is used as phase field). The choice in (1.5), besides regularizing the minimum appearing in (1.4), permits to obtain simple solutions for one-dimensional crack profiles. Correspondingly the fracture energy, at least in one spatial dimension, has only a very minor dependence on the regularization parameter \(\varepsilon \). This proposal, which was further developed in [75], has rapidly become very influential in the mechanics literature. We refer to the review [76] for a discussion of mechanical applications.
Recently Feng et al. [52] have shown how the expression in (1.5) can be modified in order to reproduce (almost) arbitrary cohesive laws, and gave an analytical expression for the required form of \(f_\varepsilon \). Further, their approach permits to distinguish between mode-I, mode-II and mixed-mode fracture. In [56], the phase field approach is studied from an energetic perspective, obtaining a variationally consistent formulation which can account for the crack direction in mixed-mode cohesive fracture. A comparison of the phase-field model from [77] with simpler standard models of the Ambrosio-Tortorelli type is discussed in [32]. An extension of the model in (1.3)–(1.4) to finite elasticity, including a separation between tensile and compressive stresses that treats the microcrack-closure-reopening effect, was presented in [65].
In this paper we study the approximation of vector-valued cohesive models of the type (1.2) via phase-field models of the type (1.3) with the damage coefficient (1.4), as proposed in [33]. In particular, we extend the results of [33] to a geometrically nonlinear framework (even restricting to a scalar-valued setting we extend [33] to the case of non-isotropic potentials). We refer to (2.2)–(2.5) for the specific hypotheses on \(\Psi \). The main result is given in Theorem 2.1, the precise assumptions are discussed in Sect. 2.1. In addition, we stress that this work, on the one side represents an intermediate step to the analysis of the analogous model in the linearized elasticity setting, where symmetrized gradients replace full gradients, which is often used in numericals simulations of cohesive fracture; and on the other side, it is a necessary preliminary analysis to the general study of the convergence of critical points, in the spirit of the one-dimensional result [23].
In order to illustrate our result, let us consider the simplest model for the energy density \(\Psi \) in finite kinematics and \(m=n\),
With this choice, our main result Theorem 2.1 states that the phase-field energies (1.3) \(\Gamma \)-converge in the \(L^1\)-topology as \(\varepsilon \rightarrow 0\) to the energy (1.2), with
and
for every \(\xi \in \mathbb {R}^{m\times n}\), \(z\in \mathbb {R}^m\), \(\nu \in S^{n-1}\), where \(g_\textrm{scal}\) is the surface energy density appearing in the scalar model (cf. formula (4.4) for the definition of \(g_\textrm{scal}\), item (iii) in Proposition 3.12 with \(W=h^\textrm{qc}\) and \(l=h^{\textrm{qc},\infty }\) to justify the second equality, and Corollary 3.5 for the third equality). As remarked above, g coincides with l asymptotically for infinitesimal amplitudes. Even in this simple case, the expression for W is somewhat implicit, as it involves a quasiconvex envelope, which in most cases can only be approximately computed numerically. We remark that even \(\Psi _2\) itself as defined in (1.6) is not quasiconvex, we refer to [74, Example 4.2] for an explicit formula for its quasiconvex envelope \(\Psi _2^{\textrm{qc}}\) in the two-dimensional case.
From the mathematical point of view, the main interest of the paper is precisely to provide a comprehensive analysis of such an energy growth degeneracy (quadratic-to-linear) in a vector-valued setting. While it is in general easy to guess the order of the degeneracy by a compactness argument, it is usually very difficult to keep track of the exact contribution of each term of the energy and to understand their mutual interactions. In the vector-valued case, this consists in solving a system of nonlinear PDE’s. Not being able to solve directly such system, the guess of the limit densities and the proof of their relevant properties is a much more delicate issue, which we discuss below in details. Indeed, one of the main difficulties in proving Theorem 2.1 is to identify the correct limit densities W, g, and l, given the density \(\Psi \) and the damage coefficient \(f_\varepsilon \) of the phase-field (1.3). We first show that one cannot expect that the cohesive energies that arise in the limit of our approximation exhaust all possible energies of the form (1.2), with densities W, g, and l satisfying the growth conditions and matching properties specified above. Indeed, we prove that, even in the simplest case \(\Psi (\xi ):=|\xi |^2\), W is not convex (see Lemma 2.5 below). Thus, at least in this case, the limit energy is not given by the relaxation of a functional defined on \(SBV(\Omega )\) (cf. [15, Remark 2.2]). Convex functions may be obtained as densities of the bulk term of the energy under more specific choices of the damage variable (see for example [24], where the damage variable is a characteristic function).
The effective surface energy density g of the \(\Gamma \)-limit of the family \((\mathcal {F}_\varepsilon )\) is defined in an abstract fashion by an asymptotic minimization formula as the \(\Gamma \)-limit of a simpler family of functionals computed on functions jumping on a hyperplane (cf. (2.12)). Alternative characterizations of g useful along the proofs are provided both in Propositions 3.1 and 3.2, in which we show that the test sequences in the very definition of g can be assumed to be periodic in \((n-1)\) mutually orthogonal directions and with \(L^2\) integrability, and in Proposition 3.3, where g is represented in terms of an asymptotic homogenization formula. Finally, the energy density l of the Cantor part turns out to coincide with the recession function \(W^\infty \) of W. Furthermore, an explicit characterization of l in terms of \(\Psi \) is given in Proposition 3.10.
The proof of the lower bound in BV is based on the blow-up technique. Roughly, to get the local estimate for the diffuse part given \((u_\varepsilon ,v_\varepsilon )\rightarrow (u,v)\) in \(L^1\), we analyze the asymptotic behaviour of the phase-field energies \(\mathcal {F}_\varepsilon \) restricted on the \(\delta \)-superlevel sets of \(v_\varepsilon \), \(\delta \in (0,1)\), and then let \(\delta \uparrow 1\). More precisely, in Lemma 4.4 we bound from below \(\mathcal {F}_\varepsilon (u_\varepsilon ,v_\varepsilon )\) in (1.3) pointwise with a functional defined on (G)SBV, that is independent of \(v_\varepsilon \) and that is computed on a truncation of \(u_\varepsilon \) with the characteristic function of a suitable superlevel set of \(v_\varepsilon \) (depending on \(\delta \)). This is actually true up to an error related to the measure of the corresponding sublevel set of \(v_\varepsilon \), and up to prefactors depending on \(\delta \) which are converging to 1 as \(\delta \uparrow 1\) for the volume term and vanishing for the surface term. The lower semicontinuity in \(L^1\) of the diffuse part of such a functional then implies the lower bound. In addition, a slight variation of this argument shows directly that \((GBV(\Omega ))^m\) is the domain of the \(\Gamma \)-limit. For the relevant functional space we refer to [45] (see also the comments in Sect. 4.1).
Instead, to prove the local estimate for the surface part we show that under a surface scaling assumption we may replace \(v_\varepsilon \) by its truncation at the threshold \(\gamma _\varepsilon \), being \(\gamma _\varepsilon \) the smallest \(z\in [0,1]\) satisfying \(f_\varepsilon (z)=1\). The mentioned asymptotic minimization formula defining g then provides a natural lower bound. The liminf inequality in GBV is finally obtained by a further truncation argument.
The upper bound in BV is proven through an integral representation argument. In particular, a direct computation provides a rough linear estimate from above, in fact optimal for the diffuse part. This allows to apply the representation result for linear functionals given in [20]. The sharp estimate for the surface density is obtained using the aforementioned characterization of g involving periodic boundary conditions. The full upper bound in GBV follows by a truncation argument.
Finally, we recall that in the scalar case several different choices for \(f_\varepsilon \) are possible without changing the overall effect of the approximation (cf. [33, Section 4]). A negative power-law divergence at 1 however leads to a corresponding power-law behaviour of g close to 0 (cf. [33, Theorem 7.4]). We expect these findings to have a natural generalization to the current vectorial setting, this requires additional technical ingredients that will be the object of future work [34].
The paper is structured as follows. In Sect. 2.1 we present the model, introducing the main definitions and stating the \(\Gamma \)-convergence result in Theorem 2.1. In Sect. 2.2 we focus on a simplified model and we prove that in this case the limiting volume energy density W, obtained by quasiconvexification as in (1.7), is not convex (Lemma 2.5). In Sect. 3 several properties of the surface and Cantor densities are discussed. In particular, Propositions 3.1 and 3.2 deal with the change of boundary conditions within the minimum problem defining g. Proposition 3.3 provides an equivalent expression of g. Sect. 4 is devoted to the proof of the lower bound: Proposition 4.1 proves the surface estimate in BV. The lower bound in BV for the diffuse part is addressed in Proposition 4.2. Finally, in Theorem 4.9, the lower bound is extended to the full space GBV via a continuity argument (cf. Proposition 4.8). The proof of the upper bound is the object of Sect. 5, which concludes the proof of Theorem 2.1. Finally, Sect. 6 addresses the problems of compactness and convergence of minimizers.
2 Model
2.1 General Definitions
In the entire paper \(\Omega \subset \mathbb {R}^n\) is a bounded, open set with Lipschitz boundary, \(\mathcal {A}(\Omega )\) denotes the family of open subsets of \(\Omega \) and \(|\cdot |\) denotes the Euclidean norm, \(|{\xi }|^2:=\sum _{ij}{\xi }_{ij}^2=\textrm{Tr}\,\big ({\xi }^T{\xi }\big )\) for \({\xi }\in \mathbb {R}^{m\times n}\).
For all \(\varepsilon >0\) we consider the functional \(\mathcal {F}_\varepsilon :L^1(\Omega ;\mathbb {R}^{m+1})\times \mathcal {A}(\Omega )\rightarrow [0,\infty ]\) given by
if \((u,v)\in W^{1,2}(\Omega ;\mathbb {R}^m)\times W^{1,2}(\Omega ;[0,1])\) and \(\infty \) otherwise, where for every \(s\in [0,1)\) we set

and \(\ell >0\) is a parameter representing the critical yield stress. We write briefly \(\mathcal {F}_\varepsilon (u,v):=\mathcal {F}_\varepsilon (u,v;\Omega )\), and analogously for all the functionals that shall be introduced in what follows.
We assume that \(\Psi :\mathbb {R}^{m\times n}\rightarrow [0,\infty )\) is continuous and such that
We assume the ensuing limit to exist, that is,
and that it is uniform on the set of \(\xi \) with \(|\xi |=1\). This means that for every \(\delta >0\) there is \(t_\delta >0\) such that \(|\Psi (t\xi )/t^2-{\Psi _\infty }(\xi )|\le \delta \) for all \(t\ge t_\delta \) and all \(\xi \) with \(|\xi |=1\), which is the same as
By scaling, \({\Psi _\infty }(t\xi )=t^2{\Psi _\infty }(\xi )\) and in particular \({\Psi _\infty }(0)=0\). Uniform convergence also implies \({\Psi _\infty }\in C^0(\mathbb {R}^{m\times n})\).
We define \(h:\mathbb {R}^{m\times n}\rightarrow [0,\infty )\) by

and denote by \(h^\textrm{qc}\) its quasiconvex envelope,
From (2.3) we infer that for every \(\xi \in \mathbb {R}^{m\times n}\)
Let \(h^{\textrm{qc},\infty }\) be its recession function,
We remark that the definitions of \(h^{\textrm{qc},\infty }\) and \({\Psi _\infty }\) differ, to reflect the different growth of the two functions, quadratic for \(\Psi \) and linear for h. Recall that \(h^{\textrm{qc},\infty }\) is itself a quasiconvex function [57, Rem. 2.2 (ii)]. Therefore, it is locally Lipschitz continuous (cf. for instance [40, Theorem 5.3 (ii)]). Moreover, in Proposition 3.10 below we shall prove that

where the latter quantity is defined as in (2.7)–(2.9). We remark that, at variance with the convex case, one cannot in general replace the \(\limsup \) in (2.9) by a limit [67, Theorem 2].
For all open subsets \(A\subseteq \mathbb {R}^n\), \(u\in W^{1,2}(A;\mathbb {R}^m)\) and \(v\in W^{1,2}(A;[0,1])\) it is convenient to introduce the functional
The first term is interpreted to be zero whenever \(\nabla u=0\), even if \(v=1\). For any \(\nu \in S^{n-1}\) we fix a cube \(Q^\nu \) with side length 1, centered in the origin, and with one side parallel to \(\nu \). We write \(Q^\nu _r:=rQ^\nu \). We define \(g:\mathbb {R}^m\times S^{n-1}\rightarrow [0,\infty )\) by
Here \(u_j\in W^{1,2}(Q^\nu ;\mathbb {R}^m)\) and \(v_j\in W^{1,2}(Q^\nu ;[0,1])\); obviously one can restrict to sequences \(v_j\rightarrow 1\) in \(L^1(Q^\nu )\). We refer to Sect. 3 for the discussion of several properties of g.
We will prove the following result:
Theorem 2.1
Let \(\mathcal {F}_\varepsilon \) be the functional defined in (2.1). Then for all \((u,v)\in L^1(\Omega ;\mathbb {R}^{m+1})\) it holds
where
if \(u\in (GBV\cap L^1(\Omega ))^m\) and \(v=1\) \(\mathcal {L}^n\)-a.e., and \(\mathcal {F}_0(u,v):=\infty \) otherwise.
Remark 2.2
One can imagine several natural generalizations of Theorem 2.1. For example, one could allow \(\Psi \) to take negative values, replacing (2.3) by
Whereas in purely elastic models like (1.1) one can add a constant to the energy density without any change in the analysis, the presence of the prefactor \(f_\varepsilon ^2(v)\) renders this modification nontrivial, and influences several steps in the proof. Indeed, the construction in Step 1 of the proof of Theorem 5.2 shows that the definition of h in (2.6) needs to be replaced by

Alternatively, one could replace the quadratic growth of \(\Psi \) in (2.3) by p-growth, \(p>1\). The requirement that the effective energy scales linearly for large strains leads to corresponding adaptations in the other parts of the functional.
For simplicity we only address here the growth condition in (2.3).
Notation. For A open we denote by \(\mathcal {M}^+(A)\) the set of positive Radon measures on the set A, and by \(\mathcal {M}_b^+(A)\) the subset of bounded measures. For \(A\in \mathcal {A}(\Omega )\),
and correspondingly for the \(\Gamma \text{- }\limsup \). We drop the dependence on the reference set A if \(A=\Omega \). We refer to Sect. 4.1 (see also [5, Lemma 2.10] or [45, Theorem 2.7]) for the definition of the vector measure \(D^cu\), under the hypotheses that \(u\in (GBV(\Omega ))^m\).
2.2 Simplified Model
In this Section we consider the simplified case \(\Psi _\mathrm {{simp}}({\xi }):=|{\xi }|^2\), the corresponding unrelaxed energy density \(h_\mathrm {{simp}}:\mathbb {R}^{m\times n}\rightarrow [0,\infty )\),
its quasiconvex envelope \(h_\mathrm {{simp}}^\textrm{qc}\) as in (2.7), and its recession function \(h_\mathrm {{simp}}^{\textrm{qc},\infty }\) as in (2.9). These functions only depend on the space dimension and the single parameter \(\ell >0\), which could be eliminated by scaling.
In this case it is possible to obtain simple closed-form expressions for several of the quantities defined above. However, an explicit characterization of the quasiconvex envelope in (2.7) remains difficult. Indeed, we show in Lemma 2.5(iii) below that even in this simplified setting the result is not convex. Since it has linear growth, lower bounds with polyconvexity cannot be used, and an explicit determination of \(h^\textrm{qc}_\mathrm {{simp}}\) seems difficult. We believe this to be a strong indication that in most cases of interest the function \(h^\textrm{qc}\) can only be approximated numerically, and not computed explicitly. Lemma 2.5 and this observation are not used in the proof of Theorem 2.1.
Lemma 2.3
For \(n,m\ge 1\) let \(h_\mathrm {{simp}}:\mathbb {R}^{m\times n}\rightarrow [0,\infty )\) be defined as in (2.14). Then:
-
(i)
its convex envelope is
$$\begin{aligned} h_\mathrm {{simp}}^\textrm{conv}(\xi )={\left\{ \begin{array}{ll} |\xi |^2 , &{} \text { if } |\xi |\le \frac{\ell }{2},\\ \ell |\xi |-\frac{\ell ^2}{4},&{} \text { if } |\xi |> \frac{\ell }{2}; \end{array}\right. } \end{aligned}$$(2.15) -
(ii)
\(\ell |\xi |-\frac{\ell ^2}{4}\le h_\mathrm {{simp}}^\textrm{qc}(\xi )\le \ell |\xi |\) for all \(\xi \in \mathbb {R}^{m\times n}\);
-
(iii)
\(h_\mathrm {{simp}}^{\textrm{qc},\infty }(\xi )=\ell |\xi |\) and the \(\limsup \) in (2.9) is a limit.
Proof
(i): To prove (2.15) we consider \(h_\textrm{scal}:[0,\infty )\rightarrow [0,\infty )\) defined by
and compute its convex envelope
Let \(\eta \in \mathbb {R}^{m\times n}\) with \(|\eta |=1\). Then \(h_\mathrm {{simp}}(t\eta )=h_{\textrm{scal}}(t)\), hence \(h_\mathrm {{simp}}^\textrm{conv}(t\eta )\le {h_\textrm{scal}^\textrm{conv}} (t)\). This proves one inequality in (2.15). At the same time, \(h^\textrm{conv}_{\textrm{scal}}(|\xi |)\le h_{\textrm{scal}}(|\xi |)=h_\mathrm {{simp}}(\xi )\), and the function \(\xi \mapsto {h_\textrm{scal}^\textrm{conv}}(|\xi |)\) is convex, since \(h^\textrm{conv}_{\textrm{scal}}\) is convex and nondecreasing in \([0,\infty )\) and \(\xi \mapsto |\xi |\) is convex. This proves the second inequality in (2.15).
(ii): This follows immediately from the fact that \(\ell |\xi |-\frac{\ell ^2}{4}\le h^\textrm{conv}_{\mathrm {{simp}}}(\xi )\le h_{\mathrm {{simp}}}^\textrm{qc}(\xi )\le h_{\mathrm {{simp}}}(\xi )\le \ell |\xi |\) for any \(\xi \in \mathbb {R}^{m\times n}\).
(iii): This follows immediately from the definition and (ii). \(\square \)
We next prove that the quasiconvex envelope \(h_\mathrm {{simp}}^\textrm{qc}\) is not convex. For this we need a linear algebra statement that we present first.
Lemma 2.4
Let
and consider for \({\xi }\in \mathbb {R}^{m\times n}\) the linear map \(T:\mathbb {R}^{m\times n\times n}_\textrm{sym}\rightarrow \mathbb {R}^{m\times n\times n}\) of the form
If \(\textrm{rank}\,{\xi }\ge 2\), then T is injective. In particular, it has an inverse \(S:T(\mathbb {R}^{m\times n\times n}_\textrm{sym})\rightarrow \mathbb {R}^{m\times n\times n}_\textrm{sym}\).
Proof
It suffices to show that there is no \(\Gamma \in \mathbb {R}^{m\times n\times n}_\textrm{sym}\) with \(T\Gamma =0\) and \(\Gamma \ne 0\). We assume it exists and define \(v\in \mathbb {R}^n\) componentwise by
Then \(T\Gamma =0\) is equivalent to
hence \(\Gamma _{ijk}={\xi }_{ij}v_k\), for all i, j, and k. Moreover, \(\Gamma \ne 0\) in turn implies that \(v\ne 0\). From \(\Gamma \in \mathbb {R}^{m\times n\times n}_\textrm{sym}\) we obtain
As \(\textrm{rank}\,{\xi }\ge 2\) there is a vector \(w\in \mathbb {R}^n\) with \(v\cdot w=0\) and \({\xi }w\ne 0\). We take the scalar product of the previous equation with w and obtain
which gives \(0=v_j ({\xi }w)_i\) for all i and j. As \(v\ne 0\) and \({\xi }w\ne 0\), this is a contradiction. \(\square \)
Lemma 2.5
Let \({\xi }\in \mathbb {R}^{m\times n}\).
-
(i)
If \(|{\xi }|\le \frac{\ell }{2}\), then \(h_\mathrm {{simp}}({\xi })=h_\mathrm {{simp}}^\textrm{qc}({\xi })=h_\mathrm {{simp}}^\textrm{conv}({\xi })\).
-
(ii)
If \(\textrm{rank}\,{\xi }\le 1\), then \(h_\mathrm {{simp}}^\textrm{qc}({\xi })=h_\mathrm {{simp}}^\textrm{conv}({\xi })\).
-
(iii)
If \(\textrm{rank}\,{\xi }\ge 2\) and \(|{\xi }|>\frac{\ell }{2}\), then \(h_\mathrm {{simp}}^\textrm{conv}({\xi })<h_\mathrm {{simp}}^\textrm{qc}({\xi })\).
Proof
We work for \(\ell =1\) (the general case can be reduced to this one by a rescaling), to shorten notation we write h for \(h_\mathrm {{simp}}\).
(i): It is clear that \(h^\textrm{conv}\le h^\textrm{qc}\le h\). If \(|{\xi }|\le \frac{1}{2}\) then \(h^\textrm{conv}({\xi })=h({\xi })\) (cf. (2.15)), and the assertion then follows.
(ii): If \(\textrm{rank}\,{\xi }=1\) with \(|{\xi }|>\frac{1}{2}\), then for any \(t>|{\xi }|\) one has
and by rank-one convexity of \(h^\textrm{qc}\) we obtain
Taking \(t\rightarrow \infty \) shows that \(h^\textrm{qc}({\xi })\le |{\xi }|-\frac{1}{4}=h^\textrm{conv}({\xi })\). Recalling \(h^\textrm{conv}\le h^\textrm{qc}\) concludes the proof.
(iii): We assume that \(\textrm{rank}\,{\xi }\ge 2\) and \(|{\xi }|> \frac{1}{2}\), and show that \(h^\textrm{conv}({\xi })<h^\textrm{qc}({\xi })\). From the explicit formulas given in Lemma 2.3(i) we know that \(h^\textrm{conv}({\xi })<h({\xi })\), from general theory \(h^\textrm{conv}\le h^\textrm{qc}\).
Assume by contradiction that \(h^\textrm{conv}({\xi })=h^\textrm{qc}({\xi })\). Then there is a sequence \(\varphi _j\in C^{\infty }((0,1)^n;\mathbb {R}^m)\) such that \(\varphi _j(x)={\xi }x\) on \(\partial (0,1)^n\) and
We consider the affine function \(L:\mathbb {R}^{m\times n}\rightarrow \mathbb {R}\),
One easily checks that \(h^\textrm{conv}(t{\xi })=L(t{\xi })=t|\xi |-\frac{1}{4}\) for \(t\ge \frac{1}{2|{\xi }|}\) (cf. (2.15)), and since \(|{\xi }|>\frac{1}{2}\) this in particular holds for \(t= 1\). Linearity and the boundary values of \(\varphi _j\) imply
Subtracting from (2.21), and letting \(g:=h-L\), leads to
We next show that \(g({\eta })\) controls the distance of the matrix \({\eta }\) from the set \(\mathbb {R}{\xi }\). To do this, for \({\eta }\in \mathbb {R}^{m\times n}\) we define the orthogonal projections
so that \(|{\eta }|^2=|{\eta }^\parallel |^2+|{\eta }^\perp |^2\) and \(L({\eta })= {\eta }^\parallel -\frac{1}{4}\).
We first consider the case \(|{\eta }|\ge 1\), so that \(h({\eta })=|{\eta }|\). Assume for a moment that both \({\eta }^\parallel \) and \({\eta }^\perp \) do not vanish. Letting \(\gamma :=|{\eta }^\perp |/|{\eta }^\parallel |\),
Let now \(\varepsilon \in (0,1]\). If \(\gamma \le \varepsilon \), then \(|{\eta }^\perp |\le \varepsilon |{\eta }^\parallel |\). Otherwise, by monotonicity of \(t\mapsto (\sqrt{1+t^2}-1)/t\) we have \(g({\eta })\ge (\sqrt{1+\varepsilon ^2}-1)|{\eta }^\perp |/\varepsilon \). Therefore
for all \({\eta }\in \mathbb {R}^{m\times n} \text { with }|{\eta }|\ge 1\) (the two cases \({\eta }^\parallel =0\) and \({\eta }^\perp =0\) follow by continuity). If instead \(|{\eta }|\le 1\),
Therefore for any \(\varepsilon \in (0,1]\) we have for all \({\eta }\in \mathbb {R}^{m\times n} \text { with } |{\eta }|\le 1\)
Combining (2.23) and (2.24) we see that for any \(\varepsilon \in (0,1]\) there is \(C_\varepsilon >0\) such that for all \({\eta }\in \mathbb {R}^{m\times n}\)
In particular, for any j we have
We integrate over \((0,1)^n\), take the limit \(j\rightarrow \infty \) and recall that \(g(\nabla \varphi _j)\rightarrow 0\) in \(L^1\) by (2.22). We obtain
for any \(\varepsilon \in (0,1]\). By (2.21) and Lemma 2.3(ii) the sequence \(\nabla \varphi _j\) is bounded in \(L^1\), and since \(\varepsilon \) was arbitrary we conclude that
We next prove that (2.25) implies that \(\nabla \varphi _j\) converges to the constant \({\xi }\) strongly in weak-\(L^1\). To do this we show that standard singular integral estimates imply rigidity. To simplify notation, we write \(u_j(x):=\varphi _j(x)-{\xi }x\) and \(R_j:=\nabla \varphi _j^\perp = \nabla u_j^\perp \), both extended by zero to the rest of \(\mathbb {R}^n\), in the next steps. We observe that
where \({\tilde{{\xi }}}:=\frac{{\xi }}{|{\xi }|}\). Taking a derivative, and writing the components, we obtain
with T obtained from \({\tilde{{\xi }}}\) as in Lemma 2.4. Let S be the inverse operator. Then
so that in particular \(\Delta u_j\) is given by a linear combination of the components of \(\nabla R_j\), with coefficients which depend only on \({\xi }\). As \(u_j(x)=0\) outside \((0,1)^n\), we obtain, denoting by N the fundamental solution of Laplace’s equation in \(\mathbb {R}^n\) (which solves \(-\Delta N=\delta _0\)),
for every \(r=1,\dots ,n\), where we have set \({(\Lambda _r(R_j))}_{cdk}:={\partial _r\partial _k} N*(R_j)_{cd}\) (recall that \(R_j=0\) outside of \((0,1)^n\)), and \((\textrm{Tr}\,\Gamma )_l:=\sum _{i=1}^n\Gamma _{lii}\), for every \(l=1,\dots ,m\) and \(\Gamma \in \mathbb {R}^{m\times n\times n}\). By [72, Theorem 4(b), page 42] we see that the operator \(R\mapsto \Lambda _{{r}}(R)\) is of weak type (1, 1), so that
with c depending only on \({\xi }\). Recalling the definition of \(u_j\) and \(R_j\) as well as (2.25),
To conclude the proof we choose \(z\in (h^\textrm{conv}({\xi }), h({\xi }))\) (here we use again that \(|{\xi }|>\frac{1}{2}\)). By continuity of h, there is \(\delta >0\) such that \(h(\eta )\ge z\) for all \(\eta \in \mathbb {R}^{m\times n}\) with \(|\eta -{\xi }|<\delta \). By definition of the weak-\(L^1\) norm,
Therefore, recalling that \(h\ge 0\) pointwise,
This contradicts (2.21) and concludes the proof. \(\square \)
3 Energy Densities of the Surface and Cantor Part
In this section we discuss several properties of the energy densities g and \(h^{\textrm{qc},\infty }\). We warn the reader that while the results dealing with g contained in Sect. 3.1 and 3.2 will be crucial in the proof of Theorem 2.1, those in Sect. 3.3 will not be employed in that proof. Actually, Proposition 3.9 and Corollary 3.11 take advantage of Theorem 2.1 itself (in particular of the lower semicontinuity of \(\Gamma \)-limits).
3.1 Equivalent Characterizations of \(g(z,\nu )\)
We show below that we may reduce the test sequences in the definition of \(g(z,\nu )\) in (2.12) to those converging in \(L^2\) and satisfying periodic boundary conditions in \((n-1)\) directions orthogonal to \(\nu \) and mutually orthogonal to each other. This is the content of the next two propositions, which will be crucial in the proof of the upper bound for the surface part (Theorem 5.2 Step 2). The proof draws inspiration from that of [19, Lemma 4.2]. We fix a mollifier \(\varphi _1\in C^\infty _c(B_1)\), with \(\int _{B_1}\varphi _1{\textrm{d}}x=1\), and set \(\varphi _\varepsilon (x):=\varepsilon ^{-n}\varphi _1(x/\varepsilon )\) in \(B_\varepsilon \).
Proposition 3.1
Assume an optimal sequence in (2.12) converges in \(L^2(Q^\nu ;\mathbb {R}^{m+1})\). Then there are \(\varepsilon _j\rightarrow 0\), \((u_j^*,v_j^*)\rightarrow (z\chi _{\{x\cdot \nu >0\}},1)\) in \(L^2(Q^\nu ;\mathbb {R}^{m+1})\), with \(v_j^*\in [0,1]\) \(\mathcal {L}^n\)-a.e. in \(Q^\nu \), such that
and
Proof
Step 1. Construction of \(u_j^*\) and \(v_j^*\). Pick \(\varepsilon _j\rightarrow 0\), \(v_j\) and \(u_j\rightarrow z\chi _{\{x\cdot \nu >0\}}\) in \(L^2(Q^\nu ;\mathbb {R}^m)\) such that
To simplify the notation we write
Obviously \(\Vert U_j-z\chi _{\{x\cdot \nu >0\}}\Vert _{L^2(Q^\nu )}\rightarrow 0\), so that \( \Vert u_j-U_j\Vert _{L^2(Q^\nu )}\rightarrow 0\). Moreover, by construction \(U_j=z\chi _{\{x\cdot \nu >0\}}\) if \(|x\cdot \nu |\ge \varepsilon _j\), \(V_j=0\) if \(|x\cdot \nu |\le \varepsilon _j\), and \(V_j=1\) if \(|x\cdot \nu |\ge 3\varepsilon _j\). Therefore, by \({\Psi _\infty }(0)=0\) and \(f(0)=0\), we have
as \(\Vert \nabla V_j\Vert _{L^{\infty }(\mathbb {R}^m)}\le \frac{c}{\varepsilon _j}\), where c is a constant independent of \(j\in \mathbb {N}\).
Next, we choose a sequence \(\eta _j\rightarrow 0\) such that
and set \(K_j:=\lfloor \eta _j/\varepsilon _j\rfloor \), we can assume \(K_j\ge 4\). We let \({\hat{R}}_k^j:=Q^\nu _{1-k\varepsilon _j}{\setminus } Q^\nu _{1-(k+1)\varepsilon _j}\), where we write for brevity \(Q^\nu _r:=rQ^\nu \) for the scaled cube. We select \(k_j\in \{{K_j+1},\dots , {2K_j}\}\) such that, writing \(R_j:={\hat{R}}_{k_j}^j\),
and
We fix \(\theta _j\in C^1_c(Q^\nu _{1-k_j\varepsilon _j})\) with \(\theta _j=1\) on \(Q^\nu _{1-(k_j+1)\varepsilon _j}\) and \(|\nabla \theta _j|\le 3/\varepsilon _j\), and define
The construction of \(v_j^*\) is more complex. In the interior part, it should match \(v_j\). In the exterior, \(V_j\). In the interpolation region, it should be not larger than \(v_j\) and \(V_j\), but also not larger than \(1-\eta _j\). Therefore we first define
which coincides with \(1-\eta _j\) in the interpolation region \(R_j\), and with 1 at distance larger than \(\eta _j\varepsilon _j\) from it, then
which coincides with \(V_j\) outside \(Q^\nu _{1-(k_j+1)\varepsilon _j}\), and with 1 inside \(Q^\nu _{1-(k_j+3)\varepsilon _j}\) as well as for \(|x\cdot \nu |\ge 3\varepsilon _j\) (cf. the definition of \(V_j\)), and finally
We then combine these three ingredients to obtain
On \(\partial Q^\nu \) the first and the last term are equal to 1, hence \(v_j^*={\hat{V}}_j=V_j\).
Step 2. Estimate of the elastic energy. By the definition of \(u_j^*\),
therefore in \(R_j\)
We recall that \(v_j^*\le \min \{v_j, V_j, 1-\eta _j\}\) in \(R_j\) and that \({[0,1)\ni }t\mapsto t/(1-t)\) is increasing. Since by construction \(v_j^*=V_j=0\) on \(\{\nabla U_j\ne 0\}{\cap R_j}\) the term \({\Psi _\infty }(\nabla U_j)\) can be ignored. Therefore
Integrating over \(R_j\) and using (3.5) in the first term, (3.4) in the second one,
Using first that the definition of \(K_j\) implies \(\lim _{j\rightarrow \infty } K_j\varepsilon _j/\eta _j=1\) and then (3.3),
Therefore
Using again that the supports of \(\nabla U_j\) and \(V_j\) are disjoint, we have
Therefore
Step 3. Estimate of the energy of the phase field. By the definition of \(v^*_j\),
From (3.6) we have \(|1-{\hat{v}}_j|\le \eta _j\) with \(|\{{\hat{v}}_j\ne 1\}|\le c\varepsilon _j\) and \(|\nabla {\hat{v}}_j|\le 1/\varepsilon _j\) with \(|\{\nabla {\hat{v}}_j\ne 0\}|\le c\varepsilon _j\eta _j\), so that
From the definition of \(V_j\) and \({\hat{V}}_j\), we see that \(|\{{\hat{V}}_j\ne 1\}|\le c\eta _j\varepsilon _j\) and \(\varepsilon _j|\nabla {\hat{V}}_j|\le c\), so that
Similarly, \({\tilde{v}}_j=v_j\) in \({Q^\nu _{1-k_j\varepsilon _j}}\), \(|{\tilde{v}}_j-1|\le |v_j-1|\), and \(|\nabla {\tilde{v}}_j|\le |\nabla v_j|+2/(k_j\varepsilon _j)\) in \(Q^\nu {\setminus } Q^\nu _{1-k_j\varepsilon _j}\) lead to
Recalling \(k_j\ge {K_j+1}\rightarrow \infty \) and \(\eta _j\rightarrow 0\), (3.10) leads to
Combining this with (3.9) concludes the proof. \(\square \)
We are now ready to perform the claimed reduction on the test sequences in the definition of \(g(\cdot ,\nu )\) in (2.12). To this aim we fix a sequence \((a_k)_k\subset (0,\infty )\) such that \(a_k<a_{k+1}\), \(a_k\uparrow \infty \), and such that there are functions \(\mathcal {T}_k\in {C^1_c}(\mathbb {R}^m;\mathbb {R}^m)\) satisfying
and \(\Vert \nabla \mathcal {T}_k\Vert _{L^\infty (\mathbb {R}^m)}\le 1\). Following De Giorgi’s averaging/slicing procedure on the codomain, the family \(\mathcal {T}_k\) will be used in several instances along the paper to obtain from a sequence converging in \(L^1\) to a limit belonging to \(L^\infty \), a sequence with the same \(L^1\) limit which is in addition equi-bounded in \(L^\infty \). Moreover, this substitution can be done up to paying an error in energy which can be made arbitrarily small.
Proposition 3.2
For any \((z,\nu )\in \mathbb {R}^m\times S^{n-1}\) and any \(\varepsilon _j^*\downarrow 0\) there is \((u_j^*,v_j^*)\rightarrow (z\chi _{\{x\cdot \nu >0\}},1)\) in \(L^2(Q^\nu ;\mathbb {R}^{m+1})\), with \(v_j^*\in [0,1]\) \(\mathcal {L}^n\)-a.e. in \(Q^\nu \), such that
and
Proof
Step 1. Reduction to an optimal sequence in (2.12) converging in \(L^2(Q^\nu ;\mathbb {R}^{m+1})\). Let \(\varepsilon _j\rightarrow 0\), \((u_j,v_j)\rightarrow (z\chi _{\{x\cdot \nu >0\}},1)\) in \(L^1(Q^\nu ;\mathbb {R}^{m+1})\) be such that
Recall that \(v_j\in [0,1]\) \(\mathcal {L}^n\)-a.e. in \(Q^\nu \), therefore \(v_j\rightarrow 1\) in \(L^2(Q^\nu )\). We claim that for all \(j,\,M\in \mathbb {N}\) there is \(k_{M,j}\in \{M+1,\ldots ,2M\}\) such that
where \(c>0\) is a constant independent of M and j. If \({a_M}>1+|z|=1+\Vert z\chi _{\{x\cdot \nu >0\}}\Vert _{L^\infty (Q^\nu )}\) then \({\mathcal {T}_{k_M,j}}(u_j)\rightarrow z\chi _{\{x\cdot \nu >0\}}\) in \(L^2(Q^\nu ;\mathbb {R}^m)\), and (3.13) yields
which in turn implies by the arbitrariness of \(M\in \mathbb {N}\),
We are left with establishing (3.13). To this aim consider \(\mathcal {T}_k(u_j)\) and note that
We estimate the second term in (3.14). The growth conditions on \(\Psi \) (cf. (2.3)) and \(\Vert \nabla \mathcal {T}_k\Vert _{L^\infty (\mathbb {R}^m)}\le 1\) yield for a constant \(c>0\)
Collecting (3.14) and (3.15) and using \(\mathcal {F}_{\varepsilon _j}^\infty (u_j,v_j;A)+\mathcal {F}_{\varepsilon _j}^\infty (0,v_j;B)\le \mathcal {F}_{\varepsilon _j}^\infty (u_j,v_j;A\cup B)\) for A and B disjoint we conclude that
Let now \(M\in \mathbb {N}\), by averaging there exists \(k_{M,j}\in \{M+1,\ldots ,2M\}\) such that
i.e. (3.13).
Step 2. Conclusion. In view of Step 1 there is an optimal sequence for \(g(z,\nu )\) in (2.12) converging in \(L^2(Q^\nu ;\mathbb {R}^{m+1})\). Let \((\varepsilon _k, u_k, v_k)\) be the sequence from Proposition 3.1. Since \(\lim _{k\rightarrow \infty }\lim _{j\rightarrow 0} \varepsilon _j^*/\varepsilon _k=0\), we can select a nondecreasing sequence \(k(j)\rightarrow \infty \) such that \(\lambda _j:=\varepsilon _j^*/\varepsilon _{k(j)}\rightarrow 0\). We let \({\tilde{Q}}^\nu :=(\textrm{Id}-\nu \otimes \nu )Q^\nu \subset \nu ^\perp \subset \mathbb {R}^n\) and select \(x_1, \dots , x_{I_j}\in {\tilde{Q}}^\nu \), with \(I_j:= \lfloor 1/\lambda _j\rfloor ^{n-1}\), such that \(x_i+{\tilde{Q}}^\nu _{\lambda _j}\) are pairwise disjoint subsets of \({\tilde{Q}}^\nu \). We set
and
where \(U_j^*\) and \(V_j^*\) are defined as in (3.2) using \(\varepsilon _j^*\). One easily verifies that \(U_j^*(x)=U_{k(j)}(\frac{x-y}{\lambda _j})\) for all \(y\in \nu ^\perp \), and the same for V. By the boundary conditions (3.1), these functions are continuous and therefore in \(W^{1,2}(Q^\nu ;\mathbb {R}^{m+1})\). We further estimate
Taking \(j\rightarrow \infty \), and recalling that \(\limsup _{j} \mathcal {F}^{\infty }_{\varepsilon _{k(j)}}(u_{k(j)}, v_{k(j)}; Q^\nu )\le g(z,\nu )\), concludes the proof. \(\square \)
In what follows we provide an equivalent characterization for the surface energy g in the spirit of [33, Proposition 4.3].
Proposition 3.3
For any \((z,\nu )\in \mathbb {R}^m\times S^{n-1}\) one has
where
Proof
For every \((z,\nu )\in \mathbb {R}^m\times S^{n-1}\) and \(T>0\) set
We first prove that
Indeed, if \(T_j\uparrow \infty \) is a sequence achieving the superior limit on the left-hand side above, thanks to Proposition 3.2 we may consider \((u_j,v_j)\in W^{1,2}(Q^\nu ;\mathbb {R}^{m+1})\) with \(0\le v_j\le 1\), \((u_j,v_j)\rightarrow (z\chi _{\{x\cdot \nu >0\}},1)\) in \(L^2(Q^\nu ;\mathbb {R}^{m+1})\),
and
Then, define \((\tilde{u}_j(y),\tilde{v}_j(y)):=\big (u_j(\frac{y}{T_j}),v_j(\frac{y}{T_j})\big )\) for \(y\in Q^\nu _{T_j}\), and note that by a change of variable it is true that
and that \((\tilde{u}_j,\tilde{v}_j)\in \mathcal {U}^{T_j}_{z,\nu }\) in view of (3.18). Then, by (3.19), the choice of \(T_j\) and the definition of \(g_T(z,\nu )\) we conclude straightforwardly (3.17).
In order to prove the converse inequality
we assume for the sake of notational simplicity \(\nu =e_n\). We then fix \(\rho >0\) and take \(T>6\), depending on \(\rho \), and \((u_T,v_T)\in \mathcal {U}^T_{z,e_n}\) such that
Let \(\varepsilon _j\rightarrow 0\) and set
with \(d\in \mathbb {Z}^{n-1}\times \{0\}\). Then, \((u_j,v_j)\rightarrow (z\chi _{\{x\cdot {e_n} >0\}},1)\) in \(L^1(Q^{e_n};\mathbb {R}^{m+1})\), and letting \(I_{\varepsilon _j}:=\{d\in \mathbb {Z}^{n-1}\times \{0\}:\,\varepsilon _j (Q^{{e_n}}_T+d)\subset \subset Q^{e_n}\}\), a change of variable yields (cf. also the discussion after (3.2))
by the choice of \((u_T,v_T)\) and T (cf. (3.21)). As \(\rho \rightarrow 0\) we get (3.20).
Estimates (3.17) and (3.20) yield the existence of the limit of \(g_T(z,\nu )\) as \(T\uparrow \infty \) and equality (3.16), as well. \(\square \)
With this representation of g at hand we can obtain a version of Proposition 3.2 which also accounts for a regularization term of the form \(\eta _\varepsilon \int \Psi (\nabla u){\textrm{d}}x\).
Proposition 3.4
For any \(\varepsilon _j\downarrow 0\) and \(\eta _j\downarrow 0\) with \(\eta _j/\varepsilon _j\rightarrow 0\), and any \((z,\nu )\in \mathbb {R}^m\times S^{n-1}\) there is \((u_j,v_j)\rightarrow (z\chi _{\{x\cdot \nu >0\}},1)\) in \(L^2(Q^\nu ;\mathbb {R}^{m+1})\), with \(v_j\in [0,1]\) \(\mathcal {L}^n\)-a.e. in \(Q^\nu \), such that
and
Proof
We use the same construction as above (without loss of generality, explicitly written only for \(\nu =e_n\)), and compute similarly
To conclude the proof it suffices to choose \(T_j\rightarrow \infty \) so slow that \(\eta _j C_{T_j}/\varepsilon _j\rightarrow 0\). \(\square \)
Corollary 3.5
If \(\Psi {{_\infty }}(\xi )=|\xi |^2\), then \(g(z,\nu )=g_\textrm{scal}(|z|)\) for all \((z,\nu )\in \mathbb {R}^m\times S^{n-1}\), where \(g_\textrm{scal}\) is defined as the right-hand side of equation (3.16) with \(n=m=1\).
For an equivalent definition of \(g_\textrm{scal}\) see equation (4.4) below and [33, Proposition 4.3].
Proof
By [33, Proposition 4.3] or by Proposition 3.3, the following characterization holds for \(g_\textrm{scal}\):

with

and

Let \((z,\nu )\in \mathbb {R}^m\times S^{n-1}\), \(z\ne 0\). We first prove that
If \(T>0\) and \((u,v)\in \mathcal {U}^T_{z,\nu }\) (see Proposition 3.3 for the definition of \( \mathcal {U}^T_{z,\nu }\)), then for \(\mathcal {H}^{n-1}\)-a.e. \(y\in {\tilde{Q}}^\nu _T:=(\textrm{Id}-\nu \otimes \nu )Q^\nu _T\subset \nu ^\perp \) the slices
belong to \(\mathcal {U}^T_{|z|}\) and satisfy by Fubini’s theorem

Taking the infimum over \((u,v)\in \mathcal {U}^T_{z,\nu }\) and passing to the limit \(T\rightarrow \infty \) we get (3.22).
Let us show now that
Let \(T>0\) and \((\alpha ,\beta )\in \mathcal {U}^{T}_{|z|}\). Fixed \(\varepsilon _j\rightarrow 0\), we will construct a competitor \((u_j,v_j)\) for the problem (2.12) defining g. We set
Hence by a change of variables we have \(\Vert u_j-z\chi _{\{x\cdot \nu >0\}}\Vert _{L^1(Q^\nu )}\rightarrow 0\) and

Therefore, we conclude that

As \((\alpha ,\beta )\in \mathcal {U}^T_{|z|}\) varies, we obtain (3.23). \(\square \)
Remark 3.6
The same argument shows that if \(\Psi \) satisfies \(\Psi {_\infty }(\xi )\ge \Psi {_\infty }(\xi \nu \otimes \nu )\) for every \(\xi \in \mathbb {R}^{m\times n}\) and \(\nu \in S^{n-1}\), then for all \((z,\nu )\in \mathbb {R}^m\times S^{n-1}\)

where

3.2 Structural Properties of \(g(z,\nu )\)
We next deduce the coercivity properties of g.
Lemma 3.7
There is \(c>0\) such that, for all \(z,\nu \in \mathbb {R}^m\times S^{n-1}\),
We provide here a direct proof of the lemma. Alternatively, these bounds may be derived estimating \(\mathcal {F}_\varepsilon \) by its 1D counterpart (as in (4.2) below) and recalling the bounds holding for \(g_\textrm{scal}\), see [33, Prop. 4.1].
Proof
We start with the lower bound. Let \(z\in \mathbb {R}^m\), \(\nu \in S^{n-1}\), and fix sequences \(\varepsilon _j\rightarrow 0\), \(v_j\) and \(u_j\rightarrow z\chi _{{\{x\cdot \nu >0\}}}\) in \(L^1(Q^\nu ;\mathbb {R}^m)\) such that \(\mathcal {F}^{\infty }_{\varepsilon _j}(u_j,v_j; Q^\nu )\rightarrow g(z,\nu )\). For every j and \(y_j\in \nu ^\perp \cap Q^\nu \) we define \(v_j^*\in W^{1,2}((-\frac{1}{2},\frac{1}{2});[0,1])\) and \(u_j^*\in W^{1,2}((-\frac{1}{2},\frac{1}{2});\mathbb {R}^m)\) by \(v_j^*(t):=v_j(y_j+t\nu )\) and \(u_j^*(t):=u_j(y_j+t\nu )\). The set of \(y_j\in \nu ^\perp \cap Q^\nu \) such that
has measure at least \(\frac{2}{3}\) and, using (2.3) to estimate \(\frac{1}{c}|(u_j^*)'|^2(t) \le {\Psi _\infty }(\nabla u_j)(y_j+t\nu )\), the set of \(y_j\in \nu ^\perp \cap Q^\nu \) such that
also has measure at least \(\frac{2}{3}\). Therefore we can fix \(y_j\) such that both inequalities hold. If \(g(z,\nu )<\infty \), then necessarily \(v_j^*\rightarrow 1\) in \(L^2((-\frac{1}{2},\frac{1}{2}))\), and it has a continuous representative. We can therefore assume that \(\sup v_j^*\ge \frac{3}{4}\) for large j. If \(\inf v_j^*\le \frac{1}{2}\) then
Otherwise, \(v_j^*\ge \frac{1}{2}\) pointwise and
Since \( \Vert u_j^*-z\chi _{t\ge 0}\Vert _{L^1((-\frac{1}{2},\frac{1}{2}))}\rightarrow 0\), there are \(t_j, t'_j\) such that \(u_j^*(t_j)\rightarrow 0\), \(u_j^*(t_j')\rightarrow z\), and therefore \(\liminf _{j\rightarrow \infty } \int _{(-\frac{1}{2},\frac{1}{2})} |(u_j^*)'| {\textrm{d}}t\ge \liminf _{j\rightarrow \infty } |u_j^*(t_j)-u_j^*(t_j')|=|z|\). We conclude that \(\liminf _{j\rightarrow \infty }\mathcal {F}_{\varepsilon _j}^{\infty }({u_j,v_j};Q^\nu )\ge c (1\wedge \ell |z|)\).
We turn to the upper bound. We define \(u_j(x):=u_j^*(x\cdot \nu )\), \(v_j(x):=v_j^*(x\cdot \nu )\), where, denoting by AI the affine interpolation between the boundary data in the relevant segments,
If \(\ell {|z|}<1\), then the upper bound in (2.3) leads to
If instead \(\ell {|z|}\ge 1\) the first term vanishes, and
\(\square \)
We prove next the subadditivity and continuity of g.
Lemma 3.8
-
(i)
For any \(\nu \in S^{n-1}\) and \(z^1,z^2\in \mathbb {R}^m\) one has
$$\begin{aligned} g(z^1+z^2,\nu )\le g(z^1,\nu )+g(z^2,\nu ). \end{aligned}$$ -
(ii)
\(g\in C^0(\mathbb {R}^m\times S^{n-1})\).
Proof
(i): Fix \(z^1,z^2\in \mathbb {R}^m\), \(\nu \in S^{n-1}\). Let \((u_j^i, v_j^i)\) be the sequences from Proposition 3.2 corresponding to \(\varepsilon _j:=1/j\) and the pair \((\nu ,z^i)\), for \(i=1,2\). We implicitly extend both periodically in the directions of \(\nu ^\perp \cap Q^\nu \), and constant in the direction \(\nu \). In particular, for \(\{x\cdot \nu \ge \frac{1}{2}\}\) we have \(u_j^i=z^i\) and \(v_j^i=1\); for \(\{x\cdot \nu \le -\frac{1}{2}\}\) we have \(u_j^i=0\) and \(v_j^i=1\) for \(i\in \{1,2\}\) and all j.
We use a rescaling similar to the one of Proposition 3.2. We fix a sequence \(M_j\in \mathbb {N}\), \(M_j\rightarrow \infty \), and define \((u_j,v_j)\in W^{1,2}(\mathbb {R}^n;\mathbb {R}^m\times [0,1])\) by
and, correspondingly,
By the periodicity of \((u^i_j,v^i_j)\) in the directions of \(\nu ^\perp \cap Q^\nu \), these maps belong to \(W^{1,2}(Q^\nu ;\mathbb {R}^m)\). Furthermore, \(u_j=0\) and \(v_j=1\) if \(x\cdot \nu \le -\frac{1}{M_j}\), \(u_j=z^1+z^2\) and \(v_j=1\) if \(x\cdot \nu \ge \frac{1}{M_j}\), and \((u_j,v_j)\) is \(\frac{1}{M_j}\)-periodic in the directions of \(\nu ^\perp \cap Q^\nu \). Therefore, by changing variables we find
so that \(u_j\rightarrow (z^1+z^2)\chi _{\{x\cdot \nu \ge 0\}}\) in \(L^1(Q^\nu ;\mathbb {R}^m)\). Arguing similarly, we infer
The conclusion follows taking the limit \(j\rightarrow \infty \).
(ii): By (i) and Lemma 3.7 we have \(g(z,\nu )\le g(z',\nu )+c\ell |z-z'|\), which implies that for any \(\nu \in S^{n-1}\) the function \(g(\cdot ,\nu )\) is \(c\ell \)-Lipschitz continuous. Therefore it suffices to prove continuity in \(\nu \) at any fixed z.
Since \({\Psi _\infty }\) is continuous and positive on the compact set \(S^{nm-1}\subseteq \mathbb {R}^{m\times n}\), there is a monotone modulus of continuity \(\omega :[0,\infty )\rightarrow [0,\infty )\), with \(\omega _\rho \rightarrow 0\) as \(\rho \rightarrow 0\), such that
This implies that
(it suffices to insert \(\eta /|\eta |\) and \(\eta R/|\eta |\) in the above expression).
Fix \(\nu \in S^{n-1}\), a sequence \(\varepsilon _j\rightarrow 0\), and let \((u_j, v_j)\) be as in Proposition 3.2, extended periodically in the directions of \(\nu ^\perp \cap Q^\nu \) and constant along \(\nu \), as in the proof of (i). Let \({\tilde{\nu }}\in S^{n-1}\), \({\tilde{\nu }}\ne \nu \), and choose \(R\in O(n)\) such that \(\nu =R{\tilde{\nu }}\) and \(|R-\textrm{Id}|\le c |\nu -{\tilde{\nu }}|\) (for example, R can be the identity on vectors orthogonal to both \(\nu \) and \({\tilde{\nu }}\), and map \(({\tilde{\nu }},{\tilde{\nu }}^\perp )\) to \((\nu ,\nu ^\perp )\) in this two-dimensional subspace). We fix a sequence \(M_j\rightarrow \infty \) (for example, \(M_j:=j\)) and define
From \(u_j\rightarrow z\chi _{\{x\cdot \nu \ge 0\}}\) in \(L^1_\textrm{loc}(\mathbb {R}^n;\mathbb {R}^m)\) we obtain \({\tilde{u}}_j\rightarrow z\chi _{{\{x\cdot {\tilde{\nu }}\ge 0\}}}\). Further, \(\nabla {\tilde{u}}_j(x)=M_j\nabla u_j (M_jRx){R}\), which implies, recalling (3.24),
Inserting in the definition of \(\mathcal {F}_{\varepsilon _j}^{\infty }({\tilde{u}}_j, {\tilde{v}}_j; Q^{{\tilde{\nu }}})\) and using a change of variables leads to

We observe that, although \({R}{\tilde{\nu }}=\nu \), we cannot in general expect \({R}Q^{{\tilde{\nu }}}=Q^\nu \). However, as \((u_j,v_j)\) are periodic in the directions orthogonal to \(\nu \), the \((n-1)\)-dimensional square \(\nu ^\perp \cap M_j{R}Q^{{\tilde{\nu }}}\) can be covered by at most \(M_j^{n-1} + c M_j^{n-2}\) disjoint translated copies of the \((n-1)\)-dimensional unit square \(\nu ^\perp \cap Q^\nu \). Therefore

\(\square \)
3.3 Density of the Cantor Part
We study now the behaviour of the surface energy density g at small jump amplitudes. The next result is probably well known to experts. Despite this, we give a self-contained proof since we have not found a precise reference in the literature. Similar constructions are performed in [7, Proposition 5.1] for isotropic functionals defined on vector-valued measures. The \(L^1\) lower semicontinuity of \(\mathcal {F}_0\) is assumed to hold in Proposition 3.9 below, as already mentioned at the beginning of Sect. 3. Such a property follows, for instance, from the validity of Theorem 2.1. We stress again that Proposition 3.9 is not used in the proof of Theorem 2.1, rather it provides a further piece of information on g showing its linear behavior at small amplitudes.
Proposition 3.9
Assume that the functional \(\mathcal {F}_0\) defined in (2.13) is \(L^1(\Omega ;\mathbb {R}^m)\) lower semicontinuous. Then, for all \(\nu \in S^{n-1}\) we have
Proof
With fixed \(\nu \in S^{n-1}\), let \(x_0\in \Omega \) and \(\rho >0\) be such that \(Q^\nu _\rho (x_0)\subset \Omega \). Upon translating and scaling, it is not restrictive to assume \(x_0=0\) and \(\rho =1\). For every \(z\in \mathbb {R}^m\) consider the sequence
where \(\varphi (t):=(t\wedge 1)\vee 0\) for every \(t\in \mathbb {R}\). Clearly, \(w_j\rightarrow u_z(x):=z\chi _{\{x\cdot \nu \ge 0\}}\) in \(L^1(Q^\nu ;\mathbb {R}^m)\), and thus by the \(L^1(Q^\nu ;\mathbb {R}^m)\) lower semicontinuity of \(\mathcal {F}_0\) we conclude that

On the other hand, given \(z\in \mathbb {R}^m\) and any couple of sequences \(z_j\rightarrow z\) and \(t_j\rightarrow 0{^+}\), denote by \(M_j\) the integer part of \(t_j^{-1}\) and define for every \(k\in \mathbb {N}\), \(k\ge 3\),
We show that \(u_{j,k}\) converges, as \(j\rightarrow \infty \), to \(w_k\) as defined in (3.25) for every \(k\ge 3\). Indeed, for \(s:=x\cdot \nu \in [\frac{i}{kM_j},\frac{i+1}{kM_j})\subseteq {[0,\frac{1}{k})}\) we have
uniformly in i, hence \(\Vert w_k-u_{j,k}\Vert _{L^\infty (Q^\nu ;\mathbb {R}^m)}\rightarrow 0\) as \(j\rightarrow \infty \). Further,

Therefore, by the \(L^1(Q^\nu ;\mathbb {R}^m)\) lower semicontinuity of \(\mathcal {F}_0\) we conclude that
As this holds for every sequence, this implies
Indeed, the superior limit in the definition of \(h^{\textrm{qc},\infty }\) is actually a limit on rank-1 directions being \(h^{\textrm{qc},\infty }\) convex on those directions.
Let now \(\widetilde{z}_j\rightarrow 0\) be a sequence for which
Upon setting \(z_j:=\frac{\widetilde{z}_j}{{|}\widetilde{z}_j{|}}\), up to subsequences we may assume that \(z_j\rightarrow z_\infty \in S^{n-1}\). In addition, \(t_j:={|}\widetilde{z}_j{|}\rightarrow 0\). Therefore, being \(h^{\textrm{qc},\infty }\) one-homogeneous we have that
By the latter equality, by (3.27) and by the continuity of \(h^{\textrm{qc},\infty }\) we infer
The conclusion follows at once from (3.26) and (3.28). \(\square \)
We now identify \(h^{\textrm{qc},\infty }\) explicitly as stated in (2.10).
Proposition 3.10
For all \(\xi \in \mathbb {R}^{m\times n}\)

Proof
With fixed \(\xi \in \mathbb {R}^{m\times n}\), the very definition of h in (2.6) and the growth condition (2.3) easily imply

Let \(\varepsilon >0\), then for every \(t>0\) consider \(\varphi _t\in {C^\infty _c}(Q_1;\mathbb {R}^m)\) such that
Note that

so that

Therefore, being \(h\ge 0\) (cf. again (2.3)) from (3.30) we infer that

from which we conclude that

From Propositions 3.9 and 3.10 we deduce straightforwardly the ensuing statement.
Corollary 3.11
For all \(\nu \in S^{n-1}\) we have

We conclude this section by proving that, under our hypotheses, the superior limit in the definition of  is in fact a limit and that the operations of quasi-convexification and of recession for
is in fact a limit and that the operations of quasi-convexification and of recession for  commute.
commute.
Proposition 3.12
We have that
-
(i)
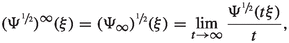 for all \(\xi \in \mathbb {R}^{m\times n}\);
for all \(\xi \in \mathbb {R}^{m\times n}\); -
(ii)
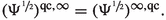
-
(iii)
In the special case \(\Psi _2(\xi ):=\textrm{dist}^2(\xi ,\textrm{SO}(n))\) one obtains \(h^{\textrm{qc},\infty }(\xi )=\ell |\xi |\) for all \(\xi \in \mathbb {R}^{m\times n}\).
Proof
The second equality in (i) follows immediately from (2.4). Then, the first is a consequence of the very definition of recession function. Alternatively, by (2.5) we infer that, for all \(\delta >0\), there is \(C_\delta >0\) satisfying

This, together with the definition of recession function, implies (i).
(ii) Since  , we immediately deduce
, we immediately deduce  . By [57, Rem. 2.2(ii)],
. By [57, Rem. 2.2(ii)],  is quasiconvex, hence
is quasiconvex, hence  .
.
Let us check the converse inequality. Let \(\xi \in \mathbb {R}^{m\times n}\). By definition of quasi-convexification and (3.31) we have

for all \(\varphi \in C^\infty _c((0,1)^n;\mathbb {R}^m)\). Hence, taking the infimum over \(\varphi \) gives

Since  and therefore
and therefore  are positively one-homogeneous, we obtain
are positively one-homogeneous, we obtain

which yields the thesis.
(iii) From the definition of \(\Psi _2\) one easily obtains  . As this function is quasiconvex, it coincides with
. As this function is quasiconvex, it coincides with  , the assertion follows then from (ii) and Proposition 3.10. \(\square \)
, the assertion follows then from (ii) and Proposition 3.10. \(\square \)
4 Lower Bound
4.1 Domain of the Limits
In order to characterize the compactness properties and the space in which the limit is finite it is useful to consider the scalar simplification of the functional, \(\mathcal {F}_\varepsilon ^\textrm{scal}:W^{1,2}(A;\mathbb {R}\times [0,1])\rightarrow [0,\infty ]\),
From (2.3), one immediately obtains that for any \((u,v)\in W^{1,2}(A;\mathbb {R}^m\times [0,1])\)
with the same constant \(c\ge 1\) as in (2.3). In particular, [33, Prop. 6.1] implies that if \((u_\varepsilon ,v_\varepsilon )\rightarrow (u,v)\) in \(L^1(\Omega ;\mathbb {R}^{m+1})\) with
then \(u\in (GBV(\Omega ))^m\) and \(v=1\) \(\mathcal {L}^n\)-a.e. \(\Omega \) (for a different proof see Remark 4.7). In addition, for every \(i\in \{1,\ldots ,m\}\)
Here \(h_\textrm{scal}^{\textrm{conv}}:[0,\infty )\rightarrow [0,\infty )\) is the convex function explicitly defined by
(cf. (2.16)–(2.17)). We remark that it coincides with the simplified model \(h_\mathrm {{simp}}\) for \(m=1\) (cf. Lemma 2.3). Further, \(g_\textrm{scal}:[0,\infty )\rightarrow [0,1]\) is the function implicitly defined by
where \(\mathcal U_t:=\{\alpha ,\,\beta \in W^{1,2}((0,1)):\, \alpha (0)=0,\,\alpha (1)=t,\,0\le \beta \le 1,\,\beta (0)= \beta (1)=1\}\). In particular, \(g_\textrm{scal}\) satisfies
-
(i)
\(g_\textrm{scal}\) is subadditive: \(g_\textrm{scal}(t_1+t_2)\le g_\textrm{scal}(t_1)+g_\textrm{scal}(t_2)\) for every \(t_1,\,t_2\in [0,\infty )\),
-
(ii)
\(0\le g_\textrm{scal}(t)\le 1\wedge \ell t\),
-
(iii)
\(\frac{g_\textrm{scal}(t)}{t}\rightarrow \ell \) as \(t\rightarrow 0^+\)
(cf. formula (1.6) in [33, Theorem 1.1] for the definition of \(g_\textrm{scal}\), and [33, Section 4] for further properties).
In formula (4.3) the total variation of the Cantor part of the scalar function \(u_i\in GBV(\Omega )\), \(|D^cu_i|(\Omega )\), is defined as the least upper bound of the family of measures \(|D^c\big ((u_i\wedge k)\vee (-k)\big )|(\Omega )\), for \(k>0\) (cf. [7, Definition 4.33, Theorem 4.34]). A similar construction can be performed for every \(u\in (GBV(\Omega ))^m\).
Precisely, [5, Lemma 2.10] or [45, Theorem 2.7] give that for every \(u\in (GBV(\Omega ))^m\) for which \(|D^cu|\) is a finite measure on \(\Omega \), one can construct a vector measure on \(\Omega \) with total variation coinciding exactly with \(|D^cu|(B)\) for every Borel subset B of \(\Omega \). For this reason such a vector measure, is denoted by \(D^cu\). Let us briefly recall the construction of \(D^cu\). To this aim, the family of truncations \(\mathcal {T}_k\) defined in (3.11) is employed. Indeed, for every \(u\in (GBV(\Omega ))^m\) such that \(|D^cu|\) is a finite measure on \(\Omega \), it is possible to show that the following limit exists for every Borel subset B of \(\Omega \)
In addition, \(\lambda \) is actually independent from the chosen family of truncations. The set function \(\lambda \) turns out to be a vector Radon measure on \(\Omega \), and moreover equality \(|\lambda |(B)=|D^cu|(B)\) is true for every B as above.
Finally, for functions \(u\in (GBV(\Omega ))^m\) satisfying estimate (4.3) it is also true that
(cf. [5, Proposition 2.12, Remark 2.13]), here one works with the one-point compactification of \(\mathbb {R}^m\). We remark that we deal with \((GBV(\Omega ))^m\) and not with the strictly larger space \(GBV(\Omega ;\mathbb {R}^m)\), which is not even a vector space, see [7, Remark 4.27]. Using the notation of [45, Definition 3.1], the domain of finiteness of the functional \(\mathcal {F}_0\) in (2.13) can be written precisely as \((GBV_\star (\Omega ))^m\times \{1\}\), where \((GBV_\star (\Omega ))^m\) is the space of functions \(u\in (GBV(\Omega ))^m\) such that the energies (4.3), computed for the truncations \((u_i\wedge k)\vee (-k)\), are bounded uniformly with respect to k, for \(i\in \{1,\ldots ,m\}\).
4.2 Surface Energy in BV
We prove below the lower bound in BV for the surface term. We recall that the definition of the surface energy density g has been given in (2.12).
Proposition 4.1
Let \(u\in BV(\Omega ;\mathbb {R}^m)\), and \((u_\varepsilon ,v_\varepsilon )\rightarrow (u,1)\) in \(L^1(\Omega ;\mathbb {R}^{m+1})\). Then for all \(A\in \mathcal {A}(\Omega )\)
where g has been defined in (2.12).
Proof
Let \((u_\varepsilon ,v_\varepsilon )\rightarrow (u,1)\) in \(L^1(\Omega ;\mathbb {R}^{m+1})\) be such that
Up to subsequences and with a small abuse of notation, we can assume that the previous lower limit is in fact a limit. Let us define the measures \(\mu _\varepsilon \in \mathcal {M}^+_b(A)\)

Extracting a further subsequence, we can assume that
as \(\varepsilon \rightarrow 0\), for some \(\mu \in \mathcal {M}^+_b(A)\), so that
Equation (4.7) will follow once we have proved that

We will prove the last inequality for points \(x_0\in J_u\cap A\) such that

where \(\nu :=\nu _u(x_0)\) and \(Q^\nu _\rho (x_0){:=x_0+\rho Q^\nu }\) is the cube centred in \(x_0\), with side length \(\rho \), and one face orthogonal to \(\nu \). We remark that such conditions define a set of full measure in \(J_u\cap A\).
For \(x_0\in J_u\cap A\) as above, we get

where we used (4.8) and
We introduce

and compute
where in the last step we used that the definition of \(\gamma _\varepsilon \) implies \(1-\gamma _\varepsilon =\ell \gamma _\varepsilon \varepsilon ^{1/2} {\le \ell \varepsilon ^{1/2}}\). Therefore

By (2.5), for every \(\delta \in (0,1)\) one has \(\Psi (\xi )\ge (1-\delta ){\Psi _\infty }(\xi )\) for \(\xi \) sufficiently large. As \({\Psi _\infty }\) is continuous, there is \(C(\delta )>0\) such that
We choose \(\delta _\rho \rightarrow 0\) such that \(\rho C(\delta _\rho )\rightarrow 0\). As \(\varepsilon f^2({\tilde{v}}_\varepsilon )\le 1\), we have
with \(\rho ^{1-n} \mathcal {L}^n(Q_\rho ^\nu ) C(\delta _\rho )=\rho C(\delta _\rho )\rightarrow 0\) as \(\rho \rightarrow 0\). We conclude by (4.10) that

where \(\mathcal {F}_\varepsilon ^{\infty }\) has been defined in (2.11). Setting \(y:=(x-x_0)/\rho \in Q^\nu \), and changing variable in the previous expression we get

where \(w^\rho (y):=w(\rho y+x_0)\) for \(y\in Q^\nu \). Recalling that \(u_\varepsilon \rightarrow u\) in \(L^1(\Omega ;\mathbb {R}^m)\), by diagonalization we can find subsequences \(\{\rho _k\}_k\) and \(\{\varepsilon (\rho _k)\}_k\) such that \(u_{\varepsilon (\rho _k)}^{\rho _k}\rightarrow [u](x_0)\chi _{\{y\cdot \nu >0\}}+u^-(x_0)\) in \(L^1(Q^\nu ;\mathbb {R}^m)\) and

Being \(\mathcal {F}_\varepsilon ^{\infty }\) invariant for translations of the first argument, we find

that is (4.9), and this concludes the proof. \(\square \)
4.3 Diffuse Part in BV
Proposition 4.2
Let \(u\in BV(\Omega ;\mathbb {R}^m)\), \((u_\varepsilon ,v_\varepsilon )\rightarrow (u,1)\) in \(L^1(\Omega ;\mathbb {R}^{m+1})\), \(A\in \mathcal {A}(\Omega )\). Then
where \(h^\textrm{qc}\) and \(h^{\textrm{qc},\infty }\) have been defined in (2.6)–(2.9).
We remark that this statement can be proven using the lower-semicontinuity result by Fonseca and Leoni [55, Th. 1.8], following an argument similar to that used in [5, Subsection 4.1]. Instead, our proof is based on the following result from [3, Theorem 4.1], see also [7, Theorem 5.47].
Theorem 4.3
(Ambrosio-Dal Maso) Let \(\phi :\mathbb {R}^{m\times n}\rightarrow [0,\infty )\) be quasiconvex and such that
and define \(F:L^1(\Omega ;\mathbb {R}^m)\rightarrow \mathbb {R}\) by
Then for any \(u\in BV(\Omega ;\mathbb {R}^m)\) we have
where \(\phi ^\infty (\xi ):=\limsup _{t\rightarrow \infty } \phi (t\xi )/t\). In particular the latter functional is lower semicontinuous with respect to the strong \(L^1(\Omega ;\mathbb {R}^m)\) convergence.
We start with a truncation result.
Lemma 4.4
There are two functions \(\alpha ,\beta :(0,1)\rightarrow (0,1)\), with \(\lim _{\delta \uparrow 1}\alpha _\delta =1\) and \(\lim _{\delta \uparrow 1}\beta _\delta =0\), such that for any \(\varepsilon >0\), \((u_\varepsilon ,v_\varepsilon )\in W^{1,2}(\Omega ;\mathbb {R}^m\times [0,1])\), \(\delta \in (0,1)\) and \(A\in \mathcal {A}(\Omega )\) there is \({\tilde{u}}_\varepsilon ^\delta \in GSBV(A;\mathbb {R}^m)\) such that
where \(H_\delta \) is defined for \(A\in \mathcal {A}(\Omega )\) and \(w\in L^1(A;\mathbb {R}^m)\) by
If one has \((u_\varepsilon ,v_\varepsilon )\rightarrow (u,1)\) in \(L^1(\Omega ;\mathbb {R}^{m+1})\) as \(\varepsilon \rightarrow 0\), then \({\tilde{u}}_\varepsilon ^\delta \rightarrow u\) in \(L^1(A;\mathbb {R}^{m})\) as \(\varepsilon \rightarrow 0\), for any fixed \(\delta \in (0,1)\).
We stress that, for the sake of notational simplicity, we will omit here and below the explicit dependence of \({\tilde{u}}^\delta _\varepsilon \) on the set A.
Proof
We fix \(\delta \in (0,1)\) and \(\varepsilon >0\). We compute, for any pair \((u,v)\in W^{1,2}(\Omega ;\mathbb {R}^{m} \times [0,1])\),

where h has been introduced in (2.6) and \(\Phi :[0,1]\rightarrow [0,\frac{1}{2}]\) is defined by
We observe that \(\Phi \) is strictly increasing, \(\Phi (1)=\frac{1}{2}\) and in particular \(\Phi \) is bijective. By the coarea formula,
Therefore there is \({\bar{t}}\in (\Phi (\delta ^2),\Phi (\delta ))\) such that
We define
(dropping the dependence on both \(\varepsilon \) and \(\delta \) from \({\tilde{u}}\)) and obtain from (4.14),
We recall that \({\bar{t}}\ge \Phi (\delta ^2)\) and that \(\Phi \) is increasing, define \(\alpha _\delta :=\delta ^3\), \(\beta _\delta :=\sqrt{1- \delta ^2}(\Phi (\delta )-\Phi (\delta ^2))\), and conclude
We also remark that \(\Vert {\tilde{u}}-u\Vert _{L^1(A)} \le \Vert u\Vert _{L^1(\{v\le \Phi ^{-1}({\bar{t}})\})}\), hence, if the sequence \(u_\varepsilon \) is equiintegrable and \(v_\varepsilon \rightarrow 1\) in \(L^1(A)\), we obtain that \(u_\varepsilon -{\tilde{u}}_\varepsilon \rightarrow 0\) in \(L^1(A;\mathbb {R}^m)\). \(\square \)
The next lemma is a minor reformulation of [64, Lemma 5.1]. The latter improves the statement of [7, Theorem 3.95] on the convergence of the blow-ups of a BV-function in a Cantor point. A more general version of this result can be found in [70, Lemma 10.6].
Lemma 4.5
Let \(u\in BV(\Omega ;\mathbb {R}^m)\) and let \(\eta :\Omega \rightarrow S^{m-1}\), \(\xi :\Omega \rightarrow S^{n-1}\) be Borel maps such that \(D^cu=\eta \otimes \xi |D^cu|\). Then, for \(|D^cu|\)-a.e. \(x\in \Omega \) and for all given \(\mu \in \mathcal {M}^+(\Omega )\), there exists a sequence \(\rho _i\rightarrow 0\), as \(i\rightarrow \infty \), such that
as \(i\rightarrow \infty \), for some nondecreasing function  with
with

where \(u_{Q^{\xi (x)}_{\rho _i}(x)}\) denotes the average of u over \(Q^{\xi (x)}_{\rho _i}(x)\).
Proof
For simplicity we will denote \(Q_1:=Q^{\xi (x)}\), \(Q_\rho (x):=x+\rho Q_1\), and
By general properties of BV functions (4.17) holds for the entire family \(\rho \rightarrow 0\) and by Radon-Nikodym differentiation
\(|D^cu|\)-a.e. \(x\in \Omega \). Up to a further \(|D^cu|\)-negligible set, [7, Theorem 3.95] and [64, Lemma 5.1] provide a sequence \(\rho _i\rightarrow 0\) such that
as \(i\rightarrow \infty \), for some \(\gamma \in \mathcal {M}^+(Q_1)\) with \(\gamma (Q_1)=1\) and some nondecreasing function  with
with  .
.
Let us check that the sequence \(\rho _i\rightarrow 0\) can be chosen such that (4.16) holds. Indeed, fixed \(i\in \mathbb {N}{\setminus } \{0\}\), we have \(\mu (\partial Q_{s\rho _i}(x_0))=0\) for \(\mathcal {L}^1\)-a.e.  . Moreover, the maps
. Moreover, the maps

are continuous as \(s\rightarrow 1^-\), respectively for the convergences \(L^1(Q_1;\mathbb {R}^m)\) and weak*-\(\mathcal {M}(Q_1)\), by definition of \(u^{\rho }_x\) and \(t_{\rho }\). Hence, we can find \(s_i\in (0,1)\) such that (4.16), (4.17) and the \(L^1(Q_1,\mathbb {R}^m)\) convergence in (4.18) hold for \(s_i\rho _i\) in place of \(\rho _i\).
We next check (4.19). By (4.21) and (4.22) we have that \(|Du_x|\le \gamma \). Hence, for \(t\in (0,1)\) such that \(\gamma (\partial Q_t)=0\), recalling that \(|Du^{\rho _i}_x|(Q_1)=\gamma (Q_1)=1\), we obtain
We infer that
and letting \(t\rightarrow 1^-\) gives \(Du^{\rho _i}_x(Q_1)\rightarrow Du_x(Q_1)\) as \(i\rightarrow \infty \). In conclusion
and then  . This gives (4.19) by monotonicity of \(\chi \). Finally, \(|Du_x|(Q_1)=1\) provides the strict-\(BV(Q_1;\mathbb {R}^m)\) convergence in (4.18). \(\square \)
. This gives (4.19) by monotonicity of \(\chi \). Finally, \(|Du_x|(Q_1)=1\) provides the strict-\(BV(Q_1;\mathbb {R}^m)\) convergence in (4.18). \(\square \)
Proof of Proposition 4.2
Step 0: Preparation. We assume \((u_\varepsilon ,v_\varepsilon )\rightarrow (u,1)\) in \(L^1(\Omega ;\mathbb {R}^{m+1})\) for some \(u\in BV(\Omega ;\mathbb {R}^m)\). Let \(A\subseteq \mathcal {A}(\Omega )\), \(\delta \in (0,1)\) and let \({\tilde{u}}_\varepsilon ^\delta \) be as in Lemma 4.4. We define the measure

so that \(\mu _\varepsilon ^\delta (A)=H_\delta ({\tilde{u}}_\varepsilon ^\delta ;A)\le \mathcal {F}_\varepsilon (u_\varepsilon ,v_\varepsilon ;A) + {h(0)\mathcal {L}^n(A\cap \{v_\varepsilon \le \delta \})}\). Passing to a subsequence we can assume that \(\displaystyle {\lim _{\varepsilon \rightarrow 0}}\mathcal {F}_\varepsilon ({u_\varepsilon ,v_\varepsilon };A)\) exists finite and that \(\mu _\varepsilon ^\delta \rightharpoonup \mu ^\delta \) weakly\(^*\) in the sense of measures on A as \(\varepsilon \rightarrow 0\), for some \(\mu ^\delta \in \mathcal {M}^+_b(A)\). If we can show that
and
for all \(\delta \in (0,1)\), then the conclusion follows.
Step 1: Absolutely continuous part. We prove (4.23). We can assume that the left-hand side is finite. First we observe that for \(\mathcal {L}^n\)-a.e. \(x_0\in A\) one has
where \(Q_\rho (x_0):=x_0+(-\frac{1}{2}\rho ,\frac{1}{2}\rho )^n\) and \(I:=\{\rho \in (0, {\frac{2}{\sqrt{n}}}\textrm{dist}(x_0,\partial A)):\, \mu ^\delta (\partial Q_\rho (x_0))=0\}\). We define \(u^\rho :Q_1\rightarrow \mathbb {R}^m\) by
By the properties of BV, for \(\mathcal {L}^n\)-a.e. \(x_0\in A\), after possibly extracting a further subsequence, \(u^\rho (y)\rightarrow \nabla u(x_0)y\) in \(L^1(Q_1;\mathbb {R}^m)\) as \(\rho \rightarrow 0\). We further define
so that \(u^\rho _\varepsilon \rightarrow u^\rho \) in \(L^1(Q_1;\mathbb {R}^m)\) as \(\varepsilon \rightarrow 0\) for any fixed \(\rho >0\) (and \(\delta \in (0,1)\)). We take a diagonal subsequence so that \(w_i(y):=u^{\rho _i}_{\varepsilon _i}(y)\rightarrow \nabla u(x_0)y\) in \(L^1(Q_1;\mathbb {R}^m)\) and
We fix \(M\in \mathbb {N}\) and for every i, by averaging we choose \(k_i\in \{M+1,\dots , 2M\}\) such that
which implies that \({\hat{w}}_i:=\mathcal {T}_{k_i}(w_i)\), with \(\mathcal {T}_{k_i}\) defined in (3.11), obeys
Indeed, in view of (2.8) and \(\Vert \nabla \mathcal {T}_{k_i}\Vert _{L^\infty (\mathbb {R}^m)}\le 1\) we have
The inequality in (4.27) then follows from (4.26).
Moreover, note that if \({a_M}>\Vert \nabla u(x_0)y\Vert _{L^\infty (Q_1)}+1\) then \(w_i\rightarrow \nabla u(x_0)y\) implies \({\hat{w}}_i\rightarrow \nabla u(x_0)y\) in \(L^1(Q_1;\mathbb {R}^m)\).
We recall that \(\mathcal {T}_{k_i}\in C^1\) implies \(\mathcal {H}^{n-1}(J_{{\hat{w}}_i}\cap Q_1)\le \mathcal {H}^{n-1}(J_{w_i}\cap Q_1)\). From (4.25) and \(\rho _i\rightarrow 0\) we deduce \(\mathcal {H}^{n-1}(J_{w_i}\cap Q_1)\rightarrow 0\) and, with \(|{\hat{w}}_i|\le a_{M+1}\) pointwise,
and therefore
With (4.25) and (4.27), using that \(w_i\rightarrow \nabla u(x_0)y\) in measure, we get
By the lower semicontinuity of the functional in the left-hand side (Theorem 4.3) and \({\hat{w}}_i\rightarrow \nabla u(x_0)y\) in \(L^1(Q_1;\mathbb {R}^m)\) we deduce
for \(\mathcal {L}^n\)-a.e. \(x_0\), every M, and every \(\delta \). This proves (4.23).
Step 2: Cantor part. We prove (4.24). By Alberti’s rank-one theorem we can assume without loss of generality that
with \(\eta (x_0)\in S^{m-1}\), \(\xi (x_0)\in S^{n-1}\) for \(|D^cu|\)-a.e. \(x_0\in A\). We fix a unit cube \(Q_1:=Q^{\xi (x_0)}\) with one face orthogonal to \(\xi (x_0)\), write \(Q_\rho (x_0):=x_0+\rho Q_1\), and select a sequence \(\rho _i\rightarrow 0\) as in Lemma 4.5, applied for the given \(u\in BV(\Omega ,\mathbb {R}^m)\) and \(\mu :=\mu ^\delta \).
As above, for \(|D^cu|\)-a.e. \(x_0\) one has
We define
so that, defining \(u_{x_0}(y):=\eta (x_0)\chi _{x_0}(y\cdot \xi (x_0))\), \(\lim _{\rho \rightarrow 0}\lim _{\varepsilon \rightarrow 0 }u_\varepsilon ^\rho = u_{x_0}\) in \(L^1(Q_1;\mathbb {R}^m)\) (for every \(\delta \in (0,1)\)) and
Taking a diagonal subsequence we see that there is \(\varepsilon _i\rightarrow 0\) such that
with \(|Du_{x_0}|(Q_1)=1\), and setting \(t_i:=t_{\rho _i}\rightarrow \infty \),
We fix \(M>0\) and, by averaging, for every i choose \(k_i\in \{M+1,\dots , 2M\}\) such that
which implies that \({\hat{w}}_i:={\mathcal {T}_{k_i}(w_i)}\in SBV\cap L^\infty (Q_1;\mathbb {R}^m)\) obeys, arguing as in Step 1 above and by taking into account that \(t_i\rightarrow \infty \),
Further, since \(\chi \) is bounded, for M sufficiently large we have \(r_i:=\Vert {\hat{w}}_i-u_{x_0}\Vert _{L^1(Q_1)} \rightarrow 0\). For every i we select \(q_i\in (1-r_i^{1/2},1)\) such that
where \({\hat{w}}_i^-\) and \(u_{x_0}^+\) denote the inner and outer trace, respectively, and define
Then, the choice of \(q_i\), (4.29), and \(\rho _i t_{i}\rightarrow 0\) yield
In addition, we get from (2.8) and \(t_i\rightarrow \infty \)
Further, \(w_i^*\in BV(Q_1;\mathbb {R}^m)\) and \(\textrm{supp}(w_i^*-u_{x_0})\subset \subset Q_1\). By [7, Lemma 5.50] and Theorem 4.3
Therefore, being  a rank-one matrix, the latter estimate together with (4.30) and (4.31) yield that
a rank-one matrix, the latter estimate together with (4.30) and (4.31) yield that
Recalling (4.29), we infer that
for every M sufficiently large. Therefore, by letting \(M\rightarrow \infty \) we conclude that
As  , this and (4.28) conclude the proof of (4.24). \(\square \)
, this and (4.28) conclude the proof of (4.24). \(\square \)
The lower bound in BV follows at once from the lower bounds for the surface and the diffuse parts.
Theorem 4.6
Let \(u\in BV(\Omega ;\mathbb {R}^m)\). Then, for all \(A\in \mathcal {A}(\Omega )\)
where \(\mathcal {F}_\varepsilon \) and \(\mathcal {F}_0\) have been defined in (2.1) and (2.13).
Proof
For simplicity, we will prove the statement for \(A=\Omega \). We argue by localization. Assume that \((u_\varepsilon ,v_\varepsilon )\rightarrow (u,1)\) in \(L^1(\Omega ;\mathbb {R}^{m+1})\), with \(u\in BV(\Omega ;\mathbb {R}^m)\), and that
Set

and notice that \(\mu \) is a monotone set function which is superadditive on disjoint open sets, \(\lambda \) is a positive Borel measure and \(\psi _i\) are positive Borel functions satisfying
thanks to Propositions 4.1 and 4.2. By [28, Proposition 1.16] we conclude
which gives the thesis. \(\square \)
Remark 4.7
From the argument in Lemma 4.4 one can also deduce directly that \(u\in (GBV(\Omega ))^m\). Indeed, consider \((u_\varepsilon ,v_\varepsilon )\rightarrow (u,v)\) in \(L^1(\Omega ;\mathbb {R}^{m+1})\) with \(\sup _\varepsilon \mathcal {F}_\varepsilon (u_\varepsilon ,v_\varepsilon )<\infty \). Necessarily \( v=1\) \(\mathcal {L}^n\)-a.e. on \(\Omega \). Moreover, with fixed \(\delta \in (0,1)\), keeping the notation introduced in Lemma 4.4, using the growth conditions on h (see (2.8)) we get
for some positive constant c depending on \(\delta \) and on \(\mathcal {L}^n(\Omega )\). In particular, for each component \((\tilde{u}_\varepsilon ^\delta )_i\) of \(\tilde{u}_\varepsilon ^\delta \), \(i\in \{1,\ldots ,n\}\), we have \((\tilde{u}_\varepsilon ^\delta )_i\in GSBV(\Omega )\) and
Then, if \(k>0\) and \(\tau _k(s):=(s\vee k)\wedge (-k)\), from the estimate above we infer that \(|D(\tau _k((\tilde{u}_\varepsilon ^\delta )_i))|(\Omega )\le C_k\), with \(C_k>0\) depending on k and on the sequence, but not on \(\varepsilon \). Therefore, there is a subsequence that converges weakly in \(BV(\Omega )\). This implies, recalling that \(\tilde{u}_\varepsilon ^\delta \rightarrow u\) in \(L^1(\Omega ;\mathbb {R}^m)\) as \(\varepsilon \rightarrow 0\) for all \(\delta \in (0,1)\), that \(\tau _k(u_i)\in BV(\Omega )\) for all k. In conclusion, we deduce that \(u_i\in GBV(\Omega )\), for all \(i\in \{1,\ldots ,n\}\), and thus \(u\in (GBV(\Omega ))^m\).
4.4 Lower Bound in GBV
In this section we extend the validity of the lower bound Theorem 4.6 to every \(u\in (GBV(\Omega ))^m\). We first prove that the functional \(\mathcal {F}_0\) is continuous under truncations.
Proposition 4.8
Let \(\mathcal {F}_0\) and \(\mathcal {T}_k\) be defined as in (2.13) and (3.11), respectively. Then, for all \(u\in (GBV(\Omega ))^m\) with \(\mathcal {F}_0(u,1)<\infty \) we have
Proof
We prove the convergence of the volume, Cantor and surface terms separately. It is useful to recall for the rest of the proof that \(\Vert \nabla \mathcal {T}_k\Vert _{L^\infty (\mathbb {R}^m)}\le 1\).
For the volume part, we observe that (2.8) implies \(|\nabla u|\in L^1(\Omega )\). We have \(\nabla (\mathcal {T}_k(u))=\nabla u\) for \(\mathcal {L}^n\)-a.e. \(x\in \Omega _k:=\{|u|\le a_k\}\), therefore in view of (2.8) we get
so that, as \(a_k\rightarrow \infty \) as \(k\uparrow \infty \), we conclude
For the surface term we recall that \(J_{\mathcal {T}_k(u)}\subseteq J_u\) for every \(k\in \mathbb {N}\) with \(\nu _{\mathcal {T}_k(u)}=\nu _u\) for \(\mathcal H^{n-1}\)-a.e. \(x\in J_{\mathcal {T}_k(u)}\). Then, thanks to (4.6) we infer that \((\mathcal {T}_k(u))^\pm \rightarrow u^\pm \), \(\chi _{J_{\mathcal {T}_k(u)}}\rightarrow \chi _{J_u}\) and \(|[\mathcal {T}_k(u)]|\le |[u]|\) \(\mathcal H^{n-1}\)-a.e. in \(J_u\), and then we conclude
thanks to Lemmata 3.7 and 3.8 (ii) and to the Dominated Convergence Theorem.
For what the Cantor part of the energy is concerned, by (2.8) we have that \(0\le h^{\textrm{qc},\infty }(\xi )\le c |\xi |\). Further, the definitions of \(\mathcal {T}_k\) and of \(D^cu\) outlined in (4.5) yield in particular

Thus,
and therefore
which concludes the proof. \(\square \)
We are ready to prove the lower bound for generalized functions of bounded variations.
Theorem 4.9
Let \(u\in (GBV(\Omega ))^m\). Then
where \(\mathcal {F}_\varepsilon \) and \(\mathcal {F}_0\) have been defined in (2.1) and (2.13).
Proof
Let \(u\in (GBV(\Omega ))^m\) and let \((u_\varepsilon ,v_\varepsilon )\in {W^{1,2}}(\Omega ; \mathbb {R}^{m+1})\) be such that \((u_\varepsilon ,v_\varepsilon )\rightarrow (u,1)\) in \(L^1(\Omega ;\mathbb {R}^{m+1})\), with \(v_\varepsilon \in [0,1]\) \(\mathcal {L}^n\)-a.e. in \(\Omega \). Without loss of generality we can suppose that \(\liminf _{\varepsilon \rightarrow 0}\mathcal {F}_{\varepsilon }(u_\varepsilon ,v_\varepsilon )<\infty \), that the latter is actually a limit (up to a subsequence not relabeled), and that \((u_\varepsilon ,v_\varepsilon )\rightarrow (u,1)\) \(\mathcal {L}^n\)-a.e. in \(\Omega \). In particular, from Sect. 4.1 we infer that \(u\in (GBV(\Omega ))^m\), with \(|\nabla u|\in L^1(\Omega )\) and satisfying (4.6) and (4.3), so that \(\mathcal {F}_0(u,1)<\infty \).
Recalling the definition of the truncation \(\mathcal {T}_k\) in (3.11), we have that \(\mathcal {T}_k(u_\varepsilon )\rightarrow \mathcal {T}_k(u)\) in \(L^1(\Omega ;\mathbb {R}^m)\) for any k and that \(\mathcal {T}_k(u)\in BV({\Omega };\mathbb {R}^m)\), being \(\mathcal {F}_0(u,1)<\infty \). Hence, we can apply Theorem 4.6 to say that
We claim that for all \(M\in \mathbb {N}\) there is \(k_{M}\in \{M+1,\dots ,2M\}\) independent of \(\varepsilon \) such that after extracting a further subsequence
for some \(c>0\) independent of \(\varepsilon \) and of M. Given this for granted, we get by (4.34), (4.35) and by the convergence \(u_\varepsilon \rightarrow u\) in measure
Finally, using the continuity under truncations for \(\mathcal {F}_0\) established in Proposition 4.8, we obtain
and hence (4.33).
It remains to prove (4.35). To this aim we argue as in Proposition 3.2 using De Giorgi’s averaging-slicing method on the range. First, for all \(k\in \mathbb {N}\) we split the energy contributions
By (2.3) and the definition of \(\mathcal {T}_k\), the last but one term in the previous expression can be estimated as
for some \(c>0\). Summing (4.36) and (4.37) and averaging, we conclude that there exists \(k_{M,\varepsilon }\in \{M+1,\dots ,2M\}\) such that
for some \(c>0\). As \(\varepsilon \rightarrow 0\), there exists a subsequence of \(\{k_{M,\varepsilon }\}\) that is independent of \(\varepsilon \). This yields (4.35) and concludes the proof. \(\square \)
5 Upper Bound
In this Section we prove the \(\Gamma -\limsup \) inequality in Theorem 2.1. In order to be able to obtain existence of minimizers for the perturbed functionals (see Sect. 6), we consider a perturbed version of the functional which includes an additional uniformly coercive term, and prove the upper bound directly for the modified functional. We fix a function \(\eta :(0,1]\rightarrow [0,1]\) such that
and define
where \(\mathcal {F}_\varepsilon \) has been defined in (2.1).
One key ingredient in the proof of the upper bound is that the \(\overline{\Gamma }\)-limit of \(\mathcal {F}_\varepsilon ^\eta \) satisfies the hypotheses of [20, Theorem 3.12], so that it can be represented as an integral functional. Its diffuse and surface densities will be identified by a direct computation.
In order to prove that \(\overline{\Gamma }\text {-}\lim _{\varepsilon \rightarrow 0}\mathcal {F}_\varepsilon ^{{\eta }}(u,1;\cdot )\) is a Borel measure, we first check the weak subadditivity of the \(\Gamma \)-upper limit of \(\mathcal {F}_\varepsilon ^{{\eta }}\).
Lemma 5.1
Let \(u\in L^1(\Omega ;\mathbb {R}^m)\), let \(A',A,B\in \mathcal {A}(\Omega )\) with \(A'\subset \subset A\), then
where \(\mathcal {F}_\varepsilon ^\eta \) has been defined in (5.2).
Proof
To simplify the notation let us set \(\mathcal {F}'':=\Gamma (L^1)\hbox {-}\limsup _{{\varepsilon \rightarrow 0}}\mathcal {F}_\varepsilon ^\eta \). It is not restrictive to assume that the right-hand side of (5.3) is finite, so that \(u\in {(GBV\cap L^1(A\cup B))^m}\). Let \((u_\varepsilon ^A,v_\varepsilon ^A),\ (u_\varepsilon ^B,v_\varepsilon ^B)\in {W^{1,2}}(\Omega ;\mathbb {R}^{m+1})\) be such that
and
for \(J\in \{A,B\}\).
Step 1. Estimate (5.3) is valid if \(u\in BV\cap L^2(A\cup B;\mathbb {R}^m)\) and (5.5) holds for two sequences converging to u in \(L^2(\Omega ;\mathbb {R}^m)\). For \(\delta :=\textrm{dist}(A^\prime ,\partial A)>0\) and some \(M\in \mathbb {N}\), we set for all \(i\in \{1,\ldots ,M\}\)
and \(A_0:=A^\prime \), so that \(A_{i-1}\subset \subset A_i\subset A\). Let \(\varphi _i\in C_c^1(\Omega )\) be a cut-off function between \(A_{i-1}\) and \(A_i\), i.e., \(\varphi _i|_{A_{i-1}}=1\), \(\varphi _i|_{A_{i}^c}=0\), and \(\Vert \nabla \varphi _i\Vert _{L^\infty (\Omega )}\le \frac{2\,M}{\delta }\). Then, we define
and
For \(i\in \{2,\ldots ,M-1\}\), \((u_\varepsilon ^i,v_\varepsilon ^i)\in {W^{1,2}}(\Omega ;\mathbb {R}^{m+1})\). Arguing exactly as in [33, Lemma 6.2], for all \(\varepsilon >0\) we can find an index \(i_\varepsilon \in \{2,\dots ,M-1\}\) such that
Passing first to the limit as \(\varepsilon \rightarrow 0\) and then as \(M\rightarrow \infty \) we obtain (5.3) having assumed that \(u_\varepsilon ^J\rightarrow u\) in \(L^2(\Omega ;\mathbb {R}^m)\), \(J\in \{A,B\}\).
Step 2. Estimate (5.3) is valid if \(u\in (GBV\cap L^1(A\cup B))^m\). We use De Giorgi’s slicing/averaging techniques on the co-domain by employing the truncation functions introduced in (3.11). The argument is analogous to that developed in Step 1 of Proposition 3.2.
Note that if \(u\in (GBV(A\cup B))^m\) then \(\mathcal {T}_k(u)\in BV\cap L^\infty (A\cup B;\mathbb {R}^m)\). In addition, for all \(k\in \mathbb {N}\) and \(J\in \{A,B\}\) it is easy to check that \(\mathcal {T}_k(u_\varepsilon ^J)\in W^{1,2}(\Omega ;\mathbb {R}^m)\), that \(\mathcal {T}_k(u_\varepsilon ^J)\rightarrow \mathcal {T}_k(u)\) as \(\varepsilon \rightarrow 0\) in \(L^2({\Omega };\mathbb {R}^m)\), and that
We estimate the last but one term. The growth conditions on \(\Psi \) (cf. (2.3)) and \(\Vert \nabla \mathcal {T}_k\Vert _{L^\infty (\mathbb {R}^m)}\le 1\) yield for a constant \(c>0\)
Collecting (5.8) and (5.9) we conclude that
Let now \(M\in \mathbb {N}\), by summing up the latter inequality for both A and B and by averaging, there exists \(k_{\varepsilon ,M}\in \{M+1,\ldots ,2M\}\) such that
Up to a subsequence, we may take the index \(k_{\varepsilon ,M}=k_M\), i.e. to be independent of \(\varepsilon \). Therefore, passing to the limit as \(\varepsilon \rightarrow 0\), the convergence \(u_\varepsilon ^J\rightarrow u\) in measure for \(J\in \{A,B\}\), (5.4), (5.5), (5.10) and Step 1 yield
Eventually, since \(\mathcal {T}_{k_M}(u)\rightarrow u\) in \(L^1(\Omega ;\mathbb {R}^m)\) as \(M\uparrow \infty \), by the lower semicontinuity of \(\mathcal {F}''\) for the \(L^1(\Omega ;\mathbb {R}^m)\) convergence we conclude (5.3). \(\square \)
We are now ready to prove the upper bound inequality.
Theorem 5.2
Let \(\mathcal {F}_{\varepsilon }^\eta \) and \(\mathcal {F}_0\) be defined in (5.2) and (2.13), respectively. For every \((u,v)\in L^1(\Omega ;\mathbb {R}^{m+1})\) it holds that
Proof
Given a subsequence \((\mathcal {F}_{\varepsilon _k}^\eta )\) of \((\mathcal {F}_\varepsilon ^\eta )\), there exists a further subsequence, not relabeled, which \(\overline{\Gamma }\)-converges to some functional \(\widehat{\mathcal {F}}\), that is,
where \(\mathcal {F}'\) and \(\mathcal {F}''\) denote here the \(\Gamma (L^1)\)-lower and upper limits of \(\mathcal {F}_{\varepsilon _k}^\eta \) and where the subscript \(_-\) denotes the inner regular envelope of the relevant functional ( [41, Definition 16.2 and Theorem 16.9]).
We remark that \(\widehat{\mathcal {F}}(u,v;\cdot )\) is the restriction of a Borel measure to open sets by [41, Theorem 14.23]. Indeed, \(\widehat{\mathcal {F}}(u,v;\cdot )\) is increasing and inner regular by definition; additivity follows from (5.14), once one checks that \((\mathcal {F}')_-\) is superadditive and \((\mathcal {F}'')_-\) is subadditive. The former condition is a direct consequence of the additivity of \(\mathcal {F}_{\varepsilon }(u,v;\cdot )\) and [41, Proposition 16.12]. The latter follows from Lemma 5.1 along the lines of [41, Proposition 18.4], using Lemma 5.1 instead of [41, (18.6)].
We divide the proof of (5.13) into several steps. First note that it is sufficient to prove it for \(v=1\) \(\mathcal {L}^n\)-a.e. on \(\Omega \).
Step 1. Estimate on the diffuse part for \(u\in BV(\Omega ;\mathbb {R}^m)\). We first prove a global rough estimate for \(\mathcal {F}''\) which actually turns out to be sharp for the diffuse part if \(u\in BV(\Omega ;\mathbb {R}^m)\). To this aim we set \(H:L^1(\Omega ;\mathbb {R}^m)\times \mathcal {A}(\Omega )\rightarrow [0,\infty ]\) as
if \(u\in W^{1,1}(\Omega ;\mathbb {R}^m)\), and \(\infty \) otherwise, where h has been defined in (2.6). We next prove the bound
for \(u\in W^{1,1}(\Omega ;\mathbb {R}^m)\). Given this estimate for granted, on setting \(H^{*}:L^1(\Omega ;\mathbb {R}^m)\times \mathcal {A}(\Omega )\rightarrow [0,\infty ]\)
if \(u\in W^{1,1}(\Omega ;\mathbb {R}^m)\), and \(\infty \) otherwise, the lower semicontinuity of \(\mathcal {F}''\) with respect to the \(L^1(\Omega ;\mathbb {R}^m)\) topology and the relaxation result with respect to the sequential weak topology in \(W^{1,1}(\Omega ;\mathbb {R}^m)\) in [4, Statement III.7] (or [40, Theorem 9.1]) imply then that
In turn, from the estimate above, Theorem 4.3 finally yields
for every \(u\in BV(\Omega ;\mathbb {R}^m)\). Therefore, the bound
follows for every \(u\in BV(\Omega ;\mathbb {R}^m)\) and \(A\in \mathcal {A}(\Omega )\).
To prove (5.16), assume first that u is an affine function, say \(u{(x)}=\xi x+b\), with \(\xi \in \mathbb {R}^{m\times n}\), \(b\in \mathbb {R}^m\). Then, the pair

is such that \((u_k,v_k)\rightarrow (u,1)\) in \(L^2(\Omega ;\mathbb {R}^m)\times L^1(\Omega )\) and recalling \(\eta _{\varepsilon _k}\rightarrow 0\)

Instead, if
we get
Therefore, we conclude (5.16) for every affine function u in view of the last two estimates.
Assume now that \(u\in C^0(\Omega ;\mathbb {R}^m)\) is a piecewise affine function, say \(u{(x)}=\sum _{i=1}^N(\xi _ix+b_i)\chi _{\Omega _i}(x)\), with \(\xi _i\in \mathbb {R}^{m\times n}\), \(b_i\in \mathbb {R}^m\), and \(\Omega _i\in \mathcal {A}(\Omega )\) disjoint and with Lipschitz boundary, and such that \(\mathcal {L}^n(\Omega \setminus \cup _{i=1}^N\Omega _i)=0\). Then, set
where for each \(i\in \{1,\ldots ,N\}\)

and \(\{\varphi _i\}_{1\le i\le N}\) is a partition of unity subordinated to the covering \(\{\Omega _i^\delta \}_{1\le i\le N}\) of \(\Omega \), \(\Omega _i^\delta \) an open \(\delta \)-neighborhood of \(\Omega _i\) for \(\delta >0\), i.e. \(\varphi _i\in C^\infty _c(\Omega _i^\delta )\), \(0\le \varphi _i\le 1\), \(\varphi _i=1\) on \(\Omega _i^{-\delta }\), \(\sum _{i=1}^N\varphi _i=1\) in \(\Omega \) (we write \(\Omega _i^{-\delta }:=\{x: B_\delta (x)\subseteq \Omega _i\}\)). Then, a straightforward computation shows that
where c depends on \(\ell \), \(\Psi \), and \(\xi _1,\dots , \xi _N\). Therefore we conclude (5.16) when u is piecewise affine, namely as \(\delta \rightarrow 0\) in the latter inequality we have
If \(u\in W^{1,1}(\Omega ;\mathbb {R}^m)\), we consider an extension of u itself (still denoted by u for convenience) to \(W^{1,1}_0(\Omega ';\mathbb {R}^m)\), for some open and bounded \(\Omega '\supset \supset \Omega \) (recall that \(\Omega \) is assumed to be Lipschitz regular). Then, we use a classical density result [50, Proposition 2.1 in Chapter X] to find \(u_k\in W^{1,1}_0(\Omega ';\mathbb {R}^m)\) piecewise affine such that \(u_k\rightarrow u\) in \(W^{1,1}(\Omega ';\mathbb {R}^m)\). The continuity of H for the \(W^{1,1}(\Omega ;\mathbb {R}^m)\) convergence, and the lower semicontinuity of \(\mathcal {F}''\) for the \(L^1(\Omega ;\mathbb {R}^{m+1})\) convergence finally imply (5.16).
Step 2. Inner regularity of \(\mathcal {F}''(u,1;\cdot )\) and existence of the \(\Gamma (L^1)\)-limit in \(A\in \mathcal A(\Omega )\) for \(u\in BV(\Omega ;\mathbb {R}^m)\). First we show that if \(u\in BV(\Omega ;\mathbb {R}^m)\) then
Given an open set A and \(\delta >0\), we can find open sets \(A'\), \(A''\), and C, with \(A'\subset \subset A''\subset \subset A\) and \(A\setminus A'\subset C\), such that \(\mathcal H(u;C)\le \delta \), where \(\mathcal H\) is defined in (5.18). Then, by Lemma 5.1 and (5.19) we get
Hence, (5.20) holds true and in turn by (5.14) we have
so that the \(\Gamma \)-limit of \(\mathcal {F}_{\varepsilon _k}^{{\eta }}(u,1;\cdot )\) exists and coincides with \({\widehat{\mathcal {F}}}(u,1;\cdot )\) for all \(u\in BV(\Omega ;\mathbb {R}^m)\).
Step 3. Integral representation of the \(\Gamma (L^1)\)-limit on \(BV(\Omega ;\mathbb {R}^m)\times \{1\}\). We now would like to represent \({\widehat{\mathcal {F}}}\) as an integral functional through [20, Theorem 3.12] and to estimate its diffuse and surface densities. In order to satisfy the coercivity hypothesis [20, Eq. (2.3’)], we introduce an auxiliary functional
for all \(u\in BV(\Omega ;\mathbb {R}^m)\), where \(\lambda \in (0,1]\) is a small parameter. Indeed, (4.2), (4.3), (2.16) and (5.19) yield
for all \(u\in BV(\Omega ;\mathbb {R}^m)\) and for some \(c>0\). Note that \(\widehat{\mathcal {F}}_\lambda \) also satisfies the continuity hypothesis [20, Eq. (2.4)], since
for all \((u,v)\in {W^{1,2}}(\Omega ;\mathbb {R}^{m+1})\), \(z,b\in \mathbb {R}^m\), \(A\in \mathcal {A}(\Omega )\), and analogous properties then hold for \(\widehat{\mathcal {F}}\).
The integral representation result [20, Theorem 3.12] then applies to \(\widehat{\mathcal {F}}_{\lambda }+c\mathcal {L}^n\) and gives, for \(u\in BV(\Omega ;\mathbb {R}^m)\) and \(A\in \mathcal {A}(\Omega )\), taking also into account the aforementioned translational invariance,
where
for \(\xi \in \mathbb {R}^{m\times n}\), Q being a cube with side length 1 centered in the origin;
for \(z\in \mathbb {R}^m\), \(\nu \in S^{n-1}\), \(Q^{\nu }\) being a cube with side length 1 and a face orthogonal to \(\nu \) and \(w_z:=z\chi _{\{x\cdot \nu >0\}}\);
for \(\xi \in \mathbb {R}^{m\times n}\). Let us estimate separately the three densities above. First, observe that by (5.19) we have
so that
for all \(\xi \in \mathbb {R}^{m\times n}\). We next show that
for \(z\in \mathbb {R}^m\), \(\nu \in S^{n-1}\). From (5.22) we have
In turn, by definition of \({\widehat{\mathcal {F}}}\) for every sequence \(({\tilde{u}}_{{k}},{\tilde{v}}_{{k}})\rightarrow (w_z,1)\) in \(L^1(\delta \,Q^{\nu };\mathbb {R}^{m+1})\) we have
The proof of (5.25) therefore reduces to the construction of a suitable sequence \(({\tilde{u}}_{{k}},{\tilde{v}}_{{k}})\), which depends implicitly on \(\delta \in (0,1)\), z and \(\nu \). By Proposition 3.4 applied with the sequences \(\varepsilon _k^*:=\varepsilon _k/\delta \) and \(\eta _k^*:=\eta _{\varepsilon _k}\), there are \((u_k^*,v_k^*)\rightarrow (w_z,1)\) in \(L^2(Q^\nu ;\mathbb {R}^{m+1})\), such that
and
We define \(({\tilde{u}}_k,{\tilde{v}}_k)\in L^2(\delta \,Q^\nu ;\mathbb {R}^{m+1})\) by
Obviously \(({\tilde{u}}_k,{\tilde{v}}_k)\rightarrow (w_z,1)\) in \(L^2({\delta \, Q^\nu };\mathbb {R}^{m+1})\). A change of variable and a straightforward computation using \(\varepsilon _k=\delta \varepsilon _k^*\) yield
Fixed \(\rho >0\), by (2.5) we have
for \(|\xi |\) large, and then
for some \(C(\rho )>0\) and all \(\xi \in \mathbb {R}^{m\times n}\). Then, with (5.30)
Similarly, from the growth conditions in (2.3) and (5.30),
Summing these two estimates,
and taking the limit \(k\rightarrow \infty \), by (5.27), (5.28) and (5.29),
We divide by \(\delta ^{n-1}\) and take the limit \(\delta \rightarrow 0\). Comparing with (5.26),
and since \(\rho \) was arbitrary (5.25) follows.
In conclusion, as \(\lambda \rightarrow 0\), estimates (5.23), (5.24) and (5.25) imply that for all \(u\in BV(\Omega ;\mathbb {R}^m)\)
This, together with the lower bound Theorem 4.6 allows to identify uniquely the \(\Gamma \)-limit of the subsequence \(\mathcal {F}_{\varepsilon _k}^{{\eta }}\). Finally, Urysohn’s property ( [41, Proposition 8.3]) extends the result to the whole family \(\mathcal {F}_{\varepsilon }^\eta \).
Step 4. Representation of the \(\Gamma (L^1)\)-limit on \((GBV(\Omega ))^m\times \{1\}\). To extend the validity of (5.13) to \(u\in (GBV(\Omega ))^m\) we argue by truncation. Indeed, if \(k\in \mathbb {N}\) and \(\mathcal {T}_k\) is the truncation operator defined in (3.11), then by Steps 1–3 we infer that
The conclusion then follows by the \(L^1\)-lower semicontinuity of \(\mathcal {F}''\) and by Proposition 4.8. \(\square \)
We are ready to prove Theorem 2.1.
Proof of Theorem 2.1
The lower bound has been proven in Theorem 4.9. The upper bound follows by Theorem 5.2 with \(\eta _\varepsilon =0\). \(\square \)
6 Compactness and Convergence of Minimizers
Next theorem establishes the compactness of sequences equibounded in energy and in \(L^1\).
Theorem 6.1
Let \(\mathcal {F}_{\varepsilon }\) be defined in (2.1). If \((u_\varepsilon ,v_\varepsilon )\in {W^{1,2}}(\Omega ;\mathbb {R}^{m+1})\) is such that
then there exists a subsequence \((u_j,v_j)\) of \((u_\varepsilon ,v_\varepsilon )\) and a function \(u\in (GBV\cap L^1(\Omega ))^m\) such that \(u_j\rightarrow u\) \(\mathcal {L}^n\)-a.e. and \(v_j\rightarrow 1\) in \(L^1(\Omega )\).
Proof
This follows arguing componentwise, that is, estimating \(\mathcal {F}_{\varepsilon }\) with its one-dimensional counterpart evaluated in a component, and applying the one-dimensional compactness result obtained in [33, Theorem 3.3] as done in Sect. 4.1 (see also the argument in Remark 4.7). \(\square \)
Convergence of minimizers and of minimum values follow now in a standard way by Theorems 2.1 and 6.1. Let \(\eta _\varepsilon >0\) be as in (5.1), i.e. such that  as \(\varepsilon \rightarrow 0\), consider the corresponding family \(\mathcal {F}_\varepsilon ^\eta \) defined in (5.2) and let \(w\in L^q(\Omega ;\mathbb {R}^m)\), with \(q>1\). Let now \(\mathcal {G}_\varepsilon ,\,\mathcal {G}_0:{L^q(\Omega ;\mathbb {R}^{m})\times L^1(\Omega )}\rightarrow [0,\infty ]\) be defined as
as \(\varepsilon \rightarrow 0\), consider the corresponding family \(\mathcal {F}_\varepsilon ^\eta \) defined in (5.2) and let \(w\in L^q(\Omega ;\mathbb {R}^m)\), with \(q>1\). Let now \(\mathcal {G}_\varepsilon ,\,\mathcal {G}_0:{L^q(\Omega ;\mathbb {R}^{m})\times L^1(\Omega )}\rightarrow [0,\infty ]\) be defined as
and
where \(\mathcal {F}_\varepsilon \) and \(\mathcal {F}_0\) have been defined in (2.1) and (2.13), respectively.
The assumption on the asymptotic ratio  as \(\varepsilon \rightarrow 0\) is needed to avoid that the term \(\eta _\varepsilon \Psi (\nabla u)\) competes with the term \((1-v)^2/\varepsilon \), overall influencing the limit behaviour. Indeed, if \(\eta _\varepsilon \sim \varepsilon \), we expect to gain a control on |[u]|, so loosing the limit cohesive effect (compare with [53]).
as \(\varepsilon \rightarrow 0\) is needed to avoid that the term \(\eta _\varepsilon \Psi (\nabla u)\) competes with the term \((1-v)^2/\varepsilon \), overall influencing the limit behaviour. Indeed, if \(\eta _\varepsilon \sim \varepsilon \), we expect to gain a control on |[u]|, so loosing the limit cohesive effect (compare with [53]).
Instead, the addition of the term \(\eta _\varepsilon \Psi (\nabla w)\) is instrumental to guarantee the existence of a minimizer for \(\mathcal {G}_\varepsilon \), provided that \(\Psi \) is quasiconvex. In general, the coercivity of \(\mathcal {G}_\varepsilon \) only ensures existence of minimizing sequences \((u_\varepsilon ^j)_j\) converging weakly in \(W^{1,{2}}(\Omega ;\mathbb {R}^m)\) to some \({\bar{u}}_\varepsilon \) minimizing the relaxation of \(\mathcal {G}_\varepsilon \). Since existence at fixed \(\varepsilon \) does not interact with the \(\Gamma \)-convergence, we state our result for asymptotically minimizing sequences.
Corollary 6.2
Let \((u_\varepsilon ,v_\varepsilon )\in {W^{1,2}}(\Omega ;\mathbb {R}^{m+1})\) be such that
where \(m_\varepsilon :=\inf _{(u,v)\in {W^{1,2}}(\Omega ;\mathbb {R}^{m+1})}\mathcal {G}_\varepsilon (u,v)\). Then \(v_\varepsilon \rightarrow 1\) in \(L^1(\Omega )\) and a subsequence of \(u_\varepsilon \) converges in \(L^q(\Omega ;\mathbb {R}^m)\) to a solution of
Moreover, \(m_\varepsilon \) tends to the minimum value of \(\mathcal {G}_0\).
Proof
The proof of the corollary will be divided in three steps.
Step 1. \(\Gamma \)-limit of \(\mathcal F_\varepsilon ^\eta \) in \(L^q\times L^1\). We check that passing from the \(L^1\times L^1\) to the \(L^q\times L^1\) topology, the expression of the \(\Gamma \)-limit of \(\mathcal {F}_\varepsilon ^\eta \) remains the same
The lower bound is an immediate consequence of that in \(L^1\times L^1\) (Theorem 4.9, being the \(L^q\) convergence stronger than the \(L^1\) convergence).
As for the upper bound, we argue by truncation. First take a subsequence of \(\mathcal {F}_\varepsilon ^\eta \) (not relabelled for convenience) and fix \(u\in BV\cap L^\infty (\Omega ;\mathbb {R}^m)\) with \(\mathcal {F}_0(u,1)<\infty \). Then Theorem 5.2 yields the existence of a sequence \((u_\varepsilon ,v_\varepsilon )\in W^{1,2}(\Omega ;\mathbb {R}^{m+1})\), such that \((u_\varepsilon ,v_\varepsilon )\rightarrow (u,1)\) in \(L^1{(\Omega ;\mathbb {R}^{m+1})}\) and
Fix \(M\in \mathbb N\) large enough such that \(a_M>\Vert u\Vert _\infty \) (see (3.11) for the definition of \(a_M\)) and, for every \(\varepsilon >0\), choose \(k_{\varepsilon ,M}\in \{{M+1},\dots ,2M\}\) such that
This implies
with \(\mathcal {T}_{k_{\varepsilon ,M}}(u_\varepsilon )\) uniformly bounded in \(L^\infty \), \(\mathcal {T}_{k_{\varepsilon ,M}}\) being defined in (3.11). This argument has been used several times throughout the paper, see for example Theorem 4.9. Passing to a further subsequence in \(\varepsilon \), we can take \(k_{\varepsilon ,M}=k_M\) independent of \(\varepsilon \). Since \((\mathcal {T}_{k_M}(u_\varepsilon ))_\varepsilon \) is uniformly bounded in \(L^\infty \) and M is large, we get \(\mathcal {T}_{k_M}(u_\varepsilon )\rightarrow \mathcal {T}_{k_M}(u)=u\) in \(L^q{(\Omega ;\mathbb {R}^m)}\) and in particular \(\mathcal {L}^n(\{a_{M+1}<|u_\varepsilon |\})\rightarrow 0\) as \(\varepsilon \rightarrow 0\), hence
Diagonalizing with respect to M and recalling the lower estimate, we conclude that every subsequence of \(\{\mathcal {F}_\varepsilon ^\eta \}_\varepsilon \) has a subsequence that \(\Gamma (L^q\times L^1)\)-converges to \(\mathcal {F}_0\) in \(L^\infty (\Omega ;\mathbb {R}^m)\times L^1(\Omega )\). Finally Urysohn’s lemma gives the convergence of the entire sequence in the same space.
Let us consider now the general case \(u\in (GBV\cap L^q(\Omega ))^m\). Then \(\mathcal {T}_k(u)\in ({BV\cap L^\infty (\Omega )})^m\), with \(\mathcal {T}_k\) again defined by (3.11), and
by the first part of the proof. As \(k\rightarrow \infty \) we have \(\mathcal {T}_k(u)\rightarrow u\) in \(L^q{(\Omega ;\mathbb {R}^m)}\) and we conclude by the lower semicontinuity of the \(\Gamma \)-limsup and the continuity of \(\mathcal {F}_0\) (see Proposition 4.8).
Step 2. \(\Gamma \)-limit of \(\mathcal {G}_\varepsilon \) in \(L^1\times L^1\). We check now that
The lower bound simply follows by Theorem 4.9 using \(\eta _\varepsilon \ge 0\) and the lower semicontinuity of \(\int _\Omega |w-u|^q{\textrm{d}}x\) with respect to the convergence in \(L^1\). In particular, if \(\Gamma (L^1\times L^1)\text {-}\liminf _{\varepsilon \rightarrow 0}\mathcal {G}_\varepsilon (u,v)<\infty \), then \(u\in (GBV(\Omega )\cap L^q)^m\) and \(v=1\) \(\mathcal {L}^n\)-a.e. on \(\Omega \).
As for the upper bound, from Step 1 we know that for all \(u\in (GBV(\Omega )\cap L^q)^m\) there exists a recovery sequence for \(\mathcal {F}_\varepsilon ^\eta \) in \(L^q\times L^1\). This is in particular a recovery sequence for \(\mathcal {G}_\varepsilon \) in \(L^1\times L^1\), which gives the conclusion.
Step 3. Convergence of minimizers. Let now \((u_\varepsilon ,v_\varepsilon )\in W^{1,2}\cap L^q(\Omega ;\mathbb {R}^{m+1})\) be a minimizing sequence for \(\mathcal {G}_\varepsilon \). Being
Theorem 6.1 gives the existence of a function \(u\in (GBV(\Omega )\cap L^q)^m\) and of a subsequence, not relabelled, such that \(u_\varepsilon \rightarrow u\) \(\mathcal {L}^n\)-a.e. on \(\Omega \) and \(v_\varepsilon \rightarrow 1\) in \(L^1{(\Omega ;\mathbb {R}^m)}\). In addition, by Hölder inequality

and the right-hand side tends to 0 since \(u_\varepsilon \rightarrow u\) in measure on \(\Omega \). Also, \((u_\varepsilon -u)\chi _{\{|u_\varepsilon -u|\le 1\}}\rightarrow 0\) in \(L^1{(\Omega ;\mathbb {R}^m)}\) by dominated convergence, hence we conclude that \(u_\varepsilon \rightarrow u\) in \(L^1{(\Omega ;\mathbb {R}^m)}\).
By Step 2 and a general property of \(\Gamma \)-convergence [41, Corollary 7.20], we conclude that (u, 1) is a minimizer of \(\mathcal {G}_0\) and that \(\mathcal {G}_\varepsilon (u_\varepsilon ,v_\varepsilon )\rightarrow \mathcal {G}_0(u,1)\). Finally, we check that in fact \(u_\varepsilon \rightarrow u\) in \(L^q{(\Omega ;\mathbb {R}^m)}\). From the previous steps we have
so that
Together with the pointwise convergence, this implies \(u_\varepsilon \rightarrow u\) in \(L^q{(\Omega ;\mathbb {R}^m)}\) by generalized dominated convergence. \(\square \)
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Alicandro, R., Braides, A., Shah, J.: Free-discontinuity problems via functionals involving the \(L^1\)-norm of the gradient and their approximations. Interfaces Free Bound. 1, 17–37, 1999
Artina, M., Cagnetti, F., Fornasier, M., Solombrino, F.: Linearly constrained evolutions of critical points and an application to cohesive fractures. Math. Models Methods Appl. Sci. 27, 231–290, 2017
Ambrosio, L., Dal Maso, G.: On the relaxation in \(BV(\Omega ; \mathbb{R}^{m})\) of quasi-convex integrals. J. Funct. Anal. 109, 76–97, 1992
Acerbi, E., Fusco, N.: Semicontinuity problems in the calculus of variations. Arch. Ration Mech. Anal. 86, 125–145, 1984
Alicandro, R., Focardi, M.: Variational approximation of free-discontinuity energies with linear growth. Commun. Contemp. Math. 4, 685–723, 2002
Ambrosio, L., Faina, L., March, R.: Variational approximation of a second order free discontinuity problem in computer vision. SIAM J. Math. Anal. 32, 1171–1197, 2001
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Mathematical Monographs. The Clarendon Press, New York (2000)
Almi, S.: Energy release rate and quasi-static evolution via vanishing viscosity in a fracture model depending on the crack opening. ESAIM Control Optim. Calc. Var. 23, 791–826, 2017
Ambrosio, L., Lemenant, A., Royer-Carfagni, G.: A variational model for plastic slip and its regularization via \(\Gamma \)-convergence. J. Elast. 110, 201–235, 2013
Ambrosio, L., Tortorelli, V.M.: Approximation of functional depending on jumps by elliptic functional via \(\Gamma \)-convergence. Commun. Pure Appl. Math. 43, 999–1036, 1990
Ambrosio, L., Tortorelli, V.M.: On the approximation of free discontinuity problems. Boll. Un. Mat. Ital. B 7(6), 105–123, 1992
Barenblatt, G.I.: The Mathematical Theory of Equilibrium Cracks in Brittle Fracture. In Advances in Applied Mechanics, Vol. 7 pp. 55–129. Academic Press, New York, 1962
Belz, S., Bredies, K.: Approximation of the Mumford-Shah functional by phase fields of bounded variation. Anal. Appl. (Singap.) 19, 183–217, 2021
Bellettini, G., Coscia, A.: Discrete approximation of a free discontinuity problem. Numer. Funct. Anal. Optim. 15, 201–224, 1994
Braides, A., Coscia, A.: The interaction between bulk energy and surface energy in multiple integrals. Proc. Roy. Soc. Edinb. Sect. A 124, 737–756, 1994
Bonacini, M., Conti, S., Iurlano, F.: Cohesive fracture in 1D: quasi-static evolution and derivation from static phase-field models. Arch. Ration. Mech. Anal. 239, 1501–1576, 2021
Braides, A., Dal Maso, G., Garroni, A.: Variational formulation of softening phenomena in fracture mechanics: the one-dimensional case. Arch. Ration. Mech. Anal. 146, 23–58, 1999
Burger, M., Esposito, T., Zeppieri, C.I.: Second-order edge-penalization in the Ambrosio–Tortorelli functional. Multiscale Model. Simul. 13, 1354–1389, 2015
Barroso, A.C., Fonseca, I.: Anisotropic singular perturbations–the vectorial case. Proc. Roy. Soc. Edinb. Sect. A 124, 527–571, 1994
Bouchitté, G., Fonseca, I., Mascarenhas, L.: A global method for relaxation. Arch. Ration. Mech. Anal. 145, 51–98, 1998
Bourdin, B., Francfort, G.A., Marigo, J.-J.: The variational approach to fracture. J. Elast. 91, 5–148, 2008
Braides, A., Gelli, M.S.: From discrete systems to continuous variational problems: an introduction. In Topics on Concentration Phenomena and Problems with Multiple Scales, volume 2 of Lect. Notes Unione Mat. Ital., pp. 3–77. Springer, Berlin, 2006
Bonacini, M., Iurlano, F.: Convergence of critical points for a phase-field approximation of 1d cohesive fracture energies. arXiv:2309.17064, 2023
Babadjian, J.-F., Iurlano, F., Rindler, F.: Concentration versus oscillation effects in brittle damage. Commun. Pure Appl. Math. 74, 1803–1854, 2021
Burke, S., Ortner, C., Süli, E.: An adaptive finite element approximation of a variational model of brittle fracture. SIAM J. Numer. Anal. 48, 980–1012, 2010
Burke, S., Ortner, C., Süli, E.: An adaptive finite element approximation of a generalized Ambrosio–Tortorelli functional. Math. Models Methods Appl. Sci. 23, 1663–1697, 2013
Bourdin, B.: Numerical implementation of the variational formulation for quasi-static brittle fracture. Interfaces Free Bound. 9, 411–430, 2007
Braides, A.: Approximation of free-discontinuity problems, volume 1694 of Lecture Notes in Mathematics. Springer, Berlin, 1998.
Bar, L., Sochen, N., Kiryati, N.: Image deblurring in the presence of impulsive noise. Int. J. Comput. Vis. 70, 279–298, 2006
Cagnetti, F.: A vanishing viscosity approach to fracture growth in a cohesive zone model with prescribed crack path. Math. Models Methods Appl. Sci. 18, 1027–1071, 2008
Caffarelli, L., Cagnetti, F., Figalli, A.: Optimal regularity and structure of the free boundary for minimizers in cohesive zone models. Arch. Ration. Mech. Anal. 237, 299–345, 2020
Chen, L., de Borst, R.: Phase-field modelling of cohesive fracture. Eur. J. Mech.-A/Solids 90, 104343, 2021
Conti, S., Focardi, M., Iurlano, F.: Phase field approximation of cohesive fracture models. Annales de l’Institut Henri Poincaré / Analyse non linéaire 33, 1033–1067, 2016
Conti, S., Focardi, M., Iurlano, F.: Superlinear cohesive fracture models as limits of phase field functionals. in preparation, 2024
Cicalese, M., Focardi, M., Zeppieri, C.I.: Phase-field approximation of functionals defined on piecewise-rigid maps. J. Nonlinear Sci. 31, 1–25, 2021
Chambolle, A.: An approximation result for special functions with bounded deformation. J. Math. Pures Appl. 9(83), 929–954, 2004
Chambolle, A.: Addendum to: “An approximation result for special functions with bounded deformation” [J. Math. Pures Appl. (9) 83 (2004), no. 7, 929–954; mr2074682]. J. Math. Pures Appl. (9), 84:137–145, 2005
Crismale, V., Lazzaroni, G., Orlando, G.: Cohesive fracture with irreversibility: quasistatic evolution for a model subject to fatigue. Math. Models Methods Appl. Sci. 28, 1371–1412, 2018
Cagnetti, F., Toader, R.: Quasistatic crack evolution for a cohesive zone model with different response to loading and unloading: a Young measures approach. ESAIM Control Optim. Calc. Var. 17, 1–27, 2011
Dacorogna, B.: Direct methods in the calculus of variations, volume 78 of Applied Mathematical Sciences, 2nd edn. Springer, New York, 2008.
Dal Maso, G.: An introduction to \(\Gamma \) -convergence. Progress in Nonlinear Differential Equations and their Applications, vol. 8. Birkhäuser Boston Inc., Boston, MA, 1993.
Dal Maso, G., Garroni, A.: Gradient bounds for minimizers of free discontinuity problems related to cohesive zone models in fracture mechanics. Calc. Var. Partial Differ. Equ. 31, 137–145, 2008
Dal Maso, G., Iurlano, F.: Fracture models as \(\Gamma \)-limits of damage models. Commun. Pure Appl. Anal. 12, 1657–1686, 2013
Dal Maso, G., Orlando, G., Toader, R.: Fracture models for elasto-plastic materials as limits of gradient damage models coupled with plasticity: the antiplane case. Calc. Var. Partial Differ. Equ., 55:Art. 45, 39, 2016.
Dal Maso, G., Toader, R.: A new space of generalised functions with bounded variation motivated by fracture mechanics. Nonlinear Differ. Equ. Appl. NoDEA 29, 63, 2022
Dal Maso, G., Zanini, C.: Quasi-static crack growth for a cohesive zone model with prescribed crack path. Proc. Roy. Soc. Edinb. Sect. A 137, 253–279, 2007
del Piero, G., Truskinovsky, L.: A one-dimensional model for localized and distributed failure. J. Phys. IV 8, 95–102, 1998
del Piero, G., Truskinovsky, L.: Macro- and micro-cracking in one-dimensional elasticity. Int. J. Sol. Struct. 38, 1135–1148, 2001
Dugdale, D.: Yielding of steel sheets containing slits. J. Mech. Phys. Solids 8, 100–108, 1960
Ekeland, I., Temam, R.: Convex Analysis and Variational Problems. Classics in Applied Mathematics. Society for Industrial and Applied Mathematics, 1999
Fokoua, L., Conti, S., Ortiz, M.: Optimal scaling laws for ductile fracture derived from strain-gradient microplasticity. J. Mech. Phys. Solids 62, 295–311, 2014
Feng, Y., Fan, J., Li, J.: Endowing explicit cohesive laws to the phase-field fracture theory. J. Mech. Phys. Solids 152, 104464, 2021
Focardi, M., Iurlano, F.: Asymptotic analysis of Ambrosio-Tortorelli energies in linearized elasticity. SIAM J. Math. Anal. 46, 2936–2955, 2014
Freddi, F., Iurlano, F.: Numerical insight of a variational smeared approach to cohesive fracture. J. Mech. Phys. Solids 98, 156–171, 2017
Fonseca, I., Leoni, G.: On lower semicontinuity and relaxation. In: Proceedings. Section A, Mathematics-The Royal Society of Edinburgh 131, 519, 2001
Feng, Y., Li, J.: A unified regularized variational cohesive fracture theory with directional energy decomposition. Int. J. Eng. Sci. 182, 103773, 2023
Fonseca, I., Müller, S.: Relaxation of quasiconvex functionals in \(BV(\Omega ; {\mathbb{R}}^{p})\) for integrands \(f(x, u,\nabla u)\). Arch. Ration. Mech. Anal. 123, 1–49, 1993
Francfort, G.A., Marigo, J.-J.: Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 46, 1319–1342, 1998
Focardi, M.: On the variational approximation of free-discontinuity problems in the vectorial case. Math. Models Methods Appl. Sci. 11, 663–684, 2001
Fusco, N.: An overview of the Mumford–Shah problem. Milan J. Math. 71, 95–119, 2003
Henao, D., Mora-Corral, C., Xu, X.: \(\Gamma \)-convergence approximation of fracture and cavitation in nonlinear elasticity. Arch. Ration. Mech. Anal. 216, 1–67, 2014
Iurlano, F.: Fracture and plastic models as \(\Gamma \)-limits of damage models under different regimes. Adv. Calc. Var. 6, 165–189, 2013
Iurlano, F.: A density result for GSBD and its application to the approximation of brittle fracture energies. Calc. Var. Partial Differ. Equ. 51, 315–342, 2014
Larsen, C.J.: Quasiconvexification in \(W^{1,1}\) and optimal jump microstructure in BV relaxation. SIAM J. Math. Anal. 29, 823–848, 1998
Lammen, H., Conti, S., Mosler, J.: A finite deformation phase field model suitable for cohesive fracture. J. Mech. Phys. Solids 178, 105349, 2023
Larsen, C.J., Slastikov, V.: Dynamic cohesive fracture: models and analysis. Math. Models Methods Appl. Sci. 24, 1857–1875, 2014
Müller, S.: On quasiconvex functions which are homogeneous of degree 1. Ind. Univ. Math. J. 41, 295–301, 1992
Negri, M., Scala, R.: A quasi-static evolution generated by local energy minimizers for an elastic material with a cohesive interface. Nonlinear Anal. Real World Appl. 38, 271–305, 2017
Negri, M., Vitali, E.: Approximation and characterization of quasi-static \(H^1\)-evolutions for a cohesive interface with different loading-unloading regimes. Interfaces Free Bound. 20, 25–67, 2018
Rindler, F.: Calculus of variations, vol. 5. Springer, 2018
Shah, J.: Curve evolution and segmentation functionals: application to color images. In Proceedings IEEE ICIP, 1996
Stein, E.M.: Singular Integrals. Princeton Univ Press, Princeton, 1970
Thomas, M., Zanini, C.: Cohesive zone-type delamination in visco-elasticity. Discrete Contin. Dyn. Syst. Ser. S 10, 1487–1517, 2017
Šilhavý, M.: Rank 1 convex hulls of isotropic functions in dimension 2 by 2. In Proceedings of Partial Differential Equations and Applications (Olomouc, 1999), vol. 126, pp. 521–529, 2001.
Wu, J.-Y., Nguyen, V.P.: A length scale insensitive phase-field damage model for brittle fracture. J. Mech. Phys. Solids 119, 20–42, 2018
Wu, J.-Y., Nguyen, V.P., Nguyen, C.T., Sutula, D., Sinaie, S., Bordas, S.P.: Phase-field modeling of fracture. Adv/. Appl. Mech. 53, 1–183, 2020
Wu, J.-Y.: A unified phase-field theory for the mechanics of damage and quasi-brittle failure. J. Mech. Phys. Solids 103, 72–99, 2017
Funding
Open access funding provided by Università degli Studi di Firenze within the CRUI-CARE Agreement. This work was partially supported by the Deutsche Forschungsgemeinschaft through Project 211504053/SFB1060 and Project 441211072/SPP2256.
M.F. is a member of GNAMPA of INdAM.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Non-financial Interests
The authors have no relevant financial or non-financial interests to disclose.
Conflicts of interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Financial Interest
All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.
Proprietary Interests
The authors have no financial or proprietary interests in any material discussed in this article.
Additional information
Communicated by A. Braides.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Conti, S., Focardi, M. & Iurlano, F. Phase-Field Approximation of a Vectorial, Geometrically Nonlinear Cohesive Fracture Energy. Arch Rational Mech Anal 248, 21 (2024). https://doi.org/10.1007/s00205-024-01962-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00205-024-01962-4




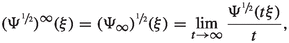 for all
for all