Abstract
We introduce a data-driven approach to the modelling and analysis of viscous fluid mechanics. Instead of including constitutive laws for the fluid’s viscosity in the mathematical model, we suggest directly using experimental data. Only a set of differential constraints, derived from first principles, and boundary conditions are kept of the classical PDE model and are combined with a data set. The mathematical framework builds on the recently introduced data-driven approach to solid-mechanics (Kirchdoerfer and Ortiz in Comput Methods Appl Mech Eng 304:81–101, 2016; Conti et al. in Arch Ration Mech Anal 229:79–123, 2018). We construct optimal data-driven solutions that are material model free in the sense that no assumptions on the rheological behaviour of the fluid are made or extrapolated from the data. The differential constraints of fluid mechanics are recast in the language of constant rank differential operators. Adapting abstract results on lower-semicontinuity and \({\mathscr {A}}\)-quasiconvexity, we show a \(\Gamma \)-convergence result for the functionals arising in the data-driven fluid mechanical problem. The theory is extended to compact nonlinear perturbations, whence our results apply not only to inertialess fluids but also to fluids with inertia. Data-driven solutions provide a new relaxed solution concept. We prove that the constructed data-driven solutions are consistent with solutions to the classical PDEs of fluid mechanics if the data sets have the form of a monotone constitutive relation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, a significantly increasing availability of data has lead to new approaches in applied mathematics, such as materials science and (turbulence models in) fluid dynamics. These approaches are aimed at systematically exploiting the data in order to avoid high computational costs or modelling based computational errors. Particularly in machine learning-based engineering and numerical simulations this has attained considerable attention. In contrast, a rigorous mathematical theory is yet to be made available.
In this article, a new data-driven approach to the mathematical modelling and analysis of viscous fluid mechanics is introduced.
Traditional mathematical models that describe viscous fluid flow are based on force balance equations, such as conservation of momentum and mass on the one hand, and on certain constitutive laws that account for the viscous behaviour of a fluid on the other hand. Both of these together lead to systems of partial differential equations, such as the Navier–Stokes system, for which different analytical and numerical solution concepts are used in order to describe the flow behaviour of the fluid. In this traditional PDE-based approach, data is only used in order to determine constitutive laws for the fluid viscosity.
The data-driven approach proposed in this paper aims to exploit available data (strain–stress pairs) directly and to incorporate them into a constrained minimisation problem the solution of which is a field of strain–stress pairs that still satisfies the differential constraints, but also approximates the given data set best.
1.1 First principles for incompressible fluid mechanics
The behaviour of an incompressible fluid at any instant t in time may be described by its velocity field \(u:x\mapsto u(x)\in {\mathbb {R}}^d\) which induces a strain(-rate) \(\epsilon :x\mapsto \epsilon (x)\in {\mathbb {R}}^{d\times d}_{\textrm{sym}}\)
the symmetric gradient of the velocity field. Moreover the fluid generates a stress field \(\sigma :x\mapsto \sigma (x)\in {\mathbb {R}}^{d\times d}_{\textrm{sym}}\) which, in the case of an inertialess fluid, satisfies
with an external force density \(f:x\mapsto f(x)\in {\mathbb {R}}^d\). Both (1.1) and (1.2) are prescribed differential constraints and are also called compatibility conditions. The strain \(\epsilon \) and the stress \(\sigma \) cannot be any field – they have to be a symmetric gradient of another field in the first, and admit a predefined divergence in the second case. For fluids with inertia the force balance (1.2) has to be complemented by the inertial forces proportional to \(\partial _t u+(u\cdot \nabla )u\). This results (after suitable non-dimensionalisation) in the equation
However, in this paper we restrict our analysis to the stationary case \(\partial _t u = 0\), i.e. we study the problem
Since our analysis is mainly based on variational arguments suited for stationary problems, we postpone the time-dependent case to a separate work.
1.2 The PDE-based approach: constitutive laws for viscous fluids
Hitherto, the modelling and analysis of a rich set of phenomena in viscous fluid mechanics relies on constitutive laws describing the relation between the strain field \(\epsilon \) and the stress field \(\sigma \). A commonly used relation is
which relies on the assumption that the stress comprises two components – the term \(\sigma _{\text {p}}=-\pi {{\,\textrm{id}\,}}\) induced by the pressure \(\pi \), and the viscous stress \({{\tilde{\sigma }}} =2\mu (|\epsilon |)\epsilon \). Here, \(\mu :s\mapsto \mu (s)\in {\mathbb {R}}_+\) denotes the viscosity of the fluid. This depends on the strain rate and measures the resistance of the fluid to deformation. Mathematically, the pressure \(\pi :x\mapsto \pi (x)\in {\mathbb {R}}\) is the Lagrange multiplier corresponding to the incompressibility condition \({{\,\textrm{div}\,}}u=0\). In the simplest model of a viscous fluid, the viscosity \(\mu \) is assumed to be constant \(\mu \equiv {{\,\textrm{const}\,}}\) and the corresponding fluid is called Newtonian. In other words, the relation between the viscous forces and the local strain rate is perfectly linear, the constant viscosity being the factor of proportionality. In the case of an inertialess incompressible Newtonian fluid one obtains the well-known Stokes equations
For incompressible Newtonian fluids with inertia one obtains the (stationary) Navier–Stokes equations
Although it is reasonable in many practical applications to assume a fluid being Newtonian, real fluids that account for viscosity are in fact non-Newtonian, i.e. they feature a nonlinear relation between the stress \(\sigma \) and the rate of strain \(\epsilon \). A widely-used constitutive relation is given by
and the corresponding fluid’s are called power-law fluids or Ostwald–de Waele fluids. The exponent \(\alpha > 0\) denotes the so-called flow-behaviour exponent and \(\mu _0 > 0\) is the flow consistency index. In the case \(0< \alpha < 1\) the fluid exhibits a shear-thinning behaviour as its viscosity decreases with increasing shear-rate, while the fluid is called shear-thickening in the case \(\alpha > 1\). In this case the viscosity is an increasing function of the shear rate. The corresponding stationary non-Newtonian Navier–Stokes system reads as
For \(\alpha =1\) we recover a Newtonian behaviour. In practice, constitutive laws for the viscosity are derived from experimental measurements. This is done by determining the parameters inside a prescribed class of laws, for instance \(\mu _0\) and \(\alpha \) in the case of power-law fluids (1.5), to best approximate the measured data. A large part of the mathematical knowledge in the mechanics of viscous fluids comes from the theoretical and numerical analysis of partial differential equations such as Stokes equation and Navier–Stokes equation, that are derived using constitutive laws. Here, a lot of progress has been made by allowing for increasingly general classes of (nonlinear) viscosity laws (see for example [17, 19, 21, 22]).
1.3 A variational data-driven approach
Nowadays, the availability of data and the possibility to mine them is increasing drastically. In the present work, instead of including constitutive laws in the mathematical models, we suggest to directly use data in order to find the strain field \(\epsilon \) and the stress field \(\sigma \) that satisfy the respective differential constraints and, at the same time, approximate the data best. In order to realise this mathematically, we are inspired by the articles [7, 16], where a similar approach has first been introduced in the context of solid mechanics.
In the present paper, data sets consist of strain–stress pairs \((\epsilon ,\sigma )\in {\mathbb {R}}^{d\times d}\times {\mathbb {R}}^{d\times d}\). We might think of these data as being extracted from one or several experiments but more generally data represent any available information about the fluid (cf. [7]). This information might be obtained by preprocessing actual measurements of other physical quantities, refined numerical simulations, or theoretical considerations (like invariance under rotations). We emphasise that the step of preprocessing is also necessary when deriving constitutive laws from measurements.
The motivation for replacing the classical PDE-based approach by the data-driven approach is the following. Once one accepts the fundamental assumptions (first principles) about the nature of the fluid leading to the differential constraints, the PDE-based approach generates two errors with respect to modelling the real world: First, the experimental equipment is imperfect, leading to measurement errors. Second, the fitting of a material law to the experimental data introduces a modelling error. The data-driven approach entirely avoids this second step.
Turning to the remaining source of errors, with perfect equipment and infinitely many measurements, we expect to recover the viscosity law of the fluid (if it exists). In reality, measurements are however restricted by
-
the inaccuracy of the equipment leading to a measurement error;
-
a limited number of data points. This comprises both ‘density of measurements’ (i.e. given a strain \(\epsilon \in {\mathbb {R}}^{d\times d}\), how many data points lie in a neighbourhood of \(\epsilon \)?), as well as ‘range of measurement’ (how large is the range of values of \(\epsilon \) that can be measured in the experiment?).
Nevertheless, if over the course of several consecutive measurement series the measurement error decreases or the density and range of data points increases, we expect the experimental data to converge to the material law. Mathematically, we give consideration to this behaviour by introducing different notions of data convergence. In this paper, we restrict ourselves to the study of the following two settings:
-
data with increasing quality and an unbounded range of measurements;
-
data with increasing quality and a bounded but increasing range of measurements.
An overview of the possible settings and where they are discussed in this paper is given in Table 1.
In the case of non-increasing accuracy, measurements for a given strain rate \(\epsilon \in {\mathbb {R}}^{d\times d}\) might be located in a neighbourhood of the exact value with a certain likelihood. In this case, the set of data converges in a weak sense to some distribution, see [4]. See also [28] for the analysis of single outliers in measurements.
1.4 Related results on data-driven approaches
In the past years, the drastically increasing availability of large and diverse data has lead to new data-driven approaches in (mathematical) fluid mechanics and materials science. In the context of this paper it seems worthwhile to explicitly address data-driven elasticity models and data-driven turbulence models.
The scientific contributions in the field of data-driven elasticity models are particularly noteworthy from the methodological point of view, as many of the mathematical tools used in this paper are based on ideas of [7, 16]. In the context of an elastic body deforming under the effect of external forces, the relevant fields are, similarly to the case of fluid mechanics, the strain \(\epsilon \) and the stress \(\sigma \). In [7, 8, 16] a (material-dependent) strain–stress relation is replaced by data. The data-driven elasticity framework and our approach differ in the kind of constraints that strain and stress field have to satisfy. Note in particular that in the case of elasticity the strain need not be tracefree but more importantly our constraint set is merely semilinear as opposed to linear in the elasticity case.
From the application-oriented point of view also the efforts made in data-driven turbulence modelling are of great interest. We recall that the present paper is only concerned with the stationary Navier–Stokes equations. However, once one considers the time-dependent setting, one of the big challenges is the onset of turbulent behaviour driven by the inertia of the fluid.
Hitherto, experimental and numerical data have mostly been used in order to gain insights into aspects of modeling and to validate numerical and analytical results. More recently, significant effort has been made in the utilisation of data in order to systematically inform turbulence models and/or to quantify and reduce modelling errors and uncertainties. Since it is numerically prohibitive to model turbulence up to very small scales, on the conceptual level, the data-driven approaches are based on the observation that it is advantageous to replace small scale turbulence by effective models that take into account the effects that microscopic dynamics have on large scale averaged quantities (for example via an effective viscosity). The question how these quantities depend on the small scales is also known as the closure problem. In this context we refer to two classical approaches for this problem – Large Eddy Simulations and the Reynolds Averaged Navier–Stokes system.
The Large Eddy Simulation has been proposed in [29]. The basic idea is to first ignore the computationally expensive smallest length scales and to first consider only the large scales of (turbulent) the Navier–Stokes flow with high Reynolds number on a rather coarse grid. Then sub-grid-scale models [23] are introduced in order to deal with the unsteadyness of the flow, i.e. with the small scales. The closure problem consists in finding appropriate sub-grid-scale models, due to the nonlinear dependence of the large scales on the small scales.
The general idea of the Reynolds Averaged Navier–Stokes system is to decompose the quantities of interest into averaged mean quantities that take into account the large scales and fluctuating quantities that take turbulent fluctuations into account. Using this decomposition one can derive equations for the bulk behaviour of the average quantities such as the mean velocity. However, the so-called Reynolds stress appearing in this equations depends on the turbulent fluctuations. As a remedy one tries to express the turbulent quantities in terms of the average quantities. We refer the reader for instance to the review article [10]. This is hitherto done by means of constitutive laws.
Linear constitutive laws for the relation between the Reynolds stresses and the mean strain rate have thus far not provided satisfactory predictive accuracy in many engineering-relevant flows [6, 26]. For this reason more involved nonlinear laws have been proposed [6, 30]. Alternatively, Deep Learning approaches based on data have been proposed (cf. for instance [18]).
1.5 Mathematical approach for the data-driven problem and main results
We follow the mathematical approach proposed in [7] in a solid mechanical context. To this end, we first split the stress \(\sigma = -\pi {{\,\textrm{id}\,}}+ {\tilde{\sigma }}\) into \(\pi {{\,\textrm{id}\,}}= -\tfrac{1}{d} {{\,\textrm{tr}\,}}(\sigma ) {{\,\textrm{id}\,}}\) and its viscous part \({\tilde{\sigma }}\).
Throughout the paper we assume that the data set \({\mathscr {D}}\) comprises pairs \((\epsilon ,{\tilde{\sigma }})\) of strain and viscous stress only. The pressure \(\pi \) (i.e. the trace of \(\sigma \)) is not included in the data set, since we allow \(\pi \) to attain arbitrary values. This is due to the fact that the pressure does not play a role in the constitutive law for the viscosity but arises as a Lagrange multiplier corresponding to the incompressibility constraint.
Given a data set \({\mathscr {D}}_n=\{(\epsilon _\beta ,{\tilde{\sigma }}_\beta )\}_{\beta \in B_n}\), consisting of pairs \((\epsilon _\beta ,{\tilde{\sigma }}_\beta )\) of symmetric and trace-free matrices in \({\mathbb {R}}^{d\times d}\), we consider the functional
as a measure for the distance of functions \((\epsilon ,{\tilde{\sigma }})\), defined on a simply connected and bounded \(C^1\)-domain \(\Omega \subset {\mathbb {R}}^d\), to the data set. Here, \({\mathscr {C}}\) is the constraint set of fields \(\epsilon ,{\tilde{\sigma }}\) satisfying the prescribed differential constraints and suitable boundary conditions, and \({{\,\textrm{dist}\,}}(\cdot ,\cdot )\) is a suitable distance function.
In the present paper, the set of differential constraints is given by (1.1) in combination with either the inertialess force balance or the stationary Navier–Stokes force balance. That is, we study both the linear constraint set
as well as the nonlinear constraint set
The set of constraints is complemented by suitable boundary conditions. Typical boundary conditions in fluid mechanics are the no-slip condition
and the Navier-slip condition
Here, \(\lambda \geqq 0\) is the inverse of the so-called slip length and \(\nu \) denotes the outer normal to \(\partial \Omega \). Moreover, \(T\partial \Omega \) denotes the tangential bundle of \(\partial \Omega \). The case of free slip \(\tau \cdot \sigma \nu =0\) for \(\tau \in T\partial \Omega \) is included via \(\lambda =0\). The second condition in (1.11) expresses the non-permeability of the boundary.
Less natural is the Neumann type boundary condition
In the linear case (1.8), we are able to handle all three types of boundary conditions (1.10), (1.11), and (1.12). In the nonlinear case (1.9), we are able to handle the physical boundary conditions (1.10) and (1.11). In some cases we allow for inhomogeneous boundary conditions, i.e. non-zero right-hand sides.
Coming back to (1.7), a minimiser (or a minimising sequence) of the functional \(I_n\) always satisfies the compatibility conditions for \(\epsilon \) and \({\tilde{\sigma }}\) and is as close to the experimental data \({\mathscr {D}}_n\) as possible.
In the case in which a sequence \({\mathscr {D}}_n\) of data sets approximates a limiting set \({\mathscr {D}}\), corresponding to a constitutive law, it is expected that the minimisers \(v_n=(\epsilon _n,{\tilde{\sigma }}_n)\) of the functional \(I_n\) converge to a solution v of the PDE corresponding to the constitutive law. One main contribution of the present article is to specify conditions under which this is true. We use the following notion for convergence of data sets:
Definition 1.1
We say that a sequence of closed sets \({\mathscr {D}}_n\) converges to \({\mathscr {D}}\), \({\mathscr {D}}_n \rightarrow {\mathscr {D}}\), if the following is satisfied:
-
(i)
Fine approximation on bounded sets: There are sequences \(a_n\rightarrow 0\) and \(R_n\rightarrow \infty \) such that for all \(n\in {\mathbb {N}}\) and for all \(z \in {\mathscr {D}}\) with \(|z| < R_n\), it holds that
$$\begin{aligned} {{\,\textrm{dist}\,}}(z, {\mathscr {D}}_n) \leqq a_n (1 + |z|). \end{aligned}$$ -
(ii)
Uniform approximation on bounded sets: There are sequences \(b_n\rightarrow 0\) and \(S_n\rightarrow \infty \) such that for all \(n\in {\mathbb {N}}\) and for all \(z_n \in {\mathscr {D}}_n\) with \(|z_n| < S_n\), it holds that
$$\begin{aligned} {{\,\textrm{dist}\,}}(z_n,{\mathscr {D}}) \leqq b_n (1 + |z_n|). \end{aligned}$$
Here, \(|\cdot | = {{\,\textrm{dist}\,}}(\cdot ,0)\) defines a pseudo-norm.
The sequences \(a_n\) and \(b_n\) represent the relative error, while \(S_n\) and \(R_n\) describe the measurement range. Note that condition (i) ensures that every point in the limiting set is approximated by data points in \({\mathscr {D}}_n\) while condition (ii) ensures that the \({\mathscr {D}}_n\) approximates \({\mathscr {D}}\) uniformly.
Moreover, the notion of convergence introduced in Definition 1.1 (ii) is justified from an experimental point of view. Indeed, for a given experimental setup we expect the measurements to be precise only within a certain range, \(|z| \leqq S_n\). For instance, in the experiment conducted by Couette [9], the aim of which was to measure the viscosity of a fluid, the range \(S_n\) is linked to the aspect ratio of the rotating cylinders. In the setting of this article, the absolute error is allowed to grow with the range of measurements, which extends the setting studied in [7], where the absolute errors are required to converge to zero.
From a mathematical point of view, the above notion of convergence is justified by the observation that we may restrict the analysis to p-equi-integrable recovery sequences in the \(\Gamma \)-convergence result below. Indeed, the first main result of this article is
-
\(\Gamma \)-convergence (Theorem 5.11 and Theorem 5.15): If \({\mathscr {D}}_n \rightarrow {\mathscr {D}}\) and the \({\mathscr {D}}_n\) satisfy a certain growth condition, then \(I_n\) \(\Gamma \)-converges to
$$\begin{aligned} I^*(\epsilon ,{\tilde{\sigma }}) = {\left\{ \begin{array}{ll} \int _\Omega {\mathscr {Q}}_{{\mathscr {A}}}{{\,\textrm{dist}\,}}\bigl (\left( \epsilon (x),{\tilde{\sigma }}(x)\right) ,{\mathscr {D}}\bigr ) \;\textrm{d}x, &{} (\epsilon ,{\tilde{\sigma }}) \in {\mathscr {C}}\\ \infty , &{} \text {else}, \end{array}\right. } \end{aligned}$$where \({\mathscr {Q}}_{{\mathscr {A}}}\) is a suitable convex envelope of the distance function corresponding to the differential operators defining the compatibility conditions (1.1) and (1.2).
There are two main challenges in the proof of this result. One difficulty is the suitable modification of sequences of functions while preserving differential constraints and given boundary conditions. To overcome this challenge we prove the following result, which might be of independent interest:
-
p-equi-integrability and boundary conditions (Theorem 3.9) If a weakly convergent sequence \(u_n\) of \(L_p\)-functions on \(\Omega \subset {\mathbb {R}}^d\) satisfies some differential constraint \({\mathscr {A}}u_n=0\) for a constant coefficient (and constant rank) differential operator \({\mathscr {A}}\), we can modify \(u_n\) slightly in the sense of closeness in \(L_r\) for \(r < p\). The modified sequence still satisfies the differential constraint and the same boundary conditions, but is p-equi-integrable (i.e. no concentrations of mass occur).
This modification result, together with slight adaptations of existing theory on relaxation subject to a linear differential constraint, yields Theorem 5.11. Moreover, overcoming the second challenge, we show that the relaxation result continues to hold when we include compact nonlinear perturbations in the constraint set \({\mathscr {C}}\), see Theorem 3.13. This includes in particular the inertia term \([u \mapsto (u\cdot \nabla )u]: W^1_p(\Omega ;{\mathbb {R}}^d) \rightarrow W^{-1}_q(\Omega ;{\mathbb {R}}^d)\), whenever \(p> 3d/(d+2)\) and \(1/p + 1/q = 1\).
In the case of a data set given by a constitutive law, data-driven solutions provide a new solution concept. Another main result of this article proves that, in the case of monotone constitutive laws, this solution concept is compatible with the concept of weak solutions to PDEs:
-
Consistency (Sect. 6): If the data set \({\mathscr {D}}\) corresponds to a monotone constitutive law, e.g. \({\mathscr {D}}=\{(\epsilon ,\vert \epsilon \vert ^{\alpha -1}\epsilon )\}\) in the case of power-law fluids, and if the corresponding PDE admits a solution, then for a map \(v=(\epsilon ,{\tilde{\sigma }})\) the following three statements are equivalent:
-
(i)
v is a minimiser of \(I^*\), i.e. a solution to the relaxed data-driven problem;
-
(ii)
\(I^*(v) = 0\), i.e. there exists a sequence \(v_n \rightharpoonup v\) with \(I(v_n) \rightarrow 0\);
-
(iii)
v is a solution to the corresponding PDE (i.e. to (1.6) in the nonlinear case) in the classical weak sense.
-
(i)
In the case of non-monotone constitutive laws, the requirement \(I^*(v)=0\) amounts to a relaxed solution concept that might be useful for instance in order to deal with viscoelastic fluids.
1.6 Outline of the paper
Section 2 shows how the fluid mechanical problems fit into the general theory of constant rank operators. In Sect. 2.1 we introduce relevant notation and recall the notion of \(\Gamma \)-convergence with respect to the weak topology of \(L_p\)-spaces. In Section 2.1.4 we recall the generalised form of Problem (1.7), where the differential constraint \((\epsilon ,{\tilde{\sigma }}) \in {\mathscr {C}}\) is written abstractly as \({\mathscr {A}}v=0\) and the distance function is replaced by some function  . In Sect. 2.2 it is demonstrated that the fluid mechanical setting fits into this abstract framework.
. In Sect. 2.2 it is demonstrated that the fluid mechanical setting fits into this abstract framework.
An abstract theory for lower-semicontinuity of functionals under linear differential constraints has been developed by Fonseca & Müller ([12], see also [2]) and we recall these results at the beginning of Sect. 3. The remainder of Sect. 3 is devoted to the modification of the corresponding arguments to fit the fluid mechanical setting of the present paper. In particular, we show the crucial Theorem 3.9, which allows us to modify sequences to be equi-integrable, while still respecting both the differential constraints and the boundary conditions. This result is used to extend relaxation results, previously obtained in [2], to the situation of a semilinear differential constraint in Theorem 3.13.
For Sects. 4–6 we return to the fluid mechanical setting and apply the abstract results of Sect. 3.
In Sect. 4 we discuss two different notions of data convergence on a purely set-theoretic level; in particular these notions of convergence are not directly connected to the differential constraints. First, in Section 4.1 we introduce a form of data convergence which corresponds to fixed range of measurement (lower-left entry of Table 1) and show that this is equivalent to a suitable notion of convergence for the unconstrained functionals
For results about \(\Gamma \)-convergence of constrained functionals of type (1.7), however, we can weaken the notion of convergence to Definition 1.1. This type of convergence is examined in Sect. 4.2. The reason for this convergence being of interest for \(\Gamma \)-convergence, is discussed already at the beginning of Sect. 3 in Theorem 3.6.
The abstract results of Sect. 3 and results about distance functions to data sets \({\mathscr {D}}_n\) of Sect. 4 are combined in Sects. 5. In Section 5.1 and Section 5.2 we introduce the data-driven problem both for inertialess fluids and fluids with inertia. We show that, given boundary conditions and a suitable pointwise coercivity condition, the functionals \(I_n\) in (1.7) are coercive on the phase space V. Therefore, we can apply results from Sect. 3 to get the respective \(\Gamma \)-convergence result (Theorem 5.11 and Theorem 5.15).
Finally, Sect. 6 links the (relaxed) data-driven problem \(I^{*}(v)=0\) to the partial differential equations obtained by including a constitutive law in the modelling. We show that if the data set \({\mathscr {D}}\) coincides with the set obtained by a monotone constitutive law, i.e. \({\mathscr {D}}= \{(\epsilon ,{\tilde{\sigma }}) :{\tilde{\sigma }}= 2\mu (\vert \epsilon \vert )\epsilon \}\), then solutions to the relaxed data-driven problem are weak solutions to the classical PDE problem and vice versa.
2 Functional Analytic Setting of the Fluid Mechanical Problem
In this section we introduce an abstract functional analytic framework that offers a convenient way to reformulate the differential constraints. First, in Section 2.1, we recall the notion of \(\Gamma \)-convergence and the notion of constant rank operators. The latter requires a short reminder on some results from Fourier analysis. In Section 2.2 we show how the differential operators appearing in the fluid mechanical applications fit into the framework of constant rank operators.
2.1 \(\Gamma \)-convergence and constant rank operators
2.1.1 Underlying function spaces
Let \(\Omega \subset {\mathbb {R}}^d\) be a bounded, simply connected set with \(C^1\)-boundary and let
be the set of symmetric trace-free matrices in \({\mathbb {R}}^{d\times d}\). We mainly study functions \(v :\Omega \rightarrow Y \times Y\) and we shall write \(v = (\epsilon ,{\tilde{\sigma }})\) to denote their components and \(\sigma = -\pi {{\,\textrm{id}\,}}+ {\tilde{\sigma }}\) for a function \(\pi :\Omega \rightarrow {\mathbb {R}}\). One might think of \(\epsilon \) as the strain and \({\tilde{\sigma }}\) the viscous part of the stress. For \(1< p,q< \infty \) with \(1/p+1/q=1\), we consider the phase space
equipped with the norm
We call \(Y \times Y \) the local phase space. Recall that we assume throughout the paper that the pressure \(\pi \) (i.e. the trace of \(\sigma \)) is not considered as part of the data. Consequently, each data set \({\mathcal {D}}_n\) is a subset of \(Y\times Y\). In order to introduce a distance on \(Y \times Y\), for pairs \((\epsilon _i,{\tilde{\sigma }}_i)\in Y \times Y\), \(i=1,2\), we define
and therewith
The function \(d(\cdot ,\cdot )\) is defined by taking the p-th, respectively the q-th root of \({{\,\textrm{dist}\,}}(\cdot ,\cdot )\), in order to guarantee that the triangle inequality is satisfied. Thus, \(d(\cdot ,\cdot )\) defines a metric on \(Y\times Y\).
Accordingly, we define the distance on the phase space V by
We start by proving that the distance function \(d(\cdot ,\cdot )\), introduced in (2.1), defines a metric.
Lemma 2.1
The map \(d :(Y \times Y) \times (Y \times Y) \rightarrow {\mathbb {R}}\) is a metric.
Proof
Positivity, definiteness and symmetry are clear. The triangle inequality follows from the elementary inequality
with if being valid for all \(a_i,b_i \in [0,\infty )\), \(i=1,2\), and \(p \geqq q\). Indeed, assume withput loss of generality that \(p \geqq q\). Then, since the functions \(s \mapsto s^{q/p},s\mapsto s^{1/p}\, s\in {\mathbb {R}}\), are concave, we obtain
\(\square \)
In what follows we embed \(\Omega \) into the d-dimensional torus \({\mathbb {T}}_d\) when it is convenient. Without loss of generality we therefore assume that \(\Omega \) is compactly contained in \((0,1)^d\). In general we use C as a generic constant. However, we use specific constants whenever it is convenient.
2.1.2 \(\Gamma \)-convergence
In this subsection we recall some well-known results on \(\Gamma \)-convergence that are frequently used throughout the paper. We use this notion of convergence to consider the behaviour of functionals of type (1.7) and (1.13) under convergence of the data.
Definition 2.2
Let (X, d) be a metric space. A sequence of functionals \(I_n :X \rightarrow [-\infty ,\infty ]\), \(\Gamma \)-converges to \(I :X \rightarrow [-\infty ,\infty ]\), in symbols \(I= \Gamma -\lim _{n \rightarrow \infty } I_n\), whenever the following is satisfied:
-
(i)
liminf-inequality: For all \(x \in X\) and for all sequences \(x_n \rightarrow x\) we have
$$\begin{aligned} I(x) \leqq \liminf _{n \rightarrow \infty } I_n(x_n). \end{aligned}$$ -
(ii)
limsup-inequality: For all \(x \in X\) there exists a sequence \(x_n \rightarrow x\) (called the recovery sequence) such that
$$\begin{aligned} I(x) \geqq \limsup _{n \rightarrow \infty } I_n(x_n). \end{aligned}$$
Remark 2.3
-
(i)
In metric spaces the constant sequence \(I_n =I\) possesses a \(\Gamma \)-limit \(I^{*}\), namely the lower-semicontinuous hull of I, given by
$$\begin{aligned} I^{*}(x) = \inf _{x_n \rightarrow x } \liminf _{n \rightarrow \infty } I(x_n). \end{aligned}$$(2.3)\(I^*\) is called the relaxation of I.
-
(ii)
If each \(x_n\) is a minimiser of \(I_n\) and \(x_n \rightarrow x\), then x is a minimiser of I.
-
(iii)
One may define \(\Gamma \)-convergence on topological spaces, cf. [11]. This reproduces the definition on metric spaces when equipped with the standard topology. Weak convergence is not metrisable on Banach spaces. However, it is metrisable on bounded sets of reflexive, separable Banach spaces. Hence, if a functional I satisfies a certain growth condition; i.e.
$$\begin{aligned} \alpha (\Vert x \Vert ) \leqq I(x) \end{aligned}$$(2.4)for a function \(\alpha :[0,\infty ) \rightarrow {\mathbb {R}}\) with \(\alpha (t) \rightarrow \infty \) as \(t \rightarrow \infty \), we may use the metric for weak convergence defined on bounded sets of the Banach space and treat the Banach space together with the weak topology as a metric space.
-
(iv)
In topological spaces, especially in Banach spaces equipped with the weak topology, the constant sequence \(I_n=I\) does in general not possess a sequential \(\Gamma \)-limit, as the infimum in (2.3) does not need to be a minimum.
-
(v)
If I does not satisfy the growth condition (2.4), it is possible to consider the sequential \(\Gamma \)-limit, given as in Definition 2.2. However, this might not exist, even if the topological \(\Gamma \)-limit of a sequence of functionals exists. In particular, the constant sequence might not have a sequential \(\Gamma \)-limit.
In the following we only consider the sequential \(\Gamma \)-limit of sequences in the weak topology of some Banach space (usually \(L_p \times L_q\)). If the functional I is coercive in the sense of (2.4), then the sequential \(\Gamma \)-limit coincides with the topological \(\Gamma \)-limit.
The following lemma links \(\Gamma \)-convergence to uniform convergence of functionals.
Lemma 2.4
(Uniform convergence and \(\Gamma \)-convergence) Let V be a reflexive, separable Banach space equipped with the weak topology. Suppose that \(I_n, I :V \rightarrow [-\infty ,\infty ]\), such that \(I_n \rightarrow I\) uniformly on bounded sets of V. If the sequential \(\Gamma \)-limit of the constant sequence I exists, then also \(I_n\) possesses a \(\Gamma \)-limit and
Note that the sequential \(\Gamma \)-limit of the constant sequence I exists if the functional is coercive.
Proof
If \(v_n \rightharpoonup v\) is a bounded sequence in V, we have
Therefore,
which establishes both the \(\limsup \)-inequality and the \(\liminf \)-inequality. \(\square \)
2.1.3 Korn–Poincaré inequality
In this subsection, we revisit a combination of Korn’s inequality (i.e. the full gradient is controlled by its symmetric part) and Poincare’s inequality to obtain an estimate of the form
This estimate is a straightforward consequence of the p-Korn inequality and the Poincaré inequality, cf. for instance [5]. For the convenience of the reader we provide the proof. In what follows we use the notation
Lemma 2.5
(Abstract Korn–Poincaré inequality) Let \(1<p<\infty \) and \(\Omega \subset {\mathbb {R}}^d\) be open, connected, and bounded with \(C^1\)-boundary. Then the following is true:
-
(i)
There is a constant \(C=C(p,\Omega )\), such that for any \(u \in W^1_p(\Omega ;{\mathbb {R}}^d)\) we have that
$$\begin{aligned} \Vert u - (A_u x +b_u) \Vert _{W^1_p} \leqq C \Vert \nabla u + \nabla u^T \Vert _{L_p}, \end{aligned}$$where
 and
and 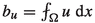 .
. -
(ii)
Let \(X \subset W^1_p(\Omega ;{\mathbb {R}}^d)\) be a closed subspace, such that
$$\begin{aligned} X \cap \left\{ A x + b :A \in {\mathbb {R}}^{d \times d}_{\textrm{skew}}, b \in {\mathbb {R}}^d\right\} = \{0\}. \end{aligned}$$Then there is a constant \(C=C(p,\Omega ,X)\), such that for any \(u \in X\) we have that
$$\begin{aligned} \Vert u \Vert _{W^{1}_p} \leqq C \Vert \nabla u + \nabla u^T \Vert _{L_p}. \end{aligned}$$
Proof
(i) Recall that there is a first-order differential operator \({\tilde{{\mathscr {A}}}}\) with constant coefficients, such that
Therefore, we can bound
Using Nečas’ lemma [1, 25] for functions with zero mean twice and writing  , we get that
, we get that
To obtain an inequality featuring only the skew-symmetric part \(A_u = \tfrac{1}{2}\left( A'_u \right) {- (A'_u)^T}\) note that by the triangle inequality
The statement follows by estimating each term on the right-hand side by \(C \Vert \nabla u + \nabla u^T \Vert _{L_p}\). For the first term we combine (2.7) and (2.6) to obtain
Using Poincaré’s and Jensen’s inequalities, the second term can be estimated by

(ii) Note that the space
is finite-dimensional. As a consequence, if \({\tilde{P}} :W^{1,p}(\Omega ;{\mathbb {R}}^d) \rightarrow {\tilde{X}}\) is a projection, then there is a constant C(X), such that
Indeed, if (2.8) were false, then there would exist a sequence \(u_n \subset X\) with \(\Vert u_n \Vert _{W^1_p} =1\) and \(\Vert u_n - P u_n \Vert _{W^1_p} \rightarrow 0\) as \(n \rightarrow \infty \). As \(P u_n \in {\tilde{X}}\) is bounded and \({{\tilde{X}}}\) is finite dimensional, there is a subsequence \(P u_{n_j}\) converging strongly to some \(y \in {\tilde{X}}\). Since \(\Vert u_n - P u_n \Vert _{W^1_p} \rightarrow 0\), this implies \(u_{n_j} \rightarrow y\) in \(W^1_p(\Omega ;{\mathbb {R}}^d)\). But this is a contradiction, as X is closed, \(\Vert u_{n_j} \Vert _{W^1_p} =1\) and \(X \cap {\tilde{X}} = \{0\}\). Part (i) in combination with (2.8) yields (ii), since \(Pu=A_ux+b_u\). \(\square \)
2.1.4 Constant rank operators
In this subsection we introduce the version of constant rank operators used in this paper. To this end, we slightly adapt the notion of homogeneous constant rank operators [24] since the differential operator \({\mathscr {A}}(\epsilon ,{\tilde{\sigma }})= ({{\,\textrm{curl}\,}}{{\,\textrm{curl}\,}}^T \epsilon , {{\,\textrm{div}\,}}{\tilde{\sigma }})\) appearing in the fluid mechanical application is only componentwise homogeneous.
We consider a differential operator \({\mathscr {A}}\) defined on functions \( v :\Omega \rightarrow {\mathbb {R}}^{m_1} \times {\mathbb {R}}^{m_2}\) defined via
where \({\mathscr {A}}_1\) and \({\mathscr {A}}_2\) are homogeneous constant coefficient differential operators of order \(k_i\), \(i=1,2\), i.e.,
Recall that the Fourier symbols corresponding to the operators defined in (2.9) are given by
Definition 2.6
\({\mathscr {A}}=({\mathscr {A}}_1,{\mathscr {A}}_1)\) satisfies the constant rank property if both \({\mathscr {A}}_1\) and \({\mathscr {A}}_2\) satisfy the constant rank property; that is, if
The characteristic cone of \({\mathscr {A}}\) is defined as
The operator \({\mathscr {A}}\) satisfies the spanning property whenever
Remark 2.7
If \(u_i \in W^{k_i}_{p_i}({\mathbb {T}}_d;{\mathbb {R}}^{m_i})\) can be written as
then \(u_i \in \ker {\mathscr {A}}_i\) if and only if for all \(\xi \in {\mathbb {Z}}^d {\setminus }\{0\}\) we have \({\hat{u}}_i(\xi ) \in \ker {\mathscr {A}}_i[\xi ]\). If, in addition, the operators \({\mathscr {A}}_i\) satisfy the constant rank property, then \({\mathbb {Z}}^d \setminus \{0\}\) can be replaced by \({\mathbb {R}}^d {\setminus } \{0\}\).
2.1.5 Fourier symbols and Fourier multipliers
In this subsection, we recall some important facts about constant rank differential operators that are connected to the Fourier transform on the d-torus \({\mathbb {T}}_d\). As we can consider the constraint operators \({\mathscr {A}}_1\) and \({\mathscr {A}}_2\) separately, we assume \({\mathscr {A}}' :C^{\infty }({\mathbb {R}}^d;{\mathbb {R}}^m) \rightarrow C^{\infty }({\mathbb {R}}^d;{\mathbb {R}}^l)\) to be a constant coefficient differential operator of order \(k_{{\mathscr {A}}'}\), i.e.,
Analogously, we consider \({\mathscr {B}}':C^{\infty }({\mathbb {R}}^d;{\mathbb {R}}^h) \rightarrow C^{\infty }({\mathbb {R}}^d;{\mathbb {R}}^m)\) a constant coefficient differential operator of order \(k_{{\mathscr {B}}'}\). We call \({\mathscr {B}}'\) a potential of \({\mathscr {A}}'\), whenever the corresponding Fourier symbols satisfy
If \(v \in C^{\infty }({\mathbb {T}}_d;{\mathbb {R}}^m) \cap L_p({\mathbb {T}}_d;{\mathbb {R}}^m)\), \(1 \leqq p < \infty \), we may write
For such v and \({\mathbb {W}} :{\mathbb {R}}^d {\setminus } \{0\} \rightarrow {{\,\textrm{Lin}\,}}({\mathbb {R}}^m;{\mathbb {R}}^l)\), we may define a linear operator W on \(C^{\infty }({\mathbb {T}}_d;{\mathbb {R}}^m) \cap L_p({\mathbb {T}}_d;{\mathbb {R}}^m),\ 1 \leqq p < \infty \), by
such that \(W(v) :{\mathbb {T}}_d \rightarrow {\mathbb {R}}^l\). If W maps boundedly into some function space, W(v) can be defined for general \(v \in L_p({\mathbb {T}}_d;{\mathbb {R}}^m)\), \(1 \leqq p < \infty \), by using density. Such an operator W is called Fourier multiplier. The algebraic identity (2.11) in combination with standard Fourier multiplier theory leads to the following statements:
Proposition 2.8
([27]) Let \({\mathscr {A}}' :C^{\infty }({\mathbb {R}}^d;{\mathbb {R}}^m) \rightarrow C^{\infty }({\mathbb {R}}^d;{\mathbb {R}}^l)\) be a differential operator as in (2.10). Then the following holds true:
-
(i)
\({\mathscr {A}}'\) satisfies the constant rank property if and only if there exists a potential \({\mathscr {B}}' :C^{\infty }({\mathbb {R}}^d;{\mathbb {R}}^h) \rightarrow C^{\infty }({\mathbb {R}}^d;{\mathbb {R}}^m)\) of \({\mathscr {A}}'\).
-
(ii)
If \({\mathscr {B}}'\) is a potential of \({\mathscr {A}}'\), there exists a Fourier multiplier operator \({\mathscr {B}}'^{-1} :L_q ({\mathbb {T}}_d;{\mathbb {R}}^m) \rightarrow W^{k_{{\mathscr {B}}'}}_q({\mathbb {T}}_d;{\mathbb {R}}^h)\) of order \(-k_{{\mathscr {B}}'}\), such that for any \(1<q< \infty \) we have
$$\begin{aligned} \Vert {\mathscr {B}}' \circ {\mathscr {B}}'^{-1} v - (v -{\hat{v}}(0)) \Vert _{L_q} \leqq C_q \Vert {\mathscr {A}}' v \Vert _{W^{-k_{{\mathscr {A}}'}}_q}, \end{aligned}$$for some positive constant \(C_q > 0\) that does only depend on q.
For weakly, but not strongly, convergent sequences on bounded sets, there are essentially two possible effects. There can be oscillations and concentrations. For weak lower-semicontinuity results, oscillations are much easier to handle than concentrations. The notion of p-equi-integrability prevents concentration.
Definition 2.9
A set \(X \subset L_p({\mathbb {T}}_d;{\mathbb {R}}^m)\) is called p-equi-integrable if
Lemma 2.10
Let \(W :C^{\infty }({\mathbb {T}}_d;{\mathbb {R}}^m) \rightarrow C^{\infty }({\mathbb {T}}_d;{\mathbb {R}}^m)\) be a 0-homogeneous Fourier multiplier. Then, for any \(1<p<\infty \) the following holds true:
-
(i)
\(W :L_p({\mathbb {T}}_d;{\mathbb {R}}^m) \rightarrow L_p({\mathbb {T}}_d;{\mathbb {R}}^m)\) is bounded;
-
(ii)
W is continuous from \(L_p({\mathbb {T}}_d;{\mathbb {R}}^m)\) to \(L_p({\mathbb {T}}_d;{\mathbb {R}}^m)\) with respect to the weak topology of \(L_p({\mathbb {T}}_d;{\mathbb {R}}^m)\);
-
(iii)
If \(X \subset L_p({\mathbb {T}}_d;{\mathbb {R}}^m)\) is a p-equi-integrable and bounded set, then W(X) is also p-equi-integrable.
Proof
(i) Part (i) follows from the Mikhlin–Hörmander multiplier theorem (e.g.[12, 14]).
(ii) This follows from the fact that the adjoint operator \(W^{*}\) is bounded from \(L_{p'}({\mathbb {T}}_d;{\mathbb {R}}^m)\) to \(L_{p'}({\mathbb {T}}_d;{\mathbb {R}}^m)\).
(iii) In order to verify the p-equi-integrability of W(X), we follow the the lines of the proof of [12, Lemma 2.17].
Step 1: Construction of a truncated sequence. There exists \(R>0\) and for all \(\varepsilon >0\) there exists a \(\delta >0\), such that we have
For \(a > 0\) consider the function \(\tau _a :{\mathbb {R}}^m \rightarrow {\mathbb {R}}^m\), defined by
Then, for fixed \(a >0\) and \(u \in X\), the set \(\{\tau _a\circ u:u\in X\}\) is bounded in \(L_{\infty }({\mathbb {T}}_d;{\mathbb {R}}^m)\). Therefore, by (i), the set \(\{W(\tau _a\circ u):u \in X\}\) is bounded in \(L_r({\mathbb {T}}_d;{\mathbb {R}}^m)\) for \(r \geqq p\).
Step 2: p-equi-integrability of the truncated sequence. We show that, for fixed \(a \in {\mathbb {N}}\), the set \(\{ W(\tau _a \circ u ) \}_{u \in X}\) is p-equi-integrable.
Taking Step 1 into account, this follows from the fact that any bounded set \(X' \subset L_{2p}({\mathbb {T}}_d;{\mathbb {R}}^m)\) is already p-equi-integrable. To prove this, assume for contradiction that there exists a bounded set \(X'\subset L_{2p}({\mathbb {T}}_d;{\mathbb {R}}^m)\) that is not p-equi-integrable. Then there exist \(u_n \subset X'\), \(E_n \subset {\mathbb {T}}_d\) with \(\vert E_n \vert \rightarrow 0\), as \(n \rightarrow \infty \), and an \(\varepsilon >0\), such that
By Jensen’s inequality this implies
which contradicts the assumption that \(u_n\) is bounded in \(L_{2p}({\mathbb {T}}_d;{\mathbb {R}}^m)\) and that \(\vert E_n \vert \rightarrow 0\).
We conclude that, for any \(\varepsilon >0\), there is \(\delta _a(\varepsilon )>0\), such that, for all \(u \in X\) we have the implication
Step 3: p-equi-integrability of W(X). We show that Step 2 together with p-equi-integrability of X implies that W(X) is p-equi-integrable.
Using p-equi-integrability and boundedness, we may estimate
Therefore, we find that
Let now \(\varepsilon >0\). By (2.14), there exists \(a(\varepsilon ) \in {\mathbb {R}}_{+}\), such that
In combination with (2.12), for all sets E with measure smaller than \(\delta _{a(\varepsilon )}(\varepsilon /2)\), this yields
Therefore, the set W(X) is p-equi-integrable. \(\square \)
2.2 The differential operator \({\mathscr {A}}\) for problems in fluid mechanics
In this section, we discuss how the fluid mechanical constraints (1.8) and (1.9) fit into the previously outlined abstract setting. We consider the two differential operators
as follows:
The Fourier symbol of the differential operator \({\mathscr {A}}_1\) is given by
For \({\mathscr {A}}_2\), the Fourier symbol reads as
For a fixed \(\xi \in {\mathbb {R}}^d \setminus \{0\}\), the set \(\ker {\mathscr {A}}_1[\xi ] \times \ker {\mathscr {A}}_2[\xi ]\) is given as follows. Let \(Y_{\xi } \subset Y\) be defined as
where \(a \odot \xi = \frac{1}{2}\left( a \otimes \xi + \xi \otimes a\right) \) is the symmetric tensor product. Note that \(Y_{\xi }\) is a \((d-1)\)-dimensional subspace of Y. Then
meaning that the space dimension of \(\ker {\mathscr {A}}_1[\xi ]\) is \((d-1)\) and
where \(\pi _{{\tilde{\sigma }}}\) is defined as the unique \(\pi \in {\mathbb {R}}\), such that \({\mathscr {A}}_2[\xi ]({\tilde{\sigma }},\pi ) =0\), i.e.,
The differential condition \({{\,\textrm{curl}\,}}{{\,\textrm{curl}\,}}^T \epsilon =0\) for \(\epsilon \in L_p({\mathbb {T}}_d;Y)\) with \(\int _{T_d} \epsilon \;\textrm{d}x=0\) encodes that \(\epsilon \) is a symmetric gradient, i.e. there is \(u \in W^1_p({\mathbb {T}}_d;{\mathbb {R}}^d)\) satisfying
The differential operator
can be treated as if it was a potential of \({\mathscr {A}}_1\).
Remark 2.11
Due to the additional constraint \({{\,\textrm{div}\,}}u=0\), \({\mathscr {B}}_1\) is not a potential to \({\mathscr {A}}_1\) in the sense of (2.11). In particular, Proposition 2.8 cannot be applied directly. Note, however that a function \(u \in W^1_p({\mathbb {T}}_d;{\mathbb {R}}^d)\) with zero average satisfies the differential constraint \({{\,\textrm{div}\,}}u=0\) if and only if
for a suitable function \(U \in W^{2,p}\left( {\mathbb {T}}_d;{\mathbb {R}}^{d \times d}_{\textrm{skew}}\right) \), where \({{\,\textrm{curl}\,}}^{*}\) is the adjoint of \({{\,\textrm{curl}\,}}\); in other words \({{\,\textrm{curl}\,}}^{*}\) is a potential of \({{\,\textrm{div}\,}}\). In particular, this also means that if \(\epsilon = \tfrac{1}{2}\left( \nabla u + \nabla u^T\right) \), then there exists \(U \in W^2_p\left( {\mathbb {T}}_d;{\mathbb {R}}^{d \times d}_{\textrm{skew}}\right) \) such that
Consequently, \({{\tilde{{\mathscr {B}}}}}_1 = \tfrac{1}{2}\left( \nabla +\nabla ^T\right) \circ {{\,\textrm{curl}\,}}^{*}\) is a potential of \({\mathscr {A}}_1\).
For the purpose of applying Fourier methods, we can use the symmetric gradient \({\mathscr {B}}_1\) on divergence-free matrices instead of the true potential. The suitable inverse of \({\mathscr {B}}_1\) in the Fourier space is
which is a Fourier multiplier of order \(1+(-2)=-1\).
The potential to the differential operator \({\mathscr {A}}_2\) is not relevant in this setting. Let us remark that the condition
for \(({\tilde{\sigma }},\pi ) \in L_q({\mathbb {T}}_d;Y \times {\mathbb {R}})\) and \(f \in W^{-1,p}({\mathbb {T}}_d;{\mathbb {R}}^d)\), can be rewritten in terms of \({\tilde{\sigma }}\) only, as
Another strategy to tackle the linear problem from a ”purely“ Fourier analytic perspective would be to ”forget“ about the pressure \(\pi \) by using the operator \({\tilde{{\mathscr {A}}}}_2({\tilde{\sigma }}) = {{\,\textrm{curl}\,}}\circ {{\,\textrm{div}\,}}{\tilde{\sigma }}\). Note that in this approach the operator \({{\,\textrm{curl}\,}}\circ {{\,\textrm{div}\,}}\) acting on \({\tilde{\sigma }}\) is the adjoint operator of \(\tfrac{1}{2} \left( \nabla +\nabla ^T\right) \circ {{\,\textrm{curl}\,}}^{*}\) which acts on U. For the non-linear problem, cf. Section 5.2, this approach yields the equation
We believe however, that from the fluid dynamical point of view it is more instructive to include the pressure \(\pi \in L_q(\Omega )\) by sticking to the more physical equation
3 Existence of Minimisers: Weak Lower-Semicontinuity and Coercivity
It is the structure of the differential constraints, with constant rank operators of different order, the quasilinear perturbation of the otherwise linear constraints, the boundary conditions, and the natural location of \(\epsilon \) and \({\tilde{\sigma }}\) in different spaces, which necessitates Sect. 3, where all of these challenges are adressed in an abstract setting.
3.1 \({\mathscr {A}}\)-Quasiconvexity
In order to study weak lower-semicontinuity results, we first introduce the notion of \({\mathscr {A}}\)-quasiconvexity for a constant rank operator \({\mathscr {A}}=({\mathscr {A}}_1,{\mathscr {A}}_2)\) as defined in the previous section.
Definition 3.1
A (measurable and locally bounded) function  is called \({\mathscr {A}}\)-quasiconvex if for all \(z=(z_1,z_2) \in {\mathbb {R}}^{m_1} \times {\mathbb {R}}^{m_2}\) and for all test functions \(\psi =(\psi _1,\psi _2) \in {\mathscr {T}}_{{\mathscr {A}}}\) with
is called \({\mathscr {A}}\)-quasiconvex if for all \(z=(z_1,z_2) \in {\mathbb {R}}^{m_1} \times {\mathbb {R}}^{m_2}\) and for all test functions \(\psi =(\psi _1,\psi _2) \in {\mathscr {T}}_{{\mathscr {A}}}\) with

it holds that

For  we define the \({\mathscr {A}}\)-quasiconvex envelope
we define the \({\mathscr {A}}\)-quasiconvex envelope  of
of  as
as

 is called \(\Lambda _{{\mathscr {A}}}\)-convex if for all \(z \in {\mathbb {R}}^{m_1}\times {\mathbb {R}}^{m_2}\) and all \(w \in \Lambda _{{\mathscr {A}}}\) the function
is called \(\Lambda _{{\mathscr {A}}}\)-convex if for all \(z \in {\mathbb {R}}^{m_1}\times {\mathbb {R}}^{m_2}\) and all \(w \in \Lambda _{{\mathscr {A}}}\) the function

is convex.
Note that the \({\mathscr {A}}\)-quasiconvex envelope  of a continuous function
of a continuous function  is the largest \({\mathscr {A}}\)-quasiconvex function smaller than
is the largest \({\mathscr {A}}\)-quasiconvex function smaller than  [12]. Moreover, a function
[12]. Moreover, a function  is \({\mathscr {A}}\)-quasiconvex if and only if
is \({\mathscr {A}}\)-quasiconvex if and only if  .
.
Proposition 3.2
(Properties of \({\mathscr {A}}\)-quasiconvex functions) Let \({\mathscr {A}}= ({\mathscr {A}}_1,{\mathscr {A}}_2)\) be a differential operator satisfying the constant rank property and the spanning property and let  . Then the following holds true:
. Then the following holds true:
-
(i)
If
 is locally bounded and \({\mathscr {A}}\)-quasiconvex, then
is locally bounded and \({\mathscr {A}}\)-quasiconvex, then  is continuous;
is continuous; -
(ii)
if
 is continuous, then
is continuous, then  is \({\mathscr {A}}\)-quasiconvex and for all \(z\in {\mathbb {R}}^{m_1} \times {\mathbb {R}}^{m_2}\) it holds that
is \({\mathscr {A}}\)-quasiconvex and for all \(z\in {\mathbb {R}}^{m_1} \times {\mathbb {R}}^{m_2}\) it holds that 
-
(iii)
if
 is continuous and \({\mathscr {A}}\)-quasiconvex, then
is continuous and \({\mathscr {A}}\)-quasiconvex, then 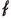 is \(\Lambda _{{\mathscr {A}}}\)-convex;
is \(\Lambda _{{\mathscr {A}}}\)-convex; -
(iv)
if
 is \({\mathscr {A}}\)-quasiconvex, \(1< p,q< \infty \) and for all \(z\in {\mathbb {R}}^{m_1} \times {\mathbb {R}}^{m_2}\) it holds that
is \({\mathscr {A}}\)-quasiconvex, \(1< p,q< \infty \) and for all \(z\in {\mathbb {R}}^{m_1} \times {\mathbb {R}}^{m_2}\) it holds that 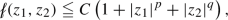
then
 is locally Lipschitz continuous and
is locally Lipschitz continuous and 
where \(\alpha = (p-1)q/p\) and \(\beta = (q-1)p/q\).
Statements (i)–(iii) are slight adaptions of [12, Section 3] for the case of first-order operators to the higher-order case. Statement (iv) is a (p, q)-adaptation of [13, 15, 20], where the \(L_p\)-setting is treated. The proof relies on the fact that any \({\mathscr {A}}\)-quasiconvex function is \(\Lambda _{{\mathscr {A}}}\)-convex.
3.2 Weak lower-semicontinuity under differential constraints
Throughout this paragraph we consider \(1<p,q<\infty \), a Carathéodory function  and functionals \(I,J:L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2}) \rightarrow {\mathbb {R}}\) defined by
and functionals \(I,J:L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2}) \rightarrow {\mathbb {R}}\) defined by

The next proposition is a straight-forward adaption of the semi lower-continuity result [12, Theorem 3.6] to the (p, q)-setting.
Proposition 3.3
Let \(1<p,q<\infty \), let  be a Carathéodory function, and assume that there exists \(C>0\) such that the following growth condition is satisfied:
be a Carathéodory function, and assume that there exists \(C>0\) such that the following growth condition is satisfied:

Moreover, let  be \({\mathscr {A}}\)-quasiconvex for a.e. \(x \in \Omega \), where \({\mathscr {A}}=({\mathscr {A}}_1,{\mathscr {A}}_2)\) is a constant rank operator with \({\mathscr {A}}_i\) having rank \(k_i\). Then the following holds true:
be \({\mathscr {A}}\)-quasiconvex for a.e. \(x \in \Omega \), where \({\mathscr {A}}=({\mathscr {A}}_1,{\mathscr {A}}_2)\) is a constant rank operator with \({\mathscr {A}}_i\) having rank \(k_i\). Then the following holds true:
-
(i)
Along all sequences \(v_n \rightharpoonup v\) in \(L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\) with \({\mathscr {A}}v_n \rightarrow {\mathscr {A}}v\) strongly in \(W^{-k_1}_p(\Omega ;{\mathbb {R}}^{m_1}) \times W^{-k_2}_q(\Omega ;{\mathbb {R}}^{m_2})\) the functional J is sequentially weakly lower-semicontinuous, i.e.
$$\begin{aligned} J(v) \leqq \liminf _{n \rightarrow \infty } J(v_n); \end{aligned}$$ -
(ii)
the functional I is sequentially weakly lower-semicontinuous on \(L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\).
We do not provide the proof of Proposition 3.3 here, since it is largely analogous to the proof of [12, Theorem 3.6], which is based on a suitable notion of equi-integrable sequences. In the (p, q)-setting, the right notion of equi-integrability is the following:
Definition 3.4
A set \(X \subset L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\) is called (p, q)-equi-integrable, if for all \(\varepsilon >0\) there exists a \(\delta >0\), such that
that is \(\{ v_1 \}_{v \in X}\) and \(\{ v_2 \}_{v \in X}\) are p-equi-integrable and q-equi-integrable, respectively.
The key insight for Proposition 3.3 is that it suffices to consider (p, q)-equi-integrable sequences. This is the content of the following proposition which is again a straightforward adaption of the p-setting:
Proposition 3.5
Let \(1<p,q < \infty \) and let  be a Carathéodory function satisfying the growth condition (3.5). Let \(v_n \rightharpoonup v\) in \(L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\) and suppose that there is a (p, q)-equi-integrable sequence \(w_n \subset L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\) such that for some \(\theta \) with \(\max \left( 1/p,1/q\right)<\theta <1\) it holds that
be a Carathéodory function satisfying the growth condition (3.5). Let \(v_n \rightharpoonup v\) in \(L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\) and suppose that there is a (p, q)-equi-integrable sequence \(w_n \subset L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\) such that for some \(\theta \) with \(\max \left( 1/p,1/q\right)<\theta <1\) it holds that
Then we have that
The proof of Proposition 3.5 is contained in the proof of the following theorem:
Theorem 3.6
Let \(1<p,q < \infty \) and let \(X \subset L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\) be weakly closed. Moreover, let  be Carathéodory functions. We define the functionals \(I^X_n, I^X :X \rightarrow {\mathbb {R}}\) as
be Carathéodory functions. We define the functionals \(I^X_n, I^X :X \rightarrow {\mathbb {R}}\) as

Suppose that X satisfies the following condition:
-
(H1)
For all bounded sequences \(v_n \subset X\) there exists a (p, q)-equi-integrable sequence \(w_n \subset X\), such that \(w_n-v_n \rightarrow 0\) in measure.
Suppose further that  satisfy that
satisfy that
-
(H2)
there exists a constant \(C>0\), such that for all \((z_1,z_2) \in {\mathbb {R}}^{m_1} \times {\mathbb {R}}^{m_2}\) and almost every \(x \in \Omega \) we have

-
(H3)
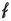 and
and 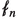 are uniformly continuous on bounded sets of \( {\mathbb {R}}^{m_1} \times {\mathbb {R}}^{m_2}\), i.e. there exists a monotone function \(\nu _R:[0,\infty )\rightarrow {\mathbb {R}}\) with \(\nu _R(s)\rightarrow 0\) as \(s\rightarrow 0\), such that for all \(n\in {\mathbb {N}}\), all \(z_1,z_2 \in {\mathbb {R}}^{m_1}\times {\mathbb {R}}^{m_2}\) with \(\vert z_1 \vert , \vert z_2 \vert \leqq R\), and for almost every \(x \in \Omega \):
are uniformly continuous on bounded sets of \( {\mathbb {R}}^{m_1} \times {\mathbb {R}}^{m_2}\), i.e. there exists a monotone function \(\nu _R:[0,\infty )\rightarrow {\mathbb {R}}\) with \(\nu _R(s)\rightarrow 0\) as \(s\rightarrow 0\), such that for all \(n\in {\mathbb {N}}\), all \(z_1,z_2 \in {\mathbb {R}}^{m_1}\times {\mathbb {R}}^{m_2}\) with \(\vert z_1 \vert , \vert z_2 \vert \leqq R\), and for almost every \(x \in \Omega \): 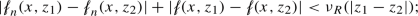
-
(H4)
the functionals with integrands
 converge uniformly on equi-integrable subsets, i.e. for all equi-integrable sets \(B \subset L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_1})\) and for all \(\varepsilon >0\) there exists \(n_{\varepsilon } \in {\mathbb {N}}\), such that for all \(v \in B\) and all \(n \geqq n_{\varepsilon }\) it holds
converge uniformly on equi-integrable subsets, i.e. for all equi-integrable sets \(B \subset L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_1})\) and for all \(\varepsilon >0\) there exists \(n_{\varepsilon } \in {\mathbb {N}}\), such that for all \(v \in B\) and all \(n \geqq n_{\varepsilon }\) it holds 
Then the functionals \(I^X_n\) and \(I^X\) enjoy the following properties:
-
(i)
for all sequences \(v_n \rightharpoonup v\) in X, there is a sequence \(w_n \rightharpoonup v\) in X such that
$$\begin{aligned} \limsup _{n \rightarrow \infty } I^X_n(w_n) \leqq \liminf _{n \rightarrow \infty } I^X(v_n); \end{aligned}$$ -
(ii)
for all sequences \(v_n \rightharpoonup v\) in X, there is a sequence \({\bar{w}}_n \rightharpoonup v\) in X such that
$$\begin{aligned} \limsup _{n \rightarrow \infty } I^X({\bar{w}}_n) \leqq \liminf _{n \rightarrow \infty } I^X_n(v_n); \end{aligned}$$ -
(iii)
if the sequential \(\Gamma \)-limit of the constant sequence \(I^X\) exists, then the sequential \(\Gamma \)-limit of \(I^X_n\) exists and
$$\begin{aligned} \Gamma - \lim _{n \rightarrow \infty } I_n^X = \Gamma - \lim _{n \rightarrow \infty } I^X. \end{aligned}$$
Note that the constraint set \({\mathscr {C}}\) in the fluid mechanical application is weakly closed and may thus play the role of the set X.
Proof
(i) The main idea of the proof is to show that a suitable version of Proposition 3.5 holds, namely that sequences \(w_n \subset X\) as in (H1) already satisfy (i). To this end, let \(v_n \subset X\) be bounded, and let \(w_n \subset X\) be a (p, q)-equi-integrable sequence, such that \(w_n - v_n \rightarrow 0\) in measure. Then we have that

Due to (H4) and the (p, q)-equi-integrablility of \(w_n\) the first term tends to 0. In order to estimate the second term, let \(L > 0\) be a constant such that \(\Vert v_n\Vert _{L_p}, \Vert w_n\Vert _{L_p} \leqq L\). Then, using (H2), for any \(R>0\) we obtain

The first integral on the right-hand side of this inequality converges to 0 as \(n \rightarrow \infty \), since \(w_n - v_n \rightarrow 0\) in measure by (H1). Moreover, since the sequence \(w_n\) is (p, q)-equi-integrable, the second integral can be bounded by a constant \(c_R\) with \(c_R \rightarrow 0\) as \(R \rightarrow \infty \). Consequently,

and we conclude that
(ii) The second statement is obtained in the same way by swapping the roles of  and
and  . Note that we can uniformly estimate
. Note that we can uniformly estimate

as all  have the same modulus of continuity on bounded sets, cf. (H3).
have the same modulus of continuity on bounded sets, cf. (H3).
(iii) If the sequential \(\Gamma \)-limit of \(I^X\) exists (we denote it by \(I^{X*}\)), then for all \(v \in X\) the following holds true.
-
(a)
Every sequence \(v_n \subset X\) with \(v_n \rightharpoonup v\) in X satisfies \(I^{X*}(v) \leqq \liminf _{n \rightarrow \infty } I^X (v_n)\).
-
(b)
There exists a sequence \(v_n \subset X\) with \(v_n \rightharpoonup v\) in X, such that \(I^{X*}(v) \geqq \limsup _{n \rightarrow \infty } I^X(v_n)\).
The \(\liminf \)-inequality for \(I_n^X\) is ensured by (ii), i.e. if \(v_n \rightharpoonup v\) in X, then
as \({{\bar{w}}}_n \rightharpoonup v\) in X. On the other hand, the \(\limsup \)-inequality follows from (i): the recovery sequence \(v_n\) (or at least a suitable subsequence) can be modified to an equi-integrable recovery sequence \(w_n\). By (i), we find that
This completes the proof. \(\square \)
The main challenge in applying Theorem 3.6 to the case in which X is a set given by differential constraints and boundary conditions is to verify Hypothesis (H1). In Sect. 4 we check the conditions (H2)–(H4) on the integrand  . To verify (H1), for a given sequence \(v_n\) we need to construct a suitable (p, q)-equi-integrable modification \(w_n\) that conserves both the differential constraints and the boundary conditions. For this purpose we need the following two auxiliary results:
. To verify (H1), for a given sequence \(v_n\) we need to construct a suitable (p, q)-equi-integrable modification \(w_n\) that conserves both the differential constraints and the boundary conditions. For this purpose we need the following two auxiliary results:
Lemma 3.7
Let \((X,d_X)\) be a complete metric space. Suppose that \(x_n\) is a sequence in X, such that \(x_n \rightarrow x\) and that, for \(m \in {\mathbb {N}}\), we have \({x_{n,m}}\) with
Then \(x_{n,m} \rightarrow x\) uniformly in m, as \(n \rightarrow \infty \).
Proof
Let \(\varepsilon >0\). Then there exists \(m_{\varepsilon } \in {\mathbb {N}}\), such that for all \(m \geqq m_{\varepsilon }\)
and an \(N_{\varepsilon }\), such that for all \(n>N_{\varepsilon }\) we find that
Moreover, there are \(N^1,\ldots ,N^{m_{\varepsilon }}\), such that for all \(m=1,\ldots ,m_\varepsilon \) it holds
Choosing \(N = \max \{N_{\varepsilon }, N^1,\ldots ,N^{m_{\varepsilon }}\}\) yields that for any \(n >N\) and \(m \in {\mathbb {N}}\) we have
which is the required uniform convergence. \(\square \)
The following result is due to [12, Lemma 2.15]. It allows to construct (p, q)-equi-integrable modified sequences. However, in general these modified sequences fail to conserve the constraints.
Proposition 3.8
Let \(v_n\) be a bounded sequence in \(L_p(\Omega ;{\mathbb {R}}^m)\). Then there exists a p-equi-integrable sequence \({\tilde{v}}_n\) with the following properties:
-
(i)
for almost every \(x \in \Omega \) we have \(\vert {\tilde{v}}_n(x) \vert \leqq \vert v_n(x) \vert \);
-
(ii)
for every \(q<p\) we have \(\lim _{n \rightarrow \infty } \Vert v_n - {\tilde{v}}_n \Vert _{L_q} =0\).
The following theorem allows us to obtain modified sequences that continue to satisfy both differential constraints and boundary conditions:
Theorem 3.9
(Equi-integrable sequences & boundary values) Suppose that \({\mathscr {A}}: C^{\infty }({\mathbb {R}}^d;{\mathbb {R}}^m) \rightarrow C^{\infty }({\mathbb {R}}^d;{\mathbb {R}}^l)\) is a homogeneous differential operator of order \(k_{{\mathscr {A}}}\), satisfying the constant rank property and that \({\mathscr {B}}\) is a potential of \({\mathscr {A}}\) in the sense of (2.11). Let \(\Omega \subset {\mathbb {R}}^d\) be an open and bounded set with Lipschitz boundary. Let \(v_n \rightharpoonup 0\) in \(L_p(\Omega ;{\mathbb {R}}^m)\) and \({\mathscr {A}}v_n \rightarrow 0\) in \(W^{-k_{{\mathscr {A}}}}_p(\Omega ;{\mathbb {R}}^l)\). Then there exists a sequence \(w_n \subset W^{k_{{\mathscr {B}}}}_p(\Omega ;{\mathbb {R}}^h)\) such that the following holds true:
-
(i)
the sequence \(\sum _{j=0}^{k_{{\mathscr {B}}}} \vert \nabla ^j w_n \vert \) is p-equi-integrable;
-
(ii)
\(\Vert {\mathscr {B}}w_n - v_n \Vert _{L_q} \rightarrow 0\), as \(n \rightarrow \infty \) for any \(q<p\);
-
(iii)
\(w_n\) is compactly supported in \(\Omega \).
The main difficulty in the proof compared to the statement without boundary values in [12] is to obtain the compact support.
Proof
Step 1: Construction of the sequence. We assume by scaling that \(\Omega \subset \subset (0,1)^d\), i.e. it may be viewed as a subset of the d-dimensional torus \({\mathbb {T}}_d\). We extend \(v_n\) by 0 outside \(\Omega \). Let \(m \in {\mathbb {N}}\). We define open sets \(V_m\) and \(U_m\), such that \(V_m \subset \subset U_m \subset \subset \Omega \); in particular,
Then there exist \(\varphi _m \in C_c^{\infty }(V_m)\) with \(\varphi _m \equiv 1\) on \(U_m\) and \(\psi _m \in C_c^{\infty }(\Omega )\) with \(\psi _m \equiv 1\) on \(V_m\), such that for all \(k,m \in {\mathbb {N}}\)
By Proposition 3.8 there exists a p-equi-integrable sequence \({\tilde{v}}_n\), such that \(\Vert {\tilde{v}}_n - v_n \Vert _{L_q} \rightarrow 0\) for \(q<p\). Therefore, as \(v_n\) converges weakly to 0, so does \({\tilde{v}}_n\). We define
We claim that we can take an appropriate diagonal sequence \(w_{n,m(n)}\) with \(m(n) \rightarrow \infty \), as \(n \rightarrow \infty \), such that \(w_{n,m(n)}\) satisfies the requirements of Theorem 3.9. The purpose of the following steps is to construct such a sequence m(n).
Step 2: Estimates on \({\bar{v}}_{n,m}\). First, we show that
To this end, note that there is a constant \(C>0\), such that
since \(\Omega \) has Lipschitz boundary. Then we deduce that
As \({\tilde{v}}_n\) is p-equi-integrable, the right-hand side converges to 0, as \(m \rightarrow \infty \). Thus, (3.7) is established.
Second, we bound the \(W^{-k_{{\mathscr {A}}}}_q\)-norm of \({\mathscr {A}}{\bar{v}}_{n,m}\). We claim that there exists a sequence \(M_1(n)\) with \(M_1(n) \rightarrow \infty \), as \(n \rightarrow \infty \), such that for all m(n) with \(m(n) \leqq M_1(n)\) and \(m(n) \rightarrow \infty \), as \(n \rightarrow \infty \), there exists \(1<q<p\) such that
Note that if \({\tilde{v}}_n\) is in \(C^k(\Omega ;{\mathbb {R}}^m)\), then we may write
Therefore, by applying the definition of \(W^{-k_{{\mathscr {A}}}}_q({\mathbb {T}}_d;{\mathbb {R}}^l)\), we may estimate
Due to density of \(C^k(\Omega ;{\mathbb {R}}^m)\) in \(L_p(\Omega ;{\mathbb {R}}^m)\), inequality (3.10) is still valid even if \({\tilde{v}}_n\) is merely in \(L_p(\Omega ;{\mathbb {R}}^m)\). With the estimates for the derivatives of \(\varphi \) we get that
Note that, on the one hand, \({\mathscr {A}}{\tilde{v}}_n \rightarrow 0\) in \(W^{-{k_{{\mathscr {A}}}}}_q(\Omega ;{\mathbb {R}}^l)\), as \({\mathscr {A}}v_n \rightarrow 0\) in \(W^{-{k_{{\mathscr {A}}}}}_p(\Omega ;{\mathbb {R}}^l)\) and \({\tilde{v}}_n - v_n \rightarrow 0\) in \(L_q(\Omega ;{\mathbb {R}}^m)\) for \(q<p\). On the other hand, as \({\tilde{v}}_n\) is bounded in \(L_p(\Omega ;{\mathbb {R}}^m)\) and weakly converging to 0, \({\tilde{v}}_n \rightarrow 0\) in \(W^{-1}_q(\Omega ;{\mathbb {R}}^m)\) strongly, due to the compact embedding of \(L_q(\Omega ;{\mathbb {R}}^m)\) into \(W^{-1}_q(\Omega ;{\mathbb {R}}^m)\). Therefore, choosing
we get that
Last, let us note that due to equi-integrability of \({\tilde{v}}_n\) and \(\vert {\bar{v}}_{n,m} \vert \leqq \vert {\tilde{v}}_n \vert \), also the set \(\{ {\bar{v}}_{n,m} \}_{n,m \in {\mathbb {N}}}\) is equi-integrable.
Step 3: Upper Bound on \(\Vert {\mathscr {B}}w_{n,m} -v_n \Vert _{L_q}\). First, we note that, by definition, \(w_{n,m}\) is compactly supported in \(\Omega \) for any \(m \in {\mathbb {N}}\), as \(\psi _m\) is compactly supported in \(\Omega \). Moreover, it holds that
We already established by the choice of \({\tilde{v}}_n\) (c.f. Proposition 3.8), that \(\mathrm {(IV)} \rightarrow 0\), as \(n \rightarrow \infty \). Furthermore, \(\mathrm {(III)} \rightarrow 0\), as \(n \rightarrow \infty \), whenever \(m=m(n) \rightarrow \infty \), cf. (3.7). Proposition 2.8 yields
The first term tends to 0 by (3.12), whenever \(m(n) \leqq M_1(n)\) is a sequence diverging to \(\infty \) as \(n \rightarrow \infty \), while the mean of \({\tilde{v}}_{n,m(n)}\) converges to zero since \({\tilde{v}}_n\rightharpoonup 0\) and because of (3.7). It remains to bound \(\mathrm {(I)}.\) To this end, note that the triangle inequality and then Hölder’s inequality imply that
The first term vanishes (uniformly in \(n\in {\mathbb {N}}\)) as \(m\rightarrow \infty \), due to the uniform \(L_p\) bound on \({\mathscr {B}}{\bar{w}}_{n,m}\), as the operator \(W=\nabla ^{k_{{\mathscr {B}}}} \circ {\mathscr {B}}^{-1}\) is a 0-homogeneous, smooth Fourier multiplier. Moreover, for the second summand note that due to Lemma 2.10 (ii) W is continuous from \(L_q({\mathbb {T}}_d;{\mathbb {R}}^m)\) to \(L_q({\mathbb {T}}_d;{\mathbb {R}}^h\otimes ({\mathbb {R}}^{d})^{\otimes k_{\mathscr {B}}})\) in the weak topology. Recall, that \({\tilde{v}}_n \rightharpoonup 0\), as \(n \rightarrow \infty \) in \(L_p({\mathbb {T}}_d;{\mathbb {R}}^m)\), that \({\bar{v}}_{n,m}\) is uniformly bounded in \(L_p({\mathbb {T}}_d;{\mathbb {R}}^m)\) and for fixed \(m \in {\mathbb {N}}\), \({\bar{v}}_{n,m} = \varphi _m {\tilde{v}}_n \rightharpoonup 0\). The weak topology of \(L_p({\mathbb {T}}_d;{\mathbb {R}}^m)\) is metrisable on bounded sets, whence we may apply Lemma 3.7 to get that the convergence
is uniform in \(m \in {\mathbb {N}}\). Again, by the boundedness of W, it holds that
For \(s<p^{*} = dp/(d-p)\), the embedding \(W^{k_{{\mathscr {B}}}}_p({\mathbb {T}}_d;{\mathbb {R}}^h) \hookrightarrow W^{k_{{\mathscr {B}}}-1}_s({\mathbb {T}}_d;{\mathbb {R}}^h)\) is compact. Hence, uniform weak convergence of \(\nabla ^{k_{{\mathscr {B}}}} {\bar{w}}_{n,m}\), together with Poincaré’s inequality, imply that
This holds in particular for \(s=p<p^*\). Therefore, choosing \(M_2(n)\) as
implies for any sequence m(n) with \(m(n) \leqq \min \{M_1(n),M_2(n)\}\) and \(m(n) \rightarrow \infty \), the inequality
Step 4: Equi-integrability of \(w_{n,m}\). It remains to show that we may choose the diagonal sequence \(w_{n,m(n)}\) in such a fashion, that \(\nabla ^j w_{n,m(n)}\) is still p-equi-integrable for all \(1 \leqq j \leqq k_{{\mathscr {B}}}\). Note that
The sequence \({\bar{w}}_{n,m}\) is uniformly bounded in m and n in \(W^{k_{{\mathscr {B}}}}_p({\mathbb {T}}_d;{\mathbb {R}}^m)\), as \({\bar{v}}_{n,m}\) is uniformly bounded in \(L_p({\mathbb {T}}_d;{\mathbb {R}}^m)\) and \({\mathscr {B}}^{-1}\) maps \(L_p({\mathbb {T}}_d;{\mathbb {R}}^m)\) to \(W^{k_{{\mathscr {B}}}}_p({\mathbb {T}}_d;{\mathbb {R}}^h)\). Hence, for \(j<k_{{\mathscr {B}}}\), \(\nabla ^j {\bar{w}}_{n,m}\) is bounded in \(L_r({\mathbb {T}}_d;{\mathbb {R}}^h\otimes ({\mathbb {R}}^{d})^{\otimes j})\) for some \(r>p\) and thus \(\vert \psi _m\nabla ^j {\bar{w}}_{n,m} \vert \leqq \vert \nabla ^j {\bar{w}}_{n,m}\vert \) is p-equi-integrable. Furthermore, observe that we have the pointwise estimate
Hence, for p-equi-integrability it suffices to show that there is \(M_3(n) \rightarrow \infty \), as \(n \rightarrow \infty \), such that for \(i < k_{{\mathscr {B}}}\) the sets
are p-equi-integrable. Indeed, (3.15) is clear, even for \(m \in {\mathbb {N}}\), instead of only \(m \leqq M_3(n)\), using again that \(W = \nabla ^{k_{{\mathscr {B}}}} \circ {\mathscr {B}}^{-1}\) is a smooth 0-homogeneous Fourier multiplier. On the other hand, \(\nabla ^{k_{{\mathscr {B}}}} {\bar{w}}_{n,m} = W( {\tilde{v}}_{n,m})\) and \(W( {\tilde{v}}_{n,m})\) is p-equi-integrable for \(m,n \in {\mathbb {N}}\) by Step 1. In (3.14) we have already established the convergence
for all \(s < p^{*}\). Let now \(s\in (p,p^{*})\) be fixed. Then for all measurable sets E we find that

Note that \(\vert E\vert ^{\frac{s-p}{p}} \rightarrow 0\), as \(\vert E \vert \rightarrow 0\). Hence we assume that \(m \leqq M_3(n)\), with \(M_3\) defined as
We conclude that for any \(0 \leqq j \leqq k_{{\mathscr {B}}}\) the set
is p-equi-integrable.
Finally, choosing a sequence \(m(n) \rightarrow \infty \), as \(n \rightarrow \infty \), with \(m(n) \leqq \min \{M_1(n),M_2(n),M_3(n)\} \rightarrow \infty \) completes the proof. \(\square \)
Corollary 3.10
(Preservation of boundary conditions) Let \(\Omega \subset {\mathbb {R}}^d\) be an open and bounded set with Lipschitz boundary. Suppose that \({\mathscr {A}}:C^{\infty }({\mathbb {R}}^d;{\mathbb {R}}^m) \rightarrow C^{\infty }({\mathbb {R}}^d;{\mathbb {R}}^l)\) is a homogeneous differential operator of order \(k_{{\mathscr {A}}}\), satisfying the constant rank property. Let \(v \in L_p(\Omega ;{\mathbb {R}}^m)\) and let \(v_n \subset L_p(\Omega ;{\mathbb {R}}^m)\), such that \(v_n \rightharpoonup v\) in \(L_p(\Omega ;{\mathbb {R}}^m)\) and \( {\mathscr {A}}v_n \rightarrow {\mathscr {A}}v\) in \(W^{-k_{{\mathscr {A}}}}_p(\Omega ;{\mathbb {R}}^l)\). Suppose that \({\mathscr {B}}\) is a potential of \({\mathscr {A}}\).
-
(i)
Suppose that v can be written as \(v= {\mathscr {B}}u\). There exists a sequence \(u_n \subset W^{k_{{\mathscr {B}}}}_p(\Omega ;{\mathbb {R}}^h)\), such that
-
(a)
\(u_n - u\) is compactly supported in \(\Omega \);
-
(b)
\({\mathscr {B}}u_n\) is p-equi-integrable;
-
(c)
\(\Vert {\mathscr {B}}u_n - v_n \Vert _{L_{r}(\Omega )} \rightarrow 0\) for some \(1<r<p\).
-
(a)
-
(ii)
There is a sequence \({{\bar{v}}}_n \subset L_p(\Omega ;{\mathbb {R}}^m)\), such that
-
(a)
\({\mathscr {A}}{{\bar{v}}}_n = {\mathscr {A}}v\);
-
(b)
\({{\bar{v}}}_n-v\) is compactly supported in \(\Omega \);
-
(c)
\({{\bar{v}}}_n\) is p-equi-integrable;
-
(d)
\(\Vert {{\bar{v}}}_n-v_n \Vert _{L_{r}(\Omega )} \rightarrow 0\) for some \(1<r<p\).
-
(a)
Corollary 3.10 is used to modify sequences of functions in the constraint set \({\mathscr {C}}\) to obtain equi-integrable sequences while at the same time preserving differential constraints and boundary conditions. Note that in problems of fluid mechanics the boundary conditions are typically given for u, the potential of \(\epsilon \), therefore part (i) is suitable for boundary conditions on the fluid velocity u being the potential of the strain. On the other hand, boundary conditions for \(\sigma \) are directly given in terms of the stress. Hence part (ii) is suitable there.
3.3 Relaxation
If the function  is not \({\mathscr {A}}\)-quasiconvex, the functional I in (3.4) fails to be weakly lower-semicontinuous. Hence, we cannot ensure existence of minimisers just by using the direct method in the calculus of variations. However, when studying the data-driven problem, it is enough to consider approximate minimisers, i.e. minimising sequences \(v_n\) with \(I(v_n)\) converging to the infimum of I, and their weak limits \(v^{*}\). In the following, we define a functional \(I^{*}\) such that it is the relaxation of I. Thus, any weak limit \(v^{*}\) of a minimising sequence is a minimiser of \(I^{*}\) and, vice versa, any minimiser of \(I^{*}\) is a weak limit of approximate minimisers.
is not \({\mathscr {A}}\)-quasiconvex, the functional I in (3.4) fails to be weakly lower-semicontinuous. Hence, we cannot ensure existence of minimisers just by using the direct method in the calculus of variations. However, when studying the data-driven problem, it is enough to consider approximate minimisers, i.e. minimising sequences \(v_n\) with \(I(v_n)\) converging to the infimum of I, and their weak limits \(v^{*}\). In the following, we define a functional \(I^{*}\) such that it is the relaxation of I. Thus, any weak limit \(v^{*}\) of a minimising sequence is a minimiser of \(I^{*}\) and, vice versa, any minimiser of \(I^{*}\) is a weak limit of approximate minimisers.
3.3.1 Relaxation under a linear differential constraint
We recall the definition of I from (3.4). For simplicity, we use for the quasiconvex envelope of a function  the short-hand notation
the short-hand notation

Note that by Proposition 3.3 the functional \(I^{*}\) given by

is weakly lower-semicontinuous in \(L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\). That \(I^*\) is indeed the relaxation of I is a consequence of the following (linear) result [2].
Proposition 3.11
Let \((v_1,v_2) \in L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\). Furthermore, let  satisfy the following assumptions:
satisfy the following assumptions:
-
(A1)
 is a Carathéodory function;
is a Carathéodory function; -
(A2)
there is \(C>0\) such that for almost every \(x \in \Omega \) and \((v_1,v_2)\in {\mathbb {R}}^{m_1}\times {\mathbb {R}}^{m_2}\) it holds that

Then, for any \(\varepsilon >0\) there exists a bounded sequence \(v^n=(v_{1,n}^{\varepsilon },v_{2,n}^{\varepsilon })\) in \(L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\), such that
-
(i)
\(v_{1,n}^{\varepsilon } \rightharpoonup v_1\) in \(L_p(\Omega ;{\mathbb {R}}^{m_1})\) and \(v_{2,n}^{\varepsilon } \rightharpoonup v_2\) in \(L_q(\Omega ;{\mathbb {R}}^{m_2})\) as \(n \rightarrow \infty \);
-
(ii)
\({\mathscr {A}}_1 v_{1,n}^{\varepsilon } = {\mathscr {A}}_1 v_1\) and \({\mathscr {A}}_2 v_{2,n}^{\varepsilon } = {\mathscr {A}}_2 v_2\);
-
(iii)
\(v_n^{\varepsilon }\) is almost a recovery sequence, i.e.

Remark 3.12
The (almost) recovery sequence \(v_n^\epsilon \) in Proposition 3.11 is bounded in \(L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\) with a bound that depends on \(\varepsilon \). Consequently, a priori we might not be able to take a weakly convergent diagonal sequence \(v_n^{\varepsilon (n)}\), such that

However, for fixed \(v=(v_1,v_2) \in L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\), let us define the constraint set \({\mathscr {C}}_v\) as the set of functions \((w_1,w_2) \in L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\) satisfying
We say that a functional J is coercive on \({\mathscr {C}}_v\), provided
If \(J :v \mapsto \int _{\Omega } f(x,v) \;\textrm{d}x\) is coercive, there is a uniform bound on the \(L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;{\mathbb {R}}^{m_2})\)-norm of \(v_n^{\varepsilon }\). By taking a diagonal sequence of \(v_n^{\varepsilon }\) we may conclude the existence of a recovery sequence \(v_n\) satisfying

Coercivity as defined in (3.18) is classically obtained by assuming that
This strong pointwise coercivity condition is however not suitable for our setting. The distance function to a set K only satisfies (3.19) if the set K is bounded. Instead, we use a weaker coercivity condition of the type
In general, \(v_1 \cdot v_2\) does not have a good pointwise bound. Nevertheless, in the fluid mechanical setting, appropriate boundary conditions allow us to bound the integral \(\int _{\Omega } v_1 \cdot v_2 \;\textrm{d}x\), cf. Section 5.
3.3.2 Relaxation under a semi-linear differential constraint
As above, let \(\Omega \subset {\mathbb {R}}^d\) be an open and bounded domain with Lipschitz boundary. Instead of considering a linear differential constraint, e.g.
we include a semilinear term. In the fluid mechanical setting this semilinear term is given by
where u is uniquely determined by \(\epsilon \) due to boundary conditions and the constraint \(\epsilon = \tfrac{1}{2}(\nabla u +\nabla u^T)\).
We fix a suitable general setting. Let, as before \({\mathscr {A}}_1 :L_p(\Omega ;{\mathbb {R}}^{m_1}) \rightarrow W^{-k_1}_p(\Omega ;{\mathbb {R}}^{l_1}) \) be a constant rank operator with a potential \({\mathscr {B}}_1 :W^{k_{{\mathscr {B}}_1}}_p(\Omega ;{\mathbb {R}}^{h_1}) \rightarrow L_p(\Omega ;{\mathbb {R}}^{m_1})\) and \({\mathscr {A}}_2 :L_q(\Omega ;{\mathbb {R}}^{m_2}) \rightarrow W^{-k_2}_p(\Omega ;{\mathbb {R}}^{l_2})\) be a constant rank operator. In addition, we require the semilinear term to satisfy the following:
-
(A3)
\(\theta :\Omega \times {\mathbb {R}}^{h_1} \times ({\mathbb {R}}^{h_1} \otimes {\mathbb {R}}^d) \ldots \times ({\mathbb {R}}^{h_1} \times {\mathbb {R}}^{h_1} \otimes ({\mathbb {R}}^d)^{\otimes k_{{\mathscr {B}}_1}} \rightarrow {\mathbb {R}}^{m_1}\) is a continuous map;
-
(A4)
The map \(\Theta \) defined on \(W^{k_{{\mathscr {B}}_1}}_p(\Omega ;{\mathbb {R}}^{h_1})\) via
$$\begin{aligned} (\Theta u)(x) = \theta \bigl (x,u(x),\nabla u(x),\ldots ,\nabla ^{k_{{\mathscr {B}}_1}}u(x)\bigr ) \end{aligned}$$is continuous from the weak topology of \(W^{k_{{\mathscr {B}}_1}}_p(\Omega ;{\mathbb {R}}^{h_1})\) to the strong topology of \(L_r(\Omega ;{\mathbb {R}}^{l_2})\) for some \(r>q\).
We study the following set of constraints:
Theorem 3.13
Let  satisfy the assumptions (A1)–(A2) from Proposition 3.11 and let \(\Theta :L_p(\Omega ;{\mathbb {R}}^{m_1}) \rightarrow W^{-1}_r(\Omega ;{\mathbb {R}}^{l_2})\) and \({\mathscr {A}}_1\), \({\mathscr {A}}_2\) satisfy the aforementioned hypotheses (A3)–(A4). Suppose that \(u_1 \in W^{k_1}_p(\Omega ;{\mathbb {R}}^{h_1})\) and \(v=(v_1,v_2) \in L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;Y \times {\mathbb {R}})\), such that \(u_1 = {\mathscr {B}}_1 v_1\) and \({\mathscr {A}}_2 v_2 = \Theta (u_1)\). Then, for all \(\varepsilon > 0\), there exist bounded sequences \(u_{1,n}^{\varepsilon } \subset W^{k_1}_p(\Omega ;{\mathbb {R}}^{h_1})\) and \(v_{n}^{\varepsilon } \subset L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;Y \times {\mathbb {R}})\) such that
satisfy the assumptions (A1)–(A2) from Proposition 3.11 and let \(\Theta :L_p(\Omega ;{\mathbb {R}}^{m_1}) \rightarrow W^{-1}_r(\Omega ;{\mathbb {R}}^{l_2})\) and \({\mathscr {A}}_1\), \({\mathscr {A}}_2\) satisfy the aforementioned hypotheses (A3)–(A4). Suppose that \(u_1 \in W^{k_1}_p(\Omega ;{\mathbb {R}}^{h_1})\) and \(v=(v_1,v_2) \in L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;Y \times {\mathbb {R}})\), such that \(u_1 = {\mathscr {B}}_1 v_1\) and \({\mathscr {A}}_2 v_2 = \Theta (u_1)\). Then, for all \(\varepsilon > 0\), there exist bounded sequences \(u_{1,n}^{\varepsilon } \subset W^{k_1}_p(\Omega ;{\mathbb {R}}^{h_1})\) and \(v_{n}^{\varepsilon } \subset L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;Y \times {\mathbb {R}})\) such that
-
(i)
\({\mathscr {B}}_1 u_{1,n}^{\varepsilon } = v_{1,n}^{\varepsilon }\);
-
(ii)
\(u_{1,n}^{\varepsilon } - u_1\) is supported in \(\Omega _n \subset \subset \Omega \);
-
(iii)
\({\mathscr {A}}_2 v_{2,n}^{\varepsilon } = {\mathscr {A}}_2\Theta (u_{1,n}^{\varepsilon })\);
-
(iv)
\(v_{2,n}^{\varepsilon }-v_2\) is supported in \(\Omega _n \subset \subset \Omega \);
-
(v)
\(v_{n}^{\varepsilon }\) is almost a recovery sequence, i.e. it satisfies

Remark 3.14
-
(i)
The statement of Theorem 3.13 is quite strong concerning boundary conditions. Indeed, the recovery sequence consisting of \(u_{1,n}^\varepsilon \) and \(v_{2,n}^\varepsilon \) preserves both the boundary conditions of \(u_1\) and the boundary conditions of \(v_2\). Thus, it is possible to use the statement independently of the particular boundary conditions (Dirichlet, Neumann, ...) in Sect. 5.
-
(ii)
Remark 3.12 is still valid in the setting of Theorem 3.13. More precisely, if we have a coercivity condition on the functional restricted to functions obeying 3.21 and some boundary conditions, then we may find a recovery sequence satisfying (i)–(iv) and

Proof of Theorem 3.13
By the linear relaxation result Proposition 3.11 there exists a sequence \(({\bar{v}}_{1,n},{\bar{v}}_{2,n}) \subset L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;Y \times {\mathbb {R}})\) weakly converging to \(v=(v_1,v_2)\) satisfying

By Proposition 3.5 and Corollary 3.10 we may take \({\tilde{u}}_{1,n}^{\varepsilon } \in W^{k_1}_p(\Omega ;{\mathbb {R}}^h)\), and \({\tilde{v}}_n \in L_p(\Omega ;{\mathbb {R}}^{m_1}) \times L_q(\Omega ;Y \times {\mathbb {R}})\), such that
-
(i)
\({\tilde{v}}_{1,n}^{\varepsilon }= {\mathscr {B}}_1 {\tilde{u}}_{1,n}^{\varepsilon }\);
-
(ii)
the first \(k_1\)-derivatives of \({\tilde{u}}_{1,n}^{\varepsilon }\) are p-equi-integrable;
-
(iii)
\({\tilde{v}}_{2,n}^{\varepsilon }\) is q-equi-integrable;
-
(iv)
\({\mathscr {A}}_2 {\tilde{v}}_{2,n}^{\varepsilon }= {\mathscr {A}}_2 \Theta (u_1)\);
-
(v)
the functions \({\tilde{u}}_{1,n}^{\varepsilon }\) and \({\tilde{v}}_{2,n}^{\varepsilon }\) satisfy the boundary conditions
$$\begin{aligned} {\left\{ \begin{array}{ll} \textrm{spt}({\tilde{u}}_{1,n}^{\varepsilon }-u_1) \subset \Omega _n &{} \\ \textrm{spt}({\tilde{v}}_{2,n}^{\varepsilon } -v_2) \subset \Omega _n \end{array}\right. } \end{aligned}$$for some \(\Omega _n \subset \subset \Omega \);
-
(vi)
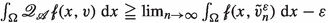 .
.
We set \(v_1^n={\tilde{v}}_{1,n}^{\varepsilon }\) and \(u_{1,n}^{\varepsilon }={\tilde{u}}_{1,n}^{\varepsilon }\) and modify \({\tilde{v}}_{2,n}^{\varepsilon }\) by
such that \({\mathscr {A}}_2 v_{2,n}^{\varepsilon } = \Theta (u_{1,n}^{\varepsilon })\). In particular, we solve the following equation:
But we know that \(w_{2,n}^{\varepsilon } = \Theta (u_{1,n}^{\varepsilon }) - \Theta (u_1)\) already is a solution to this system. As \(u_{1,n}^{\varepsilon }-u_1\) is supported inside \(\Omega _n \subset \subset \Omega \), so is \(u_{1,n}^{\varepsilon }\) due to the definition of the map \(\Theta \), cf. (A3) and (A4). Due to weak-strong continuity we have
Then \(v_{2,n}^{\varepsilon }:= {\tilde{v}}_{2,n}^{\varepsilon } + w_{2,n}^{\varepsilon }\) still is q-equi-integrable, as \({\tilde{v}}_{2,n}^{\varepsilon }\) is q-equi-integrable and \(w_{2,n}^{\varepsilon }\) bounded in \(L_r(\Omega ;Y \times {\mathbb {R}})\) for some \(r>q\); hence also p-equi-integrable. Moreover, as \(v_{1,n}^{\varepsilon } \rightharpoonup v_1\) in \(L_p(\Omega ;Y)\) and \(\Theta \) is weak-strong continuous,
and we conclude by Proposition 3.5 that

As \({\tilde{v}}_{2,n}^{\varepsilon } - v_2\) is compactly supported in \(\Omega \), \(v_{2,n}^{\varepsilon } -v_2\) satisfies the demanded boundary conditions and \({\mathscr {A}}v_{2,n}^{\varepsilon } ={\mathscr {A}}_2 \Theta (v_{1,n}^{\varepsilon })\). Hence, (up to a subsequence) \(v_n^{\epsilon }\) is almost a recovery sequence. \(\square \)
Remark 3.15
The statement of Theorem 3.13 is taylored towards its application for fluid dynamics, cf. Section 5.2. Observe that in the proof of Theorem 3.13, a main step was to solve the differential equation
together with suitable boundary conditions. This equation is solved by the observation, that \((\Theta (u_{1,n}^{\varepsilon })- \Theta (u_1))\) already satisfies the boundary conditions.
If we generalise the setting to other non-linearities, we need more assumptions on the non-linearity. For example, consider a constraint like
for some map \(\zeta :W^{k_{{\mathscr {B}}_1}}_p(\Omega ;{\mathbb {R}}^{h_1}) \rightarrow W^{-k_{{\mathscr {A}}_1}}_q(\Omega ;{\mathbb {R}}^{h_2})\). Then weak-strong continuity is not enough, as one also needs to solve the analogue of (3.22) with suitable boundary conditions. If for example, \({\mathscr {A}}_2 = {{\,\textrm{div}\,}}\), then a further condition is as follows: Whenever \(u_1\) and \(u'_1\) satisfy \(\textrm{spt}(u_1-u'_1) \subset \subset \Omega \), then \(\int \zeta (u_1)-\zeta (u'_1) \;\textrm{d}x =0\) (such that the divergence-equation is solvable, cf. [3]).
4 Convergence of Data Sets
In this section, we define two different notions of data convergence, i.e. we define a suitable topology on closed subsets of \(Y\times Y\). We show that these notions are equivalent to convergence of the unconstrained functionals J in (1.13). In particular, these notions of data convergence are independent of the underlying differential constraint. Recall that we assume that the data consist of pairs of strain \(\epsilon \) and the viscous part \({\tilde{\sigma }}\) of the stress; the pressure \(\pi \) is not part of the data.
4.1 Data convergence on bounded sets
Definition 4.1
Let \(Y \times Y \) be equipped with the metric \(d:Y \times Y \rightarrow {\mathbb {R}}\) and \(({\mathscr {D}}_n), {\mathscr {D}}\) be closed, nonempty subsets of \(Y\times Y\). We say that \({\mathscr {D}}_n\) converges to \({\mathscr {D}}\) strongly in the topology \({\mathscr {T}}_{bd }\), \({\mathscr {D}}_n \overset{bd}{\longrightarrow }{\mathscr {D}}\), if the following is satisfied:
-
(i)
Uniform approximation: There exists a sequence \(a_n \rightarrow 0\), such that for all \(n\in {\mathbb {N}}\) and for all \(z=(\epsilon , {\tilde{\sigma }}) \in {\mathscr {D}}\) it holds that
$$\begin{aligned} {{\,\textrm{dist}\,}}(z,{\mathscr {D}}_n) \leqq a_n (1 + \vert \epsilon \vert ^p + \vert {\tilde{\sigma }}\vert ^q ). \end{aligned}$$ -
(ii)
Fine approximation: There exists a sequence \(b_n \rightarrow 0\), such that for all \(n\in {\mathbb {N}}\) and for all \(z_n=(\epsilon _n,{\tilde{\sigma }}_n) \in {\mathscr {D}}_n\) it holds that
$$\begin{aligned} {{\,\textrm{dist}\,}}(z_n,{\mathscr {D}}) \leqq b_n (1 + \vert \epsilon _n \vert ^p + \vert {\tilde{\sigma }}_n \vert ^q). \end{aligned}$$
We consider the functionals defined on V by
Theorem 4.2
Let \({\mathscr {D}}_n,{\mathscr {D}}\) be closed, nonempty subsets of \(Y\times Y\). The following statements are equivalent:
-
(i)
\({\mathscr {D}}_n \overset{bd}{\longrightarrow }{\mathscr {D}}\);
-
(ii)
For all \(v \in V\) it holds that
$$\begin{aligned} \lim _{n \rightarrow \infty } J_n(v) = J(v) \end{aligned}$$and this convergence is uniform on bounded subsets of V.
Proof
‘(i) \(\Rightarrow \) (ii)’. Suppose without loss of generality that \(0 \in {\mathscr {D}}\). Otherwise we translate the underlying space which at most changes \(a_n,b_n\) by a bounded factor. Let \(v \in V\), with \(\int _{\Omega } {{\,\textrm{dist}\,}}(v,0) \;\textrm{d}x \leqq R\). We assume without loss of generality that \(p\geqq q\). Then for \(n \in {\mathbb {N}}\) we may estimate
where \(w_n(x) \in {\mathscr {D}}_n\) is a point in \({\mathscr {D}}_n\) such that \(d(v(x),w_n(x)) = d(v(x),{\mathscr {D}}_n)\). Note that, as \(0 \in {\mathscr {D}}\) and due to the uniform approximation property, we obtain a pointwise bound on \(w_n\), i.e. \(d(w_n(x),0) \leqq 2 d(v(x),0)\) for n large enough. Therefore, for some \(\varepsilon >0\) we get
Note that \(\int _{\Omega } d(v,{\mathscr {D}}_n)^p \;\textrm{d}x \) is bounded from above (for n large enough) by \(2 \int _{\Omega } d(v,0)^p \;\textrm{d}x \leqq 2R\) as \(0 \in {\mathscr {D}}\) and 0 is approximated uniformly by elements of \({\mathscr {D}}_n\). Therefore, for any \(\delta >0\) we may choose \(\varepsilon \) and \(n_0 \in {\mathbb {N}}\) such that for all \(n > n_0\) we have
Consequently, there exists \(\delta (R,n) \rightarrow 0\), such that for all \(v \in V\) with \(\int _{\Omega } {{\,\textrm{dist}\,}}(v,0) \;\textrm{d}x \leqq R\) it holds that
For the lower bound on J(v) we can do the same calculation using fine instead of uniform approximation and find that for any \(v \in V\) with \(\int _{\Omega } {{\,\textrm{dist}\,}}(v,0) \;\textrm{d}x \leqq R\) we have
We argue as for the lower bound, to obtain \({\tilde{\delta }}(R,n) \rightarrow 0\), such that for all \(v \in V\) with \(\int {{\,\textrm{dist}\,}}(v,0) \;\textrm{d}x \leqq R\)
Therefore, the convergence \(J_n(v) \rightarrow J(v)\) is uniform on bounded subsets of V.
‘(ii)\(\Rightarrow \) (i)’. We prove the statement by contradiction. Suppose first, that \({\mathscr {D}}\) is not uniformly approximated, i.e. there exists \(a >0\) and a subsequence \(z_{n_k}=(\epsilon _{n_k},{\tilde{\sigma }}_{n_k}) \subset {\mathscr {D}}\), such that
We assume without loss of generality that \(0 \in {\mathscr {D}}\). Let \(\Sigma _{n_k}\) be a subset of \(\Omega \) with measure \(\vert \Omega \vert (1+{{\,\textrm{dist}\,}}(z_{n_k},0))^{-1}\). We define
Then \(\int _{\Omega } {{\,\textrm{dist}\,}}(v_{n_k},0)\) is bounded uniformly from above by \(\vert \Omega \vert \). Furthermore,
On the other hand,
Therefore, \(J_n(v)\) does not converge to J(v) uniformly on bounded sets of V.
If \({\mathscr {D}}_n\) is not a fine approximation of \({\mathscr {D}}\), the argument is similar. Then there exists \(b>0\) and a subsequence \(z_{n_k} \in {\mathscr {D}}_{n_k}\), such that,
Again, assume that \(0 \in {\mathscr {D}}\). We may assume that there exists a sequence \(z'_n \rightarrow 0\) with \(z'_n \in {\mathscr {D}}_n\), otherwise for \(v \equiv 0\), it holds that
Let \(\Sigma _{n_k}\) be a subset of \(\Omega \) with measure \(\vert \Omega \vert (1+{{\,\textrm{dist}\,}}(z_{n_k},0))^{-1}\) and define
As argued before, \(\int _{\Omega } {{\,\textrm{dist}\,}}(v_{n_k},{\mathscr {D}}) \;\textrm{d}x \) is bounded uniformly by \(\vert \Omega \vert \) and for \(k \in {\mathbb {N}}\) we find that
But, for the distance to \({\mathscr {D}}\) we have
Therefore, the convergence \(J_n(v) \rightarrow J(v)\) cannot be uniform on bounded subsets of V. \(\square \)
The definition of this type of convergence is motivated by Lemma 2.4. In particular, we have as a consequence that if \({\mathscr {D}}_n \overset{bd}{\longrightarrow }{\mathscr {D}}\), then the sequential \(\Gamma \)-limit of \(J_n\) and of the constant sequence J coincide, i.e
4.2 Data convergence on equi-integrable sets
Definition 4.3
We say that a sequence of closed sets \({\mathscr {D}}_n \subset Y \times Y\) converges to \({\mathscr {D}}\) in the \({\mathscr {T}}_{eq }\)-topology, \({\mathscr {D}}_n \overset{eq}{\longrightarrow }{\mathscr {D}}\), if the following is satisfied.
-
(i)
Fine approximation on bounded sets: There are sequences \(a_n\rightarrow 0\) and \(R_n\rightarrow \infty \) such that for all \(n\in {\mathbb {N}}\) and for all \(z \in {\mathscr {D}}\) with \(|z| < R_n\), it holds that
$$\begin{aligned} {{\,\textrm{dist}\,}}(z, {\mathscr {D}}_n) \leqq a_n (1 + |z|). \end{aligned}$$ -
(ii)
Uniform approximation on bounded sets: There are sequences \(b_n\rightarrow 0\) and \(S_n\rightarrow \infty \) such that for all \(n\in {\mathbb {N}}\) and for all \(z_n \in {\mathscr {D}}_n\) with \(|z_n| < S_n\), it holds that
$$\begin{aligned} {{\,\textrm{dist}\,}}(z_n,{\mathscr {D}}) \leqq b_n (1 + |z_n|). \end{aligned}$$
Remark 4.4
The following statements are equivalent to the uniform approximation on bounded sets:
-
For all \(R>0\) there is a sequence \(a_n^R \rightarrow 0\) such that for all \(z \in {\mathscr {D}}\) with \({{\,\textrm{dist}\,}}(z,0)<R\) we have
$$\begin{aligned} {{\,\textrm{dist}\,}}(z,D_n) \leqq a_n^R (1 + \vert \epsilon \vert ^p + \vert {\tilde{\sigma }}\vert ^q). \end{aligned}$$ -
For all \(a>0\) and \(R>0\), there is an n(a, R) such that for all \(z \in {\mathscr {D}}\) with \({{\,\textrm{dist}\,}}(z,0) < R\) and \(n >n(a,R)\) we have
$$\begin{aligned} {{\,\textrm{dist}\,}}(z,D_n) \leqq a (1 + \vert \epsilon \vert ^p + \vert {\tilde{\sigma }}\vert ^q). \end{aligned}$$
Similar equivalent statements hold for the fine approximation on bounded sets.
Theorem 4.5
Let \({\mathscr {D}}_n,{\mathscr {D}}\) be closed, nonempty subsets of \(Y\times Y\). The following statements are equivalent:
-
(i)
\({\mathscr {D}}_n \overset{eq}{\longrightarrow }{\mathscr {D}}\) in the \({\mathscr {T}}_{eq }\)-topology.
-
(ii)
The functionals \(J_n\) converge uniformly to J on (p, q)-equi-integrable subsets of V. That is, if \(X \subset V\) is (p, q)-equi-integrable, then
$$\begin{aligned} \lim _{n \rightarrow \infty } \sup _{v \in X} \vert J_n(v) - J(v) \vert =0. \end{aligned}$$
Proof
‘(i) \(\Rightarrow \) (ii)’: The proof is similar to the proof of Theorem 4.2. We only prove that fine and uniform approximation imply that, for a (p, q)-equi-integrable subset \(X \subset V\), we have
The converse inequality follows similarly. For simplicity assume that \(0 \in {\mathscr {D}}\) and that \(p \geqq q\). For some fixed \(R>0\) we estimate
We now estimate both integrals on the right-hand side from below and start with the second term. The set \(X \subset V\) is (p, q)-equi-integrable. Hence, there is an increasing function \(\omega :{\mathbb {R}}_+ \rightarrow {\mathbb {R}}_+\) such that
The set X is bounded. Thus, defining
we find that the measure of \(\{ {{\,\textrm{dist}\,}}(v,0) > R\}\) is bounded by \(MR^{-1}\). Consequently, we obtain
We turn to the first term in (4.4). If \({{\,\textrm{dist}\,}}(v(x),0) \leqq R\), we may find some \(w(x)\in {\mathscr {D}}\) with \({{\,\textrm{dist}\,}}(w(x),0) \leqq (2^p+2^q)R\), and
Due to uniform approximation for all w(x), we can estimate for n large enough
Together with (4.5) this implies
Choosing \(R(\varepsilon )\) and n large enough, then for any \(\varepsilon \) there is \(n_{\varepsilon }\), such that
which establishes (4.3).
‘(ii) \(\Rightarrow \) (i)’: This implication is a consequence of the same counterexamples as in Theorem 4.2. Indeed, suppose that the sets \({\mathscr {D}}_n\) do not uniformly approximate \({\mathscr {D}}\) on bounded sets. Then there exist \(R>0\), \(a>0\) and a sequence \(z_{n_k} \subset {\mathscr {D}}\), such that \({{\,\textrm{dist}\,}}(z_n,0) \leqq R\) and
By the same construction as in the proof of Theorem 4.2, that is
we obtain a sequence, such that \(J(v_{n_k}) =0\) and \(J_n(v_{n_k})\geqq a \vert \Omega \vert \) with \(v_{n_k}\) uniformly bounded in \(L_{\infty }(\Omega ;Y\times Y)\) and hence \(v_{n_k}\) is also (p, q)-equi-integrable. For fine approximation the argument is again very similar. \(\square \)
5 The data-driven problem in fluid mechanics
In this section we apply the theory developed in the previous sections to the setting of fluid mechanics. We thus specialise to an explicit set of constraints \({\mathscr {C}}\) consisting of differential constraints and boundary conditions. In Section 5.1 we consider the case of inertialess fluids, leading to a set of linear differential constraints. In Section 5.2 we consider nonlinear differential constraints. In both cases we work with the following boundary conditions defined on three mutually disjoint and relatively open parts of the boundary \(\Gamma _D,\Gamma _R,\Gamma _N\subset \partial \Omega \) that satisfy
and have \(C^1\)-boundary as subsets of the manifold \(\partial \Omega \). We consider \((\epsilon ,{\tilde{\sigma }}) \in L_p(\Omega ;Y) \times L_q(\Omega ;Y )\) with an associated velocity field \(u:\Omega \rightarrow {\mathbb {R}}^d\), where \(\epsilon =\tfrac{1}{2} \left( \nabla u+\nabla u^T\right) \) and a pressure field \(\pi :\Omega \rightarrow {\mathbb {R}}\), such that u and \(\sigma =-\pi {{\,\textrm{id}\,}}+{\tilde{\sigma }}\) satisfy the following boundary conditions.
-
(D): No-slip/Dirichlet boundary conditions:
$$\begin{aligned} u = g\quad \text {on } \Gamma _D \quad \text {for } g\in W^{1-1/p}_p(\Gamma _D;{\mathbb {R}}^d). \end{aligned}$$ -
(R): Navier-slip/Robin boundary conditions:
$$\begin{aligned} {\left\{ \begin{array}{ll} u\cdot \nu =g_\nu \\ P_{T\partial \Omega }\left( ({\tilde{\sigma }}- \pi {{\,\textrm{id}\,}})\nu +\lambda u\right) = h_\tau \end{array}\right. }\quad \text {on } \Gamma _R \end{aligned}$$for \(g_{\nu } \in W^{1-1/p}_p(\Gamma _R)\) and \(h_\tau \in W^{-1/q}_q(\Gamma _R;{\mathbb {R}}^d)\). Here, \(\lambda \geqq 0\) is the inverse slip-length and \(P_{T\partial \Omega }\) is the orthogonal projection to the tangent space. Note that the second equation can equivalently be cast as
$$\begin{aligned} P_{T\partial \Omega }\left( {\tilde{\sigma }}\nu +\lambda u\right) = h_\tau \quad \text {on } \Gamma _R. \end{aligned}$$(5.1) -
(N): Neumann boundary conditions:
$$\begin{aligned} ({\tilde{\sigma }}- \pi {{\,\textrm{id}\,}})\nu =h \quad \text {on } \Gamma _N \quad \text {for } h\in W^{-1/q}_q(\Gamma _N;{\mathbb {R}}^d). \end{aligned}$$
Remark 5.1
-
(i)
The boundary conditions for u can be understood as conditions for \(\epsilon \) in a suitable weak formulation. For instance, if \(\Gamma _D = \partial \Omega \), then (D) is equivalent to the following condition on \(\epsilon \). For any \(\varphi \in W^1_q(\Omega ;Y)\) with \({{\,\textrm{div}\,}}\varphi =0\) we have
$$\begin{aligned} \int _\Omega \epsilon \cdot \varphi \;\textrm{d}x = \int _{\partial \Omega } g (\varphi \cdot \nu ) \;\textrm{d}{{\mathcal {H}}}^{d-1}. \end{aligned}$$However, since an \(\epsilon \) that is contained in the constraint set \({\mathscr {C}}\) automatically admits a corresponding u (see (linD) below and following explanation), we write the conditions directly for u. A similar remark applies to the appearance of \(\pi \).
-
(ii)
The Navier-slip boundary condition (R) requires \(P_{T\partial \Omega }u\in W_q^{-1/q}(\Gamma _R;{\mathbb {R}}^d)\) since the other two terms in (5.1) are contained in this space. Since \(\epsilon \in L_p(\Omega ;Y)\), and by Lemma 2.5 together with a trace estimate, we have \(u\in W^{1-1/p}_p(\Gamma _R;{\mathbb {R}}^d)\). The space \(W^{1-1/p}_p(\Gamma _R)\) embeds into \(W^{-1/q}_q(\Gamma _R)\), whenever either \(p\geqq q\) or
$$\begin{aligned} 1-\tfrac{1}{p} - \tfrac{d-1}{p} \geqq -\tfrac{1}{q} - \tfrac{d-1}{q}. \end{aligned}$$Thus, since \(q= \tfrac{p}{p-1}\), we require
$$\begin{aligned} p \geqq \tfrac{2d}{d+1}. \end{aligned}$$(5.2)We can therefore treat the Navier-slip boundary condition in the physically relevant dimensions \(d=2\) and \(d=3\) for \(p\geqq 4/3\) and for \(p\geqq 3/2\), respectively.
-
(iii)
The Navier boundary condition (R) includes the so called free-slip boundary condition for \(\lambda =0\).
-
(iv)
For simplicity we assume in the following that either \(\Gamma _N=\partial \Omega \) or \(\Gamma _D\ne \emptyset \). This allows us to control \(\Vert u\Vert _{W^1_p}\) in terms of \(\Vert \epsilon \Vert _{L_p}\) and the boundary data via the Korn–Poincaré inequality, cf. Lemma 2.5. If \(\Gamma _R\ne \emptyset \), while \(\Gamma _D=\emptyset \), it becomes tedious to specify under which conditions this control can still be obtained. See Lemma 5.2 and Remark 5.3 below.
-
(v)
We specify further conditions, under which the boundary condition for \(({\tilde{\sigma }}- \pi {{\,\textrm{id}\,}})\nu \) is well-defined below, as there are differences between the case with and without inertia.
In order to obtain a Korn–Poincaré type inequality, u has to be uniquely determined by the above boundary conditions
and the constraint
or the conditions must be invariant under renormalisation by rigid body motions.
Lemma 5.2
(Validity of the Korn–Poincaré inequality under boundary conditions) Let \(\Omega \subset {\mathbb {R}}^d\) be open and bounded with \(C^1\)-boundary and let \(\partial \Omega = {\bar{\Gamma }}_D \cup {\bar{\Gamma }}_R\cup {\bar{\Gamma }}_N\) be as specified above. Moreover, suppose that \(g\in W^{1-1/p}_p(\partial \Omega ;{\mathbb {R}}^d)\), \(g_{\nu }\in W^{1-1/p}_p(\partial \Omega )\) and that for all \(A \in {\mathbb {R}}^{d \times d}_{\textrm{skew}},~b \in {\mathbb {R}}^d\) we have that
Then the following statements hold true:
-
1.
If \(u_1\) and \(u_2\) satisfy (5.3) and
$$\begin{aligned} \nabla u_1 + \nabla u_1^T = \nabla u_2 + \nabla u_2^T, \end{aligned}$$then \(u_1=u_2\).
-
2.
For all \(u \in W^{1,p}(\Omega ;{\mathbb {R}}^d)\) obeying (5.3) with \(\Gamma _D \ne \emptyset \), the Korn–Poincaré inequality
$$\begin{aligned} \Vert u \Vert _{W^{1,p}} \leqq C (1+ \Vert \nabla u + \nabla u^T \Vert _{L_p}) \end{aligned}$$(5.5)holds for a constant \(C=C(\Omega ,\Gamma _D,\Gamma _R,g,g_{\nu },p)\).
Proof
(i): The assertion follows from the fact that if \(\nabla u_1 + \nabla u_1^T = \nabla u_2 + \nabla u_2^T\), then \(u_1-u_2 = Ax +b\) for some \(A \in {\mathbb {R}}^{d \times d}_{\textrm{skew}}\) and \(b \in {\mathbb {R}}^d\). Condition (5.4) then implies that \(A=0\) and \(b=0\).
(ii): The vector space \(X \subset W^1_p(\Omega ;{\mathbb {R}}^d)\) of functions satisfying the homogeneous boundary conditions in (5.3) satisfies, due to (5.4),
By transposition we get the inhomogeneous version (5.5) for the affine space of functions satisfying (5.3). \(\square \)
Remark 5.3
Indeed, (5.4) is a rather weak condition on the set \(\Omega \). For example, in dimension \(d=2\), the weakest boundary condition in the case \(\Gamma _D=\emptyset \) would be
Since \({\mathbb {R}}^{d\times d}_{\textrm{skew}}\) is one-dimensional, we can explicitly set
It follows that the only sets not satisfying (5.4) are such that \(\Gamma _R\) is a subset of concentric circles. Moreover, if \(\Gamma _D\ne \emptyset \), then (5.4) is automatically satisfied.
In dimension \(d=3\), the situation is similar. Indeed, if \(\Gamma _D\ne \emptyset \), then (5.4) is satisfied. If \(\Gamma _D=\emptyset \), then, if \(\Gamma _R\) is a subset of the boundary of a domain that is rotationally symmetric around a certain axis, (5.4) is not satisfied.
Remark 5.4
Uniqueness of u is only important for fluids with inertia. For inertialess fluids, u only appears in the constraints through boundary conditions. Therefore, even if \(\epsilon = \tfrac{1}{2}(\nabla u_1 + \nabla u_1^T) = \tfrac{1}{2}(\nabla u_2 + \nabla u_2^T)\) for \(u_1 \ne u_2\) enjoying the same boundary conditions, it does not matter for the system of equations whether we take \(u_1\) or \(u_2\). In contrast, for fluids with inertia, the contribution \((u \cdot \nabla ) u\) in the differential constraints causes the choice of u to be important. Therefore, in the linear setting, even if the prescribed boundary conditions (D), (R) and (N) allow to choose different \(u \in W^{1}_p(\Omega ;{\mathbb {R}}^d)\), for example if \(\Gamma _N=\partial \Omega \), we may project onto a subspace that does not allow multiple solutions to
Consequently, we can apply Lemma 2.5 in this situation.
5.1 Inertialess fluids
In this section we study inertialess fluids leading to the set of linear differential constraints from (1.8). That is, we consider
where \(f\in L_q(\Omega ;{\mathbb {R}}^d)\) is given. Both Robin- and Neumann boundary conditions are well-defined as \(({\tilde{\sigma }}- \pi {{\,\textrm{id}\,}}), \textrm{div} ({\tilde{\sigma }}- \pi {{\,\textrm{id}\,}}) \in L_q(\Omega )\). Combining this with the Dirichlet boundary condition, the constraint set is given by
Note that the statement ‘\((\epsilon ,{\tilde{\sigma }})\) satisfies (linD)’ means that there are \(u\in W^1_p(\Omega ;{\mathbb {R}}^d)\) and \(\pi \in L_q(\Omega )\) such that (linD) is satisfied. For data sets \({\mathscr {D}}_n, {\mathscr {D}}\subset Y \times Y\) we consider the functionals \(I_n\) and I as in (1.7).
5.1.1 Coercivity
In this subsection we verify coercivity of the functionals \(I_n\) and I.
Definition 5.5
We call a function  \(\mathbf {(p,q)}\)-coercive, if there exist \(C_1,C_2>0\) and \(\gamma \in {\mathbb {R}}\) such that
\(\mathbf {(p,q)}\)-coercive, if there exist \(C_1,C_2>0\) and \(\gamma \in {\mathbb {R}}\) such that

We say that  has \(\mathbf {(p,q)}\)-growth, if there is \(C_0>0\) such that
has \(\mathbf {(p,q)}\)-growth, if there is \(C_0>0\) such that

For \(v \in V\) we define the functional

in analogy to (1.7).
Remark 5.6
In Sect. 4 we examine data convergence without the differential constraints, in particular we study the unconstrained functional J. In general, we do not expect a coercivity statement of the type
In the following we prove that coercivity follows in the presence of the differential constraints together with suitable boundary conditions, i.e. it holds that
We can include the term \(\epsilon \cdot {\tilde{\sigma }}\) on the right-hand side of (5.6) because it is a Null-Lagrangian. This becomes clear in Remark 5.7 and in the proof of Lemma 5.8 below. In some sense we only require coercivity away from the collinearity set \(\{(\epsilon ,{\tilde{\sigma }}): \epsilon =\beta {\tilde{\sigma }}, \beta \in {\mathbb {R}}\}\). Because we expect \(\epsilon \) and \({\tilde{\sigma }}\) to be colinear for classical fluids, this kind of transversal coercivity is a natural condition for the distance to the data sets which takes the role of  later on.
later on.
Remark 5.7
For the purpose of exposition, we prove a coercivity result for functions on the torus. Here, averages of the functions \((\epsilon ,{\tilde{\sigma }})\) take over the role of boundary values and the role of the differential constraints can be isolated more clearly.
Let  be (p, q)-coercive. We claim that there are constants \(C_1,C_2>0\), such that for any \((\epsilon _0,{\tilde{\sigma }}_0) \in Y \times Y\) and all \((\epsilon ,{\tilde{\sigma }}) \in L_p({\mathbb {T}}_d;Y) \times L_q({\mathbb {T}}_d;Y)\) satisfying
be (p, q)-coercive. We claim that there are constants \(C_1,C_2>0\), such that for any \((\epsilon _0,{\tilde{\sigma }}_0) \in Y \times Y\) and all \((\epsilon ,{\tilde{\sigma }}) \in L_p({\mathbb {T}}_d;Y) \times L_q({\mathbb {T}}_d;Y)\) satisfying
for some \(\pi \in L_q({\mathbb {T}}_d)\), we have the following coercivity:

We compute
Therefore,
We conclude that

Using the boundary conditions instead of averages, we obtain coercivity of the functional also on bounded domains, as long as the integrand is (p, q)-coercive.
Lemma 5.8
(Coercivity in \(\Omega \) with boundary values) Suppose that \(f,g,g_\nu ,h_\tau \), and h are given as in (linD), (D), (R), and (N). We assume that either \(\Gamma _N=\partial \Omega \) or \(\Gamma _D\ne \emptyset \). If \(\Gamma _R\ne \emptyset \), then we additionally assume \(p\geqq 2d/(d+1)\). Suppose that  is (p, q)-coercive and has (p, q)-growth. Then there are \(C_3,C_4>0\),such that for I from (5.7) and for all \(v=(\epsilon ,{\tilde{\sigma }}) \in V\)
is (p, q)-coercive and has (p, q)-growth. Then there are \(C_3,C_4>0\),such that for I from (5.7) and for all \(v=(\epsilon ,{\tilde{\sigma }}) \in V\)
Proof
We may assume that \(v \in {\mathscr {C}}_{{{\,\textrm{lin}\,}}}\), otherwise there is nothing to show. By the coercivity of  we have
we have

Since \(v\in {\mathscr {C}}_{{{\,\textrm{lin}\,}}}\),
for some u with
due to the Korn-Poincaré inequality from Lemma 5.2(ii). Furthermore we have the following estimate
which is due to \(- {{\,\textrm{div}\,}}{\tilde{\sigma }}+\nabla \pi =f\). Let us now estimate the last term in (5.10). The following computations will be done under the assumption that all functions are smooth. The statement follows by density. Observe that
On the one hand, we have the following estimate for the bulk term:
On the other hand, the boundary contribution can be estimated on the Dirichlet part by
and on the Navier part by first isolating the term with the sign
and then estimating
and on the Neumann part by
Inserting (5.15) into (5.12) and using the result together with (5.13), (5.14), (5.16), and (5.17) in (5.10) yields
where we used Young’s inequality in the last step and the constants depend on \(d,\Omega ,f,g,g_\nu ,h,h_\tau \). \(\square \)
Lastly we check, that indeed the function \({{\,\textrm{dist}\,}}(\cdot ,{\mathscr {D}})\) is (p, q)-coercive if \({\mathscr {D}}\) contains data for which ‘\(\epsilon \) and \({\tilde{\sigma }}\) are aligned well enough’.
Lemma 5.9
The distance function \({{\,\textrm{dist}\,}}(\cdot ,{\mathscr {D}})\) to a set \({\mathscr {D}}\subset Y \times Y\) is (p, q)-coercive if and only if there are \(c_1 \in {\mathbb {R}}\) and \(c_2>0\), such that
Remark 5.10
Condition (5.19) means that the data very roughly behaves like a power law for data points with large strain, i.e. \(\sigma \sim \beta \vert \varepsilon \vert ^{\alpha -1} \varepsilon \) whenever \((\sigma ,\epsilon ) \in {\mathscr {D}}\) for \(\alpha = p-1\). The factor \(\beta \) however might depend on the strain \(\epsilon \).
Proof
‘\(\Longrightarrow \)’: Suppose first that the distance function to \({\mathscr {D}}\) is (p, q)-coercive, i.e.
Then, for all \((\epsilon ,{\tilde{\sigma }}) \in {\mathscr {D}}\) we have
and therefore,
‘\(\Longleftarrow \)’: For the converse direction we need to prove that the distance function to the set
is (p, q)-coercive. The constant \(c_2\) only makes \({\mathscr {D}}\) thicker by a finite amount. To see this, for \((\epsilon ,{\tilde{\sigma }})\in {\mathscr {D}}\), write \({\tilde{\sigma }}=\alpha \epsilon +{\tilde{\sigma }}^\perp \) with \(\epsilon \cdot {\tilde{\sigma }}^\perp =0\) and define \({\tilde{\sigma }}_\beta =\alpha \epsilon +\beta {\tilde{\sigma }}^\perp \). Since \(\epsilon \cdot {\tilde{\sigma }}=\alpha |\epsilon |^2\) we must have \(\vert {\tilde{\sigma }}^\perp \vert ^q\leqq c_2+c_\alpha |\epsilon |\) because of \((\epsilon ,{\tilde{\sigma }})\in {\mathscr {D}}\). Then \(|{\tilde{\sigma }}_\beta |^q\leqq c_{q} |\alpha \epsilon |^q+\beta ^q|{\tilde{\sigma }}^\perp |^q\) while \(\epsilon \cdot {\tilde{\sigma }}=\epsilon \cdot {\tilde{\sigma }}_\beta \). Decreasing \(\beta \), we find a \({\tilde{\sigma }}_\beta \) such that \(c_1 \epsilon \cdot {\tilde{\sigma }}> \vert \epsilon \vert ^p + \vert {\tilde{\sigma }}\vert ^q\)and such that \({{\,\textrm{dist}\,}}((\epsilon ,{\tilde{\sigma }}),(\epsilon ,{\tilde{\sigma }}_\beta ))\) is bounded independently of \((\epsilon ,{\tilde{\sigma }})\).
Thus, we may assume that \(c_2=0\) since this only shifts \(C_2\) in (5.6). Then \({\mathscr {D}}\) is (p, q)-homogeneous, i.e. \((\epsilon ,{\tilde{\sigma }}) \in {\mathscr {D}}\Rightarrow (\lambda \epsilon , \lambda ^{p/q} {\tilde{\sigma }})\in {\mathscr {D}}\) for all \(\lambda >0\). This in turn implies that the distance function is (p, q)-homogeneous, i.e.
for all \(\lambda >0\). Let \(S= \{\vert \epsilon \vert ^p + \vert {\tilde{\sigma }}\vert ^q=1\}\) be the unit sphere. Then the set
is compact and has positive distance to \({\mathscr {D}}\), i.e. there exists \(a>0\) such that
Hence, setting
we have
where we use that the right-hand side is smaller than 0 on in the complement of E, while it is smaller than a in E. This and (5.20) show that the distance function \({{\,\textrm{dist}\,}}\) is (p, q)-coercive. \(\square \)
5.1.2 \(\Gamma \)-convergence
Theorem 5.11
(\(\Gamma \)-convergence in the linear setting) Let \({\mathscr {D}}_n,{\mathscr {D}}\subset Y\times Y\) be closed, nonempty sets, and let \({\mathscr {C}}_{{{\,\textrm{lin}\,}}}\) be given by (linC). Moreover, suppose that
-
(i)
The distance functions to \({\mathscr {D}}_n\) and \({\mathscr {D}}\) are uniformly (p, q)-coercive, i.e. there are \(c_1,c_2\), such that
$$\begin{aligned} {\mathscr {D}}_n,{\mathscr {D}}\subset \{ (\epsilon ,{\tilde{\sigma }}) \in V \times V :c_1 \epsilon \cdot {\tilde{\sigma }}+c_2 > \vert \epsilon \vert ^p + \vert {\tilde{\sigma }}\vert ^q\}; \end{aligned}$$ -
(ii)
\({\mathscr {D}}_n \overset{eq}{\longrightarrow }{\mathscr {D}}\);
-
(iii)
if \(\Gamma _R\ne \emptyset \), let \(p\geqq \frac{2d}{d+1}\).
Then the functional \(I_n\) \(\Gamma \)-converges to \(I^{*}\), where
Proof
The hypotheses of Theorem 3.6 are all satisfied with  ,
,  and \(X={\mathscr {C}}_{{{\,\textrm{lin}\,}}}\). Indeed, (H1) is Corollary 3.10, (H4) is the assumption \({\mathscr {D}}_n \overset{eq}{\longrightarrow }{\mathscr {D}}\) and (H2) is satisfied by distance functions of sets, such that \({\mathscr {D}}, {\mathscr {D}}_n \cap B(0,R) \ne \emptyset \) for some \(R>0\). This in turn follows from nonemptyness and \({\mathscr {D}}_n \overset{eq}{\longrightarrow }{\mathscr {D}}\). Condition (H3) follows from the fact that the functions
and \(X={\mathscr {C}}_{{{\,\textrm{lin}\,}}}\). Indeed, (H1) is Corollary 3.10, (H4) is the assumption \({\mathscr {D}}_n \overset{eq}{\longrightarrow }{\mathscr {D}}\) and (H2) is satisfied by distance functions of sets, such that \({\mathscr {D}}, {\mathscr {D}}_n \cap B(0,R) \ne \emptyset \) for some \(R>0\). This in turn follows from nonemptyness and \({\mathscr {D}}_n \overset{eq}{\longrightarrow }{\mathscr {D}}\). Condition (H3) follows from the fact that the functions  in our setting are distance functions, hence even locally Lipschitz continuous. Finally, the set \(X={\mathscr {C}}_{{{\,\textrm{lin}\,}}}\) is weakly closed because for a bounded sequence \(v_n=(\epsilon _n,{\tilde{\sigma }}_n)\subset V\) the pressure \(\pi _n\) satisfies, after suitable renormalisation,
in our setting are distance functions, hence even locally Lipschitz continuous. Finally, the set \(X={\mathscr {C}}_{{{\,\textrm{lin}\,}}}\) is weakly closed because for a bounded sequence \(v_n=(\epsilon _n,{\tilde{\sigma }}_n)\subset V\) the pressure \(\pi _n\) satisfies, after suitable renormalisation,
and is thus also bounded. Since the differential constraints (linD) are linear, it is possible to take the limit for a subsequence. Therefore, Theorem 3.6 implies that \(I_n\) \(\Gamma \)-converges to the \(\Gamma \)-limit of I, which is given by \(I^*\) due to Proposition 3.11. \(\square \)
Remark 5.12
Theorem 4.5 establishes equivalence between data convergence and uniform convergence of \(J_n\) towards J if there is no differential constraint \({\mathscr {A}}v=0\). It is not clear whether such an equivalence holds for the constrained functionals \(I_n\) and I. Indeed, in an abstract degenerate setting, e.g. \(\ker {\mathscr {A}}[\xi ] =\{0\}\) for all \(\xi \in {\mathbb {R}}^d {\setminus } \{0\}\), so that only constant functions are in \(\ker {\mathscr {A}}\), it is easy to see that the equivalence does not hold. In this case, uniform approximation for bounded/equi-integrable functions in the constraint set \({\mathscr {C}}\) is equivalent to pointwise uniform approximation on bounded sets. That is, there are \(R_n \rightarrow \infty \) and \({\tilde{a}}_n \rightarrow 0\), such that for all \(z \in {\mathscr {D}}\) with \({{\,\textrm{dist}\,}}(z,0) \leqq R_n\)
This is considerably weaker than the notions of convergence introduced in Definition 4.1 and Definition 4.3. A similar notion holds for fine approximation. Nevertheless, from a physical viewpoint, the pointwise data convergence \({\mathscr {D}}_n \overset{eq}{\longrightarrow }{\mathscr {D}}\) is a reasonable assumption and we are thus not interested in a complete characterisation of convergence for the constrained functionals.
5.2 Fluids with inertia
In this subsection we consider the system of differential constraints, corresponding to a fluid with inertia
Regarding the boundary conditions, we make the following assumptions throughout this subsection:
-
(B1)
\(\Gamma _N=\emptyset \), i.e. there are only no-slip and Navier-type boundary conditions;
-
(B2)
\(\Gamma _D\ne \emptyset \);
-
(B3)
One of the following two statements is true
-
(B3a)
\(p> \frac{3d}{d+1}\);
-
(B3b)
\(g=0, g_v=0\) and \(h_\tau =0\).
-
(B3a)
Note that assumption (B3b) represents the important case of a non-permeable boundary. In comparison to the linear problem (linD), the set (nlD) of differential constraints admits a direct coupling between \(\epsilon \) and \({\tilde{\sigma }}\) through the inertial term \((u \cdot \nabla ) u\). For this set of differential constraints to still be meaningful, the inertial term \((u \cdot \nabla ) u\) needs to be in the same space as f, \({{\,\textrm{div}\,}}{\tilde{\sigma }}\), and \(\nabla \pi \). Since \(u\in W^{1}_p(\Omega ;{\mathbb {R}}^d)\), for \(p<d\) (otherwise we use \(u\in W^{1}_r(\Omega ;{\mathbb {R}}^d)\) for all \(r<d\)), we have by embedding \(u\in L_{dp/(d-p)}(\Omega ;{\mathbb {R}}^d)\) and thus \(u\otimes u\in L_{dp/(2d-2p)}(\Omega ;{\mathbb {R}}^{d\times d})\), which implies \((u \cdot \nabla ) u={{\,\textrm{div}\,}}(u\otimes u)\in W^{-1}_{dp/(2d-2p)}(\Omega ;{\mathbb {R}}^d)\). In order for this space to be contained in \(W^{-1}_q(\Omega ;{\mathbb {R}}^d)\), we must have
which implies
Throughout this section we assume that (5.22) holds. This includes the Newtonian case \(p=2\) in the physical dimensions \(d=2,3\). We shortly discuss the requirements on the boundary conditions. Recall that \(\tilde{\sigma }\) obeys the equation
which is well-defined in \(W_q^{-1}\left( \Omega ; \mathbb {R}^d\right) \), but the right-hand side has additional regularity, which allows for trace theorems. Observe that \((u \cdot \nabla ) u\) is contained in \(L_q\left( \Omega ; \mathbb {R}^d\right) \), whenever \(p>\frac{3 d}{d+1}\), such that for those exponents the regularity of the boundary conditions is fine. However, the proof Lemma 5.13 reveals that the dual pairing of g with \(\left( \tilde{\sigma }-\pi \right. \) id) v (on \(\Gamma _D\) ) and the dual pairings of \(g_v\) with \(\left( \tilde{\sigma }-\pi \right. \) id)v and of \(h_\tau \) with u (on \(\Gamma _R\) ) need to be well-defined. Therefore, one needs to assume additional regularity, e.g. that \(h_\tau \in W_q^{-1 / q}\left( \Gamma _R ; \mathbb {R}^d\right) \), which is a higher regularity than expected. For simplicity, we therefore stick with zero boundary conditions if \(p<\frac{3 d}{d+1}\).
In this subsection we consider the constraint set
5.2.1 Coercivity in the semilinear case
In this subsection we check that functionals of the form (5.7), with \({\mathscr {C}}_{{{\,\textrm{nl}\,}}}\) given by (nlC), are still coercive.
Lemma 5.13
(Coercivity in the semi-linear setting) Let \(p \geqq 3d/(d+2)\) and assume that the assumptions (B1)–(B3) hold. Let  be (p, q)-coercive and let \({\mathscr {C}}_{{{\,\textrm{nl}\,}}}\) be given by (nlC). Then there are constants \(C_3,C_4>0\), such that
be (p, q)-coercive and let \({\mathscr {C}}_{{{\,\textrm{nl}\,}}}\) be given by (nlC). Then there are constants \(C_3,C_4>0\), such that

Proof
Similarly to the proof of Lemma 5.8, we need to estimate \(\int \epsilon \cdot {\tilde{\sigma }}\;\textrm{d}x\), as for any \((\epsilon ,{\tilde{\sigma }}) \in Y \times Y\)

Since \(v\in {\mathscr {C}}_{{{\,\textrm{nl}\,}}}\), there is a u such that
for some u, where
due to the Korn–Poincaré inequality, Lemma 2.5 and Lemma 5.2. Furthermore, we have the estimate
which is due to \(- {{\,\textrm{div}\,}}{\tilde{\sigma }}+\nabla \pi =f-\left( u\cdot \nabla \right) u\).
Indeed, repeating the calculation from the proof of Lemma 5.8 and then using the nonlinear force balance, we obtain
For the first term we use (5.25) to bound
For the boundary term we consider the cases (B3a) and(B3b) separately.
Case (B3a): We split \(\partial \Omega =\overline{\Gamma _D\cup \Gamma _R}\) and start with
Note that \(W^{1-1/p}_p(\Gamma _D)\) embeds into \(L_3(\partial \Omega )\), whenever
This holds in view of assumption (5.22). For the other part of the boundary we estimate
For the terms without sign we obtain
Inserting (5.30) into (5.27) and using the result together with (5.28), (5.29), (5.31), and the (p, q)-coercivity of  , yields
, yields
where we use Young’s inequality and the fact that \(p>2\).
Case (B3b): Since \(g=0, g_v=0\), and \(h_\tau =0\), the boundary term simplifies to
By inserting (5.32) into (5.27) and the (p, q)-coercivity of  , we obtain
, we obtain
where we use again Young’s inequality.
\(\square \)
5.2.2 Continuity of \(\,\Theta (u) = u \otimes u \)
To verify the assumptions of Theorem 3.13, in particular the weak closedness of \({\mathscr {C}}_{\ln }\), we show that the map
is continuous from the weak topology of \(W^{1}_p(\Omega ;{\mathbb {R}}^d)\) to the strong topology of \(L_r(\Omega ;Y)\) for some \(r>q\).
Lemma 5.14
Let \(p>3d/(d+2)\). Then there is an \(r > q = p/(p-1)\), such that \(\Theta \) is continuous from \(W^{1}_p(\Omega ;{\mathbb {R}}^d)\), equipped with the weak topology, into to \(L_r(\Omega ;Y)\).
In view of Korn’s inequality (Lemma 2.5) bounded sets in \(L_p(\Omega ;Y)\) are mapped to bounded sets in \(W^1_p(\Omega ;{\mathbb {R}}^d)\) by the map \(\epsilon \mapsto u\). Hence, the map \(\Theta \) might also be seen as a map \(\epsilon \mapsto u \otimes u\).
Proof
For \(p\geqq d\) the result immediately follows from the case \(p<d\) by first embedding into \(W^{1}_\tau (\Omega ;{\mathbb {R}}^d)\) for some \(\tau <d\). Thus, let \(p<d\). Then \(W^{1}_p(\Omega ;{\mathbb {R}}^d)\) embeds compactly into \(L_s(\Omega ;{\mathbb {R}}^d)\) for all \(s < dp/(d-p)\). In particular, for every weakly convergent sequence \(u_n \subset W^{1}_p(\Omega ;{\mathbb {R}}^d)\), the sequence
converges strongly in \(L_r(\Omega ;{\mathbb {R}}^d)\) for \(r<dp/(2d-2p)\). This can be satisfied at the same time as \(r>q=p/(p-1)\) if and only if \(p>3d/(d+2)\). \(\square \)
5.2.3 \(\Gamma \)-convergence with semilinear constraint
Theorem 5.15
(\(\Gamma \)-convergence in the semilinear setting) Let \({\mathscr {D}}_n,{\mathscr {D}}\subset Y\times Y\) be closed, nonempty sets and let \({\mathscr {C}}_{{{\,\textrm{nl}\,}}}\) be given by (nlC). Moreover, suppose that:
-
(i)
The distance functions to \({\mathscr {D}}_n\) and \({\mathscr {D}}\) are uniformly (p, q)-coercive, i.e. there are \(c_1,c_2\), such that
$$\begin{aligned} {\mathscr {D}}_n,{\mathscr {D}}\subset \{ (\epsilon ,{\tilde{\sigma }}) \in V \times V :c_1 \epsilon \cdot {\tilde{\sigma }}+c_2 > \vert \epsilon \vert ^p + \vert {\tilde{\sigma }}\vert ^q\}; \end{aligned}$$ -
(ii)
\({\mathscr {D}}_n \overset{eq}{\longrightarrow }{\mathscr {D}}\);
-
(iii)
\(p> \frac{3d}{d+2}\);
-
(iv)
assumptions (B1)–(B3) hold.
Then the functional \(I_n\) \(\Gamma \)-converges to \(I^{*}\), where
Proof
The proof is very similar to the proof of Theorem 5.11. Indeed, as the constraint set \({\mathscr {C}}_{{{\,\textrm{nl}\,}}}\) is weakly closed by Lemma 5.14, the only difficulty, given \(v \in {\mathscr {C}}_{{{\,\textrm{nl}\,}}}\), is to find a recovery sequence lying in \({\mathscr {C}}_{{{\,\textrm{nl}\,}}}\). This is achieved in Theorem 3.13. \(\square \)
6 Consistency of Data-Driven Solutions and PDE Solutions in the Case of Material Law Data
In this section we consider data that are given by a constitutive law, i.e.
for a viscosity \(\mu :{\mathbb {R}}\rightarrow {\mathbb {R}}\). We compare the solutions obtained by the classical PDE approach to minimisers of the data-driven functional. As before, we assume \(\Gamma _N=\emptyset \) and call a pair \((\epsilon ,{\tilde{\sigma }}) \in L_p(\Omega ;Y) \times L_q(\Omega ;Y)\) a weak solution to the stationary Navier–Stokes equation, if there is \(u \in W^{1}_p(\Omega ;{\mathbb {R}}^d)\) and a pressure \(\pi \in L_q(\Omega )\), such that
where (6.1)\(_3\) has to be satisfied in \(W^{-1}_q(\Omega ;{\mathbb {R}}^d)\). Note that the system (6.1) is equivalent to
We may interpret the convergence of data sets discussed in Sect. 4 as an increase of the accuracy of measurement. If a constitutive law exists, then the limit \({\mathscr {D}}\) of data sets \({\mathscr {D}}_n\) should represent this law. Since we assume that the set \({\mathscr {D}}\) is given by a constitutive law \(\epsilon \mapsto {\tilde{\sigma }}_c(\epsilon )\), we consider data sets
For typical constitutive laws, a solution to the induced partial differential equation (6.2) exists and it is natural to ask whether (approximate) solutions to the data-driven problem with \({\mathscr {D}}_n\) converge to a solution of (6.2). It turns out that this is true if the constitutive relation is monotone. Indeed, assume that \((\epsilon ,{\tilde{\sigma }}) \in {\mathscr {C}}_{{{\,\textrm{nl}\,}}}\), i.e. that the differential constraints
are satisfied. If in addition \(I(u)=0\), and thus u is a minimiser, then we have
Consequently, a minimiser of I satisfying \(I(u)=0\) is a solution to the partial differential equation. Conversely, given a constitutive law \({\tilde{\sigma }}_c\) and a weak solution to the partial differential equation (6.2), we may construct the set \({\mathscr {D}}\) as in (6.3) and observe that any solution to the partial differential equation (6.2) is also a minimiser of I.
If the data set \({\mathscr {D}}\) is a limit of measurement data sets \({\mathscr {D}}_n\), it is not clear a priori whether a sequence of (approximate) minimisers \(u_n\) of \(I_n\) converges weakly to a solution u to the partial differential equation because we can only infer \(I^{*}(u)=0\) and not \(I(u)=0\). This is addressed in the following proposition, which directly follows from the relaxation statement Theorem 5.15.
Proposition 6.1
Let \(p > 3d/(d+2)\) and let \(\epsilon \mapsto {\tilde{\sigma }}_c(\epsilon )\) be a given constitutive law. Moreover, assume that the corresponding data set \({\mathscr {D}}\) is given by (6.3), such that the distance function \({{\,\textrm{dist}\,}}(\cdot ,\cdot )\) is (p, q)-coercive. If the partial differential equation (6.2) admits a weak solution v, i.e. \(\min _{v \in {\mathscr {C}}} I(v)=0\), then a function \(v^{*}\) is a minimiser of \(I^{*}\) if and only if
almost everywhere. Moreover, if
then any such approximate solution \(v^{*}\) is already a solution to the partial differential equation (6.2).
In the following we characterise some constitutive laws satisfying (6.4). To this end, we study the set
Definition 6.2
Let \(1<p<\infty \) and \(q=p/(p-1)\). For a set \({\mathscr {D}}\subset Y \times Y\) we define the \({\mathscr {A}}\)-(p, q)-quasiconvex hull of \({\mathscr {D}}\) as
We call a set \({\mathscr {D}}\subset Y \times Y\) \({\mathscr {A}}\)-(p, q)-quasiconvex if \({\mathscr {D}}={\mathscr {D}}^{(p,q)}\).
6.1 Newtonian fluids
In the Newtonian setting the fluid’s viscosity is constant, i.e. \(\mu (|\epsilon |) \equiv \mu _0 > 0\) and hence the relation between the local strain \(\epsilon \) and the viscous stress \({\tilde{\sigma }}\) is linear with \({\tilde{\sigma }}= 2\mu _0 \epsilon \). In the following, we assume without loss of generality that \(\mu _0=1/2\). That is, we have \(p=q=2\) and the constitutive law is given by the data set
Note that, in terms of \(\epsilon \) and \({\tilde{\sigma }}\), the Newtonian data set \({\mathscr {D}}_{{\mathscr {N}}}\) and the distance function \({{\,\textrm{dist}\,}}(\cdot ,\cdot )\) can be written as
Since in this case \({{\,\textrm{dist}\,}}((\cdot ,\cdot ),{\mathscr {D}}_{{\mathscr {N}}})\) is already a convex function, it is also \({\mathscr {A}}\)-quasiconvex and we have that
Consequently, we observe that the \({\mathscr {A}}\)-(2, 2)-quasiconvex hull \({\mathscr {D}}^{(2,2)}_{{\mathscr {N}}}\) of \({\mathscr {D}}_{{\mathscr {N}}}\) is given by
Therefore, any solution to the data-driven problem for Newtonian fluids is also a weak solution to the partial differential equation, in the sense that \(u \in W^{1,p}(\Omega ;{\mathbb {R}}^d)\) satisfies
and the boundary conditions (D), (R).
6.2 Power-law fluids
In the case of power-law fluids, the constitutive law for the fluid’s viscosity is \(\mu (|\epsilon |) = \mu _0 |\epsilon |^{\alpha -1}\epsilon \) with given flow-consistency index \(\mu _0 > 0\) and flow-behaviour exponent \(\alpha > 0\). Consequently, we have \({\tilde{\sigma }}= 2\mu _0 |\epsilon |^{\alpha -1}\). As above, we set without loss of generality \(\mu _0 =1/2\). In the previously used notation, we thus consider \(1< p < \infty \), \(q=p/(p-1)\) and \(\alpha = p/q = 1/(p-1)\) and suppose that the material law is given by the data set
Observe that, for \(\alpha \ne 1\), the set \({\mathscr {D}}_{\mathscr {P}}\) is not convex. Consequently, also the corresponding distance function is not convex. However,
It turns out that the \({\mathscr {A}}\)-(p, q)-quasiconvex hull \({\mathscr {D}}^{(p,q)}_{\mathscr {P}}\) of \({\mathscr {D}}_{\mathscr {P}}\) in fact coincides with the data set \({\mathscr {D}}_{\mathscr {P}}\). In order to verify this, we rely on the following observation (see also [32]):
Lemma 6.3
Let \({{\,\textrm{dist}\,}}(\cdot ,{\mathscr {D}})\) be (p, q)-coercive. Then

where \(T_{p,q}\) is the set of all continuous functions  satisfying
satisfying
-
 is \({\mathscr {A}}\)-quasiconvex;
is \({\mathscr {A}}\)-quasiconvex; -
 for all \(z \in {\mathscr {D}}\);
for all \(z \in {\mathscr {D}}\); -
 .
.
Proof
‘\(\mathbf {\supseteq }\)’: Since \({\mathscr {Q}}_{{\mathscr {A}}}{{\,\textrm{dist}\,}}(\cdot ,{\mathscr {D}})\) is contained in \(T_{p,q}\), it is clear that  is a subset of \({\mathscr {D}}^{(p,q)}\).
is a subset of \({\mathscr {D}}^{(p,q)}\).
‘\(\mathbf {\subseteq }\)’: Suppose now that \((\epsilon _0,{\tilde{\sigma }}_0) \in {\mathscr {D}}^{(p,q)}\). Then there exists a sequence \((\epsilon _n,{\tilde{\sigma }}_n) \in L_p({\mathbb {T}}_d;Y) \times L_q({\mathbb {T}}_d;Y)\) with zero average, satisfying the differential constraint such that
Due to the coercivity of the distance function we can bound
Take now  . Then
. Then  is locally Lipschitz continuous thanks to Proposition 3.2 (iv). Define \(w_n = (\epsilon '_n,{\tilde{\sigma }}_n')\) as the projection of \((\epsilon _0+\epsilon _n,{\tilde{\sigma }}_0+{\tilde{\sigma }}_n)\) onto \({\mathscr {D}}\). Then, in view of (6.5) we find that,
is locally Lipschitz continuous thanks to Proposition 3.2 (iv). Define \(w_n = (\epsilon '_n,{\tilde{\sigma }}_n')\) as the projection of \((\epsilon _0+\epsilon _n,{\tilde{\sigma }}_0+{\tilde{\sigma }}_n)\) onto \({\mathscr {D}}\). Then, in view of (6.5) we find that,
The local Lipschitz continuity of  and the boundedness of \((\epsilon _n,{\tilde{\sigma }}_n)\) now imply
and the boundedness of \((\epsilon _n,{\tilde{\sigma }}_n)\) now imply

Using \({\mathscr {A}}\)-quasiconvexity of  , (6.6), and the non-positivity of
, (6.6), and the non-positivity of  this implies
this implies

Eventually, we find that  and the proof is complete.
and the proof is complete.
\(\square \)
Corollary 6.4
Let \(p,q,\alpha \) and \({\mathscr {D}}_{{\mathscr {P}}}\) be as before. Then
Proof
Lemma 6.3 implies that we only need to find a function  , which is \({\mathscr {A}}\)-quasiconvex, is non-positive in \((\epsilon ,{\tilde{\sigma }})\) if and only if \((\epsilon ,{\tilde{\sigma }}) \in {\mathscr {D}}_{{\mathscr {P}}}\) and has (p, q)-growth. The function
, which is \({\mathscr {A}}\)-quasiconvex, is non-positive in \((\epsilon ,{\tilde{\sigma }})\) if and only if \((\epsilon ,{\tilde{\sigma }}) \in {\mathscr {D}}_{{\mathscr {P}}}\) and has (p, q)-growth. The function

exactly satisfies these assertions. Therefore, \({\mathscr {D}}_{{\mathscr {P}}}^{(p,q)} = {\mathscr {D}}_{{\mathscr {P}}}\). \(\square \)
6.3 Monotone material laws
Again, consider \(1< p < \infty \), \(q=p/(p-1)\) and \(\alpha =p/q\). We consider a constitutive law
for a viscosity \(\mu \in C\bigl ({\mathbb {R}}_+;{\mathbb {R}}_+\bigr )\). For better readability we omit the factor 2 in (6.7) in the following calculations. Furthermore, throughout this subsection we assume that the material law \({\tilde{\sigma }}(\cdot )\) is monotone, i.e. for all \(\epsilon _1,\epsilon _2 \in Y\) we have
and we denote \(a :=\lim _{s \rightarrow 0} \mu (s) s\). The data set \({\mathscr {D}}_{{\mathscr {M}}}\) corresponding to the constitutive law \(\epsilon \mapsto {\tilde{\sigma }}(\epsilon )\) is given as follows (cf. Fig. 1):
Remark 6.5
-
(i)
Monotonicity of such a radial-symmetric function \({\tilde{\sigma }}(\epsilon )\) is equivalent to monotonicity of its one-dimensional counterpart
$$\begin{aligned} s \longmapsto \mu (s) s. \end{aligned}$$Therefore, the limit \(a= \lim _{s\rightarrow 0} \mu (s)s\) is well-defined.
-
(ii)
The setting includes the previously discussed cases of Newtonian and power-law fluids, as well as Ellis-law fluids [31]. Furthermore, it allows the strain–stress graph to have a discontinuity at zero, so-called Herschel-Bulkley fluids, cf. [22].
Theorem 6.6
Let \(p,q,\alpha \) and \({\mathscr {D}}_{{\mathscr {M}}}\) be as above. Then we have
Proof
As for the proof of Corollary 6.4 for the power-law case, it suffices to find \({\mathscr {A}}\)-quasiconvex separating functions (Lemma 6.3). For \((\epsilon _0,{\tilde{\sigma }}_0) \in {\mathscr {D}}_{{\mathscr {M}}}\) we define the function (cf. Fig. 1).

This function is \({\mathscr {A}}\)-quasiconvex (even \({\mathscr {A}}\)-quasiaffine, i.e.  and
and  are \({\mathscr {A}}\)-quasiconvex) and has (p, q)-growth, as
are \({\mathscr {A}}\)-quasiconvex) and has (p, q)-growth, as

To conclude that \({\mathscr {D}}_{{\mathscr {M}}}^{(p,q)} = {\mathscr {D}}_{{\mathscr {M}}}\) we still need to show that
-
(i)
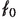 is non-positive on \({\mathscr {D}}_{{\mathscr {M}}}\);
is non-positive on \({\mathscr {D}}_{{\mathscr {M}}}\); -
(ii)
for all \((\epsilon ,{\tilde{\sigma }}) \notin {\mathscr {D}}_{{\mathscr {M}}}\) there is \((\epsilon _0,{\tilde{\sigma }}_0) \in {\mathscr {D}}_{{\mathscr {M}}}\), such that
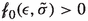 .
.
(i): Take \((\varepsilon ,{\tilde{\sigma }}) \in {\mathscr {D}}\). Suppose that \(\vert \varepsilon \vert \geqq \vert \varepsilon _0 \vert \) (the other case is rather similar). Then

(ii): Suppose that \((\epsilon ,{\tilde{\sigma }}) \notin {\mathscr {D}}_{{\mathscr {M}}}\). If \(\epsilon \ne 0\), this means that \({\tilde{\sigma }}\ne \mu (|\varepsilon |) \varepsilon \). In that case, consider
and \({\tilde{\sigma }}_t= \mu (|\epsilon _t|) \epsilon _t\). If \(\varepsilon =0\), simply take \(\epsilon _t= t e_{11}\). For now, take \(\epsilon \ne 0\), the other case is quite similar. Then for \(t<0\) small enough

as the map
is continuous. Hence, there is \(t<0\), such that
To summarise, there is a function  , such that
, such that  , whenever \((\epsilon ,{\tilde{\sigma }}) \notin {\mathscr {D}}_{{\mathscr {M}}}\). \(\square \)
, whenever \((\epsilon ,{\tilde{\sigma }}) \notin {\mathscr {D}}_{{\mathscr {M}}}\). \(\square \)
Remark 6.7
Starting from the constitutive law \(\epsilon \mapsto {\tilde{\sigma }}_c(\varepsilon )\), there are two choices for \({\mathscr {D}}_{{\mathscr {M}}}\). We may define \({\mathscr {D}}_{{\mathscr {M}}}\) as in (6.8) or only take the set \({\overline{{\mathscr {D}}}}_{\varepsilon }\) introduced in (6.8). For the \({\mathscr {A}}\)-quasiconvex hull this does not make a difference, i.e.
Indeed, (6.9) can be verified by calculating the \(\Lambda _{{\mathscr {A}}}\)-convex hull of the set \({\overline{{\mathscr {D}}}}_{\varepsilon }\) (that is, we successively take convex combinations along \(\Lambda _{{\mathscr {A}}}\)). The \(\Lambda _{{\mathscr {A}}}\)-convex hull is a subset of the \({\mathscr {A}}\)-quasiconvex hull. Therefore, it suffices to show that the \(\Lambda _{{\mathscr {A}}}\)-convex hull of \({\overline{{\mathscr {D}}}}_{\varepsilon }\) contains \({\mathscr {D}}_{{\mathscr {M}}}\). This in turn follows from the fact that
Using this observation, the \(\Lambda _{{\mathscr {A}}}\)-convex hull of \(\{(0,{\tilde{\sigma }}) :\vert {\tilde{\sigma }}\vert = a\} \subset {\overline{{\mathscr {D}}}}_{\varepsilon }\) is the convex hull \({\mathscr {D}}_0\). Consequently, the \(\Lambda _{{\mathscr {A}}}\)-convex hull and therefore also the \({\mathscr {A}}\)-quasiconvex hull of \({\overline{{\mathscr {D}}}}_{\varepsilon }\) contain \({\mathscr {D}}_{{\mathscr {M}}}\).
Data availability
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
References
Amrouche, C., Girault, V.: Decomposition of vector spaces and application to the stokes problem in arbitrary dimension. Czech. Math. J. 44(1), 109–140, 1994
Braides, A., Fonseca, I., Leoni, G.: A-quaisconvexity: Relaxation and homeogenization. ESAIM: Control Optim. Calculus Var. 5, 539–577, 2000
Bogovskii, M.: Solution of the first boundary value problem for the equation of continuity of an incompressible medium. Soviet Math. Dokl. 20, 1094–1098, 1979
Conti, S., Hoffmann, F., Ortiz, M.: Model-free data-driven inference. 2021
Ciarlet, P.G.: Chinese Annals of Mathematics. Series B 31, 607–618, 2010
Craft, T.J., Launder, B.E., Suga, K.: Development and application of a cubic Eddy-viscosity model of turbulence. Int. J. Heat Fluid Flow 17(2), 108–115, 1996
Conti, S., Müller, S., Ortiz, M.: Data-driven problems in elasticity. Arch. Ration. Mech. Anal. 229, 79–123, 2018
Conti, S., Müller, S., Ortiz, M.: Data-driven finite elasticity. Arch. Ration. Mech. Anal. 237(1), 1–33, 2020
Couette, M.: Études sur le frottement des liquides. Annales de Chimie et de Physique 21(6), 433–510, 1890
Duraisamy, K., Iaccarino, G., Xiao, H.: Turbulence modeling in the age of data. Annu. Rev. Fluid Mech. 51(1), 357–377, 2019
Dal Maso, G.: An Introduction to \(\Gamma \)-convergence. Progress in nonlinear differential equations and their applications. Birkhauser, Boston, MA 1993
Fonseca, I., Müller, S.: A-quasiconvexity, lower-semicontinuity and Young measures. SIAM J. Math. Anal. 30(6), 1355–1390, 1999
Guerra, A., Raiţă, B.: Quasiconvexity, null Lagrangians, and Hardy space integrability under constant rank constraints. arXiv:1909.03923 2019
Grafakos, L.: Classical Fourier Analysis. Graduate Texts in Mathematics. Springer Verlag, 3 edition 2014
Kirchheim, B., Kristensen, J.: On rank one convex functions that are homogeneous of degree one. Arch. Ration. Mech. Anal. 221, 527–558, 2016
Kirchdoerfer, T., Ortiz, M.: Data-driven computational mechanics. Comput. Methods Appl. Mech. Eng. 304, 81–101, 2016
Ladyženskaja, O.A.: New equations for the description of the motions of viscous incompressible fluids, and global solvability for their boundary value problems. Trudy Mat. Inst. Steklov. 102, 85–104, 1967
Ling, J., Kurzawski, A., Templeton, J.: Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 807, 155–166, 2016
Málek, J., Nečas, J., R\(\mathring{u}\)žička, M.: On the non-Newtonian incompressible fluids. Math. Models Methods Appl. Sci.3(1), 35–63, 1993
Matousek, J., Plechác, P.: On Functional Separately Convex Hulls. Discrete Comput. Geom. 19, 105–130, 1998
Málek, J., Pražák, D., Steinhauer, M.: On the existence and regularity of solutions for degenerate power-law fluids. Differ. Integr. Equ. 19(4), 449–462, 2006
Málek, J., R\(\mathring{u}\)žička, M., Shelukhin, V.V.: Herschel–Bulkley fluids: existence and regularity of steady flows. Math. Models Methods Appl. Sci.15(12), 1845–1861, 2005
Maulik, R., San, O., Rasheed, A., Vedula, P.: Subgrid modelling for two-dimensional turbulence using neural networks. J. Fluid Mech. 858, 122–144, 2019
Murat, F.: Compacité par compensation: condition necessaire et suffisante de continuité faible sous une hypothése de rang constant. Ann. Sc. Norm. Sup. Pisa 8, 69–102, 1981
Necas, J.: Equations aux dérivés partielles, chapter Sur les normes équivalentes dans \(W^{(k)}_p(\Omega )\) et sur la coercivité des formes formellement positives, pages 102–128. Les Presses de l’Université de Montreal 1966
Pope, S.B.: Turbulent Flows. Cambridge University Press, Cambridge (2000)
Raiţă, B.: Potentials for A-quasiconvexity. Calc. Var. 58, 105, 2019
Röger, M., Schweizer, B.: Relaxation analysis in a data driven problem with a single outlier. Calc. Var. Partial Differ. Equ.59(4), Paper No. 119, 22, 2020
Smagorinsky, J.: General circulation experiments with the primitive equations. Mon. Weather Rev. 91(3), 99, 1963
Wallin, S., Johansson, A.V.: An explicit algebraic Reynolds stress model for incompressible and compressible turbulent flows. J. Fluid Mech. 403, 89–132, 2000
Weidner, D.E., Schwartz, L.W.: Contact-line motion of shear-thinning liquids. Phys. Fluids 6, 3535–3538, 1994
Yan, B.: Semiconvex hulls of quasiconformal sets. J. Convex Anal. 8(1), 269–278, 2001
Acknowledgements
We thank Michael Ortiz for insightful discussions. Moreover, we acknowledge support by the Hausdorff Center for Mathematics (GZ 2047/1, Project-ID 390685813). C. L. has been partially supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the collaborative research centre ‘The mathematics of emergent effects’ (CRC 1060, Project-ID 211504053).
Funding
Open Access funding enabled and organized by Projekt DEAL. Partial financial support was received from the Hausdorff Center for Mathematics (GZ 2047/1, Project-ID 390685813). C. L. has partially been supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the collaborative research centre ‘The mathematics of emergent effects’ (CRC 1060, Project-ID 211504053).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Communicated by M. Ortiz.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lienstromberg, C., Schiffer, S. & Schubert, R. A Data-Driven Approach to Viscous Fluid Mechanics: The Stationary Case. Arch Rational Mech Anal 247, 30 (2023). https://doi.org/10.1007/s00205-023-01849-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00205-023-01849-w



 and
and 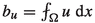 .
. is locally bounded and
is locally bounded and  is continuous;
is continuous; is continuous, then
is continuous, then  is
is 
 is continuous and
is continuous and 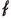 is
is  is
is 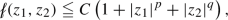
 is locally Lipschitz continuous and
is locally Lipschitz continuous and 

 and
and  are uniformly continuous on bounded sets of
are uniformly continuous on bounded sets of 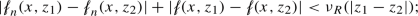
 converge uniformly on equi-integrable subsets, i.e. for all equi-integrable sets
converge uniformly on equi-integrable subsets, i.e. for all equi-integrable sets 
 is a Carathéodory function;
is a Carathéodory function;



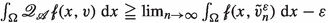 .
. is
is  for all
for all  .
.
 for a given
for a given  is non-positive on
is non-positive on  .
.