Increasing returns and labor markets in a predator–prey model

Abstract

The purpose of this work is to study the joint interaction of three founding elements of modern capitalism, namely endogenous technical change, income distribution, and labor markets, within a low-dimensional nonlinear dynamic setup extending the Goodwin model. Going beyond the conservative structure typical of the predator–prey model, we insert an endogenous source of energy, namely a Kaldor–Verdoorn (KV) increasing returns specification, that feeds the dynamics of the system over the long run and in that incorporates a transition to an (anti)-dissipative framework. The qualitatively dynamics and ample array of topological structures reflect a wide range of Kaldorian stylized facts, as steady productivity growth and constant shares of income distribution. The intensity of learning regimes and wage sensitivity to unemployment allow to mimic some typical traits of both Competitive and Fordist regimes of accumulation, showing the relevance of the demand-side engine, represented by the KV law, within an overall supply-side framework. High degrees of learning regimes stabilize the system and bring it out of an oscillatory trap. Even under regimes characterized by low degrees of learning, wage rigidity is able to stabilize the business cycle fluctuations and exert a positive effect on productivity growth.

1 Introduction

Is it possible to integrate a process of increasing returns of technical change with a conflicting class structure typical of a predator–prey model? If yes, how does productivity growth react to different elasticities to aggregate demand? How are unemployment and income distribution affected by the interaction between labor markets and endogenous technical change? To address these questions, this work develops an extension of the Goodwin model (Goodwin 1967).

The original model represents one of the most elegant, symbolic (but also stylized) representations of the recurrent cycles occurring in the capitalist system due to the conflicting class structure between capitalists and workers. Based on the Lotka–Volterra-type predator–prey biological model (Lorenz 1993), the Goodwin model presents a low-dimensional nonlinear dynamical system, wherein business cycle fluctuations are due to functional income distribution showing opposing relations between profits and wages. The nature of such fluctuations is entirely endogenous, and in that the class struggle between predators and preys lies, providing a formalization of Marx’s conflicting nature of capitalism (Dutt 1992; Shaikh 2016).

The model has been so seminal that an entire strand of literature has emerged with the attempt of modifying and extending the original framework, both from a purely modeling perspective and from an economic one. From the modeling perspective, extensions (Pohjola 1981; Velupillai 1979) have been proposed to overcome the topological structural instability of the system (Veneziani and Mohun 2006). From an economic perspective, extensions focus on the dynamics of price formation through variations in the labor market equation (Desai 1973), or to include new components such as the role of government expenditure (Wolfstetter 1982). The majority of these extensions were in continuous time, while among discrete-time models, the paper by Canry (2005) advances beyond the original Classic supply-side scaffold and integrates a Keynesian endogenous source of demand. The contribution in Dosi et al. (2015) had the dual scope of overcoming structural instability and including endogenous sources of demand generation by comparing alternative profit-led and demand-led investment drivers and labor market configurations.

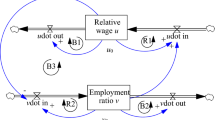
So far, the majority of extensions has devoted few or no attention to the endogenization of technical progress, which in the model is constantly increasing at an exogenous rate. Exogeneity in productivity growth impedes any type of feedback mechanism from demand to supply, and, at the opposite, from productivity growth to labor markets and income distribution. In the following, we intend to overcome the lack of a proper treatment of technical change and to study the ensuing feedback loops. In order to do this, in addition to the two original state variables – employment rate and wage share – we include a third element in the predator–prey scheme to allow the system to endogenously increase vis-á-vis its internal state. The specification we adopt encompasses a reduced form of the Kaldor–Verdoorn (KV) law in order to study the feedback from demand and income distribution to increasing returns and vice-versa (Verdoorn 1949; Kaldor 1966).

By including increasing returns, we make the original Goodwin model able to account for the three characteristic elements of a modern capitalist system – namely, income distribution, labor market, and technical change, within a framework of both endogenous growth and business cycle. After introducing the new model specification, we analyze a series of feedback dynamics by means of local sensitivity analysis upon alternative configurations of the parameter space. Our scenario analysis is performed upon two parameters, namely, the learning coefficient, which is the elasticity to economies of scale, and the wage elasticity to (un)employment as a proxy of labor market flexibility. By varying the intensity of learning opportunities and labor market flexibility, we intend to capture how the transition from informal economic systems – characterized by the absence of any type of increasing returns and employment protection in labor markets – to advanced capitalist systems – wherein technical change is affected by demand and labor markets are more regulated and less volatile – affects the overall growth in labor productivity.

The paper is structured as follows. In Section 2, we present the theoretical underpinnings behind the extension of the Goodwin model through a formalization á la Kaldor–Verdoorn. In Section 3, we present the newly developed model including labor productivity as an increasing returns source, and we discuss the ensuing stability properties. In Section 4, we present a battery of simulations, comparing alternative stages of development of economic systems, by means of local sensitivity analysis on key parameters. Section 5 analyses the feedback mechanisms from income distribution to labor productivity growth. Finally, our conclusions are presented in Section 6, together with a discussion on limitations and possible extensions.

2 Increasing returns and dissipative systems: Beyond the Goodwin model

The lack of an explicit endogenous dynamics of technical change in the Goodwinian modeling tradition implies the setting being silent upon one of the main sources driving economic progress, typical of modern capitalism (Schumpeter 1942). Indeed, a long research tradition has studied and modeled endogenous technical change by means of a complex system approach (Arthur 2009; Dosi and Virgillito 2021; Dosi et al. 2022; Dosi 2023), emphasizing the role of evolution and increasing returns on knowledge accumulation to explain the very process of growth. In addition, the joint hypotheses of exogenous technical change and of Say’s law make the Goodwinian model a conservative system, in line with the Lotka–Volterra framework (Lorenz 1993).

At the opposite side, socio-economic systems are rarely conservative and technical progress is exactly one of the main reasons for violation of such dynamics. Indeed, endogenous technical progress allows the system to grow and generate more resources than those used. In this respect, the final output tends to be more than the used inputs, with a typical (anti)-dissipative structure, whereby with (anti)-dissipative systems we consider those endogenously generating activity – or energy from a physics perspective. Economies seen as complex evolving systems are therefore more appropriately characterized by such type of structures, wherein, beyond regular cycles, also out-of-equilibrium dynamics, as bifurcations and chaos, do emerge (Nicolis and Prigogine 1977; Dosi et al. 2015).

In this paper, by preserving the predator–prey setup, we insert an endogenous source of technical change into the unstable, cyclical, and conflicting dynamics of the Goodwin model, turning the system into a dissipative one. Endogenous technical change might however be both a dis-equilibrating (Arrow 1996; Dosi and Nelson 2010) and a coordinating force. From the Schumpeterian perspective of the arrival of new technologies and paradigms, endogenous technical change creates destruction, more or less creative, but with a final result of reorganizing the system. From a Kaldor–Verdoorn (henceforth KV) perspective (Kaldor 1966, 1972), technical change, rather than being a dis-equilibrium force, tends to create quite ordered dynamic increasing returns. According to the KV law, increasing returns occur in those sectors of activity, particularly manufacturing ones, more exposed to demand growth, in that, they are systematic, rather than erratic. In fact, the KV law is based on a dynamic principle formalizing the role of aggregate demand as a driver of labor productivity growth. In this setting, beyond supply-side investment formation and capital accumulation, productivity growth emerges out of demand.

In line with the KV law, we introduce an endogenous source of technical change, making the dynamics of labor productivity dependent on the employment rate. Indeed, the employment rate can be considered a proxy of the general level of activity, being a procyclical and coincident variable with output. Therefore, an increase in the employment rate due to a phase of expansion of the cycle, driven by an increase in production (and so by capital accumulation), stimulates the accumulation of knowledge and feeds the dynamics of continuous learning. These processes are indeed at the core of increasing returns that, according to Smith (Kaldor 1972; Young 1928), stimulate the rate of growth of labor productivity through the generation of economies of scale.

During an expansionary phase of the business cycle, capitalists will increase their labor demand, leading to an increase in the employment rate. Compared to the basic Goodwin model, an increase in the employment rate will not only lead to an increase in workers’ real wages, due to the standard Phillips curve mechanism, but, at the same time, will have a positive impact on labor productivity growth. Such positive influence of the level of activity, proxied by the employment rate, on the rate of productivity is expressed through the KV coefficient (i.e., learning coefficient) capturing the effects of increasing returns and economies of scale. The coefficient value – corresponding to the degree of the system dependence on increasing returns – modulates the impact of the level of activity on the growth of labor productivity. In that, the coefficient is also a proxy for the stage of economic development of each single capitalist trajectory: low levels of the coefficient represent economies in which the KV law is weak, such as pre-industrial organizations, while high levels of the coefficient represent economies in which learning regimes are strong, which is typical for advanced manufacturing economies.

The dynamics of labor productivity becomes part of the class struggle: considering the conflicting nature of capitalism and the co-existence of increasing returns underlying the learning dynamics of the system, different degrees of labor market elasticity (wage elasticity) may affect labor productivity dynamics and ensuing income distribution. The conflict is therefore exerted over an endogenous product. By introducing increasing returns into a Goodwin model, we link an (anti)-dissipative learning dynamics with a perpetual class struggle between capitalists and workers, substantiated in the symbiotic relationship between income distribution, strength of the labor market, and technical change.

3 The model

Before introducing the new model specification, let us briefly recall the main assumptions and specification of the original model.

3.1 The Goodwin model

The main assumptions of the model read as follows:

• Two economic forces: employment effect and profits effect.

• A constant productivity growth rate $\alpha >0$.

• A constant population growth rate $\beta >0$.

• A constant capital/output ratio $\sigma >0$.

• Wages are entirely spent, profits are entirely saved and reinvested.

• Output growth rate equals profit rate.

• The equilibrium growth rate will be equal to a natural growth rate given by the sum of population and productivity growth rates.

• Technical progress is assumed to be Harrod-neutral.

• All quantities are real.

Productivity growth rate a, defined as output per capita, grows according to:

$$\begin{aligned} \dot{a}/{a}=\dot{q}/q-\dot{l}/l=\alpha \end{aligned}$$

(1)

Labor demand growth rate is defined as:

$$\begin{aligned} \frac{\dot{l}}{l}=\frac{(1-u)}{\sigma }-\alpha \end{aligned}$$

(2)

Employment growth rate is defined as:

$$\begin{aligned} \frac{\dot{v}}{v}=\frac{(1-u)}{\sigma }-(\alpha +\beta ) \end{aligned}$$

(3)

The positive relation between real wages and employment is expressed by means of a linearized Phillips curve:¹

$$\begin{aligned} (\dot{w}/{w})= -\gamma + \rho v \end{aligned}$$

(4)

The final equations are expressed in terms of the employment rate v and the share of wages u:

$$\begin{aligned} \dot{v}=[(1/\sigma -(\alpha +\beta ))-u/\sigma ]v \end{aligned}$$

(5)

$$\begin{aligned} \dot{u}=[-(\alpha +\gamma )+\rho v]u \end{aligned}$$

(6)

We can rewrite the system in the following way, obtaining the Lotka–Volterra type of formulation:

$$\begin{aligned} \dot{v}&=(a-b u)v \nonumber \\ \dot{u}&=(-c+dv)u \end{aligned}$$

(7)

According to the Lotka–Volterra system (Eq. 7) of the Goodwin model, the distributive conflict (i.e., the class struggle) generates endogenous cyclical patterns in capital accumulation, proxied by employment rate and wage share. The model reproduces in a stylized way the oscillatory and unstable nature of the capitalist system, characterized by persistent oscillations. For this reason, the economy could never converge to an equilibrium point, around which persistent limit cycles are generated.

3.2 Introducing increasing returns in a predator–prey model

In the following, we present the basic structure of our extended two-dimensional predator–prey model with a (anti)-dissipative energy source, namely, increasing returns.

To do that, we provide an explicit functional form for the dynamics of labor productivity, according to the KV specification:

$$\begin{aligned} \frac{\dot{a}}{a}=\alpha ^{'}v, \quad \alpha ^{'}\in [0,1] \end{aligned}$$

(8)

Labor demand growth is equal to:

$$\begin{aligned} \frac{\dot{l}}{l}=\frac{1-u}{\sigma }-\alpha 'v \end{aligned}$$

(9)

Hence, the employment growth rate is given by the following dynamic equation:

$$\begin{aligned} \frac{\dot{v}}{v}=\frac{1-u}{\sigma }-\beta - \alpha 'v, \quad v\in [0,1] \end{aligned}$$

(10)

Differently from the original model, the variation in the employment rate now negatively depends on the level of employment rate in itself, implying that its growth trajectories over time are anchored to a level of employment, reflecting the influence of an endogenous force of technical change. This is the first implication of the endogenous dynamics in technical change.

Conversely, the pure dynamics of wage growth is not affected by the introduction of an endogenous component in technical change:

$$\begin{aligned} \frac{\dot{w}}{w}=-\gamma +\rho v, \quad \gamma ,\rho >0 \end{aligned}$$

(11)

However, the variation in the wage share is also affected by the new specification. In fact, income distribution now depends on the difference between the wage elasticity to unemployment, a proxy for the strength of workers power, and the rate of endogenous productivity $(\rho - \alpha ^{'})$:

$$\begin{aligned} \frac{\dot{u}}{u}=-\gamma +(\rho -\alpha ^{'})v, \quad u\in [0,1] \end{aligned}$$

(12)

In our version, the representation of modern capitalism is described by a two-dimensional non-linear dynamical system, including (i) an endogenous source of technical change, (ii) labor markets and (iii) income distribution. In this version, technical change becomes an active part of the distributive conflict and therefore influences, in a structural way, the symbiotic relationship between wages and profits.

The system, obtained by combining Eqs. 10 and 12, reads as:

$$\begin{aligned} \dot{v}&= \left[ \frac{1-u}{\sigma } - \alpha ^{'}v - \beta \right] \cdot v =g_1(v,u) \nonumber \\ \dot{u}&= \left[ -\gamma + (\rho - \alpha ^{'})v \right] \cdot u = g_2(v,u) \end{aligned}$$

(13)

3.3 Stability analysis

In the following, we focus on the topological behavior of the system in Eq. 13, presenting the fixed points and performing the stability analysis. The system has two fixed points, a trivial $(v_1^*, u_1^*)$, and a non-trivial one $(v^\star _2, u^\star _2)$:

$$\begin{aligned} (v^\star _2, u^\star _2)=\left[ \frac{\gamma }{(\rho - \alpha ^{'})}, 1- \left( \frac{\alpha ^{'}\gamma }{(\rho - \alpha ^{'})} + \beta \right) \cdot \sigma \right] \end{aligned}$$

(14)

To analyze the local stability of the fixed point in Eq. 14, we compute the Jacobian matrix of the system in Eq. 13. The Jacobian matrix has the following specification:

$$\begin{aligned} \mathcal {J}= \begin{pmatrix} \left[ \frac{{\partial \dot{v}}}{{\partial v}} \right] _{v^\star , u^\star } &{} \left[ \frac{{\partial \dot{v}}}{{\partial u}} \right] _{v^\star , u^\star } \\ \left[ \frac{{\partial \dot{u}}}{{\partial v}} \right] _{v^\star , u^\star } &{} \left[ \frac{{\partial \dot{u}}}{{\partial u}} \right] _{v^\star , u^\star } \end{pmatrix}= \begin{pmatrix} \frac{1-u}{\sigma } - 2\alpha ^{'}\cdot v - \beta &{} -\frac{v}{\sigma } \\ (\rho -\alpha ^{'})\cdot u &{} -\gamma + (\rho -\alpha ^{'})\cdot v \end{pmatrix} \end{aligned}$$

Specifically, the above matrix, evaluated at Eq. 14, assumes the form:

$$\begin{aligned} \mathcal {J}_{(v^\star , u^\star )}= \begin{pmatrix} -\frac{\alpha ^{'}\gamma }{(\rho - \alpha ^{'})} &{} \qquad -\frac{\gamma }{(\rho -\alpha ^{'})\sigma }\\ (\rho -\alpha ^{'})(1-\beta \sigma )-\alpha ^{'}\gamma \sigma &{} \qquad 0 \end{pmatrix} \end{aligned}$$

(15)

The only economically meaningful fixed point is Eq. 14; and differently from the original model, the technical change coefficient enters the closed form solutions and the related eigenvalues of the Jacobian matrix (Eq. 15). Hence, technical change has an explicit effect on the stability of the system shown in Eq. 13. Moreover, changes in critical parameters entering the fixed points closed form may also result in topological changes, giving rise to the emergence of local bifurcations (Lorenz 1993; Orlando et al. 2021).

4 Simulations

In order to study the possible changes in the topological structure of the model, we perform a battery of simulations on two critical parameters, namely, the learning rate, $\alpha '$, and the wage elasticity to unemployment, $\rho$, on the macrodynamics of the system, considering the analysis of eigenvalues and the possible birth of local bifurcations. The varying intensity of these two parameters gives rise to different scenarios which might be read as alternative configurations of the macroeconomic system, embedding different stages of economic development, hereby represented by the intensity of learning regimes and degrees of labor market rigidity.

Table 1 presents the baseline parameters of the model, and the range of variations we are going to consider, given that $v,u \in [0,1]$ interval.

4.1 Special case 1: The conservative Goodwin setup

Let us now look at the purely conservative case by imposing $\alpha ^{'}=0$. System Eq. 13 becomes as follows:

$$\begin{aligned} \dot{v}&=\left[ \frac{1-u}{\sigma } - \beta \right] \cdot v =h_1(v,u) \nonumber \\ \dot{u}&= \left[ -\gamma + \rho \cdot v \right] \cdot u = h_2(v,u) \end{aligned}$$

(16)

In this case, the system is purely conservative. There are two fixed points, but only one is economically meaningful.

$$\begin{aligned} (v_{2}^\star , u_{2}^\star )=\left[ \frac{\gamma }{\rho }, 1-\sigma \beta \right] \end{aligned}$$

(17)

According to the eigenvalues of the Jacobian matrix of system Eq. 16,² this configuration can be considered a purely supply-led economy, characterized by a macro-behavior without any leakage of energy, inasmuch the learning coefficient does not exert any effect.

Figure 1 presents the limit cycle dynamics associated to the supply-led setup, which perfectly corresponds with the Goodwinian conservative framework of an economy without any sustained source of technical change.

Table 1 Baseline parameter values and range of variation

Fig. 1

Macrodynamics with $\alpha ^{'}$=0

4.2 Special case 2: Decreasing returns

In the following, we present another special case represented by the condition of a negative $\alpha '$. This scenario is equivalent to a case of decreasing returns. While the case is economically equivalent to “unlearning regimes” or anti-cumulative learning paths, formally it is relevant to study the effects of different values of the parameter in order to understand the nature of the fixed point. In case of negative values of the parameter, whose boundary condition in order to get the wage share and employment rate in the [0, 1] interval is $\alpha '=-0.05$, the fixed point is an unstable focus presenting exploding oscillations, as shown in Fig. 2a. The phase portrait dynamics is presented in Fig. 2b. In this range of parameter values, the complex and conjugated eigenvalues possess a positive real part.

Comparing the two special cases, it appears that increasing values of the learning coefficient help in stabilizing the system. Therefore, in the following, we shall assess the role of increasing values of $\alpha '$ in the positive range in order to test the effects of cumulative learning regimes.

Fig. 2

Macrodynamics with $\alpha ^{'}<0$

4.3 Stages of development: Variation in $\alpha '$

We start by asking what is the effect of the increase in the learning coefficient $\alpha '$ on the dynamics of modern capitalism, hereby represented by the dissipative predator–prey model (Eq. 13). We interpret the strength of the learning coefficient of the KV law as a force that differently manifests along alternative stages of capitalist development, and therefore associated with distinct phases of modern capitalism. Our interpretation derives from the fact that learning regimes and economies of scale are typical of the manufacturing sector, being the latter a trait of industrializing capitalist systems exiting from informal, putting-out, agricultural settings. Therefore, low values of the coefficient act in pre-industrial systems, while the opposite holds for high values.

In the baseline setup, shown in Fig. 3, we report a system behavior that recalls the Goodwinian pattern in the coupled symbiotic dynamic between profits and wages. Being the value of the learning coefficient is dramatically low, vis-á-vis our range of parameter variations, simulation results show that economies characterized by a poor dependence on increasing returns exhibit strong macroeconomic instability and business cycle volatility, manifested through the oscillatory dynamics in income distribution. The low, almost zero, elasticity of productivity growth to employment rate, proxy for the level of economic activity, means that the economic system is not able to fully exploit economies of scale. Therefore, learning by doing processes are so irrelevant that they do not allow for any generation of increasing returns in labor productivity growth over the long run. Indeed, the model keeps the qualitative typical conservative structure of the Lotka–Volterra setting.

Fig. 3

Macrodynamics with $\alpha ^{'}$=0.001

Employment rate and wage share, shown in Fig. 3a and b, respectively, manifest a structural weakness: indeed, low sensitivity of productivity growth to employment rate exacerbates the unstable and conflicting nature of capitalism, because productivity growth is not able to sufficiently stimulate any endogenous form of “energy” accumulation. Therefore, within the predator–prey skeleton, a slow dynamism in labor productivity exacerbates the class struggle and does not support the system in obtaining the necessary force to get out of an oscillatory dynamic. Notably, oscillations are wide, characterized by large upswing and downswing phases. A high amplitude of cycles implies large and perpetual instability in the economy, with a full range of potential values that both variables can reach. In fact, the lack of any benefit derived from the levels of output (employment rate) for productivity growth makes wages even further compressed by profits vis-á-vis the standard Goodwin model, and the ensuing conflicting dynamics results to be exacerbated.

Fig. 4

Macrodynamics with $\alpha ^{'}$=0.2

The absence of an endogenous engine capable of fueling the whole system over the long run not only contributes to making the economy unstable, as in the classic Goodwin setup, but, at the same time, does not allow for a proper coordination between the components of the system. Low learning regimes coexist with a persistent weakly stable and cyclic loop of macrodynamics, as shown in Fig. 3d. Due to learning processes not able to generate sufficient increasing returns, the macroeconomic dynamic stops and locks in an oscillatory trap induced by a very low learning coefficient. Adopting the metaphor of the “bicycle postulate” (Dosi and Virgillito 2021), it is as if the slow learning dynamics, typical of initial development stages of modern capitalism, are not able to generate enough kinetic energy to progress and move forward. This implies floating to infinity around a weakly stable fixed point, as in Fig. 3c, by resembling Goodwinian patterns. Although there is a slight change in the nature of the eigenvalues related to this configuration when compared to Special Case 1, there is no evident topological and qualitative change at the macrodynamic level. This points out that such a weak source of increasing returns is insufficient to properly coordinate the elements of modern capitalism.

Let us now present the effects of increasing the learning coefficient, in Fig. 4 showing the temporal evolution of the employment rate, wage share and the two-dimensional phase portrait, respectively. Firstly, let us notice a qualitative change in the nature of the fixed point in Eq. 14. Indeed, a stable focus, as shown in Fig. 4c, occurs. From a topological point of view (Szücs et al. 2012), the learning coefficient, $\alpha '$, is the bifurcation parameter of the system in Eq. 13. Our analysis concentrates on local bifurcations, that is topological changes of the system around the fixed points that can be analyzed by linearization (Kuznetsov 1998). In a neighborhood of the fixed point, moving from a null value of the learning coefficient, coinciding with a Goodwinian pattern, through a phase of an oscillatory loop for low values, toward a stabilization of the macrodynamics for high values, the presence of an (anti)-dissipative source of energy gives rise to the birth of a local bifurcation. The phase transition from a center to a stable focus is exactly due to the intensity of the learning parameter. Specifically, the change in the topological structure is due to the emergence of an inverse Hopf bifurcation.

Hopf bifurcation arises in the presence of non-conservative dynamical systems (Lorenz 1993). Consequently, the transition of the fixed point from a center to a focus is evidence that, compared to the original Goodwin model, we have introduced an (anti)-dissipative component due to an endogenous technical change source. The (anti)-dissipative structure is, however, a source of stabilization for the system. In fact, contrary to the conservative setup characterized by low, or even null, levels of $\alpha '$, as the parameter increases, the sensitivity of the system to economies of scale induces a progressive change in the trajectories that tend to converge towards a stable focus. Due to the loss of fragility and oscillatory properties of the system as the bifurcation parameter increases, the introduction of an endogenous source of technical change helps to remove the trajectories of the system from a corridor of instability (Lorenz 1993). Until the elasticity of the capitalist system with respect to economies of scale is null or very low, the conflicting and symbiotic dynamic of the two predator–prey components is persistently characterized by a Goodwinian pattern. Higher learning coefficients allow the fixed point to exit from the oscillatory trap, as shown in Fig. 5, where the 3D diagram of the inverse Hopf bifurcation is shown. The nature of the Hopf bifurcation is subcritical, that is, from the center, emerging at $\alpha '=0$, the system, for higher values of the coefficient, converges to a stable focus.

Fig. 5

Summary of the behavior of the system under different values of $\alpha '$: Hopf Bifurcation

High elasticity of productivity growth to economies of scale is an attribute of advanced stages of modern capitalism, in line with the North–South literature and the KV law empirical detection (Kaldor 1960; Fingleton and McCombie 1998; McCombie et al. 2002; Deleidi et al. 2021). In advanced stages, increasing returns generated by learning-by-doing processes driven by demand grant exponentially and persistently growing labor productivity. The gains from sustained productivity growth, in terms of output and related capital accumulation, allow capitalists to compensate for the increase in real wages derived by the expansion of the business cycle. Therefore, the wage share tends to stabilize, as shown in Fig. 4b. Consequently, the profit share stabilizes as well. In that, the class struggle dynamics is tamed and the respective distributive shares will no longer be subject to wide fluctuations thanks to the effect of the endogenous source of technical progress, which indeed stabilizes the whole economic cycle and allows to escape from the purely oscillatory and unstable dynamics. At the same time, the employment rate (Fig. 4a) also tends to stabilize and loses persistent fluctuations, endemic of an economy marked by low learning coefficients.

In terms of empirical counterparts, our results are in line with the Kaldorian stylized facts (Kaldor 1961), according to which distributive shares of wages and profits are constant over the long run, and not perpetually oscillating as predicted by the predator–prey model. The Kaldorian stylized facts were identified in a historical phase wherein the stimulus to growth and coordination of the economic system originated from the manufacturing sector, the engine of growth (Kaldor 1960). Increasing returns are able to smooth the cycle, promoting a coordination among the different domains (Dosi and Orsenigo 1988; Dosi and Virgillito 2021). Beyond constant distributive shares over the long run, the introduction of increasing returns allows to regulate and depict different stages of economic development, just varying the intensity of the learning coefficient. Indeed, the change in the topological nature of the fixed point with respect to higher levels of $\alpha '$ allows to distinguish different phases of capitalist development, characterized by different degrees of stability/instability and macroeconomic fragility (Aglietta 1976; Boyer and Saillard 2002), mapped by the amplitude of oscillations. In fact, a stabilization of income distribution emerges thanks to an energy-pushing technical change component, the latter allowing to keep coupled the joint dynamics between real wages and labor productivity. Technical change therefore has a beneficial and stabilizing effect on functional income distribution, meaning that gains from productivity growth are not fully appropriated by capitalists, but are rather transferred into wages, due to the fact that employment level stabilizes and anchors employment growth, in both directions.

4.4 Flexibility in labor markets: Variation in $\rho$

Let us now analyze the impact on the macroeconomic dynamics of a change in the parameter capturing the elasticity of real wages to employment rate, that is the coefficient of the Phillips curve (from here on, PC). We consider the intensity of the elasticity of wage changes to employment rate as a thermometer of the strength (weakness) of the class conflict, expressing the wage sensitivity to variations in employment rate and, as such, a proxy for labor power. In the following, we present a transition dynamics from a quasi-inelastic, rigid, labor market to a setup characterized by high levels of elasticity, and therefore of flexibility. Low levels of $\rho$ stand for high labor power, while, at the opposite, high levels of $\rho$ stand for low labor power.

Figures 6a and 7a show the effects on the employment rate trajectory of the transition from a rigid to a flexible labor market. In the rigid configuration, the labor market is very insensitive to business cycle fluctuations. Even in the absence of strong learning regimes, a lower wage elasticity reduces the amplitude of oscillations of the cycle, dampening volatility in the employment rate, as Fig. 6a shows. This setup ensures a higher employment rate, since it fluctuates in a range of values with higher mean levels when compared to the opposite case, depicted in Fig. 7a. Under flexible labor markets, the amplitude of oscillations is such that the employment rate can even reach the boundary values. This is due to a decline in the real wage growth rate, largely affected by business cycles, and to a consequent reduction in the share of income distributed to workers. Indeed, a very flexible labor market further discourages any possibility of recovery in recessionary periods, and exacerbates macroeconomic fragility and cycle volatility of the system.

In line with the employment rate trajectory, Fig. 6b shows that higher wage rigidity limits the boundary values in the wage share oscillations. Lower volatility for wage earners is also reflected in capitalists’ earnings. On the contrary, as shown in Fig. 7b, volatility and fluctuations in the wage share are much sharpened under flexible labor markets, making the whole system more unstable, including profits and their investment. Overall, the transition from a rigid to a flexible labor market influences the coupled dynamics of employment rate and wage share, whose trajectories in the two-dimensional space are represented in Figs. 6c and 7c, in a rigid and a flexible setup, respectively.

Fig. 6

Macrodynamics with $\rho$=0.1

Wage flexibility does not necessarily guarantee a good coordination of the entire capitalist system which, instead, benefits from a higher degree of wage rigidity. In addition to being qualitatively consistent with some stylized facts of the post-war phase of modern capitalism (Boyer and Saillard 2002; Dosi and Virgillito 2019), our simulations are also in line with agent-based modeling results that have highlighted the detriment effects of labor market flexibilization on micro, meso, and macroeconomic dynamics (Dosi et al. 2017, 2018a, b). In general, high degrees of labor power on the class struggle conflict appear to act as business cycles and crises stabilizers. At the opposite, low degrees of labor power exacerbate the effects of recessionary periods.

Fig. 7

Macrodynamics with $\rho$=0.5

5 Feedback mechanisms to productivity growth

In this section, we analyze the effects of alternative setups of both stages of development and degrees of wage elasticity on the dynamics of labor productivity growth in order to detect the feedback mechanisms from KV law and income distribution fueling economic growth.

5.1 Learning regimes and productivity dynamics

In the following, we show the feedback effects upon labor productivity of two different parametrizations of the learning coefficient. Starting with the baseline parametrization, in Fig. 8a, under a low learning coefficient, productivity growth is weakly stimulated by the KV effect. Low learning coefficients are not able to spur economic growth due to low opportunities for increasing returns in the economic activity. Indeed, over 200 time steps, productivity increases from an initial value of 1 to a final value of 1.035. Strong feedback effects of increasing values of $\alpha '$ are shown instead in Fig. 8b, where the dynamics of labor productivity is now presented in the case of a high learning coefficient. In this setting, high gains in productivity growth are presented, with the final level of productivity after 200 time steps reaching the level of $10^4$.

Which is the speed of learning in the system? Or better, how much time does the system take in order to benefit from learning regimes? We zoom into the case of $\alpha '=0.2$, by focusing on the first 50 steps. We first analyze the first 50 time steps in Fig. 9a and we then move to the whole time range in Fig. 9b. By comparing the two figures, a time-to-learn effect in the system emerges, which maps into a threshold behavior reached at $t=100$. Indeed, the step-wise dynamics that we detect in the baseline configuration and in the high learning regime one until $t=50$ are very similar. The system requires a given amount of time to absorb the gains from such learning opportunities, while the dynamic becomes exponential after a given time-to-learn threshold is overcome. This time-to-learn effect mimics the time necessary to build increasing returns, and with a micro-level perspective, the time required by workers to accumulate knowledge and know-how (Hartley 1965; Dosi and Nelson 2010). The time-to-learn represents the propagation speed to feed effects into the system (Young 1928).

Fig. 8

Labor productivity dynamics

Fig. 9

Time-to-learn threshold point in labor productivity, $\alpha '=0.2$

Fig. 10

Labor productivity dynamics

5.2 Labor power and productivity dynamics

Let us now discuss the feedback effects from a rigid to a flexible labor market on productivity growth, whose parametrizations represent two different degrees of labor power in the economy. In Fig. 10 we present the dynamics of labor productivity under a rigid (Fig. 10a) and a flexible (Fig. 10b) labor market regime, keeping the other parameters at the baseline configuration. Under a more inelastic wage growth vis-á-vis employment rate ($\rho =0.1$), even under a baseline parametrization of low learning regimes ($\alpha '=0.001$), wage rigidity prevents the labor market from being exposed to large cycle fluctuations. Therefore, although the chances to reap the benefits of increasing returns are quite low, wage rigidity, via dampening oscillations, is more conducive to labor productivity growth, although of low levels, as shown by a quite smooth linear trend dynamics. The increase in productivity originates from the positive feedback mechanisms of small amplitudes in the cycle oscillations, e.g., from the pattern of income distribution affecting economic growth.

At the opposite, the case of high wage elasticity to employment rate is a volatility-fueling setting, characterized by a labor market more prone to business cycle fluctuations. Large oscillations in income distribution translate into large fluctuations in the employment rate, which tends to be less stable. The weak and oscillating employment dynamics causes a slowdown in productivity growth because of low output accumulation and volatility in learning opportunities. In fact, instability in income distribution maps into unstable productivity dynamics, which keeps growing but with a distinct, slow-moving step-wise dynamics.

Notably, positive and negative feedback from income distribution to productivity growth not only manifest in the amplitude of oscillations but also in the final level of accumulated productivity reached during the same time period ($t=200$), which under high labor power and low wage sensitivity to employment increases more than 10 p.p. compared to a 2 p.p. increase under the low labor power setting.

5.3 Coordination setups and bifurcation regions

So far, we have performed a local, one at-a-time, parameter analysis. We now move to a two-dimensional bifurcation diagram in order to detect the regions of the system behavior with respect to a two-dimensional parameter setup. The underlying question we address is what are the parameter constellations, and ensuing economic configurations, which allow to reach coordination patterns, defined as (i) phases of cumulative and increasing growth, coupled with (ii) low degrees of fluctuations in income distribution.

Fig. 11

Bifurcation parameters space

Figure 11 shows the bifurcation regions where different configurations of the two parameters determine alternative dynamic trajectories of the system, as marked by colors. We detect a greater complexity than the original Goodwin model, with a division of the phase portrait into three areas, depending on the values of the elasticity of the labor market $\rho$ (ordinate axis) and the learning coefficient $\alpha '$ (abscissa axis).

To briefly summarize, a higher elasticity to scale economies and increasing returns contributes to make convergent the entire dynamics towards a stable focus, with ensuing effects upon the dampening of oscillations in employment rate and wage share. This implies an exponential productivity growth after a period of adaptation of the system to the impulse originated by increasing returns, what we defined the time-to-learn effect. At the same time, wage rigidity has a positive (and therefore dampening) effect on the oscillatory dynamics of employment rate and wage share, with a propagation feedback on labor productivity growth, through the long run KV relationship.

The two-parameter diagram allows having a synthetic and joint look on both dynamics.

• Gray area: for null or low values of $\alpha '$ (low dependence of the system on scale economies) and for values of $\rho$ relatively low (wage rigidity), the macrodynamics of the system assumes a Goodwinian pattern, that is, presents persistent limit cycles or oscillatory dynamics. The emergence of such Goodwinian trajectories is due to a low energy input from the endogenous source of technical change. This oscillatory dimension is found both in two- (employment rate vs. wage share, Fig. 3c) and in three-dimensional space (oscillatory loop, Fig. 3d). Even with a low wage elasticity able to guarantee small fluctuations in the limit cycles, very low values of $\alpha ^{'}$ nail the system into a stage of capitalism characterized by fragility and cyclical behavior. This proves that the bifurcation parameter that induces a phase transition is $\alpha '$.

• Yellow area: for increasing values of $\alpha '$ and for low values of $\rho$ (in some intervals of the diagram even lower than those of the gray area), there is a topological change of the macrodynamics with the emergence of a bifurcation region. This region represents the combinations of wage elasticities and learning coefficients that give birth to (an inverse) Hopf bifurcation: from an oscillatory dynamics (Goodwinian setup) to a stable configuration due to the phase transition from limit cycles to a stable focus. As a result, positive feedback chains emerge from the interaction of low labor market elasticity (or high labor power), greater macroeconomic stability, and sustained labor productivity growth, thanks to higher $\alpha '$ values that give the necessary stimulus to the system to grow and self-coordinate over the long run, out of the oscillatory trap. Hence, a form of coordination among labor markets, income distribution, and endogenous technical change emerges as a necessary condition for this macrodynamic regime.

• White area: value combinations of the two parameters leading to explosive trajectories and divergence from any stationary point, such as the dynamic center or the stable focus. This area represents one of the drawbacks of the model which, being based on a Lotka–Volterra skeleton, remains characterized by an inherent structural instability.

6 Conclusions

The aim of this work has been to study the joint interaction of three founding elements of modern capitalism, namely, endogenous technical change, income distribution, and labor markets, within a low-dimensional nonlinear dynamic setup. By going beyond the conservative structure typical of the predator–prey model, we inserted an endogenous source of energy, a Kaldor–Verdoorn increasing returns specification, which fed the dynamics of the system over the long run and in that incorporated a transition to an (anti)-dissipative framework.

Our extension allows us to enrich the dynamics of the Goodwin model and to include a new element in the dynamics of modern capitalism, which is endogenous productivity growth. Firstly, our model is able to reproduce some typical dynamics of the Goodwin original model. For low values of the endogenous response coefficient of labor productivity, the limit cycles are kept. This reflects the unstable and conflicting nature of capitalism. At the same time, by increasing the learning coefficient, there is a gradual but constant transition towards a less oscillatory and fragile dynamics, attracted by a stable focus. With respect to the original framework, productivity growth acts as a kinetic force that in the long run is able to keep together the conflicting elements of modern capitalism.

The qualitative dynamics and ample array of topological structures reflect a wide range of Kaldorian stylized facts, as constant productivity growth and constant income distribution shares (Kaldor 1961; Boyer and Saillard 2002; Dosi and Virgillito 2019). Indeed, the intensity of learning regimes and wage sensitivity to employment allow mimicking some typical traits of both Competitive and Fordist regimes of accumulation, and the eventual transition from one configuration to another. We show the relevance of the demand-side engine represented by the KV law, within an overall supply-side framework typical of the Goodwin model. High degrees of learning regimes stabilize the system and bring it out of an oscillatory trap. Even under a low degree of learning regimes, wage rigidity is able to stabilize the fluctuations of business cycle and to exert a positive effect on productivity growth.

External validations of our model’s results can be found in a series of germane models coupling the dynamics of technical change and labor markets, both in agent-based setting (Dosi et al. 2017, 2018b) and in extensions of the Goodwin model (Fatás-Villafranca et al. 2012). In particular, Fatás-Villafranca et al. 2012 introduce a Schumpeterian dynamics in R &D, giving rise to long waves and innovation cycles. Notably, the amplitude of the cycles in the two models is comparable, particularly under conditions of low degrees of increasing returns and high degrees of wage flexibility to employment. The interaction of the coupled dynamics between technological regimes, innovation waves, and amplitude of the labor market cycles represents an avenue for further research, particularly in a historical phase characterized, as it is, by structural transformations in the technology and labor market domains.

Limitations of our model include, first, the lack of one-to-one realism, in terms of modeling dimensionality and counterpart empirical evidence, and, second, the continuous time setting, poorly appropriate to model discrete time decisions. Therefore, future advancements entail a discrete time version of the model (Goodwin 1990; Dosi et al. 2015), together with the possible inclusion of a North–South gap and international trade, in order to increase the dimensionality of the system and account for other relevant patterns of modern capitalism, such as specialization and persistent structural asymmetries between countries/regions. In addition, considering that some of the Kaldorian stylized facts, as the constant functional income distribution, are losing empirical relevance, it would be interesting to move beyond a predator–prey setting, and possibly allowing for a declining wage share, as a result of the Neoliberal turn, embedding therefore the structural weakening of labor power over the long run. Alternatively, the study of a counterbalancing dissipative effect acting against the KV law, like financialization and retained profits not invested, would be a relevant extension to embrace forms of rentified capitalism (Dosi and Virgillito 2019; Dosi et al. 2024). Finally, the modeling of sources of inflation, extending the model via a price equation and studying formation of wage-spiral vs. profit-spiral configurations, is a further avenue of research.

Appendices

Appendix A: Hopf bifurcation

Let us now demonstrate the topological change due to the increase in the learning coefficient, as shown in Fig. 5. We rely on the theorem of existence of the Hopf bifurcation (Hassard et al. 1981):

Proposition 1

The non-linear dynamical system (Eq. 13), at the fixed point $(v^\star , u^\star )$, Eq. 14, exhibits a family of periodic solution for $\alpha _{0}^{'}=0$.

Proof

The two conditions for a nonlinear dynamical system to exhibit the appearance (or disappearance) of a family of periodic solutions are:

$$\begin{aligned} \text {Re}(\lambda _{\alpha _{0}})=0, \quad \text {Im}\quad \lambda _{\alpha _{0}^{'}} \ne 0 \nonumber \\ \left[ \frac{d \hspace{0.3pc} \text {Re}(\alpha ^{'})}{d\quad \alpha ^{'}} \right] _{\alpha ^{'}=\alpha _{0}^{'}}&\ne 0 \end{aligned}$$

(18)

Given our dynamical system, we can verify that the two above conditions are met:

$$\begin{aligned} \text {Re}(\lambda _{{\alpha ^{'}= 0}})= 0, \quad \text {Im}\hspace{0.3pc}\lambda _{{\alpha ^{'}= 0}}&= \pm 0.3047\cdot i \ne 0 \nonumber \\ \left[ \frac{d \hspace{0.3pc} \text {Re}(\alpha ^{'})}{d\hspace{0.3pc} \alpha ^{'}} \right] _{\alpha ^{'}=\alpha ^{'}_{(\cdot )> 0}}&< 0 \end{aligned}$$

(19)

$\square$

Appendix B: Robustness checks

In the following, we report some robustness checks on the other parameters of the model. Although we have proven that the parameters of relevance are $\alpha '$ and $\rho$, these robustness checks complete the whole parameter analysis of the system. Table 2 shows the range of variation from the baseline setting. Below, we report the simulations. The values are chosen such that the boundary conditions are always satisfied, so that the employment rate and wage share do not lose economic significance. For each of the parameters of interest, we perform a simulation exercise at high and low levels of the range of variation.

Table 2 Range of parameters values

Fig. 12

Macrodynamics with low (0.27) and high (0.61) values of $\sigma$

Fig. 13

Macrodynamics with low (0.75) and high (1.5) values of $\beta$

Fig. 14

Macrodynamics with low (0.05) and high (0.25) values of $\gamma$

Regarding the capital-output ratio $\sigma$, although analyzed at its boundary conditions, the topological nature of the system keeps assuming the original Goodwinian patterns, as shown in Fig. 12 in which the system is trapped into an oscillatory loop. Regarding the rate of exogenous population growth (see Fig. 13), the Goodwinian behavior keeps persisting, with no effect on productivity dynamics and in general on possible phase transitions. Finally, for the parameter $\gamma$, shown in Fig. 14, the intercept of the PC, starting from a floor value in the baseline scenario, is stretched until 0.25. Even at this juncture, the oscillatory and highly unstable nature of the macrodynamics of the system persists, with a slight difference in the amplitude of the oscillations, now less marked than in the baseline scenario.

After carrying out this robustness analysis, we confirm that the macrodynamic behavior á la Goodwin persists even in the above scenarios. The topological nature of the system is not affected in a structural way (Veneziani and Mohun 2006), regardless of the values assigned to the other parameters. Therefore, the learning coefficient $\alpha ^{'}$, the bifurcation parameter of the system, is the only one governing the phase transition due to the insertion of a non-conservative force, which causes the emergence of a Hopf bifurcation. Notably, the three parameters, rather than affecting the topological structure, affect the path of productivity growth, which can exert both step-wise versus smoother linear trends, vis-á-vis the alternative parameter settings.