A new approach for evaluating experienced assembly complexity based on Multi Expert-Multi Criteria Decision Making method

Abstract

In manufacturing, complexity is considered a key aspect that should be managed from the early phases of product and system design to improve performance, including productivity, efficiency, quality, and costs. The identification of suitable methods to assess complexity has always been of interest to researchers and practitioners. As complexity is affected by several aspects of different nature, it can be assessed from objective or subjective viewpoints or a combination of both. To assess experienced complexity, the analysis relies on the subjective evaluations given by practitioners, usually expressed on nominal or ordinal scales. However, methods found in the literature often violate the properties of the scales, potentially leading to bias in the results. This paper proposes a methodology based on the analysis of categorical data using the multi expert-multi criteria decision making method. A number of criteria are adopted to assess assembly complexity and, from subjective evaluations of operators, product assembly complexity is assessed at an individual level and then, aggregating results, at a global level. A comparison between experienced complexity and an objective assessment of complexity is also performed, highlighting similarities and differences. The assessment of experienced complexity is much more straightforward and less demanding than objective assessments. However, this study showed that it is preferable to use objective assessments for highly complex products as individuals do not discriminate between different complexity levels. An experimental campaign is conducted regarding a manual assembly of ball-and-stick products to show the applicability of the methodology and discuss the results.

1 Introduction

Complexity of manufacturing products and systems has long been a subject of great interest by both researchers and practitioners. Recent studies have shown that complexity is one of the main factors impacting operator and manufacturing process performance, including assembly time, quality defects, and production costs (Ameri et al. 2008; Falck and Rosenqvist 2014; Alkan et al. 2018). In addition, complexity in assembly processes is not only related to performance and KPIs but also to the design of the workspace and equipment needed on the factory floor (Alkan et al. 2016; Sinha and Suh 2018). For this reason, assessing and managing the different sources of complexity is essential for companies to achieve their competitiveness goals.

In the literature, complexity is defined and analyzed from several perspectives and, accordingly, methods to estimate complexity are manifold, as will be detailed in the following Sect. 2. Typically, assembly complexity involves objective and subjective perspectives. Objective aspects include product complexity and sequence complexity, whilst subjective aspects involve personal factors (training, creativity, experience, etc.) and operation and management strategy (Li and Wieringa 2000). Although objective assessment allows the assessment of actual sources of complexity, subjective complexity provides a more holistic view and offers a more situation-oriented understanding of the effects of complexity (Bystrom and Barfield 1999).

The relationship between objective and subjective complexity has been the subject of several studies, and has been analyzed both quantitatively and qualitatively (Li and Wieringa 2000; Mattsson 2013; Alkan 2019). The present study aims to define a relationship between operator-experienced complexity and objective complexity, estimated using the structural model first proposed by Sinha et al. (2012), adopting the multi expert-multi criteria decision making method (Yager 1993). The methodology allows obtaining, starting from some assembly criteria, (1) an individual complexity assessment (at the level of the individual operator) and (2) an overall assessment of product complexity (aggregating the individual assessments). Unlike previous models proposed in the literature, the proposed approach differs in that it uses appropriate methods to analyze and manage categorical data (i.e. the evaluations provided by operators/practitioners). Indeed, very often, operations not admitted by ordinal/nominal scales, such as ratios between categorical data, are performed, thus violating scale properties, leading to a distortion in the results (Stevens 1946; Franceschini et al. 2004). This approach is applied to a manual assembly of products and related structural and experienced complexity are compared. In detail, the following Research Questions (RQs) are addressed:

• RQ1: Is there a statistically significant association between individual experienced complexity and objective complexity?

• RQ2: Does the variability of individual experienced complexity values remain constant as the objective complexity of products changes?

• RQ3: Is there a statistically significant association between overall experienced complexity and objective complexity?

• RQ4: On average, does each change in objective complexity result in a change in operators' perceived complexity?

The method used in the present study is easier to apply, immediate and less expensive than models that objectively assess complexity. Indeed, it does not require any parameter estimates and complex calculations, but instead involves collecting data and analysing the subjective evaluations provided by operators. The results emerging from this study show that this method is preferable for low and medium complexity levels, while it is less accurate than objective assessment for highly complex product since individuals struggle to discriminate between increasing levels of complexity.

The remainder of the paper is organized into five sections. Section 2 summarizes the main definitions of product complexity and approaches used to assess complexity. In Sect. 3, the methodology proposed to assess experienced assembly complexity is presented. Section 4 illustrates a case study concerning the practical application of the proposed methodology in a manual assembly process. Section 5 illustrates experimental results and discussions. Finally, Sect. 6 concludes the paper.

2 Theoretical background

This section reviews existing scientific definitions of product complexity from different perspectives and summarizes the main approaches used to assess complexity of manufacturing systems/products adopted by practitioners and researchers.

2.1 Defining product complexity

Several articles and reviews already exist addressing methods to assess and manage complexity in manufacturing (Simon 1991, 1996; De Toni et al. 2001; ElMaraghy and Urbanic 2004; Samy and ElMaraghy 2010; ElMaraghy et al. 2012; Liu and Li 2012; Efthymiou et al. 2016; Alkan et al. 2018). Herbert Simon (1996) defined complexity as the main problem of handling systems: “Roughly, by a complex system I mean one made up of a large number of parts that interacts in a non-simple way. In such systems the whole is more than the sum of the parts, not in an ultimate, metaphysical sense but in the important pragmatic sense that, given the properties of the parts and the laws of their interaction, it is not a trivial matter to infer the properties of the whole”. In the scientific literature, complexity is defined and modelled by authors both from a broad and a narrow standpoint. From the narrow sense, complexity is defined by the quantity, relationship, and variety of process elements. On the other hand, from the broader sense, any instinctive characteristic can be part of complexity. Three following perspectives of product complexity can be identified according to Liu and Li (2012): (1) structuralist, (2) resource requirement and (3) interaction. In the structuralist perspective, the complexity of a task is defined by its structure, e.g. it can be defined as a function of the number of task elements and the relationships between them. A complex task may have many task elements, and the task elements may be interconnected with each other. Models belonging to this perspective analyze systems through characteristics such as size, variety of components, architecture, and the amount and clarity of information, see e.g. Wood (1986), Rothrock et al. (2005), Ham et al. (2012) and Alkan and Harrison (2019). In the second perspective, the resource requirement, task complexity refers to the use of resources by operators, or other similar concepts in Human Information Processing (HIP), such as visual, auditory, cognitive, and psychomotor resources, knowledge, skills, and even time. The definition is based on the idea that task performers consume more resources the more complex the process becomes (Park 2009; Bedny et al. 2012; Wickens and McCarley 2019). Such resources are attributable to the human sphere and relate to the understanding and processing of information. However, in addition to the knowledge and the visual, auditory and manual skills of the task performers, it is impossible to disregard the intrinsic attributes of the process which, growing in number, variety and uncertainty, increase the cognitive effort required. Finally, in the interaction perspective, task complexity is defined as a product of the interaction between the task and the characteristics of the task performer (e.g. idiosyncratic needs, prior knowledge and experience). Thus, according to the definition of complexity within this perspective, the same system, objectively complex, can be perceived differently. Researchers supporting this research line are concerned with subjective task complexity from the perspective of the task performers (Brown and Miller 2000; Greitzer 2005). According to this view, task complexity is a relative concept (Gonzalez et al. 2005).

Table 1 summarizes the main definitions of task complexity, as reported in the review of Liu and Li (2012), by categorizing them into the three perspectives, i.e. structuralist, interaction and resource requirement.

Table 1 Main definitions of task complexity subdivided into the three perspectives of complexity [adapted from Liu and Li (2012)]

2.2 Methods for assessing assembly complexity

In the scientific literature, several methods have been adopted to assess product complexity in manufacturing. Most of these methods link product complexity, particularly in assembly processes, to the physical attributes of the products to be assembled or the process sequence for the assembly. In contrast, although manual assembly is a widespread preference, especially in high-wage countries, research on human cognition and information processing has not received sufficient attention from both industry and academia (Zaeh et al. 2009). Thus, the variables that influence the complexity of assembly tasks, and accordingly the associated performance, are not fully understood. In Table 2, the most common methods adopted by practitioners and researchers to assess the complexity of production systems/products are summarized, highlighting their benefits and limitations.

Table 2 Summary table reporting common methods to assess complexity in manufacturing, with indication of their pros and cons

Table 2 highlights the many different methods developed in the literature for assessing the complexity of systems and products. From such an analysis, distinctive features emerge that are accordingly used by researchers to evaluate and manage complexity, also referred to as symptoms (Alkan et al. 2018). These features may be categorized into four categories: (1) nonlinear behaviours of systems, which are linked to unstable dynamic phenomena, (2) uncertainties in the operational flow, (3) system physical situation (i.e. variety, quantity and information content of system elements and their interrelations), and (4) indicators of human perceptions. Furthermore, by analysing pros and cons of methods, it emerges that few studies have addressed the practical viability by companies, how they can be linked to specific industrial needs and how they can be related to the different phases of a production system engineering life cycle.

Determining both the available engineering data at a given life cycle stage and the appropriate complexity assessment method is challenging for companies to codify within rules or best practices, as this remains unclear and generates uncertainty during method selection. Consequently, the appropriate assessment method should be selected based on the available data, often aligned to a design/engineering phase. In Table 2, as it will be described in Sect. 2.3, both objective and subjective methods for assessing complexity are included. It is important to note that completely objective approaches to measuring complexity are not always feasible. Consequently, approaches such as surveys and questionnaires, while susceptible to the subjectivity of respondents, still offer valuable information if following a systematic approach. Therefore, this paper aims to formulate a rigorous approach to assessing complexity using a subjective perspective, which is then compared with a purely objective method to highlight its benefits and criticalities.

2.3 Objective versus subjective assessment of complexity

Task and product complexity have been interpreted by researchers and practitioners from both objective and subjective standpoints (Liu and Li 2012), as shown in Table 2. In the objective viewpoint, task complexity is directly related to task characteristics and is independent of task performers (Wood 1986). Conversely, the subjective interpretation considers task complexity as a combined property of task and task performer characteristics (Byström and Järvelin 1995; Vakkari 1999). Subjective complexity is also referred to in the literature as experienced, perceived, or psychological complexity. When the complexity of the task exceeds the performer's ability, the performer will perceive the complexity of the task. Thus, complexity sometimes becomes a "state of mind," which influences how the task performer executes the task (Liu and Li 2012; Mattsson 2013).

Referring to the three perspectives mentioned in Sect. 2.1 (see Table 1), in the structuralist and resource requirement perspectives, complexity is typically described as an objective characteristic of the process, while complexity is rather defined as a subjective experience in the interactionist perspective.

Objective and subjective assessments of complexity have their strengths and weaknesses, which have been discussed or empirically analyzed by many researchers (Byström and Järvelin 1995; Maynard and Hakel 1997; Alkan 2019). The objective assessment is generally relatively specific, while the subjective one is relatively global (Schwab and Cummings 1976; Baccarini 1996; Byström 1999). Typically, authors argue that objective assessment provides a solid and rigorous basis for concise and standardized formulation, albeit it is difficult to be applied in complex and dynamic real-world situations. On the contrary, subjective assessment provides a more situation-bound understanding of the effect of task complexity and has practical implications because of availability; however, it mixes the effects of task, task performer and environment, resulting in a loss of generalization across tasks.

Although objective and subjective complexity seem to have unavoidable shortcomings and appear incompatible with each other, they are interdependent and complementary. First, there is a causal connection between them. The subjective complexity of the task depends on the objective complexity of the task, which is emphasized by several studies (Li and Wieringa 2000; Topi et al. 2005; Alkan 2019). Second, the formulation of subjective complexity should validate the objective assessment of complexity. Thus, an artificial division between objective and subjective complexity will result in an inconclusive and incomplete knowledge base (Cummings et al. 2010). Only by considering the objective and subjective complexity together, a greater understanding of the task and the relationship between the task and the task performer can be obtained.

At this point, the structural model for objective assessment of complexity (Sinha et al. 2012) is described in Sect. 2.3.1, while a detailed debate on the tension between subjective and objective complexity, which deepens the above discussion, is presented in Sect. 2.3.2.

2.3.1 Structural complexity model

In the scientific literature regarding product assembly complexity, a model addressing the assessment of complexity from an objective standpoint was firstly proposed by Sinha et al. (2012), and then used in several studies (Alkan et al. 2017; Alkan 2019; Verna et al. 2021a, b, 2022a). In such a model, the molecular orbital theory developed by Huckel (1932) is applied to the engineering domain to analyze the complexity of cyber-physical systems. The analogy behind the model is between the configuration energy of molecular systems and the complexity of engineering systems. In detail, in Huckel model, the configuration energy of atomic orbitals is expressed as a function of (1) self-energy of individual atoms in isolation, (2) interaction energy between interconnecting atoms, and (3) effects of the topology of molecular system (Hückel 1932). In this context, the configuration energy delineates the distinctive ability of the interacting system to react to its environment, and higher values exhibit increasing effort needed to develop/manage the system. Similarly, a cyber-physical system can be represented by several components that are connected in different ways: each component can be thought of as an atom, and the interfaces between them as inter-atomic interactions, i.e. chemical bonds (Sinha et al. 2012). In this framework, product complexity can be associated with the intrinsic structure of the system and, thus, the individual entities in the system, their linkages, and the architectural structure of the system (Sinha 2014). This model was then adopted and validated in a number of subsequent studies to quantify complexity of industrial products, e.g., pressure recording devices, printing systems and wrapping machines (Sinha 2014; Alkan et al. 2017; Alkan and Harrison 2019; Verna et al. 2021b).

Assembly complexity is defined as (Sinha 2014; Alkan 2019):

$$C = C_1 + C_2 \cdot C_3 .$$

(1)

The three components of the structural complexity, $C_1$, $C_2$ and $C_3$, are described below.

$C_1$ is defined as the handling complexity, and is the sum of complexities of individual product parts. It is calculated as shown in Eq. (2):

$$C_1 = \mathop \sum \limits_{p = 1}^N \gamma_p ,$$

(2)

where $N$ is the total number of product parts and $\gamma_p$ is the handling complexity of part p. The parameter $\gamma_p$ denotes the technical/ergonomic difficulty/effort associated with managing and interacting with the product part in an isolated condition, without requiring information about the system architecture. It is measured by the degree to which the part has physical characteristics that lead to difficulties or problems during its handling in manual and automated assembly operations. In previous studies, $\gamma_p$ was estimated using different approaches, including a function of standard handling time (Alkan 2019) and an exponential function to derive a score from constituting elements of a part (Alkan and Harrison 2019), the so-called Lucas Method to derive a normalized handling index (Alkan et al. 2017).

$C_2$ represents the complexity of connections (or liaisons). It is the sum of the complexities of pair-wise connections existing in the product structure, as follows:

$$C_2 = \mathop \sum \limits_{p = 1}^{N - 1} \mathop \sum \limits_{r = p + 1}^N \varphi_{pr} \cdot a_{pr},$$

(3)

where $\varphi_{pr}$ is the complexity in achieving a connection between parts p and r, and $a_{pr}$ is the (p, r)th entry of the binary adjacency matrix AM of the product. AM is a symmetric matrix of size NxN where each element designates the existence of an assembly liaison between two components. In detail, $a_{pr}$ can assume two values as follows:

$$a_{pr} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if there is a connection between}}\,p\,{\text{and}}\,r} \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$

(4)

The complexity $\varphi_{pr}$ can be assessed by the standard completion time of the connection in isolated conditions (Alkan 2019), by a fraction of the connected component complexities depending on the nature of the connectivity (Alkan and Harrison 2019), or by the normalized fitting index from the Lucas Method (Alkan et al. 2017). Note that in Eq. (3), the connection between parts is considered only once.

Finally, $C_3$ is the topological complexity and represents the complexity related to the architectural pattern of the assembled product. It can be obtained from the matrix energy E_AM of the adjacency matrix, which is designated by the sum of the corresponding singular values $\delta_q$ (Nikiforov 2007; Sinha 2014), as follows:

$$C_3 = \frac{{E_{AM} }}{N} = \frac{{\sum_{q = 1}^N {\delta_q } }}{N},$$

(5)

where E_AM stands for graph energy (or matrix energy) and $N$ stands for the number of parts (i.e. the number of nodes). As the adjacency matrix AM is a symmetric matrix of size N_X N with the diagonal elements being all zeros, the singular values correspond to the absolute eigenvalues of the adjacency matrix (Li et al. 2012; Sinha 2014).

Matrix energy regimes for graphs with a given number of nodes can be divided into (1) hyperenergetic regime, (2) hypoenergetic regime and (3) intermediate or transition regime. The hyperenergetic regime is defined by graph energy greater than or equal to that of a fully connected graph, i.e. $E_{AM} \ge 2\left( {N - 1} \right)$, and the hypoenergetic regime is defined as $E_{AM} < N$. Consequently, the intermediate regime is defined as $N \le E_{AM} < 2\left( {N - 1} \right)$. Hence, in terms of topological complexity metric, the regimes are defined as hyperenergetic when $C_3 \ge 2\left( {1 - 1/N} \right)$, hypoenergetic when $C_3 < 1$, and intermediate regime when $1 \le C_3 < 2\left( {1 - 1/N} \right)$. Note that for hyperenergetic regimes, $C_3$ can be approximated to 2 when $N$ is sufficiently large. Translating the graph structures to system architectural patterns, hyperenergetic regimes are associated with distributed architectures, hypoenergetic regimes with centralized architectures, and intermediate regimes with hierarchical, or layered, architecture. Accordingly, $C_3$ increases as the system topology shifts from centralized to more distributed architectures (Sinha 2014). Examples of real systems characterized by distributed architectures are printing systems and aircraft-geared turbofan engines (Sinha 2014), while laptops have more centralised architectures as most components are connected to their base panel.

Therefore, $C_3$ represents the intricateness of structural dependency among assembly and requires knowledge of the complete architecture of the system and, in this sense, contrary to the previous terms $C_1$ and $C_2$, denotes a global effect whose influence could be perceived during the system integration phase (Sinha 2014). Therefore, the term $C_2 \cdot C_3$ in Eq. (1) can be referred to as a general indicator of the system integration effort that allows distinguishing product architectures with similar parts and connections complexities.

2.3.2 Tension between objective and subjective assessment of complexity

As mentioned at the beginning of Sect. 2.3, objective and subjective assessments of complexity have elements in common while differing greatly in others. For these reasons, it can be argued that a tension exists between the two complexity paradigms, which has been explored and discussed in previous studies (Li and Wieringa 2000; ElMaraghy et al. 2012; Alkan et al. 2018).

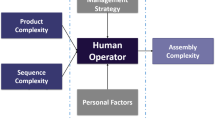
In detail, the main differences that exist between objective and subjective complexity are that objective complexity is more standardized, while subjective complexity is situation-dependent, and objective complexity is rather specific, while subjective complexity can be considered more global. In addition, the two paradigms seem incompatible, but it is challenging to consider them together, not independently of each other. In Fig. 1, the conceptual framework for manual assembly complexity is represented. In this framework, both objective and subjective aspects are included. Objective aspects may be categorized into product complexity and sequence complexity, while subjective aspects belonging to human operators into personal factors (e.g. willingness, training, expertise, etc.) and operation and management strategy (Rouse and Rouse 1979; Li and Wieringa 2000; Alkan 2019).

Fig. 1

Conceptual framework for manual assembly complexity (Li and Wieringa 2000; Alkan 2019)

As shown in Fig. 1, the objective perspective clearly links complexity to the characteristics of the process without taking into account the characteristics of performers. From this viewpoint, complexity is merely a process characteristic that can be measured. Contrarily, complexity is seen from a subjective standpoint as a union of performance and process features.

According to Liu and Li (2012), a performer begins to regard a process as complex when its intricacy exceeds his physical and/or mental capabilities. A human operator's perception of complexity during a manual assembly operation is defined similarly by Li and Wieringa (2000) as a reflection of: (1) objective complexity made up of product- and sequence-related complexities; (2) personal characteristics like training, experience, creativity, and personal characteristics such as education, training, creativity, level of engagement, personal attributes, etc., and (3) the operation strategy developed through his own experience. According to Bystrom and Barfield (1999), a purely objective perspective of complexity is to be preferred since it allows an assessment of all actual sources and elements of complexity. On the other hand, some authors argue that a purely objective evaluation is hardly applicable to real industrial contexts such as manufacturing plants (Shibata 2002; Liu and Li 2012; Verna et al. 2022b). Indeed, proponents of subjective complexity believe that subjective complexity offers a more situation-oriented understanding of the effects of complexity and provides a more comprehensive vision (Bystrom and Barfield 1999). Notwithstanding, it is more difficult to identify and analyze the effects of all the factors that may influence complexity.

Figuring out which approach, objective or subjective or a mix of the two, to use in assessing complexity is not a trivial issue. Often this choice is dictated by production-driving factors. For example, if engineers want to determine the complexity of a product in the early stages of design, thus in the absence of a prototype, subjective approaches are not applicable. Conversely, if a general method that can apply to different types of production is needed, then objective approaches fail as they are designed for specific applications.

The tension between objective and subjective complexity has been addressed in several studies, often at the qualitative level (Li and Wieringa 2000; Mattsson 2013). The relation between the two perspectives was addressed quantitatively by Alkan (2019). The study results showed a superlinear relation described by a sigmoid function between subjective and objective product complexity. In detail, after a stagnation point, perceived complexity reaches saturation and thus products with increasing objective complexities can no longer be distinguished by operators. The study points out that behind the relationship between subjective and objective complexity also lies the issue that subjective complexity assessment may underestimate the actual complexity that can be described by objective complexity. Likewise, there could be situations in which the evaluation of subjective complexity may overestimate the objective complexity. Despite this initial effort in modelling a relationship between objective and subjective complexity, the method proposed by Alkan (2019) does not properly manage and analyze data on operators' perceived complexities. Indeed, perceived complexity values defined using a five-levels ordinal scale [Green (1), Green–Yellow (2), Yellow (3), Yellow–Red (4), Red (5)] are then normalized between 0 and 1 for developing a non-linear regression model with objective complexity. Thus, information initially provided on the ordinal scale is arbitrarily interpreted and utilized on a quantitative scale with different properties from the first one. In other words, the original ordinal scale is transformed into a new cardinal scale characterized by metric and integer number composition properties. This arbitrary “promotion” of the scale properties brings about a series of problems in the perceived complexity interpretation. In more detail, the data numbering involves the definition of the perceived complexity on a formally broader scale than the original one, which generates a fictitious increase in its resolution. The numbering, acknowledging “metrological properties” higher than actually possessed by collected information, can therefore cause a “distortion” effect, which can partially or entirely distort the contents (Franceschini and Rossetto 2002, 2007).

In light of these remarks, the present study aims to further investigate the relationship between experienced assembly complexity and product complexity by proposing a new methodology to assess subjective complexity appropriately handling ordinal data gathered from interviews with operators. This approach may contribute to a better understanding of cause-and-effect relationships between the two different complexity perspectives. The comparison between experienced and objective assessment of complexity, highlighting similarities and differences, may also allow guidelines to be given to practitioners on when it is preferable to use one paradigm rather than the other for complexity assessment.

3 Method to assess experienced assembly complexity

As mentioned in Sect. 2, experienced (or perceived) assembly complexity is strictly related to the operator's capability to understand, manage and carry out the assembly to be performed. As a consequence, it is different from objective complexity, which is instead an intrinsic property of the system (Alkan et al. 2018). In light of this, a product, or more in general, an engineering system, can be perceived as more complex than its actual complexity by an operator without technological knowledge, experience and/or adequate equipment (ElMaraghy et al. 2012). Experienced assembly complexity may be affected by multiple factors, including the objective complexity of the system, the operator's training, experience, creativity, degree of involvement, and distinctive individual traits (Li and Wieringa 2000).

In this study, experienced assembly complexity is assessed at two different levels as follows: (1) individual operators’ level and (2) global level, by averaging individual operators’ assessments.

An overall scheme of the methodology proposed in this study is illustrated in Fig. 2.

Fig. 2

Schematic of the methodology for assessing experienced complexity of assembly

In the proposed methodology, it is deliberately chosen not to include cognitive-related aspects of the operators and their ability to handle a certain level of complexity (e.g., skills, training level, cultural and organisational factors, knowledge and willingness) to make the method as general as possible and applicable in different production contexts. Nevertheless, these cognitive-related aspects open research questions that need to be addressed in future research.

3.1 Assessment at individual operators’ level

Regarding the first level, individual experienced assembly complexity is assessed through subjective evaluations of operators regarding a number i = 1, …, 16 of criteria, assigned on an ordinal scale ranging from 1 to 5. The criteria used to distinguish manual assembly operations in terms of complexity are taken from the study of Falck et al. (2017a), in which the authors aimed at demonstrating that proactive criteria assessment enables the prevention of costly assembly errors and the creation of sustainable and cost-efficient assembly conditions even in the early stages of production (Falck et al. 2017a). The list of 16 criteria and the corresponding interpretation is given in Table 3. Such criteria are slightly modified from the list proposed by Falck et al. (2017a) to better suit the case study that will be described in the next Sect. 4.

Table 3 Complexity criteria of manual assembly, adapted from Falck et al. (2017a) to suit the ball-and-stick case study (described in Sect. 4)

It should be noted that although some criteria seem similar, e.g. criteria 1 and 9, they differ substantially. Criterion 1 concerns whether the operator can look for better ways to speed up assembly or avoid problems during operations. Indeed, to save time and avoid mistakes, operators may be inclined to invent and use their strategies to perform tasks. On the other hand, criterion 9, refers to the order in which each step of the assembly process is performed. It should also be noted that the complexity criteria presented in this paper are not necessarily a full list of all existing criteria, but they are a comprehensive set of criteria intended to provide an overall assessment of the experienced complexity of individuals, as it was demonstrated in different manufacturing sectors (Falck et al. 2016, 2017b) and will be experimentally demonstrated in Sect. 4.

Once the criteria have been formulated, the procedure requires that each operator k assigns, for a specific product j, an importance to each criterion i, i.e. I_ijk, depending on how relevant he considers the specific criterion to be for low product complexity. In addition to importance, each operator k was asked to express a degree of accordance with each criterion i in relation to the assembled product j, i.e. V_ijk. In both cases, five-level ordinal scales were used, which are summarized in Table 4. The importance of each criterion I_ijk has therefore a different meaning from the degree of accordance V_ijk for a given scale level, although they are expressed on an ordinal scale with the same levels to ensure uniformity in operators' responses. As an example, for an operator k, a specific criterion may be deemed negligible for a simple assembly (such as criterion 14 regarding the intuitiveness of assembly), and therefore assigned L₁—Negligible for I_ijk. However, the same operator may fully agree that the product can be assembled without instructions, and thus assigning L₅—Totally agree for V_ijk.

Table 4 Scale levels and semantic meanings for the assessment of product low-complexity criteria importance (I_ijk) and accordance degree with the criteria (V_ijk)

Ordinal scales, often linguistic, differ from cardinal scales as the concept of distance is not defined and their sole property is ordering (Agresti 2003). Although numerical conversion of verbal information simplifies subsequent analyses, it gives rise to two very significant problems: (1) numerical coding implies the introduction of a distance between the levels of the scale, and (2) the choice of a specific numerical coding over another may result in a change in the results obtained. Since a specific encoding may result in a misrepresentation of the original information, a correct approach could rely exclusively on the properties of ordinal scales. For this reason, the proposed approach avoids going through an artificial conversion into cardinal scales and improperly using synthesis operators for measuring position and dispersion, i.e. arithmetic mean and standard deviation, respectively (Franceschini et al. 2005, 2007).

Then, the evaluations on the importance and accordance degree of the 16 criteria provided by operators are combined to provide a first estimation of the experienced product complexity at the level of individual evaluator. In order to deal with linguistic ordinal scales, Yager’s multi expert-multi criteria decision making (ME-MCDM) method is adopted as synthesis approach (Yager 1993). Such a method was originally developed to integrate expert opinions expressed on linguistic scales, often vague and difficult to estimate (Yager 1995; Noor-E-Alam et al. 2011). The fields of application are various, ranging from service design to evaluation of risk priorities in manufacturing (Franceschini and Galetto 2001; Barravecchia et al. 2018). This method is adopted in the proposed approach to combine weighted partial accordance degrees assessed on the 16 complexity criteria. Authors decided to use such a method, instead of alternative approaches, e.g. Analytic Hierarchy Process (Saaty 2008), because in the early design phases, the process engineer is usually unable to provide evaluations on a ratio scale. On the other hand, an artificial promotion of data, originally given on ordinal scales, into ratings given on ratio scales could lead to a distortion of the final results (Stevens 1946; Franceschini et al. 2004).

The method addresses the general problem of aggregating individual operator evaluations to obtain an overall synthetic linguistic value (Yager 1993). It involves maximum, minimum and negation operators to combine linguistic information provided for non-equally important criteria. The underlying logic of Yager’s ME-MCDM method is that, while low-importance criteria should marginally affect the overall aggregated value, highly important criteria should significantly contribute to the definition of the aggregated evaluation. In the proposed approach, the aggregated evaluation of a certain product j expressed by the operator k (E_jk) can then be calculated, by adopting a fuzzy logic, as follows:

$$E_{jk} = {\text{Min}}_i \left[ {{\text{Max}}\left\{ {{\text{Neg}}\left( {I_{ijk} } \right),V_{ijk} } \right\}} \right],$$

(6)

being ${\text{Neg}}\left( {L_x } \right) = L_{t - x + 1}$ the negation of $L_x$, with $L_x$ the xth level of the scale and t the number of scale levels, i.e. 5 in this case. For instance, ${\text{Neg}}\left( {L_5 } \right) = L_1$ and ${\text{Neg}}\left( {L_4 } \right) = L_2$.

The aggregated evaluations obtained by Eq. (6) are values expressed on a five-scale level, where the lowest level represents high complexity and the highest level corresponds to low complexity, as the criteria listed in Table 3 are low-complexity criteria. Accordingly, to derive the final indicator of the individual experienced complexity of a certain product j expressed by the operator k (IEC_jk), where the lowest level of the scale corresponds to low complexity, a negation of the scale is performed, according to Eq. (7):

$$IEC_{jk} = t - E_{jk} + 1.$$

(7)

Table 5 reports the five-level ordinal scale of resulting individual experienced complexity.

Table 5 Scale levels and semantic meanings for the assessment of individual experienced complexity (IEC_jk)

Thus, following the proposed aggregation method, given a certain product j, if an operator k were to assign all criteria the level L₅—“Indispensable” for importance and L₅—“Totally agree” for agreement, then the individual experienced complexity $IEC_{jk}$ would be L₁—“Low”, considering the product extremely simple and believing that all criteria are essential for a simple assembly. Conversely, if the operator assigned L₅—“Indispensable” for all criteria importance and L₁—“Totally disagree” for agreement degrees, then his individual experienced complexity would be L₅—“High”, since he considers the product extremely complex and believes that all criteria are essential for a simple assembly. A different case would be if the operator assigned L₁—“Totally disagree” for agreement degrees but deemed all criteria negligible, thus providing L₁—“Negligible” for importance. In such a case, the procedure leads to obtain L₁—“Low” for the individual experienced complexity.

Figure 3 illustrates an operational scheme of the proposed procedure for a generic product j. In the scheme, for the sake of simplicity, only two operators are considered, namely A and B. For each product j, low-assembly complexity criteria are contained in the middle of the scheme, the upper part of the scheme reports the importance of assembly low-complexity criteria (I_ijk), the degrees of accordance with the criteria (V_ijk) are in the bottom part, while an assessment of the individual experienced complexity $\left( {IEC_{jk} } \right)$ can be found in the right part of the scheme.

Fig. 3

Operational scheme of the proposed approach to derive individual experienced complexity of a product j $\left( {IEC_{jk} } \right)$ by two operators (k = A, B) from importance of assembly low-complexity criteria (I_ijk) and accordance degree with the criteria (V_ijk)

To exemplify the proposed methodology, a pedagogical example is proposed in “Pedagogical example to derive product experienced complexity at level of individual operator” section of the “Appendix”.

3.2 Assessment at global level

Regarding the second level of the analysis, aimed at obtaining an overall value of experienced complexity of a product j $\left( {EC_j } \right)$ from the individual assessments, a sort of averaging of judgments is performed, without violating the properties of the ordinal scale. This synthetic measure of overall operator opinion allows designers to make decisions based on an “average” rating. Thus, the global experienced complexity is proposed as a practical indicator to synthesize individual values, although the authors are aware that any synthesis, useful and practical as it may be, inevitably results in the loss of part of the initial information (Franceschini et al. 2019). In detail, the operator Ordered Weighted Average (OWA), firstly introduced by Yager and Filev (Yager 1993; Filev and Yager 1994), is used, as defined below:

$${\text{OWA}} = {\text{Max}}_{k = 1}^n \left[ {{\text{Min}}\left\{ {Q\left( k \right), b_k } \right\}} \right],$$

(8)

where

• $Q\left( k \right) = L_{f\left( k \right)} \,\left( {k = 1, 2, \ldots ,n} \right)$ is the average linguistic quantifier (the weights of the OWA operator), with $f\left( k \right) = {\text{Int}}\left\{ {1 + \left[ {k\frac{t - 1}{n}} \right]} \right\}.$

  L_f(k) is the f(k)th level of the linguistic scale (for example, L_f(k) = L₁ if f(k) = 1).

• Int(a) is a function that gives the integer closest to a.

• t is the number of scale levels (5 in this case).

• n is the sample size.

• b_k is the kth element of the sample previously ordered in decreasing order (i.e. the IEC_jk values in this case).

This operator is an emulator of the arithmetic mean which can take values only in the set of levels of the original ordinal scale, thus avoiding the problems of numerical codification of ordinal scale levels. Accordingly, from individual experienced complexity evaluations (IEC_jk), an overall evaluation is derived, for each product j, by implementing Eq. (8):

$$EC_j = {\text{Max}}_{k = 1}^n \left[ {{\text{Min}}\left\{ {Q\left( k \right), IEC_{jk} } \right\}} \right]$$

(9)

A pedagogical example is provided in “Pedagogical example to derive product experienced complexity at global level” section of the “Appendix” to illustrate and clarify how the experienced complexity at global level can be obtained by OWA operator.

3.3 Analysis of experienced complexity at individual operators and global levels

In this section, the methodologies adopted to analyze the experienced complexity values at level of individual operator and global level, i.e. aggregating individual operators’ values, are described. In detail, the obtained values of complexity derived as discussed in the previous Sects. 3.1 and 3.2 can be compared with objective assessment of product complexity, using the structural complexity model described in Sect. 2.3.1.

Regarding the first level of the analysis, the relationship between objective assessment of complexity and individual experienced complexity of products can be modeled using Ordinal Logistic Regression (OLR), as experienced complexity is an ordinal response defined using a linguistic scale (McCullagh 1980). OLR, also called ordinal logit or proportional odds model, is an ordinal regression model that only applies to data that meet the proportional odds assumption. Furthermore, the coefficients in the linear combination are not estimated using ordinary least squares, but rather by maximum likelihood, computed by using iteratively reweighted least squares (McCullagh 1980). To analyze and interpret the key results of the OLR, two steps should be followed, as described below (Agresti 2003; Powers and Xie 2008).

• 1. Analyze the association between the response (individual experienced complexity) and the term (structural complexity)

  If the p-value for the term is lower than the significance level selected, the association between the response and the term is statistically significant. Furthermore, OLR estimates a coefficient for each term in the model. The constant coefficients, in combination with the coefficients for the term, form a series of binary regression equations. The first equation estimates the probability of the first event occurring. The second equation estimates the probability that the first or second event will occur, and so on. The coefficients are useful for determining whether a change in the predictor variable makes any of the events more or less likely. Positive coefficients make the first event and the events that are closer to it more likely as the predictor increases. Negative coefficients make the last event and the events closer to it more likely as the predictor increases.

  In OLR, odd ratios are also provided. The odds ratio compares the odds of two events. The odds of an event are the probability that the event occurs divided by the probability that the event does not occur. For continuous predictors, odds ratios that are greater than 1 indicate that the first event and the events closer to the first event are more likely as the predictor increases. Odds ratios that are less than 1 indicate that the last event and the events that are closer to it are more likely as the predictor increases.

• 2. Determine how well the model fits the data

  A model obtained by ordinal logistic regression fits the data well if the p-values for the Goodness-of-Fit Tests are greater than the significance level. This condition indicates that there is insufficient evidence to state that the model does not fit the data adequately. In addition, the measures of association should be examined. Higher values reveal a better predictive capacity. In particular, the Somers’ D, Goodman and Kruskal indices vary between − 1 and 1. Kendall's index generally ranges between − 2/3 and 2/3. Values close to 0, in all cases, reveal that the model does not have predictive ability.

In addition to OLR, also the methods described below for analyzing data at global level may be used.

Regarding the second level of the analysis, the relationship between objective assessment of complexity and experienced complexity at global level of products can be analyzed by means of Analysis of Variance (ANOVA) and measures of association suitable for categorical data. OLR cannot be used because no replicates are present. When only a continuous predictor is used in the analysis, the one-way ANOVA may be performed by flipping the model, so that the predictor variable is the experienced complexity, while the outcome variable is the continuous variable, i.e. objective complexity (Agresti 2003; Powers and Xie 2008). Furthermore, nonparametric measures of association may be used to assess the strength and direction of the association that exists between the continuous and the ordinal variable, e.g. Spearman rank-order correlation coefficient and Kendall’s coefficient of rank correlation (Agresti 2003).

4 Experimental case study

In this section, an experimental case study is considered in which the proposed methodology to assess experienced assembly complexity is applied, and then the obtained results are compared with an objective assessment of complexity.

In the experimentation, assembled products used to assess experienced complexity and then compare it with objective complexity based on structural paradigm are molecular structures assembled using balls and sticks. In the scientific literature, such molecular structures are widely recognized as reference objects to emulate the corresponding real cyber-physical products by using atoms as product's constituent parts and bonds as connections (Sinha 2014; Alkan et al. 2017; Alkan 2019; Alkan and Harrison 2019). Connections emulated by bonds can be of different types, such as physical/mechanical connections, material/fluid flow, energy flow, and information/control signal flow (Sinha 2014). Ball-and-stick structure assembly is mainly a construction activity, entailing the elaboration of visual and/or geometric information and the ability to assemble a certain structure. Thus, choosing such structures is dictated by both (1) minimizing the confounding effects that would occur in real productions, such as dynamic and organizational issues of engineering systems, and (2) performing experimental tests by isolating and controlling the effects of product complexity.

Twelve different ball-and-stick structures (see Fig. 4 and Table 6) with different levels of product structural complexity were selected and built using some molecular modeling kits (Orbit™ by 3B Scientific^®) based on clear 2D and 3D work instructions.

Fig. 4

Ball-and-sticks molecular structures used in the experiments (ID 1–ID 12), detailed in Table 6

Table 6 Structural characteristics and complexity of the molecular structures used in the experiments (calculated according to the model described in Sect. 2.3.1)

The assembly experiments were scheduled for 8 days, involving in total 52 assembly operators. In detail, on each day, at most 7 operators were involved in product assembly, supported by a quality controller who monitored the work. The assembly operators were students of the course “Quality Engineering” in the 2nd year of the Master of Science in Management Engineering program at Politecnico di Torino (Italy), with no previous experience in industrial assembly. Each operator had to assemble all 12 molecular structures, randomly assigned. The molecule assembly operations did not follow a particular assembly sequence to minimize the effects of sequence complexity. The models consisted of different atoms (i.e. balls) and bonds (i.e. sticks), in the quantities specified in Table 6. As for atoms, five different types were involved: carbon (grey), hydrogen (white), nitrogen (blue), oxygen (red), and sulfur (yellow). As for connections, two types of chemical bonds were included, namely single covalent bonds made using rigid connectors and double covalent bonds made using flexible connectors. Each type of atom and connector was placed in a specific box (see Fig. 5), where the operator selected the corresponding part following the 2D and 3D assembly instructions provided.

Fig. 5

Assembly workstation

5 Results and discussion

For each of the molecular structures, the structural complexity C was calculated, according to the model proposed in Sect. 2.3.1. Part and connection complexities were estimated from the average time acquired from preliminary experiments performed by the operators by randomizing the tasks to minimize learning effects. In detail, the average handling time, i.e. the time to locate the box, move the arm to pick position, pick the relevant atom and return the arm to work position, was used to estimate part complexity $\gamma_p$, see Eq. 2. The average completion time of a connection between a pair of atoms in isolated conditions was used to estimate connection complexity $\varphi_{pr}$, see Eq. 3. Such a time includes the handling of the connector and atoms, and the joining process, i.e. (a) locating the connection holes, (b) orienting and positioning the atoms and bond, (c) connecting the bond to both atoms, (d) arranging the connection, and (e) a final inspection. Each operator took three measurements of times, resulting in an average handling time of individual atoms of 2.80 s, an average connection time using a rigid connector of 8.95 s and using a flexible connector of 9.75 s. After normalizing average times based on the longest time, the following complexities were derived: $\gamma_p = 0.29$, $\varphi_{pr} = 0.92$ for rigid connections and $\varphi_{pr} = 1.00$ for flexible connections. Thus, according to Eqs. (1), (2), (3) and (5), respectively, complexities of parts, complexity of connections, topological complexity and overall structural complexity for each structure were obtained, as listed in Table 6.

Before the operators carried out the assembly of the 12 structures throughout the workday, some preliminary information was given, and some simple assemblies of structures (other than those being experimentally tested) were proposed. Then, the 52 operators were asked to fill in one-time the importances related to each of the 16 criteria listed in Table 3 (I_ijk) according to the evaluation scale provided in Table 4. After the assembly of each structure, the operator had to assess the degree of agreement with respect to each criterion (V_ijk) according to the scale levels listed in Table 4. Thus, in total, 52 importance evaluations for each criterion were obtained, and 52 degrees of agreement were collected for each criterion related to each of the 12 structures. In Table 7, an extract of the evaluations provided by operators for structure ID 1 is shown.

Table 7 Evaluations on product low-complexity criteria importance (I_ijk) and agreement degree (V_ijk) obtained by two operators (A and B) for the structure ID 1 and final experienced complexity at level of individual evaluator

To evaluate if the 16 criteria selected for the analysis compose a suitable set to assess complexity, a correlation analysis was performed, using Spearman's coefficient since the agreements are expressed on ordinal scale. In the correlation table, provided in Table 8 in “Additional results on the experimental case study” section of the “Appendix”, all the correlation coefficients are positive, indicating a positive relationship between the criteria, since are all formulated to assess low complexity. Such a result confirms that the assessments were given consistently. All correlation coefficients are between 0.447 (between criterion 1 and 9) and 0.815 (between criterion 7 and 15), and there are no correlations very close to 1, which would justify the elimination of some criteria as redundant. Also, using the Principal Component Analysis (PCA), which aims at determining the minimum number of principal components that account for most of the variation in the data (Johnson and Wichern 2014), it is obtained that all the criteria are equally important to represent experiencSed complexity and that all are necessary to explain the variation in the data. See for more details Figs. 6 and 7 in “Additional results on the experimental case study” section of the “Appendix”.

Fig. 6

Interval plot of structural complexity (C) versus individual experienced complexity (IEC) representing mean value and 95% confidence interval of each level of IEC

Fig. 7

Overall experienced complexity (EC) versus structural complexity (C) for the 12 molecular structures used in the experiments

The evaluations are then aggregated by Eqs. (6) and (7) to obtain the individual experienced complexity at level of individual evaluator k, for a certain product j (IEC_jk). For instance, for the assessment provided in Table 7, the values obtained are L₃ (medium product experienced complexity) for operator A and L₁ (low product experienced complexity) for operator B (Table 8).

Individual experienced complexity levels are analyzed using OLR, as described in Sect. 3.3. In Table 9, the logistic regression table is reported.

Table 8 Logistic regression table (Powers and Xie 2008)

As shown in Table 9, there is a statistically significant association between the experienced complexity and the objective complexity since the p-value associated with the predictor is less than the significance level of 5%, and also since the p-value for the test that all slopes are zero is less than 0.05 (i.e. < 0.0005). Thus, changes in product complexity are associated with changes in the probabilities that the different individual experienced complexity perceived by operators occur. Since structural complexity is a continuous predictor, the odds ratio of 0.97 indicates that as C increases, the last event and those close to it, i.e. high levels of individual experienced complexity, become more likely. The negative coefficient associated with the structural complexity confirms this result since the last event and those close to it are more likely as individual experienced complexity increases. In addition, the p-value of goodness-of-fit tests is greater than 0.05, not providing evidence that the model is inadequate.

Considering the measures of association reported in Table 10, high values of Somers' D, Goodman–Kruskal gamma, and Kendall's tau-a indicate that the model has good predictive ability.

Table 9 Measures of association between individual experienced complexity and predicted probabilities (Powers and Xie 2008)

Thus, in responding to the first research question RQ1 (reported in Sect. 1), the following finding is obtained:

Finding 1

A statistically significant association exists between individual experienced complexity and objective complexity.

This finding is in line with the previous study proposed by Alkan (2019), in which a sigmoid function between product complexity and perceived complexity was derived.

Furthermore, a one-way ANOVA is performed. In the interval plot illustrated in Fig. 6, it is evident that the means of objective complexity calculated for each level of experienced complexity are statistically different, since the 95% confidence intervals for the means do not overlap. Also, using the Tukey Method, all differences between means are statistically significant at 95% confidence level. Moreover, the Spearman rank-order correlation coefficient is 0.663 with a p-value < 0.0005.

It has to be noted from Fig. 6 that variability in results appears to be low for structures with low and high structural complexity, while for molecular structures with intermediate structural complexity, human perception of product complexity varies greatly. Accordingly, in relation to the research question RQ2 (as per Sect. 1), the following finding is identified:

Finding 2

The variability in individual experienced complexity values does not remain constant as the objective complexity of the products varies as it is lower for low and high objective complexities and higher for intermediate complexities.

This novel finding, not analyzed in previous studies, is not trivial. These differences in the experienced complexity of structures with intermediate complexity are plausibly caused by several factors that distinguish operators, including their skills, training, cultural factors, etc. Therefore, further investigation will need to be conducted by including in the analysis variables related to cognitive aspects of individuals.

According to Eq. (9), all the obtained experienced complexity at level of individual operator are aggregated using the OWA operator to derive an overall assessment of complexity of each molecular structure. Results are illustrated in Fig. 7, where global experienced complexity is related to objective complexity of structures (see Table 6). Note that in the last point (i.e., C = 181 and EC = L₄), two molecular structures (ID 11 and ID 12) are conflated.

As shown in Fig. 7, as structural (objective) complexity increases, overall experienced complexity also tends to increase. However, from structure ID 5, operators attribute, on average, the medium–high level of complexity to all molecular structures, perceiving them to be equally complex. This result is reasonable as beyond a certain level the human operator cannot distinguish different levels of complexity. The threshold at which levels of objective complexity are indistinguishable by individuals may vary across individuals since it is linked to the operator’s ability to understand and manage the assembly operation under consideration. Thus, cognitive-related factors such as cultural and organizational factors, level of experience, skills and knowledge of operators, may result in shifts at the threshold. These cognitive aspects and their effect on that threshold need to be further investigated in future research.

Results at global level are analyzed using one-way ANOVA and measures of association. The ANOVA table is provided in Table 11.

Table 10 ANOVA table for overall experienced complexity

From the ANOVA, since p-value is less than the significance level of 5%, the null hypothesis that all means of structural complexity for the three values of overall experienced complexity are equal is rejected. To determine whether the mean difference between specific pairs of groups is statistically significant the Tukey Method is adopted (Montgomery et al. 2009). From such a test, it is highlighted that two groups can be distinguished: a first group containing experienced complexity at level L₄, and a second group containing levels L₃ and L₂. In detail, the difference between means of objective complexity of structures with assigned experienced complexity L₃ and L₂ is not statistically different at 95% confidence level. On the contrary, the means of objective complexities with L₄ and L₂, and L₄ and L₃ levels of experienced complexity are significantly different. Accordingly, for less complex structures (with C less than 95), there is no significant difference from the perspective of experienced complexity since operators, on average, are unable to distinguish between low-medium (L₂) and medium (L₃) complexity. On the other hand, operators, on average, distinguish well between molecules with medium–low (L₂) and medium–high (L₄) complexity, and between those with medium (L₃) and medium–high (L₄) complexity. It should be highlighted that overall experienced complexity with levels L₁ and L₅ are not obtained since the OWA operator tends to flatten the results, not assigning the minimum and maximum levels of the scale unless (almost) all individual evaluations agree (Franceschini et al. 2004). Finally, the Spearman rank-order correlation coefficient is 0.832 with a p-value of 0.001.

In light of these results, the following findings answer, respectively, to the research questions RQ3 and RQ4 (reported in Sect. 1):

Finding 3

A statistically significant association exists between global experienced complexity and objective complexity.

Finding 4

On average, variations in objective complexity do not result in a change in perceived complexity by operators:

• (a) After a certain threshold, operators do not distinguish between different levels of objective complexity;

• (b) No significant difference is evidenced between structures with experienced medium–low complexity and medium complexity.

Finding 3 reflects what has been obtained in previous studies relating subjective and objective complexity (Alkan 2019), as mentioned above in Finding 1. Also Finding 4(a) finds evidence in previous studies, where it was observed that assemblers start to perceive the assembly operations as complex when the product complexity reaches a stagnation point (Alkan 2019). As future work, this threshold (or stagnation point) will need to be modelled in a multidimensional way considering aspects ranging from personal to operations management strategies. Finally, Finding 4(b) represents a novelty compared to previous studies and highlights that further investigation is needed to explain such differences in individuals' perceptions.

6 Conclusions

Complexity in manufacturing plays a pivotal role since if not correctly managed may reduce company performance in terms of productivity, efficiency, costs and quality.

Manufacturing complexity involves many aspects, including objective features, e.g. product complexity and sequence complexity, and subjective features, e.g. operator factors and operation/management strategy. Models adopted in the literature and by practitioners to assess manufacturing complexity are manifold and may consider only some or all aspects of complexity.

Subjective assessments of complexity are based on the analysis of operators’ evaluations, which are typically defined on nominal/ordinal scales. Accordingly, the scale in which experienced complexity is defined is typically an ordinal scale (e.g., typical levels are low complexity, medium complexity, high complexity, etc.). On the other hand, objective assessment of complexity relies on product/process characteristics, such as the number of parts and connections, assembly sequence, etc.

Identifying a relationship between experienced complexity and objective complexity may be of great assistance to production and design engineers to enhance the production process and related performance measures. Although in the literature some attempts to model the relationship between the different perspectives (objective and subjective) have been made, methods often violate the properties of the ordinal scales, potentially leading to distortion in the results.

The present paper proposes a structured methodology to assess the experienced complexity of a manual assembly starting from 16 assembly complexity criteria. Evaluation of the importance and agreement degrees on such criteria are aggregated using the multi expert-multi criteria decision making method. As a result, experienced complexity is obtained from two different levels: (1) at the level of individual operator, and (2) at an overall level, aggregating all individual complexity assessments. The proposed approach and related data analysis only rely on the use of synthesis operators and statistical tools suitable for categorical data, representing a novelty with respect to methods assessing experienced complexity used in previous studies.

Results obtained in an experimental campaign in which assembly of molecular structures was performed showed that a statistically significant association exists between the individual experienced complexity and the objective complexity (answer to RQ1), and that as structural complexity increases, high levels of individual experienced complexity become more likely. This result is in line with previous studies conducted in the field in which a sigmoid function relationship was derived between perceived and objective complexity (Alkan 2019). On the other hand, the results propose new and original insights with regard to the variability of individual data. Indeed, at individual level, variability in experience complexity appears to be low for structures with low and high structural complexity, while is more pronounced for molecular structures with intermediate structural complexity (answer to RQ2). These results may be attributed to differences in the ability of operators to handle a certain level of complexity and cognitive aspects (e.g., training, knowledge, cultural and organizational factors), which need to be investigated in future works. At global level, results showed that a statistically significant association exists between the overall experienced complexity and the objective complexity (answer to RQ3). Moreover, in response to RQ4, it was observed that, from a certain level of structural complexity, operators no longer perceive differences in complexity, in line with the results obtained in previous works (Alkan 2019). Instead, the original results that emerge by analyzing the global complexity values are that there is no significant difference between structures with experienced medium–low complexity and medium complexity. Differences in the perception of different levels of complexity and the threshold at which levels of objective complexity are indistinguishable for individuals are related to cognitive factors, such as cultural and organizational factors, level of experience, skills and knowledge of practitioners. Consequently, these aspects require further consideration in future research.

Engineers may adopt such results to understand experienced complexity in real production environments to minimize experienced complexity and the point at which the operator fails to discriminate between different levels of complexity to ensure alignment between experienced and objective complexity. To this aim, future works will have to investigate whether operator assistance systems and methods, such as augmented reality applications and collaborative systems using cobots could be used to reduce the subjects' perception of complexity. Preliminary studies in this direction have been proposed by Gervasi et al. (2022), but require further investigation. In addition, discerning experienced complexity from actual product complexity may affect the design and analysis of assembly operations and may increase the accuracy of predictions of performance measures such as costs, defects, productivity, and learning effects.

Assessing product complexity using questionnaires and evaluations provided by operators is undoubtedly much more straightforward and less costly than objectively assessing complexity, as in the case of the structural complexity model. However, this study showed that using experienced complexity to assess product complexity is appropriate for products with low and medium complexity, but not for high levels of complexity. Indeed, moving towards very complex products, it would be more appropriate to use complexity models based exclusively on objective data, as the operator cannot discern between different complexity levels.

Finally, the authors will apply the proposed approach to a real production environment and test if the obtained results can be extended to industrial products. Real-world assembly operations may require more cognitive and planning effort than ball-and-stick molecular assembly. Accordingly, the same level of product complexity may be experienced as even more complex by the operator. Thus, it is even more crucial that high levels of product complexity should be identified and minimized in the real world to reduce the experience complexity.

Appendix

1.1 Pedagogical example to derive product experienced complexity at level of individual operator

Consider a generic product j and a generic operator k. For the sake of simplicity, only three low-complexity criteria are considered, i.e. criteria 1, 2 and 3. Table 12 reports the evaluations on the importance and degree of accordance provided by the operator, respectively I_ijk and V_ijk. In the table, the results of the steps described in Sect. 3.1 are reported, as well as the final value of experience complexity at level of individual operator. In such an example, the product j is classified as medium–high complex.

Table 11 Simple example of calculation of experienced complexity for a generic product j by operator k, considering 3 low-complexity criteria (i = 1, 2, 3)

Table 12 Spearman rank-order correlation coefficients between the agreement assessments of the 16 complexity criteria of manual assembly, described in Table 3

1.2 Pedagogical example to derive product experienced complexity at global level

Consider a generic product j, the scale with t = 5 levels, namely L₁, L₂, L₃, L₄ and L₅, i.e. the levels of the scale of experienced complexity given in Table 5, and a sample of size of n = 10 operators, whose elements, previously ordered in decreasing order, are {L₅, L₅, L₅, L₄, L₄, L₃, L₃, L₃, L₂, L₁}.

The weights of the OWA operator are as follows:

• Q(1) = L₁;

• Q(2) = Q(3) = L₂;

• Q(4) = Q(5) = Q(6) = L₃;

• Q(7) = Q(8) = L₄;

• Q(9) = Q(10) = L₅.

The following result is obtained, by implementing Eq. (9):

$${\text{OWA}} = {\text{Max}}\left[ {{\text{Min}}\left\{ {L_1 ,L_5 } \right\},{\text{Min}}\left\{ {L_2 ,L_5 } \right\},{\text{Min}}\left\{ {L_2 ,L_5 } \right\},{\text{Min}}\left\{ {L_3 ,L_4 } \right\},{\text{Min}}\left\{ {L_3 ,L_4 } \right\},{\text{Min}}\left\{ {L_3 ,L_3 } \right\},{\text{Min}}\left\{ {L_4 ,L_3 } \right\},{\text{Min}}\left\{ {L_4 ,L_3 } \right\},{\text{Min}}\left\{ {L_5 ,L_2 } \right\},{\text{Min}}\left\{ {L_5 ,L_1 } \right\}} \right] = L_3 .$$

Thus, according to Eq. (9), the experienced complexity at general level of the product $\left( {EC_j } \right)$ is L_3. The OWA calculation can be represented graphically by the intersection of the ‘ascending stair’ (OWA weights) and the ‘descending stair’ (ordered sample elements), as shown in Fig. 8 (Franceschini et al. 2005).

Fig. 8

Adapted from Franceschini et al. (2005)

Graphical representation of the overall experienced complexity calculation by the OWA operator.

1.3 Additional results on the experimental case study

See Table 12 and Figs. 9 and 10.

Fig. 9

Scree plot displaying the number of the principal component versus its corresponding eigenvalue (Johnson and Wichern 2014)

Fig. 10

Loading plot showing the coefficient of each variable for the first two components (Johnson and Wichern 2014)