Skip to main content
SpringerLink
Log in

Linear instability of the lid-driven flow in a cubic cavity

  • Original Article
  • Published:
Theoretical and Computational Fluid Dynamics Aims and scope Submit manuscript

Abstract

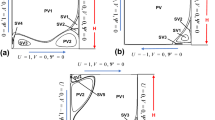
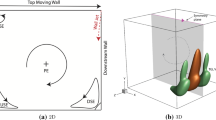
Primary instability of the lid-driven flow in a cube is studied by a linear stability approach. Two cases, in which the lid moves parallel to the cube sidewall or parallel to the diagonal plane, are considered. It is shown that Krylov vectors required for application of the Newton and Arnoldi iteration methods can be evaluated by the SIMPLE procedure. The finite volume grid is gradually refined from \(100^{3}\) to \(256^{3}\) nodes. The computations result in grid converging values of the critical Reynolds number and oscillation frequency that allow for Richardson extrapolation to the zero grid size. Three-dimensional flow and most unstable perturbations are visualized by a recently proposed approach that allows for a better insight into the flow patterns and appearance of the instability. New arguments regarding the assumption that the centrifugal mechanism triggers the instability are given for both cases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Shankar, P.N., Deshpande, M.D.: Fluid mechanics in the driven cavity. Ann. Rev. Fluid Mech. 32, 93–136 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  2. Kuhlmann, H.C., Romano F.: The lid-driven cavity. In: Computational Modelling of Bifurcations and Instabilities in Fluid Dynamics. In: A. Gelfgat (ed.) Springer, Berlin (2018)

  3. Deshmuck, R., McNamara, J.J., Liang, Z., Kolter, J.Z., Abhijit, G.: Model order reduction using sparse coding exemplified for the lid-driven cavity. J. Fluid Mech. 808, 189–223 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  4. Kalita, J.C., Gogoi, B.B.: A biharmonic approach for the global stability analysis of 2D incompressible viscous flows. Appl. Math Model. 40, 6831–6849 (2016)

    Article  MathSciNet  Google Scholar 

  5. Nuriev, A.N., Egorov, A.G., Zaitseva, O.N.: Bifurcation analysis of steady-state flows in the lid-driven cavity. Fluid Dyn. Res. 48, 061405 (2016)

    Article  MathSciNet  Google Scholar 

  6. Babu, V., Korpela, S.A.: Numerical solution of the incompressible, three-dimensional Navier–Stokes equations. Comput. Fluids 23, 675–691 (1994)

    Article  MATH  Google Scholar 

  7. Albensoeder, S., Kuhlmann, H.C.: Accurate three-dimensional lid-driven cavity flow. J. Comput. Phys. 206, 536–558 (2006)

    Article  MATH  Google Scholar 

  8. Liberzon, A., Feldman, Y., Gelfgat, A.Y.: Experimental observation of the steady—oscillatory transition in a cubic lid-driven cavity. Phys. Fluids 23, 084106 (2011)

    Article  Google Scholar 

  9. Feldman, Y., Gelfgat, A.Y.: On pressure-velocity coupled time-integration of incompressible Navier–Stokes equations using direct inversion of Stokes operator or accelerated multigrid technique. Comput. Struct. 87, 710–720 (2009)

    Article  Google Scholar 

  10. Feldman, Y., Gelfgat, A.Y.: Oscillatory instability of a 3D lid-driven flow in a cube. Phys. Fluids 22, 093602 (2010)

    Article  Google Scholar 

  11. Hammami, F., Ben-Cheikh, N., Campo, A., Ben-Beya, B., Lili, T.: Prediction of unsteady states in lid-driven cavities filled with an incompressible viscous fluid. Int. J. Mod. Phys. C 23, 1250030 (2012)

    Article  MATH  Google Scholar 

  12. Mynam, M., Pathak, A.D.: Lattice Boltzmann simulation of steady and oscillatory flows in lid-driven cubic cavity. Int. J. Mod. Phys. C 24, 1350005 (2013)

    Article  Google Scholar 

  13. Chang, H.W., Hong, P.Y., Lin, L.S., Lin, C.A.: Simulations of flow instability in three dimensional deep cavities with multi relaxation time lattice Boltzmann method on graphic processing units. Comput. Fluids 88, 866–871 (2013)

    Article  MATH  Google Scholar 

  14. Kuhlmann, H.C., Albensoeder, S.: Stability of the steady three-dimensional lid-driven flow in a cube and the supercritical flow dynamics. Phys. Fluids 26, 024104 (2014)

    Article  Google Scholar 

  15. Anupindi, K., Lai, W., Frankel, S.: Characterization of oscillatory instability in lid driven cavity flows using lattice Boltzmann method. Comput. Fluids 92, 7–21 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  16. Loiseau, J.C., Robinet, J.C., Leriche, E.: Intermittency and transition to chaos in the cubical lid-driven cavity flow. Fluid Dyn. Res. 48, 061421 (2016)

    Article  MathSciNet  Google Scholar 

  17. Gómez, F., Gómez, R., Theofilis, V.: On three-dimensional global linear instability analysis of flows with standard aerodynamics codes. Aerosp. Sci. Technol. 32, 223–234 (2014)

    Article  Google Scholar 

  18. Lopez, J.M., Welfert, B.D., Wu, K., Yalim, J.: Transitions to complex dynamics in the cubic lid-driven cavity. Phys. Rev. Fluids 2, 074401 (2017)

    Article  Google Scholar 

  19. Povitsky, A.: High-incidence 3-D lid-driven cavity flow. AIAA Paper, 2847 (2001)

  20. Povitsky, A.: Three-dimensional flow in cavity at yaw. Nonlinear Anal. Theory Methods Appl. 63, e1573–e1584 (2005)

    Article  MATH  Google Scholar 

  21. Feldman, Y., Gelfgat, A.Y.: From multi- to single-grid CFD on massively parallel computers: numerical experiments on lid-driven flow in a cube using pressure-velocity coupled formulation. Comput. Fluids 46, 218–223 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  22. Feldman, Y.: Theoretical analysis of three-dimensional bifurcated flow inside a diagonally lid-driven cavity. Theor. Comput. Fluid Dyn. 29, 245–261 (2015)

    Article  Google Scholar 

  23. Gulberg, Y., Feldman, Y.: On laminar natural convection inside multi-layered spherical shells. Int. J. Heat Mass Transf. 91, 908–921 (2015)

    Article  Google Scholar 

  24. Gelfgat, A.Y.: Visualization of three-dimensional incompressible flows by quasi-two-dimensional divergence-free projections. Comput. Fluids 97, 143–155 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  25. Gelfgat, A.Y.: Visualization of three-dimensional incompressible flows by quasi-two-dimensional divergence-free projections in arbitrary flow regions. Theor. Comput. Fluid Dyn. 30, 339–348 (2016)

    Article  Google Scholar 

  26. Patankar, S.V.: Numerical Heat Transfer and Fluid Flow. Taylor & Francis, London (1980)

    MATH  Google Scholar 

  27. van der Vorst, H.: Iterative Krylov Methods for Large Linear Systems. Cambridge Univ Press, Cambridge (2003)

    Book  MATH  Google Scholar 

  28. Bayly, B.J.: Three-dimensional centrifugal-type instabilities in inviscid two-dimensional flows. Phys. Fluids 31, 56–64 (1988)

    Article  MATH  Google Scholar 

  29. Lanzerstorfer, D., Kuhlmann, H.C.: Global stability of the two-dimensional flow over a backward-facing step. J. Fluid Mech. 693, 1–27 (2012)

    Article  MATH  Google Scholar 

  30. Albensoeder, S., Kuhlmann, H.C., Rath, H.J.: Three-dimensional centrifugal-flow instabilities in the lid-driven-cavity problem. Phys. Fluids 13, 121–135 (2001)

    Article  MATH  Google Scholar 

  31. Feldman, Y.: Direct numerical simulation of transitions and supercritical regimes in confined three-dimensional recirculating flows, Ph.D. Thesis, Tel-Aviv University (2010)

  32. Roache, P.J.: Perspective: a method for uniform reporting of grid refinement studies. J. Fluids Eng. 116, 405–413 (1994)

    Article  Google Scholar 

  33. Sorensen, D.C.: Implicit application of polynomial filters in a k-step Arnoldi method. SIAM J. Matrix Anal. Appl. 13, 357–385 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  34. Scott, J.A.: An Arnoldi code for computing selected eigenvalues of sparse real unsymmetric matrices. ACM Trans. Math. Softw. 21, 432–475 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  35. Edwards, W.S., Tuckerman, L.S., Friesner, R.A., Sorensen, D.C.: Krylov methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 110, 82–102 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  36. Tuckerman, L.S., Barkley, D.: Bifurcation analysis for time-steppers. In: Doedel, K., Tuckerman, L. (eds.) Numerical Methods for Bifurcation Problems and Large-Scale Dynamical Systems. IMA Volumes in Mathematics and Its Applications, vol. 119, pp. 453–466. Springer, New York (2000)

  37. Tuckerman, L.S., Bertagnolio, F., Daube, O., Le Quéré, P., Barkley, D.: Stokes preconditioning for the inverse Arnoldi method. In D. Henry, A. Bergeon, Vieweg Göttingen (eds.) Continuation Methods for Fluid Dynamics (Notes on Numerical Fluid Dynamics, 74), pp. 241–255 (2000)

  38. Gelfgat, A.Y.: Krylov-subspace-based steady state and stability solvers for incompressible flows: replacing time steppers and generation of initial guess. In: A. Gelfgat (ed.) Computational Modelling of Bifurcations and Instabilities in Fluid Dynamics. Springer, 2018 (to appear)

  39. Chorin, A.J.: Numerical solution of the Navier–Stokes equations. Math. Comput. 22, 745–762 (1968)

    Article  MathSciNet  MATH  Google Scholar 

  40. Vitoshkin, H., Gelfgat, A.Y.: On direct inverse of Stokes, Helmholtz and Laplacian operators in view of time-stepper-based Newton and Arnoldi solvers in incompressible CFD. Commun. Comput. Phys. 14, 1103–1119 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  41. Lynch, R.E., Rice, J.R., Thomas, D.H.: Direct solution of partial differential equations by tensor product methods. Numer. Math. 6, 185–199 (1964)

    Article  MathSciNet  MATH  Google Scholar 

  42. Gelfgat, A.Y.: Stability of convective flows in cavities: solution of benchmark problems by a low-order finite volume method. Intl. J. Num. Methods Fluids 53, 485–506 (2007)

    Article  MATH  Google Scholar 

  43. Gelfgat, A.Y.: Implementation of arbitrary inner product in global Galerkin method for incompressible Navier–Stokes equation. J. Comput. Phys. 211, 513–530 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  44. Poliashenko, M., Aidun, C,K.: A direct method for computation of simple bifurcations. J. Comput. Phys 121, 246–260 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  45. Gervais, J.J., Lemelin, D., Pierre, R.: Some experiments with stability analysis of discrete incompressible flows in the lid-driven cavity. Int. J. Numer. Meth. Fluids 24, 477–492 (1997)

    Article  MATH  Google Scholar 

  46. Fortin, A., Jardak, M., Gervais, J.J., Pierre, R.: Localization of Hopf bifurcations in fluid flow problems. Int. J. Numer. Meth. Fluids 24, 1185–1210 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  47. Auteri, F., Parolini, N., Quartapelle, L.: Numerical investigations on the stability of singular driven cavity flow. J. Comput. Phys. 183, 1–25 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  48. Peng, Y.F., Shiau, Y.H., Hwang, R.R.: Transition in a 2-D lid-driven cavity flow. Comput. Fluids 32, 337–352 (2003)

    Article  MATH  Google Scholar 

  49. Abouhamza, A., Pierre, R.: A neutral stability curve for incompressible flows in a rectangular driven cavity. Math. Comput. Model. 38, 141–157 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  50. Cadou, J.M., Potier-Ferry, M., Cochelin, B.: A numerical method for the computation of bifurcation points in fluid mechanics. Eur. J. Mech. B/Fluids 25, 234–254 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  51. Sahin, M., Owens, R.G.: A novel fully-implicit finite volume method applied to the lid-driven cavity problem. Part II. Linear stability analysis. Int. J. Numer. Meth. Fluids 42, 79–88 (2003)

    Article  MATH  Google Scholar 

  52. Boppana, V.B.L., Gajjar, J.S.B.: Global flow instability in a lid-driven cavity. Int. J. Numer. Meth. Fluids 62, 827–853 (2010)

    MathSciNet  MATH  Google Scholar 

  53. Tiesinga, G., Wubs, F.W., Veldman, A.E.P.: Bifurcation analysis of incompressible flow in a driven cavity by the Newton–Picard method. J. Comput. Appl. Math. 140, 751–772 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  54. Kalita, J.C., Gogoi, B.B.: A biharmonic approach for the global stability analysis of 2D incompressible viscous flows. Appl. Math. Model. 40, 6831–6849 (2016)

    Article  MathSciNet  Google Scholar 

  55. Gelfgat, A.Y., Molokov, S.: Quasi-two-dimensional convection in a 3D laterally heated box in a strong magnetic field normal to main circulation. Phys. Fluids 23, 034101 (2011)

    Article  Google Scholar 

  56. Brès, C.A., Colonius, T.: Three-dimensional instabilities in compressible flow over open cavities. J. Fluid Mech. 599, 309–339 (2008)

    Article  MATH  Google Scholar 

  57. Barkley, D., Gomes, G., Gabriela, M., Henderson, D.: Three-dimensional instability in flow over a backward-facing step. J. Fluid Mech 473, 167–190 (2002)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Faculty of Engineering, Tel-Aviv University, Ramat Aviv, 69978, Tel-Aviv, Israel

    Alexander Yu. Gelfgat

Authors
  1. Alexander Yu. Gelfgat
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alexander Yu. Gelfgat.

Additional information

Communicated by Vassilis Theofilis.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gelfgat, A.Y. Linear instability of the lid-driven flow in a cubic cavity. Theor. Comput. Fluid Dyn. 33, 59–82 (2019). https://doi.org/10.1007/s00162-019-00483-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00162-019-00483-1

Keywords

Search

Navigation