Effect of the Reynolds number on flow bifurcations and eddy genesis in a lid-driven sectorial cavity

Abstract

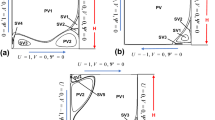
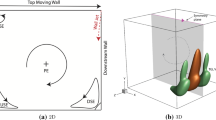
This paper presents the two-dimensional (2D) steady incompressible flow in a lid-driven sectorial cavity. In order to analyze the flow structures, the 2D Navier–Stokes equations are solved by using the finite element method. Different cases of the cavity aspect ratio A and three cases of the speed ratios $(S=-1,0,1)$ of the upper and the lower lids are considered. The finite element formulation for the governing equations is adopted via the velocity-pressure formulation. By varying A for each S, the effect of the Reynolds number on the streamline patterns and their bifurcations are investigated in range $Re\in [0,200]$. A comparison between the obtained results and some earlier studies is presented.

Appendix: Construction of shape functions

To facilitate the construction of shape functions, an isoparametric mapping which maps (x, y) cartesian coordinates to $(\xi ,\eta )$ local coordinates was used. In addition, curved-sides elements are quite useful in practice, principally for modeling curved boundaries. Due to this facilities, isoparametric mapping was used rather than direct approach (for more details see [4]).

Fig. 15

a The parent element b The real element

Figure 15a shows the parent element in $\xi ,\eta$-space; Fig. 15b shows the parent element mapped onto a curved-sided real element in x, y-space. Firstly, the parent element was examined, then the shape functions are developed on the parent element and finally the mapping of the parent element onto the real element was constituted. The latter, results in the parent shape functions was mapped into shape functions on the real element.

The parent element may have any triangular shape. However, a regular shape is desirable because real elements that are severely distorted from the parent shape cause numerical problems. Therefore, regularly shaped reel elements are generally most useful. We selected a isosceles triangle, due to it’s computation advantages (see [4]).

The parent shape functions are developed by using the interpolation property $\phi _{i}(\xi _{i},\eta _{i})=\delta _{ij.}$ The trial solution in the parent element is a complete 2-D polynomial, then each shape function may contain any of the terms in a 2-D polynomial. Thus, for node 1,

$$\begin{aligned} \phi _{1}(\xi ,\eta )=\alpha _{1}+\alpha _{2}\xi +\alpha _{3}\eta +\alpha _{4}\xi ^{2}+\alpha _{5}\xi \eta +\alpha _{6}\eta ^{2} \end{aligned}$$

(20)

where the interpolation property requires that

$$\begin{aligned} \phi _{1}(\xi _{1},\eta _{1})= & {} 1 \nonumber \\ \phi _{1}(\xi _{j},\eta _{j})= & {} 0 \qquad \quad j=2,3,4,5,6 \end{aligned}$$

(21)

Applying conditions Eqs. (21) to (20) yields six equations:

$$\begin{aligned} \begin{array}{ccccccccccccc} \alpha _{1} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} = &{} 1 \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ \alpha _{1} &{} + &{} \alpha _{2} &{} &{} &{} + &{} \alpha _{4} &{} &{} &{} &{} &{} = &{} 0 \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ \alpha _{1} &{} &{} &{} + &{} \alpha _{3} &{} &{} &{} &{} &{} + &{} \alpha _{6} &{} = &{} 0 \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ \alpha _{1} &{} + &{} \frac{1}{2}\alpha _{2} &{} &{} &{} + &{} \frac{1}{4}\alpha _{4} &{} &{} &{} &{} &{} = &{} 0 \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ \alpha _{1} &{} + &{} \frac{1}{2}\alpha _{2} &{} + &{} \frac{1}{2}\alpha _{3} &{} + &{} \frac{1}{4}\alpha _{4} &{} + &{} \frac{1}{4}\alpha _{5} &{} + &{} \frac{1}{4}\alpha _{6} &{} = &{} 0 \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ \alpha _{1} &{} &{} &{} + &{} \frac{1}{2}\alpha _{3} &{} &{} &{} &{} &{} + &{} \frac{1}{4} \alpha _{6} &{} = &{} 0 \end{array} \end{aligned}$$

(22)

solving Eq. (22) yields

$$\begin{aligned} \phi _{1}(\xi ,\eta )=\left[ 1-\xi -\eta \right] \left[ 1-2\left( \xi +\eta \right) \right] \end{aligned}$$

(23)

and in a similar fashion it shown that

$$\begin{aligned} \phi _{2}(\xi ,\eta )= & {} \xi \left( 2\xi -1\right) \nonumber \\ \phi _{3}(\xi ,\eta )= & {} \eta \left( 2\eta -1\right) \nonumber \\ \phi _{4}(\xi ,\eta )= & {} 4\xi \left[ 1-\xi -\eta \right] \nonumber \\ \phi _{5}(\xi ,\eta )= & {} 4\xi \eta \nonumber \\ \phi _{6}(\xi ,\eta )= & {} 4\eta \left[ 1-\xi -\eta \right] \end{aligned}$$

(24)

and for pressure,

$$\begin{aligned} \beta _{1}(\xi ,\eta )= & {} 1-\xi -\eta \nonumber \\ \beta _{2}(\xi ,\eta )= & {} \xi \nonumber \\ \beta _{3}(\xi ,\eta )= & {} \eta \end{aligned}$$

(25)

These shape functions are identical for each element.

There are several ways to establish such a mapping. The most widely used at present is the isoparametric approach

$$\begin{aligned} x=\mathop {\textstyle \sum }\limits _{k=1}^{6}x_{k}^{(e)}\phi _{k}^{(e)}(\xi ,\eta ) \nonumber \\ y=\mathop {\textstyle \sum }\limits _{k=1}^{6}x_{k}^{(e)}\phi _{k}^{(e)}(\xi ,\eta ) \end{aligned}$$

(26)

The Jacobian plays an important role in the FE analysis of isoparametric elements. The analytical test for acceptability of the 2-D mapping is

$$\begin{aligned} \left| J^{(e)}(\xi ,\eta )\right| >0 \end{aligned}$$

(27)

where $\left| J^{(e)}(\xi ,\eta )\right|$ is the Jacobian, which is the determinant of the Jacobian matrix (i.e., the Jacobian must be positive everywhere inside the element and on the boundary, see [4]). The Jacobian in 2-D is the ratio of an infinitesimal area in the parent element to the corresponding infinitesimal area in the real element that it is mapped into:

$$\begin{aligned} dx\,dy=\left| J^{(e)}(\xi ,\eta )\right| d\xi d\eta \end{aligned}$$

(28)

The Jacobian matrix is given by

$$\begin{aligned} J^{(e)}(\xi ,\eta )=\left[ \begin{array}{ccc} \frac{\partial x}{\partial \xi } &{} &{} \frac{\partial y}{\partial \xi } \\ &{} &{} \\ \frac{\partial x}{\partial \eta } &{} &{} \frac{\partial y}{\partial \eta } \end{array} \right] =\left[ \begin{array}{ccc} J_{11}^{(e)}(\xi ,\eta ) &{} &{} J_{12}^{(e)}(\xi ,\eta ) \\ &{} &{} \\ J_{21}^{(e)}(\xi ,\eta ) &{} &{} J_{22}^{(e)}(\xi ,\eta ) \end{array} \right] . \end{aligned}$$

(29)

Hence

$$\begin{aligned} \left| J^{(e)}(\xi ,\eta )\right| =\frac{\partial x}{\partial \xi } \frac{\partial y}{\partial \eta }-\frac{\partial x}{\partial \eta }\frac{ \partial y}{\partial \xi } \end{aligned}$$

The derivatives of the coordinate transformation are obtained from Eq. (26):

$$\begin{aligned} \begin{array}{ccc} J_{11}^{(e)}\left( \xi ,\eta \right) =\frac{\partial x}{\partial \xi } =\mathop {\textstyle \sum }\limits _{k=1}^{6}x_{k}^{(e)}\frac{\phi _{k}(\xi ,\eta )}{\partial \xi } &{} &{} J_{12}^{(e)}\left( \xi ,\eta \right) =\frac{\partial y}{\partial \xi } =\mathop {\textstyle \sum }\limits _{k=1}^{6}y_{k}^{(e)}\frac{\phi _{k}(\xi ,\eta )}{\partial \xi } \\ \begin{array}{c} \\ J_{21}^{(e)}\left( \xi ,\eta \right) =\frac{\partial x}{\partial \eta } =\mathop {\textstyle \sum }\limits _{k=1}^{6}x_{k}^{(e)}\frac{\phi _{k}(\xi ,\eta )}{\partial \eta } \end{array} &{} &{} \begin{array}{c} \\ J_{22}^{(e)}\left( \xi ,\eta \right) =\frac{\partial y}{\partial \eta } =\mathop {\textstyle \sum }\limits _{k=1}^{6}y_{k}^{(e)}\frac{\phi _{k}(\xi ,\eta )}{\partial \eta } \end{array} \end{array} \end{aligned}$$

(30)

and the derivatives of the shape functions are obtained from Eqs. (23) and (24). In addition, the derivatives $\frac{\partial \phi _{i}^{(e)}}{\partial x}$ and $\frac{\partial \phi _{i}^{(e)}}{\partial y}$ are obtained by using the chain rule:

$$\begin{aligned} \begin{array}{ccc} \frac{\partial \phi _{i}}{\partial \xi } &{} = &{} \frac{\partial \phi _{i}}{ \partial x}\frac{\partial x}{\partial \xi }+\frac{\partial \phi _{i}}{ \partial y}\frac{\partial y}{\partial \xi } \\ &{} &{} \\ \frac{\partial \phi _{i}}{\partial \eta } &{} = &{} \frac{\partial \phi _{i}}{ \partial x}\frac{\partial x}{\partial \eta }+\frac{\partial \phi _{i}}{ \partial y}\frac{\partial y}{\partial \eta } \end{array} \end{aligned}$$

(31)

Hence

$$\begin{aligned} \left\{ \begin{array}{c} \frac{\partial \phi _{i}}{\partial \xi } \\ \\ \frac{\partial \phi _{i}}{\partial \eta } \end{array} \right\} =\left[ J^{(e)}\right] \left\{ \begin{array}{c} \frac{\partial \phi _{i}}{\partial x} \\ \\ \frac{\partial \phi _{i}}{\partial y} \end{array} \right\} . \end{aligned}$$

(32)

Equation (32) can be written as:

$$\begin{aligned} \left\{ \begin{array}{c} \frac{\partial \phi _{i}}{\partial x} \\ \\ \frac{\partial \phi _{i}}{\partial y} \end{array} \right\} =\left[ J^{(e)}\right] ^{-1}\left\{ \begin{array}{c} \frac{\partial \phi _{i}}{\partial \xi } \\ \\ \frac{\partial \phi _{i}}{\partial \eta } \end{array} \right\} \end{aligned}$$

(33)

where $\left[ J^{(e)}\right] ^{-1}$ is inverse of the Jacobian matrix in Eq. (29).