1 Introduction

Nanomaterials, including nanocomposites, are commonly used in such areas of medicine as cardiology, neurology or orthopaedics (Wei and Ma 2004; Hoppen et al. 1990; Robinson et al. 1989; de Groot et al. 1996). The present trends related to materials for orthopaedic implants indicate the “nano” direction. Researches in the area show the superiority of nanomaterials over the conventional materials (Webster and Ejiofor 2004). This pertains not only to nanometals but also to nanocomposites, nanobioceramics and nanopolymers.

The natural intervertebral discs, as well as artificial ones, are subjected mainly to compressive forces. During bending a part of annulus fibrosus is compressed, the nucleus migrates towards the opposite direction which generates additional stress state in the other part of annulus fibrosus. The intervertebral disc is then capable to carry considerable compressive loads (Krag et al. 1987). Artificial intervertebral disks are experimentally verified mainly in compressive tests but also in torsional and bending tests. Such tests give information on the strength of disk prostheses, i.e. on the basis of the experimental results one can decide whether or not the tested prosthesis can be clinically applied. In the paper Büttner-Janz et al. (1989) the authors tested one of the most frequently applied intervertebral disk prostheses, i.e. SB Charité. They performed biomechanical static and dynamic compressive tests on two SB Charité prostheses. They reported three strain–stress characteristics in the form of hysteresis loops where the maximal loads corresponded to the stress values of 9, 22 and 40 MPa. They did not observe any microscopic changes in the metallic plates; however, bulge of the polyethylene core was visible. Similar compressive tests have been performed recently on prosthesis of another type, namely nucleus-sparing prosthesis (Buttermann and Beaubien 2009). A review of clinical application and some biomechanical aspects of various types of intervertebral disk prostheses is presented in Gamradt and Wang (2005).

The research delivered in this paper comprises compressive tests of various types, which were performed in order to determine hyperelastic and viscoelastic constants of the material in interest and formulate a constitutive law for it. The subject of the study is polyurethane nanocomposite. Polyurethane is a polymer that is created in the result of additive polymerisation of multifunctional isocyanates into amines and alcohols. The presence of the urethane groups in the main monomers is the factor that makes the polyurethane different from the other polymers. The polyurethane consists of two different structural segments, hard segment and soft segment. This is very advantageous in the context of the polyurethane application as one of the lumbar disc prosthesis components. The hard segment behaviour is stiff whereas the response of the other one is elastic.

In order to enhance the mechanical properties of the polyurethane, nanoparticles of carbon nanotubes were introduced in the matrix (Koerner et al. 2005). It is obvious that the more regular the dispersion of the nanoparticles in the matrix, the better mechanical properties of the polyurethane nanocomposite. Also the amount of nanoparticles influences the mechanical properties. The most popular way to evenly disperse nanoparticles in polymer-based resins is the sonification process (Schulz et al. 2006). Good dispersion of the nanoparticles in the matrix depends on variety of factors, such as the sonification time, the stirring speed, selection of dispersion solvents, and temperature of the mixture. The nanocomposite studied in the paper was produced by ultrasonically mixing polyurethane with the carbon nanotubes at the temperature 50 ∘C and in the ultrasonic bath at 40 kHz. The amount of 0.05 % weight of the nanoparticles was introduced into the matrix. The production process of the nanocomposite analysed in the paper is described in detail in Ryszkowska et al. (2007). The authors obtained some nanocomposites with bundles and agglomerates of the nanoparticles. However, they managed to elaborate such production conditions that the size of the agglomerates was very small. Therefore, the nanocomposite was modelled in the constitutive formulation as an isotropic and homogeneous material.

Polyurethane has been used for many years for production of implant components (Lelah and Cooper 1986; Lambda et al. 1998). They are characterised by high-degree biocompatibility, high resistance to degradation in human body and high wet angle, which is very important to avoid cell growth in the implantation region. Various groups (polyestradiols) resistant to hydrolytic degradation are used to produce polyurethane (Ryszkowska et al. 2010). The approach of the constitutive equation formulation presented in the paper, based on application of a potential function form ψ, is well described in the literature (Truesdell and Noll 1992; Coleman 1964; Pawlikowski 2012). It is a very convenient approach as it makes it possible to take into account various phenomena, such as ability of a material to dissipate energy, relation between reaction and deformation rate of a material, anisotropy of a material by means of structural tensors, etc. Potential energy of elasticity per unit of volume is the physical interpretation of potential function ψ, which is also referred to as strain energy density. The energy must be invariant to the coordinate system transformation. Thus, potential energy has to depend on invariants of the tensors used to describe the material’s behaviour.

The strain energy density ψ is a scalar function of one tensorial variable, i.e. the deformation gradient F. The second-order tensor F represents the mapping of the deformation from the reference state to the deformed configuration. It is assumed that ψ vanishes in the reference configuration, i.e. at time t=0. Thus, in the initial state the deformation gradient F=I, where I is the unit tensor. It is known from physical observations that the potential function increases monotonically with deformation. Thus, ψ attains its global minimum in the reference configuration which is a stress-free state (Eq. (1)):

$$ \psi( \mathbf{I} ) = 0,\qquad \psi( \mathbf{F} ) \ge 0. $$
(1)

Another restriction that is placed on the strain energy density is that in order to expand a body infinitely or to compress a body to the volume of zero, an infinite amount of energy is needed. This is expressed in Eqs. (2) and (3):

(2)
(3)

It is obvious that the potential function and the resulting constitutive equations must satisfy some requirements. Those requirements result from mathematical theory and the physical nature of the materials:

  1. (i)

    convexity,

  2. (ii)

    objectivity,

  3. (iii)

    material-frame indifference.

The constraint (i) is a fundamental one for existence and uniqueness of the solution in the boundary value analysis (Carter and Hayes 1977; Linde 1994). In order to obtain a numerical solution in cases where an analytical one is not possible, one has to ensure the uniqueness of the solution. For this requirement, confidence in numerical results is essential.

The objectivity constraint (ii), which is also referred to as observer invariance demand, means that the state of deformation of a body cannot depend on the position of the observer registering the motion. In other words, two observers in different positions will observe the identical deformation of a body at one instance.

The third constraint (iii) is closely related to the previous one. It states that a rigid motion of a deformed body does not influence the value of the energy of the body.

In a general viscoelastic or visco-hyperelastic constitutive equation formulation one has to take into account the principle of fading memory developed by Coleman and Noll (1961). It takes into consideration the deformation history and states that the deformation which occurred in the recent time history influences in a greater degree the actual state of stress than the deformation which occurred in the more distant time history. The principle is mathematically expressed as

$$ \mathbf{S} = \mathbf{S}^{e} \bigl( \mathbf{C} ( t ) \bigr) + \int_{0}^{t} \aleph \bigl( \mathbf{G} ( t - s ),s;\mathbf{C} ( t ) \bigr)\,\mathrm{d}s, $$
(4)

where S is the second Piola–Kirchhoff stress tensor, S e the elastic second Piola–Kirchhoff stress tensor, C the right Cauchy tensor defined as C=F T F, ℵ a general tensor-valued function that depends on variables G(t−s) and s. In Eq. (4), s represents the historical time variable and t is the current time.

The first objective of the paper is to implement the curve-fitting procedure to verify which of the known hyperelastic potential functions is adequate for describing pure hyperelastic response of the polyurethane. In the study the material is assumed to be incompressible and isotropic. The pure hyperelastic material constants are optimised on the basis of experimental data by means of the author’s code realising Levenberg–Marquardt algorithm for least-squares curve-fitting. The data from uniaxial monotonic compression tests comprising only the loading phase is utilised in this part of the study.

The second objective of the paper, the crucial one, is to combine two theories to determine the long-term visco-hyperelastic constitutive equation for the material using non-linear approach. The first theory was described by Taylor et al. (1970) and developed by Goh et al. (2004). By means of this theory the hereditary integral in Eq. (4) is numerically solved. The theory is based on theoretical relaxation curve-fitting to the experimental one. It has to be emphasised that no particular number of relaxation times and the corresponding characteristic amplitudes is imposed. The second theory implements the algorithm described by Ciambella et al. (2010) and is applied in order to determine the number of characteristic times and corresponding characteristic amplitudes. The code based on the algorithm, which is utilised in the study, “decides” how many relaxation times are needed to describe the rheological response of the material of interest. The combination of the two theories allows one to formulate a constitutive model for the material which describes well its rheological behaviour, i.e. relaxation phenomenon, dependence on strain rate, and hysteresis loop.

In order to attain the first objective, uniaxial compression tests have been performed. The tests consisted only of the loading phase carried out at the strain rate \(\dot{\lambda} = 10~\mathrm{min}^{- 1}\) until the strain of approx. 20 % was achieved. Here λ denotes a stretch ratio along the load direction. The following hyperelastic potential functions have been studied: Ogden, Neo-Hookean, Yeoh and Mooney–Rivlin. In this part of the paper not only was the adequate hyperelastic model determined for the polyurethane nanocomposite but also the pure hyperelastic constants were identified.

In the second part of the study, ramp relaxation tests and uniaxial monotonic compression tests were performed. In the relaxation tests the samples were compressed until the 10 % strain was attained and the change of force was measured for approx. 30 min. During the strength tests the samples were monotonically compressed at three different strain rates, \(\dot{\lambda} = 0.1~\mathrm{min}^{- 1}, \dot{\lambda} = 1~\mathrm{min}^{- 1}\) and \(\dot{\lambda} = 10~\mathrm{min}^{ - 1}\). Deformation in the load direction and in the perpendicular one was measured in the loading and unloading phases. The evaluation of the visco-hyperelastic constants was performed in two stages. First the theoretical model was matched to the relaxation data to compute the number of the characteristic times and amplitudes and identify their values as well as those of strain-dependant constants. In the second stage the values of the characteristic amplitudes and strain-dependant constants were recalibrated by theoretical curve-fitting to the experimental one obtained from the uniaxial compression tests. In this stage the relaxation times were constant and equalled the values obtained from relaxation curve-fitting.

Generally, the overall research program presented in the paper consists of the following steps:

  • determine hyperelastic potential function on the basis of uniaxial monotonic compression tests (loading phase only),

  • identify relaxation times on the basis of relaxation tests,

  • calibrate the hyperelastic constants and characteristic amplitudes on the basis of uniaxial monotonic compression tests comprising the loading and unloading phases (hysteresis loop) and performed at three different strain rates.

2 Theoretical background

Equation (4) represents a general constitutive law that takes into account elastic and long-term memory contributions. The elastic part of the equation can be calculated using the formula

(5)

Equation (5) satisfies the thermodynamic restrictions if no dissipation occurs during the elastic deformation.

To determine the hyperelastic model for the nanocomposite the following potential functions were considered:

  • Ogden (Ogden 1972): \(\psi_{\mathrm{O}} = \sum_{p = 1}^{N} \frac{\mu_{p}}{\alpha_{p}}( \lambda_{1}^{\alpha _{p}} + \lambda_{2}^{\alpha _{p}} + \lambda_{3}^{\alpha _{p}} - 3 )\),

  • Neo-Hookean (Rivlin 1997): ψ NH=c 1(I 1−3),

  • Yeoh (Yeoh 1993): ψ Y=c 1(I 1−3)+c 2(I 1−3)2+c 3(I 1−3)3,

  • Mooney–Rivlin (Macosko 1994): ψ MR=c 10(I 1−3)+c 01(I 2−3),

where μ p ,α p ,c 1,c 2,c 3, c 10, c 01 are material constants; I 1,I 2 the first and the second invariants of the right Cauchy stress tensor, respectively; λ 1,λ 2,λ 3 the stretch ratios along the principle axes.

In the case of uniaxial compression the deformation gradient tensor takes the form presented in Eq. (6):

(6)

Thus, one can define the right Cauchy stress tensor:

(7)

Since the material is assumed to be incompressible and isotropic, then λ 1 λ 2 λ 3=1,λ 2=λ 3. Thus, denoting λ 1=λ, Eq. (7) takes the form of Eq. (8):

(8)

Using Eq. (5), constitutive formulae relating the elastic second Piola–Kirchhoff stress with stretch ratio along the load direction can be derived for the considered hyperelastic models:

  • Ogden: \(S_{\mathrm{O}}^{e} = \frac{1}{\lambda^{2}}\sum_{p = 1}^{N} ( \mu_{p}\lambda^{\alpha _{p}} - \mu_{p}\lambda^{ - \frac{1}{2}\alpha _{p}} )\),

  • Neo-Hookean: \(S_{\mathrm{NH}}^{e} = \frac{1}{\lambda^{3}}2c_{1}( \lambda^{3} - 1 ) \),

  • Yeoh: \(S_{\mathrm{Y}}^{e} = \frac{2}{\lambda^{5}}( 3( c_{3}\lambda^{6} - 6c_{3}\lambda^{4} + 4c_{3}\lambda^{3} + 9c_{3}\lambda^{2} - 12c_{3}\lambda + 4c_{3} ) )( \lambda^{3} - 1 ) + \frac{2}{\lambda^{5}}( 2c_{2}\lambda^{4} - 6c_{2}\lambda^{2} + 4c_{2}\lambda + c_{1}\lambda^{2} )( \lambda^{3} - 1 ) \),

  • Mooney–Rivlin: \(S_{\mathrm{MR}}^{e} = \frac{2}{\lambda^{4}}( c_{10}\lambda^{4} + c_{01}\lambda^{3} - c_{10}\lambda - c_{01} )\).

The Neo-Hookean model is derived from the Ogden model by setting N=1,α=2. The Mooney–Rivlin model is also a particular case of the Ogden model. It can be derived from it with N=2,α 1=2,α 2=−2. The Yeoh stress model, derived from a third-order strain energy function ψ Y, is a phenomenological model for nearly incompressible materials. In general it depends on three invariants of the right Cauchy stress tensor; however, in the case of an incompressible material it is a function of only the first invariant I 1. In the Ogden model the integer N can have any value. In this paper three Ogden models are considered: with N=2,N=3 and N=4.

The hyperelastic constants in the above equations were calibrated on the basis of compression tests data. Also, on the basis of the curve-fitting analysis it was decided which of the six considered hyperelastic models, i.e. Ogden N=2, Ogden N=3, Ogden N=4, Neo-Hooke, Yeoh and Mooney–Rivlin, was taken into account in the further visco-hyperelastic law formulation.

In non-linear visco-hyperelasticity the stress depends on both time and strain. Thus, the general constitutive equation can be formulated in the form

(9)

where: S is the second Piola–Kirchhoff stress, S e(λ) strain-dependant function, g(t) time-dependant function. The sign ∗ denotes the convolution of S e and g. The function g(t) may be defined by means of the Prony series (Fung 1965):

(10)

In Eq. (10), g i represents characteristic amplitudes, τ i relaxation times, n number of relaxation times and characteristic amplitudes needed to describe visco-hyperelastic response of the material, and \(g_{\infty } = 1 - \sum_{i - 1}^{n} g_{i}\).

Since ∗ in Eq. (9) denotes the convolution of S e and g, the equation takes the form

(11)

Equation (11) can, in turn, be split into a long-term hyperelastic response and a visco-hyperelastic contribution:

(12)

The stress S(t) is now a function of only time t if the strain history λ(t) is known.

The integral in Eq. (12) may be computed using the algorithm presented in Goh et al. (2004), which is based on finite increments of time. Following the derivation introduced in Goh et al. (2004), Eq. (12) can be written in the form

(13)

where Δt is the time increment and h i (t) represents the stress at the previous time step. As the initial stress and strain in the material are known, the stress at time t>0 can be easily calculated.

3 Experimental set-up

The experiments were carried out on an MTS Bionix System. Six samples were experimentally studied. The specimens were cylindrically shaped with the diameter-to-height ratio \(\frac{d}{h} = 0.98\) (Fig. 1). In all the experiments the contact surfaces between the sample and the compressing plates (Fig. 1) were kept lubricated in order to minimise the friction and avoid barrel-like deformation of the samples. It was assumed that stress and strain are uniformly distributed in the samples. All the experiments were performed in the average temperature 20±1∘ C. All the samples were subjected to four loading-unloading cycles to eliminate the possible Mullins effect. Prior to every test the samples were compressed and uncompressed with the same strain rate four times to the strain corresponding to that attained during the tests.

Fig. 1
figure 1

Geometry of the specimens

Full size image

The uniaxial monotonic tests were conducted in order to select the best hyperelastic model for the nanocomposite mechanical behaviour. The samples were compressed at the constant strain rate \(\dot{\lambda} = 10~\mathrm{min}^{- 1}\) until the strain λ=0.80 was achieved. The experimental curves were then utilised in the process of curve-fitting and calibration of the constants.

Next, relaxation tests and compression tests with loading and unloading phases were performed. In the relaxation process the samples were compressed from the initial deformation λ=1 to the stretch λ=0.90 within approx. 1 s with constant strain rate. Thereafter, the sample strain was held fixed for 30 min. The stress and strain histories of the relaxation process are shown in Fig. 2(a) and (b), respectively.

Fig. 2
figure 2

Relaxation test: stress history (a), strain history (b)

Full size image

The loading/unloading compression tests were performed at three strain rates, \(\dot{\lambda} = 0.1~\mathrm{min}^{- 1}, \dot{\lambda} = 1~\mathrm{min}^{ - 1}\) and \(\dot{\lambda} = 10~\mathrm{min}^{ - 1} \). The constant identification process was conducted for the three experimental curves at the same time. Deformation was measured by means of videoextensometer in two directions, i.e. in the loading and in the perpendicular direction. The assumption of the material incompressibility was verified. In Fig. 3(a) change of the measured stretch ratio in the perpendicular direction λ 2 is compared with the theoretical stretch calculated on the basis of the assumption. In Fig. 3(b) the determinant of the deformation gradient tensor as a function of displacement is shown for one sample compressed at the three strain rates. Assumption of incompressibility requires that \(\operatorname{det}\mathbf{F} = 1\). It is clearly seen that the material incompressibility can be assumed with very low error.

Fig. 3
figure 3

Assumption of incompressibility: theoretical and measured stretch ratio along the perpendicular direction vs. time (a), determinant of deformation gradient tensor for the three strain rates vs. sample deformation (b)

Full size image

The samples after having been tested were left unloaded for at least 24 hours before they were examined again. Five experimental tests, i.e. compression (loading phase), relaxation and compression at three strain rates (loading/unloading phases), were performed on each sample. The diagram in Fig. 4 shows the exact plan of the experimental tests. In this diagram the use of the test results is also presented.

Fig. 4
figure 4

Diagram of the experimental plan: specification of experiments performed on each sample (left column), activities completed by utilising the experimental results (right column)

Full size image

4 Identification of relaxation times and characteristic amplitudes

The integral in Eq. (12) was solved numerically by means of the Matlab code realising the algorithm presented in the paper Goh et al. (2004). The relaxation times were calibrated by implementation of the code in the iterative outline described in Ciambella et al. (2010). The constant identification was performed by minimisation of the error between the theoretical and experimental data in each sampling time points:

$$ \min_{\mathbf{p} \in \Re }f( \mathbf{p} ) = \min_{\mathbf{p} \in \Re }\Biggl( \sum _{i = 1}^{n} \bigl[ \bigl( S( t,\mathbf{p} ) \bigr)_{i} - \bigl( \tilde{S}( t ) \bigr)_{i} \bigr]^{2} \Biggr), $$
(14)

where \(( \tilde{S}( t ) )_{i} \) are the values of stress measured at sampling times t i ,i=1,…,l, and (S(t,p)) i are values of stress predicted by Eq. (12). The latter depends not only on time but also on the material parameters assembled in vector p that spans the subset ℜ which is a member of space R k(k=m+2n). Thus, p can be written in the form

$$ \mathbf{p} = \{ \kappa_{1},\ldots ,\kappa_{m},g_{1}, \ldots ,g_{n},\tau_{1},\ldots ,\tau_{n} \}. $$
(15)

It should be noted that κ 1,…,κ m may represent either of the hyperelastic constant sets of the considered hyperelastic models. The constraints defined in Eq. (16) have to be fulfilled:

$$ 0 \le g_{i} < 1,\qquad \sum_{i = 1}^{n} g_{i} < 1,\qquad \tau_{i} \ge 0. $$
(16)

The iterative calibration of relaxation times comprises the following steps:

  • the range of characteristic times [τ min,τ max] is determined such that τ min equals to the sampling rate and τ max is the overall time of the experiment;

  • the interval [τ min,τ max] is divided into n equal parts according to the following pattern:

(17)

where \(\Delta = \frac{\mathrm{log}_{\mathrm{10}}\frac{\tau_{\max }}{\tau_{\min}}}{n - 1}\);

  • minimisation problem (14) is solved;

  • a new set of \(\tau_{i}^{h + 1} \) of relaxation times for the next time step is determined following the rules: if a characteristic amplitude \(g_{i}^{h} \), minimising (14), is lower than a given threshold, the corresponding characteristic time \(\tau_{i}^{h}\) is discarded, whereas if \(g_{i}^{h} \) is higher than the threshold, the corresponding characteristic time is left unchanged and in the vicinity new relaxation times are added, according to following formula:

$$ \tau_{i - 1}^{h + 1} = \tau_{i}^{h}10^{ - ( \frac{\Delta }{3} )^{h}}, \qquad \tau_{i}^{h + 1} = \tau_{i}^{h}, \qquad \tau_{i + 1}^{h + 1} = \tau_{i}^{h}10^{ ( \frac{\Delta }{3} )^{h}} . $$
(18)

The starting point of the minimisation problem (14) in step h+1 is the solution calculated in the previous step h. The initial values of the constants \(g_{i - 1}^{h + 1} \) and \(g_{i + 1}^{h + 1} \), corresponding to the new relaxation times, are set to zero. The last two steps are repeated either until all the scalar coefficients g i exceed the threshold, or until the decrement of the objective function between the consecutive steps is acceptably low.

5 Results

5.1 Hyperelastic model determination

The results presented in this chapter begin with the finding of the adequate hyperelastic model for the elastic contribution in the visco-hyperelastic constitutive equation for the nanocomposite. Four hyperelastic models were considered: Ogden, Neo-Hookean, Yeoh and Mooney–Rivlin. The model determination was performed on the basis of compression tests carried out under the same environmental conditions on six specimens at the strain rate \(\dot{\lambda} = 10~\mathrm{min}^{- 1}\). Although the strain–stress curves practically overlap, there can be noticed some discrepancies, especially for larger deformation (Fig. 5). One can also notice some deviations in the strain–stress curve for sample 2. It is believed that the reason for this lies in the fact that the sample had some internal flaws in its structure, like microcracks or nanoparticle bundles. The stress in Fig. 5 is the second Piola–Kirchhoff stress in the loading direction. Therefore, the mean results will be presented in the following figures. The curve-fitting process was performed for every strain–stress curve and the hyperelastic constants were identified for every specimen. Then, the mean theoretical and experimental curves were determined and the mean constants were calculated for every considered hyperelastic model.

Fig. 5
figure 5

Strain–stress curves obtained for the six samples at the rate \(\dot{\lambda} = 10~\mathrm{min}^{-1}\)

Full size image

In order to decide which of the models best describes the hyperelastic contribution, also the relative error as a measure of the theoretical curve-fitting to the experimental one was calculated at every sampling point using the formula (Ogden et al. 2004):

$$ \mathit{err}_{i} = \frac{| ( S( t,\mathbf{p} ) )_{i} - ( \tilde{S}( t ) )_{i} |}{\max ( 0.5,| \tilde{S}( t ) | )}. $$
(19)

In Fig. 6(a) the values of mean error for every sample are shown for the considered models. In Fig. 6(b) the mean error versus time is presented for every hyperelastic model.

Fig. 6
figure 6

Distribution of mean relative error for the samples: versus hyperelastic models (a), versus time (b)

Full size image

In Fig. 7 the results of curve-fitting for the considered models are shown. Analysing Figs. 6 and 7 it can be easily noticed that the best hyperelastic model for the material of interest is either the Mooney–Rivlin (MR) or the Ogden model with N=4 (O4). The mean value of the relative error calculated over the entire curve-fitting time is approx. 8 % for MR and 5 % for O4 (Fig. 6(a)). However, the error at the end of the curve-fitting procedure is 0.76 % (MR) and 1.42 % (O4), whereas for the other considered models it is much higher (Fig. 6(b)), i.e. 7.66 % (Ogden N=2), 4.16 % (Ogden N=3), 5.82 % (Neo-Hookean) and 7.14 % (Yeoh). Thus, both Ogden with N=4 and Mooney–Rivlin models will be utilised to describe hyperelastic behaviour of the material. The values of hyperelastic constants for the best models are gathered in Table 1. These values will be the initial ones in the relaxation curve-fitting when the hyperelastic constants will be recalibrated and the viscous ones will be identified.

Fig. 7
figure 7

Mean second Piola–Kirchhoff stress in the load direction versus stretch ratio for the considered hyperelastic models: Ogden N=2 (a), Ogden N=3 (b), Ogden N=4 (c), Neo-Hookean (d), Yeoh (e), Mooney–Rivlin (f)

Full size image
Table 1 Hyperelastic constants of Ogden model (N=4) and Mooney–Rivlin model
Full size table

It should be noted that in Eq. (15) now m=8 for the model O4 and m=2 for the model MR. Whereas the constants κ i are equal: for Ogden model (N=4)—κ i =μ i (i=1,3,5,7), κ i =α i (i=2,4,6,8) and for Mooney–Rivlin model—κ 1=c 10,κ 2=c 01. Thus, the rank of vector p depends only on n, i.e. the number of relaxation times, which is to be determined in the next subsection.

5.2 Visco-hyperelastic model determination

The number of relaxation times n was determined on the basis of relaxation tests performed on the six samples. In Fig. 8, second Piola–Kirchhoff stress in the loading direction versus time in the relaxation tests is presented for all the samples. It can be seen that the stress distributions for all the samples, apart from sample 2, practically overlap.

Fig. 8
figure 8

Second Piola–Kirchhoff stress in the load direction versus time curves obtained in relaxation tests for all the samples

Full size image

Therefore, it was decided that the determination of the relaxation times would be based on one of the relaxation curves, i.e. relaxation curve for sample 6. The discrepancy between the curve of sample 2 and those of the rest of the samples results in inaccurate experiment realisation.

In Fig. 9, a graphical representation of relaxation times and characteristic amplitudes identification is presented for the two considered models. In the course of the calibration, also the Mooney–Rivlin and Ogden hyperelastic constants were newly identified. The values of the constants are shown in Table 2.

Fig. 9
figure 9

Graphical representation of relaxation curve-fitting: for Ogden model (N=4) (a), for Mooney–Rivlin model (b)

Full size image
Table 2 Constants of Ogden model (N=4) and Mooney–Rivlin model calibrated on the basis of relaxation test
Full size table

The error calculated by Eq. (19) versus the experiment time is shown in Fig. 10. The mean value of the relative errors equals 3.07 % for the model O4 and 2.73 % for the model MR, whereas at the end of curve-fitting procedure they were 2.99 and 2.95 %, respectively. The values of the relative errors indicate very good fitting of the theoretical curves to the experimental ones.

Fig. 10
figure 10

Relative error versus relaxation test time: Ogden model (N=4) (a), Mooney–Rivlin model (b)

Full size image

In order to formulate more reliable constitutive equation for the material, the hyperelastic constants were recalibrated as well as were the characteristic amplitudes by fitting the theoretical curves to those obtained in the loading/unloading compression tests performed at three strain rates, i.e. \(\dot{\lambda} = 0.1~\mathrm{min}^{- 1}, \dot{\lambda} = 1~\mathrm{min}^{ - 1} \) and \(\dot{\lambda} = 10~\mathrm{min}^{ - 1}\). The calibration was conducted at the three rates simultaneously. The relaxation times were set constant. The strain rate span is quite wide, which allows to formulate a more general constitutive law.

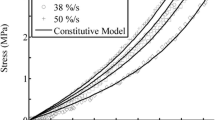
In Figs. 11 and 12 graphical representations of the curve-fitting for the Ogden (N=4) and the Mooney–Rivlin model, respectively, are presented. The stress here is represented by the mean second Piola–Kirchhoff stress in the load direction. The experimental hysteresis and the theoretical match are presented separately for each strain rate.

Fig. 11
figure 11

Mean second Piola–Kirchhoff stress in the load direction versus time representing curve-fitting for the three strain rates (Ogden model (N=4)): \(\dot{\lambda} = 0.1~\mathrm{min}^{- 1}\) (a), \(\dot{\lambda} = 1~\mathrm{min}^{ - 1}\) (b) and \(\dot{\lambda} = 10~\mathrm{min}^{ - 1} \) (c)

Full size image
Fig. 12
figure 12

Mean second Piola–Kirchhoff stress in the load direction versus time representing curve-fitting for the three strain rates (Mooney–Rivlin model): \(\dot{\lambda} = 0.1~\mathrm{min}^{- 1}\) (a), \(\dot{\lambda} = 1~\mathrm{min}^{ - 1}\) (b) and \(\dot{\lambda} = 10~\mathrm{min}^{ - 1}\) (c)

Full size image

For the model O4 the mean relative error values of the experimental curve-fitting for the three strain rates, i.e. \(\dot{\lambda} = 0.1~\mathrm{min}^{ - 1}, \dot{\lambda} = 1~\mathrm{min}^{ - 1} \) and \(\dot{\lambda} = 10~\mathrm{min}^{ - 1}\), equal 14.13, 19.69 and 24.20 %, respectively. The values of the relative error for the same strain rates for the model MR equal 8.2, 13.2 and 18.1 %, respectively. The final values of the visco-hyperelastic constants are listed in Table 3.

Table 3 The visco-hyperelastic constants of Ogden model (N=4) and Mooney–Rivlin model recalibrated on the basis of the loading/unloading compression tests at the three strain rates, i.e. \(\dot{\lambda} = 0.1~\mathrm{min}^{ - 1}\), \(\dot{\lambda} = 1~\mathrm{min}^{ - 1}\) and \(\dot{\lambda} = 10~\mathrm{min}^{ - 1}\)
Full size table

In the constitutive model (12) the number of relaxation times is equal n=6 for the Ogden and n=7 for the Mooney–Rivlin model. The values of relaxation times τ i are shown in Table 2 whereas the visco-hyperelastic constants μ p ,α p (p=1,…,8),c 10,c 01 and characteristic amplitudes g i are presented in Table 3.

In order to validate the formulated constitutive laws for the polyurethane, the theoretical relaxation curve and the experimental one were graphically compared (Fig. 13). The theoretical relaxation curves are represented by Eq. (13). The constants in the equation were taken from Table 2 (relaxation times) and Table 3 (hyperelastic constants and characteristic amplitudes).

Fig. 13
figure 13

Validation of the constitutive law for the polyurethane nanocomposite: Ogden model (N=4) (a), Mooney–Rivlin model (b)

Full size image

6 Conclusions and perspectives

In the paper, visco-hyperelastic constitutive models were determined for the polyurethane nanocomposite, which is to be implemented as one of the components of the intervertebral lumbar disc. In the first step of the formulation, two pure hyperelastic models were established for the material in interest. On the basis of uniaxial compressive tests performed at the rate \(\dot{\lambda} = 10~\mathrm{min}^{ - 1}\) the hyperelastic constants of the Ogden (N=4) and the Mooney–Rivlin models were determined. This was done using the code written in Matlab which realised the Levenberg–Marquardt algorithm for minimising the distance between the measured point data and the theoretical one (Sun and Yuan 2006). It seems that the Ogden model a little bit better simulates the hyperelastic behaviour than the Mooney–Rivlin model. However, the visco-hyperelastic simulations showed that the models are rather equally good to sufficiently simulate the rheological behaviour of the material.

In the second step, the non-linear theory of viscoelasticity was utilised to formulate visco-hyperelastic constitutive formulae. Here also, the number of relaxation times as well as characteristic constants was determined on the basis of the relaxation test data. In the process of constant identification the same optimising procedure was used. However, the procedure was modified so that it determined the needed number of relaxation times. Next, having set the values of the characteristic times from the relaxation tests, the other visco-hyperelastic constants were recalibrated on the basis of compressive tests performed with the loading and unloading phases (hysteresis effect) at three strain rates, i.e. \(\dot{\lambda} = 0.1~\mathrm{min}^{ - 1}, \dot{\lambda} = 1~\mathrm{min}^{ - 1} \) and \(\dot{\lambda} = 10~\mathrm{min}^{ - 1}\).

The general approach based on the formulation or selection of a potential function to derive the constitutive equation is very common and is willingly used especially in the cases of biological tissues and materials (Pioletti and Rakotomanana 2000; Fung 1993; Weiss and Gardiner 2001). Some of the researches are related to viscoelastic constant identification from relaxation tests and constant strain rate tests, e.g. Haut and Little (1972). However, in the present study the relaxation times are set constant and their values are established a priori. The advantage of the approach presented in the paper is that the number of the relaxation times and the characteristic constants in the Prony series is determined from best theoretical relaxation curve-fitting. The formulated constitutive laws are valid for wide range of strain rates, take into account long-term viscoelastic effects and model also the hysteresis loop. The material in the study is considered incompressible and isotropic. The former assumption was proved in the paper; the latter is rather obvious since the material is produced by casting method and the nanoparticles are uniformly distributed in the matrix.

It seems that combination of the theory to calculate numerically the hereditary integral and that incorporating the algorithm of determination of relaxation times works fine. The curve match for the three strain rates is good considering the fact that the hysteresis loop was simulated. The combination allows one to formulate a constitutive law for quite a wide strain rate range, which also describes the relaxation phenomenon.

The validation of the obtained constitutive laws presented graphically in Fig. 12 shows that after recalibration of the visco-hyperelastic constants the modelled curve does not correspond perfectly to the experimental relaxation curve. This might be due to the fact that the recalibration process was carried out on the basis of the hysteresis curves obtained experimentally at the three strain rates simultaneously. In addition to this, the strain rate span was considerably wide. This also might have affected the validation. However, it seems that the overall character of the relaxation process is modelled by the constitutive law sufficiently well.

The final values of the hyperelastic constants seem to be too low. Shear modulus G calculated from formula

$$ G = 2( c_{10} + c_{01} ) $$
(20)

is equal approximately G=12.22 MPa. The same shear modulus can be calculated also by means of the Ogden model constants:

$$ G = \frac{1}{2}\sum_{p = 1}^{8} \mu_{p}\alpha_{p}. $$
(21)

The value of G so calculated is equal approximately G=14.20 MPa. From measurements of the deformation in the longitudinal and transverse directions Poisson’s ration was calculated. Its approximate value is ν=0.45. Now, incorporating the very well-known equation relating G in terms of E and ν, one can calculate Young modulus of the material. Its value is about E=21 MPa. It seems to be quite low, especially in comparison to that of polyethylene, which is 990 MPa (Maksimov et al. 2004). Polyethylene is the material usually used as an inlay in intervertebral disc prostheses.

The further studies will concentrate on enhancement of mechanical properties of the material. It can be done by changing the amount and/or the kind of nanoparticles, by changing the chemical composition of the matrix, or by changing both the nanocomposite components’ characteristics. Such alterations would affect the values of the material constants but would not affect the general mechanical response of the nanocomposite to loading. It is believed that the formulated constitutive laws will be valid also for the nanocomposite of the same type but with different amount of nanoparticles.

The next step of the study is focused on implementation of the constitutive model in a finite element (FE) system. Nonlinear FE analyses are solved such that a configuration close to a known equilibrium state, which allows for a balance between incrementally applied load and the current stress field in the material, is searched. In this case, the elasticity tensor has to be derived and implemented in the iterative solution process, see e.g. Weiss et al. (1996) and Suchocki (2011).

The material version of the elasticity tensor ℂ is derived from the second derivative of the strain energy function ψ with respect to the right Cauchy–Green deformation tensor C (Holzapfel 2000):

(22)

It has to be emphasised that the components of the 4th-order tensor ℂ in Eq. (22) are not constant. They vary in general as a function of C. The components of tensor ℂ are to be derived analytically or calculated by means of the code that is to be written according to the algorithm presented in Sun et al. (2008).