Adaptive topology optimization of fail-safe truss structures

Abstract

Avoidance of disproportionate and progressive collapse, often termed ‘fail-safe design’, is a key consideration in the design of buildings and infrastructure. This paper addresses the problem of fail-safe truss topology optimization in the setting of plastic design, where damage is defined as a moveable circular region in which members are considered to have zero strength for that particular load case. A rigorous and computationally efficient iterative solution strategy is employed in both the dual (member adding) and primal (damage-case adding) problems simultaneously, which allows cases of high complexity and many damage cases (maximum of 16290 potential members and 16291 damage cases) to be solved to the global optimum. Common member-based damage definitions (e.g. damage to any one member) are shown to be highly dependent on the nodal grid; in the limiting case completely negating the effect of the fail-safe constraints. The method proposed in this article does not have such limitations, enabling a more sophisticated and robust treatment of fail-safe design. Moreover, the global minimization and high resolutions create new benchmarks for the least-material designs of ‘fail-safe’ structures using rigid-plastic materials. A number of example structures are considered (short cantilever, square cantilever, multi-span truss), and the effects of damage radius, location, and structure rationalisation are discussed.

1 Introduction

High-profile cases of disproportionate collapse include Ronan Point apartment in 1968 (Pearson and Delatte 2005), Alfred P. Murrah Federal Building in 1995 (Tagel-Din and Rahman 2006), and the World Trade Centre buildings in 2001 (Bažant and Verdure 2007). Such events often lead to changes in regulatory requirements (e.g. European Committee for Standardization 2006; U.S. General Services Administration 2013), as well as increased attention among the engineering community. Accordingly, resistance to the effects of disproportionate collapse is now an important consideration in structural design.

Whilst significant advancements have been made in the field of structural optimization over recent years, optimal structures by their very nature possess low, if any, redundancy. This problem was neatly articulated in the 1858 poem The wonderful “one-hoss-shay” (Holmes 1858), where the titular one-horse carriage, made such that the weakest part was “as strong as the rest”, catastrophically failed after 100 years of use, “All at once, and nothing first, just as bubbles do when they burst”.

To avoid such catastrophic failures, there is a clear need to develop accurate and computationally efficient tools to improve the resilience of optimal structures against disproportionate collapse. This paper investigates such an approach, termed ‘fail-safe truss optimization’. Similar to the ‘member adding’ scheme (Gilbert and Tyas 2003; He et al. 2019), here a damage load case adding approach is developed in addition, which allows rigid-plastic problems of relatively large size (e.g., 16290 members, and 16291 damage cases) to be solved rigorously (i.e. guaranteeing the same solution as that obtained by solving the full problem with all damage load cases). Using this new approach, it will be shown that the problem inherent in continuum fail-safe optimization – i.e. defining a member for the purpose of applying failure – also becomes a challenge in fail-safe truss optimization when problems of topology (as opposed to sizing) optimization are considered.

The remainder of the paper is structured as follows: first, salient literature is reviewed in Sect. 2, then a basic formulation considering damage to a single member is outlined in Sect. 3, and is applied to a simple example in Sect. 4. From this, issues are identified which cause the per-member damage definition to be deemed impractical. Alternative means of defining damage cases are therefore proposed in Sect. 5. Due to the large size of the optimization problems given in both Sect. 3 and 5, adaptive working-set type approaches are described in Sect. 6, which allow these formulations to be solved for larger problem sizes. The efficacy of this approach is then demonstrated on a range of examples in Sect. 7, and conclusions are drawn in Sect. 8.

2 Literature Review

The terms progressive collapse and disproportionate collapse refer to events whereby damage to a relatively small part of a structure results in damage or collapse over a much larger area. Here, the term ‘disproportionate’ relates to the final magnitude — a disproportion between the triggering event and the resulting failure – whilst the term ‘progressive’ emphasises the mechanism by which this failure propagates through a structure (Starossek and Haberland 2010). Typical approaches to assess the likelihood of disproportionate collapse involve removal of a critical element and assessment of the damaged structure’s ability to resist the applied loading. This is inherently a dynamic problem (Pretlove et al. 1991), but static methods are often used to reduce computational demand via the use of dynamic amplification factors (Khandelwal and El-Tawil 2011; U.S. General Services Administration 2013; Ruth et al. 2006; McKay et al. 2012).

A related term, robustness, refers to the ability of a structure to avoid or mitigate the effects of progressive collapse, i.e. insensitivity to local failure (Starossek and Haberland 2011, p. 625). Robustness is typically achieved through the addition of redundancy and/or compartmentalisation (Masoero et al. 2013). It is worth highlighting the difference between use of this term in a progressive/disproportionate collapse context, and its use in a structural optimization context; the latter referring to cases where problem parameters are ambiguous or uncertain (Gabrel et al. 2014). When applied to structural topology optimization, this may also be termed Reliability-Based Topology Optimization (RBTO) (Kharmanda et al. 2004; Kim et al. 2006; Guest and Igusa 2008). This field focuses on the probability of failure under given uncertainties such as a change in Young’s modulus (material uncertainty), loading conditions, or geometric imperfections.

The problem of explicitly resisting disproportionate collapse is addressed in the field of structural optimization research under the terminology ‘fail-safe’ design, a term also common in the aerospace industry (Niu 1999). In contrast to RBTO, fail-safe topology optimization focuses on ensuring the performance of the optimized structure after damage has occurred, i.e. damage to any one structural member should not cause global failure to occur. This is problematic in the context of topology optimization as structural members are not defined in advance and emerge only as the optimal design is calculated. This was addressed by Jansen et al. (2014) via the ‘failure-patch approach’, where structural damage is introduced as a square void zone of pre-defined size, to be applied at every finite element grid individually, resulting in a computationally expensive problem. Zhou and Fleury (2016) extended this approach to 3D, and proposed reducing the number of required failure patches whilst imposing a maximum length scale to ensure the full cross-section of a member would be damaged. Ambrozkiewicz and Kriegesmann (2018) used an active-set method to reduce the number of damage cases, whilst Wang et al. (2020) used the stress in the structure to guide the selection of which damage cases to include. Hederberg and Thore (2021) allow the damage patches to move, using a ‘moving morphable components’ approach, allowing the optimizer to identify critical failure locations.

These methods are each based on continuum topology optimization, and output structures formed in a single piece of material. For larger structures, such as buildings, it is usual to assemble the structure from many smaller members. Therefore, truss based approaches, such as the ground structure method of Dorn et al. (1964), are typically more appropriate. Whether obtained through numerical methods or analytically from the Michell-Hemp optimility criteria (Michell 1904; Hemp 1973), optimized truss forms are always statically determinate, with no structural redundancy. This is intuitive, as the most efficient load path will be used, and any others neglected; but it does mean that all members become critical, with any one member’s removal causing failure by mechanism.

The idea of fail-safe truss optimization was proposed by Sun et al. (1976). As it is necessary to consider the full structural response under every prescribed damage condition, the size of the optimization problem grows rapidly, thus the problems which could be solved were significantly limited by the computational resources available (up to 72 bars, 5 damage cases). Feng and Moses (1986) defined the term ‘residual strength index’ as the ratio between the strength of the system after structural damage has occurred and strength of the undamaged system. In general, residual strength index is taken as 0.667 to 0.8 (Feng 1988) for modest damage cases, i.e. single members. Frangopol and Curley (1987) also highlight the importance of the material’s ductility in the calculation of damage effects, but again the need to re-calculate structural response under each damage case limited the size of problems which were addressed.

With the power of modern computing technology, interest in computational optimization is increasing substantially. Mohr et al. (2014) developed a method to explicitly obtain truss structures with a specific degree of redundancy. This approach generates multiple complete structures within the design domain, which are then combined to form a resulting structure which can withstand removal or damage to the entirety of a given sub-structure. Compared to formulations explicitly requiring the damage of a single member, this is likely to be over-conservative. Kanno (2017) sets the problem of redundant optimization in the context of reliability based optimization, with the uncertainty being in which of the members are damaged in the worst case. The results show that, in the optimal solution, multiple damage cases may be equally critical.

Lüdeker and Kriegesmann (2019) included bending capacity in the structural members of their structures, which is of particular interest as the use of bending capacity is often one of the most practical methods used to provide resistance to disproportionate collapse. However, of the examples considered, the obtained structures are mainly loaded axially. Stolpe (2019) proposed a working-set methodology to reduce the number of damage conditions which must be considered simultaneously. As only compliance optimization was considered, globally optimal solutions (for the prescribed ground structure) could be obtained, and the proposed working-set method maintained this. The method was used to solve problems with up to 272 members and 36856 cases (i.e. degradation of any 2 members) which required up to 13150 s CPU time, whilst for the more typical problems where damage is inflicted to any 1 member (i.e. 272 cases) the CPU time required was 193 s. This approach was extended to incorporate constraints on eigen-frequency and stresses by Dou and Stolpe (2021, 2022), and it was noted that the combination of stress constraints and elastic compatibility resulted in a singularity-like effect, where partial damage to members resulted in a higher objective value than complete damage. The problems considered in these three papers use mainly adjacent-connectivity ground structures – i.e. structural members exist only horizontally, vertically and at $\pm 45^\circ$ – thus they fall mainly into the category of lattice size optimization, rather than allowing true optimal truss layouts to be obtained.

Kirby et al. (2022) obtained analytical solutions for fail safe design of simple structures subject to the complete damage of one or more members. Both minimum compliance and minimum volume problems were considered. It was found that, as the resolution increased, the fail-safe designs tended towards the form of the non-fail-safe result.

The fail-safe truss optimization studies mentioned above assume that the structure is constructed from a linear-elastic material; in some cases stress constraints are introduced to ensure this, whilst in other studies it is simply assumed. Yet, as noted by McKay et al. (2012), it is both common in practice and can produce more efficient designs if the plastic range is used. Therefore, standard linear-elastic finite-element models which are commonly used in structural design practice today (especially at the conceptual design stage) would not be appropriate for this application. More suitable are the detailed analysis methods specifically designed for use on damaged structures. These often use elasto-plastic material models, leveraging the plasticity found in most common construction materials to allow for re-distribution of loads to alternative load-paths. These advanced approaches can also integrate material non-linearities and realistic damage models to give an accurate depiction of the structure at failure. However, such analyses can take hours to run, placing them well beyond the scope of integration within an optimization process.

To provide a computationally tractable formulation for an optimization problem, a simplified model must be adopted. In the aftermath of an extreme event which has damaged the structure, ultimate limit states (e.g. strength) are likely to be of greater importance than serviceability limit states (e.g. deflection limits). The rigid-plastic material model aims to represent the ultimate limit state, whilst maintaining computational simplicity. As this is a simplified model, it is important to be aware of the limitations and assumptions, for example the assumption that unlimited plastic deformation is permitted, or the lack of an explicit damage model. More advanced analysis methods should therefore be used to verify designs, especially during the detailed design phase of a project.

For truss layout optimization, rigid-plastic material models are also attractive as they result in computationally efficient linear programming problems, and permit the use of the member-adding method (Gilbert and Tyas 2003; Pritchard et al. 2005; Sokół and Rozvany 2013; He et al. 2019) which can further reduce the computational effort required. For these reasons, rigid-plastic materials will be assumed here.

3 Basic methodology

In this section, a simple formulation for fail-safe truss optimization will be proposed which is based on the standard layout optimization formulation for rigid-plastic materials. The standard plastic layout optimization formulation for a problem with m potential members, n nodes and a load case set ${\mathbb {F}}$ can be written as:

where k is the load case index; ${\textbf{a}} = [a_1, a_2, ..., a_m]^T$ is a vector of optimization variables representing the cross-section area of each potential truss bar, and ${\textbf{q}}_k = [q_{1,k}, q_{2,k}, ..., q_{m,k}]^T$ is a vector of optimization variables representing the axial force in each potential truss bar in case k. The vector ${\textbf{l}} = [l_1, l_2, ..., l_m]^T$ contains the lengths of each potential truss bar, while the plastic yield stress of the material is given by $\sigma _+$ and $\sigma _-$ in tension and compression respectively. The vector ${\textbf{f}}_k = [f^x_{1,k}, f^y_{1,k}, f^x_{2,k}, ..., f^y_{n,k}]$ contains the external forces applied at each node in the x and y directions and ${\textbf{B}}$ is an equilibrium matrix containing direction cosines.

The formulation is now modified to ensure that failure in any one member does not lead to collapse of the frame. This requires that a statically admissible set of bar forces in the (remaining) members is possible for each damaged member. This is implemented with each damage-case acting much like the different load-cases in (1); a separate set of bar forces ${\textbf{q}}_k$ is defined for each, and equilibrium and yield constraints are independently imposed. Scaling of ${\textbf{f}}_k$ could be undertaken for damaged cases to provide an implementation of dynamic amplification factor, but for simplicity this is neglected here. Thus, the external forces ${\textbf{f}}_k$ will no longer vary from case to case, and will be simply denoted as ${\textbf{f}}$.

In this paper, damage to any member is assumed to be complete, leaving the member with no force-carrying capacity. Therefore, damage to members is modelled by setting the axial force, $q_{i,k}$, to zero in the relevant case. For simplicity, it is assumed that the indices of potential members and their relevant damage case correspond, i.e. that member k is damaged in case k.

The fail-safe optimization problem can now be written as:

where the new constraint (2e) imposes that the $k^\text {th}$ bar carries no force in case k. The set ${\mathbb {C}} = \{1,2,3,...,p\}$ contains p damage load cases (in this case p = m). Note that partial reduction in member capacity could be introduced by replacing (2e) with yield constraints modified with the desired damage factor applied to a. However, unlike the elastic case considered by Dou and Stolpe (2021, 2022) there are no compatibility constraints to cause the existence of singularities, and so full damage is expected to be the critical case.

It is conceptually simple to extend (2) to also consider multiple non-damage load cases as in classical layout optimization problems; however, for sake of simplicity, this extension is not considered here.

It should also be noted, that the problem (2) is substantially larger and more computationally challenging than (1). With a single load-case and a fully connected ground structure ($m \mathop {\propto }\limits _{\sim }n^2$), problem (1) requires $2m \mathop {\propto }\limits _{\sim }n^2$ variables and up to $2m + 2n \mathop {\propto }\limits _{\sim }n^2$ constraints. Meanwhile, (2) requires $m + m^2 \mathop {\propto }\limits _{\sim }n^4$ variables and $m(2m+2n+1)\mathop {\propto }\limits _{\sim }n^4$ constraints. Thus, problem (2) also increases in size at a much faster rate as the number of nodes increases.

4 A (de-)motivational example

Fig. 1

Short cantilever example: Results with three-bar ground structure (a) problem definition, (b) Nominal design, (c) Fail-safe plastic design, (d)-(f) Forces in the fail-safe plastic design for each damage case

Fig. 2

Short cantilever example: Convergence of form with increasing nodal resolution. Note that even the largest bars represented here have cross-sectional areas of less than $0.1\frac{F}{\sigma }$, whilst the bars of the nominal designs have cross-section area $0.707\frac{F}{\sigma }$, and of the three-bar fail-safe design have areas up to $1.414\frac{F}{\sigma }$

Fig. 3

Short cantilever example: Results with extended design domain and nodal spacings of (a) L, (b) $\frac{L}{8}$, (c) $\frac{L}{128}$

Fig. 4

Short cantilever example: Solutions of problems with increasing nodal resolution. (a) optimal volume, (b) Time taken to solve problem

Stolpe (2019, section 1.2) describes a motivating three-bar truss example equivalent to that shown in Fig. 1a. The ground structure consists of three potential truss bars, and the material to be used has the same plastic yield stress in tension and compression, which will be denoted as $\sigma$. This example will now be used to demonstrate that, as the resolution of the problem increases, it becomes ineffective to define damage based on the removal of a single member.

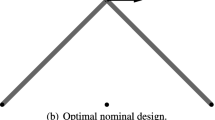
A non-fail-safe, or nominal, design (such as may be obtained by (1)) uses just two of the potential truss bars, as shown in Fig. 1b. In the nominal design each bar has area $\frac{\sqrt{2}}{2}\frac{F}{\sigma }$, giving a total volume of $2\frac{FL}{\sigma }$.

If the same problem is solved using the fail-safe formulation, (2), then the obtained solution is as shown in Fig. 1c. This has a volume of $5\frac{FL}{\sigma }$, over twice that of the nominal design. Note that this solution is slightly different to the compliance-based optimal fail-safe design given by Stolpe (2019), where all three bars were found to take equal cross-section areas; a detailed discussion of the reasons for this may be found in Appendix 1.

The bar forces in the fail-safe structure for each damage case are shown in Fig 1d–f. However, this 3-bar problem cannot truly be said to be a problem of layout optimization. To provide insights into optimal layout for this problem, it will be prudent to follow the advice of Rozvany (2009), who suggests examining the behaviour of the problem as the resolution is increased and extrapolating this to the case with infinite resolution. In Figs. 2, 3 and 4 the line support is extended to a distance of 2L above and below the level of the force application; and is discretized with an increasing number of equally spaced nodes (located on the support line only, c.f. Fig. 9). It can be observed that the solution is tending towards the volume of the nominal solution, $2\frac{FL}{\sigma }$. Furthermore, using the extrapolation scheme proposed by Darwich et al. (2010), the extrapolated volume for the infinite-resolution problem lies within 0.07% of the nominal volume.

In the limiting case of infinitesimal nodal spacing, these results suggest an optimal form consisting of two ‘bundles’ of infinitesimally thin members, connecting the loaded point to points on the support line which are infinitesimally close to elevations of $\pm L$. This structure therefore becomes almost identical to the nominal solution in Fig. 1a, but with each member replaced by a bundle of infinitesimal members, thereby bypassing the per-member damage requirement.

Further examples, which will be shown in Section 7, will demonstrate that this is not a problem-specific issue, but applies to many scenarios. Furthermore, a similar effect was observed by Kirby et al. (2022) in the optimization of fail-safe structures using elastic material, implying that this is likely to be a ubiquitous feature of optimal fail-safe designs when structural freedom is increased.

If the fail-safe design is being sought principally for reasons of fracture resistance (as in the cases of Kirby et al. 2022), then structures using bundles of members following the nominal solution may be an appropriate and efficient solution. However, disproportionate collapse in buildings is typically caused by accidental actions, e.g. explosions or impacts. In these cases, it is the spatial separation which differentiates one member from another, rather than material boundaries. Therefore, in a building design context, the bundles would likely be considered as a single member, and such designs would not be acceptable. To address this issue, the following section will describe alternative approaches to define damage cases.

5 Definitions of damage

The previous section showed that the common, per-member, definition of damage is not appropriate for use in problems of topology (rather than size) optimization. This section will describe a fail-safe layout optimization formulation with a more general definition of damage. Specific damage cases which will be used in Section 7 will also be outlined.

To define a general damage case k, the set ${\mathbb {D}}_k$ will be used; this set contains the indices of each member that is damaged in case k. This allows the general fail-safe optimization problem to be written as:

where ${\textbf{D}}_k$ is a diagonal matrix, where each element $d_{i,i}^k$ is given by:

$$\begin{aligned} d_{i,i}^k = \left\{ \begin{array}{ll} 1, \quad \text {if } i \in {\mathbb {D}}_k\\ 0, \quad \text {otherwise.} \end{array} \right. \end{aligned}$$

(4)

This will result in (3e) containing many constraints of the form $0=0$, which may be removed.

Fig. 5

Damage case defined by point $p_k$ and radius $r_k$. Thicker black members show those damaged in the given load-case, whilst thin grey members are undamaged. For this damage case, $\mathbb {D}_k$ would contain the indices of the members shown with thick black lines

Table 1 Some terminology and methods based on the sequential addition of violated (primal or dual) constraints to a reduced master problem

Note that (3) is a generalisation of (2), and the per-member damage can be implemented by generating damage cases:

$$\begin{aligned} {\mathbb {D}}_k = \{k\} \forall k \in 1, 2, ..., m \end{aligned}$$

(5)

for a problem with m potential members.

In general, the sets ${\mathbb {D}}_k$ can be chosen arbitrarily, allowing great flexibility in describing damage appropriate to a scenario. In this paper, the main approach used will be to simultaneously damage all members which lie within a circle defined by a point $\textrm{P}_k$ and a radius $r_k$. Formally,

$$\begin{aligned} {\mathbb {D}}_k = \{i \mid \textrm{distance}(\textrm{P}_k, i) \le r_k \ \} \forall k \in 1, 2, ..., p \end{aligned}$$

(6)

where p is the number of damage-cases. The function $\textrm{distance}(\textrm{P}_k, i)$ is defined as the minimum distance between the point $\textrm{P}_k$ and the line segment which is the center-line of the potential member with index i. The values of $\textrm{P}_k$ and $r_k$ must be defined for each case k in advance. Here, $r_k$ will, for simplicity, be kept uniform for all k, and will thus be denoted by r. An example of a damage case defined in this way is shown graphically in Fig. 5.

This approach is somewhat similar to the ‘failure patch approach’ used in continuum methods (Jansen et al. 2014), although here the check on whether an element is within/outside the region is performed on the center-line only. However, we emphasise that the damage cases, represented by ${\mathbb {D}}_k$, may be chosen entirely freely by the user, allowing this framework to be used with any generic or problem-specific definitions for damage.

6 Adaptive solution strategies

6.1 Existing adaptive techniques

The optimization problems (2) and (3) may become intractable as the number of potential truss members and damage cases increases. This section will present solution strategies which can significantly reduce the computational cost.

Consider that a new constraint is to be added to an existing optimization problem, ${\mathcal {P}}$; if the new constraint is satisfied at the optimal solution to ${\mathcal {P}}$, then that same solution is also the optimum of the problem including the new constraint. Whilst this statement may appear trivial, it underpins a number of powerful techniques for solving large optimization problems. Table 1 outlines a number of methods which implement this principle. In this paper, we use the term ‘adaptive’ (see e.g. Sokół and Rozvany 2013; He et al. 2019) to cover all methods of this type.

In the remainder of this section, adaptive techniques will be applied to the solution of problem (3). In Section 6.2, the approach will be applied to add constraints to the dual problem, whilst in Section 6.3 adaptive techniques are applied to the primal problem. Finally, in Section 6.4, it is shown that these two techniques can be applied simultaneously.

6.2 Dual adaptivity (member-adding)

The member adding procedure was developed by Gilbert and Tyas (2003) and extended to multiple load-case problems by Pritchard et al. (2005) and He et al. (2019), whilst Sokół and Rozvany (2013) provide an alternative implementation. In this approach, a ground structure is generated from a sub-set, ${\mathbb {M}}'$, of the set of all potential members ${\mathbb {M}}$. Members in ${\mathbb {M}}'$ are said to be active, whilst those not in ${\mathbb {M}}'$ are inactive.

This approach is based on the dual of the standard layout optimization problems. The dual of problem (3) is written as:

$$\begin{aligned} \max _{{\textbf{u}}_k, {\textbf{y}}^+_k, {\textbf{y}}^-_k, {\textbf{z}}_k} \sum _{\forall k \in {\mathbb {C}}}({\textbf{f}}^T{\textbf{u}}_k) \end{aligned}$$

(7a)

$$\begin{aligned} \text {subject to } \big ({\textbf{y}}^+_k - {\textbf{y}}^-_k + {\textbf{z}}_k&= {\textbf{B}}^T {\textbf{u}}_k\big )_{\forall k\in {\mathbb {C}}} \end{aligned}$$

(7b)

$$\begin{aligned} \sum _{\forall k \in {\mathbb {C}}} (\sigma _+ {\textbf{y}}^+_k + \sigma _- {\textbf{y}}^-_k)&\le {\textbf{l}} \end{aligned}$$

(7c)

$$\begin{aligned} \big ({\textbf{y}}^+_k, {\textbf{y}}^-_k&\ge 0\big )_{\forall k \in {\mathbb {C}}} \end{aligned}$$

(7d)

where ${\textbf{u}}$ is a vector of optimization variables representing virtual deflections at each unsupported degree of freedom, ${\textbf{y}}^+_k$ and ${\textbf{y}}^-_k$ are vectors of optimization variables representing virtual extension in load case k. ${\textbf{z}}_k$ is a vector containing optimization variables $z_{i,k}$ where member i is damaged in case k ($i \in {\mathbb {D}}_k$), and zeros otherwise. Also note that constraints (7b)-(7d) are the Karush-Kuhn-Tucker (KKT) conditions of Problem (3), so if there is no constraint violation in the dual problem, the optimum solution is identified.

Problem (7) is identical to the dual of the nominal problem (2), with the exception of the addition of ${\textbf{z}}_k$. This change means that (7b) can be satisfied with $y_{i,k}^+ = y_{i,k}^- = 0$ whenever member i is damaged in case k. Thus the member adding procedure can be implemented in the same manner as for the nominal problem, but neglecting any cases in which the member under consideration is damaged.

As with the member adding process for the nominal problem, adding members will never increase the volume of the structure. Therefore,

$$\begin{aligned} V_{{\mathbb {M}}} \le V_{{\mathbb {M}}'} \end{aligned}$$

(8)

Where $V_{\mathbb {M}}$ is the optimal volume for a certain problem using a ground structure containing all members ${\mathbb {M}}$, and $V_{{\mathbb {M}}'}$ is the optimal volume for the problem when using a ground structure consisting of only the active set of potential members, ${\mathbb {M}}'$.

6.3 Primal adaptivity (damage-case adding)

Here, a concept similar to the member adding method will also be used to enable only a subset of the damage cases to be considered initially. The approach is also similar to the working-set approach used by Stolpe (2019) in the context of elastic optimization. Initially, the problem (3) is written using only a subset of the set of all required damage cases, ${\mathbb {C}}' \subseteq {\mathbb {C}}$, and this reduced problem is solved. Similarly to the member-adding process, damage cases in ${\mathbb {C}}'$ are referred to as active, and those not in ${\mathbb {C}}'$ as inactive.

Once the reduced problem is solved, it is easy to check if a potential damage case c (which was previously inactive) is violated. Firstly, the violation of damage case c is calculated separately for each active damage case $k\in {\mathbb {C}}'$, using the axial force values ${\textbf{q}}_k$ from the reduced problem, i.e.

$$\begin{aligned} \big (\gamma _{c, k} = \sum _{i\in {\mathbb {D}}_c} |q_{i,k}|\big )_{\forall k \in {\mathbb {C}}'} \end{aligned}$$

(9)

where $\gamma _{c,k}$ is the violation of damage case c under the internal forces condition of case k. If $\gamma _{c,k} = 0$ then the values in ${\textbf{q}}_k$ can be used as the values of ${\textbf{q}}_c$, and would satisfy all relevant constraints. Thus there is no need to explicitly add case c to the problem. Note that case c is appropriately addressed when there is at least one case k which provides a valid set of forces, so cases only need to be considered for addition when $(\gamma _{c,k}>0) \forall k\in {\mathbb {C}}'$. Thus the overall violation of case c is defined as

$$\begin{aligned} \beta _{c} = \min _{k \in {\mathbb {C}}'}\gamma _{c,k} \end{aligned}$$

(10)

As previously mentioned, only cases where $\beta _c > 0$ are violated and need to be added to the problem. Furthermore, to improve computational efficiency, only a limited number of load cases are added per iteration. To prioritise which cases should be added, this paper uses a simple heuristic based only on the values of $\beta _c$ and ${\mathbb {D}}_c$. This has been identified as an area where there is significant potential for future work to identify more effective heuristics to improve speed. It is important to note that changes to this heuristic will have no effect on the reported minimum volume¹, as long as all cases are checked and found to have no violation at the final iteration.

For the simple heuristic used here, the violated damage cases $\{c\mid \beta _c>0\}$ are first sorted in descending order of the value $\beta _c$, to give an ordered set ${\mathbb {V}} = (v_1, v_2, ...)$, where $\beta _{v_1} \ge \beta _{v_2}$ etc. Case $v_1$ (with the largest violation) is first added to the (initially empty) set ${\mathbb {A}}$, which will contain the set of damage cases added in this iteration. Then the remaining cases in ${\mathbb {V}}$ are considered in order; each case c is only added to ${\mathbb {A}}$ if over half of the damaged members in ${\mathbb {D}}_c$ are not damaged in any case currently in ${\mathbb {A}}$, i.e. if $|{\mathbb {D}}_c \cap (\bigcup _{k\in {\mathbb {A}}} {\mathbb {D}}_k)|\ge 0.5|{\mathbb {D}}_c|$ then c is added to ${\mathbb {A}}$. This prevents multiple damage cases – which have very similar effects on the structure – from being added simultaneously.

Here up to $\lceil \frac{p}{10}\rceil$ potential cases are added in each iteration, i.e. $|{\mathbb {A}}|\le \lceil \frac{p}{10}\rceil$, where $p= |{\mathbb {C}}|$. If there are insufficient violated cases in ${\mathbb {V}}$, or insufficient differences between these cases, then fewer cases may be added. The set of active cases ${\mathbb {C}}'$ is then updated by adding the contents of set ${\mathbb {A}}$, and the next iteration begins.

Note that when damage-case adding process is used, the volume of the structure will increase with each iteration, i.e.:

$$\begin{aligned} V_{{\mathbb {C}}} \ge V_{{\mathbb {C}}'} \end{aligned}$$

(11)

where $V_{\mathbb {C}}$ is the volume of the problem with all damage cases included, whilst $V_{{\mathbb {C}}'}$ is the optimal volume given by the problem with a subset, ${\mathbb {C}}'$, of damage cases included. At convergence, this relationship will be satisfied by equality.

6.4 Combined adaptivity

In previous approaches (such as the examples in Tab. 1), adaptive methods have been applied only to the primal or the dual problem. In this section, it will be shown that it is possible to employ the primal and dual adaptive processes simultaneously with only a few extra considerations. As the number of variables $q_{i,k}$ is proportional to the number of members multiplied by the number of cases, this new technique of applying both adaptive approaches simultaneously allows the procedure to be initialised using a comparatively very small problem. In this paper, problems using combined adaptivity will be initialised with a ground structure of adjacent connectivity, and only the undamaged case.

Fig. 6

Convergence characteristics, using optimal volumes ($V_{\mathbb {C}}^{\mathbb {M}}$, $V_{{\mathbb {C}}'}^{{\mathbb {M}}'}$, $V_{\mathbb {C}}^{{\mathbb {M}}'}$ and $V_{{\mathbb {C}}'}^{\mathbb {M}}$) of the four problems discussed in Section 6.4: (a) Closing the gap between lower and upper bounds via combined adaptivity (shaded area indicates primal and dual violations). When no violation is detected (i.e., $V_{{\mathbb {C}}'}^{{\mathbb {M}}} = V_{{\mathbb {C}}'}^{{\mathbb {M}}'} = V_{{\mathbb {C}}}^{{\mathbb {M}}'}$), the inequality conditions ensure that $V_{{\mathbb {C}}'}^{{\mathbb {M}}'} = V_{{\mathbb {C}}}^{{\mathbb {M}}}$ (i.e., the adaptive solution converges to that obtained by solving the full problem). (b) Convergence of example problem showing volumes of the four problems discussed in Section 6.4 for each iteration. Example problem is the short cantilever example (Sec. 7.1) with 45 nodes and damage radius 0.1L

The convergence of the combined adaptivity process initially appears strange, as the volume will variously rise and fall as the iterations progress. However, the solution upon convergence will still be identical to that obtained by considering all cases and all bars from the outset. To demonstrate why this must be the case, it is necessary to consider the solutions to four related problems:

• The full problem, with all possible damage cases ${\mathbb {C}}$ and all possible members ${\mathbb {M}}$ in the ground structure, having optimal volume $V_{\mathbb {C}}^{\mathbb {M}}$. Shown in black in Fig. 6.

• The sub-problem used in the combined adaptive process, with a subset ${\mathbb {C}}'$ of the damage cases and a subset ${\mathbb {M}}'$ of members in the ground structure, having optimal volume $V_{{\mathbb {C}}'}^{{\mathbb {M}}'}$. Shown in green in Fig. 6.

• A problem containing all damage cases ${\mathbb {C}}$ but only the active ground structure of members ${\mathbb {M}}'$, with optimal volume $V_{\mathbb {C}}^{{\mathbb {M}}'}$. Shown in red in Fig. 6.

• A problem containing only the active damage cases ${\mathbb {C}}'$ but with all potential members ${\mathbb {M}}$, with optimal volume $V_{{\mathbb {C}}'}^{\mathbb {M}}$. Shown in blue in Fig.6.

As it is known that adding members to the ground structure cannot increase the volume, from (8) the following inequality conditions hold:

$$\begin{aligned} V_{\mathbb {C}}^{\mathbb {M}}&\le V_{\mathbb {C}}^{{\mathbb {M}}'} \end{aligned}$$

(12)

$$\begin{aligned} V_{{\mathbb {C}}'}^{\mathbb {M}}&\le V_{{\mathbb {C}}'}^{{\mathbb {M}}'} \end{aligned}$$

(13)

Furthermore, since adding additional damage cases cannot decrease the optimal volume, from (11) the following inequality conditions hold:

$$\begin{aligned} V_{\mathbb {C}}^{\mathbb {M}}&\ge V_{{\mathbb {C}}'}^{\mathbb {M}} \end{aligned}$$

(14)

$$\begin{aligned} V_{\mathbb {C}}^{{\mathbb {M}}'}&\ge V_{{\mathbb {C}}'}^{{\mathbb {M}}'} \end{aligned}$$

(15)

These inequalities do not permit any conclusions to be drawn about the relative values of $V_{\mathbb {C}}^{\mathbb {M}}$ (the master problem volume) and $V_{{\mathbb {C}}'}^{{\mathbb {M}}'}$ (the adaptive problem) in the general case. This is demonstrated graphically in Figure 6b, where the green points (representing $V_{{\mathbb {C}}'}^{{\mathbb {M}}'}$) may be either above or below the black line (representing $V_{\mathbb {C}}^{\mathbb {M}}$). In particular, for the case shown, iteration 6 has an adaptive problem volume, $V_{{\mathbb {C}}'}^{{\mathbb {M}}'}$, which is higher than the master problem volume, $V_{\mathbb {C}}^{\mathbb {M}}$, whilst in other iterations the converse is true.

The inequalities (12)-(15) may however be combined as follows:

$$\begin{aligned} V_{{\mathbb {C}}'}^{{\mathbb {M}}}&\le V_{{\mathbb {C}}'}^{{\mathbb {M}}'} \le V_{{\mathbb {C}}}^{{\mathbb {M}}'} \end{aligned}$$

(16)

$$\begin{aligned} V_{{\mathbb {C}}'}^{{\mathbb {M}}}&\le V_{{\mathbb {C}}}^{{\mathbb {M}}} \le V_{{\mathbb {C}}}^{{\mathbb {M}}'} \end{aligned}$$

(17)

In other words, the volumes of both the master problem and adaptive sub-problem, $V_{{\mathbb {C}}'}^{{\mathbb {M}}'}$ and $V_{{\mathbb {C}}}^{{\mathbb {M}}}$, lie in a range bounded by $V_{{\mathbb {C}}'}^{{\mathbb {M}}}$ (lower bound) and $V_{{\mathbb {C}}}^{{\mathbb {M}}'}$ (upper bound). This is also illustrated in Fig. 6.

This range may be tightened to encompass just a single value when primal and dual violation are not present. Specifically, once the member adding checks have been completed without finding any violation, it is known that (13) is satisfied with equality. Then by combining with (14) it is found that:

$$\begin{aligned} V_{{\mathbb {C}}'}^{{\mathbb {M}}} = V_{{\mathbb {C}}'}^{{\mathbb {M}}'} \le V_{\mathbb {C}}^{\mathbb {M}} \end{aligned}$$

(18)

i.e. any solution where there are no members to add is a lower bound on the true solution

If the damage-case adding checks have been completed without finding any violation, then (15) must be satisfied with equality. Combining this with (12) gives:

$$\begin{aligned} V_{{\mathbb {C}}}^{{\mathbb {M}}'}&= V_{{\mathbb {C}}'}^{{\mathbb {M}}'} \ge V_{\mathbb {C}}^{\mathbb {M}} \end{aligned}$$

(19)

These two relationships can only be simultaneously satisfied when $V_{\mathbb {C}}^{\mathbb {M}} = V_{{\mathbb {C}}'}^{{\mathbb {M}}'}$, as is illustrated graphically in Fig. 6. Thus it is demonstrated that when a sub-problem has no violated members (in the dual problem) and no violated damage cases (in the primal problem), then its optimal volume will be identical to the optimal volume of the full problem.

Therefore, the only requirement to demonstrate convergence is that, in the final iteration, both the primal and dual adaptive processes are checked and find no violation. The choice of whether to add members and/or damage cases may be made freely at each iteration. In the examples which follow, potential members are checked and added to the ground structure at every iteration. Meanwhile damage cases are only checked/added when the volume decrease between the previous two iterations is less than 1%, due to the larger impact on problem size from the addition of damage cases. Final termination of the solution process occurs only when both checks find no violation.

6.4.1 Infeasible sub-problems

An issue which can arise when both adaptive methods are combined is that a damage case may be added when the members in the current ground structure are not sufficient to carry the loading in that case. When only one of the two adaptive processes are used, infeasible sub-problems generally only arise for situations wherein the full problem is also infeasible.²

To demonstrate the issue, consider the problem in Fig 7 (this is Example II of Stolpe 2019). The first iteration considers the members which give adjacent connectivity (shown solid in Fig 7) and only the undamaged case, the solution to this is two disconnected bars, as given by Stolpe (2019, Fig.3b), and this solution cannot be improved by adding any further members. Therefore the algorithm proceeds to add required damage cases.

Fig. 7

Parallel forces example: Demonstration of potential infeasible sub-problem. Potential members present in an adjacent connectivity ground structure are shown as solid lines, and other potential members shown as dashed lines. Potential members which would be damaged (have zero force) under a damage case affecting the green circle are shown in grey

Assume that the damage case indicated by the green circle in Fig. 7 is added in the next iteration, members which are damaged and cannot take any force in this case are shown in grey. The problem will thus become infeasible as only the lines in solid black are available to carry the loading in this damage case, and they go to a single point/hinge on the bottom chord below the damaged point. (If only the primal adaptivity is used, then both the solid black and dashed black lines would be available to carry this case, and the problem would still be feasible.)

When the primal problem is infeasible, the member adding process cannot proceed, as virtual displacements are not available. In the kinematic setting, the problem becomes unbounded, with one or more virtual displacements tending to infinity (i.e. moving freely and forming a mechanism). The Mosek (MOSEK ApS 2020) solver which is here used to solve the linear optimization problems will return an unbounded ray if it identifies that a problem is unbounded. In this case, the unbounded ray in the kinematic problem will describe the virtual displacements of a mechanism. For use of this approach with solvers which do not return this information, see the alternative approach in Appendix 2.

Table 2 Parallel forces example: solution progress. Bar thickness in Solution column represents bar area. Thick members in the violated members column are those to be added, thin members are those already in the ground structure. In the violated damage cases column, previously added damage cases are shown as filled circles, the damage case to be added is shown with a solid line, other violated damage cases are shown with dotted line

The virtual displacement values forming the unbounded ray can be used in the adaptive process in almost the same manner as the standard virtual displacements. The only change is that any non-zero virtual strain caused by displacements from a mechanism implies that the relevant bar has potential to improve the solution. This can be easily achieved by scaling the virtual displacements by some large value.

6.5 Step-by-step solution

To illustrate the process, the problem in Fig 7 will be solved, and the solutions shown at each step.

Damage cases will be defined as occurring at the central four nodes, with damage radius r of one fifth of the nodal spacing; in this scenario, this radius results in only members which connect to the node being damaged in each case. Note that damage points centered on either of the support points would result in an infeasible problem, as the remaining single point support would be inadequate to provide restraint. Similarly, damage centered on a loaded point would prevent that force from being supported, and thus would also result in an infeasible problem.

Fig. 8

Parallel forces example: solution with per-member damage

The nominal solution to this problem is two disconnected bars, as is obtained in iteration 1 of Tab. 2 (since the procedure is initialised with only the undamaged case), this has a volume of 6.00. Note that in both iterations 1 and 3, there are multiple equally-violated cases by the definition used here, thus it is arbitrary which is chosen for addition. The final solution has a volume of 15.50, over 2.5 times the volume of the nominal structure.

The problem has also been solved using the per-member damage definition (5), in this case the volume of the fail-safe structure is 14.41, a 140% increase over the nominal structure and the resulting structure is shown in Fig. 8. As expected, this is a slightly lower volume than was obtained for per-node damage (Table 2) as the per-node damage requirement is more onerous (i.e. involves damage to multiple members simultaneously). In the results of Stolpe (2019), the objective function increased by 190% from the nominal to the fail-safe design under complete damage to 1 member. Both the results of Kanno (2017) and Stolpe (2019) for this problem appear to be doubly symmetric, however the solution using the plastic formulation used here does not have a vertical axis of symmetry. It is possible that this may be caused by the existence of multiple equally optimal solutions, but this has not been investigated further here.

7 Examples

7.1 Short cantilever

The short cantilever problem from section 4 will now be revisited using the methods described in Sections 5 and 6. As these approaches allow larger problems to be solved, the more general problem will be considered, with nodes spread throughout the design domain, rather than just along the support line as previously.

Fig. 9

Short cantilever problem: Comparison between various definitions of damage. (a) volumes using various damage definitions. (b)-(e) optimal solutions with $11\times 21$ grid of nodes and various damage definitions: (b) per-member damage cases ($p=16290$), (c)-(e) damage at points on a $6\times 11$ grid ($p=66$) with (c) $r=0.1L$, (d) $r=0.15L$ and (e) $r=0.25L$

Fig. 10

Short cantilever problem: (a) CPU time taken to solve problem with per-member damage and various resolutions, solution speed with and without adaptive methods. (b) Number of members and damage cases considered at each iteration of the adaptive solution process for the case with 231 nodes - i.e. the largest result in part a - for which the full problem contains 16290 potential members and 16291 potential damage cases

Firstly, the adaptive solution method will be used with damage cases defined individually for each member in the ground structure, i.e using damage cases defined by (5). Nodes are spread on a Cartesian grid with equal spacings in the x and y direction, whilst the domain is taken to extend a distance of L above and below the elevation of the load. Figure 9 gives the volumes as the resolution is increased. As previously, it can be seen that the results tend towards a volume of 2 as resolution is increased; qualitatively, the structure again tends towards ‘bundles’ of members following the lines of the nominal solution (c.f. Fig. 9b and 1b).

Figure 9 also shows results for the same problem with damage defined using circular damage regions applied at points on a regular $6\times 11$ grid. Due to the unevenness of the convergence (caused by the interaction between the node spacing and damage locations) the extrapolation method of Rozvany (2009) and Darwich et al. (2010) has not been employed here. Nonetheless, it can be seen that, as resolution increases, these solutions are converging towards solutions distinct from the original, nominal result.

To quantify the effectiveness of the proposed solution strategies proposed in Sect. 6, the problem with per-member damage cases has been solved with and without the various adaptivity methods. In all cases, identical values for the optimal volume were obtained using every strategy, verifying the reasoning in Sect. 6. Fig. 10a shows the time taken using each method. It can be seen that for all but the smallest problems, the combined adaptivity strategy is the fastest; in the largest case solved using all approaches (66 nodes, i.e. a $6\times 13$ grid) the combined adaptivity process reduces the time required by a factor of 41 (43 s compared to 1774 s $\approx$ 30 minutes without adaptive methods).

Note also that the non-adaptive approach could not be used for the larger problem sizes. This is not due to the time taken, but rather the amount of memory required to hold the full problem. The largest problem solved here using the non-adaptive method used a $6\times 11$ grid of nodes, resulting in a problem with 1361 members, and 1362 damage cases; this problem required approximately 8GB of memory, whilst a problem with a grid of $7\times 13$ nodes would imply a problem requiring some 43GB of memory. Meanwhile the largest problem solved using the adaptive strategy involved a grid of $11\times 21$ nodes, allowing 16290 potential members, and 16291 potential damage cases; yet the largest sub-problem explicitly solved required just 1765 members and 305 damage cases, the size of each sub-problem solved can be seen in Fig. 10b.

The problem was also solved using the primal/dual adaptive strategies individually. Using the primal adaptive (damage-case adding) strategy only resulted in a moderate reduction in time taken (up to a factor of 4). Conversely, using the dual adaptive (member adding) strategy alone actually increased the time taken in many cases. This is because this strategy involves solving multiple problems which each contain all of the damage cases and are therefore much larger than those solved when primal adaptivity is used.

7.2 Square cantilever

This example is based on Example III of Stolpe (2019), comprising a square $9\times 9$ grid of nodes at unit spacing, with supports on the left side and a downwards force on the bottom right corner. The problem is initially solved using a ground structure allowing only adjacent connectivity, see results in Table 3 and Fig. 11. Imposing per-member damage in this case increases the structure’s volume by 66% above the volume of the nominal solution. In the elastic solution of Stolpe (2019), imposing complete failure of a single member was found to increase worst-case compliance by 55%.

If the ground structure is now permitted to contain all non-overlapping connections between nodes (as shown in Table 3), then the imposition of fail-safe constraints for a single member failing results in an increase in volume of just 17%. From the solution shown in Table 3, it can be seen that this structure is again approaching the form of the associated nominal solution, with nearly coincident members again leading to the formation of ‘bundles’ following the form of the nominal structure.

Fig. 11

Square example: Volumes for fail-safe structures with various connectivity and damage radius

Table 3 Square example: Results with different damage conditions with various damage definitions. Volume changes given based on the relevant nominal design. For point-based damage, all damage cases present in the final iteration are shown

The problem will now be considered with damage cases based on circles about points. The points $p_k$ defining the damage cases will be spread over a grid with half the nodal spacing of the nodes in the ground structure; this means that, in the adjacent connectivity case, the intersections of two diagonal members will be the center of a damage case. Initially the damage radius r will be set to $0.353\approx \frac{\sqrt{2}}{4}$, i.e. the largest damage radius such that members at a 45$^\circ$ are not removed by damage points centred midway between two (horizontally or vertically adjacent) nodes. The results of this for both adjacent and full connectivity ground structures are shown in Table 3, along with the set ${\mathbb {C}}'$ of damage circles which were active in the final iteration. It can be seen that, for the adjacent connectivity ground structure, damage applied to nodes or at the intersections of two diagonals were almost always deemed more critical than damage halfway along a horizontal or vertical member.

This problem is very sensitive to the damage case applied just above the loaded point. With the damage radius used here, $r=0.353$, the damage case applied directly above the load removes all members connected to the loaded point and at an angle less than $45^\circ$ to the vertical. Any increase in r will also remove the bar at $45^\circ$; for the adjacent connectivity ground structure, this will result in an infeasible problem, as now only the horizontal member connects to the load. For the full connectivity ground structure, a bar at a shallower angle can be used. However, as shown in Fig. 11, this results in a sudden volume increase of 28% when $r = \frac{\sqrt{2}}{4}$, and a continuing rapid increase in volume beyond this point.

Fig. 12

Square example: Results fully connected ground structure and damage applied at points on left edge only, (a) $r=0.353$, (b) $r=1.55$

To provide results which are less susceptible to this sensitivity, this problem has been run with just the left-most column of damage cases. Results are shown in Fig. 12, with the volumes again plotted in Fig 11. Observe that there is now a high level of sensitivity to the number of support points which may be removed simultaneously, with sudden jumps in volume at $r = 0.5, 1, 1.5$ (i.e. when damage cases can remove 2, 3 and 4 support points simultaneously).

7.3 Multi-span structure

The final example concerns a multi-span structure, resembling a transfer truss or bridge. The geometry of the problem, as well as the nominal solution, is shown in Fig. 13.

For comparison purposes, a simple manual approach has been undertaken, approximating a real-world process. First, single load-case results were found for manually chosen key damage cases; in this scenario damage cases centered on each support point have been used (Fig 14a-b, and mirror images thereof). These four structures are then combined by taking the largest area for each potential member to give the structure shown in Fig. 14c.

Fig. 13

Spanning Example: Problem setup and nominal solution

Fig. 14

Spanning example: Results using simple, manual method. (a) - (b) Nominal solutions under single damage case with $r=1.6$, (c) superposition of (a), (b), and their mirror images

For the method proposed here, it is assumed that damage is caused by ground-based hazards (e.g. impacts from vehicles), thus damage cases have been defined as circular regions centered on any node in the the bottom two rows. This will also avoid the issues of sensitivity to damage occurring around load application points, as noted in the previous example.

To simplify the structures produced, a simple post-processing filter has been used. For this, the resulting structure from the proposed adaptive process was altered by removing any member which had a cross-section area less than a certain percentage of the largest area in the structure; values of up to 10% have been tested. The filtered structure was then subjected to a size optimization, again using (3). As the number of members has been greatly reduced, it was found to be unnecessary to use the adaptive solution process in the filtering stage, instead the problem with all possible damage cases and all remaining members was solved directly.

Fig. 15

Spanning Example: Resulting volume and number of members for various values of damage radius, r with filtering of areas below 0.01%, 1% 2%, ... 10% of largest cross-section area. (Filter levels which produced an infeasible size optimization problem are excluded). The letters adjacent to the nominal damaged results refer to Fig. 14

Figure 15 shows the volume and number of structural members for various damage radii and filtering levels, selected structural forms are shown in Fig. 16. Note that, in this case, even a small damage radius results in a large increase in the structural volume. This is because any damage case containing one of the supported nodes removes that support, significantly increasing the span of the structure. It can be seen that the results using the method proposed here have a lower volume than the result in Fig. 14c, and the filtered result in Fig. 16d also has fewer structural members. Furthermore, the structure in Fig 14c is likely to be invalid under damage cases other than the four which were explicitly considered. Therefore, the nominal designs (e.g., from Figs. 13 or 14) are not always appropriate benchmarks for ‘fail-safe’ design problems. Instead, the optimum solutions obtained by the proposed method can be used as new benchmarks for this type of problems.

Figure 17 shows the forces in the filtered structure ($r = 1.6$, filtering members with areas below 10% of the maximum). It can be seen that some damage cases produce internal force states which are equally well suited to address damage applied at other, physically remote, locations; for example, the forces shown in Fig. 17c could also apply in the case that the right-most column was damaged. This further supports the hypothesis that is is unnecessary to explicitly consider every damage case, and suggests that the speed of the adaptive process could be further increased by improvements to the heuristics used to select the order in which damage cases are added.

Fig. 16

Spanning example, results with various filtering levels for $r=1.6$. (a) 0.01%, (b) 4%, (c) 9%, (d) 10%

Fig. 17

Spanning example, load-paths under selected damage cases. Blue members are fully stressed in compression,and red members are fully stressed in tension; darker members carry lower stresses. Relevant damage case shown in green

8 Conclusions

A computationally efficient adaptive procedure has been presented for the solution of the fail-safe truss topology optimization problem. This has been used to solve problems with over 16000 members and 16000 possible damage cases to the global optimum, generating new benchmarks for the least-material designs of ‘fail-safe’ structures. The proposed method greatly reduces the size of the optimization problem, by explicitly considering only a sub-set of both the potential members and of the damage cases, giving substantial improvements in both solution time (speed up factor of 41) and memory needed to solve the problem. It has been demonstrated that the optimal volume obtained using this method will be identical to that obtained by solving the full problem in a single step.

The method proposed here has allowed for the solution of problems at significantly higher nodal resolutions than was possible previously. From this, it has been found that a per-member definition of damage, as is common in both industry and previous academic studies, becomes ill-defined as resolution increases. In the extreme case, the fail-safe solution becomes effectively identical to the nominal solution, with the exception that each bar of the nominal solution is replaced with a bundle of many very close, very thin structural members.

To counter this, the method has been defined in a way that permits the use of arbitrary pre-defined damage cases, allowing flexibility to adapt to different problems. Examples with damage inflicted to all structural members in a circular region have been used to demonstrate the applicability of the method. It has been observed that the volume, and even feasibility, of the problems is very strongly dependent on the precise damage definitions used. As such, further application-specific studies are suggested to define these for scenarios of interest.

To summarise, the proposed method provides a flexible and computationally tractable approach to the fail-safe truss topology optimization problem.

Replication of Results A python script based on He et al. (2019) and extended to implement the methods presented here is available in the Electronic Supplementary Materials.

Appendices

Appendix A: Stress based and compliance based formulations

This appendix will consider the simple three-bar problem solved using a rigid-plastic material in Section 4 of the present work, and using an elastic material, as in Section 1.2 of Stolpe (2019). Similarities and differences between the two methods will be discussed.

This problem has a ground structure containing just three bars, as shown in Fig. 1a. Considering anti-symmetry about the horizontal axis, this can be reduced to just two independent bar areas, the area of the horizontal bars $a_h$ and the area of the diagonal bars $a_d$. Further, if a limit on the total volume is imposed, as in common in compliance-based design problems, then the number of independent variables can be reduced to just one (in plastic context, it would be usual to consider this final step by normalising the volume based on the applied load, but this would have the same effect).

Fig. 18

Three-bar example: Analysis of all possible designs. (a) Nominal and worst-case compliance. (b) Worst-case stress. The dashed line represents the plastic stress-limited optimum structure obtained here, whilst the dash-dotted line represents the elastic compliance-optimized structure obtained by Stolpe (2019)

In this way, Fig. 18 shows results of linear-elastic analysis of all possible solutions to the three-bar problem, where solutions with thicker horizontal bars lie to the left of the plots, and those with thicker diagonal bars lie on the right. Figure 18a shows the compliance of each structure in the nominal case, as well as in the worst-case of the three damage conditions. The worst-case always occurred under removal of a diagonal member (removal of either diagonal having an identical impact), whilst the removal of the horizontal member resulted in a compliance equal to the nominal case. The solutions corresponding to the compliance-based (Stolpe 2019) and plastic stress-based (Sec. 4) formulations are marked.

We note that Stolpe (2019) uses ‘compliance’ as referring to the compliance in the nominal case (i.e. giving a value of $1+2\sqrt{2}$ for the compliance-optimized structure). Thus statements such as the fail-safe conditions causing ‘an increase of more than 35% in the objective function’ are not strictly true. The objective in Stolpe ’s (2019) formulation is the worst-case compliance, which actually increases by 266% in this case, as shown in Fig 18. For comparison, the objective function (volume) in the stress based formulation increases by 150% with the introduction of the fail-safe constraints.

Figure 18b displays the worst-case stress under any of the three damage cases for all possible structures, this assumes plastic material behaviour, and therefore differs from the results of Kirby et al. (2022). It can be observed that there is a cusp at $a_d=0.4$. For solutions right of this point, the worst-case stress occurs in the horizontal bar when one of the diagonals is damaged. For solutions left of this point, the worst-case again occurs with damage to a diagonal bar, but now the remaining diagonal is critical. At $a_d=0.4$ both members are equally stressed in this damage case, and the worst-case stress is minimized.

Note that the plastic stress-constrained optimum structure obtained in this paper also gives the minimum peak stresses under elastic material modelling. This likely not a general result, and may have been caused by the statically determinate nature of the ground-structure under each damage condition. Nonetheless, it is important to note that the strongest (i.e. stress-based optimum) and stiffest (i.e. compliance-based optimum) are not, in general, coincident under fail-safe constraints. As fail-safe constraints are likely to concern behaviour under extreme or emergency conditions, the considerations of strength (ultimate limit states) are likely to be more important than those of stiffness (serviceability limit states). Furthermore, it should be noted that both the linear-elastic and rigid-plastic material models incorporate many assumptions and simplifications, and more complex models may produce optima which are different again.

Appendix B: Addressing infeasible sub-problems

If the solver used to handle the reduced problems does not return an unbounded ray for problems which are primal infeasible/dual unbounded, then the following modification can be used to provide practical virtual displacements with which it is possible to obtain and, crucially, rank potential members which are violated. This problem is a modified version of (3), which is kinematically restricted, i.e. statically relaxed, in such a way that the kinematic problem cannot become unbounded.

This modified problem, in the kinematic setting, involves adding limits on the virtual deflections (in the positive and negative x and y directions) possible at each point. The limit, ${\bar{u}}$ is set to a large value; as ${\bar{u}}$ tends to infinity, the modified problem tends to the original problem. Converting this modification to the static setting, the added limits become four added slack forces per node (in positive and negative x and y directions). These slack forces are penalised in the objective function with a coefficient of ${\bar{u}}$; a suitable physical interpretation of this is that the slack forces represent forces in a bar connecting to some distant imagined support, thus the value ${\bar{u}}$ would be equal to the stress in the bar multiplied by the distance to the imaginary support. Again, as ${\bar{u}}$ increases, these imaginary supports have less and less influence and the problem tends towards the original.

${\bar{u}}$ should be chosen large enough that the imaginary supports are only triggered for cases where the real structure is not feasible, but coefficients which are too large may have an adverse effect on the numerical performance of the optimization algorithm. Initial testing has shown that a suitable value for, ${\bar{u}}$ is the sum of the horizontal and vertical ranges of the design domain, divided by the smallest value of yield stress amongst the potential members.