Topology optimization of scale-dependent non-local plates

Abstract

The main objective of this work is to extend finite element-based topology optimization problem to the two-dimensional, size-dependent structures described using weakly non-local Cosserat (micropolar) and strongly non-local Eringen’s theories, the latter of which finds an application for the first time, to the best of Authors’ knowledge. The optimum material layouts that minimize the structural compliance are attained by means of Solid Isotropic Material with Penalization approach, while the desired smooth, mesh-independent, binary solutions are obtained using density filter accompanied by volume preserving Heaviside projection method. The algorithms are enhanced by including an element removal and reintroduction strategy to reduce the computational cost, and to prevent spurious excessive distortion of elements with very low density. Example problems of practical importance are investigated under the assumption of linear elasticity to validate the code and to clearly demonstrate the influence of internal length scales and different non-locality mechanisms on final configurations. Obtained macro-scale optimum topologies admit the characteristics of corresponding continuum theories, and appear to be in agreement with the mechanical response governed by particle interactions in micro/nanoscale.

1 Introduction

The first rational study on topology optimization dates back to the beginning of twentieth century, to the pioneering paper of Australian mechanical engineer Michell (1904) on optimum frame design, in which, the minimum quantity of material, sufficient to sustain the external forces by tensile and compressive members of identical density (named Michell truss), was searched. Following the landmark work of Bendsøe and Kikuchi (1988), the topic has gained a considerable attention, and different methodologies, all seeking to find the parameters that minimize (or maximize) the objective function for a given set of load and boundary conditions while satisfying a series of service constraints, are proposed. In general, these approaches can be categorized as density-based, level-set, phase-field and hard-kill (evolutionary) methods, depending on the nature (continuous vs. discrete), content (material density vs. structural geometry) and updating scheme (gradient-based vs. random search) of the design variable (Rozvany 2009; Sigmund and Maute 2013; Deaton and Grandhi 2014; Tyflopoulos et al. 2018). Despite the widespread application of topology optimization to classical (local) Cauchy materials, limited number of works, that are discussed later, focused on extending the problem to non-local media which are characterized by the presence of internal length parameters and spatial dispersion properties (Kunin 1968, 1982, 1983).

Non-local theories are used to describe the behaviour of complex materials with comparable internal and external length scales for their capability of maintaining the information of underlying material organization while exploiting the field descriptions (Mindlin 1964; Kunin 1984; Capriz 1989; Maugin 1993; Eringen 1999; Gurtin 2000), and suggested to be categorized as ‘implicit/weak’ and ‘explicit/strong’ depending on the nature of non-locality (Kunin 1984; Maugin 1993; Eringen 1999; Trovalusci 2014). The theories belonging to the former class are known as generalized, microcontinua or multi-field continua (Eringen 1999; Trovalusci 2014) that are enriched with additional kinematic and work-conjugated dynamic descriptors, even leading to increasing of the number of field equations, as they induce a limited (weak) non-local character manifested through these additional non-standard fields. On the other hand, the theories belonging to the latter class preserve the classical primal fields, nonetheless the equations contain integral, integro-differential or finite difference operators. Since length scale parameters are directly linked to the bulk properties, explicit models possess a strong non-local character. The non-local theory to be used is chosen depending on the characteristics of the structure to be examined (how the unit cell behaves), though in the present study, the particular attention is going to be on micropolar (Cosserat) and two-phase local/non-local Eringen’s models (Tuna et al. 2020; Tuna and Trovalusci 2020).

Implicitly non-local micropolar theory deals with media that are composed of rigid material particles enriched with the additional micro-rotational degree of freedom (Cosserat and Cosserat 1909; Nowacki 1986; Eringen 1999), and has been widely employed for describing heterogeneous materials with microstructures, such as masonry, rock assemblages, reinforced composites (Masiani and Trovalusci 1996; Forest and Sab 1998; Colatosti et al. 2021a, b). Moreover, as the theory accounts for relative rotations corresponding to skew-symmetric part of strain and to work-conjugated stress measures, it is especially suitable to describe the behaviour of anisotropic, and in particular orthotropic media (Trovalusci and Masiani 1999; Pau and Trovalusci 2014; Eremeyev and Pietraszkiewicz 2016; Fantuzzi et al. 2019, 2020).

Explicitly non-local Eringen’s model concerns with the physics of material bodies whose stress at a point is influenced by the state of strain of all other points within a neighbourhood of the body (Kröner 1967; Eringen and Edelen 1972; Eringen 2002), hence it covers the long-range interactions between material points. Although the constitutive relation has originally been introduced in integral form (Eringen 1972), it is later transformed to differential form for specific kernel functions (Eringen 1983), and finally re-organized as two-phase local/non-local form consisting of weighted mixture of both (Eringen 1984; Altan 1989). All these forms with their enhanced versions are widely employed to model size-dependent behaviour of, especially nano and micro, structures with prominent neighbour relations (e.g. carbon nanotubes, graphene sheets, atomic chains/arrays) (Polizzotto 2001; Ansari et al. 2011; Rafii-Tabar et al. 2016; Tuna and Kirca 2021; Tuna et al. 2019; Eroglu 2020; Pisano et al. 2021; Danesh et al. 2021; Naderi et al. 2021; Günay 2021). Nevertheless, their limitations must be acknowledged to avoid the improper practice leading to paradoxical results which are comprehensively reported in a current review article by Ceballes et al. (2021).

In the available literature, only a few work addresses the topology optimization problem of structures modelled by non-classical continuum theories; such as micropolar, couple stress, and strain gradient elasticity (Rovati and Veber 2007; Liu and Su 2009; Arimitsu et al. 2011; Veber and Taliercio 2012; Bruggi and Taliercio 2012; Li and Khandelwal 2015; Li et al. 2017; Da et al. 2018; Su and Liu 2020; Chen et al. 2021), while even less deals with optimal design of systems that are related to other interesting fields of applied mathematics (e.g. conduction, diffusion) governed by non-local type equations (Andrés and Muñoz 2015, 2017; Evgrafov and Bellido 2019b, 2020). In pioneering study, Rovati and Veber (2007) applied topology optimization procedure for maximum stiffness problem considering two-dimensional (2D) micropolar solids, which has then been extended to dynamic loading conditions (Bruggi and Taliercio 2012) and three-dimensional (3D) case (Veber and Taliercio 2012), while recently Chen et al. (2021) developed a parametrized level-set topology optimisation method to re-study the minimum compliance problem of 2D Cosserat solids. For problems with prominent bending effects, the optimum material layouts of micropolar solids turn out to be characterized by more simplified and curved structures, as a result of inherent flexural stiffness, whereas local case (Cauchy) presents truss-like structures with higher compliance. This discrepancy is also evident for other non-classical models, yet to the authors’ best knowledge, such an investigation has not been performed conducting strongly non-local Eringen’s theory of elasticity.

With this motivation, the present paper generalizes finite element (FE)-based topology optimization to the 2D size-dependent structures modelled via strongly non-local two-phase Eringen’s theory. To make a comparison with weakly non-local theories, the minimum compliance problem of micropolar solids is also adopted making some adjustments. The FE models, discretised with equi-sized quadrilateral elements, are parametrised by material densities, and the optimal layouts are looked for adopting the simple, yet efficient Solid Isotropic Material with Penalization method (SIMP; Bendsøe 1989; Zhou and Rozvany 1991; Mlejnek 1992) through a gradient-based updating scheme. By virtue of the fictitious power-law approach, intermediate values of design variables are penalized to support the formal solid/void solution while to eliminate numerical problems, such as checkerboard pattern (i.e. adjacent solid–void elements in optimised configuration) and mesh dependency (Jog and Haber 1996; Sigmund and Petersson 1998), the formulation is improved with density filter (Bourdin 2001; Bruns and Tortorelli 2001). The undesirable transition region (i.e. the grey zone appeared between solid–void elements, having intermediate density values) resulting from the filtering operation is suppressed by means of projection method (Guest et al. 2004; Wang et al. 2011), which amplifies the solution further into a solid/void field. Finally, to avoid the misleading contribution of low-density elements to structural analysis of Eringen’s non-local model, an element removal and reintroduction scheme, similar to the one proposed by Bruns and Tortorelli (2003), is embedded to the algorithms. In the framework of linear elasticity, several example problems of practical importance are investigated for different characteristic lengths to point out the influence of scale effects, and different type of non-local theories on optimised configurations.

The paper is organized as follows. In Sect. 2, the field equations of micropolar and Eringen’s non-local models are outlined by presenting their limit cases leading to Cauchy continua in the case of isotropy. Then corresponding FE formulations are derived focusing on 2D case. In Sect. 3, the mathematical formulation of topology optimization problem in the minimum compliance case is shown in a detailed manner by providing information also about element removal–reintroduction scheme. Section 4 is devoted on numerical examination in which the effect of different theories on optimal topologies are studied through individual and comparative example problems by providing a discussion on the results. Finally, in Sect. 5, concluding remarks are drawn and possible future activities are suggested.

2 Continuum theories

This section provides general information on the theories considered in the present study, and on the corresponding FE formulations that are derived regarding 2D bodies occupying a domain, $\varOmega$, and discretised using linear (i.e. four-noded) elements. The structures are assumed to be made of linear, elastic and isotropic material, and a Cartesian coordinate system, with z axis along the thickness, is used for parametrisation of positions of material points, $\mathbf{{x}}$. The formulations are derived within the linearized kinematical framework where the superscripts ${\text {M}}$ and ${\text {E}}$ refer to micropolar (Cosserat) and Eringen’s non-local models respectively. For corresponding calculations, in-house codes are developed using Wolfram Mathematica software®.

2.1 Micropolar (Cosserat) theory of elasticity

Micropolar theory belongs to generalized continua, here included in the class of ‘implicit’ non-local model, for which the material particles are described in terms of their positions and rotations. So, the theory allows the material deformation to include additional micro-rotational degree of freedom, yielding following kinematic relations for linearised case:

$$\varepsilon _{ij}^{\text {M}} = u_{i,j}^{\text {M}} + {e_{ijk}}{\phi _{k}},\quad {\chi _{kj}} = {\phi _{k,j}},$$

(1)

where $\varepsilon _{ij}^{\text {M}}$ and $\chi _{kj}$ are strain and curvature tensors, while $u_{i,j}^{\text {M}}$ and $\phi _{k}$ are displacement and micro-rotation vectors, respectively and $e_{ijk}$ is permutation symbol. If micro-rotations are constrained to coincide with the local rigid rotation (macro-rotation); i.e. ${\phi _{k}} = -\dfrac{1}{2}{e_{kmn}}{u_{m,n}}$, a special case of micropolar theory, namely couple-stress theory is obtained (Sokolowski 1972; Masiani and Trovalusci 1996).

The material body can be conceived as a collection of rigid particles that undergo both translation and rotation, and interact through traction forces $t_{i}^{\text {M}}$, and couple-tractions $m_{k}$, for which the following surface balance equations are attained:

$$t_{i}^{\text {M}} = \sigma _{ij}^{\text {M}}{n_{j}},\quad {m_{k}} = {\mu _{kj}}{n_{j}},$$

(2)

where $\sigma _{ij}^{\text {M}}$ is the skew-symmetric stress tensor and ${\mu _{kj}}$ is the couple-stress tensor, with $n_{j}$ referring to unit normal. If body forces and couples are neglected, the equilibrium equations take the following form:

$$\sigma _{ij,j}^{\text {M}} = 0,\quad {\mu _{kj,j}} - {e_{ijk}}\sigma _{ij}^{\text {M}} = 0.$$

(3)

In the context of linear elasticity, the constitutive relation between strain (and curvature) and work-conjugated stress (and couple-stress) tensors are expressed as follows for the isotropic case (Eringen 1999):

$$\begin{aligned}&\sigma _{ij}^{\text {M}}(\mathbf{{x}}) = \lambda \varepsilon _{kk}^{\text {M}}(\mathbf{{x}}){\delta _{ij}} + (\mu + \chi )\varepsilon _{ij}^{\text {M}}(\mathbf{{x}}) + \mu \varepsilon _{ji}^{\text {M}}(\mathbf{{x}}), \\&{\mu _{kj}}(\mathbf{{x}}) = \alpha {\chi _{ii}}(\mathbf{{x}}){\delta _{kj}} + \beta {\chi _{jk}}(\mathbf{{x}}) + \gamma {\chi _{kj}}(\mathbf{{x}}), \end{aligned}$$

(4)

where $\alpha$, $\beta$, $\gamma$ and $\chi$ being constants related to micropolar theory, while $\lambda$ and $\mu$ refer to generalized Lamé constants (Lakes 1995):

$$\begin{aligned}&{\lambda = \dfrac{{E\nu }}{{\left( {1 + \nu } \right) \left( {1 - 2\nu } \right) }},}\quad {\mu = G - \dfrac{\chi }{2},}\quad {G = \dfrac{E}{{2(1 + \nu )}}}. \end{aligned}$$

(5)

Here E is Young’s modulus, G is classical shear modulus and $\nu$ is Poisson’s ratio. In case $\alpha$, $\beta$, $\gamma$ and $\chi$ equal to zero, constitutive equation of classical elasticity is recovered.

The FE formulation is going to be derived for 2D case using natural coordinates ($\zeta$, $\eta$). For a micropolar domain, the nodal displacement vector of an element m; ${\mathbf{{d}}_{m}^{\text {M}}}$, is represented in terms of in-plane displacements $u_{x}$, $u_{y}$ and out-of-plane micro-rotation $\phi _{z}$:

$${\mathbf{{d}}_{m}^{\text {M}} = \left\{ {\begin{array}{*{20}{c}} {\mathbf{{d}}_{m\varepsilon }^{\text {M}}}\\ {\mathbf{{d}}_{m\phi }^{\text {M}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{\tilde{u}}_{x}^{1}}&{{\tilde{u}}_{y}^{1}}&\ldots&{{\tilde{u}}_{x}^{4}}&{{\tilde{u}}_{y}^{4}}&{{\tilde{\phi }} _{z}^{1}}&\cdots&{{\tilde{\phi }} _{z}^{4}} \end{array}} \right\} _{m}^{\text {T}}},$$

(6)

where T denotes the transpose operation, and over tilde indicates that the displacement and micro-rotation measures are approximate nodal values with superscripts referring to corresponding node number. Thereby, for an element m, the displacement and rotation fields are attained by means of interpolation operations:

$$\begin{aligned}&{\mathbf{{u}}_{m}^{\text {M}}\left( {\zeta ,\eta } \right) = {\mathbf{{N}}_{u}}{} \mathbf{{d}}_{m\varepsilon }^{\text {M}},}\quad {\varvec{\phi } _{m}^{\text {M}}\left( {\zeta ,\eta } \right) = {\mathbf{{N}}_{\phi} }{} \mathbf{{d}}_{m\phi }^{\text {M}}} \end{aligned}$$

(7)

with ${\mathbf{{N}}_{u}}$ and ${\mathbf{{N}}_{\phi} }$ being the linear shape functions:

$$\begin{array}{l} {\mathbf{{N}}_{u}}\left( {\zeta ,\eta } \right) = \left[ {\begin{array}{*{20}{c}} {{N^{1}}}&{}0\\ 0&{}{{N^{1}}} \end{array}\begin{array}{*{20}{l}} \ldots \end{array}\begin{array}{*{20}{c}} {{N^{4}}}&{}0\\ 0&{}{{N^{4}}} \end{array}} \right] ,\\ {\mathbf{{N}}_{\phi} }\left( {\zeta ,\eta } \right) = \left[ {\begin{array}{*{20}{c}} {{N^{1}}}&{} \ldots &{}{{N^{4}}} \end{array}} \right] ,\\ \begin{array}{*{20}{l}} {{N^{1}} = \dfrac{{\left( {1 - \zeta } \right) \left( {1 - \eta } \right) }}{4},}&{}\quad {{N^{2}} = \dfrac{{\left( {1 + \zeta } \right) \left( {1 - \eta } \right) }}{4},}\\ {{N^{3}} = \dfrac{{\left( {1 + \zeta } \right) \left( {1 + \eta } \right) }}{4},}&{}\quad {{N^{4}} = \dfrac{{\left( {1 - \zeta } \right) \left( {1 + \eta } \right) }}{4}}. \end{array} \end{array}$$

(8)

At this point, it should be noted that, the adoption of quadratic shape functions for the displacement field and of linear ones for the micro-rotation field would maintain the displacement-rotation compatibility by assuring the same order of interpolation in the strain tensor (Providas and Kattis 2002; Darrall et al. 2014; Godio et al. 2015). Nevertheless, depending on the investigated problem and mesh discretization, the desired accuracy can still be achieved with the shape functions of same order. In fact, this very topic was also addressed in a recent publication of this Authors’ (Tuna et al. 2020) where numerical evidence is provided on the fact that the use of linear shape functions for both fields yields satisfactory results when sufficient number of elements are used.

To obtain the corresponding strain, ${\varvec{\varepsilon }}_{m}^{\text {M}}$, and curvature, ${\varvec{\chi }}_{m}^{\text {M}}$, fields of an element m;

$$\begin{aligned}&{\varvec{\varepsilon }}_{m}^{\text {M}} = \left\{ {\varepsilon _{11}^{\text {M}},\varepsilon _{22}^{\text {M}},\varepsilon _{12}^{\text {M}},\varepsilon _{21}^{\text {M}}} \right\} _{m}^{\text {T}},\quad {\varvec{\chi }}_{m}^{\text {M}} = \left\{ {\chi _{31}^{\text {M}},\chi _{32}^{\text {M}}} \right\} _{m}^{\text {T}} \end{aligned}$$

(9)

usual procedures of FE method is followed:

$$\begin{array}{l}\displaystyle {\varvec{\varepsilon }}_{m}^{\text {M}}\left( {\zeta ,\eta } \right) = \left[ {\begin{array}{*{20}{c}} {\mathbf{{L}}_{m}^{\text {M}}{\mathbf{{N}}_{u}}}&{}{\mathbf{{M}}{\mathbf{{N}}_{\phi} }} \end{array}} \right] \mathbf{{d}}_{m}^{\text {M}} = \mathbf{{B}}_{m\varepsilon }^{\text {M}}{} \mathbf{{d}}_{m}^{\text {M}},\\ {{\varvec{\chi }}_{m}}\left( {\zeta ,\eta } \right) = \left[ {\begin{array}{*{20}{c}} {{\mathbf{{0}}_{2 \times 8}}}&{}{{\nabla _{m}}{\mathbf{{N}}_{\phi} }} \end{array}} \right] \mathbf{{d}}_{m}^{\text {M}} = \mathbf{{B}}_{m\chi }^{\text {M}}{} \mathbf{{d}}_{m}^{\text {M}}. \end{array}$$

(10)

Here ${\mathbf{{L}}_{m}^{\text {M}}}$, $\mathbf{{M}}$, and ${{\nabla _{m}}}$ refer to differential operator matrix, permutation vector and gradient operator vector, respectively, and represented as follows in natural coordinate system:

$$\begin{aligned}&\begin{array}{l}\displaystyle \mathbf{{L}}_{m}^{\text {M}} = {\left[ {\begin{array}{*{20}{c}} {\dfrac{\partial }{{\partial \zeta }}{J}_{11}^{ - 1} + \dfrac{\partial }{{\partial \eta }}{J}_{12}^{ - 1}}&{}0\\ 0&{}{\dfrac{\partial }{{\partial \zeta }}{J}_{21}^{ - 1} + \dfrac{\partial }{{\partial \eta }}{J}_{22}^{ - 1}}\\ {\dfrac{\partial }{{\partial \zeta }}{J}_{21}^{ - 1} + \dfrac{\partial }{{\partial \eta }}{J}_{22}^{ - 1}}&{}0\\ 0&{}{\dfrac{\partial }{{\partial \zeta }}{J}_{11}^{ - 1} + \dfrac{\partial }{{\partial \eta }}{J}_{12}^{ - 1}} \end{array}} \right] }_{m} \end{array}, \end{aligned}$$

(11)

$$\begin{aligned}&\begin{array}{l}\displaystyle \mathbf{{M}} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ { + 1}\\ { - 1} \end{array}} \right] ,\quad {\nabla }_{m} = {\left[ {\begin{array}{*{20}{c}} {\dfrac{\partial }{{\partial \zeta }}{J}_{11}^{ - 1} + \dfrac{\partial }{{\partial \eta }}{J}_{12}^{ - 1}}\\ {\dfrac{\partial }{{\partial \zeta }}{J}_{21}^{ - 1} + \dfrac{\partial }{{\partial \eta }}{J}_{22}^{ - 1}} \end{array}} \right] }_{m}, \end{array} \end{aligned}$$

(12)

where $J_{11}^{ - 1}$, $J_{12}^{ - 1}$, $J_{21}^{ - 1}$ and $J_{22}^{ - 1}$, denote components of inverse of the Jacobian matrix (${\mathbf{{J}}_{m}}$) that is used for a proper transformation between physical (x, y) and natural coordinates ($\zeta$, $\eta$):

$$\begin{array}{*{20}{l}} {{\mathbf{{J}}_{m}} = \left[ {\begin{array}{*{20}{l}} {\dfrac{{\partial {x_{m}}}}{{\partial \zeta }}}&{}{\dfrac{{\partial {y_{m}}}}{{\partial \zeta }}}\\ {\dfrac{{\partial {x_{m}}}}{{\partial \eta }}}&{}{\dfrac{{\partial {y_{m}}}}{{\partial \eta }}} \end{array}} \right] }&{}{\begin{array}{*{20}{l}} {{x_{m}}\left( {\zeta ,\eta } \right) = \displaystyle \sum \limits _{s = 1}^{4} {{N^{s}}\left( {\zeta ,\eta } \right) q_{x}^{s}} },\\ {{y_{m}}\left( {\zeta ,\eta } \right) = \displaystyle \sum \limits _{s = 1}^{4} {{N^{s}}\left( {\zeta ,\eta } \right) q_{y}^{s}} }, \end{array}} \end{array}$$

(13)

with $q_{x}^{s}$ and $q_{y}^{s}$ referring to x and y coordinates of sth node of corresponding element.

Constitutive relation in Eq. (4) can be expressed in terms of approximate strain and curvature fields derived in Eq. (10):

$$\begin{aligned}&{{\varvec{\sigma }}_{m}^{\text {M}}\left( {\zeta ,\eta } \right) = \mathbf{{D}}_{m\varepsilon }^{\text {M}}{} \mathbf{{B}}_{m\varepsilon }^{\text {M}}{} \mathbf{{d}}_{m}^{\text {M}}}, \\&{{{\varvec{\mu }}_{m}}\left( {\zeta ,\eta } \right) = \mathbf{{D}}_{m\chi }^{\text {M}}{} \mathbf{{B}}_{m\chi }^{\text {M}}{} \mathbf{{d}}_{m}^{\text {M}}}, \end{aligned}$$

(14)

where skew-symmetric stress, ${{\varvec{\sigma }}_{m}^{\text {M}}},$ and couple stress, ${\varvec{\mu }}_{m}$, vectors are described as follows:

$${\varvec{\sigma }}_{m}^{\text {M}} = \left\{ {\sigma _{11}^{\text {M}},\sigma _{22}^{\text {M}},\sigma _{12}^{\text {M}},\sigma _{21}^{\text {M}}} \right\} _{m}^{\text {T}},\quad {\varvec{\mu }}_{m}^{\text {M}} = \left\{ {\mu _{31}^{\text {M}},\mu _{32}^{\text {M}}} \right\} _{m}^{\text {T}}.$$

(15)

Under plane strain assumption, the elasticity matrices; $\mathbf{{D}}_{m\varepsilon }^{\text {M}}$ and ${\mathbf{{D}}_{m\chi } ^{\text {M}}}$ can be re-organized as:

$$\begin{array}{l} \mathbf{{D}}_{m\varepsilon }^{\text {M}} = {E_{m}}{} \mathbf{{D}}_\varepsilon ^{\text {M}},\quad \mathbf{{D}}_{m\chi }^{\text {M}} = {E_{m}}{} \mathbf{{D}}_\chi ^{\text {M}},\\ \begin{array}{*{20}{l}} {\mathbf{{D}}_\varepsilon ^{\text {M}} = \frac{1}{{\left( {1 + \nu } \right) }}\left[ {\begin{array}{*{20}{c}} {\frac{{(1 - \nu )}}{{\left( {1 - 2\nu } \right) }}}&{}{\frac{\nu }{{\left( {1 - 2\nu } \right) }}}&{}0&{}0\\ {\frac{\nu }{{\left( {1 - 2\nu } \right) }}}&{}{\frac{{(1 - \nu )}}{{\left( {1 - 2\nu } \right) }}}&{}0&{}0\\ 0&{}0&{}{\frac{{1}}{{2\left( {1 - {N^{2}}} \right) }}}&{}{\frac{1 - 2{N^{2}}}{{2\left( {1 - {N^{2}}} \right) }}}\\ 0&{}0&{}{\frac{1 - 2{N^{2}}}{{2\left( {1 - {N^{2}}} \right) }}}&{}{\frac{{1}}{{2\left( {1 - {N^{2}}} \right) }}} \end{array}} \right] },\\ {\mathbf{{D}}_\chi ^{\text {M}} = \frac{1}{{(1 + \nu )}}\left[ {\begin{array}{*{20}{c}} {2{l_{c}}^{2}}&{}0\\ 0&{}{2{l_{c}}^{2}} \end{array}} \right] }, \end{array} \end{array}$$

(16)

using Eq. (5) and following relations defined between material’s internal length ($l_{c}$), coupling number (N) and micropolar constants ($\gamma$, $\chi$):

$$\begin{aligned}&l_{c}^{2} = \dfrac{\gamma }{{2\left( {2\mu + \chi } \right) }} \rightarrow \gamma = \dfrac{{2l_{c}^{2}E}}{{\left( {1 + \nu } \right) }}, \\&{N^{2}} = \dfrac{\chi }{{2\left( {\mu + \chi } \right) }} \rightarrow \chi = \dfrac{{{N^{2}}E}}{{\left( {1 + \nu } \right) \left( {1 - {N^{2}}} \right) }}. \end{aligned}$$

(17)

As the final step, the element formulation of a domain, discretized with ${N_{{\text {tot}}}}$ FEs, is derived based on the minimum potential energy principle:

$$\displaystyle \frac{{\partial {\varPi ^{\text {M}}}}}{{\partial \mathbf{{d}}_{i}^{\text {M}}}} = \frac{{\displaystyle \sum \nolimits _{m = 1}^{{N_{{\text {tot}}}}} {\partial \varPi _{m}^{\text {M}}} }}{{\partial \mathbf{{d}}_{i}^{\text {M}}}}=0,\quad i = 1,2, \ldots ,{N_{{\text {tot}}}}$$

(18)

for which the total potential energy functional of an element m, $\varPi _{m}^{\text {M}}$, is represented in terms of elastic strain energy, $U_{m}^{\text {M}}$, and work potential, $W_{m}^{\text {M}}$:

$$\displaystyle \varPi _{m}^{\text {M}} = U_{m}^{\text {M}}\left[ {\mathbf{{d}}_{m}^{\text {M}}} \right] + W_{m}^{\text {M}}\left[ {\mathbf{{d}}_{m}^{\text {M}}} \right] ,$$

(19)

where

$$\begin{aligned}&{U_{m}^{\text {M}}} = \dfrac{h}{2}\int \limits _{ - 1}^{1} {\int \limits _{ - 1}^{1} {\left( {{{\left( {{\varvec{\varepsilon }}_{m}^{\text {M}}} \right) }^{\text {T}}}{\varvec{\sigma }}_{m}^{\text {M}} + {{\left( {{\varvec{\chi }}_{m}^{\text {M}}} \right) }^{\text {T}}}{\varvec{\mu }}_{m}^{\text {M}}} \right) J_{m} {\text {d}}\zeta {\text {d}}\eta } } \\&W_{m}^{\text {M}} = -\sum \limits _{j = 1}^{4} {\int \limits _{ - 1}^{1} {{{\left( {\mathbf{{d}}_{m}^{\text {M}}} \right) }^{\text {T}}}{{\left\{ {\begin{array}{*{20}{c}} {\mathbf{{N}}_{u}^{\text {T}}{} \mathbf{{fs}}_{m}}\\ {\mathbf{{N}}_{\phi} ^{\text {T}}{{\mathbf{{fc}} }_{m}}} \end{array}} \right\} }_{j}}{\text {d}}{l_{j}}} } - {\left( {\mathbf{{d}}_{m}^{\text {M}}} \right) ^{\text {T}}}{} \mathbf{{q}}_{m}^{\text {M}}. \end{aligned}$$

(20)

Here $J_{m}$ denotes the determinant of the Jacobian matrix, while subscript j refers to the edge number. ${\mathbf{{fs}}}_{m}$ and ${\mathbf{{fc}}}_{m}$ are the distributed surface traction and couple traction vectors, respectively, with ${\text {d}}l_{j}$ indicating the edge length, and $\mathbf{{q}}_{m}^{\text {M}}$ being the generalized load vector including concentrated forces and couples:

$$\begin{array}{l} \begin{array}{*{20}{l}} {{{\left. {\mathbf{{fs}}_{m}} \right| }_{j}} = {{\left\{ {\begin{array}{*{20}{c}} {{{\text {fs}}_{{x_{j}}}}}&{}{{{\text {fs}}_{{y_{j}}}}} \end{array}} \right\} _{m}^{\text {T}}}},}&{}{{{\left. {{{\mathbf{{fc}} }_{m}}} \right| }_{j}} = {{\left\{ {{{\text {fc}}_{{z_{j}}}}} \right\} }_{m}},}\\ {{{\left. {{\text {d}}l} \right| }_{j = 1,3}} = \dfrac{{{l_{\text {e}}}}}{2}{\text {d}}\eta ,}&{}{{{\left. {{\text {d}}l} \right| }_{j = 2,4}} = \dfrac{{{l_{\text {e}}}}}{2}{\text {d}}\zeta ,} \end{array}\\ {\left. {\mathbf{{N}}\left( {\zeta ,\eta } \right) } \right| _{j = 1,3}} = \mathbf{{N}}\left( { \mp 1,\eta } \right) ,\\ {\left. {\mathbf{{N}}\left( {\zeta ,\eta } \right) } \right| _{j = 2,4}} = \mathbf{{N}}\left( {\zeta , \mp 1} \right) ,\\ \mathbf{{q}}_{m}^{\text {M}} = \left\{ {\begin{array}{*{20}{l}} {f_{x}^{1}}&{}{f_{y}^{1}}&{} \ldots &{}{f_{x}^{4}}&{}{f_{y}^{4}}&{}{m_{z}^{1}}&{} \ldots &{}{m_{z}^{4}} \end{array}} \right\} _{m}^{\text {T}}. \end{array}$$

(21)

From the expressions of strain energy and work potential, it is evident that the total potential energy of an element depends only on its own displacement field hence, leads to simplification of Eq. (18):

$$\frac{{\partial U _{i}^{\text {M}}}}{{\partial \mathbf{{d}}_{i}^{\text {M}}}}+\frac{{\partial W _{i}^{\text {M}}}}{{\partial \mathbf{{d}}_{i}^{\text {M}}}} = 0,\quad i = 1,2, \ldots ,{N_{{\text {tot}}}}$$

(22)

while other terms automatically vanish. By substituting the approximate stress and strain measures given in Eqs. (10) and (14) into Eq. (20), and performing the derivation operation in Eq. (22), following element formulation is obtained:

$$\mathbf{{f}}_{m}^{\text {M}}=\left( {\mathbf{{k}}_{m\varepsilon }^{\text {M}} + \mathbf{{k}}_{m\chi }^{\text {M}}} \right) \mathbf{{d}}_{m}^{\text {M}},\quad m = 1,2, \ldots ,{N_{{\text {tot}}}},$$

(23)

where $\mathbf{{f}}_{m}^{\text {M}}$ denotes element load vector, and $\mathbf{{k}}_{m\varepsilon }^{\text {M}}$ and $\mathbf{{k}}_{m\chi }^{\text {M}}$ are the components of element stiffness matrix:

$$\begin{aligned}&\mathbf{{k}}_{m\varepsilon }^{\text {M}} = h E_{m} \int \limits _{ - 1}^{1} {\int \limits _{ - 1}^{1} {{{\left( {\mathbf{{B}}_{m\varepsilon } ^{\text {M}}} \right) }^{\text {T}}}{} \mathbf{{D}}_{\varepsilon }^{\text {M}}{} \mathbf{{B}}_{m\varepsilon } ^{\text {M}}J_{m} {\text {d}}\zeta {\text {d}}\eta } }, \\&\mathbf{{k}}_{m\chi }^{\text {M}} = h E_{m} \int \limits _{ - 1}^{1} {\int \limits _{ - 1}^{1} {{{\left( {\mathbf{{B}}_{m\chi } ^{\text {M}}} \right) }^{\text {T}}}{} \mathbf{{D}}_{\chi }^{\text {M}}{} \mathbf{{B}}_{m\chi } ^{\text {M}}J_{m} {\text {d}}\zeta {\text {d}}\eta } }. \end{aligned}$$

(24)

Here, the integrals can be computed by means of numerical integration scheme; i.e. Gauss Quadrature Method, for which $2 \times 2$ Gauss Points provide sufficient accuracy considering four-noded linear elements:

$$\sum \limits _{a = 1}^{2} {\sum \limits _{b = 1}^{2} {{w_{a}}{w_{b}}{\mathbf{{B}}_{m}^{\text {T}}}\left( {{\zeta _{a}},{\eta _{b}}} \right) \mathbf{{DB_{m}}}\left( {{\zeta _{a}},{\eta _{b}}} \right) J_{m}\left( {{\zeta _{a}},{\eta _{b}}} \right) } },$$

(25)

where ${{\zeta _{a}},{\eta _{b}}}$ stands for natural coordinates of Gauss points; $\left\{ {1/{\sqrt{3} },-1/{\sqrt{3} }} \right\}$, and ${{w _{a}},{w _{b}}}$ are the corresponding Gauss weights; $\left\{ {1,1} \right\}$.

Lastly, the global equation system is obtained by proper assemblage operations of element formulation:

$${\mathbf{{K}}^{\text {M}}}{\mathbf{{u}}^{\text {M}}} = {\mathbf{{f}}^{\text {M}}},$$

(26)

where ${\mathbf{{K}}^{\text {M}}}$ is global stiffness matrix, ${\mathbf{{u}}^{\text {M}}}$ is global nodal unknowns displacement vector and ${\mathbf{{f}}^{\text {M}}}$ is global nodal load vector.

2.2 Eringen’s non-local theory of elasticity

Eringen’s theory of elasticity is considered as an ‘explicit’ type non-local model for which the state of stress at a point; $\mathbf{{x}}$ is related to strain of all the neighbouring points; ${{\bar{\mathbf{x}}}}$ within a certain proximity by means of an attenuation type kernel function, and leading to a strong non-local character. In this theory, the primal fields of classical theory of elasticity is hold, allowing following linearised kinematic relation:

$$\varepsilon _{ij}^{\text {E}} = \frac{1}{2}\left( {{u_{i,j}^{\text {E}}} + {u_{j,i}^{\text {E}}}} \right) ,$$

(27)

where $\varepsilon _{ij}^{\text {E}}$ and $u_{i}^{\text {E}}$ refer to strain tensor and displacement vector, respectively.

For the continuum to be in balance, interactions between material points, that are characterized through traction forces $t_{i}^{\text {E}}$, are described in terms of symmetric stress tensor, $\sigma _{ij}^{\text {E}}$, and unit normal vector, $n_{j}$:

$$t_{i}^{\text {E}} = \sigma _{ij}^{\text {E}}{n_{j}}$$

(28)

which results in following equilibrium equation, in the absence of body forces:

$$\sigma _{ij,j}^{\text {E}} = 0.$$

(29)

For a linear, elastic and isotropic solid obeying to Eringen’s two-phase local/non-local model, which is basically a weighted mixture of local and non-local parts regulated via the fraction coefficient; $\xi \in \left( {0,1} \right]$, the constitutive relation between strain and stress tensors takes the following form (Eringen 1984; Altan 1989):

$$\sigma _{ij}^{\text {E}}\left( \mathbf{{x}} \right) = \xi t_{ij}^{\text {E}}\left( \mathbf{{x}} \right) + \left( {1 - \xi } \right) \int \limits _\varOmega {\tau \left( {r,\kappa } \right) t_{ij}^{\text {E}}\left( {{{\bar{\mathbf{x}}}}} \right) {\text {d}}\varOmega \left( {{{\bar{\mathbf{x}}}}} \right) },$$

(30)

where $t_{ij}$ is the classical (Cauchy) stress tensor:

$$t_{ij}^{\text {E}}\left( \mathbf{{x}} \right) = \lambda \varepsilon _{kk}^{\text {E}}\left( \mathbf{{x}} \right) {\delta _{ij}} + 2G\varepsilon _{ij}^{\text {E}}\left( \mathbf{{x}} \right)$$

(31)

with ${\tau \left( {{r},\kappa } \right) }$ denoting the kernel function that accounts for the long-range effects between source and neighbouring points depending on their Euclidean distance, r; i.e. $r = \left| {\mathbf{{x}} - {{\bar{\mathbf{x}}}}} \right|$, and the value of non-local parameter, $\kappa$. It is clear that, for a fraction coefficient equal to unity; $\xi = 1$, the second term in the right hand side of constitutive equation vanishes, and Cauchy continuum is recovered. As for the other extremity; $\xi = 0$, the model is reported to become ill-posed in case of smooth kernel functions (Romano and Barretta 2016; Evgrafov and Bellido 2019a), except for some specific problems of structural mechanics (Tuna and Kirca 2017). Since, in the scope of this paper, a smooth kernel function is to be utilized, $\xi >0$ is assumed to ensure existence and uniqueness of the solution. Thence, among widely used kernel functions; such as bell-shaped, error and bi-exponential (Eringen 1983; Polizzotto 2001; Ghosh et al. 2014), a function similar to the former one, which takes the following form for a 2D continuous domain, is used (Fig. 1):

$$\displaystyle \tau \left( {r,\kappa } \right) = \left\{ {\begin{array}{*{20}{c}} {\dfrac{2}{{\pi {\kappa ^{2}}}}\left( {1 - \dfrac{{{r^{2}}}}{{{\kappa ^{2}}}}} \right) }&{}{{\text {if}}\,\,r \le \kappa }\\ 0&{}{{\text {otherwise}}} \end{array}} \right\} .$$

(32)

Fig. 1

Section and actual view of two-dimensional kernel function

The chosen kernel function;

• (1) has a positive decaying nature that vanishes beyond a certain limit, which from now on is called influence zone ($R_{\text {I}}$), with a maximum value attained at $\mathbf{{x}} = {{\bar{\mathbf{x}}}}$ ($r=0$),

• (2) approaches to Dirac Delta function in case $\kappa \rightarrow 0$,

• (3) satisfies the normalization condition on ${A_{\infty} }$:

  $$\displaystyle \int \limits _{{A_{\infty} }} {\tau \left( {\left| {\mathbf{{x}},{{\bar{\mathbf{x}}}}} \right| ,\kappa } \right) {\text {d}}A = } \int \limits _{0}^{2\theta } {\int \limits _{0}^\infty {\tau \left( {r,\kappa } \right) r{\text {d}}r{\text {d}}\theta } } = 1.$$

  (33)

For the FE formulation of a 2D body agreeing with Eringen’s theory, nodal displacement vector, $\mathbf{{d}}_{m}^{\text {E}}$, and approximate strain field, ${\varvec{\varepsilon }}_{m}^{\text {E}}$, of an element m become identical to those of classical theory:

$$\begin{aligned}&\mathbf{{d}}_{m}^{\text {E}} = \left\{ {\begin{array}{*{20}{l}} {{\tilde{u}}_{x}^{1}}&{{\tilde{u}}_{y}^{1}}&\ldots&{{\tilde{u}}_{x}^{4}}&{{\tilde{u}}_{y}^{4}} \end{array}} \right\} _{m}^{\text {T}}, \\&{\varvec{\varepsilon }}_{m}^{\text {E}}\left( {\zeta ,\eta } \right) = \mathbf{{L}}_{m}^{\text {E}}{\mathbf{{N}}_{u}}{} \mathbf{{d}}_{m}^{\text {E}} = \mathbf{{B}}_{m}^{\text {E}}{} \mathbf{{d}}_{m}^{\text {E}}, \end{aligned}$$

(34)

where over tilde symbol implies that in-plane displacements; $u_{x}$ and $u_{y}$ are approximate nodal values and strain vector is described as follows:

$${\varvec{\varepsilon }}_{m}^{\text {E}} = \left\{ {\varepsilon _{11}^{\text {E}},\varepsilon _{22}^{\text {E}},2\varepsilon _{12}^{\text {E}}} \right\} _{m}^{\text {T}}.$$

(35)

Shape function matrix ${\mathbf{{N}}_{u}}$ appearing in Eq. (34) is same as the one given in Eq. (8), while differential operator matrix, $\mathbf{{L}}_{m}$ takes the following form considering natural coordinate system:

$$\mathbf{{L}}_{m}^{\text {E}} = {\left[ {\begin{array}{*{20}{c}} {\dfrac{\partial }{{\partial \zeta }}J_{11}^{ - 1} + \dfrac{\partial }{{\partial \eta }}J_{12}^{ - 1}}&{}0\\ 0&{}{\dfrac{\partial }{{\partial \zeta }}J_{21}^{ - 1} + \dfrac{\partial }{{\partial \eta }}J_{22}^{ - 1}}\\ {\dfrac{\partial }{{\partial \zeta }}J_{21}^{ - 1} + \dfrac{\partial }{{\partial \eta }}J_{22}^{ - 1}}&{}{\dfrac{\partial }{{\partial \zeta }}J_{11}^{ - 1} + \dfrac{\partial }{{\partial \eta }}J_{12}^{ - 1}} \end{array}} \right] _{m}}.$$

(36)

Accordingly, constitutive relation can be re-written for the below defined stress vector, ${{\varvec{\sigma }}_{m}^{\text {E}}}$:

$${\varvec{\sigma }}_{m}^{\text {E}} = \left\{ {\sigma _{11}^{\text {E}},\sigma _{22}^{\text {E}},\sigma _{12}^{\text {E}}} \right\} _{m}^{\text {T}}$$

(37)

by substituting the approximate strain field given in Eq. (34) into Eq. (30):

$$\begin{aligned}&{\varvec{\sigma }}_{m}^{\text {E}}\left( {\zeta ,\eta } \right) = {\xi _{m}}{} \mathbf{{t}}_{m}^{\text {E}} \\&\quad + \left( {1 - {\xi _{m}}} \right) \sum \limits _{n \in {R_{m}}} {\int \limits _{ - 1}^{1} {\int \limits _{ - 1}^{1} {\tau \left( {\kappa ,{r_{mn}}} \right) } } } {{\bar{\mathbf{t}}}}_{n}^{\text {E}}\left| {{{{{\bar{\mathbf{J}}}}}_{n}}} \right| {\text {d}}\bar{\zeta }{\text {d}}{\bar{\eta }}, \end{aligned}$$

(38)

where $R_{m}$ denotes the list of elements that reside in the influence zone of element m, which is detected by mapping the centre of function and nodes as illustrated in Fig. 2, and $r_{mn}$ indicates the Euclidean distance between the source point ${\mathbf{{x}}_{m}}\left( {\zeta ,\eta } \right) = \left\{ {{x_{m}\left( {\zeta ,\eta } \right) },{y_{m}\left( {\zeta ,\eta } \right) }} \right\}$, and neighbouring points ${{{{\bar{\mathbf{x}}}}}_{n}}\left( {{\bar{\zeta }} ,{\bar{\eta }} } \right) = \left\{ {{{\bar{\mathbf{x}}}_{n}\left( {{\bar{\zeta }} ,\bar{\eta }} \right) },{{{\bar{y}}}_{n}\left( {{\bar{\zeta }} ,{\bar{\eta }} } \right) }} \right\}$:

$${{r_{mn}} = \left| {{\mathbf{{x}}_{m}} - {{{{\bar{\mathbf{x}}}}}_{n}}} \right| = \sqrt{{{\left( {{x_{m}} - {{{\bar{x}}}_{n}}} \right) }^{2}} + {{\left( {{y_{m}} - {{{\bar{y}}}_{n}}} \right) }^{2}}} }$$

(39)

with over bar stating that the corresponding matrix/vector/scalar is written in terms of (${{\bar{\zeta }} ,{\bar{\eta }} }$).

Fig. 2

Illustration of influence zone of mth element such that $\left\{ {1,2, \ldots , 11, \ldots ,20,21} \right\} \in {R_{m}}$

Here $\mathbf{{t}}$ denotes the classical Cauchy stress vector:

$$\mathbf{{t}}_{m}^{\text {E}}\left( {\zeta ,\eta } \right) = \mathbf{{D}}_{m}^{\text {E}}{} \mathbf{{B}}_{m}^{\text {E}}{} \mathbf{{d}}_{m}^{\text {E}},\quad {{\bar{\mathbf{t}}}}_{n}^{\text {E}}\left( {{\bar{\zeta }} ,{\bar{\eta }} } \right) = \mathbf{{D}}_{n}^{\text {E}}{{\bar{\mathbf{B}}}}_{n}^{\text {E}}{} \mathbf{{d}}_{n}^{\text {E}}$$

(40)

while elasticity matrix, $\mathbf{{D}}_{m}^{\text {E}}$, is expressed as follows under plane strain assumption:

$$\begin{aligned}&\mathbf{{D}}_{m}^{\text {E}} = {E_{m}}{\mathbf{{D}}^{\text {E}}}, \\&{\mathbf{{D}}^{\text {E}}} = \frac{1}{{\left( {1 + \nu } \right) }}\left[ {\begin{array}{*{20}{c}} {\frac{{\left( {1 - \nu } \right) }}{{\left( {1 - 2\nu } \right) }}}&{}{\frac{\nu }{{\left( {1 - 2\nu } \right) }}}&{}0\\ {\frac{\nu }{{\left( {1 - 2\nu } \right) }}}&{}{\frac{{\left( {1 - \nu } \right) }}{{\left( {1 - 2\nu } \right) }}}&{}0\\ 0&{}0&{}{\frac{1}{2}} \end{array}} \right] . \end{aligned}$$

(41)

Finally, the element formulation of a domain, discretised with ${N_{{\text {tot}}}}$ FEs is obtained by means of principle of total potential energy:

$$\frac{{\partial {\varPi ^{\text {E}}}}}{{\partial \mathbf{{d}}_{i}^{\text {E}}}} = \frac{{\sum \nolimits _{m = 1}^{{N_{{\text {tot}}}}} {\partial \varPi _{m}^{\text {E}}} }}{{\partial \mathbf{{d}}_{i}^{\text {E}}}} = 0,\quad i = 1,2, \ldots ,{N_{{\text {tot}}}}$$

(42)

for which the total potential energy functional of an element m, $\varPi _{m}^{\text {E}}$, is expressed in terms of elastic strain energy, $U_{m}^{\text {E}}$, and work potential, $W_{m}^{\text {E}}$:

$$\varPi _{m}^{\text {E}} = U_{m}^{\text {E}}\left[ {\left\{ {\left. {\mathbf{{d}}_{n}^{\text {E}}} \right| n \in {R_{m}}} \right\} } \right] + W_{m}^{\text {E}}\left[ {\mathbf{{d}}_{m}^{\text {E}}} \right] ,$$

(43)

where

$$\begin{aligned}&U_{m}^{\text {E}} = \dfrac{h}{2}\int \limits _{ - 1}^{1} {\int \limits _{ - 1}^{1} {{{\left( {{\varvec{\varepsilon }}_{m}^{\text {E}}} \right) }^{\text {T}}}{\varvec{\sigma }}_{m}^{\text {E}}J_{m} {\text {d}}\zeta {\text {d}}\eta } } \\&W_{m}^{\text {E}} =-\displaystyle \sum \limits _{j = 1}^{4} {\int \limits _{ - 1}^{1} {{{\left( {\mathbf{{d}}_{m}^{\text {E}}} \right) }^{\text {T}}}{{\left. {\mathbf{{N}}_{u}^{\text {T}}} \right| }_{j}}{{\left. {{{\mathbf{{fs}}}_{m}}} \right| }_{j}}{\text {d}}{l_{j}}} } - {\left( {\mathbf{{d}}_{m}^{\text {E}}} \right) ^{\text {T}}}{} \mathbf{{q}}_{m}^{\text {E}}. \end{aligned}$$

(44)

Here the relations mentioned in Eq. (21) for ${{\text {d}}{l_{j}}}$, ${{{\left. {{{\mathbf{{fs}}}_{m}}} \right| }_{j}}}$ and ${{{\left. {\mathbf{{N}}_{u}\left( {\zeta ,\eta } \right) } \right| }_{j}}}$ hold while concentrated load vector is defined as

$$\mathbf{{q}}_{m}^{\text {E}} = \left\{ {\begin{array}{*{20}{l}} {f_{x}^{1}}&{f_{y}^{1}}&\ldots&{f_{x}^{4}}&{f_{y}^{4}} \end{array}} \right\} _{m}^{\text {T}}.$$

(45)

Due to the strong non-local character of Eringen’s model, accounting for long-range interactions, elastic strain energy of an element m depends on the displacement field of all the elements that reside in the influence zone of the corresponding element; ${R_{m}}$, hence cannot be omitted when taking the derivatives in Eq. (42):

$$\displaystyle \frac{{\displaystyle \sum \nolimits _{m|i \in {R_{m}}} {\partial U _{m}^{\text {E}}} }}{{\partial \mathbf{{d}}_{i}^{\text {E}}}}+\frac{{\partial W _{i}^{\text {E}}}}{{\partial \mathbf{{d}}_{i}^{\text {E}}}} = 0,\quad i = 1,2, \ldots ,{N_{{\text {tot}}}}.$$

(46)

By substituting strain and stress measures given in Eqs. (34) and (38) into the elastic strain energy, following formulation is obtained for an element m:

$$\begin{aligned} \displaystyle \mathbf{{f}}_{m}^{\text {E}} &= {\xi _{m}}{} \mathbf{{k}}_{m}^{\text {E}} + \left( {1 - {\xi _{m}}} \right) \mathbf{{k}}_{mm}^{\text {E}}{} \mathbf{{d}}_{m}^{\text {E}} \\&\quad +\displaystyle \sum _{\begin{array}{c} {\scriptstyle n \in {R_{m}}}\\ {\scriptstyle n \ne m} \end{array}} {\dfrac{{\left( {1 - {\xi _{m}}} \right) }}{2}{} \mathbf{{k}}_{mn}^{\text {E}}{} \mathbf{{d}}_{n}^{\text {E}}} \\&\quad +\displaystyle \sum _{\begin{array}{c} {\scriptstyle n|m \in {R_{n}}}\\ {\scriptstyle n \ne m} \end{array}} {\dfrac{{\left( {1 - {\xi _{n}}} \right) }}{2}{{\left( {\mathbf{{k}}_{nm}^{\text {E}}} \right) }^{\text {T}}}{} \mathbf{{d}}_{n}^{\text {E}}}, \end{aligned}$$

(47)

where $\mathbf{{f}}_{m}^{\text {E}}$ denotes element load vector, and $\mathbf{{k}}_{m}^{\text {E}}$, $\mathbf{{k}}_{mm}^{\text {E}}$, $\mathbf{{k}}_{mn }^{\text {E}}$ and $(\mathbf{{k}}_{mn }^{\text {E}})^{\text {T}}$ are the components of element stiffness matrix:

$$\begin{aligned}&{\mathbf{{k}}_{m}^{\text {E}} = h{E_{m}}\int \limits _{ - 1}^{1} {\int \limits _{ - 1}^{1} {{{\left( {\mathbf{{B}}_{m}^{\text {E}}} \right) }^{\text {T}}}{\mathbf{{D}}^{\text {E}}}{} \mathbf{{B}}_{m}^{\text {E}}{} {J_{m}}{\text {d}}\zeta {\text {d}}\eta } } ,{} {} {} } \\&{\mathbf{{k}}_{mn}^{\text {E}} = h{E_{n}}\int \limits _{ - 1}^{1} {\int \limits _{ - 1}^{1} {\int \limits _{ - 1}^{1} {\int \limits _{ - 1}^{1} {{} {\mathbf{{K}}_{mn}}{\text {d}}{\bar{\zeta }} {\text {d}}{\bar{\eta }} {\text {d}}\zeta {\text {d}}\eta } } } } }, \end{aligned}$$

(48)

and

$$\begin{aligned}&{\mathbf{{K}}_{mn}} = \tau \left( {{r_{mn}},\kappa } \right) {\left( {\mathbf{{B}}_{m}^{\text {E}}} \right) ^{\text {T}}}{\mathbf{{D}}^{\text {E}}}{{\bar{\mathbf{B}}}}_{n}^{\text {E}}{} {{{\bar{J}}}_{n}}{J_{m}}. \end{aligned}$$

(49)

The first term in element formulation [Eq. (47)] represents the local part of two-phase model, while others are related to non-locality. In fact, the third and fourth terms that are responsible for column-wise expansion of each stiffness matrix, arise from the long-range interactions in-between elements. To be more specific, the former indicates the contribution of others on mth element, whereas the latter corresponds to the influence of mth element on others. According to the expression given in Eq. (49), these terms become identical for a homogeneous domain having a uniform Young’s modulus and fraction coefficient.

Similar to micropolar continuum, integration operations are carried out adopting Gauss Quadrature Method for which the number of Gauss points is arranged to minimize the numerical error.

At the last step, global equation system is achieved by performing proper assemblage operations:

$${\mathbf{{K}}^{\text {E}}}{\mathbf{{u}}^{\text {E}}} = {\mathbf{{f}}^{\text {E}}},$$

(50)

where ${\mathbf{{K}}^{\text {E}}}$ is global stiffness matrix, ${\mathbf{{u}}^{\text {E}}}$ is global nodal unknowns displacement vector and ${\mathbf{{f}}^{\text {E}}}$ is global nodal force vector.

3 Topology optimization problem

3.1 Problem formulation

Topology optimization problem considered herein aims to find the optimal material distribution that maximizes the stiffness of a structure by minimizing the compliance function under a given set of constraints. For a self-weight free domain, parametrised by the element-based design variables; i.e. material densities, $\rho _{m}$, the corresponding mathematical formulation takes the following form (Bendsøe 1989; Sigmund 2001; Bendsoe and Sigmund 2013):

$$\begin{array}{*{20}{l}}\displaystyle {{\text {find}}:}&{}{{\varvec{\rho }} = \left\{ {{\rho _{1}},{\rho _{2}}, \ldots {\rho _{{{N}_{{\text {tot}}}}}}} \right\} }\\ {{\text {minimize}}:}&{}{c\left( {{\varvec{\rho }}} \right) = {\mathbf{{u}}^{\text {T}}}{} \mathbf{{f}}}\\ {{\text {subj}}.{} {} {\text {to}}:}&{}{\mathbf{{r}}\left( {{\varvec{\rho }}} \right) = \mathbf{{Ku}} - \mathbf{{f}} = \mathbf{{0}}}\\ {}&{}{g\left( {{\varvec{\rho }}} \right) = \dfrac{V_{\text {tot}}}{{{V_{0}}}} - {V_{\text {f}}} \le 0}\\ {}&{}{0 \le {\rho _{m}} \le 1\quad m = 1,2, \ldots ,{{\text {N}}_{{\text {tot}}}}}, \end{array}$$

(51)

where the displacement vector, $\mathbf {u}$, stiffness matrix, $\mathbf {K}$ and total material volume, $V_{\text {tot}}$, depends on the design variables vector $\varvec{\rho }$; i.e. $\forall {\rho _{m}} \in {\varvec{\rho }}$ with 0 and 1 referring to void and solid parts, respectively. c stands for the structural compliance function, which is twice of the elastic strain energy (or work potential for conservative systems), while $\mathbf{{r}}$ indicates residual unbalanced load vector, and g refers to constraint function limiting the material volume to a desired fraction, $V_{\text {f}}$, with $V_{0}$ being the volume of the design domain.

3.2 Density filter and Heaviside projection method

As the direct use of design variables in local elastic analysis causes the common issue of checkerboard pattern (i.e. adjacent solid–void elements, see Fig. 3a), and mesh dependence (Jog and Haber 1996; Sigmund and Petersson 1998), the formulation needs to be improved through different schemes, such as filtering, perimeter/gradient control methods. Among those, the sensitivity (Sigmund 1997) and density (Bourdin 2001; Bruns and Tortorelli 2001) filters become the most preferred strategies due to their simple, yet efficient character.

Fig. 3

The a original $\varvec{\rho }$, b filtered $\varvec{{\tilde{\rho }}}$, and c projected $\varvec{{{\hat{\rho }} }}$ density fields

Even though sensitivity filter is criticized as leading to an ambiguous minimized function, a relatively recent study by Sigmund and Maute (2012) adopts a different perspective. The study alludes the analogy between non-local continuum models and sensitivity regularization scheme by suggesting that the minimum compliance problem with sensitivity filtering does, in fact, correspond to minimization of strain energy of a non-local medium. Similar results are also reported for non-local linear diffusion problem investigated by Evgrafov and Bellido (2019b) by highlighting the redundancy of external regularization techniques (e.g. filtering) for the non-local model. As slightly different observations were made by Li and Khandelwal (2015) and Li et al. (2017), in which the mitigation of checkerboard pattern is attributed to the use of higher-order element formulation, and the final topologies are reported to be mesh-dependent, it can be concluded that some non-local models need additional regularization in connection with topology optimization, whereas others do not.

In order to see what happens in micropolar and Eringen’s theories, the case without filtering is also investigated. However, it is only briefly commented on in the subsequent sections since the main purpose is to compare final topologies of different non-local continua not only with each other, but also with Cauchy medium that requires filtering. In doing so, the density filter, proposed by Bourdin (2001) and Bruns and Tortorelli (2001), is adopted herein due to its ability on providing two separate density fields and on enabling the straight forward incorporation of the element removal and reintroduction strategy (Bruns and Tortorelli 2003). As illustrated in Fig. 3b, filtered densities, ${\tilde{\varvec{\rho }} }$, are obtained by mapping the original densities, ${\varvec{\rho }}$, onto design domain with taking into account the status of neighbour elements set, $N_{m}$, with the aid of a weighting function, $w_{mq}$:

$$\begin{aligned} \displaystyle&{{{\tilde{\rho }} }_{m}}\left( {\varvec{\rho }} \right) = \dfrac{{\displaystyle \sum \nolimits _{q \in {N_{m}}} {{w_{mq}}{\rho _{q}}} }}{{\displaystyle \sum \nolimits _{q \in {N_{m}}} {{w_{mq}}} }}, \\ \end{aligned}$$

(52)

where

$$\begin{aligned}&{{w_{mq}} = 1 - \dfrac{{{\Delta _{mq}}}}{{{r_{\min }}}}}\quad {\text {and}}\quad {q \in {N_{m}}}\quad {{} {} {} {\text {if}}{} {} {} {} {} {\Delta _{mq}} \le {r_{\min }}}. \end{aligned}$$

(53)

Here ${{\Delta _{mq}}}$ is the centre to centre distance between elements m, q, while $r_{\min }$ refers to user defined filter radius, that is chosen in accordance with the originally imposed constraints (e.g. size of FEs Sigmund and Maute 2013); ${r _{\min }}$ must be greater than the mesh size to include the influence of, at least the nearest, neighbour elements.

Even though density filter smoothens the original field and yields mesh-independent results that automatically preserves the material volume, the final configuration might suffer from undesirable transition region (called grey zone) with intermediate density values (Bourdin 2001; Bruns and Tortorelli 2001). A way to alleviate this drawback is to diminish the filter radius in the expense of having configurations with very thin members or using projection method that amplifies the continuous filtered field to desired binary solution (Fig. 3c) by means of a Heaviside function (Guest et al. 2004; Sigmund 2007; Guest 2009; Kawamoto et al. 2011; Xu et al. 2010; Guest et al. 2011; Wang et al. 2011):

$$\displaystyle {{{\hat{\rho }} }_{m}}\left( {\varvec{\rho }} \right) = H\left( {{{{\tilde{\rho }} }_{m}}} \right) .$$

(54)

Here ${{{\hat{\rho }} }}$ stands for physical densities, and H refers to conducted Heaviside projection function which is approximated to have a smooth continuous differentiable character. Among those, the one promoting the material formation is employed throughout this study to relate the filtered and physical densities (Guest et al. 2004):

$$\displaystyle {{{\hat{\rho }} }_{m}} = 1 - {{\text {e}}^{ - \beta {{{\tilde{\rho }} }_{m}}}} + {{\tilde{\rho }}_{m}}{{\text {e}}^{ - \beta }},$$

(55)

where the constant $\beta$ tailors the curvature of the Heaviside function such that it has a linear characteristic for $\beta =0$, while approaches to step function for $\beta \rightarrow \infty$ (see Fig. 4).

Fig. 4

Heaviside projection function for different curvature parameters, $\beta$

To ensure a stable convergence and avoid local minima, Heaviside projection method is generally used with a continuation scheme in which $\beta$ is gradually increased from an initial value, $\beta _{\text {ini}}$, to a desired magnitude, $\beta _{\max }$, as the optimization progresses (Guest et al. 2004; Andreassen et al. 2011), nevertheless bad or perturbated configurations can be obtained as enforcing volume constraint is not guaranteed unlike density filter (Xu et al. 2010; Engstrom 2016; Ferrari and Sigmund 2020):

$$\displaystyle \sum \limits _{m = 1}^{{N_{{\text {tot}}}}} {{\rho _{m}}{v_{m}}} = \sum \limits _{m = 1}^{{N_{{\text {tot}}}}} {{{{\tilde{\rho }} }_{m}}{v_{m}}} \ne \sum \limits _{m = 1}^{{N_{{\text {tot}}}}} {{{{\hat{\rho }} }_{m}}{v_{m}}},$$

(56)

where $v_{m}$ refers to volume of an element.

To mitigate this violation, the parameter increase is adjusted in a volume preserving manner: at each $t_{\beta _{\max }} = 50$ iterations or when the convergence is achieved for $\beta ^{t} < \beta _{\max }$, $\beta$ is doubled for the next iteration; ${\beta ^{t+1}} = 2{\beta ^{t}} \le \beta _{\max }$, where t refers to number of iteration. In case, the volume constraint is not satisfied to a certain extend due to this sudden increase, $\beta$ is decreased by 75%; $\beta =0.75\beta$, until the condition is met.

It should be noted that, since the continuous updating scheme of $\beta$ is computationally inefficient, simple modifications were proposed and successfully employed by researchers (Guest et al. 2011; Behrou et al. 2021). Also, more enhanced projection filters and robust strategies can be used to keep the volume constraint preserved (Xu et al. 2010; Wang et al. 2011; Ferrari and Sigmund 2020), but not considered herein.

3.3 Material interpolation

In the present study, material properties are linked to the physical element densities, $\varvec{\hat{\rho }}$, with the aid of an artificial power-law approach, so-called modified SIMP method (Bendsøe 1989; Zhou and Rozvany 1991; Sigmund 2007):

$$\begin{array}{*{20}{l}}\displaystyle {{E_{m}}\left( {\varvec{\rho }} \right) = {E_{\min }} + {\hat{\rho }} _{m}^p\left( {\varvec{\rho }} \right) \left( {{E_{0}} - {E_{\min }}} \right) }. \end{array}$$

(57)

Here $E_{0}$ and $E_{\min }$ stands for the Young’s modulus of solid and void, respectively, while to ensure the non-singularity of global stiffness matrix, a very small positive number is assigned for ${E_{\min }}$: ${10^{ - 9}}{E_{0}}$ which can be dismissed in case an element removal and reintroduction strategy is introduced into the algorithm:

$$\begin{array}{l}\displaystyle {E_{m}}\left( {\varvec{\rho }} \right) = {E_{0}} {{\hat{\rho }}} _{m}^p\left( {\varvec{\rho }} \right) . \end{array}$$

(58)

The penalization factor p ($p \ge 1$) is typically taken as $p=3$ (Sigmund 2001, 2007; Andreassen et al. 2011), and guides the problem towards a solid/void solution by penalizing intermediate density values (Bendsøe and Sigmund 1999). It should be noted that, choosing p too large or too small either cause fast convergence to a local minima or large grey zones, respectively (Sigmund and Maute 2013). In some studies with micropolar solids, different penalization parameters for translational and rotational parts of constitutive relation are considered (Rovati and Veber 2007; Veber and Taliercio 2012), while here it is taken identical.

3.4 Sensitivity analysis and update scheme

For solving the problem given in Eq. (51), a gradient-based optimization procedure established upon the optimality criteria method (Bendsøe 1995) is followed. First, the Lagrangian scheme is formulated by augmenting the objective function considering the volume constraint:

$$\mathcal {L} = c + \lambda g,$$

(59)

where $\lambda$ is the positive Lagrangian multiplier. Second, with exploiting the fact that the gradient of Eq. (59) is zero when the optimality condition is met, the equation system to be solved is obtained:

$$\frac{{\partial {{\mathcal {L}}}}}{{\partial {\rho _{m}}}} = \frac{{\partial c}}{{\partial {\rho _{m}}}} + \lambda \frac{{\partial g}}{{\partial {\rho _{m}}}}=0,\quad m = 1,2, \ldots {N_{{\text {tot}}}}$$

(60)

whereas due to adopted filtering and projection operations, chain rule must be employed to accurately obtain the sensitivities of compliance and constraint functions with respect to design variables:

$${\frac{{\partial \psi }}{{\partial {\rho _{m}}}} = \displaystyle \sum \limits _{q \in {N_{m}}} {\dfrac{{\partial \psi }}{{\partial {{{\hat{\rho }} }_{q}}}}\dfrac{{\partial {{{\hat{\rho }} }_{q}}}}{{\partial {{{\tilde{\rho }} }_{q}}}}\dfrac{{\partial {{{\tilde{\rho }} }_{q}}}}{{\partial {\rho _{m}}}}} }.$$

(61)

After some mathematical manipulations, the derivative of compliance function is obtained as follows for a self-weight free domain (i.e. external load vector is independent of the density field):

$$\dfrac{{\partial c}}{{\partial {{{\hat{\rho }} }_{q}}}} = \dfrac{{\partial {\mathbf{{U}}^{\text {T}}}}}{{\partial {{{\hat{\rho }} }_{q}}}}{} \mathbf{{KU}} = - {\mathbf{{U}}^{\text {T}}}\dfrac{{\partial \mathbf{{K}}}}{{\partial {{{\hat{\rho }} }_{q}}}}{} \mathbf{{U}}$$

(62)

which can also be represented in terms of element stiffness matrices:

$$\begin{aligned} \dfrac{{\partial {c^{\text {M}}}}}{{\partial {{\hat{\rho }} _{q}}}}&= -\dfrac{{\partial {E_{q}}}}{{\partial {{\hat{\rho }} _{q}}}}{\left( {\mathbf{{d}}_{q}^{\text {M}}} \right) ^{\text {T}}}{} \mathbf{{k}}_{0}^{\text {M}}{} \mathbf{{d}}_{q}^{\text {M}},\\ \dfrac{{\partial {c^{\text {E}}}}}{{\partial {{\hat{\rho }} _{q}}}} &= -\dfrac{{\partial {E_{q}}}}{{\partial {{\hat{\rho }} _{q}}}}{\left( {\mathbf{{d}}_{q}^{\text {E}}} \right) ^{\text {T}}}{\xi _{q}}{} \mathbf{{k}}_{0}^{\text {E}}{} \mathbf{{d}}_{q}^{\text {E}}\\ \quad - \dfrac{{\partial {E_{q}}}}{{\partial {{\hat{\rho }} _{q}}}}{\left( {\mathbf{{d}}_{q}^{\text {E}}} \right) ^{\text {T}}}\left( {1 - {\xi _{q}}} \right) \mathbf{{k}}_{qq0}^{\text {E}}{} \mathbf{{d}}_{q}^{\text {E}}\\ \quad - \dfrac{{\partial {E_{q}}}}{{\partial {{\hat{\rho }} _{q}}}}\displaystyle \sum _{\begin{array}{c} {\scriptstyle n|q \in {R_{n}}}\\ \scriptstyle q \ne n \end{array}} {{{\left( {\mathbf{{d}}_{n}^{\text {E}}} \right) }^{\text {T}}}\left( {1 - {\xi _{n}}} \right) \mathbf{{k}}_{nq0}^{\text {E}}{} \mathbf{{d}}_{q}^{\text {E}}}, \end{aligned}$$

(63)

where

$$\frac{{\partial {E_{q}}}}{{\partial {{\hat{\rho }} _{q}}}} = p\left( {{E_{0}} - {E_{\min }}} \right) {{\hat{\rho }} _{q}}^{p - 1}$$

(64)

and $\mathbf{{k}}_{0}^{\text {M}}$, $\mathbf{{k}}_{0}^{\text {E}}$, $\mathbf{{k}}_{qq0}^{\text {E}}$ and $\mathbf{{k}}_{nq0}^{\text {E}}$ are non-dimensional element stiffness matrices depending only on Poisson’s ratio. Calculating other derivatives in Eq. (61) is a straightforward task, and results in:

$$\begin{aligned}&\dfrac{{\partial g}}{{\partial {{{\hat{\rho }} }_{q}}}} = \dfrac{{\displaystyle \sum \nolimits _{m = 1}^{{N_{{\text {tot}}}}} {\dfrac{{\partial \left( {{{{\hat{\rho }} }_{m}}{v_{m}}} \right) }}{{\partial {{{\hat{\rho }} }_{q}}}}} }}{{{V_{0}}}} = \dfrac{{{v_{q}}}}{{{V_{0}}}}, \\&\dfrac{{\partial {{{\hat{\rho }} }_{q}}}}{{\partial {{{\tilde{\rho }} }_{q}}}} = \beta {e^{ - \beta {{{\tilde{\rho }} }_{q}}}} + {{\text {e}}^{ - \beta }}, \\&\dfrac{{\partial {{{\tilde{\rho }} }_{q}}}}{{\partial {\rho _{m}}}} = \dfrac{{{w_{mq}}}}{{w_{q}}},\quad {{w_{q}}}={{\displaystyle \sum \limits _{r \in {N_{q}}} {{w_{qr}}} }}. \end{aligned}$$

(65)

Finally, with employing fixed-point iteration method, the corresponding density field that fulfil Eq. (60) is determined:

$$\rho _{m}^{t + 1} = \rho _{m}^{t}\dfrac{{-\dfrac{{\partial c}}{{\partial {\rho _{m}}}}}}{{\lambda \dfrac{{\partial g}}{{\partial {\rho _{m}}}}}} = \rho _{m}^{t}{B_{m}},\quad m = 1,2, \ldots {N_{{\text {tot}}}}.$$

(66)

By further adjusting $B_{m}$ with introducing a so-called damping parameter, ${\bar{\text {n}}}$, for smoothing its value, and a positive-move limit, ${\bar{\text {m}}}$, for defining the update range (Bendsøe 1995; Sigmund 2001; Andreassen et al. 2011), the well-known form of heuristic updating scheme is derived:

$$\begin{array}{l} \rho _{m}^{t + 1} = \\ \left\{ {\begin{array}{*{20}{l}} {\max \left( {0,\rho _{m}^{t} - {\bar{\text {m}}} } \right) }&{}{{\text {if}}\,\rho _{m}^{t} B_{m}^{\bar{ {\text {n}}}} \le \max \left( {0,\rho _{m}^{t} - {\bar{\text {m}}} } \right) \,}\\ {\min \left( {1,\rho _{m}^{t} + {\bar{\text {m}}} } \right) }&{}{{\text {if}}\,\rho _{m}^{t}B_{m}^{\bar{ {\text {n}}}} \ge \min \left( {1,\rho _{m}^{t} + {\bar{\text {m}}} } \right) }\\ {\rho _{m}^{t}B_{m}^{\bar{ {\text {n}}}}}&{}{{\text {otherwise}}} \end{array}} \right\} , \end{array}$$

(67)

where the bisection method is simultaneously applied to detect the value of Lagrangian multiplier $\lambda$, that satisfies the user defined volume constraint, for which the total material volume, $V_{\text {tot}}$, is calculated continuously using physical densities [see Eq. (56)].

Similar to existing literature (Ferrari and Sigmund 2020; Behrou et al. 2021), the design domain is assumed to be converged to final configuration when following conditions are simultaneously met for a parameter $\beta$ equals to the user defined maximum value $\beta _{\max }$; $\beta ^{t}= \beta _{\max }$:

$$\begin{array}{l} \dfrac{{{{\left\| {{{{\varvec{{\hat{\rho }} }}}^{t + 1}} - {{{\varvec{{\hat{\rho }} }}}^{t}}} \right\| }_{2}}}}{{\sqrt{{N_{{\text {tot}}}}} }}< {10^{ - 4}},\quad \dfrac{{\left| {{c^{t + 1}} - {c^{t}}} \right| }}{{{c^{t}}}} < {10^{ - 6}}, \end{array}$$

(68)

where ${\left\| {} \right\| _{2}}$ refers to second norm of the vector.

3.5 Element removal/reintroduction scheme

When conducting Eringen’s non-local model, the presence of low-density elements might lead to excessive distortion and unrealistic nodal displacement fields that consequently results in misleading energy distribution and false optimal topologies, a phenomenon also encountered during optimization of non-linear structures (Bruns and Tortorelli 2003). Even though in Cauchy and micropolar models the numerical singularity arising from zero density can be tackled by the introduction of a minimum of elasticity modulus, $E_{\min }$ as in Eq. (57), in Eringen’s model this is not the case as the stiffness matrix already admits a higher condition number even in case of uniform density distribution. Combined with the material singularities, the inversion of the stiffness matrix is bound to errors, which manifests itself as highly distorted elements. To circumvent the associated numerical instabilities the current algorithm is improved by adopting the systematic element removal and reintroduction strategy proposed by Bruns and Tortorelli (2003).

The method is grounded on the idea that, for a penalization parameter greater than two ($p>2$), elements with physical densities below a prescribed threshold, $\rho _{\text {tol}}$; i.e. ${{{\hat{\rho }} }_{m}} \le {\rho _{{\text {tol}}}}$ carry a negligible contribution to the physical response of the model; hence can be dismissed from the structural analysis, alongside with the nodes completely surrounded by such elements (Fig. 5). This can simply be achieved by excluding the marked elements from global stiffness matrix, and rearranging the equation system to be solved by eliminating the rows and columns that are related to the constrained DOFs of the marked nodes, while the sensitivity analysis is performed for the entire model due to the propagation effect of density filter which might yield non-zero derivatives:

$$\forall {{{\hat{\rho }} }_{m}} \le {\rho _{{\text {tol}}}}:\exists \frac{{\partial \psi }}{{\partial {\rho _{m}}}} \ne 0\quad {\text {if}}\,\,\left( {q \in {N_{m}} \vee \frac{{\partial \psi }}{{\partial {{{\hat{\rho }} }_{q}}}} \ne 0} \right) .$$

(69)

For the same reason, the adopted scheme allows previously removed elements to be reintroduced back in a very straightforward manner. However attention must be paid to select an optimal threshold magnitude that avoids chatter between successive iterations or development of disconnected regions (i.e. structural island) which requires further treatment (Bruns and Tortorelli 2003). The way of doing this is to perform numerical experiments for various tolerance values which is suggested as $\rho _{\text {tol}}=0.05$ by Bruns and Tortorelli (2003) and $\rho _{\text {tol}}=0.1$ by Behrou et al. (2021) for different types of optimization problems, based on avoiding different final topologies. In this study, $\rho _{\text {tol}}$ up to 0.2 is considered in order to observe if it would affect the results, as presented in the subsequent sections.

Fig. 5

Illustration of element removal scheme

3.6 Algorithm and remarks

In this subsection, the algorithm is summarized briefly with highlighting the key points.

• (1) The FE model is initialized with discretisation of the domain into equi-sized four-node linear elements for which the neighbour elements set and corresponding weights that are required for density filter are attained.

• (2) Each iteration of the optimization loop starts with detecting/marking low-density elements and the nodes surrounded by such elements for removal. The structural analysis is then performed for the given loading and boundary conditions to obtain the nodal unknowns vector.

• (3) The resulting compliance function is calculated and the sensitivity analyses are performed for the whole domain to achieve the volume preserving physical and other density fields which are to be saved for the next iteration.

• (4) The algorithm checks if the termination criteria are fulfilled in order to decide whether to continue the topology optimization loop or not.

4 Numerical examples

In this section individual and comparative example problems are investigated on the basis of ‘implicit/weak’ micropolar (Cosserat), ‘explicit/ strong’ Eringen’s non-local models and classical theory of elasticity in order to validate the in-house code, and highlight the influence of size effects and different non-local theories on optimal topologies. In all the examples the material update scheme is endowed with density filter in conjunction with Heaviside projection method (Guest et al. 2004), and element removal/reintroduction strategy (Bruns and Tortorelli 2003), the effects of which are also put into evidence. All the units throughout the example problems are consistent.

4.1 Validation

4.1.1 Cauchy medium

Validation of the in-house code for Cauchy medium is performed through a classical MBB beam problem (i.e. half model of three-point bending test), in which the effects of element removal/reintroduction scheme along with Heaviside projection method (HPM) is also examined. For this purpose, a rectangular domain, with a half length of $L = 60$ and a height of $H = L/3$, filled with a uniform design variable field of $\rho _{{\text {ini}}}$ at the initial configuration, is considered (Fig. 6).

Fig. 6

Schematic of design domain of half MBB Cauchy beam model (i.e. beam under three-point bending)

The optimal material distributions, that are obtained for plane stress condition and a filter radius of ${r_{\min }} = 0.03L$, are compared with the ones reported in Andreassen et al. (2011) for the following parameter set:

$$\begin{aligned}&E = 1.0,\quad {V_f} = 0.5,\quad \nu = 0.3,\quad {\bar{{\text {m}}}} = 0.2,\quad {\bar{{\text {n}}}} = 0.5 \\&{\beta _{ini}} = 1,\quad {\beta _{\max }} = 36,\quad {\rho _{{\text {ini}}}} = V_{\text {f}},\quad {p} = 3, \end{aligned}$$

(70)

where $\rho _{{\text {ini}}}$ can be adjusted to ensure that the physical density field ${{\hat{\rho }}_{\text {ini}} }$ conforms to the volume constraint for given parameter $\beta _{\text {ini}}$.

The results, illustrated in Fig. 7, for two different mesh discretisation with $60 \times 20$ and $150 \times 50$ elements respectively, exhibit almost perfectly solid and void domains, and are found to be in a very good agreement with the literature (Andreassen et al. 2011) where slight variations can be attributed to difference in $\beta _{\max }$ values. Moreover, the analyses, that are repeated for various threshold values; ${\rho _{\text {tol}}=0.10,\,0.20}$, clearly demonstrate the independence of the optimised configurations from element removal/reintroductions scheme (Bruns and Tortorelli 2003). It also reveals the versatility of the method, since no significant discrepancy neither in terms of compliance function nor in terms of material distribution is obtained between the original and element removed models, while for the latter, total number of elements is reduced up to 49% by discarding structurally insignificant low-density elements.

Fig. 7

Optimised design of half MBB plate, modelled as Cauchy medium, reported for various element removal threshold values, ${\rho _{{\text {tol}}}}$, with specifying the compliance function, c, and number of remaining elements ${(N_{{\text {tol}}})_{{\text {final}}}}$

As depicted in Fig. 8, the structural compliance function is decreased about 71% as the optimization progresses, where the stepped characteristic of the curve originates from the update scheme of Heaviside projection parameter $\beta$. Note that, a stable convergence is ensured by limiting the increase in a volume preserving manner, where a violation up to 4% is permitted as numerical experiments reveal no difference for smaller deviations. Although, the examples could be extended for larger values of ${\rho _{\text {tol}}}$, it is not preferred herein due to possible formation of structural island in the early iteration steps, which might require introduction of additional constraints (Bruns and Tortorelli 2003).

Fig. 8

Evaluation of compliance function (c), projection parameter ($\beta$) and material distribution for half model of Cauchy plate under three-point bending (MBB) (mesh: $150 \times 50$ and $\rho _{\text {tol}}=0.1$)

4.1.2 Micropolar medium

For validation purposes in case of micropolar medium, a benchmark problem of cantilevered beam with a tip force is studied, considering following material constants; $N=0.8$, $l_{c} = 0.075L$ (Rovati and Veber 2007). The rectangular design domain is assumed to have an aspect ratio of $L/H=5/2$ (Fig. 9), while the parameters related to optimization procedure are identical to the previous example except for ${V_{\text {f}}}=0.3$, $r_{\min }=0.04L$ and ${\rho _{\text {tol}}=0.1}$.

Fig. 9

Schematic of design domain of cantilevered micropolar beam model with a tip force

The emerging topologies, depicted in Fig. 10 are in a very good agreement with corresponding literature (Rovati and Veber 2007) where the increased capacity of flexural resistance of material points of micropolar medium results in a structure that is formed by curved beam-like members. Note that, slight deviations with reference study arise from different filtering schemes (sensitivity vs. density).

Fig. 10

Variation of structural compliance (c) and optimised configurations of tip loaded cantilever micropolar plates considering cases with and without Heaviside projection method (HPM)

Although the final designs seem to be independent of the discretisation, increased number of elements improves the resolution and leads to sharper boundaries when combined with Heaviside method (HPM). Moreover, the computational advantage of element removal and reintroduction scheme is once again demonstrated with remarkable reduction of 66% in total number of elements during the process (Bruns and Tortorelli 2003). Finally, as illustrated through Fig. 11, thinner members disappear as the filter radius is increased, and density distribution becomes smoother with a raise in grey zone which seems to be persisted for the largest filter radius; $r_{\min }=0.06L$.

Fig. 11

Variation of compliance function (c) and optimised configurations of tip loaded cantilever micropolar plates with respect to filter radius ($r_{\min }/L$), considering cases with and without Heaviside projection method (HPM) (mesh: $120 \times 48$)

Figure 12 shows the final topologies of the same problem for coarse and fine discretization without any filters. For this particular case, the results turn out to be not only free of checkerboard pattern, but also mesh-independent despite the use of linear FEs. Note that the same problem with even finer discretization is examined in Rovati and Veber (2007) and same final topology is reported. Although the findings conform the suggestion of Sigmund and Maute (2012) on the analogy between optimization of non-local continuum models and minimum compliance problem with sensitivity filtering scheme, it is important to note that a rigorous mathematical analysis is required to examine the role of internal scale parameters on topology optimization problem which is out of the scope of this paper.

Fig. 12

Optimised configurations of tip loaded cantilever micropolar plates without filtering

4.2 Optimization of uniaxially loaded Eringen’s plate

Following the validation of the present optimization procedure and auxiliary algorithms, the next step is to study the contribution of long-range interactions on optimal topologies within the framework of Eringen’s non-local theory of elasticity, which is seemingly reported for the first time in the literature. As the first step of doing so, an example problem of a plate under uniaxial tension with a length to height ratio of $L/H=3$ is examined thoroughly (Fig. 13a). The non-locality is kept fixed; $\kappa = L/60$, $\xi = 0.5$, and different filtering techniques and radii are considered. It should be noted that the material constants are selected in accordance with what has been reported in the literature (e.g. Pisano et al. 2009), while the remaining parameters are the same as in Cauchy example.

Fig. 13

Schematic of design domain of uniaxially loaded a intact Eringen’s plate, and b Cauchy plate with a central crack

As depicted in Fig. 14, the nature of Eringen’s theory of elasticity covering long-range interactions between material points promotes a non-uniform density field that is independent of the mesh discretisation. Although a dog-bone shaped geometry is attained for a filter radius of $r_{\min }=0.06L$, further simulations, which use various filter radii (i.e. $r_{\min }=0.03L,$ $-0.06L$), point out that $r_{\min }$ does not only control the minimum size of the members, but also completely alters the final configurations when combined with long-range interactions (Fig. 15). To be specific, larger values of ${r _{\min }}$ increase the density around the horizontal mid-line as the optimization progresses, and eventually produces a monolithic structure; whereas smaller values of ${r _{\min }}$ suggests two branches of same thickness whether HPM is included or not. In any case, incorporation of HPM suppresses the blurring effect of density filter that is leading to topologies with ambiguous boundaries. More importantly, circumventing the grey zone with low density and high deformability reduces objective function (compliance) up to 27% by eliminating the unrealistic final configurations as can be seen for instance; $r_{\min }=0.04L$: The slight curvature of the branches, that are susceptible to bending, is overcome by means of HPM. In case of no filter, additional, very thin, vertical braces emerge since no constraint on the thickness of the members exist, as evident from Fig. 16. Furthermore, almost checkerboard free and mesh-independent topologies are observed for this particular case where the former is in line with what has been reported by Evgrafov and Bellido (2019b) in which optimization using a strongly non-local model for heat conduction is examined, and the redundancy of external regularization schemes for such a case is highlighted. However, it should be noted that, this is far from an actual proof of the correspondence of non-local parameters to a filter radius which requires a comprehensive elaboration.

Fig. 14

Optimised design of uniaxially loaded Eringen’s plates reported for a filter radius of $r_{\min }=0.06L$ considering both cases with and without Heaviside projection method (HPM) (for visualization purposes, pictures are rotated 90$^\circ$)

Fig. 15

Variation of compliance function (c) and optimised configurations of uniaxially loaded Eringen’s plates with respect to filter radius ($r_{\min }/L$), considering cases with and without Heaviside projection method (HPM) (mesh: $120 \times 40$)

Fig. 16

Optimised design of uniaxially loaded Eringen’s plates without filtering

The reason of a non-uniform density distribution in the first place seems to be the softening effect of missing neighbour relations, which is reported to be responsible for deformation gradient around the end portions of the bar (Pisano and Fuschi 2003; Pisano et al. 2009; Benvenuti and Simone 2013; Tuna and Trovalusci 2020). Being inherently more pronounced at the corners, this is compensated by the increased material formation around them, and followed by gradual decrease of thickness through to the middle, in order to reduce stress concentrations. On the other hand, a uniform plate with a constant physical density field (${{{\hat{\rho }} }}_{m} = 0.5$) is expected for the Cauchy (and also Cosserat) continuum as a result of its homogeneous response to uniaxial tension.

If the uniformity of initial strain energy distribution of local plate is disturbed through a central crack (Fig. 13b) with detaching nine symmetrically (with respect to the horizontal axis) placed nodes, the optimization procedure (performed for a filter radius of $r_{\min }=0.04L$) yields two branches of bars (see Fig. 17) which are practically identical to intact Eringen’s medium. Thereby, it can be concluded that, different sources of non-uniformity, and different distributions of initial strain energy can induce exact optimal material layouts and very similar final compliances.

Fig. 17

Optimised design of uniaxially loaded Cauchy plate with central crack reported for a filter radius of $r_{\min }=0.04L$ considering Heaviside projection method (HPM)

At this point, it should be noted that such a mesh density is definitely not sufficient to capture the stress singularity, or, stress intensity factor; however, since optimization suggest avoiding the cracked region by removing the elements around it, there is no such need.

4.3 Comparative examples

After the validation of the in-house code for Cauchy and micropolar media, and observing the effects of long-range interactions (or in another words, strong non-locality) in the framework of Eringen’s model, an example problem of practical importance; pinned plate subjected to a downwards force at the middle of the bottom edge (Fig. 18a), is studied in a comparative manner to demonstrate the influence of each theory on optimum configurations. To this aim, the rectangular design domain, that has an aspect ratio of $L/H=2$, is discretized into $80\times 40$ elements following the mesh independence demonstrated previously. To avoid numerical problems (e.g. hourglass), concentrated force is modelled as a distributed load on a very small region; L/20. Topology optimization is then performed for the following parameter set:

$$\begin{aligned}&E = 1.0,\quad {V_{\text {f}}} = 0.5,\quad \nu = 0.3,\quad {\bar{{\text {m}}}} = 0.2,\quad {\bar{{\text {n}}}} = 0.5, \\&{\beta _{ini}} = 0,\quad {\beta _{\max }} = 36,\quad {\rho _{{\text {ini}}}} = V_{\text {f}},\quad {p} = 3, \\&r_{\min }=0.0375L,\quad {\rho _{\text {tol}}=0.20}, \end{aligned}$$

(71)

where the effect of coupling number, fraction coefficient, and internal characteristic lengths are studied individually considering various material properties, the results of which are illustrated in Figs. 19 and 20 for micropolar and Eringen’s media, respectively.

$$\begin{array}{*{20}{l}} {{\text {Micropolar:}}}&{}{\begin{array}{*{20}{l}} {N = 0.10,0.50,0.75,0.90},\\ {{l_{c}}/L = 0.0125, 0.0250, 0.0375}, \end{array}}\\ {{\text {Eringen:}}}&{}{\begin{array}{*{20}{l}} {\xi = 0.10,0.25,0.50,0.90},\\ {\kappa /L = 0.0125, 0.0250, 0.0375}. \end{array}} \end{array}$$

(72)

Here the largest value of characteristic internal length (or non-local parameter) is limited to 0.0375L to avoid the need of incorporation of geodetic path in the Eringen’s formulation, which must be accounted for structures with holes and curved outer boundaries, to consider the deteriorating nature of geometric discontinuities on long-range interactions, as mentioned by Polizzotto (2001) and executed in Tuna and Trovalusci (2021).

Fig. 18

a Schematic of design domain of pinned plate, and b resulting optimized design of Cauchy plate

Fig. 19

Optimum material distributions and resulting compliances, c, of pinned micropolar plates with a point load considering a various internal lengths for a constant coupling number, $N = 0.75$, and b various coupling numbers for a constant internal length, $l_{c} = 0.0125L$

Fig. 20

Optimum material distributions and resulting compliances, c, of pinned Eringen’s plates with a point load considering a various non-local parameter for a constant fraction coefficient, $\xi = 0.25$, and b various fraction coefficients for a constant non-local parameter, $\kappa = 0.0125L$

Accordingly, in Fig. 19a, the coupling number of micropolar continuum is kept constant at $N=0.75$, and various internal lengths, $l_{c}/L=0.0125-0.0375$, are studied. Due to relatively large value of $N\in [0,1]$, the couple-stress tensor is highly affected by the parameter $l_{c}$ given the dominant bending effects in the problem via which the transition of the members from straight to curved is clearly observed. To be specific, an increase in $l_{c}$ escalates the contribution of curvatures to the strain energy, and forms a funicular main arch. Since the thickness of the segments remain unaltered, the total height of the structure decreases to satisfy the prescribed volume constraint. On the other hand, as depicted in Fig. 19b, material distributions turn out to be less sensitive to N for the relatively small value of $l_{c}=0.0125L$, where apart from the slight rounding of the top edge, no significant change from optimum Cauchy topology is attended (Fig. 18b), especially for the case with less pronounced non-locality; $N=0.10$, $l_{c}=0.0125L$.

Similar observation can be made for the topology of Eringen’s medium with the lowest of non-locality considered herein;

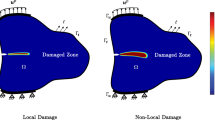
$\xi =0.90$, $\kappa =0.0125L$ (Fig. 20b). Although the effect of fraction coefficient, $\xi$, is limited for this relatively low value of non-local parameter, it still is more dominant than the coupling number is in micropolar case. Meanwhile the influence of characteristic length in Eringen’s medium is analysed in the light of Fig. 20a, in which the fraction coefficient is fixed at $\xi =0.25$, that is, 75% of the material response includes long-range interactions (with $\xi =1$ denoting the local case), while non-locality is tailored through non-local parameter, $\kappa /L=0.0125-0.0375$. In all cases, the final compliance turn out to be greater than the Cauchy continuum, which is associated with the non-locality-related softening effect of Eringen’s theory: The increased deformability, that is concentrated at the vicinity of domain boundaries due to missing neighbour relations, causes a dense region around the top edge (Fig. 21, iteration 3). Combined with the long-range interactions, this material formation is better connected with the main arms (Fig. 21, iteration 4), and leads to a higher structure than that of Cauchy. Another remarkable difference is that the junctions of the tips of the V-braces with the arms at the upper corners of the optimum shape are smaller compared to the Cauchy continuum. This is because of the ability of long-range effects to soften the stress concentrations (Tuna and Trovalusci 2020, 2021). However, in overall, the main outlook is very similar to that of Cauchy due to the fact that they share common deformation descriptors.

Fig. 21

Distribution of compliance for Cauchy and Eringen’s plates considering comparative example 1

Finally, Fig. 22 demonstrates the distribution of compliance over the optimised configurations. For comparison, the contribution of the elements are coloured by weighting each with the structural compliance, c. The extreme values at the loading and boundary regions are off the scale for all sub-figures, for the sake of seeing better the distribution. The Cosserat continuum seems to be the one with the least strain energy gradient, pointing out its ability to distribute the load, which is maintained by less deformation as evidenced from the reduction of total energy. On the other hand, the localized decrement of the stiffness around domain boundaries of Eringen’s continuum results in high gradients of strain energy, and causes the greatest compliance due to the softening effect of non-local parameter. Interestingly, for all models, the macro-scale optimum topologies admits the physics of underlying structure by being in accordance with the interactions defined between material points (Voigt 1887; Trovalusci et al. 2008; Capecchi et al. 2011; Trovalusci 2014): Roughly, the Cauchy continua assumes the particles constituting the matter interacts through forces, corresponding to bar-like connections, while micropolar continua further includes active couples, resembling to beam-like links. Based on this analogy, one can expect to obtain a truss-like structure in Eringen’s non-local model with only slight deviations from Cauchy due to existence of long-range interactions as both theories share common deformation descriptors.

Fig. 22

Contribution of the elements to the compliance (c) for different continua descriptors considering pinned plate with a concentrated load

5 Conclusion

Generalizing topology optimization method to size-de- pendent continuum theories has the utmost significance in maximizing the performance of complex materials. With this motivation, in the present paper, the update scheme of classical FE-based optimization problem is modified to analyse the design domains described on the basis of weakly/implicitly non-local micropolar and strongly/explicitly non-local Eringen’s theories, while, to the best of authors’ knowledge, this is the first time that the latter theory is used in addressing the corresponding problem.

In order to avoid mesh-dependent topologies with adjacent solid–void elements (i.e. checkerboard pattern), the formulation is endowed with density filter, the blurring effect of which is further alleviated by means of volume preserving HPM. With the aid of SIMP approach and density filter, an element removal/reintroduction strategy is easily integrated within the code to remove structurally insignificant low-density elements, that are prone to numerical instabilities. Based on the results of individual and comparative example problems, following deductions can be made about the effect different non-locality mechanisms on optimal topologies:

• Given the dominant bending effect of considered problem, the increased capacity of rotation resistance of material points of micropolar medium allows a better reduction of structural compliance with the least gradient among other models considered herein. Moreover, as the contribution of curvatures through work-conjugate stress measure becomes prominent with increased non-locality, the members of resulting topologies are transitioned from straight to curved, causing the load to be carried mainly by membrane actions.

• Despite sharing common deformation descriptors with Cauchy continuum, the topology of Eringen’s medium is essentially formed by the localized decrement of the stiffness that occurs around domain boundaries as a result of missing long-range interactions. Moreover, the capability of Eringen’s theory in distributing the stress intensity yields less material formation around stress concentration zones (such as non-convex domains in junction points). It is also interesting to observe that the optimised topology of an uniaxially loaded intact Eringen’s plate converges to that of Cauchy with a central crack albeit for different reasons, which indicates the possibility of distinct theories on providing exact topologies with different initial energy distributions.

• For all theories, the macro-scale optimum topologies confirms the physics of underlying lattice system as they are in accordance with the mechanical response governed by particle interactions, including, forces, couples and multi-body effects, while all the results become practically identical to that of Cauchy for decreasing non-locality.

• Hints on possible effects of incorporating internal length scale on topology optimization are presented through a limited number of tests. The results suggest that, the non-locality of the continua mitigates the checkerboard pattern and leads to mesh-independent results. These observations enrich the existing discussions on the role of internal scale parameters in topology optimization, and possible correspondence with filter radius which is the topic of an ongoing project.

The present study can be broadened by adopting geodetical distance to the formulation of Eringen’s model via which the case of higher non-locality can be examined. Further studies can be performed on non-local domains weakened by various types of cracks by focusing on detection of the material layouts that prevent their initiation and propagation.