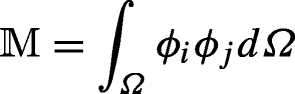A gradient-based optimization method with functional principal component analysis for efficient structural topology optimization

Abstract

Structural topology optimization (STO) is usually treated as a constrained minimization problem, which is iteratively addressed by solving the equilibrium equations for the problem under consideration. To reduce the computational effort, several reduced basis approaches that solve the equilibrium equations in a reduced space have been proposed. In this work, we apply functional principal component analysis (FPCA) to generate the reduced basis, and we couple FPCA with a gradient-based optimization method for the first time in the literature. The proposed algorithm has been tested on a large STO problem with 4.8 million degrees of freedom. Results show that the proposed algorithm achieves significant computational time savings with negligible loss of accuracy. Indeed, the density maps obtained with the proposed algorithm capture the larger features of maps obtained without reduced basis, but in significantly lower computational times, and are associated with similar values of the minimized compliance.

1 Introduction

The need for optimized solutions in structural applications has increased over the years and has become nowadays fundamental because of the limited availability of commodities, environmental impacts, increasingly stringent industrial time-to-market requests, and emerging manufacturing processes as additive manufacturing. In this framework, structural topology optimization (STO) aims at obtaining optimized performance from a structure while satisfying some functional constraints, e.g., bounds on total mass or stresses. In particular, we focus on STO, whose goal is to produce optimized structures by determining an optimal mass or volume distribution in a given design domain. Unlike other alternatives as shape and size optimization, which deal with predefined configurations, STO can virtually produce any mass distribution within the design domain.

In the literature, STO is treated as a constrained minimization problem, for which several approaches and numerical schemes have been proposed (Sigmund and Maute 2013; van Dijk et al. 2013; Munk et al. 2015). Almost all the proposed approaches are iterative, which means that the optimized mass distribution is determined by repeatedly performing structural finite element analyses (FEA) that involve the solution of the equilibrium equations for the problem under consideration. On the one hand, iterative approaches are very effective because they allow to obtain optimized solutions in a variety of situations without requiring additional assumptions. On the other hand, however, their bottleneck is the computational effort, as they require solving FEA a large number of times. For example, in a minimum compliance problem, up to 97% of the total computational time could be spent for numerically solving the equilibrium equations (Alaimo et al. 2018; Petersson 1999).

From these considerations, it becomes evident the need for reducing the computational time to solve the equilibrium equations in STO, which is a key requirement for large problems and three-dimensional applications. Reduced basis approaches represent a valid solution to such an issue, because they allow to reduce the dimensionality of the structural problem, i.e., the number of equilibrium equations to solve and, therefore, the related computational effort.

However, reduced basis approaches have been exploited in a very limited number of recent works. Gogu (Gogu 2015) constructed reduced basis on-the-fly by using the previously generated solutions of the equilibrium equations, and the reduced basis was adaptively enriched based on the STO convergence. Ferro et al. (Ferro et al. 2019) applied the principal component analysis (PCA) to the density map, obtaining an efficient numerical scheme for STO. Xiao et al. (Xiao et al. 2020) proposed a proper orthogonal decomposition (POD) scheme, related to PCA, to construct a reduced basis for the displacement field solution of FEA, to be used during the optimization; subsequently, the reduced basis is adaptively updated on-the-fly according to an error metric. Less recently, Wang et al. (Wang et al. 2007) proposed a method based on the Krylov subspaces, while Amir et al. (Amir et al. 2009) proposed the construction of a reduced order model using the combined approximations method. Finally, Yoon (Yoon 2010) used eigenmodes along with Ritz vectors for the construction of a reduced model in dynamic STO.

In this work, we propose and test a reduced basis method that relies on functional PCA (FPCA). FPCA for FEA is quite new in STO since it has only been exploited for the variable thickness sheet design problem in combination with a simulated annealing optimization heuristic (Alaimo et al. 2018); moreover, it was initially developed for uncertainty quantification (Bianchini et al. 2015). We extend the use of FPCA in STO by applying it to the class of gradient-based optimization methods, which are the most commonly used. We demonstrate that significant savings in STO computational times can be achieved with negligible loss of accuracy. In this sense, the novelty of our work is not to introduce a new numerical technique but to appropriately combine two consolidated STO methods in order to save computational time. Such methods are the gradient-based optimization, (see for example Sigmund and Maute (2013)), and the reduced basis method (FPCA), able to reduce the dimensionality of the problem.

More specifically, we employ FPCA along with a gradient-based approach, considering the code proposed in Sigmund (2001) and his gradient-based approach as a starting point for incorporating FPCA reduced basis. At each STO iteration, we convert the FEA problem into a smaller one by projecting it onto a reduced space by means of a data-driven FPCA reduced basis. The reduced problem is solved and, if error measures associated with the solution are below the given thresholds, the reduced solution is accepted; otherwise, the original FEA problem is solved and the complete solution is used to update the FPCA basis.

We decided to embed FPCA rather than PCA in the optimization because of the results reported in Bianchini et al. (2015), where FPCA has been employed for uncertainty quantification purposes. Indeed, the authors showed that FPCA clearly outperforms PCA, i.e., FPCA always turned out to be faster than PCA and well captured the behavior of the solution with less elements in the basis than PCA. As the description of the FEM solution in a reduced space is the same both for uncertainty quantification and our optimization purposes, we can consider that these results are also valid in our setting.

The remainder of the paper is structured as follows: the proposed gradient-based optimization method with FPCA is presented in Section 2; the test case used to validate our algorithm is described in Section 3, while the results are reported in Section 4; finally, discussions and conclusion of the work are drawn in Section 5.

2 Gradient-based optimization with FPCA

In this section, we present the addressed STO problem (Section 2.1), the gradient-based optimization of Sigmund (2001) (Section 2.2), and the novel contribution included in the optimization, i.e., the FPCA to generate the reduced basis (Section 2.3). Finally, we detail the overall algorithm in Section 2.4. Without loss of generality, we present the approach for two-dimensional cases; from a conceptual point of view, the approach is the same also for three-dimensional cases while, from an operational point of view, the extension is very straightforward.

2.1 Structural topology problem

We address a STO problem in which a given mass is distributed over the domain Ω in order to minimize the structural compliance:

$$ c = {\int}_{\varOmega} {\sigma} \cdot {\varepsilon} d{\varOmega} $$

where ε is the strain tensor, ${\sigma } = \mathbb {D} {\varepsilon }$ the stress tensor, and $\mathbb {D}$ the fourth-order linear elastic tensor. We assume that $\mathbb {D}$ depends on the mass density distribution as $\mathbb {D} = \rho ^{p} \tilde {\mathbb {D}}$, where $\rho \in [\rho _{\min \limits },1]$ is the mass density, p ≥ 1 a penalty coefficient, $\tilde {\mathbb {D}}$ the fourth order elastic tensor of the isotropic homogeneous bulk material, and $\rho _{\min \limits }$ a positive value close to 0.

Finally, ε is defined in terms of the displacement field u as ${\varepsilon } = \frac {1}{2} \left (\nabla \mathbf {u} + \nabla \mathbf {u}^{T} \right )$, where superscript ^T denotes transposition.

The problem is discretized following a classical FEA approach, using four-node elements with bilinear displacement functions. Accordingly, the compliance c is expressed in the form:

$$ c = \widehat{\mathbf{u}}^{T} \mathbf{f} = \sum\limits_{i = 1}^{N_{el}} {\hat{\mathbf{u}}_{i}}^{T} \mathbf{f}_{i} = \sum\limits_{i = 1}^{N_{el}} {\hat{\mathbf{u}}_{i}}^{T} \mathbf{K}_{i} \hat{\mathbf{u}}_{i} $$

(1)

where N_el is the number of elements in the discretized domain, $\hat {\mathbf {u}}_{i}$ the vector of the nodal displacements of element i, f_i the vector of the nodal forces of element i, and K_i the stiffness matrix of element i, while $\hat {\mathbf {u}}$ and f are the assembled (over all elements) displacement vector and the applied force vector, respectively. Assuming a uniform mass density ρ_i over each element i, K_i depends on ρ_i in the form $\mathbf {K}_{i} = {\rho _{i}^{p}} \tilde {\mathbf {K}}_{i}$, where $\tilde {\mathbf {K}}_{i}$ is the stiffness matrix of element i analogous to $\tilde {\mathbb {D}}$, which corresponds to a homogeneous and isotropic material.

The minimization of c, expressed as in (1), is subject to mass (volume) constraint expressed in the form:

$$ \begin{array}{@{}rcl@{}} && \sum\limits_{i = 1}^{N_{el}} \rho_{i} V_{i} = \rho^{*} V \\ && \rho_{i} \in [\rho_{\min},1] \qquad \forall i=1,\dots,N_{el} \end{array} $$

where ρ^∗ is the imposed mean density that uniquely defines the overall mass, and V_i and V are the volume of element i and the overall domain volume, respectively.

Finally, the equilibrium equations are expressed in compact form as:

$$ \mathbf{K} \hat{\mathbf{u}} = \mathbf{f} $$

(2)

where K is the assembled stiffness matrix.

2.2 Gradient-based optimization

The gradient-based minimization is an iterative procedure in which, at each iteration, the new solution in terms of ρ_i in all elements i is obtained following an optimality criterion, as proposed in Bendsøe and Sigmund (1995) and applied in Sigmund (2001).

The optimality criterion is based on the sensitivity of c with respect to the densities ρ_i in the form:

$$ \cfrac{\partial c}{\partial \rho_{i}} = \cfrac{\partial \hat{\mathbf{u}}^{T}}{\partial \rho_{i}} \mathbf{f} $$

(3)

However, there is no explicit formula that links the displacements to the density distribution. For this reason, the computation of derivatives (3) is performed by adding an adjoint term to c, in the form:

$$ c = \hat{\mathbf{u}}^{T} \mathbf{f} = \mathbf{f}^{T} \hat{\mathbf{u}} = \mathbf{f}^{T} \hat{\mathbf{u}} - \tilde{\mathbf{u}}^{T} (\mathbf{K}\hat{\mathbf{u}} - \mathbf{f}) $$

(4)

where $\tilde {\mathbf {u}}$ is an arbitrary term, and the difference in parentheses is equal to 0 thanks to (2). The gradient of c is then expressed, for each component, as:

$$ \cfrac{\partial c}{\partial \rho_{i}} = (\mathbf{f}^{T} - \tilde{\mathbf{u}}^{T} \mathbf{K}) \frac{\partial \hat{\mathbf{u}}}{\partial \rho_{i}} - \tilde{\mathbf{u}}^{T} \cfrac{\partial \mathbf{K}}{\partial \rho_{i}} \hat{\mathbf{u}} $$

(5)

which is simplified if the arbitrary term $\tilde {\mathbf {u}}$ is chosen equal to the actual displacement field $\hat {u}$, turning into:

$$ \cfrac{\partial c}{\partial \rho_{i}} = - \tilde{\mathbf{u}}^{T} \cfrac{\partial \mathbf{K}}{\partial \rho_{i}} \hat{\mathbf{u}} $$

(6)

Considering the expression of the stiffness matrix K and that ρ_i is constant over each element i, the gradient of the compliance can be computed element-wise and expressed as:

$$ \cfrac{\partial c}{\partial \rho_{i}} = - p \hat{\mathbf{u}}_{i}^{T} \rho_{i}^{(p-1)} \mathbf{K}_{i} \hat{\mathbf{u}}_{i} $$

(7)

Let us remark that (7) is valid when $\hat {\mathbf {u}}$ represents the exact solution of the equilibrium equations. This is of particular importance when considering a solution $\hat {\mathbf {u}}_{\text {rec}}$ reconstructed from the reduced space, which can be slightly different from the exact solution $\hat {\mathbf {u}}$; in this case, the complete expression (5) must be considered, or the problem must be adapted in order to use (7). In this work, as detailed in Sections 2.3 and 2.4, we consider the second alternative and we solve the problem with a modified force f_curr in such a way that $\mathbf {K} \hat {\mathbf {u}} = \mathbf {f}_{\text {curr}}$.

With (7), it is possible to iteratively update ρ_i to minimize the compliance c step by step. In particular, the new density distribution can be computed with the following heuristic approach proposed by Bendsøe and Sigmund (Bendsøe and Sigmund 1995):

$$ {\rho_{i}^{N}} = \begin{footnotesize} \begin{cases} \max (\rho_{\min},\rho_{i} - m) \\ \text{if} \rho_{i} \alpha_{i}^{\eta} \le \max(\rho_{\min}, \rho_{i} - m) \\ \rho_{i} \alpha_{i}^{\eta} \\ \text{if} \max(\rho_{\min}, \rho_{i} - m) \le \rho_{i} \alpha_{i}^{\eta} \le \min (1,\rho_{i} + m) \\ \min (1,\rho_{i} + m) \\ \text{if} \min (1,\rho_{i} + m) \le \rho_{\min} \alpha_{i}^{\eta} \end{cases} \end{footnotesize} $$

(8)

where ${\rho _{i}^{N}}$ denotes the new density of element i, m is a positive coefficient that limits density variation, $\eta = \frac {1}{2}$ is a damping coefficient, and α_i is given by the optimality condition as:

$$ \alpha_{i} = - \frac{1}{\kappa} \frac{\partial c/\partial \rho_{i}}{\partial V/{\partial \rho_{i}}} $$

(9)

where κ is a Lagrangian multiplier found through a bisectioning algorithm (Sigmund 2001).

2.3 FPCA for reduced model

The idea behind the use of FCPA in STO is to solve the equilibrium (2) in a reduced space for as many gradient-based iterations as possible. Such a reduced space, whose dimension is given by a limited number of principal displacement components, is generated by applying FPCA to a set of previously obtained solutions (Alaimo et al. 2018; Bianchini et al. 2015).

To this aim, let us consider M displacement solutions $\hat {\mathbf {u}}(\boldsymbol {\rho }_{m})$ of the equilibrium equations (with $m=1,\dots ,M$) corresponding to several realizations ρ_m of ρ, where ρ denotes the vector including all ρ_i.

The subspace spanned by these M solutions represents an approximation of the entire solution space $\mathcal {U}({\varTheta })= \left \{ \mathbf {u}(\boldsymbol {\rho }), \boldsymbol {\rho } \in {\varTheta } \right \}$, where ${\varTheta } = [\rho _{\min \limits },1]^{N_{el}}$ gathers all possible solutions of the structural problem. By applying FPCA to the subspace, we obtain the set of the K orthonormal basis functions (with 1 ≤ K ≤ M) that optimally approximate $\mathcal {U}({\varTheta })$ in terms of total explained variance.

These basis functions can be obtained by solving an eigenvalue problem that involves the covariance operator. Let us denote by $\left \{ v_{m}(\mathbf {x}), m=1,\dots ,M \right \}$ a set of M functions with cross-sectional mean $\frac {1}{M} {\sum }_{m=1}^{M} v_{m}(\mathbf {x})$ equal to 0 for each x. The corresponding empirical covariance function is:

$$ \mathbb{V}(\mathbf{s},\mathbf{t})=\frac{1}{M} \sum\limits_{m=1}^{M} v_{m}(\mathbf{s}) v_{m}(\mathbf{t}) $$

and the covariance operator is:

$$ \textbf{V}\xi: \xi(\cdot) \mapsto {\int}_{{\varOmega}} \mathbb{V}(\cdot,\mathbf{t})\xi(\mathbf{t}) d\mathbf{t} $$

Based on that, each basis function solves the following eigenproblem:

$$ \textbf{V} \xi (\mathbf{x}) = \gamma \xi(\mathbf{x}) $$

(10)

Operatively, we start from M displacement solutions $\hat {\mathbf {u}}(\boldsymbol {\rho }_{1}), \dots , \hat {\mathbf {u}}(\boldsymbol {\rho }_{M})$ corresponding to different ρ_m. We build a M × 2L matrix , where L is the number of nodes in the mesh and 2L the number of degrees of freedom.

The buffer matrix $\mathbb {U}$ is then split into two parts: the average part $\mathbb {U}_{av}$ and the residual part $\mathbb {U}_{cov}=\mathbb {U}-\mathbb {U}_{av}$ that stores the fluctuations of the solution with respect to the average.

The orthonormal basis is obtained with the functional principal components of . We use the method of snapshots as in (Alaimo et al. 2018; Bianchini et al. 2015), which is valid if 2L > M as in our case. Accordingly, the basis of rank K is obtained as follows:

• 1. Define a 2L × M matrix with

  

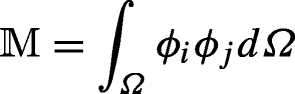
  where ϕ_k are the finite element shape functions, and $\mathbb {M}$ is a 2L × 2L matrix that can also be intended as a mass matrix.

• 2. Solve the eigenvalue problem

  

  where the eigenvalues λ_k are in descending order along k.

• 3. Choose the value of K by retaining all eigenfunctions that correspond to an eigenvalue λ_k > Λλ₁, where λ₁ is the maximum eigenvalue and Λ assumes very small values (Dulong et al. 2007).

The projection of (2) onto the reduced space of dimension K is carried out using the 2L × K matrix $\left [ {\xi }_{1}, \dots , {\xi }_{K} \right ]$, where

Let now consider the problem $\mathbf {K} \hat {\mathbf {u}} = \mathbf {f}_{\text {curr}}$, where f_curr is the modified force that allows to exploit (7). With the above projection, we may solve the following reduced problem, instead of the complete one, in the subspace spanned by the principal components:

$$ \mathbf{K}_{\text{red}} \hat{\mathbf{u}}_{\text{rs}} = \mathbf{f}_{\text{red}} $$

(11)

with

$$ \begin{array}{@{}rcl@{}} &{}\mathbf{K}_{\text{red}} = \mathbb{U}_{\text{rb}}^{T} \mathbf{K} \mathbb{U}_{\text{rb}} \end{array} $$

(12)

$$ \begin{array}{@{}rcl@{}} & \mathbf{f}_{\text{red}} = \mathbb{U}_{\text{rb}}^{T} (\mathbf{f} - \mathbf{K} \bar{\mathbf{u}}) \end{array} $$

(13)

where $\hat {\mathbf {u}}_{\text {rs}}$ denotes the solution of the problem in the reduced space and $\bar {\mathbf {u}} = \frac {1}{M} {\sum }_{m=1}^{M} \hat {\mathbf {u}}_{i}$ is the average of the solutions stored in buffer $\mathbb {U}$.

After solving (11) in the reduced space, the displacement solution is reconstructed as:

$$ \hat{\mathbf{u}}_{\text{rec}} = \bar{\mathbf{u}} + \mathbb{U}_{\text{rb}} \hat{\mathbf{u}}_{\text{rs}} $$

(14)

where subscript rec indicates that the solution is reconstructed starting from $\hat {\mathbf {u}}_{\text {rs}}$.

Although $\hat {\mathbf {u}}_{\text {rec}}$ is computationally cheaper to obtain, it is only an approximation of the actual $\hat {\mathbf {u}}$. Therefore, we must decide whether to accept $\hat {\mathbf {u}}_{\text {rec}}$ or not based on the approximation error and the quality of the solution.

The approximation error is evaluated by computing the errors e₁ and e₂ between the reconstructed force $\mathbf {f}_{\text {rec}} = \mathbf {K} \hat {\mathbf {u}}_{\text {rec}}$ and f_curr and between f_rec and f, respectively:

$$ \begin{array}{@{}rcl@{}} && e_{1} = {(\mathbf{f}_{\mathit{rec}} - \mathbf{f}_{\mathit{curr}})}^{T} \mathbb{M}_{\rho} (\mathbf{f}_{\mathit{rec}} - \mathbf{f}_{\mathit{curr}}) \\ && e_{2} = {(\mathbf{f}_{\mathit{rec}} - \mathbf{f})}^{T} \mathbb{M}_{\rho} (\mathbf{f}_{\mathit{rec}} - \mathbf{f}) \end{array} $$

The global mass matrix $\mathbb {M}_{\rho }$ is introduced to weigh less or exclude the elements with lower density ρ_i from the computation of the errors. It is computed as the assembly of elementary mass matrices, obtained for each element as

$$ \mathbb{M}_{\rho_{k}} = \rho_{k} {\int}_{{\varOmega}_{k}} \phi_{i} \phi_{j} d{\varOmega} $$

(15)

Finally, the compliance c generally decreases with the iterations in gradient-based approaches (Sigmund 2001). Therefore, to avoid too large deviations from this decreasing behavior, a reduced solution is also evaluated in terms of the difference δ_c between the compliance c obtained in the current iteration and that at the previous one.

If e₁ < τ₁, e₂ < τ₂, and δ_c < τ₃, where τ₁, τ₂, and τ₃ are fixed positive thresholds, the reconstructed solution u_rec is accepted. Otherwise, it is discarded and the complete problem (2) is solved.

2.4 Overall integrated algorithm

The algorithm reflects the iterative structure of the gradient-based optimization in Sigmund (2001), enriched by the proposed reduced basis approach based on FPCA. The basic structure of each iteration g (with $g=1,\dots ,G$) consists of solving equilibrium equations for the current density solution ρ_g, and computing the new solution ρ_g+ 1 according to (8).

The buffer $\mathbb {U}$ contains a number M of solutions between $M_{\min \limits }$ and $M_{\max \limits }$. This basic structure of the gradient-based optimization, which consists of solving the complete problem (2), is repeated for the first $M_{\min \limits }$ iterations while considering the nominal force f of the problem and storing the displacement solutions in $\mathbb {U}$. At iteration $g=M_{\min \limits }$, the matrix $\mathbb {U}_{\text {rb}}$ is also built from $\mathbb {U}$.

Starting from iteration $g=M_{\min \limits }+1$, the problem is projected onto the reduced space exploiting $\mathbb {U}_{\text {rb}}$, and the equilibrium equations are solved in the reduced space according to (11–14).

As mentioned, the reconstructed solution $\hat {\mathbf {u}}_{\text {rec}}$ is accepted if e₁ < τ₁, e₂ < τ₂, and δ_c < τ₃. In this case, the reconstructed force f_rec is also kept as the force f_curr to solve the problem at the next iteration.

If $\hat {\mathbf {u}}_{\text {rec}}$ is not accepted, the complete problem (2) is solved while considering the nominal force f. At the same time, the force f_curr to solve the problem at the next iteration is reset equal to f. Moreover, the new complete solution is included in $\mathbb {U}$; if the number of already stored solutions is equal to $M_{\max \limits }$, the oldest solution is also removed. The new $\mathbb {U}_{\text {cov}}$ is then computed with the updated $\mathbb {U}$.

At the end of each iteration g, the new density map ρ_g+ 1 is generated according to the updating scheme (8), either considering the solution $\hat {\mathbf {u}}$ of the complete problem (in the first $M_{\min \limits }$ iterations or when the reduced solution is rejected) or the reconstructed solution $\hat {\mathbf {u}}_{\text {rec}}$ (when the reduced solution is accepted starting from iteration $g=M_{\min \limits }+1$).

A detailed pseudo-code of the algorithm is reported in Algorithm 1.

The dynamic management of the buffer dimension M starting from $M_{\min \limits }$ allows to calculate, and possibly accept, reduced solutions even in the very first iterations without waiting for the first $M_{\max \limits }$ complete solutions. In fact, accepting reduced solutions even in the very first iterations is a key requirement for increasing the computational efficiency. At the same time, the upper limit $M_{\max \limits }$ allows to replace the oldest solution with the new one, thus giving preference to more recent displacement solutions that are associated with closer density distributions than the older ones.

Let us remark that, due to the approximation induced by the reconstructed displacement solution $\hat {\mathbf {u}}_{\text {rec}}$, the quantity $\mathbf {K}\hat {\mathbf {u}}_{\text {rec}} - \mathbf {f}$ is not exactly null and, therefore, expression (7) is not exact in relation to problem (2). In the literature, such an expression has been modified by adding additional terms that compensate the error, as in (Gogu 2015), but this approach requires additional computational effort at each iteration. In this work, we deal with the issue by replacing the nominal force f with f_curr. In this way, expression (7) becomes correct for the problem $\mathbf {K} \hat {\mathbf {u}} = \mathbf {f}_{\text {curr}}$ without the need to calculate additional terms. Obviously, the problem with f_curr is representative of (2) if the distance between f_curr and f is limited, as verified by the conditions e₁ < τ₁ and e₂ < τ₂ together.

3 Experimental validation

We compare our algorithm with the case in which the reduced basis approach is not exploited and all gradient-based iterations are performed with the complete problem, as in (Sigmund 2001).

Analyses have been conducted on the well-known Messerschmitt-B̈olkow-Blohm (MBB) beam problem. It consists of a simply-supported rectangular domain of size 2n_x × n_y elements, with a vertical downward force F applied in the midpoint of the lower side (force module equal to 1). Thanks to the symmetry, only half of the domain is studied, as represented in Fig. 1. We consider n_x = 2000 and n_y = 1200 elements in the analyses, which define a computationally demanding problem having more than 4.8 million degrees of freedom.

Fig. 1

Structural scheme of the considered MBB beam with domain Ω, boundary conditions, symmetry boundary conditions on the left, and applied force F

Moreover, the following parameter values are assumed:

• penalty p = 3;

• minimum density $\rho _{\min \limits }=0.001$;

• number M of solutions in the buffer between $M_{\min \limits }=2$ and $M_{\max \limits }=20$;

• parameter Λ to include eigenfunctions equal to 10^− 12;

• error threshold τ₁ = 10^− 4;

• error threshold τ₂ = 4τ₁;

Experiments have been conducted by considering the following three factors and related levels:

• mean density ρ^∗ for mass constraint: {0.3,0.5,0.7};

• radius for mesh filter r: {5,10,15} nodes;

• increment threshold τ₃: {2,4,8};

In addition to these experiments, different $M_{\min \limits }$ and $M_{\max \limits }$ values were tested for ρ^∗ = 0.5, r = 5, and τ₃ = 2.

Each setting of ρ^∗ and r is also solved with no reduced basis to get a reference solution for comparison. In particular, a number of iterations G = 100 are assumed to get the reference compliance $\tilde {c}$ of the setting without reduced basis. This value of G has shown to be large enough to guarantee convergence; indeed, we also tested greater numbers of iterations, up to G = 1000, and we observed very limited variations of $\tilde {c}$, lower than 2%, between iteration g = 100 and iteration g = 1000.

4 Results

Table 1 shows the reference $\tilde {c}$ obtained with no reduced basis with G = 100 iterations for each setting of ρ^∗ and r, together with the corresponding computational time. Moreover, it shows the CPU time to reach the reference $\tilde {c}$ plus 5% and 10% for each τ₃, and the percentage reduction with respect to the CPU time to reach the same compliance without reduced basis.

Table 1 Results from the experiments for each combination of ρ_i, r, and τ₃ with $M_{\min \limits }=2$ and $M_{\max \limits }=20$: reference $\tilde {c}$ with G = 100 iterations without reduced basis and corresponding CPU time; time to reach the reference $\tilde {c}$ plus 5% and 10% with the proposed algorithm and percentage reduction with respect to the computational time to reach the same value without reduced basis

The results show that the proposed algorithm is almost always able to find similar values of compliance c with respect to the reference $\tilde {c}$ obtained with no reduced basis by the original method of Sigmund (Sigmund 2001), for at least one value of τ₃. Moreover, a significant CPU time saving is always obtained. A reduction up to 52% and equal to at least 25% in most cases is observed when considering the reference $\tilde {c}$ plus 5%, and the reduction is even higher when considering $\tilde {c}$ plus 10%, being up to 68%. These higher reductions show that the largest gain is obtained in the first iterations, where the gradient-based optimization gives higher c reduction per iteration. Thus, the algorithm proved to be effective in these iterations, and this confirms the effectiveness of the dynamic buffer management to start using reduced problems early.

It is worth remarking that the reduced solutions are rejected because the condition δ_c < τ₃ is not respected, while the conditions e₁ < τ₁ and e₂ < τ₂ are always respected even with the low imposed thresholds. Moreover, a deeper analysis of Table 1 shows that the computational gain is not strictly correlated to the value of τ₃, due to the fact that the time gain is affected by competing factors. On the one hand, smaller τ₃ values prevent instability of the whole algorithm and the need of restarting from higher values of c; on the other hand, this greater stability is paid for with a higher number of complete FEA iterations, which are clearly more expensive in terms of CPU time.

Figure 2a, b and c show the evolution of the best known compliance c as a function of the CPU time and the number of iterations, respectively, for ρ^∗ = 0.5 and r = 5, under the different values of τ₃ together with the case with no reduced basis. We may observe a faster reduction of the objective function c over time when adopting our algorithm with FPCA reduced basis, which corresponds to the shorter CPU times reported in Table 1 to get $\tilde {c}$ plus 5% and 10%. In fact, although the convergence is slower in terms of iterations, the lower computational time required to solve the reduced problem makes the overall computational time shorter when exploiting FPCA. The red points in Fig. 2a and c highlight that the best known c always decreases in correspondence of a complete solution, and that a complete solution is required on average in only 26% or 27% of the iterations. Anyway, even when the objective function increases due to a bad representation of the solution with few bases (and the best known c remains constant over a certain time period), our algorithm is still able to redirect to acceptable values of c, which are even better than the case with no reduced basis at the same CPU time.

Fig. 2

Evolution of the objective function c. a Best known solution c as a function of the CPU time (truncated at 2 ⋅ 10⁵ s) for ρ^∗ = 0.5, r = 5, $M_{\min \limits }=2$, and $M_{\max \limits }=20$ under different τ₃ values; b best known solution c as a function of the CPU time (truncated at 2 ⋅ 10⁵ s) for ρ^∗ = 0.5, r = 5, and τ₃ = 2 under different $M_{\min \limits }$ and $M_{\max \limits }$ values; c best known solution c as s function of the number of iterations (truncated at 100 iterations) for ρ^∗ = 0.5, r = 5, $M_{\min \limits }=2$, and $M_{\max \limits }=20$ under different τ₃ values; d best known solution c as s function of the number of iterations truncated at 100 iterations) for ρ^∗ = 0.5, r = 5, and τ₃ = 2 under different $M_{\min \limits }$ and $M_{\max \limits }$ values. A red marker indicates the execution of a complete problem

Figures 3, 4, and 5 show the density maps obtained with the proposed algorithm when $\tilde {c}$ plus 5% is reached and the corresponding maps from the case with no reduced basis after G = 100 iterations. The maps are reported for each setting of ρ^∗ and r, and for τ₃ = 2. When $\tilde {c}$ plus 5% is not reached within G = 100 iterations by our algorithm for τ₃ = 2 (i.e., with {ρ^∗,r} equal to {0.3,15} and {0.5,10}), the map obtained from the algorithm at iteration g = 100 is reported. The maps from our algorithm show to capture the larger features of the solution. Moreover, although topologically different for some details, compared with the maps obtained with no reduced basis, our maps correspond to similar values of compliance c.

Fig. 3

Density maps for ρ^∗ = 0.3 and r = 5 (left column), r = 10 (central column) or r = 15 (right column). Upper row shows the maps from the proposed algorithm without post-processing with τ₃ = 2 when $\tilde {c}$ plus 5% is reached; central row shows the post-processed maps after 5 supplementary complete solutions; lower row shows the maps obtained with no reduced basis at 100 iterations. a r = 5, algorithm. b r = 10, algorithm. c r = 15, algorithm. d r = 5, post-processing. e r = 10, post-processing. f r = 15, post-processing. g r = 5, complete. h r = 10, complete. i r = 15, complete

Fig. 4

Density maps for ρ^∗ = 0.5 and r = 5 (left column), r = 10 (central column) or r = 15 (right column). Upper row shows the maps from the proposed algorithm without post-processing with τ₃ = 2 when $\tilde {c}$ plus 5% is reached; central row shows the post-processed maps after 5 supplementary complete solutions; lower row shows the maps obtained with no reduced basis at 100 iterations. a r = 5, algorithm. b r = 10, algorithm. c r = 15, algorithm. d r = 5, post-processing. e r = 10, post-processing. f r = 15, post-processing. g r = 5, complete. h r = 10, complete. i r = 15, complete

Fig. 5

Density maps for ρ^∗ = 0.7 and r = 5 (left column), r = 10 (central column), or r = 15 (right column). Upper row shows the maps from the proposed algorithm without post-processing with τ₃ = 2 when $\tilde {c}$ plus 5% is reached; central row shows the post-processed maps after 5 supplementary complete solutions; lower row shows the maps obtained with no reduced basis at 100 iterations. a r = 5,algorithm. b r = 10,algorithm. c r = 15,algorithm. d r = 5, post-processing. e r = 10, post-processing. f r = 15, post-processing. g r = 5, complete. h r = 10, complete. i r = 15, complete

To clean the maps obtained by the algorithm from zones with intermediate density, a post-processing of the solution is considered, which consists of executing 5 additional iterations in which the complete problem is solved. Results show the effectiveness of this post-processing. In fact, it does not significantly change the structure of the maps, but at the same time, it effectively cleans intermediate density regions and eliminates local irregularities. Table 2 also shows that the modulus of the compliance variation induced by post-processing is always less than 1.20% and on average equal to 0.78%. Therefore, we may argue that the presence of intermediate material in the maps obtained with the proposed algorithm involves only a small variation on the compliance which is, on average, less than 0.78%. At the same time, the maps cleaned by the post-processing are different from those in the case with no reduced basis. This could highlight the presence of local optimal solutions, or that the gap requires other iterations to be eliminated. We highlight that the post-processing has a limited impact on the computational time. In fact, assuming that all complete solutions require the same time, the percent gain obtained by the algorithm is reduced by only the 5%.

Table 2 Compliance c for different values of r, ρ^∗, and τ₃ = 2 before post-processing (from the proposed algorithm) and after post-processing (with 5 supplementary complete solutions), with relative variation after post-processing

4.1 Impact of buffer dimension M

Additional experiments are run to analyze the impact of the $M_{\min \limits }$ and $M_{\max \limits }$. Figure 2b and d show the best known compliance c as a function of the CPU time and the number of iterations, under different $M_{\min \limits }$ and $M_{\max \limits }$ values, for the case with ρ^∗ = 0.5, r = 5, and τ₃ = 2. As longer tracts with a constant best known c correspond to solutions with unstable c over the iterations, we may notice that the solution is far more stable when using a higher buffer size in terms of both $M_{\min \limits }$ and $M_{\max \limits }$. In particular, a higher $M_{\min \limits }$ value avoids the destabilization of the solution in the very first iterations of the algorithm (red line in the figure), but at the price of a higher computational cost during the initial phase when the buffer starts to collect the solutions to build up the first reduced basis.

5 Discussions and conclusion

In this work, we propose an algorithm that makes the gradient-based optimization proposed by Sigmund and Maute (2013) for STO more computationally efficient. In particular, we couple this gradient-based optimization with the FPCA method to generate reduced basis, onto which the equilibrium equations are projected at several optimization iterations. Unlike few similar works available in the literature, we exploit FPCA rather than PCA or POD because FPCA appears to be generally faster and well captures the behavior of the solution with less elements in the basis (Alaimo et al. 2018). Moreover, to face the gap between the solution reconstructed from the reduced space and the exact solution of the complete problem, we have decided to modify the problem by means of f_curr, which allows us to avoid the additional calculations required to compute corrective terms. These two innovations have made our approach alternative with respect to the others proposed in the literature and suitable for practical applications, where computational time is the bottleneck.

The proposed algorithm has been tested on a large problem with more than 4.8 million degrees of freedom, much larger than the problems considered to test similar approaches. Results confirm that the reduced FEA problem is exploited in the 73–74% of the optimization iterations (Fig. 2a and c), guaranteeing limited errors below τ₁, τ₂, and τ₃. This allows to reduce the STO computational times by the 50.3% on average (with minimum 25.5% and maximum 68.8%) to reach $\tilde {c}$ plus 10% and by the 31.4% on average (with minimum 7.2% and maximum 52.1%) to reach $\tilde {c}$ plus 5% in the experiments.

We remark that, while the uniqueness of the STO optimal solution has been proved for p = 1 (Petersson 1999), ill-posedness of the problem for higher p values (e.g., p = 3 used in this work) is well known (Bendsøe and Sigmund 1995; Tovar and Khandelwal 2010). Consequently, rather than simply being an approximation, the maps obtained using FPCA could represent optimal alternative solutions. In fact, by modifying the problem by means of f_curr, we do not follow the same sequence of solutions followed without reduced basis, allowing the procedure to move to other regions where different minima can be found. Obviously, we stopped the iterations when we reached a predefined gap with respect to the reference compliance $\tilde {c}$ to pursue time savings, but the evolution could lead to a different solution even in the subsequent iterations.

We believe this is the reason why our density maps with 5% or 10% gap are practically equivalent to those with reference $\tilde {c}$ and those at convergence when the gradient-based STO is performed without reduced basis, although they are only similar from a topological point of view. But, by exploiting reduced basis through FPCA, these solutions are obtained in a drastically lower CPU time.

As mentioned, our strategy to include f_curr has avoided additional calculations to compute corrective terms to adapt relation (6), as carried out in Gogu (2015). However, in this way, the reduced problems generate solutions with an increase of c in a few iterations. But, at the same time, the compliance c is reduced so much in the next iteration with a complete FEA solution to provide significant gain in the overall computing time. Our future work will consist in defining the best thresholds τ₁, τ₂, and τ₃ in order to optimize this trade-off. Furthermore, we will compare the proposed strategy with f_curr with different alternatives in which corrective terms are added in (6).

From an application point of view, we will apply the proposed algorithm to several practical cases. For example, we will consider the computational gain when performing a pre-screening of different layouts, such as orientations or alternative features, while limiting a finer analysis without reduced basis to the selected layout only. At the same time, we can exploit the computational gain to explore different initializations of the optimization procedure in a reduced time.