Three-dimensional fluid topology optimization for heat transfer

Abstract

In this work, an in house topology optimization (TO) solver is developed to optimize a conjugate heat transfer problem: realizing more complex and efficient coolant systems by minimizing pressure losses and maximizing the heat transfer. The TO method consists in an idealized sedimentation process in which a design variable, in this case impermeability, is iteratively updated across the domain. The optimal solution is the solidified region uniquely defined by the final distribution of impermeability. Due to the geometrical complexity of the optimal solutions obtained, this design method is not always suitable for classic manufacturing methods (molding, stamping....) On the contrary, it can be thought as an approach to better and fully exploit the flexibility offered by additive manufacturing (AM), still often used on old and less efficient design techniques. In the present article, the proposed method is developed using a Lagrangian optimization approach to minimize stagnation pressure dissipation while maximizing heat transfer between fluid and solid region. An impermeability dependent thermal conductivity is included and a smoother operator is adopted to bound thermal diffusivity gradients across solid and fluid. Simulations are performed on a straight squared duct domain. The variability of the results is shown on the basis of different weights of the objective functions. The solver builds automatically three-dimensional structures enhancing the heat transfer level between the walls and the flow through the generation of pairs of counter rotating vortices. This is consistent to solution proposed in literature like v-shaped ribs, even if the geometry generated is more complex and more efficient. It is possible to define the desired level of heat transfer and losses and obtain the closest optimal solution. It is the first time that a conjugate heat transfer optimization problem, with these constraints, has been tackled with this approach for three-dimensional geometries.

1 Introduction

In modern gas turbines, the turbine entry temperature (TET) exceeds the melting point of the used alloys, reaching up to 2200 K in the advanced engines (Chyu and Siu 2013). Efficient coolant systems must be employed to make turbine blades resistant against fusion and mechanical stresses. Coolant systems are mainly characterized by internal channels optimized to reduce pressure losses. Turbulators and other microstructures are used instead to promote heat transfer between solid parts and coolant fluid. The design of such channels, position, and shape of turbulators is still a complex subject of study. The main goal is increasing heat transfer while reducing thermal gradients across the blades and minimize the energy used for coolant purpose (Saha and Acharja 2014). Temperature uniformity is strongly required to avoid cracks and ensure high level of reliability; this aspect is still considered one of the greatest challenges in gas turbine production (Bunker 2007; Montomoli et al. 2012). In order to predict the metal temperature accurately, it is important to carry out a conjugate heat transfer (CHT) method, where the thermal field in the fluid and the solid are solved at the same time. There are mainly two methodologies, using a single solvers for fluid and solid region or using ad hoc solver for the solid part (Montomoli et al. 2009). In this work a single code is used for fluid and solid domains because it is required by the optimization process. Several methods have been proposed for the optimization of CHT problem in gas turbines. It is crucial to consider this aspect specially in small gas turbines and when there are strong thermal gradients, as in HP components (Verstraete 2008). The majority of the available work is based on shape optimization and conjugate heat transfer (Verstraete et al. 2013). However, shape optimization is based on an “a priori” definition of the baseline geometry, taking into account the manufacturability limits. Relatively complex geometry cannot always be produced using actual manufacturing processes. With the introduction of additive manufacturing (AM), the design envelope changed and we do not have anymore such limits. However, the design and optimization methods are still considering these constraints. AM allows the production of three-dimensional metal components, directly from digital models, avoiding processes as stamping, molding, and bending. Major limitations of this technique, such as poor mechanical properties of layered material and low resolution for small components, have reduced exponentially in the last year due to the large interest towards the versatility of this technique (Ford 2014; Additive Manufacturing 2013; Ibabe et al. 2014). For instance, the possibility to increase structural complexity and efficiency of mechanical components is expected to have a relevant impact in coolant system technology (Jones et al. 2015). Shape optimization is not able to fully exploit the potential of this manufacturing method. The natural next step is finding those complex and efficient geometries, suitable for AM. Topology optimization (TO) is expected to be a satisfying solution. The key idea of TO is to iteratively update a scalar variable, usually impermeability, across a domain, respecting a set of constraints and minimizing a multi-objective function. At the end of the process, the solution is found as the region with relatively high impermeability, i.e., the solidified optimum structure. This process bears resemblance to the physical sedimentation of particles in a fluid. For this reason, we will refer to that as an idealized sedimentation process.

Geometries obtained in this way show high levels of complexity. Complex channels, fractals, ribs, and series of fluid splitters are examples of the structures present in the final geometries. Those structures cannot be produced using actual manufacturing processes but only exploiting the flexibility offered by additive manufacturing. First introduction of topology optimization can be found in the 1980s in Bendsoe and Sigmund (2004), Lavrov et al. (1980), Gibiansky and Cherkaev (1997), Glowinski (1984), and Goodman et al. (1986). Since then, the technique has been used mainly for structural problems. A wide introduction can be found in Bendsoe and Kikuchi (1988). In the last 20 years the technique has been also considered for other physical problems like aerodynamics and electromagnetism. Only recently, this application has been extended to fluid-thermal dynamics problem, i.e., considering both Navier-Stokes equations and convection-conduction equations. In 2009, Dede used TO to optimized power dissipation and mean temperature across a uniformly heated domain (Dede 2009; Dede et al. 2014). In the same year, Yoon considered a two-dimensional TO approach for the cooling of a hot plate by mean of an external coolant flow (Yoon 2010). An extension of this work has been published in 2011, with the application of the same method to a hierarchical system of microchannels (Dede 2011). In 2013, Matsumori improved the method by using a conjugate heat transfer equation, taking simultaneously into account both the fluid and the solid part (Matsumori et al. 2014). In the same year, Koga performed TO on a three-dimensional uniformly heated medium (Koga et al. 2013). In 2014, Marck and Alexandersen further refined the model expressing thermal conductivity as a function of impermeability (Marck and Privat 2014; Alexandersen et al. 2014). In 2015, Dede, Alexandersen, and Kentaro performed further analysis on three-dimensional TO methods for thermal exchange in fluid domain with a heat sink in Dede et al. (2015), Alexandersen et al. (2016), and Yaji et al. (2015).

In 2013, in Marck et al. a full conjugate heat convection-conduction equation is used together with a moving asymptotes method: a coolant flow is injected from the inlet of a two-dimensional domain to be expelled by the outlet. The domain is not uniformly heated, but heat is directly diffused from the domain walls (Marck et al. 2013). A similar problem is tackled in Pietropaoli et al. in 2016 by using a steepest descent gradient method for the optimization process (Pietropaoli et al. 2017).

Using uniformly heated walls as boundary condition, this problem is a simplification of the coolant channel optimization for turbine blades. In this work, a similar model is applied to three-dimensional geometry, such as a square duct. The optimization is carried in order to increase heat transfer while reducing stagnation pressure dissipation of the coolant flow. A description of the problem is present in the work together with the relative governing equations and boundary conditions. The optimization process is built in TOffee, the house code based on the adjoint optimization method presented in Pietropaoli et al. (2017).

2 Method description

This section describes briefly the structure of TOffee, the in house optimization code for additive manufacturing. Topology optimization emulates an idealized sedimentation process, where the sediments represent the boundaries of the optimized geometries. The overall algorithm is an adjoint VoF method, where the solid material is identified by associating to each point of the domain a scalar value, usually impermeability or porosity. This variable is updated during the optimization routine in order to minimize a multi-objective function subject to a set of constraints. At the end of the process, the material distribution allows to find the solid optimized structures identified with high impermeability regions. A formal definition of the method needs the introduction of some mathematical entities:

• A design domain Ω. It is the spatial domain in which the solution is sought. In this work, the domain is a three-dimensional bounded open set;

• A set of state variables X. In this work, pressure p, velocity vector v, and temperature T are considered;

• A set of design variables Y. In this work, only impermeability α is used, better described as a Brinkman penalization coefficient in the following session. Impermeability is naturally expressed as a scalar between 0 (fluid region) and $\infty$ (solid region). For clear numerical reasons, impermeability has to be bounded with a relatively high value $\alpha _{\max }$. The advantage of this choice is the possibility to re-scale the quantity of interest and express it as $\alpha =\alpha _{\max } \gamma$, where γ ∈ [0,1] is the re-scaled design variable such that the region is fluid when γ = 0 and solid when γ = 1. Fluid parameters will be easily expressed as a function of γ.

• Design constraints R. They are a set of equalities and inequalities expressed for X and Y. In this case, they are identified by the governing equations of the fluid , that is an expression for the pressure R_p, one for the i − th velocity component $R_{v_{i}}$ and one for the temperature R_T;

• A set of feasible solutions Σ_Ω. Each element 𝜃 = 𝜃(X, Y ) of this set is a state of the system that verifies all the constraints;

• A multi-objective function F, usually expressed as a combination of many objective functions.

  The optimization process aims to minimize (or to maximize according to necessity) the multi-objective function F that is to find a feasible solution 𝜃 such that F(𝜃) = F(X, Y ) is a minimum of the set F(Σ_Ω).

3 Governing equations for porous media

The VoF algorithm is shown below. The fraction variable is the impermeability. A variable impermeability is here taken into account by adopting idealized porous media fluid equations as governing equations of the system. Governing equations R_p, $R_{v_{i}}$ and R_T are defined below and they express the fluid optimization constraints as

$$ R_{p}=R_{v_{i}}=R_{T}= 0 $$

(1)

for i = 1,2,3. Note that we will use a vectorial notation R_v instead of $R_{v_{i}},\ i = 1,2,3,$ when needed. The flow is considered incompressible and at constant density ρ,

$$ R_{p} = \nabla \cdot v $$

(2)

A modified steady Navier-Stokes equation expresses the balance of momentum,

$$ R_{v} = \rho {(}v\cdot \nabla {)} v + \nabla p - \nabla \cdot (\mu (\nabla v + \nabla^{t} v)) + \alpha_{\max}\gamma v $$

(3)

The impermeability appears in the penalization Brinkman term ($\alpha _{\max }\gamma v)$. This is a model of the resistance applied to the flow: when γ = 0, no resistance is made and the momentum equation is the Navier-Stokes equation. For increasing values of γ, the penalization coefficient forces the magnitude of v to approach 0, emulating a solid material (Marck and Privat 2014). The impermeability dependence is introduced also in the energy equation by using a variable thermal conductivity k,

$$ R_{T} = \rho c \ v \cdot \nabla T - \nabla \cdot (k \nabla T) $$

(4)

In this work, the thermal conductivity k is defined as a linear interpolation between the minimum value corresponding to the fluid (k_f) and the maximum value corresponding to the solid (k_s), that is

$$ k= k(\gamma) = k_{f} + (k_{s}-k_{f}) \gamma $$

(5)

The implementation of the boundary conditions follows what proposed by Nel et al. (2014) and this work uses the same assumptions. Differently from Nel et al. (2014) in this work, the energy equation is also present and the code is three-dimensional. At walls, no slip conditions are imposed, and isothermal conditions is used for the temperature, T_wall (that in this case is an hot surface, the maximum temperature in the domain). At the inlet, both velocity and temperature are prescribed, with uniform constant distributions, respectively v_in and T_in, with T_in < T_wall (the temperature of the inlet flow is lower than the solid surface temperature in this case). At the outlet, constant pressure is imposed, where the code is using, as reference pressure, the exit pressure so the value imposed of P at the exit is set to zero. For the velocity and the temperature gradients at the outlet, no gradients perpendicular to the surface are imposed as in Nel et al. (2014) (Table 1).

Table 1 Boundary conditions v and T. T_in and T_wall represent respectively the inlet and the wall temperature; whereas, v_in indicates the inlet velocity of the coolant flow

The geometrical constraints specified here are only the physical boundaries of the domain. Other geometrical constraints can be added without any loss of generality. Furthermore, in this work no volume constraints are imposed of the portion of domain that can be occupied by solid material.

4 Multi - objective function

A multi-objective function is defined here as a linear combination of stagnation pressure dissipation, f₁, and temperature gain of the coolant flow, f₂. They are expressed respectively as the mechanical energy and the temperature flux through the domain boundaries Γ, namely,

$$ f_{1} = - {\int}_{\Gamma}\left( p+\frac{1}{2}\rho|v|^{2} \right)v_{n} d {\Gamma} $$

(6)

$$ f_{2} = + {\int}_{\Gamma}\left( \rho c T \right)v_{n} d{\Gamma} $$

(7)

where v_n = v ⋅ n with n the normalized outward-pointing normal vector. The weighted combination of the objective is then defined as

$$ F= \omega_{1}f_{1} - \omega_{2} f_{2} $$

(8)

where ω₁ and ω₂ are positive constants used to tune the relative weight of the objectives during the optimization process. The negative weighting of f₂ is justified by the need of maximizing the temperature gain while minimizing F.

5 Continuous fluid adjoint optimization

For the adjoint optimization, we follow the work in Giles and Pierce (2000) and Cea (1986). The approach defined here is a special case of general continuous adjoint optimization.

As a general formulation, following the nomenclature already introduced in Section 2, the optimization problem can be concisely written as

$$\text{minimize}\qquad F(X,\gamma), $$

$$\text{subject to}\qquad R(X,\gamma)= 0 $$

where, as stated before, X represents the set of state variables p, v, and T, γ the design variable and R the set of constraints, in this case identified by the governing equations R_p, R_v, and R_T.

For the fluid adjoint optimization, as shown by Qian and Dede (2016) and Dilgen et al. (2018), a Lagrangian approach is considered to tackle the minimization problem. Precisely, the augmented objective function is considered, i.e., the Lagrangian functional

$$ L=F-{\int}_{\Omega}{ q R_{p}+ w\cdot R_{v}+\tau R_{T} d {\Omega}}, $$

(9)

where q, w, and τ are, respectively, Lagrange multiplier functions enforcing the constraints R_p = 0, R_v = 0, and R_T = 0. Following the terminology used by Giles and Pierce (2000), we refer to q, w, and τ as adjoint variables. The variables p, v, T are clearly functions of the design variable γ and, similarly, the adjoint variables q, w, and τ should also depend on γ. Thus, to (locally) optimize F with respect to γ one can look for a state 𝜃 = (X, γ) and adjoint variables such that the variation of L with respect to γ vanishes.

To compute the variation of F an adjoint formulation is used. Considering the total variation dL, we have

$$\begin{array}{@{}rcl@{}} dL &=& \left( \frac{\partial F}{\partial X} - {\int}_{\Omega}{ q \frac{\partial R_{p}}{\partial X} + w\cdot \frac{\partial R_{v}}{\partial X} +\tau \frac{\partial R_{T}}{\partial X} \ d {\Omega}} \right)dX \\ &&+ \left( \frac{\partial F}{\partial \gamma} - {\int}_{\Omega}{ q \frac{\partial R_{p}}{\partial \gamma} + w\cdot \frac{\partial R_{v}}{\partial \gamma} +\tau \frac{\partial R_{T}}{\partial \gamma} \ d {\Omega}} \right) d\gamma\\ \end{array} $$

(10)

where the symbols $\frac {\partial (-)}{\partial X}$ and $\frac {\partial (-)}{\partial \gamma }$ indicate the partial derivative with respect to the state variables and the design variable respectively. The adjoint variable q, w, and τ are computed in order to satisfy the following relations, i.e., the adjoint equations,

$$ \frac{\partial F}{\partial X} = {\int}_{\Omega} q \frac{\partial R_{p}}{\partial X} + w \cdot \frac{\partial R_{v}}{\partial X} +\tau \frac{\partial R_{T}}{\partial X} \ d {\Omega} $$

(11)

It follows that

$$ dL = \left( \frac{\partial F}{\partial \gamma} - {\int}_{\Omega} q \frac{\partial R_{p}}{\partial \gamma} + w\cdot \frac{\partial R_{v}}{\partial \gamma} +\tau \frac{\partial R_{T}}{\partial \gamma} d {\Omega} \right) d\gamma $$

(12)

from which the variation dL/dγ can be obtained.

At this point, a local minimum of the objective function F is computed through an iterative process, progressively updating the distribution of γ across the domain by means of the information coming from the sensitivity function exploiting the steepest descent method as in Bigs (2008), that is, the relation

$$ D \gamma = - \frac{d L}{d \gamma} $$

(13)

where Dγ represents the variation of γ between to consecutive iterations of the process. To achieve that, at each iteration the set of governing equation and adjoint equations are solved together with the relative boundary conditions.

In order to derive an explicit set of adjoint equations and the correct boundary conditions to apply, we consider, in (11), variations of the state variables, ∂p, ∂v, and ∂T. As shown in the Appendix, it is possible to integrate by parts the elements of relation (11) in order to group the resulting terms by ∂p, ∂v, and ∂T. In this way, the adjoint equations can be re-written as

$$\begin{array}{@{}rcl@{}} && {\int}_{\Omega}(\partial p) R_{q} +(\partial v)\cdot R_{w} + (\partial T) R_{\tau} d{\Omega} + \\ && {\int}_{\Gamma}(\partial p) BC_{q} + (\partial v)\cdot BC_{w} + (\partial T) BC_{\tau} \ d{\Gamma} + \\ && {\int}_{\Gamma}BC_{1}({\partial} v,w) d{\Gamma}+{\int}_{\Gamma}BC_{2}({\partial} T,\tau) \ d{\Gamma} = 0 \end{array} $$

(14)

where R_q, R_w, and R_τ constitute the adjoint operators of R_p, R_v, and R_T, whereas BC_q, BC_w, BC_τ, BC₁, and BC₂ are the surface contributions coming from integrating by part relation (11). In more details:

$$\begin{array}{@{}rcl@{}} R_{q} &=& \nabla \cdot w \end{array} $$

(15)

$$\begin{array}{@{}rcl@{}} R_{w} &=& -\rho v\cdot (\nabla w + \nabla^{t} w) - \nabla q \\ &&- \nabla \cdot(\mu (\nabla w + \nabla^{t} w)) + \alpha_{\max} \gamma w + \rho c \tau \nabla T \end{array} $$

(16)

$$\begin{array}{@{}rcl@{}} R_{\tau} &=& -\rho c v\cdot \nabla \tau - \nabla \cdot(k \nabla \tau) \end{array} $$

(17)

$$\begin{array}{@{}rcl@{}} BC_{q} &=& - w_{n} - \omega_{1} v_{n} \end{array} $$

(18)

$$\begin{array}{@{}rcl@{}} BC_{w} &=& - q n - \rho (w \cdot v )n - \rho w v_{n} - \mu (n \cdot \nabla w ) \\ &&-\omega_{1} (\rho v_{n} v + (p + \frac{1}{2} \rho |v|^{2} )) n - \omega_{2} \rho c T n \end{array} $$

(19)

$$\begin{array}{@{}rcl@{}} BC_{\tau} &=& - \rho c \tau v_{n} - k \nabla \tau \cdot n - \omega_{2} \rho c v_{n} \end{array} $$

(20)

$$\begin{array}{@{}rcl@{}} BC_{1} &=& \mu (n \cdot \nabla \partial v ) \cdot w \end{array} $$

(21)

$$\begin{array}{@{}rcl@{}} BC_{2} &=& \tau k (\partial \nabla T) \cdot n \end{array} $$

(22)

Solving (11) for q, w, and τ is obtained by vanishing all the volume and surface integral terms in (14). For the volume terms, it follows that for any variation of the state variables, the explicit form of the adjoint equations is found for $R_{q} = R_{w_{i}}=R_{\tau }= 0$. To be noticed that the adjoint equations have a similar structure of the governing equations. However, relation R_w contains also the transpose gradient of the adjoint velocity in the advection term and the source term ρcτ∇T as a result of the integration by parts in the advection term of the energy equation. To vanish the surface terms, instead, it must hold $BC_{q}=BC_{w_{i}}=BC_{\tau }=BC_{1}=BC_{2} = 0$. This relations give the set of the adjoint boundary conditions that q, w, and τ must verify on the border of the domain. In particular, considering the set of boundary conditions for the governing equations, adjoint boundary conditions can be specified for the different parts, that is inlet, outlet, and walls. Please note that it is more practical to consider separately the normal component and the tangential vector of the adjoint velocity, respectively w_n = w ⋅ n and w_ti = (w ⋅ t_i)t_i with t_i components of the unit vector tangential to w.

• Inlet and walls Velocity and temperature are prescribed as constant so (19) and (20) are not considered because the respective terms in (14) vanish automatically. The pressure is in general not constant then

  $$w_{n} = - \omega_{1} v_{n} $$

  Operating a decomposition of ∇ across the normal component n and the tangential components t_i, the following relation holds

  $$0 = \partial (\nabla \cdot v ) = \nabla \cdot \partial v = (n \cdot \nabla)\partial v_{n} + (t_{i} \cdot \nabla)\partial v_{t_{i}} $$

  The tangential components of the velocity $v_{t_{i}}$ are zero. It follows that (n ⋅∇)∂v_n = 0 and consequently, to vanish (21)

  $$(n \cdot \nabla ) (\partial v_{t_{i}} ) \cdot w_{t_{i}} = 0 $$

  that implies $w_{t_{i}}= 0$. Finally, to vanish (21), it follows that τ = 0.

• Outlet The pressure is prescribed as p = 0 so (18) is not considered because the respective term in (14) is automatically zero. The components perpendicular to the surface of the velocity and temperature gradients are imposed as zero, so (21) vanishes. Taking the tangential components of relation (19), the condition for the tangential components $w_{t_{i}}$ is found as

  $$- \rho w_{t_{i}} v_{n} - \mu (n \cdot \nabla w_{t_{i}} ) -\omega_{1} \rho v_{n} v_{t_{i}} = 0 $$

  By taking the normal component, instead, the boundary conditions for q and w_n are obtained from

  $$\begin{array}{@{}rcl@{}} q &=& - \rho (w \cdot v ) - \rho w_{n} v_{n} - \mu (n \cdot \nabla w_{n} ) -\omega_{1} \rho v_{n} v_{n} \\&&- \omega_{1} \left( \frac{1}{2} \rho |v|^{2} \right) - \omega_{2} \rho c T \end{array} $$

  A similar approach is used in Othmer et al. (2007). Finally, to vanish (20), the conditions for the adjoint temperature is found,

  $$(\tau + \omega_{2} )\rho c v_{n} + k\nabla \tau \cdot n = 0 $$

Finally, after solving the set of governing and adjoint equations, the variation dL/dγ can be computed through relation (12). Precisely, we have

$$ \frac{dL}{d \gamma} = \alpha_{\max} v\cdot w + \tau (k_{s} - k_{f}) {\Delta} T $$

(23)

so, an iterative process to find the solution is built by mean of the steepest descent method. Equation (13) is discretized in order to find the updated distribution on impermeability (γ_new) as a function of the actual distribution γ:

$$ \gamma_{new}=\gamma - h \left( \alpha_{\max} v\cdot w + \tau (k_{s} - k_{f}) {\Delta} T \right) $$

(24)

where h is a constant deriving by the approximation of the volume integral. This constant can be chosen in order to tune the speed of convergence. Furthermore, the relation (24) should be adapted in order to avoid non physical negative impermeability and to avoid the impermeability term $\alpha _{\max }\gamma$ to exceed the threshold value $\alpha _{\max }$ that is

$$ \gamma_{new}=\max \left\{ 0, \min \left\{ 1 , \gamma - h \left( {\alpha_{\max}} v\cdot w + \tau (k_{s} - k_{f}) {\Delta} T \right) \right\} \right\} $$

(25)

Validations of the code have been carried out (Pietropaoli et al. 2017) comparing the results with experimental data by Von Karman Institute (Verstraete et al. 2013).

6 Fluid topology optimization of a straight squared duct

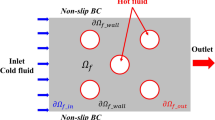
Relatively simple three-dimensional test cases have been adopted for the simulations. At first, a straight squared duct, with an aspect ratio of 1:6 is used, Fig. 1. The inlet face is pointed by the arrow whereas the outlet is the opposite square face. A coolant flow is injected by the inlet at constant velocity, with Reynolds number $Re \sim 1000$, and at constant temperature, T = 800 K. Walls temperature is kept as constant, 1800 K. Density and specific heat are consider as constant across the domain, ρ = 0.44 kg/m³ and c = 1.1 × 10³J/(kgK). The thermal conductivity of the coolant flow is k_f = 5.8 × 10^− 2W/(mK) whereas k_s = 25 W/(mK). A squared uniform mesh is generated in the domain, 50 cells on the shortest edges and 300 on the longest.

Fig. 1

Design domain for the straight square duct. Inlet face is pointed by the arrow. The outlet face is on the opposite side of the geometry

Since no volume constraints are imposed on α, when optimizing only for pressure losses, trivial solution is found and the sedimentation process does not produce any internal structure in the geometry. When using a nonzero heat transfer weight, ω₂ > 0, the flow pattern becomes more complex. Figures 2 and 3 show respectively an inlet and an outlet end view of the solution obtained using ω₁ = 1 and ω₂ = 0.01. The structure is connected and touches the external walls in proximity of the inlet and the outlet. In order to show the complexity of the coolant pattern, velocity streamlines of the coolant flow are shown in Figs. 4 and 5. The color is consistent with the temperature of the particle generating the streamlines: from fluid inlet temperature, 800 K (blue), to fluid outlet temperature, 1800 K (red). In Fig. 5, the origin of the streamlines are randomly generated with uniform distribution across the inlet patch. For the sake of clarity, in Fig. 6, streamlines origins are distributed on a diagonal segment across the squared inlet patch: in this case is easier to follow how the internal structure forces spreading and mixing motions of the fluid particles in order to enhance thermal exchange. Moreover, a diagonal planar section is taken into account to show the efficiency of heat exchange inside the domain, Figs. 6 and 7. The complex pattern of the streamlines is further shown in Fig. 8. In the picture, the view is perpendicular to the inlet plane. The color of the streamlines is chosen consistently with the angular velocity magnitude of the fluid particle generating the streamline, showing that the symmetric structures are pairs of counter rotating vortices.

Fig. 2

Inlet view: geometry optimized for pressure losses and heat transfer. In this case, ω₁ = 1 whereas ω₂ = 0.01

Fig. 3

Outlet view: geometry optimized for pressure losses and heat transfer. In this case, ω₁ = 1 whereas ω₂ = 0.01

Fig. 4

Velocity streamlines around the solution for the squared duct. The color is consistent with the local temperature of the coolant flow, from blue (800 K) to red (1800K).

Fig. 5

Velocity streamlines around the solution, generated from a transversal segment at the inlet. The color is consistent with local temperature of the coolant flow, from blue (800 K) to red (1800 K)

Fig. 6

Diagonal planar section for the straight squared duct

Fig. 7

Temperature distributions across the diagonal planar section of the squared duct. From top to bottom, heat transfer weight has been progressively increased: top ω₂ = 0; center ω₂ = 0.0001; bottom ω₂ = 0.01

Fig. 8

Velocity streamlines: the view direction is perpendicular to the inlet face. The color of the streamlines is consistent with the angular velocity magnitude of the fluid particle

When ω₂ = 0, the heat is mainly conducted from the walls. For increasing ω₂ = 0, instead, advection processes lead to a more efficient heat exchange, bringing to an almost completely hot exiting flow when ω₂ = 0.01. Table 2 and Fig. 9 show the percentage pressure drop and temperature gain for different choices of ω₂, while ω₁ = 1. Relative pressure drop and relative temperature gain are expressed with respect to the reference values obtained optimizing pressure losses only (ω₁ = 1, ω₂ = 0). The relation is nonlinear. For a thermal exchange, improvement of nearly 5%, the pressure drop is 15% higher, whereas for an improvement of approximately 7.5%, the pressure drop is nearly double. Table 2 contains also the proportion of volume occupied by the solid region for each test. The nonlinear dependence of the objective functions on ω₂ is confirmed. In fact, adding more than 30% of solid material within the design domain produces a relatively small increase of the thermal objective function, while drastically increasing the pressure drop.

Table 2 First column: percentage relative pressure drop

Fig. 9

Percentage relative pressure drop and temperature gain. The reference value on the origin is obtained with ω₁ = 1 and ω₂ = 0

7 Conclusion

This paper presents a new application of fluid topology optimization. Full three-dimensional geometries have been automatically optimized considering both pressure losses and heat exchange as objective. For the first time TO has been applied on a simplification of gas turbine heat transfer problem. Ducts and solid structures shapes inside the cavity have been optimized in order to enhance heat transfer while minimizing pressure losses of the coolant fluid. In this sense, the problem is a simplification of the internal coolant system of a gas turbine blade. A formulation for conjugate heat transfer is used in the paper. The design domain is considered as idealized porous medium with variable impermeability, updated in each iteration by using a Lagrangian adjoint approach. Complex and connected structures are automatically generated inside a straight squared duct (test case). Different choices of the objective functions weights have an influence on the efficiency of the heat exchange inside the domain. The dependence of the objective functions on the weights is nonlinear. Relatively small improvements on the heat exchange efficiency lead to consistent increase of the volume occupied by the solid region and, consequently, to relatively high pressure drop. Axial and diagonal symmetric fluid structures are visible along the main direction of both the geometry. The stability of the results open the way to the adoption of this technique to the design for additive manufacturing, possibly with many application in the design of a new advanced internal coolant system for turbine blades.

Appendix

This section contains the main derivations for the adjoint equation and the relative adjoint boundary conditions. The variation of the state variables is concisely indicated with the symbol ∂. Essentially, to obtain (14) from (12), integration by parts is applied.

For the first integrand term in (12) it holds:

$$\begin{array}{@{}rcl@{}} {\int}_{\Omega}q \partial R_{p} d {\Omega} &=& {\int}_{\Omega} q \nabla \cdot \partial v \ d {\Omega} = {\int}_{{\Gamma}} q \partial v \cdot n d{\Gamma} \\&&- {\int}_{\Omega}\nabla q \cdot \partial v \ d{\Omega} \end{array} $$

For the second one, it might be useful to remind that for any tensor A and vector x it holds

$$\nabla \cdot (A \cdot x ) = A : \nabla x + x \cdot (\nabla \cdot A) $$

where the symbol “ : ” indicates the trace of the scalar product, that is A : ∇x = tr(A ⋅∇x).

Let σ(−) be the symmetric stress tensor, namely σ = (∇ + ∇^t). It holds

$$\begin{array}{@{}rcl@{}} \nabla \cdot (\sigma (\partial v) \cdot w ) &=& \nabla \cdot (w \cdot \sigma (\partial v)) \text{and}\ \ \sigma(\partial v) : \nabla w \\&=& \sigma(w) : \nabla \partial v \end{array} $$

Thanks to the last identity, we have

$$\begin{array}{@{}rcl@{}} {\int}_{\Omega} w\cdot (\nabla \cdot \sigma(\partial v))\ d {\Omega} = {\int}_{\Gamma} w \cdot \sigma (\partial v) \cdot n \ d {\Gamma} \\ -{\int}_{\Gamma} \partial v \cdot \sigma (w) \cdot n \ d{\Gamma} + {\int}_{\Omega}\partial v \cdot (\nabla \cdot \sigma(w))\ d {\Omega} \end{array} $$

as a consequence of

$$\begin{array}{@{}rcl@{}} \nabla \cdot (w \cdot \sigma (\partial v)) &-& w\cdot (\nabla \cdot \sigma(\partial v)) = \nabla \cdot (\partial v \cdot \sigma(w)) \\&-& \partial v \cdot (\nabla \cdot \sigma(w)) \end{array} $$

Applying this to the second term of (12) we obtain

$$\begin{array}{@{}rcl@{}} &&{\int}_{\Omega}w \cdot \partial R_{v} \ d{\Omega} \\ &=& {\int}_{\Omega}w \cdot \left( \rho\ (\partial v \cdot \nabla) v + \rho\ (v \cdot \nabla) \partial v + \nabla \partial p \right.\\&&\left.- \mu \nabla \cdot \left( \nabla \partial v + \nabla^{t} \partial v \right) + \alpha_{\max} \gamma \ \partial v \right) \ d {\Omega} \\ &=&{\int}_{{\Gamma}} \rho (w \cdot v ) \partial v \cdot n \ d{\Gamma} - {\int}_{\Omega} \rho \left( \partial v \cdot \nabla w \right) \cdot v \ d{\Omega} \\ && + {\int}_{{\Gamma}}\rho \left( w \cdot \partial v \right)v \cdot n \ d{\Gamma}- {\int}_{\Omega} \rho \left( v \cdot \nabla w \right) \cdot \partial v \ d{\Omega}\\ && + {\int}_{{\Gamma}} \partial p\ w \cdot n \ d{\Gamma}- {\int}_{\Omega} \partial p\ \nabla \cdot w \ d{\Omega} \\ && - {\int}_{{\Gamma}}\mu\ w \cdot \nabla \partial v \cdot n \ d{\Gamma} + {\int}_{{\Gamma}}\mu \ \nabla w \cdot \partial v \cdot n \ d{\Gamma}\\&&- {\int}_{\Omega} \mu\ (\nabla \cdot \nabla w ) \cdot \partial v \ d{\Omega}\\ && - {\int}_{{\Gamma}}\mu\ w \cdot \nabla^{t} \partial v \cdot n \ d{\Gamma} + {\int}_{{\Gamma}}\mu\ \nabla^{t} w \cdot \partial v \cdot n \ d{\Gamma}\\&&- {\int}_{\Omega}\mu\ (\nabla \cdot \nabla^{t} w ) \cdot \partial v \ d{\Omega} + {\int}_{\Omega}\alpha_{\max} \gamma w \cdot \partial v \ d{\Omega} \end{array} $$

Finally, for the third integrand term in (12), we have

$$\begin{array}{@{}rcl@{}} &&{\int}_{\Omega} \tau \partial R_{T} \ d{\Omega} \\ &=& {\int}_{\Omega} \tau \left( \rho c \ \partial v \cdot \nabla T + \rho c \ v \cdot \nabla \partial T - \nabla \cdot \left( k \nabla \partial T \right) \right) \ d{\Omega}\\ &=& + {\int}_{\Omega}\rho c \ \tau \nabla T \cdot \partial v \ d{\Omega}\\ && + {\int}_{{\Gamma}} \rho c \ \tau \partial T \ v \cdot n \ d{\Gamma}- {\int}_{\Omega}\rho c \ \partial T \ v \cdot \nabla \tau \ d{\Omega}\\ &&- {\int}_{{\Gamma}}\tau k \partial \nabla T \cdot n \ d{\Gamma}+ {\int}_{{\Gamma}} k \partial T \nabla \tau \cdot n \ d{\Gamma}\\&&- {\int}_{\Omega}\nabla \cdot \left( k \nabla \tau \right) \partial T \ d{\Omega} \end{array} $$

Remark 1

The adjoint momentum equation can be explicitly written in two different versions. In fact, using the Gauss’ divergence theorem for the derivation of R_w, the term

$$ {\int}_{\Omega}w \cdot \rho\ (\partial v \cdot \nabla) v \ d {\Omega} $$

(26)

can be expressed as

$$\begin{array}{@{}rcl@{}} &&{\int}_{\Gamma}\rho (w \cdot v ) \partial v \cdot n \ d{\Gamma} - {\int}_{\Omega} \rho \left( \partial v \cdot \nabla w \right) \cdot v \ d{\Omega} \\ &=& {\int}_{\Gamma} \rho (w \cdot v ) \partial v \cdot n \ d{\Gamma} - {\int}_{\Omega} \rho \left( v \cdot \nabla^{t} w \right) \cdot \partial v \ d{\Omega}. \end{array} $$

(27)

Alternatively, the term in (26) can be simply re-written as

$$\begin{array}{@{}rcl@{}} {\int}_{\Omega}w \cdot \rho (\partial v \cdot \nabla^{t} v) \ d{\Omega} &=& {\int}_{\Omega}\rho (\partial v \cdot \nabla^{t} v) \cdot w \ d{\Omega}\\&& = {\int}_{\Omega} \rho (w \cdot \nabla v) \cdot \partial v \ d{\Omega} \end{array} $$

(28)

The quantities in (27) and (28) represent the same value. In this work and similarly to Nel et al. (2014), Othmer et al. (2007), and Qian and Dede (2016), we use the first formulation to obtain the advection term of (16). If using the second formulation, instead, the advection term would be written as ρ(−v ⋅∇w + w ⋅∇v), consistently to Yaji et al. (2015). The two versions are equivalent and produce the same results if not considering relatively small discrepancies coming from the numeric of the solving the two different methods. The only difference is in the derivation of the methods and, in particular, of the boundary conditions: in fact no surface contribution are given when adopting form (28), whereas the surface correction ρ(w ⋅ v)n to be included in the adjoint boundary conditions appears when adopting (27).

Remark 2

The transpose gradient terms, ∇^tv and ∇^tw, do not appear in (19) and (21) for the following reason: Considering now

$$\begin{array}{@{}rcl@{}} &&\!{\int}_{\Gamma}\left( (\nabla \partial v + \nabla^{t} \partial v) \cdot w - (\nabla w + \nabla^{t} w ) \cdot \partial v \right) \cdot n \ d {\Gamma}\\ \!&=&\! {\int}_{\Omega}\nabla \cdot \left( (\nabla \partial v + \nabla^{t} \partial v) \cdot w - (\nabla w + \nabla^{t} w ) \cdot \partial v \right) \ d {\Omega}\\ \!&=&\! {\int}_{\Omega}\sigma(\partial v ) : \nabla w - \sigma (w) : \nabla \partial v + w \cdot (\nabla \cdot (\nabla \partial v + \nabla^{t} \partial v ))\\ &&{-} \partial v \cdot (\nabla \cdot (\nabla w + \nabla^{t} w )) \ d {\Omega}\\ \!&=&\! {\int}_{\Omega}w \cdot (\nabla \cdot (\nabla \partial v )) {-} \partial v \cdot (\nabla \cdot (\nabla w )) \ d {\Omega} \end{array} $$

since ∇⋅ (∇^tw) = ∇(∇⋅ w) = 0 for equation R_q = 0 and ∇⋅ (∇^t∂v) = ∇(∇⋅ ∂v) = 0 for equation R_p = 0.