Skip to main content
SpringerLink
Log in

General decay rates for the wave equation with mixed-type damping mechanisms on unbounded domain with finite measure

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

This paper is concerned with the study of the uniform decay rates of the energy associated with the wave equation subject to a locally distributed viscoelastic dissipation and a nonlinear frictional damping

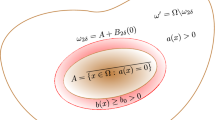
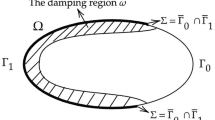
$$u_{tt}- \Delta u+ \int_0^t g(t-s){\rm div}[a(x)\nabla u(s)]\,{\rm d}s + b(x) f(u_t)=0\,\quad {\rm on} \quad \Omega\times]0,\infty[,$$

where \({\Omega\subset\mathbb{R}^n, n\geq 2}\) is an unbounded open set with finite measure and unbounded smooth boundary \({\partial\Omega = \Gamma}\). Supposing that the localization functions satisfy the “competitive” assumption \({a(x)+b(x)\geq\delta>0}\) for all \({x\in \Omega}\) and the relaxation function g satisfies certain nonlinear differential inequalities introduced by Lasiecka et al. (J Math Phys 54(3):031504, 2013), we extend to our considered domain the prior results of Cavalcanti and Oquendo (SIAM J Control Optim 42(4):1310–1324, 2003). In addition, while in Cavalcanti and Oquendo (2003) the authors just consider exponential and polynomial decay rate estimates, in the present article general decay rate estimates are obtained.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alabau-Boussouira F., Cannarsa P., Guglielmi R.: Indirect stabilization of weakly coupled systems with hybrid boundary conditions. Math. Control Relat. Fields 1(4), 413–436 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  2. Alabau-Boussouira F.: New trends towards lower energy estimates and optimality for nonlinearly damped vibrating systems. J. Differ. Equ. 249(5), 1145–1178 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  3. Alabau-Boussouira F.: A unified approach via convexity for optimal energy decay rates of finite and infinite dimensional vibrating damped systems with applications to semi-discretized vibrating damped systems. J. Differ. Equ. 248(6), 1473–1517 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  4. Alabau-Boussouira F.: Convexity and weighted integral inequalities for energy decay rates of nonlinear dissipative hyperbolic systems. Appl. Math. Optim. 51(1), 61–105 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  5. Alabau-Boussouira F.: Observabilité frontière indirecte de systèmes faiblement couplés. (French. English, French summary)[Indirect boundary observability of a weakly coupled wave system]. C. R. Acad. Sci. Paris Sér. I Math. 333(7), 645–650 (2001)

    Article  MathSciNet  Google Scholar 

  6. Ali Mehmeti F., Nicaise S.: Nemytskij’s operators and global existence of small solutions of semilinear evolution equations on nonsmooth domains. Commun. Part. Differ. Equ. 22(9-10), 1559–1588 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  7. Bae J.J., Nakao M.: Energy decay for the wave equation with boundary and localized dissipations in exterior domains. Math. Nachr. 278(7-8), 771–783 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  8. Bardos C., Lebeau G., Rauch J.: Sharp sufficient conditions for the observation, control, and stabilization of waves from the boundary. SIAM J. Control Optim. 30(5), 1024–1065 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  9. Bociu L., Rammaha M., Toundykov D.: On a wave equation with supercritical interior and boundary sources and damping terms. Math. Nachr. 284(16), 2032–2064 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  10. Cavalcanti M.M., Domingos Cavalcanti V.N., Dias Silva F.R.: Uniform decay rates for the wave equation with nonlinear damping locally distributed in unbounded domains with finite measure. SIAM J. Control Optim. 52(1), 545–580 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  11. Cavalcanti M.M., Domingos Cavalcanti V.N., Fukuoka R., Soriano J.A.: Asymptotic stability of the wave equation on compact manifolds and locally distributed damping: a sharp result. Arch. Ration. Mech. Anal. 197(3), 925–964 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  12. Cavalcanti M.M., Domingos Cavalcanti V.N., Fukuoka R., Soriano J.A.: Asymptotic stability of the wave equation on compact surfaces and locally distributed damping–a sharp result. Trans. Am. Math. Soc. 361(9), 4561–4580 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  13. Cavalcanti M.M., Domingos Cavalcanti V.N., Fukuoka R., Toundykov D.: Stabilization of the damped wave equation with Cauchy–Ventcel boundary conditions. J. Evol. Equ. 9(1), 143–169 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  14. Cavalcanti M.M., Domingos Cavalcanti V.N., Martinez P.: General decay rate estimates for viscoelastic dissipative systems. Nonlinear Anal. 68(1), 177–193 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  15. Cavalcanti M.M., Domingos Cavalcanti V.N., Lasiecka I.: Irena Well-posedness and optimal decay rates for the wave equation with nonlinear boundary damping–source interaction. J. Differ. Equ. 236(2), 407–459 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  16. Cavalcanti M.M., Oquendo H.P.: Frictional versus viscoelastic damping in a semilinear wave equation. SIAM J. Control Optim. 42(4), 1310–1324 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  17. Cavalcanti M.M., Domingos Cavalcanti V.N., Ma T.F., Soriano J.A.: Global existence and asymptotic stability for viscoelastic problems. Differ. Integral Equ. 15(6), 731–748 (2002)

    MATH  MathSciNet  Google Scholar 

  18. Cavalcanti, M.M., Domingos Cavalcanti, V.N.: Introdução à teoria das distribuições e aos espaços de Sobolev. (Portuguese) [Introduction to distribution theory and Sobolev spaces] Editora da Universidade Estadual de Maringá (Eduem), Maringá, p. 452 (2009). ISBN: 978-85-7628-195-5

  19. Chen G.: A note on the boundary stabilization of the wave equation. SIAM J. Control Optim. 19(1), 106–113 (1981)

    Article  MATH  MathSciNet  Google Scholar 

  20. Chen G.: Control and stabilization for the wave equation in a bounded domain. SIAM J. Control Optim. 17(1), 66–81 (1979)

    Article  MATH  MathSciNet  Google Scholar 

  21. Daoulatli M., Lasiecka I., Toundykov D.: Uniform energy decay for a wave equation with partially supported nonlinear boundary dissipation without growth restrictions. Discrete Contin. Dyn. Syst. Ser. S 2(1), 67–94 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  22. Eller M., Lagnese J., Nicaise S.: Decay rates for solutions of a Maxwell system with nonlinear boundary damping. Special issue in memory of Jacques-Louis Lions. Comput. Appl. Math. 21(1), 135–165 (2002)

    MATH  MathSciNet  Google Scholar 

  23. Fabrizio M., Polidoro S.: Asymptotic decay for some differential systems with fading memory. Appl. Anal. 81(6), 1245–1264 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  24. Guesmia A., Messaoudi S.A.: A general decay result for a viscoelastic equation in the presence of past and finite history memories. Nonlinear Anal. Real World Appl. 13(1), 476–485 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  25. Lasiecka I., Messaoudi S., Mustafa M.: Note on intrinsic decay rates for abstract wave equations with memory. J. Math. Phys. 54(3), 031504 (2013)

    Article  MathSciNet  Google Scholar 

  26. Lasiecka I., Toundykov D.: Regularity of higher energies of wave equation with nonlinear localized damping and a nonlinear source. Nonlinear Anal. 69(3), 898–910 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  27. Lasiecka I., Tataru D.: Uniform boundary stabilization of semilinear wave equations with nonlinear boundary damping. Differ. Integral Equ. 6(3), 507–533 (1993)

    MATH  MathSciNet  Google Scholar 

  28. Liu K.: Locally distributed control and damping for the conservative systems. SIAM J. Control Optim. 35(5), 1574–1590 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  29. Liu, W.-J., Zuazua E.: Decay rates for dissipative wave equations. Papers in memory of Ennio De Giorgi (Italian). Ricerche Mat. 48, suppl., 61–75 (1999)

  30. Martinez P.: A new method to obtain decay rate estimates for dissipative systems with localized damping. Rev. Mat. Complut. 12(1), 251–283 (1999)

    MATH  MathSciNet  Google Scholar 

  31. Martinez P.: A new method to obtain decay rate estimates for dissipative systems. ESAIM Control Optim. Calc. Var. 4, 419–444 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  32. Motai T.: Asymptotic behavior of solutions to the Klein-Gordon equation with a nonlinear dissipative term. Tsukuba J. Math. 15(1), 151–160 (1991)

    MATH  MathSciNet  Google Scholar 

  33. Muñoz Rivera J.E., Peres Salvatierra A.: Asymptotic behaviour of the energy in partially viscoelastic materials. Q. Appl. Math. 59(3), 557–578 (2001)

    MATH  Google Scholar 

  34. Nakao, M.: Decay and global existence for nonlinear wave equations with localized dissipations in general exterior domains. New trends in the theory of hyperbolic equations, 213–299. Oper. Theory Adv. Appl., 159, Birkhäuser, Basel (2005)

  35. Nakao M., Jung I.H.: Energy decay for the wave equation in exterior domains with some half-linear dissipation. Differ. Integral Equ. 16(8), 927–948 (2003)

    MATH  MathSciNet  Google Scholar 

  36. Nakao M.: Decay of solutions of the wave equation with a local nonlinear dissipation. Math. Ann. 305(3), 403–417 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  37. Nakao M.: Decay of solutions of the wave equation with a local degenerate dissipation. Israel J. Math. 95, 25–42 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  38. Nicaise S., Valein J.: Stabilization of second order evolution equations with unbounded feedback with delay. ESAIM Control Optim. Calc. Var. 16(2), 420–456 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  39. Nicaise S., Pignotti C.: Stabilization of the wave equation with boundary or internal distributed delay. Differ. Integral Equ. 21(9-10), 935–958 (2008)

    MATH  MathSciNet  Google Scholar 

  40. Nicaise S., Pignotti C.: Stability and instability results of the wave equation with a delay term in the boundary or internal feedbacks. SIAM J. Control Optim. 45(5), 1561–1585 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  41. Said-Houari B., Falcão Nascimento F.A.: Global existence and nonexistence for the viscoelastic wave equation with nonlinear boundary damping-source interaction. Commun. Pure Appl. Anal. 12(1), 375–403 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  42. Serrin J., Todorova G., Vitillaro E.: Existence for a nonlinear wave equation with damping and source terms. Differ. Integral Equ. 16(1), 13–50 (2003)

    MATH  MathSciNet  Google Scholar 

  43. Toundykov D.: Optimal decay rates for solutions of a nonlinear wave equation with localized nonlinear dissipation of unrestricted growth and critical exponent source terms under mixed boundary conditions. Nonlinear Anal. 67(2), 512–544 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  44. Todorova, G., Yordanov, B.: Nonlinear dissipative wave equations with potential. Control methods in PDE-dynamical systems, 317–337. Contemp. Math., 426, Amer. Math. Soc., Providence, RI (2007)

  45. Todorova G., Yordanov B.: Critical exponent for a nonlinear wave equation with damping. J. Differ. Equ. 174(2), 464–489 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  46. Vancostenoble J., Martinez P.: Optimality of energy estimates for the wave equation with nonlinear boundary velocity feedbacks. SIAM J. Control Optim. 39(3), 776–797 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  47. Zuazua E.: Exponential decay for the semilinear wave equation with localized damping in unbounded domains. J. Math. Pures Appl. (9) 70(4), 513–529 (1991)

    MATH  MathSciNet  Google Scholar 

  48. Zuazua E.: Exponential decay for the semilinear wave equation with locally distributed damping. Commun. Part. Differ. Equ. 15(2), 205–235 (1990)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Departamento de Matemática, Universidade Estadual de Maringá, Maringá, PR, 87020-900, Brazil

    Flávio R. Dias Silva & José H. Rodrigues

  2. Departamento de Matemática, Universidade Estadual do Ceará-FAFIDAM, Limoeiro do Norte, CE, 62930-000, Brazil

    Flávio A. F. Nascimento

Authors
  1. Flávio R. Dias Silva
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Flávio A. F. Nascimento
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. José H. Rodrigues
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Flávio A. F. Nascimento.

Additional information

PhD students at UEM, partially supported by CAPES and a grant of CNPq, Brazil.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dias Silva, F.R., Nascimento, F.A.F. & Rodrigues, J.H. General decay rates for the wave equation with mixed-type damping mechanisms on unbounded domain with finite measure. Z. Angew. Math. Phys. 66, 3123–3145 (2015). https://doi.org/10.1007/s00033-015-0547-5

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00033-015-0547-5

Mathematics Subject Classification

Keywords

Search

Navigation