Contractive Multivariate Zipper Fractal Interpolation Functions

Abstract

In this paper we introduce a new general multivariate fractal interpolation scheme using elements of the zipper methodology. Under the assumption that the corresponding Read-Bajraktarevic operator is well-defined, we enlarge the previous frameworks occurring in the literature, considering the constitutive functions of the iterated function system whose attractor is the graph of the interpolant to be just contractive in the last variable (so, in particular, they can be Banach contractions, Matkowski contractions, or Meir-Keeler contractions in the last variable). The main difficulty that should be overcome in this multivariate framework is the well definedness of the above mentioned operator. We provide three instances when it is guaranteed. We also display some examples that emphasize the generality of our scheme.

1 Introduction

In 1986, M. Barnsley (see [3]), based on the concept of iterated function system (for short IFS) introduced by J. Hutchinson (see [10]), developed the theory of fractal interpolation functions which turned out to be an impressive device in the study of non-linear phenomena in nature.

A fractal interpolation function (for short FIF) is a continuous function interpolating a given set of data such that its graph is the attractor of some IFS. Such functions offer two benefits: the free choice of scaling factor and the self-similarity feature. In relation to the classical approximants, FIFs yield a more detailed approximation for non-smooth functions. Ergo they are used in image compression, signal processing, bio-engineering etc. [14] and [18] are excellent treaties on the topic of fractal interpolation.

Later on, in 1990, P. Massopust (see [13]) generalized the concept of FIF by constructing fractal interpolation surfaces. For more results along this line of research, see, for example, [4, 6, 8, 11, 12].

In 2002, V. Aseev (see [1]) introduced the concept of zipper which provides another way to construct self-similar sets. See also [2]. Later on (see [5]), in 2020, this methodology of zipper was used to derive a univariate interpolation scheme. For some other connected works (including the study of zipper fractal interpolation surfaces) see: [9, 19, 24,25,26].

In this paper we introduce a multivariate fractal interpolation scheme using elements of the zipper methodology. In Sect. 3, under the assumption that the corresponding Read-Bajraktarevic operator is well-defined, we enlarge the previous frameworks occurring in the literature, considering the constitutive functions of the iterated function system whose attractor is the graph of the interpolant to be just Edelstein contractions (i.e. contractive) in the last variable (so, in particular, they can be Banach contractions, Matkowski contractions, or Meir-Keeler contractions in the last variable). The main difficulty that should be overcome in this multivariate framework is the well definedness of the above mentioned operator. We provide three instances when it is guaranteed. The first one is presented in Sect. 4 and the other two (concerning the bivariate case) in Sects. 5 and 6. Finally, in Sect. 7, we display some examples (linked with the settings considered on Sects. 5 and 6) which emphasize the generality of our scheme.

2 Preliminary Facts

Definition 1

A function $f:X\rightarrow X$, where (X, d) is a metric space, is called a Meir-Keeler contraction if for every $\varepsilon >0$ there exists $\delta >0$ such that for all $x,y\in X$ the following implication is valid:

$$\begin{aligned} \varepsilon \le d(x,y)<\varepsilon +\delta \;\;\Rightarrow \;\;d(f(x),f(y))<\varepsilon . \end{aligned}$$

Definition 2

A function $f:X\rightarrow X$, where (X, d) is a metric space, is called an Edelstein contraction (or contractive) if for all $x,y\in X$ the following implication is valid:

$$\begin{aligned} x\ne y \;\;\Rightarrow \;\;d(f(x), f(y)) < ~ d(x,y). \end{aligned}$$

Theorem 1

(see [15]). If (X, d) is a complete metric space and $f:X\rightarrow X$ is a Meir-Keeler contraction, then f is a Picard operator i.e. there exists a unique fixed point $x^*$ and ${\lim }_{n \rightarrow \infty }f^{[n]}(x) = x^*$ for all $x\in X$, where $f^{[n]}$ means $\underset{n\text {-times}}{\underbrace{f\circ \dots \circ f}}$.

Theorem 2

(see [7]). If (X, d) is a compact metric space and $f:X\rightarrow X$ is a Edelstein contraction, then f is a Picard operator.

Remark 1

It is well-known that each Banach contraction is a Meir-Keeler contraction and each Meir-Keeler contraction is an Edelstein contraction. On compact spaces, the family of Edelstein contractions coincide with the family of Meir-Keeler contractions (see [15]).

Given a metric space (X, d), by $P_{\text {cp}}(X)$ we designate the set $\{A\subseteq X~|~A\ne \emptyset \text {~and~}A \text {~is compact}\}$ and by h we denote the Hausdorff-Pompeiu metric.

Definition 3

A pair $\left( (X,d),(f_i)_{i \in \{1,2,\dots ,n\}}\right) :=\mathcal {S}$ is called an iterated function system (for short IFSs) if (X, d) is a complete metric space and $f_i:X\rightarrow X$ is continuous for each $i\in \{1,2,\dots ,n\}$.

The function $F_{\mathcal {S}}: P_{\text {cp}}(X) \rightarrow P_{\text {cp}}(X)$, given by

$$\begin{aligned} F_{\mathcal {S}}(K) = \underset{i=1}{\overset{n}{\cup }}f_i(K), \end{aligned}$$

for all $K\in P_{\text {cp}}(X)$, is called the fractal operator associated with $\mathcal {S}$.

If $F_{\mathcal {S}}$ is a Picard operator, then its fixed point $A_{\mathcal {S}}$ is called the attractor of ${\mathcal {S}}$.

Theorem 3

(see [10]). In the framework of Definition 3, if $f_i$’s are Banach contractions, then $F_{\mathcal {S}}$ is a Picard operator.

Theorem 4

(see [17]). In the framework of Definition 3, if $f_i$’s are Edelstein contractions and X is compact, then $F_{\mathcal {S}}$ is a Picard operator.

Let us recall the basic facts concerning the fractal interpolation functions which are due to Barnsley (see [3]).

Let us consider:

• $\{(x_i, y_i) \in \mathbb {R}^2~|~i\in \{0,1,\dots ,n\}\}$ a set of data points such that $x_0<x_1<\dots <x_n$

• $I=[x_0,x_n]$ and $I_i=[x_{i-1},x_i]$ for all $i\in \{1,2,\dots ,n\}$

• $L_i:I\rightarrow I_i$ given by

  $$\begin{aligned} L_i(x)=a_ix+b_i, \end{aligned}$$

  for all $x\in I$ and $i\in \{1,2,\dots ,n\}$ such that $L_i(x_0) = x_{i-1}$ and $L_i(x_n) = x_{i}$ for all $i\in \{1,2,\dots ,n\}$

• $\mathcal {K}\in P_{\text {cp}}(\mathbb {R})$ such that $\{y_0,y_1,\dots ,y_n\}\subset \mathcal {K}$

• $F_i: I \times \mathcal {K} \rightarrow \mathcal {K}$ Lipschitz with respect to the first variable, Banach contraction with respect to the second variable and satisfying

  $$\begin{aligned} F_i(x_0,y_0)=y_{i-1}~~~~\text {and}~~~~F_i(x_n,y_n)=y_{i}, \end{aligned}$$

  for all $i\in \{1,2,\dots ,n\}$

• the IFS $\mathcal {S}=\left( (I \times \mathcal {K},\Vert .\Vert _2),(W_i)_{i \in \{1,2,\dots ,n\}}\right) ,$ where $W_i:I\times \mathcal {K}\rightarrow I\times \mathcal {K}$ is given by

  $$\begin{aligned} W_i(x, y)= (L_i(x), F_i(x, y)), \end{aligned}$$

for all $(x,y) \in I \times \mathcal {K}$ and $i \in \{1,2,\dots ,n\}$.

Then $F_\mathcal {S}$ is a Picard operator and there exists a unique continuous function $f^*:I \rightarrow \mathcal {K}$ such that

$$\begin{aligned} G_{f^*}=A_{\mathcal {S}}\;\; \text {and}\;\;f^*(x_i)=y_i, \end{aligned}$$

for all $i\in \{0,1,\dots ,n\}$, where $G_f$ denotes the graph of the function f.

The functions obtained in this way are called fractal interpolation functions (for short FIFs).

Later on P. Massopust (see [13]) generalized Barnsley’s theory. He introduced the fractal interpolation surfaces which are continuous functions $f^*:D\rightarrow \mathbb {R,}$ where $D\subseteq \mathbb {R}^2$ is a triangular domain, that interpolate certain sets of data $\{(x_i,y_j,z_{ij})~|~i\in \{1,2,\dots ,n\},j\in \{1,2,\dots ,m\}\}\subseteq D$.

3 Contractive Zipper FIF on $\mathbb {R}^n$

Let $n\in \mathbb {N}, m_1,m_2,\dots ,m_n\in \mathbb {N}$ and

$$\begin{aligned} \left\{ \left( x_{1i_1},x_{2i_2},\dots ,x_{ni_n},z_{i_1i_2\dots i_n}\right) \in \mathbb {R}^{n+1}|p\in \{1,2,\dots ,n\},i_p\in \{0,1,\dots ,m_p\}\right\} , \end{aligned}$$

be a given set of data such that

$$\begin{aligned} x_{p0}<x_{p1}<\cdots <x_{pm_p}, \end{aligned}$$

for all $p\in \{1,2,\dots ,n\}$.

Let us choose the signature $\varepsilon =(\varepsilon _p)_{p=1}^n,$ where

$$\begin{aligned} \varepsilon _p=(\varepsilon _{p1},\varepsilon _{p2},\dots ,\varepsilon _{pm_p})\in \{0,1\}^{m_p}. \end{aligned}$$

We use the following notation:

$$\begin{aligned} I_p= & {} [x_{p0},x_{pm_p}],~~~~~~~~~~~~~~~~~~~I_{pi_p}=[x_{p(i_p-1)},x_{pi_p}],\\ \mathcal {C}= & {} I_1\times I_2\times \cdots \times I_n,~~~~~~~~~\mathcal {C}_{i_1i_2\cdots i_n}=I_{1i_1}\times I_{2i_2}\times \cdots I_{ni_n}, \end{aligned}$$

for all $p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}$.

Remark 2

Note that

$$\begin{aligned} I_p= \bigcup \limits _{\begin{array}{c} i_p\in \{1,2,\dots ,m_p\} \end{array}}I_{pi_p} \end{aligned}$$

and

$$\begin{aligned} \mathcal {C}=\bigcup \limits _{\begin{array}{c} p\in \{1,2,\dots ,n\}\\ i_p\in \{1,2,\dots ,m_p\} \end{array}}\mathcal {C}_{i_1i_2\cdots i_n}. \end{aligned}$$

Let $L_{pi_p}:I_{p}\rightarrow I_{pi_p}$ be given by

$$\begin{aligned} L_{pi_p}(x)=a_{pi_p}x+b_{pi_p}, \end{aligned}$$

for all $x\in I_p,p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\},$ where

$$\begin{aligned} a_{pi_p}=\frac{x_{p(i_p-\varepsilon _{pi_p})}-x_{p(i_p-1+\varepsilon _{pi_p})}}{x_{pm_p}-x_{p0}} \end{aligned}$$

and

$$\begin{aligned} b_{pi_p}=x_{p(i_p-1+\varepsilon _{pi_p})}-\frac{x_{p(i_p-\varepsilon _{pi_p})}-x_{p(i_p-1+\varepsilon _{pi_p})}}{x_{pm_p}-x_{p0}}x_{p0}. \end{aligned}$$

Remark 3

Note that

$$\begin{aligned} |a_{pi_p}|<1, \end{aligned}$$

for all $p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}$.

Let $L_{i_1\cdots i_n}:\mathcal {C}\rightarrow \mathcal {C}_{i_1\cdots i_n}$ be given by

$$\begin{aligned} L_{i_1\cdots i_n}(x_1,x_2,\dots ,x_n)=\left( L_{1i_1}(x_1),L_{2i_2}(x_2),\dots ,L_{ni_n}(x_n)\right) , \end{aligned}$$

for all $x_p\in I_{p},$ $p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}$.

Remark 4

Note that, for all $p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}$,

• (i) $L_{i_1\cdots i_n}$ is one-to-one.

• (ii) If:

  $$\begin{aligned} \varepsilon _{pi_p}=0,~~~~\text {then}~~~~L_{pi_p}(x_{p0}) =x_{p(i_p-1)}~~~~~\text {and}~~~~L_{pi_p}(x_{pm_p})=x_{pi_p}; \\ ~~~~~~\varepsilon _{pi_p}=1,~~~~\text {then}~~~~L_{pi_p} (x_{p0})=x_{pi_p}~~~~~~~~~\text {and}~~~~L_{pi_p}(x_{pm_p})=x_{p(i_p-1)}. \end{aligned}$$

• (iii) Consequently

  $$\begin{aligned} L_{i_1\cdots i_n}(x_{1e_1},x_{2e_2},\dots ,x_{ne_n})=\left( x_{1\sigma _1(e_1)},x_{2\sigma _2(e_2)},\dots , x_{n\sigma _n(e_n)}\right) , \end{aligned}$$

  (1)

  for all $e_p \in \{0,m_p\}$ and $p\in \{1,2,\dots ,n\}$, where

  $$\begin{aligned} \sigma _p(e_p):={\left\{ \begin{array}{ll} i_p-1+\varepsilon _{pi_p} &{}\text {if}\;e_p=0,\\ i_p-\varepsilon _{pi_p} &{}\text {if}\; e_p=m_p. \end{array}\right. } \end{aligned}$$

Let us consider $\mathcal {K}\in P_{\text {cp}}(\mathbb {R})$ such that

$$\begin{aligned} \{z_{i_1i_2\dots i_n}~|~p\in \{1,2,\dots ,n\},i_p\in \{0,1,\dots ,m_p\}\}\subset \mathcal {K} \end{aligned}$$

and for all $p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}$, we consider $F_{i_1i_2\dots i_n}:\mathcal {C}\times \mathcal {K}\rightarrow \mathcal {K}$ satisfying the following two conditions:

• (i)
  $$\begin{aligned} ~~~~~~~~~F_{i_1i_2\dots i_n}(x_{1e_1},x_{2e_2},\dots ,x_{ne_n},z_{e_1e_2\cdots e_n})=z_{\sigma _1(e_1)\sigma _2(e_2)\cdots \sigma _n(e_n)}, \end{aligned}$$

  (2)

  for all $e_p \in \{0,m_p\};$

• (ii) there exist $r_{pi_p}\in [0,\infty )$ and an Edelstein contraction map $h_{i_1i_2\dots i_n}:\mathcal {K}\rightarrow \mathcal {K}$ such that

  $$\begin{aligned}&|F_{i_1\dots i_n}(x_1,\dots ,x_n,z)-F_{i_1\dots i_n}(x_1',\dots ,x_n',z')|\nonumber \\ {}&\quad \le \sum _{p=1}^{n}r_{pi_p}|x_p-x_p'|+|h_{i_1\dots i_n}(z)-h_{i_1\dots i_n}(z')|, \end{aligned}$$

  (3)

  for all $(x_1,\dots ,x_n,z),(x_1',\dots ,x_n',z') \in \mathcal {C} \times \mathcal {K}$.

Let us consider the IFS

$$\begin{aligned} \mathcal {S}=\left( (\mathcal {C}\times \mathcal {K},\Vert .\Vert _2),(W_{i_1i_2\cdots i_n})_{p\in \{1,2,\dots ,n\},i_p\in \{1,2,\dots ,m_p\}}\right) , \end{aligned}$$

where $W_{i_1i_2\cdots i_n}:\mathcal {C}\times \mathcal {K}\rightarrow \mathcal {C}\times \mathcal {K}$ is given by

$$\begin{aligned} \begin{aligned} W_{i_1i_2\cdots i_n}&(x_1,x_2,\dots ,x_n,z){} {} \\ {}&=\left( L_{i_1i_2\cdots i_n}(x_1,x_2,\dots ,x_n),F_{i_1i_2\dots i_n}(x_1,x_2,\dots ,x_n,z)\right) , \end{aligned} \end{aligned}$$

for all $(x_1,x_2,\dots ,x_n,z)\in \mathcal {C}\times \mathcal {K},p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}$.

Let $\mathcal {G}^{*}$ be a closed subset of

$$\begin{aligned} ~\mathcal {G}= & {} \{f:\mathcal {C}\rightarrow \mathcal {K}~|~f ~\text {is continuous}, f(x_{1i_1},\dots ,x_{ni_n})\\ {}{} & {} \quad =z_{i_1\dots i_n}~\text {for all}~ p\in \{1,\dots ,n\},i_p\in \{0,m_p\}\} \end{aligned}$$

endowed with the uniform metric $\rho$ and let us suppose that the Read-Bajraktarevic type operator $T:\mathcal {G}^{*}\rightarrow \mathcal {G}^{*}$ given by

$$\begin{aligned}{} & {} T(f)(x_1,x_2,\dots ,x_n)\!=\!F_{i_1\dots i_n}\left( L_{i_1\cdots i_n}^{-1}(x_1,x_2,\dots ,x_n),f(L_{i_1\cdots i_n}^{-1}\right. \\{} & {} \left. \quad (x_1,x_2,\dots ,x_n))\right) , \end{aligned}$$

for all $f\in \mathcal {G}^{*}, (x_1,x_2,\dots ,x_n) \in \mathcal {C}_{i_1\cdots i_n},p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}$ is well-defined.

Remark 5

If $n=1$ it is well-known that T is well-defined. For $n\ge 2$ the issue of well-definedness of T becomes problematic. In Sects. 4, 5 and 6, we will work under some supplementary conditions which guarantee that T is well-defined.

Lemma 1

$$\begin{aligned} T(f)(x_{1i_1},x_{2i_2},\dots ,x_{ni_n})=z_{i_1i_2\dots i_n}, \end{aligned}$$

for all $f\in \mathcal {G}^*,p\in \{1,2,\dots ,n\}$ and $i_p\in \{0,1,\dots ,m_p\}$.

Proof

For $f\in \mathcal {G}^*,p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}$, we have

$$\begin{aligned}&T(f)(x_{1i_1},x_{2i_2},\dots ,x_{ni_n})\\ {}&=F_{i_1i_2\dots i_n}\left( L_{i_1i_2\cdots i_n}^{-1}(x_{1i_1},x_{2i_2},\dots ,x_{ni_n}),f(L_{i_1i_2\cdots i_n}^{-1}(x_{1i_1},x_{2i_2},\dots ,x_{ni_n}))\right) \\&\overset{{(1)}}{=}F_{i_1i_2\dots i_n}(x_{1e_1},x_{2e_2},\dots ,x_{ne_n},f(x_{1e_1},x_{2e_2},\dots ,x_{ne_n})\\&=F_{i_1i_2\dots i_n}(x_{1e_1},x_{2e_2},\dots ,x_{ne_n},z_{e_1e_2\cdots e_n})\\&\overset{{(2)}}{=}z_{i_1i_2\dots i_n}, \end{aligned}$$

where

$$\begin{aligned} e_p={\left\{ \begin{array}{ll} m_p, &{}\text {if}\;\varepsilon _{pi_p}=0,\\ 0, &{}\text {if}\; \varepsilon _{pi_p}=1, \end{array}\right. } \end{aligned}$$

for all $p\in \{1,2,\dots ,n\}.$

Similarly, we get the conclusion if $i_p=0$ for some of $p\in \{1,2,\dots ,n\}$. $\square$

Theorem 5

T is a Meir-Keeler contraction, so it is a Picard operator.

Proof

Let us choose an arbitrary $\varepsilon >0$.

Taking into account Remark 1, for all $p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}$, there exists $\delta _{i_1i_2\dots i_n}>0$ such that, for all $x \in \mathcal {C}$ and $z, z' \in \mathcal {K}$, the following implication is valid:

$$\begin{aligned} \varepsilon \le |z-z'|<\varepsilon +\delta _{i_1i_2\dots i_n}~~\Rightarrow ~~|F_{i_1i_2\dots i_n}(x,z)-F_{i_1i_2\dots i_n}(x,z')|<\varepsilon . \end{aligned}$$

Let $f,g \in \mathcal {G}^{*}$ such that

$$\begin{aligned} \varepsilon \le \rho (f,g)<\varepsilon +\delta , \end{aligned}$$

where

$$\begin{aligned} \delta =\min \{\delta _{i_1i_2\dots i_n}~|~p\in \{1,2,\dots ,n\}, i_p\in \{1,2,\dots ,m_p\}\}. \end{aligned}$$

Claim.

$$\begin{aligned} |F_{i_1i_2\dots i_n}(x,f(x))-F_{i_1i_2\dots i_n}(x,g(x))|<\varepsilon , \end{aligned}$$

for all $x\in \mathcal {C},p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}.$

Justification of the claim.

If $\varepsilon \le |f(x) - g(x)|$, then we have

$$\begin{aligned} |F_{i_1i_2\dots i_n}(x,f(x))-F_{i_1i_2\dots i_n}(x,g(x))|<\varepsilon , \end{aligned}$$

since $f(x),g(x)\in \mathcal {K}$ and $|f(x)-g(x)|\le \rho (f,g)<\varepsilon +\delta$.

Otherwise

$$\begin{aligned} |F_{i_1i_2\dots i_n}(x,f(x))-F_{i_1i_2\dots i_n}(x,g(x))|\overset{{(3)}}{\le }|f(x) - g(x)|<\varepsilon . \end{aligned}$$

Now the justification of the claim is complete.

Thus, we get

$$\begin{aligned} \begin{aligned} \rho (Tf,Tg)&=\underset{x\in \mathcal {C}}{\max }~|Tf(x)-Tg(x)|\\ {}&=\underset{\begin{array}{c} p\in \{1,2,\dots ,n\}\\ i_p\in \{1,2,\dots ,m_p\} \end{array}}{\max }~\underset{x\in \mathcal {C}_{i_1\cdots i_n}}{\max }~|F_{i_1\dots i_n}(L_{i_1\cdots i_n}^{-1}(x),f(L_{i_1\cdots i_n}^{-1}(x)))\\ {}&\quad -F_{i_1\dots i_n}(L_{i_1\cdots i_n}^{-1}(x),g(L_{i_1\cdots i_n}^{-1}(x)))|\overset{Claim}{<}\varepsilon . \end{aligned} \end{aligned}$$

Hence, T is a Meir-Keeler contraction and via Theorem 1, we conclude that T is a Picard operator. $\square$

Remark 6

Based on Theorem 5, there exists a unique function $f^*\in \mathcal {G}^{*}$ such that

$$\begin{aligned} T(f^*)=f^*~ ~\text {and}~~\underset{n\rightarrow \infty }{\lim }T^{[n]}(f)=f^*, \end{aligned}$$

for all $f\in \mathcal {G}^{*}.$

So, taking into account Lemma 1, we get

$$\begin{aligned} f^*(x_{1i_1},x_{2i_2},\dots ,x_{ni_n})=z_{i_1i_2\dots i_n}, \end{aligned}$$

for all $p\in \{1,2,\dots ,n\}$ and $i_p\in \{0,1,\dots ,m_p\}$.

Remark 7

• (i) For

  $$\begin{aligned} \theta =\underset{p\in \{1,\dots ,n\}}{\min }~\left\{ \frac{1-\underset{i_p\in \{1,\dots ,m_p\}}{\max }~|a_{pi_p}|}{1+\underset{i_p\in \{1,\dots ,m_p\}}{\max }~r_{pi_p}}\right\} \overset{\text {Remark } 3}{>}0, \end{aligned}$$

  let us consider the metric $d_{\theta }$, on $\mathbb {R}^{n+1}$, given by

  $$\begin{aligned} d_{\theta }((x_1,x_2,\dots ,x_n,z),(x_1',x_2',\dots ,x_n',z')):=\sum _{p=1}^{n}|x_p-x_p'|+\theta |z-z'|, \end{aligned}$$

  for all $(x_1,x_2,\dots ,x_n,z),(x_1',x_2',\dots ,x_n',z')\in \mathbb {R}^{n+1}$. Note that $d_{\theta }$ and the Euclidean metric are equivalent.

• (ii) If two metrics are equivalent, then the corresponding Hausdorff metrics are also equivalent.

Theorem 6

$W_{i_1i_2\cdots i_n}$ is an Edelstein contraction with respect to $d_{\theta }$ for all $p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}$.

Proof

Note that

$$\begin{aligned} |a_{pi_p}|+ \theta r_{pi_p}<1, \end{aligned}$$

(4)

for all $p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}$.

Since $h_{i_1i_2\cdots i_n}$ is an Edelstein contraction, we obtain

$$\begin{aligned}&d_{\theta }(W_{i_1i_2\cdots i_n}(x_1,x_2,\dots ,x_n,z),W_{i_1i_2\cdots i_n}(x_1',x_2',\dots ,x_n',z'))\\&~~~~~~=\sum _{p=1}^{n}|L_{pi_p}(x_p)-L_{pi_p}(x_p')|+\theta |F_{i_1\dots i_n}(x_1,\dots ,x_n,z)-F_{i_1\dots i_n}(x_1',\dots ,x_n',z')|\\&~~~~~~\overset{{(3)}}{\le } \sum _{p=1}^{n}(|a_{pi_p}|+\theta r_{pi_p})|x_p-x_p'|+\theta |h_{i_1\dots i_n}(z)-h_{i_1\dots i_n}(z')|\\&~~~~~~\overset{{(4)}}{<}\sum _{p=1}^{n}|x_p-x_p'|+\theta |z-z'|=d_{\theta }((x_1,x_2,\dots ,x_n,z),(x_1',x_2',\dots ,x_n',z')), \end{aligned}$$

for all $p\in \{1,2,\dots ,n\}, i_p\in \{1,2,\dots ,m_p\}$ and $(x_1,x_2,\dots ,x_n,z),(x_1',x_2',\dots ,x_n',z')\in \mathcal {C}\times \mathcal {K}$ with $(x_1,x_2,\dots ,x_n,z)\ne (x_1',x_2',\dots ,x_n',z')$. $\square$

Corollary 1

$F_{\mathcal {S}}$ is a Picard operator.

Proof

In view of Remark 7, $(\mathcal {C}\times \mathcal {K},d_{\theta })$ is compact, and the Hausdorff metrics corresponding to $\Vert .\Vert _2$ and $d_{\theta }$ are equivalent.

From Theorem 6 and Theorem 4, we can conclude that $F_{\mathcal {S}}$ is a Picard operator with respect to the Hausdorff metric corresponding to $d_{\theta }$.

The equivalence of Hausdorff metrics corresponding to $\Vert .\Vert _2$ and $d_{\theta }$ ensures that $F_{\mathcal {S}}$ is a Picard operator with respect to the Hausdorff metric corresponding to $\Vert .\Vert _2$. $\square$

Proposition 7

$$\begin{aligned} G_{f^*}=A_{\mathcal {S}}. \end{aligned}$$

Proof

Since $f^*$ is the fixed point of T, we have

$$\begin{aligned} W_{i_1i_2\cdots i_n}(G_{f^*})&=\left\{ W_{i_1i_2\cdots i_n}(x,f^*(x))~|~x\in \mathcal {C}\right\} \\&=\left\{ \left( L_{i_1i_2\cdots i_n}(x),F_{i_1i_2\dots i_n}(x,f^*(x))\right) ~|~x\in \mathcal {C}\right\} \\&=\left\{ \left( L_{i_1i_2\cdots i_n}(x),f^*\left( L_{i_1i_2\cdots i_n}(x)\right) \right) ~|~x\in \mathcal {C}\right\} \\&=\{(x,f^*(x)~|~x\in \mathcal {C}_{i_1i_2\cdots i_n}\}, \end{aligned}$$

for all $p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}$.

Therefore

$$\begin{aligned} G_{f^*}=\underset{p\in \{1,2,\dots ,n\},i_p\in \{1,2,\dots ,m_p\}}{\bigcup }W_{i_1i_2\cdots i_n}(G_{f^*})=F_{\mathcal {S}}(G_{f^*}). \end{aligned}$$

Since $G_{f^*}\in P_{\text {cp}}(\mathcal {C}\times \mathcal {K})$, the uniqueness of the fixed point of $F_{\mathcal {S}}$ implies that $G_{f^*}=A_{\mathcal {S}}$. $\square$

Remark 8

Since from Proposition 7 and Remark 6, we have

$$\begin{aligned} G_{f^*}=A_{\mathcal {S}} \end{aligned}$$

and

$$\begin{aligned} f^*(x_{1i_1},x_{2i_2},\dots ,x_{ni_n})=z_{i_1i_2\dots i_n}, \end{aligned}$$

for all $i_p\in \{0,1,\dots ,m_p\}$ and $p\in \{1,2,\dots ,n\}$, we call $f^*$ a contractive multivariate zipper fractal interpolation function.

4 The First Instance When T is well-defined

In this section we work under the following supplementary conditions which are natural in view of [16, 20, 23]:

($\alpha$):

$$\begin{aligned} \varepsilon _p=(0,1,0,1,\dots )~~~~\text {or}~~~~\varepsilon _p= (1,0,1,0,\dots ), \end{aligned}$$

for all $p\in \{1,2,\dots ,n\}$;

($\beta$):

$$\begin{aligned} F_{i_1i_2\dots i_n}(x,z)=F_{\delta (i_1i_2\dots i_n;j)}(x,z), \end{aligned}$$

(5)

for all $x=(x_1,x_2,\dots ,x_n)\in \mathcal {C}$ with $x_j=x_{je_j},$ $z\in \mathcal {K},j\in \{1,2,\dots ,n\},p\in \{1,2,\dots ,j-1,j+1,\dots ,n\},i_p\in \{1,2,\dots ,m_p\}, i_j\in \{1,2,\dots ,m_j-1\}$ and $e_j \in \{0,m_j\}$, where

$$\begin{aligned} \delta (i_1i_2\dots i_n;j):={\left\{ \begin{array}{ll} i_1\dots i_{j-1}(i_{j}+1)i_{j+1}\dots i_n &{}\text {if}\;j\in \{1,2,\dots ,n-1\},\\ i_1i_2\dots (i_n+1) &{}\text {if}\;j=n; \end{array}\right. } \end{aligned}$$

($\gamma$):

$$\begin{aligned} \mathcal {G}^{*}=\mathcal {G}. \end{aligned}$$

Lemma 2

T is well-defined.

Proof

Let $f\in \mathcal {G}^{*}$ and $i=(i_1,i_2,\dots ,i_n)\in \{1,2,\dots ,m_1-1\}\times \{1,2,\dots ,m_3-1\}\times \dots \times \{1,2,\dots ,m_n-1\}$.

Let us consider $x=(x_1,x_2,\dots ,x_n)\in \mathcal {C}_{i}\cap \mathcal {C}_{\delta (i;j)}$ for some $j\in \{1,2,\dots ,n\}$ with $x_j=x_{je_j}$.

For $p\in \{1,2,\dots ,n\}$, let us denote $x_p'=L_{pi_p}^{-1}(x_p)$.

Viewing x as an entity belonging to $\mathcal {C}_{i}$, T(f)(x) is

$$\begin{aligned} {\left\{ \begin{array}{ll} F_{i}\left( x_1',\dots ,x_{jm_j},\dots ,x_n',f(x_1',\dots ,x_{jm_j},\dots ,x_n')\right) ,&{}\text {if}\; \varepsilon _{ji_j}=0,\\ F_{i}\left( x_1',\dots ,x_{j0},\dots ,x_n',f(x_1',\dots ,x_{j0},\dots ,x_n')\right) , &{}\text {if}\; \varepsilon _{ji_j}=1 \end{array}\right. } \end{aligned}$$

and viewing x as an entity belonging to $\mathcal {C}_{\delta (i;j)}$, T(f)(x) is

$$\begin{aligned} {\left\{ \begin{array}{ll} F_{\delta (i;j)}\left( x_1',\dots ,x_{j0},\dots ,x_n',f(x_1',\dots ,x_{j0},\dots ,x_n')\right) ,&{}\text {if}\; \varepsilon _{j(i_j+1)}=0,\\ F_{\delta (i;j)}\left( x_1',\dots ,x_{jm_j},\dots ,x_n',f(x_1',\dots ,x_{jm_j},\dots ,x_n')\right) , &{}\text {if}\; \varepsilon _{j(i_j+1)}=1. \end{array}\right. } \end{aligned}$$

Taking into account $(\alpha )$ and $(\beta )$, we conclude that Tf(x) is the same in both situations.

Now, let us consider

$$\begin{aligned} x=(x_1,x_2,\dots ,x_n)\in \mathcal {C}_{i}\cap \mathcal {C}_{\delta (i;j)}\cap \mathcal {C}_{\delta (i;j+1)}\cap \mathcal {C}_{\delta ^*(i;j)}, \end{aligned}$$

for some $j\in \{1,2,\dots ,n-1\}$ with $x_j=x_{ji_j}$ and $x_{j+1}=x_{(j+1)i_{j+1}}$, where

$$\begin{aligned} \delta ^*(i;j):={\left\{ \begin{array}{ll} i_1\cdots i_{j-1}(i_j+1)(i_{j+1}+1)i_{j+2}\cdots i_n &{}\text {if}\;j\in \{1,2,\dots ,n-2\},\\ i_1i_2\dots (i_{n-1}+1)(i_n+1) &{}\text {if}\;j=n-1. \end{array}\right. } \end{aligned}$$

By the previous argument, T(f)(x) is the same if we consider:

• $x\in \mathcal {C}_{i}$ and $x\in \mathcal {C}_{\delta (i;j)};$

• $x\in \mathcal {C}_{\delta (i;j+1)}$ and $x\in \mathcal {C}_{\delta ^*(i;j)};$

• $x\in \mathcal {C}_{i}$ and $x\in \mathcal {C}_{\delta (i;j+1)}.$

Thus, T(f)(x) does not depent an viewing x as an entity of $\mathcal {C}_{i}, \mathcal {C}_{\delta (i;j)},$ $\mathcal {C}_{\delta (i;j+1)}$ or $\mathcal {C}_{\delta ^*(i;j)}$.

By continuing this process, we infer that $T(f):\mathcal {C}\rightarrow \mathcal {K}$ is a well-defined continuous function.

In view of Lemma 1, we conclude that $T(f)\in \mathcal {G}^{*}$ for all $f\in \mathcal {G}^{*}$. $\square$

5 The Second Instance when T is well-defined

In this section we work under the following supplementary conditions which are inspired from [12]:

($\alpha$):

$n=2$;

($\beta$):

$$\begin{aligned} \varepsilon _p=(0,1,0,1,\dots ), \end{aligned}$$

for all $p\in \{1,2\}$;

($\gamma$):

$F_{i_1i_2}:\mathcal {C}\times \mathcal {K}\rightarrow \mathcal {K}$ is given by

$$\begin{aligned} F_{i_1i_2}(x_1,x_2,z)=\alpha _{i_1i_2}x_1+\beta _{i_1i_2}x_2+\gamma _{i_1i_2}x_1x_2+h(z)+\eta _{i_1i_2}, \end{aligned}$$

for all $(x_1,x_2,z)\in \mathcal {C}\times \mathcal {K}$ and $(i_1,i_2)\in \{1,2,\dots ,m_1\}\times \{1,2,\dots ,m_2\}$, where $\alpha _{i_1i_2}, \beta _{i_1i_2}, \gamma _{i_1i_2}$ and $\eta _{i_1i_2}$ are constants and $h:\mathcal {K} \rightarrow \mathcal {K}$ is an Edelstein contraction;

($\delta$):

$$\begin{aligned} \mathcal {G}^{*}=\mathcal {G}. \end{aligned}$$

The ‘join-up’ condition (2) implies

$$\begin{aligned} \begin{aligned} \gamma _{i_1i_2}&=\frac{1}{(x_n-x_0)(y_m-y_0)}\left( z_{(i_1-\varepsilon _{1i})(i_2-\varepsilon _{2j})}+z_{(i_1-1+\varepsilon _{1i})(i_2-1+\varepsilon _{2j})}\right. \\ {}&\qquad -z_{(i_1-\varepsilon _{1i})(i_2-1+\varepsilon _{2j})}-z_{(i_1-1+\varepsilon _{1i})(i_2-\varepsilon _{2j})}\\ {}&\qquad \left. -\left( h(z_{nm})+h(z_{00})-h(z_{n0})-h(z_{0m})\right) \right) , \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} \alpha _{i_1i_2}&\!=\!\frac{(z_{(i_1\!-\!\varepsilon _{1i})(i_2\!-\!1\!+\!\varepsilon _{2j})}\!-\!z_{(i_1\!-\!1\!+\!\varepsilon _{1i})(i_2\!-\!1\!+\!\varepsilon _{2j})})\!-\!(h(z_{n0})\!-\!h(z_{00}))\!-\!\gamma _{i_1i_2}y_0(x_n\!-\!x_0)}{x_n\!-\!x_0},\\ \beta _{i_1i_2}&\!=\!\frac{(z_{(i_1\!-\!1\!+\!\varepsilon _{1i})(i_2\!-\!\varepsilon _{2j})}\!-\!z_{(i_1\!-\!1\!+\!\varepsilon _{1i})(i_2\!-\!1\!+\!\varepsilon _{2j})})\!-\!(h(z_{0m})\!-\!h(z_{00}))\!-\!\gamma _{i_1i_2}x_0(y_m\!-\!y_0)}{y_m\!-\!y_0}\\ \text{ and }&\\ \eta _{i_1i_2}&=z_{(i_1-\varepsilon _{1i})(i_2-\varepsilon _{2j})}-\alpha _{i_1i_2}x_n-\beta _{i_1i_2}y_m-\gamma _{i_1i_2}x_ny_m-h(z_{nm}), \end{aligned} \end{aligned}$$

for all $(i_1,i_2)\in \{1,2,\dots ,m_1\}\times \{1,2,\dots ,m_2\}$.

The function $F_{i_1i_2}:\mathcal {C}\times \mathcal {K}\rightarrow \mathcal {K}$ can be written as

$$\begin{aligned} F_{i_1i_2}(x_1,x_2,z)= & {} h(z)+\underset{(k_1,k_2)\in \{i_1-1,i_2-1\}\times \{i_1,i_2\}}{\sum }\left( z_{k_1k_2}-h(z_{\sigma _1^{-1}(k_1) \sigma _2^{-1}(k_2)})\right) \\{} & {} \Phi _{\sigma _1^{-1}(k_1)\sigma _2^{-1}(k_2)}(x_1,x_2), \end{aligned}$$

for all $(x_1,x_2,z)\in \mathcal {C}\times \mathcal {K}$ and $(i_1,i_2)\in \{1,2,\dots ,m_1\}\times \{1,2,\dots ,m_2\}$, where

$$\begin{aligned} \sigma _p^{-1}(k):={\left\{ \begin{array}{ll} m_p\varepsilon _{pi_p} &{}\text {if}\;k=i_p-1,\\ m_p(1-\varepsilon _{pi_p}) &{}\text {if}\;k=i_p, \end{array}\right. } \end{aligned}$$

for all $p\in \{1,2\}$ and $\Phi _{j_1j_2}:[x_{10},x_{1m_1}]\times [x_{20},x_{2m_2}] \rightarrow [0,1]$ with $j_p\in \{0,m_p\},p\in \{1,2\},$ are given by

$$\begin{aligned} \Phi _{00}(x)= & {} \frac{(x_{1m_1}-x_1)(x_{2m_2}-x_2)}{(x_{1m_1}-x_{10}) (x_{2m_2}-x_{20})},~~~~\Phi _{0m_2}(x)=\frac{(x_{1m_1}-x_1)(x_2-x_{20})}{(x_{1m_1}-x_{10})(x_{2m_2}-x_{20})},\\ \Phi _{m_10}(x)= & {} \frac{(x_1-x_{10}) (x_{2m_2}-x_2)}{(x_{1m_1}-x_{10})(x_{2m_2}-x_{20})},~~~~\Phi _{m_1m_2}(x)= \frac{(x_1-x_{10})(x_2-x_{20})}{(x_{1m_1}-x_{10})(x_{2m_2}-x_{20})}, \end{aligned}$$

for all $x=(x_1,x_2)\in [x_{10},x_{1m_1}]\times [x_{20},x_{2m_2}]$.

Lemma 3

$$\begin{aligned} F_{i_1i_2}(L_{1i_1}^{-1}(x_1),x_2,z)=F_{(i_1+1)i_2}(L_{1(i_1+1)}^{-1}(x_1),x_2,z), \end{aligned}$$

for all $(i_1,i_2)\in \{1,2,\dots ,m_1-1\}\times \{1,2,\dots ,m_2\}$ and $(x_1,x_2,z)\in \{x_{1i_1}\}\times [x_{2(i_2-1)},x_{2i_2}]\times \mathcal {K}$, if $m_1\ne 1$, and

$$\begin{aligned} F_{i_1i_2}(x_1,L_{2i_2}^{-1}(x_{2}),z)=F_{i_1(i_2+1)}(x_1,L_{2(i_2+1)}^{-1}(x_{2}),z), \end{aligned}$$

for all $(i_1,i_2)\in \{1,2,\dots ,m_1\}\times \{1,2,\dots ,m_2-1\}$ and $(x_1,x_2,z)\in$ $[x_{1(i_1-1)},x_{1i_1}]\times \{x_{2i_2}\}\times \mathcal {K},$ if $m_2\ne 1$.

Proof

Let us assume $m_1\ne 1$ and $(i_1,i_2)\in \{1,2,\dots ,m_1-1\}\times \{1,2,\dots ,m_2\}$.

Observe that:

• (i) If $i_1=2n_1+1,$ for some $n_1\in \mathbb {N},$ then we have

  $$\begin{aligned} F_{i_1i_2}(x,z)=&\,h(z)+(z_{(i_1-1)(i_2-1)}-h(z_{0\sigma _2^{-1}(i_2-1)})) \Phi _{0\sigma _2^{-1}(i_2-1)}(x)\nonumber \\&\,+(z_{(i_1-1)i_2}-h(z_{0 \sigma _2^{-1}(i_2)}))\Phi _{0\sigma _2^{-1}(i_2)}(x)\nonumber \\&\,+(z_{i_1(i_2-1)}-h(z_{m_1\sigma _2^{-1}(i_2-1)}))\Phi _{m_1\sigma _2^{-1}(i_2-1)}(x)\nonumber \\&\, +(z_{i_1i_2}-h(z_{m_1\sigma _2^{-1}(i_2)}))\Phi _{m_1\sigma _2^{-1}(i_2-1)}(x), \end{aligned}$$

  (6)

  for all $(x,z)\in \mathcal {C}\times \mathcal {K}$;

• (ii) If $i_1=2n_1,$ for some $n_1\in \mathbb {N},$ then we have

  $$\begin{aligned} F_{i_1i_2}(x,z)=&\,h(z)+(z_{(i_1-1)(i_2-1)}-h(z_{m_1\sigma _2^{-1} (i_2-1)}))\Phi _{m_1\sigma _2^{-1}(i_2-1)}(x)\nonumber \\&\,+(z_{(i_1-1)i_2}-h (z_{m_1\sigma _2^{-1}(i_2)}))\Phi _{m_1\sigma _2^{-1}(i_2)}(x)\nonumber \\&\,+(z_{i_1(i_2-1)}-h(z_{0\sigma _2^{-1}(i_2-1)}))\Phi _{0\sigma _2^{-1}(i_2-1)}(x)\nonumber \\&\,+(z_{i_1i_2} -h(z_{0\sigma _2^{-1}(i_2)}))\Phi _{0\sigma _2^{-1}(i_2)}(x), \end{aligned}$$

  (7)

  for all $(x,z)\in \mathcal {C}\times \mathcal {K}$.

Note that

$$\begin{aligned} L_{1i_1}^{-1}(x_{1i_1})=L_{1(i_1+1)}^{-1}(x_{1i_1})={\left\{ \begin{array}{ll} x_{1m_1} &{}\text {if}\;i_1=2n_1+1~\text {for some}~n_1\in \mathbb {N},\\ x_{10} &{}\text {if}\;i_1=2n_1~\text {for some}~n_1\in \mathbb {N}, \end{array}\right. } \end{aligned}$$

(8)

Thus, if $i_1=2n_1+1,$ for some $n_1\in \mathbb {N},$ then we have

$$\begin{aligned} \begin{aligned}&F_{i_1i_2}(L_{1i_1}^{-1}(x_1),x_2,z)\overset{(6)}{=}\ h(z)+(z_{i_1(i_2-1)}-h(z_{m_1\sigma _2^{-1}(i_2-1)}))\\ {}&\qquad \Phi _{m_1\sigma _2^{-1} (i_2-1)}(x_{1m_1},x_2) +(z_{i_1i_2}-h(z_{m_1\sigma _2^{-1}(i_2)})) \Phi _{m_1\sigma _2^{-1}(i_2-1)}(x_{1m_1},x_2) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&F_{(i_1+1)i_2}(L_{1(i_1+1)}^{-1}(x_1),x_2,z)\overset{(7)}{=}h(z)+(z_{i_1(i_2-1)} -h(z_{m_1\sigma _2^{-1}(i_2-1)}))\\ {}&\qquad \Phi _{m_1\sigma _2^{-1}(i_2-1)} (x_{1m_1},x_2) +(z_{i_1i_2}-h(z_{m_1\sigma _2^{-1}(i_2)})) \Phi _{m_1\sigma _2^{-1}(i_2-1)} (x_{1m_1},x_2), \end{aligned} \end{aligned}$$

for all $(x_1,x_2,z)\in \{x_{1i_1}\}\times [x_{2(i_2-1)},x_{2i_2}]\times \mathcal {K}$.

Then we have

$$\begin{aligned} F_{i_1i_2}(L_{1i_1}^{-1}(x_1),x_2,z)=F_{(i_1+1)i_2}(L_{1(i_1+1)}^{-1}(x_1),x_2,z), \end{aligned}$$

for all $(x_1,x_2,z)\in \{x_{1i_1}\}\times [x_{2(i_2-1)},x_{2i_2}]\times \mathcal {K}$, if $i_1=2n_1+1$ for some $n_1\in \mathbb {N}.$

Similar arguments ensure that the above equality is true if $i_1=2n_1,$ for some $n_1\in \mathbb {N}$.

In the similar way, we can prove

$$\begin{aligned} F_{i_1i_2}(x_1,L_{2i_2}^{-1}(x_{2}),z)=F_{i_1(i_2+1)}(x_1,L_{2(i_2+1)}^{-1}(x_{2}),z), \end{aligned}$$

for all $(i_1,i_2)\in \{1,2,\dots ,m_1\}\times \{1,2,\dots ,m_2-1\}$ and $(x_1,x_2,z)\in$ $[x_{1(i_1-1)},x_{1i_1}]\times \{x_{2i_2}\}\times \mathcal {C}$. $\square$

Lemma 4

T is well-defined.

Proof

Let $f\in \mathcal {G}^{*}$ and $(i_1,i_2)\in \{1,2,\dots ,m_1-1\}\times \{1,2,\dots ,m_2-1\}$.

Let us consider

$$\begin{aligned} (x_{1},x_2)\in \mathcal {C}_{i_1i_2}\cap \mathcal {C}_{(i_1+1)i_2}=\{x_{1i_1}\}\times [x_{2(i_2-1)},x_{2i_2}]. \end{aligned}$$

We have

$$\begin{aligned}&F_{i_1i_2}\left( L_{1i_1}^{-1}(x_{1i_1}),L_{2i_2}^{-1}(x_2),f\left( L_{1i_1}^{-1}(x_{1i_1}),L_{2i_2}^{-1}(x_2)\right) \right) \\ {}&\overset{\text {Lemma}~ 3}{=}F_{(i_1+1)i_2}\left( L_{1(i_1+1)}^{-1}(x_{1i_1}),L_{2i_2}^{-1}(x_2),f\left( L_{1i_1}^{-1}(x_{1i_1}),L_{2i_2}^{-1}(x_2)\right) \right) \\ {}&\quad \overset{(8)}{=}F_{(i_1+1)i_2}\left( L_{1(i_1+1)}^{-1}(x_{1i_1}),L_{2i_2}^{-1}(x_2),f\left( L_{1(i_1+1)}^{-1}(x_{1i_1}),L_{2i_2}^{-1}(x_2)\right) \right) . \end{aligned}$$

Thus, $Tf(x_{1i_1},x_{2})$ is the same if we view $(x_{1i_1},x_{2})$ as an element of $\mathcal {C}_{i_1i_2}$ and as an element of $\mathcal {C}_{(i_1+1)i_2}$.

In a similar manner, we prove that $Tf(x_1,x_{2i_2})$ is the same if we view $(x_1,x_{2i_2})$ as an element of $\mathcal {C}_{i_1i_2}$ and as an element of $\mathcal {C}_{i_1(i_2+1)}$.

By using Lemma 1, we conclude that $T(f)\in \mathcal {G}^*$. $\square$

Remark 9

Similarly we can extend this construction to an arbitrary $n\in \mathbb {N}$.

Let us choose

$$\begin{aligned} \varepsilon _p=(0,1,0,1,\dots ), \end{aligned}$$

for all $p\in \{1,2,\dots ,n\}$.

Let us consider $F_{i_1i_2\dots i_n}:\mathcal {C}\times \mathcal {K}\rightarrow \mathcal {K}$ given by

$$\begin{aligned}&F_{i_1i_2\dots i_n}(x_1,x_2,\dots ,x_n,z)=\sum _{j=1}^{n}\alpha _{i_1i_2\dots i_n}(j)x_j+\sum _{1\le j_1\le j_2\le n}\alpha _{i_1i_2\dots i_n}(j_1,j_2)x_{j_1}x_{j_2}\\ {}&~~~~~~~~~~~~~+\cdots +\sum _{1\le j_1\le j_2\le \dots \le j_p\le n}\alpha _{i_1i_2\dots i_n}(j_1,j_2,\dots ,j_p)x_{j_1}x_{j_2}\dots x_{j_p}\\ {}&~~~~~~~~~~~~~+\cdots +\alpha _{i_1i_2\dots i_n}(1,2,\dots ,n)x_{1}x_{2}\dots x_{n} +h(z)+\alpha _{i_1i_2\dots i_n}\\&~~~~~~~~~=\sum _{p=1}^{n}\sum _{1\le j_1\le j_2\le \dots \le j_p\le n}\alpha _{i_1i_2\dots i_n}(j_1,j_2,\dots ,j_p)x_{j_1}x_{j_2}\dots x_{j_p}+h(z)+\alpha _{i_1i_2\dots i_n}, \end{aligned}$$

for all $x_p\in I_p, z\in \mathcal {K},p\in \{1,2,\dots ,n\}$ and $i_p\in \{1,2,\dots ,m_p\}$, where $\alpha _{i_1i_2\dots i_n}$ and $\alpha _{i_1i_2\dots i_n}(j_1,j_2,\dots ,j_p)$’s are constants, and $h:\mathcal {K} \rightarrow \mathcal {K}$ is an Edelstein contraction.

Then we can prove that

$$\begin{aligned} F_{i_1i_2\dots i_n}(x,z)=F_{\delta (i_1i_2\dots i_n;j)}(x,z), \end{aligned}$$

for all $x=(x_1,x_2,\dots ,x_n)\in \mathcal {C}$ with $x_j=L_{ji_{j}}^{-1}(x_{ji_j})=L_{j(i_{j}+1)}^{-1}(x_{ji_j}),$ $z\in \mathcal {K},j\in \{1,2,\dots ,n\},p\in \{1,2,\dots ,j-1,j+1,\dots ,n\},i_p\in \{1,2,\dots ,m_p\}$ and $i_j\in \{1,2,\dots ,m_j-1\}$, where

$$\begin{aligned} \delta (i_1i_2\dots i_n;j):={\left\{ \begin{array}{ll} i_1\dots i_{j-1}(i_{j}+1)i_{j+1}\dots i_n &{}\text {if}\;j\in \{1,2,\dots ,n-1\},\\ i_1i_2\dots (i_n+1) &{}\text {if}\;j=n. \end{array}\right. } \end{aligned}$$

The previous equality guarantees that T is well-defined (see Lemma 2 and Lemma 4).

6 Third Instance when T is well-defined

In this section we work under the following supplementary conditions which are natural in view of [21, 22]:

($\alpha$):

$n=2$;

($\beta$):

$$\begin{aligned} z_{i_10}=z_{i_1m_2}=z_{0i_2}=z_{m_1i_2}:=z^*, \end{aligned}$$

for all $i_1\in \{0,1,2,\dots ,m_1\}$ and $i_2\in \{0,1,2,\dots ,m_2\}$;

($\gamma$):

$F_{i_1i_2}:\mathcal {C}\times \mathcal {K}\rightarrow \mathcal {K}$ is given by

$$\begin{aligned} F_{i_1i_2}(x_1,x_2,z)=\alpha _{i_1i_2}x_1+\beta _{i_1i_2}x_2+\gamma _{i_1i_2}x_1x_2+h_{i_1i_2}(z)+\eta _{i_1i_2}, \end{aligned}$$

for all $(x_1,x_2,z)\in \mathcal {C}\times \mathcal {K}$ and $(i_1,i_2)\in \{1,2,\dots ,m_1\}\times \{1,2,\dots ,m_2\}$, where $\alpha _{i_1i_2}, \beta _{i_1i_2}, \gamma _{i_1i_2}$ and $\eta _{i_1i_2}$ are constants and $h_{i_1i_2}:\mathcal {K} \rightarrow \mathcal {K}$ is an Edelstein contraction;

($\delta$):

$$\begin{aligned} \mathcal {G}^*&=\left\{ f\in \mathcal {G}~|~f(x_{10},x_2)=f(x_{1m_1},x_2)=f(x_1,x_{20})=f(x_1,x_{2m_2})=z^*\right. \\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \quad \left. ~\text {for all}~x_1\in I_1, x_2\in I_2\right\} . \end{aligned}$$

Lemma 5

T is well-defined.

Proof

Let $f\in \mathcal {G}^{*}$ and $(i_1,i_2)\in \{1,2,\dots ,m_1-1\}\times \{1,2,\dots ,m_2-1\}$.

Let us consider

$$\begin{aligned} (x_{1i_1},x_2)\in \mathcal {C}_{i_1i_2}\cap \mathcal {C}_{(i_1+1)i_2}=\{x_{1i_1}\}\times [x_{2(i_2-1)},x_{2i_2}] \end{aligned}$$

and $\lambda \in [0,1]$  such that 

$$\begin{aligned} x_2=(1-\lambda )x_{2(i_2-1)}+\lambda x_{2i_2}. \end{aligned}$$

Since $L_{2i_2}(x_{2e_{21}})=x_{2(i_2-1)}$ and $L_{2i_2}(x_{2e_{22}})=x_{2i_2}$, we obtain

$$\begin{aligned} L_{2i_2}^{-1}(x_2)&=L_{2i_2}^{-1}((1-\lambda )x_{2(i_2-1)}+\lambda x_{2i_2}) =(1-\lambda )L_{2i_2}^{-1}(x_{2(i_2-1)})+\lambda L_{2i_2}^{-1}(x_{2i_2})\nonumber \\&=(1-\lambda )x_{2e_{21}}+\lambda x_{2e_{22}}. \end{aligned}$$

(9)

Using the notation

$$\begin{aligned} e_{11}={\left\{ \begin{array}{ll} m_1 &{}\text {if}\;\varepsilon _{1i_1}=0,\\ 0 &{}\text {if}\; \varepsilon _{1i_1}=1, \end{array}\right. }~~~~~~e_{21}={\left\{ \begin{array}{ll} 0 &{}\text {if}\;\varepsilon _{2i_2}=0,\\ m_2 &{}\text {if}\; \varepsilon _{2i_2}=1, \end{array}\right. } \\ e_{22}={\left\{ \begin{array}{ll} m_2 &{}\text {if}\;\varepsilon _{2i_2}=0,\\ 0 &{}\text {if}\; \varepsilon _{2i_2}=1, \end{array}\right. }~~~~~~e_{12}={\left\{ \begin{array}{ll} 0 &{}\text {if}\;\varepsilon _{1(i_1+1)}=0,\\ m_1 &{}\text {if}\; \varepsilon _{1(i_1+1)}=1, \end{array}\right. } \end{aligned}$$

treating $(x_{1i_1},x_2)$ as an entity belonging to $\mathcal {C}_{i_1i_2}$, we have

$$\begin{aligned}&Tf(x_{1i_1},x_2)=F_{i_1i_2}\left( L_{1i_1}^{-1}(x_{1i_1}),L_{2i_2}^{-1}(x_2),f \left( L_{1i_1}^{-1}(x_{1i_1}),L_{2i_2}^{-1}(x_2)\right) \right) \\ {}&\overset{\text {Remark}~4,~\text {ii)}}{=}F_{i_1i_2} \left( x_{1e_{11}},L_{2i_2}^{-1}(x_2),f\left( x_{1e_{11}},L_{2i_2}^{-1}(x_2) \right) \right) \\ {}&\overset{(9)}{=}F_{i_1i_2}\left( x_{1e_{11}},(1-\lambda )x_{2e_{21}}+\lambda x_{2e_{22}},z^*\right) \\&=\alpha _{i_1i_2}x_{1e_{11}}+\beta _{i_1i_2}\left( (1-\lambda )x_{2e_{21}}+\lambda x_{2e_{22}}\right) +\gamma _{i_1i_2}x_{1e_{11}}\left( (1-\lambda )x_{2e_{21}}+\lambda x_{2e_{22}}\right) \\ {}&~~+h_{i_1i_2}(z^*)+\eta _{i_1i_2}\\&=(1-\lambda )\left( \alpha _{i_1i_2}x_{1e_{11}}+\beta _{i_1i_2}x_{2e_{21}} +\gamma _{i_1i_2}x_{1e_{11}}x_{2e_{21}}+h_{i_1i_2}(z^*)+\eta _{i_1i_2}\right) \\&~~+\lambda \left( \alpha _{i_1i_2}x_{1e_{11}}+\beta _{i_1i_2}x_{2e_{22}} +\gamma _{i_1i_2}x_{1e_{11}}x_{2e_{22}}+h_{i_1i_2}(z^*)+\eta _{i_1i_2}\right) \\&=(1-\lambda )F_{i_1i_2}\left( x_{1e_{11}},x_{2e_{21}},z^*\right) +\lambda F_{i_1i_2}\left( x_{1e_{11}},x_{2e_{22}},z^*\right) \\&\overset{(2)}{=}(1-\lambda )z_{i_1(i_2-1)}+\lambda z_{i_1i_2} \end{aligned}$$

and treating $(x_{1i_1},x_2)$ as an entity belonging to $\mathcal {C}_{(i_1+1)i_2}$, similarly, we obtain

$$\begin{aligned} Tf(x_{1i_1},x_2)&=F_{(i_1+1)i_2}\left( L_{1(i_1+1)}^{-1} (x_{1i_1}),L_{2i_2}^{-1}(x_2),f\left( L_{1(i_1+1)}^{-1} (x_{1i_1}),L_{2i_2}^{-1}(x_2)\right) \right) \\ {}&=F_{(i_1+1)i_2} \left( x_{1e_{12}},L_{2i_2}^{-1}(x_2),f\left( x_{1e_{12}},L_{2i_2}^{-1}(x_2) \right) \right) \\ {}&=F_{(i_1+1)i_2}\left( x_{1e_{12}},(1-\lambda )x_{2e_{21}}+\lambda x_{2e_{22}},z^*\right) \\&=(1-\lambda )F_{(i_1+1)i_2}\left( x_{1e_{12}},x_{2e_{21}}, z^*\right) +\lambda F_{(i_1+1)i_2}\left( x_{1e_{12}},x_{2e_{22}},z^*\right) \\&=(1-\lambda )z_{i_1(i_2-1)}+\lambda z_{i_1i_2}. \end{aligned}$$

Thus, $Tf(x_{1i_1},x_2)$ is the same in both situations.

In a similar manner, we prove that $Tf(x_1,x_{2i_2})$ is the same if we view $(x_1,x_{2i_2})$ as an element of $\mathcal {C}_{i_1i_2}$ and as an element of $\mathcal {C}_{i_1(i_2+1)}$.

By using Lemma 1, we conclude that $T(f)\in \mathcal {G}$.

Similar arguments ensure that

$$\begin{aligned} Tf(x_{1e_1},(1-\lambda )x_{2(i_2-1)}+\lambda x_{2i_2})=(1-\lambda )z_{e_1(i_2-1)}+\lambda z_{e_1i_2}=z^* \end{aligned}$$

and

$$\begin{aligned} Tf((1-\lambda )x_{1(i_1-1)}+\lambda x_{1i_1},x_{2e_2})=(1-\lambda )z_{(i_1-1)e_2}+\lambda z_{i_1e_2}=z^*, \end{aligned}$$

for all $\lambda \in [0,1],i_1\in \{1,2,\dots ,m_1\}, i_2\in \{1,2,\dots ,m_2\}, e_1\in \{0,m_1\}$ and $e_2\in \{0,m_2\}$.

Consequently

$$\begin{aligned} Tf(x_{1e_1},x_2)=Tf(x_1,x_{2e_2})=z^*, \end{aligned}$$

for all $x_1\in I_1, x_2\in I_2, e_1\in \{0,m_1\}$ and $e_2\in \{0,m_2\}$.

Hence, $T(f)\in \mathcal {G}^{*}$ for all $f\in \mathcal {G}^{*}$. $\square$

Remark 10

Let us consider an arbitrary data set

$$\begin{aligned} \Delta :=\left\{ \left( x_{1i_1},x_{2i_2},z_{i_1i_2}\right) \in \mathbb {R}^{3}~|~i_1\in \{0,1,\dots ,m_1\},i_2\in \{0,1,\dots ,m_2\}\right\} , \end{aligned}$$

with $x_{p0}<x_{p1}<\cdots <x_{pm_p}$ for all $p\in \{1,2\}$.

Let us choose another data set

$$\begin{aligned} \tilde{\Delta }{} & {} :=\left\{ \left( \tilde{x}_{1i_1},\tilde{x}_{2i_2},\tilde{z}_{i_1i_2}\right) \in \mathbb {R}^{3}~|~i_1\in \{-1,0,\dots ,m_1+1\},\right. \\{} & {} \left. \quad i_2\in \{-1,0,\dots ,m_2+1\}\right\} , \end{aligned}$$

such that:

• (i) $\tilde{x}_{p(-1)}<\tilde{x}_{p0}<\cdots <\tilde{x}_{p(m_p+1)}$ for all $p\in \{1,2\}$;

• (ii) $\tilde{x}_{1i_1}={x}_{1i_1}, \tilde{x}_{2i_2}={x}_{2i_2}$ and $\tilde{z}_{i_1i_2}={z}_{i_1i_2}$ for all $i_1\in \{0,1,\dots ,m_1\}$ and $i_2\in \{0,1,\dots ,m_2\}$;

• (iii) $\tilde{z}_{i_1(-1)}=\tilde{z}_{i_1(m_2+1)}=\tilde{z}_{(-1)i_2}=\tilde{z}_{(m_1+1)i_2}$ for all $i_1\in \{-1,0,\dots ,m_1+1\}$ and $i_2\in \{-1,0,\dots ,m_2+1\}$.

Then based on Remark 8 and Lemma 5, for the data $\tilde{\Delta }$, we get a contractive multivariate zipper fractal interpolation function $\tilde{f}_{\varepsilon }:[\tilde{x}_{1(-1)},\tilde{x}_{1(m_1+1)}]\times [\tilde{x}_{2(-1)},\tilde{x}_{2(m_2+1)}]\rightarrow \mathcal {K}$ and its restriction to $[{x}_{10},{x}_{1m_1}]\times [{x}_{20},{x}_{2m_2}]$ interpolates $\Delta$.

7 Examples

Let us consider the data set

$$\begin{aligned} \{(x_{1i_1},x_{2i_2},z_{i_1i_2})\in \mathbb {R}^3~|~i_1,i_2\in \{0,1,2\}\} \end{aligned}$$

with

$$\begin{aligned} x_{10}=0,x_{11}=\frac{1}{4},x_{12}=1,x_{20}=0,x_{21}=\frac{1}{2},x_{22}=1 \end{aligned}$$

and

$$\begin{aligned} z_{00}=z_{01}=z_{02}=z_{20}=z_{21}=z_{22}=z_{10}=z_{12}=\frac{1}{4},z_{11}=\frac{1}{2}. \end{aligned}$$

For $i_1,i_2\in \{1,2\},$ let us consider $h_{i_1i_2}:[-1,1]\rightarrow [-1,1],$ given by

$$\begin{aligned} h_{11}(z)=\frac{1}{2}z,~~~h_{12}(z)=\frac{1}{2}z^2,~~~h_{21}(z)=\frac{1+z}{2+z},~~~h_{22}(z)=\frac{1}{4}z, \end{aligned}$$

for all $z\in [-1,1]$.

The first example

For $\varepsilon _1=\varepsilon _2=(0,0)$, we consider

$$\begin{aligned}&L_{11}(x_1,x_2)=\left( \frac{1}{4}x_1,\frac{1}{2}x_2\right) ,\\&\qquad F_{11} (x_1,x_2,z)=\frac{1}{4}x_1x_2+h_{11}(z)+\frac{1}{8},\\&L_{12}(x_1,x_2)=\left( \frac{1}{4}x_1,\frac{1}{2}x_2+\frac{1}{2}\right) ,\\&\qquad F_{12}(x_1,x_2,z)=\frac{1}{4}x_1-\frac{1}{4}x_1x_2+h_{12}(z)+\frac{7}{32},\\&L_{21}(x_1,x_2)=\left( \frac{3}{4}x_1+\frac{1}{4},\frac{1}{2}x_2\right) ,\\&\qquad F_{21}(x_1,x_2,z)=\frac{1}{4}x_2-\frac{1}{4}x_1x_2+h_{21}(z)+\frac{-11}{36},\\&L_{22}(x_1,x_2)=\left( \frac{3}{4}x_1+\frac{1}{4},\frac{1}{2}x_2+\frac{1}{2} \right) ,\\&\qquad F_{22}(x_1,x_2,z)=-\frac{1}{4}(x_1+x_2-x_1x_2)+h_{22}(z)+\frac{7}{16}, \end{aligned}$$

for all $x_1,x_2\in [0,1]$ and $z\in [-1,1]$.

The second example

For $\varepsilon _1=(0,1)$ and $\varepsilon _2=(1,0)$, we consider

$$\begin{aligned}&L_{11}(x_1,x_2)=\left( \frac{1}{4}x_1,\frac{-1}{2}x_2+\frac{1}{2} \right) ,\\&\qquad F_{11}(x_1,x_2,z)=\frac{1}{4}x_1-\frac{1}{4}x_1x_2+h_{11}(z)+\frac{1}{8},\\&L_{12}(x_1,x_2)=\left( \frac{1}{4}x_1,\frac{1}{2}x_2+\frac{1}{2}\right) ,\\&\qquad F_{12} (x_1,x_2,z)=\frac{1}{4}x_1-\frac{1}{4}x_1x_2+h_{12}(z)+\frac{7}{32},\\&L_{21}(x_1,x_2)=\left( \frac{-3}{4}x_1+1,\frac{-1}{2}x_2+\frac{1}{2}\right) ,\\&\qquad F_{21}(x_1,x_2,z)=\frac{1}{4}x_1-\frac{1}{4}x_1x_2+h_{21}(z)-\frac{11}{36},\\&L_{22}(x_1,x_2)=\left( \frac{-3}{4}x_1+1,\frac{1}{2}x_2+\frac{1}{2}\right) ,\\&\qquad F_{22}(x_1,x_2,z)=\frac{1}{4}x_1-\frac{1}{4}x_1x_2+h_{22}(z)+\frac{3}{16}, \end{aligned}$$

for all $x_1,x_2\in [0,1]$ and $z\in [-1,1]$.

Note that, for both examples, we have

• $$\begin{aligned} F_{i_1i_2}(x_1,x_2,z)\in [-1,1], \end{aligned}$$

  for all $x_1,x_2\in [0,1], z\in [-1,1]$;

• $F_{i_1i_2}$’s satisfy the condition (2);

• $F_{i_1i_2}$’s are Lipschitz with respect to $x_1$ and $x_2$;

• $F_{i_1i_2}$’s are Edelstein contractions with respect to z;

• $F_{12}$ and $F_{21}$ are not Banach contractions with respect to z;

• the condition $\beta )$ from Sect. 6 is satisfied.

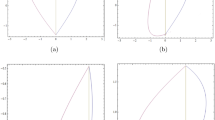
Therefore, according with Remark 8, there exist contractive multivariate zipper interpolation functions (which are called contractive fractal interpolation surfaces). Their graphical representations are given in Fig. 1 and Fig. 2.

Fig. 1

The graphical representation for the first example

Fig. 2

The graphical representation for the second example

The third example Let us consider:

• the data set

  $$\begin{aligned} \{(x_{1i_1},x_{2i_2},z_{i_1i_2})\in \mathbb {R}^3~|~i_1,i_2\in \{0,1,2\}\} \end{aligned}$$

  with

  $$\begin{aligned} x_{10}=0,x_{11}=1,x_{12}=2,x_{20}=0,x_{21}=1,x_{22}=2 \end{aligned}$$

  and

  $$\begin{aligned} z_{00}=\frac{1}{2},z_{01}=\frac{3}{4},z_{02}=\frac{1}{4},z_{10}=\frac{1}{4},z_{11}=1,z_{12}=\frac{1}{2},z_{20}=1,z_{21}=\frac{3}{4},z_{22}=1, \end{aligned}$$

• the signatures $\varepsilon _1=\varepsilon _2=(0,1)$,

• the Edelstein contraction map $h:[0,2]\rightarrow [0,2],$ given by

  $$\begin{aligned} h(z)=\frac{z}{1+z}, \end{aligned}$$

  for all $z\in [0,2]$,

• $$\begin{aligned} L_{11}(x_1,x_2)=\left( \frac{x_1}{2},\frac{x_2}{2} \right) ,~~~~~~~~~~~~~~~~~F_{11}(x_1,x_2,z)&=\frac{-5x_1}{24}+\frac{23x_2}{120}+\frac{11x_1x_2}{120}\\ {}&\quad +h(z)+\frac{1}{6},\\ L_{12}(x_1,x_2)=\left( \frac{x_1}{2},\frac{-x_2}{2}+{2}\right) ,~~~~~~~~F_{12} (x_1,x_2,z)&=\frac{x_1}{24}+\frac{19x_2}{60}-\frac{x_1x_2}{30}\\ {}&\quad +h(z)-\frac{1}{12},\\ L_{21}(x_1,x_2)=\left( \frac{-x_1}{2}+{2},\frac{x_2}{2}\right) ,~~~~~~~~F_{21} (x_1,x_2,z)&=\frac{-11x_1}{24}-\frac{7x_2}{120}+\frac{13x_1x_2}{60}\\ {}&\quad +h(z)+\frac{2}{3},\\ L_{22}(x_1,x_2)=\left( \frac{-x_1}{2}+{2},\frac{-x_2}{2}+{2}\right) ,F_{22}(x_1,x_2,z)&=\frac{-x_1}{3}-\frac{7x_2}{120}+\frac{37x_1x_2}{240}\\ {}&\quad +h(z)+\frac{2}{3}, \end{aligned}$$

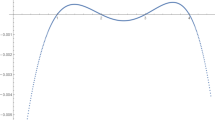
  for all $x_1,x_2\in [0,1]$ and $z\in [0,2]$. Since all the conditions from Sect. 5 are satisfied, there exists a continuous contractive fractal interpolation surface whose graphical representation is given in Fig. 3.

Fig. 3

The graphical representation for the third example