Abstract
We consider a two-phase elliptic–parabolic moving boundary problem modelling an evaporation front in a porous medium. Our main result is a proof of short-time existence and uniqueness of strong solutions to the corresponding nonlinear evolution problem in an \(L^p\)-setting. It relies critically on nonstandard optimal regularity results for a linear elliptic–parabolic system with dynamic boundary condition.

Similar content being viewed by others
References
Bazalii, B.V., Degtyarev, S.P.: Solvability of a problem with an unknown boundary between the domains of a parabolic and an elliptic equations. Ukr. Math. J. 41(10), 1155–1160 (1989)
Denk, R., Kaip, M.: General Parabolic Mixed Order Systems in \(L_p\) and Applications, Operator Theory: Advances and Applications, vol. 239. Birkhäuser, Boston (2013)
Denk, R., Saal, J., Seiler, J.: Inhomogeneous symbols, the Newton polygon, and maximal \(L^p\)-regularity. Russ. J. Math. Phys. 15, 171–191 (2008)
Escher, J.: Classical solutions to a moving boundary problem for an elliptic–parabolic system. Interfaces Free Boundaries 6, 175–193 (2004)
Frolova, E.: Solvability in Sobolev spaces of a problem for a second order parabolic equation with time derivative in the boundary condition. Port. Math. 56, 419–441 (1999)
Il’ichev, A.T., Shargatov, V.A.: Dynamics of water evaporation fronts. Comput. Math. Math. Phys. 53, 1350–1370 (2013)
Il’ichev, A.T., Tsypkin, G.G.: Catastrophic transition to instability of evaporation front in a porous medium. Eur. J. Mech. B Fluids 27, 665–677 (2008)
Ladyženskaya, O.A., Solonnikov, V.A., Ural’ceva, N.N.: Linear and Quasi-Linear Equations of Parabolic Type. AMS, Providence (1968)
Lippoth, F., Prokert, G.: Stability of equilibria of a two-phase Stokes–Osmosis problem. Interfaces Free Boundaries 18, 161–179 (2016)
Prüss, J., Saal, J., Simonett, G.: Existence of analytic solutions for the classical Stefan problem. Math. Ann. 338, 703–755 (2007)
Schubert, G., Straus, J.M.: Gravitational stability of water over steam in vapour-dominated geothermal systems. J. Geophys. Res. 85, 6505–6512 (1980)
Solonnikov, V.A., Frolova, E.V.: \(L_p\)-theory for the Stefan problem. J. Math. Sci. 99, 989–1006 (2000)
Triebel, H.: Theory of Function Spaces. Birkhäuser, Boston (1983)
Acknowledgements
The research leading to this paper was carried out in part while the second author enjoyed the hospitality of the Institute of Applied Mathematics of Leibniz University Hannover. Moreover, we express our gratitude to E.V. Frolova, J. Seiler, and M. Wilke for helpful comments and discussions.
Funding
Funding was provided by Gottfried Wilhelm Leibniz Universität Hannover and Technische Universiteit Eindhoven.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no affiliation with any organization with a direct or indirect financial interest in the subject matter discussed in the manuscript.
Additional information
Communicated by H. Amann
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Parameter dependent elliptic problems
Remark A.1
Let \(X_i\), \(Y_i\), \(i=0,1\) be Banach spaces, \(q\in (1,\infty )\), \(J=(0,T)\). Assume \(Y_1\hookrightarrow Y_0\),
and define \(u\in L_\infty (J,X_0)\) by
Then \(u(t)=A(t)^{-1}(F(t)-K(t)u(t))\) and therefore \(u\in L_q(J,X_1)\), with estimate
Lemma A.2
Let \(0<\beta<\alpha <1\), \(\subset \mathbb {R}^n\) be a domain with \(d := {\mathrm{diam}}D \le 1\) and \(\phi \in BUC^\alpha (D)\) such that \(\phi (x_0)=0\) for some \(x_0 \in D\). Then
Proof
We have for \(x,y \in D\)
\(\square \)
Lemma A.3
(Hölder estimates for coefficients in remainder terms).
Let
\(a\in Z^0(\Omega )\), \(\xi _0\in \Omega \), \(a(\xi _0,0)=0\), \(\lambda \in (0,1)\), \(\tau _0 \in J\). Let \(\Omega _\lambda := \Omega _-\cap B(\xi _0,\lambda ) \ne \emptyset \), \(Q_{\lambda ,\tau _0} := \Omega _\lambda \times (0,\tau _0)\). Then
and
Proof
We rewrite
and estimate the terms on the right separately. (The second term will be interpreted both as a function on \(\Omega \) and as a function on \(\Omega \times J\) which is constant with respect to t.) Trace and embedding theorems yield \(a(\cdot ,0)\in BUC^{2\theta _3}(\Omega )\),
and thus by Lemma A.2
Furthermore, as \(2\theta _2<1-\frac{n+1}{p}\) we have by embedding
and by restriction
with estimate
Consequently, using \({\hat{a}}|_{t=0}=0\),
Together with (A.1) this implies the result. \(\square \)
Let \(a_{ij}\in Z^0(\Omega )\) be uniformly elliptic, i.e.
for some \(\mu >0\). Let \(b_i\in Y^-_\tau \), \(f\in Y^-(\Omega _-)\), \(g\in X^-_{{\mathrm{tr}}}(\Omega _-)\).
Lemma A.4
Let \(M=\max \{\Vert a_{ij}\Vert _{Z^0},{\Vert b_i\Vert _{{\tilde{Y}}^-_\tau }},\mu ^{-1}\}.\) There are constants C(M), \(T_0(M)\) such that for \(T\le T_0\), there is precisely one solution \(u\in X^-\) to the time-dependent elliptic problem
It satisfies
If \(g=0\) and  then
then  .
.
Proof
1. We first show \(u\in L_p(J,H^2_p(\Omega _-))\) with the corresponding estimate. For this we set
and aim at the application of Remark A.1. F clearly satisfies the assumptions.
1.1. For \(v\in X_0\), \(t\in J\) we have
due to the embeddings \({\tilde{Y}}^-_\tau \hookrightarrow L^\infty (J_\tau , W^{-\theta }_p(\Omega _-))\) and \(X_0\hookrightarrow BUC^{1+\theta '}(\Omega _-)\) for a suitable \(\theta '\in (\theta ,1)\) and the pointwise multiplicator property ([13] Theorem 3.3.2)
So \(K\in L_\infty (J,{{\mathcal {L}}}(X_0,Y_0))\). Furthermore,
where we use the embedding \(X_0\hookrightarrow BUC^1(\Omega _-)\). This shows \(K\in L_p({{\mathcal {L}}}(X_0,Y_1))\).
1.2. By parallel reasonings, we get \(A\in BUC(J,{{\mathcal {L}}}(X_1,Y_1))\), \(A+K\in BUC(J,{{\mathcal {L}}}(X_0,Y_0))\) with norms depending only on M. The fact that for \(t\in J\) we have \(A(t)\in {{\mathcal {L}}}_{is}(X_1,Y_1)\), with \(\Vert A(t)^{-1}\Vert _{{{\mathcal {L}}}(Y_1,X_1)}\) depending only on \(\Vert a_{ij}\Vert _{Z^0(\Omega )}\) and \(\mu \) follows from standard theory on elliptic boundary value problems. To get \(A(t)+K(t)\in {{\mathcal {L}}}_{is}(X_0,Y_0)\) one proceeds as in the proof of [13] Theorem 4.3.3., with slight modifications due to the fact that the coefficients of A and K are not \(C^\infty \). The proof remains valid, anyway, as by (A.3) and interpolation we have estimates for the lower order term of the type
for any \(\varepsilon >0\). Note also that we have to use (A.3) together with Lemma A.2 (with \(\beta =\theta \), \(\alpha =\theta '\)) to estimate the highest-order error terms occurring from freezing of the coefficients.
As all assumptions of the above remark are valid, we conclude \(u\in L_p(J,H^2_p(\Omega _-))\) and
2. By arguments as above, we have
hence \(K\in W_p^{\theta }(J,{{\mathcal {L}}}(X_0,Y_0))\) and by parallel arguments \(A\in W_p^{\theta }(J,{{\mathcal {L}}}(X_0,Y_0))\), with norms depending on \(\Vert a_{ij}\Vert _{Z^0(\Omega )}\), \(\Vert b_i\Vert _{Y^-(\Omega _-)}\). Write \({\hat{A}} := A+K\). By Step 1.2, \({\hat{A}}(0)\in {{\mathcal {L}}}_{is}(X_0.Y_0)\), and therefore there is a \(\delta >0\) such that the open ball \({{\mathcal {B}}}\) in \({{\mathcal {L}}}(X_0,Y_0)\) centered at \({\hat{A}}(0)\) with radius \(\delta \) lies in \({{\mathcal {L}}}_{is}(X_0,Y_0)\), and the operator \(\mathop {\mathrm{inv}}\) given by \(\mathop {\mathrm{inv}}(B)=B^{-1}\) is in \(BUC^1({{\mathcal {B}}},{{\mathcal {L}}}(Y_0,X_0))\). Because \({\hat{A}}\) is continuous in time with values in \({{\mathcal {L}}}(X_0,Y_0)\), by shrinking J if necessary, we can arrange that \({\hat{A}}(t)\in {{\mathcal {B}}}\) for all \(t\in J\). Therefore we have
and from this it follows straightforwardly that \(\mathop {\mathrm{inv}}\circ {\hat{A}}\in W_p^\theta (J,{{\mathcal {L}}}(Y_0,X_0))\). Finally from this and \(F\in W_p^\theta (J,Y_0)\) we get \(u\in W_p^\theta (J,W_p^{{2}-\theta }(\Omega _-))\) and
\(\square \)
1.2 Uniform anisotropic embeddings, multiplications and related estimates
For the proof of our main result it is essential that the constant in the maximal regularity estimate of Theorem 3.1 is independent of T (at least for T small). However, the constants in usual embedding theorems (like \(W^1_q(J)\hookrightarrow L^\infty (J)\), \(q\in [1,\infty )\)) are easily seen to blow up as J becomes small. The following lemma and its corollaries ensure that this does not occur when one considers only subspaces with vanishing trace(s) at \(t=0\).
Lemma A.5
Let \(m \in \mathbb {N}\), \(q \in (1,\infty )\), \(\sigma _1 = 0\) or \(\sigma _1 \in (1/q, 1]\). Let further \(1/q < \sigma _2 \le \cdots \le \sigma _m \le 1\) and \(\sigma _1 \le \sigma _2\). Let \(X_1,...,X_m\) be Banach spaces such that \(X_1 \hookrightarrow X_2 \hookrightarrow \cdots \hookrightarrow X_m\). Given \(T \in (0,\infty ]\), let
There exist bounded linear operators \(\mathcal {E}_T: W(T) \rightarrow W\) and a constant \(C > 0\) such that
for all \(T \in (0,\infty ]\), \(u \in L_q(0,T;X_i)\) and \(i = 1,...,m\), and (in case that either \(\sigma _1 \in (1/q, 1]\) or \(\sigma _1 = 0\) and \(m \ge 2\))
for all \(T \in (0,\infty ]\) and  .
.
Proof
For \(m = 1\) and \(0 < T \le T_0\) this is stated and proved in Proposition 6.1 in [10]. The case of a general \(m \in \mathbb {N}\) is an immediate consequence. Moreover, a careful inspection of the proof shows that the constant C can be chosen independent of \(T > T_0\), too. \(\square \)
Corollary A.6
Let \(q \in (1,\infty )\), \(\delta \ge 0\), \(1/q + \delta < \sigma \le 1\) and let X be a Banach space. Given \(T \in (0,\infty ]\) we have \(W_q^\sigma ((0,T),X) \hookrightarrow BUC^\delta ((0,T),X)\). There exists a constant \(C > 0\) such that
for all \(T \in (0,\infty ]\) and  .
.
Corollary A.7
Let \(q \in (1,\infty )\), \(2 \delta + \sigma \le 2\). Given \(T \in (0,\infty ]\) we have
There exists a constant \(C > 0\) such that
for all \(T \in (0,\infty ]\) and  .
.
Let X, Y, Z be Banach spaces whose elements can be interpreted as real-valued functions on the same domain of definition. Then there is a pointwise product \((u,v)\mapsto uv\) on \(X\times Y\). We write
if for all \((u,v)\in X \times Y\) we have \(uv \in Z\) and there is an \(M>0\) such that
Lemma A.8
Let \(q \in (1,\infty )\), \(1> \rho> \sigma > 1/q\), \(T > 0\) and let X, Y, Z be Banach spaces s.t. \(X \cdot Y \hookrightarrow Z\). The following holds true:
-
(i)
\(C([0,T],X) \cdot L_q(0,T;Y) \hookrightarrow L_q(0,T;Z)\) and
$$\begin{aligned} \Vert u v \Vert _{L_q(0,T;Z)} \le M \Vert u \Vert _{C([0,T],X)} \Vert v \Vert _{L_q(0,T;Y)} \end{aligned}$$for all \(u \in C([0,T],X)\), \(v \in L_q(0,T;Y)\).
-
(ii)
\(C^\rho ([0,T],X) \cdot W_q^\sigma ((0,T),Y) \hookrightarrow W_q^\sigma ((0,T),Z)\) and
$$\begin{aligned} \Vert uv \Vert _{W_q^\sigma ((0,T),Z)}\le & {} C(\rho ,\sigma ,q,M) \; \big [ \Vert u \Vert _{L_\infty (0,T;X)} \Vert v \Vert _{W_q^\sigma ((0,T),Y)} \\&+ \, T^{\rho -\sigma + 1/q} \Vert v \Vert _{L_\infty (0,T;Y)} \Vert u \Vert _{C^{\rho }([0,T],X)} \big ] \end{aligned}$$for all \(u \in C^{\rho }([0,T],X)\), \(v \in W_q^\sigma ((0,T),Y)\).
-
(iii)
\(W_q^\sigma ((0,T),X) \cdot W_q^\sigma ((0,T),Y) \hookrightarrow W_q^\sigma ((0,T),Z)\) and
$$\begin{aligned} \Vert uv \Vert _{W_q^\sigma ((0,T),Z)}\le & {} C(q,M) \; \big [ \Vert u \Vert _{L_\infty (0,T;X)} \Vert v \Vert _{W_q^\sigma ((0,T),Y)} \\&+ \, \Vert v \Vert _{L_\infty (0,T;Y)} \Vert u \Vert _{W_q^\sigma ((0,T),X)} \big ] \end{aligned}$$for all \(u \in W_q^\sigma ((0,T),X)\), \(v \in W_q^\sigma ((0,T),Y)\).
Proof
The first statement is trivial. Let \(u \in C^\rho ([0,T],X)\), \(v \in W_q^\sigma ((0,T),Y)\). We have
and
All our assertions follow easily from these estimates. \(\square \)
An immediate consequence is the following
Lemma A.9
Under the assumptions of Lemma A.8 we have
for all  ,
,  and \(0 \le \varepsilon < \sigma - 1/q\). Moreover,
and \(0 \le \varepsilon < \sigma - 1/q\). Moreover,
for all  ,
,  and \(0 \le \varepsilon < \sigma -1/q\).
and \(0 \le \varepsilon < \sigma -1/q\).
Remark A.10
(Product estimate, elliptic phase). Let \(q \in (1,\infty )\), \(N \in \mathbb {N}\) and let \(D \subset \mathbb {R}^N\) be open. Lemmas A.8 and A.9 guarantee smallness of terms
for small values of T and  by choosing \(Y=Z=W_q^{-\sigma }(D)\), \(X = W_q^{1-\sigma }(D)\) (\(1/q< \sigma < 1/2\)) and \(Y=Z=L_q(D)\), \(X = W_q^{1-\sigma }(D)\) (\(1/q< \sigma < 1-N/q\)), respectively.
by choosing \(Y=Z=W_q^{-\sigma }(D)\), \(X = W_q^{1-\sigma }(D)\) (\(1/q< \sigma < 1/2\)) and \(Y=Z=L_q(D)\), \(X = W_q^{1-\sigma }(D)\) (\(1/q< \sigma < 1-N/q\)), respectively.
Observe that the conditions \(1/q< \sigma < 1/2\) and \(1/q< \sigma < 1-N/q\) are both satisfied if \(\frac{1}{q}\frac{q-1}{q-N}< \sigma < \frac{1}{2}(1-\frac{N+1}{q})\) and \(q > N-1\).
Lemma A.11
Let \(N \in \mathbb {N}\), \(1> \sigma > 1/q\), \(1 \ge r > \frac{N-1}{q-1/\sigma }\) and let U be an open set in \(\mathbb {R}^{N-1}\). For \(T \in (0,\infty ]\) let
Then \(E(T) \hookrightarrow BUC((0,T) \times U)\) and E(T) is a Banach algebra. There exists a constant \(C > 0\) such that
-
(i)
\(\Vert u \Vert _\infty \le C \Vert u \Vert _{E(T)}\) for all \(T \in (0,\infty ]\) and
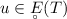 ;
; -
(ii)
\(\Vert uv \Vert _{E(T)} \le C ( \Vert u \Vert _\infty \Vert v \Vert _{E(T)} + \Vert v \Vert _\infty \Vert u \Vert _{E(T)} )\) for all \(T \in (0,\infty ]\) and
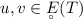 (where \(\Vert \cdot \Vert _\infty \) denotes the sup of a function over the set \((0,T) \times M\)).
(where \(\Vert \cdot \Vert _\infty \) denotes the sup of a function over the set \((0,T) \times M\)).If \(\delta \in [0,1]\), \(r > \frac{N-1}{q(1-\delta )}\) and \(\delta \sigma > 1/q + \varepsilon \), then \(E(T) \hookrightarrow BUC^{\varepsilon }((0,T),BUC(U))\) and there is a constant \(C > 0\) such that
-
(iii)
\(\Vert u \Vert _\infty \le C T^{\varepsilon } \Vert u \Vert _{E(T)}\)
for all \(T \in (0,\infty ]\) and  .
.
Proof
The embedding \(E(T) \hookrightarrow BUC((0,T) \times U)\) is stated and proved in Lemma 4.4 in [3] and the estimate (i) follows straightforwardly from Lemma A.5, Corollary A.6. Observe that for a.e. \(t \in (0,T)\)
since \(r> \frac{N-1}{q-1/\sigma } > \frac{N-1}{q}\). Hence,
and, as calculations similar to (A.4) show,
Assertion (ii) is now an easy consequence of this and of Lemma A.5, Corollary A.6. Assertion (iii) follows from Lemma 4.3 in [3] and again Lemma A.5, Corollary A.6. \(\square \)
Remark A.12
For \(r=1-1/q\) the conditions \(r > \frac{N-1}{q-1/\sigma }\), \(\sigma > 1/q\) are satisfied if \(\sigma > \frac{1}{q} \frac{q-1}{q-N}\). In this case, \(1/(q\sigma ) < (q-N)/(q-1)\). If \(\delta \in (1/(q\sigma ), (q-N)/(q-1))\), we have \(1-1/q > (N-1)/(q(1-\delta ))\) and \(\delta \sigma > 1/q\). Thus, (identifying \(\Gamma \) with \(\mathbb {R}^{n-1}\)) Lemma A.11 applies to the space \(Y_\theta ^B(\Gamma )\) frequently used in this paper.
1.3 Some auxiliary results concerning localizations
Let \(r \in (0,1)\), \(q \in [1,\infty )\), and let \(\{ \Omega ^{(k)} \}_{k \in \mathcal {K}}\) be the collection of sets defined in the proof of Lemma 3.5. Suppose further that
-
\(f \in C^\infty (\Gamma )\), \(\{ f_k \}, \{ g_k \} \subset C^\infty (\Gamma )\), \(\hbox {supp}(f_k) \subset \Omega ^{(k)}\) (\(k \in \mathcal {K}\));
-
\(\{ \psi _k \} \subset C^\infty (\Gamma )\) are such that \(\hbox {supp}(\psi _k) \subset \Omega ^{(k)}\) and \(\vert \partial ^\alpha \psi _k \vert _\infty \le C \lambda ^{-\alpha }\) uniformly for \(k \in \mathcal {K}\).
Lemma A.13
We have
and
Proof
1. Let \(x \in \Gamma \). Since x is an element of at most \(N_0\) of the sets \(\Omega ^{(k)}\), the sum \(\sum _{k \in \mathcal {K}} |f_k(x)|\) has at most \(N_0\) nonzero summands. Hence
2. Let \((x,y) \in \Gamma \times \Gamma \). Then the sum \(\sum _{k \in \mathcal {K}} |f_k(x) - f_k(y)|\) has at most \(2 N_0\) nonzero summands. Hence
The assertion follows from the definition of the intrinsic norms
\(\square \)
Remark A.14
A special case of Lemma A.13 are the estimates
and
A direct consequence of Lemma A.13 and a standard approximation argument is
Corollary A.15
Let \(V_\theta ^B(\Gamma )\), \(V \in \{ X,Y \}\) and p be as in Sect. 3.1. Then
for \(u_k \in V_\theta ^B(\Gamma )\).
Lemma A.16
We have that
and
Proof
Inequality (A.10) is obvious. For (A.11) note that
This implies
Inequality (A.12) follows from
and (A.13) is obtained by combining (A.14), (A.15) and the fact that \(|\mathcal {K}| \sim \lambda ^{-n+1}\). \(\square \)
Remark A.17
In the same way as above one obtains
\(i=1,\dots ,n-1\). From this one concludes
for  , p as in Sect. 3.1, and some \(\delta > 0\).
, p as in Sect. 3.1, and some \(\delta > 0\).
Rights and permissions
About this article
Cite this article
Lippoth, F., Prokert, G. Well-Posedness for a Moving Boundary Model of an Evaporation Front in a Porous Medium. J. Math. Fluid Mech. 21, 40 (2019). https://doi.org/10.1007/s00021-019-0438-1
Accepted:
Published:
DOI: https://doi.org/10.1007/s00021-019-0438-1
Keywords
- Elliptic–parabolic system
- moving boundary
- Stefan problem
- Hele-Shaw problem
- inhomogeneous symbol
- parabolic evolution equation





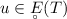 ;
;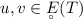 (where
(where