Skip to main content
SpringerLink
Log in

A Review: High Amplitude Vibration and Jump Phenomena Attenuation Methods in Different Dynamic Systems

  • Conference paper
  • First Online:
Recent Advancements in Mechanical Engineering

Part of the book series: Lecture Notes in Mechanical Engineering ((LNME))

  • 383 Accesses

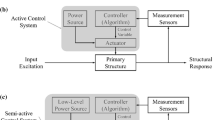
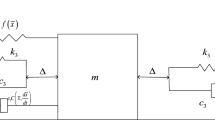
Abstract

In this review paper, the research findings regarding the jump phenomena, vibration issue and a broad range of attenuation techniques for the issues in different dynamic systems are well succinct. In the field of dynamics, the interaction between the drive and the driven source is always an interesting point of research to perceive the characteristic of non-ideal vibrating systems. In this article, we broadly categorized the investigation and vibration attenuation techniques for different dynamic system into three types, namely optimization of the system design parameter, optimization of drive parameter and smart methods. In the first category, various research articles are briefed to deliver the optimization technique for foundation element parameters such as spring, damper and bearing to reduce heavy-duty vibration amplitude. In the second category, a bunch of research findings are described to showcase that optimizing the electrical input and drive torque may help to attenuate resonant vibration. In the third part, some smart methods like the use of a magnetic bearing, magneto-rheological damper and shape memory alloy to suppress the chaotic behavior of the system in the resonance region are addressed. Nowadays, practice of the smart technique is growing faster and it is an emerging research option for the attenuation of the vibration in highly dynamic systems.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 129.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 169.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Sommerfeld A (1902) Contributions to the dynamic expansion of strength theory. Phys J 3:266–284

    Google Scholar 

  2. Samantary A (2009) Steady-state dynamics of a non-ideal rotor with internal damping and gyroscopic effects. Nonlinear Dyn 56:443–451

    Article  Google Scholar 

  3. Dasgupta S, Samantaray A, Bhattacharyya R (2010) Stability of an internally damped non-ideal flexible spinning shaft. Int J Non-Linear Mech 2010:286–293

    Article  Google Scholar 

  4. Tsuchida M, Guilherme L, Balthazar M (2005) On chaotic vibrations of a non-ideal system with two degrees of freedom. J Sound Vibr 282:1201–1207

    Article  Google Scholar 

  5. Tsuchida M, Guilherme K, Balthazar J, Silva G, Cheshankov B (2003) On regular and irregular vibrations of a non-ideal system with two degrees of freedom. 1:1 resonance. J Sound Vib 260:949–960

    Article  Google Scholar 

  6. Sado D, Kot M (2007) Chaotic vibration of an autoparametrical system with a non ideal source of power. J Theor Appl Mech 45:119–131

    Google Scholar 

  7. El-badawy A (2007) Behavioural investigation of a nonlinear nonideal vibrating system. J Vib Control 13:203–217

    Article  MathSciNet  Google Scholar 

  8. Cveticanin L, Zukovic M, Cveticanin D (2017) Two degree of freedom oscillator coupled to a non-ideal source. Int J Non-Linear Mech 94:1–21

    Article  Google Scholar 

  9. Bisoi A, Samantaray AK, Bhattacharyya R (2017) Sommerfeld effect in a two-disk rotor dynamic system at various unbalance conditions. Meccanica 53:681–701

    Article  MathSciNet  Google Scholar 

  10. Bisoi A, Samantaray AK, Bhattacharyya R (2017) Sommerfeld effect in a gyroscopic overhung rotor-disk system. Nonlinear Dyn 88(3):1565–1585

    Article  Google Scholar 

  11. Zhang X, Li Z, Li M, Wen B (2020) Stability and sommerfeld effect of a vibrating system with two vibrator driven separately by induction motors. IEEE. https://doi.org/10.1109/TMECH.2020.3003029

  12. Krasnopolskaya S (1994) Acoustic chaos caused by the sommerfeld effect. J Fluids Struct 8:803–815

    Article  Google Scholar 

  13. Dantas H, Balthazar M (2003) On the appearance of a Hopf bifurcation in a non-ideal mechanical problem. Mech Res Commun 30:493–503

    Article  MathSciNet  Google Scholar 

  14. Bola R, Balthazar M, Felix P (2007) On an approximate analytical solution to non-linear vibrating problem excited by a non-ideal motor. Nonlinear Dyn 50:841–847

    Article  Google Scholar 

  15. Mattos CM, Balthazar M (1999) On the dynamics of an armature controlled DC motor mounted on an elastically supported Table. In: 15th Brazilian Congress of Mechanical Engineering, Aguas de Lindoia, Sao Paulo, 22–26 Nov pp. 1–10

    Google Scholar 

  16. Munteanu L, Brisan C, Chiroiu V, Dumitriu D, Ioan R (2014) Chaos–hyperchaos transition in a class of models governed by sommerfeld effect. Nonlinear Dyn 78:1877–1889

    Article  MathSciNet  Google Scholar 

  17. Shad MR, Michon G, Berlioz A (2011) Modeling and analysis of nonlinear rotordynamics due to higher order deformations in bending. Appl Math Model 35:2145–2159

    Article  MathSciNet  Google Scholar 

  18. Jan A, Roman S, Grażyna S (2015) Decomposition of governing equations in the analysis of resonant response of a nonlinear and non-ideal vibrating system. Nonlinear Dyn 82:299–309

    Google Scholar 

  19. Asghari M, Hashemi M (2017) The couple stress-based nonlinear coupled three-dimensional vibration analysis of microspinning Rayleigh beams. Nonlinear Dyn 87:1315–1334

    Article  Google Scholar 

  20. Hosseini S (2013) Dynamic stability and bifurcation of a nonlinear in-extensional rotating shaft with internal damping. Nonlinear Dyn 74:345–358

    Article  MathSciNet  Google Scholar 

  21. Lawrence NV, Josiah DK, Raymond HP (2016) A new method for predicting critical speeds in rotordynamics. J Eng Gas Turbines Power 138:22541–22546

    Google Scholar 

  22. Zhang X, Wen B, Zhao C (2016) Theoretical study on synchronization of two exciters in a nonlinear vibrating system with multiple resonant types. Nonlinear Dyn 85:141–154

    Article  MathSciNet  Google Scholar 

  23. Dimentberg MF, McGovern L, Norton R, Chapdelaine J, Harrison R (1997) Dynamics of an unbalanced shaft interacting with a limited power supply. Nonlinear Dyn 13:171–187

    Article  Google Scholar 

  24. Gu P, Dubowsky S, Mavroidis C (1998) The design implication of chaotic and near chaotic vibrations in machines. In: Proceeding of the 1998 ASME design technical conferences, Atlanta, GA. 13–16 Sept, pp 1–11

    Google Scholar 

  25. Goncalves PJP, Silveira M, Petrocino EA, Balthazar JM (2016) Double resonance capture of a two degree of freedom oscillator coupled to a non-ideal motor. Meccanica 51:2203–2214

    Article  MathSciNet  Google Scholar 

  26. Gonçalves P, Silveira M, Junior B, Balthazar J (2014) The dynamic behavior of a cantilever beam coupled to an on-ideal unbalanced motor through numerical and experimental analysis. J Sound Vib 333:5115–5129

    Article  Google Scholar 

  27. Sinha A, Bharti S, Samantary A, Bhattacharya R (2020) Sommerfeld effect in a single-DOF system with base excitation from motor driven mechanism. Mech Mach Theory 148:103–108

    Article  Google Scholar 

  28. Kovriguine DA (2012) Synchronization and sommerfeld effect as typical resonant patterns. Arch Appl Mech 82:591–604

    Article  Google Scholar 

  29. Alexander F, Drozdetskaya O (2016) On the averaging in strongly damped systems: the general approach and its application to asymptotic analysis of the Sommerfeld effect. In: IUTAM 19 symposium analytical methods in nonlinear dynamics, vol. 43, pp 43–52

    Google Scholar 

  30. Zukovic M, Cveticanin L (2009) Chaos in non-ideal mechanical system with clerance. J Vib Control 15(8):1229–1246

    Article  MathSciNet  Google Scholar 

  31. Varanis M, Balthazar J, Silva A, Mereles A, Pederiva R (2018) Remark on sommerfeld effect characterization in the wavelet domain. J Vib Control 1–11

    Google Scholar 

  32. Arbex H, Balthazar J, Pontes jr B, Brasil R, Felix J, Tusset A, Bueno A (2014) On nonlinear dynamics nehaviour and control of a new model of magnetically leitated vibrating system excited by an unbalanced DC motor of limited power supply. Brazilizn Soc Mech Sci Eng 37:1139–1150

    Google Scholar 

  33. Felix J, Balthazar JM, Brasil R (2009) Comments on nonlinear dynamics of a non-ideal duffing- rayleigh oscillator: Numerical and analytical approaches. J Sound Vib 319:1136–1149

    Article  Google Scholar 

  34. Cveticanin L, Zukovic M (2015) Non-ideal mechanical system with an oscillator with rational nonlinearity. J Vib Control 21:2149–2164

    Article  MathSciNet  Google Scholar 

  35. Shina A, Samantarya AK, Bharti SK, Bhattacharya R (2018) Sommerfeld effect and passive energy reallocation in self synchronizing system. ASME, pp 1–10

    Google Scholar 

  36. Frolov KV, Krasnopolskaya TS (1988) Sommerfeld effect in system without internal damping. Plenum Publishing Corporation 23:19–24

    Google Scholar 

  37. Jha AK, Dasgupta SS (2020) Suppression of sommerfeld effect in a non-ideal discrete rotor system with fractional order external damping. Europian J Mech 79(103873)

    Google Scholar 

  38. Fernando HM, Bento RP, Silveira M (2013) Influence of ideal and non-ideal excitation sources on the dynamics of a nonlinear vibro-impact system. J Theor Appl Mech 51:763–774

    Google Scholar 

  39. Karthikeyan M, Bisoi A, Samantaray A, Bhattacharyya R (2015) Sommerfeld effect characterization in rotors with non-ideal drive from ideal drive response and power balance. Mech Mach Theory 91:269–288

    Article  Google Scholar 

  40. Iwatsubo T, Kanki H, Kawai R (1972) Vibration of asymmetric rotor through critical speed with limited power supply. J Mech Eng Sci 14(3):184–194

    Article  Google Scholar 

  41. Bisoi A, Samantaray A, Bhattacharyya R (2017) Control strategies for DC motors driving rotor dynamic systems through resonance. J Sound Vib 411:304–327

    Google Scholar 

  42. Bisoi A, Samantaray AK, Bhattacharyya R (2014) Sommerfeld effect characterisation in multi-disk rotor dynamic system with non-ideal drive through semi-analytical methods. In: Proceedings of ICTACEM, IIT Kharagpur

    Google Scholar 

  43. Bharti SK, Bisoi A, Sinha A, Samantaray A, Bhattacharyya R (2019) Sommerfeld effect at forward and backward critical speeds in a rigid rotor shaft system with anisotropic supports. J Sound Vib 442:330–349

    Article  Google Scholar 

  44. Tusset AM, Balthazar JM, Felix J (2012) On elimination of chaotic behaviour in a non-ideal portal frame structural system using both passive and active controls. J Vib Control 19(6):803–813

    Article  Google Scholar 

  45. Shina A, Bharati SK, Samantary AK, Chakraborty G, Bhattaharya R (2018) Sommerfeld effect in an oscillator with a reciprocating mass. Nonlinear Dyn 93:1719–1739

    Article  Google Scholar 

  46. Fradkov A, Tomchina O, Tomchin D (2011) Controlled passage through resonance in mechanical systems. J Sound Vib 330:1065–1073

    Article  Google Scholar 

  47. Cveticanin L, Zukovic M (2015) Motion of a motor-structure non-ideal system. European J Mech A/Solids 53:229–240

    Article  MathSciNet  Google Scholar 

  48. Castao KA, Goes LC, Balthazar JM (2010) A note on the attenuation of the sommerfeld effect of a non-ideal system taking into account a MR damper and the complete model of a DC motor. 17(7):1112–1118

    Google Scholar 

  49. Piccirillo V, Tusset AM (2014) Dynamical jump attenuation in a non-ideal system through a magnetorheological damper. J Theor Through Magnetorheological Damper 52:595–604

    Google Scholar 

  50. Wauer J, Suherman S (1997) Vibration suppression of rotating shafts passing through resonances by switching shaft stiffness. J Vib Acoust 120:170–180

    Article  Google Scholar 

  51. Wu X, Naugle C, Meagher J (2016) A full spectrum analysis methodology applied to an anisotropic overhung rotor. J Appl Mech Eng 5:1–10

    Article  Google Scholar 

  52. Jha AK, Dasgupta SS (2019) Attenuation of sommerfeld effect in an internally damped eccentric shaft-disk system via active magnetic bearings. Meccanica 54:311–320

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mechanical Engineering, National Institute Technology, Silchar, India

    Mohd Anis Ansari, Prabina Kumar Meher, Alfa Bisoi & Agnimitra Biswas

Authors
  1. Mohd Anis Ansari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Prabina Kumar Meher
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alfa Bisoi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Agnimitra Biswas
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Prabina Kumar Meher .

Editor information

Editors and Affiliations

  1. Materials Modification (United States), Fairfax, VA, USA

    T. S. Sudarshan

  2. National Institute Of Technology Silchar, Silchar, India

    K. M. Pandey

  3. National Institute Of Technology Silchar, Silchar, India

    R. D. Misra

  4. National Institute Of Technology Silchar, Silchar, India

    P. K. Patowari

  5. Department of Mechanical Engineering, National Institute of Technology Agartala, Agartala, India

    Swapan Bhaumik

Rights and permissions

Reprints and permissions

Copyright information

© 2023 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Ansari, M.A., Meher, P.K., Bisoi, A., Biswas, A. (2023). A Review: High Amplitude Vibration and Jump Phenomena Attenuation Methods in Different Dynamic Systems. In: Sudarshan, T.S., Pandey, K.M., Misra, R.D., Patowari, P.K., Bhaumik, S. (eds) Recent Advancements in Mechanical Engineering. Lecture Notes in Mechanical Engineering. Springer, Singapore. https://doi.org/10.1007/978-981-19-3266-3_28

Download citation

  • DOI: https://doi.org/10.1007/978-981-19-3266-3_28

  • Published:

  • Publisher Name: Springer, Singapore

  • Print ISBN: 978-981-19-3265-6

  • Online ISBN: 978-981-19-3266-3

  • eBook Packages: EngineeringEngineering (R0)

Publish with us

Policies and ethics

Search

Navigation