Keywords

1 Introduction

A ship will subject to a large surging moment due to the broaching phenomenon caused by surf-riding. The centrifugal force generated by serious yaw motion can lead to ships capsizes, especially for small vessels or high-speed vessels. Surf-riding is a condition in which a ship is captured by a wave in advance at a wave speed under conditions of waves or wake waves. Broaching is the violent shaking motion of the ship. Even if the maximum rudder angle is reversed, the heading phenomenon cannot be changed. Under normal circumstances, surf-riding is a prerequisite for broaching. The stability assessment method of surf-riding /broaching is divided into three levels, the safety margin is from high to low, and the judgment method is from simple to complex [1]. The third level needs to be directly evaluated, and there is no standardized conclusion. In recent years, domestic and foreign scholars have carried out various studies on the surf-riding/broaching. Spyrou [2] also conducted a nonlinear dynamic analysis for ship broaching. Umeda et al. [3] attempted to develop a more consistent mathematical model for capsizing associated with surf-riding/broaching in following and quartering waves by taking most of the second-order terms of the waves into account. Yu et al. [4] used the wave theory to calculate the surge force, utilized Melnikov method to predict the threshold value of surf-riding and used numerical analysis to solve the thrust and drag equilibrium equations, and the calculation program of the second-generation weakness of surf-riding/ broaching is developed. Chu [5] determined the surf-riding phenomenon by constructing a new Melnikov function of surge system to calculate the first-order zero threshold value. On the basis of summarizing the previous research results, based on the 4DOF maneuvering equation, this paper focuses on the surf-riding and surge of the ship in the following and quartering seas by simplifying it into 1DOF maneuvering equations. Then, the Melnikov method is used to calculate the critical Froude number required in the second level criteria and plot the ship's velocity and displacement phase diagrams. The study presented in this paper can lay a theoretical foundation for the direct calculation of the intact stability of the second generation.

2 The Maneuvering Equations for 4DOF

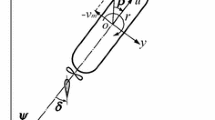
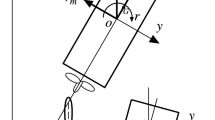
The 4DOF maneuvering equations of the ship can be expressed as [6]:

$$ \dot{\xi } = \left\{ {u\cos \chi - v\sin \chi - c} \right\} $$
(1)
$$ {\dot{\text{u}}} = {{\left\{ {T\left( {u;n} \right) - R\left( u \right) + X_{W} \left( {\xi_{G} ,\chi } \right)} \right\}} \mathord{\left/ {\vphantom {{\left\{ {T\left( {u;n} \right) - R\left( u \right) + X_{W} \left( {\xi_{G} ,\chi } \right)} \right\}} {\left( {m + m_{x} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {m + m_{x} } \right)}} $$
(2)
$$ \dot{v} = {{\left\{ {\begin{array}{*{20}l} { - \left( {m + m_{x} } \right)ur + Y_{v} \left( {u;n} \right)v + Y_{r} \left( {u;n} \right)r + Y_{\phi } \left( u \right)\phi } \\ { + Y_{\delta } \left( {u;n} \right)\delta + Y_{w} \left( {\xi_{G} ,\chi } \right)} \\ \end{array} } \right\}} \mathord{\left/ {\vphantom {{\left\{ {\begin{array}{*{20}c} { - \left( {m + m_{x} } \right)ur + Y_{v} \left( {u;n} \right)v + Y_{r} \left( {u;n} \right)r + Y_{\phi } \left( u \right)\phi } \\ { + Y_{\delta } \left( {u;n} \right)\delta + Y_{w} \left( {\xi_{G} ,\chi } \right)} \\ \end{array} } \right\}} {\left( {m + m_{y} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {m + m_{y} } \right)}} $$
(3)
$$ \dot{\chi } = r $$
(4)
$$ \dot{r} = {{\left\{ \begin{gathered} N_{v} \left( {u;n} \right)v + N_{r} \left( {u;n} \right)r + N_{\phi } \left( u \right)\phi \hfill \\ + N_{\delta } \left( {u;n} \right)\delta + N_{w} \left( {\xi_{G} ,\chi } \right) \hfill \\ \end{gathered} \right\}} \mathord{\left/ {\vphantom {{\left\{ \begin{gathered} N_{v} \left( {u;n} \right)v + N_{r} \left( {u;n} \right)r + N_{\phi } \left( u \right)\phi \hfill \\ + N_{\delta } \left( {u;n} \right)\delta + N_{w} \left( {\xi_{G} ,\chi } \right) \hfill \\ \end{gathered} \right\}} {\left( {I_{zz} + J_{zz} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {I_{zz} + J_{zz} } \right)}} $$
(5)
$$ \dot{\phi } = p $$
(6)
$$ \dot{p} = {{\left\{ \begin{gathered} m_{x} Z_{H} ur + K_{v} \left( {u;n} \right)r + K_{r} \left( {u;n} \right)r + K_{\phi } \left( u \right)\phi \hfill \\ + K_{\delta } \left( {u;n} \right)\delta + K_{w} \left( {\xi_{G} ,\chi } \right) - mgGZ\left( \phi \right) \hfill \\ \end{gathered} \right\}} \mathord{\left/ {\vphantom {{\left\{ \begin{gathered} m_{x} Z_{H} ur + K_{v} \left( {u;n} \right)r + K_{r} \left( {u;n} \right)r + K_{\phi } \left( u \right)\phi \hfill \\ + K_{\delta } \left( {u;n} \right)\delta + K_{w} \left( {\xi_{G} ,\chi } \right) - mgGZ\left( \phi \right) \hfill \\ \end{gathered} \right\}} {\left( {I_{xx} + J_{xx} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {I_{xx} + J_{xx} } \right)}} $$
(7)
$$ {{\dot{\delta } = \left\{ { - \delta - \left( {\chi - \chi_{c} } \right)} \right\}} \mathord{\left/ {\vphantom {{\dot{\delta } = \left\{ { - \delta - \left( {\chi - \chi_{c} } \right)} \right\}} {TE}}} \right. \kern-\nulldelimiterspace} {TE}} $$
(8)

where Xw and Yw are wave force, Nw and Kw are wave moments, ξG is the longitudinal coordinate of the ship center of gravity. u is the speed of surge, v is the speed of sway, N is the movement of yaw, K is the movement of roll, the superscripts of u, v, N, K are hydrodynamic coefficients except for the wave force. χ is the heading angle, χc is the designed heading angle, r is the speed of yaw, φ is the angle of roll, p is the speed of roll, δ is the rudder angle. There is a dot on the letter that represents the first derivative of time. T is the thrust, R is the resistance, n is the propeller speed, c is the wave velocity. m and mx, my represent the hull mass and additional mass, respectively, I and J are the moment of inertia and the additional moment of inertia, respectively, ZH is the center of the sway force, g is the acceleration of gravity, GZ is the restorative arm, TE is the constant of steering gear set as 0.63.

3 The Analysis of Hull Form Data and 1DOF Model

A fishing boat is selected within this study. The basic parameters of the ship hull shown in Table 1.

Table 1. The general properties of a fishing boat
Full size table

The wave condition used in this study is as follow: Wave steepness h/λ = 1/10, Wavelength λ = 34.5 m. By reading a large amount of literatures, surf-riding always occurs when the wavelength λ is close to the ship length L. Therefore, λ/L = 1 is selected as the wave condition within this study and the wave steepness is set as 1/10 based on existing literature.

Since the wave condition calculated in this section is completely random and without tailgating, the heading angle is equal to zero. Then, the Eq. (1) to Eq. (8) will be simplified as follows. First, the predetermined heading χc, the steering angle χ and the rudder angle δ are set as zero. The ship has no sway force when sailing along a straight line. Without considering the capsizing, the yaw moment can also be ignored. Therefore, the simplified equations can be written as:

$$ \dot{\xi }_{G} = \left\{ {u - c} \right\} $$
(9)
$$ \dot{u} = \{ T(u;n) - R(u) + X_{w} (\xi_{G} ,\chi )\} /(m + m_{x} ) $$
(10)

It can be seen from the Eqs. (9) and (10) that the surf-riding motion within the waves is an 1DOF model.

4 Phase Diagram Analysis

Phase analysis is the main tool to study the mechanism of ship’s surf-riding. What presents in the phase diagram is a velocity vs. displacement plot. Each curve of the phase diagram is called a phase trajectory, and each phase trajectory corresponds to a set of initial conditions. The following will be specifically analyzed by fishing boat combined with the wave parameters given in Table 2.

4.1 Change the Propeller Speed with the Given Initial Conditions

This section will first calculate the critical Froude number of the fishing boat by Melnikov method. The results are shown in Table 2.

Table 2. The calculation of the critical Froude number
Full size table

It can be seen from the Table 2 that the results calculated with Melnikov method is almost as good as the results calculated with direct method. Therefore, Table 2 is selected as the reference for calculating the initial state in this section. Next, the calculation results of the maneuvering equation are used for argumentation as followed.

$$ T\left( {c;n} \right) - R\left( c \right) + X_{W} \left( {\xi_{G} } \right) = 0 $$
(11)

It can be seen from Fig. 1(a) that the trajectory tends to a certain point slowly, indicating the position and state of surf-riding. To show this, the calculation time is increased to 250 s. As shown in Fig. 1(b), it is easy to find that the phase diagram trajectory is finally fixed at one point with coordinates (−0.922, 7.335). The speed is close to the wave speed, and the displacement have a certain gap from −1.2048 mentioned above.

Fig. 1.
figure 1

Surf-riding phase diagram

Full size image

In this case it is very difficult to simulate the wave motion exceeding the ship's surge motion. Next, the propeller speed is changed to 6 m/s, the remaining values are unchanged and calculated for 100 s, as shown in Fig. 2. It’s easy to catch the direction of the trajectory in the surf-riding phase diagram, that is, the initial point is finally focused on one point. The surging phase diagram will be an infinitely long curve. Therefore, the arrow given in Fig. 2 is the direction of the trajectory. The ship speed increases shapely before 40 s and reaches a stable state. The reason for occurring an oscillation state is that the ship constantly passes through the wave crests and troughs and is constantly subjected to positive wave forces and negative wave forces.

Fig. 2.
figure 2

The surging phase diagram at n = 6

Full size image
Fig. 3.
figure 3

A comparison of the surf-riding and surging phase diagrams

Full size image

Next, the Fig. 1(a) and Fig. 2 are now placed in the same phase diagram for comparison, as shown in Fig. 3. The two trajectories start from the same point and finally enter two completely different motion states. The major similarity for these two curves is that the two trajectories’ speeds are increasing at first. However, the orange curve is ultimately affected by the wave force, and the ship speed approaches the wave speed, while the blue curve cannot maintain a stable speed affected by the wave exciting force.

4.2 Change the Initial Speed with the Given Initial Conditions

Fig. 4.
figure 4

The ship’s surging phase diagram

Full size image
Fig. 5.
figure 5

The ship’s surf-riding phase diagram

Full size image

Figure 4 shows that the ship is captured by the waves, accelerated by the wave force but does not reach the wave speed and finally becomes a surging motion mode. Figure 5 shows that the propeller thrust cannot be maintained at the current speed and decelerated and is captured by the waves and eventually accelerated to the wave speed. In conclusion, the closer the ship speed is to the wave speed, the easier the ship is surf-riding.

4.3 The Calculation of the Critical Froude Number Using the Phase Analysis Method

Through analysis, it can be found that the propeller speed and the initial speed of the ship are the two important parameters affecting a ship’s surf-riding. In this section, the phase analysis method is used to obtain the critical Froude number.

Fig. 6.
figure 6

The ship’s surging phase diagram

Full size image
Fig. 7.
figure 7

The ship’s surf-riding phase diagram

Full size image

After changing the initial speed, it is obvious that it takes longer to calculate and judge the ship's motion. This is because the ship will perform a surging motion firstly when the ship speed accelerates to a speed close to that in still water. At this time, the state of motion will change. Taking the fishing boat as an example, the simulation time is approaching 300 s. The result shows that the ship tends to surf-riding. The surging movement shows a completely periodic change. If the surging of the periodic variation is to be simulated, a longer calculation time is required. The propeller speeds in Fig. 6 and Fig. 7 are 2.7 and 2.9, respectively, with very little difference. However, the ship presents a completely different motion state, and its motion parameters also change greatly.

Fig. 8.
figure 8

A comparison of surging phase diagram and surf-riding phase diagram

Full size image

As can be seen from Fig. 8(a), before the ship moves to the wave-300 m, the form of motion is similar. When the ship speed accelerates to 6 m/s, the two diagrams bifurcate. In the surging phase diagram, the ship speed is still changing alternately between acceleration and deceleration with little change trend. In the phase diagram of surf-riding, the ship speed suddenly increases from 5 m/s to 9 m/s and finally stabilizes at the wave speed. The black line in the figure is equivalent to the asymptotic line of the two trajectories, and the phase diagram of the section from −330 m to −300 m is magnified to compare, as shown in Fig. 8(b).

5 Conclusion

In this paper, the 4DOF maneuvering equation is simplified into a 1DOF maneuvering equation to study the critical conditions for the ship’s surf-riding and surging in waves. According to the phase diagram, it can be found that the critical speed is the intermediate value of the changed phase diagram, which is between 2.7 and 2.9. This is consistent with the critical propeller speed 2.8642 calculated by the Melnikov equation. According to the analysis above, 2.8642 is an approximation, not the critical value, in the phase diagram, and the phase diagram can determine the range of the value. It is noteworthy that if a real threshold is input, the phase diagram should enter the surf-riding at the unstable equilibrium point.