Keywords

1 Introduction

Increasing mass customization and product complexity combined with shorter product life cycles require agile, flexible, and smart production systems in manufacturing technology [13]. In addition, future studies on the topic of manufacturing technology are required to be subordinated to the maxim of resource efficiency. In forming technology, the forming tools play a key role as the link between semi-finished products and machines and directly impact the flexibility of a forming process [2]. To be more precise, kinematic forming processes such as three-roll-push bending [3] or incremental swivel bending [11] have inherent flexibility due to their shape-giving tool movement. In contrast, tool-bound processes like stamping are limited regarding an achievable variety of geometries.

State-of-the-art forming tools are typically solid and oversized steel parts generating an unnecessarily high level of energy consumption for the tool production along the entire value chain and in the operation of the tools. This research gap can be addressed by combining lightweight construction with topology optimization to obtain an efficient design tool for forming tool development. On account of the fact that Additive Manufacturing (AM) methods enable the fabrication of complex-shaped and topology-optimized tools [2]—in comparison to conventional manufacturing methods—the combination of lightweight construction, topology optimization, and AM is of significant interest.

Xu et al. [12] show that a blank holder’s weight can be decreased by 28.1% using topology optimization methods with a negligible impact on structural performance. Burkart et al. [1] point out that their achieved weight reduction of a blank holder by over 20% using topology optimization can reduce dynamic press loads by 40% resulting in an extended process window with shorter cycle times. Besides the established and in industrial finite element software implemented continuum topology optimization methods based on Solid Isotropic Material with Penalization Method (SIMP) [10], also algorithm-driven optimization based on mathematical programming [5] can be used for early-stage design optimization of truss-like lattice structures. Reintjes and Lorenz [7] show a large-scale truss topology optimization of additively manufactured lattice structures based on the high performance of commercial (mixed-integer) linear programming software like CPLEX.

Considering lightweight construction and topology optimization, this paper presents a new algorithm-driven optimization workflow for additively manufactured forming tools, mainly consisting of mathematical programming, numerical topology optimization, and verification via numerical simulation. We distinguish strictly between the rigid-body equilibrium of forces calculated via a mixed-integer linear program and a verification of the results via a linear-elastic and a non-linear-elastic numerical analysis. Based on the algorithm-driven optimization workflow we optimize a demonstrator tool of a segmented blank holder. Finally, we give an outlook on how an optimized lattice structure can be used as a mechanism for in-process modification of local surface geometry and local structural stiffness.

Fig. 1.
figure 1

Flexibility levels of forming tools (left) and demonstrator of a segmented blank holder (right)

Full size image

2 Mathematical Optimization and the Application to a Segmented Blank Holder

Within the Centre of Smart Production Design Siegen (SMAPS), we investigate sensoric and actuatoric forming tools with the aim of self-adjustable surfaces. Targeting the adaption of contact pressure distribution, dynamic compensation of part springback, and change of geometry for part variant diversity, different scales of surface adjustment are needed, as illustrated in Fig. 1 left [4]. As a vision, future forming tools will have the self-adjusting capability to control material flow and react to changing process conditions. To this end, a deep understanding of the forming process itself, sensor and actuator integration, as well as a force transmitting tool structure that is able to change surface geometry and stiffness locally, is necessary. A simple demonstrator for such a flexible tool is shown in Fig. 1 right. The segmented blank holder consists of a housing with thread holes at the bottom (3), a cover (1), and a segmented inlay structure for force transmission (2). The surface adjustment can be realized by the infeed of one screw per segment. Tests were carried out with different arrangements and infeeds of the screws. The basic proof of concept was done by measurement of the surface deformation using Gom ARAMIS, which showed different surface profiles dependent on the screw setup [4]. We examine how such a force transmitting inlay can be generated using truss-like lattice structures generated by algorithm-driven design optimization. First, a linear static finite element simulation using Altair Optistruct was performed to obtain the load case for mathematical optimization. We assume that the insert is loaded by a screw force of \(F_{screw} = 4.5\ \text {kN}\) and a contact pressure between workpiece and inlay, resulting in the process force \(F_{process} = 13.5\ \text {kN}\), see Fig. 2. The reaction load is the contact pressure \(p_{cover}\) between the cover and the inlay. After a transformation of the stress given in the Finite Element Analysis (FEA) into linear constraints (point loads), we get a formulation suitable for a Mixed-Integer Linear Program (MILP) inclusive of physical uncertainty in the parameters of the optimization model.

Fig. 2.
figure 2

Load case for the FEA (left) and point loads for the MILP (right)

Full size image

3 CAD-Based Mathematical Optimization

The design process of complex truss-like lattice structures in Computer-Aided Design (CAD) is inefficient and limits the number of parts (members) to be automatically built in a CAD model [8, 9]. For the reasons stated, transforming large-scale mathematical optimization results into a CAD model is not a straightforward task. Our first research concerning this problem found that using an Autodesk Inventor Professional Add-In, we were able to generate 6084 round structural elements (volume bodies) in 20 h and 24 min [6, 7]. To further improve computational efficiency, in order to be able to define a part as a structural element rather than only as a volume body and allow an easy geometry preparation for numerical analysis, we developed a direct CAD creation (Ansys SpaceClaim 2020 R2) in addition to a history-based CAD creation (Autodesk Inventor Professional). Our Ansys SpaceClaim Add-In construcTOR, see Fig. 3, allows CAD engineers to generate algorithm-driven design iteration studies within the Ansys Workbench. The Add-In involves a Graphical User-Interface (GUI) and bidirectional linkage to CPLEX 12.6.1, see Fig. 3, such that no profound knowledge about mathematical optimization is needed. To avoid local stress peaks at the intersection of members during numerical analysis, we post-process the intersection of members. For this purpose, a solid sphere (near-side body only) merging into the members with a diameter at least equal to the diameter of the member with the largest cross-section is added. The large number of parts given in Table 1 details that we were able to lift the limitation dictated by history-based modeling, see [7]. Besides, a significant reduction in computational time and memory usage depending on the type of implementation, geometrical complexity of the member’s cross-section and instance size exist. We compared the execution time and memory usage divided into the generation of the members and the faceting of Ansys SpaceClaim 2020 R2. In both cases, we used the beam class of the SpaceClaim API V19 and our own implementation as volume bodies.

Fig. 3.
figure 3

CAD-integrated mathematical optimization of lattice structures using the construcTOR GUI

Full size image
Table 1. Benchmark of different implementation types\(^\mathrm{{a}}\)
Full size table
Table 2. Variables
Full size table
Table 3. Sets and Parameters
Full size table

Mixed-Integer Linear Program for Truss Optimization

In order to formally represent the ground structure (see Fig. 2) an undirected graph \(G=(V,\,E)\) is used with vertices (frictionless joints) and connecting edges (straight and prismatic members). Additionally, a set of bearings \(B\subset V\) must be specified. Note that the vertices are fixed in space, as angles between two possible members and distances between joints matter in our modeling approach. We additionally require that the resulting structure is symmetrical with respect to two symmetry planes, see Fig. 2. We use the function \(R:E \rightarrow E\), mapping edge e to its representative R(e) in order to enforce that the members at edges e and R(e) share the same cross-sectional area with respect to the given symmetry. Due to manufacturing restrictions a member must have a minimum cross-sectional area. Therefore, we use a binary variable \(x_e\) to indicate the existence of a member at edge \(e\in E\) with a specified minimum cross-sectional area and a continuous variable \(a_e\) to specify its additional (optional) cross-sectional area. The continuous variable \(n_e\) represents the normal force in a member at edge e and \(r_b\) specifies the bearing reaction force of bearing b. The variables and parameters used in our model are given in Tables 2 and 3, respectively. We use bold letters when referring to vectors. With respect to the considered application, the external forces \(\mathbf {F}\) are taken from numerical simulations of the blank holder (\(F_{process}\) and \(p_{cover}\)) and the bearing reaction forces r are corresponding to \(F_{screw}\).

$$\begin{aligned} \min&\sum _{e \in E}L_e\left( A_{\min } \cdot x_{R(e)} + a_{R(e)} \right) \end{aligned}$$
(1)
$$\begin{aligned} \text {s.t.}&\, S\vert n_e \vert \le \sigma _y \left( A_{\min } \cdot x_{R(e)} + a_{R(e)}\right)&\forall \, e \in E \end{aligned}$$
(2)
$$\begin{aligned}&\sum _{e \in I(b)} n_{e}^d +F_{b}^d +r_{b}^d =0&\forall \, b \in B ,\, d\in \{x,y,z\}\end{aligned}$$
(3)
$$\begin{aligned}&\sum _{e \in I(v)} n_{e}^d + F_{v}^d =0&\forall \, v \in V\setminus B ,\, d\in \{x,y,z\}\end{aligned}$$
(4)
$$\begin{aligned}&a_{R(e)} \le (A_{\max } - A_{\min })x_{R(e)}&\forall \, e \in E \end{aligned}$$
(5)
$$\begin{aligned}&\sum _{v \in V} \mathbf {V}(b,v) \times \mathbf {F}_{v} + \sum _{b' \in B} \mathbf {V}(b,b')\times \mathbf {r}_{b'}=\mathbf {0}&\forall \, b \in B \end{aligned}$$
(6)
$$\begin{aligned}&\sum _{v \in V} \mathbf {F}_{v} + \sum _{b \in B}\mathbf {r}_b=\mathbf {0}&\end{aligned}$$
(7)
$$\begin{aligned}&\mathbf {x} \in \{0,1\}^E,\ \mathbf {a} \in \mathbb {Q}_+^E,\ \mathbf {r} \in \mathbb {Q}^{B\times 3},\ \mathbf {n} \in \mathbb {Q}^E&\end{aligned}$$
(8)

The Objective Function (1) aims at minimizing the volume of the resulting stable and symmetric complex space truss considering the external static load case. Constraint (2) ensures that the local longitudinal stress in a member must not exceed the member’s yield strength taking into account a factor of safety. Constraints (3) and (4) ensure the static equilibrium at each vertex of the structure. The decomposition of \(n_e\) into its components \(n_e^d\) with respect to each direction in space \(d \in \{x,y,z\}\) is attained by standard vector decomposition, exploiting the invariant spatial and angular relationships due to the invariant ground structure. Variables indicating an additional cross-sectional area are bound to be zero by Constraint (5) if no member is present. Constraints (6) and (7) define the equilibrium of moments by resolution of the external forces and ensure, in combination with Constraints (3) and (4), that the resulting structure is always a static system of purely axially loaded members. In particular, the cross product \(\mathbf {V}(b,v) \times \mathbf {F}_{v}\) is the moment caused by the external force \(\mathbf {F}_{v}\) on bearing b with lever arm \(\mathbf {V}(b,v)\). Analogously, \(\mathbf {V}(b,b')\times \mathbf {r}_{b'}\) is the moment about bearing b caused by the bearing reaction force at \(b'\). For the case of the segmented blank holder, see Fig. 2, solutions for \(A_{min} = \{0.79,3.14,7.07\}\ \text {mm}^{2}\) are shown in Fig. 4. Table 4 displays the computational resultsFootnote 1. For our experiments we consider a basic vertex distance of 10 mm and the material aluminum with yield strength \(\sigma _y=0.19 \ \text {GPa}\).

Fig. 4.
figure 4

\(A_{min}\) = (left) \(0.79\,\text {mm}^{2}\), (middle) \(3.14\,\text {mm}^{2}\), (right) \(7.07\,\text {mm}^{2}\)

Full size image
Table 4. Computational results
Full size table
Fig. 5.
figure 5

Comparison of the FEA of three lattice structures generated by MILP

Full size image

4 Finite Element Analysis and Shape Optimization

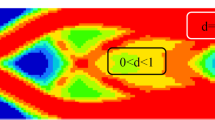
To validate the mathematical optimization results, linear static FEAs are performed using Altair OptiStruct. The load case is analogous to the load case shown in Fig. 4. The geometries showed in Fig. 4 are discretized with solid elements of type CTETRA with a nominal element edge length of 0.5 mm. Note that through this volumetric mesh each node of the lattice structure can transmit rotary moments, which is contrary to the assumptions of the MILP model. Another difference between both models is the material behavior: While the MILP model cannot consider constitutive material equations without costly linearization, a linear-elastic material (MATL1) is implemented in the FEA model with an elastic modulus of aluminum of \(E = 70\ \text {GPa}\). The results of the FEAs are shown in Fig. 5, whereby for simplicity reasons, we take advantage of the double symmetry and visualize just a quarter of the model. We see that the stresses in all three models are, in general, below the yield strength of \(\sigma _y = 0.19\ \text {GPa}\). From this we conclude that the design suggestion by mathematical optimization is a solution with good mechanical performance and geometrical properties for this load case. Nevertheless, it turns out that some higher stressed positions exist. To overcome this problem, we suggest adding an FEA based free-shape optimization to the algorithm-driven design process. To this end, high stressed areas are identified whose shape OptiStruct is allowed to change, as exemplary shown in Fig. 6 for one lattice node. In the initial state (Fig. 6 left) there are maximum von Mises stresses of about 0.5 GPa. The objective of the optimization is to move the grid points of the finite element mesh, which are defined in the design region, in normal direction of this surface until the upper bound stress constraint of 0.19 GPa is satisfied. After 3 iterations (Fig. 6 middle) the surface is slightly shaped and after 15 iterations (Fig. 6 right) we see the final geometry of the lattice node, where the upper bound stress constraint of 0.19 GPa is satisfied. Consequently, the mechanical strength of the structure is given after this optimization.

Fig. 6.
figure 6

Shape optimization: (left) v. Mises stress in the initial state, (middle) geometry of the node after 5 iterations, (right) geometry after 15 iterations

Full size image
Fig. 7.
figure 7

Forming tool with in-process adjustable active fool surfaces

Full size image

5 Conclusion and Outlook

We investigated an algorithm-driven optimization workflow for designing additively manufactured lightweight forming tools using the example of a flexible blank holder. To this end, an interactive CAD-tool was used for pre- and postprocessing the solution of a MILP optimization for truss-like lattice structures. As a minimum cross-sectional area is essential due to design restrictions in AM and symmetry can be exploited to effectively optimize structural systems, we introduced a MILP model considering continuous cross-sectional areas of the lattice members and two planes of symmetry. Finally, finite element based simulations and shape optimizations were performed to validate and improve the design suggestions supported by the preceding CAD-based mathematical optimization. Our research has highlighted that CAD-based mathematical optimization is an efficient and reliable tool for preliminary designing truss-like lattice structures for forming tools. Using finite element shape optimizations, highly stressed areas can be geometrically modified, resulting in an overall usable design. However, there is still a need for discussion that the degrees of freedom of a lattice node in the FEA differ from the degrees of freedom in the MILP model. We claim that a node in the MILP model cannot transmit rotary moments. On the contrary, due to the postprocessing of the MILP optimization solutions to merged volumes and the consequently volumetric meshing, a lattice node in the FEA can transmit rotary moments. This fact is one reason for the stress peaks in the FEA. Another reason for the stress peaks is that no constitutive material equations and no geometry are implemented in the MILP model. Therefore, it cannot take local stresses into account, which, however, underlines the importance of our workflow. Further work needs to be done to establish a component library, including joints for our Ansys SpaceClaim Add-In construcTOR. As shown in Fig. 7, we are currently investigating forming tools with in-process adjustable active tool surfaces to control material flow. Based on analysis of the interaction between local tool surface properties and the forming result, we will define process-time dependent, necessary displacement, and stiffness at the links between force transmitting lattice structure and tool surface. A new method based on our workflow will be investigated to fulfill these requirements. We will build mechanical mechanisms for adjustable surfaces and structural stiffness through technical joints instead of a solid volume at a lattice node or variable-length lattice members.