Bridging mixed integer linear programming for truss topology optimization and additive manufacturing

Abstract

One crucial advantage of additive manufacturing regarding the optimization of lattice structures is that there is a reduction in manufacturing constraints compared to classical manufacturing methods. To make full use of these advantages and to exploit the resulting potential, it is necessary that lattice structures are designed using optimization. Against this backdrop, two mixed integer programs are developed in order to use the methods of mathematical optimization in the context of topology optimization on the basis of a fitted ground structure method. In addition, an algorithm driven product design process is presented to systematically combine the areas of mathematical optimization, computer aided design, finite element analysis and additive manufacturing. Our developed computer aided design tool serves as an interface between state-of-the-art mathematical solvers and computer aided design software and is used for the generation of design data based on optimization results. The first mixed integer program focuses on powder-based additive manufacturing, including a preprocessing that allows a multi-material topology optimization. The second mixed integer program generates support-free lattice structures for additive manufacturing processes usually depending on support structures, by considering geometry-based design rules for inclined and support-free cylinders and assumptions for location and orientation of parts within a build volume. The problem to strengthen a lattice structure by local thickening or beam addition or both, with the objective function to minimize costs, is modeled. In doing so, post-processing is excluded. An optimization of a static area load with a practice-oriented number of connection nodes and beams was manufactured using the powder-based additive manufacturing system EOS INT P760.

1 Introduction

Additive Manufacturing (AM), originally referred to as rapid prototyping and commonly known as three-dimensional printing, is an additive process for rapid form manufacturing, where the final object is created by adding material in layers; each layer is a thin cross section of the part derived from the original 3D-Computer Aided Design (CAD) data (Burns 1993; Gibson et al. 2014). This differs from conventional processes such as subtractive processes (i.e., milling or drilling), formative processes (i.e., casting or forging) and joining processes (i.e., welding or fastening), see Conner et al. (2014).

One crucial advantage of AM, in relation to optimization for lightweight construction, is that there is a reduction in manufacturing constraints compared to classical manufacturing methods (Gibson et al. 2014). As stated by Jared et al. (2017), AM offers unprecedented opportunities to design complex structures optimized for performance envelops inaccessible under conventional manufacturing constraints, so that a realization of engineered materials with microstructures and properties, that are impossible via traditional synthesis techniques, becomes possible.

Enthused by these capabilities, optimization design tools have experienced a recent revival (Jared et al. 2017). Optimization and AM are considered as ideal couples and optimization techniques can play a vital role in the future development of the AM technology, if proper and efficient algorithms are developed (Gebisa and Lemu 2017). We focus on the optimization of lattice structures, as they offer some advantageous properties from a design perspective, such as lower weight, better performance and stability due to the large network of structural beams, good energy absorption and high thermal and acoustic insulation compared to its solid counterpart (Gibson and Ashby 1997; Liu et al. 2018).

To make full use of the advantages of AM and to exploit the resulting potential, the parts have to be designed previously using new optimization methods, see Gibson et al. (2014). In accordance with Jared et al. (2017), geometric complexity becomes truly free, or at least significantly cheaper, if capability gaps and challenges in materials, processes and optimization tools are addressed. For this reason, the advantage in complexity and the complete manufacturing freedom of AM, described in Conner et al. (2014), are used by our algorithm driven product design process, see Sect. 2.

Topology Optimization (TO) is an optimization method that employs mathematical tools to optimize the material distribution in a part to be designed (Gebisa and Lemu 2017). Since most TO results require post-processing, there are practical limitations for combining AM and TO techniques. Multiple agreements between the design and manufacturing experts are necessary, so that multiple optimal solutions, depending on the prioritization of manufacturability or design or both, occur. Accordingly, the final design often deviates from the global optimum in terms of mass and stiffness (López and Stroobants 2019).

Research in the field of Design for Additive Manufacturing (DfAM) (Thompson et al. 2016) has been primary focused on parts design, taking advantage of the design freedom of AM, driven by a better industrial adoption. Despite this development, AM is able to manufacture fully functional parts depending on little or no assembly operations. For this reason, we focus on a DfAM methodology depending on part design and manufacturability. Considering manufacturability, design freedom and post-processing, we introduce two Mixed-Integer Linear Program (MILP) optimizations to support the design and manufacturing experts with a global optimum.

From a design perspective, the global optimum is equivalent to using the complete manufacturing freedom of AM. From a manufacturing perspective, any feasible solution is manufacturable and implies a known or no post-processing effort. The interaction between the design and manufacturing experts is minimized, which implies time and cost-savings and a paradigm shift from production-ready (manufacturable) design to function-oriented design, which is a characteristic of AM (Hague et al. 2003; Langelaar 2016). In contrast to heuristics, mathematical optimization provides a duality gap. We offer this duality gap to design and manufacturing experts as a standard to evaluate heuristic optimization methods concerning the global optimum, despite the possibility of a high computing effort.

According to Tejani et al. (2018), Truss Topology Design (TTD) is a design problem posed to find an initial truss layout while, in the later design stages, shape, and sizing optimizations are carried out. Thus, the sub-areas of TTD are size optimization, shape optimization and TO (Tejani et al. 2018). With regard to TTD, various optimization types appear to offer value for AM respectively. There have been various methods for TTD (Achtziger et al. 1992; Bendsøe et al. 1994; Ben-Tal and Nemirovski 1997; Ohsaki and Katoh 2005; Achtziger and Stolpe 2007, 2008, 2009). Modeling trusses, in general, leads to non-convex non-linear problems. Mars (2013) presents three different ways to deal with non-convex non-linear TTD problems. One way is to replace the non-convex constraint by a big-M formulation with binary variables so that non-convexity still exists but is changed to binary variables. After a transformation of the non-linear parts of the TTD problem into linear constraints we get a MILP. Another way is a reformulation as a convex problem, which results in a semidefinite problem. The third way considered by Mars (2013) is a reformulation of the problem using dual variables and a version of the Farkas-Lemma (Jagannathan and Schaible 1983). This yields a quadratic problem.

Nemirovski (2001) formulates a truss as a Quadratic Program (QP) and transforms it into a Second-order Cone Program (SOCP). Stolpe and Svanberg (2003) deal with TO of discretized continuum structures. It is shown that a large class of non-linear 0–1 TO problems, including stress- and displacement-constrained minimum weight problems, can equivalently be modeled as linear mixed 0–1 problems. Furthermore it is shown that non-linear mixed 0–1 TO problems can equivalently be cast as either linear or convex quadratic mixed 0–1 problems (Stolpe 2007). Gally et al. (2018) provide a Mixed-Integer Semidefinite Program (MISDP) for a optimal placement of active beams for buckling control in truss structures under beam failures. Also a robust TTD with beams via a Mixed-Integer Nonlinear Semidefinite Program (MINSDP) is stated (Gally et al. 2015).

Beside the problem of optimum TTD considering an equilibrium of forces and stress constraints based on the ground structure method (Achtziger 1996), a MILP, a QP and a Semidefinite Program (SDP) have their advantages (Gally et al. 2015). These programs can be partly extended for discrete beam thicknesses, vibrations, active elements, multiple load cases, time-invariant systems and an uncertainty set implemented by an ellipsoid containing nominal loads (Gally et al. 2015; Kuttich 2018). The control of uncertainties in load-bearing lattice structures, with the use of mathematical programs and the optimal combination of passive and active structural elements within lattice structures, appear to be of particular importance for mechanical engineering (Kuttich 2018).

The basic combinational nature of TO, i.e., finding the optimal set of beams for a lattice structure, which remains in structural optimization problems, has been proved to be NP-hard (Wang et al. 2013). Heuristic approaches, such as genetic algorithms, have been applied for structural optimization problems with stress and buckling constraints (Rajeev and Krishnamoorthy 1997). However, these fairly general approaches are restricted to small-scale problems and are not suitable for AM (Wang et al. 2013). Besides, according to Mars (2013), solving large SDPs with many binary variables is quite computationally expensive, so it is obvious to try a reformulation of the semidefinite TTD for AM problem as a MILP and solve it with the help of established standard solvers like CPLEX (CPLEX 2019). Exact and efficient algorithms with problem-specific adaptions can be implemented to determine the global optimum. Additional binary variables dependent on the AM process and its standards can be used to implement further geometry-based construction and design constraints.

We will use the so-called static Timoshenko beam theory for constant cross sections (Eugster 2015), which allows us to formulate a MILP. The assumptions regarding the Timoshenko beam theory, see Sect. 3.2, make it possible to solve large instances and overcome the creative human process of engineering complex lightweight lattice structures, which leads to practical relevance for AM. Our approach provides design and manufacturing experts with a global optimum, time savings and a holistically DfAM methodology.

Since the validation and verification method of our desired workflow, as typically demanded in Technical Operations Research, see Sect. 6, is based on an Finite Element Analysis (FEA), we distinguish strictly between rigid-body equilibrium of forces calculated via a MILP and a verification of the results via a linear-elastic and a non-linear-elastic numerical analysis of our parts. On the one hand, by adopting a rigid-body equilibrium instead of the non-linear theory of elasticity, the MILP can solve large instances and exploit its advantages. On the other hand, simplification is not a disadvantage, since FEA is in any case necessary as part of the failure analysis in the product development process and provides a linear-elastic and non-linear-elastic numerical analysis. Synergy effects between both areas are generated.

In this paper, for powder-based AM and extrusion-based AM, two MILPs adapted to standards (ISO 2013; VDI 2015; ISO 2017; VDI 2019) are introduced, see Sects. 4.5 and 4.6. The two MILPs TTD$_{\mathrm{{l;p}}}$ (linear;powder-based AM) and TTD$_{\mathrm{{l;s}}}$ (linear;support needed) are developed in order to define a statically determined lattice structure, which is minimal in terms of costs, volume and material consumption under the influence of external forces, based on a fitted ground structure method. The MILP TTD$_{\mathrm{{l;p}}}$ defines a lattice structure for powder-based AM processes regardless of support structures and the MILP TTD$_{\mathrm{{l;s}}}$ defines a lattice structure for AM processes depending on support structures. The MILP TTD$_{\mathrm{{l;s}}}$ considers geometry-based design rules for inclined and support-free cylinders/beams manufactured with AM processes depending on support structures (VDI 2019) and assumptions for location and orientation of parts within a build volume (ISO 2013). Furthermore, the stress and buckling constraints are simplified in both TTD models. The MILP TTD$_{\mathrm{{l;s}}}$ aims at realizing support-free lattice structures. Both MILPs use preprocessed beam diameters and materials, so that multi-material lattice structures are possible.

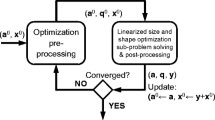
In addition, an optimization-oriented design workflow, see Fig. 12, is developed in order to exploit the advantages of optimization for AM fully. The optimization-oriented design workflow addresses four [(1)–(4)] interdisciplinary sub-areas; Operations Research (1), AM (2) as the manufacturing method and a link between this sub-areas in the form of a 3D-CAD (3) tool and a validation via an FEA (4).

In Reintjes et al. (2018), a method to minimize lateral deflection (buckling) for TTD for AM is presented. The critical load of a beam in a lattice structure, based on Euler’s critical load model (Timoshenko et al. 1962), is implemented by a MILP including geometry-based design constraints. It is shown that in addition to the static design of lattice structures using a MILP, simultaneous geometry-based optimizations are possible concerning geometry-based design constraints. Reintjes et al. (2019) present large three-dimensional lattice structures, characterized by an appropriate assembly space and level of granularity, whereby non-linear material behavior is neglected. The target function is to reduce costs and material. The design is made up of cellular structures resulting from a static load case. A control of the density of the truss is possible through penalty parameters implemented in the MILP constraints. Reintjes and Lorenz (2019) provide a MILP for TTD for AM and a related design tool for additively manufactured multi-material lattice structures. An optimization-oriented construction workflow is presented in order to exploit the advantages of TTD for AM fully. A bottom-up construction methodology and a 3D-CAD tool to realize a MILP to 3D-CAD workflow is described. A part manufactured with Selective Laser Sintering (SLS) and a numerical validation are presented. The results presented in this article are based on our preliminary work mentioned above.

This paper is organized as follows. Section 2 presents our construction characteristics, as a construction methodology for large-scale design optimization of additively manufactured multi-material lattice structures. Section 3 recasts the basic problem statements in TTD for AM and associated kinematic indeterminacy. Furthermore, a design space and a design problem is formulated. Section 4 is divided into six subsections. Section 4.1 presents preliminary work for our MILP models. Besides Sect. 4.2 illustrates how, due to the implementation of geometry-based design rules, the problem naturally becomes a MILP, which is suspected to be NP-hard. Section 4.3 explains preprocessing. Necessary decision variables, parameters and sets are defined in Sect. 4.4. Building on the previous three sections, a MILP specifying lattice structures for powder-based AM processes (TTD$_{\mathrm{{l;p}}}$) and a MILP defining support-free lattice structures for AM processes (TTD$_{\mathrm{{l;s}}}$) are presented in Sects. 4.5 and 4.6. Following Sect. 5 describes the 3D-CAD tool. Section 6 presents our optimization-oriented design workflow to use our MILPs to produce additively manufactured lattice structures. Section 7 presents numerical results and additively manufactured lattice structures. We conclude in Sect. 8.

The paper is divided into two parts: Sects. 2 and 3 provide a comprehensive overview of TTD, whereas Sects. 4–7 describe our algorithm driven product design process. The two parts may be considered separately.

2 Our construction methodology for AM

To systematically explore the area of mathematical optimization (modeling), CAD (construction), FEA (validation) and the area of AM processes (realization), we adapt the methodology of (Altherr et al. 2016). Figure 1 describes the development of an efficient additively manufactured lattice structure. The methodology is divided into two phases: the decision phase (1–4) and the action phase (5–7).

In the first step (1), customer and designer have to agree on a technical specification, which is a fair balance of loading case, costs and manufacturability, inspired by Pelz et al. (2012). The loading case is determined by the practical use of the planned part and the associated part strength and thus taken to be immutable. The manufacturability depends on the chosen AM process (4) and its standards.

The objective function (2) minimizes the material, volume and costs. An upper bound for the costs is determined by the selected Ground Structure (GS) (3), the chosen AM process, standards and AM constraints (4). Furthermore, preprocessed beam types with different beam cross sections and costs, which are proportional to the volume and the material consumed, affect the upper bound. In the next step, a MILP is used as the artificial topology designer tool (5) to determine the optimal topology/global optimum. The optimization results are implemented in a 3D-CAD tool and afterward numerically analyzed via an FEA (6). The AM process set in step (4) is used for realization (7).

The manufacturability and mechanical compliance with standards are ensured since in step (4) all manufacturing restrictions are implemented as constraints in the MILP. In order to increase the manufacturing accuracy of the chosen AM process, at the expanse of costs, standard design rules for part production aiming at a high manufacturing accuracy (VDI 2015) can be included in the artificial topology designer tool (5). These standard design rules will limit the solution space and thus counteract the “complexity for free” phenomenon of AM, see Conner et al. (2014). In AM, complexity is said to be free, as the product is made layer-by-layer so that costs and manufacturing time is independent of the part complexity (Atzeni and Salmi 2012). To take full advantage of the phenomenon “complexity for free”, standards should be used in a targeted manner, as we aim to overcome the creative human process of design and construction, with the help of a mathematically and algorithmically driven product design process, inspired by Pelz et al. (2012).

Fig. 1

The TOR pyramid—a step by step guide towards an algorithm driven product design process, based on Pelz et al. (2012)

3 Main concepts of truss topology design for AM

Section 3 is divided into five subsections. Sect. 3.1 defines the basic problem statements in TTD and associated kinematic indeterminacy. Preparations towards a lattice structure design problem as MILP are introduced in Sect. 3.2. The assumptions of our MILPs TTD$_{\mathrm{{l;p}}}$ and TTD$_{\mathrm{{l;s}}}$ regarding the displacements, the equilibrium of forces and the moment equilibrium are introduced. A concept of design space constraints for an AM system is proposed in Sect. 3.3. Our assumptions regarding the assembly space of an AM system and our ground structure method adapted for AM are introduced. In Sect. 3.4, our algorithm driven optimization for a support-free part is compared with other methods in this field of research. Section 3.5 extends the established FEA driven product design process by a preliminary design determined by our algorithm driven product design process.

3.1 Basic problem statements in truss topology design for AM and the associated kinematic indeterminacy

Since the beginning of the 20th century there have been various studies on TTD. Since then, TTD has been a growing field of research, combining different areas of engineering with mathematics. In addition to classical applications such as the optimality of Michell structures (Michell 1904), which are used in civil engineering for the design and volume optimization of space structures, there have recently been remarkable efforts to combine TTD and AM. The following is a brief overview of the models that support the combination of TTD and AM, considering that we want to formulate MILPs.

3.1.1 Basic problem statements

The following models have been obtained from Bendsøe (2009), whereat mechanisms and rigid body motions are excluded. Let E and V denote the set of edges (possible beams) and the set of vertices (possible connection nodes) of a truss, respectively. We will denote that a truss $T = \{b_1,\ldots ,b_{m}\}$ is a set of beams with $T \subseteq E$, i.e., T indicates at which edges in E a beam is placed. Let $A_{b},L_{b}$ denote the cross-sectional area and length of a beam b, respectively. It is assumed that all beams are made of linear elastic materials,¹

with Young’s modulus $E_{b}$ (Dym and Shames 1973) defining the relationship between stress (force per unit area) and strain (proportional deformation) in a material in the linear elasticity regime of a uniaxial deformation. The volume of a truss T is

$$\begin{aligned} V_T=\sum _{b \in T} \nu _{b} , \end{aligned}$$

(1)

with the beam volumes $\nu _{b}=A_{b} L_{b,b} \in \{b_1,\ldots , b_{m}\}$. As usual, the static equilibrium is expressed as

$$\begin{aligned} \pmb {B} \pmb {q}= \pmb {p} , \end{aligned}$$

(2)

where $\pmb {q}$ is the member force vector, $\pmb {p}$ is the nodal force vector of the free degrees of freedom and $\pmb {B}$ the compatibility matrix, which relate element displacements to system displacements (De Borst et al. 2012).

The basic problem statement in terms of member forces (single load truss problem) is formulated as a stress based minimum mechanical compliance problem (TTD$_{\mathrm{{c}}}$, see Table 1) using the minimum complementary energy principle (Bendsøe 2009). Problem TTD$_{\mathrm{{c}}}$ is simultaneous convex in member forces and member volumes.

The traditional formulation of TTD in terms of member forces (TTD$_{\mathrm{{p;a}}}$, see Table 1) is valid for single load, plastic design (Rozvany 1984; Topping 1993; Bendsøe and Kikuchi 1993). This single load, plastic design problem is typically stated as a minimum weight design problem, for all trusses that satisfy a static equilibrium within certain constraints on stresses in the individual beams. With the same stress constraint value $Q_{b}$ for both tension and compression, the formulation is in the form of an Linear Program (LP). Cheng and Jiang (1992) and Kirsch (1993) outline that the stress constraints are written in terms of member forces in order to give a consistent formulation. They further state, that for some truss problems, the stress in several members will converge to a finite non-zero level as the member areas converge to zero, but the member forces will converge to zero. This fact should be observed for any truss design problem involving stress constraints (Cheng and Jiang 1992; Kirsch 1993).

Just as in Bendsøe (2009), let $q_{b}^+,q_{b}^-,\sigma _{b}$ donate the member forces tension, member forces compression and stress constraint value $\sigma _{b}$ for both tension and compression, respectively, so that designs for which all beams with non-zero beam area have stresses at the maximum allowed level $Q_{b}$ (fully stressed designs) occur. Furthermore

$$\begin{aligned} t_{b}=\frac{L_{b}}{Q_{b}}(q_{b}^++q_{b}^-),\text {with}\ \pmb {q}=(\pmb {q^+}-\pmb {q^-}),\quad \pmb {q^+}, \pmb {q^-} \ge 0 \end{aligned}$$

(3)

applies, so that one can write the problem TTD$_{\mathrm{{p;a}}}$ also as an LP, see problem TTD$_{\mathrm{{p;b}}}$. The equivalence of the problems TTD$_{\mathrm{{p;a}}}$ and TTD$_{\mathrm{{p;b}}}$ is described in Dorn (1964), with a discussion on how the force formulations are convenient for studying static determinacy of solutions. The objective function of the problem TTD$_{\mathrm{{p;b}}}$ is the weight of the truss structure. As reported by Kirsch and Rozvany (1993), a basic solution to the problem TTD$_{\mathrm{{p;b}}}$ encompasses the existence of a minimum mass truss topology with an amount of beams not exceeding the degrees of freedom. If there exists such a basic solution with only non-zero forces (areas), this is a statically determined truss; otherwise, the truss will have a unique force field for the given load and will be kinematically indeterminate (Bendsøe 2009). Problem TTD$_{\mathrm{{p;a}}}$ can be extended to a multiple load LP (TTD$_{\mathrm{{p;c}}}$, see Table 1) using a set of $k =\{1, \ldots , s\}$ different load cases where the self-weight loads are considered. Thus, the sum

$$\begin{aligned} \sum _{b \in T}{t_{b}\pmb {g_{b}}}, \end{aligned}$$

(4)

with $\pmb {g_{b}}$ denoting the specific nodal gravitational force vector due to self-weight and external loads must be considered, see Eqs. (7b) and (8b).

3.1.2 Kinematic compatibility

The validation and verification method of our artificial topology design process is an FEA and therefore we are able to distinguish strictly between rigid-body equilibrium of forces calculated via a MILP and a verification of the results via a linear-elastic and a non-linear-elastic numerical analysis (FEA) of our parts.

For this reason, in accordance with Bendsøe (2009), it is helpful that the problems TTD$_{\mathrm{{p;a}}}$, TTD$_{\mathrm{{p;b}}}$ and TTD$_{\mathrm{{p;c}}}$ are at first problems in plastic design, as the kinematic compatibility is ignored and their use in elastic design is justified by the possibility of finding statically determinate solutions. In addition, the listed problems could be solved using sparse, primal-dual interior point LP-methods or the simplex algorithm (Bendsøe 2009). We exploit the advantages of both methods. On the one hand, we will focus on solving efficiently large-scale TTD problems with practical relevance for AM with the help of standard solvers; on the other hand, we will verify our results via a linear-elastic and non-linear-elastic numerical analysis, which is in any case part of an FEA driven product design process (Kurowski 2006).

Kirsch (1989), Kirsch (1993) and Topping (1992) state to be well known, that most commonly statically indeterminate solutions result in the case of a multiple load plastic design (problem TTD$_{\mathrm{{p;c}}}$). If kinematic compatibility is required, a further redesign with an FEA becomes necessary in addition to the in any case required FEA validation for elastic design. This further redesign to satisfy kinematic compatibility for elastic design leads to high effort/costs, leading to problem TTD$_{\mathrm{{p;c}}}$ being non-practical.

The problem TTD$_{\mathrm{{p;b}}}$ is adapted since its solution is statically determinate and an FEA can be used subsequently for validation only instead of redesigning the part. Problem TTD$_{\mathrm{{p;b}}}$ is modified and extended by geometry-based design rules for AM, resulting in the MILPs TTD$_{\mathrm{{l;p}}}$ and TTD$_{\mathrm{{l;s}}}$, see Sects. 4.5 and 4.6.

Table 1 TTD models

3.2 Preparations towards a lattice structure design problem as MILP

The MILPs TTD$_{\mathrm{{l;p}}}$ and TTD$_{\mathrm{{l;s}}}$ use the so-called static Timoshenko beam theory for constant cross sections, see Fig. 3. We assume a beam to be a structure, which has one of its dimensions much larger than the other two dimensions. It follows, that the cross sections of a beam do not deform in a significant manner under the influence of transverse or axial loads, and therefore the beam is assumed to be rigid. Besides, allowing no transverse shearing forces and bending moments, the displacement functions depend on the coordinates along the axis of the beam. The only allowed loads are external line-, and area-loads modeled as concentrated forces acting on nodes. We claim a linear-elastic isotropic material, with the given deformation restrictions causing no transverse stresses to occur.

3.2.1 Beam

We will consider $E_{b}$ and $I_{b}$ as the Young’s modulus and the area moment of inertia of a beam $b = {\{i,j\}}$, respectively. We will denote by $\kappa _{b}$, $L_{b}$, $A_{b}$, $G_{b}$ the Timoshenko shear coefficient, the length, the cross section area and the shear modulus of a beam b, respectively. The Timoshenko beam theory is equivalent to the Euler-Bernoulli beam theory so that the inequality (9) applies. Using the Timoshenko beam theory

$$\begin{aligned}&\frac{E_{b}I_{b}}{\kappa _{b} L_{b}^2A_{b}G_{b}} \ll 1 , \end{aligned}$$

(9)

$$\begin{aligned}&\frac{\partial E_{b}}{\partial \psi _{b}} = \frac{\partial G_{b}}{\partial \psi _{b}} = 0 , \end{aligned}$$

(10)

$$\begin{aligned}&\frac{\partial A_{b}}{\partial \psi _{b}} = \frac{\partial I_{b}}{\partial \psi _{b}} = 0 , \end{aligned}$$

(11)

applies, whereby $\psi _{b}$ is the beam axis of a beam $b = {\{i,j\}}$. The basis for equation (10) is formulated based on Hooke’s law (Rychlewski 1984), which states a linear dependency between stress and strain. In reality, the linear part is the elastic part of the material property that can be described by the Young’s modulus $E_{b}$. The shear modulus $G_{b}$ (Roylance 2008) is defined as the ratio of shear stress to shear strain. The area moment of inertia/second area moment $I_{b}$ (Gibson 2016) is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. It is used to determine the deflection and stress caused by a moment applied to a beam. Equation (10) forces a homogeneous material and equation (11) forces a constant cross section, neglecting manufacturing inaccuracies of AM processes.

The Timoshenko shear coefficient $\kappa _{b}$ (Cowper 1966) relates to the Poisson’s ratio $\mu _{b}$ (Lakes 1987), which is the negative of the ratio of signed transverse strain to signed axial strain. Concerning these works, we may assume $\kappa _{b}$ to be constant. The shear coefficient $\kappa _{b}$ is set to

$$\begin{aligned} \kappa _{b} = \frac{6(1+\mu _{b})}{7+6\mu _{b}} = \frac{9}{10} \end{aligned}$$

(12)

for a circular cross section $A_{b}$.

The physical assumptions of the Timoshenko beam theory have to be preprocessed, see inequality (9) and Eqs. (10) to (12), as they cannot be added explicitly to the MILP, which can only contain linear constraints unlike a non-linear programming problem (NLP).² This is possible since inequality (9) and equations (10) to (12) only depend on the dimension and material properties of a beam. Therefore, dimension and material of a beam are input parameters of our MILPs, see Sects. 4.5 and 4.6.

3.2.2 Force equilibrium

Let $\mathbf{u } \in {\mathbb {R}}^d$ and $\mathbf{K }(\mathbf{A },\mathbf{I }) \in {\mathbb {R}}^{d \times d}$ denote the vector of nodal displacements, where d is the number of translatoric degrees of freedom of displacements and the stiffness matrix, respectively. The vectors of the cross-sectional area $A_{b}$ and area moment of inertia $I_{b}$ of a beam $b = {\{i,j\}}$ are written as $\mathbf{A } = (A_{b} \mid b \in E)$ and $\mathbf{I } = (I_{b} \mid b \in E)$. The external load is stated as $\mathbf{f} \in {\mathbb {R}}^d$. The formulation of the equilibrium equation (13), the decomposition into the force-balance equation (14), along with the following conclusions refer to Kureta and Kanno (2014). The equilibrium equation

$$\begin{aligned} \mathbf{K }(\mathbf{A },\mathbf{I })\mathbf{u }=\mathbf{f } \end{aligned}$$

(13)

can be decomposed into the force-balance equation written as

$$\begin{aligned} \sum _{b \in E} \sum _{l=1}^{3} s_{b,l} \mathbf{b }_{b,l} = \mathbf{f } \end{aligned}$$

(14)

and the relations between the generalized stresses and the displacement vector written as

$$\begin{aligned} s_{b,l} = k_{b,l} \mathbf{b }_{b,l}^\top \mathbf{u }, \quad l=1,2,3; \quad \forall b \in E . \end{aligned}$$

(15)

here ${\mathbf{b}}_{b,1}, {\mathbf{b}}_{b,2}, {\mathbf{b}}_{b,3} \in {\mathbb {R}} \ (\forall b \in E)$ are constant vectors with respect to the local coordinate system of a beam $b = {\{i,j\}}$. Constants $k_{b,1}, k_{b,2}, k_{b,3} \in {\mathbb {R}} \ (\forall b \in E)$ are defined by

$$\begin{aligned} k_{b,1}&= \frac{E_{b} A_{b}}{L_{b}^0} , \end{aligned}$$

(16)

$$\begin{aligned} k_{b,2}&= \frac{1}{L_{b}}\left( \frac{L_{b}^2}{12 E_{b} I_{b}} + \frac{1}{\kappa _{e} G_{b} A_{b}}\right) ^{-1} , \end{aligned}$$

(17)

$$\begin{aligned} k_{b,3}&= \frac{E_{b} I_{b}}{L_{b}^0} , \end{aligned}$$

(18)

where $L_{b}^0$ is the undeformed length of a beam $b = {\{i,j\}}$. Note that the coefficients $k_{b,1}, k_{b,2}, k_{b,3} \in {\mathbb {R}}$ are determined by the material selected for a beam, so that we can preprocess inequality (9) along with equations (10) to (12) and (16) to (18). In line with Kureta and Kanno (2014) it is defined that $k_{b,2} = 0$ if $E_{b} = G_{b} = 0$, see equation (17).

By elimination of the displacement vector $s_{b,i}$, equations (14) and (15) revert to equation (13). The decomposition into the force-balance equation (14) is a fundamental concept of our MILPs since we want to specify the equilibrium of forces as a hard constraint and the cost per beam type as a soft constraint, resulting from the preprocessed beam volume and material specification. A hard constraint is selected as a constraint for the variables that are required to be satisfied. By implication a soft constraint is a constraint that is allowed to be violated. The force-balance equation (14) can be used in combination with a binary variable $x_{i,j}$ to indicate whether a beam is present between nodes $i,j \in V$, see (24b) to (24d) and (24g). The binary variable $x_{i,j}$ is used to implement further geometry-based construction and design standards (VDI 2019, 2015; ISO 2013), see Sect. 3.4.

3.2.3 Moment equilibrium

Let $m_{k}$ and $m_{l}$ denote two moments in Newton metre acting centrically at two adjacent nodes, where $k,l \in V$. The lever arms of the moments $m_{k}$ and $m_{l}$ are positioned in relation to the global coordinate system $F_{WP_{x,y,z}}^G$ of the reference volume ${\mathbb {V}}$, as described in Sect. 3.3 and shown in Figs. 2 and 3. Let $T=\{0,1,\ldots ,n\}$ denote a set of different beam types t and $F_{i,j}$ the force vector in Newton between the directly adjacent nodes $i \in V$ and $j \in V$.

As stated in inequality (19), we assume a linear elastic strains plastic behavior, with the plastic section modulus $Z_{b} = \infty$ of a beam $b = {\{i,j\}}$. The stress $c_{t,i,j}$ of a beam b of type t in Pascal is stated as

$$\begin{aligned} \frac{|F_{i,j} |}{{A_{b}}} + \overbrace{\frac{max \{|m_{k} |, |m_{l} |\}}{Z_{b}}}^{\approx 0} \le c_{t,i,j} \, . \end{aligned}$$

(19)

The upper bound of the stress $\overline{c}_{t,i,j}$, affected by the safety factor $\gamma \in ]1,+\infty [$, is given by the equation

$$\begin{aligned} \overline{c}_{t,i,j} = \frac{c_{t,i,j}}{\gamma } \, . \end{aligned}$$

(20)

3.3 Design space

3.3.1 Manufacturing constraints

As can be seen in Fig. 2, a in relation to the front side of the AM system upwardly directed construction is postulated. The build origin (0, 0, 0) is placed on the origin of the machine coordinate system and thus coincides with the origin of the assembly space ${\mathbb {A}}$. The build direction z coincides with the positive y-direction of each coordinate system. The build surface is located on the x, z-plane and corresponds to the spanned plane of the assembly space ${\mathbb {A}}$ on the x, z-plane. It is assumed that the build platform of the AM system is sufficiently dimensioned and the feed region and overflow region allow the planned reference volume ${\mathbb {V}}$. The build platform of the AM system is located in the negative y-direction.

The layer thickness is known as constant, fully dense and near net shape, so that the accuracy is assumed as sufficient. The preprocessing of the upper bound of stress $\overline{c}_{t,i,j}$ is therefore realistic, see cases (21). According to ISO (2013), the right-hand rule for positive rotations, in relation to the origin of the reference volume ${\mathbb {V}}$, is applied. All dimensions between the three bounding boxes are known. The assembly space ${\mathbb {A}}$, also known as master bounding box, is determined by the used AM system and is therefore independent of the part orientation. The initial build orientation is assumed to be as shown in Fig. 2. A part reorientation is permissible so that no restrictions arise at part nesting (Canellidis et al. 2013). The reference volume ${\mathbb {V}}$ can change as a result of a part reorientation, so we assume the reference volume ${\mathbb {V}}$ to be an arbitrary oriented bounding box. Figure 2 illustrates the difference between the reference volume ${\mathbb {V}}$ and the GS ${\mathbb {G}}$, although that in some cases ${\mathbb {G}} \equiv {\mathbb {V}}$ may occur.

Fig. 2

Division of the design space

3.3.2 Assembly space

Since AM is a layered manufacturing process, the build orientation of a part towards the assembly space has a significant impact on the part quality (e.g., accuracy and surface finish) and costs. Also, the support structure depending on the support contact area and the build time are affected. In order to be able to define the direction of our part towards the assembly space, we need to make some assumptions. The terminology is derived from ISO (2017).

Let ${\mathbb {A}}$ be the assembly space of an AM system, represented by a polyhedron as an open subset of ${\mathbb {R}}^3$. Let ${\mathbb {V}} \subset {\mathbb {A}}$ be the reference volume to be replaced by a lattice structure. The classification of the assembly space ${\mathbb {A}}$ enables us to distinguish between internal and external support structures. Any type of support structure within ${\mathbb {V}}$ is defined as an internal support structure. A support structure outside of ${\mathbb {V}}$, but forced to be connected to the load-bearing structure, is defined as an external support structure. Besides, the classification of the assembly space ${\mathbb {A}}$ is done for minimization of ${\mathbb {V}}$, in order to save computing effort and to optimize the utilization of the assembly space ${\mathbb {A}}$. The classification is the formal basis for part decomposition, in detail orientation decisions for single- and multi-parts and packing problems, see Oh et al. (2018).

Fig. 3

Beam $B_{\tilde{t},i,j}$ and related local coordinate systems $F_{WP_{\check{x},\check{y},\check{z}}}$ and $F_{WP_{\hat{x},\hat{y},\hat{z}}}$

3.3.3 Ground structure

Following our aim to develop MILPs, which can be applied to large-scale TTD for AM in consideration of geometry-based design rules, we focus on a GS with low complexity. Therefore, only directly adjacent nodes as possible beam connections are considered. The angles $r_{i,j,x}, r_{i,j,y}, r_{i,j,z}$ between two possible beams in the primary planes of a local coordinate system $F_{WP_{x,y,z}}$ are fixed to $45^\circ$, see Fig. 3 and Table 2. Consequently, the GS in Fig. 4 is not the set of all possible connection nodes. According to Bendsøe (2009), this approach may obviously lead to designs that are not the best ones for the chosen set of connection nodes, but the approach implicitly allows for restrictions on the possible spectrum of beam lengths as well as for the study of the optimal subset of beams of a given truss layout. In consideration of our assumptions, three beam lengths arise, which is the minimum for a three-dimensional lattice structure with diagonal and bracing beams. Different GSs can be set up by adjusting the angles $r_{i,j,x}, r_{i,j,y}, r_{i,j,z}$. Recesses can be created by setting $x_{i,j} = 0$ for the desired volume.

Fig. 4

Illustration of the ground structure method

The GS is rotated around one axis of the global coordinate system $F_{WP_{x,y,z}}^G$, if a force component in any direction in space $Q_{i,x}, Q_{i,y}, Q_{i,z} \in {\mathbb {R}}_+$, resulting from a applied concentrated force $Q_i$ at a node $i\in V$, is introduced. A local coordinate system $F_{WP_{x,y,z}}$ is introduced centrically on that node and the node is considered as a force application point. The local coordinate system $F_{WP_{x,y,z}}$ is a parallel shift with respect to the axes of the global coordinate system $F_{WP_{x,y,z}}^G$ and is used for preprocessing the three force components $F^{\alpha }_{i,j} = F_{i,j} r_{i,j,\alpha }, \ \alpha \in \{x,y,z\}$, see (24b) to (24d). A modeling of the angular relationships between the force components $F^{x}_{i,j}, F^{y}_{i,j}, F^{z}_{i,j}$ and the global coordinate system $F_{WP_{x,y,z}}^G$ is avoided. Any force distribution angle can be preprocessed.

3.4 Support structure optimization

AM is divided into seven groups: vat photopolymerization, material jetting, binder jetting, powder bed fusion, material extrusion, directed energy deposition and sheet lamination (ISO 2017). As we focus on the optimization of lattice structures for AM, a description of the individual AM processes is not given, see Wong and Hernandez (2012) for a brief review of AM.

According to Jiang et al. (2018), the reason for using support structures is to ensure printability in the manufacturing process, since a three-dimensional model with overhanging, hole or edge features will need support structures for successful manufacturing as printed materials will not be able to stand in position through layer-wise fabrication and the associated stair-stepping effect (Quan et al. 2015).

The main support methods for AM processes are honeycomb support, sparse tree support, tree-like support, space-efficient branching support, bridge support and grain support (Jiang et al. 2018). In addition to the physical necessity for support structures, depending on the AM process and the part geometry, the support structures increase material consumption, manufacturing costs and post-processing effort. Post-processing can have a negative impact on the part quality or even prevent manufacturability and should be minimized or excluded.

Using support structures, a toolless and post-processing free manufacturing is not possible. An optimization of the support structures would lead to a reduction in the material consumption during the production process and a significant reduction of the time and effort required during post-processing (Lindecke et al. 2018). The internal and external support structure is defined by the GS ${\mathbb {G}}$. Therefore, the GS needs to be extended by the volume defining the possible external support structure.

Removability has to be considered, especially for an internal support structure. If the internal support structure is irremovable because of no direct access to the support structure, which likely occur for lattice structures manufactured with AM, the support structure has to be considered in the part design and validation as force-bearing. Also, a self-printability requirement is necessary, as the support structure itself should not require a support structure (Jiang et al. 2018). In line with Langelaar (2016), existing TO approaches do not consider AM-specific limitations during the design process, resulting in designs that are not self-supporting.

The main categories of methods minimizing the need for support structures for AM can be divided into two subgroups; either the original part is kept intact or the original part is redesigned, see Fig. 5. We extend the main categories of support structure methods for AM by a global optimization in terms of a support-free part, see Sect. 4.6.

Fig. 5

Main categories of support structure methods for AM, based on Jiang et al. (2018)

Research in the field of support structures for AM has primarily focused on reducing the print time, characterization and optimization of the support materials used and post-processing (Jiang et al. 2018).

Vaidya and Anand (2016) presented a new approach for minimizing support structures in conjunction with Dijkstra’s shortest path algorithm to generate optimized support structures. They subsequently used a numerical model to proof that the optimized support can withstand the planned load case. Vanek et al. (2014) proposed a tree-like support structure generation method for Fused Deposition Modeling (FDM) which can reduce manufacturing time and costs. As in the previous method, a numerical analysis is necessary because the method is geometry-based and considers the angle and length of the support structure. The geometry-based optimization and the numerical verification of the stability are strictly separated.

Our DfAM methodology depends on part design and manufacturability and it does not require a numerical model to proof that the optimized support can withstand the planned load case. Any feasible solution is manufacturable and implies no post-processing effort if support is impermissible. We consider the support structure as a subset of the load-bearing lattice structure and optimize both structures in a single task.

3.5 Algorithm driven product design process

The established application of using the FEA as a design tool, see Fig. 6, is to change the design process from iterative cycles of “design, prototype, test” (traditional product design process) into a streamlined process (FEA driven product design process) where prototypes are used only for final design verification. With the use of FEA, design iterations are moved from physical space of prototyping and testing into virtual space of computer based simulations (Kurowski 2006). The goal is to establish a safe and cost-effective product design process.

We extend this FEA driven product design process by a preliminary design determined by our mathematically and algorithmically driven artificial topology design process, see Fig. 6. Mathematical optimization and FEA (simulation) is used concurrently within the design process, whereby mathematical optimization is used first for topology and shape optimization and FEA only for validation.

Fig. 6

Traditional, FEA and algorithm driven product design process

4 Mixed integer programming for truss topology design

Section 4 is divided into six subsections. Section 4.1 presents preliminary work for our MILP models. Besides Sect. 4.2 illustrates how due to the implementation of geometry-based design rules the problem naturally becomes a MILP which is suspected to be NP-hard. Preprocessing is explained in Sect. 4.3. Necessary decision variables, parameters and sets are defined in Sect. 4.4. Building on the previous three sections, a MILP specifying lattice structures for powder-based AM processes (TTD$_{\mathrm{{l;p}}}$) and a MILP defining support-free lattice structures for AM processes (TTD$_{\mathrm{{l;s}}}$) are presented in Sects. 4.5 and 4.6.

4.1 Preliminaries

The following assumptions refer to the MILPs TTD$_{\mathrm{{l;p}}}$ and TTD$_{\mathrm{{l;s}}}$. Characteristics of AM are tool-less manufacturing, the elimination of geometric restrictions in general and the paradigm shift from production-ready to function-oriented design (Hague et al. 2003; Langelaar 2016). The tool-less production is given a priori by the AM process, whereby we serve the other two characteristics with our MILPs TTD$_{\mathrm{{l;p}}}$ and TTD$_{\mathrm{{l;s}}}$. On the one hand, the function-oriented design is obtained by the objective function of the MILPs; on the other hand, the elimination of geometric restrictions is obtained by variable beam lengths based on the GS, along with the possibility of different beam cross sections and diameters, see Sect. 3.2. The fundamental phenomena of AM “complexity for free” is to be fully exploited by the objective function, to achieve a holistic design approach and overcome conventional manufacturing constraints, see Jared et al. (2017).

Using AM for lattice structures, no standardized shaped parts and connections, as well as associated costs, are necessary. For this reason, assembly costs are not taken into account in the MILPs TTD$_{\mathrm{{l;p}}}$ and TTD$_{\mathrm{{l;s}}}$, as a connection node only consists of an accumulation of cured material. If our MILPs are formulated for a classical construction application, the influence of standard fasteners and time differences during the assembly can be considered by additional constraints.

A formulation of the equilibrium of forces as a soft constraint and cost per beam type as a hard constraint is not practicable for our MILPs. Due to the assumptions of Sect. 3.2 the potential energy stored in all beams, given by the mechanical compliance, would be a soft constraint. We avoid a formulation of the mechanical compliance, since we distinguish strictly between rigid-body equilibrium of forces calculated via a MILP and a verification of the results via linear-elastic and non-linear-elastic numerical analysis of our parts.

We set up the MILPs TTD$_{\mathrm{{l;p}}}$ and TTD$_{\mathrm{{l;s}}}$ in terms of beam forces for single load, plastic design. Both MILPs are stated as a minimum weight design problem, for all trusses that satisfy static equilibrium within certain constraints on the stresses in the individual beams. The same stress constraint value is valid for both, tension and compression.

4.2 LP versus MILP

Clearly, if all binary variables and the corresponding constraints in TTD$_{\mathrm{{l;p}}}$ or TTD$_{\mathrm{{l;s}}}$ are omitted, the result is one of the LPs TTD$_{\mathrm{{c}}}$, TTD$_{\mathrm{{p;a}}}$, TTD$_{\mathrm{{p;b}}}$, TTD$_{\mathrm{{p;c}}}$, of Table 1, see Sects. 4.5 and 4.6. By omitting the binary variable $x_{i,j}$, it is no longer possible to model geometry-based design rules depending on the AM process. Furthermore, it is no longer possible to use preprocessed beam diameters and materials, so that multi-material lattice structures could be realized.

To implement geometry-based design rules the problem naturally becomes a MILP and we suspect it to be NP-hard. We see no other opportunity than to introduce the binary variable $x_{i,j}$ indicating whether a beam is present between two adjacent nodes $i\in V$ and $j\in V$ and force $F_{i,j}$ to the target function, see constraints (24a) and (24k).

4.3 Preprocessing

According to equation (20) the safety factor $\gamma$ modifies the upper bound of the capacity $c_{t,i,j}$ of a beam $\{i,j\}$ of type t. The force components in every direction in space $Q_{i,x}, Q_{i,y}, Q_{i,z} \in {\mathbb {R}}_+$, resulting from a applied concentrated force $Q_i$ at a node $i\in V$ are decomposed, as described in Sect. 3.2.2. The angles between two possible beams in the primary planes of the local coordinate system $F_{WP_{x,y,z}}$ are fixed to $45^\circ$, so that $r_{i,j,x}, r_{i,j,y}, r_{i,j,z} \in \{0,\frac{1}{\sqrt{2}},1\}$, the GS and the critical upskin and downskin angle $\upsilon _{cr} = \delta _{cr} = 45^\circ$, as described in Sect. 4.6.2, applies. It is ensured that $L_{b}^0 = N(t(b)) \cdot \tau$ is fulfilled, whereat N(t(b)) is the number of layers needed for a beam b of type t manufactured with the layer thickness $\tau$. The undeformed length of a beam $L_{b}^0$ is a multiple of the layer thickness $\tau$, which reduces production inaccuracies.

Concerning the preparations towards a lattice structure design problem as MILP, see Sect. 3.2, the costs of a beam of type $t cost_t \in {\mathbb {{R}}_+}$ are preprocessed and proportional to the volume and material consumed. Moreover, the different capacities $\overline{c}_{t,i,j} \in {\mathbb {R}}_+$ of a beam type t are preprocessed, see cases (21). Let $\overline{c}_{t,i,j} \in {\mathbb {R}}_+$ be the preprocessed upper bound of the stress of a beam type t between the nodes $i \in V$ and $j \in V$ with the associated material constitution $M_t = (\kappa _t,L_t,A_t,E_t,G_t,I_t)$ and dimension $D_t = (A_t,L_t)$. We define $\overline{F}_{t,i,j} \in {\mathbb {R}}$, to be the preprocessed upper bound of the axial force ${F}_{t,i,j}$ between the nodes $i,j \in V$ depending on the beam b of type t. The set $U \subseteq E$ is defined as the set of void beams. The following generic cases - to clarify the preprocessing - are differentiated:

$$\begin{aligned} \overline{c}_{t,i,j} = {\left\{ \begin{array}{ll} \overline{F}_{t,i,j}, & \{i,j\} \in E \setminus U \\ 0, & \{i,j\} \in U \end{array}\right. } \end{aligned}$$

(21)

Furthermore, constraints (22) and (23) determine the positions $L_{i,x}, \ L_{i,y}$ of a node $i \in V$. The positions $L_{i,x}, \ L_{i,y}$ are measured from the global coordinate system $F_{WP_{x,y,z}}^G$ ($L_{1,x}=L_{1,y}=0$) aligned with the axis x, y, z of the directions in space. We define the length width and height of the reference volume ${\mathbb {V}}$ stated as the number of connection nodes in each direction in space to be $\overline{x}, \overline{y}, \overline{z} \in {\mathbb {N}}$. The positions $L_{i,x}, \ L_{i,y}$ are used to determine the lever arms of the global statical area moment, see constraints (24e) and (24f).

$$\begin{aligned}&L_{i,x}=(i \mod (\,\overline{\!{x}}\,\overline{\!{z}}-1)) \mod \,\overline{\!{x}} \quad \forall i \in V \end{aligned}$$

(22)

$$\begin{aligned}&L_{i,y}=\left\lfloor \frac{i-1}{\,\overline{\!{x}}\,\overline{\!{z}}} \right\rfloor \quad \forall i \in V \end{aligned}$$

(23)

4.4 Instance parameter

The input parameter of both MILPs are the load case ($Q_i,i \in V$). The sizing of the assembly space ${\mathbb {A}}$ is determined by the parameters $x, y, z \in {\mathbb {N}}$, which are the length, width and height of the assembly space ${\mathbb {A}}$, stated as the number of connection nodes in each direction in space. A set of connection nodes $V =\{1, \ldots , xyz\}$ results. Taking into account the undeformed length of a beam $L_{b}^0$ and the binary variable $B_{t,i,j}$ indicating if a beam b of type t is present at $\{i,j\} \in E$, the dimensions of the reference volume ${\mathbb {V}}$ are given by $B_{t,i,j}$ and $\overline{x},\overline{y},\overline{z} \in {\mathbb {N}}$.

A set of different beam types $T=\{0,1,\ldots ,n\}$ and a set of nodes V acting as bearings $B \subseteq V$ is determined. The position of a bearing in the reference volume ${\mathbb {V}}$ corresponds to the indexing of the node i. The maximum permissible load corresponds to the maximum permissible load of the bearing for a static load case. Analogous to the external forces $Q_i$, see cases (21), the bearing reaction forces $R_i$ are decomposed into the force components $R_{i,x}, R_{i,y}, R_{i,z}$ with respect to the local coordinate system $F_{WP_{x,y,z}}$ and inserted centrically at a node.

Table 2 Decision variables, parameters and sets

4.5 Our mixed integer program for powder-based AM

$$\begin{aligned}&(TTD_{\mathrm{{l;p}}}): \quad \min \sum _{i \in V} \sum _{j \in V} \sum _{t \in T} B_{t,i,j} cost_t \end{aligned}$$

(24a)

$$\begin{aligned}&\quad \text {s.t.} \sum _{\begin{array}{c} j \in NB_x({i}) \end{array}} F_{i,j}^{x} +Q_{i,x}+R_{i,x} = 0 \quad \forall i \in V \end{aligned}$$

(24b)

$$\begin{aligned}&\quad \sum _{\begin{array}{c} j \in NB_y({i}) \end{array}} F_{i,j}^{y} +Q_{i,y}+R_{i,y} = 0 \quad \forall i \in V \end{aligned}$$

(24c)

$$\begin{aligned}&\quad \sum _{\begin{array}{c} j \in NB_z({i}) \end{array}} F_{i,j}^{z} +Q_{i,z}+R_{i,z}=0 \quad \forall i \in V \end{aligned}$$

(24d)

$$\begin{aligned}&\quad \sum _{\begin{array}{c} i \in V \\ Q_{i,z} \ne 0 \end{array}}Q_{i,z} (L_{i,y}-L_{j,{y}}) \nonumber \\&\quad +\sum _{k \in B}R_{k,{z}} (L_{k,{y}}-L_{j,{y}})=0 \quad \forall j \in B \end{aligned}$$

(24e)

$$\begin{aligned}&\quad \sum _{\begin{array}{c} i \in V \\ Q_{i,z} \ne 0 \end{array}}Q_{i,z} (L_{i,x}-L_{j,{x}}) \nonumber \\&\quad +\sum _{k \in B}R_{k,{z}} (L_{k,{x}}-L_{j,{x}})=0 \quad \forall j \in B \end{aligned}$$

(24f)

$$\begin{aligned}&\quad F_{i,j}\le M x_{i,j} \quad \forall i,j \in V \end{aligned}$$

(24g)

$$\begin{aligned}&\quad F_{i,j} =-F_{j,i} \quad \forall i,j \in V \end{aligned}$$

(24h)

$$\begin{aligned}&\quad F_{i,j} \le \sum _{t \in T} c_{t,i,j} B_{t,i,j} \quad \forall i,j \in V \end{aligned}$$

(24i)

$$\begin{aligned}&\quad B_{t,i,j} =B_{t,j,i} \quad \forall i,j \in V, t \in T \end{aligned}$$

(24j)

$$\begin{aligned}&\quad \sum _{t\in T} B_{t,i,j} = x_{i,j} \quad \forall i,j \in V \end{aligned}$$

(24k)

$$\begin{aligned}&\quad R_{i,z} =0 \quad \forall i \in V \setminus B \end{aligned}$$

(24l)

$$\begin{aligned}&\quad x_{i,j}, B_{t,i,j} \in \{0,1\} \quad \forall i,j \in V, t \in T \end{aligned}$$

(24m)

The objective function of the MILP TTD$_{\mathrm{{l;p}}}$ (24a) is to create a statically determined lattice structure, which is minimal in terms of costs under the influence of external forces. The minimization of costs in the target function represents a minimization of the required construction volume and material, since these sizes are decisive for the costs.

Constraints (24b) to (24d) determine a force equilibrium at every node $i \in V$ between the decomposed external forces $Q_{i,x}, Q_{i,y}, Q_{i,z}$ and the active forces $F_{i,j}$ of the beams mounted at a node i, following the decomposed force-balance equation (14). Each node $i \in V$ is possible to be connected to a set of adjacent nodes $NB_{x}(i), NB_{y}(i), NB_{z}(i) \subseteq NB(i)$ which have a force component in the x, y or z direction in space. The decomposition of the forces $F_{i,j}$ in the directions in space x, y and z is obtained by applying the appropriate trigonometric values ($r_{i,j,x}, r_{i,j,y}, r_{i,j,z}$) in relation to the local coordinate system $F_{WP_{x,y,z}}$ of the node i.

Constraints (24e) and (24f) define a global statical area moment which results from the decomposed external forces $Q_{i,x}, Q_{i,y}, Q_{i,z}$ and the decomposed bearing reaction forces $R_{i,x}, R_{i,y}, R_{i,z}$, following the assumptions of equation (19) that we assume a linear elastic strains plastic behavior, with the plastic section modulus $Z_{b} = \infty$ of a beam $b = {\{i,j\}}$. Only vertical forces are exerted. Thus, only two moment equilibrium constraints are needed and $R_{i,x} = R_{i,y}=0 \; \; \forall i \in V$ applies. Along with constraints (24e) and (24f) the external and internal statical determinacy is ensured.

Constraint (24g) ensures that only applied beams ($B_{t,i,j}=x_{i,j}=1$) can experience active forces. Constraint (24h) represents the force equilibrium of the adjacent nodes $i \in V$ and $j \in V$ connected with one beam indicated by $B_{t,i,j} = 1$. Constraint (24i) limits the active force $F_{i,j}$ in the beam $B_{t,i,j}$ concerning the capacity $c_{t,i,j} \in {\mathbb {R}}_+$, whereas constraint (24k) guarantees that a specific beam b of type t is selected if a beam $B_{t,i,j}$ is used. Combining constraints (24j) and (24k) we get $x_{i,j} =x_{j,i} \; \; \forall i,j \in V$ which demand a used beam to withstand tension and compression, which in combination with (24h) corresponds to Newton’s third law of motion. Finally constraint (24l) sets the bearing reaction forces of non-bearing nodes to zero. Any node can be defined as a bearing.

4.6 Our mixed integer program for support-free lattice structures

Design options to ensure manufacturability for self-supporting cylindrical parts, with different geometric characteristics, are presented. Numerical key figures are defined and can be used to engineer support-free parts and ensure manufacturability. The geometric characteristics are taken from the standard VDI (2019) and the terminology is derived from ISO (2017).

4.6.1 Preparations in order to get optimization-friendly design constraints for support-free lattice structures

Sectional shape A varying sectional shape of a cylindrical part is unbounded, as the quality of a metallurgically-bonded connection is independent of the sectional shape. The transition angle $\beta$ is also unbounded. Due to different mass accumulations, a varying sectional shape can influence the dimensional accuracy.

Minimal horizontal manufactured self-supporting cylinder In the case of a minimal horizontal manufactured self-supporting cylinder, dimensional deviations due to the stair-step effect have to be taken into account. For this reason, the layer thickness $\tau$ is decisive for designing a horizontal self-supporting cylinder.

Minimal vertical manufactured self-supporting cylinder In the case of a minimal vertical manufactured self-supporting cylinder the contour path including filling has to be ensured so that the track width is decisive. Let D, $D_{h}$, $D_{v}$ be the outer diameter of a self-supporting cylinder independent of the part orientation and dependent of the horizontal/vertical orientation, respectively. For a minimum horizontal manufactured self-supporting cylinder, the outer diameter ${D_{h}}$ is set to the value range $\underline{D}_{h} \gg 2 \underline{\tau }$ and $\underline{D}_{h} \ge 4.0 \, mm$. For a minimum vertical manufactured self-supporting cylinder $\underline{D}_{v} \ge 4.0\,\mathrm{mm}$ is defined.

Overhang ${b}_{o}$ A self-supporting overhang ${b}_{o}$ specifies the overhang of a part to the build platform. A maximum self-supporting overhang $\overline{b}_{o}$ must not be exceeded, other than that a support structure is necessary. The maximum width of the self-supporting overhang $b_{o}$ indicates the extent to which no support structure is needed without manufacturing faults occurring. The value for a maximum self-supporting overhang is $\overline{b}_{o} \le 1.6 \, mm$. In the case of unknown boundaries for the maximum width of the self-supporting overhang $b_{o}$, it is recommended to comply with $\overline{b}_{o} \le 2.5\,\mathrm{mm}$.

Minimum gap size The minimum gap size describes the required gap width ${b}_{g}$ for immovable parts as a function of the surrounding cured material. It is imperative to exclude merging of the adjacent layers. The minimum vertical gap is set to $\underline{b}_{g,v} \ge 0.2\,\mathrm{mm}$ and the minimum horizontal gap to $\underline{b}_{g,h} \ge 0.3\,\mathrm{mm}$. It is recommended to arrange a gap as vertically as possible in order to avoid support structures since the stair-step effect is insignificant for vertical part orientation.

Upskin and downskin area ${\mathbb {U}}$ and ${\mathbb {D}}$ A upskin area ${\mathbb {U}}$ is a (sub-)area whose normal vector in relation to the build direction z is positive, see Fig. 7. Similarly, a downskin area ${\mathbb {D}}$ is a (sub-)area whose normal vector in relation to the build direction z is negative. The length of a cylindrical beam is defined as l.

Upskin and downskin angle $\upsilon$ and $\delta$ A upskin angle $\upsilon$ is an angle between the build platform plane and a upskin area ${\mathbb {U}}$ whose value lies between $0 ^\circ$ and $90^{\circ }$. A downskin angle $\delta$ is an angle between the build platform plane and a downskin area ${\mathbb {D}}$ whose value lies between $0^{\circ }$ (parallel to the build platform) and $90^{\circ }$ (perpendicular to the build platform), see Fig. 7. If a perpendicular normal vector exists in relation to the build direction Z ($\upsilon = \delta = 90^{\circ }$), the upskin area ${\mathbb {U}}$ and downskin area ${\mathbb {D}}$ are identical. Both areas coincide with the positive construction direction Z and no support structure is needed.

Minimum angle of inclined self-supporting cylinders The minimum angle of inclined self-supporting cylinders is limited by the downskin angle $\delta$, not by the upskin angle $\upsilon$ (VDI 2015). Inclined cylinders can be manufactured without a support structure as long as the critical downskin angle $\delta _{cr} = 45^{\circ }$ is not undershot. Depending on the downskin angle $\delta$, the manufactured self-supporting cylinder can deform during manufacturing from a certain ratio of overhang/beam length $l=L_{b}^0$ of a cylinder to the outer diameter D if no support structure is provided. Manufacturing faults may occur. The permissible $L_{b}^0/D$ ratio depends on $\delta$.

4.6.2 Implementation of design constraints for support-free lattice structures

Figure 8 shows a definition by cases for supporting a cylinder depending on the length $l=L_{b}^0$, diameter D, downskin angle $\delta$ and the use of support structures. The case distinction is implemented in the MILPs TTD$_{\mathrm{{l;p}}}$ and TTD$_{\mathrm{{l;s}}}$ by equation (25) and (26). Due to the fitted GS, $\delta _{cr} = \upsilon _{cr} =\ 45^{\circ }$ applies implicitly. It is not necessary to differentiate between the critical downskin angle $\delta _{cr}$ and the critical upskin angle $\upsilon _{cr}$ of a support-free cylinder. A part not taking the in Sect. 4.6.1 mentioned design constraints for support-free cylinders into account is classified as not ready for manufacturing.

Fig. 7

Downskin- and upskin angle $\delta$ and $\upsilon$ according to standard VDI (2019)

Fig. 8

a Cylinder with any downskin angle $\delta$ and adverse $L_{b}^0/D$ ratio. Suitable by the support structure, but not optimal in terms of material consumption and post-processing. b Cylinder suitable for material extrusion AM with minimal manufacturable downskin angle $\delta = \delta _{cr} = 45^{\circ }$ and admissible $L_{b}^0/D$ ratio. c Cylinder not suitable for material extrusion AM with $\delta \ge \delta _{cr}$ and too big $L_{b}^0/D$ ratio. According to standard VDI (2015)

We assume a part to be connected directly to the build platform without an external support structure. We define a maximum length $\overline{l} = \overline{L}_{b}^0$ of a cylindrical beam depending on the AM process so that the curl effect (VDI 2015) is excluded. A modification of internal holes to avoid support structures (Thomas 2009) is unnecessary, since the predefined GS applies and thus all internal holes/free spaces are known. Even though a varying sectional shape of a cylindrical part is unbounded, we assume $\underline{D}_{h} = \underline{D}_{v} \ge 4.0 \, mm$ to minimize dimensional accuracy and fulfill the design options for a minimum horizontal and vertical manufactured self-supporting cylinder. A change in the cross-sectional area is fixed to a transition angle of $\beta = 90^{\circ }$, so that only vertical transitions between cylindrical parts are possible, independent of the part orientation. The value for a maximum self-supporting overhang is set to $\overline{b}_{o} = 1.6\,\mathrm{mm}$. We fix the minimum horizontal and vertical gap size to $\underline{b}_{g,h},\, \underline{b}_{g,v} \ge 0.3\,\mathrm{mm}$.

The build direction z is assumed to be positive with increasing node indexing, so that a distinction between upskin and downskin areas ${\mathbb {U}}$ resp. ${\mathbb {D}}$, upskin and downskin angles $\upsilon$ resp. $\delta$, is possible. By fixing the critical upskin and downskin angle to $\upsilon _{cr} = \delta _{cr} = 45^{\circ }$ via the GS and introducing a permissible length l to diameter D ratio of a cylinder, the following two cases as implementation of the standards VDI (2019) and VDI (2015)

$$\begin{aligned} \upsilon _{cr}&= \delta _{cr}= 45^{\circ }: L_{b}^0/D \le 5 \end{aligned}$$

(25)

$$\begin{aligned} \upsilon&= \delta = 90^{\circ } : L_{b}^0/D \le 10 \end{aligned}$$

(26)

follow. A set of cylinders with identical beam axes is considered a single cylinder. Constraint (25) identifies a cylinder manufactured angled at $45^{\circ }$ in relation to the local coordinate system $F_{WP_{x,y,z}}$ of a node. Analogous to that, constraint (26) identifies a cylinder manufactured angled at $90^{\circ }$ in relation to the local coordinate system $F_{WP_{x,y,z}}$ of a node. Constraints (25) and (26) restrict any combination of single or multiple cylinders with identical beam axes set in the GS. We can now state the model $TTD_{\mathrm{{l;s}}}$ for $k=\{2,3\}$:

$$\begin{aligned}&(TTD_{\mathrm{{l;s}}}): \quad \min \sum _{i \in V} \sum _{j \in V} \sum _{t \in T} B_{t,i,j} cost_t \end{aligned}$$

(27a)

$$\begin{aligned}&\quad \text {s.t. } \{(24b) - (24k)\} \nonumber \\&\quad 2\ell _i^o \le \sum _{j \in NB^{\backprime }(i)}x_{i,j} \le \ell _i^o +1 \quad \forall i,j \in V, o \in O \end{aligned}$$

(27b)

$$\begin{aligned}&\quad \sum _{j \in NB(i)}x_{i,j}\ge 3Z_i \quad \forall i \in V \end{aligned}$$

(27c)

$$\begin{aligned}&\quad \min (A_k)y_i \le \sum _{j \in NB(i)}x_{i,j} \le \max (A_k)y_i \quad \forall i,j \in V \end{aligned}$$

(27d)

$$\begin{aligned}&\quad \sum _{o \in O} \ell _i^o \le \frac{1}{2}\max (A_k)Z_i \quad \forall i \in V \end{aligned}$$

(27e)

$$\begin{aligned}&\quad R_{i,z}=0 \quad \forall i \in V \setminus B \end{aligned}$$

(27f)

$$\begin{aligned}&\quad x_{i,j}, y_i, \ell _i^o, Z_i, B_{t,i,j} \in \{0,1\} \quad \forall i,j \in V, t \in T, o\in O \end{aligned}$$

(27g)

The objective function of the MILP TTD$_{\mathrm{{l;s}}}$ (27a) is to create a statically determined, load-bearing and support-free lattice structure, which is minimal in terms of costs. The minimization of costs in the target function represents a minimization of the required construction volume and material following the MILP TTD$_{\mathrm{{l;p}}}$. For this reason, the constraints (27b) to (27e) present a geometry-based modeling, affecting the force equilibrium constraints (24b) to (24d) and the moment equilibrium constraints (24e) and (24f). The force and moment equilibrium constraints are bounded by (24g) to (24i).

Constraints (25) and (26) apply due to the implementation of constraints (27b) to (27g). Let O denote the set of beam combinations between two adjacent nodes that are excluded in the MILP TTD$_{\mathrm{{l;s}}}$ in opposition to TTD$_{\mathrm{{l;p}}}$ to realize a support-free lattice structure.

Constraints (27b) and (27e) identify the combination possibilities of beams between adjacent nodes $NB^{\backprime }(i)$ that would not comply with the design rules of VDI (2019) and VDI (2015). Constraint (27b) checks all adjacent nodes $NB^{\backprime }(i)$, which can require an additional beam to comply with the design rules for support-free lattice structures. All cases that require an additional beam to comply with the design rules are identified by the binary variable $\ell _i^o$ in constraint (27b). Associated in constraint (27e), the binary variable $Z_i$ indicates whether at least one additional beam is needed.

Constraint (27c) forces the model to add at least one beam between two adjacent nodes identified as critical in constraint (27b) and (27e). Constraint (27d) forces the model to set the binary variables $x_{i,j}$ and $y_i$, which corresponds to the construction of an additional beam to comply with the design rules for support-free lattice structures.

5 CAD tool

Current design methods and CAD tools are not tailored for the shape of additive manufactured lightweight lattice structures and are not yet optimized to achieve the great potential offered by AM (Rosen 2013). The innovation in the AM technology is not yet followed by an adaption in design and CAD software and tools (Azman et al. 2014).

Furthermore, the complexity of lattice structures causes the design process in CAD to be computationally inefficient (Rosen 2007). Most commercially available CAD software uses a Boundary Representation (BREP) system and is adjusted for conventional instead of additive manufacturing processes (Azman et al. 2014). The use of exact BREP geometries enables the repair and preparation of 3D geometries including all manufacturing data, but is computationally expensive. An early triangulation, i.e., converting the three-dimensional geometry into a Standard Triangle Language (STL) file, would reduce the need for computing capacity but a manipulation of the geometry is no longer possible without affecting the final part. Therefore, an early triangulation to save computing effort is impractical for our algorithm driven product design process. The CAD model should remain based on the original geometry description, e.g., a neutral data exchange format like STEP (ISO 10303), until Computer Aided Manufacturing (CAM).

For all these reasons, the generation of any kind of complex structures for AM is limited. It is necessary to develop tools (Add-Ins) for standard CAD software tailored for complex additive manufactured parts, in our application for additive manufactured lattice structures.

We developed a 3D-CAD tool, which is part of our DfAM methodology to realize an algorithm driven product design process. The 3D-CAD tool is implemented in the CAD software Autodesk Inventor Professional 2020 (Autodesk 2019). It is a bi-directional data integration between the state-of-the-art mathematical solvers and a CAD software and is used for the generation of lattice structures. The 3D-CAD tool described links the solution file of CPLEX to Autodesk Inventor Professional 2020. CAD-based design encodings of the instance data and the lattice structure are again directed to CPLEX. With our 3D-CAD tool, we provide the performance of state-of-the-art mathematical solvers to design and manufacturing experts which focus on lattice structures.

Our tool takes full advantage of the geometrical freedom of additive manufacturing by constructing each element of a lattice structure individually. It is possible to construct any type of lattice structure. The 3D-CAD tool can be used as a stand-alone software, independent of the algorithm driven product design process. A Finite Element Method (FEM) software directly adopts the CAD data and computes (on request) a linear-elastic and non-linear-elastic numerical FEA. The derivation of the high compressed 3D geometries (e.g., STL, AMF) and CAM data (e.g., machine setting, toolpath generation) is done based on the generated CAD design data.

5.1 Construction methodology

We concentrate on a construction methodology to model any lattice structure. The established approach to model an elementary structure that is multiplied in the spatial directions in space is insufficient for this purpose. On the one hand, the approach is not able to model any lattice structure (e.g., unstructured lattice structures); on the other hand, the approach depends strongly on the complexity of the elementary structure (Azman et al. 2014).

Our approach is to decompose the elementary structure into its individual parts and model each part from scratch. Figure 9 shows the modeling of one part. A plane is defined on a connection node and a profile is created. Furthermore, the profile is extruded to form a beam with a circular and constant cross-section.

Fig. 9

Construction of a beam with a circular and constant cross-section

Any lattice structure can be modeled with our construction methodology and the performance is dependent on the amount of parts but independent of the (geometric) complexity of the elementary structure, due to the individual construction of each part. In our application the individual parts are solid round beams with a constant cross-section. The decomposition of the elementary structure into its individual parts is indispensable for us since we cannot make any statement about the type of lattice structure before the TTD optimization, except to analyze the GS. In order to construct any optimization result, we assume that the lattice structures calculated by our MILPs are unstructured.

Concerning a straightforward implementation of new types of parts (e.g., hollow beams), the computation of the reference volume ${\mathbb {V}}$ (Function 1) and the modeling of a part (Function 2) are separated. If a new type of beam is required, the input parameter $A_{t,i,j}$ as the area/profile A of beam type t between the adjacent nodes i and j (see function 2) can be changed. Function 2 extrudes the new profile $A_{t,i,j}$ and creates a new kind of part.

5.2 Data processing of our MILPs

The reference volume ${\mathbb {V}}$, see Fig. 2, is the initial volume considered by our 3D-CAD tool. The finally constructed lattice structure is a subset of the GS ${\mathbb {G}}$ representing the reference volume ${\mathbb {V}}$. To implement the results of our MILPs in the 3D-CAD tool, a distinction between a lattice frame and a lattice structure is made. A lattice frame is defined by connection nodes and line segments and serves as a basis for the lattice structure. A lattice structure is created by adding topological relations to the lattice frame.

The lattice frame is implemented generating the reference volume ${\mathbb {V}}$, see Function 1, using the parameters $x, y, z \in {\mathbb {N}}$ of our MILPs. In addition, the binary variable $x_{i,j}$ specifies whether a line segment is present between nodes $i\in V$ and $j\in V$. The connection nodes of the lattice frame are read from the MILP instance file, the line segments from the MILP solution file.

The lattice structure is implemented by adding topological relations to the lattice frame. For this we use the binary variable $B_{t,i,j} \in \{0,1\}$ of our MILPs, which specifies whether a beam of type $t \in T$ is present between two nodes i and j. The binary variable $B_{t,i,j}$ is read from the MILP solution file.

The variable $F_{i,j}$ provides the generalized active force of a beam, which allows a comparison between the static structural dimensioning of the MILPs and a linear-elastic and non-linear-elastic numerical FEA. The utilization of an individual beam is defined by the comparison of the capacity $c_{t,i,j}$ (critical load) of beam type t and the force $F_{i,j}$.

Since we enable a numerical analysis, the preprocessing from Sect. 4.3, which enables a linear definition of the material constitution $M_t$ and the dimension $D_t$ of a beam type t, is resolved. The material constitution $M_t(\kappa _t,L_t,A_t,E_t,G_t,I_t)$ and the dimension $D_t(A_t,L_t)$ of a beam type t is a function of several variables and parameters. The undeformed length $L_{b}^0$ and the Timoshenko shear coefficient $\kappa _t$ of a beam type t apply to the instance parameter of the MILP. The cross section area $A_t$, shear modulus $G_t$, Young’s modulus $E_t$, variable length $L_t$ and the area moment of inertia $I_t$ apply to the material assigned in the CAD model. The material is identical to the preprocessed material of the MILP. Non-linear analysis with plastic material behavior can thus be carried out within a FEA.

5.2.1 Modeling the reference volume

The function ReferenceVolume, see Function 1, iterates over the set of connection nodes $V =\{1, \ldots , xyz\}$ representing the reference volume ${\mathbb {V}}$. Besides, all beams are modeled using the function ModelBeam, see Function 2. The connection nodes V are implemented as work points $WP_{x,y,z}$ having the same indexing as the connection nodes V. Each work point $WP_{x,y,z}$ is defined as a grounded work point in a part file and has three spatial coordinates x, y, z in relation to the origin of the reference volume ${\mathbb {V}}$ ($x=y=z=0$). All degrees of freedom of the work points are removed, so that they are fixed in space. We allow only operations needed for Function 2; defining a coordinate system, plane and a three-dimensional path in relation to a work point $WP_{x,y,z}$. The three-dimensional path is the basis for the line segment of the lattice frame.

The input to Function 1 is the MILP instance file including the preprocessed beam types and materials and the MILP solution file. The MILP instance file specifies the positions of the work points $WP_{x,y,z}$ in the reference volume ${\mathbb {V}}$ and implicit all possible beam lengths. The MILP solution file specifies which work points $WP_{x,y,z}$ are to be connected with a beam $B_{t,i,j}$. To realize a bottom-up construction methodology, the function outputs any lattice structure as an assembly (.iam) with beams as parts (.ipt).

In the first step of Function 1, the reference volume ${\mathbb {V}}$ is generated by iterating over the length x, width y and height z of the reference volume ${\mathbb {V}}$. The dimensions are indicated by the set of connection nodes V in each direction in space. The distance between two work points $WP_{x,y,z}$ arranged on a single plane are read from the instance data file of the MILP. All other distances are determined depending on the work points $WP_{x,y,z}$ in the 3D-CAD tool.

To solve the problem that the MILP does not specify the geometric relations between work points $WP_{x,y,z}$, all work points $WP_{x,y,z}$ are created first using Function 1. In a second step, see Function 2, the beams are modeled in relation to the spatial coordinates x, y, z of the work points $WP_{x,y,z}$ in relation to the origin of the reference volume ${\mathbb {V}}$. Therefore, beams can be modeled directly by indexing the work points $WP_{x,y,z}$, without any angular relationships.

5.2.2 Modeling a beam

The ModelBeam function models a beam using two neighboring work points $WP_{\check{x},\check{y},\check{z}}$, $WP_{\hat{x},\hat{y},\hat{z}}$, a beam profile $A_{t,i,j}$, the binary variable $B_{t,i,j}$, the material constitution of a beam $M_t$ and the variable $S_{i,k,d}$ for post-processing.

The function outputs a beam as a part (.ipt) positioned between two neighboring work points $WP_{\check{x},\check{y},\check{z}}$, $WP_{\hat{x},\hat{y},\hat{z}}$ of a reference volume ${\mathbb {V}}$. The material constitution $M_t(\kappa _t,L_t,A_t,E_t,G_t,I_t)$ is assigned to each beam. The use of a global or local coordinate system depends on the implementation capabilities of the Autodesk Inventor Professional 2020 API.

In the first step two local coordinate systems $F_{WP_{\check{x},\check{y},\check{z}}}$, $F_{WP_{\hat{x},\hat{y},\hat{z}}}$ are created centered on two neighboring work points $WP_{\check{x},\check{y},\check{z}}$, $WP_{\hat{x},\hat{y},\hat{z}}$. Both local coordinate systems $F_{WP_{\check{x},\check{y},\check{z}}}$, $F_{WP_{\hat{x},\hat{y},\hat{z}}}$ have a relative and absolute relation to the global coordinate system $F_{WP_{x,y,z}}^G$, see Fig. 3. Subsequent, a line segment $L_{WP_{x,y,z}}$ depending on the position in space of two neighboring work points $WP_{\check{x},\check{y},\check{z}}$, $WP_{\hat{x},\hat{y},\hat{z}}$ is created. The line segment $L_{WP_{x,y,z}}$ is defined as the central axis of a beam. Following, a plane $P_{WP_{x,y,z}}$ is created as a function of the line segment $L_{WP_{x,y,z}}$ and a work point $WP_{\hat{x},\hat{y},\hat{z}}$. The plane $P_{WP_{x,y,z}}$ is arranged orthogonally to the line segment $L_{WP_{x,y,z}}$. The plane $P_{WP_{x,y,z}}$ as a function of the line segment $L_{WP_{x,y,z}}$ and the work points $WP_{\check{x},\check{y},\check{z}},WP_{\hat{x},\hat{y},\hat{z}}$ is used to implement a construction methodology based only on the MILP data: The line segment $L_{WP_{x,y,z}}$ is dependent on the indexing from the MILP and the plane $P_{WP_{x,y,z}}$ is dependent on the line segment $L_{WP_{x,y,z}}$, except for an angular parameter which describes, that the plane is orthogonal to the line. A round cross-sectional area $C_{WP_{x,y,z}}$ as profile centered on one of the two neighboring work points $WP_{\check{x},\check{y},\check{z}}$, $WP_{\hat{x},\hat{y},\hat{z}}$ is created. The profile is extruded along the line segment to create a solid beam $B_{WP_{x,y,z}}$.

5.3 Post-processing

As can be seen in Fig. 10 left, interferences (red) and unwanted free spaces (green) inevitable occur due to the connection of beams with variable diameters at intersection points. In accordance with Nguyen and Vignat (2016), in the case of solid round beams with a constant cross-section, it is necessary to correct the intersection points between the beams, see Fig. 10 right for a detail view.

To post-process the intersection, a solid sphere needs to be added at the intersection points to fill the missing space. The radius of the added sphere surface should be at least equal to the radius of the beam with the largest cross-section. We create the sphere surface $S_{i,k,d}$ as a function of the work point $i \in V$, the maximum beam diameter $d_{i,max}$ at work point $i \in V$ and a scaling factor k, so that $S_{i,k,d} = k \cdot d_{i,max} \ \forall i \in V$ applies.

To post-process the overlapping objects, the objects are segregated through splitting at their overlap limits. Only one of the previously overlapping objects is retained so that the topology including material distribution is merged. The post-processing excludes rough contour transitions. Furthermore, the self-weight of the part, which was falsified by the material overlaps, is corrected.

This post-processing makes the part ready for AM. A correct FEA including external and self-weight loads becomes possible. Stress concentrations and singularities are expected for the FEA for two reasons; the transitions of the sphere surfaces to the beams and the transitions of multiple beams with identical beam axes. By fixing the transition angle at $\beta = 90^{\circ }$, see Sect. 3.4, sharp re-entrant corners result, which can be triggers for stress concentrations and singularities. The post-processing of the intersection points is segregated considered in our 3D-CAD tool.

Fig. 10

a Post-processing of interferences (red) and free spaces (green). b Detail view of a post-processed intersection. Fig. 10 right shows the post-processing of the smallest radius (green beam and red sphere) for a better illustration.

5.4 Case study

The data processing of Autodesk Inventor 2020 is based on the same BREP models to define the topology and geometry of parts as other CAD standard software. Therefore, our results are representative of other CAD standard software such as Dassault Systems CATIA V5 (Catia 2019) and PTC Creo Elements (Creo 2019). The performance of the 3D-CAD tool to design a cubic lattice structure was observed.

Different lattice structure sizes, see Fig. 11, are used to study the performance impact of increasing lattice structure sizes. Time and memory requirements for all necessary intermediate formats used of our algorithm driven product design process are analyzed, see Table 3. In order to achieve an accurate evaluation, three different STL and G-code (standard RS-274) file quality levels are defined.

Please note that any lattice structure can be modeled with this construction methodology, due to the individual construction of each part. The cubic elementary structure serves only for illustration purposes and can be replaced by any structure, e.g., a octet-truss elementary structure. The 3D-CAD tool is tested up to a number of 6084 beams, which takes 20 hours, 46 minutes and 30 seconds, see Table 3 and Fig. 11.

A quadratic growth of the running time, depending on the number of parts to be designed, is observed. The RAM used and the STEP³ (ISO 10303, AP 242) file size is linear dependent on the number of parts. The intermediate format STL is used in ASCII as well as binary format. Both intermediate formats and the G-code required for CAM are linear dependent on to the number of parts.

Our developed 3D-CAD tool, as part of our algorithm driven product design process, can contribute to solve the problem that current design methods and CAD tools are not tailored for the shape of additive manufactured lattice structures and are not yet optimized to achieve the enormous potential offered by the technology AM. It provides ready for manufacturing lattice structures.

Fig. 11

Lattice structure sizes to evaluate time and memory requirements

Table 3 Time and memory requirements for all necessary intermediate formats used of our algorithm driven product design process

6 Workflow: from an idea to a part

The design and manufacturing experts using our algorithm driven product design process, see Sect. 3.5, decide which circumstances are implemented by the TTD models, are preprocessed in our 3D-CAD tool, or are omitted and validated with an FEA. A data interface between the CAD software and a Computer-aided Engineering (CAE) software enables a data conversion from a geometrical representation of a part (CAD file) into a triangulated surface of a part (STL file). Once the STL file has been generated, the file is imported into a slicer software. This so-called slicer converts the STL file into a G-code file used for CAM.

The 3D-CAD tool serves as an interface between the TTD models, the FEA, CAE and finally AM. Partial problems that cannot be modeled in the TTD models, depending on their natural constraints, have to be post-processed in the 3D-CAD tool. Considering the MILPs TTD$_{\mathrm{{l;p}}}$ and TTD$_{\mathrm{{l;s}}}$, the post-processing of intersections and interferences for an FEA, see Sect. 5, are implemented by the 3D-CAD tool. Furthermore, the CAD model is prepared for an FEA in the 3D-CAD tool. Finally, a verification of the part via a linear-elastic and non-linear-elastic numerical FEA is possible. All necessary design data is available to slice and subsequently manufacture the part using any desired AM process. As the 3D-CAD tool completely processes the data and is integrated into the CAD software Autodesk Inventor Professional 2020 (Autodesk 2019), the design and manufacturing experts have access to the full range of standard CAD software via a neutral data exchange format like STEP (ISO 10303).

As shown in Fig. 12, the process is iterative. The AM process and related standards (see lower left) influence the constraints of the selected TTD models and vice versa. The design and manufacturing experts are able to control the results of the optimization (SOL file) through the assembly (STEP file) automatically generated by the 3D-CAD tool. Subsequently, an FEA (validation) can be performed. Either the design results are not sufficient, so that the constraints of the TTD have to be adapted, or the assembly can be manufactured straightforward with AM. The processing step TTD encompasses all optimization methods available or planned to our algorithm driven product design process.

Using the TTD models TTD$_{\mathrm{{l;p}}}$ and TTD$_{\mathrm{{l;s}}}$, instance variables such as the load case, material specifications and the reference volume are specified. The aim of the algorithm driven product design process is to use our optimization at the first chronological level of the design process and FEA only for validation.

Fig. 12

Schematic of our algorithm driven product design process

7 Computational study

7.1 Use case structural optimization: MILP TTD$_{\mathrm{{l;p}}}$

For the optimization CPLEX 12.6.1 is used. The construction is done with our 3D-CAD tool. The data preparation for the selective laser sintering of the lattice structure (Fig 13) with the AM system EOS INT P760 is done with the rapid prototyping software Maigcs RP (Materialise 2019). The BuildProcessor available for Magics RP is used to generate the G-code file from the STL file. There is no post-processing of the STL data; the STL data obtained from our 3D-CAD tool is sufficiently high-resolution and the transitions are post-processed appropriate, see Sect. 5.3. The numerical analysis is performed with ANSYS AIM 19.2 (ANSYS 2019).

The resulting lattice structure of the use case for the MILP TTD$_{\mathrm{{l;p}}}$ (Fig. 13) is manufactured with SLS. The assembly space ${\mathbb {A}}$ of the used AM system EOS INT P 760 is represented as a polyhedron consisting of $V =\{1, \ldots , 19285\}$ connection nodes, resulting from the dimensions of the assembly space ${\mathbb {A}}$ of the AM system EOS INT P 760 ($700 \times 380 \times 580$ mm) and a beam length of 20 mm for a beam arranged on a single plane. The reference volume ${\mathbb {V}}$ was set to the dimensions $120 \times 120 \times 120$ mm. Hence, there are 216 connection nodes in ${\mathbb {V}}$.

The four corner points of the first plane in the positive z-direction are defined as bearings, see Fig. 14. It is predetermined that the top level in the z-direction is fully developed with beams with a diameter of 6 mm. The necessary entries of the binary variable $x_{i,j}$ are set to 1, so that the predefined beams can become load-bearing by optimization. The beam diameters $\{2,4,6,8\}\,\mathrm{mm}$ together with the associated $c_{t,i,j} \in {\mathbb {R}}_+$ and $cost_t \in {\mathbb {R}}_+$ are specified as parameters. A static area load (Fig. 14) at the last plane in the positive z-direction is specified. The applied static area load is simplified by a purely vertical centric force application at each node.

Fig. 13

Additive manufactured lattice structure including bearings as single parts (SLS)

The computation time⁴ using CPLEX (manually interrupted) was 10 h 51 min. 12 permissible solutions were determined, whereby the duality gap was 55.73%. The number of beams could be reduced from 3336 (entire reference volume ${\mathbb {V}}$) to 665, which is a reduction of 80.07%.

To validate the results of the MILP, we perform a static structural-mechanical analysis. The analysis determines the deformation, stresses and strains in our lattice structure as a function of a static load case specified by the MILP. Inertia loads and dead weight are analyzed, as they are simplified in our MILP. Dynamic or damping effects are optional and not considered in this validation. The boundary conditions (Fig. 14) for the FEA are determined by the load case and the bearings of the MILP. The FEA mesh of our lattice structure is a structured mesh without mesh refinements at transitions of parts, and tetrahedral elements are used. The element size is defined as 2.0 mm and the trial function is program-controlled. The total deformation (Fig. 15) is provided as a fringe plot to visualize the results of the static structural-mechanical validation of our lattice structure.

The lattice structure is support-free, because the used AM system EOS INT P 760, as a plastic laser-sintering system for direct manufacturing, can create parts without the need for support structures. No additional (physical) post-processing is necessary for the lattice structure due to the design rules implemented in the MILPs and the post-processing in the 3D-CAD-tool. The material used for manufacturing is fine polyamide PA 2200 with a modified layer thickness of 0.12 mm.

Fig. 14

Boundary conditions of the FEA

Fig. 15

Fringe plot of the total deformation (FEA)

7.2 Use case optimization of support-free lattice structures: MILP TTD$_{\mathrm{{l;s}}}$

The following use case considers a positioning of a static area load and is a proof of concept for the MILP TTD$_{\mathrm{{l;s}}}$.

The reference volume ${\mathbb {V}}$ is set to the dimensions $120 \times 120 \times 120$ mm. The length of a beam arranged on a single plane is set to 20 mm. Hence, there are 216 connection nodes in ${\mathbb {V}}$. The four corner points of the first plane in the z-direction are defined as bearings. It is predetermined that the top level in the z-direction is fully developed with beams. The beam diameters $\{1,2,4,6,8\}$ mm and the associated $c_{t,i,j} \in {\mathbb {R}}_+$ and $cost_t \in {\mathbb {R}}_+$ are passed as parameters.

We assume that the bar diameter of 1 mm is the minimal manufacturable beam diameter for the used AM system. The assumption is based on the fact that the MILP TTD$_{\mathrm{{l;s}}}$ should have the freedom to use this minimal beam diameter, to comply with the implemented design rules for support-free lattice structures, while having the minimum of material consumption. The use case for the model MILP TTD$_{\mathrm{{l;s}}}$ is therefore identical to the use case for the MILP TTD$_{\mathrm{{l;s}}}$, except for the additional minimum beam diameter of 1 mm.

Since our geometry-based modeling in the MILP TTD$_{\mathrm{{l;s}}}$, see Sect. 4.6, is coupled to the force equilibrium constraints and the moment equilibrium constraints via the binary variable $x_{i,j}$, there is no possibility to evaluate the resulting lattice structure whether one or more beams are used to avoid a combination of beams at a node that would require a support structure. We consider the support structure in the part design, and therefore, as entire force-bearing. Nevertheless, the use case for the model TTD$_{\mathrm{{l;s}}}$ can be statistically evaluated and compared to the use case for the model TTD$_{\mathrm{{l;p}}}$.

The computation time for the use case TTD$_{\mathrm{{l;s}}}$ (manually interrupted) was 49 h and 27 min for the instance TTD$_{\mathrm{{l;s}}}$. A number of 103 permissible solutions were determined, whereby the duality gap was 64.46%.

In order to allow comparability, we make the following assumptions: As AM material extrusion process, FDM is performed on the AM system Ultimaker 2 Extended+. The support structure is designed with the supplied Slicer Cura 3.6.9 (Cura 2019). The support structure has been designed with a support overhang angle $\delta = 45^{\circ }$, brim type build plate adhesion, a grid pattern, 30% density and free placement of support structures. The material is Acrylonitrile Butadiene Styrene (ABS) with a density of 1.1 g/cm$^3$. The layer thickness was set to 0.1 mm; the beams were printed as solid material.

Table 4 shows that the model TTD$_{\mathrm{{l;s}}}$ requires $5.43 \cdot 10^4\,\mathrm{mm}^3$ less actual volume of the lattice structure ${\mathbb {L}}$ than the solution of Cura 3.6.9. This results in a 3.14% better ratio and a weight saving of 103.12 g, which corresponds to a cost-saving in material of 46.10%. The use of our MILP TTD$_{\mathrm{{l;s}}}$ ensures that no support structure and post-processing is necessary, unlike the solution of Cura 3.6.9.

Table 4 Statistics for the solutions of the use cases of the MILPs TTD$_{\mathrm{{l;p}}}$ and TTD$_{\mathrm{{l;s}}}$ and a solution calculated by Cura 3.6.9.

8 Conclusion and outlook

This paper has investigated how to systematically combine mathematical optimization, CAD, FEA and AM into an algorithm driven product design process. Mathematical optimization and FEA simulation were used within the product design process, whereby mathematical optimization was initially used for topology and shape optimization and the resulting part was validated by a linear-elastic and non-linear-elastic numerical analysis. The results showed that our product design process can be used to design additive manufactured lattice structures. Our vision is to develop tools for engineers. For this, we combined engineering and mathematical optimization through a 3D-CAD tool to profit from both areas. In addition, we were able to support design and manufacturing experts with the opportunity to find a global optimum, which is equivalent to using the complete manufacturing freedom of AM. With the 3D-CAD tool, we provided the performance of state-of-the-art mathematical solvers to design and manufacturing experts focusing on lattice structures. For the implementation of the complete algorithm driven product design process, various topics had to be covered. In the following, we conclude our contributions and identify future research directions.

8.1 Optimization for powder-based AM

For our MILP TTD$_{\mathrm{{l;p}}}$ concerning powder-based AM, we presented a preprocessing that makes it possible to define the maximum normal stress of a beam, depending on the material constitution and dimension. This allowed a multi-material mixed integer program. The preprocessing was used for the MILPs TTD$_{\mathrm{{l;p}}}$ and TTD$_{\mathrm{{l;s}}}$, whereby later in the algorithm driven product design process the preprocessing was adjusted to enable a FEA. Our MILP TTD$_{\mathrm{{l;p}}}$ generated a lattice structure for powder-based AM processes regardless of support structures, as they are not necessary for this AM process. An optimized lattice structure regarding a static area load, with a practice-oriented number of connection nodes and beams, was manufactured using the powder-based AM system EOS INT P760. As for future research for the MILP TTD$_{\mathrm{{l;p}}}$ we plan to include external heuristics, especially starting solutions in the solution strategy and to develop lower and upper bounds. Typical process-specific geometrical limitations of AM technologies like delamination of layers, curling or stair-step effects should be minimized by formulating boundary constraints, regarding to maximize the part quality. If a support structure is necessary, it should also be possible to minimize the material of the support structure by minimizing the sum of the angles between the build orientation of a beam and the build direction.

8.2 Optimization of support-free lattice structures

The MILP TTD$_{\mathrm{{l;s}}}$ generated a support-free lattice structure for AM processes usually depending on support structures, by considering geometry-based design rules for inclined and support-free cylinders (VDI 2019) and assumptions for location and orientation of parts within a build volume (ISO 2013). The problem to strengthen a lattice structure by local thickening or beam addition or both, with the objective function to minimize costs and material, was modeled. In doing so, post-processing was excluded. Compared to a support structure generation via the AM slicing application Cura 3.6.9, our method was able to obtain a cost-saving in material of 46.10% for our optimized lattice structure. In the future, we want to add an assisting structural analysis, as the most important limitation of the proposed method is that we work geometry-based via VDI (2019), under the assumption that the topology withstands the shear forces during the manufacturing process. Since the variable $x_{i,j}$ is used to define the presence of a beam, we will develop suitable heuristics to generate valid solutions in order to enable us to fix the variable $x_{i,j}$ and solve the remaining LP instead of the original MILP.

8.3 3D-CAD tool and additive manufacturing

A 3D-CAD tool implemented in the CAD software Autodesk Inventor Professional 2020, as part of our algorithm driven product design process, was presented. We focused on a construction methodology that models each part from scratch, so that any lattice structure can be modeled. The 3D-CAD tool was tested up to a number of 6084 beams, which took 20 h and 24 min. Time and memory requirements for all intermediate formats used of our algorithm driven product design process were analyzed. The results of the mathematical optimization were corrected in the 3D-CAD tool by an overlay check of the solid and surface objects. Sphere surfaces were added and overlapping material was dispensed at the intersection points. We work towards a parallel processing of assemblies for the 3D-CAD tool to increase the performance, as a quadratic growth of the running time, depending on the number of parts to be designed, was observed. Furthermore, it should be possible to directly generate STL files out of the MILP solution to bypass the CAD performance issues and produce ready-to-manufacture lattice structures. We manufactured a lattice structure with SLS, but in the future an industrial application with a complex loading case including main loads, additional loads and individual loads shall be optimized and manufactured with direct metal laser sintering. A use case including tree-like support structures is of particular interest.