Abstract
An intensive effort by the cryptographic community to minimize the round complexity of secure multi-party computation (MPC) has recently led to optimal two-round protocols from minimal assumptions. Most of the proposed solutions, however, make use of a broadcast channel in every round, and it is unclear if the broadcast channel can be replaced by standard point-to-point communication in a round-preserving manner, and if so, at what cost on the resulting security.
In this work, we provide a complete characterization of the trade-off between number of broadcast rounds and achievable security level for two-round MPC tolerating arbitrarily many active corruptions. Specifically, we consider all possible combinations of broadcast and point-to-point rounds against the three standard levels of security for maliciously secure MPC protocols, namely, security with identifiable, unanimous, and selective abort. For each of these notions and each combination of broadcast and point-to-point rounds, we provide either a tight feasibility or an infeasibility result of two-round MPC. Our feasibility results hold assuming two-round OT in the CRS model, whereas our impossibility results hold given any correlated randomness.
The full version of this paper can be found at the IACR Cryptology ePrint Archive, report 2019/1183.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Round complexity is an important efficiency measure of secure multi-party computation protocols (MPC) [40, 67], with a large body of research focusing on how it can be minimized. The “holy grail” in this thread has been two-round protocols, as single-round MPC for a large set of functions cannot be achieved [43]. The first solutions to this problem were based on strong cryptographic assumptions (FHE [5, 59], iO [34], witness encryption [42], and spooky encryption [26]), whereas more recent results showed how to build two-round MPC resilient to any number of active corruptions from standard assumptions, such as two-round oblivious transfer (OT) [9, 10, 33] or OT-correlation setup and one-way functions (OWF) [35] (we discuss the state of the art in Sect. 1.1).
The advantage of such two-round MPC protocols, however, is often dulled by the fact that the protocols make use of a broadcast channel in the case of malicious adversaries. Indeed, in practice such a broadcast channel is typically not available to the parties, who instead need to use a broadcast protocol over point-to-point communication for this task. Classical impossibility results from distributed computing imply that any such deterministic protocol tolerating (up to) t corruptions requires \(t+1\) rounds of communication [27, 28]; these bounds extend to randomized broadcast, showing that termination cannot be guaranteed in constant rounds [17, 52]. Even when considering expected round complexity, randomized broadcast would require \(\varOmega (n/(n-t))\) rounds [30] when the adversary can corrupt a majority of parties (i.e., \(t\ge n/2\)), and expected two rounds are unlikely to suffice for reaching agreement, even with weak guarantees, as long as \(t> n/4\) [24] (as opposed to expected three rounds [58]). Furthermore, while the above lower bounds consider broadcasting just a single message, known techniques for composing randomized broadcast protocols with non-simultaneous termination require a multiplicative blowup of \(c>2\) rounds [7, 20, 22, 53, 55].
The above state of affairs motivated a line of work investigating the effect in the round complexity of removing the assumption of broadcast from two-round MPC protocols [2, 4, 49, 51, 60]. In order to do so, however, one needs to settle for weaker security definitions. In other words, one needs to trade off security guarantees for lower round complexity.
In this work, we fully characterize the optimal trade-off between security and use of broadcast in two-round MPC protocols against a malicious adversary who corrupts any number of parties: In a nutshell, for each of the three standard security definitions that are achievable against such adversaries in the round-unrestricted setting—namely, security with identifiable, unanimous, or selective abort—we provide protocols that use the provably minimal number of broadcast rounds (a broadcast round is a round in which at least one party broadcasts a message using a broadcast channel). Our positive results assume, as in the state-of-the-art solutions, existence of a two-round oblivious transfer (OT) protocol in the CRS model (alternatively, OT-correlation setup and OWF), whereas our impossibility results hold for any correlated randomness setup.
1.1 Background
Starting with the seminal works on MPC [8, 16, 40, 65, 67], a major goal has been to strike a favorable balance between the resources required for the computation (e.g., the protocol’s round complexity), the underlying assumptions (e.g., the existence of oblivious transfer), and the security guarantees that can be achieved.
Since in the (potentially) dishonest-majority setting, which is the focus in this work, fairness (either all parties learn the output or nobody does) cannot be achieved generically [18], the standard security requirement is weakened by allowing the adversary to prematurely abort the computation even after learning the output value. Three main flavors of this definition—distinguished by the guarantees that honest parties receive upon abort—have been considered in the literature:
-
1.
Security with identifiable abort [19, 50] allows the honest parties to identify cheating parties in case of an abort;
-
2.
security with unanimous abort [29, 40] allows the honest parties to detect that an attack took place, but not to catch the culprits; and, finally,
-
3.
security with selective (non-unanimous) abort [41, 49] guarantees that every honest party either obtains the correct output from the computation or locally detects an attack and aborts.
We note in passing that the above ordering reflects the strength of the security definition, i.e., if a protocol is secure with identifiable abort then it is also secure with unanimous abort; and if a protocol is secure with unanimous abort, then it is also secure with selective abort. The opposite is not true in general.
A common design principle for MPC protocols, used in the vast majority of works in the literature, is to consider a broadcast channel as an atomic resource of the communication model. The ability to broadcast messages greatly simplifies protocols secure against malicious parties (see, e.g., the discussion in Goldreich’s book [39, Sec. 7]) and is known to be necessary for achieving security with identifiable abort [19]. Indeed, broadcast protocols that run over authenticated channels exist assuming a public-key infrastructure (PKI) for digital signatures [27], with information-theoretic variants in the private-channels setting [63]. Therefore, in terms of feasibility results for MPC, the broadcast resource is interchangeable with a PKI setup. In fact, if merely unanimous abort is required, even this setup assumption can be removed [29].Footnote 1
However, as discussed above, in terms of round efficiency, removing the broadcast resource is not for free and one needs to either pay with more rounds to emulate broadcast [27, 30], or lessen the obtained security guarantees. However, very few generic ways to trade-off broadcast for weaker security have been proposed. A notable case is that of Goldwasser and Lindell [41], who showed how to compile any r-round MPC protocol \(\pi \) that is designed in the broadcast model into a 2r-round MPC protocol over point-to-point channels at the cost of settling for the weakest security guarantee of selective abort, even if the original protocol \(\pi \) was secure with unanimous or identifiable abort. Interestingly, since as mentioned earlier broadcast protocols are expensive in terms of rounds and communication, most (if not all) practical implementations of MPC protocols use this compiler and therefore can only achieve selective abort [44, 45, 54, 56, 57, 66].
But even at this security cost, the compiler from Goldwasser and Lindell [41] does not achieve a round-preserving reduction as it induces a constant multiplicative blowup in the number of rounds. The reason is that, in a nutshell, this compiler has every broadcast round being emulated by a two-round echo multi-cast approach, where every party sends the message he intends to broadcast to all other parties, who then echo it to ensure that if two honest parties received inconsistent messages everyone can observe. Such a blowup is unacceptable when we are after protocols with the minimal round complexity of two rounds.
Two-round MPC protocols in the malicious setting were first explored in [37, 38], while recent years have witnessed exciting developments in two-round MPC [1,2,3,4,5, 9,10,11, 15, 25, 26, 31,32,36, 42, 49, 51, 59, 60, 64]. The current state of the art can be summarized as follows:
-
Garg and Srinivasan [33] and Benhamouda and Lin [9] showed how to balance between the optimal round complexity and minimal cryptographic assumptions for MPC in the broadcast model, by showing that every function can be computed with unanimous abort using two broadcast rounds, assuming two-round oblivious transfer (OT) and tolerating \(t<n\) corruptions.
-
In the honest-majority setting, Ananth et al. [2] and Applebaum et al. [4] showed that security with selective abort can be achieved using two point-to-point rounds assuming OWF.
-
Patra and Ravi [60] showed that in the plain model (without any setup assumptions, such as a PKI) security with unanimous abort cannot be achieved in two point-to-point rounds, and even if the first round can use a broadcast channel. As pointed out in [62], the lower-bounds proofs from [60] do not extend to a setting with private-coins setup.
While advancing our understanding of what kind of security can be achieved in two rounds, the picture derived from the results above is only partial and does not resolve the question of whether the feasibility results can be pushed further. For example, is it possible to obtain identifiable abort via two broadcast rounds for \(t<n\)? Is it possible to achieve selective abort via two point-to-point rounds for \(t<n\)? What security can be achieved when broadcast is used only in a single round in a two-round MPC protocol? This motivates the main question we study in this paper:
What is the tradeoff between the use of broadcast and achievable security in two-round MPC?
1.2 Our Contributions
We devise a complete characterization of the feasibility landscape of two-round MPC against arbitrarily many malicious corruptions, with respect to the above three levels of security (with abort) depending on availability of a broadcast channel. Specifically, we consider all possible combinations of broadcast and point-to-point rounds—where a point-to-point round consists of only point-to-point communication whereas in a broadcast round at least one party uses the broadcast channel—i.e., no broadcast round, one broadcast round, and two broadcast rounds.
Our results are summarized in Table 1. For simplicity we prove our positive results secure against a static t-adversary, for \(t<n\). Although we do not see a specific reason why an adaptive adversary cannot be tolerated, treating this stronger case would need a careful modification of our arguments; we leave a formal treatment of an adaptive adversary as an open question. All our negative results hold for a static adversary, and hence also for an adaptive adversary, since the latter is a stronger adversary. We note that due to the ordering in strength of the security definitions discussed above, any positive (feasibility) result implies feasibility for any column to its left in the same row, and an impossibility result implies impossibility for any column to its right in the same row.
Next, we give a more detailed description of the results and how they complement the current landscape.
Two Broadcast Rounds MPC. First, as a justification of our search for round-optimal protocols, we observe that as a straightforward corollary of Halevi et al. [43], we can exclude the existence of a single-round general MPC protocol—i.e., MPC for any function. This is true for any of the three security definitions, independently of whether or not the protocol uses a broadcast channel. We can thus focus our attention to protocols with two rounds.
Let us first consider the case where both rounds use a broadcast channel. A simple observation reveals that in this case the strongest notion of security with identifiable abort is feasible. Indeed, the recent results by Garg and Srinivasan [33] and Benhamouda and Lin [9] prove that assuming two-round OT, every function can be securely computed with unanimous abort, tolerating static, malicious corruptions of any subset of the parties.Footnote 2 A simple corollary shows that when starting with an inner protocol that is secure with identifiable abort (e.g., the GMW protocol [40]), the compiled protocol will also be secure with identifiable abort. The proof follows directly by inspecting either one of the proofs of [9, 33]. For completeness, we state this as a corollary below.
Corollary 1
([9, 33]). Assume the existence of a two-round OT protocol secure against a static malicious adversary in the CRS model and let \(t<n\). Then, every efficiently computable n-party function can be securely computed with identifiable abort in the CRS model using two broadcast rounds tolerating a static malicious t-adversary.
This leaves open the cases of both rounds being point-to-point rounds, and of one broadcast round and one point-to-point round, which constitute our main contributions. Interestingly, in the latter case the order of the rounds makes a difference on what security can be achieved.
Impossibility Results. We start our investigation with proving the lower bounds illustrated in Table 1. Towards this goal, we describe a simple three-party function which, due to its properties, can be used in all the associated lower bounds. At a very high level, the chosen function f enjoys two core properties that will be crucial in our impossibility proofs: First, the function takes two inputs from a dedicated party, say \(P _3\), but in any evaluation, the output depends on only one of these values (which of the two inputs is actually used is mandated by the input of the other two parties). Second, f has input independence with respect to \(P _1\)’s input, i.e., an adversary corrupting \(P _2\) and \(P _3\) cannot bias their inputs depending on \(P _1\)’s input. (See Sect. 3 for the function’s definition.)
We note in passing that all our impossibility results hold assuming an arbitrary private-coin setup and are therefore not implied by any existing work. As a result, wherever in our statements broadcast is assumed for some round, the impossibility holds even if point-to-point channels are also available in this round. The reason is that as our proofs hold assuming an arbitrary private-coins setup (e.g, a PKI), the setup can be leveraged to implement secure point-to-point communication over broadcast (using encryption). Thus, adding point-to-point communication in a broadcast round cannot circumvent our impossibilities. This is not necessarily the case when no setup is allowed by the proof, which is an additional justification for proving impossibilities which hold even assuming setup.
Here is how we proceed in gradually more involved steps to complete the impossibility landscape: As a first, easy step we show, using the line of argumentation of HLP [43], that our function f is one of the functions which cannot be computed in a single round even against any one party being semi-honest. This excludes existence of single-round maliciously secure generic MPC protocol against dishonest majorities, even if the single round is a broadcast round, and even if we are settling for security with selective abort and assume an arbitrary correlated-randomness setup (last row in Table 1).
Unanimous Abort Requires Second Round over Broadcast. Next, we turn to two-round protocols and prove impossibility for securely computing f with unanimous abort when only the first round might use broadcast, i.e., the second round is exclusively over point-to-point (rows 3 and 4 in Table 1). This implies that under this communication pattern, security with identifiable abort is also impossible. Looking ahead, this impossibility result is complemented by Theorem 11 (Item 2), which shows that security with selective abort can be achieved in this setting.
The proof is somewhat involved, although not uncommon in lower bounds, but can be summarized as follows: We assume, towards a contradiction, that a protocol \(\pi \) computing f with unanimous abort exists. We then look at an adversary corrupting \(P _1\) and define a sequence of worlds in which \(P _1\)’s second-round messages are gradually dropped—so that in the last world, (the adversarial) \(P _1\) sends no messages to the other parties. By sequentially comparing neighboring worlds, we prove that in all of them, the parties cannot abort and they have to output the output of the function evaluated on the original inputs that were given to the parties. However, as in the last scenario \(P _1\) sends no message in the second round, this means that \(P _2\) and \(P _3\) can compute the output (which incorporates \(P _1\)’s input) already in the first round. This enables a rushing adversary corrupting \(P _2\) and \(P _3\) to evaluate \(f(x_1,x_2,x_3)\) on his favorite inputs for \(x_2\) and \(x_3\) before even sending any protocol message, and depending on the output y decide whether he wants to continue playing with those inputs—and induce the output \(y=f(x_1,x_2,x_3)\) on \(P _1\)—or change his choice of inputs to some \(x_2'\) and \(x_3'\) and induce the output \(y'=f(x_1,x'_2,x'_3)\) on \(P _1\). This contradicts the second property of f, i.e., input independence with respect to \(P _1\)’s input against corrupted \(P _2\) and \(P _3\).
We note in passing that a corollary of [60, Thm. 5] (explicitly stated in the full version [61, Cor. 1]) excluded security with unanimous abort for the case of an honest majority, but only for protocols that are defined in the plain model, without any trusted setup assumptions. Indeed, as pointed out by the authors in [62], their proof technique does not extend to the setting with private-coin setup. In more detail, and to illustrate the difference, consider the setting where the first round is over broadcast (and possibly point-to-point channels) and the second is over point-to-point. The argument for ruling out unanimous abort in [61, Cor. 1] crucially relies on \(P _3\) not be able to distinguish between the case where \(P _2\) does not send messages to \(P _1\) (over a private channel) and the case where \(P _1\) claims not to receive any message. However, given a PKI and a CRS for NIZK, the private channel can be emulated over the broadcast message, and the sender can prove honest behaviour. In this case, \(P _3\) can detect the event where \(P _2\) is cheating towards \(P _1\) in the first round; hence, \(P _1\) and \(P _3\) can jointly detect the attack.
Identifiable Abort Requires Two Broadcast Rounds. As a final step, we consider the case where only the second round might use broadcast—i.e., the first round is over a point-to-point channel. In this case we prove that security with identifiable abort is impossible (row 2 in Table 1). This result, which constitutes the core technical contribution of our work, is once again, complemented by a positive result which shows how to obtain unanimous abort with this communication pattern (Theorem 11). The idea of the impossibility proof is as follows: Once again we start with an assumed protocol \(\pi \) (towards contradiction) and compare two scenarios, where the adversary corrupts \(P _1\) in the first and \(P _2\) in the second. The adversary lets the corrupted party run \(\pi \), but drops any message exchanged between \(P _1\) and \(P _2\) in the first (point-to-point) round. By comparing the views on the two scenarios we show that aborting is not an option. Intuitively, the reason is that identifiable abort requires the parties to agree on the identity of a corrupted party; but the transcripts of the two executions are identical despite the corrupted party’s identity being different, which means that if the parties try to identify a cheater, they will get it wrong (with noticeable probability) in one of the two scenarios.
Subsequently, we compare the world where \(P _2\) is corrupted with one where the adversary corrupts also \(P _1\) but has him play honestly; the correctness of the protocol (and the fact that the protocol machines are not aware of who is corrupted) ensures that despite the fact that \(P _1\) is corrupted, his initial input will be used for computing the output of the honest party (which recall cannot abort as its view is identical to the other two scenarios). In this world, \(P _2\) sends nothing to \(P _3\) in Round 1, but \(P _1\) and \(P _3\) exchange their first-round messages. Therefore, a rushing adversary can obtain \(P _3\)’s second-round message before sending any message on behalf of \(P _2\). Using this information, the adversary can run in its head two executions of the protocol using the same messages for \(P _3\) (and same first-round messages for \(P _1\)) but on different inputs for \(P _2\). This will allow extracting both inputs of \(P _3\), thereby violating the first property of the function discussed above.
Note that this proof is more involved than the previous one excluding unanimous abort. For example, while the previous proof merely required the adversary to “bias” the output, the current proof requires the adversary to extract both inputs of the honest \(P _3\); essentially, we use the indistinguishable hybrids to construct an extractor. Indeed, the above is only a sketch of the argument, and the formal proof needs to take care of a number of issues: First, since an honest \(P _3\) can detect that \(P _2\) is cheating, the security definition only guarantees that \(P _3\)’s output will be consistent with some input value of \(P _2\). In that case, it is not clear that the adversary can have strategies which yield both inputs of \(P _3\), which would exclude the possibility of the above attack. We prove that this is not the case, and that using the honest strategy, the adversary can induce an execution in which the different input distributions required by the proofs are used in the evaluation of the function. Second, in order to extract the two inputs of \(P _3\), the adversary needs to know the output as well as the effective corrupted inputs on which the function is evaluated under our above attack scenarios. We ensure this by a simple syntactic manipulation of the function, i.e., by requiring each party to locally (and privately) output its own input as used in the evaluation of the function’s output.
Observe that although our results are proved for three parties, they can be easily extended to n parties by a standard player-simulation argument [46]—in fact, because our adversary corrupts 2 out of the 3 parties, our result exclude any adversary corrupting \(t\ge 2n/3\) of the parties.
Feasibility Results. Next, we proceed to provide matching upper bounds, showing that security with unanimous abort is feasible when the second round is over broadcast (even if the first round is over point-to-point), and that security with selective abort can be achieved when both rounds are over point-to-point channels. Our results are based on the compiler of Ananth et al. [2], who focused on information-theoretic security of two-round MPC in the honest-majority setting.Footnote 3 Ananth et al. [2], initially adjusted the two-round protocol from [1] to provide information-theoretic security with unanimous abort in the broadcast model (for \(\mathsf {NC} ^1\) circuits), and then compiled it to provide security with selective abort over point-to-point channels.Footnote 4
Compiling Two-Broadcast-Round Protocols. We start by presenting an adaptation of the compiler from [2] to the dishonest-majority setting. Let \(\pi _{\mathsf {bc}} \) be a two-round MPC protocol in the broadcast model that is secure with unanimous abort. We first discuss how to compile \(\pi _{\mathsf {bc}} \) to a protocol in which the first round is over point-to-point and the second round is over broadcast.
-
In the compiled protocol, every party \(P _i\) starts by computing its first-round message in \(\pi _{\mathsf {bc}} \), denoted \(m_i^1\). In addition, \(P _i\) considers its next-message function for the second round
 (that computes \(P _i\)’s second round message based on its input \(x_i\), randomness \(r_i\), and all first-round messages). Each party “hard-wires” its input and randomness to the circuit computing
(that computes \(P _i\)’s second round message based on its input \(x_i\), randomness \(r_i\), and all first-round messages). Each party “hard-wires” its input and randomness to the circuit computing  such that given all first-round messages as input, the circuit outputs \(P _i\)’s second-round message. Next, \(P _i\) garbles this circuit and secret-shares each input label using an additive secret-sharing scheme. In the first round of the compiled protocol, each party sends to each other party over private channels his first-round message from \(\pi _{\mathsf {bc}} \) and one share of each garbled label. (Note that for all the parties, the “adjusted” second-round circuits should receive the same input values, i.e., the first-broadcast-round messages.)
such that given all first-round messages as input, the circuit outputs \(P _i\)’s second-round message. Next, \(P _i\) garbles this circuit and secret-shares each input label using an additive secret-sharing scheme. In the first round of the compiled protocol, each party sends to each other party over private channels his first-round message from \(\pi _{\mathsf {bc}} \) and one share of each garbled label. (Note that for all the parties, the “adjusted” second-round circuits should receive the same input values, i.e., the first-broadcast-round messages.) -
In case \(P _i\) didn’t receive messages from all other parties he aborts. Otherwise, \(P _i\) receives from every \(P _j\) the message \(m^1_{j\rightarrow i}\) (i.e., first-round messages of \(\pi _{\mathsf {bc}} \)) and for each input wire of the next-message function of \(P _j\), two shares: one for value 0 and the other for value 1 (recall that each bit that is broadcasted in the first round of \(\pi _{\mathsf {bc}} \) forms an input wire in each circuit). In the second round, every party sends to all other parties the garbled circuit as well as one share from each pair, according to the messages received in the first round \((m^1_{1\rightarrow i},\ldots ,m^1_{n\rightarrow i})\).
-
Next, every party reconstructs all garbled labels and evaluates each garbled circuit to obtain the second-round messages of \(\pi _{\mathsf {bc}} \). Using these messages the output value from \(\pi _{\mathsf {bc}} \) is obtained.
Proof Intuition. Intuitively, if all honest parties receive the same “common part” of the first-round message (corresponding to the first broadcast round of \(\pi _{\mathsf {bc}} \)), they will be able to reconstruct the garbled labels and obtain the second-round message of each party by evaluating the garbled circuits. Note that since the second round is over broadcast, it is guaranteed that all honest parties will evaluate the same garbled circuits using the same garbled inputs, and will obtain the same output value. If there exists a pair of parties that received different first-round messages, then none of the parties will be able to reconstruct the correct labels.
Given an adversary \(\mathcal {A} _\mathsf {{out}} \) to the outer protocol (that uses a first point-to-point round) a simulator \(\mathcal {S} _\mathsf {{out}} \) is constructed using a simulator \(\mathcal {S} _\mathsf {{in}} \) for the inner protocol (in the broadcast model). At a high level, \(\mathcal {S} _\mathsf {{out}} \) will use \(\mathcal {S} _\mathsf {{in}} \) to simulate the first-round messages of the honest parties, send them (with the appropriate synthetic adjustments) to \(\mathcal {A} _\mathsf {{out}} \), and get the corrupted parties’ first-round messages.
-
In case they are not consistent, \(\mathcal {S} _\mathsf {{out}} \) will send \(\mathsf {abort}\) to the trusted party and resume by simulating garbled circuits that output dummy values in the second round—this is secure since the labels for these garbled circuits will not be revealed.
-
In case they are consistent, \(\mathcal {S} _\mathsf {{out}} \) will use the inner simulator \(\mathcal {S} _\mathsf {{in}} \) to extract the input values of the corrupted parties and send them to the trusted party. Once receiving the output, \(\mathcal {S} _\mathsf {{out}} \) can hand it to \(\mathcal {S} _\mathsf {{in}} \) who outputs the second-round messages for the honest parties. Next, \(\mathcal {S} _\mathsf {{out}} \) will use these messages to simulate the garbled circuits of the honest parties and hand them to \(\mathcal {A} _\mathsf {{out}} \). Based on the response from \(\mathcal {A} _\mathsf {{out}} \) (i.e., the second-round messages) \(\mathcal {S} _\mathsf {{out}} \) will send \(\mathsf {abort}\) or \(\mathsf {continue}\) to the trusted party and halt.
We remark that the proof in [2] also follows this intuition; however, that proof uses specific properties of the (simulator for the) broadcast-model protocol constructed in [2] (which in turn is based on the protocol from [1]). Our goal is to provide a generic compiler, which works for any two-round broadcast-model protocol, and so our use of the simulator for the broadcast-model protocol must be black-box. For that purpose, we devise non-trivial new simulation techniques, which we believe might be of independent interest. Our proof can be adapted to demonstrate that the original compilation technique of [2] is, in fact, generic, i.e., can securely compile any broadcast-hybrid protocol.
To explain the technical challenge and our solution, let us discuss the above issue in more detail: Recall that the security definition for the stand-alone modelFootnote 5 from [39] guarantees that for every adversary there is a simulator for the ideal computation (in the current case, ideal computation with unanimous abort). The simulator is invoked with some auxiliary information, and starts by sending to the trusted party inputs for the corrupted parties (or \(\mathsf {abort}\)). Upon receiving the output value, the simulator responds with \(\mathsf {abort}\)/\(\mathsf {continue}\), and finally generates its output which is computationally indistinguishable from the view of the adversary in a protocol (where the honest parties’ outputs are distributed according to the extracted corrupted-parties’ inputs).
Given an adversary \(\mathcal {A} _\mathsf {{out}} \) for the compiled protocol \(\pi \), we would like to use the security of \(\pi _{\mathsf {bc}} \) to construct a simulator \(\mathcal {S} _\mathsf {{out}} \) and simulate the “common part” of the honest parties’ messages (i.e., the messages \(m^1_{i\rightarrow j}\) from an honest \(P _i\) to a corrupted \(P _j\)). However, the adversary \(\mathcal {A} _\mathsf {{out}} \) induces multiple adversaries for \(\pi _{\mathsf {bc}} \), one for every honest party and it is not clear which simulator (i.e., for which of these adversaries) should be used. In fact, before interacting with \(\mathcal {A} _\mathsf {{out}} \) and sending him the first-round messages of honest parties, \(\mathcal {S} _\mathsf {{out}} \) should first run one (or a few) of the aforementioned simulators to get the inputs for the corrupted parties, invoke the trusted party with the input values, and get back the output. (At this point the simulator is committed to the corrupted parties’ inputs.)Footnote 6 Only then can \(\mathcal {S} _\mathsf {{out}} \) send the output back to the inner simulator(s) and get the view of the inner adversary (adversaries) in the execution, and use it to interact with \(\mathcal {A} _\mathsf {{out}} \).
Receiver-Specific Adversaries. To solve this conundrum, we construct our simulator as follows: For every honest party \(P _j\) we define a receiver-specific adversary \(\mathcal {A} _\mathsf {{in}} ^j\) for \(\pi _{\mathsf {bc}} \), by forwarding the first-broadcast-round messages to \(\mathcal {A} _\mathsf {{out}} \) and responding with the messages \(\mathcal {A} _\mathsf {{out}} \) sends to \(P _j\) (recall that \(\mathcal {A} _\mathsf {{out}} \) can send different messages to different honest parties in \(\pi \)). By the security of \(\pi _{\mathsf {bc}} \), for every such \(\mathcal {A} _\mathsf {{in}} ^j\) there exists a simulator \(\mathcal {S} _\mathsf {{in}} ^j\).
To define the simulator \(\mathcal {S} _\mathsf {{out}} \) (for the adversary \(\mathcal {A} _\mathsf {{out}} \)), we use one of the simulators \(\mathcal {S} _\mathsf {{in}} ^j\) corresponding to the honest parties. \(\mathcal {S} _\mathsf {{out}}\) initially receives from \(\mathcal {S} _\mathsf {{in}} ^j\) either the corrupted parties’ inputs or an \(\mathsf {abort}\) message, and forwards the received message to the trusted party. If \(\mathcal {S} _\mathsf {{in}} ^j\) does not abort, \(\mathcal {S} _\mathsf {{out}} \) receives back the output value y, forwards y to \(\mathcal {S} _\mathsf {{in}} ^j\) and receives the simulated second-round messages from \(\mathcal {S} _\mathsf {{in}} ^j\)’s output. Next, \(\mathcal {S} _\mathsf {{out}} \) invokes \(\mathcal {A} _\mathsf {{out}} \) and simulates the first-round messages of \(\pi \) (using the simulated first-round messages for \(\pi _{\mathsf {bc}} \) obtained from \(\mathcal {S} _\mathsf {{in}} ^j\)), receives back the first-round messages from \(\mathcal {A} _\mathsf {{out}} \), and checks whether these messages are consistent. If so, \(\mathcal {S} _\mathsf {{out}}\) completes the simulation by constructing simulated garbled circuits that output the correct second-round messages (if \(\mathcal {A} _\mathsf {{out}} \)’s messages are consistent, the simulated messages by \(\mathcal {S} _\mathsf {{in}} ^j\) are valid for all honest parties). If \(\mathcal {A} _\mathsf {{out}} \)’s messages are inconsistent, \(\mathcal {S} _\mathsf {{out}} \) simulates garbled circuits that output dummy values (e.g., zeros), which is acceptable since the \(\mathcal {A} _\mathsf {{out}} \) will not learn the labels to open them. We refer the reader to Sect. 4.2 for a detailed discussion and a formal proof.
Selective Abort via Two point-to-point Rounds. After showing that the compiler from [2] can be adjusted to achieve unanimous abort when the first round is over point-to-point and the second is over broadcast, we proceed to achieve selective abort when both rounds are over point-to-point, facing any number of corruptions. The main difference from the previous case is that the adversary can send different garbled circuits to different honest parties in the second round, potentially causing them to obtain different output values, which would violate correctness (recall that the definition of security with selective abort permits some honest parties to abort while other obtain the correct output, but it is forbidden for two honest parties to obtain two different output values). However, we reduce this attack to the security of \(\pi _{\mathsf {bc}} \) and show that it can only succeed with negligible probability.
Organization of the Paper. Preliminaries are presented in Sect. 2. In Sect. 3 we present our impossibility results and in Sect. 4 our feasibility results. Due to space limitations, complementary material and some of the proofs can be found in the full version [23].
2 Preliminaries
In this section, we introduce some necessary notation and terminology. We denote by \(\kappa \) the security parameter. For \(n\in \mathbb {N}\), let \([n]=\{1,\cdots ,n\}\). Let \(\textsf {poly}\) denote the set of all positive polynomials and let PPT denote a probabilistic algorithm that runs in strictly polynomial time. A function \(\nu :\mathbb {N} \rightarrow [0,1]\) is negligible if \(\nu (\kappa )<1/p(\kappa )\) for every \(p\in \textsf {poly}\) and large enough \(\kappa \). Given a random variable X, we write \(x\leftarrow X\) to indicate that x is selected according to X.
2.1 Security Model
We provide the basic definitions for secure multiparty computation according to the real/ideal paradigm (see [12, 13, 39] for further details), capturing in particular the various types of unsuccessful termination (“abort”) that may occur. For simplicity, we state our results in the stand-alone setting, however, all of our results can be extended to the UC framework [13].
Real-World Execution. An n-party protocol \(\pi = (P _1,\ldots ,P _n)\) is an n-tuple of PPT interactive Turing machines. The term party \(P _i\) refers to the \(i\)’th interactive Turing machine. Each party \(P _i\) starts with input \(x_i\in \{0,1\}^*\) and random coins \(r_i\in \{0,1\}^*\). Without loss of generality, the input length of each party is assumed to be the security parameter \(\kappa \). An adversary \(\mathcal {A}\) is another interactive TM describing the behavior of the corrupted parties. It starts the execution with input that contains the identities of the corrupted parties and their private inputs, and an additional auxiliary input. The parties execute the protocol in a synchronous network. That is, the execution proceeds in rounds: Each round consists of a send phase (where parties send their messages from this round) followed by a receive phase (where they receive messages from other parties). The adversary is assumed to be rushing, which means that he can see the messages the honest parties send in a round before determining the messages that the corrupted parties send in that round.
The parties can communicate in every round over a broadcast channel or using a fully connected point-to-point network. The communication lines between the parties are assumed to be ideally authenticated and private (and thus the adversary cannot modify messages sent between two honest parties nor read them).Footnote 7
Throughout the execution of the protocol, all the honest parties follow the instructions of the prescribed protocol, whereas the corrupted parties receive their instructions from the adversary. The adversary is considered to be actively malicious, meaning that he can instruct the corrupted parties to deviate from the protocol in any arbitrary way. At the conclusion of the execution, the honest parties output their prescribed output from the protocol, the corrupted parties do not output anything and the adversary outputs an (arbitrary) function of its view of the computation (containing the views of the corrupted parties). The view of a party in a given execution of the protocol consists of its input, its random coins, and the messages it sees throughout this execution.
Definition 1
(Real-world execution). Let \(\pi = (P _1,\ldots , P _n)\) be an n-party protocol and let \(\mathcal {I} \subseteq [n]\) denote the set of indices of the parties corrupted by \(\mathcal {A} \). The joint execution of \(\pi \) under \((\mathcal {A},\mathcal {I})\) in the real model, on input vector \({\varvec{x}}= (x_1,\ldots , x_n)\), auxiliary input \(\mathsf {aux} \) and security parameter \(\kappa \), denoted \(\text{ REAL }_{\pi ,\mathcal {I},\mathcal {A} (\mathsf {aux})}({\varvec{x}},\kappa )\), is defined as the output vector of \(P _1,\ldots ,P _n\) and \(\mathcal {A} (\mathsf {aux})\) resulting from the protocol interaction.
Ideal-World Execution (with abort). We now present standard definitions of ideal computations that are used to define security with identifiable abort, unanimous abort, and selective (non-unanimous) abort. For further details see [19, 41, 50].
An ideal computation with abort of an n-party functionality f on input \({\varvec{x}}=(x_1,\ldots ,x_n)\) for parties \((P _1,\ldots ,P _n)\) in the presence of an adversary (a simulator) \(\mathcal {S} \) controlling the parties indexed by \(\mathcal {I} \subseteq [n]\), proceeds via the following steps.
-
Sending inputs to trusted party: An honest party \(P _i\) sends its input \(x_i\) to the trusted party. The adversary may send to the trusted party arbitrary inputs for the corrupted parties. Let \(x_i'\) be the value actually sent as the input of party \(P _i\).
-
Trusted party answers adversary: The trusted party computes \(y=f(x_1', \ldots , x_n')\). If there are corrupted parties, i.e., if \(\mathcal {I} \ne \emptyset \), send y to \(\mathcal {S} \). Otherwise, proceed to step Trusted party answers remaining parties.
-
Adversary responds to trusted party: The adversary \(\mathcal {S} \) can either select a set of parties that will not get the output by sending an \((\mathsf {abort},\mathcal {J})\) message with \(\mathcal {J} \subseteq [n]\setminus \mathcal {I} \), or allow all honest parties to obtain the output by sending a \(\mathsf {continue} \) message.
-
Trusted party answers remaining parties: If \(\mathcal {S} \) has sent an \((\mathsf {abort},\mathcal {J})\) message with \(\mathcal {J} \subseteq [n]\setminus \mathcal {I} \) and \(\mathcal {I} \ne \emptyset \), the trusted party sends \(\bot \) to every party \(P _j\) with \(j\in \mathcal {J} \) and y to every \(P _j\) with \(j\notin \mathcal {J} \cup \mathcal {I} \). Otherwise, if the adversary sends a \(\mathsf {continue} \) message or if \(\mathcal {I} =\emptyset \), the trusted party sends y to \(P _i\) for every \(i\notin \mathcal {I} \).
-
Outputs: Honest parties always output the message received from the trusted party while the corrupted parties output nothing. The adversary \(\mathcal {S} \) outputs an arbitrary function of the initial inputs \(\left\{ x_i\right\} _{i\in \mathcal {I}}\), the messages received by the corrupted parties from the trusted party and its auxiliary input.
Definition 2
(Ideal computation with selective abort). Let \(f :(\{0,1\}^*)^n \rightarrow (\{0,1\}^*)^n\) be an n-party functionality and let \(\mathcal {I} \subseteq [n]\) be the set of indices of the corrupted parties. Then, the joint execution of f under \((\mathcal {S}, \mathcal {I})\) in the ideal computation, on input vector \({\varvec{x}}=(x_1, \ldots , x_n)\), auxiliary input \(\mathsf {aux} \) to \(\mathcal {S} \) and security parameter \(\kappa \), denoted  , is defined as the output vector of \(P _1, \ldots , P _n\) and \(\mathcal {S} \) resulting from the above described ideal process.
, is defined as the output vector of \(P _1, \ldots , P _n\) and \(\mathcal {S} \) resulting from the above described ideal process.
We now define the following variants of this ideal computation:
-
Ideal computation with unanimous abort. This ideal computation proceeds as in Definition 2, with the difference that in order to abort the computation, the adversary simply sends \(\mathsf {abort} \) to the trusted party (without specifying a set \(\mathcal {J} \)). In this case, the trusted party responds with \(\bot \) to all honest parties. This ideal computation is denoted as
 .
. -
Ideal computation with identifiable abort. This ideal computation proceeds as the ideal computation with unanimous abort, with the exception that in order to abort the computation, the adversary chooses an index of a corrupted party \({i^*}\in \mathcal {I} \) and sends \((\mathsf {abort},{i^*})\) to the trusted party. In this case, the trusted party responds with \((\bot ,{i^*})\) to all parties. This ideal computation is denoted as
 .
.
Security Definitions. Having defined the real and ideal computations, we can now define security of protocols.
Definition 3
Let  . Let \(f:(\{0,1\}^*)^n \rightarrow (\{0,1\}^*)^n\) be an n-party functionality. A protocol \(\pi \) t -securely computes f with “type” if for every PPT real-world adversary \(\mathcal {A}\), there exists a PPT adversary \(\mathcal {S} \), such that for every \(\mathcal {I} \subseteq [n]\) of size at most t, it holds that
. Let \(f:(\{0,1\}^*)^n \rightarrow (\{0,1\}^*)^n\) be an n-party functionality. A protocol \(\pi \) t -securely computes f with “type” if for every PPT real-world adversary \(\mathcal {A}\), there exists a PPT adversary \(\mathcal {S} \), such that for every \(\mathcal {I} \subseteq [n]\) of size at most t, it holds that
3 Impossibility Results
In this section, we prove our impossibility results. Concretely, in Sect. 3.1, we argue that there is no single-round maliciously secure generic MPC protocol against dishonest majorities, even if the single round is a broadcast round, and even if we are settling for security with selective abort and we assume an arbitrary correlated-randomness setup. Subsequently, in Sect. 3.2, we prove that no generic two-round MPC protocol can achieve security with identifiable abort, while making use of broadcast in only one of the two rounds. This holds irrespective of whether the broadcast round is the first or second one. Towards this goal, we start by proving that no two-round protocol in which the broadcast round is first—i.e., the second round is over point-to-point—can achieve identifiable abort. This is proved in Theorem 1; in fact, the theorem proves a stronger statement, namely, that there is a function f such that no protocol with the above structure can securely compute f with unanimous abort.Footnote 8
Theorem 1 implies that the only option for a two-round protocol with only one broadcast round to securely compute f with identifiable abort, is if the broadcast round is the second round—i.e., the first round is over point-to-point. We prove (Theorem 7) that this is also impossible, i.e., f cannot be computed by such a protocol. This proves that the result from Theorem 11 (Item 1), which achieves security with unanimous abort in this case, is also tight and completes the (in)feasibility landscape for two-round protocols. Furthermore, we note that all the results proved in this section hold for both computational and information-theoretic security, even if we assume access to an arbitrary correlated-randomness setup.
A Simple Function. Before starting our sequence of impossibility results, we first introduce a simple function which we will use throughout this section. Consider the following three-party public-output function (i.e., all three parties receive the output): The parties, \(P _1, P _2,\) and \(P _3\), hold inputs \(x_1\in \{0,1\}\times \{0,1\}\), \(x_2\in \{0,1\}\) and \(x_3\in \{0,1\}^\kappa \times \{0,1\}^\kappa \), respectively, where \(x_1=(x_{1,1},x_{1,2})\) and \(x_3=(x_{3,1},x_{3,2})\). For a bit b we denote by \(b^\kappa \) the string resulting from concatenating \(\kappa \) times the bit b (recall that \(\kappa \) denotes the security parameter). The function is defined as follows:
Note that in the above function, the first bit of \(P _1\), i.e., \(x_{1,1}\) contributes to the computed XOR, whereas the relation between the second bit of \(P _1\), i.e., \(x_{1,2}\), and the input-bit \(x_2\) of \(P_2\) is the one which defines which of the \(x_{3,1}\) or \(x_{3,2}\) will be used in the output. One can easily verify that the following is a more compact representation of f:
The latter representation will be useful in the proof of Theorem 7.
As discussed in the introduction, the above function enjoys the following two useful properties: First, it is impossible in the ideal world (where parties and an adversary/simulator have access to a TTP for f) for the simulator to learn both inputs of \(P _3\) even if he corrupts both \(P _1\) and \(P _2\). Second, assuming the input \(x_{1,1}\) of \(P_1\) is chosen uniformly at random, it is impossible for a simulator corrupting \(P _2\) and \(P _3\) to fix the output to 0. We prove these two properties in the corresponding theorems where they are used.
3.1 Impossibility of Single-Round MPC
As a simple corollary of HLP [43] (see also [60]), we can exclude the existence of a semi-honestly secure MPC protocol for the above function.
Corollary 2
([43]). The function f cannot be computed with selective abort by a single-round protocol tolerating one semi-honest corrupted party.
Extending Corollary 2 to the multi-party case (involving more than three parties) follows using a player-simulation argument, and the following facts that are implied by our definition of security with selective abort: (1) If the adversary follows his protocol, the evaluation cannot abort even if parties are corrupted; this follows from the non-triviality condition and the fact that when the adversary follows the protocol with his corrupted parties, the protocol cannot deviate based on the fact that parties are corrupted; (2) for such an honest-looking adversary [14], the protocol achieves all the guarantees required for semi-honest security—i.e., there is a simulator which simulates the adversary’s entire view from the inputs and outputs of corrupted parties.
Corollary 3
For \(n\ge 3\), there exist an n-party function \(f_n\) for which there is no single-round protocol \(\pi \) which securely computes \(f_n\) with selective abort against even a single corruption. The statement is true even if \(\pi \) uses a broadcast channel in its single round.
3.2 Impossibility of Single-Broadcast Two-Round MPC
Having excluded the possibility of single-round MPC protocols, we next turn to two rounds. Throughout this section, we prove impossibility statements for three-party protocols (for the function f). As discussed in the introduction, all our statements can be directly extended to the multi-party setting using the straightforward extension of f to n parties (cf. function \(f_n\) in Corollary 3).
Impossibility of Unanimous Abort When Broadcast Is First Round. We start by proving impossibility of security with unanimous abort for f against corrupted majorities. Analogous to [43] we will say that an adversary learns the residual function \(f(x_1,\cdot ,\cdot )\) to denote the event that the adversary learns enough information to locally and efficiently compute \(f(x_1,x_2^*,x_3^*)\) on any (and as many) inputs \(x_2^*\) and \(x_3^*\) as he wants.
Theorem 1
There exists no two-round protocol \(\pi \) which securely computes f with unanimous abort against corrupted majorities while making use of the broadcast channel only in the first round (i.e., where the second round is over point-to-point channels). The statement is true even assuming an arbitrary correlated randomness setup.
Proof
Towards a contradiction, assume that there is protocol \(\pi =(\pi _1,\pi _2,\pi _3)\), where \(\pi _i\) is the code (e.g., interactive Turing machine) of \(P _i\), for computing f with unanimous abort which uses broadcast in its first round, but only point-to-point in the second round. Consider executions of \(\pi \) on uniformly random inputs \(x_1\) and \(x_2\) for \(P _1\) and \(P _2\) and on input \(x_3\in \{(0^\kappa ,1^\kappa ),(1^\kappa ,0^\kappa )\}\) from \(P _3\) in the following scenarios (see Fig. 1 for an illustration). In all four scenarios, the adversary uses the honest input for the corrupted party and allows him to execute his honest protocol on uniform random coins, but might drop some of the messages the corrupted party’s protocol attempts to send in Round 2.
The scenarios from the proof. All protocols are executed as specified; whenever an arrow is present it indicates that the message that the corresponding protocol would send is indeed sent; missing arrows indicate that respective messages are dropped. A shade on the background of a protocol indicates that the corresponding party is corrupted (but the adversary still executes the respective protocol on the honest input, but might drop some messages).
-
Scenario 1: The adversary corrupts \(P _1\), plays the first round according to \(\pi \) but sends no messages in the second round.
-
Scenario 2: The adversary corrupts \(P _1\), plays both rounds according to \(\pi \), but does not send his second-round message towards \(P _3\); party \(P _2\) receives his second-round message according to the honest protocol.
-
Scenario 3: The adversary corrupts \(P _1\) but plays the honest protocols in both rounds.
-
Scenario 4: No party is corrupted.
The proof of the theorem proceeds as follows: By a sequence of comparisons between the four scenarios we show that in Scenario 1, \(\pi _2\) and \(\pi _3\) cannot abort and will have to produce output equal to \(f(x_1,x_2,x_3)\) with overwhelming probability despite the fact that \(P _1\) sends no message in Round 2. This means that a (rushing)Footnote 9 adversary corrupting \(P _2\) can learn the residual function \(f(x_1,\cdot ,\cdot )\) already in Round 1 and before committing to any inputs for \(P _2\) and \(P _3\). This allows him to choose corrupted inputs depending on (the honest input) \(x_1\) violating the security (in particular the input-independence property)Footnote 10 of \(\pi \). The formal argument follows. For notational clarity, we will denote the message that \(P _i\) sends to \(P _j\) over a point to point channel in round \(\rho \) by \(m_{\rho ,i\rightarrow j}\); if in round \(\rho \) a party \(P _i\) broadcasts a messages, we will denote this message by \(m_{\rho ,i\rightarrow *}\). Due to space limitations, the proof for these claim are deferred to the full version [23].
Claim 2
In Scenario 3, parties \(P _2\) and \(P _3\) output \(f(x_1,x_2,x_3)\) with overwhelming probability.
Claim 3
In Scenario 2, parties \(P _2\) and \(P _3\) output \(f(x_1,x_2,x_3)\) with overwhelming probability.
Claim 4
In Scenario 1, parties \(P _2\) and \(P _3\) output \(f(x_1,x_2,x_3)\) with overwhelming probability.
Claim 5
An adversary corrupting \(P _2\) and \(P _3\) can learn the residual function \(f(x_1,\cdot ,\cdot )\) before \(P _2\) or \(P _3\) send any message.
To complete the proof of the theorem, we show that existence of the above adversary \(\mathcal {A} \) implies an adversary \(\mathcal {A} '\) that can break the security (in particular, the input independence) of \(\pi \). Intuitively, \(\mathcal {A} '\) will corrupt \(P _2\) and \(P _3\) and use the strategy of the adversary \(\mathcal {A} \) from the above claim to learn the residual function before committing to his own input to f; thus \(\mathcal {A} '\) is free to choose this inputs for \(P _2\) and \(P _3\) depending on \(x_1\). We next provide a formal proof of this fact by describing a strategy for biasing the output (depending on \(x_1\)) which cannot be simulated.
Concretely, consider the following \(\mathcal {A} '\) that corrupts \(P _2\) and \(P _3\): \(\mathcal {A} '\) receives \(m_{1,1\rightarrow *}\) from \(P _1\) and using \(\mathcal {A} \), for \(x_2^*=0\) and \(x_{3,1}*=0^\kappa \) and \(x_{3,2}*=1^\kappa \), \(\mathcal {A} '\) computes \(y=f(x_1,0,(0^\kappa ,1^\kappa ))\). Then, dependent on whether y is \(0^\kappa \) or \(1^\kappa \)—observe that by definition of the function, these are the only two possible outcomes given the above inputs of \(P _3\)—\(\mathcal {A} '\) distinguishes two cases:
-
Case 1: If \(y=0^\kappa \) then execute the honest protocol for \(P _2\) and \(P _3\) with these inputs, i.e., \(x_2=0\) and \(x_{3,1}=0^\kappa \) and \(x_{3,2}=1^\kappa \).
-
Case 2: If \(y=1^\kappa \), then execute the honest protocol for \(P _2\) and \(P _3\) with the inputs of \(P _3\) swapped, i.e., \(x_2=0\) and \(x_{3,1}=1^\kappa \) and \(x_{3,2}=0^\kappa \).
Note that in both cases \(P _1\) witnesses a view which is indistinguishable from the honest protocol with inputs: \(x_2=0\) and \(x_{3,1}=0^\kappa \) and \(x_{3,2}=1^\kappa \) (Case 1) or \(x_2=0\) and \(x_{3,1}=1^\kappa \) and \(x_{3,2}=0^\kappa \) (Case 2); hence, the correctness of \(\pi \) implies that with overwhelming probability if \(y=f(x_1,0,(0^\kappa ,1^\kappa ))=0^\kappa \) then \(P _1\) will output it, otherwise, i.e., if \(y=f(x_1,0,(0^\kappa ,1^\kappa ))=1^\kappa \) he will output \(y=f(x_1,0,(1^\kappa ,0^\kappa ))\); but in this latter case \(y=0^\kappa \) by the definition of f. Hence, this adversary always makes \(P _1\) output \(0^\kappa \).
To complete the proof we prove that in an ideal evaluation of f with an honest \(P _1\) and corrupted \(P _2\) and \(P _3\), if \(P _1\) uses a uniformly random input and no abort occurs, then the output can be \(0^\kappa \) with probability at most \(1/2\pm \textsf {negl}(\kappa )\).
Claim 6
For any simulator \(\mathcal {S} \) corrupting \(P _2\) and \(P _3\) and not causing the ideal execution to abort, if \(P _1\)’s input is chosen uniformly at random, then for any choice of inputs for \(P _2\) and \(P _3\), there exist a string \(z\in \{0,1\}^\kappa \) such that the output of \(P _1\) will be z or \(\bar{z}\) each with probability \(1/2\pm \textsf {negl}(\kappa ).\)
The above claim implies that for any simulator, with probability at least 1/2 the output will be different than \(0^\kappa \). Hence the adversary \(\mathcal {A} '\) (who, recall, always fixes the output to \(0^\kappa \)) cannot be simulated which contradicts the assumed security of \(\pi \).
Impossibility of Identifiable Abort. Next, we proceed to the proof of our second, and main, impossibility theorem about identifiable abort. For this proof we make the following modification to f: In addition to its output from f, every party \(P _i\) is required to locally output his own input \(x_i\). We denote this function by \(\hat{f}\). Specifically, the output of \(\hat{f}\) consists of two parts: A public part that is identical to f, which is the same for all parties (without loss of generality, we will use \(f(x_1,x_2,x_3) \) to denote this part), and a private part which for each \(P _i\) is its own input.
We remark that impossibility for such a public/private output function \(\hat{f}\) implies impossibility of public output functions via the standard reduction of private to public input functions (see [39]).
Theorem 7
The function \(\hat{f}\) cannot be securely computed with identifiable abort by a three-party protocol that uses one point-to-point round and one broadcast round, tolerating (up to) two corrupted parties. This is true even assuming an arbitrary correlated-randomness setup.
Proof
Assume, towards a contradiction, that a protocol \(\pi \) exists for the function \(\hat{f}\). First, note that due to Theorem 1, the broadcast round cannot be the first round. (This holds because security with identifiable abort implies security with unanimous abort.) Hence, the first round of \(\pi \) must be the point-to-point round and the second can be a broadcast round. In the following, we will assume that the second round uses only the broadcast channel; this is without loss of generality as we allow \(\pi \) to be in the correlated-randomness model, which means that parties might share keys that they can use to emulate point-to-point communication over the broadcast network. (Proving impossibility in the correlated-randomness model implies impossibility in the plain model.)
Consider the parties \(P _1\), \(P _2\), and \(P _3\) holding uniformly chosen inputs \(x_1,x_2,\) and \(x_3\) for \(\hat{f}\). Let \(\pi _i\) denote the code executed by \(P _i\) in \(\pi \) (i.e., \(P _i\)’s protocol machine), and consider the following scenarios (also illustrated in Fig. 2):
The scenarios from the proof. All protocols are executed as specified. A shade on the background of a protocol indicates that the corresponding party is corrupted (the adversary still executes the respective protocol on the honest input, but may drop some messages). A solid arrow indicates that the message that the corresponding protocol would send is indeed sent; cut arrows indicate that respective messages are dropped, where we illustrate which adversarial behavior is the reason for dropping a message by scissors; bold arrows indicate that this second-round message depends on the protocol having seen some incomplete transcript (due to dropped messages) in the first round and might therefore adapt its behavior accordingly.
-
Scenario 1: The adversary corrupts only \(P _3\) and has him play \(\pi _3\), but drops the message \(m_{1,3\rightarrow 2}\) that \(\pi _3\) sends to \(P _2\) in the first round (i.e., the message is never delivered to \(\pi _2\)) and does not deliver to \(\pi _3\) the message \(m_{1,2\rightarrow 3}\) received from \(P _2\) in the first round. Other than this intervention, all machines execute their prescribed code and all other messages are sent and delivered as specified by the protocol \(\pi \).
In particular, the instance of \(\pi _3\) which the adversary emulates is not aware that the message \(m_{1,3\rightarrow 2}\) (which it generated and tried to send to \(\pi _2\) in the first round) was never delivered, and is not aware that \(P _2\) did send a message \(m_{1,2\rightarrow 3}\) in the first round, which was blocked. In other words, the internal state of \(\pi _2\) (resp., \(\pi _3\)) reflects the fact that the message to \(\pi _3\) (resp., \(\pi _2\)) is sent, but the message from \(\pi _3\) (resp., \(\pi _2\)) did not arrive.
-
Scenario 2: The adversary corrupts only \(P _2\) and has him play \(\pi _2\) with the modification that he drops the first-round message \(m_{1,3\rightarrow 2}\) received from \(P _3\) (again, the message is never delivered to \(\pi _2\)) and the message \(m_{1,2\rightarrow 3}\) that \(\pi _2\) sends to \(P_3\). Other than this specific intervention, all machines execute their prescribed code and all other messages are sent and delivered as specified by the protocol \(\pi \).
In particular, the simulated instance of \(\pi _2\) is not aware that its first round message \(m_{1,2\rightarrow 3}\) for \(P _3\) was never delivered, and is not aware that \(P _3\) did send the message \(m_{1,3\rightarrow 2}\) in the first round, which was blocked, as above.
-
Scenario 3: The adversary corrupts \(P _1\) and \(P _2\). Both parties play exactly the same protocol as in Scenario 2.
First we observe the following: In all three scenarios the three machines witness the same interaction—i.e., their (joint) internal states are identically distributed. Indeed, all three adversarial strategies have the effect of execution of the prescribed protocol without the first message from \(\pi _3\) to \(\pi _2\) and from \(\pi _2\) to \(\pi _3\). Since \(\pi _1, \pi _2,\) and \(\pi _3\) are protocol-machines (interactive algorithms), their behavior cannot depend on who is corrupted. This means that their (joint) output (distribution) in Scenario 1 must be indistinguishable (in fact, identically distributed) to their output in Scenarios 2 and 3.
Now consider an execution of this protocol on uniformly random inputs. We consider the following two cases for Scenario 1, where the probabilities are defined over the choice of the correlated randomness, the random coins used by the protocols, and the randomness used for selecting the inputs, and analyze them in turn.
Case 1: The Honest Parties Abort (with noticeable probability). We prove that if an abort occurs with noticeable probability, then the security of the protocol is violated: Due to the identifiability requirement, if in Scenario 1 there is an abort, then both \(\pi _1\) and \(\pi _2\) need to output the identity of \(P _3\) (as a cheater) as he is the only corrupted party. However, since as argued above the output distributions in the two scenarios are indistinguishable, the fact that in Scenario 1, \(\pi _1\) aborts with the identity of \(P _3\) with noticeable probability implies that also in Scenario 2, \(\pi _1\) will also abort identifying \(P _3\) with noticeable probability.
By the assumption that \(\pi \) is secure with identifiable abort—which implies that honest parties agree on the identity of a corrupted party in case of abort—the latter statement implies that in Scenario 2, with noticeable probability, \(\pi _3\) will abort with the same cheater, i.e., the honest party \(P _3\) (who is running \(\pi _3\)) will abort identifying itself as a cheater contradicting the fact that \(\pi \) is secure with identifiable abort. (Security with identifiable abort only allows an abort identifying a corrupted party.) This means that the protocol cannot abort with noticeable probability which leaves Case 2, below, as the only alternative.
Case 2: The Honest Parties Do Not Abort (with overwhelming probability). We prove that an adversary corrupting \(P _1\) in addition to \(P _2\) can learn both \(x_{3,1}\) and \(x_{3,2}\) with noticeable probability, which is impossible in an ideal evaluation of \(\hat{f}\), as follows. Observe that since, in this case, the probability of aborting in Scenario 1 is negligible and the joint views of the parties are indistinguishable between the two scenarios, the probability that an abort occurs in Scenario 2 or Scenario 3 is also negligible. Furthermore, because Scenario 3 consist of the same protocols in exactly the same configuration and with the same messages dropped, the output of the protocols in Scenario 3 is distributed identically to the output of the protocol in Scenario 2, namely it is the output of the function on the actual inputs of \(P _1\) and \(P _3\) and some input from \(P _2\).
Next, observe that the security of \(\pi \) for this case implies that for every adversary in Scenario 2 there exists a simulator corrupting \(P _2\). Let \(\mathcal {A} _2\) denote the adversary that chooses an input for \(\pi _2\) uniformly at random and plays the strategy specified in Scenario 2, and let \(\mathcal {S} _2\) denote the corresponding simulator. Denote by \(X_2^*\) the random variable corresponding to the input \(x_2^*\) that \(\mathcal {S} _2\) hands to the functionality for \(\hat{f}\) on behalf of \(P _2\), and denote by \(X_1=(X_{1,1},X_{1,2})\) and \(X_3=(X_{3,1},X_{3,2})\) the random variables corresponding to the inputs of the honest parties. The following claim states that \(X_2^*\) might take any of the values 0 or 1 with noticeable probability.
Claim 8
For each \(b\in \{0,1\}\), \({\mathrm {Pr}}\left[ X_2^*=b\right] \) is noticeable.
Proof
First we note that due to input independence—i.e., because in the ideal experiment the simulator needs to hand inputs corresponding to the corrupted parties before seeing any information about the honest parties’ inputs—it must hold that \({\mathrm {Pr}}\left[ X_2^*=b\right] ={\mathrm {Pr}}\left[ X_2^*=b\mid X_1,X_3\right] \). Hence, it suffices to prove that \({\mathrm {Pr}}\left[ X_2^*=x_2^*\mid X_1,X_3\right] \) is noticeable for each of the two possible input choices \(x_2^*\in \{0,1\}\) for the simulator. Assume towards a contradiction that this is not true. This means that with overwhelming probability the simulator always inputs the same \(x_2^*=b\). Without loss of generality, assume that \(b=0\) (the argument for \(b=1\) is symmetric). Since the protocol aborts only with negligible probability, security implies that the distribution of the public output for every \(P _i\) with this simulator \(\mathcal {S} _2\) is (computationally) indistinguishable from \(f(X_1,0,X_3)=X_{1,1}^\kappa \oplus X_{3,(1+ X_{1,2})}\).
However, since \(\mathcal {S} _2\) is a simulator for \(\pi \) with adversary \(\mathcal {A} _2\) who uses a uniform input in his \(\pi _2\) emulation, this implies that the interaction of the protocols \(\pi _1, \pi _2,\) and \(\pi _3\) in Scenario 2 must also have as public output a value with distribution indistinguishable from \(X_{1,1}^\kappa \oplus X_{3,(1+ X_{1,2})}\). Now, using the fact that the views which the protocol machines in Scenario 2 and 1 are indistinguishable,Footnote 11 we can deduce that the public output in Scenario 1 needs to also be distributed indistinguishably from \(X_{1,1}^\kappa \oplus X_{3,(1+ X_{1,2})}\).
However, in Scenario 1, party \(P _2\) is not corrupted which means that the public output distribution needs to be indistinguishable from \(f(X_1,X_2,X_3^*)\), where \(X_3^*=(X_{3,1}^*,X_{3,2}^*)\) is the input distribution of the simulator \(\mathcal {S} _3\) for the corrupted \(P _3\), existence of which is implied by the security of \(\pi \). But this means that \(\mathcal {S} _3\) will have to come up with \(X_3^*\) such that the public-output distribution \(f(X_1,X_2,X_3^*)=X_{1,1}^\kappa \oplus X_2^\kappa \oplus X^*_{3,1+(X_{1,2}\oplus X_2)}\) is distributed indistinguishably from \(X_{1,1}^\kappa \oplus X_{3,(1+X_{1,2})}^*\). Since \(X_3^*\) cannot depend on \(X_1\) or \(X_2\), this is impossible.
The following claim follows directly from Claim 8 and the security of \(\pi \) (recall that we are under the assumption that Scenario 2 terminates without abort except with negligible probability).
Claim 9
For any inputs \(x_1\) and \(x_3\) for protocol-machines \(\pi _1\) and \(\pi _3\) in Scenario 2, the probability (over the input-choice of \(x_2\) and the local randomness \(r_2\) given to \(\pi _2\)) that the public output is \(x^\kappa _{1,1}\oplus x^\kappa _2\oplus x_{3,1}\) (i.e., \(x_{1,2}=x_2\)) is noticeable, and so is the probability that the public output \(x^\kappa _{1,1}\oplus x^\kappa _2\oplus x_{3,2}\) (i.e., \(x_{1,2}\ne x_2\)).
The final claim that we prove provides the attack discussed at the beginning of the proof for Case 2. We refer to the full version [23] for a proof.
Claim 10
An adversary \(\mathcal {A} \) corrupting both \(P _1\) and \(P _2\) can learn both \(x_{3,1}\) and \(x_{3,2}\) with noticeable probability.
Finally, we observe that, by the definition of the function, the probability that a simulator \(\mathcal {S}\) for the adversary \(\mathcal {A} \) from Claim 10 (who corrupts \(P _1\) and \(P _2\)) outputs both inputs of \(\pi _3\) is negligible. Hence, Claim 10 contradicts the assumed security of \(\pi \).
4 Feasibility of Two-Round MPC with Limited Use of Broadcast
In this section, we present our feasibility results, showing how to compute any function with unanimous abort when only the second round of the MPC protocol is over broadcast, and with selective abort purely over pairwise channels. More formally:
Theorem 11
Assume the existence of a two-round maliciously secure OT protocol, let f be an efficiently computable n-party function, and let \(t<n\). Then,
-
1.
f can be securely computed with unanimous abort, tolerating a PPT static, malicious t-adversary, by a two-round protocol in which the first round is over private channels and the second over broadcast.
-
2.
f can be securely computed with selective abort, tolerating a PPT static, malicious t-adversary, by a two-round protocol over private channels.
The proof of Theorem 11 follows from Lemmas 1 and 2 that show how to compile any two-broadcast-round protocol secure with unanimous (resp., selective) abort by a black-box straight-line simulation, to the desired result. Theorem 11 follows from that fact, and the two-broadcast-round MPC protocols presented in [9, 33].
The only cryptographic assumption used in our compiler is a garbling scheme that is used to garble the second-round next-message function of the protocol. As observed in [2], for the protocol from [33] the second-round next-message function is in \(\mathsf {NC} ^1\). Therefore, by using information-theoretic garbling schemes for \(\mathsf {NC} ^1\) [47, 48] and the information-theoretic two-broadcast-round protocol of [35] (in the OT-correlation model, where parties receive correlated randomness for precomputed OT [6]), we obtain the following corollary.
Corollary 4
Let f be an efficiently computable n-party function and let \(t<n\). Then,
-
1.
f can be computed with information-theoretic security and unanimous abort in the OT-correlation model, tolerating a static, malicious t-adversary, by a two-round protocol in which the first round is over private channels and the second over broadcast.
-
2.
f can be computed with information-theoretic security and selective abort in the OT-correlation model, tolerating a static, malicious t-adversary, by a two-round protocol over private channels.
Structure of Two-Round Protocols. Before proving Theorem 11, we present the notations that will be used for the proof. We consider n-party protocols defined in the correlated-randomness hybrid model, where a trusted party samples \((r_1,\ldots ,r_n)\leftarrow D_\mathsf {corr} \) from some predefined efficiently sampleable distribution \(D_\mathsf {corr} \), and each party \(P _i\) receives \(r_i\) at the onset of the protocol. For simplicity, and without loss of generality, we assume that the random coins of each party are a part of the correlated randomness. The probabilities below are over the random coins for sampling the correlated randomness and the random coins of the adversary.
The two-round n-party protocol is then defined by the set of three functions per party  . Every party \(P _i\) operates as follows:
. Every party \(P _i\) operates as follows:
-
The first-round messages are computed by the function
 , which is a deterministic function of his input \(x_i\) and randomness \(r_i\). If the first round is over broadcast it holds that \(m_{i\rightarrow 1}^1=\ldots =m_{i\rightarrow n}^1\), and we denote the unique message as \(m_i^1\).
, which is a deterministic function of his input \(x_i\) and randomness \(r_i\). If the first round is over broadcast it holds that \(m_{i\rightarrow 1}^1=\ldots =m_{i\rightarrow n}^1\), and we denote the unique message as \(m_i^1\). -
The second-round messages are computed by the next-message function
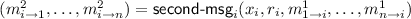 , which is a deterministic function of \(x_i\), \(r_i\) and the first-round message \(m_{j\rightarrow i}^1\) received from each \(P _j\). As before, if the second round is over broadcast we denote the unique message as \(m_i^2\).
, which is a deterministic function of \(x_i\), \(r_i\) and the first-round message \(m_{j\rightarrow i}^1\) received from each \(P _j\). As before, if the second round is over broadcast we denote the unique message as \(m_i^2\). -
The output is computed by the function \(y={\textsf {output}} _i(x_i,r_i,m_{1\rightarrow i}^1,\ldots ,m_{n\rightarrow i}^1,m_{1\rightarrow i}^2,\ldots ,m_{n\rightarrow i}^2)\), which is a deterministic function of \(x_i,r_i\) and the first-round and second-round messages.
4.1 Compiling Two-Broadcast-Round Protocols
In this section, we present a compiler which transforms a two-broadcast-round MPC protocol into a two-round protocol suitable for a point-to-point network. The compiler is based on the compiler presented in Ananth et al. [2], which considered information-theoretic honest-majority protocols that are executed over both private point-to-point channels and a broadcast channel. We adapt this compiler to the dishonest-majority setting, where the input protocol is defined purely over a broadcast channel. See the full version [23] for a formal specification of the compiler.
Let \(\pi _{\mathsf {bc}} \) be a two-round MPC protocol in the broadcast model. Initially, every party “hard-wires” his input and randomness to the circuit computing the second-round next-message function  on the first-broadcast-round messages. Next, each party garbles this circuit and secret-shares each label using an additive secret-sharing scheme.
on the first-broadcast-round messages. Next, each party garbles this circuit and secret-shares each label using an additive secret-sharing scheme.
In the first round, each party sends to each other party over private channelsFootnote 12 his first-round message from \(\pi _{\mathsf {bc}} \) and one share of each garbled label. Note that all of these “adjusted” second-round circuits (one circuit generated by each party) should receive the same input values, i.e., the first-broadcast-round messages. For each input wire, corresponding to one broadcast bit, each party receives two shares (one for value 0 and the other for value 1). In the second round, every party sends to all other parties the garbled circuit as well as one share from each pair, according to the messages received in the first round. Since each party sends the same second-round message to all others, each party can either send the second-round message over a broadcast channel (in which case it is guaranteed that all parties receive the same messages) or multicast the message over (authenticated) point-to-point channels.
Next, every party reconstructs all garbled labels and evaluates each garbled circuit to obtain the second-round messages of \(\pi _{\mathsf {bc}} \). Using these messages each party can recover the output value from \(\pi _{\mathsf {bc}} \).
4.2 Unanimous Abort with a Single Broadcast Round
We start by proving that the compiled protocol  is secure with unanimous abort when the second-round message is over a broadcast channel. Intuitively, if all honest parties receive the same “common part” of the first-round message (corresponding to the first broadcast round of \(\pi _{\mathsf {bc}} \)), they will be able to reconstruct the garbled labels and obtain the second-round message of each party by evaluating the garbled circuits. Note that since the second round is over broadcast, it is guaranteed that all honest parties will evaluate the same garbled circuits using the same garbled inputs, and will obtain the same output value. If there exist a pair of parties that received different first-round messages, then none of the parties will be able to reconstruct the correct labels.
is secure with unanimous abort when the second-round message is over a broadcast channel. Intuitively, if all honest parties receive the same “common part” of the first-round message (corresponding to the first broadcast round of \(\pi _{\mathsf {bc}} \)), they will be able to reconstruct the garbled labels and obtain the second-round message of each party by evaluating the garbled circuits. Note that since the second round is over broadcast, it is guaranteed that all honest parties will evaluate the same garbled circuits using the same garbled inputs, and will obtain the same output value. If there exist a pair of parties that received different first-round messages, then none of the parties will be able to reconstruct the correct labels.
The security of the compiled protocol reduces to the security of the broadcast-model protocol; however, some subtleties arise in the simulation. The simulation of the garbled circuits requires the simulated second-round messages for \(\pi _{\mathsf {bc}} \) (as this is the output from the garbled circuit). To simulate the second-round message of \(\pi _{\mathsf {bc}} \), the simulator must obtain the output value that corresponds to the input values that are extracted from the corrupted parties in the first round. However, since the adversary can send different first-round messages to different honest parties over the point-to-point channels, there may be multiple input values that can be extracted—in fact, the messages received by every honest party can define a different set of input values for the corrupted parties.
In more detail, given an adversary \(\mathcal {A} \) for the compiled protocol \(\pi \), we construct a simulator \(\mathcal {S} \). We would like to use the security of \(\pi _{\mathsf {bc}} \) to simulate the “common part” of the honest parties’ messages. However, the adversary \(\mathcal {A} \) induces multiple adversaries for \(\pi _{\mathsf {bc}} \), one for every honest party. For every honest party \(P _j\) we define a receiver-specific adversary \(\mathcal {A} _j\) for \(\pi _{\mathsf {bc}} \), by forwarding the first-broadcast-round messages to \(\mathcal {A} \) and responding with the messages \(\mathcal {A} \) sends to \(P _j\) (recall that \(\mathcal {A} \) can send different messages to different honest parties in \(\pi \)). By the security of \(\pi _{\mathsf {bc}} \), for every such \(\mathcal {A} _j\) there exists a simulator \(\mathcal {S} _j\).
To define the simulator \(\mathcal {S} \) (for the adversary \(\mathcal {A} \)), we use one of the simulators \(\mathcal {S} _j\) corresponding to the honest parties (the choice of which simulator to use is arbitrary). \(\mathcal {S}\) initially receives from \(\mathcal {S} _j\) either the corrupted parties’ inputs or an \(\mathsf {abort}\) message, and forwards the received message to the trusted party. If \(\mathcal {S} _j\) does not abort, \(\mathcal {S} \) receives back the output value y, forwards y to \(\mathcal {S} _j\) and receives the simulated second-round messages from \(\mathcal {S} _j\)’s output. Next, \(\mathcal {S} \) invokes \(\mathcal {A} \) and simulates the first-round messages of \(\pi \) (using the simulated first-round messages for \(\pi _{\mathsf {bc}} \) obtained from \(\mathcal {S} _j\)), receives back the first-round messages from \(\mathcal {A} \), and checks whether these messages are consistent. If so, \(\mathcal {S}\) completes the simulation by constructing simulated garbled circuits that output the correct second-round messages (if \(\mathcal {A} \)’s messages are consistent, the simulated messages by \(\mathcal {S} _j\) are valid for all honest parties). If \(\mathcal {A} \)’s messages are inconsistent, \(\mathcal {S} \) simulates garbled circuit that output dummy values (e.g., zeros), which is ok since the \(\mathcal {A} \) will not learn the labels to open them.
Lemma 1
Let f be an efficiently computable n-party function and let \(t<n\). Let \(\pi _{\mathsf {bc}} \) be a two-broadcast-round protocol that securely computes f with unanimous abort by a black-box straight-line simulation and assume that garbling schemes exist. Consider the protocol  where the first round is over secure point-to-point channels and the second round is over broadcast. Then, \(\pi \) securely computes f with unanimous abort.
where the first round is over secure point-to-point channels and the second round is over broadcast. Then, \(\pi \) securely computes f with unanimous abort.
The proof of Lemma 1 can be found in the full version [23].
4.3 Selective Abort with Two point-to-point Rounds
We proceed by proving our second result, that the compiled protocol  is secure with selective abort when the second-round message is over a point-to-point channel. The main difference from the previous case (Sect. 4.2) is that the adversary can send different garbled circuits to different honest parties in the second round, potentially causing them to obtain different output values, which would violate correctness (recall that the definition of security with selective abort permits some honest parties to abort while other obtain the correct output, but it is forbidden for two honest parties to obtain two different output values.)
is secure with selective abort when the second-round message is over a point-to-point channel. The main difference from the previous case (Sect. 4.2) is that the adversary can send different garbled circuits to different honest parties in the second round, potentially causing them to obtain different output values, which would violate correctness (recall that the definition of security with selective abort permits some honest parties to abort while other obtain the correct output, but it is forbidden for two honest parties to obtain two different output values.)
Lemma 2
Let f be an efficiently computable n-party function and let \(t<n\). Let \(\pi _{\mathsf {bc}} \) be a two-broadcast-round protocol that securely computes f with unanimous abort by a black-box straight-line simulation and assume that garbling schemes exist. Consider the protocol  where both rounds are over secure point-to-point channels. Then, \(\pi \) securely computes f with selective abort.
where both rounds are over secure point-to-point channels. Then, \(\pi \) securely computes f with selective abort.
Notes
- 1.
- 2.
- 3.
A similar technique was used by Garg et al. [35] to compile two-round MPC to a client-server MPC, albeit in the semi-honest setting.
- 4.
We note that the approach of Applebaum et al. [4] does not extend to the dishonest-majority setting in a straightforward way.
- 5.
Our choice to describe the results in the stand-alone model is for simplicity and for providing stronger impossibility results. Our feasibility results extend to the UC framework [13] via standard technical adjustments, as our simulators are black-box and straight-line. We note that the same simulation techniques discussed in this section are also needed for adjusting the proof to the UC model.
- 6.
This is challenging because we use the broadcast-hybrid protocol in a black-box manner. Restricting to subclasses of protocols with specific properties—e.g., the view of the adversary in the first round is distributed independently of the function’s output—may enable more straightforward simulation strategies.
- 7.
Private channels can be realized over authenticated channels without increasing the round complexity given a PKI for public-key encryption.
- 8.
Recall that there is a trivial reduction from security with unanimous abort to security with identifiable abort: Run the protocol and in case it aborts with the ID of some party \(P _i\), output abort and ignore the identity of the corrupted party.
- 9.
Our impossibility results consider standard, worst-case and rushing adversaries. One might investigate how the landscape looks like against non-rushing adversaries, but this is typically considered too strong an assumption for protocols, as it implies feasibility of fair exchange (a task impossible in the standard rushing-adversary with dishonest majority realm) and even in a single round. We do not consider this theoretical question here.
- 10.
Informally, input independence, a property implied by the standard simulation-based security definition (see Sect. 2.1), requires that the adversary cannot choose his inputs depending on the inputs of honest parties.
- 11.
Note that although parties \(P _3\) and \(P _2\) are corrupted in these scenarios, the corresponding adversary still executes \(\pi _3\) and \(\pi _2\), respectively and has some transmitted message dropped. Hence, we can define the view of these protocols in this concrete attack scenario although they are controlled by the adversary.
- 12.
Private channels can be realized over authenticated channels without additional rounds assuming a public-key infrastructure (PKI) for public-key encryption.
References
Ananth, P., Choudhuri, A.R., Goel, A., Jain, A.: Round-optimal secure multiparty computation with honest majority. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part II. LNCS, vol. 10992, pp. 395–424. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_14
Ananth, P., Choudhuri, A.R., Goel, A., Jain, A.: Two round information-theoretic MPC with malicious security. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part II. LNCS, vol. 11477, pp. 532–561. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_19
Applebaum, B., Brakerski, Z., Tsabary, R.: Perfect secure computation in two rounds. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018, Part I. LNCS, vol. 11239, pp. 152–174. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_6
Applebaum, B., Brakerski, Z., Tsabary, R.: Degree 2 is complete for the round-complexity of malicious MPC. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part II. LNCS, vol. 11477, pp. 504–531. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_18
Asharov, G., Jain, A., López-Alt, A., Tromer, E., Vaikuntanathan, V., Wichs, D.: Multiparty computation with low communication, computation and interaction via threshold FHE. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 483–501. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_29
Beaver, D.: Precomputing oblivious transfer. In: Coppersmith, D. (ed.) CRYPTO 1995. LNCS, vol. 963, pp. 97–109. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-44750-4_8
Ben-Or, M., El-Yaniv, R.: Resilient-optimal interactive consistency in constant time. Distrib. Comput. 16(4), 249–262 (2003)
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation (extended abstract). In: 20th ACM STOC, pp. 1–10. ACM Press (1988)
Benhamouda, F., Lin, H.: k-Round multiparty computation from k-round oblivious transfer via garbled interactive circuits. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part II. LNCS, vol. 10821, pp. 500–532. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_17
Benhamouda, F., Lin, H., Polychroniadou, A., Venkitasubramaniam, M.: Two-round adaptively secure multiparty computation from standard assumptions. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018, Part I. LNCS, vol. 11239, pp. 175–205. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_7
Boyle, E., Gilboa, N., Ishai, Y.: Group-based secure computation: optimizing rounds, communication, and computation. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part II. LNCS, vol. 10211, pp. 163–193. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_6
Canetti, R.: Security and composition of multiparty cryptographic protocols. J. Cryptol. 13(1), 143–202 (2000). https://doi.org/10.1007/s001459910006
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd FOCS, pp. 136–145. IEEE Computer Society Press (2001)
Canetti, R., Ostrovsky, R.: Secure computation with honest-looking parties: what if nobody is truly honest? (extended abstract). In: 31st ACM STOC, pp. 255–264. ACM Press (1999)
Canetti, R., Poburinnaya, O., Venkitasubramaniam, M.: Better two-round adaptive multi-party computation. In: Fehr, S. (ed.) PKC 2017, Part II. LNCS, vol. 10175, pp. 396–427. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54388-7_14
Chaum, D., Crépeau, C., Damgård, I.: Multiparty unconditionally secure protocols (extended abstract). In: 20th ACM STOC, pp. 11–19. ACM Press (1988)
Chor, B., Merritt, M., Shmoys, D.B.: Simple constant-time consensus protocols in realistic failure models. J. ACM 36(3), 591–614 (1989)
Cleve, R.: Limits on the security of coin flips when half the processors are faulty (extended abstract). In: 18th ACM STOC, pp. 364–369. ACM Press (1986)
Cohen, R., Lindell, Y.: Fairness versus guaranteed output delivery in secure multiparty computation. J. Cryptol. 30(4), 1157–1186 (2017). https://doi.org/10.1007/s00145-016-9245-5
Cohen, R., Coretti, S., Garay, J.A., Zikas, V.: Round-preserving parallel composition of probabilistic-termination cryptographic protocols. In: ICALP 2017. LIPIcs, vol. 80, pp. 37:1–37:15. Schloss Dagstuhl (2017)
Cohen, R., Haitner, I., Omri, E., Rotem, L.: Characterization of secure multiparty computation without broadcast. J. Cryptol. 31(2), 587–609 (2018). https://doi.org/10.1007/s00145-017-9264-x
Cohen, R., Coretti, S., Garay, J., Zikas, V.: Probabilistic termination and composability of cryptographic protocols. J. Cryptol. 32(3), 690–741 (2019). https://doi.org/10.1007/s00145-018-9279-y
Cohen, R., Garay, J.A., Zikas, V.: Broadcast-optimal two-round MPC. Cryptology ePrint Archive, Report 2019/1183 (2019)
Cohen, R., Haitner, I., Makriyannis, N., Orland, M., Samorodnitsky, A.: On the round complexity of randomized Byzantine agreement. In: DISC, pp. 12:1–12:17 (2019)
Cohen, R., Shelat, A., Wichs, D.: Adaptively secure MPC with sublinear communication complexity. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11693, pp. 30–60. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_2
Dodis, Y., Halevi, S., Rothblum, R.D., Wichs, D.: Spooky encryption and its applications. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part III. LNCS, vol. 9816, pp. 93–122. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_4
Dolev, D., Strong, H.R.: Authenticated algorithms for Byzantine agreement. SIAM J. Comput. 12(4), 656–666 (1983)
Fischer, M.J., Lynch, N.A.: A lower bound for the time to assure interactive consistency. Inf. Process. Lett. 14(4), 183–186 (1982)
Fitzi, M., Gottesman, D., Hirt, M., Holenstein, T., Smith, A.: Detectable Byzantine agreement secure against faulty majorities. In: 21st ACM PODC, pp. 118–126. ACM (2002)
Garay, J.A., Katz, J., Koo, C.-Y., Ostrovsky, R.: Round complexity of authenticated broadcast with a dishonest majority. In: 48th FOCS, pp. 658–668. IEEE Computer Society Press (2007)
Garg, S., Polychroniadou, A.: Two-round adaptively secure MPC from indistinguishability obfuscation. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 614–637. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_24
Garg, S., Srinivasan, A.: Garbled protocols and two-round MPC from bilinear maps. In: 58th FOCS, pp. 588–599. IEEE Computer Society Press (2017)
Garg, S., Srinivasan, A.: Two-round multiparty secure computation from minimal assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part II. LNCS, vol. 10821, pp. 468–499. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_16
Garg, S., Gentry, C., Halevi, S., Raykova, M.: Two-round secure MPC from indistinguishability obfuscation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 74–94. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_4
Garg, S., Ishai, Y., Srinivasan, A.: Two-round MPC: information-theoretic and black-box. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018, Part I. LNCS, vol. 11239, pp. 123–151. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_5
Garg, S., Miao, P., Srinivasan, A.: Two-round multiparty secure computation minimizing public key operations. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part III. LNCS, vol. 10993, pp. 273–301. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_10
Gennaro, R., Ishai, Y., Kushilevitz, E., Rabin, T.: The round complexity of verifiable secret sharing and secure multicast. In: 33rd ACM STOC, pp. 580–589. ACM Press (2001)
Gennaro, R., Ishai, Y., Kushilevitz, E., Rabin, T.: On 2-round secure multiparty computation. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 178–193. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_12
Goldreich, O.: Foundations of Cryptography: Basic Applications, vol. 2. Cambridge University Press, Cambridge (2004). ISBN 0-521-83084-2 (hardback)
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or a completeness theorem for protocols with honest majority. In: 19th ACM STOC, pp. 218–229. ACM Press (1987)
Goldwasser, S., Lindell, Y.: Secure multi-party computation without agreement. J. Cryptol. 18(3), 247–287 (2005)
Dov Gordon, S., Liu, F.-H., Shi, E.: Constant-round MPC with fairness and guarantee of output delivery. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216, pp. 63–82. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_4
Halevi, S., Lindell, Y., Pinkas, B.: Secure computation on the web: computing without simultaneous interaction. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 132–150. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_8
Hazay, C., Scholl, P., Soria-Vazquez, E.: Low cost constant round MPC combining BMR and oblivious transfer. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part I. LNCS, vol. 10624, pp. 598–628. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_21
Hazay, C., Orsini, E., Scholl, P., Soria-Vazquez, E.: Concretely efficient large-scale MPC with active security (or, TinyKeys for TinyOT). In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018, Part III. LNCS, vol. 11274, pp. 86–117. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03332-3_4
Hirt, M., Maurer, U.M.: Player simulation and general adversary structures in perfect multiparty computation. J. Cryptol. 13(1), 31–60 (2000). https://doi.org/10.1007/s001459910003
Ishai, Y., Kushilevitz, E.: Randomizing polynomials: a new representation with applications to round-efficient secure computation. In: 41st FOCS, pp. 294–304. IEEE Computer Society Press (2000)
Ishai, Y., Kushilevitz, E.: Perfect constant-round secure computation via perfect randomizing polynomials. In: Widmayer, P., Eidenbenz, S., Triguero, F., Morales, R., Conejo, R., Hennessy, M. (eds.) ICALP 2002. LNCS, vol. 2380, pp. 244–256. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45465-9_22
Ishai, Y., Kushilevitz, E., Paskin, A.: Secure multiparty computation with minimal interaction. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 577–594. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_31
Ishai, Y., Ostrovsky, R., Zikas, V.: Secure multi-party computation with identifiable abort. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 369–386. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_21
Ishai, Y., Kumaresan, R., Kushilevitz, E., Paskin-Cherniavsky, A.: Secure computation with minimal interaction, revisited. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216, pp. 359–378. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_18
Karlin, A.R., Yao, A.C.: Probabilistic lower bounds for Byzantine agreement and clock synchronization (1986). Unpublished manuscript
Katz, J., Koo, C.-Y.: On expected constant-round protocols for Byzantine agreement. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 445–462. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_27
Lindell, Y., Nof, A.: A framework for constructing fast MPC over arithmetic circuits with malicious adversaries and an honest-majority. In: ACM CCS 2017, pp. 259–276. ACM Press (2017)
Lindell, Y., Lysyanskaya, A., Rabin, T.: Sequential composition of protocols without simultaneous termination. In: 21st ACM PODC, pp. 203–212. ACM (2002)
Lindell, Y., Pinkas, B., Smart, N.P., Yanai, A.: Efficient constant round multi-party computation combining BMR and SPDZ. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216, pp. 319–338. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_16
Lindell, Y., Smart, N.P., Soria-Vazquez, E.: More efficient constant-round multi-party computation from BMR and SHE. In: Hirt, M., Smith, A. (eds.) TCC 2016, Part I. LNCS, vol. 9985, pp. 554–581. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_21
Micali, S.: Very simple and efficient Byzantine agreement. In: Papadimitriou, C.H. (ed.) ITCS 2017, LIPIcs, vol. 4266, pp. 6:1–6:1, 67, January 2017. https://doi.org/10.4230/LIPIcs.ITCS.2017.6
Mukherjee, P., Wichs, D.: Two round multiparty computation via multi-key FHE. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 735–763. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_26
Patra, A., Ravi, D.: On the exact round complexity of secure three-party computation. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part II. LNCS, vol. 10992, pp. 425–458. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_15
Patra, A., Ravi, D.: On the exact round complexity of secure three-party computation. Cryptology ePrint Archive, Report 2018/481 (2018)
Patra, A., Ravi, D.: Beyond honest majority: the round complexity of fair and robust multi-party computation. In: Galbraith, S.D., Moriai, S. (eds.) ASIACRYPT 2019, Part I. LNCS, vol. 11921, pp. 456–487. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34578-5_17
Pfitzmann, B., Waidner, M.: Unconditional Byzantine agreement for any number of faulty processors. In: Finkel, A., Jantzen, M. (eds.) STACS 1992. LNCS, vol. 577, pp. 337–350. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-55210-3_195
Quach, W., Wee, H., Wichs, D.: Laconic function evaluation and applications. In: 59th FOCS, pp. 859–870. IEEE Computer Society Press (2018)
Rabin, T., Ben-Or, M.: Verifiable secret sharing and multiparty protocols with honest majority (extended abstract). In: 21st ACM STOC, pp. 73–85. ACM Press (1989)
Wang, X., Ranellucci, S., Katz, J.: Global-scale secure multiparty computation. In: ACM CCS 2017, pp. 39–56. ACM Press (2017)
Yao, A.C.-C.: Protocols for secure computations (extended abstract). In: 23rd FOCS, pp. 160–164. IEEE Computer Society Press (1982)
Acknowledgements
We would like to thank Prabhanjan Ananth, Arpita Patra, and Divya Ravi for useful discussions and comments. We also thank the anonymous reviewers of Eurocrypt 2020 for pointing us to the client-server protocol MPC of [35].
Ran Cohen’s research was supported in part by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Project Activity (IARPA) under contract number 2019-19-020700009 (ACHILLES). Juan Garay and Vassilis Zikas were supported in part by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via 2019-1902070008.
The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of ODNI, IARPA, DoI/NBC, or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright annotation thereon.
This work was done in part while Vassilis Zikas was visiting the Simons Institute for the Theory of Computing, UC Berkeley, and UCLA.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Cohen, R., Garay, J., Zikas, V. (2020). Broadcast-Optimal Two-Round MPC. In: Canteaut, A., Ishai, Y. (eds) Advances in Cryptology – EUROCRYPT 2020. EUROCRYPT 2020. Lecture Notes in Computer Science(), vol 12106. Springer, Cham. https://doi.org/10.1007/978-3-030-45724-2_28
Download citation
DOI: https://doi.org/10.1007/978-3-030-45724-2_28
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-45723-5
Online ISBN: 978-3-030-45724-2
eBook Packages: Computer ScienceComputer Science (R0)





 (that computes
(that computes  such that given all first-round messages as input, the circuit outputs
such that given all first-round messages as input, the circuit outputs  .
. .
.

 , which is a deterministic function of his input
, which is a deterministic function of his input 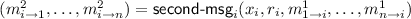 , which is a deterministic function of
, which is a deterministic function of 