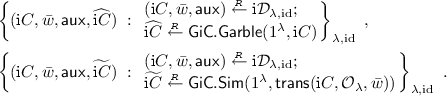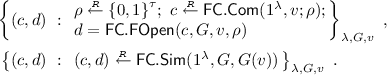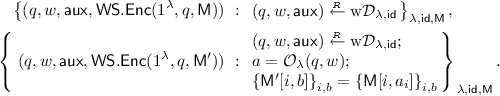k-Round Multiparty Computation from k-Round Oblivious Transfer via Garbled Interactive Circuits

Abstract

We present new constructions of round-efficient, or even round-optimal, Multi-Party Computation (MPC) protocols from Oblivious Transfer (OT) protocols. Our constructions establish a tight connection between MPC and OT: In the setting of semi-honest security, for any $k \ge 2$, k-round semi-honest OT is necessary and complete for k-round semi-honest MPC. In the round-optimal case of $k = 2$, we obtain 2-round semi-honest MPC from 2-round semi-honest OT, resolving the round complexity of semi-honest MPC assuming weak and necessary assumption. In comparison, previous 2-round constructions rely on either the heavy machinery of indistinguishability obfuscation or witness encryption, or the algebraic structure of bilinear pairing groups. More generally, for an arbitrary number of rounds k, all previous constructions of k-round semi-honest MPC require at least OT with $k'$ rounds for $k' \le \lfloor k/2 \rfloor$.

In the setting of malicious security, we show: For any $k \ge 5$, k-round malicious OT is necessary and complete for k-round malicious MPC. In fact, OT satisfying a weaker notion of delayed-semi-malicious security suffices. In the common reference string model, for any $k \ge 2$, we obtain k-round malicious Universal Composable (UC) protocols from any k-round semi-malicious OT and non-interactive zero-knowledge. Previous 5-round protocols in the plain model, and 2-round protocols in the common reference string model all require algebraic assumptions such as DDH or LWE.

At the core of our constructions is a new framework for garbling interactive circuits. Roughly speaking, it allows for garbling interactive machines that participates in interactions of a special form. The garbled machine can emulate the original interactions receiving messages sent in the clear (without being encoded using secrets), and reveals only the transcript of the interactions, provided that the transcript is computationally uniquely defined. We show that garbled interactive circuits for the purpose of constructing MPC can be implemented using OT. Along the way, we also propose a new primitive of witness selector that strengthens witness encryption, and a new notion of zero-knowledge functional commitments.

1 Introduction

A Multi-Party Computation (MPC) protocol allows m mutually distrustful parties to securely compute a functionality $f(\bar{x})$ of their corresponding private inputs $\bar{x}=x_1, \dots , x_m$, such that party $P_i$ receives the i-th component of $f(\bar{x})$. The semi-honest security guarantees that honest-but-curious parties who follow the specification of the protocol learn nothing more than their prescribed outputs. The stronger malicious security guarantees that even malicious parties who may deviate from the protocol, cannot learn more information nor manipulate the outputs of the honest parties. MPC protocols for computing general functionalities are central primitives in cryptography and have been studied extensively. An important question is: “how many rounds of interactions do general MPC protocols need, and under what assumptions?”

The round complexity of 2-Party Computation (2PC) was resolved more than three decades ago: Yao [44, 45] gave a construction of general semi-honest 2PC protocols that have only two rounds of interaction (where parties have access to a simultaneous broadcast channel¹), using garbled circuits and a 2-message semi-honest Oblivious Transfer (OT) protocol. The round complexity is optimal, as any one-round protocol is trivially broken. Moreover, the underlying assumption of 2-message semi-honest OT is weak and necessary.²

In contrast, constructing round-efficient MPC protocols turned out to be more challenging. The first general construction [32] requires a high number of rounds, O(d), proportional to the depth d of the computation. Later, Beaver, Micali, and Rogaway (BMR) reduced the round complexity to a constant using garbled circuits [5]. However, the exact round complexity of MPC remained open until recently. By relying on specific algebraic assumptions, a recent line of works constructed (i) 2-round MPC protocols relying on trusted infrastructure (e.g., a common reference string) assuming LWE [2, 14, 21, 39, 41] or DDH [9,10,11], and (ii) 2-round protocols in the plain model from indistinguishability obfuscation or witness encryption with NIZK [16, 22, 24, 28, 35], or bilinear groups [29]. However, all these constructions heavily exploit the algebraic structures of the underlying assumptions, or rely on the heavy machinery of obfuscation or witness encryption.

The state-of-the-art for malicious security is similar. Garg et al. [27] showed that 4 round is optimal for malicious MPC. So far, there are constructions of (i) 5-round protocols from DDH [1], and (ii) 4-round protocols from subexponentially secure DDH [1], or subexponentially secure LWE and adaptive commitments³ [12]. In general, for any number of round k, all known constructions of semi-honest or malicious MPC require at least $k'$ round OT for $k' \le \lfloor k/2\rfloor$. We ask the question,

$$\begin{aligned} \begin{array}{c} \textit{Can we have round-optimal MPC protocols from weak and necessary} \\ \textit{assumptions?} \end{array} \end{aligned}$$

We completely resolve this question in the semi-honest setting, constructing 2-round semi-honest MPC from 2-round semi-honest OT, and make significant progress in the malicious setting, constructing 5-round malicious MPC from 5-round delayed-semi-malicious OT, a weaker primitive than malicious OT. Our results are obtained via a new notion of garbling interactive circuits. Roughly speaking, classical garbling turns a computation, given by a circuit C and an input x, into another one $(\hat{C}, \hat{x})$ that reveals only the output C(x). Our new notion considers garbling a machine participating in an interaction: Let C (with potentially hardcoded input x) be an interactive machine that interacts with an oracle ${\mathcal {O}}$, which is a non-deterministic algorithm that computes its replies to C’s messages, depending on some witnesses ${\bar{w}}$. Garbling interactive machine turns C into $\hat{C}$, which can emulate the interaction between C and ${\mathcal {O}}$, given the witnesses ${\bar{w}}$ in the clear (without any secret encoding). It is guaranteed that $\hat{C}$ reveals only the transcript of messages in the interaction and nothing else, provided that the transcript is computationally uniquely defined, that is, it is computationally hard to find two different witnesses ${\bar{w}}, {\bar{w}}'$ that lead to different transcripts.

1.1 Our Contributions

We construct 2-round semi-honest MPC protocols in the plain model from 2-round semi-honest OT. Our construction can be generalized to an arbitrary number of rounds, establishing a tight connection between MPC and OT: For any k, k-round OT is necessary and complete for k-round MPC.⁴

Theorem 1.1

(Semi-Honest Security). For any $k \ge 2$, there is a k-round semi-honest MPC protocol for any functionality f, from any k-round semi-honest OT protocol.

The above theorem resolves the exact round complexity of semi-honest MPC based on weak and necessary assumptions, closing the gap between the 2-party and multi-party case. In the optimal 2-round setting, by instantiating our construction with specific 2-round OT protocols, we obtain 2-round MPC protocols in the plain model from a wide range of number theoretic and algebraic assumptions, including CDH [6], factoring [6],⁵ LWE [42],⁶ and constant-noise LPN with a sub-exponential security [31, 46]. This broadens the set of assumptions that round-optimal semi-honest MPC can be based on.

Going beyond semi-honest security, we further strengthen our protocols to achieve the stronger notion of semi-malicious security, as a stepping stone towards malicious security. Semi-malicious security proposed by [2] considers semi-malicious attackers that follow the protocol specification, but may adaptively choose arbitrary inputs and random tapes for computing each of its messages. We enhance our semi-honest protocols to handle such attackers.

Theorem 1.2

(Semi-Malicious Security). For any $k \ge 2$, there is a k-round semi-malicious MPC protocol for any functionality f, from any k-round semi-malicious OT protocol.

Previous semi-malicious protocols have 3 rounds based on LWE [2, 12], 2 rounds based on bilinear maps [29], or 2 rounds based on LWE but in the common reference string model [39]. We obtain the first 2-round construction from any 2-round semi-malicious OT, which is necessary and can be instantiated from a variety of assumptions, including DDH [40], QR, and N-th residuosity [36]. Furthermore, following the compilation paradigms in recent works [1, 2, 12], we immediately obtain maliciously secure Universal Composable (UC) protocols in the common reference string model [15, 18], using non-interactive zero-knowledge (NIZK).

Corollary 1.3

(Malicious Security in the CRS Model). For any $k \ge 2$, there is a k-round malicious UC protocol in the common reference string model for any functionality f, from any k-round semi-malicious OT protocol and NIZK.

Moving forward to malicious MPC protocols in the plain model, we show that, for any $k \ge 5$, k-round malicious MPC protocols can be built from k-round delayed-semi-malicious OT, which is implied by k-round malicious OT.

Theorem 1.4

(Malicious Security in the Plain Model). For any $k \ge 5$, there is a k-round malicious MPC protocol for every functionality f, from any k-round delayed-semi-malicious OT protocol.

This theorem is obtained by first showing that our k-round semi-malicious MPC protocols satisfy a stronger notion of delayed-semi-malicious security, when instantiated with a k-round OT protocol satisfying the same notion. Here, delayed-semi-malicious security guards against a stronger variant of semi-malicious attackers, and is still significantly weaker than malicious security. For instance, delayed-semi-malicious OT provides only indistinguishability-based privacy guarantees, whereas malicious OT supports extraction of inputs and simulation. In the second step, we transform our k-round delayed-semi-malicious MPC protocols into k-round malicious MPC protocols, assuming only one-way functions. This transformation relies on specific structures of our protocols. In complement, we also present a generic transformation that starts with any $(k-1)$-round delayed semi-malicious MPC protocol.

Previous 5-round malicious protocols rely on LWE and adaptive commitments [12], or DDH [1]. Our construction weakens the assumptions, and in particular adds factoring-based assumptions into the picture. Our result is one-step away from constructing round-optimal malicious MPC from weak and necessary assumptions. So far, 4-round protocols can only be based on subexponential DDH [1] or subexponential LWE and adaptive commitments [12]. A clear open question is constructing 4-round malicious MPC from 4-round OT.

Along the way of constructing our MPC protocols, we develop new techniques and primitives that are of independent interest: We propose a new notion of garbling interactive circuits, a new primitive of witness selector that strengthens witness encryption [26], and a new notion of zero-knowledge functional commitment. Roughly speaking,

• As mentioned above, garbling interactive machine transforms an interactive machine C talking to a non-deterministic oracle ${\mathcal {O}}({\bar{w}})$ using some witnesses, into a garbled interactive machine $\hat{C}$ that upon receiving the witnesses ${\bar{w}}$ in the clear (without any secret encoding) reveals the transcript of the interaction between C and ${\mathcal {O}}({\bar{w}})$ and nothing else, provided that the transcript is computationally uniquely defined.

• Witness selector strengthens witness encryption [26] in the dimension that hiding holds when it is computationally hard to find a witness that enables decryption, as opposed to when no such witnesses exist.

• Finally, we enhance standard (computationally binding and computationally hiding) commitment schemes with the capability of partially opening a commitment c to the output f(v) of a function f evaluated on the committed value v, where the commitment and partial decommitment reveal nothing more than the output f(v).

To construct 2-round MPC, we use garbled interactive circuits and functional commitments to collapse rounds of any multi-round MPC protocols down to 2, and implement garbled interactive circuits using witness selector and classical garbled circuits. Our technique generalizes the novel ideas in recent works on constructing laconic OT from DDH [19], identity based encryption from CDH or factoring [13, 23], and 2-round MPC from bilinear pairing [29]. These works can be rephrased as implementing special-purpose garbled interactive circuits from standard assumptions, and applying them for their specific applications. In this work, we implement the garbled interactive circuits, witness selector, and functional commitments needed for our constructions of MPC, from OT. The generality of our notions gives a unified view of the techniques in this and prior works.

1.2 Organization

We start with an overview of our techniques in Sect. 2. Then, after some classical preliminaries in Sect. 3, we formally define garbled interactive circuit schemes in Sect. 4. In Sect. 5, we build 2-round semi-honest MPC protocols from any semi-honest MPC protocols and (zero-knowledge) functional commitment scheme with an associated garbled interactive circuit scheme. In Sect. 6, we define witness selector schemes and show that they imply garbled interactive circuit schemes. The construction of a functional commitment scheme with witness selector from any 2-round OT (which concludes the construction of 2-round semi-honest MPC protocols from 2-round OT), as well as the extensions to k-round OT and to the semi-malicious and malicious settings are in the full version [7].

1.3 Concurrent Work

In a concurrent and independent work [30], Garg and Srinivasan also built k-round semi-honest MPC from k-round semi-honest OT. In the malicious setting, they obtained a stronger result in the CRS model, constructing 2-round UC-secure MPC from 2-round UC-secure OT in the CRS model (without requiring NIZK contrary to us). On the other hand, they did not consider malicious MPC in the plain model, whereas we constructed k-round malicious MPC from k-round delayed-semi-malicous OT for any $k \ge 5$. While both works leverage the novel ideas in [13, 19, 23, 29], the concrete techniques are different. In our language, if we see their protocols in the lens of garbled interactive circuits, each step of their garbled interactive circuit performs a NAND gate on the state of one of the parties, while each of our steps performs a full MPC round, thanks to the functional commitment. Our approach can also be seen as more modular by the introduction of garbled interactive circuits, witness selector, and functional commitments, which we believe are of independent interest.

2 Overview

Garg et al. [24] introduced a generic approach for collapsing any MPC protocol down to 2 rounds, using indistinguishability obfuscation [4, 25]. Later et al. [35] showed how to perform round collapsing using garbled circuits, witness encryption, and NIZK. Very recently, Garg and Srinivasan [29] further showed how to do collapse rounds using garbled protocols, which can be implemented from bilinear pairing groups. In this work, we perform round collapsing using our new notion of garbled interactive circuits; this notion is general and enables us to weaken the assumption to 2-round OT. (See the full version [7] for a more detailed comparison with prior works.) Below, we give an overview of our construction in the 2-round setting; construction in the multi-round setting is similar.

2.1 Round-Collapsing via Obfuscation

The basic idea is natural and simple: To construct 2-round MPC protocols for a function f, take any multi-round MPC protocols for f, referred to as the inner MPC protocols, such as, the Goldreich-Micali-Wigderson protocol [32], and try to eliminate interaction. Garg, Gentry, Halevi, and Raykova (GGHR) [24] showed how to do this using indistinguishability obfuscation. The idea is to let each player $P_i$ obfuscate their next-step circuit ${\mathsf {Next}}_i(x_i, r_i, \star )$ in an execution of the inner MPC protocol $\varPi$ for computing f, where ${\mathsf {Next}}_i(x_i,r_i,\star )$ has $P_i$’s private input $x_i$ and random tape $r_i$ hardcoded, and produces $P_i$’s next message $m_i^\ell$ in round $\ell$, on input the messages ${\bar{m}}^{<\ell } = {\{m_j^{\ell '}\}}_{j, \ell '<\ell }$ broadcast by all parties in the previous rounds,

$$\begin{aligned} {\mathsf {Next}}_i(x_i,r_i, {\bar{m}}^{< \ell }) = m_i^\ell ~. \end{aligned}$$

(1)

Given all obfuscated circuits ${\{{\mathrm {i}O}({{\mathsf {Next}}(x_i,r_i,\star )}_j)\}}$, each party $P_i$ can emulate the execution of $\varPi$ in its head, eliminating interaction completely.

The above idea achieves functionality, but not security. In fact, attackers, given the obfuscated next-step circuits of honest parties, can evaluate the residual function with the inputs of honest parties hardcoded, or even evaluate honest parties’ next-step circuits on arbitrary “invalid” messages. To avoid this, the protocol requires each party to commit to its input and random tape in the first round, $c_i {\mathop {\leftarrow }\limits ^{{}_R}}{\mathsf {Com}}(x_i, r_i)$. Then, in the second round, each party obfuscates an augmented next-step circuit ${{\mathsf {AugNext}}}_i$ that takes additionally a NIZK proof $\pi _j^{\ell '}$ for each message $m_j^{\ell '}$ it receives, and verifies the proof $\pi _j^{\ell '}$ that $m_j^{\ell '}$ is generated honestly from inputs and random tapes committed in $c_j$ (it aborts otherwise). This way, only the unique sequence of honestly generated messages is accepted by honest parties’ obfuscated circuits. In the security proof, by the security of indistinguishability obfuscation and NIZK, this unique sequence can even be hardcoded into honest parties’ obfuscated circuits, enabling simulation using the simulator of the inner MPC protocol.

2.2 Garbled Interactive Circuits

The fact that it suffices and is necessary that the honest parties’ obfuscated circuits only allow for a single meaningful “execution path” (determined by the unique sequence of honest messages), suggests that we should rather use garbling instead of obfuscation for hiding honest parties’ next-step circuits. However, the challenge is that the next-step circuits ${\mathsf {Next}}_i$ are not plain circuits: They are interactive in the sense that they takes inputs (i.e., MPC messages) generated by other parties that cannot be fixed at time of garbling. To overcome the challenge, we formalize the MPC players as interactive circuits, and propose a new notion called Garbled Interactive Circuits (GIC).

The interaction with an interactive circuit is captured via a non-deterministic ($\text {poly}$-size) oracle ${\mathcal {O}}$ that on inputs a query q and some witness w returns an answer $a = {\mathcal {O}}(q, w)$ (or $\bot$ if w is not accepting). (Note that ${\mathcal {O}}$ is non-deterministic in the sense that without a valid witness, one cannot evaluate ${\mathcal {O}}$.) An interactive circuit ${\mathrm {i}C}$ consists of a list of L next-step circuits ${\{{\mathrm {i}C}^\ell \}}_{\ell \in [L]}$. Its execution with oracle ${\mathcal {O}}$ on input a list of witnesses ${\bar{w}} = {\{{\bar{w}}^\ell \}}$ proceeds in L iterations as depicted in Fig. 1: In round $\ell$, ${\mathrm {i}C}^\ell$ on input the state ${{{st}}}^{\ell -1}$ output in the previous round, as well as the answers ${\bar{a}}^{\ell -1} = {\{a^{\ell -1}_k\}}$ from ${\mathcal {O}}$ to queries ${\bar{q}}^{\ell -1} = {\{q^{\ell -1}_k\}}$ produced in the previous round, outputs the new state ${{{st}}}^{\ell }$ and queries ${\bar{q}}^\ell = {\{q^{\ell }_k\}}$, and a (round) output $o^\ell$.

$$\begin{aligned} \forall \ell ,\qquad {\mathrm {i}C}^\ell ({{{st}}}^{\ell -1}, {\bar{a}}^{\ell -1}) = ({{{st}}}^\ell , {\bar{q}}^\ell , o^\ell ) ~, \text { where } \forall k,\ a^{\ell -1}_k = {\mathcal {O}}(q^{\ell -1}_k, w^{\ell -1}_k)~. \end{aligned}$$

The output of the execution is the list of round outputs ${\bar{o}}={\{o^\ell \}}_\ell$, and the transcript of the execution is the list of all queries, answers, and outputs $\mathsf {trans}({\mathrm {i}C}, {\bar{w}}) = {\{({\bar{q}}^\ell , {\bar{a}}^\ell , o^\ell )\}}_\ell$. In the case that any oracle answer is $a^\ell _k =\bot$, the execution is considered invalid. For simplicity of this high-level overview, we consider only valid executions and valid transcript; see Sect. 4 for more details.

Fig. 1.

Execution of an interactive circuit ${\mathrm {i}C}$ with witnesses ${\bar{w}}$

A Garbled Interactive Circuit (GIC) scheme $\mathsf {GiC}$ allows us to garble an interactive circuit $\widehat{{\mathrm {i}C}}{\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GiC.Garble}({\mathrm {i}C})$, s.t. 

• Correctness: We can evaluate $\widehat{{\mathrm {i}C}}$ with the oracle ${\mathcal {O}}$ and a list ${\bar{w}}$ of witnesses (in the clear) to obtain each round output $o^\ell = \mathsf {GiC.Eval}(\widehat{{\mathrm {i}C}},{\bar{w}}^{<\ell })$. This significantly differs from classical garbling techniques where inputs of the computation must be encoded using secrets (such as, mapping them to corresponding input keys or labels).

• Simulation Security for Unique Transcripts Distribution: Security guarantees that $\widehat{{\mathrm {i}C}}$ reveals only the transcript of execution, including all outputs, queries, and answers, and nothing else, that is, it can be simulated by $\widetilde{\mathrm {i}C}{\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GiC.Sim}(\mathsf {trans})$, provided that there is a unique transcript of execution.

The requirement on unique transcript is necessary, otherwise, security is ill-defined as there may exist different transcripts produced by using different witnesses, and the simulator cannot hardcode them all. Furthermore, garbled interactive circuit schemes are meant to be different from obfuscation and hides only a single execution path. To formalize this, there are two options:

• Statistically Unique Transcript. The easier option is requiring simulation security only for interactive circuits ${\mathrm {i}C}$ that have unique transcript no matter what witnesses are used, that is, for all ${\bar{w}}, {\bar{w}}'$, $\mathsf {trans}({\mathrm {i}C},{\mathcal {O}}, {\bar{w}}) = \mathsf {trans}({\mathrm {i}C},{\mathcal {O}}, {\bar{w}}')$. This is, however, a strong requirement.

• (Default:) Computationally Unique Transcript. The more general option is considering a distribution $\mathrm {i}\mathcal {D}$ over $({\mathrm {i}C}, {\bar{w}})$ that has computationally unique transcripts, in the sense that given $({\mathrm {i}C}, {\bar{w}})$, it is hard to find ${\bar{w}}'$ that leads to a different valid transcript, $\mathsf {trans}({\mathrm {i}C},{\mathcal {O}}, {\bar{w}}) \ne \mathsf {trans}({\mathrm {i}C},{\mathcal {O}}, {\bar{w}}')$.⁷

GIC for a computational or statistical unique-transcript distribution ensures:

$$\begin{aligned} {\left\{ \mathsf {GiC.Garble}({\mathrm {i}C}) : ({\mathrm {i}C}, {\bar{w}}) {\mathop {\leftarrow }\limits ^{{}_R}}\mathrm {i}\mathcal {D}\right\} }&\approx \\ {\left\{ \mathsf {GiC.Sim}(\mathsf {trans}({\mathrm {i}C}, {\mathcal {O}}, {\bar{w}})) : ({\mathrm {i}C}, {\bar{w}}) {\mathop {\leftarrow }\limits ^{{}_R}}\mathrm {i}\mathcal {D}\right\} }&\end{aligned}$$

Looking ahead, our 2-round MPC protocols from 2-round semi-honest oblivious transfer crucially rely on the stronger notion of GIC for computationally unique transcripts. If using GIC for statistically unique transcripts, we would need a 2-round OT protocol where the receiver’s message statistically binds its input bit, which is not a necessary assumption for constructing 2-round semi-honest MPC protocols.

2.3 Constructing GIC from Witness Selector

We start with the warm-up case of building GIC for statistically unique transcripts by combining plain garbled circuits and witness encryption. Witness Encryption (WE) proposed by Garg et al. [26], enables one to encrypt a message under an instance $\mathsf {x}$ of an NP language $\mathcal {L}$ to obtain a ciphertext $\mathsf {ct}{\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {WE.Enc}(\mathsf {x}, \mathsf {M})$; later this ciphertext can be decrypted using any witness $\mathsf {w}$ of $\mathsf {x}$, $\mathsf {M}= \mathsf {WE.Dec}(\mathsf {ct},\mathsf {w})$. The idea of combining garbled circuits and witness encryption has already appeared in three recent works by Gordon et al. [35], Cho et al. [19], and Döttling and Garg [23]. Our garbled interactive circuit scheme can be viewed as a generalization of their ideas for capturing the full power of this combination. As we explain shortly, to handle computationally unique transcripts, we need to rely on a new primitive called Witness Selector, which strengthens WE.⁸

To garble an interactive circuit ${\mathrm {i}C} = {\{{\mathrm {i}C}^\ell \}}_\ell$, a natural first attempt is garbling each next-step circuit ${\mathrm {i}C}^\ell$ as a plain circuit, yielding L garbled circuits ${\{\widehat{{\mathrm {i}C}}{}^\ell , \mathsf {key}^\ell \}}_{\ell }$, where each input wire of $\widehat{{\mathrm {i}C}}{}^\ell$ has two keys, $(\mathsf {key}^\ell [k,0],\mathsf {key}^\ell [k,1])$, one for this input bit being 0 and one for 1. The difficulty is that, to evaluate $\widehat{{\mathrm {i}C}}{}^\ell$, the evaluator must obtain keys corresponding to the honestly generated state ${{{st}}}^{\ell -1}$ and answers ${\bar{a}}^{\ell -1}$ produced in the previous round; denote these keys as $\mathsf {key}^\ell [{{{st}}}^{\ell -1}]$ and $\mathsf {key}^\ell [{\bar{a}}^{\ell -1}]$.⁹ We show how to enable this by modifying the garbled circuits ${\{\widehat{{\mathrm {i}C}}{}^\ell \}}$ as follows.

• The first idea is embedding all keys $\mathsf {key}^\ell$ for one garbled circuit $\widehat{{\mathrm {i}C}}{}^\ell$ in the previous one $\widehat{{\mathrm {i}C}}{}^{\ell -1}$, so that, $\widehat{{\mathrm {i}C}}{}^{\ell -1}$ can output directly the keys $\mathsf {key}^\ell [{{{st}}}^{\ell -1}]$ for the state ${{{st}}}^{\ell -1}$ it produces. This idea, however, does not apply for selecting keys for answers ${\bar{a}}^{\ell -1}$, as $\widehat{{\mathrm {i}C}}{}^{\ell -1}$ only computes queries ${\bar{q}}^{\ell -1}$ but not answers as it does not necessarily know the corresponding witnesses ${\bar{w}}^{\ell -1}$.

• The second idea is using WE as a “translator.” To illustrate the idea, assume that there is a single query $q^{\ell -1}$ and it has a Boolean answer $a^{\ell -1}$. In this case, let $\widehat{{\mathrm {i}C}}{}^{\ell -1}$ output a pair of WE ciphertexts $(\mathsf {ct}_0, \mathsf {ct}_1)$, where $\mathsf {ct}_b$ encrypts the key $\mathsf {key}^\ell [k,b]$ for the answer $a^{\ell -1}$ being b, under the statement $\mathsf {x}_b$ that the oracle outputs b, ${\mathcal {O}}(q^{\ell -1}, w'_b) = b$, for some witness $w'_b$. Now, the evaluator after evaluating $\widehat{{\mathrm {i}C}}{}^{\ell -1}$ obtains $\mathsf {ct}_0, \mathsf {ct}_1$. Using the witness $w^\ell$ it receives as input, it can decrypt the WE ciphertext $\mathsf {ct}^{\ell -1}_{a^{\ell -1}}$ for $a^{\ell -1} = {\mathcal {O}}(q^{\ell -1}, w^{\ell -1})$, obtaining the right key $\mathsf {key}^\ell [a^{\ell -1}]$ for evaluating the next garbled circuit.

To show security, it boils down to argue that for each garbled circuit $\widehat{{\mathrm {i}C}}{}^{\ell }$, only one key for each input wire is revealed. The security of $\widehat{{\mathrm {i}C}}{}^{\ell -1}$ ensures that only keys $\mathsf {key}^\ell [{{{st}}}^{\ell -1}]$ for the right state is revealed. On the other hand, to argue that only keys $\mathsf {key}^\ell [k,a^{\ell -1}]$ for the right answers are revealed, it crucially relies on the fact that the transcript including the answer is statistically unique. Thus, the ciphertext $\mathsf {ct}_{1-a^{\ell -1}}$ is encrypted under a false statement, and by security of WE, the label $\mathsf {key}^\ell [k,1-a^{\ell -1}]$ is hidden. We emphasize that if the transcript were only computationally unique, both WE ciphertexts $\mathsf {ct}_0, \mathsf {ct}_1$ would potentially be encrypted under true statements, as there may exist two witnesses $w_0, w_1$ that make the oracle output 0 and 1, ${\mathcal {O}}(q^{\ell -1}, w_0) = 0$, ${\mathcal {O}}(q^{\ell -1}, w_1) = 1$, even though it is computationally hard to find them; and the security of WE would be vacuous.

To handle computationally unique transcripts, WE is not the right tool. We propose a new primitive called Witness Selective (WS), which strengthens WE in two ways:

• Correctness: WS is defined for a non-deterministic oracle ${\mathcal {O}}$. One can encrypt a set of keys $\mathsf {key}= {\{\mathsf {key}[k,b]\}}_{k \in [l], b \in {\{0,1\}}}$ under a query q, $\mathsf {ct}\leftarrow \mathsf {WS.Enc}(q,\mathsf {key})$, which can later be decrypted using a witness w revealing the keys selected according to the output $a = {\mathcal {O}}(q, w)$, that is, ${\{\mathsf {key}[k,a_k]\}}_k = \mathsf {WS.Dec}(\mathsf {ct}, w)$.

• Semantic Security for Unique Answers: The security guarantee is that the WS ciphertext $\mathsf {ct}$ hides all the keys $\mathsf {key}[k, 1-a_{k}]$, provided that a is the computationally unique answer. Clearly, if it were easy to find two witnesses $w, w'$ such that, $(a = {\mathcal {O}}(q, w)) \ne (a' = {\mathcal {O}}(q,w'))$, the aforementioned semantic security cannot hold. Therefore, similarly to GIC, security is only required to hold for a distribution $\mathrm {w}\mathcal {D}$ over (q, w) that has computationally unique answers in the sense that given (q, w), it is hard to find $w'$ that makes ${\mathcal {O}}$ output a different valid answer. Then,

  $$\begin{aligned}&{\left\{ \mathsf {WS.Enc}(q,\mathsf {key}) : (q, w) {\mathop {\leftarrow }\limits ^{{}_R}}\mathrm {w}\mathcal {D}\right\} } \approx \\&{\left\{ \mathsf {WS.Enc}(q,\mathsf {key}) : (q, w) {\mathop {\leftarrow }\limits ^{{}_R}}\mathrm {w}\mathcal {D}; \ a = {\mathcal {O}}(q, w); \ \forall k, \ \mathsf {key}[k, 1-a_k] = 0 \right\} } . \end{aligned}$$

We can construct general GIC scheme for computationally unique transcript by replacing WE in the warm-up construction with WS. Slightly more precisely, each garbled circuit $\widehat{{\mathrm {i}C}}{}^{\ell -1}$ outputs a WS ciphertext $\mathsf {ct}$ encrypting keys ${\{\mathsf {key}[k, b]\}}$ for all wires corresponding to the oracle answer $a^{\ell -1}$, under the query $q^{\ell -1}$ (if there are multiple queries, simply generate one WS ciphertext for each query); then, the evaluator can use the witness $w^{\ell -1}$ to decrypt and obtain keys ${\{\mathsf {key}[k, a^{\ell -1}_k]\}}$ selected according to the oracle answer $a^{\ell -1} = {\mathcal {O}}(q^{\ell -1}, w^{\ell -1})$. Since the oracle answer (as a part of the transcript) is computationally unique, semantic security of WS ensures that the other keys ${\{\mathsf {key}[k, 1-a^{\ell -1}_k]\}}$ remain hidden, and hence we can invoke the security of the garbled circuits to argue the security of GIC.

As discussed above, WS is stronger than WE. For instance, one can use WS to encrypt a set of keys $\mathsf {key}$ under a query $q = (h,y=h(v))$ for a randomly sampled collision-resistant hash function h. With respect to the de-hashing oracle ${\mathcal {O}}(q, v')$ that outputs $v'$ if $y = h(v')$, a WS ciphertext reveals only keys ${\{\mathsf {key}[k,v_k]\}}$ selected by v, and hides others. In contrast, WE provides no security in this case. On the other hand, WS is weaker than the notion of extractable WE [33]. Roughly speaking, extractable WE guarantees that for every attacker A, there is an extractor E, such that, if A can decrypt a ciphertext encrypted under statement $\mathsf {x}$, then E can output a witness of $\mathsf {x}$. Extractable WE implies WS, and is strictly stronger as it requires knowledge extraction.

We note that so far there is no construction of general-purpose WE, let alone WS or extractable WE, from standard assumptions. This is also not the goal of this work. Instead, we show below how to construct special-purpose WS that suffices to construct 2-round MPC protocols.

2.4 Round-Collapsing via Garbled Interactive Circuits

We now revisit the round-collapsing approach, by replacing obfuscation with garbled interactive circuits. First, we observe that each player $P_i$ in the inner MPC protocol can be viewed as an interactive circuit ${\{P_i^\ell \}}$, interacting with an oracle ${\mathcal {O}}$ representing the other parties ${\{P_j\}}$, as described in Fig. 2.

Fig. 2.

Each player $P_i$ can be formalized as an interactive circuit $P_i = {\{P_i^\ell \}}$.

The important details are: In each round $\ell$, $P_i^{\ell }$ obtains through the oracle ${\mathcal {O}}$ all messages ${\bar{m}}^{\ell -1} = {\{m_j^{\ell -1}\}}_j$ output in the previous round, and additionally, it outputs a proof $\pi ^{\ell }_i$ that the message $m_i^{\ell }$ it outputs is generated honestly from its input $x_i$ and random tape $r_i$ committed in $c_i$. The message and proof are exactly the witness $w_i^\ell = (m_i^\ell , \pi ^\ell _i)$ for the query $q^\ell _i$ that players $P_j^\ell$ make in round $\ell$ to the oracle ${\mathcal {O}}$ for obtaining $P_i$’s message $a_i^\ell =m_i^\ell$ for the next round.

Therefore, we can use a GIC scheme to garble the interactive circuit representing each player $P_i$ to collapse round:

• 1. In the first round of MPC, each $P_i$ broadcasts a commitment $c_i$ to its input $x_i$ and random tape $r_i$, and

• 2. in the second round, each $P_i$ sends the garbled interactive circuit $\widehat{P}{}_i {\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GiC.Garble}({\{P^\ell _i\}})$, and

• 3. each $P_i$ emulates the execution of inner MPC in its head, by evaluating all ${\{\widehat{P}{}_j\}}$ round by round: In round $\ell$, it evaluates $o_j^\ell = (m_j^\ell , \pi _j^\ell ) = \mathsf {GiC.Eval}(\widehat{P}{}_j, {\bar{w}}^{<\ell })$, using the outputs obtained in previous rounds as witnesses, $w^{<\ell } = o^{< \ell } = {\{ (m_k^{\ell '},\pi _k^{\ell '})\}}_{k, \ell '<\ell }$. $P_i$ obtains its output when the inner MPC execution completes.

We observe that the transcript of execution of each ${\{P^\ell _i\}}$ is indeed computationally unique, as the commitments ${\{c_j\}}$ have unique committed values ${\{x_j, r_j\}}$ by the computational binding property, and lead to unique next messages ${\{m_j^\ell \}}$, by the soundness of proofs ${\{\pi _j^\ell \}}$. Therefore, the GIC scheme guarantees that the garbled interactive circuits reveals only their outputs, queries, and answers, summing up to all commitments ${\{c_j\}}$, inner MPC messages ${\{m^\ell _j\}}$, and proofs ${\{\pi _j^\ell \}}$, all of which can be made simulatable.

The MPC messages can be simulated by the simulator of the inner MPC protocol. To make commitments and proofs simulatable, the easiest way is using a standard non-interactive commitment scheme and a NIZK system, which however (1) requires a common reference string, and (2) makes the task of instantiating the associated WS scheme difficult. Recall that to instantiate the GIC scheme, we need a WS scheme for the oracle ${\mathcal {O}}$ described above, which internally verifies proofs. To solve this, we resort to a zero-knowledge Functional Commitment (FC) scheme that has a built-in special-purpose proof system. By minimizing the security requirements on this commitment, we manage to construct it, together with an associated WS scheme, from 2-message semi-honest OT (which is a necessary assumption). This gives 2-round MPC protocols in the plain model from 2-message semi-honest OT.

2.5 Functional Commitment with Witness Selector from OT

A zero-knowledge functional commitment scheme ${\mathsf {FC}}$ is computationally binding and computationally hiding, and additionally supports functional opening that is both binding and zero-knowledge. The notion of functional commitment was previously proposed by Libert et al. [37] for inner product functions, and later generalized to general functions in [3]. Here, we consider a stronger property, namely a zero-knowledge property. On the other hand, we do not require commitments nor functional decommitments to be of size constant in the length of the committed value, and our binding property only holds against semi-honest adversaries. Functional commitments were also implicitly and informally suggested by Gorbunov et al. in [34], as a way to interpret their new primitive: Homomorphic Trapdoor Functions (HTDFs). HTDFs could be used to construct our functional commitments (but the converse is not true). However, we do not know how to construct WS associated to an FC built from the HTDF proposed in [34].

• Functional Opening: For a commitment $c = {\mathsf {FC.Com}}(v; \rho )$ and a circuit G, one can generate a functional decommitment $d$ to the output of G evaluated on the committed value v, namely $m= G(v)$, using the randomness $\rho$ of the commitment $c$,

  $$ d= {\mathsf {FC.FOpen}}(c, G, m, \rho ), \quad {\mathsf {FC.FVer}}(c, G, m, d) = 1.$$

  We say that $(m,d)$ is a decommitment to (c, G); here, $d$ serves as a proof $\pi = d$ that the value committed in c evaluates to m through G in our 2-round MPC protocols.

  (Semi-Honest) Functional Binding: For an honestly generated commitment $c= {\mathsf {FC.Com}}(v;\rho )$ with random tape $\rho$, it is hard to find a decommitment $(m',d')$ to (c, G) for a different output $m'\ne m$, even given $\rho$. Note this is weaker than standard computational binding, as binding is only required for honestly generated commitments. This corresponds to distributional soundness of the proofs.

  Simulation (i.e., Zero-Knowledge): An honestly generated commitment $c {\mathop {\leftarrow }\limits ^{{}_R}}{\mathsf {FC.Com}}(v;\rho )$ (with random tape $\rho$) and decommitment $d$ can be simulated together, using only the output m, $(\tilde{c}, \tilde{d}) {\mathop {\leftarrow }\limits ^{{}_R}}{\mathsf {FC.Sim}}(c, G, m)$. This property is weaker than standard zero-knowledge, as the statement is from a distribution and is also simulated; only a single decommitment $d$ can be given for each commitment, or else simulation does not work.

A WS scheme associated with ${\mathsf {FC}}$ is for the oracle ${\mathcal {O}}^{\mathsf {FC}}$ that on input a query (c, G) and a witness $w = (m,d)$, outputs m if $(m,d)$ is a valid decommitment to (c, G), and $\bot$ otherwise. The functional binding property ensures that for any v, G, the distribution $\mathrm {w}\mathcal {D}_{v,G}$ of query $q = (c, G)$ and decommitment $w = (m, d)$ for honestly generated $c= {\mathsf {FC.Com}}(v;\rho )$, produces computationally unique oracle answer m (even given the randomness $\rho$ as auxiliary information). Despite the fact that functional commitments are only semi-honestly binding and one-time simulatable, we show that, together with an associated WS scheme, they suffice to instantiate our 2-round MPC protocols.

We show how to construct a functional commitment, and its associated WS scheme, from garbled circuits and a 2-round string 2-to-1 semi-honest OT.

OT as semi-honest binding commitment: We start with observing that any string 2-to-1 semi-honest OT gives a commitment scheme that is semi-honest binding; that is, given an honestly generated commitment $c = {\mathsf {Com}}(v;\rho )$ using a uniformly random tape $\rho$, it is hard to find a decommitment $(v',\rho ')$ that opens c to a different value $v' \ne v$ even given $\rho$. To see this, consider the parallelized version of 2-to-1 string OT, where $\mathrm {ot}_1 = \mathrm {p}\mathsf {OT}_1(x; \rho )$ generates the first flows from OT receiver for every bit $x_k$, and $\mathrm {ot}_2 = \mathrm {p}\mathsf {OT}_2(\mathrm {ot}_1, {\{\mathsf {key}[k, b]\}})$ generates the second flows from OT sender for every pair of inputs $(\mathsf {key}[k,0], \mathsf {key}[k,1])$. Combining $\mathrm {ot}_2$ with the randomness $\rho$ used for generating the first flows, one can act as the OT receiver to recover exactly one input $\mathsf {key}[k, x_k]$ at each coordinate k. We argue that the first flow $\mathrm {ot}_1 = \mathrm {p}\mathsf {OT}_1(x; \rho )$ is a semi-honest commitment to x. Suppose that it is not the case and that it is easy to find a decommitment $\rho '$ to a different value $x' \ne x$. Then a semi-honest attacker acting as OT receiver can violate the privacy of OT sender. (However, observe that $\mathrm {p}\mathsf {OT}_1(x)$ is not necessarily computationally binding, as there is no security for maliciously generated first flows of OT.)

Functional Opening: We use garbled circuits and OT (as a semi-honest binding commitment scheme) to enable functional opening. To commit to a value v, garble a universal circuit $U_v(\star ) = U(v,\star )$ with v hardcoded, and commit to all its input keys ${\{\mathsf {key}[k,b]\}}$ using $\mathrm {p}\mathsf {OT}_1$:

$$\begin{aligned} {\mathsf {FC.Com}}(v; \rho ) = c = (\widehat{U}{}_v, \mathrm {ot}_1) \ , \text { where }\ \mathrm {ot}_1[k,b] = \mathrm {p}\mathsf {OT}_1(\mathsf {key}[k,b];\ \rho [k,b])~. \end{aligned}$$

To generate a decommitment (m, d) of (c, G), simply send the keys and randomness used for generating the OT first flows ${\{\mathrm {ot}_1[k,G[k]]\}}$ selected by G. More formally, if G[k] is the k-th bit of the description of G which is used as input to $U_v$:

$$\begin{aligned} {\mathsf {FC.FOpen}}(c, G, m,\rho ) = d = {\left\{ \mathsf {key}[k, G[k]],\ \rho [k, G[k]]\right\} }. \end{aligned}$$

Verifying a decommitment $d= {\{\mathsf {key}', \rho '\}}$ w.r.t. (c, G, m) involves checking that the keys and randomness contained in $d'$ generate the OT first flows selected by G, and the garbled universal circuit $\widehat{U}{}_v$ evaluates to m on input these keys.

It is easy to see that the semi-honest binding property of $\mathrm {p}\mathsf {OT}_1$ implies the semi-honest functional binding of ${\mathsf {FC}}$, and that a pair (c, d) can be simulated relying on the security of garbled circuits and the computational hiding property (i.e., receiver privacy) of $\mathrm {p}\mathsf {OT}_1$.

WS for ${\mathsf {FC}}$: Next, to construct a WS scheme for the oracle ${\mathcal {O}}^{\mathsf {FC}}$ that verifies the functional decommitment of ${\mathsf {FC}}$, we again use garbled circuits to “enforce and hide” this verification. To encrypt a set of messages $\mathsf {M}[i,b']$ under a query (c, G), our idea is to garble the following circuit V that acts as ${\mathsf {FC.FVer}}$ (without checking (1)), and selects messages according to the output m if verification passes,

$$\begin{aligned} V({\{\mathsf {key}'[k]\}}) = {\left\{ \begin{array}{ll} {\{\mathsf {M}[i, m_i]\}} &{} \text {if } \widehat{U}{}_v({\{\mathsf {key}'[k]\}}) = m\\ \bot &{} \text {otherwise} \end{array}\right. }. \end{aligned}$$

(2)

Let $\widehat{V}{}$ be the garbled circuit, and ${\{{\mathsf {okey}}_k[j,\beta ]\}}_{j}$ the set of keys for the input wires corresponding to $\mathsf {key}'[k]$. (For clarity, we denote keys for $\widehat{V}{}$ as ${\mathsf {okey}}$.)

Given a decommitment $d= (\mathsf {key}', \rho ')$, correct WS decryption should recover messages ${\{\mathsf {M}[i,G(v)_i]\}}$ selected according to the correct output G(v) if the decommitment is valid, and $\bot$ if invalid. To enable this, what is missing is a “translation mechanism” that can achieve the following: For every k,

• Correctness: if $(\mathsf {key}'[k], \rho '[k])$ is a valid decommitment to $\mathrm {ot}_1[k, G[k]]$, it translates this pair into input keys of $\widehat{V}{}$ corresponding to $\mathsf {key}[k, G[k]]$, namely ${\{{\mathsf {okey}}_k[j,\mathsf {key}[k,G[k]]_j]\}}_j$.

• Security: the other keys ${\{{\mathsf {okey}}_k[j,1-\mathsf {key}[k,G[k]]_j]\}}_j$ are always hidden.

With such a translation mechanism, given a valid decommitment $d = \{\mathsf {key}[k, G[k]],\rho [k, G[k]]\}$, one can obtain all input keys corresponding to ${\{\mathsf {key}[k, G[k]]\}}$, and can evaluate $\widehat{V}{}$ with these keys to obtain the correct output,

$$\begin{aligned} \widehat{V}{}\left( {\left\{ {\{{\mathsf {okey}}_k[j,\mathsf {key}[k,G[k]]_j]\}}_j\right\} }_k\right) = V({\{\mathsf {key}[k,G[k]]\}}_k) = {\{\mathsf {M}[i, G(v)_i]\}}_i~. \end{aligned}$$

(3)

The security of the translation mechanism and garbled circuit $\widehat{V}{}$ guarantees that only the right messages ${\{\mathsf {M}[i, G(v)_i]\}}$ are revealed.

Our key observation is that the second flows of OT is exactly such a translation mechanism. For every OT first flows $\mathrm {ot}_1[k,G[k]]$ selected by G, generate the OT second flows using appropriate input keys of $\widehat{V}{}$ as sender’s inputs,

$$\begin{aligned} \forall k, \qquad \mathrm {ot}_2[k] {\mathop {\leftarrow }\limits ^{{}_R}}\mathrm {p}\mathsf {OT}_2(\mathrm {ot}_1[k,G[k]],\ {\{{\mathsf {okey}}_k[j,\beta ]\}}_{j,\beta })~. \end{aligned}$$

(4)

Indeed, for every k, given a valid decommitment $(\mathsf {key}[k, G[k]],\rho ')$ to $\mathrm {ot}_1[k,G[k]]$, one can act as an OT receiver to recover input keys ${\{{\mathsf {okey}}_k\left[ j,\mathsf {key}[k,G[k]]_j\right] \}}_j$, achieving correct translation. On the other hand, the OT sender’s security guarantees that the other keys ${\{{\mathsf {okey}}_k\left[ j,1-\mathsf {key}[k,G[k]]_j\right] \}}_j$ remain hidden.

Summarizing the above ideas gives the following construction of WS for ${\mathsf {FC}}$:

• $\mathsf {WS.Enc}((c,G), \mathsf {M})$: To encrypt $\mathsf {M}$ under (c, G), encryptor garbles the circuit V as in Eq. (2), and generates the second OT flows as in Eq. (4). The WS ciphertext is $\mathsf {ct}= (c, G, \widehat{V}{}, {\{\mathrm {ot}_2[k]\}})$.

• $\mathsf {WS.Dec}(\mathsf {ct},d)$: To decrypt $\mathsf {ct}$ with a decommitment $d = {\{\mathsf {key}', \rho '\}}$, the decryptor first verifies that for every k $(\mathsf {key}'[k], \rho '[k])$ is a valid decommitment of $\mathrm {ot}_1[k, G[k]]$ in c; otherwise, abort. Then, for every k, it acts as an OT receiver with input $\mathsf {key}'[k]$, randomness $\rho '[k]$, and OT sender’s message $\mathrm {ot}_2[k]$ to recover input keys of $\widehat{V}{}$ corresponding to $\mathsf {key}'[k]$. Finally, it evaluates $\widehat{V}{}$ with the obtained keys and output the messages output by $\widehat{V}{}$, as in Eq. (3).

The correctness and security of the WS scheme follows directly from the correctness and security of the translation mechanism, which are in turn implied by those of OT. See the full version [7] for more details.

Combining Sects. 2.1 to 2.5, we get a construction of a 2-round semi-honest MPC protocol from any 2-round semi-honest OT protocol using round collapsing for an inner MPC protocol.

2.6 Semi-Malicious and Malicious Security in the CRS Model

Toward achieving malicious security, we first achieve semi-malicious security. Roughly speaking, a semi-malicious party $P_j$ generates its messages according to the protocol using arbitrarily and adaptively chosen inputs and random tapes. This is formalized by letting $P_j$ “explain” each message $m^{\ell }_j$ it sends with a pair of input and random tape consistent with it, on a special witness tape. In the two-round setting, the challenge in simulating the view of $P_j$ lies in simulating honest parties’ first messages without knowing any secret information of $P_j$. This is because $P_j$ may rush to see honest parties’ first messages before outputting its own message, input, and random tape. (Observe that this is not an issue for semi-honest security, as the simulator learns the inputs and random tapes of corrupted parties first.)

Recall that in our 2-round protocols, each party $P_i$ sends functional commitments $c_i$ to its input and random tape $(x_i,r_i)$ in the first round, which are later partially decommitted to reveal $P_i$’s messages m in the inner MPC protocol. The simulation property of the functional commitment scheme ${\mathsf {FC}}$ ensures that the commitment and decommitment can be simulated together using just the message. However, this is insufficient for achieving semi-malicious security, as the simulator must simulate commitments in the first round with no information. To overcome this problem, we strengthen the simulatability of ${\mathsf {FC}}$ to equivocability, that is, simulation takes the following two steps: First, a commitment $\tilde{c}$ is simulated with no information, and later it is equivocated to open to any output m w.r.t. any circuit G. Instantiating our 2-round MPC protocols with such an equivocal functional commitment scheme, and other primitives that are semi-maliciously secure (e.g., using a semi-maliciously secure multi-round MPC protocol, and 2-round OT protocol), naturally “lift” semi-honest security to semi-malicious security.

With a simple idea, we can transform any simulatable functional commitment scheme ${\mathsf {FC}}$ into an equivocal one $\mathsf {eFC}$: Let $(\mathsf {OT}_1, \mathsf {OT}_2)$ be the sender and receiver’s algorithms of a 2-out-of-1 OT scheme.

• To commit to v, generate a ${\mathsf {FC}}$ commitment c to v, and then commit to each bit $c_i$ twice using the algorithm $\mathsf {OT}_1$, yielding the $\mathsf {eFC}$ commitment:

  $$\begin{aligned} ec = {\left\{ \mathrm {ot}_1[i,0] = \mathsf {OT}_1(c_i;\ r[i,0]),\ \mathrm {ot}_1[i,1] = \mathsf {OT}_1(c_i;\ r[i,1]) \right\} }_i \,. \end{aligned}$$

• An $\mathsf {eFC}$ decommitment (ed, G(v)) to (ec, G) contains the ${\mathsf {FC}}$ decommitment (d, G(v)) to (c, G), and the OT randomness ${\{r[i,c_i]\}}$ for generating the set of first flows ${\{\mathrm {ot}_1[i,c_i]\}}$ selected by c. Note that for any ec generated according to the above commitment algorithm, the revealed OT randomness determines the commitment c, and then the ${\mathsf {FC}}$ decommitment d determines G(v).

• Now, a commitment can be simulated by committing to both 0 and 1 in ec,

  $$\widetilde{ec} = {\{\mathrm {ot}_1[i,0] = \mathsf {OT}_1(0;\ r[i,0]),\ \mathrm {ot}_1[i,1] = \mathsf {OT}_1(1;\ r[i,1]) \}}_i \,.$$

  To decommit $\widetilde{ec}$ to output G(v), first simulate the ${\mathsf {FC}}$ commitment and decommitment $(\tilde{c}, \tilde{d})$ together using G(v), and then reveal the set of randomness ${\{r[i, \tilde{c}_i]\}}$ selected according to the simulated commitment $\tilde{c}$.

The WS scheme associated with $\mathsf {eFC}$ can be constructed similarly as that for ${\mathsf {FC}}$. The above idea is conceptually simple, but leads to nested calls of $\mathrm {p}\mathsf {OT}_1$/$\mathsf {OT}_1$, as a ${\mathsf {FC}}$ commitment c already contains OT first flows. This is not a problem when using 2-round OT, but does not extend to multi-round OT. In the full version [7], we present a more involved construction that avoids nested calls.

Malicious Security in the CRS Model. Given 2-round semi-maliciously secure protocols, in the CRS model, we can let each party prove using NIZK that each message is generated in a semi-malicious way (i.e., according to the protocol w.r.t. some input and random tape) as done in [2], which immediately gives Corollary 1.3 in the introduction. We refer the reader to [2] for more details.

Extension to k Rounds. Our 2-round semi-honest or semi-malicious constructions so far can be extended to k-round constructions, when replacing the underlying 2-round OT protocols with semi-honest or semi-malicious k-round OT protocols. See the full version [7] for more details.

2.7 Malicious Security in the Plain Model

We first show a new compilation that turns any $(k-1)$-round MPC protocol for computing f satisfying a stronger variant of semi-malicious security, called delayed-semi-malicious security, into a k-round malicious MPC protocol for f, assuming only one-way functions, for any $k \ge 5$. Roughly speaking, a delayed-semi-malicious party $P_j$ acts like a semi-malicious party, except that, it only “explains” all its messages once, before the last round (instead of explaining each of its messages after each round). This is formalized by letting $P_j$ output a pair of input and random tape before the last round (on its special witness tape) which is required to be consistent with all $P_j$’s messages. We say that a protocol is delayed-semi-malicious secure if it is secure against such adversaries. (For technical reasons, we require the protocols to have a universal simulator.) We observe that our k-round semi-malicious MPC protocols, when instantiated with a k-round delayed-semi-malicious OT become secure against delayed semi-malicious attackers (and admit a universal simulator).

To “lift” delayed-semi-malicious security to malicious security generically, our compilation builds on techniques of [1]. To illustrate the idea, consider compiling our 2-round delayed-semi-malicious MPC protocol $\varPhi$ for f into a 5-round malicious MPC protocol $\varPi$ for f. The basic idea is running $\varPhi$ for computing f, and restricting a malicious adversary A to act as a delayed-semi-malicious one $A'$ by requiring A to prove using zero-knowledge proof of knowledge (ZKPOK) that its messages in each round of $\varPhi$ are generated correctly according to some input and random tape. Unlike the CRS model, ZKPOK in the plain model requires at least 4 rounds. Sequentializing the two ZKPOK leads to a 8-round protocol. But if the ZKPOK allows for delayed-input, that is, only the last prover’s message depends on the statement and witness, then the two ZKPOK can be partially parallelized, leading to a 5-round protocol. In addition, in order to prevent mauling attacks, the ZKPOK must be non-malleable. Fortunately, Ciampi, Ostrovsky, Siniscalchi, and Visconti [20] (COSV) recently constructed a 4-round delayed-input non-malleable ZKPOK protocol from one-way functions, which suffice for our purpose. When starting from a 4-round (instead of 2-round) protocol $\varPhi$, to obtain a 5-round malicious protocol $\varPi$, we cannot afford to prove correctness of each round. But, if $\varPhi$ is delayed-semi-malicious secure, then it suffices to prove correctness only at the last two rounds, keeping the round complexity at 5.

Though the high-level ideas are simple, there are subtleties in the construction and proof. We cannot use the non-malleable ZKPOK in a black-box. This is because simulation of non-malleable ZKPOK uses rewindings and may render the $\varPhi$ instance running in parallel insecure. In addition, the COSV non-malleable ZKPOK is only many-many non-malleable in the synchronous setting, but in $\varPi$, the non-malleable ZKPOKs are not completely synchronized (ending either at the second last or the last round). Therefore, we use the COSV construction in a non-black-box way in $\varPi$ (with some simplification) as done in [1]. The specific property of COSV non-malleable ZKPOK that we rely on is that simulation requires only rewinding the second and third rounds, while (witness) extraction requires only rewinding the third and forth rounds. This means $\varPhi$ would be rewound at second/third and third/fourth rounds. The security of a generic delayed-semi-malicious protocol may not hold amid such rewinding. However, if we start with a 4-round protocol, rewindings can be circumvented if $\varPi$ contains no messages of $\varPhi$ in its third round. This means, in the rewindings of second/third and third/fourth rounds, the simulator can simply replay messages of $\varPhi$ in the main thread, keeping the instance of $\varPhi$ secure. See the full version [7] for details.

The above transformation is modular and general, but comes at a price—it only gives k-round malicious MPC from $(k-1)$-round delayed-semi-malicious OT, which is not necessary. To eliminate the gap, we leverage specific structures of our k-round delayed-semi-malicious protocols, to address the rewinding issue above. To illustrate the ideas, lets again examine the $k=5$ case.

To handle rewindings at third/fourth rounds, we observe that at the end of fourth round, each party $P_i$ proves using COSV non-malleable ZK that it has acted honestly in $\varPhi$ according to some input and random tape $(x_i, r_i)$. If in the malicious protocol $\varPi$, each party additionally commits to $(x_i, r_i)$ in the first two rounds using a statistically binding commitment scheme (and prove that its messages are generated honestly using the committed value). Then, as long as the adversary cannot cheat in the non-malleable ZK proofs, its messages in the third/fourth rounds of $\varPhi$ are determined by the commitments in the first two rounds. Therefore, the simulator can afford to continuously rewinding the adversary, until it repeats its messages in $\varPhi$ in the main execution thread. In this case, the simulator can simply replay the honest parties’ messages in $\varPhi$ in the main thread.

To handle rewindings at second/third rounds, the specific property of our protocol that we rely on is that the first 2 rounds of $\varPhi$ contains only instances of OT, whose messages do not depend on parties’ inputs. The latter holds because of the random self-reducibility of OT (hence, the sender and receiver can only use their inputs for generating their last messages). To avoid rewinding these OT instances in $\varPhi$, our idea is modifying the malicious protocol $\varPi$ as follows: In the first 2 rounds, for every OT instance $\mathsf {OT}_j$ in $\varPhi$, $\varPi$ runs two independent OT instances $\mathsf {OT}_j^0$ and $\mathsf {OT}_j^1$. In the third round, an random instance $\mathsf {OT}_j^{b_j}$ for ${b_j} \leftarrow {\{0,1\}}$ is chosen to be continued, and the other $\mathsf {OT}_j^{1-{b_j}}$ aborted—they are referred to as the real and shadow instances. Now in a rewinding of the second/third round, to avoid rewinding the real OT instances, the simulator replays the OT messages in the second round, and in the third round, continues the shadow instances $\mathsf {OT}_j^{1-{b_j}}$ and aborts the real instances $\mathsf {OT}_j^{b_j}$. Importantly, since for every pair $(\mathsf {OT}_j^0, \mathsf {OT}_j^1)$, the choice ${b_j}$ of which is real and which is shadow is random and independent, the view of the adversary in a rewinding is identical to that in the main execution thread. This guarantees that rewindings would succeed.

We remark that this idea does not apply in general. This is because to continue a random instance of a general protocol $\varPhi$ in the third round, parties may need to agree on that instance, which requires coin-tossing. In contrast, our protocol $\varPhi$ consists of many OT instances $\mathsf {OT}_j$, the decision of which of $(\mathsf {OT}_j^0,\mathsf {OT}_j^1)$ to continue can be made locally by the party who is supposed to send the third message of $\mathsf {OT}_j$ in $\varPhi$. In the full version [7], we put the above two ideas together, which gives k-round malicious OT from k-round delayed-semi-malicious OT.

A figure summarizing the results is provided in the full version [7].

3 Preliminaries

The security parameter is denoted $\lambda$. We recall the notion of polynomial-size circuit classes and families, together with the notion of statistical and computational indistinguishability in the full version [7].

For the sake of simplicity, we suppose that all circuits in a circuit class have the same input and output lengths. This can be achieved without loss of generality using appropriate paddings. We recall that for any $S$-size circuit class $\mathcal {C}= {\{\mathcal {C}_\lambda \}}_{\lambda \in \mathbb {N}}$, there exists a universal $\text {poly}(S)$-size circuit family ${\{U_\lambda \}}_{\lambda \in \mathbb {N}}$ such that for any $\lambda \in \mathbb {N}$, any circuit $C\in \mathcal {C}_\lambda$ with input and output lengths $n, l$, and any input $x\in {\{0,1\}}^n$, $U_\lambda (C, x) = C(x)$.

We make use of garbled circuit schemes. A garbled circuit scheme $\mathsf {GC}$ for a $\text {poly}$-size circuit class $\mathcal {C}= {\{\mathcal {C}_\lambda \}}_{\lambda \in \mathbb {N}}$ is defined by four polynomial-time algorithms $\mathsf {GC}=(\mathsf {GC.Gen},\mathsf {GC.Garble},\mathsf {GC.Eval},\mathsf {GC.Sim})$: (i) $\mathsf {key}{\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GC.Gen}(1^\lambda )$ generates input labels $\mathsf {key}= {\{\mathsf {key}[i, b]\}}_{i \in [n], b \in {\{0,1\}}}$; (ii) $\widehat{C}{\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GC.Garble}(\mathsf {key}, C)$ garbles the circuit $C\in \mathcal {C}_\lambda$ into $\widehat{C}$; (iii) $y= \mathsf {GC.Eval}(\widehat{C}, \mathsf {key}')$ evaluates the garbled circuit $\mathsf {GC.Garble}$ using input labels $\mathsf {key}' = {\{\mathsf {key}'[i]\}}_{i \in [n]}$ and returns the output $y\in {\{0,1\}}^l$; (iv) $(\mathsf {key}', {\widetilde{C}}) {\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GC.Sim}(1^\lambda , y)$ simulates input labels $\mathsf {key}' = {\{\mathsf {key}'[i]\}}_{i \in [n]}$ and a garbled circuit ${\widetilde{C}}$ corresponding to the output $y\in {\{0,1\}}^l$. The formal definition can be found in the full version [7]. We recall that garbled circuit schemes can be constructed from one-way functions.

4 Definition of Garbled Interactive Circuit Schemes

In this section, we define Garbled Interactive Circuit (GIC) schemes. An overview is provided in Sect. 2.2.

4.1 Interactive Circuits

We start by defining non-deterministic oracles and interactive circuits.

Definition 4.1

(Non-Deterministic Oracles). A non-deterministic oracle ${\mathcal {O}}$ is a circuit that takes as input a pair of bitstrings $(q,w) \in {\{0,1\}}^{n} \times {\{0,1\}}^{m}$, called query and witness respectively, and the output is a l-bit string or a special element $\perp$, called answer: ${\mathcal {O}}(q,w) \in {\{0,1\}}^{l} \cup \{\perp \}$. A poly-size non-deterministic oracle family is an ensemble of poly-size non-deterministic oracles ${\mathcal {O}}= {\{{\mathcal {O}}_\lambda \}}_{\lambda \in N}$.

Definition 4.2

Let ${\mathcal {O}}$ be a non-deterministic oracle. An L-round interactive circuit ${\mathrm {i}C} = {\{{\mathrm {i}C}^\ell \}}_{\ell \in [L]}$ with oracle ${\mathcal {O}}$ consists of a list of L next-step circuits.

An execution of ${\mathrm {i}C}$ with ${\mathcal {O}}$ and a list of witnesses ${\bar{w}} = {\{{\bar{w}}^{\ell }\}}_{\ell \in [L]}$ proceeds in L iterations as follows: In round $\ell \in [L]$, the next-step circuit ${\mathrm {i}C}^\ell$ on input the state ${{{st}}}^{\ell -1}$ (output in the previous round) and answers ${\bar{a}}^{\ell -1} = {\{a^{\ell -1}_k\}}_k$ (to queries ${\bar{q}}^{\ell -1} = {\{q^{\ell -1}_k\}}_k$ produced in the previous round), outputs a new state ${{{st}}}^{\ell }$, queries ${\bar{q}}^\ell = {\{q^{\ell }_k\}}_k$, and a (round) output $o^\ell$,

$$\begin{aligned} ({{{st}}}^\ell , {\bar{q}}^\ell , o^\ell ) = {\left\{ \begin{array}{ll} {\mathrm {i}C}^\ell ({{{st}}}^{\ell -1}, {\bar{a}}^{\ell -1}) &{} \text {if } \forall k,\ a^{\ell -1}_k = {\mathcal {O}}(q^{\ell -1}_k, w^{\ell -1}_k) \ne \bot \\ (\bot ,\bot ,\bot ) &{} \text{ otherwise } \end{array}\right. }~. \end{aligned}$$

The execution terminates after L rounds, or whenever $\bot$ is output. By convention, ${{{st}}}^0$ and ${\bar{q}}^0$ are empty strings.

We say that an execution is valid if it terminates after L rounds without outputting $\bot$. We call the list of witnesses ${\bar{w}}$ the witnesses of the execution. The output of the execution is the list of round outputs, denoted as ${{\mathsf {out}}}({\mathrm {i}C}, {\mathcal {O}},{\bar{w}}) = {\bar{o}} = {\{o^\ell \}}_{\ell \in [L]}$. The transcript of the execution is the list of queries, answers, and outputs, denoted as $\mathsf {trans}({\mathrm {i}C}, {\mathcal {O}}, {\bar{w}}) = {\{{\bar{q}}^\ell , {\bar{a}}^\ell , o^\ell \}}_{\ell \in [L]}$. (If the execution outputs $\bot$ in round $\ell$, ${\bar{q}}^{\ell '} = {\bar{a}}^{\ell '} =o^{\ell '} = \bot$ for all $\ell ' \ge \ell$.) Finally, we say that ${\mathrm {i}C}$ has size S if the total size of all circuits are bounded by S. In the rest of the paper, when the oracle ${\mathcal {O}}$ is clear from the context, we often omit it in the notations and write ${{\mathsf {out}}}({\mathrm {i}C},{\bar{w}})$ and $\mathsf {trans}({\mathrm {i}C},{\bar{w}})$.

4.2 Garbling Interactive Circuits

As mentioned above, an important difference between GIC schemes and classical garbled circuit schemes is that to evaluate a garbled (plain) circuit, one must obtain encoded inputs, whereas a garble interactive circuit can be evaluated with its oracle ${\mathcal {O}}$ on input an arbitrary list of witnesses, without encoding. This provides a more powerful functionality, but poses an issue on security: There may exist different lists of witnesses ${\bar{w}}, {\bar{w}}'$ that lead to executions with completely different transcripts. In this case, it is unclear how simulation can be done. To circumvent this, we only require the security of the garbling scheme to hold for distributions $\mathrm {i}\mathcal {D}$ of interactive circuits ${\mathrm {i}C}$ and witnesses ${\bar{w}}$ (with potentially some auxiliary information ${{\mathsf {aux}}}$) that have computationally unique transcripts $\mathsf {trans}({\mathrm {i}C},{\mathcal {O}}, {\bar{w}})$, in the sense that (given ${{\mathsf {aux}}}$) it is hard to find another list of witnesses ${\bar{w}}'$ that leads to an inconsistent transcript $\mathsf {trans}({\mathrm {i}C}, {\mathcal {O}},{\bar{w}})$, where inconsistency means:

Definition 4.3

(Consistent Transcripts). We say that two transcripts $\{{\bar{q}}^\ell , {\bar{a}}^\ell ,{o^\ell \}}_{\ell \in [L]}$ and ${\{{{\bar{q}}}'^\ell , {{\bar{a}}}'^\ell ,o'^\ell \}}_{\ell \in [L]}$ are consistent if for every $\ell \in [L]$, $({\bar{q}}^\ell , {\bar{a}}^\ell , o^\ell ) = ({\bar{q}}'^\ell , {\bar{a}}'^\ell , o'^\ell )$ or $({\bar{q}}^\ell , {\bar{a}}^\ell , o^\ell ) = (\bot , \bot , \bot )$ or $({\bar{q}}'^\ell , {\bar{a}}'^\ell , o'^\ell ) = (\bot , \bot , \bot )$. Otherwise, we say that the two transcripts are inconsistent.

Note that one can always produce a list of invalid witnesses that lead to an invalid execution. Therefore, difference due to outputting $\bot$ does not count as inconsistency. Next, we formally define these distributions that produce unique transcripts.

Definition 4.4

(Unique-Transcript Distribution). Let ${\mathcal {O}}= {\{{\mathcal {O}}_\lambda \}}_{\lambda \in \mathbb {N}}$ be a non-deterministic oracle family. Let $\mathrm {i}\mathcal {D}= {\{\mathrm {i}\mathcal {D}_{\lambda ,\mathrm {id}}\}}_{\lambda \in \mathbb {N}, \mathrm {id}}$ be an ensemble of efficiently samplable distributions over tuples $({\mathrm {i}C}, {\bar{w}}, {{\mathsf {aux}}})$. We say that $\mathrm {i}\mathcal {D}$ is a (computationally) unique-transcript distribution for ${\mathcal {O}}$, if

• Valid Execution: For any $\lambda \in \mathbb {N}$, any index $\mathrm {id}\in {\{0,1\}}^{\text {poly}(\lambda )}$, and any $({\mathrm {i}C}, {\bar{w}},{{\mathsf {aux}}})$ in the support of $\mathrm {i}\mathcal {D}_{\lambda ,\mathrm {id}}$, the execution of ${\mathrm {i}C}$ with ${\mathcal {O}}_\lambda$ and ${\bar{w}}$ is valid.

• Computationally Unique Transcript: For any $\text {poly}$-size circuit family $A={\{A_\lambda \}}_{\lambda }$, any sequence of indices ${\{\mathrm {id}_\lambda \}}_{\lambda }$, there is a negligible function $\mathrm {negl}$, such that for any $\lambda$:

  $$\begin{aligned}&\Pr \Big [ \mathsf {trans}({\mathrm {i}C}, {\mathcal {O}}_\lambda ,{\bar{w}}') \text { and }\mathsf {trans}({\mathrm {i}C},{\mathcal {O}}_\lambda , {\bar{w}})\text { are inconsistent} : \\&\qquad \qquad \quad ({\mathrm {i}C}, {\bar{w}},{{\mathsf {aux}}}) {\mathop {\leftarrow }\limits ^{{}_R}}\mathrm {i}\mathcal {D}_{\lambda , \mathrm {id}_\lambda }; \ {\bar{w}}' {\mathop {\leftarrow }\limits ^{{}_R}}A_\lambda ({\mathrm {i}C}, {\bar{w}},{{\mathsf {aux}}}) \Big ] \le \mathrm {negl}(\lambda ). \end{aligned}$$

It is a statistically unique-transcript distribution if the second property holds for any arbitrary-size circuit family $A = {\{A_\lambda \}}_\lambda$.

Now, we are ready to define GIC schemes.

Definition 4.5

(Garbled Interactive Circuit Schemes). Let ${\mathcal {O}}= {\{{\mathcal {O}}_\lambda \}}_{\lambda \in \mathbb {N}}$ be a non-deterministic oracle family, and $\mathrm {i}\mathcal {D}= {\{\mathrm {i}\mathcal {D}_{\lambda ,\mathrm {id}}\}}_{\lambda \in \mathbb {N}, \mathrm {id}}$ be a unique-transcript distribution for ${\mathcal {O}}$. A garbled interactive circuit scheme for $({\mathcal {O}},\mathrm {i}\mathcal {D})$ is a tuple of three polynomial-time algorithms $\mathsf {GiC}= (\mathsf {GiC.Garble},\mathsf {GiC.Eval},\mathsf {GiC.Sim})$:

• Garbling: $\widehat{{\mathrm {i}C}}{\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GiC.Garble}(1^\lambda ,{\mathrm {i}C})$ garbles an interactive circuit ${\mathrm {i}C}$ into a garbled interactive circuit $\widehat{{\mathrm {i}C}}$;

• Evaluation: $o^\ell = \mathsf {GiC.Eval}(\widehat{{\mathrm {i}C}}, {\bar{w}}^{< \ell })$ evaluates a garbled interactive circuit $\widehat{{\mathrm {i}C}}$ with a partial list of witness ${\bar{w}}^{<\ell }$, and outputs the $\ell$-th round output $o^\ell$;

• Simulation: $\widetilde{\mathrm {i}C}{\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GiC.Sim}(1^\lambda , T)$ simulates a garbled circuit $\widetilde{\mathrm {i}C}$ from a transcript T of an execution;

satisfying the following properties:

• Correctness: For any $\lambda \in \mathbb {N}$, any index $\mathrm {id}\in {\{0,1\}}^{\text {poly}(\lambda )}$, any $({\mathrm {i}C}, {\bar{w}}, {{\mathsf {aux}}})$ in the support of $\mathrm {i}\mathcal {D}_{\lambda , \mathrm {id}}$, it holds that

  $$\begin{aligned} \Pr \Big [ {\{\mathsf {GiC.Eval}(\widehat{{\mathrm {i}C}}, {\bar{w}}^{<\ell })\}}_{\ell \in [L]}&= {{\mathsf {out}}}({\mathrm {i}C}, {\mathcal {O}}_\lambda , {\bar{w}}) : \\&\qquad \qquad \quad \widehat{{\mathrm {i}C}}{\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GiC.Garble}(1^\lambda , {\mathrm {i}C}) \Big ] = 1 ; \end{aligned}$$

• Simulatability: The following two distributions are computationally indistinguishable:

  

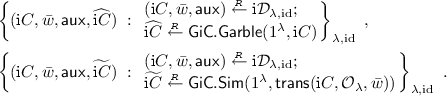
Remark 4.6

In this paper, we always consider perfect correctness for all primitives for the sake of simplicity. We could relax this notion to correctness up to a negligible error probability if, in addition, we ask that no non-uniform poly-time adversary can generate inputs and randomness which would not satisfy the correctness property, with non-negligible probability. In other words, in the case of GIC schemes, semi-maliciously generated GIC should satisfy the correctness property (except with negligible probability). This additional property is not needed for our semi-honest constructions.

5 2-Round Semi-Honest MPC Protocols

In this section, we present our construction of 2-round semi-honest MPC protocols. For that purpose, we first introduce the notion of functional commitment. We then show the MPC construction.

5.1 New Tool: Functional Commitment

Definition 5.1

((Zero-Knowledge) Functional Commitment). Let $\mathcal {G}= {\{\mathcal {G}_\lambda \}}_{\lambda \in \mathbb {N}}$ be a $\text {poly}$-size circuit class. A (zero-knowledge) functional commitment scheme ${\mathsf {FC}}$ for $\mathcal {G}$ is a tuple of four polynomial-time algorithms ${\mathsf {FC}}=({\mathsf {FC.Com}},{\mathsf {FC.FOpen}},{\mathsf {FC.FVer}},{\mathsf {FC.Sim}})$:

• Commitment: $c= {\mathsf {FC.Com}}(1^\lambda , v;\rho )$ generates a commitment $c$ of $v\in {\{0,1\}}^n$ using random tape $\rho \in {\{0,1\}}^\tau$, for the security parameter $\lambda$, where the random tape length $\tau$ is polynomial in $\lambda$;

• Functional Opening: $d= {\mathsf {FC.FOpen}}(c, G, v, \rho )$ derives from the commitment $c$ and the random tape $\rho$ used to generate it, a functional decommitment $d$ of $c$ to $y= G(v)$ for $G\in \mathcal {G}_\lambda$;

• Functional Verification: $b = {\mathsf {FC.FVer}}(c, G, y, d)$ outputs $b=1$ if $d$ is a valid functional decommitment of $c$ to $y$ for $G\in \mathcal {G}_\lambda$; and outputs $b=0$ otherwise;

• Simulation: $(c,d) {\mathop {\leftarrow }\limits ^{{}_R}}{\mathsf {FC.Sim}}(1^\lambda , G, y)$ simulates a commitment $c$ together with a functional decommitment $d$ of $c$ to $y$ for $G\in \mathcal {G}_\lambda$;

satisfying the following properties:

• Correctness: For any security parameter $\lambda \in \mathbb {N}$, for any $v\in {\{0,1\}}^n$, for any circuit $G\in \mathcal {G}_{\lambda }$, for any $\rho \in {\{0,1\}}^\tau$, it holds that if $c= {\mathsf {FC.Com}}(1^\lambda ,v;\rho )$, then:

  $$\begin{aligned} {\mathsf {FC.FVer}}(c, G, G(v), {\mathsf {FC.FOpen}}(c, G, v, \rho )) = 1; \end{aligned}$$

• Semi-Honest Functional Binding: For any polynomial-time circuit family $A={\{A_\lambda \}}_{\lambda \in \mathbb {N}}$, there exists a negligible function $\mathrm {negl}$, such that for any $\lambda \in \mathbb {N}$, for any $v\in {\{0,1\}}^{n}$, for any circuit $G\in \mathcal {G}_{\lambda }$:

  $$\begin{aligned}&\Pr \Big [ {\mathsf {FC.FVer}}(c, G, y, d) = 1 \text { and } y\ne G(v) :\\&\rho {\mathop {\leftarrow }\limits ^{{}_R}}{\{0,1\}}^\tau ; \ c= {\mathsf {FC.Com}}(1^\lambda , v; \rho ); \ (y, d) {\mathop {\leftarrow }\limits ^{{}_R}}A_\lambda (1^\lambda ,c,v,\rho ) \Big ] \le \mathrm {negl}(\lambda ); \end{aligned}$$

• Simulatability: The following two distributions are computationally indistinguishable:

  

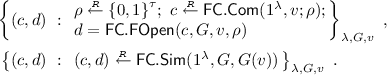
Note that the simulatability property implies the standard hiding property of commitments, if each circuit class $\mathcal {G}_\lambda$ contains a constant circuit: Consider indeed any constant circuit $C(x) = \alpha$, the fact that $(c, d)$ can be simulated from C and $\alpha$ implies that $c$ hides the message committed inside.

Let us now define the non-deterministic oracle family associated to ${\mathsf {FC}}$.

Definition 5.2

Let $\mathcal {G}= {\{\mathcal {G}_\lambda \}}_{\lambda \in \mathbb {N}}$ be a $\text {poly}$-size circuit class. Let ${\mathsf {FC}}=({\mathsf {FC.Com}},{\mathsf {FC.FOpen}},{\mathsf {FC.FVer}},{\mathsf {FC.Sim}})$ be a functional commitment scheme for $\mathcal {G}$. We define the following associated non-deterministic oracle family ${\mathcal {O}}^{\mathsf {FC}}= {\{{\mathcal {O}}^{\mathsf {FC}}_{\lambda }\}}_{\lambda \in \mathbb {N}}$:

$$ {\mathcal {O}}^{\mathsf {FC}}_\lambda ((c, G), (y, d)) = {\left\{ \begin{array}{ll} y&{}\text {if } {\mathsf {FC.FVer}}(c,G,y,d) = 1; \\ \perp &{}\text {otherwise.} \end{array}\right. } $$

5.2 Construction of 2-Round Semi-Honest MPC

Let f be an arbitrary N-party functionality.¹⁰ To construct a 2-round semi-honest MPC protocol ${\widetilde{\varPi }}$ for f, we rely on the following tools:

• A semi-honestly secure L-round MPC protocol $\varPi =({\mathsf {Next}}, {\mathsf {Output}})$ for f. We will refer to this protocol the “inner MPC protocol”.

  Recall that ${\mathsf {Next}}$ is next message function that computes the message broadcasted by party $P_i$ in round $\ell$, $m_{i}^\ell = {\mathsf {Next}}_i(x_i,r_i,{\bar{m}}^{< \ell })$, on input $x_i$ and random tape $r_i$, after receiving messages ${\bar{m}}^{< \ell } = {\{m_j^{\ell '}\}}_{j \in [N], \ell ' < \ell }$ broadcasted by parties $P_j$ on previous rounds. And ${\mathsf {Output}}$ is the output function that computes the output of party $P_i$, $y_i = {\mathsf {Output}}_i(x_i,r_i,{\bar{m}})$, after receiving all the messages ${\bar{m}} = {\{m_j^\ell \}}_{j \in [N],\ell \in [L]}$. The security parameter $\lambda$ is an implicit parameter $1^\lambda$ of ${\mathsf {Next}}$ and ${\mathsf {Output}}$.

• A functional commitment scheme ${\mathsf {FC}}=({\mathsf {FC.Com}},{\mathsf {FC.FOpen}},{\mathsf {FC.FVer}},{\mathsf {FC.Sim}})$ for the class of all $S$-size circuits with a sufficiently large polynomial bound $S$. We denote by ${\mathcal {O}}^{\mathsf {FC}}$ the associated non-deterministic oracle family defined in Definition 5.2.

• A GIC scheme $\mathsf {GiC}= (\mathsf {GiC.Garble}, \mathsf {GiC.Eval})$ for the oracle ${\mathcal {O}}^{\mathsf {FC}}$ and the unique-transcript distribution $\mathrm {i}\mathcal {D}= {\{\mathrm {i}\mathcal {D}_{\lambda ,\mathrm {id}}\}}_{\lambda \in \mathbb {N}, \mathrm {id}}$ that we define later.

We will show that using the constructions in Sect. 6 and in the full version [7], we can construct the two last tools from 2-round (semi-honest) OT. With the above tools, our 2-round MPC protocol ${\widetilde{\varPi }}=({\widetilde{\mathsf {Next}}}, \widetilde{\mathsf {Output}})$ for f proceed as follows:

Each party $P_{i}$ computes its first message $\widetilde{m}_{i}^1 = {\widetilde{\mathsf {Next}}}_{i}(x_{i},{\tilde{r}}_{i},\emptyset )$, using security parameter $\lambda$, input $x_{i}$, random tape ${\tilde{r}}_{i}$, and no messages, as follows.

• 1. Take a sufficient long substring $r_{i}$ of ${\tilde{r}}_{i}$ as the random tape for running the inner MPC protocol $\varPi$.

• 2. Commit L times to $(x_{i},r_{i})$ using the functional commitment scheme ${\mathsf {FC}}$: for $\ell \in [L]$, $c_{i}^\ell = {\mathsf {FC.Com}}(1^\lambda , (x_{i},r_{i}); \rho _i^\ell )$, where all the $\rho _i^\ell$’s (and $r_i$) are non-overlapping substrings of ${\tilde{r}}_i$.

• 3. Broadcast the first message $\widetilde{m}_{i}^1 = {\{c^\ell _{i}\}}_{\ell \in [L]}$, and keep ${\{\rho ^\ell _i\}}_{\ell \in [L]}$ secret.

Each party $P_{i}$ computes its second message $\widetilde{m}_i^2 = {\widetilde{\mathsf {Next}}}_{i}(x_{i},{\tilde{r}}_{i},{\{\widetilde{m}_j^1\}}_{j \in N})$, using all first messages ${\{\widetilde{m}_j^1\}}_{j \in N}$ as follows:

• 1. Garble the interactive circuit ${\mathrm {i}C}_i= {\{{\mathrm {i}C}^\ell _i\}}_{\ell \in [L]}$ defined in Fig. 3:

  $\widehat{{\mathrm {i}C}}_i{\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GiC.Garble}(1^\lambda , {\mathrm {i}C}_i).$

• 2. Broadcast the second message $\widetilde{m}_{i}^2 = \widehat{{\mathrm {i}C}}_i$.

Fig. 3.

The interactive circuit ${\mathrm {i}C}_i$

Each party $P_{i}$ computes its output $y_i= \widetilde{\mathsf {Output}}_{i}(x_{i},{\tilde{r}}_{i}, {\{\widetilde{m}_j^1, \widetilde{m}_j^2\}}_{j \in [N]} )$, using all first and second messages ${\{\widetilde{m}_j^1, \widetilde{m}_j^2\}}_{j \in N}$ as follows. Proceed in L iterations to evaluate the N garbled circuits ${\{\widehat{{\mathrm {i}C}}_j\}}_{j \in [N]}$ in parallel. Before iteration $\ell \in [L]$ starts, the following invariant holds:

Invariant: After the first $(\ell -1)$ iterations, $P_i$ has obtained for every $j \in [N]$ and every $\ell ' < \ell$:

• the inner MPC message $m_j^{\ell '}$ generated in the $\ell '$-th round by party $P_j$, and

• the associated functional decommitment $d_j^{\ell '}$ of $c_j^{\ell '}$ for the circuit $G_j^{\ell '}(\star ,\star ) = {\mathsf {Next}}_j(\star ,\star ,{\bar{m}}^{< \ell '})$.

We define ${\bar{w}}^{<\ell } = {\{w_j^{\ell '}\}}_{j,\ell '< \ell } = {\{(m_j^{\ell '},d_j^{\ell '})\}}_{\ell ' < \ell }$.

In the first round $\ell = 1$, all these messages and functional decommitments are empty. Thus, the invariant holds initially. With the above, $P_i$ does the following in iteration $\ell$: for every $j \in [N]$: $(m_j^\ell ,d_j^\ell ) = o^\ell _j = \mathsf {GiC.Eval}(\widehat{{\mathrm {i}C}}_j, {\bar{w}}^{< \ell })$.

After all L iterations, $P_i$ obtains the set of all messages ${\bar{m}}$, and computes the output by invoking the output function of the inner MPC protocol: $y_i= {\mathsf {Output}}_i\left( x_i,r_i, {\bar{m}}\right)$.

We now define the unique-transcript distribution $\mathrm {i}\mathcal {D}= {\{\mathrm {i}\mathcal {D}_{\lambda ,\mathrm {id}}\}}_{\lambda \in \mathbb {N}, \mathrm {id}}$ (for the garbled interactive circuit ${\mathrm {i}C}_i$) as follows: $\mathrm {id}= (i,{\bar{x}}, {\bar{r}}, {\bar{m}})$ and $\mathrm {i}\mathcal {D}_{\lambda ,\mathrm {id}}$ is

$$ {\left\{ ({\mathrm {i}C}_i,\;{\bar{w}},\;{\bar{\rho }}={\{\rho _j^\ell \}}_{j,\ell }) : \ \begin{array}{l} \forall j \in [N],\; \forall \ell \in [L], \\ \qquad \rho _j^\ell {\mathop {\leftarrow }\limits ^{{}_R}}{\{0,1\}}^{|\rho _j^\ell |}; \; c_j^\ell = {\mathsf {FC.Com}}(1^\lambda ,(x_j,r_j);\rho ^\ell _j); \\ \qquad G_j^{\ell }(\star ,\star ) = {\mathsf {Next}}_j(\star ,\star ,{\bar{m}}^{< \ell }); \\ \qquad d_j^\ell = {\mathsf {FC.FOpen}}(c^\ell _j, G_j^\ell , (x_j,r_j), \rho ^\ell _j); \\ {\bar{w}} = {\{w_j^\ell = (m_j^\ell ,d_j^\ell )\}}_{j,\ell }; {\mathrm {i}C}_i\text { defined in Fig. 3} \end{array} \right\} }. $$

The unique-transcript property follows from the semi-honest functional binding property of ${\mathsf {FC}}$. See the full version [7] for details.

We have the following theorem proven in the full version [7].

Theorem 5.3

If the inner MPC $\varPi =({\mathsf {Next}}, {\mathsf {Output}})$ is correct and secure against semi-honest adversaries, if the functional scheme ${\mathsf {FC}}$ is correct, semi-honest functional binding, and simulatable, if the garbled interactive circuit scheme $\mathsf {GiC}$ is correct and simulatable, then the MPC protocol defined above is correct and secure against semi-honest adversaries.

6 Garbled Interactive Circuit from Witness Selector

In this section, we show how to construct GIC from another tool we call witness selector, which can be seen as generalization of witness encryption to languages defined by a non-deterministic oracle family ${\mathcal {O}}$. Contrary to witness encryption, each query to ${\mathcal {O}}$ may have multiple answers, as long as at most one can be found efficiently.

We first define the notion of computationally unique-answer distribution for ${\mathcal {O}}$ and the notion of witness selector for such a distribution. Then we show how to construct a garbled interactive circuit scheme for $({\mathcal {O}},\mathrm {i}\mathcal {D})$ from any witness selector for a unique-answer distribution for ${\mathcal {O}}$ which is consistent with the unique-transcript distribution $\mathrm {i}\mathcal {D}$.

6.1 Witness Selector

Definition 6.1

(Unique-Answer Distribution). Let ${\mathcal {O}}$ be a non-deterministic oracle family. Let $\mathrm {w}\mathcal {D}= {\{\mathrm {w}\mathcal {D}_{\lambda ,\mathsf {id}}\}}_{\lambda \in \mathbb {N}, \mathsf {id}}$ be an ensemble of efficiently samplable distributions over tuples $(q,w,{{\mathsf {aux}}})$. We say that $\mathrm {w}\mathcal {D}$ is a (computationally) unique-answer distribution for ${\mathcal {O}}$ if

• Non-$\bot$ Answer: For any $\lambda \in \mathbb {N}$, any index $\mathsf {id}\in {\{0,1\}}^{\text {poly}(\lambda )}$, and any $(q,w,{\mathsf {aux}})$ in the support of $\mathrm {w}\mathcal {D}_{\lambda ,\mathsf {id}}$, ${\mathcal {O}}_\lambda (q,w) \ne \bot$.

• Computationally Unique Answer: For any $\text {poly}$-size circuit family $A={\{A_\lambda \}}_{\lambda \in \mathbb {N}}$, for any sequence of indices ${\{\mathsf {id}_\lambda \}}_{\lambda }$, there exists a negligible function $\mathrm {negl}$, such that for any $\lambda \in \mathbb {N}$:

  $$\begin{aligned} \Pr \Big [{\mathcal {O}}_\lambda (q,w')&\ne \perp \text { and }{\mathcal {O}}_\lambda (q,w') \ne {\mathcal {O}}_\lambda (q,w) : \\&\quad (q,w,{\mathsf {aux}}) {\mathop {\leftarrow }\limits ^{{}_R}}\mathrm {w}\mathcal {D}_{\lambda ,\mathsf {id}_\lambda }; \ w' {\mathop {\leftarrow }\limits ^{{}_R}}A_{\lambda }(q,w,{\mathsf {aux}}) \Big ] \le \mathrm {negl}(\lambda ). \end{aligned}$$

It is a statistically unique-answer distribution if the second property holds for any arbitrary-size circuit family $A = {\{A_\lambda \}}_\lambda$.

Definition 6.2

(Witness Selector). Let ${\mathcal {O}}= {\{{\mathcal {O}}_\lambda \}}_{\lambda \in N}$ be a non-deterministic oracle family, and $\mathrm {w}\mathcal {D}={\{\mathrm {w}\mathcal {D}_{\lambda ,\mathsf {id}}\}}_{\lambda \in \mathbb {N},\mathsf {id}}$ a unique-answer distribution for ${\mathcal {O}}$. A witness selector scheme for $({\mathcal {O}},\mathrm {w}\mathcal {D})$ is a tuple of two polynomial-time algorithms $\mathsf {WS}= (\mathsf {WS.Enc},\mathsf {WS.Dec})$:

• Encryption: $\mathsf {ct}{\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {WS.Enc}(1^\lambda , q, \mathsf {M})$ encrypts messages $\mathsf {M}={\{\mathsf {M}[i,b]\}}_{i \in [l],b\in {\{0,1\}}}$ for a query q, into a ciphertext $\mathsf {ct}$, where each message has the same length $|\mathsf {M}[i,b]| = \text {poly}(\lambda )$;

• Decryption: $\mathsf {M}' = \mathsf {WS.Dec}(\mathsf {ct}, w)$ decrypts a ciphertext $\mathsf {ct}$ into messages $\mathsf {M}' = {\{\mathsf {M}'[i]\}}_{i \in [l]}$ using a witness w;

satisfying the following properties:

• Correctness: For any security parameter $\lambda \in \mathbb {N}$, for any index $\mathsf {id}$, for any $(q,w,{{\mathsf {aux}}})$ in the support of $\mathrm {w}\mathcal {D}_{\lambda ,\mathsf {id}}$, for any messages $\mathsf {M}={\{\mathsf {M}[i,b]\}}_{i,b}$, for $a = {\mathcal {O}}(q,w)$:

  $$ \Pr \Big [ \mathsf {WS.Dec}(\mathsf {WS.Enc}(1^\lambda , q, \mathsf {M}),\; w) = {\{\mathsf {M}[i,a_i]\}}_{i \in [l]} \Big ] = 1 \,; $$

• Semantic Security: The following two distributions are indistinguishable:

  

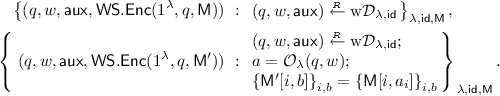
6.2 Garbled Interactive Circuit from Witness Selector

Let ${\mathcal {O}}= {\{{\mathcal {O}}_\lambda \}}_{\lambda \in \mathbb {N}}$ be a $\text {poly}$-size non-deterministic oracle family. Let $\mathrm {i}\mathcal {D}= {\{\mathrm {i}\mathcal {D}_{\lambda ,\mathrm {id}}\}}_{\lambda \in \mathbb {N}, \mathrm {id}}$ be an ensemble of efficiently samplable distributions over tuples $({\mathrm {i}C}, {\bar{w}}, {{\mathsf {aux}}})$, where ${\mathrm {i}C}$ is an L-round interactive circuit. We suppose that $\mathrm {i}\mathcal {D}$ is a unique-transcript distribution for ${\mathcal {O}}$. To construct a garbled interactive circuit scheme $\mathsf {GiC}= (\mathsf {GiC.Garble},\mathsf {GiC.Eval},\mathsf {GiC.Sim})$ for $({\mathcal {O}},\mathrm {i}\mathcal {D})$, we rely on the following tools:

• A witness selector $\mathsf {WS}=(\mathsf {WS.Enc},\mathsf {WS.Dec})$ for $({\mathcal {O}},\mathrm {w}\mathcal {D})$ where $\mathrm {w}\mathcal {D}={\{\mathrm {w}\mathcal {D}_{\lambda ,\mathsf {id}}\}}$ is a unique-answer distribution for ${\mathcal {O}}$, which is consistent with the unique-transcript distribution $\mathrm {i}\mathcal {D}$ (consistency is defined below).

• A garbled circuit scheme $\mathsf {GC}=(\mathsf {GC.Gen},\mathsf {GC.Garble},\mathsf {GC.Eval},\mathsf {GC.Sim})$ for the class of all $S$-size circuits with a sufficiently large polynomial bound $S$.

The naive notion of consistence would be: $\mathrm {i}\mathcal {D}$ is consistent with $\mathrm {w}\mathcal {D}$ if each query $q^\ell _k$ and its associated witness $w^\ell _k$ follow the same distribution as $\mathrm {w}\mathcal {D}$. Unfortunately, this is not sufficient as the adversary may learn some auxiliary information. Instead, we require that for any $\ell$ and k, the distribution of $({\mathrm {i}C}, {\bar{w}},{{\mathsf {aux}}}) {\mathop {\leftarrow }\limits ^{{}_R}}\mathrm {i}\mathcal {D}_{\lambda ,\mathrm {id}}$ can be simulated from $(q,w,{{\mathsf {aux}}}) {\mathop {\leftarrow }\limits ^{{}_R}}\mathrm {w}\mathcal {D}_{\lambda ,\mathsf {id}'}$ (for some index $\mathsf {id}'$ function of $\mathrm {id}$) in such a way that $q^\ell _k$ and $w^\ell _k$ match q and w. A formal definition is provided in the full version [7].

Fig. 4.

The augmented next message function ${\mathrm {i}C.\mathsf {AugNext}}^\ell$

The construction proceeds as follows:

• Garbling: $\widehat{{\mathrm {i}C}}{\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GiC.Garble}(1^\lambda , {\mathrm {i}C})$ garbles the interactive circuit ${\mathrm {i}C} = {\{{\mathrm {i}C}^\ell \}}_{\ell \in [L]}$ into $\widehat{{\mathrm {i}C}}$ as follows: For $\ell$ from L to 1,

  • 1. Generate input labels $\mathsf {key}^\ell {\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GC.Gen}(1^\lambda )$.

  • 2. Garble the circuit ${\mathrm {i}C.\mathsf {AugNext}}^\ell$ defined in Fig. 4:

    $\widehat{\mathrm {i}C.\mathsf {AugNext}}{}^\ell {\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GC.Garble}(\mathsf {key}^\ell ,{\mathrm {i}C.\mathsf {AugNext}}^\ell ).$

  And output $\widehat{{\mathrm {i}C}}= {\{\widehat{\mathrm {i}C.\mathsf {AugNext}}{}^\ell \}}_{\ell \in [L]}$.

• Evaluation: $o^{\ell '} = \mathsf {GiC.Eval}(\widehat{{\mathrm {i}C}},{\bar{w}}^{< \ell '})$ evaluates the garbled interactive circuit $\widehat{{\mathrm {i}C}}$ with the partial list of witnesses ${\bar{w}}^{< \ell '}$ as follows. For $\ell \in [\ell ']$, we denote by $\mathsf {key}'^\ell$ the set of input labels that we actually use to evaluate $\widehat{\mathrm {i}C.\mathsf {AugNext}}{}^\ell$ (i.e., it contains one label per input wire; $\mathsf {key}'^1$ and $\mathsf {key}'^{L+1}$ are the empty strings). $\mathsf {key}'^\ell$ is composed of two parts $\mathsf {key}'^\ell [[{{{st}}}^\ell ]]$ and $\mathsf {key}'^\ell [[{\bar{a}}^\ell ]] = {\{\mathsf {key}'^\ell [[a^\ell _k]]\}}_k$ corresponding to the input wires for ${{{st}}}^\ell$ and ${\bar{a}}^\ell$ respectively: $\mathsf {key}'^\ell = (\mathsf {key}'^\ell [[{{{st}}}^\ell ]], {\{\mathsf {key}'^\ell [[a^\ell _k]]\}}_k)$. For $\ell$ from 1 to $\ell '$, the evaluator does the following:

  • 1. Evaluate the garbled circuit $\widehat{\mathrm {i}C.\mathsf {AugNext}}{}^\ell$:

    $(\mathsf {key}'^{\ell +1}[[{{{st}}}^\ell ]],\; {\bar{q}}^\ell ,\; {\bar{\mathsf {ct}}}^\ell ,\; o^\ell ) = \mathsf {GC.Eval}(\widehat{\mathrm {i}C.\mathsf {AugNext}}{}^\ell , \mathsf {key}'^\ell ).$

  • 2. If $\ell < \ell '$, for each $k \in [|{\bar{\mathsf {ct}}}^\ell |]$, decrypt $\mathsf {ct}^\ell _k$ using the witness $w^\ell _k$:

    $\mathsf {key}'^{\ell +1}[[a^\ell _k]] = \mathsf {WS.Dec}(\mathsf {ct}^\ell _k,w^\ell _k).$

  And output $o^{\ell '}$ (except if $o^\ell = \bot$ for some $\ell \le \ell '$).

• Simulation: $\widetilde{\mathrm {i}C}{\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GiC.Sim}(1^\lambda , T)$ simulates a garbled interactive circuit $\widetilde{\mathrm {i}C}$ from a transcript $T = {\{{\bar{q}}^\ell , {\bar{a}}^\ell ,o^\ell \}}_{\ell \in [L]}$ as follows. As for evaluation, for $\ell \in [L]$, we denote by $\mathsf {key}'^\ell = (\mathsf {key}'^\ell [[{{{st}}}^\ell ]], {\{\mathsf {key}'^\ell [[a^\ell _k]]\}}_k)$ the set of input labels that we actually use as inputs to $\widehat{\mathrm {i}C.\mathsf {AugNext}}{}^\ell$ (i.e., it contains one label per input wire). For $\ell$ from L to 1, the simulator does the following:

  • 1. Define $\mathsf {key}^{\ell +1}$ to be such that $\mathsf {key}^{\ell +1}[i,b] = \mathsf {key}'^{\ell +1}[i]$ for all input wire i and all bits $b \in {\{0,1\}}$. $\mathsf {key}'^{L+1}$ and $\mathsf {key}^{L+1}$ are empty.

  • 2. Encrypt the labels generated for the round $\ell +1$ corresponding to the answer ${\bar{a}}^\ell$, using the witness selector scheme: for each k,

    $\mathsf {ct}^\ell _k {\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {WS.Enc}(1^\lambda , {\bar{q}}^\ell , \mathsf {key}^{\ell +1}[[a^\ell _k]]).$ (For $\ell = L$, ${\bar{\mathsf {ct}}}^\ell$ and $\mathsf {key}^{\ell +1}$ are empty.)

  • 3. Simulate the garbling of $\widehat{\mathrm {i}C.\mathsf {AugNext}}{}^\ell$, using its outputs $\mathsf {key}'^{\ell +1}[[{{{st}}}^\ell ]] = \mathsf {key}^{\ell +1}[{{{st}}}^\ell ]$ (for $\ell =L$, this value is empty), ${\bar{q}}^{\ell +1}$, ${\bar{\mathsf {ct}}}^\ell$, and $o^\ell$:

    $\widehat{\mathrm {i}C.\mathsf {AugNext}}{}^\ell {\mathop {\leftarrow }\limits ^{{}_R}}\mathsf {GC.Sim}(1^\lambda ,(\mathsf {key}'^{\ell +1}[[{{{st}}}^\ell ]], {\bar{q}}^{\ell }, {\bar{\mathsf {ct}}}^\ell , o^\ell )).$

We prove the following security theorem in the full version [7].

Theorem 6.3

If $\mathsf {GC}$ is correct and simulatable, if $\mathsf {WS}$ is correct and semantically secure, if $\mathrm {w}\mathcal {D}$ is unique-answer, and if $\mathrm {i}\mathcal {D}$ and $\mathrm {w}\mathcal {D}$ are consistent, then the garbled interactive circuit scheme $\mathsf {GiC}$ defined above is correct and simulatable.