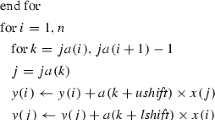1 Introduction

In this chapter describes a highly computationally efficient solver for equations of the form

$$\displaystyle \begin{aligned} \kappa \frac{\partial u}{\partial t} = \ mathcal{L} u (\boldsymbol{x}, t) + h(u,\boldsymbol{x},t), \ \ \boldsymbol{x} \in \varOmega, t > 0, {} \end{aligned} $$
(1)

with initial data u(x, 0) = u 0(x). Here \(\ mathcal {L}\) is an elliptic operator acting on a fixed domain Ω and h is lower order, possibly nonlinear terms. We take κ to be real or imaginary, allowing for parabolic and Schrödinger type equations. We desire the benefits that can be gained from an implicit solver, such as L-stability and stiff accuracy, which means that the computational bottleneck will be the solution of a sequence of elliptic equations set on Ω. In situations where the elliptic equation to be solved is the same in each time-step, it is highly advantageous to use a direct (as opposed to iterative) solver. In a direct solver, an approximate solution operator to the elliptic equation is built once. The cost to build it is typically higher than the cost required for a single elliptic solve using an iterative method such as multigrid, but the upside is that after it has been built, each subsequent solve is very fast. In this chapter, we argue that a particularly efficient direct solver to use in this context is a method obtained by combining a multidomain spectral collocation discretization (a so-called “patching method”, see e.g. Ch. 5.13 in [3]) with a nested dissection type solver. It has recently been demonstrated [1, 7, 12] that this combined scheme, which we refer to as a “Hierarchial Poincaré–Steklov (HPS)” solver, can be used with very high local discretization orders (up to p = 20 or higher) without jeopardizing either speed or stability, as compared to lower order methods.

In this chapter, we investigate the stability and accuracy that is obtained when combining high-order time-stepping schemes with the HPS method for solving elliptic equations. We restrict attention to relatively simple geometries (mostly rectangles). The method can without substantial difficulty be generalized to domains that can naturally be expressed as a union of rectangles, possibly mapped via curvilinear smooth parameter maps.

A longer version of this chapter with additional details is available at [2]. Also note that the conclusions are deferred to Part II of this paper (same issue).

2 The Hierarchical Poincaré–Steklov Method

In this section, we describe a computationally efficient and highly accurate technique for solving an elliptic PDE of the form

$$\displaystyle \begin{aligned} \begin{aligned}{}[Au](\boldsymbol{x}) =&\ g(\boldsymbol{x}),\quad&\boldsymbol{x} \in \varOmega,\\ u(\boldsymbol{x}) =&\ f(\boldsymbol{x}),\quad&\boldsymbol{x} \in \varGamma, \end{aligned} \end{aligned} $$
(2)

where Ω is a domain with boundary Γ, and where A is a variable coefficient elliptic differential operator

$$\displaystyle \begin{aligned}\displaystyle [Au](\boldsymbol{x}) = -c_{11}(\boldsymbol{x})[\partial_{1}^{2}u](\boldsymbol{x}) -2c_{12}(\boldsymbol{x})[\partial_{1}\partial_{2}u](\boldsymbol{x}) -c_{22}(\boldsymbol{x})[\partial_{2}^{2}u](\boldsymbol{x})\\\displaystyle +c_{1}(\boldsymbol{x})[\partial_{1}u](\boldsymbol{x}) +c_{2}(\boldsymbol{x})[\partial_{2}u](\boldsymbol{x}) +c(\boldsymbol{x})\,u(\boldsymbol{x}) \end{aligned} $$

with smooth coefficients. In the present context, (2) represents an elliptic solve that is required in an implicit time-descretization technique of a parabolic PDE, as discussed in Sect. 1. For simplicity, let us temporarily suppose that the domain Ω is rectangular; the extension to more general domains is discussed in Remark 1.

Our ambition here is merely to provide a high level description of the method; for implementation details, we refer to [1, 2, 7,8,9, 12, 13].

2.1 Discretization

We split the domain Ω into n 1 × n 2 boxes, each of size h × h. Then on each box, we place a p × p tensor product grid of Chebyshev nodes, as shown in Fig. 1. We use collocation to discretize the PDE (2). With \(\{\boldsymbol {x}_{i}\}_{i=1}^{N}\) denoting the collocation points, the vector u that represents our approximation to the solution u of (2) is given simply by u(i) ≈ u(x i). We then discretize (2) as follows:

  1. 1.

    For each collocation node that is internal to a box (red nodes in Fig. 1), we enforce (2) by directly collocating the spectral differential operator supported on the box, as described in, e.g., Trefethen [15].

  2. 2.

    For each collocation node on an edge between two boxes (blue nodes in Fig. 1), we enforce that the normal fluxes across the edge be continuous. For instance, for a node x i on a vertical line, we enforce that ∂u∕∂x 1 is continuous across the edge by equating the values for ∂u∕∂x 1 obtained by spectral differentiation of the boxes to the left and to the right of the edge. For an edge node that lies on the external boundary Γ, simply evaluate the normal derivative at the node, as obtained by spectral differentiation in the box that holds the node.

  3. 3.

    All corner nodes (gray in Fig. 1) are dropped from consideration. For an elliptic operator of the form (2) with c 12 = 0, it turns out that these values do not contribute to any of the spectral derivatives on the interior nodes, which means that the method without corner nodes is mathematically equivalent to the method with corner nodes, see [5, Sec. 2.1] for details. When c 12 ≠ 0, one must in order to drop the corner nodes include an extrapolation operator when evaluating the terms involving the spectral representation of the mixed derivative ∂ 2 u∕∂x 1 ∂x 2. This may lead to a slight drop in the order of convergence, but the difference is hardly noticeable in practice, and the exclusion of corner nodes greatly simplifies the implementation of the method.

Fig. 1
figure 1

The domain Ω is split into n 1 × n 2 squares, each of size h × h. In the figure, n 1 = 3 and n 2 = 2. Then on each box, a p × p tensor product grid of Chebyshev nodes is placed, shown for p = 7. At red nodes, the PDE (2) is enforced via collocation of the spectral differentiation matrix. At the blue nodes, we enforce continuity of the normal fluxes. Observe that the corner nodes (gray) are excluded from consideration

Full size image

Since we exclude the corner nodes from consideration, the total number of nodes in the grid equals N = (p − 2)(p n 1 n 2 + n 1 + n 2) ≈ p 2 n 1 n 2. The discretization procedure described then results in an N × N matrix A. For a node i, the value of A(i, :)u depends on what type of node i is:

$$\displaystyle \begin{aligned}{\mathsf{A}}(i,:){\mathsf{u}} \approx \left\{\begin{array}{l} [Au](\boldsymbol{x}_{i})\ \mbox{for any interior (red) node,}\\ 0\ \text{for any edge node (blue) not on }\varGamma,\\ \partial u /\partial n\ \text{for any edge node (blue) on }\varGamma. \end{array}\right. \end{aligned}$$

This matrix A can be used to solve BVPs with a variety of different boundary conditions, including Dirichlet, Neumann, Robin, and periodic [12].

In many situations, a simple uniform mesh of the type shown in Fig. 1 is not optimal, since the regularity in the solution may vary greatly, due to corner singularities, localized loads, etc. The HPS method can easily be adapted to handle local refinement. The essential difficulty that arises is that when boxes of different sizes are joined, the collocation nodes along the joint boundary will not align. It is demonstrated in [1, 5] that this difficulty can stably and efficiently be handled by incorporating local interpolation operators.

2.2 A Hierarchical Direct Solver

A key observation in previous work on the HPS method is that the sparse linear system that results from the discretization technique described in Sect. 2.1 is particularly well suited for direct solvers, such as the well-known multifrontal solvers that compute an LU-factorization of a sparse matrix. The key is to minimize fill-in by using a so called nested dissection ordering [4, 6]. Such direct solvers are very powerful in a situation where a sequence of linear systems with the same coefficient matrix needs to be solved, since each solve is very fast once the coefficient matrix has been factorized. This is precisely the environment under consideration here. The particular advantage of combining the multidomain spectral collocation discretization described in Sect. 2.1 is that the time required for factorizing the matrix is independent of the local discretization order. As we will see in the numerical experiments, this enables us to attain both very high accuracy, and very high computational efficiency.

Remark 1 (General Domains)

For simplicity we restrict attention to rectangular domains in this chapter. The extension to domains that can be mapped to a union of rectangles via smooth coordinate maps is relatively straight-forward, since the method can handle variable coefficient operators [12, Sec. 6.4]. Some care must be exercised since singularities may arise at intersections of parameter maps, which may require local refinement to maintain high accuracy.

The direct solver described exactly mimics the classical nested dissection method, and has the same asymptotic complexity of O(N 1.5) for the “build” (or “factorization”) stage, and then \(O(N\log N)\) cost for solving a system once the coefficient matrix has been factorized. Storage requirements are also \(O(N\log N)\). A more precise analysis of the complexity that takes into account the dependence on the order p of the local discretization shows [1] that T build ∼ N p 4 + N 1.5, and \(T_{\mathrm {solve}} \sim N\,p^{2} + N\log N\).

3 Time-Stepping Methods

For high-order time-stepping of (1), we use the so called Explicit, Singly Diagonally Implicit Runge–Kutta (ESDIRK) methods. These methods have a Butcher diagram with a constant diagonal γ and are of the form

0

0

     

2γ

γ

γ

    

c 3

a 3,1

a 3,2

γ

   

⋮

⋮

⋮

⋱

⋱

  

c s−1

a s−1,1

a s−1,2

a s−1,3

⋯

γ

 

1

b 1

b 2

b 3

⋯

b s−1

γ

 

b 1

b 2

b 3

⋯

b s−1

γ

ESDIRK methods offer the advantages of stiff accuracy and L-stability. They are particularly attractive when used in conjunction with direct solvers since the elliptic solve required in each stage involves the same coefficient matrix \((I-h\gamma \ mathcal {L})\), where h is the time-step.

In general we split the right hand side of (1) into a stiff part, F [1], that will be treated implicitly using ESDIRK methods, and a part, F [2], that will be treated explicitly (with a Butcher table denoted \(\hat c\), \(\hat A\), and \(\hat b\)). Precisely we will use the Additive Runge–Kutta (ARK) methods by Carpenter and Kennedy [11], of order 3, 4 and 5.

We may choose to formulate the Runge–Kutta method in terms of either solving for slopes or solving for stage solutions. We denote these the k i formulation and the u i formulation, respectively. When solving for slopes the stage computation is

$$\displaystyle \begin{aligned} \begin{array}{rcl} k_{i}^{n} &\displaystyle =&\displaystyle F^{[1]}(t_{n} + c_{i} \varDelta t, u^{n} + \varDelta t\sum_{j=1}^{s}a_{ij}k_{j}^{n} + \varDelta t\sum_{j=1}^{s} \hat{a}_{ij} l_{j}^{n}),\ \ i = 1,\ldots,s, \end{array} \end{aligned} $$
(3)
$$\displaystyle \begin{aligned} \begin{array}{rcl} l_{i}^{n} &\displaystyle =&\displaystyle F^{[2]}(t_{n} + c_{i} \varDelta t, u^{n} + \varDelta t\sum_{j=1}^{s}a_{ij}k_{j}^{n} + \varDelta t\sum_{j=1}^{s} \hat{a}_{ij} l_{j}^{n}), \ \ i = 1,\ldots,s. {} \end{array} \end{aligned} $$
(4)

Note that the explicit nature of (4) is encoded in the fact that the elements on the diagonal and above in \(\hat {A}\) are zero. Once the slopes have been computed the solution at the next time-step is assembled as

$$\displaystyle \begin{aligned} u^{n+1} = u^{n} + \varDelta t\sum_{j=1}^{s}b_{j}k_{j}^{n} + \varDelta t\sum_{j=1}^{s} \hat{b}_{j} l_{j}^{n}. {} \end{aligned} $$
(5)

If the method is instead formulated in terms of solving for the stage solutions the implicit solves take the form

$$\displaystyle \begin{aligned} u_{i}^{n} = u^{n} + \varDelta t \sum_{j=1}^{s} \Big( a_{ij}F^{[1]}(t_{n} + c_{j} \varDelta t, u_{j}^{n}) + \hat{a}_{ij} F^{[2]}(t_{n} + c_{j} \varDelta t, u_{j}^{n}) \Big ), \end{aligned}$$

and the explicit update for u n+1 is given by

$$\displaystyle \begin{aligned} u^{n+1} = u^{n} + \varDelta t \sum_{j=1}^{s} b_{j}(F^{[1]}(t_{n} + c_{j} \varDelta t, u_{j}^{n}) + F^{[2]}(t_{n} + c_{j} \varDelta t, u_{j}^{n})). \end{aligned}$$

The two formulations are algebraically equivalent but offer different advantages. For example, when working with the slopes we do not observe (see experiments presented in the second part of this paper) any order reduction due to time-dependent boundary conditions (see e.g. the analysis by Rosales et al. [14]). On the other hand and as discussed in some detail below, in solving for the slopes the HPS framework requires an additional step to enforce continuity.

We note that it is generally preferred to solve for the slopes when implementing implicit Runge–Kutta methods, particularly when solving very stiff problems where the influence of roundoff (or solver tolerance) errors can be magnified by the Lipschitz constant when solving for the stages directly.

Remark 2

The HPS method for elliptic solves was previously used in [10], which considered a linear hyperbolic equation

$$\displaystyle \begin{aligned} \frac{\partial u}{\partial t} = \ mathcal{L} u (\boldsymbol{x}, t), \ \ \boldsymbol{x} \in \varOmega, t > 0, \end{aligned}$$

where \(\ mathcal {L}\) is a skew-Hermitian operator. The evolution of the numerical solution can be performed by approximating the propagator \(\exp (\tau \ mathcal {L}): L^{2}(\varOmega )\rightarrow L^{2}(\varOmega )\) via a rational approximation

$$\displaystyle \begin{aligned} \exp(\tau \ mathcal{L}) \approx \sum_{m = - M}^{M} b_{m}(\tau \ mathcal{L} - \alpha_{m})^{-1}. \end{aligned}$$

If application of \((\tau \ mathcal {L} - \alpha _{m})^{-1}\) to the current solution can be reduced to the solution of an elliptic-type PDE it is straightforward to apply the HPS scheme to each term in the approximation. A drawback with this approach is that multiple operators must be formed and it is also slightly more convenient to time step non-linear equations using the Runge–Kutta methods we use here.

There are two modifications to the HPS algorithm that are necessitated by the use of ARK time integrators, we discuss these in the next two subsections.

3.1 Neumann Data Correction in the Slope Formulation

In the HPS algorithm the PDE is enforced on interior nodes and continuity of the normal derivative is enforced on the leaf boundary. Now, due to the structure of the update formula (5), if at some time u n has an error component in the null space of the operator that is used to solve for a slope k i, then this will remain throughout the solution process. Although this does not affect the stability of the method it may result in loss of relative accuracy as the solution evolves. As a concrete example consider the heat equation

$$\displaystyle \begin{aligned} u_{t} = u_{xx}, \ \ x \in [0,2], t > 0, {} \end{aligned} $$
(6)

with the initial data u(x, 0) = 1 −|x − 1|, and with homogenous Dirichlet boundary conditions. We discretize this on two leaves which we denote by α and β.

Now in the k i formulation, we solve several PDEs for the k i values and update the solution as

$$\displaystyle \begin{aligned} u^{n+1} = u^{n} + \varDelta t \sum_{j=1}^{s}b_{j}k_{j}^{n}. \end{aligned}$$

Here, even though the individual slopes have continuous derivatives the kink in u n will be propagated to u n+1. In this particular example we would end up with the incorrect steady state solution u(x, t) = 1 −|x − 1|.

Fortunately, this can easily be mitigated by adding a consistent penalization of the jump in the derivative of the solution during the merging of two leaves (for details see Section 4 in [1]). That is, if we denote the jump by [[⋅]] we replace the condition 0 = [[Tk + h k]] where Tk is the derivative from the homogenous part and h k is the derivative for the particular solution (of the slope) by the condition [[Tk + h k − Δt −1 h u]] = 0. In comparison to [1] we get the slightly modified merge formula

$$\displaystyle \begin{aligned} {\mathsf{k}}_{i,3} = \big({\mathsf{T}}^{\alpha}_{3,3} - {\mathsf{T}}^{\beta}_{3,3}\big)^{-1} \big( {\mathsf{T}}^{\beta }_{3,2}{\mathsf{k}}_{i,2} -{\mathsf{T}}^{\alpha}_{3,1}{\mathsf{k}}_{i,1} +{\mathsf{h}}_{3}^{k,\beta} -{\mathsf{h}}_{3}^{k,\alpha} - \frac{1}{\varDelta t}({\mathsf{h}}_{3}^{u,\alpha} -{\mathsf{h}}_{3}^{u,\beta}) \big), \end{aligned}$$

along with the modified equation for the fluxes of the particular solution on the parent box

$$\displaystyle \begin{aligned} \left[\begin{array}{c} {\mathsf{v}}_{1} \\ {\mathsf{v}}_{2} \end{array}\right] =&\ \left(\left[\begin{array}{ccc} {\mathsf{T}}_{1,1}^{\alpha} & {\mathsf{0}} \\ {\mathsf{0}} & {\mathsf{T}}_{2,2}^{\beta } \end{array}\right] + \left[\begin{array}{c} {\mathsf{T}}_{1,3}^{\alpha} \\ {\mathsf{T}}_{2,3}^{\beta} \end{array}\right]\, \big({\mathsf{T}}^{\alpha}_{3,3} - {\mathsf{T}}^{\beta}_{3,3}\big)^{-1} \big[-{\mathsf{T}}^{\alpha}_{3,1}\ \big|\ {\mathsf{T}}^{\beta}_{3,2}] \right) \left[\begin{array}{c} {\mathsf{k}}_{i,1} \\ {\mathsf{k}}_{i,2} \end{array}\right] +\\ &\ \left[\begin{array}{c} {\mathsf{h}}^{k,\alpha}_{1} \\ {\mathsf{h}}^{k,\beta}_{2} \end{array}\right] + \left[\begin{array}{c} {\mathsf{T}}_{1,3}^{\alpha} \\ {\mathsf{T}}_{2,3}^{\beta} \end{array}\right]\, \big({\mathsf{T}}^{\alpha}_{3,3} - {\mathsf{T}}^{\beta}_{3,3}\big)^{-1} \big({\mathsf{h}}_{3}^{\beta}-{\mathsf{h}}_{3}^{\alpha} - \frac{1}{\varDelta t}({\mathsf{h}}_{3}^{u,\alpha} -{\mathsf{h}}_{3}^{u,\beta}) \big). \end{aligned} $$

Due to space we must refer to [1] for a detailed discussion of these equations. Briefly, h k, α and h k, β above denote the spectral derivative on each child’s boundary for the particular solution to the PDE for k i and are already present in [1]. However, h u, α and h u, β, which denote the spectral derivative of u n on the boundary from each child box, are new additions.

The above initial data is of course extreme but we note that the problem persists for any non-polynomial initial data with the size of the (stationary) error depending on resolution of the simulation. We further note that the described penalization removes this problem without affecting the accuracy or performance of the overall algorithm.

Remark 3

Although for linear constant coefficient PDE it may be possible to project the initial data in a way so that interior affine functions do not cause the difficulty above, for greater generality, we have chosen to enforce the extra penalization throughout the time evolution.

Remark 4

When utilizing the u i formulation in a purely implicit problem we do not encounter the difficulty described above. This is because we enforce continuity of the derivative in \(u_{s}^{n}\) when solving

$$\displaystyle \begin{aligned} (I - \varDelta t \gamma \ mathcal{L}) u_{s}^{n} = u^{n} + \varDelta t \ mathcal{L} \Big (\sum_{j=1}^{s-1} a_{sj} u_{j}^{n} \Big) + \varDelta t \sum_{j=1}^{s-1} a_{sj} g(x,t_{n}+c_{j} \varDelta t), \end{aligned}$$

followed by the update \(u^{n+1} = u_{s}^{n}\).

3.2 Enforcing Continuity in the Explicit Stage

The second modification is to the first explicit stage in the k i formulation. Solving a problem with no forcing this stage is simply

$$\displaystyle \begin{aligned} k_{1}^{n} = \ mathcal{L} (u_{n}). \end{aligned}$$

When, for example, \(\ mathcal {L}\) is the Laplacian, we must evaluate it on all nodes on the interior of the physical domain. This includes the nodes on the boundary between two leafs where the spectral approximation to the Laplacian can be different if we use values from different leaves. The seemingly obvious choice, replacing the Laplacian on the leaf boundary by the average, leads to instability. However, stability can be restored if we enforce \(k_{1}^{n} = \ mathcal {L} (u_{n})\) on the interior of each leaf and continuity of the derivative across each leaf boundary. Algorithmically, this is straightforward as these are the same conditions that are enforced in the regular HPS algorithm, except in this case we simply have an identity equation for k 1 on the interior nodes instead of a full PDE.

Although it is convenient to enforce continuity of the derivative using the regular HPS algorithm it can be done in a more efficient fashion by forming a separate system of equations involving only data on the leaf boundary nodes. In a single dimension on a discretization with n leafs this reduces the work associated with enforcing continuity of the derivative across leaf boundary nodes from solving n × (p − 1) − 1 equations for n × (p − 1) − 1 unknowns to solving a tridiagonal system of equations n − 1 equations for n − 1 unknowns.

In two dimensions the system is slightly different, but if we have n × n leafs with p × p Chebyshev nodes on each leaf then eliminating the explicit equations for the interior nodes reduces the system to (p − 2) × 2n independent tridiagonal systems of n − 1 equations with n − 1 unknowns for a total of (p − 2) × 2n × (n − 1) equations with (p − 2) × 2n × (n − 1) unknowns.

When the u i formulation is used for a fully implicit problem the intermediate stage values still requires us to evaluate \(\ mathcal {L} u^{n}\), but this quantity only enters through the body load in the intermediate stage PDEs. The explicit first stage in this formulation is simply \(u_{1}^{n} = u^{n}\). Furthermore, while we must calculate

$$\displaystyle \begin{aligned} u^{n+1} = u^{n} + \varDelta t \ mathcal{L} \Big (\sum_{j=1}^{s} a_{sj} u_{j}^{n} \Big), \end{aligned}$$

this is equivalent to \(u_{s}^{n}\) since b j = a sj and we simply take \(u^{n+1} = u_{s}^{n}\).

When both explicit and implicit terms are present, we proceed differently. Now, the values of \(u_{i}^{n}\) look almost identical to the implicit case and we still avoid the problem of an explicit “solve” in \(u_{1}^{n}\), but we also have

$$\displaystyle \begin{aligned} u^{n+1} = u^{n} + \varDelta t \sum_{j=1}^{s} b_{j}(F^{[1]}(t_{n} + c_{j} \varDelta t, u_{j}^{n}) + F^{[2]}(t_{n} + c_{j} \varDelta t, u_{j}^{n})) \end{aligned}$$

The ESDIRK method has the property that b j = a sj, but for the explicit Runge–Kutta method we have \(b_{j} \neq \hat {a}_{sj}\). When the explicit operator F [2] does not contain partial derivatives we need not enforce continuity of the derivative and can simply reformulate the method as

$$\displaystyle \begin{aligned} u^{n+1} = u_{s}^{n} + \varDelta t \sum_{j=1}^{s}(a_{sj} - \hat{a}_{sj})F^{[2]}(t_{n} + c_{j} \varDelta t, u_{j}^{n}) \end{aligned}$$

4 Boundary Conditions

The above description for Runge–Kutta methods does not address how to impose boundary conditions for a system of ODEs resulting from a discretization of a PDE. In particular, the different formulations incorporate boundary conditions in slightly different ways.

In this work we consider Dirichlet, Neumann, and periodic boundary conditions. For periodic boundary conditions the intermediate stage boundary conditions are enforced to be periodic for both formulations. As the k i stage values are approximations to the time derivative of u, the imposed Dirichlet boundary conditions for x ∈ Γ are \(k_{i}^{n} = u_{t}(x,t_{n} + c_{i} \varDelta t)\). When solving for u i one may attempt to enforce boundary conditions using u i = u(x, t + c i Δt), x ∈ Γ. However, as demonstrated in part two of this series and discussed in detail in [14], this results in order reduction for time dependent boundary conditions.

In the HPS algorithm, Neumann or Robin boundary conditions are mapped to Dirichlet boundary conditions using the linear Dirichlet to Neumann operator as discussed for example in [1].