1 Introduction

Applications such as plug-in hybrid electric vehicles [1], renewable energy storage [2], uninterruptible power supply (UPS) systems [3], aerospace applications [4] and smart grids [5] usually need an energy storage device, which increase the popularity of the bidirectional DC-DC converters. As the DAB converter has many advantages, such as galvanic isolation, zero-voltage switching, high power density, high efficiency, and symmetric structure [6], it has been drawn more attention compared with other bidirectional DC-DC converters. Until now, researchers have focused on modeling [7], control strategies [8,9,10], design methodology [11], and modulation strategies [3, 12]. However, the complex dynamics in the digitally controlled DAB converter, caused by switching nonlinearity and control delay [13], may deteriorate the working performance and bring stability problem. However, it has not been studied in the existing literature.

Because of the inherent nonlinearity existing in DC-DC converters, the systems may always show the abnormal operation instead of the expected normal operation. To study dynamic behavior and stability of the DC-DC converters, many researchers have devoted to the modeling methods, and various kinds of complex dynamics have been investigated, such as Hopf bifurcation, period doubling bifurcation and chaos [14,15,16]. Generally, a state-space averaged model or a discrete-time model can be used to study the dynamics in converters [17, 18]. The averaged model averages each circuit variable within one switching period. Thus, this model neglects the switching details and can only detect the slow-scale dynamics of the system effectively. The discrete-time model expresses the state variables at one sampling time and the variables at an earlier sampling time by deriving an iterative function. This model can offer information of both the slow-scale and fast-scale dynamics of the system and is more accurate compared with the averaged model.

To study the dynamics in a DAB converter, an appropriate model should be developed first. Considering the small ripple requirement in averaged model [17], establishing a discrete-time model is more appropriate as the transformer current in a DAB converter is purely AC. Thus, several discrete-time models for DAB converters have been established. In [19], a discrete-time averaged model is obtained. This model averages the value of the output voltage over half switching period and suitable for half period control. In [20, 21], due to the symmetry of the transformer current and the output voltage in steady state, the discrete-time models are also established in a half switching period and suitable for half period control. In [22], a discrete-time small signal model is developed. It is established in a full switching period. However, it does not consider the ESRs in circuit. Above of all, almost all of these models have not consider the output capacitor ESR. But when one switching period control is adopted and the system loses stability under inappropriate parameters, the state variables will be unsymmetrical. The previous models suitable for half switching period control will not be suitable anymore and a more accurate model should be established. Thus, in this paper, a full discrete-time model in a whole switching period is established. This model considers all the ESRs in the circuit, including the output capacitor ESR. Using this model, the influences of the controller parameter and the output capacitor ESR on the stability of the system are discussed. Simulation and experimental results show that this full discrete-time model is effective enough and can predict the instability of the system accurately.

The rest of the paper is organized as follows. The operation principle of the digitally controlled DAB converter is briefly introduced and the full discrete-time model is established in Section 2. Then, in Section 3, based on the full discrete-time model, the stability of the DAB converter is analyzed. In Section 4, simulation and experimental results verify the theoretical analyses. Finally, conclusions are given in Section 5.

2 System description and full discrete-time modeling

2.1 System description

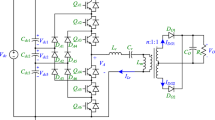
The schematic circuit of a digitally controlled DAB converter is shown in Fig. 1. It consists of a power stage and a digital control system. The power stage is composed mainly of a high frequency transformer and two H bridges.

Fig. 1
figure 1

Diagram of digitally controlled DAB converter

Full size image

The turn ratios of high-frequency transformer is 1: N . The transformer provides voltage matching and galvanic isolation between two voltage buses. Owing to the symmetrical structure, DAB converter can realize bidirectional power flow. In this paper, take the power flowing from V 1 to V 2 as an example. So V 1 is the input DC voltage, V 2 is the output voltage. L is the transformer leakage inductance, serving as an instantaneous energy storage device. R t is the sum of the line resistances, the switch on-resistors, and the transformer winding resistances. C o is the output capacitor. R C is the output capacitor ESR.

Generally, a DAB converter has four control strategies [6]. They are respectively the single phase-shift (SPS) control, the extended-phase-shift (EPS) control, the dual-phase-shift (DPS) control, and the triple-phase-shift (TPS) control. The SPS control, which is the most widely used control strategy for DAB converters [1, 6, 23], is adopted in this paper. In SPS control, v p and v s are square wave voltages with 50% duty cycle. The phase shift φ between v p and v s controls the power flow directions. Figure 2 is the operation waveforms in steady state and in this case, the power flows from the V 1-side to the V 2-side. It can be seen from Fig. 2 that there are four intervals in one switching period and the converter operates symmetrically in each half period.

Fig. 2
figure 2

Operation waveforms in steady state

Full size image

In this system, the digital controller consists of an output-voltage feedback. it samples the output voltage V 2 at the beginning of each switching period and the sampling result is compared with the voltage reference. Then, the phase shift φ is calculated through the controller and saturator, and loaded at the beginning of the next switching period. Thus, there is one step delay in the system. The saturator element limits the range of φ. When the power flows from V 1 to V 2, the range of is from 0 to π/2. When the power flows from V 2 to V 1, the range of is from −π/2 to 0.

The values of the parameters in circuit can have great effect to the stability of the system. An inappropriate parameter can make the phase shift angle φ keep oscillating. Thus, obvious oscillation phenomenon can also appear to the output voltage and the inductor current, making the system in an unstable state. So establishing an appropriate model and using the model to study the stability of the DAB converter is necessary.

2.2 Full discrete-time modeling

The discrete-time model derived in this paper assumes that transistor switching transients are negligible. It is also assumed that the input capacitance is relatively large, so the dynamics of the input capacitor are not considered. To obtain the discrete-time model of the converter, continuous time state-space equations of DAB converter in four subintervals should be derived first, each equations taking the form as

$$ \dot{\varvec{x}}(t) = \varvec{A}_{i} \varvec{x}(t) + \varvec{B}_{i} V_{1} $$
(1)

where x(t) is the state vector and x(t) = [i L v C]T; i = 1, 2, 3, 4, is corresponding to the four subintervals t 1-t 4 in Fig. 2.

The matrices A i and vectors B i in (1) are expressed in (2) and (3). It can be seen from the expressions that this paper considers the output capacitor ESR.

$$ \left\{ {\begin{array}{*{20}l} {\varvec{A}_{1} = \varvec{A}_{4} = \left[ {\begin{array}{*{20}c} { - \frac{{N^{2} R_{\text{t}} + k_{1} }}{{N^{2} L}}} & {\frac{{k_{2} }}{vL}} \\ { - \frac{{k_{2} }}{{NC_{\text{o}} }}} & { - \frac{1}{{C_{\text{o}} \left( {R_{\text{o}} + R_{\text{C}} } \right)}}} \\ \end{array} } \right]} \hfill \\ {\varvec{A}_{2} = \varvec{A}_{3} = \left[ {\begin{array}{*{20}c} { - \frac{{N^{2} R_{\text{t}} + k_{1} }}{{N^{2} L}}} & { - \frac{{k_{2} }}{NL}} \\ {\frac{{k_{2} }}{{NC_{\text{o}} }}} & { - \frac{1}{{C_{\text{o}} \left( {R_{\text{o}} + R_{\text{C}} } \right)}}} \\ \end{array} } \right]} \hfill \\ \end{array} } \right. $$
(2)
$$ \left\{ {\begin{array}{*{20}l} {\varvec{B}_{1} = \varvec{B}_{2} = \left[ {\begin{array}{*{20}c} {\frac{1}{L}} & 0 \\ \end{array} } \right] \, } \hfill \\ {\varvec{B}_{3} = \varvec{B}_{4} = \left[ { - \begin{array}{*{20}c} {\frac{1}{L}} & 0 \\ \end{array} } \right]} \hfill \\ \end{array} } \right. $$
(3)

where

$$ \left\{ {\begin{array}{*{20}l} {k_{1} = R_{\text{o}} R_{\text{C}} /\left( {R_{\text{o}} + R_{\text{C}} } \right)} \hfill \\ {k_{2} = R_{\text{o}} /\left( {R_{\text{o}} + R_{\text{C}} } \right)} \hfill \\ \end{array} } \right. $$
(4)

The discrete-time model is derived from regular sampling of the state variables of the continuous-time dynamics. Compared with the average model, the discrete-time model is obtained without making quasi-static approximation such as high switching frequency and small ripple. The discrete-time modeling process of this system can be divided into two steps. The first step is the power stage and the second step is the digital control system. As the power converter has four switching states in one switching cycle, four discrete-time models in four switching states can be derived by the state variables first, as shown in (5).

$$ \left\{ {\begin{array}{*{20}l} {{\varvec{x}}\left( {nT_{\text{s}} + t_{1} } \right) = {\text{e}}^{{{\varvec{A}}_{1} t_{1} }} \cdot {\varvec{x}}\left( {nT_{\text{s}} } \right) + {\varvec{\psi}}_{1} V_{1} } \hfill \\ {{\varvec{x}}\left( {nT_{\text{s}} + t_{1} + t_{2} } \right) = {\text{e}}^{{{\varvec{A}}_{2} t_{2} }} \cdot {\varvec{x}}\left( {nT_{\text{s}} + t_{1} } \right) + {\varvec{\psi}}_{2} V_{1} } \hfill \\ {{\varvec{x}}\left( {nT_{\text{s}} + t_{1} + t_{2} + t_{3} } \right) = {\text{e}}^{{{\varvec{A}}_{3} t_{3} }} \cdot {\varvec{x}}\left( {nT_{\text{s}} + t_{1} + t_{2} } \right) + {\varvec{\psi}}_{3} V_{1} } \hfill \\ {{\varvec{x}}\left( {\left( {n + 1} \right)T_{\text{s}} } \right) = {\text{e}}^{{{\varvec{A}}_{4} t_{4} }} \cdot {\varvec{x}}\left( {nT_{\text{s}} + t_{1} + t_{2} + t_{3} } \right) + {\varvec{\psi}}_{4} V_{1} } \hfill \\ \end{array} } \right. $$
(5)

where

$$ \left\{ {\begin{array}{*{20}l} {t_{1} = t_{3} = \varphi_{n} /(2\pi f_{\text{s}} )} \hfill \\ {t_{2} = t_{4} = 1/(2f_{\text{s}} ) - \varphi_{n} /(2\pi f_{\text{s}} )} \hfill \\ \end{array} } \right. $$
(6)
$$ \left\{ {\begin{array}{*{20}l} {{\varvec{\psi}}_{1} = \int_{0}^{{t_{1} }} {{\text{e}}^{{{\varvec{A}}_{1} t_{1} }} {\varvec{B}}_{1} } {\text{d}}t = {\varvec{A}}_{1}^{ - 1} ({\text{e}}^{{{\varvec{A}}_{1} t_{1} }} - {\varvec{I}}){\varvec{B}}_{1} V_{1} } \hfill \\ {{\varvec{\psi}}_{2} = \int_{0}^{{t_{2} }} {{\text{e}}^{{{\varvec{A}}_{2} t_{2} }} {\varvec{B}}_{2} } {\text{d}}t = {\varvec{A}}_{2}^{ - 1} ({\text{e}}^{{{\varvec{A}}_{2} t_{2} }} - {\varvec{I}}){\varvec{B}}_{2} V_{1} } \hfill \\ {{\varvec{\psi}}_{3} = \int_{0}^{{t_{3} }} {{\text{e}}^{{{\varvec{A}}_{3} t_{3} }} {\varvec{B}}_{3} } {\text{d}}t = {\varvec{A}}_{3}^{ - 1} ({\text{e}}^{{{\varvec{A}}_{3} t_{3} }} - {\varvec{I}}){\varvec{B}}_{3} V_{1} } \hfill \\ {{\varvec{\psi}}_{4} = \int_{0}^{{t_{4} }} {{\text{e}}^{{{\varvec{A}}_{4} t_{4} }} {\varvec{B}}_{4} } {\text{d}}t = {\varvec{A}}_{4}^{ - 1} ({\text{e}}^{{{\varvec{A}}_{4} t_{4} }} - {\varvec{I}}){\varvec{B}}_{4} V_{1} } \hfill \\ \end{array} } \right. $$
(7)

The discrete-time model in a whole switching cycle can be derived by integrating the four equations in (5). Let the values of x at the beginning of the n-th and the (n + 1)-th switching cycles be denoted as x n , and x n+1 respectively, so the discrete-time model of the power stage is shown in (8):

$$ \begin{aligned} {\varvec{x}}_{n + 1} & = {\text{e}}^{{{\varvec{A}}_{4} t_{4} }} \left\{ {{\text{e}}^{{{\varvec{A}}_{3} t_{3} }} \left[ {{\text{e}}^{{{\varvec{A}}_{2} t_{2} }} \left( {{\text{e}}^{{{\varvec{A}}_{1} t_{1} }} {\varvec{x}}_{n} +\, {\varvec{\psi}}_{1} V_{1} } \right) + {\varvec{\psi}}_{2} V_{1} } \right] +\, {\varvec{\psi}}_{3} V_{1} } \right\} + {\varvec{\psi}}_{4} V_{1} \\ & = {\varvec{F}}\left( {\varphi_{n} } \right){\varvec{x}}_{n} + {\varvec{G}}\left( {\varphi_{n} } \right)V_{1} \\ \end{aligned} $$
(8)

where

$$ \left\{ {\begin{array}{*{20}l} {{\varvec{F}}\left( {\varphi_{n} } \right) = {\text{e}}^{{{\varvec{A}}_{4} t_{4} }} \cdot {\text{e}}^{{{\varvec{A}}_{3} t_{3} }} \cdot {\text{e}}^{{{\varvec{A}}_{2} t_{2} }} \cdot {\text{e}}^{{{\varvec{A}}_{1} t_{1} }} } \hfill \\ \begin{aligned} {\varvec{G}}\left( {\varphi_{n} } \right) & = {\text{e}}^{{{\varvec{A}}_{4} t_{4} }} \cdot {\text{e}}^{{{\varvec{A}}_{3} t_{3} }} \cdot {\text{e}}^{{{\varvec{A}}_{2} t_{2} }} \cdot {\varvec{\psi}}_{1} + {\text{e}}^{{{\varvec{A}}_{4} t_{4} }} \cdot {\text{e}}^{{{\varvec{A}}_{3} t_{3} }} \cdot {\varvec{\psi}}_{2} \\ & \quad + \,{\text{e}}^{{{\varvec{A}}_{4} t_{4} }} \cdot {\varvec{\psi}}_{3} + {\varvec{\psi}}_{4} \\ \end{aligned} \hfill \\ \end{array} } \right. $$
(9)

To simplified calculation and guarantee the accuracy, matrix exponentials involved in (8) can be approximated by the 2-order approximations, as shown in (10)

$$ {\text{e}}^{{{\varvec{A}}_{m} t_{m} }} \approx \varvec{I} + {\varvec{A}}_{m} t_{m} + \frac{1}{2!}\left( {{\varvec{A}}_{m} t_{m} } \right)^{2} $$
(10)

where I is the unit matrix; m = 1, 2, 3, 4.

The controller system considers one step delay, as it samples V 2 periodically at the time t = nT s and updates φ at the time t = (n + 1)T s. PI-controller or higher performance controller are frequently used in the DAB system. However, our focus in this paper are the characteristics of the DAB converter instead of the controller. Thus, for simplicity, taking a proportional controller as an example, the discrete-time model of the digital control system is derives as (11), where k is the proportional controller parameter. It can be observed from the equation that this model deals with one step delay commendably.

$$ \varphi_{n + 1} = k\left( {V_{\text{ref}} - V_{2n} } \right) = k\left( {V_{{{\text{ref}}n}} - {\varvec{M}} \cdot {\varvec{x}}_{n} } \right) \in \left[ {0,\pi /2} \right] $$
(11)

where V refn is the sampling value at the beginnings of the n-th switching cycle of the reference voltage V ref; vector M describe the relationship among V 2n , i Ln and v Cn .

According to the circuit of V 2 side, the relationship among V 2, i 2 and v C can be figured out firstly. i 2 is the output current as shown in Fig. 1.

From Fig. 1, it can be easily figured out that

$$ V_{2} = \frac{{R_{\text{o}} R_{\text{C}} }}{{R_{\text{o}} + R_{\text{C}} }}i_{2} + \frac{{R_{\text{o}} }}{{R_{\text{o}} + R_{\text{C}} }}v_{\text{C}} $$
(12)

In the digital controlled DAB converter, it samples the output voltage V 2 periodically at the time t = nT s, so the discrete-time equation of (12) is as follows.

$$ V_{2n} = \frac{{R_{\text{o}} R_{\text{C}} }}{{R_{\text{o}} + R_{\text{C}} }}i_{2n} + \frac{{R_{\text{o}} }}{{R_{\text{o}} + R_{\text{C}} }}v_{{{\text{C}}n}} $$
(13)

The waveform of the inductor current i L and the output current i 2 are shown in Fig. 2. The relationship between i L and i 2 can be described in (14).

$$ \left\{ {\begin{array}{*{20}l} {i_{ 2} = i_{\text{L}} /N} \hfill & {t \in \left[ {nT_{\text{s}} + t_{1} ,nT_{\text{s}} + t_{1} + t_{2} } \right]} \hfill \\ {i_{ 2} = - i_{\text{L}} /N} \hfill & {t \in \left[ {nT_{\text{s}} ,nT_{\text{s}} + t_{1} } \right] \cup \left[ {nT_{\text{s}} + t_{1} + t_{2} ,\left( {n + 1} \right)T_{\text{s}} } \right]} \hfill \\ \end{array} } \right. $$
(14)

Thus, at the beginning of the n-th switching cycle, the relationship between i 2n and i Ln can be described as (15).

$$ i_{ 2n} { = - }i_{{{\text{L}}n}} /N $$
(15)

Finally, combined (13) and (15), the vector M is obtained as

$$ {\varvec{M}} = \left[ {\begin{array}{*{20}c} {\frac{{ - R_{\text{o}} R_{\text{C}} }}{{\left( {R_{\text{o}} + R_{\text{C}} } \right)N}}} & {\frac{{R_{\text{o}} }}{{R_{\text{o}} + R_{\text{C}} }}} \\ \end{array} } \right] $$
(16)

Above of all, (8) and (11) composes of the full discrete-time model of the digitally controlled DAB converter. Since few mathematical approximations are involved in this model, this model can be considered highly accurate and can be effectively used to predict the dynamics with the variation of parameters in the system.

3 Stability analysis of DAB converter

3.1 Jacobian matrix analysis

The parameters in circuit have great influences on the stability of the system. The inductor current and the output voltage waveforms may appear obvious oscillations if the parameters are not well selected. Thus, in this section, the dynamics and stability will be investigated with the help of the Jacobian matrix.

$$ \varvec{J} = \left. {\left[ {\begin{array}{*{20}c} {\frac{{\partial i_{{{\text{L}}\left( {n + 1} \right)}} }}{{\partial i_{{{\text{L}}n}} }}} & {\frac{{\partial i_{{{\text{L}}\left( {n + 1} \right)}} }}{{\partial V_{{{\text{C}}n}} }}} & {\frac{{\partial i_{{{\text{L}}\left( {n + 1} \right)}} }}{{\partial \varphi_{n} }}} \\ {\frac{{\partial V_{{{\text{C}}\left( {n + 1} \right)}} }}{{\partial i_{{{\text{L}}n}} }}} & {\frac{{\partial V_{{{\text{C}}\left( {n + 1} \right)}} }}{{\partial V_{{{\text{C}}n}} }}} & {\frac{{\partial V_{{{\text{C}}\left( {n + 1} \right)}} }}{{\partial \varphi_{n} }}} \\ {\frac{{\partial \varphi_{{\left( {n + 1} \right)}} }}{{\partial i_{{{\text{L}}n}} }}} & {\frac{{\partial \varphi_{{\left( {n + 1} \right)}} }}{{\partial V_{{{\text{C}}n}} }}} & {\frac{{\partial \varphi_{{\left( {n + 1} \right)}} }}{{\partial \varphi_{n} }}} \\ \end{array} } \right]} \right|_{{\left( {I_{L} ,V_{\text{C}} ,\varPhi } \right)}} $$
(17)

Using (8) and (11), the corresponding Jacobian matrix of the system can be expressed as (17). Then the characteristic equation of (17) is shown in (18).

$$ \det \left( {\lambda {\varvec{I}} - {\varvec{J}}} \right) = 0 $$
(18)

From (18), we can get all the eigenvalues \( \lambda_{J1} \), \( \lambda_{J2} \), and \( \lambda_{J2} \)of the Jacobian matrix. If at least one eigenvalue exhibits an absolute value higher than 1, then the system is unstable. If the eigenvalues move out of the unit circle from (1, 0) or (−1, 0), saddle node bifurcation or period doubling bifurcation will occur. And conjugated eigenvalues of a discrete-time model crossing out of the unite circle indicates Hopf bifurcation (or Neimarck-Sacker bifurcation) [18].

It should be mentioned that the operation point \( \left( {I_{\text{L}} ,V_{\text{C}} ,\varPhi } \right) \)need to be figured out at the same time to obtain the Jacobian matrix and the eigenvalues. Usually this operating point is in a steady-state and therefore the steady-state solution needs to be calculated. Obviously, the steady-state solution corresponds to constant phase shift angle \( \varPhi \) and state vector \( \varvec{X} = \left[ {\begin{array}{*{20}c} {I_{\text{L}} } & {V_{\text{C}} } \\ \end{array} } \right]^{\text{T}} \). Denote the subintervals t 1-t 4 and exponential matrices in (7) using capitals to represent the steady-state values as in (19).

$$ \left\{ {\begin{array}{*{20}l} {T_{1} = T_{3} = \varPhi /(2f_{\text{s}} \pi )} \hfill \\ {T_{2} = T_{4} = 1/(2f_{\text{s}} ) - \varPhi /(2f_{\text{s}} \pi )} \hfill \\ {{\varvec{\psi}}_{1} = \varvec{A}_{1}^{ - 1} ({\text{e}}^{{\varvec{A}_{1} T_{1} }} - \varvec{I}){\varvec{B}}_{1} V_{1} \, } \hfill \\ {{\varvec{\psi}}_{2} = \varvec{A}_{2}^{ - 1} ({\text{e}}^{{\varvec{A}_{2} T_{2} }} - \varvec{I}){\varvec{B}}_{2} V_{1} } \hfill \\ {{\varvec{\psi}}_{3} = {\varvec{A}}_{3}^{ - 1} ({\text{e}}^{{{\varvec{A}}_{3} T_{3} }} - \varvec{I}){\varvec{B}}_{3} V_{1} } \hfill \\ {{\varvec{\psi}}_{4} = {\varvec{A}}_{4}^{ - 1} ({\text{e}}^{{{\varvec{A}}_{4} T_{4} }} - \varvec{I}){\varvec{B}}_{4} V_{1} } \hfill \\ \end{array} } \right. $$
(19)

where \( {\text{e}}^{{{\varvec{A}}_{i} T_{i} }} = \varvec{I} + {\varvec{A}}_{i} T_{i} + 0.5\left( {{\varvec{A}}_{i} T_{i} } \right)^{2} \, \); i = 1, 2, 3, 4. Then the solution for the operating point \( \left( {I_{\text{L}} ,V_{\text{C}} ,\varPhi } \right) \) can be obtained by enforcing the periodicity: \( {\varvec{x}}_{n + 1} = {\varvec{x}}_{n} = {\varvec{X}} \) in (8), which is given by (20) and (21).

$$ {\varvec{X}} = \left( {1 - {\varvec{F}}\left( \varPhi \right)} \right)^{ - 1} {\varvec{G}}\left( \varPhi \right)V_{1} $$
(20)
$$ \varPhi = k\left( {V_{\text{ref}} - {\varvec{M}}\varvec{X}} \right) $$
(21)

The system parameters are shown in Table 1. As we know, all switches in DAB converter can achieve ZVS in whole load range when \( d \) is equal to 1 (d represents the voltage conversion ratio and \( d{ = }{{NV_{1} } \mathord{\left/ {\vphantom {{NV_{1} } {V_{2} }}} \right. \kern-0pt} {V_{2} }} \)) [24]. So in actually applications, it is optimal to let d = 1. Thus, in this paper, we use a N = 1 transformer while V 1 = V 2. If we want to change the parameters of the DAB converter, such as the transformer ratio or input and output voltage, we just change the corresponding parameters in (2) and (5), and the following method in the paper can be directly used.

Table 1 System parameters
Full size table

Based on the parameters above, the effect of the changes of k will be first investigated. The changing trend and the values of eigenvalues around the border of the unit circle with the increase of k can be respectively seen in Fig. 3a and Table 2. It can be remarked that there are three eigenvalues, and it is the conjugate eigenvalues exceed the unit circle when k increases while the third one remains practically unchanged. Therefore, when k is larger than 0.55, the system is unstable and exhibits Hopf bifurcation.

Fig. 3
figure 3

Trajectory of eigenvalues

Full size image
Table 2 Eigenvalues at R C = 0.45 Ω for various of k
Full size table

Then, the output capacitor ESR R C is taken as a bifurcation parameter to further illustrate that the choices of parameters have great effect on the stability of the system. Keep k equal to 0.47 and let R C sweep from 0.46 Ω to 0.7 Ω with steps of 0.02 Ω. The trajectory and the values of eigenvalues around the unit circle are respectively shown in Fig. 3b and Table 3. It can be remarked that there are also three eigenvalues, and it is the conjugate ones exceed the unit circle when R C increases while the third one remains practically unchanged. Thus, when R C is bigger than 0.56 Ω, the system is unstable and exhibits Hopf bifurcation.

Table 3 Eigenvalues at k = 0.47 for various of R C
Full size table

3.2 Margin of stability curve

In the industry, bifurcations are usually unexpected and avoided and the usual acceptable operation state is period-1 steady state. For example, a Hopf bifurcation can make the system operate at a several periods limit cycle and bring much wider amplitude to the output voltage and inductor current. The wider amplitudes will have greater impact on device stresses. Therefore it is necessary to draw a bifurcation boundary for practical design to avoid the occurrence of such undesirable bifurcations.

The stability boundary at different values of k and R C is demonstrated in Fig. 4. It shows that the stability boundary of k can be expanded greatly when R C is decreased. Thus, R C has great influences on the system, which points out that it is quite necessary and important to take R C into account in practice. However, it does not mean the system is always stable if R C = 0 Ω. From Fig. 4, it can be seen that when R C = 0 Ω, the system will be unstable when k is greater than 1.81.

Fig. 4
figure 4

Stability boundary

Full size image

4 Simulation results and experimental verifications

In this section, corresponding simulation and experimental studies were conducted to verify the forementioned analysis.

4.1 Simulation results

Based on Fig. 1, the model of a digitally controlled DAB converter is set up in MATLAB/Simulink. In order to simulate the time delay and the sampling and holding process, the “sample time” settings in the unit-delay and sum module are all set as T s.

Figure 5 illustrates simulation waveforms of inductor currents with 0.45 Ω output capacitor ESR when k = 0.55 and 0.57. It can be seen that the digitally controlled system is stable when k = 0.55 and unstable when k = 0.57, which is coincident with the analysis result of Fig. 3.

Fig. 5
figure 5

Simulation results (R C = 0.45 Ω)

Full size image

When R C = 0.58 Ω, the simulation waveforms when k = 0.45 and 0.47 are depicted in Fig. 6. It can be observed that the system is stable when k = 0.45 and unstable when k = 0.47. Comparing the simulation results of Figs. 5 and 6, it can be found that the increase of R C make the stability boundary of k decreased, which is consistent with the analysis result of Fig. 4.

Fig. 6
figure 6

Simulation results (R C = 0.58 Ω)

Full size image

4.2 Experimental verifications

For the practical verification, a small-scale experimental prototype was built in the laboratory. It has the same design parameter values with the simulation model to validate the numerical analysis and simulation results.

The functional diagram of the experimental prototype is shown in Fig. 7. The prototype uses “IXFK102N30P” Power MOSFETs from IXYS Corporation as all switches. The external inductor and the transformer are made of litz wires and five electrolytic capacitors are applied as the output capacitor. The converter is controlled with a TMS320F28335 DSP chip, which implements the voltage control algorithm. The output voltage is measured by a LEM Hall voltage sensor and modulated by an output voltage modulating circuit. The 1ED020I12-F driver ICs are applied in the driver circuits to realize isolation and amplification.

Fig. 7
figure 7

Functional diagram of experimental platform

Full size image

The experimental results with R C = 0.45 Ω are shown in Fig. 8. When k = 0.52, the system is stable. But when k = 0.58, low frequency oscillations appears on the waveforms of the output voltage and the inductor current. It can be found from Fig. 8b that the inductor current is asymmetrical about half switching period. This phenomenon can lead to the transformer magnetic bias and even cause the core saturation problem and audible noise. Moreover, the oscillations on the output voltage can also decrease the quality of power supply.

Fig. 8
figure 8

Experimental results (R C = 0.45 Ω)

Full size image

The experimental results with R C = 0.58 Ω are shown in Fig. 9. When k = 0.38, the system is stable. But when k = 0.48, low frequency oscillations appears on the waveforms of the output voltage and the inductor current. Comparing between Figs. 8 and 9, the experimental results validate that R C has greater influences on the system as the stability boundary is decreased significantly when R C is increased. Because of the existence of some practical limitations, such as various parasitic parameters, device model imperfections and dead effect and, there are some differences on amplitude between experimental and simulation waveforms. Furthermore, there are small deviations of k between experimental results and theoretical calculation.

Fig. 9
figure 9

Experimental results (R C = 0.58 Ω)

Full size image

5 Conclusion

In this paper, the dynamics and stability of a digitally controlled DAB converter have been analyzed. This paper presents a full discrete-time modeling method for the digitally controlled DAB converter with output voltage closed loop. The output capacitor ESR and one step delay in the digital controller are taken into account in the full discrete-time model. Based on this model, the stabilities of the DAB converter versus the proportional controller parameter and the output capacitor ESR are analyzed and then the critical values and the bifurcation types are accurately predicted. Further, this paper also finds that the stability region of the proportional controller parameter is expanded significantly when capacitor ESR R C is decreased. So when designing a DAB converter in practice, it is quite important and necessary to take R C into account. The analysis in this paper provides useful guidelines for the appropriate design and control of the converter, thereby keeping the bifurcations far enough from the normal operating conditions in parameter space.