1 Introduction

The energy storage system (ESS) plays a key role in deciding the electric vehicle’s performance and reliability [1–3]. Compared with the energy storage system solely structured by only batteries or supercapacitors, a hybrid energy storage system comprising both high power density and high energy density storage units, gains better performance, such as high power rating, high energy capacity, short response time, and extended the life cycle of the ESS [4–7]. Control, robustness, stability, efficiency, and optimization of HESS remain an essential research area [8]. How to reinforce the complementary advantages of batteries and supercapacitors, the current sharing and SOC management of battery are key issues that need to be considered [9–12].

Many studies have been done upon the dynamic power sharing between batteries and supercapacitors [13–15]. The main control objective is to achieve the dynamic allocation of high frequency power demands and low frequency power demands to the batteries and supercapacitors respectively. In [14], a piecewise linear relationship between the current of the battery and supercapacitor decides the power distribution. When the load power varies tremendously, the current of supercapacitor increases dramatically. As a result, the fluctuating power is mainly compensated by the supercapacitor with fast response. However, in the case of small variation of the load power, all the power is balanced by the battery, which leads to frequent charge and discharge cycles. This may do great harm to the battery and shorten its service life. To separate the responses in frequency between these two energy storages, the power demand are divided into low frequency and high frequency components in [15]. And through the bus and supercapacitor voltage cascaded control, the converter current references are set such that the low frequency component is supplied by the battery and the high frequency component is supplied by the supercapacitor [16]. However, only one battery and one supercapacitor are concerned, which limits its applications in the high power occasion.

In [16–21], the total current demand is derived from the difference between the energy source and load power. Then the low-frequency component of the current, namely the total current reference for the battery interfacing power converters, is generated by passing this current reference through a low-pass filter (LPF), while the rest of the current is the reference for supercapacitors. However, the calculation of the total current demand requires the information of all energy source and load power. It relies on a wide communication bandwidth with the increasing number of interfaces, which decreases the system reliability. Meanwhile, the average current control is adopted for current sharing. Such centralized energy management system relies heavily upon the energy control center itself, resulting in inadequate system reliability and scalability, which is not suitable for systems with dynamic structure.

On the other hand, the batteries have the operation limitations in practice. Without a proper battery management, it may come into being serious problems, such as the over-charging, over-discharging, imbalance of voltage among the cells. Therefore, it is a necessity to develop advanced control strategies for the battery equalization. In [16, 18–22], SOC is taken into account in energy control center with centralized control, whose drawback is the less flexible and not appropriate in an expandable system. An attenuation coefficient, with consideration of factors like battery terminal voltage and SOC, is multiplied by the battery current reference in the control loop to guarantee the efficient and safe operation of batteries in [23]. However, the current reference restriction that no power outputs once the battery voltage exceeds the bounds is too rigorous.

Combined with advantages of the conventional droop control, which features high expandability and reliability, the dual droop frequency dividing coordinated control is derived for HESS in this paper with consideration of power sharing between batteries and supercapacitors and SOC of batteries. By employing this control scheme, the dynamic power sharing between two energy storage mediums is ensured with the DC bus and supercapacitor voltage cascaded control. While dual droop control, as an extension of the conventional droop control, realizes the current sharing and SOC management of different power modules without requirement of communication, which increases the system reliability and flexibility.

2 Proposed control strategy for HESS

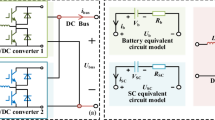
Figure 1 shows an electric vehicle propulsion system with HESS, which contains both high energy density and high power density storage elements. The battery packs, which provide power during the intermittent of the renewable energy sources, are connected to the DC bus by modular bi-directional DC-DC converters for the convenience of battery capacity expansion. While the supercapacitors are connected to the DC bus by multiple converters because of the high power rating.

Fig. 1
figure 1

Modular hybrid energy storage propulsion system

Full size image

The detailed control block of HESS is depicted in Fig. 2. C Bus is the bus capacitor, and the power fluctuation caused by the motor drive is presented by a current source i bus . For controlling the bi-directional DC/DC converters (BDCs), a cascaded control scheme using the inner current-control loop and outer voltage-control loop is realized, where i L_ref is the current reference and the current transfer function is defined as G BDC (s). i Bat , i SC are the currents of the batteries and supercapacitors, respectively. i Bus_Bat , i Bus_SC are the corresponding current into the DC bus. G vcSC (s), H vBus , V Bus_ref are the compensators, feedback coefficient and voltage reference of the DC bus voltage control loop. The corresponding definitions of supercapacitor voltage control loop are expressed as G vcBat (s), H vSC , V SC_ref . And V Bus , V SC , V Bat are the voltage of DC Bus, supercapacitor and battery. The conventional droop control is employed to realize the current sharing among the BDCs for supercapacitor, and the dual droop control is adopted for the current sharing and SOC management of the batteries. The frequency diving control method is realized through the DC bus and supercapacitor voltage cascaded control.

Fig. 2
figure 2

Modular hybrid energy storage propulsion system

Full size image

To analyze and verify the effectiveness of the control strategy, a HESS, with the combination of batteries and supercapacitor, is built with parameters listed in Table 1.

Table 1 Parameters of HESS
Full size table

2.1 Control design of power modules for supercapacitor

A DC-DC converter with droop controller can be simplified as an electric circuit with an ideal DC voltage source in series with an output resistance, as in Fig. 3. One promising way to realize droop control is by setting the virtual output impedance R droop of DC-DC converter. A schematic diagram of two parallel connected converter modules and the corresponding droop curves are depicted in Fig. 3. The difference of output currents ΔI Bus can be derived as

$$ \Delta I_{Bus} = \frac{{V_{Bus1} - V_{Bus2} }}{{R_{droop} }} $$
(1)

where V Bat1 and V Bat2 are the no-load voltage of each module.

Fig. 3
figure 3

Parallel operation of power converters with droop control and droop curves

Full size image

As presented in [19], the input current reference i SC_ref for the supercapacitor converter is used to regulate the output voltage (V Bus ) at the reference level. From Fig. 4, the virtual output impedance of the supercapacitor converter is obtained by

$$ Z_{BDC} (s) = \frac{1}{{H_{vBus} (s)G_{vcSC} (s)G_{BDC} (s)\frac{{V_{SC} }}{{V_{Bus} }}}} $$
(2)
Fig. 4
figure 4

Control scheme for supercapacitor converter

Full size image

In order to realize the V-I droop curves as shown in Fig. 3, the compensator G vcSC (s) can be derived as

$$ G_{vcSC} (s) = \frac{1}{{H_{vBus} (s)G_{BDC} (s)\frac{{V_{SC} }}{{V_{Bus} }}}}\frac{1}{{R_{d\_SC} }} $$
(3)

Hence the output impedance Z BDC (s) equals to R d_SC .

Considering n converter modules in parallel, the open loop transfer function of DC bus voltage G vBuspoc (s) is n times of G vBusoc (s), which is given by

$$ \begin{aligned} & G_{vBuspoc} (s) = nG_{vBusoc} (s) = nG_{vcSC} (s)G_{BDC} (s)\frac{{V_{SC} }}{{V_{Bus} }} \\ & \frac{1}{{C_{Bus} s}}H_{vBus} (s) = \frac{n}{{R_{d\_SC} C_{Bus} s}} \end{aligned} $$
(4)

From (4), the bandwidth of DC bus voltage loop is decided by the number of branches in parallel n and the droop coefficient R d_SC . The bandwidth of DC bus voltage loop is set at 5 Hz with consideration of the supercapacitor response time (in milliseconds). In the case of two converter modules in parallel, the droop coefficient R d_SC is 21.2 Ω. If the voltage difference between V Bat1 and V Bat2 after calibration is 0.2% of the output voltage, namely 1.6 V, the difference of output current ΔI Bus can be obtained by (1), which is 0.075 A and 4% of current in full load case. So the effect in distributing current equally is satisfied.

The open and close loop transfer function after compensation G vBuspoc (s), G vBuspc (s) are obtained by (5) and (6), while the current transfer function from battery to supercapacitor G iSC_iBatp (s) is given by (7).

$$ G_{vBuspoc} (s) = \frac{{z_{c\_Bus} }}{s} $$
(5)
$$ G_{vBuspc} (s) = \frac{{G_{vBuspoc} (s)/H_{vBus} (s)}}{{1{ + }G_{vBuspoc} (s)}} \approx \frac{{z_{c\_Bus} }}{{s + z_{c\_Bus} }}\frac{1}{{H_{vBus} (s)}} $$
(6)
$$ \begin{aligned} G_{{i_{SC} \_i_{Bat} p}} (s)&= - G_{vBuspc} (s)H_{vBus} (s)\frac{{V_{Bat} }}{{V_{SC} }} \hfill \\&\approx \frac{{z_{c\_Bus} }}{{s + z_{c\_Bus} }}\frac{{V_{Bat} }}{{V_{SC} }} \hfill \\ \end{aligned} $$
(7)

where z c_Bus equals to n/(R d_SC C Bus ).

2.2 Control design of power modules for batteries

The equation of droop control for batteries is listed as (8), where V SC0 is the no-load voltage of each module, R d_Bat is the drop coefficient and I Bat is the battery current. If all the battery converters are controlled under the same droop curve, the batteries with lower SOC will go into over discharge while those with higher SOC will be over charged, which significantly decrease the system reliability. In order to balance SOC of each battery unit, a dual droop control scheme is proposed by introducing battery SOC into droop control scheme, which is shown in Fig. 5.

$$ V_{SC} = V_{SC0} - R_{d\_Bat} I_{Bat} $$
(8)

V SC0_1, V SC0_2 are the supercapacitor voltage reference for each battery converter, which are decided with their SOCs as in (9)

$$ V_{SC0} = V_{SC0}^{ *} \,{ + }\,k_{v\_SOC} SOC $$
(9)

where \( V_{SC0}^{ *} \) is the supercapacitor voltage reference under the circumstance of the minimum SOC and k v_SOC is the secondary droop coefficient.

Fig. 5
figure 5

Dual droop control scheme for battery converters

Full size image

Equation (9) is drawn in Fig. 6, which achieves droop curves shifting up and down as presented in Fig. 5. Thus the battery with higher SOC takes in smaller current and gives out bigger current, which contributes to SOC balancing among the battery units.

Fig. 6
figure 6

Secondary droop between battery SOC and \( V_{SC0}^{ *} \)

Full size image

The difference of battery currents ΔI Bat is derived by

$$ \Delta I_{Bat} = I_{Bat1} - I_{Bat2} = \frac{{V_{SC0\_1} - V_{SC0\_2} }}{{R_{d\_Bat} }} $$
(10)
$$ \begin{aligned} V_{SC0\_1} - V_{SC0\_2}\,=\,& k_{v\_SOC} (SOC_{1} - SOC_{2} ) = \hfill \\ & k_{v\_SOC} \Delta SOC \hfill \\ \end{aligned} $$
(11)

By substituting (11) into (12), ΔI Bat is expressed as

$$ \Delta I_{Bat} = \frac{{k_{v\_SOC} \Delta SOC}}{{R_{d\_Bat} }} $$
(12)

The battery SOC is related to its initial SOC, i.e. SOC 0 and the battery current as given by

$$ SOC = SOC_{ 0} - \frac{{\int {I_{Bat} {\text{d}}t} }}{{C_{Bat} }} $$
(13)

So the difference of SOCs can be calculated as following

$$ \begin{aligned} \Delta SOC\,=\,& SOC_{1} - SOC_{2} = SOC_{{0}_{1}} - SOC_{{0}_{2}} - \hfill \\ & \frac{{\int {(I_{Bat1} - I_{Bat2} ){\text{d}}t} }}{{C_{Bat} }} = \Delta SOC_{0} - \frac{{\int {\Delta I_{Bat} {\text{d}}t} }}{{C_{Bat} }} \hfill \\ \end{aligned} $$
(14)

Carrying out Laplace transform on (12) and (14), (15) and (16) can be derived

$$ \Delta I_{Bat} (s) = \frac{{k_{v\_SOC} \Delta SOC(s)}}{{R_{d\_Bat} }} $$
(15)
$$ \Delta SOC(s) = \Delta SOC_{0} - \frac{{\Delta I_{Bat} (s)}}{{C_{Bat} s}} $$
(16)

By substituting (15) into (16), the difference of SOCs and battery currents are expressed as

$$ \Delta SOC(s) = \frac{{R_{d\_Bat} C_{Bat} s}}{{R_{d\_Bat} C_{Bat} s + k_{v\_SOC} }}\Delta SOC_{0} $$
(17)
$$ \Delta I_{Bat} (s) = \frac{{k_{v\_SOC} C_{Bat} s}}{{R_{d\_Bat} C_{Bat} s + k_{v\_SOC} }}\Delta SOC_{0} $$
(18)

According to (17), the SOC balance is a first order system so the difference of SOCs gradually deceases to zero with some decay time constant T SOC as given in (19). Consequently the difference of battery currents turns to zero, realizing the SOC balancing as demonstrated in (18).

$$ T_{SOC} = \frac{{R_{d\_Bat} C_{Bat} }}{{k_{v\_SOC} }} $$
(19)

3 Design considerations of proposed control strategy

3.1 Primary droop control parameter design

The block diagram of the supercapacitor voltage control loop is depicted in Fig. 7, where the supercapacitor is modeled as a capacitor C SC and a resistor R SC in series. And the impedance of the supercapacitor Z SC (s) = (R SC C SC s+1)/(C SC s). The relationship between the supercapacitor voltage and the battery current can be derived by

$$ v_{SC} (s) = \frac{{v_{SC\_ref} }}{{H_{vSC} (s)}} - \frac{1}{{G_{vcBat} (s)G_{BDC} (s)H_{vSC} (s)}}i_{Bat} (s) $$
(20)
Fig. 7
figure 7

Block diagram of supercapacitor voltage control loop

Full size image

In order to lower the gain around zero introduced by the supercapacitor impedance so as to suppress the batteries’ response to the power fluctuation around the zero frequency, the compensator G vcBat (s) is designed as (20) where z SC  = 1/(R SC C SC ) and the droop equation is derived by (22).

$$ G_{vcBat} (s) = \frac{1}{{H_{vSC} (s)G_{BDC} (s)}}\frac{1}{{R_{d\_Bat} }}\frac{{z_{SC} }}{{s + z_{SC} }} $$
(21)
$$ v_{SC} (s) = \frac{{v_{SC\_ref} }}{{H_{vSC} (s)}} - R_{d\_Bat} \frac{{s + z_{SC} }}{{z_{SC} }}i_{Bat} (s) $$
(22)

For the DC component, namely s = 0, the droop equation is simplified as following

$$ v_{SC} (0) = \frac{{v_{SC\_ref} }}{{H_{vSC} (0)}} - R_{d\_Bat} i_{Bat} (0) $$
(23)

The bandwidth of the supercapacitor voltage loop is set at 0.05 Hz considering the batteries response time (in seconds). In the case of two converter modules in parallel, the droop coefficient R d_SC is 0.05 Ω.

3.2 Secondary droop control parameter design

The secondary droop control between the supercapacitor voltage reference and SOC is achieved by adding a feedforward loop into the supercapacitor voltage control loop, as presented in Fig. 8. The secondary droop equation in steady state is given by

$$ V_{SC} = \frac{{v_{SC\_ref} }}{{H_{vSC} }} + k_{v\_SOC} SOC $$
(24)
Fig. 8
figure 8

Block diagram of dual droop control for battery units

Full size image

In order not to influence the stability of the supercapacitor voltage control loop, the SOC balancing time constant T SOC is set as 300 s, far larger than the corresponding time of the cross-over frequency in the supercapacitor voltage control loop (20 s). From (19), the secondary droop coefficient k v_SOC can be obtained.

3.3 System response to power fluctuation

The relationship between the control parameters and frequency response range is analyzed to theoretically verify the proposed control strategy.

The transfer block diagram of response of the supercapacitor current and battery current to power fluctuation is plotted in Fig. 9.

Fig. 9
figure 9

Transfer block diagram of response of supercapacitor current and battery current to power fluctuation

Full size image

The transfer function from the supercapacitor current to the battery current is obtained by

$$ \begin{aligned} G_{{i_{Bat} \_i_{SC} p}} (s)\,&=Z_{SC} (s)H_{vSC} (s)nG_{vcBat} (s)G_{BDC} (s) \hfill \\ & =\,\frac{{z_{c\_SC} }}{s}\frac{{V_{SC} }}{{V_{Bat} }} \hfill \\ \end{aligned} $$
(25)

where z c_SC is the crossover frequency of supercapacitor voltage control loop.

From Fig. 9, the output impedance of HESS can be calculated by

$$ \begin{aligned} Z_{op} (s) &= \frac{{v_{Bus} (s)}}{{i_{bus} (s)}} = \frac{1}{{1 + G_{vBuspoc} (s)(1 + G_{{i_{Bat} \_i_{SC} p}} (s)\frac{{V_{Bat} }}{{V_{SC} }})}} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{{C_{Bus} s}}& = \frac{s}{{(s + z_{c\_SC} )(s + z_{c\_Bus} )C_{Bus} }} \hfill \\ \end{aligned} $$
(26)

Therefore, the transfer function of the DC bus capacitor current, supercapacitor current and batteries current to power fluctuation G iCBus_ibusp (s), G iBus_SC_ibusp (s) and G iBus_Bat_ibusp (s) can be derived by

$$ G_{{i_{CBus} \_i_{bus} p}} (s) = \frac{{Z_{op} (s)}}{{\frac{1}{{C_{Bus} s}}}} = \frac{{s^{2} }}{{(s + z_{c\_SC} )(s + z_{c\_Bus} )}} $$
(27)
$$ \begin{aligned} G_{{i_{Bus\_SC} \_i_{bus} p}} (s)\,=\,& Z_{op} (s)G_{vBuspoc} (s)C_{Bus} s \hfill \\ =& \frac{{z_{c\_Bus} s}}{{(s + z_{c\_SC} )(s + z_{c\_Bus} )}} \hfill \\ \end{aligned} $$
(28)
$$ \begin{aligned} G_{{i_{Bus\_Bat} \_i_{bus} p}} (s)\,=\, & G_{{i_{Bus\_SC} \_i_{bus} p}} (s)\frac{{V_{Bus} }}{{V_{Bat} }}G_{{i_{Bat} \_i_{SC} p}} (s)\frac{{V_{Bat} }}{{V_{Bus} }} \hfill \\ = & \frac{{z_{c\_SC} z_{c\_Bus} }}{{(s + z_{c\_SC} )(s + z_{c\_Bus} )}} \hfill \\ \end{aligned} $$
(29)

Figure 10 gives the frequency response range of the DC bus capacitors, supercapacitors and batteries to the power fluctuation. It can be seen that the batteries absorb the low frequency power fluctuation while supercapacitors provide the high frequency part and the rest power is supplied by DC bus capacitors. Meanwhile, the diving frequencies are decided by the crossover frequencies of the DC bus voltage control loop and supercapacitor voltage control loop. So the HESS can be fully used through proper controller design.

Fig. 10
figure 10

Response of energy storage to DC bus power fluctuation

Full size image

4 Experimental and simulation verification

In this section, a HESS, comprising two supercapacitor converters and two battery converters with parameters as listed in Table 1, is built to demonstrate the advanced performance of the proposed control strategy.

The current sharing effect and droop character of two supercapacitor converters are displayed in Fig. 11. The no-load voltage difference before and after calibration are shown in Fig. 11a, b respectively. And the droop curve and current difference are demonstrated in Fig. 11c, which presents a good current sharing result.

Fig. 11
figure 11

Current sharing effect

Full size image

The process of SOC balancing and current equalization of batteries is shown in Fig. 12. The initial SOC difference is set to 5% and the measurement of SOC difference is calculated by the Ah-integration as presented in (14). With dual control scheme, the currents of battery units tends to equality and the SOC difference decreases gradually from the initial value 5% to 1.8% in 300 s, which is corresponding to the time constant T SOC .

Fig. 12
figure 12

Results of battery SOC equilibrium and current sharing

Full size image

Figure 13 shows the dynamic power allocation between supercapacitor and batteries when a 1 kW step load is applied to the system. The supercapacitor responses to the high frequency power fluctuation while the batteries response to the rest power. The output voltage is well regulated at DC bus voltage reference without steady state error since the supercapacitor does not response to the dc component. Meanwhile, it can be seen that the current difference in the case of ΔSOC = 3% is larger than that in the case of ΔSOC = 1.4%. So the current difference is positively correlated to ΔSOC, which helps to SOC equalization.

Fig. 13
figure 13

Dynamic response of supercapacitor and battery current to power fluctuation

Full size image

5 Conclusion

This paper proposes a dual droop-frequency diving coordinated control strategy for HESS in electric vehicle application. The dynamic power allocation is realized through the voltage cascaded control, where the DC bus voltage control loop and supercapacitor voltage control loop set the frequency range for both supercapacitor and battery, make the most use of hybrid energy storage system. On the other aspect, the dual droop control scheme provides not only current sharing between battery units but also SOC equalization without the necessity of communication, which helps to lengthen the battery cycle life and increase the system reliability and flexibility. The experimental results have proven it to be a viable solution for energy management of HESS.