A credit policy approach in a two-warehouse inventory model for deteriorating items with price- and stock-dependent demand under partial backlogging

Abstract

Advertisement of the product is an important factor in inventory analysis. Also, price and stock have an important role to attract more customers in the competitive business situations. Trade credit policy is another important role in inventory analysis. We have combined these three factors together in a two-warehouse inventory model and represented it mathematically. In addition, we have added deteriorating factor of our proposed problem with price- and stock-dependent demand under partial backlogged shortage and solved. The frequency of advertisement is considered constant for a year in this paper. The proposed model is highly nonlinear in nature. Due to highly nonlinearity, we could not find the closed form solution. In this paper, trade credit facility is taken in the perspective of retailer, and all the possible cases and subcases of the model are discussed and solved using lingo 10.0 software. The results of sensitivity analysis prove the effectiveness of the proposed model.

Introduction

Inventories are the idle stock of physical goods having economic values and are held in various forms by an organization, like raw materials, work-in-process goods, finished goods waiting for packing or transportation or use or sale in future. These stocks represent a large portion of the business investment and must be well managed to maximize profit or minimize loss. Many small business organizations cannot observe the types of losses arising from poor inventory management. Proper management and control of inventories play a vital role in a successful profit-making business.

Deterioration is nothing but the decline of quality of a product. The products that become decayed, damaged, expired, or invalid over time are referred to as deteriorating items. Deteriorating items can be divided into two categories. The first one refers to the items like meat, vegetables, fruits, medicines, flowers, etc. which become decayed, damaged, or expired over time. The second one includes the items like computer chips, mobile phones, fashion and seasonal goods that lose part or total value over time because of the invention of new technology. The concept of quality management in time must imbibe bringing prosperity in the business world. Customer satisfaction is another functional aspect of responsibility entrusted to the business houses and firms. The utility of technology in a need-based manner to improvise the business cannot be undermined. The research and innovation to that extent play a greater role to bring excellence to the commercial world. Numerous researchers have carried out research in this field, and a good number of researchers are still working on this field.

Some of the finest papers on the deteriorating-inventory model are referred here. Mukhopadhyay et al. (2004) have developed an inventory model with price-dependent demand, deterioration rate as time proportional and then the model has been solved analytically with suitable numerical example. A production-inventory model for deteriorating items with multiple market demand is proposed by He et al. (2010). Since then, Cheng and Wang (2009) have discussed trapezoidal demand which is a piecewise linear function in their model with constant deterioration. Malik and Singh (2011) have presented a deteriorating-inventory model with variable demand and solved the model using soft computing technique. Maihami and Kamalabadi (2012a, b) have considered a noninstantaneous deteriorating item for a joint pricing and inventory control model with time and price-dependent demand and presented a solution for maximizing the profit. Again Maihami and Kamalabadi (2012a, b) have built an inventory model with noninstantaneous deteriorating items under permissible delay in payments and solved with a suitable solution procedure. Taleizadeh and Nematollahi (2014) have proposed an inventory model with delay payment, managed a perishable item in a finite planning horizon and also presented an optimal solution procedure to establish the model. Taleizadeh et al. (2015) have described vendor-managed inventory model in a two-supply chain system. Here they have considered demand as deterministic and price sensitive and also in terms of deterioration. Their objective in this model is to maximize profit in an entire chain system.

Dye (2013) has presented a noninstantaneous deteriorating item in his model, to reduce deterioration rate he has introduced preservation technology investment and reached on decisions. Mishra and Shing (2011) have described an inventory model to minimize the inventory cost, where the model takes into account time-dependent demand, holding cost and deterioration. The channel coordination for a supply chain consisting of one manufacturer and one retailer and deteriorating-inventory model is presented by Cárdenas-Barrón and Sana (2014), whose proposed model considers demand as sensitive to promotional efforts and sales team’s initiatives with deterioration. An inventory model for a single deteriorating item with stock-level-dependent demand has been presented by Bhunia et al. (2015). Chatterji and Gothi (2015) have analysed an inventory model by taking into account Weibull distribution deterioration and demand as ramp type. Jaggi et al. (2015) have studied an inventory model with constant demand and deterioration; their work also discussed trade credit which helps to stimulate demand and attract retailer. Islam et al. (2016) have built an inventory model with exponentially decreasing demand with constant deterioration.

It is a well-known fact that in a fiercely competitive world, commercial advertisements play a vital role in boosting the business prospects and penetrating into overseas markets. Creative and effective advertisement not only creates the lasting impact on the customer mind, but it also fosters brand loyalty for a longer period of time. In case of new products and new market, advertisements play a much greater role to help customers to be cognizant and to get the right information and consequently to change customers’ mindset. A colossal research that focused on advertisement as a factor in creating the demand is established by many researchers. Here we have cited some of the models proposed based on advertisement as a factor. An inventory model involving defective items and incorporating marketing decision, where demand is price and advertisement dependent, has been proposed by Mondal et al. (2009), with which they have derived a solution to maximize the profit. Then, Palanivel and Uthayakumar (2015) have revisited the work of Mondal et al. (2009) and developed an inventory model with price- and advertisement-dependent demand under partial backlogging. Giri and Sharma (2014) have introduced advertising cost-dependent demand in their model and developed a model from the perspectives of manufacturers and retailers. Geetha and Uthayakumar (2016) have presented an optimal policy for a noninstantaneous deteriorating-inventory model where demand is dependent on price and advertisement. Bhunia et al. (2015) have discussed two storage inventory models considering a demand which is dependent on time, selling price and frequency of advertisement with a single deteriorating item.

At present, appropriate distribution channels, as well as optimal logistics and warehousing facilities, are part and parcel of any effective marketing system. Two-warehousing systems, in general, facilitate the reduction in costs, ensure smooth and better supply management, and allow for safe and secured upkeep of inventories for final deliveries to retail destinations. Here we are citing some notable researchers who worked on a two-warehouse system. Lee and Hsu (2009) have introduced a two-warehouse inventory model with time-dependent demand and deterioration. Liang and Zhou (2011) have derived an optimal replenishment policy for a two-warehouse inventory model under a conditionally permissible delay in payments. Sett et al. (2012) have developed a two-warehouse inventory model with the increasing demand and time-varying deterioration. Bhunia et al. (2013) have studied a two-warehouse deteriorating-inventory model with the linear trend in demand. This work has been extended by Bhunia et al. (2014a, b) using the permissible delay in payment. Sana (2016) has developed a production-inventory model for a two-stage supply chain, consisting of one manufacturer and one retailer, and derived a solution for the profit.

Without trade credit, business is unthinkable. Trade credit is the most important part of distribution channel management. Modern business thrives on credit system be it consumer credit, trade credit, or loans and advances obtained by manufactures. Actually, the trade credit system makes it possible for the flow of goods from the manufacturer via many intermediaries vide retailer to reach the end customer. That is the reason why it is the most important part of working capital management. Recently, a vast number of research papers have been published on trade credit. For instance, Cheng et al. (2009) have integrated an inventory model where trade credit linked to ordering quantity and demand is considered to be a decreasing function of price. Liao and Huang (2010) have presented an inventory model for optimizing the replenishment cycle time and discussed trade credit under deteriorating-inventory environment. Soni et al. (2010) have reviewed an inventory model with trade credit facility from the retailer’s point of view and derived a solution. Maiti (2011) has introduced a fuzzy genetic algorithm to solve an inventory model with credit-linked promotional demand in an imprecise planning horizon. Kumar et al. (2012) have developed a deterministic inventory model for price-dependent demand, and using trade credit under deteriorating environment, Liao et al. (2013) also have designed an inventory model with two warehouse systems and introduced trade credit in a supply chain system. Taleizadeh et al. (2013) have focused on delay payment system in their model and prepared a deteriorating-inventory model allowing for shortage and backlogged items. Finally, they followed an optimal solution procedure to determine the order and shortage quantities. Taleizadeh (2014) has described multiple prepayment schemes in their model and developed a deteriorating-inventory model. In addition, they presented a suitable optimal solution with relevant numerical examples. Pourmohammad Zia and Taleizadeh (2015) have considered both multiple advance payments and delayed payment in their inventory model and explained about inventory model with optimal solution. Lashgari et al. (2015) have developed an inventory model under a three-level supply chain situations considering with advance payment scheme in both up and downstream modes. Lashgari et al. (2016) have focused on two-level trade credits in their model and presented a deteriorating-inventory model with shortage and backordered items, and at last, they were able to obtain an optimal solution. Lashgari et al. (2017) have proposed a noninstantaneous deteriorating-inventory model under partial prepayment with trade credit policy and finally obtained an optimal solution for the said model. Diabat et al. (2017) have established a deteriorating-inventory model considering partial downstream delayed payment and upstream advance payment schemes under three different cases of shortages, i.e. shortage is not allowed, shortages allowed with partial backordering, and full backordering. Finally, they obtained an optimal solution procedure for the proposed model. Taleizadeh (2017a, b) has developed an inventory model with advance payment scheme under shortages with planned partial backordering and discussed a solution algorithm with suitable numerical examples to validate the model. Taleizadeh (2017a, b) again discussed deteriorating items which evaporate such as chemical raw material in his work, and derived an inventory model allowing for shortage and partially backordered items. Taleizadeh et al. (2017) have introduced an imperfect EPQ inventory model with trade credit policies and derived a closed form solution. Tavakkoli and Taleizadeh (2017) have introduced a lot sizing model for decaying item with full advance payment from the buyer and conditional discount from the supplier.

Singh et al. (2016) have derived an EOQ model with stock -dependent demand, trade credit facility in perspective of retailers, and preservation technology for reduction of deterioration. Shah and Cardenas-Barron (2015) have described an inventory model with cash discount facility, and derived the solution which helps retailer and supplier to take better decisions.

Research gap and our contribution

In this proposed model, a two-warehouse inventory model for deterioration item with trade credit policy approach with price- and stock-dependent demand under partial backlogged shortage is described. In reality, we always see that advertisement of the product has a huge impact on the point of profit. Initially an enterprise/organization decides about the quantum of advertisement depending upon the allotted budget. In that regard, we have considered the frequency of advertisement is constant. We have developed this model under the following factors.

• 1. Price- and stock-dependent demand.

• 2. Price as a constant markup rate.

• 3. Backlogging rate is length of the waiting time of the customers.

• 4. Alternative trade credit policy.

• 5. Advertisement of the product.

Due to stock-dependent demand and alternative trade credit policy, the problem is converted into a highly nonlinear problem. For this reason, we cannot be able to prove the optimality mathematically and also cannot be able to find any closed form solution. In this connection, we have solved the problem by using lingo 10.0 software and make a 3D plot in order to show the concavity graphically. Finally, we performed the sensitivity analysis in order to make a fruitful conclusion.

Assumptions and notations

The following assumptions have been made and notations used for the purpose of developing the proposed model.

Notations	Units	Description
$C_{0}$	$/order	Ordering cost
$C_{l}$	$/unit	Opportunity cost
$a$	Constant	Demand parameter $(a > 0)$
$b$	Constant	Demand parameter $(b > 0)$
P	$/unit	Selling price per unit
$C_{p}$	Units	Purchase cost per unit
$A$	Constant	Frequency of advertisement
$\gamma$	constant	Shape parameter of advertisement
$C_{4}$	$/advertisement	Advertisement cost
$C_{b}$	$/unit	Shortage cost per unit
$m( > 1)$	Constant	Mark up rate
$p$	Constant	Selling price and $p = mC_{p}$
$\alpha$	Constant	Deterioration rate at own warehouse (OW)
$\beta$	Constant	Deterioration rate at rented warehouse (RW)
$C_{d}$	$/unit	Deterioration cost
$W_{1}$	Units	Storage capacity of the (OW)
$W_{2}$	Units	Storage capacity of the (RW)
$t_{2}$	Years	Time at which the stock in OW reaches to zero
$c_{\text{ho}}$	$/unit/unit time	Holding cost per unit for OW
$c_{\text{hr}}$	$/unit/unit time	Holding cost per unit for RW
$W$	Units	Initial inventory level at OW
R	Units	Maximum backlogged units
S	Units	Maximum inventory level
$I_{r} (t)$	Units	The inventory level at any time t in (RW)
$I_{0} (t)$	Units	The inventory level at any time t in (OW)
$M$	Years	Credit period offered by the supplier
$I_{e}$	$/year	Interest earned by the supplier
$I_{p}$	$/year	Interest charged by the supplier
$\prod^{i}$	$/year	Total cyclic cost per unit time for case $i = 1,2,3,4,5,6,7$
Decision variables
t1	Years	Time at which the stock in RW reaches to zero
T	Years	The length of the replenishment cycle

Assumptions

• (i) The inventory planning horizon is infinite.

• (ii) The lot size is delivered in one batch entirely.

• (iii) Shortages, if any, are allowed and partially backlogged and shortages are accumulated with rate $\left[ {1 + \delta (T - t)} \right]^{ - 1} ,\delta > 0$.

• (iv) Lead-time is negligible, and replenishment rate is infinite.

• (v) Deterioration is considered instantaneous for both the warehouses.

• (vi) The deterioration rates in both warehouses are constant. However, the deterioration rate in rented warehouse (RW) $\beta$, due to the better facilities, is smaller than the deterioration rate $\alpha$ in own warehouse (OW), i.e. $0 < \beta < \alpha \ll 1$.

• (vii) The demand rate $D(A,p,I(t))$ is dependent on inventory level ($I(t)$), selling price (p) of the item and the frequency of advertisement (A), i.e.$D(A,p,I(t)) = A^{\gamma } (a - bp + cI(t))$ where $a,b,c,\gamma > 0$ and A is an integer.

• (viii) In this paper, we have introduced alternative trade credit policy, i.e. suppliers offered trade credit period M to the retailers. Also, during this time period, interest earned rate is $I_{e}$ and the interest charged rate is $I_{p} .$

The mathematical model

In this proposed inventory model, initially, an enterprise purchases $(S + R)$ units of a single deteriorating item. Shortly after $R$ units are utilized to fulfil the partially backlogged demand, and consequently, the on-hand inventory level becomes $S$ units of which $W_{1}$ units are stored in OW and the remaining amount $\left( {S - W_{1} } \right)$ units in RW. The inventory level in RW decreases due to the need to meet the customers’ demand, and also deterioration effect of the item reduces during the time interval $[0,t_{1} ],$ and it vanishes at time $t = t_{1}$. On the other hand, in OW during $[0,t_{1} ]$, the inventory level $W_{1}$ decreases due to deterioration only, and during $[t_{1} ,t_{2} ],$ it decreases due to resultant effect of deterioration and customers’ demand. At time $t = t_{2}$, the inventory level in OW becomes zero. Thereafter, the shortages have appeared during the time interval $[t_{2} ,T]$ , which are accumulated depending on the waiting time-length up to the new lot with a rate $\left[ {1 + \delta (T - t)} \right]^{ - 1} ,\delta > 0$. The maximum shortage level,$R$, occurs at time $t = T$. Our main object is to determine the optimal values of $A,t_{1}$ and $T,$ as a result of which, the profit per unit time of the system will be maximized, and also to obtain the corresponding values of $S$ and $R$.

The stock in rented warehouse (RW) ($0 \le t \le t_{1}$) depicted due to demand and deterioration of the items, follows the following differential equation:

$$\frac{{{\text{d}}I_{r} (t)}}{{{\text{d}}t}} + \beta I_{r} (t) = - A^{\gamma } (a - bp + cI_{r} (t)),\quad 0 \le t \le t_{1}$$

(1)

subject to conditions

$$I_{r} (t) = 0\quad {\text{at}}\;t = t_{1}$$

and

$$I_{r} (t) = S - W_{1} \quad {\text{at}}\;t = 0.$$

On solving Eq. (1) and using $I_{r} (t) = 0$ at $t = t_{1},$ one can get

$$I_{r} (t) = \frac{{A^{\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}({\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} - 1).$$

(2)

Again, using $I_{r} (t) = S - W_{1}$ at $t = 0$, in Eq. (2), one can get

$$S = W_{1} + \frac{{A^{\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}({\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} - 1).$$

(3)

On the other hand, the inventory level of owned warehouse (OW) follows the differential equation as

$$\frac{{{\text{d}}I_{0} (t)}}{{{\text{d}}t}} + \alpha I_{0} (t) = 0\quad 0 \le t \le t_{1}$$

(4)

$$\frac{{{\text{d}}I_{0} (t)}}{{{\text{d}}t}} + \alpha I_{0} (t) = - A^{\gamma } (a - bp + cI_{0} (t))\quad t_{1} < t \le t_{2}$$

(5)

$$\frac{{{\text{d}}I_{0} (t)}}{{{\text{d}}t}} = - \frac{{A^{\gamma } (a - bp)}}{1 + \delta (T - t)}\quad t_{2} < t \le T$$

(6)

subject to conditions

$$I_{o} (t) = W_{1} \quad {\text{at}}\;t = 0$$

(7)

$$I_{o} (t) = 0\quad {\text{at}}\;t = t_{2}$$

(8)

$${\text{and}}\quad I_{o} (t) = - R\quad {\text{at}}\;t = T.$$

(9)

Also $I_{o} (t)$ is continuous at $t = t_{1}$ and $t = t_{2}$.

With the help of the boundary conditions (7)–(9), the solutions of the Eqs. (4)–(6) are given by

$$I_{o} (t) = W_{1} {\text{e}}^{ - \alpha t} \quad 0 \le t \le t_{1}$$

(10)

$$I_{0} (t) = \frac{{A^{\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}({\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} - 1)\quad t_{1} < t \le t_{2}$$

(11)

$$I_{0} (t) = \frac{{A^{\gamma } (a - bp)}}{\delta }\log (1 + \delta (T - t)) - R\quad t_{2} < t \le T.$$

(12)

The continuity condition of $I_{o} (t)$ at time $t = t_{1}$ gives us

$$W_{1} {\text{e}}^{{ - \alpha t_{1} }} = \frac{{A^{\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}({\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} - 1).$$

(13)

Also from the continuity of $I_{o} (t)$ at $t = t_{2}$ , we can get

$$R = \frac{{A^{\gamma } (a - bp)}}{\delta }\log (1 + \delta (T - t_{2} )).$$

(14)

The total numbers of deteriorated items in RW and OW over the stock-in period can be calculated as follows:

$$D_{1} = \beta \int\limits_{0}^{{t_{1} }} {I_{r} (t)\,{\text{d}}t} \quad {\text{and}}\quad D_{2} = \alpha \int\limits_{0}^{{t_{2} }} {I_{0} (t)\,{\text{d}}t} .$$

Hence, we can write $\int_{0}^{{t_{1} }} {I_{r} (t)\,{\text{d}}t} = \frac{{D_{1} }}{\beta }$ and $\int_{0}^{{t_{2} }} {I_{o} (t){\mkern 1mu} {\text{d}}t} = \frac{{D_{2} }}{\alpha }$.

Again, the total numbers of deteriorated items in RW and OW over the stock-in period can be expressed in terms of the total demands in the following way:

$$D_{1} = S - W_{1} - \int\limits_{0}^{{t_{1} }} {A^{\gamma } (a - bp + cI_{r} (t)){\text{d}}t}$$

$${\text{and}}\quad D_{2} = W_{1} - \int\limits_{{t_{1} }}^{{t_{2} }} {A^{\gamma } (a - bp + cI_{o} (t)){\text{d}}t.}$$

Therefore, the total holding cost $C_{\text{hold}}$ over the entire cycle is given by

$$\begin{aligned} C_{\text{hold}} &= C_{\text{hr}} \int\limits_{0}^{{t_{1} }} {I_{r} (t)\,{\text{d}}t} + C_{\text{ho}} \int\limits_{0}^{{t_{2} }} {I_{o} (t)\,{\text{d}}t} \hfill \\ &= \frac{{C_{\text{hr}} }}{\beta }\left[ {S - W_{1} - \int\limits_{0}^{{t_{1} }} {A^{\gamma } (a - bp + cI_{r} (t)){\text{d}}t} } \right] + \frac{{C_{\text{ho}} }}{\alpha }\left[ {W_{1} - \int\limits_{{t_{1} }}^{{t_{2} }} {A^{\gamma } (a - bp + cI_{o} (t)){\text{d}}t} } \right] \hfill \\ &= C_{\text{hold1}} + C_{\text{hold2}} , \hfill \\ \end{aligned}$$

$$\begin{aligned} {\text{where}}\quad C_{\text{hold1}} &= \frac{{C_{\text{hr}} }}{\beta }\left[ {S - W_{1} - \int\limits_{0}^{{t_{1} }} {A^{\gamma } (a - bp + cI_{r} (t)){\text{d}}t} } \right] \hfill \\ &= \frac{{C_{\text{hr}} }}{\beta }\left[ {S - W_{1} - A^{\gamma } (a - bp)t_{1} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}t_{1} } \right] \hfill \\ \end{aligned}$$

$$\begin{aligned} {\text{and}}\quad C_{\text{hold2}} &= \frac{{C_{\text{ho}} }}{\alpha }\left[ {W_{1} - \int\limits_{{t_{1} }}^{{t_{2} }} {A^{\gamma } (a - bp + cI_{o} (t)){\text{d}}t} } \right] \hfill \\ &= \frac{{C_{\text{ho}} }}{\alpha }\left[ {W_{1} - A^{\gamma } (a - bp)(t_{2} - t_{1} ) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - t_{1} )} \right] \hfill \\ \end{aligned}$$

$$\begin{aligned} \therefore C_{\text{hold}} &= \frac{{C_{\text{hr}} }}{\beta }\left[ {S - W_{1} - A^{\gamma } (a - bp)t_{1} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}t_{1} } \right] \hfill \\ &\quad + \frac{{C_{\text{ho}} }}{\alpha }\left[ {W_{1} - A^{\gamma } (a - bp)(t_{2} - t_{1} ) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - t_{1} )} \right]. \hfill \\ \end{aligned}$$

(15)

Again, the total shortage cost $C_{\text{sho}}$ over the entire cycle is given by

$$\begin{aligned} C_{\text{sho}} &= - C_{b} \int\limits_{{t_{2} }}^{T} {I_{0} (t)\,{\text{d}}t} \hfill \\ \therefore C_{\text{sho}} &= C_{b} \left[ {R(T - t_{2} ) - \frac{{A^{\gamma } (a - bp)}}{\delta }.\frac{1}{\delta }\left[ { - \delta (T - t_{2} ) + (1 + \delta (T - t_{2} ))\log (1 + \delta (T - t_{2} ))} \right]} \right] \hfill \\ &= C_{b} \left[ {R(T - t_{2} ) + \frac{{A^{\gamma } (a - bp)}}{{\delta^{2} }}\left[ {\delta (T - t_{2} ) - (1 + \delta (T - t_{2} ))\log (1 + \delta (T - t_{2} ))} \right]} \right]. \hfill \\ \end{aligned}$$

(16)

The total deterioration cost (DC) during the cyclic length is

$$\begin{aligned} {\text{DC}} &= C_{\text{d}} \left[ {S - W_{1} - \int\limits_{0}^{{t_{1} }} {A^{\gamma } (a - bp + cI_{r} (t)){\text{d}}t} } \right] + C_{\text{d}} \left[ {W_{1} - \int\limits_{{t_{1} }}^{{t_{2} }} {A^{\gamma } (a - bp + cI_{o} (t)){\text{d}}t} } \right] \hfill \\ & = C_{\text{d}} \left[ {S - W_{1} - A^{\gamma } (a - bp)t_{1} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}t_{1} } \right] \hfill \\ & \quad + C_{\text{d}} \left[ {W_{1} - A^{\gamma } (a - bp)(t_{2} - t_{1} ) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - t_{1} )} \right]. \hfill \\ \end{aligned}$$

(17)

Since the shortages are not fully backlogged, there are some losses of sale, and the corresponding lost sale cost (LSC) during the entire cyclic is

$$\begin{aligned} {\text{LSC}} &= C_{l} \int\limits_{{t_{2} }}^{T} {\left( {1 - \frac{1}{1 + \delta (T - t)}} \right)D{\text{d}}t} \hfill \\ &= C_{l} A^{\gamma } (a - bp)\left[ {(T - t_{2} ) - \frac{1}{\delta }\log (1 + \delta (T - t_{2} ))} \right]. \hfill \\ \end{aligned}$$

(18)

The supplier offers the trade credit period $M$ to his retailer, and consequently, there may arise three following scenarios:

• Scenario 1: $0 < M \le t_{1}$.

• Scenario 2: $t_{1} < M \le t_{2}$.

• Scenario 3: $t_{2} < M$.

Now scenario 1 will be discussed at first, later scenario 2 and finally scenario 3.

Scenario 1: $0 < M \le t_{1}$

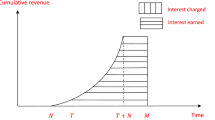
In this case, the total amount payable to the supplier is $C_{p} (S + R)$ at time $t = M$ (Fig. 1).

Fig. 1

Pictorial representation of scenario 1: $0 < M \le t_{1}$

Due to sale and interest earned, the total accumulated amount is given by

$$U_{1} = p\int\limits_{0}^{M} {D{\text{d}}t} + pI_{e} \int\limits_{0}^{M} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } + pR(1 + I_{e} M).$$

Therefore,

$$\begin{aligned} U_{1} & = p\left[ {MA^{\gamma } (a - bp) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}M} \right] \hfill \\ &\quad + pI_{e} \left[ \begin{aligned} \frac{{A^{\gamma } (a - bp)M^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{3} }}\left\{ {e^{{(\beta + cA^{\gamma } )(t_{1} - M)}} - e^{{(\beta + cA^{\gamma } )t_{1} }} } \right\} \hfill \\ &\quad + \frac{{cMA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}e^{{(\beta + cA^{\gamma } )t_{1} }} - \frac{{cA^{2\gamma } (a - bp)M^{2} }}{{2(\beta + cA^{\gamma } )}} \hfill \\ \end{aligned} \right] + pR(1 + I_{e} M). \hfill \\ \end{aligned}$$

(19)

Based on the values of $U_{1}$ and $C_{p} (S + R)$, two subscenarios may arise:

• Scenario 1.1 $U_{1} \ge C_{p} (S + R)$.

• Scenario 1.2 $U_{1} < C_{p} (S + R)$.

Scenario $U_{1} \ge C_{p} (S + R)$

In this scenario, the average profit for the cycle can be expressed as follows:

$$Z^{(1.1)} (A,n,t_{1} ,T) = \frac{X}{T},$$

where

$$\begin{aligned} X &= < {\text{excess amount after paying the amount to the supplier}} > \hfill \\ &\quad + \, < {\text{interest earned for the rest amount during the interval}}\;[M,T] > \hfill \\ &\quad + \, < {\text{total selling price during the interval}}\;[M,t_{2} ] > \hfill \\ &\quad + \, < {\text{interest earned during the interval}}\;[M,t_{2} ] > \hfill \\ &\quad + \, < {\text{interest earned during the interval}}\;[t_{2} ,T] > - {\text{TC}} \hfill \\ \end{aligned}$$

$${\text{i}}.{\text{e}}.,\quad X = \{ U_{1} - C_{p} (S + R)\} \{ 1 + I_{e} (T - M)\} + \left\{ {p\int\limits_{M}^{{t_{2} }} {D\,{\text{d}}t} + pI_{e} \int\limits_{M}^{{t_{2} }} {\int\limits_{M}^{t} D {\text{d}}u\,{\text{d}}t} } \right\}\{ 1 + I_{e} (T - t_{2} )\} - {\text{TC}}$$

and the total cost ${\text{TC}}$ of the system is given by

$${\text{TC}} = < {\text{ordering cost}} > \, + < {\text{advertisement cost}} > \, + \, < {\text{holding cost}} > + \, < {\text{shortage cost}} > + \, < {\text{deterioration cost}} > \, + \, < {\text{lost sale cost}} >$$

$${\text{i}}.{\text{e}}.,\quad {\text{TC}} = C_{o} + C_{4} A + C_{\text{hold}} + C_{\text{sho}} + {\text{DC}} + {\text{LSC}}$$

$$\begin{aligned} &= C_{o} + C_{4} A \hfill \\ &\quad + \frac{{C_{\text{hr}} }}{\beta }\left[ {S - W_{1} - A^{\gamma } (a - bp)t_{1} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}t_{1} } \right] \hfill \\ &\quad + \frac{{C_{\text{ho}} }}{\alpha }\left[ {W_{1} - A^{\gamma } (a - bp)(t_{2} - t_{1} ) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - t_{1} )} \right] \hfill \\ &\quad + C_{b} \left[ {R(T - t_{2} ) + \frac{{A^{\gamma } (a - bp)}}{{\delta^{2} }}\left[ {\delta (T - t_{2} ) - (1 + \delta (T - t_{2} ))\log \left( {1 + \delta (T - t_{2} )} \right)} \right]} \right] \hfill \\ &\quad + C_{d} \left[ {S - W_{1} - A^{\gamma } (a - bp)t_{1} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}t_{1} } \right] \hfill \\ &\quad + C_{d} \left[ {W_{1} - A^{\gamma } (a - bp)(t_{2} - t_{1} ) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - t_{1} )} \right] \hfill \\ &\quad + C_{l} A^{\gamma } (a - bp)\left[ {(T - t_{2} ) - \frac{1}{\delta }\log (1 + \delta (T - t_{2} ))} \right]. \hfill \\ \end{aligned}$$

(20)

Thus, the corresponding optimization problem is

Problem 1

${\text{Maximise}}\quad \prod^{1} (t_{1} ,T) = \frac{X}{T}$

${\text{Subject to}}\quad 0 < M \le t_{1} < t_{2} < T.$

Scenario 1.2: $U_{1} < C_{p} (S + R)$

In this scenario, the total accumulated amount at time $t = M$ is less than the total purchase cost.

Again, two cases may appear at this stage as follows:

• Case 1.2.1: Partial payment is permitted at time $t = M$.

• Case 1.2.2: Partial payment is not permitted at time $t = M$.

Case 1.2.1: Partial payment is permitted at time $t = M$

In this subscenario, let us assume that at time $t = B(B > M),$ the rest amount $C_{p} (S + R) - U_{1}$ will be paid. Therefore, the retailer has to pay the interest on the amount of $C_{p} (S + R) - U_{1}$ during the interval $\left[ {M,B} \right]$.

Hence, the total amount that will be payable at time $t = B(B > M)$ is $(C_{p} (S + R) - U_{1} )(1 + I_{p} (B - M))$.

The total amount available to the retailer

$$\begin{aligned} &= {\text{ Selling}}\;{\text{amount during the interval}}\;\left[ {M,B} \right] + {\text{ the interest earned}} \hfill \\ &= p\int\limits_{M}^{B} {D\,{\text{d}}t} + pI_{e} \int\limits_{M}^{B} {\int\limits_{M}^{t} D {\text{d}}u\,{\text{d}}t} \hfill \\ &= p\int\limits_{M}^{B} {A^{\gamma } (a - bp + cI_{r} (t))\,{\text{d}}t} + pI_{e} \int\limits_{M}^{B} {\left\{ {\int\limits_{M}^{t} {A^{\gamma } (a - bp + cI_{r} (u))\,} {\text{d}}u} \right\}\,{\text{d}}t} . \hfill \\ \end{aligned}$$

Hence, at time $t = B,$ the amount payable to the supplier is equal to the total amount available to the retailer, i.e.

$$(C_{p} (S + R) - U_{1} )(1 + I_{p} (B - M)) = p\int\limits_{M}^{B} {D{\text{d}}t} + pI_{e} \int\limits_{M}^{B} {\int\limits_{M}^{t} D {\text{d}}u{\text{d}}t} .$$

Therefore, the average profit for the cycle is given by

$$\prod^{2} (t_{1} ,T) = \frac{X}{T},$$

where

$$\begin{aligned} X &= < {\text{Total selling price during the interval}}\;\left[ {B,t_{2} } \right] > \hfill \\ & \quad + < {\text{Interest earned during the interval}}\;\left[ {B,t_{2} } \right] > \hfill \\ &\quad + < {\text{Interest earned during the interval}}\;[t_{2} ,T] > - {\text{TC}} \hfill \\ \end{aligned}$$

$${\text{i}}.{\text{e}}.,\quad X = \left\{ {p\int\limits_{B}^{{t_{2} }} {D{\text{d}}t} + pI_{e} \int\limits_{B}^{{t_{2} }} {\int\limits_{B}^{t} D {\text{d}}udt} } \right\}\{ 1 + I_{e} (T - t_{2} )\} - {\text{TC}} .$$

The total cost ${\text{TC}}$ of the system is given by

$${\text{TC}} = < {\text{ordering cost}} > \, + \, < {\text{advertisement cost}} > \, + \, < {\text{holding cost}} > \, + \, < {\text{shortage cost}} > \, + < {\text{deterioration cost}} > \, + \, < {\text{lost sale cost}} >$$

$${\text{i}}.{\text{e}}.,\quad {\text{TC}} = C_{o} + C_{4} A + C_{\text{hold}} + C_{\text{sho}} + {\text{DC}} + {\text{LSC}} .$$

Hence, in this subscenario, the corresponding optimization problem is given by

Problem 2

$${\text{Maximise}}\quad \prod^{2} (t_{1} ,T) = \frac{X}{T}$$

(21)

$${\text{Subject}}\;{\text{to}}\quad 0 < M \le t_{1} < t_{2} < T.$$

Case 1.2.2: partial payment is not permitted at time $t = M$

In this subscenario, the retailer has to pay the credit amount to the supplier. Let this time point be $B$. In this case, retailer has to pay the interest for the period $[M,B]$.

Obviously, the amount payable to the supplier is equal to the total on-hand amount available to the retailer at time $t = B$, i.e.

$$C_{p} (S + R)(1 + I_{p} (B - M)) = p\int\limits_{0}^{B} {D{\text{d}}t} + pI_{e} \int\limits_{0}^{B} {\int\limits_{0}^{t} D {\text{d}}u{\text{d}}t} + pR(1 + I_{e} B),$$

where

$$\begin{aligned} p\int\limits_{0}^{B} {D{\text{d}}t} &= p\int\limits_{0}^{B} {[A^{\gamma } (a - bp + cI_{r} (t))]{\text{d}}t} \hfill \\ &= p\left[ {BA^{\gamma } (a - bp) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}B} \right] \hfill \\ \end{aligned}$$

and

$$\begin{aligned} & pI_{e} \int\limits_{0}^{B} {\int\limits_{0}^{t} D {\text{d}}u{\text{d}}t} \hfill \\ &\quad = pI_{e} \left[ \begin{aligned} \frac{{A^{\gamma } (a - bp)B^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{3} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} \hfill \\ &\qquad + \frac{{cBA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} - \frac{{cA^{2\gamma } (a - bp)B^{2} }}{{2(\beta + cA^{\gamma } )}} \hfill \\ \end{aligned} \right]. \hfill \\ \end{aligned}$$

Therefore, the average profit for the cycle is given by

$$Z^{(1.2.2)} (A,n,t_{1} ,T) = \frac{X}{T},$$

where

$$\begin{aligned} X &= < {\text{total selling price during the interval}}\left[ {B,t_{2} } \right]{ > } \hfill \\ &\quad + < {\text{interest earned during the interval}}\;\left[ {B,t_{2} } \right] > \hfill \\ &\quad + < {\text{interest earned during the interval}}\;[t_{2} ,T] > - {\text{TC}} \hfill \\ \end{aligned}$$

$${\text{i}}.{\text{e}}.,\quad X = \left\{ {p\int\limits_{B}^{{t_{2} }} {D{\text{d}}t} + pI_{e} \int\limits_{B}^{{t_{2} }} {\int\limits_{B}^{t} D {\text{d}}u{\text{d}}t} } \right\}\{ 1 + I_{e} (T - t_{2} )\} - {\text{TC}},$$

where

$$p\int\limits_{B}^{{t_{2} }} {D{\text{d}}t} = p\left[ \begin{aligned} A^{\gamma } (a - bp)(t_{2} - B) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}(t_{1} - B) \hfill \\ - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - t_{1} ) \hfill \\ \end{aligned} \right]$$

and

$$\begin{aligned} pI_{e} \int\limits_{B}^{{t_{2} }} {\int\limits_{B}^{t} D {\text{d}}u{\text{d}}t} &= pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(t_{1} - B)^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{3} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} \} \hfill \\ &\quad + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} (t_{1} - B) - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\frac{{(t_{1} - B)^{2} }}{2} \hfill \\ \end{aligned} \right] \hfill \\ &\quad + pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(t_{2} - t_{1} )^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot (t_{2} - t_{1} ) \hfill \\ &\quad - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\frac{{(t_{2} - t_{1} )^{2} }}{2} \hfill \\ \end{aligned} \right]. \hfill \\ \end{aligned}$$

Hence, in this subscenario, the corresponding optimization problem is given by

Problem 3

$${\text{Maximise}}\quad \prod^{3} (t_{1} ,T) = \frac{X}{T}$$

(22)

$${\text{Subject to}}\quad 0 < M \le t_{1} < t_{2} < T$$

Scenario 2: $t_{1} < M \le t_{2}$

In this case, the total revenue earned by the retailer up to $t = M$ is given by (Fig. 2)

$$\begin{aligned} U_{2} &= p\int\limits_{0}^{M} {D{\text{d}}t} + pI_{e} \int\limits_{0}^{M} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } + pR(1 + I_{e} M) \hfill \\ &= {\text{Term}}1 + {\text{Term}}2 + pR(1 + I_{e} M). \hfill \\ \end{aligned}$$

(23)

Fig. 2

Pictorial representation of scenario 2: $t_{1} < M \le t_{2}$

Again two subscenarios may arise:

• Scenario 2.1 $U_{2} \ge C_{p} (S + R).$

• Scenario 2.2 $U_{2} < C_{p} (S + R) .$

Scenario 2.1: $U_{2} \ge C_{p} (S + R)$

In this subscenario, the average profit for the cycle is given by

$$\prod^{4} (t_{1} ,T) = \frac{X}{T},$$

where

$$\begin{aligned} X &= < {\text{excess amount after paying the amount to the supplier}} > \hfill \\ &\quad + < {\text{interest earned for the rest amount during the interval}}\;[M,T] > \hfill \\ &\quad + < {\text{total selling price during the interval}}\;[M,t_{2} ] > \hfill \\ &\quad + < {\text{interest earned during the interval}}\;[M,t_{2} ] > \hfill \\ &\quad + < {\text{interest earned during the interval}}\;[t_{2} ,T] > - {\text{TC}} \hfill \\ \hfill \\ \end{aligned}$$

$${\text{i}} . {\text{e}} .,\quad X = \{ U_{2} - C_{p} (S + R)\} \{ 1 + I_{e} (T - M)\} + \left\{ {p\int\limits_{M}^{{t_{2} }} {D{\text{d}}t} + pI_{e} \int\limits_{M}^{{t_{2} }} {\int\limits_{M}^{t} D {\text{d}}u{\text{d}}t} } \right\}\{ 1 + I_{e} (T - t_{2} )\} - {\text{TC}} .$$

Here, the total cost ${\text{TC}}$ of the system is given by

$${\text{TC}} = < {\text{ordering \, cost}} > \, + \, < {\text{advertisement \, cost}} > \, + \, < {\text{holding cost}} > + < {\text{shortage \, cost}} > \, + \, < {\text{deterioration \, cost}} > \, + < {\text{lost \, sale \, cost}} >$$

$${\text{i}} . {\text{e}} .,\quad {\text{TC}} = C_{o} + C_{4} A + C_{\text{hold}} + C_{\text{sho}} + {\text{DC}} + {\text{LSC}} .$$

Hence, in this subscenario, the corresponding optimization problem is given by

Problem 4

$${\text{Maximise}}\quad \prod^{4} (t_{1} ,T) = \frac{X}{T}$$

(24)

$${\text{Subject to}}\quad 0 < t_{1} < M \le t_{2} < T$$

Scenario 2.2: $U_{2} < C_{p} (S + R)$

In this scenario, two subscenarios may appear:

• Case 2.2.1: partial payment is permitted at time $t = M$.

• Case 2.2.2: partial payment is not permitted at time $t = M$.

Case 2.2.1: partial payment is permitted at time $t = M$

In this scenario, let the excess amount $C_{p} (S + R) - U_{2}$ payable to the supplier at time be $t = B$. In this case, the interest amount of $C_{p} (S + R) - U_{2}$ during the interval $\left[ {M,B} \right]$ is to be paid.

According to this condition, the amount payable to the supplier is equal to the total on-hand amount available to the retailer at time $t = B$, i.e.

$$(C_{p} (S + R) - U_{2} )(1 + I_{p} (B - M)) = p\int\limits_{M}^{B} {D{\text{d}}t} + pI_{e} \int\limits_{M}^{B} {\int\limits_{M}^{t} D {\text{d}}u{\text{d}}t} .$$

In this scenario, the corresponding constrained optimization problem can be written as follows:

Problem 5

$${\text{Maximise}}\quad \prod^{5} (t_{1} ,T) = \frac{X}{T}$$

(25)

$${\text{Subject to}}\quad 0 < t_{1} < M \le t_{2} < T.$$

Here, the average profit for the cycle is given by

$$\prod^{5} (t_{1} ,T) = \frac{X}{T},$$

where

$$\begin{aligned} X &= < {\text{total selling price during the interval}}\;[B,t_{2} ] > \hfill \\ &\quad + < {\text{interest earned during the interval}}\;[B,t_{2} ] > \hfill \\ &\quad + < {\text{interest earned during the interval}}\;[t_{2} ,T] > - {\text{TC}} \hfill \\ \end{aligned}$$

$${\text{i}} . {\text{e}} .,\quad X = \left\{ {p\int\limits_{B}^{{t_{2} }} {D{\text{d}}t} + pI_{e} \int\limits_{B}^{{t_{2} }} {\int\limits_{B}^{t} D {\text{d}}u{\text{d}}t} } \right\}\{ 1 + I_{e} (T - t_{2} )\} - {\text{TC}} .$$

Here, the total cost ${\text{TC}}$ of the system is given by ${\text{TC}} =$ < ordering cost > + < advertisement cost > + < holding cost > + < shortage cost > + < deterioration cost > + < lost sale cost >

$${\text{i}} . {\text{e}} .,\quad {\text{TC}} = C_{o} + C_{4} A + C_{\text{hold}} + C_{\text{sho}} + {\text{DC}} + {\text{LSC}} .$$

Case 2.2.2: partial payment is not permitted at time $t = M$

In this subscenario, according to this condition, the amount payable to the supplier = total oon-hand amount available to the retailer at time $t = M$, i.e.

$$C_{p} (S + R)(1 + I_{p} (B - M)) = p\int\limits_{0}^{B} {D{\text{d}}t} + pI_{e} \int\limits_{0}^{B} {\int\limits_{0}^{t} D {\text{d}}u{\text{d}}t} + pR(1 + I_{e} B).$$

In this case, the corresponding optimization problem is given by

Problem 6

$${\text{Maximise}}\quad \prod^{6} (t_{1} ,T) = \frac{X}{T}$$

(26)

$${\text{Subject to}}\quad 0 < t_{1} < M \le t_{2} < T.$$

Here, the per unit profit is given by

$$\prod^{6} (t_{1} ,T) = \frac{X}{T},$$

where $X =$ <total selling price during the interval $[B,t_{2} ]$>, + <interest earned during the interval $[B,t_{2} ]$>, + <interest earned during the interval $[t_{2} ,T]$> $- {\text{TC}}$

$${\text{i}} . {\text{e}} .,\quad X = \left\{ {p\int\limits_{B}^{{t_{2} }} {D{\text{d}}t} + pI_{e} \int\limits_{B}^{{t_{2} }} {\int\limits_{B}^{t} D {\text{d}}u{\text{d}}t} } \right\}\{ 1 + I_{e} (T - t_{2} )\} - {\text{TC}}$$

$${\text{and}}\quad {\text{TC}} = C_{o} + C_{4} A + C_{\text{hold}} + C_{\text{sho}} + {\text{DC}} + {\text{LSC}}.$$

Scenario 3: $t_{2} < M \le T$

In this case, the total revenue earned by the retailer up to $t = M$ is given by (Fig. 3)

$$U_{3} = \left\{ {p\int\limits_{0}^{{t_{2} }} {D{\text{d}}t} + pI_{e} \int\limits_{0}^{{t_{2} }} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } } \right\}\{ 1 + I_{e} (M - t_{2} )\} + pR(1 + I_{e} M).$$

Fig. 3

Pictorial representation of scenario 3: $t_{2} < M \le T$

Hence, finally the average profit for the cycle in the case can be written as

$$\prod^{7} (t_{1} ,T) = \frac{X}{T},$$

where $X =$ < excess amount >, + <i nterest earned during the interval $[M,T]$ for the excess amount > $- {\text{TC}}$

$${\text{i}} . {\text{e}} .,\quad X = \{ U_{3} - c_{p} (S + R)\} \{ 1 + I_{e} (T - M)\} - {\text{TC}} .$$

Hence, in this scenario, the corresponding constrained optimization problem can be presented as follows:

Problem 7

$${\text{Maximise}}\quad \prod^{7} (t_{1} ,T) = \frac{X}{T}$$

(27)

$${\text{Subject to}}\quad 0 < t_{1} < t_{2} < M \le T$$

Numerical example

The proposed model has one numerical example. Here, the values of the parameters used in the numerical examples seem realistic but not taken from a case study of real life. Lingo 10.0 is used solve this proposed inventory model and to find optimal values of R, T, and S along with the maximum profit of the system. The results are given below.

Example 1

$$\begin{aligned} C_{hr} &= 0.6,\;C_{ho} = 0.2,\;C_{o} = 350,\;C_{b} = 7,\;C_{p} = 9,\;C_{4} = 50,\;a_{1} = 140,\;b = 0.1,\;c = 5,\gamma = 0.03,\;\delta = 0.7, \hfill \\ W_{1} &= 300,\;M = 0.25,\;I_{e} = 0.09,\;I_{p} = .12,\;A = 5,\;\beta = 0.06,\;\alpha = 0.24,\;m_{1} = 1.5,\;c_{1} = 8,\;c_{d} = 9 \hfill \\ \end{aligned}$$

From the above numerical example, we have obtained case one that gives better optimal solution which is described below.

$$\prod^{1*} (t_{1} ,T) = \$ 6 8 1. 8 6 3 1 ,\quad t_{1}^{*} = 0. 2 5 ,\quad t_{2}^{*} = 0. 6 9 7 5 2 1 0,\quad T^{*} = 0. 7 8 0 9 5 9 8,\quad S^{*} = 3 7 5. 9 1 8 9\quad {\text{and}}\quad R^{*} = 1 1. 7 9 9 7 4.$$

Example 2

$$\begin{aligned} C_{\text{hr}} &= 0.7,\;C_{\text{ho}} = 0.3,\;C_{o} = 200,\;C_{b} = 5,\;C_{p} = 8,\;C_{4} = 50,\;a_{1} = 120,\;b = 0.05,\;c = 5,\gamma = 0.03,\;\delta = 0.5, \hfill \\ W_{1} & = 300,\;M = 0.246,\;I_{e} = 0.12,\;I_{p} = 0.15,\;A = 10,\;\beta = 0.1,\;\alpha = 0.25,\;p = 12,\;c_{1} = 4,\;c_{d} = 8. \hfill \\ \end{aligned}$$

From the above-described numerical example 2, we have obtained the second objective function that gives better optimal solution which is described below.

$$\prod^{6*} (t_{1} ,T) = \$ 5 0 5. 8 8 1 5 ,\,t_{1}^{*} = 0. 0 7 3 5 8 ,\;t_{2}^{*} = 0. 5 4 3 0 4 7 6,\;T^{*} = 0. 6 4 4 4 4 6 7,\;S^{*} = 3 1 1. 5 8 5 3\;{\text{and}}\;R^{*} = 1 2. 6 5 4 7 9.$$

Sensitivity analysis

To investigate the impacts of the changes of the numerical values of the inventory parameters on the optimal solution of earlier described numerical Example 1, a sensitivity analysis has been performed as detailed in this section for the above Example 1. This analysis has been carried out by changing the value of each parameter from − 20 to 20%—but one parameter at a time—with all the remaining parameters retaining their initial values (Table 1).

Table 1 Sensitivity analysis of Example 1 with respect to different parameters

From the above table, we can derive the following conclusions:

• When we decrease 20% on the holding cost of rented warehouse, $c_{\text{hr}},$ the system gives infeasible solution; when we increase 10–20% on the holding costs of rented warehouse $c_{\text{hr}},$ then $R^{ * }$ and $T^{ * }$ increase, and $\prod^{ * }$ decreases, and the rest parameters $S^{ * }$, $t_{1}^{ * }$ and $t_{2}^{ * }$ retain the same values. In this paper, the increases of the profit function mean an organization gains more profit, and decreases stand for organization getting lower profit. Also increased values of the other variables mean stock, shortage, and cycle length will also increase, and their decreased values mean stock, shortage, and cycle length all will decrease.

• When we decrease 10–20% on the holding cost of owned warehouse $c_{o},$ then $\prod^{ * }$ decreases, and $T^{ * }$, $R^{ * }$, $S^{ * }$, $t_{1}^{ * }$ and $t_{2}^{ * }$ increase; when we increase 10–20% on the holding cost of owned ware house $c_{o},$ then the system gives infeasible solution. Here, increases of the profit function mean an organization gains more profit and decreases stand for organization getting lower profit. Also increased values of the other variables mean stock, shortage, cycle length all will increase and decreased values mean stock, shortage, cycle length all will decrease.

• When we decrease 10–20% on the parameter $a,$ then $R^{ * }$, $t_{2}^{ * }$ and $T^{ * }$ decrease, and $S^{ * }$and $\prod^{ * }$ increase, and $t_{1}^{ * }$ retains the same value; when we increase 10–20% on the parameter $a,$ then the system gives infeasible solution. Here increases of the profit function mean an organization gains more profit, and decreases stand for organization getting lower profit. Also increased values of the other variable mean stock, shortage, cycle length all will increase, and decreased values mean stock, shortage, cycle length all will decrease.

• When we decrease 10–20% on the parameter $b,$ then $\prod^{ * }$, $R^{ * }$, $S^{ * }$ and $T^{ * }$ decrease, $t_{2}^{ * }$ increases, and $t_{1}^{ * }$ retains the same value; when we increase 10–20% on the parameter $b,$ then the system gives infeasible solution. Here increases of the profit function mean an organization gains more profit and decreases stand for organization getting lower profit. Also increased values of the other variables mean stock, shortage, and cycle length all will increase, and decreased values mean stock, shortage, and cycle length all will also decrease.

• When we decrease 10–20% on the parameter $c,$ then $R^{ * }$, $T^{ * }$, $t_{2}^{ * }$ and $t_{1}^{ * }$ decrease, and $\prod^{ * }$and $S^{ * }$ increase; when we increase 10–20% on the parameter $c,$ then the system gives infeasible solution. Here increases of the profit function mean an organization gains more profit, and decreases stand for organization getting lower profit. Also increased values of the other variables mean stock, shortage, and cycle length all will increase and decreased values mean stock, shortage, and cycle length all will decrease.

• When we decrease 10–20% on the parameter $\delta,$ then the total system gives infeasible solution; when we increase 10–20% on the parameter $\delta,$ then also system gives infeasible solution.

• When we decrease 10–20% on the parameter $A,$ then $\prod^{ * }$and $t_{2}^{ * }$ decrease, and $R^{ * }$, $S^{ * }$ and $T^{ * }$ increase, and $t_{1}^{ * }$ retains the same value; when we increase 10–20% on the parameter $A,$ then the system gives infeasible solution. Here increases of the profit function mean an organization gains more profit and decrease stands for organization getting lower profit. Also increased values of the other variables mean stock, shortage, and cycle length all will increase, and decreased values mean stock, shortage, and cycle length all will decrease.

Main contribution and practical implication

In this paper, we have introduced an alternative trade credit policy for price- and stock-dependent demand under different situations. In the real-life business world, several factors exist in inventory analysis. Some of them are

• (i) Advertisement of the product.

• (ii) Price and stock of the product.

• (iii) Deterioration of the product.

• (iv) Credit facility of the product.

In our proposed paper, we have combined these four factors together in a two-warehouse inventory system. We have represented this real-life problem mathematically considering probable possible cases. Due to highly nonlinear scenarios, we have used lingo 10.0 software to solve this problem. In this paper, we have incorporated all of these factors into alternative trade credit policy.

Conclusion

In this study, we have investigated a two-warehouse inventory model for deteriorating item with the credit policy approach. Demand is dependent on frequency of advertisement, price and stock. Due to the complexity, we have considered the frequency of advertisement as a constant in a year. We have described all the possible cases mathematically. We have solved two numerical examples, reported the optimal solution and winner case. We have presented this paper from the perspective of retailers. The proposed work is highly nonlinear in nature. We cannot solve the problem theoretically. Due to this situation, we have used the well-known software Lingo 10.0 to solve this problem. According to the sensitivity analysis, our proposed model is highly sensible.

Finally, this two-warehouse inventory model can be extended to other situations by considering several realistic features such as imperfect item, reliability of the product, weibull distribution deterioration, etc. Also, another realistic feature can be introduction of, e.g. trade credit (two levels or partial), in this study. Anyone can extend our proposed model by considering that the inventory costs are interval valued or fuzzy valued, and so can solved by any soft-computing technique.

Appendix

The total holding cost $C_{\text{hold}}$ over the entire cycle is given by

$$\begin{aligned} C_{\text{hold}} &= C_{\text{hr}} \int\limits_{0}^{{t_{1} }} {I_{r} (t){\text{d}}t} + C_{\text{ho}} \int\limits_{0}^{{t_{2} }} {I_{o} (t){\text{d}}t} \hfill \\ & = \frac{{C_{\text{hr}} }}{\beta }\left[ {S - W_{1} - \int\limits_{0}^{{t_{1} }} {A^{\gamma } (a - bp + cI_{r} (t)){\text{d}}t} } \right] + \frac{{C_{\text{ho}} }}{\alpha }\left[ {W_{1} - \int\limits_{{t_{1} }}^{{t_{2} }} {A^{\gamma } (a - bp + cI_{o} (t)){\text{d}}t} } \right] \hfill \\ &= C_{\text{hold1}} + C_{\text{hold2}} , \hfill \\ \end{aligned}$$

$$\begin{aligned} {\text{where}}\quad C_{\text{hold1}} &= \frac{{C_{\text{hr}} }}{\beta }\left[ {S - W_{1} - \int\limits_{0}^{{t_{1} }} {A^{\gamma } (a - bp + cI_{r} (t)){\text{d}}t} } \right] \hfill \\ &= \frac{{C_{\text{hr}} }}{\beta }\left[ {S - W_{1} - A^{\gamma } (a - bp)t_{1} - cA^{\gamma } \int\limits_{0}^{{t_{1} }} {\left( {\frac{{A^{\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}({\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} - 1)} \right){\text{d}}t} } \right] \hfill \\ &= \frac{{C_{\text{hr}} }}{\beta }\left[ {S - W_{1} - A^{\gamma } (a - bp)t_{1} - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}\left[ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} }}{{ - (\beta + cA^{\gamma } )}} - t} \right]_{0}^{{t_{1} }} } \right] \hfill \\ &= \frac{{C_{\text{hr}} }}{\beta }\left[ {S - W_{1} - A^{\gamma } (a - bp)t_{1} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}\left[ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} }}{{(\beta + cA^{\gamma } )}} + t} \right]_{0}^{{t_{1} }} } \right] \hfill \\ &= \frac{{C_{\text{hr}} }}{\beta }\left[ {S - W_{1} - A^{\gamma } (a - bp)t_{1} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}\left\{ {\frac{1}{{(\beta + cA^{\gamma } )}} - \frac{{{\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} }}{{(\beta + cA^{\gamma } )}} + t_{1} } \right\}} \right] \hfill \\ &= \frac{{C_{\text{hr}} }}{\beta }\left[ {S - W_{1} - A^{\gamma } (a - bp)t_{1} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}t_{1} } \right]. \hfill \\ \end{aligned}$$

$$\begin{aligned} {\text{and}}\quad C_{\text{hold2}} &= \frac{{C_{\text{ho}} }}{\alpha }\left[ {W_{1} - \int\limits_{{t_{1} }}^{{t_{2} }} {A^{\gamma } (a - bp + cI_{o} (t)){\text{d}}t} } \right] \hfill \\ &= \frac{{C_{\text{ho}} }}{\alpha }\left[ {W_{1} - A^{\gamma } (a - bp)(t_{2} - t_{1} ) - cA^{\gamma } \int\limits_{{t_{1} }}^{{t_{2} }} {\left( {\frac{{A^{\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}()} \right){\text{d}}t} } \right] \hfill \\ &= \frac{{C_{\text{ho}} }}{\alpha }\left[ {W_{1} - A^{\gamma } (a - bp)(t_{2} - t_{1} ) - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}\left[ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} }}{{ - (\alpha + A^{\gamma } c)}} - t} \right]_{{t_{1} }}^{{t_{2} }} } \right] \hfill \\ &= \frac{{C_{\text{ho}} }}{\alpha }\left[ {W_{1} - A^{\gamma } (a - bp)(t_{2} - t_{1} ) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}\left[ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} }}{{(\alpha + A^{\gamma } c)}} + t} \right]_{{t_{1} }}^{{t_{2} }} } \right] \hfill \\ &= \frac{{C_{\text{ho}} }}{\alpha }\left[ {W_{1} - A^{\gamma } (a - bp)(t_{2} - t_{1} ) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}\left[ {\frac{1}{{(\alpha + A^{\gamma } c)}} - \frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} }}{{(\alpha + A^{\gamma } c)}} + t_{2} - t_{1} } \right]} \right] \hfill \\ &= \frac{{C_{\text{ho}} }}{\alpha }\left[ {W_{1} - A^{\gamma } (a - bp)(t_{2} - t_{1} ) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - t_{1} )} \right] \hfill \\ \end{aligned}$$

$$\begin{aligned} \therefore C_{\text{hold}} &= \frac{{C_{\text{hr}} }}{\beta }\left[ {S - W_{1} - A^{\gamma } (a - bp)t_{1} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}t_{1} } \right] \hfill \\ &\quad + \frac{{C_{\text{ho}} }}{\alpha }\left[ {W_{1} - A^{\gamma } (a - bp)(t_{2} - t_{1} ) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - t_{1} )} \right] \hfill \\ \end{aligned}$$

Again, the total shortage cost $C_{\text{sho}}$ over the entire cycle is given by

$$\begin{aligned} C_{\text{sho}} &= - C_{b} \int\limits_{{t_{2} }}^{T} {I_{0} (t){\text{d}}t} \hfill \\ &= - C_{b} \int\limits_{{t_{2} }}^{T} {\left[ {\frac{{A^{\gamma } (a - bp)}}{\delta }\log (1 + \delta (T - t)) - R} \right]{\text{d}}t} \hfill \\ &= C_{b} \int\limits_{{t_{2} }}^{T} {\left[ {R - \frac{{A^{\gamma } (a - bp)}}{\delta }\log (1 + \delta (T - t))} \right]{\text{d}}t} \hfill \\ &= C_{b} \left[ {R(T - t_{2} ) - \frac{{A^{\gamma } (a - bp)}}{\delta }\int\limits_{{t_{2} }}^{T} {\log (1 + \delta (T - t)){\text{d}}t} } \right] \hfill \\ &= C_{b} \left[ {R(T - t_{2} ) - \frac{{A^{\gamma } (a - bp)}}{\delta } \cdot \Delta } \right], \hfill \\ \end{aligned}$$

$$\begin{aligned} {\text{where}}\quad \Delta &= \int\limits_{{t_{2} }}^{T} {\log (1 + \delta (T - t)){\text{d}}t} \hfill \\ &= [t\log (1 + \delta (T - t))]_{{t_{2} }}^{T} - \int\limits_{{t_{2} }}^{T} {\frac{ - \delta \,t}{1 + \delta (T - t)}{\text{d}}t} \hfill \\ &= - t_{2} \log (1 + \delta (T - t_{2} )) - \int\limits_{{t_{2} }}^{T} {\frac{1 + \delta (T - t) - (1 + \delta T)}{1 + \delta (T - t)}{\text{d}}t} \hfill \\ &= - t_{2} \log (1 + \delta (T - t_{2} )) - \int\limits_{{t_{2} }}^{T} {\left[ {1 - \frac{(1 + \delta T)}{1 + \delta (T - t)}} \right]{\text{d}}t} \hfill \\ & = - t_{2} \log (1 + \delta (T - t_{2} )) - \left[ {t - \frac{{(1 + \delta T)\log \left( {1 + \delta (T - t)} \right)}}{ - \delta }} \right]_{{t_{2} }}^{T} \hfill \\ & = - t_{2} \log (1 + \delta (T - t_{2} )) - \left[ {t + \frac{{(1 + \delta T)\log \left( {1 + \delta (T - t)} \right)}}{\delta }} \right]_{{t_{2} }}^{T} \hfill \\ & = - t_{2} \log (1 + \delta (T - t_{2} )) - \left[ {(T - t_{2} ) + \frac{(1 + \delta T)}{\delta }\{ - \log (1 + \delta (T - t_{2} ))\} } \right] \hfill \\ & = - t_{2} \log (1 + \delta (T - t_{2} )) - (T - t_{2} ) + \frac{(1 + \delta T)}{\delta }\log (1 + \delta (T - t_{2} )) \hfill \\ & = \frac{1}{\delta }\left[ { - \delta (T - t_{2} ) + (1 + \delta (T - t_{2} ))\log (1 + \delta (T - t_{2} ))} \right] \hfill \\ \end{aligned}$$

$$\begin{aligned} \therefore C_{sho} &= C_{b} \left[ {R(T - t_{2} ) - \frac{{A^{\gamma } (a - bp)}}{\delta }.\frac{1}{\delta }[ - \delta (T - t_{2} ) + (1 + \delta (T - t_{2} ))\log (1 + \delta (T - t_{2} ))]} \right] \hfill \\ &= C_{b} \left[ {R(T - t_{2} ) + \frac{{A^{\gamma } (a - bp)}}{{\delta^{2} }}[\delta (T - t_{2} ) - (1 + \delta (T - t_{2} ))\log (1 + \delta (T - t_{2} ))]} \right]. \hfill \\ \end{aligned}$$

The total deterioration cost (DC) during the cyclic length is

$$\begin{aligned} {\text{DC}} &= C_{d} \left[ {S - W_{1} - \int\limits_{0}^{{t_{1} }} {A^{\gamma } (a - bp + cI_{r} (t)){\text{d}}t} } \right] + C_{d} \left[ {W_{1} - \int\limits_{{t_{1} }}^{{t_{2} }} {A^{\gamma } (a - bp + cI_{o} (t)){\text{d}}t} } \right] \hfill \\ &= C_{d} \left[ {S - W_{1} - A^{\gamma } (a - bp)t_{1} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}t_{1} } \right] \hfill \\ &\quad + C_{d} \left[ {W_{1} - A^{\gamma } (a - bp)(t_{2} - t_{1} ) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - t_{1} )} \right]. \hfill \\ \end{aligned}$$

Since the shortages are not fully backlogged, there are some losses in sales and the corresponding lost sale cost (LSC) during the entire cyclic is

$$\begin{aligned} {\text{LSC}} & = C_{l} \int\limits_{{t_{2} }}^{T} {\left( {1 - \frac{1}{1 + \delta (T - t)}} \right)D{\text{d}}t} \hfill \\ &= C_{l} A^{\gamma } (a - bp)\int\limits_{{t_{2} }}^{T} {\left( {1 - \frac{1}{1 + \delta (T - t)}} \right){\text{d}}t} \hfill \\ &= C_{l} A^{\gamma } (a - bp)\left[ {t - \frac{\log (1 + \delta (T - t))}{ - \delta }} \right]_{{t_{2} }}^{T} \hfill \\ &= C_{l} A^{\gamma } (a - bp)\left[ {t + \frac{\log (1 + \delta (T - t))}{\delta }} \right]_{{t_{2} }}^{T} \hfill \\ &= C_{l} A^{\gamma } (a - bp)\left[ {(T - t_{2} ) - \frac{1}{\delta }\log (1 + \delta (T - t_{2} ))} \right]. \hfill \\ \end{aligned}$$

Scenario 1: $0 < M \le t_{1}$

Due to sale and interest earned, the total accumulated amount is given by

$$\begin{aligned} U_{1} &= p\int\limits_{0}^{M} {D{\text{d}}t} + pI_{e} \int\limits_{0}^{M} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } + pR(1 + I_{e} M) \hfill \\ & = {\text{Term}}1 + {\text{Term}}2 + pR(1 + I_{e} M), \hfill \\ \end{aligned}$$

where

$$\begin{aligned} {\text{Term}}1 &= p\int\limits_{0}^{M} {D{\text{d}}t} \hfill \\ &= p\int\limits_{0}^{M} {[A^{\gamma } (a - bp + cI_{r} (t))]{\text{d}}t} \hfill \\ &= p\left[ {MA^{\gamma } (a - bp) + cA^{\gamma } \int\limits_{0}^{M} {\left[ {\frac{{A^{\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}({\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} - 1)} \right]{\text{d}}t} } \right] \hfill \\ &= p\left[ {MA^{\gamma } (a - bp) + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}\left[ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} }}{{ - (\beta + cA^{\gamma } )}} - t} \right]_{0}^{M} } \right] \hfill \\ &= p\left[ {MA^{\gamma } (a - bp) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}\left[ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} }}{{(\beta + cA^{\gamma } )}} + t} \right]_{0}^{M} } \right] \hfill \\ &= p\left[ {MA^{\gamma } (a - bp) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}\left[ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} }}{{(\beta + cA^{\gamma } )}} - \frac{{{\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} }}{{(\beta + cA^{\gamma } )}} + M} \right]} \right] \hfill \\ &= p\left[ {MA^{\gamma } (a - bp) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}M} \right] \hfill \\ \end{aligned}$$

$$\begin{aligned} {\text{Term}}2 &= pI_{e} \int\limits_{0}^{M} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } = pI_{e} \int\limits_{0}^{M} {\left\{ {\int\limits_{0}^{t} {D{\text{d}}u} } \right\}} {\text{d}}t = pI_{e} \int\limits_{0}^{M} {\left\{ {\int\limits_{0}^{t} {A^{\gamma } (a - bp + cI_{r} (u)){\text{d}}u} } \right\}} {\text{d}}t \hfill \\ &= pI_{e} \int\limits_{0}^{M} {\left[ {A^{\gamma } (a - bp)t + cA^{\gamma } \int\limits_{0}^{t} {\frac{{A^{\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}} \{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - u)}} - 1\} {\text{d}}u} \right]} {\text{d}}t \hfill \\ &= pI_{e} \int\limits_{0}^{M} {\left[ {A^{\gamma } (a - bp)t + \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\left[ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - u)}} }}{{ - (\beta + cA^{\gamma } )}} - u} \right]_{0}^{t} } \right]} {\text{d}}t \hfill \\ &= pI_{e} \int\limits_{0}^{M} {\left[ {A^{\gamma } (a - bp)t - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\left[ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - u)}} }}{{(\beta + cA^{\gamma } )}} + u} \right]_{0}^{t} } \right]} {\text{d}}t \hfill \\ &= pI_{e} \int\limits_{0}^{M} {\left[ {A^{\gamma } (a - bp)t - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\left[ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} }}{{(\beta + cA^{\gamma } )}} - \frac{{{\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} }}{{(\beta + cA^{\gamma } )}} + t} \right]} \right]} {\text{d}}t \hfill \\ &= pI_{e} \int\limits_{0}^{M} {\left[ {A^{\gamma } (a - bp)t - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}e^{{(\beta + cA^{\gamma } )(t_{1} - t)}} + \frac{{cA^{2\gamma } (a - bp)e^{{(\beta + cA^{\gamma } )t_{1} }} }}{{(\beta + cA^{\gamma } )^{2} }} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}t} \right]} {\text{d}}t \hfill \\ &= pI_{e} \left[ {\frac{{A^{\gamma } (a - bp)t^{2} }}{2} - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} }}{{ - (\beta + cA^{\gamma } )}} + \frac{{cA^{2\gamma } (a - bp){\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} }}{{(\beta + cA^{\gamma } )^{2} }}t - \frac{{cA^{2\gamma } (a - bp)t^{2} }}{{2(\beta + cA^{\gamma } )}}} \right]_{0}^{M} \hfill \\ &= pI_{e} \left[ \begin{aligned} \frac{{A^{\gamma } (a - bp)M^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{3} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} \hfill \\ &\quad + \frac{{cMA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} - \frac{{cA^{2\gamma } (a - bp)M^{2} }}{{2(\beta + cA^{\gamma } )}} \hfill \\ \end{aligned} \right]. \hfill \\ \end{aligned}$$

Therefore,

$$\begin{aligned} U_{1} &= p\left[ {MA^{\gamma } (a - bp) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)}}M} \right] \hfill \\ &\quad + pI_{e} \left[ \begin{aligned} \frac{{A^{\gamma } (a - bp)M^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{3} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} \hfill \\ &quad + \frac{{cMA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}e^{{(\beta + cA^{\gamma } )t_{1} }} - \frac{{cA^{2\gamma } (a - bp)M^{2} }}{{2(\beta + cA^{\gamma } )}} \hfill \\ \end{aligned} \right] + pR(1 + I_{e} M), \hfill \\ \end{aligned},$$

where

$$\begin{aligned} p\int\limits_{M}^{{t_{2} }} {D{\text{d}}t} &= p\left[ {\int\limits_{M}^{{t_{1} }} {D{\text{d}}t} + \int\limits_{{t_{1} }}^{{t_{2} }} {D{\text{d}}t} } \right] = p\left[ {\int\limits_{M}^{{t_{1} }} {\{ A^{\gamma } (a - bp + cI_{r} (t))\} {\text{d}}t} + \int\limits_{{t_{1} }}^{{t_{2} }} {\{ A^{\gamma } (a - bp + cI_{0} (t))\} {\text{d}}t} } \right] \hfill \\ &= p\left[ \begin{aligned} A^{\gamma } (a - bp)(t_{1} - M) + cA^{\gamma } \int\limits_{M}^{{t_{1} }} {\frac{{A^{\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} - 1\} {\text{d}}t} + A^{\gamma } (a - bp)(t_{2} - t_{1} ) \hfill \\ &\quad + cA^{\gamma } \int\limits_{{t_{1} }}^{{t_{2} }} {\left( {\frac{{A^{\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}({\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} - 1)} \right){\text{d}}t} \hfill \\ \end{aligned} \right] \hfill \\ &= p\left[ {A^{\gamma } (a - bp)(t_{2} - M) + \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\left[ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} }}{{ - (\beta + cA^{\gamma } )}} - t} \right]_{M}^{{t_{1} }} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}\left[ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} }}{{ - (\alpha + A^{\gamma } c)}} - t} \right]_{{t_{1} }}^{{t_{2} }} } \right] \hfill \\ &= p\left[ \begin{aligned} A^{\gamma } (a - bp)(t_{2} - M) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}\left\{ {1 - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} } \right\} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}(t_{1} - M) \hfill \\ &\quad - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - t_{1} ) \hfill \\ \end{aligned} \right] \hfill \\ \end{aligned}$$

and

$$\begin{aligned} pI_{e} \int\limits_{M}^{{t_{2} }} {\int\limits_{M}^{t} D {\text{d}}u{\text{d}}t} &= pI_{e} \left[ {\int\limits_{M}^{{t_{1} }} {\int\limits_{M}^{t} D {\text{d}}u{\text{d}}t + \int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{{t_{1} }}^{t} D {\text{d}}u{\text{d}}t} } } \right] \hfill \\ &= pI_{e} \left[ {\int\limits_{M}^{{t_{1} }} {\int\limits_{M}^{t} {\{ A^{\gamma } (a - bp + cI_{r} (u))\} } {\text{d}}u{\text{d}}t + \int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{{t_{1} }}^{t} {\{ A^{\gamma } (a - bp + cI_{0} (u))\} } {\text{d}}u{\text{d}}t} } } \right] \hfill \\ &= pI_{e} [\Delta_{1} + \Delta_{2} ], \hfill \\ \end{aligned},$$

where

$$\begin{aligned} \Delta_{1} &= \int\limits_{M}^{{t_{1} }} {\int\limits_{M}^{t} {\{ A^{\gamma } (a - bp + cI_{r} (u))\} } {\text{d}}u{\text{d}}t} \hfill \\ &= \int\limits_{M}^{{t_{1} }} {\left[ {A^{\gamma } (a - bp)(t - M) + cA^{\gamma } \int\limits_{M}^{t} {\left\{ {\frac{{A^{\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - u)}} - 1\} } \right\}} {\text{d}}u} \right]{\text{d}}t} \hfill \\ &= \int\limits_{M}^{{t_{1} }} {\left[ {A^{\gamma } (a - bp)(t - M) + \frac{{cA^{2\gamma } (a - bp)}}{{\beta + A^{\gamma } c}}\left[ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - u)}} }}{{ - (\beta + cA^{\gamma } )}} - u} \right]_{M}^{t} } \right]{\text{d}}t} \hfill \\ &= \int\limits_{M}^{{t_{1} }} {\left[ {A^{\gamma } (a - bp)(t - M) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}(t - M)} \right]{\text{d}}t} \hfill \\ &= \left[ {A^{\gamma } (a - bp)\left( {\frac{{t^{2} }}{2} - Mt} \right) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\left\{ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} }}{{ - (\beta + A^{\gamma } c)}} - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} \cdot t} \right\} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\left( {\frac{{t^{2} }}{2} - Mt} \right)} \right]_{M}^{{t_{1} }} \hfill \\ &= \left[ \begin{aligned} A^{\gamma } (a - bp)\left( {\frac{{t_{1}^{2} }}{2} - Mt_{1} - \frac{{M^{2} }}{2} + M^{2} } \right) + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{3} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} \} \hfill \\ &\quad + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} (t_{1} - M) - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\left( {\frac{{t_{1}^{2} }}{2} - Mt_{1} - \frac{{M^{2} }}{2} + M^{2} } \right) \hfill \\ \end{aligned} \right] \hfill \\ &= \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(t_{1} - M)^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{3} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} \} \hfill \\ + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} (t_{1} - M) - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\frac{{(t_{1} - M)^{2} }}{2} \hfill \\ \end{aligned} \right] \hfill \\ &= \int\limits_{{t_{1} }}^{{t_{2} }} {\left[ {A^{\gamma } (a - bp)(t - t_{1} ) + cA^{\gamma } \int\limits_{{t_{1} }}^{t} {\left\{ {\frac{{A^{\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - u)}} - 1\} } \right\}} {\text{d}}u} \right]{\text{d}}t} \hfill \\ &= \int\limits_{{t_{1} }}^{{t_{2} }} {\left[ {A^{\gamma } (a - bp)(t - t_{1} ) + \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left[ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - u)}} }}{{ - (\alpha + cA^{\gamma } )}} - u} \right]_{{t_{1} }}^{t} } \right]{\text{d}}t} \hfill \\ &= \int\limits_{{t_{1} }}^{{t_{2} }} {\left[ {A^{\gamma } (a - bp)(t - t_{1} ) - \, \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}(t - t_{1} )} \right]} {\text{d}}t \hfill \\ &= \left[ {A^{\gamma } (a - bp)\left( {\frac{{t^{2} }}{2} - tt_{1} } \right) - \, \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}\left\{ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} }}{{ - (\alpha + cA^{\gamma } )}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot t} \right\} - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left( {\frac{{t^{2} }}{2} - tt_{1} } \right)} \right]_{{t_{1} }}^{{t_{2} }} \hfill \\ &= \left[ \begin{aligned} A^{\gamma } (a - bp)\left( {\frac{{t_{2}^{2} }}{2} - t_{2} t_{1} - \frac{{t_{1}^{2} }}{2} + t_{1}^{2} } \right) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot (t_{2} - t_{1} ) \hfill \\ - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left( {\frac{{t_{2}^{2} }}{2} - t_{2} t_{1} - \frac{{t_{1}^{2} }}{2} + t_{1}^{2} } \right) \hfill \\ \end{aligned} \right] \hfill \\ &= \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(t_{2} - t_{1} )^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot (t_{2} - t_{1} ) \hfill \\ &\quad - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\frac{{(t_{2} - t_{1} )^{2} }}{2} \hfill \\ \end{aligned} \right]. \hfill \\ \end{aligned}.$$

Therefore,

$$\begin{aligned} pI_{e} \int\limits_{M}^{{t_{2} }} {\int\limits_{M}^{t} D {\text{d}}u{\text{d}}t} &= pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(t_{1} - M)^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{3} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} \} \hfill \\ \qquad + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} (t_{1} - M) - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\frac{{(t_{1} - M)^{2} }}{2} \hfill \\ \end{aligned} \right] \hfill \\ &\quad + pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(t_{2} - t_{1} )^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot (t_{2} - t_{1} ) \hfill \\ &\quad - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\frac{{(t_{2} - t_{1} )^{2} }}{2} \hfill \\ \end{aligned} \right] \hfill \\ \end{aligned}$$

Case 1.2.1: Partial payment is permitted at time $t = M$

The total amount available to the retailer:

$$\begin{aligned} &= {\text{Selling}}\;{\text{amount}}\;{\text{during}}\;{\text{the}}\;{\text{interval}}\;\left[ {M,B} \right] + {\text{the}}\;{\text{interest}}\;{\text{earned}} \hfill \\ & = p\int\limits_{M}^{B} {D{\text{d}}t} + pI_{e} \int\limits_{M}^{B} {\int\limits_{M}^{t} D {\text{d}}u{\text{d}}t} \hfill \\ & = p\int\limits_{M}^{B} {A^{\gamma } (a - bp + cI_{r} (t)){\text{d}}t} + pI_{e} \int\limits_{M}^{B} {\left\{ {\int\limits_{M}^{t} {A^{\gamma } (a - bp + cI_{r} (u))} {\text{d}}u} \right\}{\text{d}}t} \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(B - M) + cA^{\gamma } \int\limits_{M}^{B} {\frac{{A^{\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} - 1\} {\text{d}}t} } \right] \hfill \\ & \quad + pI_{e} \int\limits_{M}^{B} {\left[ {A^{\gamma } (a - bp)(t - M) + cA^{\gamma } \int\limits_{M}^{t} {\frac{{A^{\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - u)}} - 1\} } {\text{d}}u} \right]{\text{d}}t} \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(B - M) + \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\left[ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} }}{{ - (\beta + cA^{\gamma } )}} - t} \right]_{M}^{B} } \right] \hfill \\ & \quad + pI_{e} \int\limits_{M}^{B} {\left[ {A^{\gamma } (a - bp)(t - M) + \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\left[ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - u)}} }}{{ - (\beta + cA^{\gamma } )}} - u} \right]_{M}^{t} } \right]{\text{d}}t} \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(B - M) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}(B - M)} \right] \hfill \\ & \quad + pI_{e} \int\limits_{M}^{B} {\left[ {A^{\gamma } (a - bp)(t - M) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}(t - M)} \right]} {\text{d}}t \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(B - M) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}\left\{ {{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} } \right\} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}(B - M)} \right] \hfill \\ & \quad + pI_{e} \left[ {A^{\gamma } (a - bp)\left( {\frac{{t^{2} }}{2} - Mt} \right) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}\left\{ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} }}{{ - (\beta + cA^{\gamma } )}} - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} .t} \right\} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\left( {\frac{{t^{2} }}{2} - Mt} \right)} \right]_{M}^{B} \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(B - M) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}(B - M)} \right] \hfill \\ & \quad + pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\left( {\frac{{B^{2} }}{2} - MB - \frac{{M^{2} }}{2} + M^{2} } \right) + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{3} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} \} \hfill \\ \qquad + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} (B - M) - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\left( {\frac{{B^{2} }}{2} - MB - \frac{{M^{2} }}{2} + M^{2} } \right) \hfill \\ \end{aligned} \right] \hfill \\ &= p\left[ {A^{\gamma } (a - bp)(B - M) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}(B - M)} \right] \hfill \\ & \quad + pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(B - M)^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{3} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} \} \hfill \\ \qquad + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - M)}} (B - M) - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\frac{{(B - M)^{2} }}{2} \hfill \\ \end{aligned} \right] \hfill \\ \end{aligned}$$

$$\begin{aligned} X & = < {\text{total selling price during the interval}}\;\left[ {B,t_{2} } \right] > \hfill \\ & \quad + < {\text{interest earned during the interval}}\;\left[ {B,t_{2} } \right] > \hfill \\ & \quad + < {\text{interest earned during the interval}}\;[t_{2} ,T] > - {\text{TC}} \hfill \\ \end{aligned}$$

$${\text{i}}.{\text{e}}.,\quad X = \left\{ {p\int\limits_{B}^{{t_{2} }} {D{\text{d}}t} + pI_{e} \int\limits_{B}^{{t_{2} }} {\int\limits_{B}^{t} D {\text{d}}u{\text{d}}t} } \right\}\{ 1 + I_{e} (T - t_{2} )\} - {\text{TC,}}$$

where

$$p\int\limits_{B}^{{t_{2} }} {D{\text{d}}t} = p\left[ \begin{aligned} A^{\gamma } (a - bp)(t_{2} - B) - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}(t_{1} - B) \hfill \\ & \quad - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - t_{1} ) \hfill \\ \end{aligned} \right]$$

and

$$\begin{aligned} pI_{e} \int\limits_{B}^{{t_{2} }} {\int\limits_{B}^{t} D {\text{d}}u{\text{d}}t} & = pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(t_{1} - B)^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{3} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} \} \hfill \\ \qquad + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - B)}} (t_{1} - B) - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\frac{{(t_{1} - B)^{2} }}{2} \hfill \\ \end{aligned} \right] \hfill \\ & \quad+ pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(t_{2} - t_{1} )^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot (t_{2} - t_{1} ) \hfill \\ \qquad - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\frac{{(t_{2} - t_{1} )^{2} }}{2} \hfill \\ \end{aligned} \right] \hfill \\ \end{aligned}$$

Scenario 2: $t_{1} < M \le t_{2}$

In this case, the total revenue earned by the retailer up to $t = M$ is given by

$$\begin{aligned} U_{2} & = p\int\limits_{0}^{M} {D{\text{d}}t} + pI_{e} \int\limits_{0}^{M} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } + pR(1 + I_{e} M) \hfill \\ & = {\text{Term1}} + {\text{Term2}} + pR(1 + I_{e} M), \hfill \\ \end{aligned},$$

where

$$\begin{aligned} {\text{Term1}} & = p\int\limits_{0}^{M} {D{\text{d}}t} = p\left[ {\int\limits_{0}^{{t_{1} }} {D{\text{d}}t} + \int\limits_{{t_{1} }}^{M} {D{\text{d}}t} } \right] = p\left[ {\int\limits_{0}^{{t_{1} }} {A^{\gamma } (a - bp + cI_{r} (t)){\text{d}}t} + \int\limits_{{t_{1} }}^{M} {A^{\gamma } (a - bp + cI_{o} (t)){\text{d}}t} } \right] \hfill \\ & = p\left[ \begin{aligned} A^{\gamma } (a - bp)t_{1} + cA^{\gamma } \int\limits_{0}^{{t_{1} }} {\frac{{A^{\gamma } (a - bp)}}{{\beta + A^{\gamma } c}}} \{ {\text{e}}^{{(\beta + A^{\gamma } c)(t_{1} - t)}} - 1\} {\text{d}}t \hfill \\ \qquad + A^{\gamma } (a - bp)(M - t_{1} ) + cA^{\gamma } \int\limits_{{t_{1} }}^{M} {\frac{{A^{\gamma } (a - bp)}}{{\alpha + A^{\gamma } c}}\{ {\text{e}}^{{(\alpha + A^{\gamma } c)(t_{2} - t)}} - 1\} {\text{d}}t} \hfill \\ \end{aligned} \right] \hfill \\ & = p\left[ \begin{aligned} A^{\gamma } (a - bp)t_{1} + \frac{{cA^{2\gamma } (a - bp)}}{{\beta + A^{\gamma } c}}\left[ {\frac{{{\text{e}}^{{(\beta + A^{\gamma } c)(t_{1} - t)}} }}{{ - (\beta + A^{\gamma } c)}} - t} \right]_{0}^{{t_{1} }} \hfill \\ \qquad+ A^{\gamma } (a - bp)(M - t_{1} ) + \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + A^{\gamma } c}}\left[ {\frac{{{\text{e}}^{{(\alpha + A^{\gamma } c)(t_{2} - t)}} }}{{ - (\alpha + A^{\gamma } c)}} - t} \right]_{{t_{1} }}^{M} \hfill \\ \end{aligned} \right] \hfill \\ & = p\left[ \begin{aligned} A^{\gamma } (a - bp)t_{1} - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\beta + A^{\gamma } c)t_{1} }} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + A^{\gamma } c}} \cdot t_{1} \hfill \\ \qquad + A^{\gamma } (a - bp)(M - t_{1} ) - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ {\text{e}}^{{(\alpha + A^{\gamma } c)(t_{2} - M)}} - {\text{e}}^{{(\alpha + A^{\gamma } c)(t_{2} - t_{1} )}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + A^{\gamma } c}}(M - t_{1} ) \hfill \\ \end{aligned} \right] \hfill \\ \end{aligned}$$

$$\begin{aligned} {\text{Term2}} & = pI_{e} \int\limits_{0}^{M} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } = pI_{e} \left[ {\int\limits_{0}^{{t_{1} }} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } + \int\limits_{{t_{1} }}^{M} {\int\limits_{{t_{1} }}^{t} {D{\text{d}}u{\text{d}}t} } } \right] \hfill \\ & = pI_{e} \left[ {\int\limits_{0}^{{t_{1} }} {\left\{ {\int\limits_{0}^{t} {A^{\gamma } (a - bp + cI_{r} (u)){\text{d}}u} } \right\}} {\text{d}}t + \int\limits_{{t_{1} }}^{M} {\left\{ {\int\limits_{{t_{1} }}^{t} {A^{\gamma } (a - bp + cI_{o} (u) ) {\text{d}}u} } \right\}{\text{d}}t} } \right] \hfill \\ & = pI_{e} \left[ {\Delta_{1} + \Delta_{2} } \right], \hfill \\ \end{aligned},$$

where

$$\begin{aligned} \Delta_{1} & = \int\limits_{0}^{{t_{1} }} {\left\{ {\int\limits_{0}^{t} {A^{\gamma } (a - bp + cI_{r} (u)){\text{d}}u} } \right\}} {\text{d}}t \hfill \\ & = \int\limits_{0}^{{t_{1} }} {\left[ {A^{\gamma } (a - bp)t + cA^{\gamma } \int\limits_{0}^{t} {\frac{{A^{\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - u)}} - 1\} {\text{d}}u} } \right]} {\text{d}}t \hfill \\ & = \int\limits_{0}^{{t_{1} }} {\left[ {A^{\gamma } (a - bp)t + \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\left[ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - u)}} }}{{ - (\beta + cA^{\gamma } )}} - u} \right]_{0}^{t} } \right]} {\text{d}}t \hfill \\ & = \int\limits_{0}^{{t_{1} }} {\left[ {A^{\gamma } (a - bp)t - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}\{ {\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}t} \right]} {\text{d}}t \hfill \\ & = \left[ {A^{\gamma } (a - bp) \cdot \frac{{t^{2} }}{2} - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}\left\{ {\frac{{{\text{e}}^{{(\beta + cA^{\gamma } )(t_{1} - t)}} }}{{ - (\beta + cA^{\gamma } )}} - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \cdot t} \right\} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\frac{{t^{2} }}{2}} \right]_{0}^{{t_{1} }} \hfill \\ & = \left[ {A^{\gamma } (a - bp)\frac{{t_{1}^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \cdot t_{1} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\frac{{t_{1}^{2} }}{2}} \right] \hfill \\ \hfill \\ \end{aligned}$$

$$\begin{aligned} \Delta_{2} & = \int\limits_{{t_{1} }}^{M} {\left\{ {\int\limits_{{t_{1} }}^{t} {A^{\gamma } (a - bp + cI_{o} (u)){\text{d}}u} } \right\}{\text{d}}t} \hfill \\ & = \int\limits_{{t_{1} }}^{M} {\left[ {A^{\gamma } (a - bp)(t - t_{1} ) + cA^{\gamma } \left\{ {\int\limits_{{t_{1} }}^{t} {\left\{ {\frac{{A^{\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - u)}} - 1\} } \right\}} {\text{d}}u} \right\}} \right]{\text{d}}t} \hfill \\ & = \int\limits_{{t_{1} }}^{M} {\left[ {A^{\gamma } (a - bp)(t - t_{1} ) + \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left[ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - u)}} }}{{ - (\alpha + cA^{\gamma } )}} - u} \right]_{{t_{1} }}^{t} } \right]{\text{d}}t} \hfill \\ & = \int\limits_{{t_{1} }}^{M} {\left[ {A^{\gamma } (a - bp)(t - t_{1} ) - \, \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}(t - t_{1} )} \right]{\text{d}}t} \hfill \\ & = \left[ {A^{\gamma } (a - bp)\left( {\frac{{t^{2} }}{2} - tt_{1} } \right) - \, \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}\left\{ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} }}{{ - (\alpha + cA^{\gamma } )}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot t} \right\} - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left( {\frac{{t^{2} }}{2} - tt_{1} } \right)} \right]_{{t_{1} }}^{M} \hfill \\ & = \left[ \begin{aligned} A^{\gamma } (a - bp)\left( {\frac{{M^{2} }}{2} - Mt_{1} - \frac{{t_{1}^{2} }}{2} + t_{1}^{2} } \right) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} \hfill \\ \qquad + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot (M - t_{1} ) - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left( {\frac{{M^{2} }}{2} - Mt_{1} - \frac{{t_{1}^{2} }}{2} + t_{1}^{2} } \right) \hfill \\ \end{aligned} \right] \hfill \\ & = \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(M - t_{1} )^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} \hfill \\ \qquad + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot (M - t_{1} ) - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\frac{{(M - t_{1} )^{2} }}{2} \hfill \\ \end{aligned} \right]. \hfill \\ \end{aligned}.$$

Therefore,

$${\text{Term2}} = pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{t_{1}^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \cdot t_{1} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\frac{{t_{1}^{2} }}{2} \hfill \\ \qquad + A^{\gamma } (a - bp)\frac{{(M - t_{1} )^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} \hfill \\ \qquad + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot (M - t_{1} ) - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\frac{{(M - t_{1} )^{2} }}{2} \hfill \\ \end{aligned} \right].$$

Scenario 2.1: $U_{2} \ge C_{p} (S + R)$

$X =$ < excess amount after paying the amount to the supplier >, + <i nterest earned for the rest amount during the interval $[M,T]$ >, + <t otal selling price during the interval $[M,t_{2} ]$ >, + <i nterest earned during the interval $[M,t_{2} ]$ >, + <i nterest earned during the interval $[t_{2} ,T]$ > $- {\text{TC}}$

$${\text{i}}.{\text{e}}.,\quad X = \{ U_{2} - C_{p} (S + R)\} \{ 1 + I_{e} (T - M)\} + \left\{ {p\int\limits_{M}^{{t_{2} }} {D{\text{d}}t} + pI_{e} \int\limits_{M}^{{t_{2} }} {\int\limits_{M}^{t} D {\text{d}}u{\text{d}}t} } \right\}\{ 1 + I_{e} (T - t_{2} )\} - {\text{TC,}}$$

where

$$\begin{aligned} p\int\limits_{M}^{{t_{2} }} {D{\text{d}}t} & = p\left[ {\int\limits_{M}^{{t_{2} }} {\{ A^{\gamma } (a - bp + cI_{0} (t))\} {\text{d}}t} } \right] \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(t_{2} - M) + cA^{\gamma } \int\limits_{M}^{{t_{2} }} {\left( {\frac{{A^{\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}({\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} - 1)} \right){\text{d}}t} } \right] \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(t_{2} - M) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}\left[ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} }}{{ - (\alpha + A^{\gamma } c)}} - t} \right]_{M}^{{t_{2} }} } \right] \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(t_{2} - M)\, - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - M)} \right] \hfill \\ \end{aligned}$$

and

$$\begin{aligned} pI_{e} \int\limits_{M}^{{t_{2} }} {\int\limits_{M}^{t} D {\text{d}}u{\text{d}}t} & = pI_{e} \left[ {\int\limits_{M}^{{t_{2} }} {\left\{ {\int\limits_{M}^{t} {\{ A^{\gamma } (a - bp + cI_{0} (u))\} } {\text{d}}u} \right\}{\text{d}}t} } \right] \hfill \\ & = pI_{e} \int\limits_{M}^{{t_{2} }} {\left[ {A^{\gamma } (a - bp)(t - M) + cA^{\gamma } \int\limits_{M}^{t} {\left\{ {\frac{{A^{\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - u)}} - 1\} } \right\}} {\text{d}}u} \right]{\text{d}}t} \hfill \\ & = pI_{e} \int\limits_{M}^{{t_{2} }} {\left[ {A^{\gamma } (a - bp)(t - M) + \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left[ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - u)}} }}{{ - (\alpha + cA^{\gamma } )}} - u} \right]_{M}^{t} } \right]{\text{d}}t} \hfill \\ & = pI_{e} \int\limits_{M}^{{t_{2} }} {\left[ {A^{\gamma } (a - bp)(t - M) - \, \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}(t - M)} \right]} {\text{d}}t \hfill \\ & = pI_{e} \left[ {A^{\gamma } (a - bp)\left( {\frac{{t^{2} }}{2} - tM} \right) - \, \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}\left\{ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} }}{{ - (\alpha + cA^{\gamma } )}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} .t} \right\} - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left( {\frac{{t^{2} }}{2} - tM} \right)} \right]_{M}^{{t_{2} }} \hfill \\ & = pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\left( {\frac{{t_{2}^{2} }}{2} - t_{2} M - \frac{{M^{2} }}{2} + M^{2} } \right) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} \} \hfill \\ \qquad + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} .(t_{2} - M) - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left( {\frac{{t_{2}^{2} }}{2} - t_{2} M - \frac{{M^{2} }}{2} + M^{2} } \right) \hfill \\ \end{aligned} \right] \hfill \\ & = pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(t_{2} - M)^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} \cdot (t_{2} - M) \hfill \\ \qquad - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\frac{{(t_{2} - M)^{2} }}{2} \hfill \\ \end{aligned} \right] \hfill \\ \end{aligned}$$

Case 2.2.1: Partial payment is permitted at time $t = M$.

Here the details calculation given below:

$$\begin{aligned} p\int\limits_{M}^{B} {D{\text{d}}t} & = p\left[ {\int\limits_{M}^{B} {\{ A^{\gamma } (a - bp + cI_{0} (t))\} {\text{d}}t} } \right] \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(B - M) + cA^{\gamma } \int\limits_{M}^{B} {\left( {\frac{{A^{\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}({\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} - 1)} \right){\text{d}}t} } \right] \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(B - M) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}\left[ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} }}{{ - (\alpha + A^{\gamma } c)}} - t} \right]_{M}^{B} } \right] \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(B - M)\, - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - B)}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(B - M)} \right] \hfill \\ \end{aligned}$$

and

$$\begin{aligned} pI_{e} \int\limits_{M}^{B} {\int\limits_{M}^{t} D {\text{d}}u{\text{d}}t} & = pI_{e} \left[ {\int\limits_{M}^{B} {\left\{ {\int\limits_{M}^{t} {\left\{ {A^{\gamma } (a - bp + cI_{0} (u))} \right\}} {\text{d}}u} \right\}{\text{d}}t} } \right] \hfill \\ & = pI_{e} \int\limits_{M}^{B} {\left[ {A^{\gamma } (a - bp)(t - M) + cA^{\gamma } \int\limits_{M}^{t} {\left\{ {\frac{{A^{\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - u)}} - 1\} } \right\}} {\text{d}}u} \right]{\text{d}}t} \hfill \\ & = pI_{e} \int\limits_{M}^{B} {\left[ {A^{\gamma } (a - bp)(t - M) + \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left[ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - u)}} }}{{ - (\alpha + cA^{\gamma } )}} - u} \right]_{M}^{t} } \right]{\text{d}}t} \hfill \\ & = pI_{e} \int\limits_{M}^{B} {\left[ {A^{\gamma } (a - bp)(t - M) - \, \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}\left\{ {{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} } \right\} - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}(t - M)} \right]} {\text{d}}t \hfill \\ & = pI_{e} \left[ {A^{\gamma } (a - bp)\left( {\frac{{t^{2} }}{2} - tM} \right) - \, \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}\left\{ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} }}{{ - (\alpha + cA^{\gamma } )}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} .t} \right\} - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left( {\frac{{t^{2} }}{2} - tM} \right)} \right]_{M}^{B} \hfill \\ & = pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\left( {\frac{{B^{2} }}{2} - BM - \frac{{M^{2} }}{2} + M^{2} } \right) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - B)}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} \} \hfill \\ \qquad+ \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} \cdot (B - M) - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left( {\frac{{B^{2} }}{2} - BM - \frac{{M^{2} }}{2} + M^{2} } \right) \hfill \\ \end{aligned} \right] \hfill \\ & = pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(B - M)^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - B)}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} \} \hfill \\ \qquad + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - M)}} \cdot (B - M) - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\frac{{(B - M)^{2} }}{2} \hfill \\ \end{aligned} \right], \hfill \\ \end{aligned}$$

where $X =$ <total selling price during the interval $[B,t_{2} ]$>, + <interest earned during the interval $[B,t_{2} ]$>, + <interest earned during the interval $[t_{2} ,T]$> $- {\text{TC}}$

$${\text{i}}.{\text{e}}.,\quad X = \left\{ {p\int\limits_{B}^{{t_{2} }} {D\,dt} + pI_{e} \int\limits_{B}^{{t_{2} }} {\int\limits_{B}^{t} D {\text{d}}u{\text{d}}t} } \right\}\{ 1 + I_{e} (T - t_{2} )\} - {\text{TC,}}$$

where

$$\begin{aligned} p\int\limits_{B}^{{t_{2} }} {D{\text{d}}t} &= p\left[ {\int\limits_{B}^{{t_{2} }} {\{ A^{\gamma } (a - bp + cI_{0} (t))\} {\text{d}}t} } \right] \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(t_{2} - B) + cA^{\gamma } \int\limits_{B}^{{t_{2} }} {\left( {\frac{{A^{\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}({\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} - 1)} \right){\text{d}}t} } \right] \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(t_{2} - B) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}\left[ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} }}{{ - (\alpha + A^{\gamma } c)}} - t} \right]_{B}^{{t_{2} }} } \right] \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(t_{2} - B)\, - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - B)}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - B)} \right] \hfill \\ \end{aligned}$$

and

$$\begin{aligned} pI_{e} \int\limits_{B}^{{t_{2} }} {\int\limits_{B}^{t} D du\,dt} & = pI_{e} \left[ {\int\limits_{B}^{{t_{2} }} {\left\{ {\int\limits_{B}^{t} {\left\{ {A^{\gamma } (a - bp + cI_{0} (u))} \right\}} {\text{d}}u} \right\}{\text{d}}t} } \right] \hfill \\ & = pI_{e} \int\limits_{B}^{{t_{2} }} {\left[ {A^{\gamma } (a - bp)(t - B) + cA^{\gamma } \int\limits_{B}^{t} {\left\{ {\frac{{A^{\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - u)}} - 1\} } \right\}} {\text{d}}u} \right]{\text{d}}t} \hfill \\ & = pI_{e} \int\limits_{B}^{{t_{2} }} {\left[ {A^{\gamma } (a - bp)(t - B) + \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left[ {\frac{{{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - u)}} }}{{ - (\alpha + cA^{\gamma } )}} - u} \right]_{B}^{t} } \right]{\text{d}}t} \hfill \\ & = pI_{e} \int\limits_{B}^{{t_{2} }} {\left[ {A^{\gamma } (a - bp)(t - B) - \, \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}\left\{ {{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - B)}} } \right\} - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}(t - B)} \right]} {\text{d}}t \hfill \\ & = pI_{e} \left[ {A^{\gamma } (a - bp)\left( {\frac{{t^{2} }}{2} - tB} \right) - \, \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}\left\{ {\frac{{e^{{(\alpha + cA^{\gamma } )(t_{2} - t)}} }}{{ - (\alpha + cA^{\gamma } )}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - B)}} \cdot t} \right\} - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left( {\frac{{t^{2} }}{2} - tB} \right)} \right]_{B}^{{t_{2} }} \hfill \\ & = pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\left( {\frac{{t_{2}^{2} }}{2} - t_{2} B - \frac{{B^{2} }}{2} + B^{2} } \right) + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - B)}} \} \hfill \\ \qquad + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - B)}} \cdot (t_{2} - B) - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\left( {\frac{{t_{2}^{2} }}{2} - t_{2} B - \frac{{B^{2} }}{2} + B^{2} } \right) \hfill \\ \end{aligned} \right] \hfill \\ & = pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(t_{2} - B)^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - B)}} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - B)}} \cdot (t_{2} - B) \hfill \\ \qquad - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\frac{{(t_{2} - B)^{2} }}{2} \hfill \\ \end{aligned} \right]. \hfill \\ \end{aligned}$$

Case 2.2.2: partial payment is not permitted at time $t = M$.

Here the details calculations are given below:

$$\begin{aligned} p\int\limits_{0}^{B} {D{\text{d}}t} & = p\left[ {\int\limits_{0}^{{t_{1} }} {D{\text{d}}t} + \int\limits_{{t_{1} }}^{B} {D{\text{d}}t} } \right] = p\left[ {\int\limits_{0}^{{t_{1} }} {A^{\gamma } (a - bp + cI_{r} (t)){\text{d}}t} + \int\limits_{{t_{1} }}^{B} {A^{\gamma } (a - bp + cI_{o} (t)){\text{d}}t} } \right] \hfill \\ & = p\left[ \begin{aligned} A^{\gamma } (a - bp)t_{1} - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\beta + A^{\gamma } c)t_{1} }} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + A^{\gamma } c}} \cdot t_{1} \hfill \\ \qquad + A^{\gamma } (a - bp)(B - t_{1} ) - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ {\text{e}}^{{(\alpha + A^{\gamma } c)(t_{2} - B)}} - {\text{e}}^{{(\alpha + A^{\gamma } c)(t_{2} - t_{1} )}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + A^{\gamma } c}}(B - t_{1} ) \hfill \\ \end{aligned} \right] \hfill \\ \end{aligned}$$

$$\begin{aligned} pI_{e} \int\limits_{0}^{B} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } & = pI_{e} \left[ {\int\limits_{0}^{{t_{1} }} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } + \int\limits_{{t_{1} }}^{B} {\int\limits_{{t_{1} }}^{t} {D{\text{d}}u{\text{d}}t} } } \right] \hfill \\ & = pI_{e} \left[ {\int\limits_{0}^{{t_{1} }} {\left\{ {\int\limits_{0}^{t} {A^{\gamma } (a - bp + cI_{r} (u)){\text{d}}u} } \right\}} {\text{d}}t + \int\limits_{{t_{1} }}^{B} {\left\{ {\int\limits_{{t_{1} }}^{t} {A^{\gamma } (a - bp + cI_{o} (u)){\text{d}}u} } \right\}{\text{d}}t} } \right] \hfill \\ & = pI_{e} \left[ {\Delta_{1} + \Delta_{2} } \right], \hfill \\ \end{aligned}$$

where

$$\begin{aligned} \Delta_{1} & = \int\limits_{0}^{{t_{1} }} {\left\{ {\int\limits_{0}^{t} {A^{\gamma } (a - bp + cI_{r} (u)){\text{d}}u} } \right\}} {\text{d}}t \hfill \\ & = \left[ {A^{\gamma } (a - bp)\frac{{t_{1}^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} .t_{1} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\frac{{t_{1}^{2} }}{2}} \right] \hfill \\ \end{aligned}$$

$$\begin{aligned} \Delta_{2} & = \int\limits_{{t_{1} }}^{B} {\left\{ {\int\limits_{{t_{1} }}^{t} {A^{\gamma } (a - bp + cI_{o} (u)){\text{d}}u} } \right\}{\text{d}}t} \hfill \\ & = \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(B - t_{1} )^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - B)}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} \hfill \\ \qquad + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot (B - t_{1} ) - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\frac{{(B - t_{1} )^{2} }}{2} \hfill \\ \end{aligned} \right]. \hfill \\ \end{aligned}$$

Therefore,

$$pI_{e} \int\limits_{0}^{B} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } = pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{t_{1}^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \cdot t_{1} \hfill \\ &\quad - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\frac{{t_{1}^{2} }}{2} + A^{\gamma } (a - bp)\frac{{(B - t_{1} )^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - B)}} - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} \hfill \\ & \quad+ \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot (B - t_{1} ) - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\frac{{(B - t_{1} )^{2} }}{2} \hfill \\ \end{aligned} \right],$$

where $X =$ <total selling price during the interval $[B,t_{2} ]$>, + <interest earned during the interval $[B,t_{2} ]$>, + <interest earned during the interval $[t_{2} ,T]$> $- {\text{TC}}$

$${\text{i}}.{\text{e}}.,\quad X = \left\{ {p\int\limits_{B}^{{t_{2} }} {D{\text{d}}t} + pI_{e} \int\limits_{B}^{{t_{2} }} {\int\limits_{B}^{t} D {\text{d}}u{\text{d}}t} } \right\}\{ 1 + I_{e} (T - t_{2} )\} - {\text{TC,}}$$

where

$$\begin{aligned} p\int\limits_{B}^{{t_{2} }} {D{\text{d}}t} & = p\left[ {\int\limits_{B}^{{t_{2} }} {\{ A^{\gamma } (a - bp + cI_{0} (t))\} {\text{d}}t} } \right] \hfill \\ & = p\left[ {A^{\gamma } (a - bp)(t_{2} - B)\, - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - B)}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)}}(t_{2} - B)} \right] \hfill \\ pI_{e} \int\limits_{B}^{{t_{2} }} {\int\limits_{B}^{t} D {\text{d}}u{\text{d}}t} & = pI_{e} \left[ {\int\limits_{B}^{{t_{2} }} {\left\{ {\int\limits_{B}^{t} {\{ A^{\gamma } (a - bp + cI_{0} (u))\} } {\text{d}}u} \right\}{\text{d}}t} } \right]. \hfill \\ \end{aligned}$$

Scenario 3: $t_{2} < M \le T$

In this case, the total revenue earned by the retailer up to $t = M$ is given by

$$U_{3} = \left\{ {p\int\limits_{0}^{{t_{2} }} {D{\text{d}}t} + pI_{e} \int\limits_{0}^{{t_{2} }} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } } \right\}\{ 1 + I_{e} (M - t_{2} )\} + pR(1 + I_{e} M),$$

where

$$\begin{aligned} p\int\limits_{0}^{{t_{2} }} {D{\text{d}}t} & = p\left[ {\int\limits_{0}^{{t_{1} }} {Ddt} + \int\limits_{{t_{1} }}^{{t_{2} }} {D{\text{d}}t} } \right] = p\left[ {\int\limits_{0}^{{t_{1} }} {A^{\gamma } (a - bp + cI_{r} (t)){\text{d}}t} + \int\limits_{{t_{1} }}^{{t_{2} }} {A^{\gamma } (a - bp + cI_{o} (t))dt} } \right] \hfill \\ & = p\left[ \begin{aligned} A^{\gamma } (a - bp)t_{2} - \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\beta + A^{\gamma } c)t_{1} }} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + A^{\gamma } c}} \cdot t_{1} \hfill \\ \qquad - \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + A^{\gamma } c)^{2} }}\{ 1 - {\text{e}}^{{(\alpha + A^{\gamma } c)(t_{2} - t_{1} )}} \} - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + A^{\gamma } c}}(t_{2} - t_{1} ) \hfill \\ \end{aligned} \right] \hfill \\ \end{aligned}$$

and

$$\begin{aligned} pI_{e} \int\limits_{0}^{{t_{2} }} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } & = pI_{e} \left[ {\int\limits_{0}^{{t_{1} }} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } + \int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{{t_{1} }}^{t} {D{\text{d}}u{\text{d}}t} } } \right] \hfill \\ & = pI_{e} \left[ {\int\limits_{0}^{{t_{1} }} {\left\{ {\int\limits_{0}^{t} {A^{\gamma } (a - bp + cI_{r} (u)){\text{d}}u} } \right\}} {\text{d}}t + \int\limits_{{t_{1} }}^{{t_{2} }} {\left\{ {\int\limits_{{t_{1} }}^{t} {A^{\gamma } (a - bp + cI_{o} (u)){\text{d}}u} } \right\}{\text{d}}t} } \right] \hfill \\ & = pI_{e} [\Delta_{1} + \Delta_{2} ], \hfill \\ \end{aligned}$$

where

$$\begin{aligned} \Delta_{1} & = \int\limits_{0}^{{t_{1} }} {\left\{ {\int\limits_{0}^{t} {A^{\gamma } (a - bp + cI_{r} (u)){\text{d}}u} } \right\}} {\text{d}}t \hfill \\ & = \left[ {A^{\gamma } (a - bp)\frac{{t_{1}^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \cdot t_{1} - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\frac{{t_{1}^{2} }}{2}} \right] \hfill \\ \end{aligned}$$

$$\begin{aligned} \Delta_{2} & = \int\limits_{{t_{1} }}^{{t_{2} }} {\left\{ {\int\limits_{{t_{1} }}^{t} {A^{\gamma } (a - bp + cI_{o} (u)){\text{d}}u} } \right\}{\text{d}}t} \hfill \\ & = \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{(t_{2} - t_{1} )^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} \hfill \\ \qquad + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot (t_{2} - t_{1} ) - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\frac{{(t_{2} - t_{1} )^{2} }}{2} \hfill \\ \end{aligned} \right]. \hfill \\ \end{aligned}$$

Therefore,

$$pI_{e} \int\limits_{0}^{{t_{2} }} {\int\limits_{0}^{t} {D{\text{d}}u{\text{d}}t} } = pI_{e} \left[ \begin{aligned} A^{\gamma } (a - bp)\frac{{t_{1}^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \} + \frac{{cA^{2\gamma } (a - bp)}}{{(\beta + cA^{\gamma } )^{2} }}{\text{e}}^{{(\beta + cA^{\gamma } )t_{1} }} \div t_{1} \hfill \\ \qquad - \frac{{cA^{2\gamma } (a - bp)}}{{\beta + cA^{\gamma } }}\frac{{t_{1}^{2} }}{2} + A^{\gamma } (a - bp)\frac{{(t_{2} - t_{1} )^{2} }}{2} + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{3} }}\{ 1 - {\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \} \hfill \\ \qquad + \frac{{cA^{2\gamma } (a - bp)}}{{(\alpha + cA^{\gamma } )^{2} }}{\text{e}}^{{(\alpha + cA^{\gamma } )(t_{2} - t_{1} )}} \cdot (t_{2} - t_{1} ) - \frac{{cA^{2\gamma } (a - bp)}}{{\alpha + cA^{\gamma } }}\frac{{(t_{2} - t_{1} )^{2} }}{2} \hfill \\ \end{aligned} \right].$$