Energy harvesting in a delay-induced parametric van der Pol–Duffing oscillator

Abstract

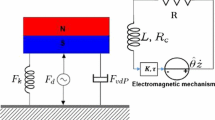
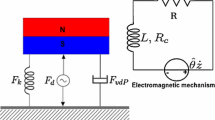
Quasi-periodic vibration-based energy harvesting is investigated in a delayed van der Pol–Duffing oscillator coupled to a delayed piezoelectric mechanism. It is assumed that the time delay in the mechanical subsystem is modulated around a mean value with a certain amplitude and frequency. The case of a delay-induced parametric resonance for which the frequency of the modulation is near twice the natural frequency of the oscillator is considered. The first- and second-step multiple scale methods are applied to obtain approximations of periodic and quasi-periodic solutions as well as the corresponding output powers. Bifurcation analysis is carried out to locate regions of existence of these solutions. The effect of different system parameters on the performance of quasi-periodic vibration-based energy harvesting is examined. The advantage of using quasi-periodic vibrations to extract energy over a broadband of system parameters away from the resonance is illustrated. Numerical simulations are conducted to validate the analytical predictions.

Appendix

$$\begin{aligned}&S_{1}=\frac{\delta }{2}-\frac{\chi \kappa (2\beta -2\alpha _{3}\cos (\frac{\omega \tau _{2}}{2}))}{(2\beta -2\alpha _{3}\cos (\frac{\omega \tau _{2}}{2}))^{2}+(\omega +2\alpha _{3}\sin (\frac{\omega \tau _{2}}{2}))^{2}}\\&\qquad -\frac{\alpha _{1}}{\omega }\sin \frac{\omega \tau _{1}}{2},\nonumber \\&\quad S_{2}=\frac{-\lambda }{8}, ~~~~S_{3}=\frac{\alpha _{2}}{2\omega }\sin \frac{\omega \tau _{1}}{2}\\&\quad S_{4}=-\frac{\alpha _{2}}{2\omega }\cos \frac{\omega \tau _{1}}{2},\nonumber \\&\quad S_{5}=\frac{\sigma }{\omega }+\frac{\chi \kappa (\omega +2\alpha _{3}\sin (\frac{\omega \tau _{2}}{2}))}{(2\beta -2\alpha _{3}\cos (\frac{\omega \tau _{2}}{2}))^{2}+(\omega +2\alpha _{3}\sin (\frac{\omega \tau _{2}}{2}))^{2}}\\&\qquad -\frac{\alpha _{1}}{\omega }\cos \frac{\omega \tau _{1}}{2},\nonumber \\&\quad S_{6}=\frac{3\gamma }{4\omega }.\ \end{aligned}$$