Positively defined color-singlet fragmentation function $g \rightarrow {\chi _{cJ}}$

Abstract

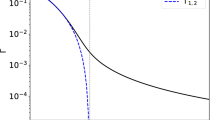
We revisit the fragmentation process $g \rightarrow {\chi _{cJ}}+g$. Contrary to what was presented previously in the literature, our fragmentation functions are strictly positive, smooth, and vanish at $z \rightarrow 1$.

Appendix: Off-shell production amplitudes for \(^3P_J^{[1]}\) states

Here we consider the gluon splitting subprocess

$$\begin{aligned} g^*(k_1,\epsilon _1,a)\rightarrow g(k_2,\epsilon _2,b) + c(p_c) + {\bar{c}}(p_{{\bar{c}}}), \end{aligned}$$

(14)

where the symbols in the parentheses indicate the momentum, the polarization, and the color of the interacting quanta. The produced quarks form a bound state $p_{\chi }=p_c+p_{{\bar{c}}}$ with spin momentum $S=1$ and angular orbital momentum $L=1$.

The calculation of this subprocess at ${{\mathcal {O}}}(\alpha _s^2)$ refers to two Feynman diagrams:

(15)

with the property ${\mathcal{M}}_1={\mathcal{M}}_2$. The color factor is universal and is equal to $\delta ^{ab}/2\sqrt{3}$. The amplitudes ${\mathcal{M}}_i$ contain spin projection operator which selects the spin-triplet $c{\bar{c}}$ state:

(16)

where $m_c$ is the c-quark mass and $\epsilon _{S}$ is the $c{\bar{c}}$ spin polarization vector.

The orbital angular momentum L is associated with the relative momentum q of the quarks in a bound state. The relative momentum q is defined as

$$\begin{aligned} p_c=\frac{1}{2}p_\chi +q,\quad p_{{\bar{c}}}=\frac{1}{2}p_\chi -q. \end{aligned}$$

(17)

According to a general formalism developed in [11, 12], the terms showing no dependence on q are identified with the contributions to the $L=0$ state; the terms linear in $q^\alpha$ are related to the $L=1$ state with the proper polarization vector $\epsilon ^\alpha$ (see below); the quadratic terms $q^\alpha q^\beta$ refer to the $L=2$ state with the polarization tensor $\epsilon ^{\alpha \beta }$; and so on. The decomposition of ${\mathcal{M}}$ in powers of q is carried out by expanding the subprocess amplitude as

$$\begin{aligned} {\mathcal{M}}(q)={\mathcal{M}}|_{q{=}0} + q^\alpha (\partial {\mathcal{M}}/\partial q^\alpha )|_{q{=}0} + ..., \end{aligned}$$

(18)

where q is assumed to be a small quantity.

The amplitude ${\mathcal{M}}(q)$ has to be multiplied by the bound state wave function $\Psi (q)$ and integrated over q. A term-by-term integration of Eq. (18) is performed using the relations

$$\begin{aligned} \int \frac{\mathrm{{d}}^3q}{(2\pi )^3}\Psi (q)= & {} \frac{1}{\sqrt{4\pi }}{\mathcal{R}}(x{=}0), \end{aligned}$$

(19)

$$\begin{aligned} \int \frac{\mathrm{{d}}^3q}{(2\pi )^3}q^\alpha \Psi (q)= & {} -i\epsilon _L^\alpha \frac{\sqrt{3}}{\sqrt{4\pi }}{\mathcal{R}}'(x{=}0), \end{aligned}$$

(20)

etc., where ${\mathcal{R}}(x)$ is the radial wave function in the coordinate representation (the Fourier transform of $\Psi (q)$). Taking the trace in (15) and selecting the terms linear in q, with further replacing q with $\epsilon _L$, yield:

$$\begin{aligned} {\mathcal{M}}_1= & {} {\mathcal{M}}_2 = 16\pi \alpha _s \sqrt{3/4\pi }\,{\mathcal{R}}'(0)/(2m_c)^{3/2} \nonumber \\&\quad \,\times \,\Bigl \{\Bigr . \,\bigl [\, (k_1 e_2)\,(\epsilon _1\epsilon _S) + (k_2\epsilon _1)\,(\epsilon _2\epsilon _S) - (k_3\epsilon _S)\,(\epsilon _1\epsilon _2) \bigr ]\nonumber \\&\quad \times \, 4m_c^2\,(k_3\epsilon _L)/(k_1 k_2)^2\nonumber \\&\quad - \bigl [ (k_1k_2)\,(\epsilon _1\epsilon _S)\,(\epsilon _2\epsilon _L) - (k_1 k_1)\,(\epsilon _1\epsilon _S)\,(\epsilon _2\epsilon _L) \bigr . \nonumber \\&\quad + (k_1 k_2)\,(\epsilon _1\epsilon _L)\,(\epsilon _2\epsilon _S) - (k_2k_2)\,(\epsilon _1\epsilon _L)\,(\epsilon _2\epsilon _S)\nonumber \\&\quad + (k_3\epsilon _S)\,(p_\chi \epsilon _1)\,(\epsilon _2\epsilon _L) - (k_3\epsilon _S)\,(p_\chi \epsilon _2)\,(\epsilon _1\epsilon _L)\nonumber \\&\quad - \bigl . (k_3\epsilon _L)\,(p_\chi \epsilon _1)\,(\epsilon _2\epsilon _S) + (k_3\epsilon _L)\,(p_\chi \epsilon _2)\,(\epsilon _1\epsilon _S) \,\bigr ] \nonumber \\&\quad /(k_1 k_2) \Bigl .\Bigr \} \end{aligned}$$

(21)

The polarization vectors $\epsilon _S$ and $\epsilon _L$ are defined as explicit four vectors. In the frame where the z axis is oriented along the quarkonium momentum vector, $p_{\chi }=(0,\,0,\,|p_{\chi }|,\,E_{\chi })$, these polarization vectors read

$$\begin{aligned} \epsilon (\pm 1) = (\pm 1,\,i,\,0,\,0)/\sqrt{2},\quad \epsilon (0) = (0,\,0,\,E_{\chi },\,|p_{\chi }|)/m_{\chi }. \end{aligned}$$

States with definite $S_z$ and $L_z$ can be translated into physical states $\chi _J$ with definite total angular momentum J and its projection $J_z$ using Clebsch–Gordan coefficients:

$$\begin{aligned} |\chi (J,J_z)\rangle =\sum _{L_z,S_z} \langle 1,L_z;1,S_z|J,J_z \rangle \;|\epsilon _L,\epsilon _S\rangle \end{aligned}$$

(22)

This completes our derivation of the production matrix element. The resulting expression has been explicitly tested for gauge invariance by substituting the gluon momenta $k_i$ for their polarization vectors $\epsilon _i$.